| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A48 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015825 | |
| Published online | 24 January 2011 | |
The structure of the magnetic field in the massive star-forming region W75N
1
Argelander-Institut für Astronomie der Universität Bonn,
Auf dem Hügel 71,
53121
Bonn,
Germany
e-mail: gsurcis@astro.uni-bonn.de
2
Instituto de Astronomía (UNA), Apdo Postal 70-264, Cd.
Universitaria, 04510- Mexico DF,
Mexico
3
Max-Planck Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
4
National Astronomical Research Institute of Thailand,
Ministry of Science and Technology,
Rama VI Rd., Bangkok
10400,
Thailand
5
Instituto de Ciencias del Espacio (CSIC)-UB/IEEC, Universitat de
Barcelona, Martí i Franquès
1, 08028
Barcelona,
Spain
6
Physics Department, DePaul University,
2219 N. Kenmore Ave., Byrne Hall
211, Chicago,
IL
60614,
USA
Received:
27
September
2010
Accepted:
16
November
2010
Context. A debated topic in star formation theory is the role of magnetic fields during the protostellar phase of high-mass stars. It is still unclear how magnetic fields influence the formation and dynamics of massive disks and outflows. Most current information on magnetic fields close to high-mass protostars comes from polarized maser emissions, which allows us to investigate the magnetic field on small scales by using very long-baseline interferometry.
Aims. The massive star-forming region W75N contains three radio continuum sources (VLA 1, VLA 2, and VLA 3), at three different evolutionary stages, and associated masers, while a large-scale molecular bipolar outflow is also present. Very recently, polarization observations of the 6.7 GHz methanol masers at milliarsecond resolution have been able to probe the strength and structure of the magnetic field over more than 2000 AU around VLA 1. The magnetic field is parallel to the outflow, suggesting that VLA 1 is its powering source. The observations of H2O masers at 22 GHz can give more information about the gas dynamics and the magnetic fields around VLA 1 and VLA 2.
Methods. The NRAO Very Long Baseline Array was used to measure the linear polarization and the Zeeman-splitting of the 22 GHz water masers in the star-forming region W75N.
Results. We detected 124 water masers, 36 around VLA 1 and 88 around VLA 2 of W75N, which indicate two different physical environments around the two sources, where VLA 1 is in a more evolved state. The linear polarization of the masers confirms the tightly ordered magnetic field around VLA 1, which is aligned with the large-scale molecular outflow, and also reveals an ordered magnetic field around VLA 2, which is not parallel to the outflow. The Zeeman-splitting measured on 20 of the masers indicates strong magnetic fields around both sources (the averaged values are |BVLA1| ~ 700 mG and |BVLA2| ~ 1700 mG). The high values of the magnetic field strengths, which come from the shock compression of the gas, are consistent with the methanol and OH magnetic field strengths. Moreover, by studying the maser properties we were also able to determine that the water masers are pumped in C-shocks in both sources.
Key words: stars: formation / masers / polarization / magnetic fields / ISM: individual objects: W75N
© ESO, 2011
1. Introduction
During the formation of low-mass stars, the magnetic field is thought to slow the collapse, to transfer the angular momentum, and to power the outflow, but its role during the formation of high-mass stars is still under debate (e.g., McKee & Ostriker 2007; Girart et al. 2009). Several questions remain unanswered because massive star-forming regions are rare and distant and often consist of a large number of protostars, consequently it is difficult to observe magnetic fields during their protostellar phase. Recently some progress has been made. Vlemmings et al. (2010) and Surcis et al. (2009, hereafter S09) have shown that the magnetic field is orthogonal to large rotating disks and parallel to molecular bipolar outflows even during the high-mass protostellar phase and not only during the formation of low-mass stars (e.g., Matsumoto & Tomisaka 2004; McKee & Ostriker 2007). They obtained their results by using methanol masers as probes of magnetic fields. In fact, the bright and narrow spectral line emission of masers is ideal for detecting, with polarimetric interferometry, both Zeeman-splitting and the orientation of the magnetic field on scales from arcsec to milliarcsec (mas). So far, the main maser species used for this purpose are H2O, OH, and CH3OH masers. Since their masing conditions are different they are located in distinct zones of massive star-forming regions. The H2O masers are detected in the denser zones with hydrogen number densities nH2 between approximately 108 and 1010 cm-3 (Elitzur et al. 1989), showing a velocity width of about 1 km s-1 and a high brightness temperature Tb > 109 K (e.g., Reid & Moran 1981). The first very long baseline interferometry (VLBI) observations of the linear and circular polarization of water maser emissions were made by Leppänen et al. (1998) and Sarma et al. (2001), respectively. Afterwards more H2O maser polarization observations were carried out by various authors, which confirmed the importance of this kind of observation in studying the role of the magnetic field in massive star formation (e.g., Imai et al. 2003; Vlemmings et al. 2006). Here we present Very Long Baseline Array (VLBA) linear and circular polarization observations of water masers in the high-mass star-forming region W75N.
All 22 GHz water maser features in W75N for which linear and/or circular polarization was detected.
W75N is an active high-mass star-forming region in the molecular complex DR21–W75 (Dickel
et al. 1978; Persi et al. 2006) at a distance of 2 kpc. At the resolution of
~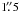 three H ii regions were identified (Haschick et al. 1981): W75N (A), W75N (B), and W75N (C). At
three H ii regions were identified (Haschick et al. 1981): W75N (A), W75N (B), and W75N (C). At
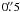 resolution, Hunter et al. (1994) detected three
subregions in W75N (B): Ba, Bb and Bc. At higher angular resolution
(~
resolution, Hunter et al. (1994) detected three
subregions in W75N (B): Ba, Bb and Bc. At higher angular resolution
(~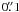 ),
Torrelles et al. (1997) resolved the subregions Ba
and Bb further (renaming them VLA 1 and VLA 3), and imaged a third weaker and more compact
H ii region between them, which they named VLA 2. A large-scale high-velocity
outflow, with an extension greater than 3 pc and a total molecular mass greater than
255 M⊙, was also detected from W75N (B) (e.g., Shepherd et al.
2003). Shepherd et al. (2003) proposed a multi-outflow scenario where VLA 2 may drive the
large-scale outflow, and VLA 1 and VLA 3 are the centers of two other small flows. So far,
it has been impossible to determine the main powering source of the 3 pc outflow. Several
authors have suggested VLA 1 as the powering source (e.g., Torrelles et al. 1997, S09 and references therein).
),
Torrelles et al. (1997) resolved the subregions Ba
and Bb further (renaming them VLA 1 and VLA 3), and imaged a third weaker and more compact
H ii region between them, which they named VLA 2. A large-scale high-velocity
outflow, with an extension greater than 3 pc and a total molecular mass greater than
255 M⊙, was also detected from W75N (B) (e.g., Shepherd et al.
2003). Shepherd et al. (2003) proposed a multi-outflow scenario where VLA 2 may drive the
large-scale outflow, and VLA 1 and VLA 3 are the centers of two other small flows. So far,
it has been impossible to determine the main powering source of the 3 pc outflow. Several
authors have suggested VLA 1 as the powering source (e.g., Torrelles et al. 1997, S09 and references therein).
Several maser species (H2O, OH, and CH3OH) have been detected in W75N (e.g., Torrelles et al. 1997; Baart et al 1986, S09), in particular around the two H II regions VLA 1 and VLA 2. The H2O maser emissions associated with VLA 1 are located along a linear structure parallel to its radio jet with a proper motion of about 2 mas/yr, while those associated with VLA 2 show a circular distribution, which is expanding with a velocity of about 5 mas/yr (Torrelles et al. 2003, hereafter T03). Only one H2O maser is associated with VLA 3 (T03). Methanol masers were detected in two groups (A and B/C) located northwest and southeast of VLA 1, respectively. Group A is along a linear structure and group B/C show an arc-like structure (S09). No CH3OH masers are associated with VLA 2 (e.g., Minier et al. 2000, S09). However, VLA 2 is the place where the most intensive OH flare took place (Alakov et al. 2005; Slysh et al. 2010). Other OH maser emission sites are situated on a ring structure around all three radio sources (Hutawarakorn et al. 2002). Based on the different activity in H2O and OH masers, Torrelles et al. (1997) suggest that these three sources are at different evolutionary stages, in particular VLA 1 is the “oldest” source of this region and VLA 3 the “youngest” one (driving a radio Herbig-Haro object, Carrasco-González et al. 2010). In this evolutionary scenario, VLA 2 is at an intermediate stage.
In order to determine and investigate the magnetic field of W75N(B), polarization observations of OH and CH3OH maser emissions have been made (e.g., Hutawarakorn et al. 2002; Fish & Reid 2007; S09). The magnetic field strength obtained from the OH maser polarization observations was ~7 mG (e.g., Hutawarakorn et al. 2002; Slysh et al. 2002). During the OH maser flare near VLA 2, Slysh & Migenes (2006) detected a strong magnetic field of more than 40 mG in several maser spots, which increased in the next observations up to 70 mG (Slysh et al. 2010). S09 measured a magnetic field strength of 50 mG around VLA 1 by studying the circular polarized emissions of methanol masers. Hutawarakorn & Cohen (1996) and S09 investigated the linear polarization of OH and CH3OH masers, respectively, and both suggested that the magnetic field is oriented along the outflow. Although the OH masers at 1.6 and 1.7 GHz are very susceptible to both internal and external Faraday rotation, at 6.7 GHz the Faraday rotation is only about 5° indicating that the finding of the large-scale magnetic field aligned with the outflow is robust.
Since the water masers, unlike the CH3OH and OH masers, are found in denser zones of the star-forming regions, it is crucial to study their polarization emission on a small scale. In fact, because they arise close to both radio sources they can give us new information on the role of the magnetic field during the massive star formation, in particular at two different evolutionary stages.
2. Observations and data reduction
We observed the massive star-forming region W75N(B) in the 616–523 transition of H2O (rest frequency: 22.23508 GHz) with the NRAO1 VLBA on November 21st 2005. The observations were made in full polarization spectral mode using 4 overlapped baseband filters of 1 MHz in order to cover a total velocity range of ≈ 50 km s-1. Two correlations were performed. One with 128 channels in order to generate all 4 polarization combinations (RR, LL, RL, LR) with a spectral resolution of 7.8 kHz (0.1 km s-1). The other one with high spectral resolution (512 channels; 1.96 kHz = 0.027 km s-1), which only contains the circular polarization combinations (LL, RR), to be able to detect Zeeman splitting of the H2O maser across the entire velocity range. Including the overheads, the total observation time was 8 h.
 |
Fig. 1 Results of the full radiative transfer χ2-model fits, for the maser that shows the highest linear polarization fraction (VLA1.19) and for the maser that shows the highest PV around VLA2 (VLA2.22). The fits yield the emerging maser brightness temperature TbΔΩ and the intrinsic maser linewidth ΔVi. Contours indicate the significance intervals Δχ2 = 0.25, 0.5, 1, 2, 3, 7, with the thick solid contours indicating 1σ and 3σ areas. |
The data were reduced using the Astronomical Image Processing Software package (AIPS) following the method of Kemball et al. (1995). The bandpass, the delay, the phase and the polarization calibration were performed on the calibrator J2202+4216, which has been used successfully by Vlemmings et al. (2006) for H2O maser polarization observations of Cepheus A. The fringe-fitting and the self-calibration were performed on one of the brightest maser features VLA 1.14 (Table 1). All calibration steps were initially performed on the dataset with modest spectral resolution after which the solutions, with the exception of the bandpass solutions that were obtained separately, were copied and applied to the high spectral resolution dataset. Stokes I (rms = 7.3 mJy beam-1), Q (rms = 6.5 mJy beam-1) and U (rms = 6.5 mJy beam-1) data cubes were created using the AIPS task IMAGR (beam-size 2.0 mas × 0.7 mas) from the modest spectral resolution dataset, while the I and V (rms = 10 mJy beam-1) cubes were imaged from the high spectral resolution dataset and for the same fields. The Q and U cubes were combined to produce cubes of polarized intensity and polarization angle. Since these observations were obtained between two VLA polarization calibration observations2, during which the linear polarization angle of J2202+4216 was constant at 13°̣5, we were able to estimate the polarization angles with a systemic error of no more than ~2°. The I and V cubes at high spectral resolution were used to determine the Zeeman splitting.
3. Analysis
3.1. Maser identification
To identify the water maser features in W75N(B) region, we used an identification process divided into three steps: 1) we used a program called “maser finder” (Curiel, pers. comm.), which is able to search for maser spots, velocity channel by velocity channel, with a signal-to-noise ratio greater than a given value (in our case, an 8-sigma limit was used); 2) we fitted the identified maser spots using the AIPS task IMFIT; and 3) we identified a maser feature, when three or more maser spots coincided spatially (within a box of 2 by 2 pixels) and each of them appeared in consecutive velocity channels. Table 1 contains the positions, velocities and peak flux densities of all the maser features found in the region.
In the first part of the process and after evaluating the global noise level of the channel map, the code searches for maser spots in the velocity map, excluding the edges of the channel map. When strong maser spots are found (for instance, with a peak flux density higher than 2 Jy beam-1), the local rms around these strong maser spots (within a predefined box, for instance, 400 by 400 pixels) is estimated, as well as the rms outside the boxes. The code identifies a maser spot when the SNR of the candidate (using the local rms) is greater than a predefined value. In the case of W75N, we have adopted a lower limit of 8-sigma. The code produces a table with the spatial location and intensity of all the identified maser spots. This procedure is repeated for each velocity channel included in the input file that is used by the code. The code also produces a script for each velocity channel that can be run inside AIPS in order to produce Gaussian fits of all the identified maser spots. After running all the AIPS scripts, a table with all the important parameters (e.g., spatial resolution, velocity, intensity) of each maser spot is produced. We then use the output table to search for maser features that fulfill the criteria described above.
 |
Fig. 2 Total intensity and circular polarization spectrum for the three maser features VLA1.07, VLA1.16, and VLA2.16. The thick red lines are the best-fit models of I and V emission obtained using the radiative transfer method (see Sect. 3.2). All maser features were centered to zero velocity. |
3.2. Polarization fitting
From the maser theory we know that the fractional linear polarization
Pl of the H2O maser emission depends on the
degree of its saturation and the angle (θ) between the maser propagation
direction and the magnetic field (e.g., Goldreich et al. 1973; Nedoluha & Watson 1992).
Even the relation between the measured polarization angle χ and the
magnetic field angle on the sky (φB) depends
on θ, with the linear polarization vector perpendicular to the field for
θ > θcrit ~ 55° (Goldreich
et al. 1973), where
θcrit is the so-called Van Vleck angle. It is therefore
important to evaluate θ for every H2O maser that shows linear
polarization emission. In order to obtain the best values for θ, we
needed to determine the emerging brightness temperature (TbΔΩ)
and the intrinsic thermal linewidth (ΔVi), which is the full
width half-maximum (FWHM) of the Maxwellian distribution of particle velocities, of the
masers with high precision. This could be done by fitting the water maser emissions with
the full radiative transfer method described by Vlemmings et al. (2006, 2010), who successfully
used it for water and methanol masers in Cepheus A. These radiative transfer methods are
based on the models for water masers of Nedoluha & Watson (1992), for which the shapes of the total intensity, linear
polarization, and circular polarization spectra depend on TbΔΩ
and ΔVi. They also found that the emerging brightness
temperature scaled linearly with (Γ + Γν), which are the maser
decay rate Γ and cross-relaxation rate Γν. Since for the
22 GHz H2O masers Γ ≲ 1 s-1 and Γν
depends on the gas temperature, we include in our fit a value
(Γ + Γν) = 1s-1, so that we could adjust the
fitted TbΔΩ values by simply scaling according to
(Γ + Γν). Note that ΔVi and
θ do not need to be adjusted. We model the observed linear polarized
and total intensity maser spectra by gridding the intrinsic thermal linewidth
ΔVi between 0.4 and 3.5 km s-1,
in steps of 0.025 km s-1, using a least square fitting routine
(χ2-model) with an upper limit of the brightness temperature
TbΔΩ = 1011 K sr. In Fig. 1 two examples are shown of the results obtained by fitting the water
maser emissions with the full radiative transfer method code. From these first fits, we
can then obtain the angles θ by considering the relation between
Pl and θ (see Vlemmings et al. 2010, for more details). The best values for
TbΔΩ and ΔVi are then included
in the full radiative transfer code to produce the I and V
models that were used for fitting the total intensity and circular polarized
spectra of the H2O masers extracted from the high-resolution I
and V cubes. The magnetic field strength along the line of sight
is evaluated by using the equation 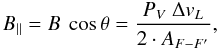 (1)where
ΔvL is the FWHM of the total intensity
spectrum, the AF − F′ coefficient, which depends on
TbΔΩ. The circular polarization fraction
(PV) are obtained from the
I and V models.
(1)where
ΔvL is the FWHM of the total intensity
spectrum, the AF − F′ coefficient, which depends on
TbΔΩ. The circular polarization fraction
(PV) are obtained from the
I and V models.
Another important aspect that must be considered in the analysis of the water masers is the degree of their saturation, which influences Pl. We are able to estimate it by considering the ratio between maser rate of stimulated emission (R) and the sum of maser decay rate and the cross-relaxation rate (Γ + Γν).
The stimulated emission rate is given by 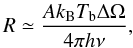 (2)where
A = 2 × 10-9 s-1 is the 22-GHz H2O
maser spontaneous rate (Goldreich & Keeley 1972), kB and h are the Boltzmann
and Planck constants, respectively, ν the maser frequency and
TbΔΩ the emerging brightness temperature adjusted at the
right Γ + Γν value. The masers are unsaturated when
R/(Γ + Γν) < 1, in the onset of
saturation when R/(Γ + Γν) ≥ 1, and fully
saturated when R/(Γ + Γν) ≈ 100 (Vlemmings
et al. 2006). Moreover, when the saturation sets
in, the maser lines start to broaden again, and this means that the observed linewidth
(ΔvL) becomes as large as ΔVi or
larger depending on the degree of the saturation.
(2)where
A = 2 × 10-9 s-1 is the 22-GHz H2O
maser spontaneous rate (Goldreich & Keeley 1972), kB and h are the Boltzmann
and Planck constants, respectively, ν the maser frequency and
TbΔΩ the emerging brightness temperature adjusted at the
right Γ + Γν value. The masers are unsaturated when
R/(Γ + Γν) < 1, in the onset of
saturation when R/(Γ + Γν) ≥ 1, and fully
saturated when R/(Γ + Γν) ≈ 100 (Vlemmings
et al. 2006). Moreover, when the saturation sets
in, the maser lines start to broaden again, and this means that the observed linewidth
(ΔvL) becomes as large as ΔVi or
larger depending on the degree of the saturation.
Although the full radiative transfer method is based on a model for general water masers, it should be noted that, when this model is applied to saturated masers, it is impossible to properly disentangle the values of TbΔΩ and ΔVi. In this case the method only provides a lower limit for TbΔΩ and an upper limit for ΔVi. For high maser brightness temperatures, i.e. greater than 109 cm-3 K sr (Nedoluha & Watson 1992), the cosθ dependence of Eq. (1) breaks down thereby introducing a more complex dependence on θ. As a result, the angle θ obtained from the fit is overestimated and, in particular, it could also reach values of 90° or greater. Consequently, the values of TbΔΩ, ΔVi and θ obtained for saturated masers could not be taken into account in the analysis of the region.
4. Results
4.1. Maser distribution
In Fig. 3 we show the distribution of the 124 22-GHz water maser features detected with the VLBA. No water maser emission with a peak flux density less than 80 mJy beam-1 is detected. All H2O masers are detected around the radio sources VLA 1 (29%, 36/124) and VLA 2 (71%, 88/124).
The water masers associated with VLA 2, which have local standard of rest velocities (VLSR) between –7.7 and 13.7 km s-1, are distributed elliptically around its 1.3 cm continuum peak. In Fig. 4 we report two ellipses obtained by fitting the positions of the water masers detected by T03 (called here ellipse 1) and in the present paper (ellipse 2), their parameters are reported in Table 2. The major axis of ellipse 2 is 64 mas larger than that of ellipse 1, the minor axes are also in the same ratio. This indicates an expansion velocity of ~4.8 mas/yr in all directions, corresponding to ~46 km s-1 (at 2 kpc). This value is consistent with the proper motion of the water masers as reported by T03. Since the expansion velocity is symmetric in all directions, we aligned the centers of the two ellipses with the position of the 1.3 cm continuum peak obtained from a Gaussian fit. Consequently we were able to overlay all water masers of the region on the continuum VLA map with an accuracy of approximately 10 mas. In this way we could also compare the positions of the masers around VLA 1 at the two different epochs. If we look at the northern masers around VLA 2, we see that the masers detected by T03 are better aligned with the ellipse 1 than the masers detected by us with ellipse 2 (Fig. 4, right panel), indicating that those masers are also moving northeastward. This movement might be due to the formation of a jet (see Fig. 3).
 |
Fig. 3 Positions of water and methanol masers superimposed on the 1.3 cm continuum contour map of the VLA1 thermal jet and VLA 2 (Torrelles et al. 1997). Contours are −3, −2, 2, 3, 4, 5, 6, 7, 8 × 0.16 mJy beam-1. Blue triangles indicate the positions of the water maser features detected with the VLBA (this paper). Red circles indicate the position of the methanol masers features detected by S09. The two arrows indicate the direction of the large-scale molecular bipolar outflow (PA = 66°). |
The water masers associated with VLA 1 can be divided into three groups, one composed of the northern masers (VLA 1A), one of the masers closest to the central protostar (VLA 1B, see
 |
Fig. 4 Left panel: a close-up view of the H2O maser features around the radio source VLA 2. Right panel: a zoom-in view of the boxed region of the left panel. The octagonal symbols are the identified maser features in present work scaled logarithmically according to their peak flux density. The maser LSR radial velocity is indicated by color. A 5 Jy beam-1 symbol is plotted for illustration in both panel. The linear polarization vectors, scaled logarithmically according to polarization fraction P1 (in Table 1), are overplotted. Two ellipses are also drawn in both panels. They are the results of the best fit of the water masers (crosses) detected by T03 (dotted ellipse, ellipse 1; epoch 1999) and of those detected in present work (solid ellipse, ellipse 2; epoch 2005). Their parameters are listed in Table 4. The synthesized beam is 2.0 mas × 0.7 mas. |
4.2. Linear and circular polarization
Linear polarization was detected in 50 masers (Table 1). In particular, about 70% of the H2O masers associated with VLA 1 show linear polarization emission. The corresponding linear polarization vectors are shown in Figs. 4 and 5 (left panel). The highest fractional linear polarization was detected in water masers related to VLA 1 (Pl ~ 26%). Eight masers associated with VLA 1 have high linear polarizations, Pl between 10% and 26%, so that the median value of linear polarizations for the masers in VLA 1 is ~ 7%. In contrast, the maximum Pl for the masers associated with VLA 2 is 6%, and the median value is much lower at 1.5%. Circular polarization was detected in 20 masers, equally distributed between VLA 1 and VLA 2.
Number, epoch, semi-major axis, semi-minor axis, and inclination from the elliptical fit of the water maser associated with VLA 2 in the two different epochs.
 |
Fig. 5 Left panel: a close-up view of the H2O maser features (octagon) around the radio source VLA 1. Right panel: a zoom-in view of the water masers group VLA 1B, here are also reported the water masers (square) detected by T03. The octagonal and the square symbols are scaled logarithmically according to their peak flux density. The maser LSR radial velocity is indicated by color. The systemic LSR radial velocity of W75N massive star-forming region is 10 km s-1 (Shepherd et al. 2003). Symbols for 3 Jy beam-1 and for 1 Jy beam-1 are shown in the lower left corner of the panels. The linear polarization vectors, scaled logarithmically according to polarization fraction P1 (in Table 1), are overplotted on the left panel. The synthesized beam is 2.0 mas × 0.7 mas. |
The rms weighted linear polarization angles of the water masers around VLA 1 and VLA 2 are ⟨ χ1 ⟩ ≈ −67° ± 40° and ⟨ χ2 ⟩ ≈ −72° ± 32°, respectively. Since the water masers of group VLA 1A show ordered linear polarization vectors, it is worthwhile evaluating its weighted polarization angles, which is ⟨ χ1A ⟩ = −20° ± 9°.
We were able to fit 42 masers with the method described in Sect. 3.2, and the results are given in columns 10 and 11 of Table 1, and two examples (i.e., VLA1.19, VLA2.22) are
reported in Fig. 1. Although the emerging brightness
temperatures for VLA 1 and VLA 2 are both in the range
108 K sr < TbΔΩ < 1010 K sr,
their weighted intrinsic maser linewidths are very different. They are
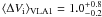 km s-1
and
km s-1
and 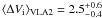 km s-1,
respectively.
km s-1,
respectively.
Finally, considering the emerging brightness temperature and the observed Pl we determined θ for those masers which we were able to fit for ΔVi and TbΔΩ. The results are given in Col. 14 of Table 1 with the errors determined by analyzing the full probability distribution functions. Eight of the H2O masers around the radio source VLA 1 (from VLA1.12 to VLA1.19, which are the closest features to the protostar) show values for θ equal to 90°. This suggests that, from the theory of the Zeeman effect, we are observing perpendicular to the magnetic field. Consequently, we should not be able to detect circular polarization from these masers. However, since we detected circular polarization in three of them (VLA1.16, VLA1.17, and VLA1.19) the measurements of θ must be affected by the degree of their saturation, as discussed in Sect. 3.2. By excluding these 8 masers, we evaluated ⟨ θ ⟩ VLA1 = 83° ± 7° and ⟨ θ ⟩ VLA2 = 85° ± 6°, which imply that the magnetic fields are close to the plane of the sky.
In Col. 13 of Table 1 we report the magnetic field strength along the line of sight obtained by fitting the high-resolution spectra of I and V (see Sect. 3.2). The masers VLA1.21, VLA2.01, and VLA2.02 do not show any linear polarization emission, but they do show circular polarization emission. Consequently we could not get TbΔΩ and ΔVi as done for the other masers that showed linear polarization emission, and to measure the magnetic field strength, we used the TbΔΩ and ΔVi values of the closest masers. In Table 1 the circular polarization fraction is also reported (Col. 12).
5. Discussion
The water masers detected using the VLBA are related to two different radio continuum sources of W75N(B), VLA 1 and VLA 2, which are thought to be in two different evolutionary stages. In the next sections, we discuss their nature as two independent groups, their polarization and finally the type of shocks that give rise to them.
5.1. H2O maser properties
As suggested by the difference between their intrinsic thermal linewidths, which is
1.5 km s-1, the masers around VLA 1 and VLA 2 appear to arise under two
different physical conditions. Using 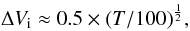 (3)we estimate the
gas temperatures in the H2O masing regions around VLA 1 and VLA 2, and find
them to be TVLA 1 ~ 400 K and
TVLA 2 ~ 2500 K, respectively. The intrinsic
thermal linewidths of the VLA 2 masers are quite similar to each other, while the three
groups of masers around VLA 1 show a difference in their ΔVi.
In particular, we find that the maser groups VLA 1A and C have similar intrinsic thermal
linewidths ( ⟨ ΔVi ⟩ = 1.0 km s-1) while the group
VLA 1B has lower values ( ⟨ ΔVi ⟩ = 0.7 km s-1).
This can come from the degree of their saturation that we can evaluate by considering
Eq. (2).
(3)we estimate the
gas temperatures in the H2O masing regions around VLA 1 and VLA 2, and find
them to be TVLA 1 ~ 400 K and
TVLA 2 ~ 2500 K, respectively. The intrinsic
thermal linewidths of the VLA 2 masers are quite similar to each other, while the three
groups of masers around VLA 1 show a difference in their ΔVi.
In particular, we find that the maser groups VLA 1A and C have similar intrinsic thermal
linewidths ( ⟨ ΔVi ⟩ = 1.0 km s-1) while the group
VLA 1B has lower values ( ⟨ ΔVi ⟩ = 0.7 km s-1).
This can come from the degree of their saturation that we can evaluate by considering
Eq. (2).
Before using Eq. (2) we have to adjust the emerging brightness temperature values as explained in Sect. 3.2. At a temperature of ~400 K, for which Γ + Γν = 3 s-1 (Nedoluha & Watson 1992), the weighted emerging brightness temperature of VLA 1B is ⟨ TbΔΩ ⟩ > 1011 K sr, which is close to the limit of full saturation, and for VLA 1A and C is ⟨ TbΔΩ ⟩ = 1010 K sr. From Eq. (2) the masers of VLA 1A and VLA 1C are thus completely unsaturated (R/(Γ + Γν) = 0.5), while VLA 1B masers are saturated (R/(Γ + Γν) > 5), even if the real degree of their saturation is unknown because of underestimating TbΔΩ. The average observed linewidth (ΔvL) of VLA 1B group, which is about 0.5 km s-1, gives us another indication of the saturation state of their H2O masers. As reported in Sect. 3.2, the intrinsic thermal linewidths for the saturated masers are overestimated so ΔvL might be larger or at least equal to ΔVi implying that the maser lines are rebroadened as expected in the saturated maser lines. As the VLA 1B masers are saturated, they have not been taken into account in our conclusions. For the other masers associated with VLA 1, we observed linewidths well below their intrinsic thermal linewidth, and this confirms that these masers are unsaturated. The masers associated with VLA 2 are unsaturated; in fact, for T ~ 2500 K (Γ + Γν = 14 s-1, Anderson & Watson 1993), we get ratios of R/(Γ + Γν) < 0.5.
From the measurements of the maser flux densities
(S(ν)) and feature angular sizes (Σ) we can estimate the
brightness temperature by the equation reported in S09, ![\begin{equation} \frac{T_{\rm{b}}}{[\rm{K}]}=\frac{S(\nu)}{[\rm{Jy}]}\cdotp \left(\frac{\Sigma^2}{[\rm{mas^2}]}\right)^{-1}\cdotp\xi_{\rm{H_{2}O}}, \label{tb} \end{equation}](/articles/aa/full_html/2011/03/aa15825-10/aa15825-10-eq410.png) (4)where
ξH2O = 1.24 × 109 mas2 Jy-1 K
is a constant factor which includes all constant values, such as the Boltzmann constant,
the wavelength, and the proportionality factor obtained for a Gaussian shape by Burns
et al. (1979). Comparing
Tb with the emerging brightness temperatures obtained from
the model, we can easily estimate ΔΩ. The Gaussian fit of the masers give a size of
0.4 mas for the water masers related to VLA 1, which indicates that they are unresolved,
while a size of 0.5 for the masers associated with VLA 2, which indicates that they are
marginally resolved. The brightness temperatures of the brightest masers in both groups
are Tb,VLA1.08 > 1.23 × 1012 K and
Tb,VLA2.24 ≈ 1012 K, for which we find
ΔΩVLA1.08 < 10-2 sr and
ΔΩVLA2.24 ≈ 10-2 sr for T = 400 K and 2500 K,
respectively. Considering all the features in Table 1, the maser beaming of the two groups are
ΔΩVLA 1 ≲ 10-2 sr
(Γ + Γν = 2 s-1) and
ΔΩVLA 2 ≈ 10-2 sr
(Γ + Γν = 14 s-1). In a tubular geometry
ΔΩ ≈ (d/l)2, where d and
l are the transverse size and length of the tube respectively. Assuming
d approximately the size of the maser features, the maser lengths are
all in the range 1012 cm ≲ l ≲ 1014 cm.
(4)where
ξH2O = 1.24 × 109 mas2 Jy-1 K
is a constant factor which includes all constant values, such as the Boltzmann constant,
the wavelength, and the proportionality factor obtained for a Gaussian shape by Burns
et al. (1979). Comparing
Tb with the emerging brightness temperatures obtained from
the model, we can easily estimate ΔΩ. The Gaussian fit of the masers give a size of
0.4 mas for the water masers related to VLA 1, which indicates that they are unresolved,
while a size of 0.5 for the masers associated with VLA 2, which indicates that they are
marginally resolved. The brightness temperatures of the brightest masers in both groups
are Tb,VLA1.08 > 1.23 × 1012 K and
Tb,VLA2.24 ≈ 1012 K, for which we find
ΔΩVLA1.08 < 10-2 sr and
ΔΩVLA2.24 ≈ 10-2 sr for T = 400 K and 2500 K,
respectively. Considering all the features in Table 1, the maser beaming of the two groups are
ΔΩVLA 1 ≲ 10-2 sr
(Γ + Γν = 2 s-1) and
ΔΩVLA 2 ≈ 10-2 sr
(Γ + Γν = 14 s-1). In a tubular geometry
ΔΩ ≈ (d/l)2, where d and
l are the transverse size and length of the tube respectively. Assuming
d approximately the size of the maser features, the maser lengths are
all in the range 1012 cm ≲ l ≲ 1014 cm.
5.2. Magnetic field in W75N(B)
5.2.1. Magnetic field strength
The magnetic field strength along the line of sight was determined from circular
polarization measurements for 20 water masers. We detected significant
( ≥ 3σ) magnetic fields toward 10 masers in VLA 1 and 7 masers in
VLA 2. The detected fields along the line of sight (B||)
range from − 400 mG to + 600 mG for the H2O masers around VLA 1 and from
− 200 mG to 1000 mG for those associated with VLA 2 (see Table 1). The wide range obtained for
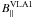 and
and 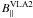 is not anomalous, and a similar range was reported for Cepheus A (Vlemmings et al. 2006). The changing in the sign indicates the
reversal of the magnetic field (negative towards the observer, positive away from the
observer) as already observed in other sources (e.g., Vlemmings et al. 2006). Since the θ values are close
to 90°, i.e. close to the plane of the sky, a slight difference in these angles can
produce an inversion of the sign of the magnetic fields. In the case of VLA 1, the
positive and negative magnetic field strengths measured for VLA 1B and VLA 1C groups
indicate a twisted magnetic field, which is not the case for VLA 2. Apart from the
H2O masers VLA2.01 and VLA2.02, which are located on the right edge of the
ellipse 2 and show positive values, the other masers in the upper left part of the
ellipse 2 (from VLA2.09 to VLA2.26) present a clear separation between positive and
negative magnetic field strengths (see Fig. 4 and
Table 1).
is not anomalous, and a similar range was reported for Cepheus A (Vlemmings et al. 2006). The changing in the sign indicates the
reversal of the magnetic field (negative towards the observer, positive away from the
observer) as already observed in other sources (e.g., Vlemmings et al. 2006). Since the θ values are close
to 90°, i.e. close to the plane of the sky, a slight difference in these angles can
produce an inversion of the sign of the magnetic fields. In the case of VLA 1, the
positive and negative magnetic field strengths measured for VLA 1B and VLA 1C groups
indicate a twisted magnetic field, which is not the case for VLA 2. Apart from the
H2O masers VLA2.01 and VLA2.02, which are located on the right edge of the
ellipse 2 and show positive values, the other masers in the upper left part of the
ellipse 2 (from VLA2.09 to VLA2.26) present a clear separation between positive and
negative magnetic field strengths (see Fig. 4 and
Table 1).
Based on these detections the absolute weighted magnetic field strengths along the line
of sight, where the weights are 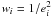 and
ei is the error of the
ith measurement, are
and
ei is the error of the
ith measurement, are 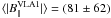 mG and
mG and
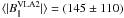 mG. In the case of VLA 1, it is
more correct to determine ⟨ | B|| | ⟩ for only the
unsaturated masers; i.e.,
mG. In the case of VLA 1, it is
more correct to determine ⟨ | B|| | ⟩ for only the
unsaturated masers; i.e., 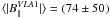 mG. The large errors are due to
the large scatter of the magnetic field strength values, which depend on the projection
effects, on the density of each water maser region, and on the local velocities of
shocks. Because of this scatter it is difficult to evaluate the true strength of the
full magnetic fields of the entire region. To compare the results obtained using
different maser species we can estimate them roughly. Since
⟨ θ ⟩ VLA1 = 83°
mG. The large errors are due to
the large scatter of the magnetic field strength values, which depend on the projection
effects, on the density of each water maser region, and on the local velocities of
shocks. Because of this scatter it is difficult to evaluate the true strength of the
full magnetic fields of the entire region. To compare the results obtained using
different maser species we can estimate them roughly. Since
⟨ θ ⟩ VLA1 = 83°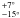 and ⟨ θ ⟩ VLA2 = 85°
and ⟨ θ ⟩ VLA2 = 85°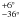 the absolute weighted magnetic field strengths are
the absolute weighted magnetic field strengths are
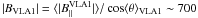 mG and
|BVLA2| ~ 1700 mG, respectively. Such high
values are also found by Vlemmings et al. (2006)
in Cepheus A. As their shock velocity is 10 km s-1, measuring a magnetic
field of 600 mG, these authors explain this high value with the presence of a nearby
magnetic dynamo.
mG and
|BVLA2| ~ 1700 mG, respectively. Such high
values are also found by Vlemmings et al. (2006)
in Cepheus A. As their shock velocity is 10 km s-1, measuring a magnetic
field of 600 mG, these authors explain this high value with the presence of a nearby
magnetic dynamo.
If the magnetic field is important throughout the collapse of a spherical cloud, the
cloud forms primarily by flows along field lines, and the conservation of magnetic flux
and of the mass imply B ∝ n0.47 (Crutcher
1999). Although the scaling of the magnetic
field in water maser is due to shocks, Vlemmings (2006, 2008) empirically showed that
even water masers with number densities up to 1011 cm-3 follow
this relation, even if in non-masing gas of similar densities the magnetic field
strengths are likely lower due to ambipolar diffusion. Hence, from the magnetic field
strengths, we can determine the number density of the cloud where the H2O
masers arise by the relation B ∝ n0.47.
Considering the pre-shock magnetic field (B|| = 16 mG)
and density
(nH2 = 109 cm-3)
obtained by S09 from methanol maser emissions, we have
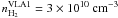 and
and 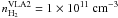 .
Similar calculation can be done considering the magnetic field strength obtained during
the OH flare near VLA 2 (Slysh et al. 2010). They
measured a magnetic field strength of about 70 mG, which is comparable to the total
magnetic field strength inferred by S09 (B = 50 mG). Since from the OH
maser observations is generally possible to get only B and not
B|| and since the flare occurred near VLA 2, in this
case we have to use the value of |BVLA2| instead of the
value of
.
Similar calculation can be done considering the magnetic field strength obtained during
the OH flare near VLA 2 (Slysh et al. 2010). They
measured a magnetic field strength of about 70 mG, which is comparable to the total
magnetic field strength inferred by S09 (B = 50 mG). Since from the OH
maser observations is generally possible to get only B and not
B|| and since the flare occurred near VLA 2, in this
case we have to use the value of |BVLA2| instead of the
value of 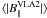 . For an OH number density of
108 cm-3, we find
. For an OH number density of
108 cm-3, we find 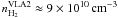 for the water masers around VLA 2, close to what is obtained considering the methanol
masers. These results, which are close to the extreme upper limit of
1011 cm-3 of the water maser thermalisation (Elitzur et al.
1989), confirm the assumptions on the
CH3OH and OH number densities and reinforce the measurements of the
magnetic field strength made by S09, Slysh et al. (2010) and in this paper. The three independent magnetic field strength values
obtained from three different maser species located at different positions show that the
magnetic field in massive star-forming regions can reach strength larger than expected.
This large unexpected values of B might be due either to the presence
of a magnetic dynamo or to the presence of very high-velocity shocks that strongly
compress the gas, and consequently increase the magnetic field strength from 50–70 mG
(pre-shock methanol-OH region) to > 1 Gauss (water maser region). For the last
hypothesis we refer the reader to Sect. 5.3.
for the water masers around VLA 2, close to what is obtained considering the methanol
masers. These results, which are close to the extreme upper limit of
1011 cm-3 of the water maser thermalisation (Elitzur et al.
1989), confirm the assumptions on the
CH3OH and OH number densities and reinforce the measurements of the
magnetic field strength made by S09, Slysh et al. (2010) and in this paper. The three independent magnetic field strength values
obtained from three different maser species located at different positions show that the
magnetic field in massive star-forming regions can reach strength larger than expected.
This large unexpected values of B might be due either to the presence
of a magnetic dynamo or to the presence of very high-velocity shocks that strongly
compress the gas, and consequently increase the magnetic field strength from 50–70 mG
(pre-shock methanol-OH region) to > 1 Gauss (water maser region). For the last
hypothesis we refer the reader to Sect. 5.3.
With regard to the orientation of the magnetic field, it is worthwhile to discuss the influence of the Faraday rotation in our observations.
5.2.2. Faraday rotation
The measurements of the linear polarization angle (χ) might be
disturbed by the foreground, ambient, and internal Faraday rotation, which are given by
![\begin{equation} \Phi[^{\circ}]=1.35 \times 10^{-15}\,D\,[\rm{cm}]\, \textit{n}_{e}\,[\rm{cm^{-3}}]\, \textit{B}_{||}\,[\rm{mG}]\,\nu^{-2}\,[\rm{GHz}], \label{fari} \end{equation}](/articles/aa/full_html/2011/03/aa15825-10/aa15825-10-eq458.png) (5)where
D is the length of the path over which the Faraday rotation occurs,
ne and B|| are
respectively the average electron density and the magnetic field along this path and
ν the frequency. For the foreground Faraday rotation (i.e. the
rotation due to the medium between the source and the observer)
φf is
0°̣4
at 22 GHz, assuming the interstellar electron density and the magnetic field are
ne ≈ 0.012 cm-3 and
B|| ≈ 2 μG, respectively.
(5)where
D is the length of the path over which the Faraday rotation occurs,
ne and B|| are
respectively the average electron density and the magnetic field along this path and
ν the frequency. For the foreground Faraday rotation (i.e. the
rotation due to the medium between the source and the observer)
φf is
0°̣4
at 22 GHz, assuming the interstellar electron density and the magnetic field are
ne ≈ 0.012 cm-3 and
B|| ≈ 2 μG, respectively.
All water masers are not in the same plane, but they arise in clouds at different depths. This depth is impossible to determine from our observations, so in order to estimate the ambient Faraday rotation (i.e. the rotation due to the ambient medium where masers arise), we assume the maximum projected separation as upper limit of D among masers close to each other with the highest velocity difference, which is Dmax ≈ 2 × 1015 cm. For the electron density, we assume the value reported by Fish & Reid (2006), ne ≈ 300 cm-3, which can produce a rotation of 90° along the path amplification of OH maser around H II regions. Considering B|| = 16 mG (S09), the ambient Faraday rotation is φa < 26°.
The internal Faraday rotation, which can destroy the linear polarization (Fish & Reid 2006), depends on the type of shock that pumps the water masers. They can either be a dissociative jump shock (J-shock) or a nondissociative continuous shock (C-shock). In the case of a C-shock, the intrinsic Faraday rotation at 22 GHz can be considered negligible because the ionization state of the gas is controlled by cosmic-ray ionization, which generates electron-molecular ion pairs at a rate of 10-17 s-1 (Kaufman & Neufeld 1996), while we have to roughly estimate its contribution for a J-shock. In this case, the electron density is ne = χe nH2, where χe is the ionization fraction (χe = 10-5 − 10-4; Kylafis & Norman 1987) and nH2 the number density of the H2O masers. In the most conservative situation, for which ne ~ 104 cm-3, we determine an internal Faraday rotation of tens of degrees, enough to destroy the linear polarization in some cases. This means that either the electron density must be much lower or, more likely, the internal Faraday rotation must be negligible, and consequently the shock must be a C-shock.
5.2.3. Magnetic field orientation
Suppose that the water masers in both sources are pumped by C-shocks (see Sect. 5.3), this means that the Faraday rotation is < 26°. Since the H2O masers associated with VLA 1 and VLA 2 indicate that there are two different magnetic fields around the two sources, it is worthwhile discussing them separately. All water masers show θ > θcrit ~ 55°; i.e., the magnetic field direction is perpendicular to the linear polarization vectors and close to the plane of the sky.
The group VLA 1A shows an orientation of the magnetic field
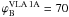 ° ± 9°, which is in good
agreement with what is reported by S09 (ϕB = 73° ± 10°).
This also confirms that the magnetic field orientation in this part of the source is
close to the direction of the large-scale molecular bipolar outflow (66°) (S09). The
other two groups VLA 1B and C show disordered linear polarization vectors, which cannot
give information on the orientation of the magnetic field. The different orientation of
the linear polarization vectors for these two groups might come from the different
depths of the masers, i.e. high values of the ambient Faraday rotation, and therefore we
can assume that the masers with angles far from −20° are located at higher depths than
those with angles close to −20° (e.g. VLA1.14).
° ± 9°, which is in good
agreement with what is reported by S09 (ϕB = 73° ± 10°).
This also confirms that the magnetic field orientation in this part of the source is
close to the direction of the large-scale molecular bipolar outflow (66°) (S09). The
other two groups VLA 1B and C show disordered linear polarization vectors, which cannot
give information on the orientation of the magnetic field. The different orientation of
the linear polarization vectors for these two groups might come from the different
depths of the masers, i.e. high values of the ambient Faraday rotation, and therefore we
can assume that the masers with angles far from −20° are located at higher depths than
those with angles close to −20° (e.g. VLA1.14).
Although around VLA 2 some H2O masers show the 90°-flip of the linear polarization angle (e.g., VLA2.15), which was also observed in some water masers in Cepheus A (Vlemmings et al. 2006), the magnetic field appears to be radial (see Fig. 4). Considering ⟨χ2⟩ ≈ −72°, the magnetic field orientation is about 18° that indicates a misalignment with the large-scale molecular bipolar outflow and the magnetic field of VLA 1, even though the inclination of both ellipses (~60°) is close to them.
The different orientation of the magnetic fields of the two sources again implies different local physical environments for VLA 1 and VLA 2, and suggests that VLA 1 is the powering source of the large-scale molecular bipolar outflow, as already indicated by S09.
5.3. J- or C-shocks?
As reported in previous papers, the H2O masers are thought to be pumped by the transition of shocks generated in the two protostars (e.g., Torrelles et al. 1997). These shocks can be either C-shocks or J-shocks. In a water masing region, C-shocks show v ≲ 50 km s-1 and a post-shock T < 4000 K (Kaufman & Neufeld 1996), while J-shocks have velocities v ≳ 45 km s-1 and a post-shock plateau temperature that depends on the pre-shock density, the shock velocity, and the observed linewidth of the water masers (Elitzur et al. 1989). Kylafis & Norman (1991) investigated the effects of the temperature on their J-shock model up to a temperature of about 1000 K, and they found that the brightness temperature starts to increase more slowly when a temperature ~500 K is reached.
We first consider VLA 1. Assuming the proper motion of the water masers reported by T03,
i.e. 19 km s-1, as the velocity of the shock and as pre-shock density, the
density of the methanol masers
nH2 = 109 cm-3 (S09), the
equation reported in Elitzur et al. (1989) for a
J-shock 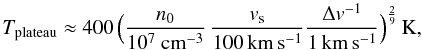 (6)where here
ΔvVLA1 = 0.5 km s-1, gives us a most likely
post-shock temperature
(6)where here
ΔvVLA1 = 0.5 km s-1, gives us a most likely
post-shock temperature 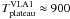 K, which is higher than the
temperature measured considering the weighted intrinsic velocity obtained from our fit
(TVLA1 ≈ 400 K). Moreover, from the model of a C-shock
described by Kaufman & Neufeld (1996), we
are able to estimate the velocity of the shock by considering the temperature
TVLA1. The model for a temperature of 400 K gives
K, which is higher than the
temperature measured considering the weighted intrinsic velocity obtained from our fit
(TVLA1 ≈ 400 K). Moreover, from the model of a C-shock
described by Kaufman & Neufeld (1996), we
are able to estimate the velocity of the shock by considering the temperature
TVLA1. The model for a temperature of 400 K gives
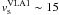 km s-1, which is
close to the proper motion of the H2O masers. Therefore, following our
arguments, the shock in VLA 1 is most likely a C-shock.
km s-1, which is
close to the proper motion of the H2O masers. Therefore, following our
arguments, the shock in VLA 1 is most likely a C-shock.
In the case of VLA 2, the plateau temperature due to a J-shock is
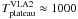 K (where
ΔvVLA2 = 0.7 km s-1, and
vVLA2 = 46 km s-1), which is less than the
temperature that we measured (TVLA2 ≈ 2500 K). The difference
of the two temperatures may be due to the turbulence velocity of the gas, which can be
determined by considering ΔVi. In fact,
ΔVi is related to the thermal and turbulence velocities by
the equation
K (where
ΔvVLA2 = 0.7 km s-1, and
vVLA2 = 46 km s-1), which is less than the
temperature that we measured (TVLA2 ≈ 2500 K). The difference
of the two temperatures may be due to the turbulence velocity of the gas, which can be
determined by considering ΔVi. In fact,
ΔVi is related to the thermal and turbulence velocities by
the equation 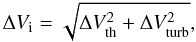 (7)and considering
Eq. (3) we are able to estimate the
turbulence velocity of the gas if a J-shock is present. The thermal velocity, which stems
from the warming up of the gas by the compression due to the passage of a shock, for a
temperature of 1000 K is
(7)and considering
Eq. (3) we are able to estimate the
turbulence velocity of the gas if a J-shock is present. The thermal velocity, which stems
from the warming up of the gas by the compression due to the passage of a shock, for a
temperature of 1000 K is 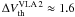 km s-1, so we have
ΔVturb ≈ 1.9 km s-1. If instead we suppose that
the shock is a C-shock from the model of Kaufman & Neufeld (1996) for TVLA2 ~ 2500 K, we get
km s-1, so we have
ΔVturb ≈ 1.9 km s-1. If instead we suppose that
the shock is a C-shock from the model of Kaufman & Neufeld (1996) for TVLA2 ~ 2500 K, we get
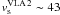 km s-1, which is
close to the expansion velocity that we determined in the present paper
(vVLA 2 = 46 km s-1). Both velocities are also
in good agreement with the velocity of 43 km s-1 measured by Slysh et al.
(2010) for the OH masers near VLA 2 obtained by
multiepoch observations. However, vVLA 2 is close to the
limit of 45 km s-1, which is considered the limit between the two types of
shocks, so we cannot rule one of them out by only considering the velocity. Since we
obtain well-ordered high linear polarization fraction and linear polarization vectors, we
have to suppose that the Faraday rotation is at most ~20°; otherwise, the
vectors no longer appear to be aligned with the large structure (i.e., ellipse 2). This
condition is only met if the internal Faraday rotation is small; in other words, if the
shock is a C-shock (Kaufman & Neufeld 1996). Therefore, we strongly suggest that there is a C-shock also in VLA 2 even
if a J-shock cannot be completely ruled out.
km s-1, which is
close to the expansion velocity that we determined in the present paper
(vVLA 2 = 46 km s-1). Both velocities are also
in good agreement with the velocity of 43 km s-1 measured by Slysh et al.
(2010) for the OH masers near VLA 2 obtained by
multiepoch observations. However, vVLA 2 is close to the
limit of 45 km s-1, which is considered the limit between the two types of
shocks, so we cannot rule one of them out by only considering the velocity. Since we
obtain well-ordered high linear polarization fraction and linear polarization vectors, we
have to suppose that the Faraday rotation is at most ~20°; otherwise, the
vectors no longer appear to be aligned with the large structure (i.e., ellipse 2). This
condition is only met if the internal Faraday rotation is small; in other words, if the
shock is a C-shock (Kaufman & Neufeld 1996). Therefore, we strongly suggest that there is a C-shock also in VLA 2 even
if a J-shock cannot be completely ruled out.
From the equation ![\begin{equation} \frac {B_{\rm{maser}}}{[\rm mG]}\approx80\sqrt{\frac{n_{\rm{H_{2}}}}{[10^{8}\,\rm{cm^{-3}}]}}\cdotp \frac{v_{\rm{s}}} {[10\,\rm{km\,s^{-1}}]}, \label{Cmag} \end{equation}](/articles/aa/full_html/2011/03/aa15825-10/aa15825-10-eq500.png) (8)where
nH2 is the pre-shock density and
vs the velocity of the shock, we can verify our assumption
about the pre-shock density and the rough estimation of
| BVLA1 | and | BVLA2 | .
Equation (8) is valid for both types of
shocks (Kaufman & Neufeld 1996).
Considering nH2 = 109 cm-3
as before, we get |BVLA1| ≈ 500 mG and
|BVLA2| ≈ 1200 mG, which are consistent with the rough
values reported in Sect. 5.2, making the presence of
a magnetic dynamo unnecessary. Finally, from our results we can strongly depict the
following scenario for VLA 1: the hot gas in a C-shock pumps the water masers and at the
same time the warm dust associated with this shock emits infrared photons, which pumps the
methanol masers in the pre-shock region, as already suggested in S09.
(8)where
nH2 is the pre-shock density and
vs the velocity of the shock, we can verify our assumption
about the pre-shock density and the rough estimation of
| BVLA1 | and | BVLA2 | .
Equation (8) is valid for both types of
shocks (Kaufman & Neufeld 1996).
Considering nH2 = 109 cm-3
as before, we get |BVLA1| ≈ 500 mG and
|BVLA2| ≈ 1200 mG, which are consistent with the rough
values reported in Sect. 5.2, making the presence of
a magnetic dynamo unnecessary. Finally, from our results we can strongly depict the
following scenario for VLA 1: the hot gas in a C-shock pumps the water masers and at the
same time the warm dust associated with this shock emits infrared photons, which pumps the
methanol masers in the pre-shock region, as already suggested in S09.
6. Conclusions
We observed the 22 GHz water masers in full polarization mode in the massive star-forming region W75N with the VLBA. We
detected 124 water masers around the two radio sources VLA 1 and VLA 2, which appear to be in two different evolutionary stages; i.e., VLA 1 is more evolved and a radio jet has not formed yet in VLA 2. From our observations, we have shown that these two sources separated in the sky by ~1′′ (2000 AU) have different local physical environments. In particular, the linear polarization indicates that the magnetic field around VLA 1 is aligned well with the large-scale molecular bipolar outflow, while the magnetic field is well-ordered around the shell-like expanding gas associated with VLA 2. The detection of Zeeman-splitting indicates an absolute weighted magnetic field strengths |BVLA1| ~ 700 mG and |BVLA2| ~ 1700 mG. We were also able to determine the type of shocks that pump the water masers associated with both sources. They both are C-shocks, even though a J-shock cannot completely be ruled out in the case of VLA 2. We suggest VLA 1 as the driving source of the large-scale molecular bipolar outflow.
Acknowledgments
We wish to thank an anonymous referee and the editor for making useful suggestions that have highly improved the paper. G.S. and W.H.T.V. acknowledge support by the Deutsche Forschungsgemeinschaft (DFG) through the Emmy Noether Reseach grant VL 61/3-1. S.C. acknowledges support from CONACYT grant 60581. J.M.T. acknowledges support from MICINN (Spain) AYA2008-06189-C03 (co-funded with FEDER funds) and from Junta de Andalucía (Spain).
References
- Alakov, A. V., Slysh, V. I., Popov, M. V., et al. 2005, Astron. Lett., 31, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, N., & Watson, W. D. 1993, ApJ, 407, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Baart, E. E., Cohen, R. J., Davies, R. D., et al. 1986, MNRAS, 219, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. O., Owen, F. N., & Rudinick, L. 1979, AJ, 84, 1683 [NASA ADS] [CrossRef] [Google Scholar]
- Carrasco-González, C., Rodríguez, L. F., Torrelles, J. M., et al. 2010, AJ, 139, 2433 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Dickel, J. R., Dickel, H. R., & Wilson, W. J. 1978, ApJ, 223, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M., Hollenbach, D. J., & McKee, C. F. 1989, ApJ, 346, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Fish, V. L., & Reid, M. J. 2006, ApJS, 164, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Fish, V. L., & Reid, M. J. 2007, ApJ, 656, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Girart, J. M., Beltrán, M. T., Zhang, Q., et al. 2009, Science, 324, 1408 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Goldreich, P., & Keeley, D. A. 1972, ApJ, 174, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., Keeley, D. A., & Kwan, J. Y. 1973, ApJ, 179, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Haschick, A. D., Reid, M. J., Burke, B. F., et al. 1981, ApJ, 244, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, T. R., Taylor, G. B., Felli, M., et al. 1994, A&A, 284, 215 [NASA ADS] [Google Scholar]
- Hutawarakorn, B., & Cohen, R. J. 1996, ASPC, 97, 532 [NASA ADS] [Google Scholar]
- Hutawarakorn, B., Cohen, R. J., & Brebner, G. C. 2002, MNRAS, 330, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Imai, H., Horiuchi, S., Deguchi, S., & Kameya, O. 2003, ApJ, 595, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufman, M. J., & Neufeld, D. A. 1996, ApJ, 456, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Kemball, A. J., Diamond, P. J., & Cotton, W. D. 1995, A&AS, 110, 383 [Google Scholar]
- Kylafis, N. D., & Norman, C. A. 1987, ApJ, 323, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Kylafis, N. D., & Norman, C. A. 1991, ApJ, 373, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Leppänen, K., Liljeström, T., & Diamond, P. 1998, ApJ, 507, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumoto, T., & Tomisaka, K. 2004, ApJ, 616, 266 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Minier, V., Booth, R. S., & Conway, J. E. 2000, A&A, 362, 1093 [NASA ADS] [Google Scholar]
- Nedoluha, G. E., & Watson, W. D. 1992, ApJ, 384, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Persi, P., Tapia, M., & Smith, H. A. 2006, A&A, 445, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., & Moran, J. M. 1981, ARA&A, 19, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Sarma, A. P., Troland, T. H., & Romney, J. D. 2001, ApJ, 554, L217 [NASA ADS] [CrossRef] [Google Scholar]
- Shepherd, D. S., Testi, L., & Stark, D. P. 2003, ApJ, 584, 882 [NASA ADS] [CrossRef] [Google Scholar]
- Slysh, V. I., & Migenes, V. 2006, MNRAS, 369, 1497 [Google Scholar]
- Slysh, V. I., Migenes, V., Val’tts, I. E., et al. 2002, ApJ, 564, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Slysh, V. I., Alakov, A. V., & Migenes, V. 2010, MNRAS, 404, 1128 [NASA ADS] [Google Scholar]
- Surcis, G., Vlemmings, W. H. T., Dodson, R., et al. 2009, A&A, 506, 757 (S09) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torrelles, J. M., Gómez, J. F., Rodríguez, L. F., et al. 1997, ApJ, 489, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Torrelles, J. M., Patel, N. A., Anglada, G., et al. 2003, ApJ, 598, L115 (T03) [NASA ADS] [CrossRef] [Google Scholar]
- Vlemmings, W. H. T. 2008, A&A, 484, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vlemmings, W. H. T., Diamond, P. J., van Langevelde, H. J., et al. 2006, A&A, 448, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vlemmings, W. H. T., Surcis, G., Torstensson, K. J. E., et al. 2010, MNRAS, 404, 134 [NASA ADS] [Google Scholar]
All Tables
All 22 GHz water maser features in W75N for which linear and/or circular polarization was detected.
Number, epoch, semi-major axis, semi-minor axis, and inclination from the elliptical fit of the water maser associated with VLA 2 in the two different epochs.
All Figures
 |
Fig. 1 Results of the full radiative transfer χ2-model fits, for the maser that shows the highest linear polarization fraction (VLA1.19) and for the maser that shows the highest PV around VLA2 (VLA2.22). The fits yield the emerging maser brightness temperature TbΔΩ and the intrinsic maser linewidth ΔVi. Contours indicate the significance intervals Δχ2 = 0.25, 0.5, 1, 2, 3, 7, with the thick solid contours indicating 1σ and 3σ areas. |
| In the text | |
 |
Fig. 2 Total intensity and circular polarization spectrum for the three maser features VLA1.07, VLA1.16, and VLA2.16. The thick red lines are the best-fit models of I and V emission obtained using the radiative transfer method (see Sect. 3.2). All maser features were centered to zero velocity. |
| In the text | |
 |
Fig. 3 Positions of water and methanol masers superimposed on the 1.3 cm continuum contour map of the VLA1 thermal jet and VLA 2 (Torrelles et al. 1997). Contours are −3, −2, 2, 3, 4, 5, 6, 7, 8 × 0.16 mJy beam-1. Blue triangles indicate the positions of the water maser features detected with the VLBA (this paper). Red circles indicate the position of the methanol masers features detected by S09. The two arrows indicate the direction of the large-scale molecular bipolar outflow (PA = 66°). |
| In the text | |
 |
Fig. 4 Left panel: a close-up view of the H2O maser features around the radio source VLA 2. Right panel: a zoom-in view of the boxed region of the left panel. The octagonal symbols are the identified maser features in present work scaled logarithmically according to their peak flux density. The maser LSR radial velocity is indicated by color. A 5 Jy beam-1 symbol is plotted for illustration in both panel. The linear polarization vectors, scaled logarithmically according to polarization fraction P1 (in Table 1), are overplotted. Two ellipses are also drawn in both panels. They are the results of the best fit of the water masers (crosses) detected by T03 (dotted ellipse, ellipse 1; epoch 1999) and of those detected in present work (solid ellipse, ellipse 2; epoch 2005). Their parameters are listed in Table 4. The synthesized beam is 2.0 mas × 0.7 mas. |
| In the text | |
 |
Fig. 5 Left panel: a close-up view of the H2O maser features (octagon) around the radio source VLA 1. Right panel: a zoom-in view of the water masers group VLA 1B, here are also reported the water masers (square) detected by T03. The octagonal and the square symbols are scaled logarithmically according to their peak flux density. The maser LSR radial velocity is indicated by color. The systemic LSR radial velocity of W75N massive star-forming region is 10 km s-1 (Shepherd et al. 2003). Symbols for 3 Jy beam-1 and for 1 Jy beam-1 are shown in the lower left corner of the panels. The linear polarization vectors, scaled logarithmically according to polarization fraction P1 (in Table 1), are overplotted on the left panel. The synthesized beam is 2.0 mas × 0.7 mas. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


