| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201014867 | |
| Published online | 21 January 2011 | |
Dust properties along anomalous extinction sightlines
II. Studying extinction curves with dust models
1
INAF, Astronomical Observatory,
Vicolo dell’Osservatorio 5,
35122
Padova,
Italy
e-mail: paola.mazzei@oapd.inaf.it
2
Department of Astronomy, Vicolo dell’Osservatorio 3, 35122
Padova,
Italy
Received:
26
April
2010
Accepted:
22
November
2010
Context. Studies of the dust extinction in the Galaxy have found that the large majority of sight lines analyzed obey a simple relation depending on one parameter, the total-to-selective extinction coefficient, RV. Different values of RV are able to match the whole extinction curve in different environments, thus characterize normal extinction curves. However anomalous curves i.e, curves which deviate strongly from this simple behavior have been observed in the Galaxy as well as external galaxies.
Aims. More than sixty curves with large ultraviolet deviations from their best-fit one-parameter curve are analyzed. The extinction curves are fitted with dust models to shed light on the properties of the grains along selected lines of sight, the processes affecting them, and their relations with the environmental characteristics.
Methods. The extinction curve models are developed using the latest prescriptions for grain-size distributions capable of describing one-parameter curves for RV values from 3.1 to 5.5. These models, extended here down to RV = 2.0, allow us to compare the resulting properties of our deviating curves with those of normal curves in a self-consistent framework, and thus to recover the relative trends overcoming the modeling uncertainties.
Results. In addition to 20 anomalous curves extracted from the same sample for study in a previous paper and revised here to account for the latest updates, these curves represent the largest, homogeneous sample of anomalous curves studied so far with dust models. Our results show that the ultraviolet deviations are driven by a larger amount of small grains than predicted for lines of sight where extinction depends on only one parameter. Moreover, the dust-to-gas ratios of anomalous curves are lower than the same values for no deviating lines of sight.
Conclusions. Both shocks and grain-grain collisions should destroy dust grains, hence reduce the amount of the dust trapped in the grains, modify the size distribution of the dust, and increase the small-to-large grain size ratio. Therefore, the extinction properties derived should correspond to sight lines where shocks and high velocity flows perturb the physical state of the interstellar medium and leave their signature on the dust properties.
Key words: dust, extinction / ISM: clouds / open clusters and associations: general / galaxies: ISM
© ESO, 2011
1. Introduction
Dust extinction in the Galaxy is very complex, there being large variations from region to region. A successful attempt to interpret the observed behavior of extinction curves in our own Galaxy from near-IR to ultraviolet (UV) was given by Cardelli et al. (1989, CCM in the following). They found a relation between the whole shape of the extinction curve and the total-to-selective extinction coefficient, RV. With only very few exceptions, Galactic extinction curves so far observed tend to follow this relation within the uncertainties in the calculated RV values and extinction curves (Clayton et al. 2000; Gordon et al. 2003; Valencic et al. 2004, and references therein). Different values of RV are a rough indicator of the different environmental conditions affecting the grain-size distribution: low-RV values arise along sight lines with more small grains than high-RV sight lines. However, as pointed out by Cardelli & Clayton (1991), Mathis & Cardelli (1992), and in several recent papers (Mazzei & Barbaro 2008, and references therein) anomalous curves, i.e., curves that deviate from this simple behavior, still exist in our own Galaxy. Valencic et al. (2004) found that seven per cent of their sample of 417 International Ultraviolet Explorer (IUE) extinction curves combined with Two-Micron All-Sky Survey (2MASS) photometry, deviate from the CCM law by more than three times the standard deviation (3σ). Moreover, the CCM law does not apply outside the Galaxy. Gordon et al. (2003) showed that the vast majority of measured extinction curves in the Large and Small Magellanic Clouds do not obey the CCM law, even if a continuum of dust properties exists. Fitzpatrick & Massa (2009) concluded that to fit the visible-infrared region of the extinction curve two parameters at least are needed. The power-law model for the near-IR extinction law provides an excellent fit to most extinction curves, but the value of the power index varies significantly from sight-line-to-sight-line and increases with the wavelength.
The interest in these problems is increasing because suitable extinction corrections, which allow us to properly account for galaxy properties (i.e., colors and luminosities of nearby as well as of distant galaxies) are needed to improve our knowledge of galaxy evolution. Thus, our understanding of the dust extinction properties, in particular their dependence on the environment, are challenges to modern cosmology.
In this paper, we build-on the analysis of Mazzei & Barbaro (2008, Paper I in the following) by studying the behavior of a new class of extinction curves identified for the same sample defined in that paper where 785 extinction curves were compared with the relations derived by CCM for a variety of RV values in the range 2 − 6. The curves were classified as normal if they fitted at least one of the CCM curves or otherwise anomalous. In particular, all the curves retained deviate by more than 2σ from their CCM best-fit law, at least at one UV wavelength. By fitting the observed data with extinction curves provided by dust grain models, we aim to achieve insight into the properties of the grains along selected lines of sight, the processes affecting them, and their relations with the environmental characteristics. The extinction curve models are based on the prescriptions of Weingartner & Draine (2001) i.e., using their grain-size distributions and recent updates (Draine & Li 2007). Models of Weingartner & Draine (2001), which are able to describe normal curves for RV values of 3.1, 4.0 and 5.5, are extended down to RV = 2.0 and updated following Draine & Li (2007). All of these models allow us to compare the resulting properties, of both normal and anomalous curves, in a self-consistent framework, thus recover the relative trends.
The plan of the paper is the following. Section 2 summarizes the sample of extinction curves and the method used to derive their anomalous behavior, more details about these points are given in Paper I; Sect. 3 is devoted to the dust models developed to provide the best-fit model for the selected curves. All the models, for both anomalous and normal curves, are computed using the grain-size distributions of Weingartner & Draine (2001) with the updates of Draine & Li (2007); we indicate these models as WD in the following. In Sect. 4, the results for all these models are presented in terms of dust-to-gas ratios, abundance1 ratios, and small-to-large grain size ratios of the dust trapped into the grains along extinction curves. Results from Paper I are also revised to account for the afore mentioned implementation, to compare of the properties of the whole sample of anomalous sightlines. Section 5 is devoted to the Fitzpatrick & Massa (1988, 1990) parameterization of all our models. We aim to compare the properties of our sample with those of the larger sample of parameterized sightlines in the literature available so far (Valencic et al. 2004). In Sect. 6, we present our conclusions.
2. The sample
We gathered the UV data from the Astronomical Netherlands Satellite (ANS) photometry catalog of Wesselius et al. (1982). The UV observations were performed in five UV bands with central wavelengths (and widths) 1549 (149), 1799 (149), 2200 (200), 2493 (150), and 3294 (101) Å. Of the approximately 3500 stars in the ANS catalog, Savage et al. (1985) derived UV extinction excesses for 1415 normal stars of spectral type earlier than B7. These color excesses (Table 1 of Savage et al. 1985), E(λ − V) for λ cited above, are interpreted with reference to the photoelectric V band, starting from UV magnitudes listed in the ANS catalog and the intrinsic colors of Wu et al. (1980). Absolute calibrations of UV fluxes were performed as described by Wesselius et al. (1982). E(B − V) data are also listed in the Table 1 of the same catalog.
To avoid large errors in the color excesses, only those lines of sight with
E(B − V) ≥ 0.2 were retained, amounting
to 785 curves. From such a sub-sample, Barbaro et al.
(2001) singled out 78 lines of sight which they defined as anomalous. Their
analysis were extended in Paper I by considering
near-IR magnitudes from 2MASS catalog to derive the intrinsic infrared-color indices by
using Wegner’s calibrations (1994). For each observed curve covering the IR and UV regions,
the following quantities were minimized by applying a weighted least squares fit of the
different standard CCM relations ![\begin{equation} \delta (x_r)_{i,j}=\left[ \kappa (x_r)_{j} - \kappa (x_r)_{i}\right] / \sigma_{\kappa(x_r)_i} , \end{equation}](/articles/aa/full_html/2011/03/aa14867-10/aa14867-10-eq11.png) (1)where the index
r refers to all the eight wavelengths, i.e., the five UV ones from Savage et al. (1985), cited above, and the three IR
wavelengths. By assuming that
xr = 1/λr
and
κ(xr) = E(λr − V)/E(B − V),
the values of
κ(xr)i
refer to the observed curves (index i) and
κ(xr)j
to the CCM curve corresponding to each RV value
ranging from ≃ 2 to 6. The
σκ(xr)i,
are computed following Eq. (3) of Wegner
(2002)
(1)where the index
r refers to all the eight wavelengths, i.e., the five UV ones from Savage et al. (1985), cited above, and the three IR
wavelengths. By assuming that
xr = 1/λr
and
κ(xr) = E(λr − V)/E(B − V),
the values of
κ(xr)i
refer to the observed curves (index i) and
κ(xr)j
to the CCM curve corresponding to each RV value
ranging from ≃ 2 to 6. The
σκ(xr)i,
are computed following Eq. (3) of Wegner
(2002)![\begin{equation} \sigma_{\kappa(x_{r})}^2=\left[\frac{1}{E(B-V)}\right]^2 \left[\sigma^2_{m_{\lambda_r}} +\sigma_{V}^2+\sigma^2_{r,m}\right]+\left[\frac {\kappa(x_{r})\sigma_{E(B-V)}} {E(B-V)}\right]^2 , \end{equation}](/articles/aa/full_html/2011/03/aa14867-10/aa14867-10-eq20.png) (2)accounting for: i)
a conservative maximum color excess error,
σE(B − V), of 0.04 mag; ii) a
root-mean-square deviation of the observation at .55 μm,
σV, of 0.01 mag (Savage et al. 1985); iii) a root-mean-square deviation of the photometric
observation at wavelength λr,
σmλr,
ranging from 0.001 − 0.218 mag (Wesselius et al.
1982) in the UV range and given by the 2MASS catalog in the IR one; and iv)
classification errors and errors in the intrinsic colors, i.e,
σr,m, as given in Table 1B of Meyer & Savage (1981) in the UV range and derived
from Wegner (1994) in the IR one.
(2)accounting for: i)
a conservative maximum color excess error,
σE(B − V), of 0.04 mag; ii) a
root-mean-square deviation of the observation at .55 μm,
σV, of 0.01 mag (Savage et al. 1985); iii) a root-mean-square deviation of the photometric
observation at wavelength λr,
σmλr,
ranging from 0.001 − 0.218 mag (Wesselius et al.
1982) in the UV range and given by the 2MASS catalog in the IR one; and iv)
classification errors and errors in the intrinsic colors, i.e,
σr,m, as given in Table 1B of Meyer & Savage (1981) in the UV range and derived
from Wegner (1994) in the IR one.
For each line of sight, the residual differences at the five UV wavelengths between the observed data and the best-fit standard CCM curve, as in Eq. (1), were evaluated. Only lines for which at least one of these |δr| exceeds (or equals) two were retained. This defined the 2δ sample.
As pointed out in Paper I, this approach differs from that of Barbaro et al. (2001), both because IR data were not yet available and the anomalous character is defined here by separately analyzing each UV wavelength, i.e., considering δr, instead of using a criterion based on the combination of all UV data (i.e., Δ2, see Barbaro et al. 2001, for more details). There are 84 lines of sight in such a new sample, i.e., more than 10% of the selected initial sample, 27 (3.4%) with at least one |δr| > 3. These percentages are higher than those expected from random error analysis, as pointed out in Paper I.
The five UV wavelengths cited above correspond to the values x = 6.46, 5.56, 4.55, 4.01, and 3.04, respectively. The behavior of δ(4.55) > 0, more or less in correspondence with that of the bump, and of δ(6.46) < 0, in correspondence with that of the far-UV rise, was shown for the whole sample in Fig. 1 of Paper I. There are fifteen sight lines with δ(4.55) > 0 and δ(6.46) < 0, called type A anomalous curves, that were analyzed in Paper I as well as five sight lines with δ(4.55) < 0 and δ(6.46) > 0, defined type B anomalous curves. Type A curves are characterized by weaker bumps and steeper far-UV rises than expected from their best-fit CCM curve, which is worse by more than 2σ for at least one UV wavelength for each of them. Type B curves have stronger bumps and smoother far-UV rises than expected for CCM curves that provide best-fit solutions to the observations.
Here we focus on type C curves, i.e., sixty-four lines of sight, 76% of the 2δ sample. The behavior of type C curves can also be recovered here by looking at Fig. 1. For all of these curves, with the exception of five curves only, the corresponding best-fit standard CCM curve is always well above (≥2σ at least one UV wavelength) the observed data (Fig. 1, top panel). For five of them, two belonging to the 2δ sample, i.e., BD+59 2829 and BD+58 310, and three to the 3δ sample, i.e., HD 14707, HD 282622, and BD+52 3122, the corresponding best-fit standard CCM curve is well below the observed data, with some exception at x = 3.04 (Fig. 1, bottom panel).
In Table 1, the main properties of type C curves are presented: names (Col. 1), spectral types (Col. 2), reddening (Col. 3), V magnitudes (Col. 4) all from Savage et al. (1985), and RV (Col. 5). The RV values in Table 1, obtained by minimizing by means of a weighted least squares fit with different CCM relations the quantities in Eq. (1) using IR the extinction data only, agree with estimates of RV following prescriptions of Fitzpatrick (1999); the errors were computed with the same method used in Paper I (Geminale & Popowski 2004), which accounts for mismatch errors affecting the color excesses to the larger extent.
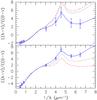 |
Fig. 1 Top panel: extinction data of HD 168785 (open circles) compared with our best-fit dust model (blue) continuous line (see Sect. 3), and the best-fit standard CCM curves corresponding to the whole spectral range, (black) dotted line, and to the IR data only, (red) dashed line. Bottom panel: extinction data of BD+58 310 (open circles) compared with our best-fit dust model (blue) continuous line, and the corresponding best-fit standard CCM curves with the same symbols as in the top panel. |
Properties of type C anomalous curves.
The first twenty-two lines of sight in Table 1 belong to the 3δ sample.
We note that HD 392525 corresponds to BD + 57 2525, and HD 282622 to BD + 30 748.
From the SIMBAD CDS database2 about 8% of our sight lines correspond to Be stars (i.e., HD 21455, HD 28262, HD 326327, HD 392525, and BD + 59 2829), and 9% to variable stars (i.e., HD 1337, HD 14707, HD 28446, HD 141318, HD 217035, BD + 31 3235); these represent about 17% of type C curves.
In the following analysis, we removed from the sample BD + 56 586, since a negative color excess E(.33 − V), −0.01, corresponds to this line of sight, which is indicative of mismatch errors (Papaj et al. 1991; Wegner 2002). We also removed from the sample HD 1337, an eclipsing binary of β Lyrae type in SIMBAD, also marked as a variable in Savage et al. (1985), and HD 137569, a post-AGB star (SIMBAD). Their extreme RV values, 0.60 ± 0.18 and 1.10 ± 0.18 (Table 1) are outside the range of explored standard CCM relations (Fitzpatrick 1999).
The selected lines of sight probe a wide range of dust environments, as suggested by the large spread in the measured RV values. In particular, HD 141318 and BD+58 310 are extreme cases: HD 141318 with RV equal to 1.95 ± 0.18 and BD+58 310 with RV = 5.65 ± 0.47 (Table 1).
Best-fit parameters of WD grain-size distributions of type C curves.
3. Models
Models of the extinction curves were computed according to the prescriptions of Weingartner & Draine (2001) and Draine & Li (2007). The novelty of these models is that the grain-size distribution is based on more recent observational constraints in the optical and infrared spectral domains (see Weingartner & Draine 2001, and references therein). This distribution, a revision of the Mathis et al. (1977) size distribution (see Clayton et al. 2003, for a discussion on grain size distribution history), accounts for two populations of spherical grains: amorphous silicate (Si) and carbonaceous grains (C), the latter consisting of graphite grains and polycyclic aromatic hydrogenated (PAH) molecules. Their optical properties, which depend on their geometry and chemical composition, are described by Li & Draine (2001b,a) and Draine & Li (2007), and account for new laboratory data, i.e., the near-IR absorption spectra measured by Mattioda et al. (2005), as well as the spectroscopic observations of PAH emission from dust in nearby galaxies (Draine & Li 2007, and references therein).
The Weingartner & Draine (2001) size distribution (see their Eq. (4)) allows for both a smooth cutoff in grain size a > at, and a change in the slope d ln ngr/d ln a for a < at. This requires several parameters that can be determined by comparing the observed curve using the Levenberg-Marquardt algorithm (Weingartner & Draine 2001)3. Table 2 presents the grain-size distribution parameters derived from our best-fit dust models of type C extinction curves where: bC is the abundance of carbon (per H nucleus) in the double log-normal very small grain population (see Table 2 and Eqs. (12) − (14) of Draine & Li 2007), αg and αs are the power-law indices of the C and Si grain-size distributions, respectively, βg and βs their curvature parameters, at,g and at,s their transition sizes, and ac,g and ac,s their upper cutoff radii.
Best-fit parameters of WD grain-size distributions of CCM curves with small RV values.
These models, indeed, depend on ten parameters since ac,s is constant (Weingartner & Draine 2001; Paper I). Figure 1 compares the observed extinction curves of two type C lines with the corresponding best-fit models.
The values of these parameters capable of reproducing the observed wavelength-dependent extinction law in the local Milky Way (MW), i.e., the observational fits of Fitzpatrick (1999) for RV values 3.1, 4.0, and 5.5 and different bC amounts, corresponding to twenty-five models, are derived by Weingartner & Draine (2001, Figs. 8 − 12; see also Draine 2003. Li & Draine (2002) showed that these grain models are also consistent with the observed IR emission from diffuse clouds in the MW and SMC. The observational fits of Fitzpatrick (1999), in turn, closely agree with standard CCM curves for the same RV values until RV is smaller than 5.5 (Fitzpatrick 1999, his Fig. 7). Moreover, as pointed out in Paper I, the extinction curves of Weingartner & Draine (2001) are almost unaffected by taking into account the latest updates (Draine & Li 2007). Thus, WD models are useful tools for providing insight into the properties of dust trapped in grains along normal lines of sight or small deviating extinction lines (i.e. < 2σ). However, since the majority of RV values in Table 1 are smaller than 3.1, we computed a new set of WD parameters capable of reproducing normal, CCM curves with total-to-selective extinction coefficients from 2.9 and 2.0, that we list in Table 3 for each pair of values (RV, bC), as in Weingartner & Draine (2001). The last two columns of this table show volumes of carbonaceous and silicate populations normalized to their abundance/depletion-limited values, i.e., 2.07 × 10-27 cm-3 H-1 and 2.98 × 10-27 cm-3 H-1, respectively (Weingartner & Draine 2001). As discussed by Draine (2003) and Draine (2004), models in Table 1 of Weingartner & Draine (2001) slightly exceed the abundance/depletion-limited values of silicon grains (≤20%) and we assume that this value is the maximum allowed. Figure 2 shows two normal curves of our sample with small RV, their best-fit standard CCM curves, and, as a comparison, WD dust grain models to fit the data. Properties of all these models, of both normal and anomalous curves, are given in the next section in terms of dust-to-gas ratios, abundance ratios, and small-to-large grain size ratios of the dust trapped into the grains along these extinction curves.
There are several distinct interstellar dust models that simultaneously fit the observed extinction, infrared emission, and abundances constraints (Zubko et al. 2004). Models of WD allow us to compare the results of our deviating curves here with those of normal curves, in a self-consistent framework.
4. Results
For a given chemical composition of the grains, the total volume occupied by the dust
grains, Vg, which includes the total volume per hydrogen atom of
each grain type, is directly related to the dust-to-gas ratio,
ρd/ρH, as described in
Eqs. (3) − (6) of Paper I, i.e., 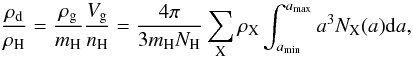 (3)where the integral is
computed for the given size distributions of the grains, i.e., from parameters in
Table 2 for both anomalous and normal curves, in
both Table 1 of Weingartner & Draine (2001),
accounting for latest updating (Draine & Li
2007), and Table 3.
(3)where the integral is
computed for the given size distributions of the grains, i.e., from parameters in
Table 2 for both anomalous and normal curves, in
both Table 1 of Weingartner & Draine (2001),
accounting for latest updating (Draine & Li
2007), and Table 3.
 |
Fig. 2 Top panel: HD 39136, a normal curve of our sample (blue filled squares) whose best-fit standard CCM curve corresponds to RV = 2.85 ± 0.47 (red dotted line). The (magenta) long-dashed line is computed as the seventh model in Table 1 of Weingartner & Draine (2001), RV = 3.1, including latest updating (Draine & Li 2007); the (green) short-dashed line is our best-fit dust model: the fifth model in Table 3. Bottom panel: HD 12323, a normal curve of our sample (blue filled squares) whose best-fit standard CCM curve corresponds to RV = 2.30 ± 0.51 (red dashed line); the (green) continuous line is the best-fit dust model: the thirteenth model in Table 3. |
The number of atoms of an element per interstellar H nucleus trapped in the grains, i.e., the C/H and Si/H abundances, and the same fractions compared with the solar values, i.e., C/C⊙ and Si/Si⊙, can be computed from the ρd/ρH ratio of each type of grains. The solar values of carbon and silicon dust abundances adopted to achieve this aim are, as in Paper I, (C/H)⊙ = 3.3 × 10-4, and (Si/H)⊙ = 3.65 × 10-5; the average mass in our own galaxy of one carbon grain is 19.93 × 10-24 g/cm3 and of one silicon grain 28.7 × 10-23 g/cm3, as in Weingartner & Draine (2001); these values are in good agreement with estimates by Clayton et al. (2003) of (C/H)⊙ = 3.2 × 10-4 and (Si/H)⊙ = 4.0 × 10-5.
The properties of the grains along type A and B anomalous curves, investigated in Paper I, indicate that B curves are characterized by a number of small silicon grains that is lower than for normal curves with the same RV, and lower than A curves too; they are also characterized by a larger number of small carbon grains as A curves are. These results, revised here to account for the updates provided by Draine & Li (2007), are included in the figures to allow comparisons. The main change caused by these improvements (Table 2 of Draine & Li 2007), is related to the number of carbon atoms per total H in each of the log-normal components (Eqs. (11)−(14) of Draine & Li 2007). Appreciable effects occur when the parameters of grain-size distribution provide a larger number of small carbon grains than the number required to fit normal lines, thus in the case of anomalous lines.
In the figures, error bars of WD normal curves span the range of values of different models corresponding to the same RV value (Sect. 3).
Properties of the dust trapped into the grains along type C curves.
The results of our WD best-fit models of type C curves are reported in Table 4: the name of the sight line is indicated in Col. 1, the dust-to-gas ratio in units of 10-2 in Col. 2, the abundance ratios in Cols. 3 and 4, the small-to-large grain size ratios of carbon, RC, in Col. 5 and of silicon grains, RSi, in Col. 6, the RV value in Col. 7, and the E(B − V)/NH ratio in Col. 8. Here, as in the following, we define small grains as those of size a ≤ 0.01 μm, and large grains those of size larger than this value.
The following conclusions can be derived by comparing the results presented in Table 4 with those derived from the same dust grain models of normal extinction curves (Sect. 3):
-
i)
Dust population models generally infer substantial abun-dances of elements in grain material, approaching or exceed-ing the abundances believed to be appropriate to interstellarmatter (Draine 2003, and references therein).It is remarkable that, according to our models, the predictedamount of carbon that condenses onto grains along the ma-jority of our sight lines is lower than the average Galacticvalue (Fig. 3). Only three anomalous curves,HD 37061, HD 21455, andHD 164492, require C/H abundance largerthan the solar value. Moreover, for about 74% of our models oftype C curves, the predicted C/H ratio does notexceed a fraction 0.7 − 0.6 of C cosmic abundance which is accepted, although with large uncertainties, as the average amount of carbon trapped in grains (Draine 2009). No anomalous line model exceeds the solar value of the silicon abundance.

Fig. 3 Abundances of the dust locked up into the grains along our anomalous sight lines compared with the solar values (see text); (green) open circles are for type C curves, and (black) squares represent normal curves computed with WD parameters corresponding to seven different RV values, i.e. forty-nine models (Sect. 3). We also include the results of type A and B extinction models (Paper I), (red) stars and (blue) filled triangles, respectively, revised here to account for the latest model updates (Draine & Li 2007) (see text).
-
ii)
The dust-to-gas ratio of type C curves is linked to the E(B − V)/N(H) ratio by the relation
 (4)with dispersion
0.076 (dashed line in Fig. 4) and
E(B − V)/N(H)
in units of the average Galactic value, i.e.,
1.7 × 10-22 mag cm2 (Bohlin
et al. 1978). Accounting for all our anomalous curves, we derive
(4)with dispersion
0.076 (dashed line in Fig. 4) and
E(B − V)/N(H)
in units of the average Galactic value, i.e.,
1.7 × 10-22 mag cm2 (Bohlin
et al. 1978). Accounting for all our anomalous curves, we derive
 (5)with dispersion
0.13, (continuous line in Fig. 4), in close
agreement with the results of Paper I, although
with a slightly smaller correlation index, 0.92 instead of 0.95. Therefore, anomalous
curves are characterized by dust-to-gas ratios lower than the average Galactic value.
In particular, no type C extinction curve exceeds the critical Galactic value of 0.01
(Barbaro et al. 2004, and references therein),
independently of its carbon grain abundance (see i)). Extinction curves of our sample
with a
E(B − V)/N(H)
ratio equal to the average Galactic value, exhibit their anomalous character due to a
dust-to-gas ratio lower than normal curves. Moreover, their
E(B − V)/N(H)
can depend on the dust-to-gas ratio when
RV does not, unlike the behavior
expected for normal extinction curves (Fig. 5,
top panel). Hence, while anomalous curves can also be found in environments with
normal reddening properties, strong deviations from the average reddening Galactic
value are a signature of an anomaly as shown in Fig. 5, bottom panel, and discussed in Barbaro
et al. (2004).
(5)with dispersion
0.13, (continuous line in Fig. 4), in close
agreement with the results of Paper I, although
with a slightly smaller correlation index, 0.92 instead of 0.95. Therefore, anomalous
curves are characterized by dust-to-gas ratios lower than the average Galactic value.
In particular, no type C extinction curve exceeds the critical Galactic value of 0.01
(Barbaro et al. 2004, and references therein),
independently of its carbon grain abundance (see i)). Extinction curves of our sample
with a
E(B − V)/N(H)
ratio equal to the average Galactic value, exhibit their anomalous character due to a
dust-to-gas ratio lower than normal curves. Moreover, their
E(B − V)/N(H)
can depend on the dust-to-gas ratio when
RV does not, unlike the behavior
expected for normal extinction curves (Fig. 5,
top panel). Hence, while anomalous curves can also be found in environments with
normal reddening properties, strong deviations from the average reddening Galactic
value are a signature of an anomaly as shown in Fig. 5, bottom panel, and discussed in Barbaro
et al. (2004). -
iii)
In the vast majority of the cases, the expected small-to-large grain size ratios of anomalous lines differ from the corresponding values expected for WD CCM curves (Fig. 6). Anomalous curves are generally characterized by a number of small carbonaceous grains that is larger than inferred by normal curves, whereas the small-to-large size ratios of Si grains span a wider range, from smaller to larger values than normal lines. Only five anomalous curves have normal values of both these ratios, BD+59 2829 and BD+58 310, belonging to the 2δ sample, and HD 14707, HD 282622, BD+52 3122, to the 3δ sample. For these sightlines, their best-fit standard CCM curve in the UV range is below the observed data, as outlined in Sect. 2 (Fig. 1, bottom panel).

Fig. 4 Behavior of the dust-to-gas ratio, ρd/ρH, normalized to the average Galactic value, 0.01, with the E(B − V)/NH ratio in units of 1.7 × 10-22 cm2 mag (Bohlin et al. 1978); symbols are as in the previous figure. The dashed line shows the relation for type C curves (Eq. (4)) and the continuous line for all the anomalous curves analyzed (Eq. (5)).

Fig. 5 Top panel: RV values and the corresponding E(B − V)/NH ratios in units of 1.7 × 10-22 mag cm2, as derived from our WD dust grain models (see text); symbols are as in the previous figures; the dashed line connects the results of WD models of normal curves corresponding to seven different RV values (Sect. 3); the range in bold-face on the x-axis shows the expected deviation of Galactic curves (Bohlin et al. 1978). Bottom panel: behavior of the reddening E(B − V) (Savage et al. 1985) as a function of the predicted total hydrogen column density; continuous line shows the average Galactic relationship found by analyzing a large sample of sight lines whose HI and H2 column densities were measured: E(B − V)/N(H) = 1.7 × 10-22 mag cm2 (Bohlin et al. 1978); symbols are the same as in the previous figures.

Fig. 6 Predicted small-to-large grain size ratios for carbonaceous and silicate grains of anomalous sight lines compared with the range spanned by WD models of CCM curves (continuous lines) for the same range of RV values.

Fig. 7 Expected behavior of the small-to-large grain size ratio of silicate (top panel) and carbonaceous dust (bottom panel) versus RV values along anomalous sight lines compared with the same along CCM curves (open squares) computed with WD parameters (Sect. 3). Continuous line in the top panel corresponds to the relationship y = ( − 0.37 ± 0.03) + (3.30 ± 0.09), with dispersion 0.18 and anti-correlation index − 0.91, that applies to normal lines. Continuous line in the bottom panel shows the relationship for the whole sample of anomalous curves y = ( − 0.25 ± 0.03)x + (5.83 ± 0.09) with dispersion 0.19 and correlation index − 0.65.

Fig. 8 Expected behavior of the small-to-large grain size ratio of silicate (top panel) and carbonaceous dust (bottom panel) versus the silicon and carbonaceous dust abundances, respectively, of anomalous sight lines; continuous line holds for Si grains of the whole sample y = (0.43 ± 0.06)x + ( − 1.55 ± 0.13) with dispersion 0.34 and correlation index 0.60. Symbols are the same as in the previous figures.
-
iv)
The small-to-large size ratio of Si grains is almost independent of the selective extinction coefficient, RV (r = − 0.20), unlike the normal curves. For these curves, this ratio anti-correlates strongly with RV (Fig. 7, top panel). The same ratio of carbon grains for type C curves is, indeed, anti-correlated with RV having an anti-correlation index r = − 0.80, in contrast to the WD CCM lines (Fig. 7, bottom panel). This anti-correlation is somewhat weakened by including all the anomalous curves in the sample.
-
v)
From the analysis of Fig. 8, top panel, the small-to-large size ratio of Si grains along anomalous lines is correlated with the Si abundance (continuous line in Fig. 8); type C curves are more correlated (r = 0.73). The models predict Si abundances up to a hundred times lower than solar values.
Compared with the properties of the environments where other types of lines of sight occur, the properties typical of C types can, on average, be summarized as indicated below and reported in Table 5, where the mean values and their errors are in the same units as in Table 4, and N indicates WD normal curves:
-
1.
The small-to-large size ratio of carbonaceous grains is almostsix times higher than the average value found for normal curvesand is comparable to the average value of type Aand B curves.
-
2.
The small-to-large size ratio of silicon grains is smaller than the average value of A types and almost three times larger than that of type B curves, although it is like that of normal curves.
-
3.
The average amount of carbon that condenses into grains is slightly lower than the expected Galactic abundance trapped into grains, 0.7 − 0.6; that is the value of normal curves as derived here from the same grain models. Type A reaches the maximum value allowed, which is almost three times larger than that of B curves displaying the lower value.
-
4.
All the anomalous curves have a Si abundance lower than that of normal curves; type C, in particular, has the lowest value.
Therefore, type C sight lines must contain, on average, dust abundances lower than the abundances trapped into the grains along normal lines, in particular of silicate grains, as well as small-to-large grain size ratios of carbonaceous dust larger than expected for normal curves. These properties are different from those expected for A and B curves. The former, in particular, correspond to sight lines with the highest abundances of carbonaceous dust and the latter ones to lines of sight with both the lowest carbon abundances and the lowest small-to-large grain size ratio of silicon dust, i.e., the largest Si grains.
The different properties of the dust locked into the grains along anomalous sight lines can be recovered by accounting for the violent nature of the interstellar medium. Shocks and grain-grain collisions should both destroy dust grains, so reducing the amount of the dust trapped in the grains, and modify the normal size distribution of the dust increasing the small-to-large grain size ratio, as discussed in the next section.
5. Discussion
Table 6 presents the values of the Fitzpatrick & Massa (1988, 1990) parameters (FM parameters in the following) of type C curves derived from our models, since a correct estimate of these parameters from only five UV color excesses is impossible.
The properties of our sample can then be compared with those of Valencic et al. (2004), the largest, homogeneous sample of Galactic extinction curves with known FM parameters and RV values available so far. Valencic et al. (2004) found that the CCM extinction law, with suitable RV values, applies for 93% of their 417 sight lines and that only four lines deviate by more than 3σ. They conclude that the physical processes that give rise to grain populations that have CCM-like exctinction dominate the interstellar medium.
Sixteen of the curves considered here were studied by Valencic et al. (2004), five belonging to the 3δ sample (HD 14357, HD 37061, HD 164492, HD 191396, BD + 57 252) and eleven to the 2δ sample (HD 54439, HD 96042, HD 141318, HD 149452, HD 152245, HD 168137, HD 248893, HD 252325, BD + 59 2829, BD + 62 2154, and BD + 63 1964). By comparing their parameterized UV extinction curves at the five ANS wavelengths with our ones, we find meaningful differences, i.e., larger than three σr at one wavelength or more, for all the common curves of the 3δ sample, unless for BD + 57 252 which closely agrees with our data. For the sight lines belonging to the 2δ sample, three curves (i.e., HD 168137, HD 252325, and HD149452) show differences larger than two σr at four wavelengths, one curve (i.e., HD 248893) at two wavelengths and four curves (i.e., HD 152245, BD + 59 2829, BD + 62 2154, and BD + 63 1964) at one wavelength. That of HD 96042 closely agrees with our data, and the remaining curves, i.e., HD 54439 and HD 141318, show only differences lower than two σr at one wavelength.
We note, however, that the spectral type and luminosity class of Valencic et al. (2004) are based on spectral properties in the UV rather than in the visible spectral range as in Savage et al. (1985); moreover the color excesses used by Valencic et al. (2004) are derived from IUE (International Ultraviolet Explorer) spectra using the pair method, whereas Savage et al. (1985) used the ANS photometry and intrinsic colors by Wu et al. (1980) described in Sect. 2.
Figure 9 compares the FM parameters of sixteen common sight lines here together with those (eight) in Paper I.
Average properties of the dust locked up into the grains of WD extinction models.
FM parameters of type C anomalous curves.
 |
Fig. 9 Open circles and stars (black) show the FM parameters of sixteen extinction curves derived from our best-fit dust models in Sect. 3 together with those of eight curves in Paper I, respectively; asterisks (red) are for the same curves by Valencic et al. (2004); continuous lines show the relations derived by Valencic et al. (2004, see their Table 6). |
5.1. The FM parameterization
In the following, we define 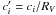 for
i = 2, 3, and 4,
for
i = 2, 3, and 4,  , and
xo and γ to be the same, to compare our
results with those of Valencic et al. (2004). The
data in Table 6 concern the parameterization in
terms of the normalized color excesses, i.e.,
κ(λ) = E(λ − V)/E(B − V),
whereas the primed symbols, i.e.,
, and
xo and γ to be the same, to compare our
results with those of Valencic et al. (2004). The
data in Table 6 concern the parameterization in
terms of the normalized color excesses, i.e.,
κ(λ) = E(λ − V)/E(B − V),
whereas the primed symbols, i.e., 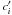 , are in terms of
A(λ)/AV.
Figures 10 − 12, compare the FM parameters of all our anomalous curves with both the FM
parameters derived from WD CCM curves (Sect. 3), and the sample of Valencic et al. (2004, their Table 5). Figures 10 − 12 show the relations
between the different parameters. Relationships with (anti)/co-relation index,
r, larger than (−)0.4 are reported in Table 7 for WD normal CCM curves, in Table 8 for C types, and in Table 9 for all the
anomalous sight lines.
, are in terms of
A(λ)/AV.
Figures 10 − 12, compare the FM parameters of all our anomalous curves with both the FM
parameters derived from WD CCM curves (Sect. 3), and the sample of Valencic et al. (2004, their Table 5). Figures 10 − 12 show the relations
between the different parameters. Relationships with (anti)/co-relation index,
r, larger than (−)0.4 are reported in Table 7 for WD normal CCM curves, in Table 8 for C types, and in Table 9 for all the
anomalous sight lines.
Looking at Figs. 10 − 12 important agreements with the results of Valencic et al. (2004) are clearly evident, as well as similar trends as the WD normal curves. These points indicate that dust models of anomalous curves, which most closely fit ANS data, are not biased by the low resolution of these data. In particular:
 |
Fig. 10 Black points show the FM parameters of extinction curves in Valencic et al. (2004); open circles (green) are the FM parameters of C type anomalous curves as derived from our models (see Sect. 3), (red) stars and (blue) triangles are the same of A and B types, and (cyan) open squares of WD CCM models (see text); black continuous lines are the relationships in Table 9 with r > 0.50, (cyan) dashed lines are the same for WD CCM curves (Table 7). |
 |
Fig. 11 FM parameters of our extinction curves compared with the sample of Valencic et al. (2004); symbols are as in the previous figure; dotted lines in the bottom bottom panel are correlations for A and B types (Paper I). |
 |
Fig. 12 FM parameters of all our curves compared with the sample of Valencic et al. (2004); symbols are as in Fig. 10. |
-
i)
The correlation between c
 ,
the bump height, and 1/RV (Fig. 10) for the whole sample exhibits the same slope
as both the WD normal curves (Table 7) and
the sample of Valencic et al. (2004), which
has the same correlation index as our sample (slope 3.48 ± 0.24, and dispersion
0.25). Each type of anomalous curve indeed obeys a different relation: B curves show
the stronger correlation index (r = 0.99) and the steeper slope
(6.77 ± 0.46); A curves have an intermediate correlation index,
r = 0.64, but the lower slope, 2.10 ± 0.64.
,
the bump height, and 1/RV (Fig. 10) for the whole sample exhibits the same slope
as both the WD normal curves (Table 7) and
the sample of Valencic et al. (2004), which
has the same correlation index as our sample (slope 3.48 ± 0.24, and dispersion
0.25). Each type of anomalous curve indeed obeys a different relation: B curves show
the stronger correlation index (r = 0.99) and the steeper slope
(6.77 ± 0.46); A curves have an intermediate correlation index,
r = 0.64, but the lower slope, 2.10 ± 0.64. -
ii)
Γ, the full width at half maximum (FWHM) of the bump, spans a large range of values by changing 1/RV as the sample of Valencic et al. (2004), perhaps reflecting a wide range of environments (Cardelli & Clayton 1991). No correlation is found for our sample as well as each anomalous type, unlike WD CCM models.
-
iii)
For the whole sample of anomalous curves, c
 ,
the far-UV (FUV) non-linear rise, and
1/RV correlate with a lower
correlation index than WD normal curves but have almost the same slope; B types have
a stronger correlation (r = 0.87) than C types, whereas A types
display any correlation (r = − 0.20). The sample of Valencic et al. (2004) shows a weaker
correlation, r = 0.38, and a higher slope, 0.51 ± 0.06, than our
findings for the total sample.
,
the far-UV (FUV) non-linear rise, and
1/RV correlate with a lower
correlation index than WD normal curves but have almost the same slope; B types have
a stronger correlation (r = 0.87) than C types, whereas A types
display any correlation (r = − 0.20). The sample of Valencic et al. (2004) shows a weaker
correlation, r = 0.38, and a higher slope, 0.51 ± 0.06, than our
findings for the total sample. -
iv)
The correlation between
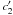 and
and
 (Fig. 11) illustrate the tight constraints
of the linear components of the extinction. The whole sample of anomalous curves is
more strongly correlated (Table 9) than
type C curves (Table 8). Their slope agrees
within the errors with the findings of Valencic
et al. (2004, their Table 6) but is steeper than that derived from WD CCM
models, at more than three times the error. As discussed in the previous section,
this difference is a consequence of the smaller amount of dust grains with normal
and large sizes, which affects the optical portion of the extinction curve of
anomalous sight lines compared to normal lines.
Table 7
(Fig. 11) illustrate the tight constraints
of the linear components of the extinction. The whole sample of anomalous curves is
more strongly correlated (Table 9) than
type C curves (Table 8). Their slope agrees
within the errors with the findings of Valencic
et al. (2004, their Table 6) but is steeper than that derived from WD CCM
models, at more than three times the error. As discussed in the previous section,
this difference is a consequence of the smaller amount of dust grains with normal
and large sizes, which affects the optical portion of the extinction curve of
anomalous sight lines compared to normal lines.
Table 7Relations between FM parameters of WD CCM curves.
Table 8Relations between FM parameters of type C anomalous curves.
Table 9Relations between FM parameters of all the anomalous curves.
-
v)
The parameters
 and
and
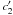 do not
correlate (r = 0.17) for the whole sample of anomalous curves, in
agreement with the findings of Valencic et al.
(2004, and references therein). Thus, the carriers of the FUV non-linear
rise are not the same as the optical linear rise. For WD CCM curves, these
parameters, indeed, are correlated. A weak correlation arises for C types
(Table 8).
do not
correlate (r = 0.17) for the whole sample of anomalous curves, in
agreement with the findings of Valencic et al.
(2004, and references therein). Thus, the carriers of the FUV non-linear
rise are not the same as the optical linear rise. For WD CCM curves, these
parameters, indeed, are correlated. A weak correlation arises for C types
(Table 8). -
vi)
Our results between
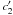 and
γ (r = − 0.31) agree with those of Valencic et al. (2004, and references therein)
who do not find any correlation. For WD CCM models, these parameters are
anti-correlated, wider bumps are found in extinction curves with weaker linear
rises.
and
γ (r = − 0.31) agree with those of Valencic et al. (2004, and references therein)
who do not find any correlation. For WD CCM models, these parameters are
anti-correlated, wider bumps are found in extinction curves with weaker linear
rises. -
vii)
For the whole sample of anomalous curves, we find the same correlation between
 and
γ as that of Valencic et al.
(2004) (Table 9), with a correlation
index slightly lower than theirs (their Table 6, r = 0.58). As the
bump FWHM increases, this means that the bump strength also increases. The C types
display a tighter correlation with a steeper slope than the whole sample here. Jenniskens & Greenberg (1993) attributed
this relation, at least partly, to the fitting procedure whereas, following Fitzpatrick & Massa (1988), these
parameters are truly related in some way. WD CCM curves span a shorter range of
γ and
and
γ as that of Valencic et al.
(2004) (Table 9), with a correlation
index slightly lower than theirs (their Table 6, r = 0.58). As the
bump FWHM increases, this means that the bump strength also increases. The C types
display a tighter correlation with a steeper slope than the whole sample here. Jenniskens & Greenberg (1993) attributed
this relation, at least partly, to the fitting procedure whereas, following Fitzpatrick & Massa (1988), these
parameters are truly related in some way. WD CCM curves span a shorter range of
γ and  values,
which are anti-correlated.
values,
which are anti-correlated. -
viii)
There is almost no correlation between
 and
and
 (Fig. 12) for both the whole sample
(r = 0.24) and type C curves (r = 0.25), as well
as for the sample of Valencic et al. (2004)
(r = 0.31), whereas the correlation is strong for WD CCM curves.
As discussed in Paper I, A types are weakly
anti-correlated (r = − 0.56) and B types are strongly correlated
(r = 0.92).
(Fig. 12) for both the whole sample
(r = 0.24) and type C curves (r = 0.25), as well
as for the sample of Valencic et al. (2004)
(r = 0.31), whereas the correlation is strong for WD CCM curves.
As discussed in Paper I, A types are weakly
anti-correlated (r = − 0.56) and B types are strongly correlated
(r = 0.92).
Therefore, looking at the same figures, several important differences arise between our sample and that of Valencic et al. (2004):
-
i)
There is a weak relation betweenxo, the bump position (μm-1), and 1/RV that is stronger for type C curves, at variance with the results of both Valencic et al. (2004) and WD CCM models (r = 0.31).
-
ii)
For the whole sample of anomalous curves,
 and
γ are anti-correlated in the sense that a broader bump is found
along sight lines with a smaller FUV non-linear rise; by considering only type A
curves, the anti-correlation index increases (r = − 0.87),
whereas, by considering only C types, the anti-correlation index decreases
(Table 8). No correlation is found by Valencic et al. (2004), while Carnochan (1986), Fitzpatrick & Massa (1988), and Jenniskens & Greenberg (1993) obtained an opposite trend, in the
sense that a wider bump is found along sight lines with a larger FUV rise. We note
that WD CCM curves show a very similar trend as anomalous curves, although with a
steeper slope and a higher anti-corelation index. This finding cannot be ascribed to
the coarser wavelength sampling of the ANS data since a similar trend arises from
dust models fitting complete extinction curves. This is provided by the different
dust components that play the job in our models.
and
γ are anti-correlated in the sense that a broader bump is found
along sight lines with a smaller FUV non-linear rise; by considering only type A
curves, the anti-correlation index increases (r = − 0.87),
whereas, by considering only C types, the anti-correlation index decreases
(Table 8). No correlation is found by Valencic et al. (2004), while Carnochan (1986), Fitzpatrick & Massa (1988), and Jenniskens & Greenberg (1993) obtained an opposite trend, in the
sense that a wider bump is found along sight lines with a larger FUV rise. We note
that WD CCM curves show a very similar trend as anomalous curves, although with a
steeper slope and a higher anti-corelation index. This finding cannot be ascribed to
the coarser wavelength sampling of the ANS data since a similar trend arises from
dust models fitting complete extinction curves. This is provided by the different
dust components that play the job in our models. -
iii)
The parameters
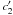 and
and
 do not
correlate for the whole sample of anomalous curves (r = − 0.05) as
well as for C types (r = 0.06), at variance with the results of
Valencic et al. (2004, their Table 6,
r = 0.49 and with those of WD normal curves. However, when
considering separately type A and B curves good correlations are found, though with
very different slopes (Paper I). In
particular, looking at Fig. 11, A and B curves
outline the lower and upper limits of the region where C curves are superimposed on
normal ones. The correlation occurring separately for A and B types suggests that
some fraction of the linear rise is associated with the bump (Carnochan 1986) but in a different proportion for these types, as
discussed in Paper I. The C type curves,
characterized by properties of their grain populations of values in-between those of
A and B types, as outlined in the previous section, do not have the same proportion
of grains contributing to the bump and to the linear rise, thus do not correlate.
do not
correlate for the whole sample of anomalous curves (r = − 0.05) as
well as for C types (r = 0.06), at variance with the results of
Valencic et al. (2004, their Table 6,
r = 0.49 and with those of WD normal curves. However, when
considering separately type A and B curves good correlations are found, though with
very different slopes (Paper I). In
particular, looking at Fig. 11, A and B curves
outline the lower and upper limits of the region where C curves are superimposed on
normal ones. The correlation occurring separately for A and B types suggests that
some fraction of the linear rise is associated with the bump (Carnochan 1986) but in a different proportion for these types, as
discussed in Paper I. The C type curves,
characterized by properties of their grain populations of values in-between those of
A and B types, as outlined in the previous section, do not have the same proportion
of grains contributing to the bump and to the linear rise, thus do not correlate.
Hence, anomalous curves exhibit bump properties, i.e., bump width, bump height, bump
strength, 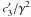 , and bump
position, that are strongly correlated whereas the same properties are independent of the
linear rise
, and bump
position, that are strongly correlated whereas the same properties are independent of the
linear rise 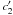 . Neither WD CCM
models, nor the sample of Valencic et al. (2004)
show any correlation with the bump position. Moreover, the bump height,
. Neither WD CCM
models, nor the sample of Valencic et al. (2004)
show any correlation with the bump position. Moreover, the bump height,
 correlates with the
linear rise,
correlates with the
linear rise, 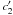 , for both the
sample of Valencic et al. (2004) and WD CCM models
(Table 7), though with different slopes, showing
that bump properties are driven by different dust components, in contrast to what happens
for anomalous curves.
, for both the
sample of Valencic et al. (2004) and WD CCM models
(Table 7), though with different slopes, showing
that bump properties are driven by different dust components, in contrast to what happens
for anomalous curves.
WD models of normal curves show a good correlation between the bump area,
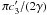 , and the FUV non-linear
rise, indicating that the same grain populations are implied by these features, whereas C
type curves show a weak correlation, which becomes weaker when we consider the whole
sample of anomalous curves (r = 0.40), since A types do not correlate
(r = − 0.28).
, and the FUV non-linear
rise, indicating that the same grain populations are implied by these features, whereas C
type curves show a weak correlation, which becomes weaker when we consider the whole
sample of anomalous curves (r = 0.40), since A types do not correlate
(r = − 0.28).
Therefore, several extinction properties of type C anomalous curves differ from those of CCM curves computed with the same dust models and corresponding to the same RV values, showing that mechanisms working in the environments of anomalous curves are different from those in the environments of normal curves.
5.2. Insight into environmental conditions
The results here derived from dust grain models (Weingartner & Draine 2001; Draine & Li 2007) show that the dust-to-gas ratios predicted for our sample are lower than the average Galactic value (Sect. 4). A types, in particular, have the largest, average value of such a ratio, whereas C types the lowest, average value. This trend is a consequence of the under-abundance of Si grains, which, for A types, is on average 1.5 times less than that of normal, CCM curves computed with the same grain models. However, it is at least three times greater than that of type C curves (Table 5). Moreover, the anomalous behavior of type C curves is driven by a larger population of small grains than the normal population, i.e., that characterizing lines of sight with extinction properties similar to those of CCM curves.
Many theoretical studies have faced the problem of the influence of shock waves on grains and their size distributions (Jones 2009a,b; and Draine 2009, for a review). As much as 5% − 15% of the initial grain mass (a ≥ 0.005 μm) may end up in very small fragments with a ≃ .0014 μm in shock waves expanding in a warm interstellar medium with shock velocities between 50 and 200 km s-1 (Jones et al. 1996). High velocity shocks affect grains through sputtering reducing the number of small particles, while in shocks with lower velocities grain-grain collisions alter the size distribution by increasing the small-to-large grain size ratio (Jones 2005). Following Cowie (1978), silicate grains may almost be destroyed by velocity shocks higher than ≃ 80 km s-1, while graphite grains need to have velocities higher than 100 km s-1. Jones et al. (1996) found that, for a shock velocity of 100 km s-1, the percentage of the initial mass of silicate grains destroyed can increase from 18% to 37% by increasing the average density of the pre-shock gas, n0, from 0.25 to 25 cm-3; for the same conditions, the percentage of the initial mass of carbonaceous grains destroyed increases from 7% to 13%. Detailed descriptions of the various grain destruction mechanisms and grain lifetime in the interstellar medium were presented by Jones et al. (1996) and Jones (2004). Moreover, for shocks with high velocities, the destruction of silicate grains by sputtering can reduce the depletion of Si (Barlow & Silk 1977). Guillet et al. (2009) found that silicon dust is destroyed in J-type shocks slower than 50 km s-1 by vaporisation not sputtering.
To gather information on the physical nature and the behavior of grains, the knowledge of the environments crossed by the sightlines is essential as the shape of the extinction curves. Unfortunately, the knowledge of the environmental properties is advancing slowly, since various relevant data are still not available for many sightlines, as for the column density of the different gas constituents and the depletion of the most important chemical elements. However, for several anomalous lines of sight analyzed in Paper I, of A and B types, there is convincing evidence that their environments have been processed by shock waves. Similar conditions are reported in the literature for some lines of sight of C type that have been here analyzed, as summarized in the following.
Multi-object spectroscopy toward h e χ Persei open clusters (Points et al. 2004) revealed the great complexity of the interstellar Na I absorption in the Perseus arm gas. Velocities from −75 down to −20 km s-1, are typical of this region. The intermediate velocity (−50 km s-1) component revealed in the south region of χ Persei, to which HD 14357 belongs, corresponds to an intervening interstellar cloud (Points et al. 2004).
HD 37061 is a translucent sight line (van Dishoeck & Black 1989) that crosses M 43, an apparently spherical HII region ionized by its star, HD 37061.
The triple star HD 28446 (DL Cam), with its Hα emission region, is located near the top of a ring of dust and small dark clouds in the Cam OB1 layer (Straižys & Laugalys 2007).
The sight line HD 73420 crosses the Vela OB1 association including the Vela X-1 binary pulsar system (Reed 2000).
The line of sight HD 152245 crosses a bright HII region, RCW 113/116, associated with several isolated molecular clouds located at the edge of evolved HII regions. They are thought to result from the fragmentation of the dense layer of material swept up by the expanding HII region (Urquhart et al. 2009).
Georgelin et al. (1996) report Hα and CO velocities respectively of −20 and −25 km s-1 in NGC 6193, to which HD 149452 belongs.
In the nebula Simeiz 55 to which HD 191396 belongs, high-velocity motions are reported (Esipov et al. 1996).
HD 248893 belongs to the Crab Nebula, which is a well-known supernova remnant (Wu 1981).
HD 252325 sight line crosses the compact HII region/molecular cloud complex G189.876 + 0.156, which has been squeezed by the stellar wind of massive stars (Qin et al. 2008).
HD 253327 is one of the ionizing stars of the compact HII region/molecular cloud complex G192.584 − 0.041, where a stellar wind is sweeping up the surrounding material (Qin et al. 2008).
The young open cluster NGC 6823, to which HD 344784 and BD + 23 3762 belong, at the edge of the Vulpecula rift molecular cloud, arises in a region where star formation is probably triggered by external shocks (Fresneau & Monier 1999).
The sight line BD + 62 338 crosses the most notable Galactic-plane high-velocity cloud complex, named complex H by Wakker & van Woerden (1991), where the velocity of the neutral hydrogen cloud relative to the local standard of rest is −201 km s-1 (Wakker 2001).
6. Conclusions
To enhance our knowledge of the extinction properties, more than sixty extinction curves taken from the same sample as defined in Paper I have been analyzed. In that paper, 785 UV extinction curves from the ANS catalog and IR data from 2MASS catalog (Sect. 2) were compared with standard CCM curves for a variety of RV values in the range 2 − 6. The curves were classified as normal if they provide an accurate fit to at least one of the CCM curves or anomalous otherwise. Eighty-four curves were retained that deviate by more than two σ from their standard CCM best-fit law at least at one UV wavelength (Eq. (2)). In this paper, sixty-four anomalous sight lines, defined as type C curves (Sect. 2), have been examined. For the majority of these lines, the corresponding best-fit CCM curve is always well above the UV data ( ≥ 2σ for at least one UV wavelength; Fig. 1, top panel). In Paper I, the extinction properties of twenty anomalous curves of different types, A and B type, have been studied. Type A curves are characterized by weaker bumps and steeper far-UV rises than expected from their standard best-fit CCM curve, that is worse, of course, by more than 2σ for at least one UV wavelength in each of them; type B curves show stronger bumps and smoother far-UV rises.
By fitting the observed curves with extinction curves provided by dust grain models, we have gained insight into the properties of the grains, the processes affecting them, and their relations with the environmental characteristics along selected lines of sight.
The selected sightlines represent the largest, homogeneous sample of extinction curves exhibiting large UV deviations from the CCM law, analyzed so far with dust models.
The models are calculated using the prescriptions of Weingartner & Draine (2001), i.e., their grain-size distributions and the most recent model updates (Draine & Li 2007), as in Paper I. Models of Weingartner & Draine (2001) are able to reproduce the observed wavelength-dependent extinction law of normal curves in the local MW for RV values 3.1, 4.0, and 5.5, in the Large Magellanic Cloud, and the Small Magellanic Cloud (SMC, bar region); moreover these models are also consistent with the observed IR emission from diffuse clouds in the MW and the SMC (Li & Draine 2002), and in several nearby galaxies (Liu et al. 2010, and references therein). This choice, the same as in Paper I, allows us to compare the results of our deviating curves with the same as normal curves in a self-consistent framework, and thus to recover the relative trends of the dust properties along selected sight lines overcoming the modeling uncertainties, which are widely discussed by Draine (2009). Since our anomalous sample extends to small RV values, down to 2.0, twenty-four dust models of CCM curves with RV smaller than 3.1 are built up with the same grain models to allow the comparison.
The results derived from models, of both CCM curves and anomalous lines of sight, are presented in terms of dust-to-gas ratios, abundance ratios, and small-to-large grain size ratios of the dust locked up into the grains following the recipes in Sect. 4. Results of Paper I are also revised to account for recent updating (Draine & Li 2007) (Sects. 3 and 4). Moreover, FM parameterization of all the dust models is performed in order to compare the results with the sample of Valencic et al. (2004).
Anomalous curves show bump properties, i.e., bump width, bump strength, bump height, and bump position that are strongly correlated with each other but all independent of the linear rise (Figs. 11 and 12). Neither the WD CCM models, nor the sample of Valencic et al. (2004) show any correlation with the bump position, and their bump height and linear rise are correlated, implying that the mechanisms working in the environments of anomalous curves differ from those in the environments of normal curves. Type C extinction curves require, indeed, dust abundances lower than normal sight lines, especially of silicate grains. Moreover, a number of small grains of carbonaceous dust larger than expected for normal curves with the same RV value is derived. These properties also differ from those expected for A and B types, not only in terms of abundances, but also of small-to-large grain size ratios. The B type curves, in particular, correspond to sight lines with the lowest small-to-large grain size ratios of silicate dust, compared also to WD CCM curves. Carbonaceous grains do not have clearly different values of this ratio between anomalous types. However, their ratios are almost six times larger than those of WD normal lines with the same RV.
The anomalous extinction properties analyzed here should arise along sight lines where shocks and high velocity flows perturb the physical state of the interstellar medium leaving their signature on the dust properties. Evidence of this nature has been reported in the previous section. Shocks and grain-grain collisions should modify the size distribution of the dust, increasing the number of small grains or, for relatively high velocity shocks, destroy them, reducing the amount of the dust trapped into the grains (Guillet et al. 2009; Jones 2009a,b; Draine 2009). As discussed in Paper I, to interpret the results derived for B anomalous lines of sight, we need to invoke both a lower small-to-large silicate grain size ratio and a larger ratio for carbonaceous ones, relative to normal curves. This can be achieved by a relatively high velocity shock that produces a sputtering or vaporisation process that is successful in destroying small silicate grains, while achieving only a partial destruction of carbonaceous ones, that increases the number of smaller particles of such a component. Along A sight lines slower velocity shocks than along B sight lines should be required to produce only a partial destruction of large size grains of both the dust components increasing the number of smaller particles. Moreover, type C extinction properties are indicative of environments where the abundance of dust trapped into the grains is about two times less than that characterizing type A and B environments, and three times less than that of normal, CCM lines.
Acknowledgments
We thank Anna Geminale who help us to extract our sample and an anonymous referee whose useful suggestions help us to improve the paper.
References
- Barbaro, G., Mazzei, P., Morbidelli, L., Patriarchi, P., & Perinotto, M. 2001, A&A, 365, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbaro, G., Geminale, A., Mazzei, P., & Congiu, E. 2004, MNRAS, 353, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Barlow, M. J., & Silk, J. 1977, ApJ, 215, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., & Clayton, G. C. 1991, AJ, 101, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carnochan, D. J. 1986, MNRAS, 219, 903 [NASA ADS] [Google Scholar]
- Clayton, G. C., Gordon, K. D., & Wolff, M. J. 2000, ApJS, 129, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, G. C., Wolff, M. J., Sofia, U. J., Gordon, K. D., & Misselt, K. A. 2003, ApJ, 588, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L. 1978, ApJ, 225, 887 [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2004, BAAS, 36, 1614 [NASA ADS] [Google Scholar]
- Draine, B. T. 2009, in Interstellar Dust from Astronomical Observations to Fundamental Studies, ed. F. Boulanger, C. Joblin, A. Jones, & S. Madden, EAS Publ. Ser., 35, 245 [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Esipov, V. F., Lozinskaya, T. A., Mel’Nikov, V. V., et al. 1996, Pis ma Astronomicheskii Zhurnal, 22, 571 [NASA ADS] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 1988, ApJ, 328, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 1990, ApJS, 72, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2009, ApJ, 699, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Fresneau, A., & Monier, R. 1999, AJ, 118, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Geminale, A., & Popowski, P. 2004, Acta Astron., 54, 375 [NASA ADS] [Google Scholar]
- Georgelin, Y. M., Russeil, D., Marcelin, M., et al. 1996, A&AS, 120, 41 [Google Scholar]
- Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillet, V., Jones, A., & Pineau Des Forêts, G. 2009, in Interstellar Dust from Astronomical Observations to Fundamental Studies, ed. F. Boulanger, C. Joblin, A. Jones, & S. Madden, EAS Publ. Ser., 35, 219 [Google Scholar]
- Jenniskens, P., & Greenberg, J. M. 1993, A&A, 274, 439 [NASA ADS] [Google Scholar]
- Jones, A. P. 2004, in Astrophysics of Dust, ed. A. N. Witt, G. C. Clayton, & B. T. Draine, ASP Conf. Ser., 309, 347 [Google Scholar]
- Jones, A. P. 2005, in ESA Special Publication, ed. A. Wilson, ESA Spec. Publ., 577, 239 [Google Scholar]
- Jones, A. 2009a, in Interstellar Dust from Astronomical Observations to Fundamental Studies, ed. F. Boulanger, C. Joblin, A. Jones, & S. Madden, EAS Publ. Ser., 35, 3 [Google Scholar]
- Jones, A. 2009b, in Interstellar Dust from Astronomical Observations to Fundamental Studies, ed. L. Pagani & M. Gerin, EAS Publ. Ser., 34, 107 [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., & Draine, B. T. 2001a, ApJ, 554, 778 [Google Scholar]
- Li, A., & Draine, B. T. 2001b, ApJ, 550, L213 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., & Draine, B. T. 2002, ApJ, 576, 762 [Google Scholar]
- Liu, G., Calzetti, D., Yun, M. S., et al. 2010, AJ, 139, 1190 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., & Cardelli, J. A. 1992, ApJ, 398, 610 [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Mattioda, A. L., Hudgins, D. M., & Allamandola, L. J. 2005, ApJ, 629, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzei, P., & Barbaro, G. 2008, MNRAS, 390, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, D. M., & Savage, B. D. 1981, ApJ, 248, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Papaj, J., Krelowski, J., & Wegner, W. 1991, MNRAS, 252, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Points, S. D., Lauroesch, J. T., & Meyer, D. M. 2004, PASP, 116, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, S., Wang, J., Zhao, G., Miller, M., & Zhao, J. 2008, A&A, 484, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reed, B. C. 2000, AJ, 119, 1855 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., Massa, D., Meade, M., & Wesselius, P. R. 1985, ApJS, 59, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Straižys, V., & Laugalys, V. 2007, Baltic Astron., 16, 167 [Google Scholar]
- Urquhart, J. S., Morgan, L. K., & Thompson, M. A. 2009, A&A, 497, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valencic, L. A., Clayton, G. C., & Gordon, K. D. 2004, ApJ, 616, 912 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1989, ApJ, 340, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Wakker, B. P. 2001, ApJS, 136, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Wakker, B. P., & van Woerden, H. 1991, A&A, 250, 509 [Google Scholar]
- Wegner, W. 2002, Baltic Astron., 11, 1 [Google Scholar]
- Wegner, W. 1994, MNRAS, 270, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Wesselius, P. R., van Duinen, R. J., de Jonge, A. R. W., et al. 1982, A&AS, 49, 427 [Google Scholar]
- Wu, C.-C. 1981, ApJ, 245, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, C., Gallagher, J. S., Peck, M., Faber, S. M., & Tinsley, B. M. 1980, ApJ, 237, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V., Dwek, E., & Arendt, R. G. 2004, ApJS, 152, 211 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Best-fit parameters of WD grain-size distributions of CCM curves with small RV values.
Average properties of the dust locked up into the grains of WD extinction models.
All Figures
 |
Fig. 1 Top panel: extinction data of HD 168785 (open circles) compared with our best-fit dust model (blue) continuous line (see Sect. 3), and the best-fit standard CCM curves corresponding to the whole spectral range, (black) dotted line, and to the IR data only, (red) dashed line. Bottom panel: extinction data of BD+58 310 (open circles) compared with our best-fit dust model (blue) continuous line, and the corresponding best-fit standard CCM curves with the same symbols as in the top panel. |
| In the text | |
 |
Fig. 2 Top panel: HD 39136, a normal curve of our sample (blue filled squares) whose best-fit standard CCM curve corresponds to RV = 2.85 ± 0.47 (red dotted line). The (magenta) long-dashed line is computed as the seventh model in Table 1 of Weingartner & Draine (2001), RV = 3.1, including latest updating (Draine & Li 2007); the (green) short-dashed line is our best-fit dust model: the fifth model in Table 3. Bottom panel: HD 12323, a normal curve of our sample (blue filled squares) whose best-fit standard CCM curve corresponds to RV = 2.30 ± 0.51 (red dashed line); the (green) continuous line is the best-fit dust model: the thirteenth model in Table 3. |
| In the text | |
 |
Fig. 3 Abundances of the dust locked up into the grains along our anomalous sight lines compared with the solar values (see text); (green) open circles are for type C curves, and (black) squares represent normal curves computed with WD parameters corresponding to seven different RV values, i.e. forty-nine models (Sect. 3). We also include the results of type A and B extinction models (Paper I), (red) stars and (blue) filled triangles, respectively, revised here to account for the latest model updates (Draine & Li 2007) (see text). |
| In the text | |
 |
Fig. 4 Behavior of the dust-to-gas ratio, ρd/ρH, normalized to the average Galactic value, 0.01, with the E(B − V)/NH ratio in units of 1.7 × 10-22 cm2 mag (Bohlin et al. 1978); symbols are as in the previous figure. The dashed line shows the relation for type C curves (Eq. (4)) and the continuous line for all the anomalous curves analyzed (Eq. (5)). |
| In the text | |
 |
Fig. 5 Top panel: RV values and the corresponding E(B − V)/NH ratios in units of 1.7 × 10-22 mag cm2, as derived from our WD dust grain models (see text); symbols are as in the previous figures; the dashed line connects the results of WD models of normal curves corresponding to seven different RV values (Sect. 3); the range in bold-face on the x-axis shows the expected deviation of Galactic curves (Bohlin et al. 1978). Bottom panel: behavior of the reddening E(B − V) (Savage et al. 1985) as a function of the predicted total hydrogen column density; continuous line shows the average Galactic relationship found by analyzing a large sample of sight lines whose HI and H2 column densities were measured: E(B − V)/N(H) = 1.7 × 10-22 mag cm2 (Bohlin et al. 1978); symbols are the same as in the previous figures. |
| In the text | |
 |
Fig. 6 Predicted small-to-large grain size ratios for carbonaceous and silicate grains of anomalous sight lines compared with the range spanned by WD models of CCM curves (continuous lines) for the same range of RV values. |
| In the text | |
 |
Fig. 7 Expected behavior of the small-to-large grain size ratio of silicate (top panel) and carbonaceous dust (bottom panel) versus RV values along anomalous sight lines compared with the same along CCM curves (open squares) computed with WD parameters (Sect. 3). Continuous line in the top panel corresponds to the relationship y = ( − 0.37 ± 0.03) + (3.30 ± 0.09), with dispersion 0.18 and anti-correlation index − 0.91, that applies to normal lines. Continuous line in the bottom panel shows the relationship for the whole sample of anomalous curves y = ( − 0.25 ± 0.03)x + (5.83 ± 0.09) with dispersion 0.19 and correlation index − 0.65. |
| In the text | |
 |
Fig. 8 Expected behavior of the small-to-large grain size ratio of silicate (top panel) and carbonaceous dust (bottom panel) versus the silicon and carbonaceous dust abundances, respectively, of anomalous sight lines; continuous line holds for Si grains of the whole sample y = (0.43 ± 0.06)x + ( − 1.55 ± 0.13) with dispersion 0.34 and correlation index 0.60. Symbols are the same as in the previous figures. |
| In the text | |
 |
Fig. 9 Open circles and stars (black) show the FM parameters of sixteen extinction curves derived from our best-fit dust models in Sect. 3 together with those of eight curves in Paper I, respectively; asterisks (red) are for the same curves by Valencic et al. (2004); continuous lines show the relations derived by Valencic et al. (2004, see their Table 6). |
| In the text | |
 |
Fig. 10 Black points show the FM parameters of extinction curves in Valencic et al. (2004); open circles (green) are the FM parameters of C type anomalous curves as derived from our models (see Sect. 3), (red) stars and (blue) triangles are the same of A and B types, and (cyan) open squares of WD CCM models (see text); black continuous lines are the relationships in Table 9 with r > 0.50, (cyan) dashed lines are the same for WD CCM curves (Table 7). |
| In the text | |
 |
Fig. 11 FM parameters of our extinction curves compared with the sample of Valencic et al. (2004); symbols are as in the previous figure; dotted lines in the bottom bottom panel are correlations for A and B types (Paper I). |
| In the text | |
 |
Fig. 12 FM parameters of all our curves compared with the sample of Valencic et al. (2004); symbols are as in Fig. 10. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


