| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201016118 | |
| Published online | 05 January 2011 | |
Letters to the Editor
Radial transport of refractory inclusions and their preservation in the dead zone
1
Laboratoire de Minéralogie et de Cosmochimie du Muséum (LMCM), CNRS
& Muséum National d’Histoire Naturelle, UMR 7202,
57 rue Cuvier,
75005
Paris,
France
e-mail: ejacquet@mnhn.fr
2
CEA, Irfu, SAp,
Centre de Saclay, 91191
Gif-sur-Yvette,
France
3
UMR AIM, CEA-CNRS-Univ. Paris VII, Centre de Saclay,
91191
Gif-sur-Yvette,
France
Received:
10
November
2010
Accepted:
21
December
2010
Calcium-aluminum-rich inclusions (CAIs) are the oldest solar system solids known in primitive meteorites (chondrites). They predate the other components by 1–2 Myr, and likely condensed within a short time interval, close to the Sun in the gaseous protoplanetary disk. Their preservation must counterbalance both the sunward drift caused by gas drag and the general inward motion of the entraining gas. We propose that an efficient outward transport of CAIs can be achieved by advection as a result of the viscous expansion of the disk, provided it is initially less than 10 AU in size, which we argue is plausible from both observational and theoretical points of view. Gas drag would stop this outward motion within 105 yr. However, by that time, a magnetically dead zone would have developed as gravitational instabilities fade away, which would trap CAIs for a significant fraction of the disk lifetime because of the reduced advection velocities. The dead zone would also prevent outward diffusion of subsequently condensed CAIs, contributing to their observed narrow age range. This preservation mechanism is independent of the outward transport scenario (before the dead zone formation) and a natural consequence of considering the source of turbulence in accretion disks.
Key words: accretion, accretion disks / instabilities / magnetohydrodynamics (MHD) / meteorites, meteors, meteoroids
© ESO, 2011
1. Introduction
Chondrites are the most primitive meteorites and provide an invaluable record of early solar system processes.They consist of millimeter-sized solids set in a fine-grained matrix, the most abundant of which are chondrules, silicate spherules produced by rapid melting and cooling of precursor material (e.g. Connolly & Desch 2004). Another noteworthy, albeit rarer component of chondrites are refractory inclusions,in particular submillimeter- to centimeter-sized calcium-aluminum-rich inclusions (CAIs). Thermodynamic calculations suggest that they condensed at temperatures of ~1400–1800 K from a gas of solar composition, although many have since melted and/or partially evaporated.With an age of ~4568 Myr (e.g. Bouvier et al. 2007), CAIs are the oldest known solar system solids. Intriguingly, primary formation of CAIs – at least those of CV chondrites – seems restricted to an interval of a few 104 yr (Bizzarro et al. 2004), while chondrule formation apparently began 1–2 Myr later and lasted ~2 Myr (Villeneuve et al. 2009). Despite some variation in CAI mineralogy among chondrite groups, similarities indicate that all CAIs formed in a common environment, likely close to the Sun, and were then transported to chondrite-forming regions (e.g. MacPherson 2005). Outward transport is also needed for two CAIs identified in dust returned from comet Wild 2 (e.g. Zolensky et al. 2006).
Transport and/or production mechanisms of CAIs must have been efficient because their mass fraction in some chondrites – a few percent, e.g. Hezel et al. (2008) – is comparable with what in situ condensation from a solar gas would have achieved. Moreover, these mechanisms must offset the sunward drift induced by gas drag on solids (Weidenschilling 1977) and the general inward motion of accreting gas, which partially entrains the solids. These combined phenomena typically entail a drift into the Sun within a few 105 yr for millimeter-sized bodies.
Proposed CAI transport scenarii either involve jets such as the X-Wind model (Shu et al. 2001), or operate solely inside the disk, e.g. with turbulent diffusion (e.g. Bockelée-Morvan et al. 2002; Cuzzi et al. 2003; Ciesla 2010), gravitational instabilities (GI; Boss 2004), or meridional circulation – an hypothetical outward flow around the midplane (e.g. Takeuchi & Lin 2002; Ciesla 2009). As originally formulated in the literature, jet models and meridional circulation should operate over most of the disk’s lifetime and thus would not reproduce per se the narrow age range of CV CAIs. Conversely, turbulent diffusion and GI would be efficient only in the early phases. As Cuzzi et al. (2003) emphasize, disk evolution definitely matters.
In this letter, we sketch a scenario (depicted in Fig. 1) of CAI transport and preservation in the disk: we adopt in Sect. 2 a small and massive initial disk (stage “A” in Fig. 1). As described in Sect. 3, viscous heating enables CAI condensation sufficiently far from the Sun to have CAIs entrained outward by disk expansion (stage “B”), before they are stopped by gas drag (stage “C”). As GI fade away, a dead zone forms, where the magnetorotational instability (MRI) does not operate, in which CAIs are effectively trapped for a few Myr until chondrite accretion (stage “D”) because of reduced advection velocity. This is the subject of Sect. 4. The model and its limitations are discussed in Sect. 5.
2. Disk model
 |
Fig. 1 Cartoon of the proposed scenario: CAIs form in an initially compact and massive disk A), which undergoes viscous expansion, entraining CAIs outward B), building up a leaky reservoir that is eventually released at large heliocentric distances C), while a dead zone emerges and traps CAIs until chondrite accretion D). |
Observations of class 0 objects have not yet unambiguously identified disks, suggesting that many disks may have begun by being very compact (Maury et al. 2010; Hennebelle & Ciardi 2009, and references therein). The lower range of plausible values of the precollapse cloud’s rotation velocity and size actually allow a centrifugal radius – the maximum stellocentric distance where infalling material lands on the equatorial plane – less than ~10 AU (Pickett et al. 1997; Zhu et al. 2010). Hydrodynamical simulations of protostellar collapse by Tscharnuter et al. (2009) result within ~104 yr in the buildup of a compact disk with a hot inner region extending to 4 AU. Moreover, magnetic braking during the collapse has been shown to be able to remove angular momentum efficiently enough to allow small disk sizes, depending on the relative inclination between angular momentum and the magnetic field threading the cloud (Hennebelle & Fromang 2008; Hennebelle & Ciardi 2009).
We therefore consider an early epoch where the disk size is a few AU, and adopt, for
greater definition, the surface density profile of the self-similar model taken from Lynden-Bell & Pringle (1974), similarly to Cuzzi et al. (2003): 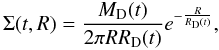 (1)with
MD(t) and
RD(t) the disk mass and characteristic
radius, respectively, at time t. This model assumes that the viscosity
(1)with
MD(t) and
RD(t) the disk mass and characteristic
radius, respectively, at time t. This model assumes that the viscosity
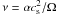 (with
cs the isothermal sound speed, Ω the Keplerian angular
velocity and α a dimensionless parameter) is time-independent
and proportional to the heliocentric distance R, and therefore may
be written as
(with
cs the isothermal sound speed, Ω the Keplerian angular
velocity and α a dimensionless parameter) is time-independent
and proportional to the heliocentric distance R, and therefore may
be written as 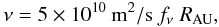 (2)with
fν a dimensionless factor, and
RAU the heliocentric distances expressed in AU. In the disk
outer regions dominated by the irradiation temperature (here
∝ R−1/2, with nominal
Tirr(1 AU) = 280K), our nominal
fν = 1 corresponds to a constant
α = 10-2. RD increases linearly
with time and satisfies
(2)with
fν a dimensionless factor, and
RAU the heliocentric distances expressed in AU. In the disk
outer regions dominated by the irradiation temperature (here
∝ R−1/2, with nominal
Tirr(1 AU) = 280K), our nominal
fν = 1 corresponds to a constant
α = 10-2. RD increases linearly
with time and satisfies 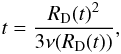 (3)the origin of times being a
mathematical singularity where all mass resides at the center. Angular momentum conservation
implies that
(3)the origin of times being a
mathematical singularity where all mass resides at the center. Angular momentum conservation
implies that 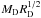 is constant. We take a nominal
is constant. We take a nominal 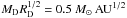 , a
reasonable value because, in evolved phases, the disk, whose radius is
>102 AU, may be expected to have a mass larger than
that of the “minimum mass solar nebula” (MMSN), 0.01–0.02 M⊙
(Hayashi 1981). Moreover, one-zone models of
embedded accretion disks by Kratter et al. (2008)
yield a disk-to-star mass ratio of a few tenths during the infall phase.
, a
reasonable value because, in evolved phases, the disk, whose radius is
>102 AU, may be expected to have a mass larger than
that of the “minimum mass solar nebula” (MMSN), 0.01–0.02 M⊙
(Hayashi 1981). Moreover, one-zone models of
embedded accretion disks by Kratter et al. (2008)
yield a disk-to-star mass ratio of a few tenths during the infall phase.
It is important to note, based on Eq. (3), that within ~1 Myr the disk, though initially small, will attain 102–103 AU as observed for class II objects.
3. Outward transport via viscous expansion
In the self-similar model, the vertically averaged radial gas velocity is (Lynden-Bell & Pringle 1974) 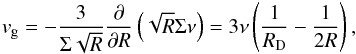 (4)where the second equality
uses the surface density profile given by Eq. (1). Beyond the turnover radius
Rswitch = RD/2,
vg is outward (positive).
(4)where the second equality
uses the surface density profile given by Eq. (1). Beyond the turnover radius
Rswitch = RD/2,
vg is outward (positive).
In the inner disk, viscous dissipation generates a contribution to the local temperature
that dominates that of irradiation by the Sun. Using Chambers
(2009)’s formulae, but sticking to the prescribed viscosity profile given by
Eq. (2), the former is
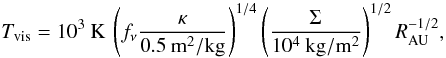 (5)with κ the
(constant) opacity. Initially, as shown in Fig. 2, the
“CAI factory” (Cuzzi et al. 2003) extends beyond
Rswitch, allowing CAIs to be advected outward from where they
condensed (stage “B” in Fig. 1) until
Rswitch exits the CAI factory on a timescale of
104−105 yr (see Fig. 2). This
alone would account for the narrow age range of CV CAIs.
(5)with κ the
(constant) opacity. Initially, as shown in Fig. 2, the
“CAI factory” (Cuzzi et al. 2003) extends beyond
Rswitch, allowing CAIs to be advected outward from where they
condensed (stage “B” in Fig. 1) until
Rswitch exits the CAI factory on a timescale of
104−105 yr (see Fig. 2). This
alone would account for the narrow age range of CV CAIs.
The CAIs cannot be entrained arbitrarily far, however. The gas drag in the Epstein regime
indeed induces a drift with respect to the gas (e.g. Weidenschilling 1977): 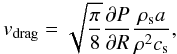 (6)with P,
ρ the gas pressure and density, and ρs,
a the CAI internal density and radius, respectively.
vdrag is inward and roughly inversely
proportional to ρ. Thus, for a given CAI size, at sufficiently
large heliocentric distances, vdrag dominates
vg and the net CAI velocities are directed inward. Therefore,
CAI velocities in the early phase are positive over a finite range of heliocentric distances
only, bounded by two “stagnation” points (i.e. heliocentric distances where the CAI velocity
is zero). After some expansion, these stagnation points merge and the velocities are
directed inward throughout the disk from that time onward. If, in the self-similar model,
the position of the outer stagnation point is taken to be stationary in time, this yields
the maximum transport range of solids Rmax and the corresponding
time tmax1:
(6)with P,
ρ the gas pressure and density, and ρs,
a the CAI internal density and radius, respectively.
vdrag is inward and roughly inversely
proportional to ρ. Thus, for a given CAI size, at sufficiently
large heliocentric distances, vdrag dominates
vg and the net CAI velocities are directed inward. Therefore,
CAI velocities in the early phase are positive over a finite range of heliocentric distances
only, bounded by two “stagnation” points (i.e. heliocentric distances where the CAI velocity
is zero). After some expansion, these stagnation points merge and the velocities are
directed inward throughout the disk from that time onward. If, in the self-similar model,
the position of the outer stagnation point is taken to be stationary in time, this yields
the maximum transport range of solids Rmax and the corresponding
time tmax1:
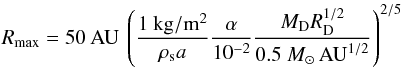 (7)
(7)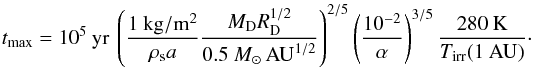 (8)For fiducial disk
parameters, solids can thus be transported outward for tens of AUs within ~105
yr. Because the CAIs must have departed from a sufficiently hot disk region, their transport
range may be somewhat smaller than Rmax (e.g. ~10 AU in
Fig. 2).
(8)For fiducial disk
parameters, solids can thus be transported outward for tens of AUs within ~105
yr. Because the CAIs must have departed from a sufficiently hot disk region, their transport
range may be somewhat smaller than Rmax (e.g. ~10 AU in
Fig. 2).
 |
Fig. 2 Space-time diagram of the self-similar model. Dashed lines mark the trajectory of CAIs with ρsa = 1 kg/m2 and the black continuous line indicates the locus of Rswitch. The MRI-inactive areas are shaded in blue (dead zone), with the 1500 K isotherm (a typical CAI condensation temperature) drawn as a continuous blue line. Regions prone to GI in the absence of viscous dissipation are shaded in red. Once the (GI-free) dead zone reaches a significant fraction of the disk mass, the disk model is no longer self-consistent, and disk evolution is expected to slow down, as is the sunward drift of CAIs in the dead zone. The conclusion is that CAIs can be transported to the dead zone before its formation. |
4. Preservation of CAIs in the dead zone
In the self-similar model the return to the Sun, which essentially follows the gas, is completed for t = 4.9tmax2, that is, largely before chondrite accretion. Although the estimates here are conservative, because they ignore random-walk turbulent motions (e.g. Cuzzi et al. 2003; Ciesla 2010), the problem is especially acute for centimeter-sized CAIs common in CV chondrites (with ρsa = 10–100 kg/m2). The purpose of this section is to show that the appearance of a dead zone, which slows down the inward motion of the solids, solves the preservation issue.
Indeed, thus far we have not addressed the question of the driver of accretion, and hence the maximum domain of validity of the model. These drivers are thought to result from GI and/or the MRI. The red zone in Fig. 2 shows the maximal domain (calculated ignoring heating by local turbulence) where GI-induced turbulence can occur, assuming a threshold value for the Toomre parameter Q ≡ Ωcs/πGΣ of Qc = 2 (see e.g. Kratter et al. 2008). Although GI may be important in the early phases, MRI-powered turbulence is believed to prevail after the disk has significantly expanded. The blue zone shows where neither temperature (below an activation threshold here fixed at 1500 K) nor cosmic rays (limited to an attenuation depth of 103kg/m2) yield the minimum ionization fraction required for the MRI (Gammie 1996). Thus, wherever the blue zone is not overlaid by the red one, α values assumed by the self-similar model (10-3−10-2) cannot be self-consistently sustained, and a dead zone, with reduced accretion, results within 104−105 yr at a few AU (stage “C” in Fig. 1). This is before the CAIs have returned to the Sun.
In the evolved stages of the disk (no longer captured by the self-similar model, because its simple α prescription breaks down), the inner edge of the dead zone will move inward to a fraction of an AU, while its outer edge will lie at tens of AU (e.g. Sano et al. 2000; Ilgner & Nelson 2006; Bai & Goodman 2009). The dead zone would then persist over most of the gas disk’s lifetime: Fromang et al. (2002) and Terquem (2008) found e.g. dead zones in steady α-disks for a wide parameter range, including mass accretion rates at the lower end (~10-9 M⊙/yr) of those of observed T Tauri objects (Hartmann et al. 1998).
Accretion is reduced in the dead zone, and the gas density is high enough to also reduce
vdrag (stage “D” in Fig. 1). Using Eqs. (4) and (6), the CAI drift timescale is 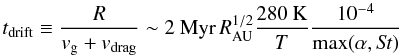 (9)The
Stokes number
St = πρsa/2Σ
is related to the gas drag and α to advection. Note that this general
order-of-magnitude estimate is independent of the previous history of the disk.
α would not exceed 10-4 in the dead zone (Fleming & Stone 2003) and the surface density
would likely be in the range
104−105kg/m2 (Terquem 2008), so that millimeter-sized bodies satisfy
St ≤ 10-4. This should ensure survival for a few Myr at a few
AU.
(9)The
Stokes number
St = πρsa/2Σ
is related to the gas drag and α to advection. Note that this general
order-of-magnitude estimate is independent of the previous history of the disk.
α would not exceed 10-4 in the dead zone (Fleming & Stone 2003) and the surface density
would likely be in the range
104−105kg/m2 (Terquem 2008), so that millimeter-sized bodies satisfy
St ≤ 10-4. This should ensure survival for a few Myr at a few
AU.
After the formation of the dead zone, the CAI production would essentially be confined to the inner active zone. Indeed, an important point is that the temperature of the thermal activation of the MRI is on the order that of CAI condensation. Beyond the inner edge of the dead zone, the temperature will drop significantly below this value because of the drop of the turbulence level. Because diffusion from inside this boundary would be negligible, CAIs formed after the dead zone appearance would not be sent to the chondrite-forming regions in significant amounts.
5. Discussion
Using viscous expansion of the disk to transport solids in general (Wehrstedt & Gail 2002; Garaud 2007; Hughes & Armitage 2010) or specifically CAIs (Ciesla 2010) – with the recognition that their observed age distribution is narrowed because CAI transport rapidly becomes inefficient –, is not new. However, the input parameters of the runs of Ciesla (2010) always placed the CAI formation region inside Rswitch and therefore required diffusion to send CAIs to the spreading zone. In Sect. 2 we argued that an initial disk even more compact than envisioned by Ciesla (2010) is conceivable and gave a prime role to advective transport. Its advantage is that the CAI-to-gas ratio would essentially retain its original order of magnitude, which seems required to account for the high mass fraction of CAIs in some chondrites. It would also explain the high proportion of crystalline silicates in comets (Wooden et al. 2005; Hughes & Armitage 2010). Finally, a small disk size would allow turbulent mixing to achieve a significant initial degree of isotopic (and chemical) homogeneity in it, as is generally observed in meteorites (e.g. Cassen & Summers 1983; Yang & Ciesla 2010). Regardless of the importance of advection, turbulent diffusion would help outward transport of CAIs and consequently, as far as the latter is concerned, the difference between this (very simplified) study and those of Bockelée-Morvan et al. (2002); Cuzzi et al. (2003); Ciesla (2010); Hughes & Armitage (2010), is quantitative, not qualitative, in nature. Because this model (or those listed just above) describes the origin and evolution of CAIs disk-wide, one prediction is that the key constraint of the restricted formation interval, hitherto drawn only from CV chondrites, should pertain to CAIs of most if not all chondrite groups.
We caution that infall should be taken into account in the future, although we ignored it in this study. This will require dedicated numerical simulations. Conceivably, outward expansion of the bulk of the disk beyond the centrifugal radius and appearance of the dead zone could be linked to a drop of the infall rate: matter supply would then be insufficient to sustain GI and would no longer overwhelm viscous-stress-driven flow past the centrifugal radius (e.g. Zhu et al. 2010). In their protostellar collapse simulations, Tscharnuter et al. (2009) also reported outward directed flows near the midplane in the hot inner disk, lasting a few millenia only (possibly because of their high assumed turbulence level), and mentioned the possible relevance for CAI formation.
At the end of Sect. 3 we observed that the self-similar model fails to preserve CAIs when extrapolated over 1 Myr. This seems a general property of simple α-models. Ciesla (2010) found the discrepancy with observed CAI abundance to be between one and two orders of magnitude. He also noted that lower values of α, while slowing down disk evolution, would also reduce CAI production because of the lower temperatures. Cuzzi et al. (2003) already noted this shortcoming and proposed that the inward drift of meter-sized migrators could maintain a 10–100-fold enhanced abundance of condensable matter above solar in the “CAI factory”, hereby compensating for their subsequent dilution in the nebula. However, this enhanced metallicity would yield partial pressures of oxygen in excess of those inferred from the Ti3 + /Ti4 + ratio in CAI pyroxene (Grossman 2010) unless the migrators entered the CAI factory with C/O ≳ 1 (see Eq. (24) in Grossman et al. 2008). This value lies far above that of the (chemically primitive) matrices of chondrites though and is consistent with the high end only of the range spanned by comet samples and interplanetary dust particles (e.g. Rietmeijer 1998; Sandford et al. 2008). Moreover, any enhancement would be limited by the amount of migrators in the outer disk (Ciesla 2010), in particular for relatively compact disks. Ciesla (2010) also argues that preferential settling of CAIs to the midplane could enhance their concentration in chondrites. With regard to the CAI drift timescale, it is unclear however when the low values of the surface densities (~102 kg/m2) he implies in his estimate, which are two orders of magnitude below the MMSN at a few AU, would hold, especially in conjunction with low turbulence levels.
Our point is that a solution to this problem naturally presents itself when the sources of
the turbulence that drives mass accretion are considered. Indeed, as pointed out in Sect. 4,
simple α-models are not self-consistent throughout the disk extent and the
evolution in the context of MRI- and/or GI-driven accretion. The formation of a dead zone is
a general, unavoidable feature of accretion disks (Zhu
et al. 2010): for instance, in a steady α-disk, the mass accretion
rate (Ṁ = 3πΣν) below which
Q right outside the inner MRI-active zone, evaluated with the passive
irradiation temperature, exceeds Qc is given by
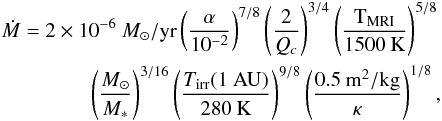 (10)which
is therefore a lower bound for the appearance of the dead zone in this case. Thus, the
preservation mechanism outlined in Sect. 4 is actually fairly independent of the compact
disk expansion scenario of Sect. 3. Ciesla (2010)
mentioned among alternative possibilities that a slowing of the disk evolution would explain
CAI survival; this study thus provides a way to realize this. That a dead zone blocks
diffusion from the inner active zone would also account for the restricted formation
interval of CAIs incorporated in chondrites, regardless of the dominating transport
mechanism (advection, diffusion...) before the dead zone formation. The presence of a dead
zone is also constrained by the Myr spread in age observed for chondrules (whose sizes are
similar to that of CAIs) from individual chondrites (e.g. Villeneuve et al. 2009) by virtue of Eq. (9). Finally, although we showed the necessity of the formation of the dead zone,
how this formation occurs has yet to be ascertained. Because the
viscosity drops outward around the inner boundary of the dead zone, a net
outward flow may be expected there according to the first equality in Eq. (4) – perhaps even independently of the
compactness of the disk –, before some steady state with uniformly inward accretion sets in.
Detailed numerical simulations of dead zone formation are definitely needed.
(10)which
is therefore a lower bound for the appearance of the dead zone in this case. Thus, the
preservation mechanism outlined in Sect. 4 is actually fairly independent of the compact
disk expansion scenario of Sect. 3. Ciesla (2010)
mentioned among alternative possibilities that a slowing of the disk evolution would explain
CAI survival; this study thus provides a way to realize this. That a dead zone blocks
diffusion from the inner active zone would also account for the restricted formation
interval of CAIs incorporated in chondrites, regardless of the dominating transport
mechanism (advection, diffusion...) before the dead zone formation. The presence of a dead
zone is also constrained by the Myr spread in age observed for chondrules (whose sizes are
similar to that of CAIs) from individual chondrites (e.g. Villeneuve et al. 2009) by virtue of Eq. (9). Finally, although we showed the necessity of the formation of the dead zone,
how this formation occurs has yet to be ascertained. Because the
viscosity drops outward around the inner boundary of the dead zone, a net
outward flow may be expected there according to the first equality in Eq. (4) – perhaps even independently of the
compactness of the disk –, before some steady state with uniformly inward accretion sets in.
Detailed numerical simulations of dead zone formation are definitely needed.
Acknowledgments
We thank Dr F. J. Ciesla for his constructive review that significantly improved the quality and the clarity of the manuscript.
References
- Bai, X., & Goodman, J. 2009, ApJ, 701, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Bizzarro, M., Baker, J. A., & Haack, H. 2004, Nature, 431, 275 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bockelée-Morvan, D., Gautier, D., Hersant, F., Huré, J., & Robert, F. 2002, A&A, 384, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boss, A. P. 2004, ApJ, 616, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, A., Blichert-Toft, J., Moynier, F., Vervoort, J. D., & Albarède, F. 2007, Geoch. Cosmoch. Acta, 71, 1583 [Google Scholar]
- Cassen, P., & Summers, A. 1983, Icarus, 53, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 2009, ApJ, 705, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, F. J. 2009, Icarus, 200, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, F. J. 2010, Icarus, 208, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Connolly, Jr., H. C., & Desch, S. J. 2004, Chemie der Erde/Geochemistry, 64, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Cuzzi, J. N., Davis, S. S., & Dobrovolskis, A. R. 2003, Icarus, 166, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Fleming, T., & Stone, J. M. 2003, ApJ, 585, 908 [NASA ADS] [CrossRef] [Google Scholar]
- Fromang, S., Terquem, C., & Balbus, S. A. 2002, MNRAS, 329, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Garaud, P. 2007, ApJ, 671, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Grossman, L. 2010, M&PS, 45, 7 [NASA ADS] [Google Scholar]
- Grossman, L., Beckett, J. R., Fedkin, A. V., Simon, S. B., & Cielsa, F. J. 2008, in Oxygen in the solar system, ed. G. J. MacPherson (MSA), 93 [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Progr. Theoret. Phys. Suppl., 70, 35 [CrossRef] [Google Scholar]
- Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Ciardi, A. 2009, A&A, 506, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hezel, D. C., Russell, S. S., Ross, A. J., & Kearsley, A. T. 2008, M&PS, 43, 1879 [NASA ADS] [Google Scholar]
- Hughes, A. L. H., & Armitage, P. J. 2010, ApJ, 719, 1633 [NASA ADS] [CrossRef] [Google Scholar]
- Ilgner, M., & Nelson, R. P. 2006, A&A, 445, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kratter, K. M., Matzner, C. D., & Krumholz, M. R. 2008, ApJ, 681, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- MacPherson, G. J. 2005, Treatise on Geochemistry, ed. Davis, A. M., Holland, H. D., & Turekian, K. K. (Elsevier B), 201 [Google Scholar]
- Maury, A. J., André, P., Hennebelle, P., et al. 2010, A&A, 512, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, B. K., Durisen, R. H., & Link, R. 1997, Icarus, 126, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Rietmeijer, F. 1998, in Planetary materials, ed. J. J. Papike (MSA), 2–01–2–95 [Google Scholar]
- Sandford, S. A., Messenger, S., DiSanti, M., Keller, L., & Altweg, K. 2008, Oxygen in the solar system, ed. G. J. MacPherson (MSA), 247–272 [Google Scholar]
- Sano, T., Miyama, S. M., Umebayashi, T., & Nakano, T. 2000, ApJ, 543, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Shang, H., Gounelle, M., Glassgold, A. E., & Lee, T. 2001, ApJ, 548, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T., & Lin, D. N. C. 2002, ApJ, 581, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Terquem, C. E. J. M. L. J. 2008, ApJ, 689, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Tscharnuter, W. M., Schönke, J., Gail, H., Trieloff, M., & Lüttjohann, E. 2009, A&A, 504, 109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villeneuve, J., Chaussidon, M., & Libourel, G. 2009, Science, 325, 985 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wehrstedt, M., & Gail, H. 2002, A&A, 385, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Wooden, D. H., Harker, D. E., & Brearley, A. J. 2005, in Chondrites and the Protoplanetary Disk, ed. A. N. Krot, E. R. D. Scott, & B. Reipurth, ASP Conf. Ser., 341, 774 [Google Scholar]
- Yang, L., & Ciesla, F. J. 2010, in Lunar and Planetary Institute Science Conference Abstracts, Lunar and Planetary Inst. Technical Report, 41, 1461 [Google Scholar]
- Zhu, Z., Hartmann, L., & Gammie, C. 2010, ApJ, 713, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Zolensky, M. E., Zega, T. J., Yano, H., et al. 2006, Science, 314, 1735 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Figures
 |
Fig. 1 Cartoon of the proposed scenario: CAIs form in an initially compact and massive disk A), which undergoes viscous expansion, entraining CAIs outward B), building up a leaky reservoir that is eventually released at large heliocentric distances C), while a dead zone emerges and traps CAIs until chondrite accretion D). |
| In the text | |
 |
Fig. 2 Space-time diagram of the self-similar model. Dashed lines mark the trajectory of CAIs with ρsa = 1 kg/m2 and the black continuous line indicates the locus of Rswitch. The MRI-inactive areas are shaded in blue (dead zone), with the 1500 K isotherm (a typical CAI condensation temperature) drawn as a continuous blue line. Regions prone to GI in the absence of viscous dissipation are shaded in red. Once the (GI-free) dead zone reaches a significant fraction of the disk mass, the disk model is no longer self-consistent, and disk evolution is expected to slow down, as is the sunward drift of CAIs in the dead zone. The conclusion is that CAIs can be transported to the dead zone before its formation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


