| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 15 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201015597 | |
| Published online | 29 November 2010 | |
Cross-calibration of the X-ray instruments onboard the Chandra, INTEGRAL, RXTE, Suzaku, Swift, and XMM-Newton observatories using G21.5–0.9⋆
1
Japan Aerospace Exploration Agency, Institute of Space and
Astronautical Science, 3-1-1
Yoshino-dai, Chuo-ku, Sagamihara, Kanagawa
252-5210,
Japan
e-mail: tsujimot@astro.isas.jaxa.jp
2
European Space Agency, European Space Astronomy
Centre, 28691
Villanueva de la Cañada,
Madrid,
Spain
3
Harvard-Smithsonian Center for Astrophysics,
MS-70, 60 Garden Street,
Cambridge, MA
02138,
USA
4
Department of Physics and Astronomy, University of
Leicester, Leicester
LE1 7RH,
UK
5
INAF, Istituto di Astrofisica Spaziale e Fisica
Cosmica, via del Fosso del
Cavaliere, 100
00133
Roma,
Italy
6
National Aeronautics and Space Agency, Goddard Space Flight
Center, Code 662, Laboratory for X-ray Astrophysics, Greenbelt, MD
20771,
USA
Received:
16
August
2010
Accepted:
14
September
2010
Context. For many years, X-ray astronomy missions have used the Crab nebula as a celestial calibration source for the X-ray flux and spectral shape. However, the object is often too bright for current and future missions equipped with instruments with improved sensitivity.
Aims. We use G21.5–0.9, a pulsar-wind nebula with a time-constant power-law spectrum and a flux of a few milli-Crab in the X-ray band, as a viable, fainter substitute to the Crab. Using this source, we conduct a cross-calibration study of the instruments onboard currently active observatories: Chandra ACIS, Suzaku XIS, Swift XRT, and XMM-Newton EPIC (MOS and pn) for the soft-band, and INTEGRAL IBIS-ISGRI, RXTE PCA, and Suzaku HXD-PIN for the hard band.
Methods. We extract spectra from all instruments and fit under the same astrophysical assumptions. We compare the spectral parameters of the G21.5–0.9 model: power-law photon index, H-equivalent column density of the interstellar photoelectric absorption, and flux in the soft (2–8 keV) or hard (15–50 keV) energy band.
Results. We identify systematic differences in the best-fit parameter values unattributable to statistical scatter of the data alone. We interpret these differences as due to residual cross-calibration problems. The differences can be as large as 20% and 9% for the soft-band flux and power-law index, respectively, and 46% for the hard-band flux. The results are plotted and tabulated as a useful reference for future calibration and scientific studies using multiple missions.
Key words: instrumentation: detectors / X-rays: individuals: G21.5 / 0.9
© ESO, 2010
1. Introduction
From the successful launch to the end of the mission, all X-ray observatories put tremendous effort into the flight calibrations of their instruments using celestial objects to test their response models and to monitor changes in their performance. Most such efforts have been made by each observatory independently from the others, using similar methodologies and often the same targets. For the purpose of facilitating communication and comparison of results among various calibration teams, an international consortium for instrumental cross-calibration was established, which is named the International Astronomical Consortium for High Energy Calibration (IACHEC)1.
As part of the IACHEC activities, we present the results of a comparison study of G21.5–0.9 using the currently active X-ray missions. The purpose of this paper is to compare the flux and spectral shape in the X-ray bandpass of this time-constant power-law source and to identify systematic differences among various instruments. The benefits for the community are two-fold: (1) the comparison result is useful for improving the calibration and interpretation of data from other celestial objects obtained by different instruments; (2) this study will be a basis to establish G21.5–0.9 as a viable flight calibration source for the X-ray flux and spectral shape, substituting the traditionally-used Crab nebula (Kirsch et al. 2005; Weisskopf et al. 2010), which is often too bright for contemporary and future instruments with improved sensitivity.
Participating missions for the comparison study are the Chandra X-ray Observatory (Weisskopf et al. 2002), the International Gamma-ray Astrophysics Laboratory (INTEGRAL, Winkler et al. 2003), the Rossi X-ray Timing Explorer (RXTE, Bradt et al. 1993), Suzaku (Mitsuda et al. 2007), Swift (Gehrels et al. 2004), and XMM-Newton (Jansen et al. 2001) observatories.
We use the following instruments: the Advanced CCD Imaging Spectrometer (ACIS, Garmire et al. 2003) onboard Chandra, the INTEGRAL Soft Gamma-Ray Imager (ISGRI, Lebrun et al. 2003) equipped with the IBIS telescope (Ubertini et al. 2003), the Proportional Counter Array (PCA, Jahoda et al. 1996) onboard the RXTE, the X-ray Imaging Spectrometer (XIS, Koyama et al. 2007) and the Hard X-ray Detector (HXD, Kokubun et al. 2007; Takahashi et al. 2007) PIN component onboard Suzaku, the X-Ray Telescope (XRT, Burrows et al. 2004) onboard Swift, and the European Photon Imaging Camera (EPIC) MOS-type (Turner et al. 2001) and pn-type (Strüder et al. 2001) CCDs onboard XMM-Newton. The dispersive X-ray spectrometers onboard Chandra and XMM-Newton are out of the scope of this study. Readers can also refer to Snowden (2002), in which two past missions ASCA (GIS and SIS) and ROSAT (PSPC) are compared with Chandra (ACIS) and XMM-Newton (EPIC) using the same object.
The instruments used in our study are divided into two groups: the soft-band instruments (Chandra ACIS, Suzaku XIS, Swift XRT, XMM-Newton EPIC-MOS and EPIC-pn) sensitive below ~10 keV and the hard-band instruments (INTEGRAL IBIS-ISGRI, RXTE PCA, and Suzaku HXD-PIN) sensitive above ~10 keV. The instruments with imaging capability are all the soft-band instruments with X-ray optics and INTEGRAL IBIS-ISGRI with a coded mask. All the soft-band instruments employ X-ray CCD devices, which have imaging and medium-resolution (E/ΔE ~ 30–50) spectroscopic capability.
The plan of this paper is as follows. In Sect. 2, we describe the X-ray properties of G21.5–0.9 and discuss the advantages and limitations of this source as a calibration source. In Sect. 3, we present the basic properties of the participating instruments, the data sets, and the processing of the data. In Sect. 4, we first set up the procedures for event extraction and spectral fitting, which are common among all the instruments as much as possible (Sect. 4.1). We then present the fitting results from each individual instrument and justify the common procedures. We also discuss the effect of some major systematic uncertainties arising from the procedures (Sect. 4.2). Finally, we assemble all spectra for joint fitting (Sect. 4.3). In Sect. 5, we compare the results among all the participating instruments and identify systematic cross-calibration uncertainties. We also compare the differences found in the present work with those in other studies. We summarize in Sect. 6.
2. Object: G21.5–0.9
Pulsar wind nebulae (PWNe) are a small class of supernova remnants with intrinsically bright non-thermal X-ray emission, including the prototypical Crab nebula, 3C 58, Kes 75, PSR B0540–69, PSR B1509–58, and G21.5–0.9. PWNe are suited for X-ray flux calibration due to their constant total X-ray flux over human time scales. The brightness and power-law index of the spectrum change spatially across a PWN, but the integrated spectrum can be represented by a single power-law in practice. Therefore, they can also be used for calibrating the spectral shape, i.e., the power-law index in X-ray photon spectra. Indeed, the Crab nebula has been used as a standard X-ray flux and spectral shape calibration source for decades.
G21.5–0.9 is a PWN powered by the pulsar PSR J1833–1034 with a period of 61.8 ms (Gupta et al. 2005; Camilo et al. 2006). The age and distance of the object are estimated as 870 yr (Bietenholz & Bartel 2008) and 4.8 kpc (Tian & Leahy 2008), respectively. The object is a bright X-ray emitter. The Einstein observatory resolved the object into several structures of different spatial scales (Becker & Szymkowiak 1981). The EXOSAT and Ginga satellites showed that the X-ray spectrum is represented by a power-law model (Davelaar et al. 1986; Asaoka & Koyama 1990), arguing for the PWN nature of this source.
G21.5–0.9 has several advantages over other PWNe as a celestial calibration source: (1) it is fainter than the Crab nebula by a factor of ~500, which places it in a reasonable flux range to match the dynamic ranges of contemporary and future missions; (2) it is compact in size for its distance and youth, mitigating the effects caused by spatial differences of mirror and detector responses; (3) it has a very simple circular distribution of brightness and spectral hardness, presumably because of the pole-on geometry, making the source and background extraction easy; (4) the spectrum is flatter than other PWNe, so it can be used to calibrate detectors over a wide range of energies including those above 10 keV; (5) the soft (<1 keV) photons contribute little to the spectrum due to a large interstellar extinction of ≳1022 cm-2. Therefore, the calibration uncertainty stemming from the accumulation of contaminating material on CCDs, which plagues both ACIS and XIS, can be decoupled; (6) no pulsation is confirmed in the X-ray band, which indicates that the spectrum does not change in pulse phase like the Crab nebula; (7) because of these properties, G21.5–0.9 has been used as a calibration source for Chandra, Swift, and XMM-Newton. We can exploit the wealth of existing data sets.
The source also has some limitations: (1) G21.5–0.9 is extended by ~3′ and is not adequate to calibrate dispersive spectrometers; (2) the object is located close to the Galactic plane with a rich population of bright X-ray binaries, which makes source confusion non-negligible for instruments without imaging capability (PCA and HXD-PIN); (3) the spectrum suffers a large interstellar extinction, leaving few photons in the energy band below ~1 keV. Soft-band calibration sources are needed to complement G21.5–0.9, which is covered by other IACHEC studies (e.g., Beuermann 2006; Plucinsky et al. 2008).
 |
Fig. 1 Chandra ACIS-S3 image of G21.5–0.9. The spatial components and the nearby source SS 397 are labeled. The source extraction region of 165″ is indicated by the solid circle. |
Several spatial structures are known in the X-ray image. Figure 1 shows a Chandra ACIS-S3 view of the object. At the center, the “core” is found (Slane et al. 2000), which is the neutron star with a power-law spectrum. The X-ray pulsation is yet to be found from the pulsar (La Palombara & Mereghetti 2002; Camilo et al. 2006). The core is actually resolved with a size of ~2″, possibly representing the pulsar wind termination shock (Slane et al. 2000). Surrounding this is the “plerion”, ~30″ in size, which is a synchrotron nebula. The spectral hardness decreases as the distance from the core increases, indicating the synchrotron loss of high energy electrons as a function of energy. A larger, fainter structure, the “halo”, is found around the plerion, which is ~150″ in size. The halo also shows a power-law spectrum with hardness decreasing as distance increases (Warwick et al. 2001). The origin of the halo is different from that of the plerion. One idea is that the halo is dust-scattered light from the plerion (Bandiera & Bocchino 2004). Upon these non-thermal features, there is a faint knot ~1′̣5 north of the core, called the “North Spur”. Based on the thermal spectral features, it is considered to be ejecta from the supernova explosion (Bocchino et al. 2005).
Some PWNe (e.g., the Crab nebula) show time-variable filaments. In G21.5–0.9, Matheson & Safi-Harb (2010) have used archival Chandra data to detect some localized variable emission near the pulsar. However, the contribution of these variable features to the total flux of G21.5-0.9 is negligible (≲1%) and therefore our analysis is not affected by these features.
An unrelated point source is found ~2′̣0 southwest of the core. This object is identified as the emission-line star SS 397 (Stephenson & Sanduleak 1977; Warwick et al. 2001). The source is a γ Cas analogue, which is a small class of Be stars known to show weakly variable X-ray flux with extreme hardness.
All of these spatial structures can be separated only by telescopes with good angular resolution. Because the participating instruments in our cross-calibration study include those with low angular resolution or the lack thereof, we use a source extraction region large enough to encompass all of these structures. We ignore the contaminating thermal emission from the North Spur, which is very faint (~0.1% of the non-thermal emission). We retrieved all the Chandra archival data to examine the behavior of the unrelated neighboring source SS 397, and found that the source is variable by a factor of a few, but has a negligible flux even at the brightest level. The total X-ray spectrum in our extraction region is dominated by the integration of the spatially-varying power-law emission from G21.5–0.9. We only treat the integrated spectrum, which we approximate as a single power-law spectrum. The reduced χ2 values in our fitting show that this approach is valid for the present data set.
3. Instruments, data, and processing
3.1. Chandra ACIS
3.1.1. Instruments
ACIS is an X-ray imaging-spectrometer consisting of the ACIS-I and ACIS-S CCD arrays. The imaging capability is unprecedented with a half-power diameter (HPD) of ~1″ at the on-axis position. We use one of the CCD chips (ACIS-S3) in the ACIS-S array. The ACIS-S3 chip is a back-side illuminated device sensitive in the 0.2–10 keV band. The chip has 1024 × 1024 pixels covering a 8′̣4 × 8′̣4 area.
List of data sets and their basic properties.
3.1.2. Data
The Chandra data were retrieved from the archive. A total of 41 ACIS observations were available with G21.5-0.9 at various detector positions. We chose seven full-frame observations with the object close to but offset from the center of the ACIS-S3 chip (CS0–CS6; Table 1), so that the chip encompasses the entire spatial structure of the source and leaves some area for background event extraction (Fig. 2). We also supplemented these data with three ACIS-S3 sub-array observations (CS7–CS9; Table 1) to evaluate the effect of pile-up (Sect. 4.2.1). The data were taken in timed exposure mode with a frame time of 3.2 s for the full frame (CS0–CS6) observations and 0.84 s for the sub-array (CS7–CS9) observations.
 |
Fig. 2 Layout of the fields of view (solid squares) and the background extraction regions (dashed rectangles) for each ACIS-S3 full-frame data set (CS0–6) in different colors. The source extraction region (solid circle) is displaced from the image center, leaving the other side of the image for the background extraction region (5′̣5 × 1′̣9). |
3.1.3. Processing
We processed the data using calibration database (CALDB) version 4.2 and CIAO version 4.2. The redistribution matrix functions (RMFs) and the auxiliary response files (ARFs) were generated for each data set. The RMFs take into account the spatial dependence of the detector response. The ARFs take into account the flux outside of the extraction region, although this is not a significant issue for the ACIS-S3 data as the resolved object is entirely contained in the source extraction region (Fig. 2).
3.2. INTEGRAL IBIS-ISGRI
3.2.1. Instruments
The IBIS telescope is a payload of INTEGRAL. It is composed of two layers of detectors. The upper layer is ISGRI, sensitive in the energy range 15–1000 keV. ISGRI is equipped with a CdTe detector array of 128 × 128 pixels with a spectral resolution of ~9% at 100 keV. The IBIS has a coded mask, giving the instrument imaging capability with an unprecedented angular resolution of 12′ FWHM in this band. The full-coded field of view is ~9° square.
3.2.2. Data
The IBIS data were obtained from a set of ~4000 IBIS Science Window data sets taken in a time period of 5 years from March 2003 to March 2008. We checked the source light curve in the 18–60 keV band and found that it is constant at a count rate of ~0.9 s-1. Therefore, we stacked all the data sets.
3.2.3. Processing
The standard INTEGRAL Off-line Scientific Analysis (OSA) version 8.0 was used to obtain images and spectra. We used the standard IBIS response files released in the OSA 8.0 distribution. The IBIS ARFs are computed in each year to incorporate the updated systematic uncertainties, which could affect the analysis of bright sources. Due to the very long time span for the observations of this source, we computed an average ARF for the total spectrum, which was weighted by the total exposure time in each calibration period.
3.3. RXTE PCA
3.3.1. Instruments
The PCA is a proportional counter array consisting of five proportional counter units (PCU1–5). The counters are filled with Xe gas and are sensitive at 2–60 keV. The instrument is unique in its high timing accuracy, large effective area, and modest spectral resolution of ~1 keV at 6 keV. There are no focussing optics but the collimator limits the field of view to ~1° square.
3.3.2. Data
We retrieved the archival data of G21.5-0.9 observed on 1997 November 8 (Table 1). We extracted the PCA spectrum from the standard2 PCA data mode, which provides spectral information in 129 channels with a time resolution of 16 s.
The electron flux stayed lower than 0.2 counts s-1 PCU-1 and no PCU breakdown events occurred during the entire observation. Data from all PCUs and all layers were combined into one spectrum. All five PCUs were operational during the entire observation, except for South Atlantic Anomaly (SAA) passages.
3.3.3. Processing
We excluded events during times when the elevation angle from the Earth rim was smaller than 10° and during SAA passages and 30 min thereafter. The remaining net exposure time is 21 ks.
The background spectrum and the RMF were calculated using the latest versions of the pcabackest (version 3.8) and pcarmf (version 11.7) tools. The background spectrum was scaled down by 1.3% to match the Standard2 rate in channels 110–128, corresponding to energies higher than 75 keV where no source counts are expected.
3.4. Suzaku XIS and HXD-PIN
3.4.1. Instruments
The XIS is an X-ray imaging-spectrometer equipped with four X-ray CCDs sensitive in the 0.2–12 keV band. One is a back-side illuminated (XIS1) device and the others are front-side illuminated (XIS0, 2, and 3) devices. The entire XIS2 and a part of the XIS0 are nonfunctional due to putative micro-meteorite hits, hence are not used in this paper. The four CCDs are located at the focal plane of four co-aligned X-ray telescopes with a HPD of ~2′̣0. Each XIS sensor has 1024 × 1024 pixels and covers a 17′̣8 × 17′̣8 view, which encompasses the entire G21.5–0.9 structure and leaves ample room to construct background spectra.
The PIN is a component of the HXD covering 10–70 keV. It is a non-imaging detector composed of 64 Si PIN diodes at the bottom of well-type collimators surrounded by GSO anti-coincidence scintillators. The effective area monotonically decreases as the distance increases from the field center, with a full width at zero intensity (FWZI) view of ~70′ square.
3.4.2. Data
We executed a Suzaku observation dedicated to the present study on 2009 October 10 for 40 ks using the XIS and the HXD. The target was placed at the XIS nominal position. The XIS was operated in the normal clocking mode with a frame time of 8 s.
Within the FWZI square view of the PIN, two other sources were found in the INTEGRAL source catalog (Bird et al. 2010); 4U 1835–11 and AX J1831.2–1008 at 26′̣4 and 42′̣7 from the field center. Because both unrelated sources have intensities less than 0.2% of G21.5–0.9 in the ISGRI 20–60 keV band, we ignore the contribution of these sources in the PIN spectrum.
3.4.3. Processing
The data were processed with pipeline processing version 2.4 and were reduced using HEASoft version 6.8–6.9.
For the XIS, the RMFs and ARFs were generated using the xisrmfgen and xissimarfgen tools. The former takes into account the positional difference of the detector response. The latter is based on a ray-tracing simulation, which is designed to compensate for photons lost outside of the extraction region. The tool also takes into account the surface brightness distribution of incoming X-rays to calculate the effective area under the assumption that the spectrum is uniform across the emitting region. We used the combined ACIS-S3 image (Fig. 1) as the true spatial distribution.
For the PIN, the background consists of astrophysical and instrumental background. The former is dominated by the cosmic X-ray background (CXB). We used the instrumental background spectrum and the detector response files distributed by the instrument team. We simulated the CXB spectrum using the energy response and added it to the instrumental background to subtract the CXB contribution. G21.5–0.9 is assumed to be point-like when generating the spatial response of the detector.
3.5. Swift XRT
3.5.1. Instruments
The XRT comprises a Wolter-I telescope, which focuses X-rays onto an X-ray CCD device identical to the ones flown on the XMM-Newton EPIC-MOS instrument (Burrows et al. 2004). The CCD, which is responsive to 0.2–10 keV X-rays, has a dimension of 600 × 600 pixels, covering a 23′̣6 × 23′̣6 field. The mirror has a HPD of ~18″ and gives astrometric accuracies of a few arcseconds.
As Swift’s primary science goal is to rapidly respond to gamma-ray bursts (GRBs), the XRT was designed to operate autonomously, so that it could measure GRB light curves and spectra over seven orders of magnitude in flux. In order to mitigate the effects of pile-up, the XRT automatically switches between different CCD readout modes depending on the source brightness. Two frequently-used modes are: Windowed Timing (WT) mode, which provides 1D spatial information in the central 7′̣8 of the CCD with a time resolution of 1.8 ms, and Photon Counting (PC) mode, which allows full 2D imaging-spectroscopy with a time resolution of 2.5 s.
The XRT’s thermoelectric cooler power supply system apparently failed shortly after launch, resulting in CCD operating temperatures ranging from –75 to –50 °C instead of the intended –100 °C. In order to reduce the dark current and overall noise level caused by the higher operating temperatures, the CCD substrate voltage (Vss) was raised from 0 to 6 V on 2007 August 30. While this allowed the CCD to operate a few degrees warmer, it had the minor drawback of reducing the quantum efficiency (QE) both at high energies (≳5 keV) and just below the Si edge (1.5–1.84 keV). The Vss = 6 V calibration modifications required to correct the changes of QE have been completed for the WT mode but not for the PC mode, at the time of writing; the latter will be released in due course. The XRT CCD in-flight calibration is described in Godet et al. (2009).
3.5.2. Data
G21.5–0.9 is used as a routine calibration source for the XRT as its heavily absorbed spectrum is useful to verify the high energy redistribution properties of the CCD. Since the object is an extended source and it is difficult to subtract background adequately for the WT data, we present only results from PC mode observations.
As Swift has a flexible observing schedule, often interrupted by GRBs, observations are divided into ObsIDs containing one or more snapshots, where each snapshot has a typical exposure of 1–2 ks. For a faint source like G21.5–0.9, it is necessary to accumulate data from different ObsIDs for any given epoch.
We retrieved 18 observations from the UK Swift Science Data Centre. To minimize the effect of vignetting, the observations were selected so that the source lay within 10′ of the CCD bore-sight, avoiding pointings that have large off-axis angles. The data were grouped into four epochs, split into two groups: before (SX0 and SX1) and after (SX2 and SX3) the Vss change (Table 1). Typical exposures were 17–18 ks per epoch.
3.5.3. Processing
The data were processed with Swift software version 3.5, which was made available with HEASoft version 6.8.
For each epoch, a summed exposure map was computed, accounting for CCD bad columns and telescope vignetting. The exposure maps were then used to create extended source ARF files by subdividing the source extraction region into boxes and calculating an average ARF over the regions, weighted by the relative exposure and counts in each box. For this analysis, CALDB v011 RMF and ARFs were used.
3.6. XMM-Newton EPIC
3.6.1. Instruments
The EPIC is composed of two different types of X-ray CCD devices; two units of MOS-type (MOS1 and MOS2) covering 0.15–12 keV and one unit of pn-type covering 0.15–15 keV. The three devices are located at the focal plane of three co-aligned telescopes with a HPD of ~15″.
The MOS1 and MOS2 cameras consist of an array of seven front-illuminated CCD chips, each of which has 600 × 600 pixels covering a ~10′̣9 × 10′̣9 square region. The pn-type has a 2 × 6 back-illuminated CCD array, each of which has 200 × 64 pixels covering a ~13′̣6 × 4′̣4 rectangular region.
3.6.2. Data
XMM-Newton observed G21.5–0.9 several times within the field of view of the EPIC camera. We used the data with the target placed at the center of the camera taken on 2000 April 7 (Table 1). The observation was performed with the medium-thickness filter and full-frame mode for the CCD clocking.
 |
Fig. 3 Layout of the field of view of the central chip of the two MOS arrays (solid square), the MOS and pn source extraction region (solid circle), and the MOS background extraction region (dashed annulus) overlaid on the pn image. The pn chip gaps and bad columns are apparent in the image. |
 |
Fig. 4 Radial profile of background-unsubtracted 0.5–8 keV counts for the soft-band instruments. The counts are normalized to the value at the center. The radii of the source extraction apertures are shown by the dashed lines. |
In the MOS arrays, the object is located at the center of the central CCD of both arrays. The entire spatial structure is contained in a chip. In the pn-array, G21.5–0.9 is located at the bottom of CCD number 4 and the structure spreads across neighboring CCDs (Fig. 3).
3.6.3. Processing
The data were reduced using XMM-Newton Science Analysis System (SAS) version 10 (Gabriel et al. 2004) and the latest calibration files available at the time of reduction (August 2010). Event lists were generated using the data reduction meta-tasks e[mp]proc with the default settings. The data were screened to remove intervals of high particle background.
Response files were generated using the rmfgen and arfgen tasks. We took into account the spatial distribution of the extended X-ray emission by calculating a coarse detector map around the G21.5-0.9 centroid, which was convolved with the spatially-dependent effective area to produce the appropriate transfer function for the extraction region. The SAS does not support correction for photons lost outside of the source extraction region. However, we consider that this is negligible by taking a source extraction region large enough to encompass most photons to the level of 10-3 of the peak (Fig. 4).
4. Analysis and results
4.1. Overall procedure
4.1.1. Source extractions for soft-band instruments
For the soft-band instruments, we extracted source events from a 165″ circle centered at the pulsar PSR J1833–1034 at (RA, Dec) = (18:33:33.57, −10:34:07.5) in the equinox J2000.0. The radius was chosen as a compromise to be large enough to encompass a significant fraction of the entire structure of G21.5–0.9 as well as the negligible unrelated emission (Fig. 4) yet small enough to be contained in the field of view of all the instruments. The Suzaku XIS, with a larger telescope HPD than the others, is the only exception; we chose a larger source extraction radius of 300″, which contains a significant fraction of the source photons (Fig. 4). The background events were extracted from various regions optimized for each instrument, which is discussed individually in Sect. 4.2.
4.1.2. Fitting procedure
We assembled the source and background spectra, RMFs, and ARFs for all the instruments. Using XSPEC package version 12.6, we fitted the background-subtracted spectra. We applied the spectral model pegpwrlw attenuated by the interstellar photoelectric absorption model TBabs (Wilms et al. 2000). The former is the same as the conventional power-law model except that it uses the flux between the designated lower and upper energies, not the normalized flux at 1 keV, as a free parameter for the intensity. This decouples the often-entangled parameters of the index (Γ) and normalization in power-law fitting. The flux was evaluated in the energy ranges 2–8 keV (FX,soft) and 15–50 keV(FX,hard) for the soft-band and hard-band instruments respectively. The Verner et al. (1996) model was used for the photoelectric absorption cross sections, and the Wilms et al. (2000) model was used for the metal abundance for the derivation of the H-equivalent extinction column density (NH).
For the soft-band instruments, we used the common energy range of 1–8 keV for fitting. All CCDs are Si-based, and thus have sensitivity in a similar energy range. For the hard-band instruments, the inhomogeneity of the detecting technique did not allow us to use a common energy range. So, we used different ranges optimized for each instrument: 18–150 keV for INTEGRAL ISGRI, 5.0–30 keV for RXTE PCA, and 15–70 keV for Suzaku PIN. Because the power-law index of PWN spectra changes with energy range, the choice of different energy ranges for fitting might introduce systematic uncertainty.
Spectra were binned with the number of counts per bin specified in Table 1. The model was fitted to minimize the χ2 statistics and was considered statistically acceptable if the null hypothesis probability was larger than 5%. Statistical uncertainties for the best-fit values were derived as the 1σ deviations.
4.2. Individual fitting and systematic uncertainties
We now fit the spectra individually for each participating instrument following the common procedure set up in Sect. 4.1. We justify the choice of our spectral model by showing that all the fits yield statistically acceptable results. We also discuss systematic uncertainties arising from the common procedure. Spectra obtained from the same instrument and with the same response (CS0–6, SX0–1, and SX2–3) are fitted jointly after confirming that individual spectra give consistent results.
4.2.1. Chandra ACIS
The Chandra ACIS-S3 data (CS0–CS6) were taken at different epochs. G21.5–0.9 was placed at different detector positions, displaced 1′̣17–1′̣32 from the chip center. The background spectra were accumulated from different regions (Fig. 2). Statistically-acceptable best-fit models were obtained; results are listed in Table 2 and the CS0 spectrum is shown as a representative example in Fig. 5.
 |
Fig. 5 ACIS-S3 (CS0) spectrum and the best-fit model. The upper panel shows the data (crosses) and best-fit model (solid line), while the lower panel shows the residuals to the fit. The range used for fitting is shown with grey shading. The spectrum is binned to achieve 30σ in each bin only for display. |
In order to evaluate the systematic uncertainty caused by inhomogeneities in the data sets, we compared the best-fit parameters among the different observations (Fig. 6). For each parameter (NH, Γ, and FX,soft), the seven values were tested against the null hypothesis that they deviate from a constant value. For all parameters, the hypothesis was rejected, implying that there is no statistical reason to claim any difference among the data sets. We thus combined all spectra and fitted them jointly to obtain a statistically-acceptable best-fit model. The result is appended in Table 2 as CS0–6.
 |
Fig. 6 Comparison of best-fit values (with 1σ statistical uncertainties) for spectral parameters from the full-frame ACIS-S3 data. The solid line and grey shaded regions respectively indicate the best-fit and 1σ statistical uncertainty range from the joint fitting. |
 |
Fig. 7 Comparison of best-fit values (with 1σ statistical uncertainties) for the spectral parameters from joint fits of the full-frame (black) and the sub-array (red) data at different outer source extraction radii. The inner radius was fixed at 0. The ratio of the two is shown by the green crosses and on the right horizontal axis. |
Due to the superb imaging capability of ACIS, the full-frame data suffer slight pile-up at the peak of the surface brightness distribution of the object. We conclude that this effect is negligible for our cross-calibration comparison based on the following assessment. We compared the results of the full-frame and sub-array fits at different outer source extraction radii (rout) within the field of view of the sub-array data (Fig. 7). A shorter frame time for the sub-array data reduces the frequency of pile-up. In Fig. 7, we see two trends as rout increases. The first is the monotonic change of the spectral shape (NH and Γ) both for the full-frame and sub-array data, which stems from spatial changes of the spectrum intrinsic to G21.5–0.9. The second is the decreasing differences between the full-frame and sub-array results, which are due to the alleviation of the pile-up effect. Beyond 20″, the results of the two data sets are stable with a full-frame to sub-array ratio of 1 except for a 4% difference in FX,soft. We believe that the FX,soft difference is a separate issue with an unidentified origin. In fact, we find a similar discrepancy in a comparison of an annular region, in which the inner 30″ circle including the bright core was removed to avoid pile-up. The FX,soft difference between the full-frame and sub-array data was again found to be ~3.5%, which exceeds the statistical uncertainty of ~2.0%. We thus conclude that the major cause of the FX,soft discrepancy is not pile-up.
4.2.2. INTEGRAL IBIS-ISGRI
The IBIS-ISGRI detected emission from G21.5–0.9 at a significance level of ~35σ. The spectrum consists of 12 channels spaced almost equally on a logarithmic scale (Fig. 8). The interstellar extinction cannot be constrained by the IBIS-ISGRI data alone, so we fixed it to 2.99 × 1022 cm-2, the value obtained from the joint fitting of the soft-band instruments (Sect. 4.3.1). A statistically-acceptable best-fit model was obtained, which is shown in Fig. 8 and Table 2.
In order to compare with the previous work by de Rosa et al. (2009) for the same object, we fitted the spectrum with the same model (a single power-law) used in their work. The derived index and flux in the 20–100 keV range are 2.0 (1.9–2.1) and 5.3 (5.1 − 5.5) × 10-11 erg s-1 cm-2, whereas de Rosa et al. (2009) found 2.2 ± 0.1 and 5.2 × 10-11 erg s-1 cm-2. These are consistent within the statistical uncertainties.
4.2.3. RXTE PCA
The non-imaging nature and large field of view of the PCA lead to a considerable contamination by unrelated emission ubiquitous in the direction of G21.5-0.9. Two major sources of contamination are the Galactic ridge X-ray emission, evident from the excess emission at 6–7 keV (Fig. 9), and the CXB emission.
In order to subtract the contribution of the unrelated emission, we used data (ObsID = 20266-01-35-06S) obtained in a control field devoid of bright sources at the Galactic coordinate of (l,b) = (21.999, − 0.005), which is 1°̣01 away from G21.5-0.9 at (21.501, − 0.885). We fitted the two spectra at the control field and at G21.5–0.9 jointly. For the former, a model was applied to represent the unrelated emission, which is a power-law continuum plus a Gaussian line for the blended Fe lines at 6–7 keV, attenuated by a fixed interstellar extinction of NH = 3 × 1022 cm-2. For the latter, the model representing the G21.5–0.9 spectrum was added. The interstellar extinction to G21.5–0.9 was fixed to 2.99 × 1022 cm-2 as for the IBIS-ISGRI fitting. All parameters in the model for the unrelated emission were common between the two spectra, except for a flux rescaling factor for the G21.5–0.9 spectrum with respect to the control field spectrum.
Statistically-acceptable best-fit models were obtained and are shown in Fig. 9. The best-fit parameters for the G21.5–0.9 model are summarized in Table 2. Those for the unrelated emission model are; Γ = 2.39 (2.25–2.51), FX,hard = 1.50 (1.24 − 1.83) × 10-11 erg s-1 cm-2, Egau = 6.56 (6.53–6.59) keV, σgau = 0.40 (0.34–0.45) keV, and Ngau = 3.85 (3.57 − 4.18) × 10-4 s-1 cm-2, where Egau, σgau, and Ngau are the center energy, width, and flux of the Gaussian model. In the 15–50 keV range, it is estimated that the contribution of the unrelated emission accounts for 21% of the total emission in the G21.5-0.9 spectrum. Note that the uncertainty in the control-field flux was not propagated to derive the numbers in Table 2.
 |
Fig. 9 PCA spectrum and the best-fit model. In the upper panel, the best-fit model (thick brown solid line) is decomposed into the G21.5–0.9 (brown dotted line) and the unrelated (orange dotted line) emission components. The other symbols follow Fig. 5. |
4.2.4. Suzaku XIS and HXD-PIN
Background events were extracted from an annulus with inner and outer radii of 5′̣0 and 7′̣0, concentric to the source extraction region. The calibration of the XIS is uncertain around the Si K edge. We excluded events in the 1.8–2.0 keV range in the fitting. We independently fitted each of the three XIS spectra and the PIN spectrum. Statistically-acceptable best-fit models were obtained and are shown in Fig. 10 and Table 2.
 |
Fig. 10 XIS and PIN spectra and best-fit model. The XIS spectra are binned to achieve 30σ in each bin only for display. The symbols follow Fig. 5. |
Unlike the other soft-band instruments, the ARF generator for the XIS compensates for photons lost outside of the source extraction region. This is a source of systematic uncertainty. In order to evaluate this, we fitted the spectra constructed from different outer source extraction radii (rout). The inner radius was fixed to 0′. The ARFs were generated by assuming a point-like source or a surface brightness distribution like that shown in Fig. 1. Figure 11 summarizes the result that the best-fit spectral parameters converge as rout increases for both assumptions in generating the ARFs. For rout = 5′, the radius we use to compare with the other instruments, we can safely assume that the uncertainty due to the compensation of lost photons is negligible.
 |
Fig. 11 Best-fit values and 1σ uncertainties for the spectral parameters with different outer source extraction radii. Black symbols indicate that the ARF was calculated assuming the source brightness distribution of the ACIS-S3 image. Red symbols indicate that a point-like source was assumed. Here, we use the result from the joint fit to the three XIS devices, since the result of the individual fits gives the same trend. |
4.2.5. Swift XRT
Figure 12 shows the summed XRT image from which the radial profile (Fig. 4) was calculated. Overplotted on the image are the source (solid) and background (dashed) extraction regions. The background was chosen from an annulus with some additional circles to increase the area from the region with maximum and uniform exposure.
 |
Fig. 12 XRT image of G21.5–0.9. The source (solid) and background (dashed) regions used for the spectral analysis are shown. |
For each of the four epochs of data (Table 1), we performed individual fitting. We further grouped all the data sets before and after the Vss change for joint fitting. Statistically-acceptable best-fit models were obtained, which are shown in Fig. 5 (the SX0 fitting as a representative) and Table 2.
 |
Fig. 13 XRT (SX0) spectrum and best-fit model. The spectrum is binned to achieve 30σ in each bin only for display. The symbols follow Fig. 5. |
There is a clear difference in the spectral parameters obtained from data taken before and after the Vss change (Fig. 14), with the latter showing a slightly steeper but more absorbed spectrum than the former. Within each group, NH and Γ are consistent with each other. The discrepancy in the parameters is caused by the slight QE change incurred after the Vss was altered. The calibration of this effect is ongoing. We hereafter use the result obtained for the data before the change (SX0 and SX1). We see a notable difference in FX,soft between SX0 and SX1. We could not identify the cause for the difference and ignore it as a statistical scatter.
 |
Fig. 14 Comparison of best-fit values (with 1σ statistical uncertainties) for the spectral parameters from the XRT fits. The solid line and grey shaded regions indicate the best-fit and 1σ statistical uncertainty range from joint fitting. |
4.2.6. XMM-Newton EPIC
In order to ensure that the fluxes measured by the three EPIC cameras correspond to the same region in the sky, as well as to provide a correction factor for the lost sky area due to bad pixels/columns and chip gaps, we applied a common detector mask during the accumulation of the spectral products (“masked spectra” hereafter). This mask was generated by multiplying the detector masks produced by the SAS task emask on the individual EPIC cameras2. For the correction factor to compensate for the masked area, we extracted a MOS1 spectrum from the full 165″ extraction circle (“unmasked spectrum”). We chose the MOS1 detector, because it was only marginally affected by CCD artifacts in our data. We calculated the flux ratio between the unmasked and the masked spectra, which is 1.091 in the 2–8 keV energy range. Finally, we multiplied that ratio to the flux obtained from the “masked” spectra to derive the flux in the full 165″ circle.
The background spectra for the two MOS cameras were extracted from an annulus with inner and outer radii of 3′̣3 and 5′̣0, concentric to the source extraction region. The background region is also contained in the central CCD chip with the source region (Fig. 3).
Unlike the MOS cameras, the background extraction for the pn camera is not straight-forward. The source spreads across multiple CCDs (Fig. 3) and the background level is known to have a measurable position dependence, particularly along the readout direction. We therefore extracted a spectrum from blank sky data (Carter & Read 2007) using the same extraction region as the source, and used it as the background spectrum. Out-of-time events were removed in the pn data.
We fitted individual spectra from the three EPIC devices. A statistically-acceptable best-fit model was obtained, which is shown in Fig. 15 and Table 2.
 |
Fig. 15 EPIC spectra and the best-fit model. The spectra are binned to achieve 30σ in each bin only for display. The symbols follow Fig. 5. |
In the pn result, a deviation is seen below 1.5 keV, which is not observed in any other instrument at a comparable level. The origin of this feature is currently unknown. Possible explanations are residual uncertainties in the background subtraction (the pn background has a complex spatial structure whose modeling for extended sources close to the bore-sight position is non-trivial) and residual inaccuracies in the calibration of the redistribution. Notwithstanding the origin of this feature, we assessed the effect of the deviation to the best-fit parameter values by altering the lower energy (Emin) in the fitting (Fig. 16). The upper energy (Emax) was fixed to 8.0 keV. Toward lower energies in Emin, the best-fit NH and Γ values change monotonically. The global trend, however, is common among MOS1, MOS2, and pn, implying that the <1.5 keV deviation only seen in the pn does not affect the pn fitting results. This is conceivable since the pn spectrum has dominant counts in 1.5–Emax keV band. We thus ignore the effect of the <1.5 keV deviation hereafter.
 |
Fig. 16 Best-fit values (with 1σ uncertainties) for the spectral parameters, using different lower energy values in the fitting. |
4.3. Joint fitting of all data
We assembled all spectra and responses and attempted a joint fitting separately for the soft-band and hard-band instruments. The procedures follow the individual fitting in Sect. 4.2. The seven ACIS-S3 spectra were treated as one. The two XRT data sets (SX2 and SX3) were discarded and the remaining two (SX0 and SX1) were used as one.
4.3.1. Soft-band instruments
For the soft-band joint fitting, we first fitted the spectra with all spectral parameters (NH, Γ, FX,soft) tied among all instruments. The best-fit model was statistically rejected due mainly to the inconsistent normalizations among the instruments. Statistical uncertainties were not derived as the goodness of fit was very low.
We therefore introduced an additional normalization rescaling parameter for all instruments with respect to a fixed FX,soft value of 5.69 × 10-11 erg s-1 cm-2, which is the best-fit value from the joint fitting above. Note that this value is not the most likely value for the absolute flux. The derived value can be easily biased by the instruments yielding a larger number of counts than the others, regardless of whether they are better calibrated or not. Nevertheless, it is the value that best represents our datasets. We obtained a result, which was still statistically unacceptable, but was much improved in the goodness of fit (Table 2). The comparison of FX,soft is shown in Fig. 17.
 |
Fig. 17 Comparison of the best-fit FX,soft or FX,hard values (with 1σ statistical uncertainties) from the joint fitting done with the other parameters (Γ and NH) tied among all the soft-band or hard instruments. |
4.3.2. Hard-band instruments
We took the same approach in the joint fitting of the hard-band instruments except that NH was fixed to 2.99 × 1022 cm-2 (the value from the soft-band joint fitting). First, we fitted all spectral parameters (Γ, FX,hard) tied among all instruments, which was unsuccessful for the same reason as for soft-band joint fitting. We therefore introduced a normalization rescaling parameter for each spectrum and obtained a statistically-acceptable best-fit model (Table 2). The comparison of the FX,hard is shown in Fig. 17.
5. Discussion
5.1. Comparison of fitting results
 |
Fig. 18 Scatter plot of the best-fit Γ versus NH values (with the 1σ uncertainties) for all soft-band instruments. |
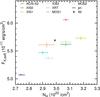 |
Fig. 19 Scatter plot of the best-fit NH versus FX, soft values (with the 1σ statistical uncertainties) for all soft-band instruments. |
 |
Fig. 20 Scatter plot of the best-fit Γ versus FX,soft values (with the 1σ statistical uncertainties) for all soft-band instruments. |
 |
Fig. 21 Scatter plot of the best-fit Γ versus FX,hard values (with the 1σ uncertainties) for all hard-band instruments. |
We now compare all the results. The values in Table 2 are plotted in four scatter plots (Figs. 18–21) for every combination of two spectral parameters.
5.1.1. Identifying systematic differences
For identifying significant systematic uncertainties, we assume that instrument A and B
have the best-fit values and 1σ statistical uncertainties for a certain
spectral parameter x as
x(A) ± Δx(A) and
x(B) ± Δx(B). The statistical
uncertainty is nearly symmetric in the upper and lower directions in all parameters
(Table 2), so we take the mean of the two for
Δx(A) and Δx(B). If the
modulus of the logarithm of the ratio exceeds three times the convolved statistical
uncertainty as 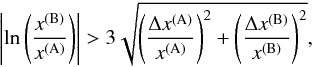 (1)we conclude that the two instruments A and
B have a significant systematic difference in x.
(1)we conclude that the two instruments A and
B have a significant systematic difference in x.
In the soft band, we have eight instruments (ACIS-S3, XIS0, XIS1, XIS3, XRT, MOS1, MOS2, and pn) and three parameters (NH, Γ, and FX,soft). Figure 18 shows that NH and Γ are coupled, so we only consider Γ. For each parameter, we have 28 combinations, where a combination is a comparison of the parameters for a pair of instruments. In the hard band, we have three instruments (PIN, PCA, and ISGRI) and two parameters (Γ and FX,hard). For each parameter, we have 3 combinations. A total of 62 combinations were examined. The identified systematic differences are shown in bold faces in Tables 3–6.
5.1.2. Soft-band comparison
In the flux comparison, 20 out of 28 combinations show a significant difference (Table 3). The ACIS-S3 flux is larger than all the others. The pn flux is smaller than all the others. The three XIS instruments (XIS0, XIS1, and XIS3) are consistent with each other and the two MOS cameras are consistent with each other. XRT is consistent with the three XIS devices and MOS1. The largest difference, between ACIS-S3 and pn, is 20%.
In the index comparison, 15 out of 28 combinations show a significant difference (Table 4). As for the flux, the three XIS instruments and the two MOS cameras are consistent among themselves. The largest difference, between XIS1 and pn, is 9%.
Note that Γ can absorb a part of the uncertainty of NH in the fitting or vice versa due to their degeneracy, resulting in an overestimation of the uncertainty. This is particularly visible in the XIS fitting (Fig. 10), where the residuals in the 3–10 keV band indicate that a flatter Γ would be more appropriate. However, a flatter Γ would have fit the data in the 1–2 keV range worse than a steeper Γ. In order to focus solely on Γ, we did the fit in the 2.0–8.0 keV band with the NH fixed to 2.99 × 1022 cm-2. Figure 22 shows the result; the inconsistency among Γ narrows in comparison to Fig. 20.
 |
Fig. 22 Same as Fig. 20, but with the fitting performed in the 2.0–8.0 keV band with a fixed NH value to focus on the difference in Γ in the hard band. |
5.1.3. Hard-band comparison
In the flux comparison, 2 out of 3 combinations in FX,hard are significantly different (Table 5). ISGRI is smaller than the other two. The greatest difference, between ISGRI and PIN, is as large as 46%. In the index comparison, all three instruments are consistent with each other (Table 6).
5.2. Comparison with other studies
5.2.1. Internal cross-calibration studies
We compared our results with cross-calibration results for instruments onboard the same satellite (i.e., XIS0, XIS1, and XIS3 for Suzaku and EPIC-MOS1, EPIC-MOS2, and EPIC-pn for the XMM-Newton), referring to the technical notes issued by their calibration teams. Both observatories use these instruments simultaneously, so we can mitigate the effects caused by changes of the instrumental performance over time in these comparisons.
In the Suzaku XIS study (Ishida et al. 2007), the Crab nebula was used to compare the power-law index and flux in the 1–10 keV band at the XIS nominal position. Their results are consistent with the present study. XIS0, 1, 3 are consistent with each other to better than 3% both in flux and power-law index. The back-side illuminated device (XIS1) is slightly larger in flux and steeper in power-law index than the front-side illuminated devices (XIS0 and XIS3).
In the XMM-Newton EPIC study (Gabriel et al. 2008), G21.5–0.9 was also used to compare the power-law index and flux in 2–10 keV band using the same data set. Their results show that the flux increases in the sequence of MOS2, MOS1, and pn, which is inconsistent with our result. This is due to the caveat of the bad pixel/column treatment in the older SAS versions described in Sect. 4.2.6. In fact, without considering this caveat, we obtained the same result as Gabriel et al. (2008).
In another XMM-Newton EPIC study (Stuhlinger et al. 2008), several extra-galactic point-like sources were used to compare the flux in six energy bands. Point sources are less affected by the SAS caveat than extended sources like G21.5–0.9. In the two energy bands closest to ours (1.5–4.0 and 4.0–10.0 keV), the flux is larger for MOS1 and MO2 than pn by ~5%, which is the same trend that we found.
5.2.2. External cross-calibration studies
We also compared our results with other cross-calibration studies across multiple missions. The number of such studies is small; in fact, we could only find a few studies comparing Chandra and XMM-Newton, often with outdated software versions. We refer to another IACHEC study by Nevalainen et al. (2010), in which 11 relaxed clusters of galaxies are used. In this study, the 2–7 keV band spectra were fitted with an optically-thin thermal plasma model to derive the plasma temperature and flux. The ACIS-I, ACIS-S, and EPIC instruments were used. ACIS-I and ACIS-S were confirmed to be consistent with each other and were treated as one.
In the flux comparison, ACIS was significantly larger than the three EPIC cameras by 5–10%. Among the three EPIC instruments, pn is lower than the other two by ~5%. Both discrepancies are consistent with our result.
In the temperature comparison, ACIS and pn were consistent with each other. Among the EPIC instruments, pn and MOS (MOS1 and MOS2 were combined) were also consistent with each other. In order to compare to the cluster temperature result, we fitted the G21.5–0.9 spectra in the same energy band with a power-law model attenuated by a fixed NH value of 2.99 × 1022 cm-2 and substituted the softness of the index for the temperature. We found that the consistency in the spectral softness among ACIS-S3 and the three EPIC cameras is also found with G21.5–0.9.
6. Conclusion
We used the pulsar wind nebula G21.5–0.9 to conduct a cross-calibration study of instruments onboard the currently working X-ray astronomy missions. The archival and original data were accumulated for Chandra ACIS-S3, INTEGRAL IBIS-ISGRI, RXTE PCA, Suzaku XIS and HXD-PIN, Swift XRT, and XMM-Newton EPIC-MOS and EPIC-pn.
We conducted coherent spectral fitting for all the data using methods as common as possible. We tabulated and plotted the results in order to be a useful reference. We compared the results in all combinations of two different instrument pairs for the spectral parameters, and identified many systematic differences unattributable to the statistical uncertainties alone. Most differences are consistent with those reported in previous studies of a similar purpose.
Many factors can cause systematic differences between instruments, including (1) inaccurate calibration of either or both of the two compared instruments; (2) the limitations of G21.5–0.9 as a calibration source; and (3) inappropriate choice of the source extraction aperture, the spectral models, background, energy ranges, etc. These factors are entangled, and our aim is to discriminate the causes belonging to (1). We addressed some of the concerns belonging to (3) in Sect. 4.2 and showed that these effects are minor. The limitations of G21.5–0.9 as a calibration source (Sect. 2) are unavoidable. After all, there is no perfect celestial calibration source. Therefore, the only practical approach is to conduct similar comprehensive comparison studies using a variety of celestial sources and to identify systematic differences commonly seen in various studies. More IACHEC papers will follow, which will serve for this purpose.
The systematic differences should not be left as they are. We feel that the current level of differences among various instruments (or even within the same observatory) can be lessened. For example, we described in this study that (1) the Chandra ACIS-S3 full-frame and the sub-array data appear to have inconsistent normalization; (2) the Swift XRT results remain inconsistent before and after the substrate voltage changes or even at two epochs before the change for flux; (3) Suzaku XIS is not well calibrated at the energies around the Si I K edge; (4) the EPIC-pn shows a deviation in the low energy tail of the spectrum; and (5) the three EPIC instruments are inconsistent with each other.
Scientific measurements can be no better than the calibration accuracies. Continuous calibration efforts are required to keep the instruments reliable and to maximize the scientific output. We hope that the present study will help such efforts, which the entire community relies upon.
See http://www.iachec.org/index.html for detail.
SAS users should be aware that this procedure does not work with SAS versions 10 and earlier. Due to a formal error in the header of the mask file, the mask description is not correctly propagated in the spectral file header, and arfgen cannot properly apply the bad area correction on “masked” spectra. We modified the header of the mask file manually in order to cope with this problem. A solution to this problem is expected to be available in SAS versions later then 10.0.
Acknowledgments
We thank the members of the IACHEC for sharing their results prior to publication and Marcus G. Kirsch who took a leadership role in setting up this consortium. We acknowledge Dai Takei and Kei Saitou for their
help in Suzaku data reduction. A.P.B. and A.M.R. acknowledges support from the Science and Technology Facilities Council.
References
- Asaoka, I., & Koyama, K. 1990, PASJ, 42, 625 [NASA ADS] [Google Scholar]
- Bandiera, R., & Bocchino, F. 2004, Adv. Space Res., 33, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., & Szymkowiak, A. E. 1981, ApJ, 248, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K. 2006, A&A, 460, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bietenholz, M. F., & Bartel, N. 2008, MNRAS, 386, 1411 [NASA ADS] [CrossRef] [Google Scholar]
- Bird, A. J., Bazzano, A., Bassani, L., et al. 2010, ApJS, 186, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bocchino, F., van der Swaluw, E., Chevalier, R., & Bandiera, R. 2005, A&A, 442, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradt, H. V., Rothschild, R. E., & Swank, J. H. 1993, A&AS, 97, 355 [NASA ADS] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2004, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conf. Ser., ed. K. A. Flanagan, & O. H. W. Siegmund, 5165, 201 [Google Scholar]
- Camilo, F., Ransom, S. M., Gaensler, B. M., et al. 2006, ApJ, 637, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, J. A., & Read, A. M. 2007, A&A, 464, 1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davelaar, J., Smith, A., & Becker, R. H. 1986, ApJ, 300, L59 [NASA ADS] [CrossRef] [Google Scholar]
- de Rosa, A., Ubertini, P., Campana, R., et al. 2009, MNRAS, 393, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, C., Denby, M., Fyfe, D. J., et al. 2004, in Astronomical Data Analysis Software and Systems (ADASS) XIII, ed. F. Ochsenbein, M. G. Allen, & D. Egret, ASP Conf. Ser., 314, 759 [Google Scholar]
- Gabriel, C., Ibarra, A., Gonzalez-Riestra, R., et al. 2008, in XMM-SOC-USR-TN, XMM-Newton Science Operation Centre and XMM-Newton Science Survey Centre, 17, 1 [Google Scholar]
- Garmire, G. P., Bautz, M. W., Ford, P. G., Nousek, J. A., & Ricker, Jr., G. R. 2003, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conf. Ser., ed. J. E. Truemper, & H. D. Tananbaum, 4851, 28 [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Godet, O., Beardmore, A. P., Abbey, A. F., et al. 2009, A&A, 494, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gupta, Y., Mitra, D., Green, D. A., & Acharyya, A. 2005, Current Science, 89, 853 [NASA ADS] [Google Scholar]
- Ishida, M., Suzuki, K., & Someya, K. 2007, in JX-ISAS-SUZAKU-MEMO, ed. Suzaku Team, 11, 1–7 [Google Scholar]
- Jahoda, K., Swank, J. H., Giles, A. B., et al. 1996, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conf. Ser., ed. O. H. Siegmund, & M. A. Gummin, 2808, 59 [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirsch, M. G., Briel, U. G., Burrows, D., et al. 2005, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conf. Ser., ed. O. H. W. Siegmund, 5898, 22 [Google Scholar]
- Kokubun, M., Makishima, K., Takahashi, T., et al. 2007, PASJ, 59, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, K., Tsunemi, H., Dotani, T., et al. 2007, PASJ, 59, 23 [Google Scholar]
- LaPalombara, N., & Mereghetti, S. 2002, A&A, 383, 916 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebrun, F., Leray, J. P., Lavocat, P., et al. 2003, A&A, 411, L141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matheson, H., & Safi-Harb, S. 2010, ApJ, 724, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsuda, K., Bautz, M., Inoue, H., et al. 2007, PASJ, 59, 1 [Google Scholar]
- Nevalainen, J., David, L., & Guainazzi, M. 2010, A&A, 523, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plucinsky, P. P., Haberl, F., Dewey, D., et al. 2008, in SPIE Conf. Ser., 7011 [Google Scholar]
- Slane, P., Chen, Y., Schulz, N. S., et al. 2000, ApJ, 533, L29 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Snowden, S. L. 2002, unpublished [arXiv:astro-ph/0203311] [Google Scholar]
- Stephenson, C. B., & Sanduleak, N. 1977, ApJS, 33, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stuhlinger, M., Kirsch, M. G. F., Santos-Lleo, M., et al. 2008, in XMM-SOC-CAL-TN, ed. XMM-Newton Science Operation Centre, 52, 1 [Google Scholar]
- Takahashi, T., Abe, K., Endo, M., et al. 2007, PASJ, 59, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tian, W. W., & Leahy, D. A. 2008, MNRAS, 391, L54 [NASA ADS] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Warwick, R. S., Bernard, J., Bocchino, F., et al. 2001, A&A, 365, L248 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weisskopf, M. C., Brinkman, B., Canizares, C., et al. 2002, PASP, 114, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Guainazzi, M., Jahoda, K., et al. 2010, ApJ, 713, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Winkler, C., Courvoisier, T., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Chandra ACIS-S3 image of G21.5–0.9. The spatial components and the nearby source SS 397 are labeled. The source extraction region of 165″ is indicated by the solid circle. |
| In the text | |
 |
Fig. 2 Layout of the fields of view (solid squares) and the background extraction regions (dashed rectangles) for each ACIS-S3 full-frame data set (CS0–6) in different colors. The source extraction region (solid circle) is displaced from the image center, leaving the other side of the image for the background extraction region (5′̣5 × 1′̣9). |
| In the text | |
 |
Fig. 3 Layout of the field of view of the central chip of the two MOS arrays (solid square), the MOS and pn source extraction region (solid circle), and the MOS background extraction region (dashed annulus) overlaid on the pn image. The pn chip gaps and bad columns are apparent in the image. |
| In the text | |
 |
Fig. 4 Radial profile of background-unsubtracted 0.5–8 keV counts for the soft-band instruments. The counts are normalized to the value at the center. The radii of the source extraction apertures are shown by the dashed lines. |
| In the text | |
 |
Fig. 5 ACIS-S3 (CS0) spectrum and the best-fit model. The upper panel shows the data (crosses) and best-fit model (solid line), while the lower panel shows the residuals to the fit. The range used for fitting is shown with grey shading. The spectrum is binned to achieve 30σ in each bin only for display. |
| In the text | |
 |
Fig. 6 Comparison of best-fit values (with 1σ statistical uncertainties) for spectral parameters from the full-frame ACIS-S3 data. The solid line and grey shaded regions respectively indicate the best-fit and 1σ statistical uncertainty range from the joint fitting. |
| In the text | |
 |
Fig. 7 Comparison of best-fit values (with 1σ statistical uncertainties) for the spectral parameters from joint fits of the full-frame (black) and the sub-array (red) data at different outer source extraction radii. The inner radius was fixed at 0. The ratio of the two is shown by the green crosses and on the right horizontal axis. |
| In the text | |
 |
Fig. 8 ISGRI spectrum and best-fit model. The symbols follow Fig. 5. |
| In the text | |
 |
Fig. 9 PCA spectrum and the best-fit model. In the upper panel, the best-fit model (thick brown solid line) is decomposed into the G21.5–0.9 (brown dotted line) and the unrelated (orange dotted line) emission components. The other symbols follow Fig. 5. |
| In the text | |
 |
Fig. 10 XIS and PIN spectra and best-fit model. The XIS spectra are binned to achieve 30σ in each bin only for display. The symbols follow Fig. 5. |
| In the text | |
 |
Fig. 11 Best-fit values and 1σ uncertainties for the spectral parameters with different outer source extraction radii. Black symbols indicate that the ARF was calculated assuming the source brightness distribution of the ACIS-S3 image. Red symbols indicate that a point-like source was assumed. Here, we use the result from the joint fit to the three XIS devices, since the result of the individual fits gives the same trend. |
| In the text | |
 |
Fig. 12 XRT image of G21.5–0.9. The source (solid) and background (dashed) regions used for the spectral analysis are shown. |
| In the text | |
 |
Fig. 13 XRT (SX0) spectrum and best-fit model. The spectrum is binned to achieve 30σ in each bin only for display. The symbols follow Fig. 5. |
| In the text | |
 |
Fig. 14 Comparison of best-fit values (with 1σ statistical uncertainties) for the spectral parameters from the XRT fits. The solid line and grey shaded regions indicate the best-fit and 1σ statistical uncertainty range from joint fitting. |
| In the text | |
 |
Fig. 15 EPIC spectra and the best-fit model. The spectra are binned to achieve 30σ in each bin only for display. The symbols follow Fig. 5. |
| In the text | |
 |
Fig. 16 Best-fit values (with 1σ uncertainties) for the spectral parameters, using different lower energy values in the fitting. |
| In the text | |
 |
Fig. 17 Comparison of the best-fit FX,soft or FX,hard values (with 1σ statistical uncertainties) from the joint fitting done with the other parameters (Γ and NH) tied among all the soft-band or hard instruments. |
| In the text | |
 |
Fig. 18 Scatter plot of the best-fit Γ versus NH values (with the 1σ uncertainties) for all soft-band instruments. |
| In the text | |
 |
Fig. 19 Scatter plot of the best-fit NH versus FX, soft values (with the 1σ statistical uncertainties) for all soft-band instruments. |
| In the text | |
 |
Fig. 20 Scatter plot of the best-fit Γ versus FX,soft values (with the 1σ statistical uncertainties) for all soft-band instruments. |
| In the text | |
 |
Fig. 21 Scatter plot of the best-fit Γ versus FX,hard values (with the 1σ uncertainties) for all hard-band instruments. |
| In the text | |
 |
Fig. 22 Same as Fig. 20, but with the fitting performed in the 2.0–8.0 keV band with a fixed NH value to focus on the difference in Γ in the hard band. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


