| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015166 | |
| Published online | 30 November 2010 | |
Spectra disentangling applied to the Hyades binary θ2 Tauri AB: new orbit, orbital parallax and component properties⋆,⋆⋆
1
Koninklijke Sterrenwacht van België, Ringlaan 3, 1180
Brussel, Belgium
e-mail: kbtorres2003@yahoo.com.br, patricia.lampens@oma.be
2
GEPI & UMR CNRS 8111, Observatoire de Paris,
92195
Meudon Cedex,
France
3
IPR Université de Rennes 1, Campus de Beaulieu 3, 35042
Rennes Cedex,
France
4
Astronomical Institute, Academy of Sciences of the Czech
Republic, 25165
Ondřejov, Czech
Republic
Received:
7
June
2010
Accepted:
4
October
2010
Aims.θ2 Tau is a detached and single-lined interferometric-spectroscopic binary as well as the most massive binary system of the Hyades cluster. The system revolves in an eccentric orbit with a periodicity of 140.7 days. Its light curve furthermore shows a complex pattern of δ Scuti-type pulsations. The secondary has a similar temperature but is less evolved and fainter than the primary. In addition, it is rotating more rapidly. Since the composite spectra are heavily blended, the direct extraction of radial velocities over the orbit of component B was hitherto unsuccessful. Our aim is to reveal the spectrum of the fainter component and its corresponding Doppler shifts in order to improve the accuracy of the physical properties of this important “calibrator” system.
Methods. Using high-resolution spectroscopic data recently obtained with the Elodie (Observatoire de Haute-Provence, France) and Hermes (Roque de Los Muchachos, La Palma, Spain) spectrographs, and applying a spectra disentangling algorithm to three independent data sets including CfA spectra (Oak Ridge Observatory, USA), we derived an improved spectroscopic orbit. We next used a code based on simulated annealing and general least-squares minimization to refine the orbital solution by performing a combined astrometric-spectroscopic analysis based on the new spectroscopy and the long-baseline data from the Mark III optical interferometer.
Results. As a result of the performed disentangling, and notwithstanding the high degree of blending, the velocity amplitude of the fainter component is obtained in a direct and objective way. Major progress based on this new determination includes an improved computation of the orbital parallax (still consistent with previous values). Our mass ratio is in good agreement with the older estimates of Peterson et al. (1991, 1993), but the mass of the primary is 15–25% higher than the more recent estimates by Torres et al. (1997) and Armstrong et al. (2006).
Conclusions. The evolutionary status of both components is re-evaluated in the light of the revisited properties of θ2 Tau AB. Due to the strategic position of the components in the turnoff region of the cluster, the new determinations imply stricter constraints for the age and the metallicity of the Hyades cluster. We conclude that the location of component B can be explained by current evolutionary models, but the location (and the status) of the more evolved component A is not trivially explained and requires a detailed abundance analysis of its disentangled spectrum. The improved accuracy (at the 2% level) on the stellar masses provides a useful basis for the comparison of the observed pulsation frequencies with suitable theoretical models.
Key words: astrometry / techniques: high angular resolution / binaries: visual / binaries: spectroscopic / stars: fundamental parameters / stars: individual:θ2Tauri
Based on observations obtained at the 1.93-m telescope of the Observatoire de Haute Provence, the 1.2-m Mercator telescope at the Roque de los Muchachos Observatory (in the framework of the Hermes Consortium) and the 1.5-m Wyeth telescope at Oak Ridge Observatory.
Full Table 4 is only available in electronic form at http://www.aanda.org
© ESO, 2010
1. Introduction
A modern research topic that we are currently pursuing is the study of binary and multiple stars with at least one pulsating component. The advantages of studying pulsating components in well-detached systems are manyfold, e.g. both the theories of stellar evolution and of stellar pulsation can be accurately tested and refined. Accurate component properties compared to suitably chosen theoretical isochrones indeed allow to obtain information on the object’s age and evolutionary path and are usually necessary to help discriminate among various possible pulsation models.
We selected the δ Scuti star θ2 Tau for a careful study for three reasons: (a) it is a detached, spectroscopic binary resolved by long-baseline interferometry (Armstrong et al. 2006, hereafter AM06); (b) it is a member of the Hyades open cluster at a mean distance of 45 pc (Perryman et al. 1998); (c) the evolutionary status of the primary component is still under heavy debate (Torres et al.1997, hereafter TSL97; Lastennet et al.1999, and AM06).
θ2 Tau (HD 28319 = HIP 20894 = 78 Tau) is the most massive
main-sequence star of the Hyades cluster: it is located at the main-sequence turnoff region
of the isochrone best fitting the individual members of the cluster (Lebreton et al. 2001, hereafter LE01). It forms a quadruple system with
θ1 Tau (=77 Tau), a common proper motion companion at an
angular separation of 5 6 .
The brighter component is a single-lined spectroscopic binary (SB1) which was resolved by
long-baseline interferometry (Shao et al. 1991; Pan et al. 1992; Hummel
& Armstrong 1992). The orbital period of the binary is 140.7 days with an
eccentricity of about 0.7. The primary component, θ2 Tau A, has
been classified as A7 III and rotates with Vsini =
70 km s-1(Frémat et al. 2006). It is very
hard to detect the secondary, θ2 Tau B, spectroscopically
because the Doppler shifts are only a fraction of the width of its broad spectral lines. The
secondary is less evolved and therefore fainter than θ2 Tau A.
TSL97 treated θ2 Tau as a double-lined spectroscopic
binary (SB2) using a 2D-cross correlation method in which they considered the extra pull of
the secondary in order to obtain improved radial velocities of the primary component.
However, they were unable to obtain reliable radial velocity measurements for
θ2 Tau B and they only observed its (orbital) influence on the
velocities of the brighter companion. For these reasons, also the mass ratio could not be
directly determined. Still, they were able to derive a interferometric-spectroscopic orbit
and to determine the component masses and the distance of the binary by exploring and
assuming a range of values for the mass ratio and the rotational velocity of the secondary
star. The orbital parallax of their solution agrees well with the Hipparcos trigonometric
parallax (Perryman & ESA 1997). The outcome is
that the components have different projected rotational velocities: TSL97 obtained a best
fit assuming KB = 38 km s-1 and
VBsini = 110 km s-1, with
resulting component masses of
MA = 2.42 ± 0.30 M⊙ and
MB = 2.11 ± 0.17 M⊙. Recently,
the component masses and luminosities have been redetermined by AM06. From their
interferometric data coupled to the Hipparcos secular (i.e. proper-motion based) parallax
(de Bruijne et al. 2001) and a compatible choice of
spectroscopic orbits, these authors obtained component masses of
MA = 2.15 ± 0.12 M⊙ and
MB = 1.87 ± 0.11 M⊙.
6 .
The brighter component is a single-lined spectroscopic binary (SB1) which was resolved by
long-baseline interferometry (Shao et al. 1991; Pan et al. 1992; Hummel
& Armstrong 1992). The orbital period of the binary is 140.7 days with an
eccentricity of about 0.7. The primary component, θ2 Tau A, has
been classified as A7 III and rotates with Vsini =
70 km s-1(Frémat et al. 2006). It is very
hard to detect the secondary, θ2 Tau B, spectroscopically
because the Doppler shifts are only a fraction of the width of its broad spectral lines. The
secondary is less evolved and therefore fainter than θ2 Tau A.
TSL97 treated θ2 Tau as a double-lined spectroscopic
binary (SB2) using a 2D-cross correlation method in which they considered the extra pull of
the secondary in order to obtain improved radial velocities of the primary component.
However, they were unable to obtain reliable radial velocity measurements for
θ2 Tau B and they only observed its (orbital) influence on the
velocities of the brighter companion. For these reasons, also the mass ratio could not be
directly determined. Still, they were able to derive a interferometric-spectroscopic orbit
and to determine the component masses and the distance of the binary by exploring and
assuming a range of values for the mass ratio and the rotational velocity of the secondary
star. The orbital parallax of their solution agrees well with the Hipparcos trigonometric
parallax (Perryman & ESA 1997). The outcome is
that the components have different projected rotational velocities: TSL97 obtained a best
fit assuming KB = 38 km s-1 and
VBsini = 110 km s-1, with
resulting component masses of
MA = 2.42 ± 0.30 M⊙ and
MB = 2.11 ± 0.17 M⊙. Recently,
the component masses and luminosities have been redetermined by AM06. From their
interferometric data coupled to the Hipparcos secular (i.e. proper-motion based) parallax
(de Bruijne et al. 2001) and a compatible choice of
spectroscopic orbits, these authors obtained component masses of
MA = 2.15 ± 0.12 M⊙ and
MB = 1.87 ± 0.11 M⊙.
As a member of a well-studied cluster, both the metallicity and the distance of θ2 Tau are known within narrow boundaries. Such a large amount of information concerning the fundamental properties of the components of a detached binary system (with components in a different evolutionary phase) has led to various attempts of confrontation with stellar evolutionary models. Before Hipparcos (Perryman & ESA 1997), Królikowska (1992) concluded that the evolutionary status of θ2 Tau was either in the thick H(ydrogen)-shell burning phase (without overshooting) or in the H-core burning phase (with overshooting). From the location in a colour-magnitude diagram and a best fit with an isochrone of age ≈ 630 Myr and metallicity Z = 0.027, TSL97 (using Bertelli et al. 1994 ’s models) concluded that the primary is in a phase near H-core exhaustion, immediately preceding the phase of overall contraction. But, because both binarity and fast rotation may affect the colour indices, the uncertainty remained. Lastennet et al. (1999) used the binary to evaluate various stellar evolution models stating that “the three theoretical models allow to fit correctly the system (...) in agreement with the more recent constraints available about the metallicity of the Hyades cluster”. They found that the primary could be in the H-core burning (end) phase or in the H-shell burning (beginning) phase depending on its metallicity. In an extensive study of the Hyades cluster, de Bruijne et al. (2001) again used θ2 Tau and concluded that the agreement with the CESAM isochrones (including convective core overshoot) was remarkably good. LE01 derived a maximum age of 650 Myr and the initial helium content of the cluster by comparing the mass-luminosity relation based on a set of five binaries also containing θ2 Tau with predictions from models appropriate for the Hyades (using Y = 0.26). They issued a warning for the stars located in the turnoff region claiming that “the interpretation is complicated by the effects of rotation and overshooting that make either model or photometric data uncertain” and that “improvement of the mass of θ2 Tau A would certainly better constrain the overshooting by anchoring the star more precisely on its isochrone”. More accurate masses is precisely what AM06 obtained. However, the lower masses and/or brighter luminosities do not conform with some of the recent stellar evolutionary models, i.e. Girardi et al. (2000) and LE01, for the age and metallicity of the Hyades. Finally, Yıldız et al. (2006) tried to model both components of θ2 Tau using models including differential rotation. They concluded that good agreement was found for θ2 Tau A with Z = 0.024 and an age of 700 Myr. However, the same model could not explain the location of the secondary component in the colour-magnitude diagram. The evolutionary status of both components of θ2 Tau is therefore still a non-trivial issue.
The system has one more attractive feature: its primary component is a typical multiperiodic δ Scuti star. Various multi-site campaigns have been conducted. Breger et al. (1989) obtained five closely spaced and stable frequencies, all of which had amplitudes below 0.01 mag. They discarded rotational splitting since it could not explain the observed frequency separations and proposed a mixture of modes of different l and m values. Kennelly et al. (1996) discussed a large set of radial velocity and line profile data from which up to seven frequencies emerged with only three frequencies in common with the previous analysis. They suggested long-term (>6 yr) amplitude variability and a combination of low and high degree modes. Amplitude variability on a 10 yr time scale is also claimed by Li et al. (1997). Both components are located within the lower Cepheid instability strip (where the δ Scuti stars are observed) but it seems well established that the more massive primary is the pulsating star (Breger et al. 1989; Kennelly et al. 1996). The results of a vast multi-site campaign (Breger et al. 2002) revealed the presence of 11 frequencies in the range 10−15 c/d and 2 frequencies in the range 26−27 c/d (see also Poretti et al. 2002). After having modelled the light-time corrections, they attributed the first 11 frequencies to pulsations of the primary component while the last two frequencies probably originate from the secondary component. Currently, because of the limited frequency range of the detected modes, the complex frequency spectrum does not allow a proper mode identification.
Because they are located in the turnoff region of the cluster, the exact locations of both stars in the H-R diagram allow to distinguish between different evolutionary models and different isochrones, thus making them extremely useful for the constraints they impose on the chemical composition and the age of the Hyades (provided that their physical properties can be determined very accurately). As “calibrator stars”, they could indicate how important the mixing processes (such as convective core overshooting or rotational mixing) are in the internal layers of stars from the Hyades cluster (LE01). The knowledge of accurate fundamental component properties furthermore holds good potential for a reliable pulsation modelling of the two stars.
The outline of this article is the following: the observations are presented in Sect. 2 while the analysis method of spectra disentangling is explained in some detail in Sect. 3. In Sect. 4, we will compare the component spectra obtained from the application of the spectra disentangling method with an observed spectrum of a reference star as well as with synthetic spectra. Especially in the case of the fainter component, not easily discernable in the observed composite spectra, this will show that the mathematically reconstructed spectra are plausible from the viewpoint of physics. Section 5 deals with the orbital analysis obtained by combining both spectroscopic and interferometric data. In Sect. 6, we thoroughly discuss the quality of our results and their implication in the light of the component’s evolutionary stages. We end by mentioning the new perspectives and the planned future work.
2. Observations
The spectroscopic data consist of (a) 44 échelle spectra (R = 42 000; S/N1 ~200−300 in V; resolution element of 7.1 km s-1) obtained by us with Elodie at the 1.93 m telescope of the Observatoire de Haute-Provence covering the wavelength range from 389.5 to 681.5 nm; (b) 13 échelle spectra (R ~ 85 000; S/N ~ 220−340 in V; resolution element of 3.5 km s-1) obtained by us with the Hermes spectrograph at the 1.2 m Mercator telescope located at the Roque de Los Muchachos Observatory, La Palma, covering the wavelength range from 377 to 900 nm; (c) 70 échelle spectra (R ~ 35 000; S/N ~ 50; resolution element of 8.5 km s-1) obtained by TSL97 using the center for astrophysics (CfA) spectrograph mounted on the 1.5 m Wyeth reflector at the Oak Ridge Observatory, covering a wavelength range of 26 Å around 519 nm; (d) 16 single-order coudé spectra (R ~ 25 000; S/N ~ 100–200; resolution element of 14 km s-1) obtained at the 2-m telescope of the Ondřejov Observatory of the Astronomical Institute of the Academy of Sciences of the Czech Republic, covering the wavelength range 517–589 nm.
The Elodie data were reduced using the Intertacos pipeline (Baranne et al. 1996) available at the telescope, while the Hermes data were treated using the Hermes reduction pipeline (Raskin et al. 2010). These reduction procedures perform the order extraction, the offset and flat-field correction, and the wavelength calibrations. The resulting wavelength scale was corrected for the Earth’s motion relatively to the barycenter of the solar system using the Iraf software package. The spectra collected at the Ondřejov Observatory were reduced with the procedure described by Škoda & Šlechta (2002).
In total, 127 spectra2 covering the entire orbital cycle and full range in radial velocity amplitude were available for the analysis3. We furthermore made use of 34 best-fit angular separations (ρ) and position angles (θ) derived from the measurements obtained by Armstrong et al. (1992), Hummel & Armstrong (1992) and AM06 with the Mark III long-baseline optical interferometer.
3. Spectra disentangling
Spectral intervals used in the spectra disentangling analysis.
Our analysis was divided in two steps: (a) the determination of the orbital parameters from a selected wavelength region; and (b) the computation of the intrinsic component spectra, keeping the orbital parameters fixed during the convergence, for other wavelength regions (cf. Table 1).
In step (a), the search for the orbital parameters was done using 127 spectra weighted according to their S/N ratio in the wavelength region R3 (cf. Table 1). This region was chosen for it allows the highest accuracy on the determination of the component radial velocities among all selected regions (cf. Fig. 1: the standard deviation shows a deep local minimum in that region).
 |
Fig. 1 Uncertainty of the radial velocity information content as a function of wavelength, assuming S/N = 100. The standard deviation, SRV, was computed over a 60 Å wide interval, shifted with a step of 10 Å. The primary and secondary are represented, respectively by a full and a dashed line. Each wavelength region (Table 1) is represented by a small horizontal line. |
![\begin{equation} \chi^2 = \sum_j W(t) [I_{{\rm obs},t}(j) - (\ell_{\rm A} I_{\rm A} (j + \delta_{{\rm A},t})+\ell_{\rm B} I_{\rm B} (j + \delta_{{\rm B},t})]^2, \label{Eq1} \end{equation}](/articles/aa/full_html/2011/01/aa15166-10/aa15166-10-eq42.png) (1)where
Iobs,t(j) represents a set
of normalized composite spectra at orbital phase t and
pixel j with weight W(t),
IA(j) and
IB(j) are the two component spectra,
δA,t and
δB,t are the component Doppler shifts. The
component’s respective (time-independent) light contributions are indicated by
ℓA and ℓB. Since a complex
structure with secondary minima was revealed in the χ2 space
(due to the broad lines of the secondary component), a search for the global minimum was
executed for a grid of KB-values (Fig. 2). The final spectroscopic orbit computation was performed with
KB = 43.4 km s-1 determined from this grid search
(cf. Table 3, upper panel). We adopted an uncertainty
of the order of 0.5 km s-1 on this value, corresponding to treating as equivalent
all the solutions with 298 840 < χ2 < 298 850, as
indicated by Fig. 2. Unfortunately, Fourier
disentangling does not (yet) include any error estimation of the orbital elements.
(1)where
Iobs,t(j) represents a set
of normalized composite spectra at orbital phase t and
pixel j with weight W(t),
IA(j) and
IB(j) are the two component spectra,
δA,t and
δB,t are the component Doppler shifts. The
component’s respective (time-independent) light contributions are indicated by
ℓA and ℓB. Since a complex
structure with secondary minima was revealed in the χ2 space
(due to the broad lines of the secondary component), a search for the global minimum was
executed for a grid of KB-values (Fig. 2). The final spectroscopic orbit computation was performed with
KB = 43.4 km s-1 determined from this grid search
(cf. Table 3, upper panel). We adopted an uncertainty
of the order of 0.5 km s-1 on this value, corresponding to treating as equivalent
all the solutions with 298 840 < χ2 < 298 850, as
indicated by Fig. 2. Unfortunately, Fourier
disentangling does not (yet) include any error estimation of the orbital elements. 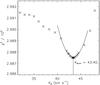 |
Fig. 2 Distribution of the χ2 of the solutions derived by spectra disentangling as a function of the radial velocity semi-amplitude of the secondary. |
In order to verify whether the numerical problem is well-conditioned, the condition numbers Cm (i.e. the ratio of the largest to the smallest eigenvalue in the covariance matrix) for the set of equations for each Fourier mode m was computed (see Fig. 3). log C is a rough measure of the loss of precision on the Fourier amplitudes in the component spectra, expressed in units of number of digits. One digit is lost, relative to the bottom value of log C, in the m = 1 mode and this provoked a low-level sinusoidal undulation in the reconstructed spectra (see Hensberge et al.2008 for more explanation).
 |
Fig. 3 Logarithm of the condition number (log C) versus the Fourier mode computed for θ2 Tau using the radial velocities derived with FDBinary. |
The indeterminacy of the m = 0 mode implies that the light ratio between
the two components has to be estimated from external information. Therefore, it was
determined for each spectral region using the differential magnitude (Δm)
measurements reported by AM06 (cf. their Table 3). A
linear dependence of Δm on λ represents these measurements
within their uncertainties. A weighted fit gives: 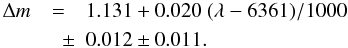 (2)The zero-point at the weighted average
wavelength of 6361 Å was chosen such that the constant and the gradient are uncorrelated.
Equation (2) fixes the light ratio (see
black line in Fig. 5), used to renormalize the
component spectra, with the central wavelength
λ = λcj of
each region j (cf. Table 1)
substituted in the equation.
(2)The zero-point at the weighted average
wavelength of 6361 Å was chosen such that the constant and the gradient are uncorrelated.
Equation (2) fixes the light ratio (see
black line in Fig. 5), used to renormalize the
component spectra, with the central wavelength
λ = λcj of
each region j (cf. Table 1)
substituted in the equation.
In a first step, we fixed the value of the luminosity ratio in order to verify whether the disentangled component spectra are consistent with the assumption of equal line blocking, since both components have very similar colours (Peterson et al. 1993) and must have the same overall chemical composition. Figure 4 compares the line blocking for each spectral region in both components. The result is sensitive to sub-percent changes in the continuum levels, in other words, to the solution of the Fourier mode m = 0. Physical constraints on pseudo-continuum data points deliver limits to the coupled continuum placement (represented by grey and black symbols). The diagonal in the figure represents the locus of equal line blocking. As seen from this figure, the assumption of equal line blocking is nowhere (i.e. in none of the studied regions) in contradiction with the allowed range of the choice of the continuum levels. Under this assumption, the offset in continuum level of the primary’s spectrum may be larger than the previously derived limits (see, for example, R6 in Fig. 4), but it will never exceed the level of 0.5%. Such an offset remains insignificant in the context of the present study.
Therefore, in a second step, we evaluated which range of continuum positions was acceptable around the one for assumed equal line blocking, and, in turn, estimated the range of possible monochromatic luminosity ratios from the disentangled component spectra. Figure 5 shows that our spectroscopic estimates are in concordance with the interferometric ones, though are less accurate than the latter. The grey intervals represent the possible values for ℓB/ℓA derived from the renormalization procedure (Ilijić et al. 2004) used to correct the disentangled component spectra into physically meaningful spectra.
 |
Fig. 4 Line blocking of θ2 Tau AB for each of the 7 spectral regions described in Table 1. See Sect. 3. |
 |
Fig. 5 Determination of the light contributions of θ2 Tau AB, using the disentangled component spectra. The grey vertical bars represent the acceptable values for ℓB/ℓA, for each spectral region (Table 1). The ℓB/ℓA predicted by AM06 are also shown (i.e. black diamonds with error bars), as well as Eq. (2) (straight black line). The grey line represents the slope of the flux ratio curve of two synthetic spectra with a difference of temperature corresponding to +200 K, in the sense (component B – component A). See Sects. 3 and 4.1. |
4. Component spectra
4.1. Comparison with a reference stellar spectrum
We compared the reconstructed component spectra to the observed spectrum of the δ Scuti star HD 2628 (Vsini ~ 20 km s-1) which is classified as A7 III, as is also the case of the binary system θ2 Tau AB (AM06). For visual concordance, the reference spectrum was shifted by 39.5 km s-1 and broadened by 66 km s-1 and 118 km s-1 in order to match the spectra of component A and B respectively.
Figure 6 shows how well the reconstructed component spectra agree with the reference star spectrum, especially for the spectrum of component A which matches better the luminosity class of HD 2628. The spectra of component B may, at the one per cent level, still be affected by low-amplitude wiggles corresponding to larger uncertainties in the solution of the m = 2 or even slightly higher Fourier modes. The position and shape of the lines coincide well, showing the power of the spectra disentangling technique in reconstructing component spectra without any a priori assumptions about their spectral features. Note, however, that the shape of the Balmer Hβ-line (Fig. 6, panels R2) indicates a slight temperature difference between the two components of θ2 Tau and the reference star (HD 2628 is about 400 K cooler than θ2 Tau AB).
 |
Fig. 6 Comparison between the reconstructed component spectra of θ2 Tau AB (grey) and the spectrum of HD 2628 (black), for the regions listed in Table 1. The latter spectrum was broadened by 66 and 118 km s-1, respectively for components A and B, and shifted by 39.5 km s-1. |
4.2. Comparison with synthetic spectra
In order to determine Vsini and the system velocity γ, we also compared the reconstructed spectra with synthetic spectra in the regions R3 to R5 of Table 1 and averaged the results.
Independently fitting the Hα and Hβ-lines of each component spectrum, an average effective temperature over these two H-lines was determined: 7800 ± 170 K for component A and B. We also derived two limits for the temperature difference, ΔTeff,B − A, by computing synthetic spectra with slightly different temperatures and by imposing that their flux ratio curve should pass through all interferometric measurements (cf. black error bars in Fig. 5). Note that this curve is more sensitive in the bluest part of the wavelength range. These limits suggest a temperature difference, ΔTeff,B − A, ranging from +100 to +500 K (best fit at +200 K, cf. grey line), which is also consistent with our derived values of the component temperatures, considering their uncertainty.
A small difference in effective temperature is also confirmed by the interferometric measurement of the colour difference of ~−0.006 mag (Peterson et al. 1993). For both components, log g was estimated from the averaged effective temperatures and the components luminosities (see Sect. 5.2). Table 2 summarizes the atmospheric parameters of θ2 Tau using the synthetic spectra and compares them with the parameters adopted (except VBsini and γ, which were determined by TSL97).
The Str mgren photometric data provided by the
General Catalogue of Photometric Data (Mermilliod
et al.1997) for
θ2 Tau: V = 3.41,
b − y = 0.100, m1 = 0.197,
c1 = 1.012, u − b = 1.606,
and β = 2.831, confirm these effective temperatures. Indeed, a combined
effective temperature Teff,AB = 7928 K results from an updated
version of the standard calibration by Moon &
Dworetsky (1985) (Napiwotski, priv. comm.).
mgren photometric data provided by the
General Catalogue of Photometric Data (Mermilliod
et al.1997) for
θ2 Tau: V = 3.41,
b − y = 0.100, m1 = 0.197,
c1 = 1.012, u − b = 1.606,
and β = 2.831, confirm these effective temperatures. Indeed, a combined
effective temperature Teff,AB = 7928 K results from an updated
version of the standard calibration by Moon &
Dworetsky (1985) (Napiwotski, priv. comm.).
Atmospheric parameters of θ2 Tau A and B.
 |
Fig. 7 Intrinsic spectra of θ2 Tau A and B (in black) compared to synthetic spectra computed for the Hyades metallicity ([Fe/H] = +0.14 in red; [Fe/H] = +0.19 in green; LE01), and the solar metallicity (in blue). The luminosity ratio is fixed to 0.35. The Teff, Vsini and log g values were fixed to those ones described in Table 2. |
5. Combined orbital analysis
Accurate orbital solutions of stellar systems are obtained when different techniques are used together to provide input data to a single least-squares analysis, thereby leading to the simultaneous determination of all the parameters, also including an independent determination of the distance to the system. To this aim, a combined interferometric-spectroscopic analysis of θ2 Tau was performed (Lampens et al. 2009). Unfortunately, to our knowledge, no software is available that directly combines the orbital solution of spectral disentangling with the astrometry. Thus, radial velocities must be specified, with uncertainties. These uncertainties will define the relative weights of the radial velocities with respect to those of the relative positions (interferometry). We used 2 × 127 radial velocities obtained from the Elodie, Hermes and CfA spectra and 34 best-fit angular separations ρ and position angles θ (Sect. 2).
5.1. Input radial velocities and their uncertainties
There exist two options for the input radial velocities: (a) we may derive radial velocities applying the cross-correlation technique using the reconstructed component spectra as templates; or (b) we may compute radial velocities from the spectroscopic orbit derived with FDBinary. The first delivers “observed” (noisy) measurements, but the orbit derived from them will not exactly correspond to the orbit derived with FDBinary. The orbit that would be derived from the radial velocities resulting from the cross-correlation is of slightly inferior quality than the self-consistent orbit obtained from FDBinary. Hence, option (b) was preferred. Nevertheless, we checked that choosing option (a) is consistent with the combined astrometric-spectroscopic solution. We also evaluated the radial velocity information content in the spectral region, assuming that random noise largely dominates the error budget in order to derive associated uncertainties (see e.g. Fig. 1). In this sense, these estimates are lower limits to the true uncertainties. The principles for a single-star spectrum are elaborated in several papers, e.g. Verschueren & David (1999) and for a binary in Hensberge et al. (2000). The latter uncertainties essentially contain a correction factor (relative to the single-star case) for the correlation at a given orbital phase between the spectral gradients in the Doppler-shifted component spectra, and a multiplicative factor inversely proportional to the contribution of the component to the total light (Vaz et al., in prep.). Typical uncertainties thus derived are given by the following median values: σ(RVA) = 0.15 and σ(RVB) = 0.68 km s-1 (Elodie spectra); σ(RVA) = 0.10 and σ(RVB) = 0.54 km s-1 (Hermes spectra); σ(RVA) = 0.65 and σ(RVB) = 3.10 km s-1 (CfA spectra). In addition, we also made sure that these uncertainties in radial velocity are compatible with the scatter that one would obtain by (re)computing the radial velocities from the range of acceptable orbits derived with FDBinary which correspond to equivalent solutions in the χ2 plane (see Fig. 2). Table 4 lists the uncertainties on the component radial velocities derived with FDBinary.
5.2. Final orbital elements
The combined solution was computed using the code vbsb2, which performs a global exploration of the parameter space followed by a local least-squares minimization (Pourbaix 1998). The essence of the method resides in a simultaneous adjustment of various data types performed in two steps: (a) the minimum of the objective function is globally searched following the principles of simulated annealing (SA, Metropolis et al. 1953); and (b) the best estimate of a large number of trials provides the starting point of a local least-squares minimization (using the procedure of Broyden-Fletcher-Goldstrab-Shanno).
Table 3 (bottom panel) lists the orbital elements and their standard deviations obtained after 200 runs with SA, exploring a small interval around the period provided by TSL97. The orbital elements were slightly updated in the combined astrometric-spectroscopic solution (cf. Table 3), without significant effect on the derived component spectra. Interestingly, our determinations of the mass ratio (0.754 ± 0.001) and KB are in close agreement with the first estimates derived by Peterson (1991) and Peterson et al. (1993) (see Table 1 in AM06 for the mass ratio estimate using Peterson’s corrected radial velocities).
Orbital solutions of θ2 Tau A and B from various techniques.
θ2 Tau AB radial velocities.
 with respect to our solution as we follow
the spectroscopic convention (while TSL97 followed Pan
et al. (1992), hereafter PS92). The marginally significant change in the value of
the eccentricity places it now in-between the discordant values of TSL97 and AM06. As an
additional check, we verified that the residuals in both position angle and angular
separation show no systematic offset and the standard deviations,
σ(O−C)θ = 1.2o
and σ(O−C)ρ = 0.47 mas, agree with
the published error bars on the measurements.
with respect to our solution as we follow
the spectroscopic convention (while TSL97 followed Pan
et al. (1992), hereafter PS92). The marginally significant change in the value of
the eccentricity places it now in-between the discordant values of TSL97 and AM06. As an
additional check, we verified that the residuals in both position angle and angular
separation show no systematic offset and the standard deviations,
σ(O−C)θ = 1.2o
and σ(O−C)ρ = 0.47 mas, agree with
the published error bars on the measurements.
In conclusion, the astrometric part of the combined solution is in excellent agreement with the pure astrometric solution computed by AM06, except (marginally) for the eccentricity. Our value is also constrained by the spectroscopic data, and lies in-between the value derived by AM06 and that of TSL97 (see Table 3). Also note that the uncertainties of the visual orbital elements are very similar to those published by AM06.
The new orbital parallax has a relative error, σπ/π, of 0.5%, which is several times more precise than the one of TSL97 (π = 21.22 mas, σπ/π = 3.6%) and the ones measured by the Hipparcos astrometric satellite (Perryman & ESA1997: π = 21.89 mas, σπ/π = 3.8%; van Leeuwen2007: π = 21.69 mas, σπ/π = 2.1%). Though the value of the new parallax is slightly smaller, it remains compatible with these formerly derived values, within the larger uncertainties of these previous determinations. However, the new value is in disagreement with the secular parallax derived by de Bruijne et al. (2001) (see Table 3 (σπ/π = 1.6%) and Sect. 6.1).
The combined orbital solution is graphically illustrated by Fig. 8 (astrometric observations and combined solution) and 9 (spectroscopic observations and combined solution). The astrometric-spectroscopic orbital solution previously derived by TSL97 is shown for comparison. We remark that these authors adopted some visual orbital elements of the preliminary orbit published by PS92 in their combined analysis. The most conspicuous difference between both studies (ours – TSL97) is the larger radial velocity amplitude of component B, while there is excellent agreement for the radial velocity curve of component A over the entire phase range. Note that, even though a homogeneous coverage in orbital phase was achieved, we still do not have a perfect coverage in radial velocity in the critical part of the orbit where the radial velocity is changing fastest (only 13% of the spectra have a radial velocity larger than 24.8 km s-1 for component A).
At this stage, it is relevant to compare and explain the uncertainties quoted in Table 3. Here, we list the formal errors of a (local) least-squares minimization process. These show a significant improvement of (at least) a full order of magnitude over the errors listed by TSL97. However, TSL97 did not compute their solution using full least-squares analysis (since the interferometric data were not available to them). In addition, some of their uncertainties were derived by way of Monte Carlo simulations assuming Gaussian errors on the various parameters. As already mentioned, with regard to the astrometric part of the solution, TSL97 adopted the visual orbital elements and the corresponding errors from PS92. Compared to this and other previous analyses performed with (subsets of) the Mark III data, the astrometric orbit derived by AM06 shows a major improvement in quality: from their Table 3, a factor of about 10 was gained in the accuracy of the visual orbital elements over that of the previous studies. Our work merely confirms the very high quality of their orbital solution.
On the other hand, with regard to the uncertainties in the spectroscopic part of the combined solution, we notice that the higher quality (higher S/N) of the 44 Elodie and 13 Hermes spectrahas led to the extraction of 5–10 times more precise radial velocities: the quality of the radial velocities is expected to be 5 times better if the ratio of their typical uncertainties is considered (e.g. Elodie versus CfA, see Sect. 5.1), and 10 times better if the ratio of the typical rms residual is considered (TSL97 derived a rms residual of 1.7 km s-1 in RVA whereas we have rms residuals of 0.15 and 0.20 km s-1 in RVA and RVB, respectively, over the entire data set). The gain might be somewhat larger considering the larger amount of spectra (127 instead of 70 spectra), as well as the robustness of the applied disentangling technique (the radial velocities in the observed spectra are bound by a Keplerian orbit which probably lowers the bias in the different parameters) and the improved astrometric orbit. But the somewhat less favourable distribution over the orbital velocity range of the new spectra in comparison with the CfA ones,might have limited the gain achieved. Hence, an overall improvement of a factor of (at least) 5 can be expected compared to TSL97. As a matter of fact, Table 3 suggests a gain with a factor slightly larger than 10 in the radial-velocity amplitudes.
This difference can be understood as these formal errors remain underestimates of the true errors. For example, the error mentioned for KA is ± 0.04 km s-1, which is about 3 times better than the median error in radial velocity extracted for that component (see Sect. 5.1). This seems reasonable. However, the error mentioned for KB is ± 0.14 km s-1, which is about 5 times better than the median error in radial velocity extracted for that component (see Sect. 5.1). An uncertainty 2 (perhaps 3) times as large for KB might be closer to the true uncertainty value, in particular if we also consider the shape of the χ2 minimum in Fig. 2. Indeed, the formal error based on an increase by a unit of χ2 is 0.15 km s-1 (assuming a perfect parabolic shape near minimum), i.e. similar to the uncertainty listed in Table 3. However, such an estimate corresponds to a strict lower limit of the uncertainty since it assumes random errors. With resampled data and the ambiguity in tracing of the continuum levels, uncertainties on subsequent pixels get correlated, which unavoidably contributes to introducing some bias in one spectrum with respect to the others. To stay on the safe side, we will adopt from hereon an error twice as large for KB, i.e. ± 0.28 km s-1 (instead of ± 0.14 km s-1). As a consequence of the laws of error propagation, we will also consider a larger error contribution of the semi-axis major αB (the semi-axis major of component B with respect to the centre of mass expressed in km s-1) and on MA by a factor of 2. The former leads to an error budget on the orbital parallax increased by a factor of 1.4 (determined by the ratio of the apparent and the true semi-axis major).
 |
Fig. 8 Combined orbital solution plotted with the astrometric data from Armstrong et al. (2006). |
 |
Fig. 9 Combined orbital solution (full lines) plotted with component radial velocities(symbols “°” for component A and “□” for component B) derived with FDBinary. Combined orbital solution derived by TSL97 (dashed lines). The different data sets obtained with the Elodie (observatoire de haute-provence, OHP), Hermes (Roque de Los Muchachos Observatory, LPA) and CfA spectrographs are represented by the different shades of grey, see legend. |
Adopting the new parallax of Table 3 and ΔmV = 1.11 ± 0.01 mag (derived from Eq. (2)) we obtain the following component absolute magnitudes: MvA = 0.33 ± 0.03 mag and MvB = 1.44 ± 0.03 mag. This determination is more accurate than before (thanks to the improved parallax determination) and remains in good agreement with the one provided by TSL97. However, it differs from that by AM06 at the 3σ-level.
Fundamental properties of θ2 Tau A and B components.
6. Comparison with evolutionary models
6.1. Previous status
Various attempts to compare the components’ locations in the Hertzsprung-Russell (H-R) diagram with evolutionary models have already been done, though not always with great success. The importance of finding the correct evolutionary models may also have implications for the entire Hyades cluster. Lastennet et al. (1999) tested 3 independent sets of stellar evolutionary tracks: those of the Geneva and Padova groups (cf. Lastennet et al. 1999, for the references) and those of Claret & Giménez (1992). They found some discrepant results from isochrone fits for 3 visual binaries using the Hipparcos parallaxes (including θ2 Tau) and were unable to find a single isochrone passing through the locations of both components of V818 Tau (van Bueren 22). However, LE01 remarked that the models previously used (taken from the literature) did not match the cluster’s chemical composition. Using the location of V818 Tau, these authors were able to exclude the isochrone at 625 Myr with the solar-scaled abundance for He (Y = 0.28), and derived the improved value Y = 0.255 ± 0.009. They furthermore concluded that an isochrone with ([Fe/H] = +0.19, Y = 0.27) matched best the observed main-sequence of the Hyades, whereas a chemical composition with both ([Fe/H] = +0.19, Y = 0.27) and ([Fe/H] = +0.14, Y = 0.26) fitted well the locations of the 5 considered binaries (including θ2 Tau). In the turnoff region, rotational effects complicate the interpretation but the overall agreement is good (see Fig. 12 from LE01). However, in order to discriminate between the different models (e.g. with or without overshooting), the accuracy on the component masses, also of θ2 Tau, was still insufficient.
AM06 adopted the dynamical parallaxes based on the Hipparcos proper motions (de Bruijne et al. 2001) to revise the orbital solution of θ2 Tau (we recall that this parallax is inconsistent with our determination). These authors derived a total mass of 4.03 ± 0.20 M⊙. Using the spectroscopic mass ratio of TSL97, they computed the component masses and luminosities. They were however unsuccessful at modelling the component locations in the mass-luminosity and the Hertzsprung-Russell diagrams, even though they corrected the luminosities and the colours for the rotational effects assuming 3 different inclination angles: in each case, the masses appeared too small for the observed luminosities. Therefore, they claimed that the component properties of θ2 Tau did not match the current evolutionary tracks. However, the He abundance used in their model fits is not appropriate for the Hyades.
 |
Fig. 10 Location of θ2 Tau AB in the Hertzsprung-Russell diagram. The curves represent evolutionary tracks for the masses corresponding to θ2 Tau AB, the metallicity of the Hyades (following LE01) and three levels of overshooting, αOV (different black curves as indicated in the legend) and an isochrone of age of 650 Myr (red curve), all computed using the code Cesam (Morel & Lebreton 2008). |
6.2. Current status
The revised component properties (cf. Table 5) and, maybe more importantly, the higher accuracy with which they were obtained, make it worthwhile to review the location of the components of θ2 Tau in the evolutionary diagram. An isochrone model with the age and the chemical composition of the Hyades should be fitting the parameter box of both stars within the quoted uncertainties. We may also expect that sharper constraints might be put on the age and the abundance determination of the cluster, given the fact that the accuracies are (expected to be) of the order of 2% on the component masses and of the order of 4% on the component luminosities (i.e. an improvement with a factor of 6–7 with respect to previous determinations). This was already the case with V818 Tau (LE01), an eclipsing-spectroscopic binary whose component masses are known within 1% (Peterson & Solensky 1988).
In Fig. 10, we plotted the locations of θ2 Tau A and B in the H-R diagram using the temperatures and the masses from Table 5. We compare these locations with theoretical evolutionary tracks adopting the Hyades composition derived by LE01 ([Fe/H] = +0.14 and Y = 0.26). Three different values of overshooting were considered: zero overshoot (full lines), and overshoot values of 0.2 and 0.4, in units of the pressure scale height Hp (dashed, respectively dotted lines). As can be clearly seen from Fig. 10, the track with M = 2.16 M⊙ and zero overshoot passes through the box of component B (at an age of ≈ 600 Myr), while the tracks with M = 2.86 M⊙ are way too luminous compared to the location of the box representing component A. Nevertheless, an isochrone model of age 650 Myr and with the same chemical composition (thin line) passes through both boxes. We conclude that component B is indeed on the main sequence (as previous authors did), whereas the interpretation for component A remains enigmatic: neither convective core overshooting nor rapid rotation can be invoked to explain the observed discrepancy. Taking into account gravitational darkening due to rapid rotation would shift its observed location in the wrong direction (its non-rotating counterpart would be hotter if seen equator-on and fainter if seen pole-on, Frémat et al.2005). However, while non-zero overshoot would make the star evolve more rapidly (the star will be younger at the tams position), turbulent diffusion due to rapid rotation would make the star evolve more slowly (the star would be older at the tams position, Meynet & Maeder2000), shifting the observed location in the right direction. Another possibility which seems more plausible, is a change in chemical composition – in the sense of a higher metallicity. Interestingly, the disentangled spectra are going in the same sense. This, however, needs to be confirmed by a detailed chemical analysis of the component spectra.
Because of its location on the tip of the turnoff region, precisely θ2 Tau A was critical to the choice of the chemical composition suitable for the Hyades cluster in LE01’s work. It might be necessary to look into a few other solutions again. In particular, the higher metallicity and higher helium abundance of the ([Fe/H] = +0.19 and Y = 0.27) model, which fitted well the remainder of main-sequence stars in the cluster, should be re-investigated. However, such a detailed confrontation is beyond the scope of the present work. Furthermore, and for the first time, the availability of the disentangled component spectra opens the way to an abundance determination in both components as if they were single stars. The resulting disentangled component spectra thus provide two additional “calibrator” stars useful in a consistent analysis of the chemical composition of cluster members.
7. Summary
The fainter component of the system rotates rapidly such that its lines are continuously blended with those of the primary during the whole orbit. This resulted in a broad range of mass ratios published in the literature, ranging from 0.73 to 0.873. The spectra disentangling technique has proven, under these difficult conditions, to be adequate to obtain reliable orbital parameters as well as the intrinsic spectra of both components. These spectra, obtained from a pure mathematical technique without any a priori information about the component spectral features, permitted us to derive consistent and accurate atmospheric properties such as the component effective temperatures (Teff,A = Teff,B = 7800 ± 170 K and the respective projected rotational velocities (VAsini = 68.4 ± 1.5 km s-1 and VBsini = 113 ± 6 km s-1). The value for the mass ratio we found is: q = 0.754 ± 0.002. Furthermore, the component spectra were shown to closely reproduce the characteristics of an observed reference spectrum (using the single star HD 2628). From the comparison with synthetic spectra, we found that enhanced metallicity was needed to model θ2 Tau A and B, as expected for two members of the Hyades cluster.
The combined (astrometric-spectroscopic) analysis permitted us to determine the orbital parallax (20.90 ± 0.14 mas) as well as the component masses (MA = 2.86 ± 0.06 M⊙ and MB = 2.16 ± 0.02 M⊙) with a high accuracy. Adopting this new parallax, we obtained the component absolute magnitudes MvA = 0.33 ± 0.03 mag and MvB = 1.44 ± 0.03 mag. A further improvement of the accuracy on the orbital parameters might be gained if the interval around periastron passage were more intensively covered. Indeed, at present, 76% of the spectra cover half the period around apastron, whereas only 24% cover half the period around periastron. It might also be worthwhile to extend the spectral range used for the application of spectra disentangling by one order of magnitude (with respect to the present range of 26 Å) provided that sufficient spectra obtained near the epoch of periastron passage are included as well. Obviously, covering this crucial orbital phase with more Elodie or Hermes spectra should lead to a significant improvement. Ideally, the distribution of the spectra should be homogeneous over the entire range of Doppler velocities.
From the confrontation between the observed masses and luminosities and evolutionary tracks adopting the Hyades composition derived by LE01, we conclude that component B is on the main sequence. The interpretation for component A, however, remains problematic. We investigated a number of possibilities (such as convective core overshooting, fast rotation) to explain the observed discrepancy but it would appear from this first analysis that a change in chemical composition – in the sense of a higher metallicity – might be necessary.
The resulting disentangled component spectra open the way to an abundance analysis in the components of θ2 Tau as if they were single stars. This will be useful in the discussion concerning the true chemical composition of the Hyades cluster. We intend to perform such an analysis making use of the semi-automatic method that we developed for A and F-type stars (Hekker et al. 2009).
Online material
Online material
θ2 Tau AB radial velocities.
The 44 spectra from the Elodie spectrograph can be retrieved directly from the Elodie database (http://atlas.obs-hp.fr/elodie/). The 70 spectra from the Harvard Smithsonian center for astrophysics (CfA) and the 13 ones from the Hermes spectrograph are available upon request from the authors of the paper Torres et al. (1997) and from us, respectively.
Acknowledgments
K. B. V. Torres, Y. Frémat and P. Lampens gratefully acknowledge support in the framework of the following projects financed by the Belgian Federal Science Policy: the project “Disentangled Components of Multiple Stars as Laboratories of Stellar Evolution” (Supplementary Researcher 2008–2009) and the Action-1 project “Pulsation, Chemical Composition and Multiplicity in Main-Sequence A-F Stars” (Ref. MO/33/018). In addition, K. B. V. Torres acknowledges funding from the Brazilian agencies CNPq, CAPES and FAPEMIG. We thank Drs. D. Pourbaix and S. Ilijić for supplying their respective codes FDBinary and vbsb2. We furthermore thank the Optical Infrared Co-ordination Network (opticon, a major international collaboration supported by the Research Infrastructures Programme of the European Commission’s Sixth Framework Programme) for the observing runs being funded by its Trans-National Access Programme (Ref. 2005/042 and 2006/042) as well as Dr. G. Torres for providing us the spectra collected at the Oak Ridge Observatory. The Hermes project is a collaboration between the KULeuven, the Université Libre de Bruxelles and the Royal Observatory of Belgium with contributions from the Observatoire de Genève (Switzerland) and the Thüringer Landessternwarte Tautenburg (Germany). Hermes is funded by the Fund for Scientific Research of Flanders (FWO) under the grant G.0472.04, from the Research Council of K. U. Leuven under grant GST-B4443, from the Fonds National de la Recherche Scientifique under contracts IISN4.4506.05 and FRFC 2.4533.09, and financial support from Lotto (2004) assigned to the Royal Observatory of Belgium. The Ondřejov Observatory is supported by the project with reference AV0Z10030501. We thank P. Škoda’s collaborators, from Ondřejov Observatory, Czech Republic, for kindly taking 16 spectra of θ2 Tau. Last but not least, we thank the referee for some very useful suggestions. This work made use of the Simbad astronomical data base operated by the CDS, Strasbourg (France) and the ADS bibliography.
References
- Armstrong, J. T., Mozurkewich, C. A., & Hummel, D. 1992, in High-Resolution Imaging by Interferometry, ed. J. M. Beckers, & F. Merkle, 673 [Google Scholar]
- Armstrong, J. T., Mozurkewich, D., Hajian, A. R., et al. 2006, AJ, 131, 2643, (AM06) [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&AS, 106, 275 [NASA ADS] [Google Scholar]
- Breger, M., Garrido, R., Huang, L., et al. 1989, A&A, 214, 209 [NASA ADS] [Google Scholar]
- Breger, M., Pamyatnykh, A. A., Zima, W., et al. 2002, MNRAS, 336, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., & Giménez, A. 1992, A&AS, 96, 255 [NASA ADS] [Google Scholar]
- de Bruijne, J. H. J., Hoogerwerf, R., & de Zeeuw, P. T. 2001, A&A, 367, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frémat, Y., Lampens, P., Van Cauteren, P., & Robertson, C. W. 2006, Mem. Soc. Astron. Ital., 77, 174 [NASA ADS] [Google Scholar]
- Frémat, Y., Zorec, J., Hubert, A., & Floquet, M. 2005, A&A, 440, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [Google Scholar]
- Hensberge, H., Ilijić, S., & Torres, K. B. V. 2008, A&A, 482, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Frémat, Y., Lampens, P., et al. 2009, MNRAS, 396, 1689 [NASA ADS] [CrossRef] [Google Scholar]
- Hensberge, H., Pavlovski, K., & Verschueren, W. 2000, A&A, 358, 553 [NASA ADS] [Google Scholar]
- Hummel, C. A., & Armstrong, J. T. 1992, in Complementary Approaches to Double and Multiple Star Research, ed. H. A. McAlister, & W. I. Hartkopf, ASP Conf. Ser., 32, IAU Colloq., 135, 552 [Google Scholar]
- Ilijić, S., Hensberge, H., Pavlovski, K., & Freyhammer, L. M. 2004, in Spectroscopically and Spatially Resolving the Components of the Close Binary Stars, ed. R. W. Hilditch, H. Hensberge, & K. Pavlovski, ASP Conf. Ser., 318, 111 [Google Scholar]
- Kennelly, E. J., Walker, G. A. H., Catala, C., et al. 1996, A&A, 313, 571 [Google Scholar]
- Królikowska, M. 1992, A&A, 260, 183 [NASA ADS] [Google Scholar]
- Lampens, P., Torres, K., Frémat, Y., & Hensberge, H. 2009, in American Institute of Physics Conference Series, ed. J. A. Guzik, & P. A. Bradley, 1170, 446 [Google Scholar]
- Lastennet, E., Valls-Gabaud, D., Lejeune, T., & Oblak, E. 1999, A&A, 349, 485 [NASA ADS] [Google Scholar]
- Lebreton, Y., Fernandes, J., & Lejeune, T. 2001, A&A, 374, 540, (LE01) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, Z., Zhou, A., & Yang, D. 1997, PASP, 109, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Mermilliod, J., Mermilliod, M., & Hauck, B. 1997, A&AS, 124, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] [Google Scholar]
- Moon, T. T., & Dworetsky, M. M. 1985, MNRAS, 217, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pan, X., Shao, M., & Colavita, M. M. 1992, in Complementary Approaches to Double and Multiple Star Research, ed. H. A. McAlister, & W. I. Hartkopf, 502, ASP Conf. Ser., 32, IAU Colloq. 135, (PS92) [Google Scholar]
- Perryman, M. A. C., & ESA 1997, The HIPPARCOS and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission, ESA Special Publication, 1200 [Google Scholar]
- Perryman, M. A. C., Brown, A. G. A., Lebreton, Y., et al. 1998, A&A, 331, 81 [NASA ADS] [Google Scholar]
- Peterson, D. M. 1991, in The Formation and Evolution of Star Clusters, ed. K. Janes, ASP Conf. Ser., 13, 592 [Google Scholar]
- Peterson, D. M., & Solensky, R. 1988, ApJ, 333, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, D. M., Stefanik, R. P., & Latham, D. W. 1993, AJ, 105, 2260 [NASA ADS] [CrossRef] [Google Scholar]
- Poretti, E., Buzasi, D., Laher, R., Catanzarite, J., & Conrow, T. 2002, A&A, 382, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pourbaix, D. 1998, A&AS, 131, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing, ed. W. H. Press, S. A. Teukolsky, W. T. Vetterling, & B. P. Flannery [Google Scholar]
- Raskin, G., Van Winckel, H., Hensberge, H., et al. 2010, A&A, in press [Google Scholar]
- Shao, M., Colavita, M. M., Hines, B. E., et al. 1991, BAAS, 23, 830 [NASA ADS] [Google Scholar]
- Škoda, P., & Šlechta, M. 2002, Publications of the Astronomical Institute of the Czechoslovak Academy of Sciences, 90, 22 [NASA ADS] [Google Scholar]
- Torres, G., Stefanik, R. P., & Latham, D. W. 1997, ApJ, 485, 167, (TSL97) [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verschueren, W., & David, M. 1999, A&AS, 136, 591 [Google Scholar]
- Yıldız, M., Yakut, K., Bakış, H., & Noels, A. 2006, MNRAS, 368, 1941 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Uncertainty of the radial velocity information content as a function of wavelength, assuming S/N = 100. The standard deviation, SRV, was computed over a 60 Å wide interval, shifted with a step of 10 Å. The primary and secondary are represented, respectively by a full and a dashed line. Each wavelength region (Table 1) is represented by a small horizontal line. |
| In the text | |
 |
Fig. 2 Distribution of the χ2 of the solutions derived by spectra disentangling as a function of the radial velocity semi-amplitude of the secondary. |
| In the text | |
 |
Fig. 3 Logarithm of the condition number (log C) versus the Fourier mode computed for θ2 Tau using the radial velocities derived with FDBinary. |
| In the text | |
 |
Fig. 4 Line blocking of θ2 Tau AB for each of the 7 spectral regions described in Table 1. See Sect. 3. |
| In the text | |
 |
Fig. 5 Determination of the light contributions of θ2 Tau AB, using the disentangled component spectra. The grey vertical bars represent the acceptable values for ℓB/ℓA, for each spectral region (Table 1). The ℓB/ℓA predicted by AM06 are also shown (i.e. black diamonds with error bars), as well as Eq. (2) (straight black line). The grey line represents the slope of the flux ratio curve of two synthetic spectra with a difference of temperature corresponding to +200 K, in the sense (component B – component A). See Sects. 3 and 4.1. |
| In the text | |
 |
Fig. 6 Comparison between the reconstructed component spectra of θ2 Tau AB (grey) and the spectrum of HD 2628 (black), for the regions listed in Table 1. The latter spectrum was broadened by 66 and 118 km s-1, respectively for components A and B, and shifted by 39.5 km s-1. |
| In the text | |
 |
Fig. 7 Intrinsic spectra of θ2 Tau A and B (in black) compared to synthetic spectra computed for the Hyades metallicity ([Fe/H] = +0.14 in red; [Fe/H] = +0.19 in green; LE01), and the solar metallicity (in blue). The luminosity ratio is fixed to 0.35. The Teff, Vsini and log g values were fixed to those ones described in Table 2. |
| In the text | |
 |
Fig. 8 Combined orbital solution plotted with the astrometric data from Armstrong et al. (2006). |
| In the text | |
 |
Fig. 9 Combined orbital solution (full lines) plotted with component radial velocities(symbols “°” for component A and “□” for component B) derived with FDBinary. Combined orbital solution derived by TSL97 (dashed lines). The different data sets obtained with the Elodie (observatoire de haute-provence, OHP), Hermes (Roque de Los Muchachos Observatory, LPA) and CfA spectrographs are represented by the different shades of grey, see legend. |
| In the text | |
 |
Fig. 10 Location of θ2 Tau AB in the Hertzsprung-Russell diagram. The curves represent evolutionary tracks for the masses corresponding to θ2 Tau AB, the metallicity of the Hyades (following LE01) and three levels of overshooting, αOV (different black curves as indicated in the legend) and an isochrone of age of 650 Myr (red curve), all computed using the code Cesam (Morel & Lebreton 2008). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


