| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014967 | |
| Published online | 08 December 2010 | |
The birth rate of subluminous and overluminous type Ia supernovae
1
School of Physics and Chemistry, Henan Polytechnic University,
Jiaozuo
454000,
PR China
e-mail: xiangcunmeng@hotmail.com
2
Department of Physics, Shangqiu Normal University,
476000
Shangqiu, PR
China
3
Key Laboratory of Modern Astronomy and Astrophysics (Nanjing
University) Ministry of Education, 210093
Nanjing, PR
China
4
College of Physics and Electronic Information, Dali University,
671003
Dali, PR
China
5
National Astronomical Observatories, Chinese Academy of Sciences,
100012
Beijing, PR
China
6
Department of Astronomy, Beijing Normal University,
100875
Beijing, PR
China
Received: 10 May 2010
Accepted: 24 October 2010
Context. Based on the single degenerate (SD) scenario, a super-Chandrasekhar mass model derived from the rapid rotation of a progenitor star may account for the overluminous type Ia supernovae (SNe Ia) like SN 2003fg. Previous authors calculated a series of binary evolution and showed the parameter spaces for the super-Chandrasekhar mass model. Another team developed an equal-mass double degenerate (DD) model to explain subluminous SNe Ia like SN 1991bg. But they did not show the evolution of the birth rate of these peculiar SNe Ia or compared them with absolute birth rates from observations.
Aims. We aim to show the evolution of the birth rates of these peculiar SNe Ia based on the results of these other works, and compare the birth rates with observations to check whether these model may account for all the peculiar SNe Ia.
Methods. We carried out a series of binary population synthesis calculations and considered two methods of common envelope (CE) evolution, i.e. α-formalism and γ-algorithm.
Results. We found that the evolution of the birth rate of these peculiar SNe Ia heavily dependen on how the CE evolution is treated. The overluminous SNe Ia may only occur for α-formalism with low CE ejection efficiency, and the delay time of the SNe Ia is between 0.4 and 0.8 Gyr. The upper limit of the contribution rate of the supernovae to all SN Ia is less than 0.3%. The delay time of subluminous SNe Ia from equal-mass DD systems is between 0.1 and 0.3 Gyr for α-formalism with α = 3.0, but longer than 9 Gyr for α = 1.0. The range of the delay time for γ-algorithm is very wide, i.e. longer than 0.22 Gyr, even as long as 15 Gyr. The subluminous SNe Ia from equal-mass DD systems may only account for no more than 1% of all SNe Ia observed.
Conclusions. The super-Chandrasekhar mass model may account for a part of the 2003fg-like supernovae and the equal-mass DD model may explain some 1991bg-like events, too. In addition, based on the comparison between theories and observations, including the birth rate and delay time of the 1991bg-like events, we found that the γ-algorithm is more likely to be an appropriate prescription of the CE evolution of DD systems than the α-formalism if the equal-mass DD system is the progenitor of 1991bg-like SNe Ia.
Key words: white dwarfs / supernovae: general / supernovae: individual: SN 2003fg / supernovae: individual: SN 1991bg
© ESO, 2010
1. Introduction
In their function as one of the distance indicators, type Ia supernovae (SNe Ia) showed their importance in determining cosmological parameters, which resulted in the discovery of the accelerating expansion of the universe (Riess et al. 1998; Perlmutter et al. 1999). The result is exciting and suggests the presence of dark energy. At present, SNe Ia are proposed to be cosmological probes for testing the evolution of the dark energy equation of state with time and testing the evolutionary history of the universe (Riess et al. 2007; Kuznetsova et al. 2008; Howell et al. 2009). They were even chosen to check the general relativity (Zhao et al. 2010). However, the nature of SNe Ia is still unclear, especially their progenitor system (Hillebrandt & Niemeyer 2000; Leibundgut 2000). It is widely believed that a SN Ia is produced from the thermonuclear runaway of a carbon-oxygen white dwarf (CO WD) in a binary system (Arnett 1982). Based on the nature of the WD companion, two basic scenarios have been discussed for about three decades. One is the single degenerate (SD) model (Whelan & Iben 1973; Nomoto et al. 1984), i.e. the companion may be either a main-sequence (MS) or a slightly evolved star (WD + MS), or a red giant star (WD + RG), or a helium star (WD + He star), and the model is widely investigated by many groups (Yungelson et al. 1995; Li et al. 1997; Hachisu et al. 1999a,b; Nomoto et al. 1999; 2003; Langer et al. 2000; Han & Podsiadlowski 2004; Chen & Li 2007; Han 2008; Meng & Yang 2010b; Lü 2009; Wang et al. 2009a,b; Wang et al. 2010). The other scenario is the double degenerate (DD) model (Iben & Tutukov 1984; Webbink 1984), in which a system of two CO WDs loses orbital angular momentum by means of gravitational wave radiation and finally merges. Although the birth rate and the distribution of its delay time (DDT, delay time: between the episode of star formation producing progenitor systems and the occurrence of SNe Ia) from this channel is comparable to observations (Han 1998; Yungelson & Livio 1998; 2000; Tutukov & Yungelson 2002; Mennekens et al. 2010) and some SNe Ia such as SN 2003fg and SN 2005hj may likely result from the channel (Howell et al. 2006; Quimby et al. 2007), some numerical simulations showed that the most probable fate of the coalescence is an accretion-induced collapse and, finally, neutron star formation (see the review by Hillebrandt & Niemeyer 2000). Generally, the WD mass at the moment of explosion is equal for the SD model (the so-called Chandrasekhar mass model) or less than the Chandrasekhar limit (the sub-Chandrasekhar mass model), while larger than the limit for DD model (super-Chandrasekhar mass model).
The most remarkable property of SNe Ia is their apparently homogeneous nature. This characteristic is interpreted as the observable consequence of a model where the progenitors of SNe Ia are CO WDs that have increase their mass to close to the Chandrasekhar limit via mass transfer in a binary system. Nevertheless, observations of two peculiar events, i.e. SN 1991T and SN 1991bg, raised questions about the uniformity of SNe Ia. Motivated by these discoveries, Phillips (1993) suggested a relation between the absolute magnitude of SNe Ia at maximum light and the magnitude drop of the B light curve during the first 15 days following maximum. When SNe Ia are applied as distance indicator, the relation is adopted.
The peak brightness of SN 1991bg was ~2.0 mag fainter in B than that of normal SNe Ia, and its light curve declined unusually fast following maximum (Filippenko et al. 1992b; Leibundgut et al. 1993). SN 1991bg was identified by Branch & Miler (1993) as intrinsically subluminous. The low peak luminosity indicated a low amount of 56Ni, i.e. about 0.07 M⊙ (Mazzali et al. 1997). Generally, the subluminous property of the SN 1991bg may be explained by a sub-Chandrasekhar mass model from a CO WD + He star system or a merger of CO WD and He WD (Branch et al. 1995; Livio 1999; 2003). However, Pakmor et al. (2010) recently suggested an alternative scenario, i.e. subluminous 1991bg-like events may be from the mergers of equal-mass CO WDs of M ~ 0.9 M⊙. Although the light curve from the merger model is broader than that of 1991bg-like events, the synthesized spectra, red color, and low expansion velocities are all close to those observed for 1991bg-like events. They claimed that the events from the merger of equal-mass WDs should occur with a rate of ≈2−11% of all SNe Ia. However, Pakmor et al. (2010) discussed a relative birth rate to various SNe Ia progenitor channels rather than the absolute ones from observations. One of the purposes in this paper is to present the evolution of the birth rate of the subluminous 1991bg-like events from the mergers of equal-mass WDs and to compare the birth rate with those from observations.
SN 1991T is an overluminous event, and its light curve declined slowly after maximum luminosity (Filippenko et al. 1992a; Phillips et al. 1992; 1999), which is often taken as an indication of a large 56Ni mass (Höflich et al. 1995; Nugent et al. 1997; Pinto & Eastman 2001). Nevertheless, Kasen et al. (2004) suggested a second, physically very different route to explain the peculiarities of SN 1991T – one could be peering down an ejecta hole, which is caused by the existence of the companion at the moment of supernova explosion. This suggestion was upheld by a detailed binary population synthesis (BPS) study (Meng & Yang 2010a). Therefore, it is possible that 1991T-like supernovae have not any special properties in physics except for the viewing angle of an observer.
The SN 2003fg was observed to be 2.2 times overluminous than a normal SN Ia and the amount of 56Ni was inferred to be 1.3 M⊙, which requires a super-Chandrasekhar mass explosion (~2.1 M⊙, Astier et al. 2006; Howell et al. 2006). Since the detection of SN 2003fg, another three 2003fg-like events were discovered, i.e. SN 2006gz (Hicken et al. 2007), SN 2007if (Scalzo et al. 2010; Yuan et al. 2010) and SN 2009dc (Tanaka et al. 2010; Yamanaka et al. 2010). These supernovae are usually assumed to have formed from the mergers of DD systems, where the total mass of the DD systems exceeds the Chandrasekhar mass limit. However, a super-Chandrasekhar WD may also exist in a SD system, where the massive WD is supported by rapid rotation (Yoon & Langer 2005; Howell et al. 2006). For example, Maeda & Iwamoto (2009) showed that the properties of SN 2003fg are more consistent with an aspherical explosion of a super-Chandrasekhar WD supported by a rapid rotation. Considering the influence of rotation on accreting WD, Yoon & Langer (2004) found that a WD under a special condition may rotate differentially. Using the result of Yoon & Langer (2004), Chen & Li (2009) calculated the evolution of close binaries consisting of a CO white dwarf and a normal companion, and obtained the parameter space in an orbital period-secondary mass (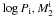 ) plane for super-Chandrasekhar SNe Ia. However, they did not present the evolution of the birth rate of the super-Chandrasekhar SNe Ia either. In this paper, we will show the evolution by a detailed BPS study.
) plane for super-Chandrasekhar SNe Ia. However, they did not present the evolution of the birth rate of the super-Chandrasekhar SNe Ia either. In this paper, we will show the evolution by a detailed BPS study.
In Sect. 2, we describe our BPS method. We show the BPS results in Sect. 3, and the discussions and conclusions are given in Sect. 4.
2. Binary population synthesis
2.1. Super-Chandrasekhar SNe Ia
The study of Chen & Li (2009) is based on a WD + MS system and their results were summarized in an orbital period-secondary mass (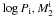 ) plane. According to the situation of the primary in a primordial system at the onset of the first Roche lobe overflow (RLOF), there are three evolutionary channels contributing to the WD + MS system, the He star channel, the EAGB channel and the TPAGB channel (see Meng et al. 2009; and Meng & Yang 2010b, for details about the channels). In this paper, the TPAGB channel is the dominant one because the initial mass of WD for overluminous SNe Ia is larger than 1.0 M⊙, and the other two channels do not contribute to the overluminous because the initial WD mass from this channel is always smaller than 1.0 M⊙ (see also Fig. 8 in Meng et al. 2009). For all three channels, a common envelope (CE) phase is expected. After the formation of the WD + MS systems, the systems continue to evolve, the secondaries may also fill their Roche lobes at a stage and RLOF starts. We assume that if the initial orbital period,
) plane. According to the situation of the primary in a primordial system at the onset of the first Roche lobe overflow (RLOF), there are three evolutionary channels contributing to the WD + MS system, the He star channel, the EAGB channel and the TPAGB channel (see Meng et al. 2009; and Meng & Yang 2010b, for details about the channels). In this paper, the TPAGB channel is the dominant one because the initial mass of WD for overluminous SNe Ia is larger than 1.0 M⊙, and the other two channels do not contribute to the overluminous because the initial WD mass from this channel is always smaller than 1.0 M⊙ (see also Fig. 8 in Meng et al. 2009). For all three channels, a common envelope (CE) phase is expected. After the formation of the WD + MS systems, the systems continue to evolve, the secondaries may also fill their Roche lobes at a stage and RLOF starts. We assume that if the initial orbital period, 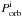 , and the initial secondary mass,
, and the initial secondary mass, 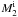 , of a SD system located in the appropriate regions in the (
, of a SD system located in the appropriate regions in the (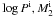 ) plane for super-Chandrasekhar SNe Ia at the onset of RLOF, a super-Chandrasekhar SN Ia is then produced.
) plane for super-Chandrasekhar SNe Ia at the onset of RLOF, a super-Chandrasekhar SN Ia is then produced.
2.2. Subluminous SNe Ia
Pakmor et al. (2010) also made a BPS study about 1991bg-like events based on their merging model from equal-mass DD systems, where the components are both massive and the mass ratio is only slightly less than one, i.e. the primary masses are in the range of 0.85–1.05 M⊙ with a mass ratio of 0.9 < q < 1.0. Because the results from the large WD mass (as large as 1.05 M⊙) will more likely lead to more luminous SNe Ia, not 1991bg-like events, we critically limit that the range of WD mass is between 0.83 and 0.9 M⊙ in this paper (see also Pakmor et al. 2010). A primordial binary system may become a DD system after one or two CE phases (Han 1998; Ruiter et al. 2009). There are three sub-categories to form the DD system contributing to the subluminous SNe Ia. Below, we briefly outline the three sub-categories: Case 1, 2, and 3.
Case 1 (2RLOF + 2CE): Although the evolutionary channel for Case 1 is similar, the parameters of the primordial binaries for different CE treatment are different (see next subsection). For an α-formalism, the primordial zero-age main sequence (ZAMS) mass of primaries is in the range of 5.2 M⊙ to 5.7 M⊙, and the mass ratio (m2 / m1) is between 0.59 and 0.7, and the primordial separation is close, i.e. from 30 R⊙ to 60 R⊙. For a γ-algorithm, the primordial ZAMS mass of primaries is in the range of ~5.35 M⊙ to 7.1 M⊙, and the mass ratio is between 0.35 and 0.53, and the primordial separation is even more close, i.e. from 17 R⊙ to 30 R⊙. Because of the close separation, the primary fills its Roche lobe when it is crossing the Hertzprung Gap (HG), and then a stable RLOF occurs. The primary loses its hydrogen-rich envelope and then becomes a helium star, where mass ratio reverses at a point. The helium star may fill its Roche lobe again after its central helium is exhausted, where the RLOF is also dynamically stable for a low-mass ratio. During the two stable RLOF, the separation may increase greatly for material transferring from light component to heavy one, after which the system finally becomes a very wide WD + MS system, where the separation may be as large as 400 R⊙. The secondary fills its Roche lobe during HG, which leads to a CE for a high mass ratio (~10). After the CE ejection, the mass donor becomes a helium star and continues to evolve. The helium star fills its Roche lobe once again after the exhaustion of the central helium, and a second CE ensues (mass ratio ~2). Thus a DD system forms. However, the final separation is heavily dependent on the treatment of the CE, i.e. ≤0.6 R⊙ for the α-formalism, while 2–3 R⊙ for the γ-algorithm, which is the dominant factor resulting in a different delay time of SNe Ia for the different treatment of the CE.
Case 2 (RLOF + CE): for this case, the mass ratio for primordial binary system is very close to 1, i.e. larger than 0.94, and the primordial ZAMS mass of the primary is between 3.75 and 4.1 M⊙. The primordial system has a very wide separation (wider than 2500 R⊙), which permits the primary to evolve to the thermal pulsing asymptotic giant branch (TPAGB) stage before it fills its Roche lobe, after which a stable RLOF occurs. At this stage, the secondary is a horizontal branch (HB) star (central helium burning). The system consists of a CO WD and a HB star after the RLOF. The secondary fills its Roche lobe again at TPAGB stage and a CE forms for a high-mass ratio (~7). After the CE ejection, the orbit decays greatly and a DD system forms with a separation of 0.2 to 2 R⊙. Then, the delay time of the subluminous SNe Ia from this sub-category is less than 2 Gyr.
Case 3 (one CE): the primordial ZAMS mass of primaries is around 4 M⊙ and the mass ratio is almost 1, i.e. larger than 0.999. The primordial separation is from 1200 R⊙ to 1600 R⊙, and thus both primary and secondary are at TPAGB stage when the primary fills its Roche lobe, which results in a CE. After the CE ejection, a DD system forms with a separation of ~3 R⊙. The delay time of SNe Ia from this sub-category is longer than 9 Gyr.
Following the DD system, gravitational wave radiation (GW) dominates the evolution of the system on a timescale tGW (Landau & Lifshitz 1962), 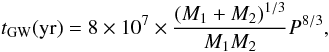 (1)where P is the orbital period of the DD system in hours, and M1 and M2 are the mass of the two white dwarf in solar mass, respectively. Then, the time elapsed from the birth of primordial binary system to the occurrence of SN Ia is equal to the sum of the timescale on which the secondary star becomes a WD and the orbital decay time. We assume that if M1 and M2 are both in the range of 0.83–0.9 M⊙ and the elapsed time is less than 15 Gyr, a subluminous SN Ia is produced.
(1)where P is the orbital period of the DD system in hours, and M1 and M2 are the mass of the two white dwarf in solar mass, respectively. Then, the time elapsed from the birth of primordial binary system to the occurrence of SN Ia is equal to the sum of the timescale on which the secondary star becomes a WD and the orbital decay time. We assume that if M1 and M2 are both in the range of 0.83–0.9 M⊙ and the elapsed time is less than 15 Gyr, a subluminous SN Ia is produced.
2.3. Common envelope
As mentioned above, CE is very important for the formation of SD and DD systems. During binary evolution, the mass ratio (q = Mdonor / Maccretor) is crucial. If it is larger than a critical mass ratio, qc, mass transfer between the two components is dynamically unstable and a CE forms (Paczy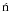 ski 1976). The ratio qc varies with the evolutionary state of the donor star at the onset of RLOF (Hjellming & Webbink1987; Webbink 1988; Han et al. 2002; Podsiadlowski et al. 2002; Chen & Han 2008). In this study, we adopt qc = 4.0 when the donor star is on MS or crossing HG. This value is supported by detailed binary evolution studies (Han et al. 2000; Chen & Han 2002; 2003). If the primordial primary is on the first giant branch (FGB) or the asymptotic giant branch (AGB), we use
ski 1976). The ratio qc varies with the evolutionary state of the donor star at the onset of RLOF (Hjellming & Webbink1987; Webbink 1988; Han et al. 2002; Podsiadlowski et al. 2002; Chen & Han 2008). In this study, we adopt qc = 4.0 when the donor star is on MS or crossing HG. This value is supported by detailed binary evolution studies (Han et al. 2000; Chen & Han 2002; 2003). If the primordial primary is on the first giant branch (FGB) or the asymptotic giant branch (AGB), we use ![\begin{equation} q_{\rm c}=\left[1.67-x+2\left(\frac{M_{\rm c}}{M}\right)^{\rm 5}\right]/2.13, \label{eq:qc} \end{equation}](/articles/aa/full_html/2011/01/aa14967-10/aa14967-10-eq37.png) (2)where Mc is the core mass of the donor star, and x = dlnR1 / dlnM is the mass-radius exponent of the donor star and varies with composition. If the mass donors (primaries) are naked helium giants, qc = 0.748 based on Eq. (2) (see Hurley et al. 2002, for details).
(2)where Mc is the core mass of the donor star, and x = dlnR1 / dlnM is the mass-radius exponent of the donor star and varies with composition. If the mass donors (primaries) are naked helium giants, qc = 0.748 based on Eq. (2) (see Hurley et al. 2002, for details).
Embedded in the CE are the dense core of the donor star and the secondary. Owing to frictional drag with the envelope, the orbit of the embedded binary decays, and a large part of the orbital energy released in the spiral-in process is injected into the envelope (Livio & Soker 1988). It is generally assumed that the CE is ejected if 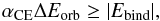 (3)where ΔEorb is the orbital energy released, Ebind is the binding energy of CE, and αCE is CE ejection efficiency, i.e. the fraction of the released orbital energy used to eject the CE. Because the thermal energy in the envelope is not incorporated into the binding energy, αCE may be greater than 1 (see Han et al. 1995, for details about the thermal energy). In this paper, we set αCE to 1.0 or 3.01. After the CE, the orbital separation at the onset of the CE, ai, becomes af which is determined by
(3)where ΔEorb is the orbital energy released, Ebind is the binding energy of CE, and αCE is CE ejection efficiency, i.e. the fraction of the released orbital energy used to eject the CE. Because the thermal energy in the envelope is not incorporated into the binding energy, αCE may be greater than 1 (see Han et al. 1995, for details about the thermal energy). In this paper, we set αCE to 1.0 or 3.01. After the CE, the orbital separation at the onset of the CE, ai, becomes af which is determined by 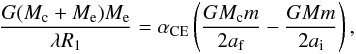 (4)where λ is a structure parameter relaying on the evolutionary stage of the donor, M, Mc, and Me are the masses of the donor, the donor envelope and the core, respectively, R1 is the radius of the donor, and m is the companion mass. In this paper, we take the structure parameter to be a constant, i.e. λ = 0.5 (de Kool et al. 1987). Thus, the final orbital separation of a binary system after the CE phase af is given by
(4)where λ is a structure parameter relaying on the evolutionary stage of the donor, M, Mc, and Me are the masses of the donor, the donor envelope and the core, respectively, R1 is the radius of the donor, and m is the companion mass. In this paper, we take the structure parameter to be a constant, i.e. λ = 0.5 (de Kool et al. 1987). Thus, the final orbital separation of a binary system after the CE phase af is given by 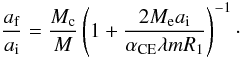 (5)The description above may well produce the distribution of WD + MS systems as noticed by Zorotovic et al. (2010; see also Hurley et al. 2002), while it is possibly difficult for the description to produce a close pair of white dwarfs. Nelemans et al. (2000) and Nelemans & Tout (2005) suggested an alternative algorithm equating the angular momentum balance, which may explain the formation of all kinds of close binaries:
(5)The description above may well produce the distribution of WD + MS systems as noticed by Zorotovic et al. (2010; see also Hurley et al. 2002), while it is possibly difficult for the description to produce a close pair of white dwarfs. Nelemans et al. (2000) and Nelemans & Tout (2005) suggested an alternative algorithm equating the angular momentum balance, which may explain the formation of all kinds of close binaries: 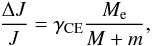 (6)where J is the total angular momentum and ΔJ is the change of the total angular momentum during the common envelope phase. Implicitly assuming the conservation of energy, the final orbital separation af after the CE is then given by
(6)where J is the total angular momentum and ΔJ is the change of the total angular momentum during the common envelope phase. Implicitly assuming the conservation of energy, the final orbital separation af after the CE is then given by 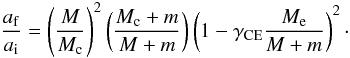 (7)Based on the results in Nelemans & Tout (2005), we set γCE = 1.5.
(7)Based on the results in Nelemans & Tout (2005), we set γCE = 1.5.
Following Nelemans & Tout (2005), we call the the formalism for Eq. (3) the α-formalism and that of Eq. (6) the γ-algorithm. In this paper, we treat CE evolution with the two algorithms.
2.4. Basic parameters for Monte Carlo simulations
To investigate the birthrate of SNe Ia, we followed the evolution of 4 × 107 binaries via Hurley’s rapid binary evolution code (Hurley et al. 2000; 2002). The descriptions above for super-luminous SNe Ia from the SD model and the subluminous ones from the equal-mass DD systems are incorporated into the code. The primordial binary samples are generated in a Monte Carlo way and a circular orbit is assumed for all binaries. The basic parameters for the simulations are as follows: (1) a constant star formation rate (SFR) of 5 M⊙ yr-1 over the past 15 Gyr or a single star burst of 1011M⊙; (2) the initial mass function (IMF) of Miller & Scalo (1979); (3) the mass-ratio distribution is constant; (4) all stars are members of binary systems and the distribution of separations is constant in log a for wide binaries, where a is the orbital separation, and falls off smoothly at small separation, where a = 10 R⊙ is the boundary for wide and close binaries; (5) solar metallicity, i.e. Z = 0.02 (see Meng & Yang 2010b, for details of the parameter input).
3. Results
3.1. Single star burst
Figure 1 shows the evolution of the birth rate of overluminous (the thick line) and subluminous (the thin lines) SNe Ia with different CE treatments, where a single star burst is assumed. An imposing property in the figure is that the results are heavily dependent on the treatment of CE evolution. For overluminous SNe Ia, only an α-formalism with α = 1.0 may produce SNe Ia. This is mainly derived from constraint of the parameter space for overluminous SNe Ia and the different evolutionary channels for WD + MS systems. Based on the results in Chen & Li (2009), a CO WD may explode as an overluminous SN Ia only when its initial mass is larger than 1.0 M⊙. As described in Sect. 2.1, there are three channels that may produce a WD + MS system, but the TPAGB channel is the only one leading to a WD + MS system with an initial WD mass larger than 1.0 M⊙. The primordial binary system experiencing the TPAGB channel has a very long orbital period, i.e. longer than 1000 days, which means a low binding energy of CE (Meng et al. 2009). Because of the low binding energy of the CE and a long primordial orbital period, αCE has a remarkable influence on CO+WD systems from the TPAGB channel. Generally, if a CE can be ejected, a low αCE produces a shorter orbital-period WD + MS system, which is more likely to fulfill the conditions for overluminous SNe Ia. Therefore, we only obtain overluminous SNe Ia when αCE = 1.0 (see also Meng et al. 2009). For WD + MS systems, the effect of the γ-algorithm is similar to that of the α-formalism with αCE = 3.0 (Nelemans & Tout 2005). Thus no overluminous SNe Ia is produced for the γ-algorithm.
It is clearly shown in Fig. 1 that most of overluminous SNe Ia occur between 0.4 and 0.8 Gyr. This is mainly determined by the high initial companion mass of WD (see Figs. 2 and 3 in Chen & Li 2009). In addition, the peak value of the birth rate for overluminous SNe Ia is lower than that for normal SNe Ia from WD + MS systems by about two orders of magnitude (see Han & Podsiadlowski 2004; Meng et al. 2009).
Both α-formalism and γ-algorithm may produce the subluminous SNe Ia. However, the subluminous SNe Ia may be from different sub-categories for different CE treatment. For an α-formalism, subluminous SNe Ia are produced from Case 1 only when αCE has a high value, i.e. αCE = 3.0. Because a binary system has experienced two CE phase for Case 1 before it becomes a DD system suitable for subluminous SNe Ia, a low αCE means a shorter orbital period, even a merger before CE ejection, and then no subluminous SNe Ia. Actually, when αCE = 1.0, all the binary system suitable for subluminous SNe Ia merger before a DD system forms, except those from Case 3. Because the primordial binary systems from Case 3 have a very large separation, their final separation is also very large after a CE phase. Thus, the delay time from this channel is very long, i.e. longer than 9 Gyr. Whatever, the birth rate from this channel is too low, i.e. the peak value is only 10-6 yr-1 (see the thin solid line in Fig. 1). Even for αCE = 3.0, the result of subluminous SNe Ia significantly differs from that for the γ-algorithm. The subluminous SNe Ia occur between 0.1 and 0.3 Gyr for α = 3.0, while they explode with a very wide age range for the γ-algorithm, i.e. longer than 0.22 Gyr and even as long as 15 Gyr. The subluminous SNe Ia for γ-algorithm come from two subcategories, i.e. Case 2 with delay time shorter than 2 Gyr, while Case 1 with delay time longer than 2 Gyr.
 |
Fig. 1 Evolution of the birthrates of super-luminous SNe Ia from SD channel and subluminous SNe Ia from the merge of equal-mass DD systems for a single starburst of 1011 M⊙ for different CE treatments. The thick line is the result for overluminous SNe Ia, while the thin lines are the results for subluminous SNe Ia. |
Another impressive property in Fig. 1 is that the peak value of the birth rate is lower than that from observations by at least two orders of magnitude (Totani et al. 2008; Maoz et al. 2010a; Maoz & Badenes 2010), and the shape of the DDT in this figure also significantly differs from observations (Maoz et al. 2010b). The best-fitted DDT from observations follows t-1 (Totani et al. 2008; Maoz et al. 2010b), while the DDT is a narrow peak for the super-luminous SNe Ia from the SD channel and the subluminous ones from the merge of equal-mass DD systems under an α-formalism. Although the DDT for the subluminous under the γ-algorithm is not a narrow peak, its shape still does not follow t-1. These results are good evidence for the subgroup nature of 2003fg-like and 1991bg-like SNe Ia.
3.2. Constant star-formation rate
Figure 2 shows Galactic birthrates of SNe Ia for overluminous and subluminous SNe Ia. Our simulations give an upper limit of the birth rate of overluminous SNe Ia from WD + MS systems, i.e. ~8 × 10-6 yr-1 (thick solid line), which is lower than the Galactic birthrate inferred observationally by about three orders of magnitude (3–4 × 10-3 yr-1, van den Bergh & Tammann 1991; Cappellaro & Turatto 1997; Li et al. 2010). Consequently, the overluminous SNe Ia from WD + MS systems could be very rare events. The upper limit of the birth rate of subluminous SNe Ia from the equal-mass DD systems is only slightly higher than that of overluminous SNe Ia, i.e. ~3 × 10-5 yr-1, and the subluminous SNe Ia from DD systems are accordingly rare events as well.
4. Discussions and conclusions
4.1. Birth rate
According to the results of Chen & Li (2009), we found that the 2003fg-like supernovae from SD systems contribute to no more than 0.3% of all SNe Ia. The contribution rate is low and seems not to account for the discovery of four 2003fg-like events at present. Considering that the delay time of the 2003fg-like supernova from the SD systems should be less than 0.8 Gyr (see Fig. 1) and SN 2009dc may be from an old population, the model of Chen & Li (2009) may thus account for a part of the 2003fg-like supernovae.
The Galactic birth rate for super- (Col. 3) and subluminous (Col. 4) SNe Ia with different BPS parameters (Col. 2), where a constant star formation rate (5 M⊙ yr-1) is assumed over the past 15 Gyr.
We found that the subluminous SNe Ia from an equal-mass DD system may at most account for 1% of all SNe Ia observed. But Pakmor et al. (2010) found that their model should occur with a rate of ≃2−11% of the total SN Ia rate, which seems consistent with the observation rate of 1991bg-like supernovae with errors (16% ± 7%, Li et al. 2001). However, their high birth rate is given with regard to other possible SNe Ia progenitor formation channels, rather than to that from observations. Because no progenitor model may account for the birth rate of SNe Ia derived observationally at present2, the birth rate in Pakmor et al. (2010) might be overestimated. Then, the equal-mass DD systems may be the progenitors of some1991bg-like supernovae.
4.2. Age
We find that if an overluminous SNe Ia is from a WD + MS system, its delay time should be shorter than 0.8 Gyr, which means that there is new star formation during the recent 0.8 Gyr in the host galaxies of the overluminous SNe Ia if the SNe Ia are from WD + MS systems. At present, there are four documented examples of overluminous SNe Ia explosions with an derived progenitor mass higher than the Chandrasekhar mass limit, i.e. SN 2003fg, 2006gz, 2007if and 2009dc. Amoung the four SNe Ia, only the host galaxy of SN 2009dc was suspected to have no significant information of star formation because it is an S0 galaxy and inspection of its SDSS images show uniformly red color (Yamanaka et al. 2010).
The delay time of 1991bg-like events is very different based on the treatment of CE. For α = 3.0, the delay time is shorter than 0.3 Gyr, while longer than 9 Gyr for α = 1.0. The range of delay time for γ-algorithm is very wide, longer than 0.22 Gyr and even as long as 15 Gyr. Thus, our results provide a possibility to test which treatment of CE may work for the CE evolution of equal-mass DD systems via measuring the progenitor age of 1991bg-like events. Now, many SNe Ia like SN 1991bg were discovered and it is apparent that they favor E and S0 galaxies, i.e. more than 60% of 1991bg-like events are found in E/S0 galaxies and the remainder are found in early-type spiral galaxies (Howell 2001), and then the subluminous SNe Ia are expected to arise in old (>1 Gyr) stellar population (Sullivan et al. 2006). For example, the host galaxy of SN 1991bg, NGC 4371, is an elliptical galaxy and its age is approximately 14 ± 2.5 Gyr (Trager et al. 2000). Although this age relies on the assumption of a single star burst and is model-dependent, the results of Trager et al. (2000) provided a lower limit of 10 Gyr for the age of the progenitor of SN 1991bg (Howell 2001). The simulation of α = 1.0 seems to favor this long age, but the birth rate from the simulation is too low to compare it with observations, and the age range for the simulation is also too narrow. Considering that the simulation of α = 3.0 also cannot explain the old population nature of 1991bg-like SNe Ia, the α-formalism may not explain the properties of these subluminous events. In our simulation for the γ-algorithm, Case 1 (older than 2 Gyr) dominates the subluminous SNe Ia and contributes to more than 95% of these SNe Ia. This means that most of 1991bg-like events belong to an old population, while there are still a few of the subluminous SNe Ia favoring a young population, which is more consistent with the statistic results of Howell (2001) than the α-formalism, at least qualitatively. In addition, the birth rate for the γ-algorithm is also closer to that of observations (Sullivan et al. 2006). Consequently, our results are more likely to favor the γ-algorithm3. One may argue that since the simulation of α = 1.0 may produce the old subluminous SNe Ia as obtained in Pakmor et al. (2010), our conclusion is possibly dependent on the parameters of BPS simulation, such as the distributions of mass ratio and eccentricity. We checked the influence of the distributions of mass ratio and eccentricity on the birth rates of the special SNe Ia under the assumption of an α-formalism. We find that the influence on the super-luminous SNe Ia is insignificant (see Table 1), while on the subluminous SNe Ia it cannot be neglected. The distribution of n(q) = 2q favors the high-mass ratio, and then may enhance the contribution of Case 3 and the birth rate of the subluminous SNe Ia, but the enhancement is moderate by about a factor of 2 and the birth rate is still much lower than that derived observationally (see Table 1). An elliptical orbit is more possible to deduce the CE evolution than a circular orbit. So, under the distribution of n(e) = 2e, the contribution of Case 1 is significantly enhanced, as is subsequently the birth rate of the subluminous SNe Ia (see Table 1). However, the distribution of n(e) = 2e almost dose not affect Case 3. Because the delay time from Case 1 is very short, i.e. shorter than 0.3 Gyr, most of 1991bg-like events (more than 97%) should be from very young population if α-formalism works for the subluminous SNe Ia, which conflicts with observations (Howell 2001). So, our basic conclusion cannot be influenced by the BPS parameters4. However, recall that our conclusion is critically dependent on the result of Pakmor et al. (2010), i.e. the 1991bg-like supernovae are from equal-mass DD systems, which are only a part of SNe Ia from DD systems, not all DD systems.
In summary, we show the evolution of the birth rate of overluminous SNe Ia from SD systems and subluminous SNe Ia from equal-mass DD systems, and find that the birth rate of the SNe Ia is very low. Our results indicate that the model of Chen & Li (2009) may account for some 2003fg-like supernova, as does the model of Pakmor et al. (2010) for 1991bg-like events. In addition, depending on the simulation of Pakmor et al. (2010), the results in our paper favor the γ-algorithm for the CE evolution of equal-mass DD systems.
Via reconstructing the evolution of post-common-envelope binaries (PCEB) consisting of a white dwarf and a main-sequence star, Zorotovic et al. (2010) obtained a relative low αCE value, where the internal energy of the envelope was included.
The DD model may explain the observational birth rate of SNe Ia (Han 1998; Yungelson & Livio 1998; 2000), but earlier numerical simulations showed that the most probable fate of the coalescence of DD systems is an accretion-induced collapse and, finally, neutron star formation (Saio & Nomoto 1985; see also the review by Hillebrandt & Niemeyer 2000).
Note: after analyzing the evolution of a new sample of PCEBs, Zorotovic et al. (2010) found that the classical α-formalism seems to be an appropriate prescription of CE evolution and it turns out that this constrains the outcome of the CE evolution much more than the γ-algorithm.
Acknowledgments
We are grateful to the anonymous referee for his/her constructive suggestions, which improve the manuscript greatly. This work was supported by the Natural Science Foundation of China under grant Nos. 10873011, 10963001 and 11003003 and the Project of the Fundamental and Frontier Research of the Henan Province under grant No. 102300410223 and Program for the Science & Technology Innovation Talents in the Universities of the Henan Province.
References
- Arnett, W. D. 1982, ApJ, 253, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Astier, P., Guy, J., Regnault, N., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Branch, D., Livio, M., Yungelson, L. R., et al. 1995, PASP, 107, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., & Miler, D. L. 1993, ApJ, 405, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellaro, E., & Turatto, M. 1997, in Thermonuclear Supernovae, ed. P. Ruiz-Lapuente, R. Cannal, & J. Isern (Dordrecht: Kluwer), 77 [Google Scholar]
- Chen, X., & Han, Z. 2002, MNRAS, 335, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Chen X., & Han, Z. 2003, MNRAS, 341, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., & Han, Z. 2008, MNRAS, 387, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, W., & Li, X. 2007, ApJ, 658, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, W., & Li, X. 2009, ApJ, 702, 686 [NASA ADS] [CrossRef] [Google Scholar]
- de Kool, M., van den Heuvel, E. P. J., & Pylyser, E. 1987, A&A, 183, 47 [NASA ADS] [Google Scholar]
- Filippenko, A. V., Richmond, M. W., Matheson, T., et al. 1992a, ApJ, 384, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Filippenko, A. V., Richmond, M. W., Branch, D., et al. 1992b, AJ, 104, 1543 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., Nomoto, K., et al. 1999a, ApJ, 519, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 1999b, ApJ, 522, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z. 1998, MNRAS, 296, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z. 2008, ApJ, 677, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., & Podsiadlowski, Ph. 2004, MNRAS, 350, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1995, MNRAS, 272, 800 [NASA ADS] [Google Scholar]
- Han, Z., Tout, C. A., & Eggleton, P. P. 2000, MNRAS, 319, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, Ph., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., & Niemeyer, J. C. 2000, ARA&A, 38, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Hicken, M., Garnavich, P. M., Prieto, J. L., et al. 2007, ApJ, 669, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Höflich, P., Khokhlov, A. M., & Wheeler, J. C. 1995, ApJ, 444, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A. 2001, ApJ, 554, L193 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A., Sullivan, M., Nugent, P. E., et al. 2006, Nature, 443, 308 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Howell, D. A., Conley, A., Della Valle, M., et al. 2009, [arXiv:0903.1086] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Hjellming, M. S., & Webbink, R. F. 1987, ApJ, 318, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I., Jr., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., Nugent, P., Thomas, R. C., & Wang, L. 2004, ApJ, 610, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Kuznetsova, N., Barbary, K., Connolly, B., et al. 2008, ApJ, 673, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1962, The Classical Theory of Fields (Oxford: Pergamon) [Google Scholar]
- Langer, N., Deutschmann, A., Wellstein, S., et al. 2000, A&A, 362, 1046 [NASA ADS] [Google Scholar]
- Leibundgut, B. 2000, A&ARv, 10, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Leibundgut, B., Kirshner, R. P., Phillips, M. M., et al. 1993, AJ, 105, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Li, X. D., & van den Heuvel, E. P. J. 1997, A&A, 322, L9 [NASA ADS] [Google Scholar]
- Li, W. D., Filippenko, A. V., Treffers, R., et al. 2001, ApJ, 546, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W. D., Chornock, R., Leaman, J., et al. 2010, [arXiv:1006.4613] [Google Scholar]
- Lü, G., Zhu, C., Wang, Z., & Wang, N. 2009, MNRAS, 396, 1086 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Soker, N. 1988, ApJ, 329, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M. 1999, in Type Ia Suppernova: Theory and Cosmology, ed. J. Truran, & T. Niemeyer (New York: Cambridge Univ. Press), 33 [Google Scholar]
- Livio M., 2003, in From Twilight to Highlight: The Physics of supernova, ESO/Springer serious, ESO Astrophysics Symposia, ed. W. Hillebrandt, & B. Leibundgut, (Berlin: Springer), 33 [Google Scholar]
- Maeda, K., & Iwamoto, K. 2009, MNRAS, 394, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., & Badenes, C. 2010, MNRAS, 407, 1314 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Mannucci, F., Li, W., et al., 2010a, MNRAS, in press, [arXiv:1002.3056] [Google Scholar]
- Maoz, D., Sharon, K., & Gal-Yam, A. 2010b, ApJ, 722, 1879 [Google Scholar]
- Mazzali, P. A., Chugai, N., Turatto, M., et al. 1997, MNRAS, 284, 151 [NASA ADS] [Google Scholar]
- Meng, X., & Yang, W. 2010a, MNRAS, 401, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., & Yang, W. 2010b, ApJ, 710, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., Chen, X., & Han, Z. 2009, MNRAS, 395, 2103 [NASA ADS] [CrossRef] [Google Scholar]
- Mennekens, N., Vanbeveren, D., De Greve, J. P., & De Donder, E. 2010, A&A, 515, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, G. E., & Scalo, J. M. 1979, ApJS, 41, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., & Tout, C. A. 2005, MNRAS, 356, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., Verbunt, F., Yungelson, L. R., et al. 2000, A&A, 360, 1011 [NASA ADS] [Google Scholar]
- Nomoto, K., Thielemann, F.-K., & Yokoi, K. 1984, ApJ, 286, 644 [Google Scholar]
- Nomoto, K., Umeda, H., Hachisu, I., et al. 1999, in Type Ia Suppernova: Theory and Cosmology, ed. J. Truran, & T. Niemeyer (New York: Cambridge Univ. Press), 63 [Google Scholar]
- Nomoto, K., Uenishi, T., Kobayashi, C., et al. 2003, in From Twilight to Highlight: The Physics of supernova, ESO/Springer serious, ESO Astrophysics Symposia, ed. W. Hillebrandt, & B. Leibundgut (Berlin: Springer), 115 [Google Scholar]
- Nugent, P., Baron, E., Branch, D., Fisher, A., & Hauschildt, P. H. 1997, ApJ, 485, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1976, in Structure and Evolution of Close Binaries, ed. P. P. Eggleton, S. Mitton, & J. Whelan (Dordrecht: Kluwer), 75 [Google Scholar]
- Pakmor, R., Kromer, M., Röopke, F. K., et al. 2010, Nature, 463, 61 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M., Wells, L. A., Suntzeff, N. B., et al. 1992, AJ, 103, 1632 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M., Lira, P., Suntzeff, N. B., et al. 1999, AJ, 118, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Pinto, P. A., & Eastman, R. G. 2001, NewA, 6, 307 [Google Scholar]
- Podsiadlowski, Ph., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Quimby, R., Höflich, P., & Wheeler, J. C. 2007, ApJ, 666, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D. 1975, Mem. R. Soc. liège, 6ième Serie, 8, 369 [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Strolger, L.-G., Casertano, S., et al. 2007, ApJ, 659, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiter, A., Belczynski, K., & Fryer, C. 2009, ApJ, 699, 2026 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., & Nomoto, K. 1985, A&A, 150, L21 [NASA ADS] [Google Scholar]
- Scalzo, R. A., Aldering, G., Antilogus, P., et al. 2010, ApJ, 713, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Le Borgne, D., & Pritchet, C. J., et al. 2006, ApJ, 648, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Kawabata, K. S., Yamanaka, M., et al. 2010, ApJ, 714, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Totani, T., Morokuma, T., Oda, T., et al. 2008, PASJ, 60, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., Faber, S. M., Worthey, G., & González, J. J. 2000, AJ, 119, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Tutukov, A. V., & Yungelson, L. R. 2002, Astron. Rep., 46, 667 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S., & Tammann, G. A. 1991, ARA&A, 29, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Meng, X., Chen, X., & Han, Z. 2009a, MNRAS, 395, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Chen, X., Meng, X., & Han, Z. 2009b, ApJ, 701, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Li, X., & Han, Z. 2010, MNRAS, 401, 2729 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1988, in The Symbiotic Phenomenon, ed. J. Mikolajewska, M. Friedjung, S. J. Kenyon, & R. Viotti (Kluwer: Dordrecht), 311 [Google Scholar]
- Whelan, J., & Iben, I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Yamanaka, M., Kawabata, K. S., Kinugasa, K., et al. 2010, ApJ, 707, L118 [Google Scholar]
- Yang, W., Meng, X., & Li, Z. 2010, MNRAS, 409, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S. C., & Langer, N. 2004, A&A, 419, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S. C., & Langer, N. 2005, A&A, 435, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yuan, F., Quimby, R. M., Wheeler, J. C., et al. 2010, ApJ, 715, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Yungelson, L., & Livio, M. 1998, ApJ, 497, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Yungelson, L., & Livio, M. 2000, ApJ, 528, 108 [CrossRef] [Google Scholar]
- Yungelson, L., Livio, M., Tutukov, A., et al. 1995, ApJ, 447, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, G., Giannantonio, T., Pogosian, L., et al. 2010, PhRvD, 81, 3510 [Google Scholar]
- Zorotovic, M., Schreiber, M., & Gänsiche, B. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
The Galactic birth rate for super- (Col. 3) and subluminous (Col. 4) SNe Ia with different BPS parameters (Col. 2), where a constant star formation rate (5 M⊙ yr-1) is assumed over the past 15 Gyr.
All Figures
 |
Fig. 1 Evolution of the birthrates of super-luminous SNe Ia from SD channel and subluminous SNe Ia from the merge of equal-mass DD systems for a single starburst of 1011 M⊙ for different CE treatments. The thick line is the result for overluminous SNe Ia, while the thin lines are the results for subluminous SNe Ia. |
| In the text | |
 |
Fig. 2 Similar to Fig. 1 but for a constant star-formation rate of 5 M⊙ yr-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


