| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201014960 | |
| Published online | 30 November 2010 | |
The black holes of radio galaxies during the “Quasar Era”: masses, accretion rates, and evolutionary stage⋆
1
Institut d’Astrophysique Spatiale, CNRS, Université Paris-Sud
11,
Bât. 120–121,
91405
Orsay,
France
e-mail: nicole.nesvadba@ias.u-psud.fr
2
European Southern Observatory, Karl-Schwarzschild Strasse, Garching bei München,
Germany
3
GEPI, Observatoire de Paris, CNRS, Université Denis
Diderot, Meudon,
France
4
SUPA, Institute for Astronomy, Royal Observatory,
Blackford Hill, Edinburgh, UK
5
Instituto de Astronomía, UNAM, 04510
México, DF, Mexico
6
Department of Physics and Astronomy, University of
Nevada, South Maryland
Parkway, Las Vegas,
NV,
USA
Received: 9 May 2010
Accepted: 13 September 2010
We present an analysis of the AGN broad-line regions of 6 powerful radio galaxies at z ~ 2 (HzRGs), which is part of a study of a sample of 50 HzRGs with rest-frame optical imaging spectroscopy obtained at the VLT. In 6 galaxies we detect luminous (ℒ(Hα) = few × 1044 erg s-1), spatially unresolved, broad (FWHM ≥ 10 000 km s-1) Hα line emission from the nucleus (HαBLRs), consistent with broad-line regions of supermassive black holes with masses of few × 109 M⊙ and accretion luminosities of a few percent of the Eddington luminosity. In two galaxies we also detect HβBLRs, suggesting relatively low extinction of AV ~ 1 mag, which agrees with constraints from X-ray observations. Overall, we find HαBLRs in ~20% of the galaxies where Hα is observed. By relating black hole and bulge mass, we find a possible offset towards higher black-hole masses of at most ~0.6 dex relative to nearby galaxies at a given host mass, although each individual galaxy is within the scatter of the local relationship. If not entirely from systematic effects, this would then suggest that the masses of the host galaxies have increased by at most a factor ≈4 since z ~ 2 relative to the black-hole masses, perhaps through accretion of satellite galaxies or because of a time lag between star formation in the host galaxy and AGN fueling. We also compare the radiative and mechanical energy output (from jets) of our targets with predictions of recent models of “synthesis” or “grand unified” AGN feedback, which postulate that AGN with similar radiative and mechanical energy output rates to those found in our HzRGs may be nearing the end of their period of active growth. We discuss evidence that they may reach this stage at the same time as their host galaxies.
Key words: galaxies: evolution / galaxies: high-redshift / galaxies: nuclei / galaxies: active / galaxies: jets / galaxies: star formation
© ESO, 2010
1. Introduction
One of the most remarkable discoveries in extragalactic astronomy in the past decade is the close relationship between the masses of supermassive black holes and several properties of their bulges, such as stellar mass (Magorrian et al. 1998; Häring & Rix 2004), stellar velocity dispersion (“M-σ relation” Gebhardt et al. 2000; Ferrarese 2002; Tremaine et al. 2002; Ferrarese 2002), and the concentration parameter (Graham et al. 2001). Theoretical arguments suggest that the most fundamental of these may be a relationship with the binding energy of the bulge (Hopkins et al. 2007; Younger et al. 2008) or perhaps with the dark-matter halo (Booth & Schaye 2010).
A popular way to interpret these relationships is by postulating that supermassive black holes may regulate their own growth, as well as that of their host galaxies, by coupling a small fraction of their energy output to the surrounding gas. This heats and unbinds significant fractions of the gas, by inhibiting star formation (“AGN feedback”, e.g. Silk & Rees 1998; Springel et al. 2005; Bower et al. 2006; Croton et al. 2006; Cattaneo et al. 2007; Ciotti & Ostriker 2007; Sijacki et al. 2007; Merloni & Heinz 2008; Ciotti et al. 2009; Fanidakis et al. 2010). The scaling relations of black hole mass with the bulge parameters are a major observational constraint to gauging the “efficiency” of this process, the fraction of the energy output of the AGN that is being injected into the interstellar medium of the host galaxy (typically a few × 0.1%, e.g. Di Matteo et al. 2005; Merloni & Heinz 2008; Shankar et al. 2009; Körding et al. 2008).
A large number of observational studies have been dedicated to finding direct observational constraints for the (co-)evolution of black holes and their host galaxies across cosmic time (e.g., Shields et al. 2003; Walter et al. 2004; McLure et al. 2006; Peng et al. 2006; Shields et al. 2006; Woo et al. 2006; Treu et al. 2007; Alexander et al. 2008; Coppin et al. 2008; Shen et al. 2008; Wang et al. 2010). Amongst those, studies of AGN at redshifts z ≳ 2 are particularly interesting, since these redshifts correspond to the epoch when powerful AGN were most abundant (Pei 1995) and when massive galaxies evolved most quickly (e.g., Caputi et al. 2006). However, since we know little about the underlying physics of how AGN interact with their environments and whether feedback occurs in AGN and host galaxies of all types at these redshifts, it is difficult to link black-hole properties and feedback directly. This is particularly true in light of recent galaxy evolution models, which postulate that supermassive black holes may interact with their environments at different stages of their evolution in different ways, where thermal feedback may dominate at some epochs, and mechanical feedback may at others (Churazov et al. 2005; Croton et al. 2006; Sijacki et al. 2007; Merloni & Heinz 2008; Fanidakis et al. 2010; Ciotti et al. 2009).
Using integral-field spectroscopy of the ionized emission-line gas in high-redshift radio galaxies at z ≥ 2 we recently identified energetic, kpc-scale outflows of ionized gas corresponding to significant fractions of their interstellar medium (a few × 1010 M⊙; Nesvadba et al. 2006, 2007, 2008b). These ionized gas masses are comparable to the cold molecular gas masses in these galaxies (e.g., Papadopoulos et al. 2000; De Breuck et al. 2003, 2005; Nesvadba et al. 2009), suggesting that a significant fraction of the interstellar medium participates in the outflows. Outflow velocities are of order of the escape velocity of massive galaxies. These may be the observational signatures of energetic AGN-driven winds, making the black holes of HzRGs particularly interesting targets.
Unfortunately, nuclear broad-line regions (BLRs) in HzRGs are very rarely observed, because the central regions are obscured in these type II AGN. This has significantly hampered observational efforts to characterize their black-hole properties. Most notably, at redshifts z ≥ 2, BLRs have only been anecdotally reported for 4 HzRGs (Röttgering et al. 1997; Larkin et al. 2000; Nesvadba et al. 2006; Humphrey et al. 2007), and their black-hole properties have not yet been fully discussed. McLure et al. (2006) studied the redshift evolution of the black-hole bulge mass relationship for powerful radio-loud AGN out to z ≤ 2 (with 6 radio galaxies at 1.5 ≤ z ≤ 2.0 and one quasar at z = 2.0), but relied on the BLRs of quasars for the black-hole properties and on radio galaxies for the host properties, assuming that the only difference between radio-loud quasars and radio galaxies in a given redshift range was in their orientation. This has not yet been proven for high-redshift AGN, where evolutionary effects may be at least as important (e.g. Hopkins et al. 2006).
Here we discuss the properties of supermassive black holes in 6 powerful radio galaxies at z ~ 2−2.5 (HzRGs), in which we detect broad Hα line emission with FWHM ≥ 10 000 km s-1 originating in a compact region near the nucleus. The similarity to broad-line quasars suggests this is nuclear broad-line emission from the AGN. The emission lines are luminous, but less so than in powerful, optically selected quasars, making it possible to study AGN and host properties for the same objects. We discuss black-hole masses and accretion rates, and use the stellar mass estimates of Seymour et al. (2007) to place these galaxies on the black-hole bulge mass relationship. We also compare radiative and mechanical energy output rates with predictions from recent AGN feedback models (Churazov et al. 2005; Sijacki et al. 2007; Merloni & Heinz 2008; Fanidakis et al. 2010), which suggest that black holes with similar properties as those in our targets may be in a critical transition phase from radiatively efficient to radiatively inefficient accretion.
Throughout the paper we adopt a flat H0 = 70 km s-1 Mpc-1 concordance cosmology with ΩM = 0.3 and ΩΛ = 0.7.
2. Observations and sample selection
All data were taken with the near-infrared integral-field spectrograph SINFONI (Tecza et al. 2000; Bonnet et al. 2004) at the Very Large Telescope of ESO in the H and K bands. SINFONI is an image slicer giving a field of view of 8″ × 8″ with a pixel scale of 250 mas in the seeing-limited mode. These observations are part of an ongoing survey of HzRGs at z ≳ 2. Our sample currently consists of 50 powerful radio galaxies at z ≳ 2, which were selected according to radio power and radio size. All targets have steep-spectrum radio sources. They include a significant fraction of the known radio galaxies with confirmed redshifts at z ≥ 2 observable from the VLT and at suitable redshifts for near-infrared observations. All are type-2 AGN, classified by narrow rest-frame UV emission lines and a high HeII/CIV line ratio. The results of the full survey will be discussed in a series of upcoming papers. Here we focus on the nuclear properties of the 6 galaxies that have broad Hα line emission with properties consistent with originating in AGN broad-line regions. We defer a full analysis of the spatially-extended line emission to a subsequent paper, but emphasize that the present galaxies are consistent with having outflows very similar to those described by Nesvadba et al. (2006, 2007, 2008b).
 |
Fig. 1 Spectra of 5 of the HzRGs with BLRs seen in Hα and SINFONI observations (for the spectrum of MRC1138-262 see Nesvadba et al. 2006). Top to bottom: MRC0156-252, MRC1017-220, TXS1113-178, MRC1558-003, and MRC2025-218. The BLR of MRC0156-252 and MRC1558-003 were detected through longslit spectroscopy by Larkin et al. (2000) and Humphrey et al. (2007), respectively. All spectra are smoothed by 5 pixels (corresponding to 25 Å or ~340 km s-1) to emphasize the BLR. This is only for the sake of visualization, the analysis was performed on the unsmoothed spectra. |
Most data were obtained with the H + K grating giving a spectral resolving power R = 1500 and a spectral coverage between 1.45 μm and 2.4 μm. Total on-source exposure times were between 45 min and 6 h per source. MRC1138-262 was observed in the H and the K band individually, with R ~ 3000 and 4000, respectively, and with on-source exposure times of 75 and 140 min, respectively. (The data of MRC1138-262 have previously been described by Nesvadba et al. 2006, but without a dedicated analysis of its nuclear properties.) We reduced all data sets with our custom data reduction software, which is optimized to study high-redshift galaxies. For details of the data reduction procedure, see, e.g., Nesvadba et al. (2006, 2008a). Data were calibrated using nearby bright stars observed at similar air masses to the targets at the beginning or end of each observation. We used the same stars to monitor the size of the seeing disk with SINFONI and the same setup as for the data. Typically, the seeing was between 0.5″ and 1.5″, corresponding to a spatial resolution of 4−12 kpc at a redshift z ~ 2.5.
Observed wavelengths, redshifts, full-width a half maximum, fluxes of the Hα and Hβ broad lines, and V-band extinctions.
 |
Fig. 2 Close-up of the Hα spectral region of MRC0156-003. We show the spectrum with the best fit superimposed (thick black line). Thin black lines show each individual fit component. The lower panel shows the fit residual. The line at λ = 2.03 μm is the [SII]λλ6716, 6731 doublet, where the two components are blended. At wavelengths shortward of 1.9 μm the atmospheric transmission drops to <10%. |
Three of our sources have already been known to have broad nuclear Hα line emission, but their black-hole properties have not yet been discussed in the literature. Larkin et al. (2000) discovered a broad nuclear Hα line in MRC2025-218 at z = 2.6. Nesvadba et al. (2006) identified a broad Hα emission line in MRC1138-262 at z = 2.2. Humphrey et al. (2007) report on the discovery of broad nuclear Hα emission in MRC1558−003 at z = 2.5. For MRC1558−003 and MRC2025−218 our measurements are consistent with the previous results. For TXS1113-178, Röttgering et al. (1997) find a broad CIV component consistent with the FWHM of our Hα line measurement. Eales & Rawlings (1996) report the detection of a “broad” Hα line in MRC0156-252; however, their spectrum has low signal-to-noise and they give an FWHM estimate of about 4000 km s-1. This is consistent with the integrated extended, spatially-resolved line emission in our data, and significantly narrower than the FWHM = 12 500 km s-1 we find for the broad line. In the following we use our new measurements, adopting the results published in Nesvadba et al. (2006) for MRC1138-252. A few broad lines were previously detected in radio galaxies at lower redshifts, z ~ 1−1.5 (Economou et al. 1995; Willott et al. 2000).
3. Results
Figure 1 shows the integrated spectra of our targets centered on the position of the brightest continuum emission. Spectra were extracted from 2″ × 2″ box apertures (corresponding to about twice the FWHM of the seeing disk). Broad emission-line components are apparent in all six galaxies, and are superimposed by luminous, narrow components of Hα and [NII]λλ6548, 6583. MRC1017-220 is at a redshift where the red wing of the broad line falls into a spectral region with very low atmospheric transmission between the H and the K band, so that we only detected the blue wing of the broad line and the line center, but missed most of the red wing.
Owing to the relatively broad widths of the narrow lines of typically FWHM ~ 800 km s-1, [NII] and the narrow Hα component are blended in all galaxies. The kinematics of these lines is consistent with those in the extended emission-line regions, suggesting they are part of the same outflows as seen in projection along the same line of sight as the AGN. We will discuss the extended line emission in a forthcoming paper.
 |
Fig. 3 We detected broad Hβ line emission in two of our galaxies, MRC1558-003 and MRC2025-218 (upper panels). Thick black lines show a Gaussian line profile with the same redshift and line width, which we measured for Hα, scaled to match the Hβ flux. Thick gray lines show the FeII template from Iwamuro et al. (2002), to illustrate that the contribution of FeII is negligible in both cases. We subtracted the continuum in both spectra. The middle and lower panels show the fit residual spectrum after subtracting Hβ and the position of night sky lines, respectively. |
Broad Hα luminosities, black holes masses, Eddington and bolometric luminosities, jet kinetic luminosities, and stellar masses.
3.1. Broad Hα line emission
To derive emission-line properties, we removed the continuum emission and fitted all broad and narrow line components with a set of weighted Gaussian profiles. To distinguish between broad and narrow components, we attributed zero weights to wavelengths where the narrow components (or night-sky lines) dominate1. We subtracted the broad components, and fitted the residuals with lines whose redshifts and line widths were tied to the values observed in [OIII]λ5007. Nesvadba et al. (2008b) find that, in the extended emission-line regions of HzRGs, all bright, narrow emission lines typically have very uniform kinematic properties, at least to the precision of the observations, and we find the same in the present analysis.
Broad Hα lines typically have fluxes FHα ~ 10-14−10-15 erg s-1 cm-2 and FWHMs ~ 10 000−14 000 km s-1. Values for individual targets are given in Table 1. We did not correct for Galactic foreground extinction, which is negligible at the observed near-infrared wavelengths. One broad and one narrow component were sufficient for all galaxies except MRC0156-252, for which we needed an additional Hα component of intermediate width, FWHM = 7480 km s-1 and an integrated line flux of 1.4 × 10-14 erg s-1 cm-2 (Fig. 2).
All data sets are deep enough that we would have detected Hα lines with similar luminosity and width, which suggests that HzRGs with HαBLRs may have different AGN properties or may be more highly extincted than other HzRGs. To quantify this we measured the rms at the spectral position of Hα in each of the cubes where Hα falls into the band, but was not detected. We find a typical rms of a few × 10-19 erg s-1 cm-2, and up to ~1 × 10-18 erg s-1 cm-2 for the shallowest data sets. We used Monte Carlo simulations to estimate 3σ limits on the integrated flux of these lines, assuming two line widths which are representative of the measured widths. For 1000 iterations, we can exclude line fluxes brighter than 8.7 × 10-17 erg s-1 cm-2 and 2.6 × 10-16 erg s-1 cm-2 at 3σ significance for line widths of FWHM = 9500 km s-1 and FWHM = 12 500 km s-1, respectively. This is about an order of magnitude fainter than the fluxes of the detected broad Hα lines.
3.2. Broad Hβ line emission and extinction
In the two galaxies with the deepest observations we also detected a broad Hβ component in the H-band. Figure 3 shows the broad Hβ line emission in MRC0156-252 and MRC1558-003. TXS1113-178 and MRC1138-262 have more shallow data which are not sufficient for probing Hβ line emission in a similar way. In MRC0156-252 and MRC1017-220, Hβ falls outside the near-infrared atmospheric windows.
Although the broad Hβ lines are not intrinsically faint, they are difficult to detect due to their large widths compared to the spectral sampling, imperfections in the night-sky line subtraction, superimposed narrow-line components, including [OIII]λλ4959, 5007, and the shape of the continuum. We therefore did not fit the redshift and widths of these lines individually, but used the values found for Hα to identify the lines and to estimate their fluxes. In Fig. 3 we show the expected Hβ profile for both galaxies. By scaling this spectrum we derive Hα/Hβ flux ratios of F(Hα)/F(Hβ) ~ 4−5 for both galaxies. By comparing our spectra with the FeII quasar template of Iwamuro et al. (2002) we can rule out strong FeII contamination at the wavelength of Hβ.
For an intrinsic line ratio of Hα/Hβ = 3.1 and a galactic extinction law, the observed Hα/Hβ ratios correspond to an extinction of AV ~ 1 mag. Dong et al. (2008) report very similar Hα/Hβ ratios in radio-loud AGN at low redshift, Hα/Hβ = 3.4.
Equally low extinctions are also suggested by comparing the observed Hα and X-ray fluxes. If most of the Hα line emission is due to photoionization of gas in the central few parsecs of the AGN, then simple energy conservation arguments imply that the Hα line emission cannot be more luminous than the X-ray emission. In fact, observations of nearby AGN suggest X-ray/Hα ratios of 3−20 (Ward et al. 1988; Imanishi & Terashima 2004). X-ray luminosities are available in the literature for two of our sources. Overzier et al. (2005) measure ℒX = 2 × 1045 erg s-1 at 2−6 keV for MRC0156-003, and Carilli et al. (2002) find ℒX = 4 × 1045 erg s-1 at 2−10 keV for MRC1138-262. These X-ray and Hα luminosities given in Table 2 imply a ratio of X-ray to Hα emission of ~6 for both sources. This is within the range of values suggested by Ward et al. (1988) and Imanishi & Terashima (2004), and is fully consistent with relatively low extinction along the line of sight into the AGN. Alexander et al. (2008) give similar arguments for submillimeter-selected quasars and point out that this also suggests that scattering is unlikely to play a large role for the observed Hα line fluxes. The same applies to our HzRGs.
The same comparison for two HzRGs with similar X-ray and near-infrared data (Overzier et al. 2005; Nesvadba et al. 2008b) suggests that the HαBLRs of HzRGs may generally suffer much higher extinction. Overzier et al. (2005) measure ℒX = 1 × 1044 erg s-1 for MRC0406-244 at z = 2.4 and ℒX = 6 × 1044 erg s-1 for TXS0828+193 at z = 2.6. The study of Nesvadba et al. (2008b) did not reveal any HαBLRs but allow us to place upper limits on their observed Hα luminosity of 2 × 1042 erg s-1. This corresponds to much smaller fractions of their X-ray luminosity, 1/20 for MRC0406-244 and 1/100 for TXS0828+193. It may indicate that extinction depends strongly on the individual sightline into the AGN. This is plausible if the spatial distribution of the obscuring material is inhomogeneous and clumpy.
4. The supermassive black holes of HzRGs
4.1. The frequency of HαBLRs in HzRGs
Previous discoveries of HαBLRs in HzRGs have only been anecdotal (Larkin et al. 2000; Nesvadba et al. 2006; Humphrey et al. 2007, see also Economou et al. 1995; Willott et al. 2000 at somewhat lower redshifts, z ≤ 1.5). Although we did not select a complete sample in the usual statistical sense, our targets include a significant fraction of the known HzRGs at these redshifts, and may therefore allow a rough assessment of how frequent HαBLRs may be among the most powerful radio galaxies known at z ≥ 2. Having 27 targets at redshifts where HαBLRs fall into the atmospheric windows and adding 4 HzRGs at similar redshifts of Humphrey et al. (2007) which are not in our sample, we find that HαBLRs were detected in 6/31 possible cases, corresponding to ~20% of our sample.
4.2. The nature of HαBLRs
HzRGs typically have luminous, extended line emission with complex kinematics. For example, Nesvadba et al. (2006, 2007, 2008b) find line widths of up to FWHM ~ 4000 km s-1 in the integrated spectra of HzRGs, which are due to spatially extended gas with large velocity gradients and line widths, and could mimic a BLR (see the example of MRC0156-262, Sect. 2). In our targets the Hα emission-line morphology shows a luminous, nuclear, and compact Hα emission-line component in addition to the more diffuse extended (and narrower) line emission. These broad components have no equivalent in [OIII]λ5007, unlike the emission from the diffuse gas, where the spectral profiles of Hα and [OIII]λ5007 are typically very similar (Nesvadba et al. 2007, 2008b). The absence of broad components of forbidden lines is among the prime characteristics of BLRs where the electron densities are high enough that forbidden levels are collisionally de-excited.
We take this as evidence that the HαBLRs of our targets indeed trace gas in the vicinity of the supermassive black hole, and adopt the common interpretation that this gas is approximately in virial equilibrium and is an adequate tracer of the black hole mass. Accretion rates are relatively low in our sources (Sect. 4.4) well below the values for which we may expect strong disk winds (Kurosawa & Proga 2009; Proga & Kallman 2004).
4.3. Virial mass estimates
A number of recipes have been proposed to estimate black-hole masses from the line widths and luminosities (e.g., McLure & Jarvis 2002; Vestergaard 2002; Onken et al. 2004; Peterson et al. 2004; Vestergaard & Peterson 2006), among which we choose the approach of Greene & Ho (2005) which relies on the properties of the Hα line only. This is the obvious method of choice, because Hα is the only line that is well detected in our targets.
Greene & Ho (2005) give a simple scaling for black-hole mass, MBH, as a function of the FWHM and luminosity of the Hα line, MBH = 2 × 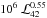 ×
× 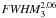 , where FWHM3 and Hα luminosity ℒ42 are given in units of 103 km s-1 and 1042 erg s-1. With this scaling and the luminosities and FWHMs given in Table 1, we find a relatively narrow range of black-hole masses of a few × 109 M⊙ and up to 2 × 1010 M⊙. Results for individual galaxies are given in Table 2.
, where FWHM3 and Hα luminosity ℒ42 are given in units of 103 km s-1 and 1042 erg s-1. With this scaling and the luminosities and FWHMs given in Table 1, we find a relatively narrow range of black-hole masses of a few × 109 M⊙ and up to 2 × 1010 M⊙. Results for individual galaxies are given in Table 2.
Applying a method calibrated for quasars to radio galaxies can potentially introduce important systematic uncertainties, in particular owing to inclination and extinction. Section 3.2 suggests that extinction does not likely play a major role. Greene & Ho (2005) find an average observed ratio of Hα/Hβ ≈ 3.5, whereas we find Hα/Hβ ≈ 4. Since black-hole mass depends only weakly on the Hα luminosity, this difference is negligible.
Orientation is perhaps a bigger concern, if our radio galaxies are on average more strongly inclined relative to the line of sight than quasars (e.g., Antonucci 1993). Greene & Ho (2005) do not find any significant difference between radio-quiet and radio-loud quasars, but it is likely that their radio-loud sample consisted mostly of flat-spectrum quasars (although they do not comment on the radio spectral index).
Jarvis & McLure (2002) compare quasars with flat and steep-spectrum radio sources and find on average a factor 1.3 broader lines in steep-spectrum quasars similar to our HzRGs, which would correspond to a bias towards higher masses by a factor 1.8. Of course we cannot exclude that HzRGs may on average be even more strongly inclined than steep-spectrum radio-loud quasars. If, for example, the BLR in such a quasar had an inclination of ~45° relative to the line of sight, and that of a radio galaxy an inclination of ~80°, then we would expect to overestimate the black hole mass by another factor ~2, which is not very different from other astrophysical uncertainties (see also, e.g., Collin et al. 2006).
Orientations near the line of sight are also disfavored by relatively uniform and moderate fractions of the luminosity of the radio core relative to the lobes of 0.7% to 10% (Carilli et al. 1997; Pentericci et al. 2000), which suggest orientations between 45° and 60° (e.g. Carilli et al. 1997). This also suggests that orientation probably does not introduce a major bias. Moreover, it is not clear whether the unified model is appropriate for high-redshift AGN, since evolutionary effects may at least play as large a role at high redshift (e.g. Hopkins et al. 2006, see also Sect. 6). When necessary in the following we state both mass estimates, the one with and the one without inclination correction.
4.4. Eddington luminosities, radiative and mechanical luminosities
The accretion luminosity of a black hole is the second fundamental parameter we estimate from our data, by relating the bolometric luminosity with the maximally possible accretion luminosity for a spherically symmetric flow (Eddington luminosity). The Eddington luminosity, ℒEdd, of a SMBH scales with black-hole mass as ℒEdd = 1.3 × 1038 M/M⊙ erg s-1 (Rees 1984). In Table 2 we list the Eddington luminosities corresponding to the black-hole masses estimated in Sect. 4.3.
The bolometric luminosity can be estimated from our data. Greene & Ho (2005) calibrated the broad Hα luminosity as a function of the continuum luminosity at 5100 Å, ℒHα = 5.25 × 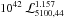 , and we adopt ℒbol = 9 λ ℒ5100 to translate the continuum luminosity at 5100 Å to the bolometric luminosity (Kaspi et al. 2000). With the black-hole properties listed in Table 2, we find accretion luminosities of 0.02−0.07 ℒEdd (0.04−0.14 ℒEdd for inclination-corrected black-hole masses, Sect. 4.3). This result is not dominated by extinction. Hα/Hβ line ratios are not much higher than those of quasars (Greene & Ho 2005), and Eddington luminosity and bolometric luminosity only weakly depend on ℒHα with powers of 0.55 and 0.86, respectively. Therefore extinction is unlikely to lower the Eddington ratios by more than ~10%.
, and we adopt ℒbol = 9 λ ℒ5100 to translate the continuum luminosity at 5100 Å to the bolometric luminosity (Kaspi et al. 2000). With the black-hole properties listed in Table 2, we find accretion luminosities of 0.02−0.07 ℒEdd (0.04−0.14 ℒEdd for inclination-corrected black-hole masses, Sect. 4.3). This result is not dominated by extinction. Hα/Hβ line ratios are not much higher than those of quasars (Greene & Ho 2005), and Eddington luminosity and bolometric luminosity only weakly depend on ℒHα with powers of 0.55 and 0.86, respectively. Therefore extinction is unlikely to lower the Eddington ratios by more than ~10%.
4.5. Kinetic luminosity of the radio source
In Sect. 6 we rely on the radiative and mechanical energy output rates of the supermassive black holes. This requires constraining the kinetic jet luminosity, which is inherently difficult, because the observed radio luminosity is not a good tracer of the energy content of the relativistic jet plasma. Consequently, jet kinetic powers are only known at an order-of-magnitude level or worse (e.g., Bicknell 1995). We adopt two different methods to estimate the kinetic power in our sources. Both methods rely on low-frequency fluxes, which we estimate from extrapolating along the power law of the radio synchrotron emission based on multi-frequency observations listed in the NED extragalactic data base.
First, we use the calibration of Bîrzan et al. (2008), who estimated the energy necessary to inflate cavities in the diffuse hot gas of massive galaxy clusters. This is a very direct empirical estimate of the jet kinetic power, but was derived for radio sources that are 2−3 orders of magnitude less powerful than those in our targets. Second, we rely on the results of Willott et al. (1999), who propose a scaling of the kinetic power as a function of the monochromatic radio flux at 151 MHz, ℒkin = 3 × 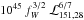 erg s-1. Here ℒ151,28 indicates the measured flux density at 151 MHz in units of 1028 W Hz-1 sr-1, and fW is a correction factor which includes the most salient astrophysical uncertainties. It is likely in the range 1−20, and we adopt a value of 10, following the arguments given in Cattaneo et al. (2009).
erg s-1. Here ℒ151,28 indicates the measured flux density at 151 MHz in units of 1028 W Hz-1 sr-1, and fW is a correction factor which includes the most salient astrophysical uncertainties. It is likely in the range 1−20, and we adopt a value of 10, following the arguments given in Cattaneo et al. (2009).
Typically we find kinetic luminosities of 5−10 × 1045 erg s-1 with the calibration of Bîrzan et al. (2008), and ~5−10 × 1046 erg s-1, corresponding to of order 0.01−0.1 ℒEdd with that of Willott et al. (1999). Results for individual galaxies are listed in Table 2.
5. Black-hole bulge mass relationship
The scaling relationships of black holes and bulges are important tracers of the (possibly self-)regulated growth of black holes and galaxies across cosmic time. Accordingly, much observational effort has been invested in tracing the redshift evolution of these relationships (e.g., Shields et al. 2003, 2006; Woo et al. 2006; Peng et al. 2006; Treu et al. 2007; Shen et al. 2008), although sometimes with contradictory results. Overall these observations advocate a relatively mild redshift evolution of a few tenths of dex out to moderate redshifts (z ≪ 1).
We now compare our HzRGs with the local relationship, relying on our black-hole mass estimates (Sect. 4.3) and the photometric mass estimates of Seymour et al. (2007). Seymour et al. estimated masses or upper limits for 70 HzRGs with Spitzer rest-frame near-infrared observations, constraining the relative contribution of the stellar component and dust at different temperatures. Photometric estimates of stellar masses are relatively robust for a range of star-formation histories, but poorly constrained ages and initial mass functions cause systematic uncertainties of factors of up to about 2−3 for plausible ages between few × 108 yrs and about 109 yrs. 5 of our galaxies are included in the sample of Seymour et al. (2007). For TXS1113-178, which is not part of this sample, we use the average mass of the Seymour et al. sample, 1011.5 M⊙. We prefer to use this average mass rather than the K-bands magnitude derived from our SINFONI cube, because the latter may be significantly contaminated by the AGN, whereas the Seymour et al. observations are near the rest-frame H-band where the stellar contribution to the overall spectral energy distribution is maximal. Moreover, the HzRGs of Seymour et al. (2007) span a narrow mass range overall, not much greater than the uncertainties in the mass estimates of individual galaxies. In the following we also assume that these are spheroid-dominated systems, consistent with the morphological studies of van Breugel et al. (1998) and Pentericci et al. (2001), and plausible for high stellar masses of few 1011 M⊙.
In Fig. 4 we show the black-hole bulge mass relationship of our HzRGs and compare it with the relationship for nearby galaxies derived by Häring & Rix (2004). Arrows mark galaxies for which Seymour et al. (2007) give upper limits on the stellar mass. A new, ongoing analysis of the Seymour et al. sample suggests that these upper limits are at most 20−50% larger than the actual masses. This is negligible for our purposes. The sole exception may be MRC1138-262 where the distinction between AGN and stellar continuum is more difficult due to the particularly powerful AGN. This analysis is based on IRAC and MIPS 24 μm and 60 μm photometry for all targets and includes a more systematic analysis of the dust emission (De Breuck et al. 2010).
 |
Fig. 4 Black-hole masses as estimated in Sect. 4.3 as a function of stellar mass of the host galaxy, taken from Seymour et al. (2007). Red dots mark the HzRG in which we detected HαBLRs, not correcting for inclination, and blue empty squares show the same galaxies with black-hole masses estimated assuming the inclination correction of Jarvis & McLure (2002). The empty circle marks TXS1113-178 for which we used the average HzRG mass of Seymour et al. (2007). Arrows mark galaxies for which Seymour et al. only provide upper limits (see text for details). Empty circles show the nearby galaxies of Häring & Rix (2004), and the black dashed line shows the best linear fit to their sample. |
We focus in the following on the ensemble properties of our sample, but each individual galaxy falls within the scatter of the local relationship (Fig. 4). This illustrates that HzRGs have at most about 4 × larger black-hole masses for a given bulge mass than expected from the local relationship (a factor 2 if we use inclination-corrected black-hole mass estimates, see Sect. 4.3). This is broadly consistent with the redshift evolution of radio-loud AGN found by McLure et al. (2006), if we extrapolate to the redshifts of our sources. McLure et al. used the observed K-band magnitudes of radio galaxies to estimate bulge masses and broad-line spectroscopy of steep-spectrum quasars out to z = 1.5−2.0, and predict an offset from the local relationship by 0.6 dex for z ≥ 2.
The offset we find is significantly less than those reported for other populations of massive, strongly star-forming galaxies at z ≥ 2, (e.g. Walter et al. 2004; Alexander et al. 2008; Coppin et al. 2008; Wang et al. 2010). The reason could be that we used stellar masses instead of dynamical masses based on the width of CO line emission like the above analyses, or it could indicate evolutionary effects. Redshifts z ≥ 1−2 are the most rapid phase in the evolution of massive galaxies, which makes observations at these redshifts particularly interesting, in spite of the observational challenges.
The offset of HzRGs relative to the local sequence is formally consistent with observations of the redshift evolution of the M-σ relationship out to moderate (z ~ 0.5) redshifts. Using, e.g., the relationship of Woo et al. (2008), we would expect an offset by a factor ~2. However, it is not clear whether this is indeed an evolutionary effect or caused by selection effects. For example, our HzRGs, which are somewhat more massive than the local sample of Häring & Rix, would fall on the relationship by Häring & Rix (2004), if the latter was somewhat steepened (within their scatter). Alternatively, e.g., Wyithe (2006) propose that black hole and bulge properties could be related through a log-quadratic rather than a log-linear relationship, in which case our targets would show no sign of evolution.
Observational biases may also contribute. For example, following Lauer et al. (2007) we may expect that the intrinsic scatter in the relationship combined with the the steep slope of the high-mass end of the galaxy mass function may bias the relationship for massive galaxies towards higher black hole masses. We argue in Sect. 7 that, whether this offset is intrinsic or not, mild offsets of factors 2−4 are not inconsistent with the basic picture where HzRGs are massive galaxies that have completed most of their growth by z ~ 2.
 |
Fig. 5 The ratio of kinetic and radiative luminosity of the AGN as a function of accretion power, following Merloni & Heinz (2008). Above a critical accretion power of a few percent of Eddington, the relationship splits into two branches to accommodate radio-loud and radio-quiet, rapidly accreting AGN with radiatively efficient accretion. Red filled and empty triangles show the radio galaxies of our sample, using different calibrations to estimate the kinetic energy from the observed radio power (Sects. 4.5, 6). Small blue squares and green circles show z ~ 2 quasars and submillimeter galaxies from Coppin et al. (2008) and Alexander et al. (2008), respectively. Small light blue triangles show z ≥ 6 quasars taken from Wang et al. (2010). Blue arrows mark the typical accretion regime of massive early-type (and typically radio-active) elliptical galaxies. Only the HzRGs fall into the critical accretion regime, where (if the scenario of Merloni & Heinz 2008, and others is fundamentally correct) we may expect to find evolved supermassive black holes near the end of their active phase of growth, as they are transiting into the low-accretion regime spanned by massive early-type galaxies. |
6. Low accretion rates of SMBHs in HzRGs
In Sect. 4.4 we used our black-hole mass estimates and broad-line luminosities to estimate accretion luminosities for our targets in the range of a few and up to about 10% Eddington. When reaching similar accretion luminosities of a few percent Eddington, Galactic “miniquasars” undergo rapid changes in their accretion properties, with dramatic effects for their X-ray and radio emission (e.g., Nowak 1995; Maccarone et al. 2003; Körding et al. 2006a,b; Fender et al. 2004). The analogy with these stellar-mass black holes has very recently inspired several authors to propose a fairly complex scenario of “synthesis” (Merloni & Heinz 2008) or “unified” (Fanidakis et al. 2010) AGN feedback, where an initial, strongly radiative phase with high accretion rates is followed by a later phase with low accretion rates, during which the radio source inhibits gas cooling and accretion through the injection of kinetic energy into the ambient medium (see also, e.g., Sijacki et al. 2007). Churazov et al. (2005) proposes that this may be accompanied by episodes of highly unstable accretion, rapid “radio flaring”, and powerful radio activity. Merloni & Heinz (2008) use the local black-hole mass function and X-ray constraints on the radiative energy output of AGN to quantify the accretion and feedback history of AGN within this scenario in a semi-empirical way.
The HzRGs of our sample have luminous (ℒbol ≥ 1046 erg s-1) AGN as well as very short-lived (a few × 106−7 yrs; Blundell & Rawlings 1999), powerful radio sources of up to 1029 W Hz-1 at 500 MHz (Miley & De Breuck 2008), and they show the signatures of fast, AGN-driven kpc-scale outflows of significant fractions of their interstellar medium (Nesvadba et al. 2006, 2008b). These are several of the characteristics expected for the “flaring” phase between radiative and kinetic feedback in the “synthesis” models, and the low accretion rates of their black holes could be another. Churazov et al. (2005) postulate that during this phase, kinetic feedback and gas heating become more efficient as accretion rates drop further, until AGN and host galaxy reach a state where very low accretion rates can efficiently balance gas cooling (Croton et al. 2006). This may be the case in nearby, massive, early-type galaxies with radio sources (Best et al. 2006; Hardcastle et al. 2007) where star formation is significantly less efficient than in ordinary star-forming galaxies (Nesvadba et al. 2010).
For a more quantitative comparison we show the ratio of kinetic to radiative energy output (derived in Sects. 4.5 and 4.4, respectively) in Fig. 5 as a function of accretion luminosity. We adopted this figure from Merloni & Heinz (2008, their Fig. 1, and use the kinetic luminosities derived with the relationship of Willott et al. (1999) and Bîrzan et al. (2008), respectively. For accretion luminosities above the critical value, the line splits to accommodate radio-quiet (lower branch) and radio-loud (upper branch) AGN. All of our targets are in the critical accretion regime, and have ratios of kinetic-to-radiative power that are near the values suggested by Merloni & Heinz (2008).
Figure 5 also shows other populations of powerful AGN in massive, intensely star-forming galaxies at z ≥ 2, like submillimeter galaxies with BLR measurements (Alexander et al. 2008), and quasars at redshift z ~ 2 and z ~ 6, respectively (taken from Coppin et al. 2008; Walter et al. 2004; Wang et al. 2010). To estimate the kinetic luminosity of the radio sources in these samples, we used the approach outlined in Sect. 4.5 and published radio fluxes, where we assumed a radio spectral index of α = −0.8. For the high-redshift AGN, this has the character of an upper limit, because the observed faint radio fluxes may be significantly contaminated, or even dominated, by star formation. Unlike the HzRGs, these galaxies do not fall into the critical accretion regime.
Similarly, the black holes in our HzRGs seem to have lower accretion luminosities than equally massive black holes studied in large quasar surveys at z ~ 2−3. For example, Kollmeier et al. (2006) find that typical accretion luminosities in their X-ray and infrared-selected quasar sample taken from the AGES survey are a factor 10 higher (but tails of their distribution extend to the same range found for HzRGs). Their selection suggests >70% completeness for black holes with masses and accretion luminosities ≥ 0.01 ℒEdd, similar to those in HzRGs, making this comparison robust (but see, e.g. Kelly et al. 2010; Schulze & Wisotzki 2010,for a discussion of the effects of incompleteness in statistical studies of the accretion history of AGN).
7. Implications for high-redshift galaxy evolution
Observational evidence is growing that the host galaxies of HzRGs may be massive galaxies seen during a late stage of their active formation phase: at all redshifts, radio galaxies are among the brightest galaxies in the K-band, suggesting they are at the upper end of the mass function (De Breuck et al. 2001; Willott et al. 2003; see also Seymour et al. 2007). At redshifts z > 3, most HzRGs are luminous submillimeter emitters with intense star formation, whereas only few galaxies are detected at lower redshifts (Archibald et al. 2001; Reuland et al. 2004). If this is not entirely from selection effects, then it may suggest that HzRGs as an ensemble are transiting from actively star-forming to passively evolving during this epoch, perhaps as a consequence of AGN feedback signaled by the extended outflows of warm ionized gas. It is interesting that this happens during the epoch where the red sequence seems to emerge (Kodama et al. 2007).
The results of Sects. 5 and 6 suggest that the black holes in HzRGs may also be nearing the end of their period of active growth. Compared to submillimeter galaxies and quasars at z ≥ 2 (Alexander et al. 2008; Coppin et al. 2008; Walter et al. 2004; Wang et al. 2010), they fall remarkably close to the local relationship between black hole and bulge mass, as can be expected if the evolution of black holes and bulges is driven by the same mechanism.
Figure 5 suggests that the accretion rates of HzRGs may have dropped to a critical value where mechanical feedback begins to dominate radiative feedback, unlike the black holes in the above mentioned submillimeter galaxies and quasars, which all have higher accretion rates. It is tempting to speculate that this transition may also have triggered the large-scale outflows of the HzRGs, which may sweep up and heat the ambient cold gas out to scales of 10s of kpc. Integral-field spectroscopy of luminous, infrared-selected quasars with moderate radio sources reveals disturbed gas kinematics, but no evidence of equally strong outflows extending over scales of 10s of kpc (Alexander et al. 2010; Polletta et al., in prep.).
Obviously, radiatively efficient accretion is maintained in HzRGs, with ℒbol = few × 1046 erg s-1, but outflow rates of a few 100 M⊙ yr-1 of warm ionized gas (ignoring other gas phases Nesvadba et al. 2006, 2008b) suggest that the gas supply for star formation and AGN activity is being depleted rapidly. Broad UV absorption lines in MRC2025-218 (Humphrey et al. 2008), reminiscent of broad absorption lines sometimes observed in quasars, suggest that outflows are also present near the black hole, making it plausible that, after the radio-loud phase, neither the supermassive black holes in HzRGs nor their host galaxies, will have enough “fuel” to maintain much more growth, unless significant amounts of cold gas are supplied, for example through a major merger. The environments of HzRGs are rich in ionized, neutral, and molecular gas (Villar-Martín et al. 2003; van Ojik et al. 1997; Nesvadba et al. 2009), but the analogy with nearby massive galaxy clusters illustrates that much of this gas can be heated by the AGN (see, e.g., McNamara & Nulsen 2007, and references therein).
Moderate, subsequent bulge growth may occur through accretion of satellite galaxies of HzRGs (Nesvadba et al. 2008b; Hatch et al. 2009). Ram-pressure stripping, tidal effects, and on-going star formation will likely have removed much of the gas in the satellites by the time they merge, in which case galaxy growth would not necessarily lead to black-hole growth (Kazantzidis et al. 2005). This is consistent with structural parameters of nearby massive early-type and cD galaxies (Weinzirl et al. 2009; Schombert 1987) and could eliminate the small offset of HzRGs from the local black-hole bulge mass relationship (if it is not entirely due to systematic effects), or else change the position of our galaxies by a few dex within the large scatter of this relationship.
8. Summary
We presented an analysis of the black-hole properties in 6 powerful radio galaxies at z ~ 2 (HzRGs), which show broad, luminous Hα line emission that we identify as emission from the AGN broad-line region (HαBLR). This study is part of an ongoing, systematic analysis of 50 HzRGs with rest-frame optical integral-field spectroscopy and with the goal of quantifying the role of AGN feedback for galaxy evolution at high redshift. Our main results are as follows.
(1) HαBLRs in HzRGs are not rare. 6/31 HzRGs at redshifts where Hα can be observed show HαBLRs, corresponding to ~20% of our sample. The broad Hα lines have emission-line luminosities of a few × 1044 erg s-1 and line widths of FWHM ≥ 10 000 km s-1. Broad Hβ lines in 2 cases and X-ray constraints suggest low extinction (AV ~ 1 mag).
(2) We estimate black-hole masses and bolometric luminosities from the Hα luminosities and line widths, finding masses of a few × 109 M⊙ and up to 1010 M⊙ which is broadly consistent with the masses of the most massive black holes in the nearby universe. Bolometric luminosities are a few percent of the Eddington luminosity, lower than in other populations of massive, intensely star-forming galaxies and quasars with black holes of similar mass.
(3) Black-hole and stellar masses suggest that HzRGs fall on the black-hole bulge mass relationship for local galaxies, formally with a small offset to lower bulge masses by at most a factor 4. Much of this offset may be from systematic effects; alternatively, it could be explained with an extended phase of accretion of (gas-poor) satellite galaxies.
(4) Relative to the Eddington luminosities, HzRGs have radiative and (through the radio source) mechanical energy output rates that are in the “critical” range expected by recent “unifie”’ AGN feedback scenarios. This could imply that they have reached the end of their period of active growth, if these models are fundamentally correct. We argue that the same is probably true for the host galaxies of HzRGs, suggesting that black hole and host galaxy could be terminating their phase of active growth at the same time.
Acknowledgments
We would like to thank the staff at Paranal for having carried out the observations and the ESO TAC for the generous allocation of observing time. We thank the referee for comments that helped substantially improve the paper. N.P.H.N. wishes to thank Elmar Körding for interesting discussions about big and small black holes near and far during a visit in Southampton. N.P.H.N. and M.D.L. wish to thank the CNRS for the continuous financial support.
References
- Alexander, D. M., Brandt, W. N., Smail, I., et al. 2008, AJ, 135, 1968 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. M., Swinbank, A. M., Smail, I., McDermid, R., & Nesvadba, N. P. H. 2010, MNRAS, 57 [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Archibald, E. N., Dunlop, J. S., Hughes, D. H., et al. 2001, MNRAS, 323, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., Kaiser, C. R., Heckman, T. M., & Kauffmann, G. 2006, MNRAS, 368, L67 [NASA ADS] [Google Scholar]
- Bicknell, G. V. 1995, ApJS, 101, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Bîrzan, L., McNamara, B. R., Nulsen, P. E. J., Carilli, C. L., & Wise, M. W. 2008, ApJ, 686, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Blundell, K. M., & Rawlings, S. 1999, Nature, 399, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnet, H., Abuter, R., Baker, A., et al. 2004, The Messenger, 117, 17 [NASA ADS] [Google Scholar]
- Booth, C. M., & Schaye, J. 2010, MNRAS, 405, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Caputi, K. I., Dole, H., Lagache, G., et al. 2006, ApJ, 637, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., Röttgering, H. J. A., van Ojik, R., Miley, G. K., & van Breugel, W. J. M. 1997, ApJS, 109, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., Harris, D. E., Pentericci, L., et al. 2002, ApJ, 567, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., Blaizot, J., Weinberg, D. H., et al. 2007, MNRAS, 377, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., Faber, S. M., Binney, J., et al. 2009, Nature, 460, 213 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Churazov, E., Sazonov, S., Sunyaev, R., et al. 2005, MNRAS, 363, L91 [NASA ADS] [Google Scholar]
- Ciotti, L., & Ostriker, J. P. 2007, ApJ, 665, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L., Ostriker, J. P., & Proga, D. 2009, ApJ, 699, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Collin, S., Kawaguchi, T., Peterson, B. M., & Vestergaard, M. 2006, A&A, 456, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coppin, K. E. K., Swinbank, A. M., Neri, R., et al. 2008, MNRAS, 389, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- De Breuck, C., van Breugel, W., Röttgering, H., et al. 2001, AJ, 121, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- De Breuck, C., Neri, R., & Omont, A. 2003, New Astron. Rev., 47, 285 [NASA ADS] [CrossRef] [Google Scholar]
- De Breuck, C., Downes, D., Neri, R., et al. 2005, A&A, 430, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Breuck, C., Seymour, N., Stern, D., et al. 2010, ApJ, 725, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dong, X., Wang, T., Wang, J., et al. 2008, MNRAS, 383, 581 [NASA ADS] [Google Scholar]
- Eales, S. A., & Rawlings, S. 1996, ApJ, 460, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Economou, F., Lawrence, A., Ward, M. J., & Blanco, P. R. 1995, MNRAS, 272, L5 [NASA ADS] [Google Scholar]
- Fanidakis, N., Baugh, C. M., Benson, A. J., et al. 2010, MNRAS, in press [arXiv:0911.1128] [Google Scholar]
- Fender, R. P., Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L. 2002, ApJ, 578, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., Erwin, P., Caon, N., & Trujillo, I. 2001, ApJ, 563, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., & Ho, L. C. 2005, ApJ, 630, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2007, MNRAS, 376, 1849 [NASA ADS] [CrossRef] [Google Scholar]
- Häring, N., & Rix, H.-W. 2004, ApJ, 604, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Hatch, N. A., Overzier, R. A., Kurk, J. D., et al. 2009, MNRAS, 395, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., Robertson, B., & Krause, E. 2007, ApJ, 669, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Humphrey, A., Villar-Martín, M., Fosbury, R., et al. 2007, MNRAS, 375, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Humphrey, A., Villar-Martín, M., Vernet, J., et al. 2008, MNRAS, 383, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Imanishi, M., & Terashima, Y. 2004, AJ, 127, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamuro, F., Motohara, K., Maihara, T., et al. 2002, ApJ, 565, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Jarvis, M. J., & McLure, R. J. 2002, MNRAS, 336, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Kazantzidis, S., Mayer, L., Colpi, M., et al. 2005, ApJ, 623, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C., Vestergaard, M., Fan, X., et al. 2010, ApJ, 719, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- Kodama, T., Tanaka, I., Kajisawa, M., et al. 2007, MNRAS, 377, 1717 [NASA ADS] [CrossRef] [Google Scholar]
- Kollmeier, J. A., Onken, C. A., Kochanek, C. S., et al. 2006, ApJ, 648, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Körding, E. G., Fender, R. P., & Migliari, S. 2006a, MNRAS, 369, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Körding, E. G., Jester, S., & Fender, R. 2006b, MNRAS, 372, 1366 [NASA ADS] [CrossRef] [Google Scholar]
- Körding, E. G., Jester, S., & Fender, R. 2008, MNRAS, 383, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Kurosawa, R., & Proga, D. 2009, MNRAS, 397, 1791 [NASA ADS] [CrossRef] [Google Scholar]
- Larkin, J. E., McLean, I. S., Graham, J. R., et al. 2000, ApJ, 533, L61 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lauer, T. R., Tremaine, S., Richstone, D., & Faber, S. M. 2007, ApJ, 670, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Maccarone, T. J., Gallo, E., & Fender, R. 2003, MNRAS, 345, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., & Jarvis, M. J. 2002, MNRAS, 337, 109 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., Jarvis, M. J., Targett, T. A., Dunlop, J. S., & Best, P. N. 2006, MNRAS, 368, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Merloni, A., & Heinz, S. 2008, MNRAS, 388, 1011 [NASA ADS] [Google Scholar]
- Miley, G., & De Breuck, C. 2008, A&ARv, 15, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvadba, N. P. H., Lehnert, M. D., Eisenhauer, F., et al. 2006, ApJ, 650, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvadba, N. P. H., Lehnert, M. D., De Breuck, C., Gilbert, A., & van Breugel, W. 2007, A&A, 475, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nesvadba, N. P. H., Lehnert, M. D., Davies, R. I., Verma, A., & Eisenhauer, F. 2008a, A&A, 479, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nesvadba, N. P. H., Lehnert, M. D., De Breuck, C., Gilbert, A. M., & van Breugel, W. 2008b, A&A, 491, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nesvadba, N. P. H., Neri, R., De Breuck, C., et al. 2009, MNRAS, 395, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvadba, N., Boulanger, F., Salome, P., et al. 2010, A&A, 521, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowak, M. A. 1995, PASP, 107, 1207 [NASA ADS] [CrossRef] [Google Scholar]
- Onken, C. A., Ferrarese, L., Merritt, D., et al. 2004, ApJ, 615, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Overzier, R. A., Harris, D. E., Carilli, C. L., et al. 2005, A&A, 433, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papadopoulos, P. P., Röttgering, H. J. A., van der Werf, P. P., et al. 2000, ApJ, 528, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Pei, Y. C. 1995, ApJ, 438, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Impey, C. D., Rix, H., et al. 2006, ApJ, 649, 616 [Google Scholar]
- Pentericci, L., Van Reeven, W., Carilli, C. L., Röttgering, H. J. A., & Miley, G. K. 2000, A&AS, 145, 121 [Google Scholar]
- Pentericci, L., McCarthy, P. J., Röttgering, H. J. A., et al. 2001, ApJS, 135, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D., & Kallman, T. R. 2004, ApJ, 616, 688 [Google Scholar]
- Rees, M. J. 1984, ARA&A, 22, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Reuland, M., Röttgering, H., van Breugel, W., & De Breuck, C. 2004, MNRAS, 353, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Röttgering, H. J. A., van Ojik, R., Miley, G. K., et al. 1997, A&A, 326, 505 [NASA ADS] [Google Scholar]
- Schombert, J. M. 1987, ApJS, 64, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze, A., & Wisotzki, L. 2010, A&A, 516, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seymour, N., Stern, D., De Breuck, C., et al. 2007, ApJS, 171, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Shankar, F., Bernardi, M., & Haiman, Z. 2009, ApJ, 694, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Greene, J. E., Strauss, M. A., Richards, G. T., & Schneider, D. P. 2008, ApJ, 680, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Shields, G. A., Gebhardt, K., Salviander, S., et al. 2003, ApJ, 583, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Shields, G. A., Menezes, K. L., Massart, C. A., & Van den Bout, P. 2006, ApJ, 641, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Sijacki, D., Springel, V., Di Matteo, T., & Hernquist, L. 2007, MNRAS, 380, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J., & Rees, M. J. 1998, A&A, 331, L1 [NASA ADS] [Google Scholar]
- Springel, V., Di Matteo, T., & Hernquist, L. 2005, MNRAS, 361, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Tecza, M., Thatte, N. A., Eisenhauer, F., et al. 2000, in SPIE Conf. Ser. 4008, ed. M. Iye, & A. F. Moorwood, 1344 [Google Scholar]
- Tremaine, S., Gebhardt, K., Bender, R., et al. 2002, ApJ, 574, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., Woo, J.-H., Malkan, M. A., & Blandford, R. D. 2007, ApJ, 667, 117 [NASA ADS] [CrossRef] [Google Scholar]
- van Breugel, W. J. M., Stanford, S. A., Spinrad, H., Stern, D., & Graham, J. R. 1998, ApJ, 502, 614 [NASA ADS] [CrossRef] [Google Scholar]
- van Ojik, R., Röttgering, H. J. A., Miley, G. K., & Hunstead, R. W. 1997, A&A, 317, 358 [NASA ADS] [Google Scholar]
- Vestergaard, M. 2002, ApJ, 571, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Villar-Martín, M., Vernet, J., di Serego Alighieri, S., et al. 2003, MNRAS, 346, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., Carilli, C., Bertoldi, F., et al. 2004, ApJ, 615, L17 [CrossRef] [Google Scholar]
- Wang, R., Carilli, C. L., Neri, R., et al. 2010, ApJ, 714, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, M. J., Done, C., Fabian, A. C., Tennant, A. F., & Shafer, R. A. 1988, ApJ, 324, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Weinzirl, T., Jogee, S., Khochfar, S., Burkert, A., & Kormendy, J. 2009, ApJ, 696, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Rawlings, S., Blundell, K. M., & Lacy, M. 1999, MNRAS, 309, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Rawlings, S., & Jarvis, M. J. 2000, MNRAS, 313, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Rawlings, S., Jarvis, M. J., & Blundell, K. M. 2003, MNRAS, 339, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J., Treu, T., Malkan, M. A., & Blandford, R. D. 2006, ApJ, 645, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J., Treu, T., Malkan, M. A., & Blandford, R. D. 2008, ApJ, 681, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Wyithe, J. S. B. 2006, MNRAS, 365, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Younger, J. D., Hopkins, P. F., Cox, T. J., & Hernquist, L. 2008, ApJ, 686, 815 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Observed wavelengths, redshifts, full-width a half maximum, fluxes of the Hα and Hβ broad lines, and V-band extinctions.
Broad Hα luminosities, black holes masses, Eddington and bolometric luminosities, jet kinetic luminosities, and stellar masses.
All Figures
 |
Fig. 1 Spectra of 5 of the HzRGs with BLRs seen in Hα and SINFONI observations (for the spectrum of MRC1138-262 see Nesvadba et al. 2006). Top to bottom: MRC0156-252, MRC1017-220, TXS1113-178, MRC1558-003, and MRC2025-218. The BLR of MRC0156-252 and MRC1558-003 were detected through longslit spectroscopy by Larkin et al. (2000) and Humphrey et al. (2007), respectively. All spectra are smoothed by 5 pixels (corresponding to 25 Å or ~340 km s-1) to emphasize the BLR. This is only for the sake of visualization, the analysis was performed on the unsmoothed spectra. |
| In the text | |
 |
Fig. 2 Close-up of the Hα spectral region of MRC0156-003. We show the spectrum with the best fit superimposed (thick black line). Thin black lines show each individual fit component. The lower panel shows the fit residual. The line at λ = 2.03 μm is the [SII]λλ6716, 6731 doublet, where the two components are blended. At wavelengths shortward of 1.9 μm the atmospheric transmission drops to <10%. |
| In the text | |
 |
Fig. 3 We detected broad Hβ line emission in two of our galaxies, MRC1558-003 and MRC2025-218 (upper panels). Thick black lines show a Gaussian line profile with the same redshift and line width, which we measured for Hα, scaled to match the Hβ flux. Thick gray lines show the FeII template from Iwamuro et al. (2002), to illustrate that the contribution of FeII is negligible in both cases. We subtracted the continuum in both spectra. The middle and lower panels show the fit residual spectrum after subtracting Hβ and the position of night sky lines, respectively. |
| In the text | |
 |
Fig. 4 Black-hole masses as estimated in Sect. 4.3 as a function of stellar mass of the host galaxy, taken from Seymour et al. (2007). Red dots mark the HzRG in which we detected HαBLRs, not correcting for inclination, and blue empty squares show the same galaxies with black-hole masses estimated assuming the inclination correction of Jarvis & McLure (2002). The empty circle marks TXS1113-178 for which we used the average HzRG mass of Seymour et al. (2007). Arrows mark galaxies for which Seymour et al. only provide upper limits (see text for details). Empty circles show the nearby galaxies of Häring & Rix (2004), and the black dashed line shows the best linear fit to their sample. |
| In the text | |
 |
Fig. 5 The ratio of kinetic and radiative luminosity of the AGN as a function of accretion power, following Merloni & Heinz (2008). Above a critical accretion power of a few percent of Eddington, the relationship splits into two branches to accommodate radio-loud and radio-quiet, rapidly accreting AGN with radiatively efficient accretion. Red filled and empty triangles show the radio galaxies of our sample, using different calibrations to estimate the kinetic energy from the observed radio power (Sects. 4.5, 6). Small blue squares and green circles show z ~ 2 quasars and submillimeter galaxies from Coppin et al. (2008) and Alexander et al. (2008), respectively. Small light blue triangles show z ≥ 6 quasars taken from Wang et al. (2010). Blue arrows mark the typical accretion regime of massive early-type (and typically radio-active) elliptical galaxies. Only the HzRGs fall into the critical accretion regime, where (if the scenario of Merloni & Heinz 2008, and others is fundamentally correct) we may expect to find evolved supermassive black holes near the end of their active phase of growth, as they are transiting into the low-accretion regime spanned by massive early-type galaxies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


