| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015481 | |
| Published online | 25 November 2010 | |
The halos of satellite galaxies: the companion of the massive elliptical lens SL2S J08544−0121⋆
1
Argelander-Institut für Astronomie,
Auf dem Hügel 71,
53121
Bonn,
Germany
e-mail: suyu@astro.uni-bonn.de
2
Excellence Cluster Universe, Technische Universität München,
Boltzmannstr. 2,
85748
Garching,
Germany
e-mail: aleksi.halkola@universe-cluster.de
3
Tuorla Observatory, Department of Physics & Astronomy,
University of Turku, Väisäläntie
20, 21500
Piikkiö,
Finland
Received:
27
July
2010
Accepted:
20
September
2010
Strong gravitational lensing by groups or clusters of galaxies provides a powerful technique to measure the dark matter properties of individual lens galaxies. We study in detail the mass distribution of the satellite lens galaxy in the group-scale lens SL2S J08544−0121 by modelling simultaneously the spatially extended surface brightness distribution of the source galaxy and the lens mass distribution using Markov chain Monte Carlo methods. In particular, we measure the dark matter halo size of the satellite lens galaxy to be
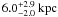 with a fiducial velocity dispersion of
with a fiducial velocity dispersion of 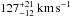 . This is the first time the size of an individual galaxy halo in a galaxy group has been measured using strong gravitational lensing without assumptions of mass following light. We verify the robustness of our halo size measurement using mock data resembling our lens system. Our measurement of the halo size is compatible with the estimated tidal radius of the satellite galaxy, suggesting that halos of galaxies in groups experience significant tidal stripping, a process that has been previously observed on galaxies in clusters. Our mass model of the satellite galaxy is elliptical with its major axis misaligned with that of the light by ~50deg. The major axis of the total matter distribution is oriented more towards the centre of the host halo, exhibiting the radial alignment found in N-body simulations and observational studies of satellite galaxies. This misalignment between mass and light poses a significant challenge to modified Newtonian dynamics.
. This is the first time the size of an individual galaxy halo in a galaxy group has been measured using strong gravitational lensing without assumptions of mass following light. We verify the robustness of our halo size measurement using mock data resembling our lens system. Our measurement of the halo size is compatible with the estimated tidal radius of the satellite galaxy, suggesting that halos of galaxies in groups experience significant tidal stripping, a process that has been previously observed on galaxies in clusters. Our mass model of the satellite galaxy is elliptical with its major axis misaligned with that of the light by ~50deg. The major axis of the total matter distribution is oriented more towards the centre of the host halo, exhibiting the radial alignment found in N-body simulations and observational studies of satellite galaxies. This misalignment between mass and light poses a significant challenge to modified Newtonian dynamics.
Key words: galaxies: halos / galaxies: groups: individual: SL2S J08544 − 0121 / gravitational lensing: strong / methods: data analysis
Based in part on observations made with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. These observations are associated with program 10876.
© ESO, 2010
1. Introduction
Observations to date indicate that the luminous parts of galaxies are embedded in dark matter halos, but properties of the dark matter halos are difficult to probe due to the scarcity of luminous dynamical tracers beyond the visible parts of galaxies (e.g., Sofue & Rubin 2001; Bender et al. 1994, and references therein). Gravitational lensing, a phenomenon where foreground mass distributions deflect the light rays from background source galaxies, provides a powerful tool to study matter distributions in the Universe because lensing is sensitive to the total matter distribution independent of the light profiles of the foreground lenses. Strong gravitational lensing occurs when a single source galaxy is lensed into multiple images; in contrast, weak gravitational lensing corresponds to weak distortions in the shape of the single lensed image of the background source.
Weak galaxy-galaxy lensing has been successfully employed to study the dark matter halo properties of galaxies both in the field (e.g., Brainerd et al. 1996; dell’Antonio & Tyson 1996; Hudson et al. 1998; Fischer et al. 2000; Smith et al. 2001; Hoekstra et al. 2003, 2004; Mandelbaum et al. 2006a,b; Parker et al. 2007; Tian et al. 2009) and in clusters (e.g., Natarajan & Kneib 1997; Natarajan et al. 2002; Limousin et al. 2007; Natarajan et al. 2009). In this method, the tangential shear signals from the distorted shapes of background galaxies around foreground galaxies are stacked together to infer the mass distributions of the foreground lens galaxies. Stacking is needed because the shear signals around individual foreground galaxies are typically too weak to constrain the mass distributions of individual lens galaxies. Consequently, scaling relations are used to characterise the average properties of the foreground lens galaxies in order to model the stacked shear signal. In the case of galaxy clusters, the cluster profile also needs to be modelled in detail to extract the residual shear signals around cluster galaxies (e.g., Limousin et al. 2005). From these studies, there is a general trend that galaxies in denser environments have smaller dark matter halo sizes.
Strong lensing has been used to constrain the size of dark matter halos in the galaxy cluster Abell 1689 (Halkola et al. 2007). Scaling relations are used to relate the halo size to the luminosity of the galaxy members. By modelling the positions of the multiple images of strongly lensed background sources, Halkola et al. (2007) found the halos of galaxies in Abell 1689 to be truncated compared to galaxies of equal luminosity in the field. This is likely due to the tidal stripping of galaxy halos by the strong gravitational potential of the galaxy cluster (e.g., Limousin et al. 2009b; Natarajan et al. 2009).
Both the galaxy-galaxy lensing and strong lensing methods mentioned above are statistical in that they average signals over many lens galaxies and study the ensemble properties of these lens galaxies. Recently, two studies of strong lensing clusters have yielded halo size measurements for individual cluster galaxies. Richard et al. (2010) modelled the cluster Abell 370 and used the multiple image positions to constrain the halo size of a cluster galaxy that lies in the vicinity of a giant gravitationally lensed arc. Donnarumma et al. (2010) analysed the cluster Abell 611 using the multiple image positions of lensed arcs, and measured the halo sizes of the brightest cluster galaxy (BCG) and several galaxies in the vicinity of the BCG. In both studies, the centroids, axis ratios and position angles of the cluster galaxies have been fixed to the observed light distributions. While studies such as the Sloan Lens ACS Survey indicate that light is generally a good tracer of mass for isolated galaxy lenses in the field (Koopmans et al. 2006; Bolton et al. 2008a,b), there can be misalignments especially for galaxies in dynamical environments such as in groups and clusters (e.g., Pereira et al. 2008). If there are misalignments in the cluster galaxies in Abell 370 and Abell 611, then fixing these lens parameter values to the observed light distribution could lead to a bias in the determination of the halo size. Allowing all parameters to vary, while avoiding the bias, would in general induce parameter degeneracies.
In this paper, we aim to constrain the halo size of the satellite galaxy of the massive elliptical lens in SL2S J08544−0121. We show how we can use strong lensing to constrain individual galaxy halo size without assumptions of scaling relations and without enforcement of mass following light. This technique works on group- and cluster-scale lens systems where lensed arcs are comparable to, or larger than, the halo sizes of group/cluster galaxies. In lens systems where a group/cluster galaxy lies close to an arc, the morphological information of the arc provides powerful constraints on the mass distribution of the galaxy. Recently, Vegetti et al. (2010) studied the system SDSS J120602.09+514229.5, which exhibits similar lensing features as in SL2S J08544−0121. They used the lensing arc to detect the presence of mass substructure (a visible dwarf satellite galaxy in this case), which demonstrates their dark matter substructure detection method (Vegetti & Koopmans 2009). Properties of the dwarf satellite such as its mass were measured, nonetheless, the halo size of the dwarf galaxy was assumed to be its theoretical tidal radius. Our aim in studying SL2S J08544−0121 is to measure the halo size of the satellite galaxy.
The paper is organised as follows. We summarise the observations of the lens system SL2S J08544−0121 in Sect. 2, and describe the reduction of the observations in Sect. 3. We present the lens modelling method and the measurement of the satellite halo size in Sect. 4. Simulations that test this method for the case of SL2S J08544−0121 are in Sect. 5. Finally, we discuss our results in Sect. 6 before concluding in Sect. 7.
Throughout the paper, parameter constraints are given by the median values with the uncertainties given by the 2.3 and the 97.7 percentiles (corresponding to 95.4% credible intervals (CI)) of the marginalised probability density distributions. We assume a flat Λ-CDM cosmology with H0 = 70 kms-1 Mpc-1 and ΩΛ = 1 − ΩM = 0.72. From the redshifts of the lens and the source galaxies in Sect. 2, one arcsecond at the lens (source) plane in SL2S J08544−0121 corresponds to 5.0 (8.5) kpc. The position angles of the galaxies are measured eastward from north.
2. Observations of SL2S J08544–0121
The lens system SL2S J08544−0121, discovered in the Canada France Hawaii Telescope Legacy Survey (CFHTLS), is part of the Strong Lensing Legacy Survey (SL2S) (Cabanac et al. 2007; Limousin et al. 2009a). Details of the observations of the lens system are described in Limousin et al. (2009a) and Limousin et al. (2010); we summarise below the relevant ones for this paper.
 |
Fig. 1 A colour image of SL2S J08544−0121 constructed from the F475W, F606W and the F814W images taken with the HST/ACS. The primary and satellite lenses are denoted by P and S, respectively. The boxes mark the multiple image systems that are shown in detail in Fig. 2. |
Hubble Space Telescope (HST) Advanced Camera for Surveys (ACS) images were obtained for this lens system in snapshot mode in three filters: F475W, F606W and F814W (ID 10876; PI Kneib). Figure 1 shows a massive galaxy, which we refer to as the primary lens galaxy (labelled P), that strongly lenses two background source galaxies: one into a bright inner arc (with its corresponding images, shown in the marked boxes) and the other into a faint outer arc (as marked on the figure). In this work, we focus on the bright inner arc because the outer arc is too faint for (i) redshift measurements and (ii) providing useful information on the system in addition to the inner arc without redshift information. Discussions of the arc hereafter refer to the inner arc unless otherwise stated. The arc is at a distance of ~5″ from the primary lens galaxy, making this a group-scale lens system. This system is special in that a galaxy, labelled S, lies near the arc.
The redshifts of the primary lens and the source are zd,P = 0.3530 ± 0.0005 and zs = 1.2680 ± 0.0003, respectively (Limousin et al. 2009a, 2010). The redshift of galaxy S is zd,S = 0.3514 ± 0.0004 (Muñoz et al., in prep.). The uncertainties in the redshift measurements are statistical only; systematic errors due to, e.g., wavelength calibration and dependence on section of spectrum for redshift extraction, are ~0.0005 (Cabanac 2010, priv. comm.). We note that a difference of Δz = 0.001 between galaxy P and galaxy S corresponds to a line-of-sight velocity difference of ~200 kms-1 at zd,P, which is consistent with the expected radial velocities in a galaxy group. Based on the proximity of galaxy S to galaxy P and their measured zd,P and zd,S, we interpret galaxy S as being physically associated with the primary lens galaxy, and we refer to galaxy S as the satellite lens galaxy. For the analysis, we use zd = zd,P as the lens redshift for the system.
The positions of the multiple images of the background source show a high degree of asymmetry: the northern image is ~8″ away from the primary lens galaxy, significantly larger than the ~5″ of the arc. This is caused by the group environment of the lens system: a concentration of galaxies is located about ~1′ to the east of the system and has similar redshifts as the lens system. Limousin et al. (2010) showed that this asymmetry can be exploited to study the global properties of the group.
3. HST image analysis
We obtain the standard CALACS pipeline1 reduced images from the ESO/ST-ECF2 Science Archive. Since single exposures were taken in each wavelength band, these images still contain cosmic rays that are subsequently masked using L.A.Cosmic (van Dokkum 2001). The data are further reduced using the MultiDrizzle package for IRAF (Fruchter et al. 2009) to correct for the geometric distortion. The output image pixel size is 0.05″.
For the reconstruction of the lensed arcs, it is important to remove any light contribution to the arcs from the lens galaxies. This is done using the GALFIT software package (Peng et al. 2002). Following, e.g., Marshall et al. (2007) and Suyu et al. (2009), the point spread function (PSF) is estimated from a star in the field. The regions around the lensed arcs, as well as those of the remaining cosmic rays, are masked for extracting the lens galaxy light. The light distribution of the primary lens is bimodal with a concentrated circular component and a smoother, more elliptical component. The satellite lens and the two components of the primary lens are fitted simultaneously with Sérsic profiles (Sersic 1968). To investigate the light distribution of the primary lens as a whole, we also fit a single Sérsic profile to the primary lens. In doing so, we mask out the core of the primary lens that shows clear bimodality in the light distribution. We set the origin of the image coordinate system to be located at the centroid of the single-component primary lens galaxy. The best fit values for the Sérsic profiles are tabulated in Table 1. The profile parameters for the satellite lens are nearly the same in both the single- and two-component modelling of the primary lens light.
Properties of the lens galaxy light distribution.
Despite the dwarfish appearance of the satellite galaxy when juxtaposed with the primary lens, the satellite galaxy is a normal elliptical galaxy based on its effective radius in Table 1 and the lensing derived velocity dispersion in Sect. 6.2 (Tollerud et al. 2010; Graves et al. 2009; Geha et al. 2003).
We have chosen to use the F606W image for our analysis since this has the highest signal-to-noise ratio (SNR) and is least affected by cosmic rays near the lensed arcs.
4. Satellite halo size from lens modelling
In this section, we describe our lens modelling of the HST data for constraining the halo size of the satellite galaxy. We model the lens system using simply-parametrised mass profiles (Sect. 4.1), and sample the posterior probability distribution of the lens parameters using Markov chain Monte Carlo (MCMC) methods (Sect. 4.2). To constrain the lens parameters, we use either the image positions of the multiply imaged source (Sect. 4.3) or the extended surface brightness distribution of the lensed source galaxy (Sect. 4.4). This allows us to quantify the amount of additional information the extended images provide on the mass distribution of the lenses.
4.1. Simply-parametrised lens profiles
For a review on gravitational lensing, we refer the reader to Schneider et al. (2006). We describe the mass distribution for the lens system as two lens galaxies (the primary and the satellite) in the presence of a constant external shear.
The primary lens galaxy is modelled as a singular pseudoisothermal elliptic mass distribution (PIEMD; Kassiola & Kovner 1993) with dimensionless surface mass density 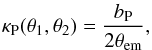 (1)where
(1)where 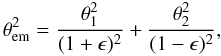 (2)(θ1,θ2) are angular coordinates on the image/lens plane, and ϵ is the ellipticity defined as ϵ ≡ (1 − q) / (1 + q) with q being the axis ratio. The strength and axis ratio of the primary lens are bP and qP, respectively. The distribution is appropriately translated by the centroid position (θ1,P, θ2,P) and rotated by the position angle φP.
(2)(θ1,θ2) are angular coordinates on the image/lens plane, and ϵ is the ellipticity defined as ϵ ≡ (1 − q) / (1 + q) with q being the axis ratio. The strength and axis ratio of the primary lens are bP and qP, respectively. The distribution is appropriately translated by the centroid position (θ1,P, θ2,P) and rotated by the position angle φP.
The satellite lens galaxy is modelled as a dual pseudo isothermal elliptical mass distribution (dPIE; Elíasdóttir et al. 2007) with a vanishing core radius, 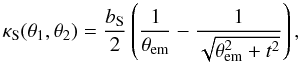 (3)where bS is the satellite lens strength, θem is defined in Eq. (2) with qS being the axis ratio of the satellite, and t is the “truncation radius” of the satellite. The dPIE distribution is suitably translated by the centroid position (θ1,S, θ2,S) and rotated by the position angle φS. The radial dependence of the three dimensional mass density distribution corresponding to Eq. (3) is
(3)where bS is the satellite lens strength, θem is defined in Eq. (2) with qS being the axis ratio of the satellite, and t is the “truncation radius” of the satellite. The dPIE distribution is suitably translated by the centroid position (θ1,S, θ2,S) and rotated by the position angle φS. The radial dependence of the three dimensional mass density distribution corresponding to Eq. (3) is 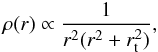 (4)where r is the three dimensional radius, rt = Ddt, and Dd is the angular diameter distance between the observer and the lens. Consequently, for r ≪ rt the mass distribution of the satellite galaxy is isothermal (ρ ∝ r-2), but for r ≫ rt the mass distribution falls off as r-4. We refer to rt as the size of the satellite dark matter halo (with the corresponding angular size as t), but note that rt is roughly the half-mass radius (e.g., Elíasdóttir et al. 2007). The fiducial velocity dispersion is defined as
(4)where r is the three dimensional radius, rt = Ddt, and Dd is the angular diameter distance between the observer and the lens. Consequently, for r ≪ rt the mass distribution of the satellite galaxy is isothermal (ρ ∝ r-2), but for r ≫ rt the mass distribution falls off as r-4. We refer to rt as the size of the satellite dark matter halo (with the corresponding angular size as t), but note that rt is roughly the half-mass radius (e.g., Elíasdóttir et al. 2007). The fiducial velocity dispersion is defined as 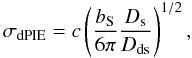 (5)where c is the speed of light, and Ds (Dds) is the angular diameter distance between the observer (lens) and the source. The Appendix in Elíasdóttir et al. (2007) shows the relation between σdPIE and the measured velocity dispersion σ ∗ .
(5)where c is the speed of light, and Ds (Dds) is the angular diameter distance between the observer (lens) and the source. The Appendix in Elíasdóttir et al. (2007) shows the relation between σdPIE and the measured velocity dispersion σ ∗ .
The constant external shear is parametrised by a shear strength γext and a shear angle φext. In terms of polar coordinates ϑ and ϕ such that θ1 = ϑcos(ϕ) and θ2 = ϑsin(ϕ), the lens potential describing the constant external shear is 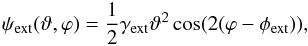 (6)where the shear centre is arbitrary since it corresponds to an unobservable constant shift in the source plane. Note that
(6)where the shear centre is arbitrary since it corresponds to an unobservable constant shift in the source plane. Note that 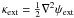 is zero. The shear position angle of φext = 0° or φext = 90° corresponds to a shearing along the θ1-direction or the θ2-direction, respectively.
is zero. The shear position angle of φext = 0° or φext = 90° corresponds to a shearing along the θ1-direction or the θ2-direction, respectively.
We have 13 lens parameters in total: 5 for the PIEMD (θ1,P, θ2,P, qP, φP, bP), 6 for the dPIE (θ1,S, θ2,S, qS, φS, bS, t) and 2 for the external shear (γext, φext). We impose uniform priors on all lens parameters. However, for t, we restrict its range to be between 0.4″ and 10″. The lower limit is set by the effective radius of the satellite galaxy (the radius within which the integrated flux of the galaxy is half its total flux) in Table 1. Any dark matter contribution to the satellite galaxy would lead to a value for t (approximately the half-mass radius) that is larger than the effective radius, assuming a roughly constant mass-to-light ratio for the luminous matter. The upper limit of 10″ is based on the expectation that a satellite halo size larger than the arc ( ~5″) will not be constrained.
4.2. MCMC sampling
We follow Dunkley et al. (2005) to achieve efficient MCMC sampling of the posterior probability density function (PDF) of the lens parameters and to test for convergence. The PDFs for the lens parameters are described in Sects. 4.3 and 4.4. Efficiency of the MCMC sampling hinges upon the proposal density distribution (which encodes the information regarding the direction and step size for obtaining the next random step in the MCMC chain). Briefly, the procedure is: (i) obtain a chain with acceptance rate of ~0.25 based on an initial guess of the proposal density distribution; (ii) update the proposal density distribution by approximating it as a multivariate Gaussian with its covariance matrix set to the covariances among the parameters of the previous chain after the burn-in phase; (iii) adjust the Gaussian widths of the proposal density distribution by a constant factor to obtain a new chain with an acceptance rate of ~0.25: a global increase (decrease) in the Gaussian widths of the proposal density distribution leads to a lower (higher) acceptance rate; (iv) repeat (ii) and (iii) until a convergent MCMC chain is obtained. We find that the proposal density distribution needs updating only a few times to achieve efficient sampling of the posterior PDF. We follow the power-spectrum convergence test introduced in Dunkley et al. (2005). In this approach, convergence is achieved when the chain is drawing samples throughout the region of high probability (so that the correlation between successive samples in the chain does not bias the posterior PDF) and when the ratio of the variance of the sample mean to the variance of the sample distribution is ≤ 0.01 (so that statistics can be obtain with good accuracy).
4.3. Lens modelling using image positions
We identify three peaks in the source surface brightness distribution in the HST F606W image. Figure 2 shows the identified image positions corresponding to each of the three peaks in the source. The three peaks are strongly lensed into 2, 4 and 7 images, respectively. We include the images around the satellite galaxy which are important for our study of the satellite. These images were not considered by Limousin et al. (2010) since the focus of their study was to probe the global properties of the galaxy group instead of local effects due to the satellite. We estimate the uncertainties in the image positions to be 0.05″, except for the image positions near the satellite galaxy whose uncertainties we take to be 0.15″ as they are more difficult to identify. The image positions provide a total of 26 constraints.
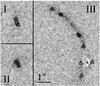 |
Fig. 2 Identification of the multiple images. The three panels (I, II and III) correspond to the regions marked in Fig. 1. These image cutouts are taken from the F606W image with the light from the lens galaxies subtracted. The triangles, circles and squares show the three multiple image systems. |
We follow Halkola et al. (2006, 2008) for the lens modelling based on image positions. The posterior PDF for the lens parameters, collectively denoted as η, given the image positions dpt is
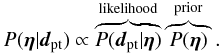 (7)The likelihood is
(7)The likelihood is ![\begin{equation} P(\vec{d}_{\rm pt} |\vec{\eta}) = \frac{1}{Z_{\rm {pt}}} \exp {\left[-\frac{1}{2}\displaystyle\sum_{j=1}^{N_{\rm sys}}\displaystyle\sum_{i=1}^{N_{\rm im}^j} \frac{\vert\vec{\theta}_{i,j}-\vec{\theta}_{i,j}^{\rm pred}(\vec{\eta})\vert^2}{\sigma_{i,j}^2} \right]}, \label{eq:like_pt} \end{equation}](/articles/aa/full_html/2010/16/aa15481-10/aa15481-10-eq94.png) (8)where Nsys is the number of multiply imaged systems (=3 in our case, corresponding to the 3 peaks in the source surface brightness distribution),
(8)where Nsys is the number of multiply imaged systems (=3 in our case, corresponding to the 3 peaks in the source surface brightness distribution), 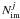 is the number of multiple images in system j, θi,j is the observed image position,
is the number of multiple images in system j, θi,j is the observed image position, 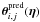 is the modelled image position, σi,j is the uncertainty in the observed image position, and Zpt is the normalisation given by
is the modelled image position, σi,j is the uncertainty in the observed image position, and Zpt is the normalisation given by 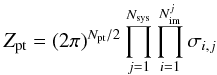 (9)with
(9)with 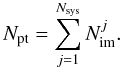 (10)Positions of the surface brightness peaks in the source plane, βj (where j = 1...Nsys), are needed to predict the image positions
(10)Positions of the surface brightness peaks in the source plane, βj (where j = 1...Nsys), are needed to predict the image positions 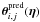 . For a given set of values for the 13 lens parameters η, we optimise for the source positions, denoted by
. For a given set of values for the 13 lens parameters η, we optimise for the source positions, denoted by 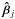 , that maximise Eq. (8). Effectively, we have marginalised over the source position parameters by approximating the likelihood as having a delta function at
, that maximise Eq. (8). Effectively, we have marginalised over the source position parameters by approximating the likelihood as having a delta function at 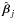 . As described in Sect. 4.1, the prior PDF, P(η), is uniform with t limited to [0.4″,10″] .
. As described in Sect. 4.1, the prior PDF, P(η), is uniform with t limited to [0.4″,10″] .
We sample the posterior PDF P(η | dpt) based on the MCMC procedure described in Sect. 4.2. The critical curves and caustics of the most probable lens model and the source positions are shown in Fig. 3. The large-scale diamond-shaped caustic curve, the astroid, is associated with the primary lens. The presence of the satellite galaxy transforms an ordinary cusp of the astroid into a pentagon-shaped caustic curve. Due to the singular nature of the satellite mass profile, there is also a “cut” (shown as a dot-dashed curve in the inset), which is the limiting case of a caustic curve (e.g., Kormann et al. 1994). Each of the three source surface brightness peaks lies in a different caustic region, and is thus multiply imaged different number of times. The source peak marked by the solid square lies outside of the main astroid caustic of the primary lens, and hence has 2 images. The solid circle is inside both the astroid caustic and the cut, and therefore has a total of 5 predicted images (the caustic crossing creates 2 additional images and the cut crossing yields 1 more). We have observed only 4 image positions (marked by open circles in Fig. 3) because the 5th predicted image, which lies near the centre of the satellite and is less magnified than the other images, could not be detected given the noise levels and the residuals of the lens galaxy light near the centre (see Fig. 2). The source marked by the solid triangle, being inside the pentagon caustic, has two more predicted images than the solid circle and is thus a 7-image system. The creation of such a 7-image system is not possible without the satellite galaxy – the primary elliptical lens galaxy with its simple astroid can only produce 4 images (excluding the central, often demagnified, image that would lie near the centre of the primary lens). All in all, we are able to reproduce all the observed image positions without predicting extra images that can be detected in the data. The root mean square separation between the observed and the corresponding predicted image positions of the most probable lens model is 0.051″.
 |
Fig. 3 Critical curves (black) and caustics (grey) of the lens models. Dashed (solid) curves correspond to the most probable lens model with image positions (extended image surface brightness) as constraints. The dot-dashed curve in the inset marks the cut of the satellite. The cross (plus) symbol denotes the modelled centroid position of the primary (satellite) lens. The three types of open symbols mark the three sets of multiple image systems. The solid symbols are the corresponding modelled source positions based on the most probable lens parameters from the extended image modelling. The shapes of the critical and caustic curves are similar for the two models, but the model based on image positions (dashed) has a rounder primary lens with higher external shear. |
The results of the MCMC sampling for a subset of the 13 parameters are shown in Fig. 4. There is a degeneracy between bP and γext: a higher lens strength produces more internal shear so that less external shear is needed to explain the configuration of the multiple images. Similarly, there is a correlation between qP (not shown) and γext: a rounder primary lens (i.e., higher qP) with less internal shear requires more external shear. The figure shows that both bS and t are not well constrained. In particular, t shows a full degeneracy in the prior range of 0.4″ and 10″. The L-shaped contours of t and bS indicate that the posterior cannot be well described by a multivariate Gaussian distribution. As a result, the multivariate Gaussian proposal density distribution is suboptimal and the efficiency of the MCMC sampling is hampered by these parameter degeneracies. In fact, we could not obtain a convergent chain with >2 × 106 samples even after several updates of the proposal density distribution due to the parameter degeneracies. The results presented in this section are based on a chain of length 106 after the burn-in phase.
 |
Fig. 4 Marginalised posterior PDF for γext (external shear strength), bP (strength of primary lens in arcseconds), bS (strength of satellite lens in arcseconds) and t (truncation radius of satellite in arcseconds) based on image position modelling. The three shaded areas show the 68.3%, 95.4% and 99.7% credible regions. The halo size of the satellite galaxy is not constrained using image positions. |
Table 2 lists the marginalised lens parameters in the second column. The value of t, which nearly spans the entire range of the prior, shows that we cannot constrain the halo size of the satellite galaxy using image positions as constraints. The remedy is to use more information, such as the surface brightness of each pixel in the extended lensed images that is described next.
Modelled lens parameter values.
4.4. Lens modelling using extended images
In order to reconstruct the spatially extended surface brightness distribution of the lensed images, we need to model both the lens mass distribution and the extended source surface brightness distribution. We follow Suyu et al. (2006) to reconstruct the source surface brightness, denoted by s, on a grid of pixels given a lens potential model. The reconstruction is a Bayesian regularised linear inversion, where we denote λ as the strength of regularisation and g as the form of regularisation. This reconstruction returns the most probable source surface brightness distribution sMP, and also the Bayesian evidence of source reconstruction, ℰ, which is equivalent to the likelihood of the lens parameters. The posterior PDF for lens parameters, η, given the extended image surface brightness, dsb, is
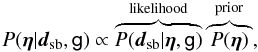 (11)where
(11)where
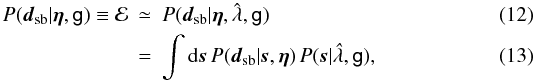 and
and 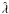 is the optimal regularisation determined by maximising P(dsb | η,λ,g). Suyu et al. (2006) gave the expression for P(dsb | η,λ,g) in their Eq. (19), and showed that the approximation in Eq. (12) is a valid one.
is the optimal regularisation determined by maximising P(dsb | η,λ,g). Suyu et al. (2006) gave the expression for P(dsb | η,λ,g) in their Eq. (19), and showed that the approximation in Eq. (12) is a valid one.
We sample the posterior of the lens parameters with MCMC methods using the Bayesian evidence ℰ of the source surface brightness reconstruction as the likelihood at each step of the chain. The priors on the satellite lens parameters are as before (described in Sect. 4.1). In the sampling process, we use 30 × 30 source pixels; the typical pixel size is ~0.035″. We find that our results are robust under changes in the number of source pixels, provided the source resolution is sufficient to describe the data ( ≳ 20 × 20). We assume the curvature form of regularisation for the source surface brightness distribution (Suyu et al. 2006), which is applicable in this case given the relatively smooth surface brightness of the lensed images. Furthermore, we fix the regularisation constant to be λavg, the average of the optimal 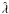 values from a short test chain (the optimal
values from a short test chain (the optimal 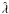 is different for different lens parameter values). In other words, we approximate Eq. (12) further and use P(dsb | η,λavg,g) for ℰ. This approximation is valid because ℰ changes by < 1 between the optimised
is different for different lens parameter values). In other words, we approximate Eq. (12) further and use P(dsb | η,λavg,g) for ℰ. This approximation is valid because ℰ changes by < 1 between the optimised 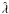 and the fixed λavg.
and the fixed λavg.
 |
Fig. 5 Marginalised posterior PDF for γext (external shear strength), bP (strength of primary lens in arcseconds), bS (strength of satellite lens in arcseconds) and t (truncation radius of satellite in arcseconds) based on extended image surface brightness modelling, plotted on the same scales as in Fig. 4. The three shaded regions show the 68.3%, 95.4% and 99.7% credible regions. For comparison, the lines show the 68.3% credible regions from Fig. 4 with image positions as constraints. In contrast to the full t-degeneracy from image position modelling, extended image modelling allows us to constrain the truncation radius of the satellite galaxy halo to be |
The resulting constraints on the lens parameters are shown in Fig. 5, plotted on the same scales as Fig. 4 for comparison. The MCMC sampling converges in <105 steps. The correlations among γext, bP and qP share similar trends as in the results of the image position modelling, but are smaller in magnitude. In contrast to Fig. 4, the strong degeneracy in t is broken with the use of the information from the extended images. The significantly tighter constraints based on the extended images are in agreement with the constraints based on image positions within the 68.3% credible regions. Table 2 shows the values for the marginalised lens parameters. In particular, the size of the satellite halo is constrained to be 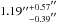 , corresponding to
, corresponding to 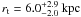 .
.
 |
Fig. 6 Extended image and source surface brightness reconstruction. From left to right: top: observed image, reconstructed image; bottom: normalised image residual (in units of the uncertainty estimated for each pixel), reconstructed source. The morphology of the lensed arc is reproduced, and the reconstructed source surface brightness distribution shows three peaks. |
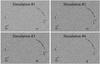 |
Fig. 7 Four simulated images designed to mimic SL2S J08544−0121 but with different input mass distributions. Simulations are labelled as #1 − 4. Details of the simulations are given in Sect. 5.1. |
The most probable image and source surface brightness reconstructions are shown in Fig. 6. The image pixels around the satellite galaxy have been excluded in the modelling due to the imperfect lens galaxy light subtraction near the galaxy centre. One of the strongly lensed images is also excluded (the rightmost triangle in panel III of Fig. 2) since it is blended with the residuals of the lens galaxy light subtraction. We opt to discard this particular lensed image to avoid including lens galaxy light residuals as false lensed features of the background source that could potentially bias our modelling. The top and the bottom-left panels show that the lensed features, apart from the cores of the lensed images, are reproduced by our model. The cores in the surface brightness clumps of galaxies tend to be sharply peaked; this leads to the visible residuals near the cores of highly magnified images due to source and image pixelisations. Nonetheless, this does not limit the modelling of the extended image structure – the reduced χ2 is 0.75. The reconstructed source in the bottom-right panel indeed exhibits three peaks in its surface brightness distribution, thus confirming our image identification in Sect. 4.3. The critical and caustic curves of the most probable lens parameters are illustrated in Fig. 3.
Comparing Tables 1 and 2, we see that the modelled φP is offset by ~30° from that of the observed light distribution, as was previously noted by Limousin et al. (2010). We attribute this to the presence of two brightness peaks in the primary lens galaxy; in such dynamically unrelaxed systems, it is not surprising that the observed light distribution inside the lensed arcs does not trace the mass probed around the arcs by strong lensing. N-body simulations show that dark matter halos can have the inner parts of their gravitational potential elongated in a different direction from that of the outer parts (e.g., Hayashi et al. 2007). Furthermore, simulations with gas indicate that the angular momentum of the galaxy embedded in a typical dark matter halo is on average more aligned with the inner parts than the outer parts of the total mass distribution (e.g., Bett et al. 2010). In addition, studies of intrinsic ellipticity correlations of luminous galaxies suggest that the mass and the light of galaxies could be misaligned by ~25°−35° (e.g., Okumura et al. 2009; Brainerd et al. 2009). The modelled position angle of the mass distribution of the satellite is also misaligned from that of the light by ~50°, and we discuss this in Sect. 6.3.
The halo size measurement is obtained by modelling the F606W image, selected based on its SNR and cosmic ray subtraction. We could have also considered the F475W and F814W images. However, the F475W image has lower SNR than the F606W image and has several cosmic rays near the lensed arcs, which would make the analysis of F475W prone to systematic effects due to cosmic ray residuals. Compared to the F606W image, the F814W image has similarly low levels of cosmic rays but lower SNR. We repeat our analysis on the F814W to check for consistency. We find that t is constrained by the F814W data and agrees with the F606W value within the uncertainties; however, the marginalised uncertainties of t from F814W is almost twice as large as that of F606W, as expected due to the lower SNR of F814W. Thus, our measurement of t from F606W is consistent with F814W and would not change drastically even if the F814W data were included. In the next section, we test the robustness of this measurement using simulations.
5. Simulation tests: robustness of halo size measurement
We create 4 simulations that mimic the image morphology of SL2S J08544−0121. In each case, we have an input model which we use to lens a background source consisting of three approximately Gaussian peaks in its surface brightness distribution, similar to the reconstructed source in Fig. 6. We then convolve the lensed image with a Gaussian PSF of FWHM 0.08″, and add uniform Gaussian noise. Figure 7 shows the images of the four simulations labelled as #1−4. The idea is to model each of the simulations using the same procedure as in the case of the real data to test the robustness of the satellite halo size measurement. The details of generating each simulation are as follows.
5.1. Inputs of the simulations
5.1.1. Simulation #1
The input mass distribution is a PIEMD for the primary lens, a dPIE for the satellite galaxy, and a constant external shear. The parameter t for the satellite is set to 2″, whereas the other parameters of the input model are chosen so that the lensed image resembles SL2S J08544−0121. This simulation corresponds to the ideal case where the lens profiles we use for modelling are identical to the profiles we use to create the simulation.
5.1.2. Simulation #2
This simulation is similar to Simulation #1 (PIEMD + dPIE + constant external shear), except the input value for the truncation radius of the satellite galaxy is t = 5″. In this simulation, the input t is approximately the extent of the lensed arc. We expect the constraints on t to weaken substantially as its value becomes comparable to, or larger than, the arc length since the morphology of the arc is not so sensitive to a halo size that extends beyond the arc. This simulation is designed to probe the limit in which we can use this method to measure the halo size of the satellite.
5.1.3. Simulation #3
In this simulation, the input primary lens mass distribution is shallower than isothermal, as one may expect for massive systems dominated by dark matter (e.g., Vegetti et al. 2010; Newman et al. 2009). Specifically, we describe the primary lens as a singular power-law ellipsoid (SPLE; Barkana 1998), and we set the slope to be γ = 1.8 (such that the density ρ3D ~ r − γ). We continue to use dPIE with t = 2″ for the satellite and input a constant external shear.
5.1.4. Simulation #4
As described in Sect. 2 and Limousin et al. (2010), SL2S J08544−0121 is in a group environment and the external shear is mainly generated by a concentration of galaxies located about ~1′ to the east. In this simulation, we create the simulated data using a singular isothermal sphere (SIS) profile for this mass concentration instead of a constant external shear. The input profiles for the lens galaxies are PIEMD and dPIE with t = 2″. This simulation tests whether a constant external shear is a good approximation for the more realistic situation where the external convergence also varies slightly across the lens system.
5.2. Modelling results of the simulations
We model each of the simulations using a PIEMD for the primary lens galaxy, a dPIE for the satellite galaxy and a constant external shear, i.e., the same profiles used to model the real data in Sect. 4. We impose similar priors as for the real data on the lens parameters: uniform with t restricted to be between [0″,10″] . In each of the four simulations, the image position modelling provides no constraints on t, supporting the results in Sect. 4.3. For modelling the extended lensed images, we employ similar image masks as that of the real data (shown in Fig. 6). Figure 8 shows the marginalised PDF of bS and t from modelling the extended images in each simulation, which we describe below in turn.
 |
Fig. 8 Marginalised posterior PDF of bS (strength of satellite lens) and t (truncation radius of satellite) for the simulations. The crosses mark the input parameter values. The three shaded areas show the 68.3%, 95.4% and 99.7% credible regions. In the cases where the truncation radius is constrained (without a full degeneracy in the prior range), the recovered value agrees with the input value within the uncertainties. |
In Simulation #1, the top-left panel of Fig. 8 shows that the modelled truncation radius of the satellite is 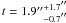 , which recovers the input value of 2″. All the other satellite lens parameters are also recovered within the uncertainties. Some of the other lens parameters that show strong degeneracies (e.g., γext, bP, and qP) have their modelled values lie along the degeneracies but are offset from the input values. Nonetheless, the measurement of t is not so sensitive to these parameters since it is mostly degenerate with bS which is recovered within the uncertainties. This simulation shows that if the profiles we use to model the galaxies match the true mass profiles, then we can recover the size of the satellite halo within the uncertainties. We have tested this result using different image masks and source resolution – in all cases, the recovered t agrees with the input value within the errors.
, which recovers the input value of 2″. All the other satellite lens parameters are also recovered within the uncertainties. Some of the other lens parameters that show strong degeneracies (e.g., γext, bP, and qP) have their modelled values lie along the degeneracies but are offset from the input values. Nonetheless, the measurement of t is not so sensitive to these parameters since it is mostly degenerate with bS which is recovered within the uncertainties. This simulation shows that if the profiles we use to model the galaxies match the true mass profiles, then we can recover the size of the satellite halo within the uncertainties. We have tested this result using different image masks and source resolution – in all cases, the recovered t agrees with the input value within the errors.
In Simulation #2, the top-right panel in Fig. 8 shows that t is now completely degenerate with bS, and in fact with all the other lens parameters. This panel is based on a MCMC chain of length 106 that has not yet converged – we have not been able to obtain a convergent chain after >2 × 106 steps, in contrast to the MCMC sampling of the other simulations that converges in ≲ 106 steps. Therefore, the results of this simulation suggest that as soon as the halo size of the satellite becomes comparable to the arc length, even information from the extended surface brightness does not allow the halo size to be determined.
In Simulation #3, there is a mismatch in the modelled profile (PIEMD) and the input profile (SPLE) for the primary lens galaxy. The bottom-left panel in Fig. 8 shows that t is unconstrained within the prior range. The main reason for the full t-degeneracy is that the model profile cannot accurately reproduce the simulated arcs because the relative thickness in the extended images is sensitive to the slope (e.g., Dye & Warren 2005; Dye et al. 2008; Suyu et al. 2010). The image residuals due to the slope mismatch diminish the amount of information on t since these image residuals are more significant than residuals caused by changes in t. Indeed, when we model the primary lens using a SPLE with a slope of 1.8 for comparison to the PIEMD model, we find that the maximum likelihood of the SPLE model is a factor of ~e13 higher than that of the PIEMD model. Furthermore, we recover the input t (= 2″) and bS values for the satellite (similar to the results of Simulation #1) when the SPLE model is used for the primary. Therefore, we also attribute the offset in the recovered satellite strength bS from the input value (shown in Fig. 8) to the slope mismatch. We note that a formal model comparison of the SPLE and PIEMD requires obtaining the Bayesian evidence of the lens models (i.e., marginalising over all the lens parameters), which is beyond the scope of this paper. This simulation shows that t is no longer constrained when the modelled profile is significantly different from the input profile in terms of the slope. This full degeneracy was not obtained in the case of the real data, confirming that the PIEMD+dPIE+shear model is a good description for the SL2S J08544−0121 system.
In Simulation #4, the modelled value of the truncation radius is unconstrained within the 95.4% CI, as shown in the bottom-right panel in Fig. 8; however, within the 68.3% CI, it is constrained to be 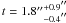 , which recovers the input value of 2″. Compared to Simulation #1, the sensitivity on t is weakened due to the mismatch between the constant external shear model and the SIS input. Since the degeneracy is not observed in the case of the real data, this suggests that the external convergence due to the environment varies weaker across the strong lens system than that of an SIS (which has κSIS ∝ 1 / θ), making the constant external shear a good approximation.
, which recovers the input value of 2″. Compared to Simulation #1, the sensitivity on t is weakened due to the mismatch between the constant external shear model and the SIS input. Since the degeneracy is not observed in the case of the real data, this suggests that the external convergence due to the environment varies weaker across the strong lens system than that of an SIS (which has κSIS ∝ 1 / θ), making the constant external shear a good approximation.
The results of the simulations indicate that if the truncation radius is constrained, then it agrees with the input value within the uncertainties.
6. Discussions
This is the first time the halo size of a satellite galaxy is measured without assuming a scaling relation and without fixing any of the satellite lens parameters based on the observed light distribution.
6.1. Tidal radius of the satellite
Is the measured halo size of ~6.0 kpc for the satellite galaxy reasonable? We can answer this question by comparing our halo size measurement to the theoretically estimated tidal radius.
The tidal radius of the satellite is the location between the primary and the satellite galaxies where the gravitational tidal force due the primary is equal to the gravitational force of the satellite. Mass particles that originally belong to the satellite and are further from the satellite centre than the tidal radius will fall into the gravitational potential of the primary lens galaxy. By approximating the satellite and primary galaxies as spherical isothermal halos, we estimate the tidal radius of the satellite halo to be 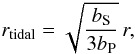 (14)where r is the three-dimensional distance between the centres of the satellite and the primary lens (Metcalf & Madau 2001). From observations and lens modelling, we have only the projected two-dimensional distance, R, between the satellite and the primary. Nonetheless, we can derive the probability distribution P(r | R) by assuming that the distribution of satellites follow the total matter distribution of the primary lens halo. This is motivated by N-body simulations that show the distribution of subhalos follow roughly the mass distribution of the host halo (e.g., Nagai & Kravtsov 2005; Klypin et al. 2010). To ensure that P(r | R) is normalised, we impose a hard cutoff for the isothermal distribution for the primary halo at rcut, i.e., we assert ρ(r) = 0 for r > rcut. For rcut between 500 kpc and 2000 kpc (the expected range for a group-scale halo), we find that our PDF for P(r | R) is insensitive to rcut for r ≪ rcut. Using the derived P(r | R), Eq. (14), the modelled lens strengths and the projected separation between the lenses of R = 5.1″ = 25.5 kpc in Table 2, we show in Fig. 9 the PDF for P(rtidal | R). Our measurement of the truncation radius of
(14)where r is the three-dimensional distance between the centres of the satellite and the primary lens (Metcalf & Madau 2001). From observations and lens modelling, we have only the projected two-dimensional distance, R, between the satellite and the primary. Nonetheless, we can derive the probability distribution P(r | R) by assuming that the distribution of satellites follow the total matter distribution of the primary lens halo. This is motivated by N-body simulations that show the distribution of subhalos follow roughly the mass distribution of the host halo (e.g., Nagai & Kravtsov 2005; Klypin et al. 2010). To ensure that P(r | R) is normalised, we impose a hard cutoff for the isothermal distribution for the primary halo at rcut, i.e., we assert ρ(r) = 0 for r > rcut. For rcut between 500 kpc and 2000 kpc (the expected range for a group-scale halo), we find that our PDF for P(r | R) is insensitive to rcut for r ≪ rcut. Using the derived P(r | R), Eq. (14), the modelled lens strengths and the projected separation between the lenses of R = 5.1″ = 25.5 kpc in Table 2, we show in Fig. 9 the PDF for P(rtidal | R). Our measurement of the truncation radius of 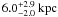 based on the lens modelling in Sect. 4.4 is thus consistent with the tidal radius PDF.
based on the lens modelling in Sect. 4.4 is thus consistent with the tidal radius PDF.
 |
Fig. 9 Probability density of the tidal radius of the satellite given the modelled projected distance of R = 25.5 kpc and the modelled lens strengths. Our halo size measurement of |
6.2. Galaxy halo size comparison
We use Eq. (5) to derive the fiducial velocity dispersion of our satellite galaxy from Table 2: 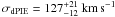 . Figure 10 shows our results in comparison to previous studies of halo sizes based on strong lensing in clusters and galaxy-galaxy lensing both in the field and in clusters. We note that different studies often employ different galaxy luminosities, scaling relations and reference luminosity/velocity dispersion, so the comparison illustrated is more qualitative than quantitative. Our measurement, marked by an inverted triangle, shows that the halo size of the satellite galaxy in SL2S J08544−0121 is significantly smaller than isolated field galaxies of comparable velocity dispersion. In fact, the satellite galaxy halo size is similar to those of galaxies in clusters. One may expect that galaxy members in group environments would have individual halos which are on average larger than those in cluster environments and smaller than isolated field galaxies. However, the primary lens galaxy in SL2S J08544−0121 is the brightest group galaxy (BGG), so the satellite galaxy is probably near the centre of the group potential3 which could make the stripping of the satellite galaxy more efficient. Indeed, hydrodynamical N-body simulations done by Limousin et al. (2009b) and the analysis of the galaxy cluster Cl 0024+16 by Natarajan et al. (2009) both indicate that in galaxy clusters, the halo size of a galaxy is smaller the closer the galaxy is to the cluster centre. Our measurement of the satellite halo size therefore supports the tidal stripping of galaxy halos in dense environments found in earlier lensing studies.
. Figure 10 shows our results in comparison to previous studies of halo sizes based on strong lensing in clusters and galaxy-galaxy lensing both in the field and in clusters. We note that different studies often employ different galaxy luminosities, scaling relations and reference luminosity/velocity dispersion, so the comparison illustrated is more qualitative than quantitative. Our measurement, marked by an inverted triangle, shows that the halo size of the satellite galaxy in SL2S J08544−0121 is significantly smaller than isolated field galaxies of comparable velocity dispersion. In fact, the satellite galaxy halo size is similar to those of galaxies in clusters. One may expect that galaxy members in group environments would have individual halos which are on average larger than those in cluster environments and smaller than isolated field galaxies. However, the primary lens galaxy in SL2S J08544−0121 is the brightest group galaxy (BGG), so the satellite galaxy is probably near the centre of the group potential3 which could make the stripping of the satellite galaxy more efficient. Indeed, hydrodynamical N-body simulations done by Limousin et al. (2009b) and the analysis of the galaxy cluster Cl 0024+16 by Natarajan et al. (2009) both indicate that in galaxy clusters, the halo size of a galaxy is smaller the closer the galaxy is to the cluster centre. Our measurement of the satellite halo size therefore supports the tidal stripping of galaxy halos in dense environments found in earlier lensing studies.
 |
Fig. 10 Comparison of the galaxy halo size measurements. For statistical measurements, rt is the fiducial truncation radius and σ is the fiducial velocity dispersion. The direct measurement of our satellite galaxy in SL2S J08544−0121 is marked by an inverted triangle, confirming the tidal stripping of galaxy halos in dense environments. |
6.3. Radial alignment of the satellite
As mentioned in Sect. 4.4, the total mass distribution of the satellite is misaligned with the observed light distribution by ~50°. Specifically, with respect to the line connecting the modelled centres of the satellite and the primary lens galaxies, the major axis of the modelled satellite mass distribution is at an angle of 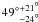 whereas the major axis of the light distribution is at 99° ± 2° (95.4% CI), where both angles are measured counterclockwise. Compared to the light distribution of the satellite, its mass distribution is elongated more towards the centre of the primary, exhibiting the so-called “radial alignment”.
whereas the major axis of the light distribution is at 99° ± 2° (95.4% CI), where both angles are measured counterclockwise. Compared to the light distribution of the satellite, its mass distribution is elongated more towards the centre of the primary, exhibiting the so-called “radial alignment”.
Studies based on both observations (e.g., Pereira & Kuhn 2005; Agustsson & Brainerd 2006; Faltenbacher et al. 2007) and N-body simulations (e.g., Pereira et al. 2008; Knebe et al. 2008a) show that the major axes of satellite galaxies (subhalos) tend to point towards the centre of mass of their host. These radial alignments are detected by averaging over many satellite galaxies. In the case of observations, the position angles of the luminous parts of the satellites are measured and compared to the direction of the host galaxy. In the case of N-body simulations, mass particles belonging to subhalos are identified, and the shapes of the subhalos are measured. By following the evolution of the alignment of the subhalos with time, Pereira et al. (2008) argued for tidal torquing as the mechanism for producing the radial alignment. One would expect that dark matter halos, being more extended and having lower spins than the galaxies, would be more easily torqued. Indeed, Knebe et al. (2008b) found that the central parts of the subhalos were less radially aligned than the subhalos as a whole. Furthermore, Pereira et al. (2008) found that the dark matter alignment was stronger than the galaxy alignment. Our measurement of the orientations of both the luminous and the total matter distributions of the satellite galaxy in SL2S J08544−0121 also hints at the stronger total matter alignment that was found for ensembles of satellites in earlier studies.
6.4. Implications for modified Newtonian dynamics
Modified Newtonian dynamics (MOND) was first suggested by Milgrom (1983) as an alternative to the existence of dark matter for explaining the flat rotation curves observed in spiral galaxies. Instead of requiring additional dark matter in the outer parts of a galaxy, MOND postulates that Newtonian gravity breaks down in this small-acceleration region, and the acceleration experienced by a test particle is larger than the Newtonian value. For a review on the subject, we refer the reader to Sanders & McGaugh (2002). Sellwood & Kosowsky (2001) pointed out several tests that could rule out simple theories of modified gravity, one of which is the misalignment between the axes of dark matter halos and those of the visible matter (i.e., mass must follow light in MOND since there is no dark matter).
In our analysis of SL2S J08544−0121, we find that the dimensionless surface mass density of the satellite galaxy, κS, is misaligned with that of the light by ~50°. Under General Relativity (GR), κS is the surface mass density of the total mass distribution, up to a constant factor. However, in MOND, the derived κS does not in general scale linearly with the surface mass density (e.g., Zhao et al. 2006). The key question for testing MOND is whether the mass distribution of the satellite galaxy that is modelled using MOND would also be misaligned with the observed light distribution. Mortlock & Turner (2001) considered gravitational lensing in MOND under the assumption that the deflection of photons is twice that of massive particles moving at the speed of light, in accordance with GR. This assumption must be valid in the Newtonian limit of any MONDian lensing theory. The authors find that while gravitational lensing deflections depend only on κ in GR (thin-lens approximation), this is no longer true in MOND where in general the deflections depend on the mass distribution of the lens along the line of sight. Nonetheless, Mortlock & Turner (2001) showed that for a typical elliptical galaxy, the thin-lens approximation holds; the deflection angles are the same as the GR predictions in the inner parts (where the projected distances are ≲ 2 kpc) and approach an asymptotic value in the outer parts. Chiu et al. (2006) found qualitatively similar trends for the deflection angles in a relativistic formulation of MOND by Bekenstein (2004; the tensor-vector-scalar theory). Therefore, modelling the satellite galaxy in MOND can be seen as modelling the satellite galaxy in GR with a different deflection angle field, or equivalently, a different mass radial profile. In a strongly lensed system, the position angle of an elliptical mass distribution is determined based on the observed image configuration and is quite insensitive to the actual radial profile of the mass distribution. Therefore, even if the satellite galaxy were modelled using MOND, it would still need to have its mass distribution elongated in a direction that is misaligned with the light by ~50° to fit the lensing observations. This misalignment cannot be explained by MOND and supports the dark matter hypothesis.
7. Conclusions
We modelled the mass distributions of the group-scale strong lens system SL2S J08544−0121 that consists of a massive elliptical lens and a satellite lens galaxy. The lens galaxies are modelled as parametrised profiles, with the truncation radius of the satellite as one parameter to characterise its halo size. Using Markov chain Monte Carlo methods to sample the lens mass parameters, we compare the results based on image position modelling and based on extended surface brightness modelling. From this we conclude:
-
In comparison to image position modelling, extendedsurface brightness modelling provides significantly tighterconstraints on the lens parameters, although the results of thetwo approaches agree within the uncertainties.
-
Image position modelling provides no constraints on the halo size of the satellite galaxy.
-
Extended surface brightness modelling constrains the halo size of the satellite to be
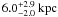 (95.4% CI).
(95.4% CI).
-
Modelling of simulations that resemble the system SL2S J08544−0121 shows the recovery of the input truncation radius if it is constrained. Our three-component lens model (consisting of PIEMD, dPIE and constant external shear) provides an adequate description of SL2S J08544 − 0121.
-
This technique works on galaxy group- or cluster-scale lenses where the galaxy member halo size is spatially less extended than features of the lensed arcs.
-
The measured satellite halo size is in agreement with its estimated tidal radius, indicating that galaxies in group environments experience tidal stripping of their halos. This confirms the tidal stripping of galaxy halos in dense environments found in numerical simulations and in previous lensing analysis of galaxy clusters.
-
The position angles of the total matter distribution and the light distribution of the satellite are misaligned by ~50°. The major axis of the total matter distribution points more towards the centre of the primary halo, consistent with the detected radial alignment of satellite galaxies in previous observational studies and numerical simulations.
-
The misalignment between mass and light of the satellite galaxy is a serious challenge to MOND.
The method developed in this paper for measuring the galaxy halo sizes is general and applicable to other lens systems. Indeed, there are already several group- and cluster-scale lens systems known to contain strong lensing arcs with nearby group or cluster galaxy member(s). This new galactic halo ruler, when applied to a sample of systems, should help advance our understanding of galaxy evolution and of the growth and assembly of galaxy groups and clusters.
More precisely, the satellite galaxy is near one of the possibly two centres of the group potential since the luminosity map of SL2S J08544 − 0121 is bimodal with one peak at the BGG and another peak at a collection of galaxies that are ~1′ east of the BGG (Limousin et al. 2010).
Acknowledgments
We thank P. Schneider, R. Cabanac, M. Limousin, P. Marshall, J. Chen, J. Hartlap, P. Behroozi for useful discussions, and Y. Mellier for helpful suggestions. We are grateful to R. Cabanac and R. Muñoz for providing us with information regarding the lens redshifts, and thank J. Richard and T. Treu for the previously published redshifts from Keck/LRIS observations. We thank the anonymous referee for helpful comments on the manuscript. S.H.S. is supported in part through the Deutsche Forschungsgemeinschaft under the project SCHN 342/7–1. A.H. acknowledges support from the Finnish Academy of Science and Letters. This research was supported in part by the DFG cluster of excellence “Origin and Structure of the Universe”. Based in part on observations made with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. These observations are associated with program 10876.
References
- Agustsson, I., & Brainerd, T. G. 2006, ApJ, 644, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Barkana, R. 1998, ApJ, 502, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Bekenstein, J. D. 2004, Phys. Rev. D, 70, 083509 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, R., Saglia, R. P., & Gerhard, O. E. 1994, MNRAS, 269, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Bett, P., Eke, V., Frenk, C. S., Jenkins, A., & Okamoto, T. 2010, MNRAS, 404, 1137 [NASA ADS] [Google Scholar]
- Bolton, A. S., Burles, S., Koopmans, L. V. E., et al. 2008a, ApJ, 682, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, A. S., Treu, T., Koopmans, L. V. E., et al. 2008b, ApJ, 684, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Brainerd, T. G., Blandford, R. D., & Smail, I. 1996, ApJ, 466, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Brainerd, T. G., Agustsson, I., Madsen, C. A., & Edmonds, J. A. 2009, ApJ, submitted [arXiv:0904.3095] [Google Scholar]
- Cabanac, R. A., Alard, C., Dantel-Fort, M., et al. 2007, A&A, 461, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiu, M., Ko, C., & Tian, Y. 2006, ApJ, 636, 565 [NASA ADS] [CrossRef] [Google Scholar]
- dell’Antonio, I. P., & Tyson, J. A. 1996, ApJ, 473, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Donnarumma, A., Ettori, S., Meneghetti, M., et al. 2010, A&A, accepted [arXiv:1002.1625] [Google Scholar]
- Dunkley, J., Bucher, M., Ferreira, P. G., Moodley, K., & Skordis, C. 2005, MNRAS, 356, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Dye, S., Evans, N. W., Belokurov, V., Warren, S. J., & Hewett, P. 2008, MNRAS, 388, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Dye, S., & Warren, S. J. 2005, ApJ, 623, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Elíasdóttir, Á., Limousin, M., Richard, J., et al. 2007, unpublished [arXiv:0710.5636] [Google Scholar]
- Faltenbacher, A., Li, C., Mao, S., et al. 2007, ApJ, 662, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, P., McKay, T. A., Sheldon, E., et al. 2000, AJ, 120, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., Hack, W., Droetboom, M., et al. 2009, in BAAS, 41, 414 [Google Scholar]
- Geha, M., Guhathakurta, P., & van der Marel, R. P. 2003, AJ, 126, 1794 [NASA ADS] [CrossRef] [Google Scholar]
- Graves, G. J., Faber, S. M., & Schiavon, R. P. 2009, ApJ, 693, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Halkola, A., Seitz, S., & Pannella, M. 2006, MNRAS, 372, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Halkola, A., Seitz, S., & Pannella, M. 2007, ApJ, 656, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Halkola, A., Hildebrandt, H., Schrabback, T., et al. 2008, A&A, 481, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayashi, E., Navarro, J. F., & Springel, V. 2007, MNRAS, 377, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Franx, M., Kuijken, K., Carlberg, R. G., & Yee, H. K. C. 2003, MNRAS, 340, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Yee, H. K. C., & Gladders, M. D. 2004, ApJ, 606, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, M. J., Gwyn, S. D. J., Dahle, H., & Kaiser, N. 1998, ApJ, 503, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kassiola, A., & Kovner, I. 1993, ApJ, 417, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Trujillo-Gomez, S., & Primack, J. 2010, ApJ, submitted [arXiv:1002.3660] [Google Scholar]
- Knebe, A., Draganova, N., Power, C., et al. 2008a, MNRAS, 386, L52 [Google Scholar]
- Knebe, A., Yahagi, H., Kase, H., Lewis, G., & Gibson, B. K. 2008b, MNRAS, 388, L34 [NASA ADS] [Google Scholar]
- Koopmans, L. V. E., Treu, T., Bolton, A. S., Burles, S., & Moustakas, L. A. 2006, ApJ, 649, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Kormann, R., Schneider, P., & Bartelmann, M. 1994, A&A, 284, 285 [NASA ADS] [Google Scholar]
- Limousin, M., Kneib, J., & Natarajan, P. 2005, MNRAS, 356, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Limousin, M., Kneib, J. P., Bardeau, S., et al. 2007, A&A, 461, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limousin, M., Cabanac, R., Gavazzi, R., et al. 2009a, A&A, 502, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limousin, M., Sommer-Larsen, J., Natarajan, P., & Milvang-Jensen, B. 2009b, ApJ, 696, 1771 [NASA ADS] [CrossRef] [Google Scholar]
- Limousin, M., Jullo, E., Richard, J., et al. 2010, A&A, 524, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandelbaum, R., Hirata, C. M., Broderick, T., Seljak, U., & Brinkmann, J. 2006a, MNRAS, 370, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Seljak, U., Kauffmann, G., Hirata, C. M., & Brinkmann, J. 2006b, MNRAS, 368, 715 [Google Scholar]
- Marshall, P. J., Treu, T., Melbourne, J., et al. 2007, ApJ, 671, 1196 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalf, R. B., & Madau, P. 2001, ApJ, 563, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Mortlock, D. J., & Turner, E. L. 2001, MNRAS, 327, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., & Kravtsov, A. V. 2005, ApJ, 618, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., & Kneib, J. 1997, MNRAS, 287, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., Kneib, J., & Smail, I. 2002, ApJ, 580, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., Kneib, J., Smail, I., et al. 2009, ApJ, 693, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Treu, T., Ellis, R. S., et al. 2009, ApJ, 706, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Okumura, T., Jing, Y. P., & Li, C. 2009, ApJ, 694, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, L. C., Hoekstra, H., Hudson, M. J., van Waerbeke, L., & Mellier, Y. 2007, ApJ, 669, 21 [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira, M. J., & Kuhn, J. R. 2005, ApJ, 627, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira, M. J., Bryan, G. L., & Gill, S. P. D. 2008, ApJ, 672, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, J., Kneib, J., Limousin, M., Edge, A., & Jullo, E. 2010, MNRAS, 402, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H., & McGaugh, S. S. 2002, ARA&A, 40, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., Kochanek, C. S., & Wambsganss, J. 2006, Gravitational Lensing: Strong, Weak and Micro, ed. P. Schneider, C. S. Kochanek, & J. Wambsganss [Google Scholar]
- Sellwood, J. A., & Kosowsky, A. 2001, in Gas and Galaxy Evolution, ed. J. E. Hibbard, M. Rupen, & J. H. van Gorkom, ASP Conf. Ser., 240, 311 [Google Scholar]
- Sersic, J. L. 1968, Atlas de galaxias australes, ed. J. L. Sersic [Google Scholar]
- Smith, D. R., Bernstein, G. M., Fischer, P., & Jarvis, M. 2001, ApJ, 551, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Sofue, Y., & Rubin, V. 2001, ARA&A, 39, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Marshall, P. J., Hobson, M. P., & Blandford, R. D. 2006, MNRAS, 371, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Marshall, P. J., Blandford, R. D., et al. 2009, ApJ, 691, 277 [Google Scholar]
- Suyu, S. H., Marshall, P. J., Auger, M. W., et al. 2010, ApJ, 711, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, L., Hoekstra, H., & Zhao, H. 2009, MNRAS, 393, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Tollerud, E. J., Bullock, J. S., Graves, G. J., & Wolf, J. 2010, ApJ, submitted [arXiv:1007.5311] [Google Scholar]
- van Dokkum, P. G. 2001, PASP, 113, 1420 [NASA ADS] [CrossRef] [Google Scholar]
- Vegetti, S., & Koopmans, L. V. E. 2009, MNRAS, 392, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Vegetti, S., Czoske, O., & Koopmans, L. V. E. 2010, MNRAS, 407, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H., Bacon, D. J., Taylor, A. N., & Horne, K. 2006, MNRAS, 368, 171 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 A colour image of SL2S J08544−0121 constructed from the F475W, F606W and the F814W images taken with the HST/ACS. The primary and satellite lenses are denoted by P and S, respectively. The boxes mark the multiple image systems that are shown in detail in Fig. 2. |
| In the text | |
 |
Fig. 2 Identification of the multiple images. The three panels (I, II and III) correspond to the regions marked in Fig. 1. These image cutouts are taken from the F606W image with the light from the lens galaxies subtracted. The triangles, circles and squares show the three multiple image systems. |
| In the text | |
 |
Fig. 3 Critical curves (black) and caustics (grey) of the lens models. Dashed (solid) curves correspond to the most probable lens model with image positions (extended image surface brightness) as constraints. The dot-dashed curve in the inset marks the cut of the satellite. The cross (plus) symbol denotes the modelled centroid position of the primary (satellite) lens. The three types of open symbols mark the three sets of multiple image systems. The solid symbols are the corresponding modelled source positions based on the most probable lens parameters from the extended image modelling. The shapes of the critical and caustic curves are similar for the two models, but the model based on image positions (dashed) has a rounder primary lens with higher external shear. |
| In the text | |
 |
Fig. 4 Marginalised posterior PDF for γext (external shear strength), bP (strength of primary lens in arcseconds), bS (strength of satellite lens in arcseconds) and t (truncation radius of satellite in arcseconds) based on image position modelling. The three shaded areas show the 68.3%, 95.4% and 99.7% credible regions. The halo size of the satellite galaxy is not constrained using image positions. |
| In the text | |
 |
Fig. 5 Marginalised posterior PDF for γext (external shear strength), bP (strength of primary lens in arcseconds), bS (strength of satellite lens in arcseconds) and t (truncation radius of satellite in arcseconds) based on extended image surface brightness modelling, plotted on the same scales as in Fig. 4. The three shaded regions show the 68.3%, 95.4% and 99.7% credible regions. For comparison, the lines show the 68.3% credible regions from Fig. 4 with image positions as constraints. In contrast to the full t-degeneracy from image position modelling, extended image modelling allows us to constrain the truncation radius of the satellite galaxy halo to be |
| In the text | |
 |
Fig. 6 Extended image and source surface brightness reconstruction. From left to right: top: observed image, reconstructed image; bottom: normalised image residual (in units of the uncertainty estimated for each pixel), reconstructed source. The morphology of the lensed arc is reproduced, and the reconstructed source surface brightness distribution shows three peaks. |
| In the text | |
 |
Fig. 7 Four simulated images designed to mimic SL2S J08544−0121 but with different input mass distributions. Simulations are labelled as #1 − 4. Details of the simulations are given in Sect. 5.1. |
| In the text | |
 |
Fig. 8 Marginalised posterior PDF of bS (strength of satellite lens) and t (truncation radius of satellite) for the simulations. The crosses mark the input parameter values. The three shaded areas show the 68.3%, 95.4% and 99.7% credible regions. In the cases where the truncation radius is constrained (without a full degeneracy in the prior range), the recovered value agrees with the input value within the uncertainties. |
| In the text | |
 |
Fig. 9 Probability density of the tidal radius of the satellite given the modelled projected distance of R = 25.5 kpc and the modelled lens strengths. Our halo size measurement of |
| In the text | |
 |
Fig. 10 Comparison of the galaxy halo size measurements. For statistical measurements, rt is the fiducial truncation radius and σ is the fiducial velocity dispersion. The direct measurement of our satellite galaxy in SL2S J08544−0121 is marked by an inverted triangle, confirming the tidal stripping of galaxy halos in dense environments. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.