EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 520 (September-October 2010) A&A, 520 (2010) A29 Full HTML
Free Access
Issue
A&A
Volume 520, September-October 2010
Article Number A29
Number of page(s) 11
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200913081
Published online 24 September 2010
A&A 520, A29 (2010)

A precise measurement of the solar differential rotation by tracing small bright coronal structures in SOHO-EIT images

Results and comparisons for the period 1998-2006[*]

H. Wöhl1 - R. Brajsa2,[*] - A. Hanslmeier3 - S. F. Gissot4

1 - Kiepenheuer-Institut für Sonnenphysik, Schöneckstr. 6, 79104 Freiburg, Germany
2 - Hvar Observatory, Faculty of Geodesy, University of Zagreb, Kaciceva 26, 10000 Zagreb, Croatia
3 - Institut für Physik, IGAM, Universität Graz, Universitätsplatz 5, 8010 Graz, Austria
4 - SIDC, Royal Observatory of Belgium, Ave. Circulaire 3, 1180 Brussels, Belgium

Received 6 August 2009 / Accepted 1 February 2010

Abstract
Aims. We precisely determine the solar rotation velocity during most of the 23rd solar cycle, in the years 1998-2006. We measure the solar differential rotation by tracing small bright coronal structures (SBCS) in SOHO-EIT images.
Methods. The 28.4 nm EIT channel was used and positions of more than 55 000 structures were measured applying an interactive and improved automatic method of data reduction.
Results. We achieve the closest representation of the observational data when all three solar differential rotation parameters are used and obtain the formula $\omega ~ (b) = 14.499 (\pm 0.006) - 2.54 (\pm 0.06) ~ {\rm sin}^2 b - 0.77 (\pm 0.09) ~ {\rm sin}^4 b$. This result represents the sidereal rotation velocity in deg day-1 and is produced by the automatic method applied in 1998-2006. A north-south rotational asymmetry and a rigid component of the solar rotation at high latitudes were found.
Conclusions. A more differential rotation profile of SBCS than of sunspots and sunspot groups was found. The rotation velocity of SBCS is very similar to those obtained by small photospheric magnetic features. The north-south rotational asymmetry of SBCS was interpreted with a model of the relationship between solar rotation and activity. The rigid component of the solar rotation at high latitudes, identifiable only from the results of the automatic method, was related to larger structures mostly identified by that method, in contrast to the interactive method, which detected smaller structures.

Key words: Sun: rotation - Sun: corona - Sun: activity

1 Introduction

Solar rotation is one of the fundamental properties of the Sun as a star and an investigation of the relationship between the solar rotation and activity is an important observational task. Measurements of the solar differential rotation provide an observational constraint on theoretical models of the rotating convection zone and the solar MHD dynamo, which appears to play a decisive role in generating and maintaining a solar magnetic field and the whole activity of the Sun (Stix 2002; Ossendrijver 2003; Rüdiger & Hollerbach 2004; Rozelot & Neiner 2009). Understanding the solar activity cycle, which is driven by a MHD dynamo, remains a key unsolved problem in solar physics, along with, e.g., the heating of the solar corona and solar flares.

In resolving these problems, sunspots have been most often used as tracers, mainly because of the long-term data sets available from various observatories, e.g., Greenwich and Mt. Wilson (Newton & Nunn 1951; Gilman & Howard 1984; Howard et al. 1984; Balthasar et al. 1986; Howard & Gilman 1986; Zappala & Zuccarello 1991; Pulkkinen & Tuominen 1998; Brajsa et al. 2002a; Ruzdjak et al. 2004, 2005, in prep.). However, apart from the advantage of long time coverage, sunspots and sunspot groups have serious disadvantages, such as their well-known complex and variable structure, a very pronounced butterfly diagram, and the enormous difference in the number of tracers present on the Sun at maximum and minimum activity.

In the present analysis, we use small bright coronal structures (SBCS) as tracers of the solar rotation determination and in this way some of the above mentioned disadvantages can be avoided. SBCS are localized tracers covering solar latitudes more uniformly than the sunspots, their latitudinal range varies during the cycle much less than for sunspots, and the difference in the number of tracers between activity maximum and minimum is much lower (e.g., Brajsa et al. 2005, and references therein). Owing to the absence of ordinary active regions, the discernibility of SBCS during the periods of the activity minimum is even better than at maximum. The SBCS are highly correlated with the coronal bright points discernible in the EUV and soft X-ray spectral regions. Their most important physical characteristics were summarized by Brajsa et al. (2004, 2008b, and references therein).

Positions of SBCS identified and traced in full-disc SOHO-EIT images, acquired during 6 months in the 1998-1999 period, were reduced and analysed for determination of solar rotation and related topics in a series of papers (Brajsa et al. 2001b, 2002b, 2004, 2008b; Vrsnak et al. 2003). For data reduction, two methods are used: an interactive one and an automatic one. In the present paper, we extend the analysis with the interactive method to two additional months in the year 1999 and apply an improved automatic method to the extensive data set obtained in the years 1998-2006 (data from a total of 93 months). A subset of this data was previously used to compare the sidereal angular rotation velocity of the SBCS and sub-photospheric layers during the declining phase of the solar cycle 23 (Zaatri et al. 2009).

2 The SOHO-EIT data set

The data set consists of several thousand full-disc full-resolution solar filtergrams recorded in the Fe XV line at the wavelength of 28.4 nm with the EIT instrument (Delaboudiniere et al. 1995) onboard the SOHO spacecraft. Images were usually taken every 6 h, i.e., with a regular cadence of 4 images per day, although sometimes there were gaps of 12 h or more between the successive images. All images were preprocessed by correcting defects (e.g., grid, CCD flat field) and the CCD offset. Additional information about the images used and their prereduction were given by Brajsa et al. (2001b).

Among the four EIT channels, we chose to use data from the 28.4 nm one since it corresponds to the highest temperature and appears to provide the sharpest image contrast, which is suitable for identifying SBCS. The contamination by the transition region emission (Mg VII, Si VII) is not a serious problem, since the magnetic field lines are anchored to the photosphere.

Measurements were performed in the period 1998-2006 covering most of the 23rd solar cycle. In the years 1998-1999, data from all calender months were not suitable for the analysis (data from only 9 months were considered), while in the period 2000-2006 data from all calender months were analysed. In Tables 3-11, the time periods are listed according to the year of observation.

3 The interactive and automatic methods of data reduction

The interactive method of data reduction is based on a visual identification of a particular SBCS that can be used as a tracer. The data reduction programs were written in IDL. All full disc solar images were visually inspected and the SBCS identified in a sequence of images. The main criterion for identifying a SBCS was checking its persistence in consecutive images at approximately the same latitude but shifted in the central meridian distance (CMD) according to the elapsed time. The CMD values of the identified features were then measured in selected consecutive images and fitted as a function of time (t). The correlation coefficient of the function CMD(t) was generally very high, implying that the tracers had been correctly identified.

More details about the interactive method, such as distinguishing between different tracer subtypes, tracing times and lifetimes of the features, as well as the intensity and area evolution were described in the papers of Brajsa et al. (2001a,b, 2008b) and of Mulec et al. (2007). The interactive method has many advantages that allow detailed studies of SBCS (e.g., Vrsnak et al. 2003; Mulec et al. 2007; Brajsa et al. 2008b), but also some important disadvantages. The main disadvantages are that the method is extremely time consuming and the difficulty in various observers applying the method in exactly the same way.

To avoid these disadvantages and to accelerate the data reduction, an automatic method was developed (Brajsa et al. 2001b, 2002b; Wöhl et al. 2001). It relies on the IDL procedure, ``Regions Of Interest (ROI) segmentation'', which was initially developed to detect and identify stars and galaxies in deep sky images of galaxy clusters. The ROI parameters that can be preset are the sharpness of the subimages (s), their circumference range (c), and the intensity range of their brightness (i). The following ROI parameters were used: s was limited to between 30 and 255 relative units, c was in the range from 30 to 80 EIT pixels (80 to 210 arcsec), and i was limited between 100 and 600 relative intensity units (Brajsa et al. 2002b). The centres of the selected subimages were automatically traced in triplets of consecutive full-disc solar images taken every 6 h and the last image in a triplet was the first one in the next triplet.

In the first phase of the application of the automatic method (Brajsa et al. 2002b), the numerically allowed latitudinal variation in the traced feature was 1 deg from one image to the next and all synodic rotation velocities outside the range 7-17 deg day-1 were excluded from further analysis. However, it was found that these criteria were not conservative enough, especially for images taken during the high solar activity phases (Brajsa et al. 2008c). The automatic method was therefore improved: the allowed change in latitude from one image to the next, to identify the same structure, was reduced from 1 to 0.8 deg, the synodic rotation velocity filter was reduced to 9.5-16.5 deg day-1, and the differential rotation gradient of -3.0 $\times$ ${\rm sin}^2 b$, where b is solar latitude, was in addition imposed.

In the present work, all data were reduced using the improved automatic method. The data from the first 6 months of the entire observational period (1998-1999; Brajsa et al. 2002b) were therefore re-reduced.

4 Results

The measured synodic rotational velocities were transformed into the sidereal ones with the time-dependent procedure taking into account the variable velocity of the Earth and SOHO in their orbits around the Sun (e.g., Rosa et al. 1995).

We used the most common representation of the solar differential rotation

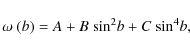
\begin{displaymath}% \omega ~ (b) = A + B ~ {\rm sin}^2 b + C ~ {\rm sin}^4 b, \end{displaymath} (1)

where $\omega$ represents the angular rotation velocity expressed in deg day-1, b the heliographic latitude, and A, B, and C the solar rotation parameters. Three different approaches to the fitting procedure were used (e.g., Brajsa et al. 1997): in the first one, the parameter C = 0; in the second one, all three parameters were used, but generally with $C \ne 0$; and in the third one, all three parameters were taken into account, but setting B = C. The third procedure was introduced by Scherrer et al. (1980) to avoid the possibility of crosstalk between the parameters B and C. In this case, Eq. (1) was transformed to $\omega (b) = y(x) = A + B(x + x^2)$ by performing the substitution $x = {\rm sin}^2 b$. We now take x + x2 = x' leading to y(x') = A + Bx', which is now fitted with the linear least squares method, as usual (e.g., Brajsa et al. 1997).

Extreme rotation velocity values, which are regarded as erroneous, were excluded in two steps called filters. In applying the first filter all sidereal rotation velocity values lower than 8 deg day-1 and higher than 18 deg day-1 were excluded regardless of the tracer's latitude. The rotation velocity parameters from Eq. (1) were then found for all remaining data points (1st step). To apply the second filter all velocity values differing by $\delta = 2.0$ deg day-1 or more from the mean curve were excluded from the data and new parameters were recalculated (2nd step). An example of the application of this two-step velocity filter is presented in Fig. 1 and Table 2. This filtering was applied when data from certain periods (months, years or longer intervals) were combined together. Thus the sum of all used tracers differs slightly when adding monthly numbers and comparing them with final annual sums. A similar result holds when the yearly results are combined to form longer periods.

4.1 The interactive method: 1998-1999

For the case C = 0, the differential rotation parameters, obtained by applying the interactive method for 8 months during 1998-1999 are given in Table 1. From these results, a combined data set was composed for the whole interval and the interactive method was applied. The solar differential rotation results for this combined data set are presented in Figs. 1 and 2 and Table 2. In Fig. 2 and Table 2, the differential rotation curves and the solar rotation parameters for all three fitting cases (described earlier) are presented.

The application of the interactive method is extremely time consuming and the results presented here are a combination of efforts of many observers. Most often the data from the same months were analysed by more than just one observer and the selection of individual results, combined and used in the present paper, is based on the monthly values published by Brajsa et al. (2001a, 2008a). In the Acknowledgements, the names of all observers who contributed to this effort are listed.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig1.eps} \end{figure} Figure 1:

Sidereal rotation velocities determined by tracing coronal bright points with the interactive method for 8 selected months during 1998-1999 (see Table 1). The data points excluded by the second filter, as described in text, are shown by crosses. The fitted differential rotation curve using all data points presented here and the error ranges of 2 deg day-1 are denoted by dotted lines. The full line indicates the differential rotation curve of the filtered data (stars). It is defined by the differential rotation parameters given in the third line of Table 2.

Open with DEXTER

Table 1:   Differential rotation parameters A and B from Eq. (1) and their standard errors M in deg day-1 for the interactive method.

Table 2:   Similar to Table 1 for the combined interactive data set from 8 months, 1998-1999.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig2.eps} \end{figure} Figure 2:

Mean values of sidereal rotation velocities obtained using the interactive method (the same data set as in Fig. 1). The averaging is performed in 5 deg latitude bins and the error bars indicate the standard errors of the means in each bin. The three lines represent least squares fits to all filtered data as indicated in the legend (see also Table 2).

Open with DEXTER

4.2 The automatic method: 1998-2006

The solar rotation parameters found by the automatic method are presented in Tables 3-11, for the nine years of observations, 1998-2006. We note that in the first two years, 1998 and 1999, not all months were covered, because of either a lack of observations or inadequate data. Later, in the period 2000-2006, in each year all 12 months were covered with observations suitable for further reduction. The results for data from a total of 93 months are therefore presented.

In these tables, the number of structures found per month, the number of triplets used per month, and the average number of structures per triplet are also given. For each month, two sets of the results were calculated: one for all tracers according to the criteria described above and another for the subsets of selected stable structures.

The identification of stable structures was performed by searching for pairs of triplets with a difference in latitude of less than 0.5 deg and continuing values in longitude, i.e., in the CMD. In general, fewer than half of the structures were found to be stable. The difference between the equatorial rotation velocity of all structures and that of the selected stable structures was found to be statistically significant at the 3$\sigma$ level. The mean of the monthly differences for those two cases is -0.030 $\pm$ 0.009 deg day-1.

Thus the stable structures exhibit a slightly higher equatorial rotation compared to all structures. This finding is similar to a result published by Hara (2009, Fig. 4) from X-ray bright points observed with Yohkoh/SXT in the years 1994 until 1997. However, in that paper a mean increase in the equatorial rotation velocity by 0.005 deg day-1 for an increase of the lifetime by one hour was found, about a factor of 2 larger than our result.

Table 12:   Similar to Tables 3-11 for the annual data sets, $N_{\rm all} = 50~589$.

Table 13:   Similar to Table 2 for the combined automatic data set from 93 months, 1998-2006.

Finally, the results for the nine years under consideration and for all time periods taken together (93 months in those nine years) are given in Tables 12 and 13, respectively. In Table 13, the solar differential rotation parameters are presented after applying the 1st and the 2nd filter, and for the three different fitting procedures.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig3.eps} \vspace*{3mm} \end{figure} Figure 3:

Similar to Fig. 2 for the automatic method, all data 1998-2006 (see Table 13).

Open with DEXTER

In Fig. 3, the mean values of sidereal rotation velocities obtained using the automatic method are given for the 5 deg latitude bins. The corresponding error bars indicate the standard errors in the means for each bin. For the three fitting procedures, the solar differential rotation curves are also given. The least squares fits were performed for all filtered data (not only for the mean values).

The error bars are very small, because of the high precision of the measurements and the huge numbers of data points in each 5-deg bin. Therefore, we present separately the 5-deg bin averages and solar differential rotation curves enlarged for the low (0-40 deg) and high (40-90 deg) latitude parts in Figs. 4 and 5, respectively. It is interesting that the application of the fitting procedure with all three parameters, A-C, allowing $B \ne C$, represents the observational data in the optimal way (Figs. 3-5), due to the excellent latitudinal coverage of the tracers used.

4.3 The north-south asymmetry of the solar rotation

Table 14:   The north-south asymmetry of the solar rotation for the results of the interactive (1998-1999) and the automatic (1998-2006) method. N - the number of traced structures.

The solar rotation parameters are given separately for the northern and southern solar hemispheres in Table 14. The results for both reduction methods, the interactive and the automatic one, are presented. For the interactive method, the difference in the equatorial rotation velocity between hemispheres (the parameter A) is very small and statistically insignificant. On the other hand, the gradient in the solar rotation (the parameter B) differs between the two solar hemispheres, the difference being statistically significant at the 1$\sigma$ level. For the automatic method, the difference in the solar rotation parameter A is statistically significant at the 1$\sigma$ level and the difference in the solar rotation parameter B is statistically significant at the 2$\sigma$ level. A smaller difference in the equatorial rotation velocity is consistent with the continuity requirement of the rotation velocity. For both methods, the southern solar hemisphere rotates more rapidly, which can also be clearly seen in Figs. 6 and 7, where the results of the interactive and automatic methods are presented, respectively.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig6.eps} \vspace*{5mm} \end{figure} Figure 7:

The north-south asymmetry for the interactive method.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig7.eps} \vspace*{5mm} \end{figure} Figure 8:

The north-south asymmetry for the automatic method.

Open with DEXTER

5 Discussion

5.1 Comparing results of interactive and automatic methods for data of 1998-1999

Table 15:   A comparison of the results obtained by the interactive and the automatic method (upper and lower parts of the table, respectively) for the 8 selected months during 1998-1999, see also Tables 1 and 2.

A comparison of the results obtained by the interactive and automatic methods was possible for 8 months in the period 1998-1999, when both methods were applied. Using the three fitting procedures, the solar differential rotation parameters calculated after the 2nd filter are presented for this case in Table 15. The mean velocity values for 5-deg latitude bins and corresponding differential rotation curves for the interactive and automatic methods are given in Fig. 8. For the interactive method, the equatorial rotation velocity and the gradient in the differential rotation are slightly larger, in comparison to the automatic method. This finding agrees with the more rigid solar rotation component found by the automatic method, which was obtained in a preliminary form by Brajsa et al. (2002b) for a smaller data set and an earlier version of the automatic method.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig8.eps} \vspace*{5mm} \end{figure} Figure 6:

A comparison of the results obtained by the interactive and the automatic method for the 8 selected months during 1998-1999, see also Table 15.

Open with DEXTER

5.2 A comparison with other data

Table 16:   A comparison of differential rotation parameters A-C from Eq. (1) for SBCS (Tables 13 and 15) with other results. R - remark.

We present a comparison of the differential rotation parameters calculated by tracing SBCS in the present work with the results obtained by other methods and tracers in Table 16. Apart from the coronal bright points and similar tracers identified in the EUV and X-ray parts of the spectrum, the results obtained by tracing sunspots, H$\alpha$ filaments, and different radio sources observed at mm wavelengths are compared with the cross-correlation of magnetic structures and measurements of Doppler shifts.

An unusual disagreement is found in Table 16, in addition to the well-known observational findings that structures consisting of concentrated magnetic fields, such as sunspots, have a more rapid rotation velocity than the surrounding plasma measured by Doppler shifts and that large-scale coronal tracers have a rigid component in their rotation. Kariyappa (2008) and Hara (2009) both measured the rotation velocity of coronal bright points in Yohkoh/SXT images during mostly overlapping time periods. However, the rotation results, especially at the solar equator, differ significantly (lines 3 and 4 in Table 16).

It is interesting that the equatorial rotation velocity of coronal bright points taken from the literature (the rotation parameter A, lines 1-8 in Table 16) vary across a wide range from 14.19 deg day-1 to 17.6 deg day-1. The same parameter for the SBCS, which partly corresponds to the coronal bright points, were found to be in a much narrower range between 14.499 deg day-1 and 14.62 deg day-1 (lines 9-17 in Table 16). At present, we have no explanation for this discrepancy, besides that in this work we used a large, homogeneous data set, leading to more common rotation values at the solar equator.

When only the first two parameters from Eq. (1) are taken into account, the SBCS parameters analysed in this work are similar to (the parameter A) or larger than (the parameter B) the corresponding values for sunspots and sunspot groups. For the parameter B, the absolute values are considered, implying that SBCS have a more differential rotation profile than sunspots. On the other hand, when all three parameters from Eq. (1) are considered, there is general agreement with the results of the photospheric magnetic fields. This is a consequence of the magnetic nature of SBCS, and the disagreement with sunspots might be caused by the superior latitudinal coverage of SBCS compared to sunspots.

5.3 The north-south asymmetry of the solar rotation compared with the solar activity status

A more rapid yet weaker differential solar rotation profile was found for the southern solar hemisphere during the subinterval (1998-1999) when the interactive method was applied and during the whole observing interval (1998-2006) when the data were reduced with the automatic method. For the automatic method, the north-south rotational asymmetry is statistically significant at the 2$\sigma$ level (Sect. 4.3., Table 14, Figs. 6 and 7). The first time interval (1998-1999) coincides with the ascending phase of the solar cycle No. 23, while the whole time period (1998-2006) embraces most of the activity maximum of the same solar cycle.

The observed north-south rotational asymmetry can be interpreted in the framework of a model of interdependence of solar rotation and activity, taking into account the balance between Reynolds and Maxwell stresses (Brun 2004; Brun et al. 2004; Brajsa et al. 2006, 2007). During most of the 23rd solar cycle, the southern solar hemisphere was more active (Temmer et al. 2006, their Fig. 6 and Table 2). This is also true for the first part of the ascending phase (1998-1999) of that solar cycle. Stronger magnetic activity in the southern solar hemisphere therefore on average suppresses, to some extent, the differential rotation. Maxwell stresses, related to the magnetic field, oppose the usual Reynolds stresses, which are the main cause of the differential character of the solar rotation.

5.4 On the rigid component of the solar rotation at high latitudes

The rotation results obtained with the automatic method of data reduction detect a rigid rotational component at high solar latitudes, roughly between 60 and 80 deg. This can be clearly seen in Figs. 3, 5, and 7. It is interesting that this rigid component is even more pronounced in the more active, southern solar hemisphere (Fig. 7). On the other hand, nothing like that was found in the results of the interactive method (Figs. 2, 6, and 8), apart from a small more rapidly rotational component at heliographic latitudes between 50 and 60 deg, but only in the southern solar hemisphere (Fig. 6). This rigid component of the solar rotation found for the automatic method is consistent with the difference between the gradients of the solar rotation, i.e., the parameter B, for the two methods. The difference is statistically significant at the 2$\sigma$ level, the rotation determined by the automatic method being more rigid (a lower absolute value of the rotation parameter B) as can be seen in Table 15.

A similar spin-up of the solar rotation, i.e., a rigid rotational component at high solar latitudes, determined by magnetic field patterns was reported by Sheeley et al. (1987) and Stenflo (1989a,b). In both cases, the solar magnetic field patterns were autocorrelated with the time lag of one solar rotation. However, this rigid component in the solar rotation was not present when the magnetic field patterns were cross-correlated in daily magnetograms separated by a couple of days (Snodgrass 1983) and in that case a typical, continuously decreasing rotation velocity profile with latitude was found.

To interpret this curious behaviour of solar magnetic field patterns, two models were proposed. Sheeley et al. (1987) proposed magnetic flux-transport models, in which supergranular diffusion and meridional motions distribute magnetic elements across the solar surface. On the other hand, Stenflo (1989a) proposed a continual replacement of evanescent surface magnetic flux by sources deep inside the convection zone. However, as pointed out by Snodgrass (1992), in both models the long-lived and the short-lived magnetic structures have different rotation properties because of different correlation procedures applied. Snodgrass (1992) claims that this difference is not due to the difference in the time lag, but is a result of a selection effect, in particular of spatial resolution. Snodgrass (1992) concludes that the autocorrelation method identifies large-scale structures, while the cross-correlation on short timescales finds small-scale features.

Finally, we can apply this line of reasoning to our results. It is well known that SBCS correspond to magnetic regions of different length scales. The rotational behaviour of SBCS is also consistent with this finding (e.g., Sect. 5.2. in the present paper). In one of our earlier works (Brajsa et al. 2002b), we reported that the automatic method chooses mostly small active regions and parts of larger, ordinary active regions, while the interactive method identifies predominantly point-like structures and small loops, i.e., coronal bright points on a smaller spatial scale. We can therefore interpret the observed spin-up of the solar rotation, found by the automatic method at high latitudes, with this selection effect. Applying the automatic method, larger objects are identified and traced, which each have a rigid rotation component.

6 Summary and conclusions

We have precisely determined the solar differential rotation by tracing small bright coronal structures (SBCS) in SOHO-EIT images during the period 1998-2006. The 28.4 nm EIT channel was used and positions of more than 55 000 structures have been measured. Both interactive and the automatic methods of data reduction were applied and their results were compared for similar time periods. The closest representation of the observational data has been obtained by using all three solar differential rotation parameters from Eq. (1) and allowing $B \ne C$. This has been possible because of the very comprehensive latitudinal coverage of the tracers used.

The results imply a more differential rotation profile of SBCS than of sunspots and sunspot groups. The rotation velocity of SBCS is very similar to those obtained for small photospheric magnetic features. This is unsurprising, since SBCS correspond mostly to small bipolar magnetic structures.

A north-south rotational asymmetry of SBCS was found and interpreted in terms of a model of the relationship between solar rotation and activity. Finally, a rigid component of the solar rotation of SBCS discovered at high latitudes by applying the automatic method, can be interpreted as the result of a selection effect. The automatic method has a greater tendency to identify larger structures, while the interactive method identifies mostly smaller features and the two types of SBCS have different rotational properties at high latitudes.

In a continuation of the present work (Jurdana-Sepic et al., in prep.), we will investigate the relationship between the parameters of the solar rotation and the solar activity using the monthly and yearly values of the solar rotation parameters presented in this work. In this way, we would like to complement some earlier studies of the coronal rotation variation (e.g., Nash et al. 1988; Rybák 1994, 2000; Altrock 2003; Brajsa et al. 2007; Gissot 2009, and references therein) and to compare those results for coronal structures with those obtained using other tracers and methods in different time periods (Table 16 in the present paper).

Acknowledgements
This project was started with the support of the Alexander von Humboldt Foundation and is related to the SOHO-EIT Proposal Brajsa_206: ``an analysis of the solar rotation velocity by tracing coronal features'' (http://umbra.nascom.nasa.gov/eit/proposals/) submitted in March 1999 by R. Brajsa, B. Vrsnak, V. Ruzdjak, D. Rosa, H. Wöhl, and F. Clette. SOHO is a project of international cooperation between ESA and NASA. We would like to thank the EIT team for developing and operating the instrument, F. Clette, J.-F. Hochedez, and J. de Patoul for providing the EIT images and helpful discussions and H. Balthasar and J. Rybák for useful comments and suggestions. Besides the coauthors of the present paper, R. Brajsa and H. Wöhl, the interactive method of data reduction was also performed by following observers: J. O. Engler, M. Kasabasic, M. Mulec, J. Rodmann, K. Schawinski-Guiton, T. J. Schuck, and A. Wegner. The authors would like to thank them sincerely for their valuable contribution to data reduction. This work is sponsored by the Air Force Office of Scientific Research, Air Force Material Command, USAF, under grant number FA8655-07-1-3093. Further, the research leading to the results presented in this paper has partly received funding from European Community's Seventh Framework Programme (FP7/2007-2013) under grant agreement No. 218816 and R.B. and A.H. acknowledge also the support from the Austrian-Croatian Bilateral Scientific Project. Finally, the authors are very thankful to the anonymous referee for suggesting many improvements of the paper and especially for pointing out an interesting rotational behaviour of SBCS at high solar latitudes.

References

  1. Adams, W. M., & Tang, F. 1977, Sol. Phys., 55, 499 [NASA ADS] [CrossRef] [Google Scholar]
  2. Altrock, R. C. 2003, Sol. Phys., 213, 23 [NASA ADS] [CrossRef] [Google Scholar]
  3. Balthasar, H., Vázquez, M., & Wöhl, H. 1986, A&A, 155, 87 [NASA ADS] [Google Scholar]
  4. Brajsa, R., Vrsnak, B., Ruzdjak, V., et al. 1991, Sol. Phys., 133, 195 [NASA ADS] [CrossRef] [Google Scholar]
  5. Brajsa, R., Ruzdjak, V., Vrsnak, B., et al. 1997, Sol. Phys., 171, 1 [NASA ADS] [CrossRef] [Google Scholar]
  6. Brajsa, R., Wöhl, H., Schuck, T. J., et al. 2001a, Hvar Obs. Bull., 25, 13 [NASA ADS] [Google Scholar]
  7. Brajsa, R., Wöhl, H., Vrsnak, B., et al. 2001b, A&A, 374, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Brajsa, R., Wöhl, H., Vrsnak, B., et al. 2002a, Sol. Phys., 206, 229 [NASA ADS] [CrossRef] [Google Scholar]
  9. Brajsa, R., Wöhl, H., Vrsnak, B., et al. 2002b, A&A, 392, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Brajsa, R., Wöhl, H., Vrsnak, B., et al. 2004, A&A, 414, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Brajsa, R., Wöhl, H., Vrsnak, B., et al. 2005, Sol. Phys., 231, 29 [NASA ADS] [CrossRef] [Google Scholar]
  12. Brajsa, R., Ruzdjak, D., & Wöhl, H. 2006, Sol. Phys., 237, 365 [NASA ADS] [CrossRef] [Google Scholar]
  13. Brajsa, R., Wöhl, H., Ruzdjak, D., et al. 2007, Astron. Nachr., 328, 1013 [NASA ADS] [CrossRef] [Google Scholar]
  14. Brajsa, R., Mulec, M., Hanslmeier, A., et al. 2008a, Cent. Eur. Astrophys. Bull., 32, 117 [NASA ADS] [Google Scholar]
  15. Brajsa, R., Wöhl, H., Vrsnak, B., et al. 2008b, Cent. Eur. Astrophys. Bull., 32, 165 [NASA ADS] [Google Scholar]
  16. Brajsa, R., Wöhl, H., Hanslmeier, A., & Gissot, S. F. 2008c, ESPM-12, Poster 2.3-32, http://espm.kis.uni-freiburg.de [Google Scholar]
  17. Brajsa, R., Romstajn, I., Wöhl, H., et al. 2009, A&A, 493, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Brun, A. S. 2004, Sol. Phys., 220, 333 [NASA ADS] [CrossRef] [Google Scholar]
  19. Brun, A. S., Miesch, M. S., & Toomre, J. 2004, ApJ, 614, 1073 [NASA ADS] [CrossRef] [Google Scholar]
  20. d'Azambuja, M., & d'Azambuja, L. 1948, Ann. Obs. Paris-Meudon, VI, VII [Google Scholar]
  21. Delaboudiniere, J. P., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162, 291 [NASA ADS] [CrossRef] [Google Scholar]
  22. Deng, Y., Wang, J., & Harvey, J. 1999, Sol. Phys., 186, 13 [NASA ADS] [CrossRef] [Google Scholar]
  23. Dupree, A. K., & Henze, W., Jr. 1972, Sol. Phys., 27, 271 [NASA ADS] [CrossRef] [Google Scholar]
  24. Gilman, P., & Howard, R. 1984, ApJ, 283, 385 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gissot, S. 2009, Ph.D. Thesis, Universite Catholique de Louvain [Google Scholar]
  26. Golub, L., Krieger, A. S., Silk, J. K., Timothy, A. F., & Vaiana, G. S. 1974, ApJ, 189, L93 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hara, H. 2009, ApJ, 697, 980 [Google Scholar]
  28. Howard, R., & Harvey, J. 1970, Sol. Phys., 12, 23 [NASA ADS] [CrossRef] [Google Scholar]
  29. Howard, R., & Gilman, P. A. 1986, ApJ, 307, 389 [NASA ADS] [CrossRef] [Google Scholar]
  30. Howard, R., Gilman, P. A., & Gilman, P. I. 1984, ApJ, 283, 373 [NASA ADS] [CrossRef] [Google Scholar]
  31. Karachik, N., Pevtsov, A. A., & Sattarov, I. 2006, ApJ, 642, 562 [NASA ADS] [CrossRef] [Google Scholar]
  32. Kariyappa, R. 2008, A&A, 488, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Komm, R. W., Howard, R. F., & Harvey, J. W. 1993, Sol. Phys., 145, 1 [NASA ADS] [CrossRef] [Google Scholar]
  34. Küveler, G., & Wöhl, H. 1983, A&A, 123, 29 [NASA ADS] [Google Scholar]
  35. Lustig, G., & Wöhl, H. 1989, A&A, 218, 299 [NASA ADS] [Google Scholar]
  36. Mulec, M., Brajsa, R., Wöhl, H., et al. 2007, Cent. Eur. Astrophys. Bull., 31, 1 [NASA ADS] [Google Scholar]
  37. Nash, A. G., Sheeley, N. R., Jr., & Wang, Y.-M. 1988, Sol. Phys., 117, 359 [NASA ADS] [CrossRef] [Google Scholar]
  38. Newton, H. W., & Nunn, M. L. 1951, MNRAS, 111, 413 [NASA ADS] [Google Scholar]
  39. Ossendrijver, M. 2003, A&ARv, 11, 287 [Google Scholar]
  40. Perez Garde, M., Vázquez, M., Schwan, H., & Wöhl, H. 1981, A&A, 93, 67 [NASA ADS] [Google Scholar]
  41. Pevtsov, A. A., & Latushko, S. M. 2000, ApJ, 528, 999 [NASA ADS] [CrossRef] [Google Scholar]
  42. Pulkkinen, P., & Tuominen, I. 1998, A&A, 332, 748 [NASA ADS] [Google Scholar]
  43. Rozelot, J.-P., & Neiner, C. 2009, The Rotation of Sun and Stars, Lect. Notes Phys., 765 [Google Scholar]
  44. Rüdiger, G., & Hollerbach, R. 2004, The Magnetic Universe (Weinheim: Wiley-VCH) [Google Scholar]
  45. Rosa, D., Brajsa, R., Vrsnak, B., & Wöhl, H. 1995, Sol. Phys., 159, 393 [NASA ADS] [CrossRef] [Google Scholar]
  46. Ruzdjak, D., Ruzdjak, V., Brajsa, R., & Wöhl, H. 2004, Sol. Phys., 221, 225 [NASA ADS] [CrossRef] [Google Scholar]
  47. Ruzdjak, D., Brajsa, R., Sudar, D., & Wöhl, H. 2005, Sol. Phys., 229, 35 [NASA ADS] [CrossRef] [Google Scholar]
  48. Rybák, J. 1994, Sol. Phys., 152, 161 [NASA ADS] [CrossRef] [Google Scholar]
  49. Rybák, J. 2000, Hvar Obs. Bull., 24, 135 [NASA ADS] [Google Scholar]
  50. Scherrer, P. H., Wilcox, J. M., & Svalgaard, L. 1980, ApJ, 241, 811 [NASA ADS] [CrossRef] [Google Scholar]
  51. Sheeley, N. R., Jr., Nash, A. G., & Wang, Y.-M. 1987, ApJ, 319, 481 [NASA ADS] [CrossRef] [Google Scholar]
  52. Snodgrass, H. B. 1983, ApJ, 270, 288 [NASA ADS] [CrossRef] [Google Scholar]
  53. Snodgrass, H. B. 1984, Sol. Phys., 94, 13 [NASA ADS] [CrossRef] [Google Scholar]
  54. Snodgrass, H. B. 1992, in The Solar Cycle, ed. K. L. Harvey, ASP Conf. Ser., 27, 71 [Google Scholar]
  55. Stenflo, J. O. 1989a, A&A, 210, 403 [NASA ADS] [Google Scholar]
  56. Stenflo, J. O. 1989b, A&ARv, 1, 3 [NASA ADS] [CrossRef] [Google Scholar]
  57. Stix, M. 2002, The Sun (Berlin: Springer-Verlag) [Google Scholar]
  58. Temmer, M., Rybak, J., Bendik, P., et al. 2006, A&A, 447, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Vrsnak, B., Brajsa, R., Wöhl, H., et al. 2003, A&A, 404, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Wöhl, H., Brajsa, R., Vrsnak, B., et al. 2001, Hvar Obs. Bull., 25, 27 [NASA ADS] [Google Scholar]
  61. Zaatri, A., Wöhl, H., Roth, M., Corbard, T., & Brajsa, R. 2009, A&A, 504, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Zappala, R. A., & Zuccarello, F. 1991, A&A, 242, 48 [Google Scholar]

Online Material

Table 3:   Differential rotation parameters A and B from Eq. (1) and their standard errors M in deg day-1 obtained applying the automatic method to monthly data sets for the year 1998.

Table 4:   Similar to Table 3 for the year 1999, $N_{\rm s/y} = 3014$.

Table 5:   Similar to Table 3 for the year 2000, $N_{\rm s/y} = 7254$.

Table 6:   Similar to Table 3 for the year 2001, $N_{\rm s/y} = 6882$.

Table 7:   Similar to Table 3 for the year 2002, $N_{\rm s/y} = 7123$.

Table 8:   Similar to Table 3 for the year 2003, $N_{\rm s/y} = 9450$.

Table 9:   Similar to Table 3 for the year 2004, $N_{\rm s/y} = 7700$.

Table 10:   Similar to Table 3 for the year 2005, $N_{\rm s/y} = 5162$.

Table 11:   Similar to Table 3 for the year 2006, $N_{\rm s/y} = 3221$.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig4.eps} \end{figure} Figure 4:

The low-latitude part of Fig. 3.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig5.eps} \end{figure} Figure 5:

The high-latitude part of Fig. 3.

Open with DEXTER

Footnotes

... 1998-2006[*]
Tables 3-11 and Figs. 4, 5 are only available in electronic form at http://www.aanda.org
...[*]
Alexander von Humboldt Research Fellow.

All Tables

Table 1:   Differential rotation parameters A and B from Eq. (1) and their standard errors M in deg day-1 for the interactive method.

Table 2:   Similar to Table 1 for the combined interactive data set from 8 months, 1998-1999.

Table 12:   Similar to Tables 3-11 for the annual data sets, $N_{\rm all} = 50~589$.

Table 13:   Similar to Table 2 for the combined automatic data set from 93 months, 1998-2006.

Table 14:   The north-south asymmetry of the solar rotation for the results of the interactive (1998-1999) and the automatic (1998-2006) method. N - the number of traced structures.

Table 15:   A comparison of the results obtained by the interactive and the automatic method (upper and lower parts of the table, respectively) for the 8 selected months during 1998-1999, see also Tables 1 and 2.

Table 16:   A comparison of differential rotation parameters A-C from Eq. (1) for SBCS (Tables 13 and 15) with other results. R - remark.

Table 3:   Differential rotation parameters A and B from Eq. (1) and their standard errors M in deg day-1 obtained applying the automatic method to monthly data sets for the year 1998.

Table 4:   Similar to Table 3 for the year 1999, $N_{\rm s/y} = 3014$.

Table 5:   Similar to Table 3 for the year 2000, $N_{\rm s/y} = 7254$.

Table 6:   Similar to Table 3 for the year 2001, $N_{\rm s/y} = 6882$.

Table 7:   Similar to Table 3 for the year 2002, $N_{\rm s/y} = 7123$.

Table 8:   Similar to Table 3 for the year 2003, $N_{\rm s/y} = 9450$.

Table 9:   Similar to Table 3 for the year 2004, $N_{\rm s/y} = 7700$.

Table 10:   Similar to Table 3 for the year 2005, $N_{\rm s/y} = 5162$.

Table 11:   Similar to Table 3 for the year 2006, $N_{\rm s/y} = 3221$.

All Figures

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig1.eps} \end{figure} Figure 1:

Sidereal rotation velocities determined by tracing coronal bright points with the interactive method for 8 selected months during 1998-1999 (see Table 1). The data points excluded by the second filter, as described in text, are shown by crosses. The fitted differential rotation curve using all data points presented here and the error ranges of 2 deg day-1 are denoted by dotted lines. The full line indicates the differential rotation curve of the filtered data (stars). It is defined by the differential rotation parameters given in the third line of Table 2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig2.eps} \end{figure} Figure 2:

Mean values of sidereal rotation velocities obtained using the interactive method (the same data set as in Fig. 1). The averaging is performed in 5 deg latitude bins and the error bars indicate the standard errors of the means in each bin. The three lines represent least squares fits to all filtered data as indicated in the legend (see also Table 2).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig3.eps} \vspace*{3mm} \end{figure} Figure 3:

Similar to Fig. 2 for the automatic method, all data 1998-2006 (see Table 13).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig6.eps} \vspace*{5mm} \end{figure} Figure 7:

The north-south asymmetry for the interactive method.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig7.eps} \vspace*{5mm} \end{figure} Figure 8:

The north-south asymmetry for the automatic method.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig8.eps} \vspace*{5mm} \end{figure} Figure 6:

A comparison of the results obtained by the interactive and the automatic method for the 8 selected months during 1998-1999, see also Table 15.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig4.eps} \end{figure} Figure 4:

The low-latitude part of Fig. 3.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13081_fig5.eps} \end{figure} Figure 5:

The high-latitude part of Fig. 3.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.