| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 16 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201014214 | |
| Published online | 17 September 2010 | |
ASOHF: a new adaptive spherical overdensity halo finder
S. Planelles - V. Quilis
Departament d'Astronomia i Astrofísica, Universitat de València, 46100 Burjassot (Valencia), Spain
Received 8 February 2010 / Accepted 24 May 2010
Abstract
We present and test a new halo finder based on the spherical
overdensity (SO) method. This new adaptive
spherical overdensity halo finder (ASOHF) is able to identify dark
matter haloes and their substructures (subhaloes) down to the scales
allowed by the analysed simulations. The code has been especially
designed for the adaptive mesh refinement cosmological codes, although
it can be used as a stand-alone halo finder for N-body codes. It has
been optimised for the purpose of building the merger tree of the
haloes. In order to verify the viability of this new tool, we have
developed a set of bed tests that allows us to estimate the performance
of the finder. Finally, we apply the halo finder to a cosmological
simulation and compare the results obtained to those given by other
well known publicly available halo finders.
Key words: dark matter - large-scale structure of Universe - galaxies: clusters: general - methods: numerical
1 Introduction
In the standard model of structure formation, small systems collapse first and then merge hierarchically to form larger structures. Galaxy clusters, which are at the top of this hierarchy, represent the most massive virialized structures in the universe and may host thousands of galaxies.
Numerical simulations of structure formation are essential tools in theoretical cosmology. During the last years, these simulations have become a powerful theoretical mechanism to accompany, interpret, and sometimes to lead cosmological observations because they bridge the gap that often exists between basic theory and observation. Their main role, in addition to many other uses, has been to test the viability of the different structure formation models, such us, variants of the cold dark matter (CDM) model, by evolving initial conditions using basic physical laws.
Historically, the use of cosmological simulations started in the 1960s (Aarseth 1963) and 1970s (e.g., Peebles 1970; and White 1976). These calculations were N-body collisionless simulations with few particles. Over the last three decades great progress has been made in the development of N-body codes that model the distribution of dissipationless dark matter particles. Besides this numerical progress, computers and computational resources have made such progress that simulations could be applied systematically as scientific tools. Their use led to important results in our knowledge of the Universe.
In addition to the treatment of the collisionless dark component of cosmological structures, hydrodynamical codes designed to describe the baryonic component of the Universe have also been developed, usually coupled with N-body codes.
The generation of the data is only a first step that carries out complex simulations to generate a huge amount of raw information. In the particular case of N-body simulations, the aggregates of millions of dissipationless dark matter particles produced in the simulations require to be interpreted and somehow compared with the observable Universe. To do so, it is necessary to identify the groups of gravitationally bound dark matter particles, which are the dark counterparts of the observable components of the cosmological structures (galaxies, galaxy clusters, etc.). These dark matter clumps are the so-called dark matter haloes, and the task to identify them in simulations is usually carried out with the help of numerical tools known as halo finders.
There are several kinds of halo finders currently widely used. All these halo-finding algorithms seem to perform exceedingly well when they deal with the identification of haloes without substructure. However, the remarkable development of N-body simulations and the applications studied with these new codes necessitated new algorithms able to deal with the scenario of haloes-within-haloes (Klyplin et al. 1999b; Moore et al. 1999; Klyplin et al. 1999a).
Motivated by the importance of working with the halo and subhalo population obtained from simulations, we present a new halo finder called ASOHF (adaptive spherical overdensity halo finder). This finder, based on the spherical overdensity (SO) method, has been especially designed to couple with the outputs of the adaptive mesh refinement (AMR) cosmological Eulerian codes. Taking advantage of the capabilities of the AMR scheme, the algorithm is able to identify dark matter haloes and their substructures (subhaloes) in a hierarchical way limited only by the resolution of the analysed simulation. Additionally, it has been optimised for building the evolutionary merger tree of the haloes. To check the viability of this new tool, we developed a simple set of tests which generates different toy models with properties completely known beforehand. This battery of tests will allow us to calibrate the real accuracy of our finder. Finally, we apply ASOHF to a cosmological simulation and compare the results with those obtained with other publicly available halo-finding algorithms, such as AFoF (van Kampen 1995) and AHF (Knollmann & Knebe 2009).
The present paper is organized as follows. In Sect. 2 we briefly describe several existing halo-finding algorithms tested in the scientific literature. In Sect. 3 we introduce the main properties of the halo finder ASOHF. In Sect. 4 we describe several idealised tests and the results of applying ASOHF to them. In Sect. 5 ASOHF is applied to a cosmological simulation, and the results are compared to those obtained by other halo finders available in the literature. Finally, in Sect. 6, we summarize and discuss our results.
2 Background
Different algorithms to identify structures and substructures in cosmological simulations have been proposed and have seen many improvements over the years. As a consequence, there are several kinds of halo finders currently widely used although, at heart, the basic idea of them all is to identify gravitationally bound objects in an N-body simulation. Let us briefly outline some of the most popular halo finders.
The classical method to identify dark matter haloes is the purely
geometrical friends-of-friends algorithm (FoF) (Davis et al. 1985). This
technique consists in finding neighbours of dark matter particles and
neighbours of these neighbours according to a given linking length
parameter. The characteristic linking length,
![]() ,
is usually
set to
,
is usually
set to ![]() 0.2 of the mean particle separation. The collection of
linked particles forms a group that is considered as a virialized
halo. The mass of the halo is defined as the sum of the mass of all
dark matter particles within the halo. Among the main advantages
of this algorithm we can point out that its results are relatively
easy to interpret and that it does not make any assumption
concerning the halo shape. The greatest disadvantage is its
rudimentary choice of linking length, which can lead to a connection of
two separate objects via the so-called ''linking bridges''. Moreover,
because structure formation is hierarchical, each halo contains
substructure and thus, different linking lengths are needed to
identify ``haloes-within-haloes''. There are several modified
implementations of the original FoF, such as the adaptive FoF (AFoF;
van Kampen 1995) or the hierarchical FoF (HFoF; Klyplin et al. 1999a),
among others, which try to overcome these limitations.
0.2 of the mean particle separation. The collection of
linked particles forms a group that is considered as a virialized
halo. The mass of the halo is defined as the sum of the mass of all
dark matter particles within the halo. Among the main advantages
of this algorithm we can point out that its results are relatively
easy to interpret and that it does not make any assumption
concerning the halo shape. The greatest disadvantage is its
rudimentary choice of linking length, which can lead to a connection of
two separate objects via the so-called ''linking bridges''. Moreover,
because structure formation is hierarchical, each halo contains
substructure and thus, different linking lengths are needed to
identify ``haloes-within-haloes''. There are several modified
implementations of the original FoF, such as the adaptive FoF (AFoF;
van Kampen 1995) or the hierarchical FoF (HFoF; Klyplin et al. 1999a),
among others, which try to overcome these limitations.
The other most general method is the spherical overdensity (SO, Lacey & Cole 1994) that uses the mean overdensity criterion for the detection of virialized haloes. The basic idea of this technique is to identify spherical regions with an average density corresponding to the density of a virialized region according the top-hat collapse. The main drawback of the SO mass definition is that it is somehow artificial, enforcing spherical symmetry on all objects, while in reality haloes often have an irregular structure (White 2002), for example, haloes that were formed in a recent merger event or haloes at high redshifts. Furthermore, defining an SO mass can be ambiguous because the corresponding SO spheres might overlap for two close density peaks. Due to these characteristics, the SO method implies oversimplifications that could lead to unrealistic results and which therefore deserve a careful treatment. Despite these apparently significant disadvantages, one of the most relevant features of this technique is that no linking length is needed to define the structures.
Almost all existing halo finders are based on either the FoF algorithm, the SO, or a combination of both methods.
The DENMAX (Bertschinger & Gelb 1991; Gelb & Bertschinger 1994) and the SKID (Weinberg et al. 1997) algorithms are similar methods. Both of them calculate a density field from the particle distribution, then gradually move the particles in the direction of the local density gradient ending with small groups of particles around each local density maximum. The FOF method is then used to associate these small groups with individual haloes. The difference between the two methods is in the calculation of the density field. DENMAX uses a grid, while SKID applies an adaptive smoothing kernel similar to that employed in SPH techniques (Gingold & Monaghan 1977; Lucy 1977). The effectiveness of these methods is limited by the technique used to determine the density field (Götz et al. 1998).
The HOP method (Eisenstein & Hu 1998) is based on a density field similar to the SKID. However, it uses a different type of particle sliding. The HOP algorithm searches for the maximum density among the n nearest neighbours of a particle and attaches the particle to the densest neighbour. Finally, it groups particles in a local density maximum, defining a virialized halo.
The BDM method (Klyplin et al. 1999a) uses randomly placed spheres with predefined radius, which are iteratively moved to the centre of mass of the particles contained in them until the density centre is found.
Completely different is the VOBOZ technique (Neyrinck et al. 2005), which uses a Voronoi tessellation to calculate the local density.
The halo finder MHF (Gill et al. 2004) took advantage of the grid hierarchy generated by the AMR code MLAPM (Knebe et al. 2001) to find the haloes in a given simulation. In most of the cosmological AMR codes, the grid hierarchy is built in such a way that the grid is refined in high-density regions and hence naturally traces the densest regions. This can be used not only to select haloes, but also to identify the substructure. The AHF (Amiga Halo Finder), which is the direct successor of the original MHF, has been recently presented and tested (Knollmann & Knebe 2009).
Similarly to SKID, in SUBFIND (Springel et al. 2001) the density of each particle is estimated with a cubic spline interpolation. In a first step, the FOF method is used and then any locally overdense region enclosed by an isodensity contour that traverses a saddle point is considered as a substructure candidate. SUBFIND runs on individual simulation snapshots, but can afterwards reconstruct the full merger tree of each subclump by using the subhalo information from previous snapshots. All subhalo candidates are then examined and unbound particles are removed.
A quite different method is provided by the code SURV (Tormen et al. 2004; Giocoli et al. 2008a,2009), which identifies subhaloes within the virial radius of the final host by following all branches of the merger tree of each halo (rather than just the main branch), in order to reconstruct the full hierarchy of substructure down to the mass resolution of the simulation.
The parallel group finder 6DFOF (Diemand et al. 2007,2006)
finds peaks in phase-space density, i.e., it links the most bound
particles inside the cores of haloes and subhaloes together. The same
objects identified by 6DFOF at different times therefore always have
quite a large fraction of particles in common (in most cases over ![]() ). This makes finding progenitors or descendants rather easy.
). This makes finding progenitors or descendants rather easy.
3 The ASOHF halo finder
The halo identification is a crucial issue in the analysis of any cosmological simulation. Inspired by this, we developed a halo finder especially suited for the results of the Eulerian cosmological code MASCLET (Quilis 2004), although it can be easily applied to the outcome of a general N-body code.
The halo finder developed for MASCLET, ASOHF, shares some features with AHF (Knollmann & Knebe 2009), which is the evolution of the original MHF halo finder (Gill et al. 2004). Although we used an identification technique based on the original idea of the SO method, the practical implementation of our finder has several steps designed to improve the performance of this method and to get rid of the possible drawbacks as well as to take advantage of an AMR grid structure.
The particular implementation of our halo finder follows several main steps.
- 1.
- In a first step, the algorithm reads the density field computed on a
hierarchy of grids provided by the simulations. Then the SO method is
applied to each density maximum: radial shells are stepped out around
each density peak until the mean overdensity falls below a given
threshold or there is a significant rising in the slope of the
density profile. The overdensity,
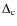 ,
depends on the adopted
cosmological model and can be approximated by the expression
(Bryan & Norman 1998)
,
depends on the adopted
cosmological model and can be approximated by the expression
(Bryan & Norman 1998)
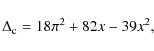
(1)
where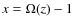 and
and
![$\Omega(z)=[\Omega_{\rm m} (1+z)^3]/ [\Omega_{\rm m}
(1+z)^3 + \Omega_\Lambda]$](/articles/aa/full_html/2010/11/aa14214-10/img9.png) .
Typical values of this contrast are
between 100 and 500, depending on the adopted cosmology.
.
Typical values of this contrast are
between 100 and 500, depending on the adopted cosmology.
Therefore, the virial mass of a halo,
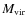 ,
is defined as the
mass enclosed in a spherical region of radius,
,
is defined as the
mass enclosed in a spherical region of radius,
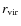 ,
with an
average density
,
with an
average density
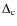 times the critical density of the Universe
times the critical density of the Universe
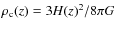
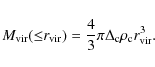
(2)
This first step, which only defines the scale of the objects we are looking for, provides a crude estimation of the position, radius and mass for each detected halo.
- 2.
- The second step takes care of possible overlaps among the preliminary haloes found in the first step. In our method, if two haloes overlap and the shared mass is larger than the 80% of the minimum mass of the implicated haloes, the less massive of them is removed from the list. On the other hand, if the shared mass is between the 40% and the 80% of the minimum mass of the haloes, the algorithm joins these haloes and computes the centre of mass of the new halo. Consequently, it removes the less massive halo from the list, and applies again the first step to the new centre of mass to obtain the physical properties of the new halo. In the end, this step provides a final number of haloes.
- 3.
- Once we have a tentative halo selection, a third step provides a more accurate sample by working only with the dark matter particles within each halo. These particles are distributed through the complete simulated volume and are not limited by cell boundaries. ASOHF can deal with several particles species (particles with different masses), providing therefore a best-mass resolution. This step is crucial to obtain a precise estimation of the main physical properties of the haloes, particularly, a new prediction for the mass and position of the centre of mass.
- 4.
- Once centres of potential haloes are found, the code checks if all particles contained in a halo are bound. It finds the final properties and the radial structure of all haloes in the same way as in the first step, but now working only with the particles. It places concentric shells around each centre and for each shell it computes the mass of the dark matter particles, the mean velocity, and the velocity dispersion relative to the mean. In order to determine whether a particle is bound or not, the code estimates the escape velocity at the position of the particles (Klyplin et al. 1999a). If the velocity of a particle is higher than the escape velocity, the particle is assumed to be unbound and is therefore removed from the halo considered. This pruning is halted when a given halo holds fewer than a fixed minimum number of particles or when no more particles need to be removed.
- 5.
- The process finishes when it verifies that the radial density profile
of the haloes is consistent with the functional form proposed by NFW
(Navarro et al. 1997) in the range from twice the force resolution to
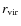
![\begin{displaymath}\rho (r)= \frac{\rho_0}{(r/r_{\rm s})^{\alpha} [1+(r/r_{\rm s})]^{\beta}} ,
\end{displaymath}](/articles/aa/full_html/2010/11/aa14214-10/img14.png)
(3)
where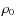 is the normalization,
is the normalization, 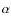 and
and 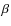 are the
inner and outer slopes respectively, and
are the
inner and outer slopes respectively, and 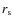 is the scale radius.
The virial and the scale radius are related through
the concentration parameter
is the scale radius.
The virial and the scale radius are related through
the concentration parameter
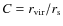 .
.
Note that this method is completely general and easily applicable to any N-body code, assuming the density field is previously evaluated on a grid or set of nested grids.
3.1 Substructure
Substructures within haloes are usually defined as locally overdense self-bound particle groups identified within a larger parent halo.
In our analysis, the process of halo-finding outlined above can be performed independently at each level of refinement of the simulation. Then our halo finder can trace haloes-in-haloes in a natural way obtaining a hierarchy of nested haloes. Moreover, it is able to find several levels of substructure within substructure. This property allows us to take advantage of the high spatial resolution provided by the AMR scheme, identifying a wide variety of objects with very different masses and scales.
Still, due to this procedure and to the nature of the AMR grid, this technique could mix real substructures and overlapping haloes. In order to deal with possible misidentifications of subhaloes, we need to implement an extra mechanism.
Let us consider two haloes from two different but consecutive
refinement levels, h1 (lower level and, hence, lower
resolution) and h2 (upper level and, therefore, higher spatial
resolution), with masses m1 and m2, radii r1 and r2, and
the velocity of the centre of mass equal to
![]() and
and
![]() ,
respectively. In our method, these haloes are considered
as host halo (lower level) and subhalo (upper level), respectively, if
they satisfy the conditions
,
respectively. In our method, these haloes are considered
as host halo (lower level) and subhalo (upper level), respectively, if
they satisfy the conditions
- 1.
-
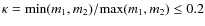
- 2.
-
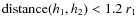
- 3.
- h2 gravitationally bound to h1.
On the other hand, given the structure of nested grids generated by the AMR scheme, it is possible that sometimes the same halo would be identified more than once in different levels with centres slightly shifted in position. To capture these duplicates, a similar criterion to that used for the substructures is used, but now with the conditions
- 1.
-
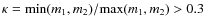
- 2.
-
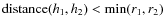
- 3.
-
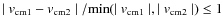 .
.
At this point, substructures are defined only on the different levels of the grid. These levels have been defined and established by the assumed refining criteria which can be fixed by the evolution, when the outputs are directly imported from a code like MASCLET, or by any other criteria, like the number of particles per cell, when ASOHF works as a stand-alone code. Thus, ASOHF is able to find substructures and assign masses to them with a good accuracy throughout most of the host halo and is only limited by the existence of refinements in the computational grid.
Once the code has acted on the different levels of resolution of the considered grid, it obtains a single halo sample classifying all the haloes in three categories according to their nature: single haloes (with or without significant substructures), subhaloes (belonging to single haloes) and poor haloes (in our method these are haloes with less than a fixed number of dark matter particles, e.g. 50, or haloes that are a misidentification of other haloes). Thus, it is possible to obtain a complete sample of objects with very different masses and scales, ranging from the biggest haloes down to the minimum scales imposed by the resolution of the analysed simulations.
One of the main advantages of our method is that the hierarchy of nested grids used by the AMR cosmological simulations is built following the density peaks, and therefore these grids are already suitably adjusted to track the dark matter haloes. Last but not least the use of AMR grids implies that we need no longer define a linking length.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14214fg1.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg27.png)
|
Figure 1: Flowchart for ASOHF. In this diagram, NL stands for the total number of analysed AMR grid levels. NH ad NH' represent the total number of tentative and final found haloes, respectively. |
| Open with DEXTER | |
3.2 Merger tree
Dark matter haloes and their mass assembly histories are essential
pieces of any non-linear structure formation theory based on the
![]() CDM model. Yet the construction of a merger tree from
the outputs of an N-body simulation is not a trivial matter. We
included in the halo finder programme a routine that is able to obtain
the evolution history of each one of the found haloes. The method of
progenitor identification is based on the comparison of lists of
particles belonging to the haloes at different moments both backwards and
forwards in time, i. e., it tracks the history of all dark matter
particles belonging to a given halo at a given epoch. This procedure
is repeated backwards in time until the first progenitor of the
considered halo is reached. This mechanism allows us not only to
know all progenitors of each halo, but also the amount of mass received
from each one of its ancestors.
CDM model. Yet the construction of a merger tree from
the outputs of an N-body simulation is not a trivial matter. We
included in the halo finder programme a routine that is able to obtain
the evolution history of each one of the found haloes. The method of
progenitor identification is based on the comparison of lists of
particles belonging to the haloes at different moments both backwards and
forwards in time, i. e., it tracks the history of all dark matter
particles belonging to a given halo at a given epoch. This procedure
is repeated backwards in time until the first progenitor of the
considered halo is reached. This mechanism allows us not only to
know all progenitors of each halo, but also the amount of mass received
from each one of its ancestors.
This mechanism can be applied to build the merging history tree of either the haloes or the subhaloes of the simulation.
This procedure is very useful when we are interested in an exhaustive analysis of all the linking relations among the haloes, for example, when we want to analyse mergers or collisions between two or more haloes, or when we are interested in following the history of individual haloes as well as different processes of halo disruption.
However, sometimes we are only interested in the main branch of the merger tree of each halo, or in other words, in a ``simplified'' merger tree. In order to have a quick estimate of the history of the main branch we included a reduced merger tree routine in the halo finder which, instead of following all particles of the haloes, looks only for the closest particle to the centre of each halo. This particle, which is supposed to be the most bound particle in the halo, is followed backwards in time until the first progenitor of the considered halo is found. With this method, each parent halo is allowed to have only one descendant.
The ASOHF method is summarized in Fig. 1, where a flowchart of the main process is shown.
3.3 Halo shapes
In ASOHF code the shape of the haloes is evaluated by approximating
their mass distribution by a triaxial ellipsoid. The axes of inertia
of the different haloes and subhaloes are evaluated from the tensor of
inertia (see e.g. Shaw et al. 2006; Cole & Lacey 1996):
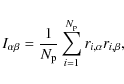
|
(4) |
where the positions ri are given with respect to the centre of mass and the summation is over all particles in the halo (
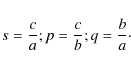
|
(5) |
An additional measure for the shape of the ellipsoid is the triaxiality parameter (Franx et al. 1991),
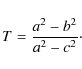
|
(6) |
An ellipsoid is considered oblate if 0<T<1/3, triaxial with 1/3<T<2/3, and prolate if 2/3<T<1.
4 Testing the halo finder
Before using the ASOHF finder in real cosmological applications, we have to be sure that it provides accurate and credible results. In order to validate and assess the robustness of our method, we developed a set of tests that will allow us to quantify the uncertainty of the halo finder algorithm and to check the properties of the haloes found with it.
In these tests we build mock distributions of dark matter particles, made by hand, resembling real outputs of cosmological simulations. Therefore, we have perfectly known distributions of dark matter particles forming a given number of cosmological structures with physical parameters completely known. Once these distributions are built, we apply the halo finder and compare the results obtained with the ones originally adopted to create the mock distributions by hand.
The different numerical implementations presented in this section
were performed assuming the following cosmological parameters: matter
density parameter,
![]() ;
cosmological constant,
;
cosmological constant,
![]() ;
baryon density parameter,
;
baryon density parameter,
![]() ;
reduced Hubble constant, h=H0/100 km s-1 Mpc
-1=0.73; power spectrum index,
;
reduced Hubble constant, h=H0/100 km s-1 Mpc
-1=0.73; power spectrum index,
![]() ;
and power
spectrum normalization,
;
and power
spectrum normalization,
![]() .
.
The set of tests was designed to help us check different aspects of interest in cosmological simulations: i) test 1 and test 2 are focussed in looking for and characterizing single haloes and subhaloes, respectively; ii) test 3 builds the merger trees of haloes; and iii) test 4 analyses big samples of haloes.
All cases considered in this section were placed in a comoving volume of 100 h-1 Mpc on a side. The computational box has been discretised with 2563 cubical cells. All our modelled haloes will be spherical, with a given dark matter density profile, mass, and radius. From now on, these artificial or modelled haloes will be called template haloes.
Depending on the test we are analysing, we need to define the number
of template haloes we want to study, the number of time outputs
(different redshifts we look at), as well as the total number of dark
matter particles to be used. The total number of particles must be
conserved during the whole evolution to guarantee mass conservation,
and it must be chosen as a compromise between having a good resolution
in mass for each halo and the computational cost. In the particular
implementation of all tests presented in this section we
assumed for simplicity's sake, equal mass dark matter particles with
masses
![]() .
.
4.1 Test 1: looking for single haloes
The first test presented is designed to check the ability of the halo finder to look for single haloes and compute their main physical properties at a given redshift: position, mass, and radius. To achieve this we generate an artificial sample of haloes with different numbers of dark matter particles, and with positions, virial radii, and virial masses fixed by hand. Then the halo finder is applied to this mock universe to verify whether the detected haloes agree with those previously made by hand.
Table 1: Mean features of the generated haloes at z=0 in test 1.
Let us describe the method to generate these artificial haloes. Assuming some general features (cosmological parameters, number of time steps, number of desired haloes and total number of particles), the properties of the haloes that populate each time step are made by hand: the number of dark matter particles within each halo (and hence, their masses) and the coordinates of their centres. With this information and the cosmological parameters the average density corresponding to a given epoch as well as the virial radius from Eq. (2) of the haloes are computed. Once the main physical properties of the haloes have been defined, each halo is created by a random distribution of dark matter particles - using the rejection sampling method (von Neumann 1951) -, in a way that its density profile is consistent with a NFW profile (Navarro et al. 1997).
In this subsection we present a case characterized by the usual
cosmological parameters and with ![]() 105 dark matter particles in a
unique time step corresponding to z=0. For this test we
generated four dark matter haloes with density profiles compatible
with NFW, in the way explained before. The main properties of
these mock haloes are summarized in Table 1.
105 dark matter particles in a
unique time step corresponding to z=0. For this test we
generated four dark matter haloes with density profiles compatible
with NFW, in the way explained before. The main properties of
these mock haloes are summarized in Table 1.
![\begin{figure}
\par\includegraphics[width=12.2cm]{14214fg2.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg48.png)
|
Figure 2: Radial dark matter density profiles for the four generated haloes compiled in Table 1 as a function of the radius at z=0 (test 1). Continuous lines stand for the input profiles of the mock haloes, whilst points represent the profiles obtained by the halo finder. |
| Open with DEXTER | |
The ASOHF halo finder was applied to this mock simulation. The
mean relative errors found in the computation of the positions and
radii are of the order of ![]() .
The masses are perfectly
recovered because all particles forming the halo are identified. Note
that although the results seem excellent, they correspond to
an extremely idealised test.
.
The masses are perfectly
recovered because all particles forming the halo are identified. Note
that although the results seem excellent, they correspond to
an extremely idealised test.
In Fig. 2 we plot the radial density profiles used as input to generate - using the rejection method - the haloes (continuous line) and the obtained profiles (dots). These last profiles were computed by averaging the dark matter density in spherical shells of a fixed logarithmic width.
We fitted a NFW density profile to each one of the obtained
profiles. The concentration, inner and outer slopes are shown in
Table 1, respectively. In Col. 7 of this Table, we present
the concentration obtained from the fitting together with the
concentration of the density profile used as input (between
parenthesis). For the inner (outer) slope of the density
profile that we denoted by ![]() (
(![]() ), the fitted value
must be compared with 1.0 (2.0), which corresponds to the value
adopted in the input profile.
), the fitted value
must be compared with 1.0 (2.0), which corresponds to the value
adopted in the input profile.
We checked that the errors encountered for the fitted profiles are mostly caused by the rejection sampling method. In this line we tested that the sampling of an input density profile with the rejection method produces particle distributions that trace the underlying density profile with a precision of a few per cent. Therefore, when the halo finder finds a halo and obtains its density profile, there is also a small error when compared with the input density profile. But it must be kept in mind that this error does not arise from the halo finder algorithm itself but from the way that this particular test has been set up.
Although this test is very simple, because it only considers four haloes in a single time step, it provides us with a powerful tool to verify the behaviour of our finder in a very basic situation. We checked many other configurations (some of them really unrealistic) with similar results. Due to its clarity and simplicity we have chosen this one to demonstrate our objective.
4.2 Test 2: looking for subhaloes
![\begin{figure}
\par\includegraphics[width=15.5cm]{14214fg3.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg50.png)
|
Figure 3: Mock distribution of a halo with three substructures: two subhaloes and one sub-subhalo (test 2). The left panel shows the 2D projection of the structures found by ASOHF. Circles represent the radii of the different structures, while the different line types stand for the different refinement levels in which the haloes have been found. The right panel shows the known distribution of dark matter particles in this test. Different colours stand for the level to which the particles belong. |
| Open with DEXTER | |
In this section we present a simple test that was designed to check the ability of ASOHF to deal with substructures.
Following the idea of test 1, we generated by hand a simple distribution of haloes placed in different levels of resolution of a very basic AMR grid similar to that of the MASCLET code. For the sake of simplicity, only three levels of refinement (the ground grid and two upper levels) were considered. The hierarchy of structures and substructures generated for this test are distributed according to these levels.
Among all configurations that we tried for this test, we chose because of its clarity a simple one in which four structures are considered: a big dark matter halo in the coarse level hosting two subhaloes where at the same time one of these subhaloes hosts a smaller subhalo, which is a sub-subhalo of the big one.
Figure 3 shows the configuration analysed in this test. A visual inspection of this plot shows that the halo finder also works properly when dealing with substructures located in different levels of an AMR grid.
Additionally, the mean relative errors given by ASOHF
in the estimation of the main properties of the generated
structures are of the order of
![]() ,
,
![]() and
and ![]() for the mass,
position, and radius, respectively.
This value together with a visual inspection of
Fig. 3 is an excellent indicator of the good performance of
ASOHF when working with structures that contain different substructures,
at least in a simple configuration like the one considered here.
for the mass,
position, and radius, respectively.
This value together with a visual inspection of
Fig. 3 is an excellent indicator of the good performance of
ASOHF when working with structures that contain different substructures,
at least in a simple configuration like the one considered here.
Because this configuration is very basic, we check this situation in Sect. 5 for a proper cosmological simulation and compare the results obtained by ASOHF with those obtained by other well known halo finders.
4.3 Test 3: testing the merger tree
Once we checked that the ASOHF finder works properly when it looks for single haloes and subhaloes, we checked how well it computes the merger tree for each.
In this section we consider several configurations characterized by the same parameters as in the previous ones, but with more than one time step. Now the idea is to generate a given number of haloes, in the simple way explained before, but forcing different time evolutions of these haloes.
We are interested in studying the most common events in the evolution of dark matter haloes: i) relaxed or isolated evolution, i.e., without important interactions or mergers with other haloes (case I); ii) ruptures or disruptions of a single halo into two or more smaller haloes owing mainly to interactions with the environment or with other haloes (case II); and iii) mergers between two or more haloes (case III). To do this we chose four haloes at a given redshift which are those compiled in Table 1, and studied their evolution in the three different cases that have into account in a simple way the most common events explained before. Then, ASOHF is applied to these artificial evolutions to compare the obtained merger trees with the generated ones.
Again, for the sake of simplicity and brevity, a reduced number of haloes will be considered, but note that more complicated configurations were studied and can be easily implemented.
Figure 4 shows the merger trees obtained by ASOHF in the different cases considered here. The top panel of Fig. 4 shows the complete merger tree obtained for the four haloes studied in each of the three cases presented here. In the bottom panel of the same figure, the same cases are represented but following only the closest particle to the centre of each halo (reduced merger tree).
The line segments joining the circles in Fig. 4 are a relevant feature of the plot because they indicate that the halo at the earlier time is considered to merge into (or to be identical to) the halo at the later time. Moreover, in the upper panel the different line types represent the percentage of mass that goes from one halo to another. Thus, a halo at later time connected with a halo at earlier time by a dash-dotted line means that up to 25% of its total mass comes from that halo at earlier time. The same idea applies to the other line types.
The horizontal axis is designed to separate the haloes according to their future merging activity. It does not directly indicate space positions, although there should be some correlation between how close two haloes are in the plot and how close they are in space (because haloes need to be close to merge later on). The vertical axis shows the redshift of each time step in the simulation. The size of each circle indicates the virial mass of each halo normalized to its final mass at the last iteration. Because the iterations go in descending order, the last iteration corresponds to the lowest redshift.
The different cases analysed in this section and their representation in Fig. 4 are discussed in detail in the subsections below.
![\begin{figure}
\par\includegraphics[height=14cm]{14214fg4.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg53.png)
|
Figure 4: Merger trees for several haloes in the three different cases analysed in Sect. 4.3 (test 3). Left, central, and right panels stand for case I, II, and III, respectively. The top panels represent the results obtained following all dark matter particles within each halo (complete merger tree), whereas the bottom panels stand for the results obtained following only the closest particle to the centre of each halo (reduced merger tree). Haloes are represented by circles whose sizes are normalized to the final mass at z=0. The different line types connecting haloes at different times in the upper plots indicate the amount of mass transferred from the progenitors to their descendants. |
| Open with DEXTER | |
4.3.1 Case I
In this first case, we study the most trivial situation. Only two time
steps corresponding to
![]() and
and
![]() are
considered. The objective is that the four haloes generated at
are
considered. The objective is that the four haloes generated at
![]() would be exactly the same as those at
would be exactly the same as those at
![]() .
The
selection of the redshifts is made in order to obtain a fast evolution
of the haloes, but it is possible to make it for time steps much more
realistic and separated in time. In any case, this selection is not
relevant to achieve our objective, which is to check the performance of the
halo finder computing the merger tree of a given halo, i.e., following
the particles that belong to a halo at a given epoch through the
evolution.
.
The
selection of the redshifts is made in order to obtain a fast evolution
of the haloes, but it is possible to make it for time steps much more
realistic and separated in time. In any case, this selection is not
relevant to achieve our objective, which is to check the performance of the
halo finder computing the merger tree of a given halo, i.e., following
the particles that belong to a halo at a given epoch through the
evolution.
The haloes at different epochs are generated in the way explained above. In this particular case, we force that the four considered haloes at both epochs would be identical, i.e., with the same particles in each one and with the same radius and position of the centre.
In order to be as clear as possible when talking about haloes at different epochs, we will use the notation hij, where istands for the iteration number (iterations in descendant order and then corresponding the iteration or time step 1 to the lowest redshift) and j for the halo number in the iteration i, respectively.
According to this notation, the generated relations between the haloes in this case are

-
![$h_{21} \Longrightarrow h_{11} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img57.png)

-
![$h_{22} \Longrightarrow h_{12} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img58.png)

-
![$ h_{23} \Longrightarrow h_{13} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img59.png)

-
![$h_{24} \Longrightarrow h_{14} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img60.png) .
.
We applied the halo finder to this artificial evolution and constructed the merger tree of the selected haloes tracking all dark matter particles for a given halo backwards in time. For each halo in this case, two merger trees, the complete and the reduced one, have been built. The left panels of Fig. 4 show the obtained results. The upper-left plot of this figure shows the complete merger tree for the considered haloes, whereas the lower-left plot represents the reduced merger tree for the same haloes.
According to these plots it is evident that for case I the halo finder tracks the correct history for all considered haloes.
Additionally, the connection lines linking the haloes at different
redshifts in the complete merger tree inform us about the percentage
of mass that each younger halo receives from its progenitors. In
this particular case, this percentage is in all cases greater than
![]() ,
in perfect agreement with the expected results (
,
in perfect agreement with the expected results (![]() ).
More precisely, the obtained results are
).
More precisely, the obtained results are

-
![$h_{21} \Longrightarrow h_{11} [99.97\%]$](/articles/aa/full_html/2010/11/aa14214-10/img64.png)

-
![$h_{22} \Longrightarrow h_{12} [99.98\%]$](/articles/aa/full_html/2010/11/aa14214-10/img65.png)

-
![$h_{23} \Longrightarrow h_{13} [99.99\%]$](/articles/aa/full_html/2010/11/aa14214-10/img66.png)

-
![$h_{24} \Longrightarrow h_{14} [99.99\%]$](/articles/aa/full_html/2010/11/aa14214-10/img67.png) .
.
4.3.2 Case II
In this case we are interested in checking the capabilities of the halo finder when some haloes suffer one or several disruptions during their evolution, when they lose mass and reduce their size. This process operates at two regimes for different reasons. This is quite common in very small size haloes. The reason is that these haloes are not really gravitationally well bound and can easily be disrupted by interactions with environment or with other haloes. For larger haloes, those mass losses are smaller and they are usually associated with tidal interactions.
To study this case we started at
![]() with the four haloes
summarized in Table 1. Now, three time steps of the haloes
evolution corresponding to
with the four haloes
summarized in Table 1. Now, three time steps of the haloes
evolution corresponding to
![]() ,
,
![]() and z=0 are
considered. The results of this situation are shown in the middle
panels (top and bottom) of Fig. 4.
and z=0 are
considered. The results of this situation are shown in the middle
panels (top and bottom) of Fig. 4.
Here the generated evolutions can be summarized in the
following relations. In a first step, the connections between the
haloes of the third (
![]() )
and the second (
)
and the second (
![]() )
iterations are
)
iterations are

-
![$h_{31} \Longrightarrow h_{21} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img68.png)

-
![$h_{32} \Longrightarrow h_{22} [100\%] ,
h_{23} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img69.png)

-
![$h_{33} \Longrightarrow h_{24} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img70.png)

-
![$h_{34} \Longrightarrow h_{25} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img71.png) .
.

-
![$h_{21} \Longrightarrow h_{12} [100\%] ,
h_{14} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img72.png)

-
![$h_{22} \Longrightarrow h_{11} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img73.png)

-
![$ h_{23} \Longrightarrow h_{13} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img59.png)

-
![$h_{24} \Longrightarrow h_{16} [100\%] ,
h_{18} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img74.png)

-
![$h_{25} \Longrightarrow h_{15} [100\%] ,
h_{17} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img75.png) .
.
After building these artificial evolutions, ASOHF was applied to this mock universe to obtain the merger trees of the involved haloes.
As we can see in the upper-middle plot (case II) of Fig. 4, the halo finder again provides very accurate
results, in perfect agreement with those exposed before. In all
cases the obtained percentages are between ![]() and
and ![]() .
Again, the value of the percentages can be explained if we take into
account that each halo has been populated with particles randomly
placed. Then, the particles positions are not always the same and
small deviations are expected.
.
Again, the value of the percentages can be explained if we take into
account that each halo has been populated with particles randomly
placed. Then, the particles positions are not always the same and
small deviations are expected.
If we compare the upper-middle plot of Fig. 4 (complete merger tree) with the lower-middle plot (reduced merger tree), the results completely agree but in the lower plot each halo is only allowed to have one descendant at maximum.
4.3.3 Case III
Here the response of the halo finder in a merger between two or more haloes is checked.
To analyse this, we started again with the same haloes and time
steps as before. Now, the different evolutions can be
summarized with the following links. In a first step the connections
between the haloes of the third (
![]() )
and the second
(
)
and the second
(
![]() )
iterations are (the same as in the previous case)
)
iterations are (the same as in the previous case)

-
![$h_{31} \Longrightarrow h_{21} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img68.png)

-
![$h_{32} \Longrightarrow h_{22} [100\%] ,
h_{23} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img69.png)

-
![$h_{33} \Longrightarrow h_{24} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img70.png)

-
![$h_{34} \Longrightarrow h_{25} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img71.png) .
.

-
![$h_{21}+h_{24}+h_{25} \Longrightarrow h_{12}
[74.49\% + 9.48\% + 16.03\%]$](/articles/aa/full_html/2010/11/aa14214-10/img77.png)

-
![$h_{22} \Longrightarrow h_{11} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img73.png)

-
![$ h_{23} \Longrightarrow h_{13} [100\%]$](/articles/aa/full_html/2010/11/aa14214-10/img59.png) .
.
From the right panels of Fig. 4 (top and bottom plots), we can deduce that despite the triple merger that has taken place in the last time step, the halo finder provides very accurate results. Indeed, the results obtained for this merger event are

-
![$h_{21}+h_{24}+h_{25} \Longrightarrow h_{12}
[74.45\% + 9.45\% + 16.08\%]$](/articles/aa/full_html/2010/11/aa14214-10/img78.png) ,
,
4.4 Test 4: analysing a sample of haloes
![\begin{figure}
\par\includegraphics[height=10cm]{14214fg5.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg79.png)
|
Figure 5: Top panel: academic mass function corresponding to the generated sample of 100 haloes for test 4. Dots represent the mass function obtained by ASOHF, whereas the continuous line corresponds to the function generated by hand. Bottom panel: relative error or difference in mass between the two distributions shown in the upper plot. |
| Open with DEXTER | |
The analysis of big samples of haloes is crucial in cosmological applications. Therefore, once we checked the halo finder works correctly looking for single haloes and constructing their merger trees, we should check what its response is when working with a large sample of haloes and computing all their properties. Once this sample of haloes is built, an academic mass function, i.e., the mass distribution of all the generated haloes, is computed.
For the sake of simplicity, only one time step corresponding to
z=0 was considered. Then a sample of 100 haloes with
masses randomly distributed between
![]() and
and
![]() ,
was generated. The position of the
centre and the radius of each halo are obtained randomly, whereas the
number of particles belonging to each one of them is derived from
their masses.
,
was generated. The position of the
centre and the radius of each halo are obtained randomly, whereas the
number of particles belonging to each one of them is derived from
their masses.
Once this mock universe was generated, the ASOHF finder was applied. Then the academic mass function of the well known distribution of haloes is compared with the mass function of the sample of haloes obtained by ASOHF.
The results obtained in this case are shown in Fig. 5, in which the number of objects of a given
mass is plotted as a function of the mass. This plot shows the
theoretical or academic mass function (continuous line) and the one
obtained by ASOHF (filled dots). As we can see, these two
distributions are almost completely superposed. As a proof of the
precision of the finder we can compare the masses of the most and less
massive haloes of the sample obtained by the two methods. Thus, the
most massive halo found by the finder has a mass of
![]() ,
whereas this halo was supposed to have a
mass of
,
whereas this halo was supposed to have a
mass of
![]() .
The same occurs for the less
massive halo, which was found by the finder to have a mass of
.
The same occurs for the less
massive halo, which was found by the finder to have a mass of
![]() ,
whereas it was supposed to have a mass of
,
whereas it was supposed to have a mass of
![]() .
In addition, as we can see in the
bottom panel of Fig. 5, the maximum value of
the relative error in mass between the theoretical and the obtained
mass functions is
.
In addition, as we can see in the
bottom panel of Fig. 5, the maximum value of
the relative error in mass between the theoretical and the obtained
mass functions is ![]()
![]() .
.
5 Comparison with other halo finders
In this section we compare the results of ASOHF with two other halo-finding mechanisms, namely AFoF (van Kampen 1995) and AHF (Knollmann & Knebe 2009). We applied these three halo finders to a cosmological simulation carried out with the cosmological code MASCLET. The main properties of this simulation are explained below.
For the AFoF run, a linking length of 0.16 times the mean DM
particle separation was used, yielding an overdensity at the
outer radius comparable to the virial overdensity used in the ASOHF
run. This linking length is obtained when scaling the standard
linking length of 0.2 by
![]() according to
the adopted cosmology (Eke et al. 1996).
according to
the adopted cosmology (Eke et al. 1996).
For the run with AHF, we used a value of 5 for the parameters with regard to the refinement criterion on the domain grid (DomRef) and on the refined grid (RefRef), respectively. To understand the role of these parameters we need to explain briefly how AHF operates. Once the user has provided the particle distribution, the first step in AHF consists in covering the whole simulation box with a regular grid of a user-supplied size. In each cell the particle density is calculated by means of a triangular shaped cloud (TSC) weighting scheme (Hockney & Eastwood 1988). If the particle density exceeds a given threshold (the refinement criterion on the domain grid, DomRef), the cell is refined and covered with a finer grid with half the cell size. On the finer grid (where it exists), the particle density is recalculated in every cell and then each cell exceeding another given threshold (the refinement criterion on refined grids, RefRef) is refined again. This is repeated until a grid is reached on which no further cell needs to be refined. Following this procedure yields a grid hierarchy constructed in a way that it traces the density field and can then be used to find haloes and subhaloes in a similar way to that used by ASOHF.
In all the runs, an equal minimum number of dark matter particles per halo was considered. This number has been set to 50 particles per halo. In spite of this consideration, we expect some differences in the final results obtained with the different halo finders. The main explanation for these expected discrepancies has to do with the different techniques used by the three methods in the generation of the density field and hence in the definition of the haloes. However, general properties of the simulation should be well described by the three finders.
5.1 Simulation details
The simulation described here was performed with the cosmological code MASCLET (Quilis 2004). This code couples an Eulerian approach based on high-resolution shock capturing techniques for describing the gaseous component with a multigrid particle mesh N-body scheme for evolving the collisionless component (dark matter). Gas and dark matter are coupled by the gravity solver. Both schemes benefit by using an AMR strategy, which permits them to gain spatial and temporal resolution.
The numerical simulation was performed assuming a spatially flat
![]() CDM cosmology with the following cosmological parameters:
matter density parameter,
CDM cosmology with the following cosmological parameters:
matter density parameter,
![]() ;
cosmological constant,
;
cosmological constant,
![]() ;
baryon density parameter,
;
baryon density parameter,
![]() ;
reduced Hubble constant, h=H0/100 km s-1 Mpc
-1=0.73; power spectrum index,
;
reduced Hubble constant, h=H0/100 km s-1 Mpc
-1=0.73; power spectrum index,
![]() ;
and power spectrum
normalization,
;
and power spectrum
normalization,
![]() .
The initial conditions were set up at
z=50, using a CDM transfer function from Eisenstein & Hu (1998) for a cube
of a comoving side length
47 h-1 Mpc. The computational
domain was discretised with 2563 cubical cells.
.
The initial conditions were set up at
z=50, using a CDM transfer function from Eisenstein & Hu (1998) for a cube
of a comoving side length
47 h-1 Mpc. The computational
domain was discretised with 2563 cubical cells.
This simulation uses a maximum of six levels of refinement, which
gives a peak spatial resolution of 3 h-1 kpc. For the dark
matter two particles species were considered to be the best mass
resolution ![]()
![]() ,
equivalent to
distribute 2563 particles in the whole box.
,
equivalent to
distribute 2563 particles in the whole box.
Table 2: General results obtained by ASOHF, AFoF and AHF at z=0.
![\begin{figure}
\par\includegraphics[height=100mm]{14214fg6.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg98.png)
|
Figure 6: Top panel: comparison of the mass functions obtained by ASOHF, AHF and AFoF at z=0. The mass function predicted by Sheth & Tormen is also shown. Bottom panel: relative difference in the number of haloes between AFoF and AHF compared to ASOHF. |
| Open with DEXTER | |
5.2 Halo mass function
![\begin{figure}
\par\includegraphics[height=90mm]{14214fg7.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg99.png)
|
Figure 7:
2D projection for haloes
at z=0. Only haloes with masses above
|
| Open with DEXTER | |
Here we present the sample of haloes obtained from the cosmological simulation by the three halo finders used in the present study, namely ASOHF, AFOF and AHF. Their main properties and differences are discussed.
The three halo finders obtained a relatively large sample of galaxy
clusters and groups spanning an approximated range of masses from
![]() to
to
![]() .
The total number of structures identified by ASOHF, AFoF, and AHF has
been 1339, 7448, and 1712, respectively. Although the numbers
and masses of the detected haloes are roughly consistent, they are, as
expected, slightly different among them.
These results are more
similar between ASOHF and AHF, whereas AFoF identifies more smaller
haloes.
.
The total number of structures identified by ASOHF, AFoF, and AHF has
been 1339, 7448, and 1712, respectively. Although the numbers
and masses of the detected haloes are roughly consistent, they are, as
expected, slightly different among them.
These results are more
similar between ASOHF and AHF, whereas AFoF identifies more smaller
haloes.
To analyse the simulation mass function, we restricted ourselves
to study the best-resolved haloes, that is those haloes with masses
above
![]() .
The number of haloes with masses above this limit and
the maximum and minimum masses (in all the sample) of the found haloes
by the different halo finders are summarized in Table 2. The
obtained results by the three finders, although very similar, are not
exactly the same. This was expected because each halo finder uses
different approximations and techniques. ASOHF
uses the grid hierarchy generated by the cosmological simulation
itself, whereas AHF has to construct a new set of grids with different
criteria because only a list of particles is provided to
them which is consequently not identical with that used by ASOHF.
.
The number of haloes with masses above this limit and
the maximum and minimum masses (in all the sample) of the found haloes
by the different halo finders are summarized in Table 2. The
obtained results by the three finders, although very similar, are not
exactly the same. This was expected because each halo finder uses
different approximations and techniques. ASOHF
uses the grid hierarchy generated by the cosmological simulation
itself, whereas AHF has to construct a new set of grids with different
criteria because only a list of particles is provided to
them which is consequently not identical with that used by ASOHF.
In Fig. 6 we compare the mass functions at z=0 of the simulation as obtained by the different halo finders in this study. We also present a comparison with the mass function proposed by Sheth & Tormen (1999) (ST).
![\begin{figure}
\par\includegraphics[height=150mm]{14214fg8.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg103.png)
|
Figure 8:
Distribution of
the halo shapes at z=0 as found by ASOHF ( left panels)
and AHF ( right panels), respectively. Only haloes with masses above
|
| Open with DEXTER | |
The obtained mass functions show a considerable dispersion mainly in
the lower limit of mass compared with the ST prediction. Note though
that the theoretical mass function proposed by ST has
been calibrated using an overdensity of
![]() (Tormen 1998), whereas in our case this overdensity is
(Tormen 1998), whereas in our case this overdensity is ![]() 374.
The bottom panel of Fig. 6 displays the
relative deviation of the mass functions obtained by AFoF and AHF
with respect to the results produced by ASOHF. Hence, a positive deviation
means that the ASOHF run found more haloes in the given bin than the
halo finder it is compared with. Generally speaking, we find good agreement
between the three mass functions, although ASOHF and AHF results
exhibit a better resemblance, which is expected because the
similarities of both methods.
374.
The bottom panel of Fig. 6 displays the
relative deviation of the mass functions obtained by AFoF and AHF
with respect to the results produced by ASOHF. Hence, a positive deviation
means that the ASOHF run found more haloes in the given bin than the
halo finder it is compared with. Generally speaking, we find good agreement
between the three mass functions, although ASOHF and AHF results
exhibit a better resemblance, which is expected because the
similarities of both methods.
Let us point out that the dispersion of the mass function when compared with the reference mass function (ST) is a well known issue. We stress that is out of the scope of this paper to discuss how representative the considered simulation is. Instead, we use this simulation to test whether the different halo finders produce similar results. In this sense, we emphasize that the three algorithms compared agree very well.
For the sake of completeness, we mention that the dispersion of the mass function is a complex topic that is abundantly discussed in the literature. A few examples, among many others, could be: i) the work by Reed et al. (2007), where the authors study the dispersion of the mass function for several simulations depending on the redshift; ii) the results of the GIMIC project (Crain et al. 2009), where an important dispersion in the mass function is shown depending on the considered region; and iii) the dispersion of the mass function found by Yaryura et al. (2010) related with very large structures.
From now on, we restrict ourselves to analyse only the main differences between the AHF and the ASOHF codes, that is, between the ``grid based on halo finders''. The reason is that these methods are more directly comparable with each other. Still, given that we use AHF as a stand-alone halo finder, differences are expected.
To have a first order comparison of the spatial distribution
of the haloes encountered by both codes, Fig. 7
shows the 2D projection along the z axis of the simulated box of all
haloes (and/or subhaloes) found by ASOHF and by AHF at z=0. We
only show those haloes or subhaloes with masses larger than
![]() .
Both panels are highly
consistent. All relevant features of the halo distribution were
caught with both methods, and therefore they seem perfectly
comparable.
.
Both panels are highly
consistent. All relevant features of the halo distribution were
caught with both methods, and therefore they seem perfectly
comparable.
The main differences between both methods arise when the smallest structures found are taken into account. Whereas the biggest structures are perfectly recognized in both plots, the smallest represent the main source of disagreement. These discrepancies may have a variety of causes, of which the most important is that the finders make use of very different techniques to compute the dark matter density distributions. Both codes create their structures of nested grids according to different criteria. Therefore, a slight change in the number of grids, especially for the small objects, could alter the way in which these objects are resolved, making them detectable or not. Leaving this issue aside, both distributions are fully comparable.
5.3 Halo shapes
The shapes of haloes are described by the axes,
![]() ,
of the
ellipsoid derived from the inertia tensor, as described in Sect.
3.3. For the sake of completeness, we have compared the
distribution of halo shapes obtained by ASOHF and AHF for haloes with
masses above
,
of the
ellipsoid derived from the inertia tensor, as described in Sect.
3.3. For the sake of completeness, we have compared the
distribution of halo shapes obtained by ASOHF and AHF for haloes with
masses above
![]() .
The obtained results
are shown in Fig. 8.
As we can deduce from
these results, haloes are generally triaxial but with a large
variation in shapes. Prolate objects have p=1, oblate objects have
q=1, and spherical objects have p=q=1.
.
The obtained results
are shown in Fig. 8.
As we can deduce from
these results, haloes are generally triaxial but with a large
variation in shapes. Prolate objects have p=1, oblate objects have
q=1, and spherical objects have p=q=1.
Our results show that the haloes are mainly spherical but with a slight preference for prolateness over oblateness. This distribution qualitatively agrees with previous results (e.g., Cole & Lacey 1996; Frenk et al. 1988; Bailin & Steinmetz 2005).
![\begin{figure}
\par\includegraphics[height=130mm]{14214fg11}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg105.png)
|
Figure 9: Merger tree of the analysed host halo. Cluster haloes are represented by circles whose sizes are normalized to the final mass at z = 0. Lines connecting haloes at different times indicate the amount of mass transferred from the progenitors to their descendants. Only the contribution of the most massive progenitors is displayed. |
| Open with DEXTER | |
Bottom panels of Fig. 8 show the triaxiallity parameter,
T, of the haloes found by ASOHF (left plot) and AHF (right plot) as a
function of halo masses. In this figure the x-axis was divided
into 12 mass bins equally spaced in logarithmic scale, and the error bars
represent ![]() uncertainties due to the number counts. The
general trends obtained from these plots agree with
previous results (e.g., Shaw et al. 2006; Allgood et al. 2006; Warren et al. 1992). As it would be naively expected, more massive
haloes tend to be less spherical and more prolate. In a hierarchical
model of structure formation, more massive haloes form later, and have
less time to relax and to form more spherical configurations. In
addition, because haloes tend to be formed by matter collapsing along
filaments, they generally lead to prolate rather than oblate
structures. Because our halo sample is statistically small, the general
trend obtained for the shape of the haloes must be taken with caution
although it agrees with previous results.
Nevertheless, even when the sample can be limited, results from
ASOHF and AHF are completely consistent.
uncertainties due to the number counts. The
general trends obtained from these plots agree with
previous results (e.g., Shaw et al. 2006; Allgood et al. 2006; Warren et al. 1992). As it would be naively expected, more massive
haloes tend to be less spherical and more prolate. In a hierarchical
model of structure formation, more massive haloes form later, and have
less time to relax and to form more spherical configurations. In
addition, because haloes tend to be formed by matter collapsing along
filaments, they generally lead to prolate rather than oblate
structures. Because our halo sample is statistically small, the general
trend obtained for the shape of the haloes must be taken with caution
although it agrees with previous results.
Nevertheless, even when the sample can be limited, results from
ASOHF and AHF are completely consistent.
5.4 Subhaloes
One of the main features of the ASOHF finder is its capacity to deal with haloes and subhaloes. In this section we compare the abundance and distribution of substructures given by ASOHF and AHF.
For the sake of comparison, we focus on the detailed analysis of the
most massive halo in the cosmological simulation previously described.
This halo has a virial mass of ![]()
![]() and
a virial radius of
and
a virial radius of ![]() 2.4 Mpc. To illustrate the time evolution
of the chosen halo, we constructed its merger tree by tracking all its
particles backwards in time. In Fig. 9 we display the merging
history of the halo. To facilitate the reading
of this figure, we only show the mergers among the most massive haloes
that contribute to build up the final halo at z=0. Otherwise, the
plot would be saturated by the amount of mergers due to small
structures, which are not very relevant from the dynamical point of
view, though. The merger tree starts at z=0 and it plots all the
most massive progenitors of the final halo in previous time-steps over
several output times of the simulation. The total mass of each halo
is represented by a circle, whose size is normalized to the mass of
the final halo at z=0. The meaning of the different line types
remains the same as in Sect. 4.3 (Fig. 4),
that is the amount of mass received by any of the progenitors. This
kind of plot not only shows the merger history, but also the different
interconnections over time. Although this halo is the most massive in
the simulation, it is far from being virialized because, as we can see
in Fig. 9, it has suffered several major mergers
during its evolution, one of which happened very recently. This makes
the process of the substructure analysis more challenging.
2.4 Mpc. To illustrate the time evolution
of the chosen halo, we constructed its merger tree by tracking all its
particles backwards in time. In Fig. 9 we display the merging
history of the halo. To facilitate the reading
of this figure, we only show the mergers among the most massive haloes
that contribute to build up the final halo at z=0. Otherwise, the
plot would be saturated by the amount of mergers due to small
structures, which are not very relevant from the dynamical point of
view, though. The merger tree starts at z=0 and it plots all the
most massive progenitors of the final halo in previous time-steps over
several output times of the simulation. The total mass of each halo
is represented by a circle, whose size is normalized to the mass of
the final halo at z=0. The meaning of the different line types
remains the same as in Sect. 4.3 (Fig. 4),
that is the amount of mass received by any of the progenitors. This
kind of plot not only shows the merger history, but also the different
interconnections over time. Although this halo is the most massive in
the simulation, it is far from being virialized because, as we can see
in Fig. 9, it has suffered several major mergers
during its evolution, one of which happened very recently. This makes
the process of the substructure analysis more challenging.
In Fig. 10 we present the analysis of this particular halo with its substructures as found by ASOHF (upper plots) and AHF (lower plots), respectively. The left column of the panel displays the 2D projection of the halo with its subhaloes. The x and y axes show the coordinates in Mpc of the haloes within the computational box. The comparison of the haloes identified by both codes deserves some comments. The main halo is located at the same coordinates and with the same mass and size in both cases. There is also a clear correlation among the largest subhaloes in both subhalo samples in sizes and masses. But there seem to be important differences in the smallest substructures. As we mentioned above, the explanation of this different performance detecting small structures is directly linked with the structure of nested grids built by the algorithms.
Subhalo mass functions have been widely studied in previous works
(e.g., De Lucia et al. 2004; Giocoli et al. 2008a; Knollmann & Knebe 2009; Gao et al. 2004; Ghigna et al. 2000), leading to the conclusion that
subhalo mass functions can be described with a power law,
![]()
![]() ,
with a logarithmic slope
,
with a logarithmic slope ![]() in the
range from 0.7 to 0.9. We computed the subhalo mass function
of the cosmological simulation used for the comparison of both halo
finders. The results are shown in the panels of the right column in
Fig. 10. These plots show the cumulative mass
functions of the subhaloes for the considered main halo as obtained
by ASOHF (top) and AHF (bottom). To facilitate the
comparison with previous results, two lines corresponding to the power
laws with values of
in the
range from 0.7 to 0.9. We computed the subhalo mass function
of the cosmological simulation used for the comparison of both halo
finders. The results are shown in the panels of the right column in
Fig. 10. These plots show the cumulative mass
functions of the subhaloes for the considered main halo as obtained
by ASOHF (top) and AHF (bottom). To facilitate the
comparison with previous results, two lines corresponding to the power
laws with values of ![]() equal to -0.7 and -0.9 are
plotted. The masses of subhaloes are normalized to the mass of the
main halo. The error bars show
equal to -0.7 and -0.9 are
plotted. The masses of subhaloes are normalized to the mass of the
main halo. The error bars show ![]() uncertainties due to the
number counts.
uncertainties due to the
number counts.
![\begin{figure}
\includegraphics[height=160mm] {14214fg9.ps}
\vspace*{0.25mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg109.png)
|
Figure 10:
Analysis of the subhalo
population of the most massive halo in our simulation.
Left panels (top and bottom plots):
subhalo population within the most massive host halo in our simulation
as found by ASOHF and AHF. The size of the circles
represents the virial radius of the different haloes. Right panels:
cumulative subhalo mass function for the most massive halo in our
simulation as found by ASOHF (upper plot) and AHF (lower plot).
Two power law fits with slopes of -0.7 and -0.9 are
also shown in these panels. Error bars show |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[height=85mm]{14214fg10}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg110.png)
|
Figure 11: 2D projection of the dark matter density field around the biggest halo in the simulation. The colour scale represents the logarithmic of the density field. Subhaloes found by ASOHF (left panel) and AHF (right panel) are superimposed being the white circles the radii of these haloes. |
| Open with DEXTER | |
From a statistical point of view, the comparison of both mass functions shows that both codes have similar capabilities when dealing with finding substructures. The fitting to a power law of the analysed data gives a slope of 0.9 for ASOHF and 0.7 for AHF. This would render the ASOHF and AHF mass functions completely consistent with previous results, because they are well fit between the two limiting power laws for substructure in haloes. Nevertheless, this conclusion must be taken with caution because, as we saw, a direct comparison of the smallest substructures is not straightforward.
We proceed to compare identified subhaloes with the real mass distribution in the main halo to deepen in the comparison of the encountered subhalo samples and assuming that a direct comparison between both methods is not always completely meaningful. Therefore, Fig. 11 shows the colour-coded dark matter column density in the main halo considered in this section together with the detected subhaloes overplotted as circles with their radii normalized to the main halo radius. The left panel of the figure corresponds to the sample obtained by ASOHF, whereas the right panel displays subhaloes identified by AHF. As we previously discussed when analysing Fig. 10, most of the substructures are unambiguously identified by both codes and with very similar features (sizes and masses). However, the smallest subhaloes are not well identified either with ASOHF or AHF. Moreover, it is striking that some of these small substructures do not match not only between both halo finders, but more intriguing, with the real mass distribution.
6 Summary and conclusions
In the last years cosmological simulations have experienced an astonishing development, producing a huge amount of computational data. Intimately related to the development of simulations, all kinds of analysis tools have arisen too. One of the most important analysis tools have become the halo finder algorithms, whose relevance is crucial when comparing simulations with observation.
The halo-finding issue has revealed itself as not trivial at all. When cosmological simulations have increased their resolution and complexity and the amount of data have grown exponentially, to find haloes can itself be an intensive computational work. Moreover, the different techniques and implementations used in the halo finders developed so far can show important differences, particularly when looking at the features of the smallest objects in the simulations.
We developed a new halo-finding code with the main idea of contributing towards constraints for a field in which only a limited number of algorithms are available and differences among codes are still relevant.
Our ASOHF code was especially designed to overcome some limitations of the original SO technique and to exploit the benefits of having a set of nested grids that track the density distribution in the analysed volume. By treating all AMR grids at a certain level of refinement (same numerical resolution) independently, the code is able to find haloes at all levels. This procedure can identify haloes in haloes in a natural way and therefore describe the properties of the substructure in cosmological objects.
The numerical scheme is also prepared to compute the merger tree of the haloes in the computational box as well as some other usual properties of these haloes such as their shapes, and density and velocity radial profiles.
We set up several idealised and controlled tests to check the capabilities of the halo finder. Although most of these tests are unreal, they allow us total control of every part of the halo-finding process. In all tests, the performance of the finder algorithm has been correct.
The next step to calibrate and test the ASOHF finder was to apply it to the outcome of a cosmological simulation and compare its results with other halo finders widely used like AHF and AFoF.
In a first instance, we compared the sample of haloes encountered by the three codes in a given cosmological simulation. A coarse comparison showed a good agreement among them. The mass functions obtained by the three finders were also very similar. We looked at the shape of the encountered haloes, finding a reasonable concordance between the results obtained by ASOHF and AHF and with previous studies.
More interestingly, we tested the abilities of ASOHF dealing with substructure in not idealised simulations. In order to check this issue, we picked up the most massive halo in the considered computational box. This halo was throughly analysed using both grid based on finders, namely, ASOHF and AHF. From the statistical point of view, the results are comparable because the subhalo mass functions are reasonably consistent. Still, the comparison object by object was not as successful because there are several noticeable differences concerning the smaller objects. To clarify this, we compared the samples of haloes obtained by both algorithms with the real mass distribution. Apparently, both codes agree among themselves and match the mass distribution for the most relevant features. However, both algorithms miss small objects when they are compared with the mass distribution. Surprisingly, the two codes do not miss the same small objects.
The explanation for this behaviour for the ASOHF finder is related to how the hierarchy of nested grids is created. We checked that some of those smaller objects are not always covered by a high resolution grid. In that case the halo finder does not identify the small haloes because it is necessary to have them defined in grids with enough numerical resolution. Although the detailed description of the AHF algorithm is out of the scope of the present paper, given that it is also a grid based on halo finder, it is very likely that the differences affecting the detection of small substructures could be caused by the same reasons as in the ASOHF code.
The ASOHF code has been recently used to study galaxy cluster mergers in a cosmological context (Planelles & Quilis 2009). The working version of the code is serial and it is written in FORTRAN 95. At present we are working on the parallel OpenMP version of the code, which will be publicly released in due course.
AcknowledgementsThis work has been supported by Spanish Ministerio de Ciencia e Innovación (MICINN) (grants AYA2007-67752-C03-02 and CONSOLIDER2007-00050) and the Generalitat Valenciana (grant PROMETEO-2009-103). S.P. thanks to the MICINN for a FPU doctoral fellowship. The authors gratefully acknowledge S. Knollmann and A. Knebe for an invaluable help regarding the use of AHF as well as for many interesting comments and discussions. The authors also wish to thank to J.M. Ibáñez and B. Gibson for useful discussions, and the anonymous referee for his/her constructive criticism. Simulations were carried out in the Servei d'Informática de la Universitat de València and the Centre de Supercomputació de Catalunya (CESCA).
References
- Aarseth, S. J. 1963, MNRAS, 126, 223 [NASA ADS] [Google Scholar]
- Allgood, B., Flores, R. A., Primack, J. R., et al. 2006, MNRAS, 367, 1781 [NASA ADS] [CrossRef] [Google Scholar]
- Bailin, J., & Steinmetz, M. 2005, ApJ, 627, 647 [Google Scholar]
- Bertschinger, E., & Gelb, J. M. 1991, Comp. Phys., 5, 164 [Google Scholar]
- Bryan, G. L., & Norman, M. L. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., & Lacey, C. 1996, MNRAS, 281, 716 [Google Scholar]
- Crain, R., Theuns, T., Dalla Vecchia, C., et al. 2009, MNRAS, 399, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Efstathiou, G., Frenk, C. S., & White, S. D. M. 1985, ApJ, 292, 381 [Google Scholar]
- De Lucia, G., Kauffmann, G., Springel, V., et al. 2004, MNRAS, 348, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Diemand, J., Kuhlen, M., & Madau, P. 2006, ApJ, 649, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Diemand, J., Kuhlen, M., & Madau, P. 2007, ApJ, 657, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., & Hu, W. 1998, ApJ, 511, 5 [Google Scholar]
- Eke, V. R., Cole, S., & Frenk, C. S. 1996, MNRAS, 282, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Franx, M., Illingworth, G., & de Zeeuw, T. 1991, ApJ, 383, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Frenk, C. S., White, S. D. M., Davis, M., & Efstathiou, G. 1988, ApJ, 327, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, L., White, S. D. M., Jenkins, A., Stoehr, F., & Springel, V. 2004, MNRAS, 355, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Gelb, J. M., & Bertschinger, E. 1994, ApJ, 436, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Ghigna, S., Moore, B., Governato, F., et al. 2000, ApJ, 544, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Gill, S. P. D., Knebe, A., & Gibson, B. K. 2004, MNRAS, 351, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Gingold, R. A., & Monaghan, J. J. 1977, MNRAS, 181, 375 [Google Scholar]
- Giocoli, C., Tormen, G., & van den Bosch, F. C. 2008, MNRAS, 386, 2135 [NASA ADS] [CrossRef] [Google Scholar]
- Giocoli, C., Tormen, G., Sheth, R. K., & van den Bosch, F. C. 2009, MNRAS, 404, 502 [Google Scholar]
- Götz, M., Huchra, J. P., & Branderberger, R. H. 1998[arXiv:astro-ph/9811393] [Google Scholar]
- Hockney, R. W., & Eastwood, J. W. 1988, Computer Simulation Using Particles (Bristol: Hilger) [Google Scholar]
- Klypin, A., Gottlöber, S., Kravtsov, A., & Khoklov, A. 1999, ApJ, 516, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Kravtsov, A., Valenzuela, O., & Prada, F. 1999, ApJ, 522, 82 [Google Scholar]
- Knebe, A., Green, A., & Binney, J. 2001, MNRAS, 325, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Knollmann, S., & Knebe, A. 2009, ApJS, 182, 624 [Google Scholar]
- Lacey, C., & Cole, S. 1994, MNRAS, 271, 676 [Google Scholar]
- Lucy, L. B. 1977, AJ, 82, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Ghigna, S., Governato, F., et al. 1999, ApJ, 524, L19 [Google Scholar]
- Navarro J., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Neyrinck, M. C., Knedin, N. Y., & Hamilton, A. J. S. 2005, MNRAS, 356, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1970, AJ, 75, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Planelles, S., & Quilis, V. 2009, MNRAS, 399, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Quilis, V. 2004, MNRAS, 352, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, D., Bower, R., Frenk, C. S., Jenkins, A., & Theuns, T. 2007, MNRAS, 374, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, L. D., Weller, J., Ostriker, J. P., & Bode, P. 2006, ApJ, 646, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R., & Tormen, G. 1999, MNRAS, 308, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Whte, S. D. M., Tormen, G. , & Kauffmann, G. 2001, MNRAS, 328, 726 [Google Scholar]
- Tormen, G. 1998, MNRAS, 297, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Tormen, G., Moscardini, L., & Yoshida, L. 2004, MNRAS, 350, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- van Kampen, E. 1995, MNRAS, 273, 295 [NASA ADS] [Google Scholar]
- von Neumann, J. 1951, Various techniques used in connection with random digits. Monte Carlo methods, Nat. Bureau Standards, 12, 36 [Google Scholar]
- Warren, M. S., Quinn, P. J., Salmon, J. K., & Zurek, W. H. 1992, 399, 405 [Google Scholar]
- Weinberg, D., Hernquist, L., & Katz, N. 1997, ApJ, 477, 8 [NASA ADS] [CrossRef] [Google Scholar]
- White, M. 2002, ApJ, 143, 241 [Google Scholar]
- White, S. D. M. 1976, MNRAS, 177, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Yaryura, C. Y., Baugh, C. M., & Angulo, R. E. 2010, MNRAS, submitted[arXiv:1003.4259] [Google Scholar]
All Tables
Table 1: Mean features of the generated haloes at z=0 in test 1.
Table 2: General results obtained by ASOHF, AFoF and AHF at z=0.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14214fg1.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg27.png)
|
Figure 1: Flowchart for ASOHF. In this diagram, NL stands for the total number of analysed AMR grid levels. NH ad NH' represent the total number of tentative and final found haloes, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.2cm]{14214fg2.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg48.png)
|
Figure 2: Radial dark matter density profiles for the four generated haloes compiled in Table 1 as a function of the radius at z=0 (test 1). Continuous lines stand for the input profiles of the mock haloes, whilst points represent the profiles obtained by the halo finder. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.5cm]{14214fg3.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg50.png)
|
Figure 3: Mock distribution of a halo with three substructures: two subhaloes and one sub-subhalo (test 2). The left panel shows the 2D projection of the structures found by ASOHF. Circles represent the radii of the different structures, while the different line types stand for the different refinement levels in which the haloes have been found. The right panel shows the known distribution of dark matter particles in this test. Different colours stand for the level to which the particles belong. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{14214fg4.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg53.png)
|
Figure 4: Merger trees for several haloes in the three different cases analysed in Sect. 4.3 (test 3). Left, central, and right panels stand for case I, II, and III, respectively. The top panels represent the results obtained following all dark matter particles within each halo (complete merger tree), whereas the bottom panels stand for the results obtained following only the closest particle to the centre of each halo (reduced merger tree). Haloes are represented by circles whose sizes are normalized to the final mass at z=0. The different line types connecting haloes at different times in the upper plots indicate the amount of mass transferred from the progenitors to their descendants. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=10cm]{14214fg5.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg79.png)
|
Figure 5: Top panel: academic mass function corresponding to the generated sample of 100 haloes for test 4. Dots represent the mass function obtained by ASOHF, whereas the continuous line corresponds to the function generated by hand. Bottom panel: relative error or difference in mass between the two distributions shown in the upper plot. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=100mm]{14214fg6.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg98.png)
|
Figure 6: Top panel: comparison of the mass functions obtained by ASOHF, AHF and AFoF at z=0. The mass function predicted by Sheth & Tormen is also shown. Bottom panel: relative difference in the number of haloes between AFoF and AHF compared to ASOHF. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=90mm]{14214fg7.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg99.png)
|
Figure 7:
2D projection for haloes
at z=0. Only haloes with masses above
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=150mm]{14214fg8.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg103.png)
|
Figure 8:
Distribution of
the halo shapes at z=0 as found by ASOHF ( left panels)
and AHF ( right panels), respectively. Only haloes with masses above
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=130mm]{14214fg11}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg105.png)
|
Figure 9: Merger tree of the analysed host halo. Cluster haloes are represented by circles whose sizes are normalized to the final mass at z = 0. Lines connecting haloes at different times indicate the amount of mass transferred from the progenitors to their descendants. Only the contribution of the most massive progenitors is displayed. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[height=160mm] {14214fg9.ps}
\vspace*{0.25mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg109.png)
|
Figure 10:
Analysis of the subhalo
population of the most massive halo in our simulation.
Left panels (top and bottom plots):
subhalo population within the most massive host halo in our simulation
as found by ASOHF and AHF. The size of the circles
represents the virial radius of the different haloes. Right panels:
cumulative subhalo mass function for the most massive halo in our
simulation as found by ASOHF (upper plot) and AHF (lower plot).
Two power law fits with slopes of -0.7 and -0.9 are
also shown in these panels. Error bars show |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[height=85mm]{14214fg10}
\end{figure}](/articles/aa/full_html/2010/11/aa14214-10/Timg110.png)
|
Figure 11: 2D projection of the dark matter density field around the biggest halo in the simulation. The colour scale represents the logarithmic of the density field. Subhaloes found by ASOHF (left panel) and AHF (right panel) are superimposed being the white circles the radii of these haloes. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


