EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 517 (July 2010) A&A, 517 (2010) A96 Full HTML
Free Access
Issue
A&A
Volume 517, July 2010
Article Number A96
Number of page(s) 37
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200913501
Published online 17 August 2010
A&A 517, A96 (2010)

A line confusion limited millimeter survey of Orion KL I. Sulfur carbon chains[*]

B. Tercero - J. Cernicharo - J. R. Pardo - J. R. Goicoechea

Centro de Astrobiología (CSIC-INTA), Departamento de Astrofísica Molecular, Ctra. de Aljalvir Km 4, 28850 Torrejón de Ardoz, Madrid, Spain

Received 19 October 2009 / Accepted 15 April 2010

Abstract
We perform a sensitive (line confusion limited), single-side band spectral survey towards Orion KL with the IRAM 30 m telescope, covering the following frequency ranges: 80-115.5 GHz, 130-178 GHz, and 197-281 GHz. We detect more than 14 400 spectral features of which 10 040 have been identified up to date and attributed to 43 different molecules, including 148 isotopologues and lines from vibrationally excited states. In this paper, we focus on the study of OCS, HCS+, H2CS, CS, CCS, C3S, and their isotopologues. In addition, we map the OCS J=18-17 line and complete complementary observations of several OCS lines at selected positions around Orion IRc2 (the position selected for the survey). We report the first detection of OCS $\nu_2 = 1$ and $\nu_3 = 1$ vibrationally excited states in space and the first detection of C3S in warm clouds. Most of CCS, and almost all C3S, line emission arises from the hot core indicating an enhancement of their abundances in warm and dense gas. Column densities and isotopic ratios have been calculated using a large velocity gradient (LVG) excitation and radiative transfer code (for the low density gas components) and a local thermal equilibrium (LTE) code (appropriate for the warm and dense hot core component), which takes into account the different cloud components known to exist towards Orion KL, the extended ridge, compact ridge, plateau, and hot core. The vibrational temperature derived from OCS $\nu_2 = 1$ and $\nu_3 = 1$ levels is $\simeq$210 K, similar to the gas kinetic temperature in the hot core. These OCS high energy levels are probably pumped by absorption of IR dust photons. We derive an upper limit to the OC3S, H2CCS, HNCS, HOCS+, and NCS column densities. Finally, we discuss the D/H abundance ratio and infer the following isotopic abundances: 12C/13C = $45\pm 20$, 32S/34S = $20\pm6$, 32S/33S = $75\pm29$, and 16O/18O =  $250 \pm 135$.

Key words: surveys - stars: formation - ISM: abundances - ISM: clouds - ISM: molecules - radio lines: ISM

1 Introduction

The Orion KL (Kleinmann-Low) cloud is the closest ($\simeq$414 pc, Menten et al. 2007) and most well studied high mass star-forming region in our Galaxy (see, e. g., Genzel & Stutzki 1989 for review). The prevailing chemistry of the cloud is particularly complex as a result of the interaction of the newly formed protostars, outflows, and their environment. The evaporation of dust mantles and the high gas temperatures produce a wide variety of molecules in the gas phase that are responsible for a spectacularly prolific and intense line spectrum (Blake et al. 1987; Charnley 1997; Brown et al. 1988).

Near- and mid-IR subarcsecond resolution imaging and (sub)millimeter interferometric observations have identified the main sources of luminosity, heating, and dynamics in the region. At first, IRc2 was believed to be the responsible for this complex environment. However, the 8-12 $\mu$m emission peak of IRc2 is not coincident with the the origin of the outflow(s) (and the Orion SiO maser origin), and its intrinsic IR luminosity ( $L\approx1000~L_{\odot}$) is only a fraction of the luminosity of the entire system (Gezari et al. 1998). In addition, 3.6-22 $\mu$m images indicate that IRc2 is resolved into four non self-luminous components. Therefore, IRc2 is not presently the powerful engine of Orion KL and its nature remains unclear (Dougados et al. 1993; Greenhill et al. 2004; Shuping et al. 2004). Menten & Reid (1995) identified the very embedded radio continuum source I (a young star with a very high luminosity without an infrared counterpart, $\simeq$10 $^5~L_\odot$, Greenhill et al. 2004; Gezari et al. 1998, located  $0\hbox{$.\!\!^{\prime\prime}$ }5$ south of IRc2) as the source coinciding with the centroid of the SiO maser distribution (Goddi et al. 2009b; Plambeck et al. 2009; Zapata et al. 2009a). They also detected the radio continuum emission of IR source n, suggesting this source as another precursor of the large-scale phenomena. In addition, Beuther et al. (2004) detected a sub-millimeter source without IR and centimeter counterparts, SMA1, previously predicted by de Vicente et al. (2002), which may be the source driving the high velocity outflow (Beuther & Nissen 2008). Thus, the core of Orion KL contains the compact HII regions I and n (in addition to BN, which was resolved with high resolution at 7 mm by Rodríguez et al. 2009), which appear to be receding from a common point, an originally massive stellar system that disintegrated $\simeq$500 years ago (Zapata et al. 2009b; Gómez et al. 2005). Finally, submm aperture synthesis line surveys provided the spatial location and extent of many molecular species (Goddi et al. 2009b; Wright et al. 1996; Beuther et al. 2005; Plambeck et al. 2009; Liu et al. 2002; Zapata et al. 2009a; Blake et al. 1996).

The chemical complexity of Orion KL has been demonstrated by several line surveys performed at different frequency ranges: 72.2-91.1 GHz by Johansson et al. (1984); 215-247 GHz by Sutton et al. (1985); 247-263 GHz by Blake et al. (1986); 200.7-202.3, 203.7-205.3 and 330-360 GHz by Jewell et al. (1989); 70-115 GHz by Turner (1989); 257-273 GHz by Greaves & White (1991); 150-160 GHz by Ziurys & McGonagle (1993); 325-360 GHz by Schilke et al. (1997); 607-725 GHz by Schilke et al. (2001); 138-150 GHz by Lee et al. (2001); 159.7-164.7 GHz by Lee & Cho (2002); 455-507 GHz by White et al. (2003); 795-903 GHz by Comito et al. (2005); 44-188 $\mu$m by Lerate et al. (2006); 486-492, 541-577 GHz by Olofsson et al. (2007) and Persson et al. (2007); and 42.3-43.6 GHz by Goddi et al. (2009a).

In spite of this large amount of data, no line confusion limited survey has been carried out so far with a large single dish telescope. We performed such a line survey towards Orion IRc2 with the IRAM 30-m telescope at wide frequency ranges (a total frequency coverage of $\simeq$168 GHz). Our main goal was to obtain a deep insight into the molecular content and chemistry of Orion KL, an archetype high mass star-forming region (SFR), and to improve our knowledge of its prevailing physical conditions. It also allows us to search for new molecular species and new isotopologues, as well as the rotational emission of vibrationally excited states of molecules already known to exist in this source. Since the amount and complexity of the data is large, we divided our analysis into families of molecules so that model development and discussions could be more focused. In this paper, we concentrate on sulfur carbon chains, in particular carbonyl sulfide OCS (see previous studies by Goldsmith & Linke 1981; Evans II et al. 1991; Wright et al. 1996; Charnley 1997), CS (previously analyzed by Hasegawa et al. 1984; Murata et al. 1991; Zeng & Pei 1995; Wright et al. 1996; Johnstone et al. 2003), H2CS (Minh et al. 1991; Gardner et al. 1984), HCS+, CCS, CCCS, and their isotopologues.

Column density calculations, and therefore the estimation of isotopic abundance ratios and molecular excitation, have improved, with respect to previous works, due to the much larger number of available lines, their consistent calibration across the explored frequency range, the up-to-date information about the physical properties of the region and molecular constants, and the use of a LVG radiative transfer code to derive reliable physical and chemical parameters. Modeled brightness temperatures obtained from a fit to all observed lines have been convolved with the telescope beam profile, assuming a given size for each cloud component, to provide accurate source-averaged, and not beam-averaged, molecular column densities.

After presenting the line survey (Sects. 2 and 3), this work concentrates on the detection of OCS, HCS+, H2CS, CS, CCS, and CCCS lines and their analysis, as well as providing upper limits to the abundance of several non-detected sulfur-carbon-chain bearing molecules such us OC3S, H2CCS, HNCS, HOCS+, and NCS (Sects. 4 to 7). This is the first of a series of papers dedicated to the analysis of the millimeter emission from different molecular families towards Orion KL.

2 Observations and data analysis

Table 1:   $\eta _{\rm MB}$ and HPBW along the covered frequency range.

The observations were carried out using the IRAM 30 m radiotelescope during September 2004 (3 mm and 1.3 mm windows), March 2005 (full 2 mm window), April 2005 (completion of 3 mm and 1.3 mm windows), and January 2007 (maps and pointed observations at particular positions). Four SiS receivers operating at 3, 2, and 1.3 mm were used simultaneously with image sideband rejections within 20-27 dB (3 mm receivers), 12-16 dB (2 mm receivers) and $\simeq$13 dB (1.3 mm receivers). System temperatures were in the range 100-350 K for the 3 mm receivers, 200-500 K for the 2 mm receivers, and 200-800 K for the 1.3 mm receivers, depending on the particular frequency, weather conditions, and source elevation. For frequencies in the range 172-178 GHz, the system temperature was significantly higher, 1000-4000 K, due to proximity of the atmospheric water line at 183.31 GHz. The intensity scale was calibrated using two absorbers at different temperatures and the atmospheric transmission model (ATM, Cernicharo 1985; Pardo et al. 2001). Table 1 shows the variation in the main beam efficiency ( $\eta _{\rm MB}$) and the half power beam width (HPBW) across the covered frequency range. The error beam contribution to the observed line intensities is negligible for heavy polyatomic molecules because their emission originates in a compact region. However, the error beam contribution of the low-J line extended emission of abundant species (HCO+, HCN, CN or CS) can be significant (up to $\simeq$10-20% of the observed intensities at 1 mm). Deriving the correct brightness temperature for these lines requires large-scale mapping.

Pointing and focus were regularly checked on the nearby quasars 0420-014 and 0528+134. Observations were made in the balanced wobbler-switching mode, with a wobbling frequency of 0.5 Hz and a beam throw in azimuth of $\pm$240''. No contamination from the off position affected our observations except for a marginal one at the lowest elevations ($\sim$25$^{\circ}$) for molecules showing low J emission along the extended ridge.

Two filter banks with $512 \times 1$ MHz channels and a correlator providing two 512 MHz bandwidths and 1.25 MHz resolution were used as backends. We pointed towards IRc2 source at $\alpha_{2000.0} = \rm 5^h 35^m 14.5^s$, $\delta_{2000.0} = -5^{\circ} 22' 30.0''$ (J2000.0) corresponding to the ``survey position''. We observed two additional positions to target both the compact ridge ( $\alpha_{2000.0} = \rm 5^h35^m 14.3^s$, $\delta_{2000.0} = -5^{\circ} 22' 37.0''$) and the ambient molecular cloud ( $\alpha_{2000.0} =\rm 5^h 35^m 15.3^s$, $\delta_{2000.0} = -5^{\circ} 22' 09.0''$). Figure 15 of Wright et al. (1996) shows a 3 mm dust image depicting all positions quoted above.

The spectra shown in all figures are in units of antenna temperature, $T^*_{\rm A}$, corrected for atmospheric absorption and spillover losses. In spite of the good receiver image-band rejection, each setting was repeated at a slightly shifted frequency (10-20 MHz) to manually identify and remove all features arising from the image side band. The spectra from different frequency settings were used to identify all potential contaminating lines from the image side band. In some cases, it was impossible to eliminate the contribution of the image side band and we removed the signal in those contaminated channels leaving holes in the data. The total frequencies blanked this way represent less than 0.5% of the total frequency coverage. Figure 1 shows our procedure for removing the image side band lines. We removed most of the features above a 0.05 K threshold.

\begin{figure} \par\includegraphics[width=8cm,clip]{13501fg01.eps} \end{figure} Figure 1:

The top panel shows two superimposed spectra corresponding to different frequency settings (112 500 and 112 520 MHz). The 40 MHz displaced line is the 115.5 GHz CO line in the image side band. The bottom panel shows the final spectrum resulting from our procedure to eliminate the image side band (see text, Sect. 2). We are confident that all lines above 0.05 K have frequencies correctly assigned.

Open with DEXTER

3 The line survey

Within the 168 GHz bandwidth covered, we detected more than 14 400 spectral features of which 10 040 were already identified and attributed to 43 molecules, including 148 different isotopologues and vibrationally excited states. Any feature covering more than 3-4 channels and of intensity greater than 0.02 K is above 3$\sigma$ and is considered to be a line in our survey. The noise was difficult to derive from the data because of the high density of lines. We computed it from the observing time and the system temperature. In the 2 mm and 1.3 mm windows, the features weaker than 0.1 K have not yet been systematically analyzed, except when searching for isotopic species with good laboratory frequencies. We thus expect to considerably increase the number of both identified and unidentified lines. We note that the number of U lines was initially much larger. Identification of some isotopologues of most abundant species (see below) allowed us to reduce the number of U-lines at a rate of $\sim$500 lines per year. We used standard procedures to identify lines above 0.2 K including all possible contributions (taking into account the energy of the transition and the line strength) from different species. Thanks to the wide frequency coverage of our survey, many rotational lines were observed for each species, hence it is possible to estimate the contribution of a given molecule to the intensity of a spectral feature where several lines from different species are blended. We applied this procedure to all our previous line surveys with the 30 m telescope (e.g., Cernicharo et al. 2000).

As an example of the scope of this line survey in the field of molecular spectroscopy, Demyk et al. (2007), Margulès et al. (2009), Carvajal et al. (2009), and Margulès et al. (2010) identified more than 600, 100, 600, and 100 lines from the 13C and 15N isotopologues of CH3CH2CN, the 13C isotopologues of HCOOCH3, and CH3OCOD, respectively. Many of the remaining U-lines are certainly due to isotopologues of other abundant species.

Figures 2, 4, and 6 show the whole data set of this Orion KL line survey at 3 mm, 2 mm and 1.3 mm respectively. Figures 3, 5, and 7 show 1 GHz wide spectra as an example in each window. We have marked the identified features with labels (molecule and transition quantum numbers) and the strongest unidentified ones as ``U''. In each figure, the top panels display the total intensity range, while the middle and the bottom ones show different zoomed images of the intensity range.

Because of the large amount of line features in the spectra, and to follow the most efficient strategy for the line identification process, we decided to proceed in steps by studying the different molecular families including all possible isotopologues and vibrationally excited states. We continue to analyze our line survey data, which we expect to make public, with all line identifications, by 2011.

\begin{figure} \par\includegraphics[angle=270, width=17cm,clip]{13501fg02.eps} \end{figure} Figure 2:

Molecular line survey of Orion KL at 3 mm. The top panel shows the total intensity scale; the middle and the bottom panels show a zoom of the total intensity. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

\begin{figure} \par\includegraphics[width=16cm,clip]{13501fg03n.eps} \end{figure} Figure 3:

Example of Orion's KL survey at 3 mm with 1 GHz bandwidth. The top panel shows the total intensity scale; the middle and the bottom panels show a zoom of the total intensity. Detected molecules are marked with labels and some unidentified features are marked as U.

Open with DEXTER

\begin{figure} \par\includegraphics[% width=16cm,clip]{13501fg04n.eps} \end{figure} Figure 4:

Molecular line survey of Orion KL at 2 mm presented similarly to Fig. 2.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=270,width=17cm,clip]{13501fg05.eps} \end{figure} Figure 5:

Example of Orion's KL survey at 2 mm with 1 GHz bandwidth. The top panel shows the total intensity scale; the middle and the bottom panels show a zoom of the total intensity. Detected molecules are marked with labels and some unidentified lines are marked as U.

Open with DEXTER

\begin{figure} \par\includegraphics[width=17cm,clip]{13501fg06n.eps} \end{figure} Figure 6:

Molecular line survey of Orion KL at 1.3 mm presented similarly to Fig. 2.

Open with DEXTER

\begin{figure} \par\includegraphics[width=17cm,clip]{13501fg07n.eps} \end{figure} Figure 7:

Example of the Orion KL survey at 1.3 mm with 1 GHz bandwidth. The top panel shows the total intensity scale; the middle and the bottom panels show a zoom of the total intensity. Detected molecules are labeled and some unidentified lines are marked as U.

Open with DEXTER

In agreement with previous works, four different spectral cloud components are generally defined in the analysis of low angular resolution line surveys where different physical components overlap in the beam. These components are characterized by different physical and chemical conditions (Blake et al. 1987,1996): (i) a narrow or ``spike'' ($\la$5 km s-1 line-width) component at $v_{\rm LSR} \simeq 9$ km s-1 delineating a north-to-south extended ridge or ambient cloud; (ii) a compact and quiescent region, the compact ridge, ( $v_{\rm LSR} \simeq 8$ km s-1, $\Delta v \simeq 3$ km s-1) identified for the first time by Johansson et al. (1984); (iii) the plateau a mixture of outflows, shocks, and interactions with the ambient cloud ( $v_{\rm LSR} \simeq 6{-}10$ km s-1, $\Delta v \ga 25$ km s-1); (iv) a hot core component ( $v_{\rm LSR} \simeq 3{-}5$ km s-1, $\Delta v \la10{-}15$ km s-1) first detected in ammonia emission Morris et al. (1980). Table 2 gives the physical parameters that we obtained for each component from the modeling of the OCS, HCS+, H2CS, CS, CCS, and CCCS line emission (Sect. 5). The assumption of a single gas temperature and density for each cloud component is the greatest simplification of our methodology. It is clear that the source structure identified by much higher angular resolution interferometric observations is far more complex than assumed in Table 2. We attempted to use more complex structures using density and temperature gradients, but the comparison with the data indicate that we do not have enough information to fit these physical gradients, even when we have many lines for some species. Therefore, we fix the physical properties to be those given in Table 2 (values derived from our data analysis) to ensure that we have only one free parameter (the column density) when modeling the spectral lines. Nevertheless, our multi-source excitation and radiative transfer approach represents a major improvement on previous works based on LTE analysis.

4 Results

4.1 OCS

Table 2:   The assumed Orion KL spectral components.

Carbonyl sulfide (OCS) has a linear structure and, because of its rotational constant (B=5932.83 MHz for 16O12C32S), it harbours up to 15 transitions per vibrational state that can be observed in the covered frequency range. Line detections in our survey include the ground vibrational state of 6 isotopologues (OCS, OC34S, OC33S, O13CS, 18OCS, O13C34S), plus two vibrationally excited states of the main isotopologue ($\nu_2 = 1$, $\nu_3 = 1$). The last two were detected here for the first time in space. Only a tentative detection is presented for 17OCS and OC36S because of the weakness of the features and/or their overlap with other spectral lines.

\begin{figure} \par\includegraphics[width=14cm,clip]{13501fg08.eps} \end{figure} Figure 8:

Observed (offseted histogram) and model (thin curves) OCS, OC34S and OC33S lines. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

\begin{figure} \par\includegraphics[width=14cm,clip]{13501fg09.eps} \end{figure} Figure 9:

Observed lines (offseted histogram) and model (thin curves) of OCS $\nu _2$ = 1 and OCS $\nu _3$ = 1. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

The rotational constants used to derive the line frequencies were taken from Golubiatnikov et al. (2005) (OCS), the NIST triatomic molecules database (OC34S and O13CS), Burenin et al. (1981b) (OC33S), Burenin et al. (1981a) (all the others OCS isotopologues), and Morino et al. (2000) (OCS vibrationally excited states). The OCS dipole moment ($\mu$ = 0.7152D) was assumed to be that measured by Tanaka et al. (1985). Observed line parameters and intensities are given in Table 3. Figures 8, A.1 and 9 show the lines that are not blended with features from other species and our best-fit-model line profiles (see Sect. 5.1). The line profiles and intensities show the contribution from the extended and compact molecular ridges, the plateau, and the hot core. In previous line surveys, the extended ridge component was discarded as a significant source of OCS line emission. However, we include it here as a requirement to reproduce the observed intensities from J = 7-6 up to J = 23-22 (main and rare isotopologues).

To constrain the model more tightly, and determine the spatial distribution of the OCS line emission, we obtained a map of the OCS J = 18-17 line and performed sensitive observations of several lines at selected positions around Orion IRc2. Figure A.2 shows the observed line profiles and integrated line intensity spatial distribution. Figure 10 shows the line emission for different velocity ranges.

The maximum integrated intensity lies approximately 3'' southwest of IRc2 (see Fig. A.2) and is a mixture of compact ridge and hot core components, in agreement with the spatial distribution found by Wright et al. (1996). The velocity structure of the OCS emission depicted in Fig. 10 shows all the cloud spectral components discussed above. The spatial distribution of the red wing ( $v_{\rm LSR}\simeq15{-}20$ km s-1) of the J = 18-17 line emission is particularly interesting. It traces an elliptical expanding shell of gas around IRc2, the low-velocity outflow. The front of the shell is traced by the emission at velocities from -10 to -1 km s-1 (blue wing), while the red part of the shell appears at 20-25 km s-1.

The observed lines at selected positions are shown in Fig. 11. Altogether, these data allow us to study the hot core, the compact ridge, and the extended ridge. Sutton et al. (1995) also observed the OCS J = 28-27 line at different positions. OCS line intensities are clearly brighter towards the compact ridge position than towards IRc2 (hot core). The antenna temperature measured towards the extended ridge position is $\simeq$1 K; however, the extended ridge contribution towards IRc2 should be larger to explain the data (see Sect. 5.1).

Table 3:   OCS observed line parameters.

Table 4 gives the parameters of the OCS lines derived by fitting Gaussian profiles to all velocity components with the CLASS software[*]. The $v_{\rm LSR}$ velocities derived for the hot core vary between 3.3 km s-1 to 5.6 km s-1due to the overlap with the other velocity components, in particular in the blueshifted wing of the line profile (see Fig. 8). Table B.1, only available online, gives the parameters of the observed lines of the most abundant isotopologues (OC34S, OC33S, and O13CS) and vibrationally excited OCS ($\nu_2 = 1$). Since these lines are much weaker than those of OCS $\nu=0$, only a single velocity component has been fitted. Because of either their weakness or heavy blending, the analysis of the other OCS isotopologues and of OCS $\nu_3 = 1$ is not possible. We note that the line parameters for OCS $\nu_2 = 1$ match those of the hot core component. This behavior is as expected since the energy of the $\nu_2 = 1$ vibrational level is 749 K, which is populated for the warmest gas component.
\begin{figure} \par\includegraphics[width=18cm,clip]{13501fg10n.eps} \end{figure} Figure 10:

OCS J = 18-17 integrated line intensity maps at different velocity ranges (indicated at the top of each panel). The integrated intensity of the maps has been multiplied by a scale factor (indicated in the panels) to maintain the same color dynamics for all maps. The interval of contours is 10 K km s-1, the minimum contour is 30 K km s-1 for the maps with velocities between -1 and 11 km s-1 and 50 K km s-1 for the rest of the panels.

Open with DEXTER

\begin{figure} \par\includegraphics[width=11.5cm,clip]{13501fg11.eps} \end{figure} Figure 11:

Some lines of OCS, OC34S and O13CS observed at different positions which correspond with different components of Orion KL. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

Table 4:   OCS velocity components from Gaussian fits.

4.2 HCS+

Four transitions of thioformyl cation (HCS+) were detected in the covered frequency range. Line frequencies and observational parameters are given in Table B.2, only available online, which contains the following information: Col. 1 gives the observed (centroid) radial velocities, Col. 2 the peak line temperature, Col. 3 the integrated line intensity, Col. 4 the quantum numbers, Col. 5 the assumed rest frequencies, Col. 6 the energy of the upper level, and Col. 7 the line strength. Rotational constants were derived from the rotational lines reported by Margulès et al. (2003). The adopted dipole moment,  $\mu = 1.958$ D, is taken from Botschwina & Sabald (1985). Line profiles and our best-fit models (see Sect. 5.2) are shown in Fig. A.3.

The HCS+ line profiles display the four Orion's spectra components. In this case, the contribution of the extended ridge component is very weak (see Sect. 5.2).

4.3 H2CS

We detected several transitions of thioformaldehyde (45 transitions of ortho and para states). We also detected H2C34S, H213CS (both p- and o- states) and HDCS isotopologues.

Line parameters are given in Table B.3, only available online, which contains the following information: Col. 1 indicates the isotopologue or the vibrational state, Col. 2 gives the observed (centroid) radial velocities, Col. 3 the peak line temperature, Col. 4 the integrated line intensity, Col. 5 the quantum numbers, Col. 6 the assumed rest frequencies, Col. 7 the energy of the upper level, and Col. 8 the line strength. Figures A.4-A.7 show the lines that are not blended with other species and our best-fit model (see Sect. 5.3). The rotational constants used to derive the line frequencies were taken from the CDMS Catalog[*] for H2CS (Maeda et al. 2008) and H213CS. The H2CS dipole moment, $\mu=1$.6491D, is the one measured by Fabricant et al. (1977). For H2C34S (ortho and para) and HDCS, the line parameters were fitted from all rotational lines reported by Minowa et al. (1997) and the observed lines towards B1 dark cloud by Marcelino et al. (2005). For HDCS, a small $\mu_{\rm b}$ dipole moment is expected, which we assumed to be identical to that of HDCO.

Line profiles and intensities indicate contributions from the extended ridge, compact ridge (very prominent), the plateau, and the hot core.

Table B.4, only available online, provides the parameters of selected lines of H2CS and its isotopologues obtained assuming Gaussian fits to the line profiles. We show only one narrow component fit (a blend of compact ridge, extended ridge, and hot core) because the wide component (plateau) cannot be fitted due to blending with other species. The main component contribution is the compact ridge. We note that for H2CS (ortho and para), $v_{\rm LSR}$, and $\Delta v$tend to values similar to these of the hot core when the $K_{\rm a}$ quantum number increases.

4.4 CS

Three transitions (J = 2-1, 3-2, 5-4) of carbon monosulfide substitutions C32S, C34S, and C33S along with four lines of 13CS and 13C34S (J = 2-1, 3-2, 5-4, 6-5) were detected. For C36S, 13C33S, and vibrationally excited CS (v=1), we present only tentative detections. Line frequencies and observational parameters are given in Table B.5, only available online, which contains the following information: Column 1 indicates the isotopologue or the vibrational state, Col. 2 gives the observed (centroid) radial velocities, Col. 3 the peak line temperature, Col. 4 the integrated line intensity, Col. 5 the quantum numbers, Col. 6 the assumed rest frequencies, Col. 7 the energy of the upper level, and Col. 8 the line strength. Line profiles for transitions that are not blended with other features are shown in Fig. A.8. The spectroscopic constants for CS and C34S are taken from Gottlieb et al. (2003), those of 13CS, C33S, C36S, 13C34S, and 13C33S from Ahrens & Winnewisser (1998), and those of CS v=1 come from Kim & Yamamoto (2003). Dipole moments ($\mu=1$.958D for CS v=0 and $\mu=1$.936D for CS v=1) were taken from Winnewisser & Cook (1968).

Line profiles from the most abundant isotopologues display the four Orion KL spectral components. At 3 mm and 2 mm, the ridge and the plateau emission dominate, at 1 mm the presence of the hot core component in the line profile is very significant. For the less abundant isotopologues (C36S, 13C34S and 13C33S), the compact ridge and hot core components are responsible for most of the line emission. The emission of CS vibrationally excited states comes mainly from the hot core component.

Line parameters for CS, C34S, C33S, 13CS, and 13C34S are given in Table B.6, only available online.

4.5 CCS

\begin{figure} \par\includegraphics[width=13.5cm,clip]{13501fg12.eps}\vspace*{-2mm} \end{figure} Figure 12:

Observed lines (offseted histogram) and model (thin curves) of CCS. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

The CCS radical ($^3\Sigma$ ground electronic state) has several transitions in the surveyed frequency range. Detected lines and main spectroscopic parameters are given in Table B.7, only available online, containing the following information: Col. 1 gives the observed (centroid) radial velocities, Col. 2 the peak line temperature, Col. 3 the quantum numbers, Col. 4 the assumed rest frequencies, Col. 5 the energy of the upper level, and Col. 6 the line strength. Rotational constants were taken from Yamamoto et al. (1990) and the dipole moment,  $\mu = 2.88$ D, comes from Lee (1997). Figure 12 shows the detected transitions that are unaffected by line overlap.

Owing to the line emission weakness, it is difficult to distinguish the different spectral cloud components in the observed line profiles. To reproduce the line intensities (see Sect. 5.5), we assumed that the hot core component is responsible for most of the observed emission. However, the line velocity centroid indicates that both the extended and compact ridge components also contribute at the observed emission. Ziurys & McGonagle (1993) found the same velocity components in their CCS observed lines (one detected and two tentative). The much lower abundances of CCS isotopologues and of vibrationally excited CCS prevent us from detecting any of their transitions above the line confusion limit.

4.6 C3S

\begin{figure} \par\includegraphics[width=14cm,clip]{13501fg13.eps} \end{figure} Figure 13:

Observed lines (offseted histogram) and model (thin curves) of C3S. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

Previously, C3S has been observed in cold dark clouds (Kaifu et al. 1987) and in the envelopes of C-rich AGB stars (Bell et al. 1993; Cernicharo et al. 1987a). Sutton et al. (1995) found a possible spectral line towards Orion hot core and compact ridge positions, but its identification as the C3S J=58-57 line was discarded because of the high energy level (475 K).

We report the first detection of C3S in warm clouds. We clearly identified 17 of the 29 rotational transitions covered in the survey. The remaining transitions are blended with lines of other species. Figure 13 shows several C3S detected lines. Line parameters are given in Table B.8, which is only available online, containing the following information: Col. 1 gives the observed (centroid) radial velocities, Col. 2 the peak line temperature, Col. 3 the quantum numbers, Col. 4 the assumed rest frequencies, Col. 5 the energy of the upper level, and Col. 6 the line strength. Rotational constants were taken from Yamamoto et al. (1987) and the dipole moment ( $\mu = 3.704$ D) was assumed to be that measured by Suenram & Lovas (1994). The line centroid velocity indicates that the emission mainly arises from the hot core. As for CCS, we could not detect any C3S isotopologues or vibrationally excited states.

5 Determination of column densities

For all detected species column densities were calculated using an excitation and radiative transfer code developed by J. Cernicharo (Cernicharo 2010, in preparation). Depending on either the selected molecule or physical conditions, we followed either a LVG (Sobolev 1958; Sobolev 1960) or LTE approach. For each cloud component, we assumed uniform physical conditions for the kinetic temperature, density, radial velocity, and line width (Table 2). We adopted these values from the data analysis (Gaussian fits and an attempt to simulate the line widths and intensities with LTE and LVG codes) as representative parameters for the different species. When a change in these values was required (e.g. C3S analysis), we indicate this in the text. Our modeling technique also takes into account the size of each component and its offset position with respect IRc2. Corrections for beam dilution were applied to each line depending on their frequency. The only free parameter is therefore the column density of the corresponding observed species. Taking into account the compact nature of most cloud components, the contribution from the error beam is negligible except for the extended ridge, which has a small contribution for all observed lines.

In addition to line opacity effects, other sources of uncertainty are related to the following:

  • adopting uniform physical conditions assumes that the physical structure of the cloud is simplified. However, parameters such as the size, kinetic temperature, and density gradients of the different components of the cloud are difficult to assess from low resolution single-dish observations. This problem can be partially overcome by analyzing many different molecular species and transitions covering a broad range of excitation conditions, as allowed by our line survey;

  • the angular resolution of any single-dish line survey is modest. Therefore, the emission from different physical components is usually blended and cannot be separated. However, important efforts have been made to separate them spectrally thanks to the availability of a large number of lines from different isotopologues and vibrational states (different opacity regimes) and a wide frequency range (different source coupling regimes);

  • pointing errors, as small as 2'', could introduce important changes in the contribution from each cloud component to the observed line profiles, especially at 1.3 mm. However, the modeled and observed line profiles never differ by more than 20%, which is compatible with the absolute calibration error of our line survey (estimated to be about 15%).


5.1 OCS


Table 5:   Column densities - OCS.

Detailed multi-source LVG excitation and radiative transfer calculations were performed to fit the OCS line emission from the extended ridge, compact ridge, and plateau. Given the lower density in these components (similar or lower than the critical densities of the observed OCS transitions), the OCS level populations should be far from LTE, thus the LVG calculation is much more appropriately adapted to interpreting the data correctly. Collisional cross-sections of OCS-H2 are taken from Green & Chapman (1978), which were calculated for temperatures in the range 10-100 K including levels up to J=13. In addition, we included levels up to J = 40 in our models. Collisional rates for J >13 levels were derived using the energy sudden approximation (Goldflam et al. 1977) and using the $\sigma$ ($0 \geq J$; $J \leq13$) rates. The LTE approximation was assumed for both the hot core and vibrationally excited OCS. For OCS $\nu _2$ = 1 and OCS $\nu_3 = 1$, we changed the velocity width parameter for the hot core component ( $\Delta v = 5$ km s-1) with respect to the value given in Table 2 to provide a closer accurate fit to the line profiles.

The beam coupling strongly affects the observed OCS lines in the different frequency ranges. At 1.3 mm, ${\it HPBW} \simeq 10''$, we lose most of the compact ridge emission when pointing to IRc2. Moreover, the different gas components are not always centered on the beam. Our model takes into account all these spatial structure effects. As an example, Fig. 10 shows the OCS emission at different velocities, with the result that at velocities of between 7 and 11 km s-1, the OCS emission peak is out side the telescope beam at 1.3 mm.

Although the relatively low dipole moment of OCS (0.715 D, Tanaka et al. 1985) helps to keep these lines optically thin, some of them, especially at the higher end of the explored J range, may be optically thick (Schilke et al. 1997; Ziurys & McGonagle 1993). The opacities were taken into account by the LVG and LTE codes. However, both LVG and LTE approximations are more appropriate for optically thin emission; hence, the column density for the main isotopologue obtained with our LVG or LTE calculations should be considered as a lower limit. The derived column densities from the lines shown in Figs. 8, A.1, and 9 are given in Table 5. We also derived the column density of OCS indirectly by means of the column density of its less abundant isotopologues to assess the line opacity effect (OC34S and O13CS assuming isotopic abundances of 32S/34S = 20 and 12C/13C = 45; the adopted isotopic abundances are an average of the values obtained in this work, see Sect. 6). Owing to the low intensity of the lines belonging to these other less abundant isotopologues, implying larger overlap problems, we can only get upper limits for their column density. We estimate the uncertainty to be in the range 20-30% for the results of OCS, O13CS, OC34S, and OCS $\nu_2 = 1$ and around 50% for OC33S, 18OCS, and OCS $\nu_3 = 1$.

The OCS column density derived from the isotopologue emission in the compact ridge and the hot core is four times higher than the column densities obtained from the lines of the main isotopologue. It appears that the OCS lines emerging from the hot core and the compact ridge are saturated, this is consistent with the optical depth estimation of Schilke et al. (1997) for the 29-28 transition of OCS ($\tau=3.5$ assuming 32S/34S = 22.5). For the plateau and the extended ridge, we obtained similar column densities using both methods indicating that the OCS main isotopologue emission towards these components is optically thin.

Table 6:   Column densities - H2CS.

The component with the highest OCS column density corresponds to the hot core with N(OCS) $_{\rm hot\;\;core} \simeq (5 \pm 1)\times10^{16}$ cm-2. In addition, to obtain a good fit to the line profiles we need to add a contribution from the extended ridge component of N(OCS) $_{\rm extended\;\;ridge} =(2.4\pm0.5)\times 10^{15}$ cm-2. However, the analysis of the emission from positions in the extended ridge far away from IRc2 (see Fig. 11) implies a much lower column density, N(OCS) $_{\rm extended\;\;ridge\;\;position} = (2.0 \pm 0.5) \times 10^{14}$ cm-2. Hence, it appears that the extended ridge also undergoes either a volume density increase or an OCS abundance increase in the direction of the hot core. Otherwise, the strong emission emerging from the hot core may affect the excitation of the OCS energy levels in the extended ridge (radiative scattering, see the HCO+ and HCN cases discussed by Cernicharo & Guèlin 1987 and González-Alfonso & Cernicharo 1993). Our results infer OCS column densities more than ten times higher than in many previous studies (Blake et al. 1987; Johansson et al. 1984; Turner 1991). These works provided beam-average column densities and do not address the determination of the column density for each cloud component. The beam-averaged results from Sutton et al. (1995) can be converted into source-averaged column densities after multiplying by the beam dilution factor ($\simeq$3 for the hot core component, assuming $d_{\rm hot\;\;core}=10''$and FWHM $_{\rm JCMT}=13.7''$ at the observed frequencies). We note that Sutton et al. (1995) found a corrected-source-averaged column density of $\simeq$ $3\times10^{16}$ cm-2 and Persson et al. (2007) estimated a source-average column density of $\simeq$ $1.7 \times 10^{16}$ cm-2 both for the hot core position whose values are 2 and 3 times lower than our result, respectively. These values compare well with our measurement above.

We estimated a difference varying from 5% to 15%, depending on the molecule, between LTE or LVG (for molecules having collisional rates available) results.

5.2 HCS+

We determine the HCS+ column density using collisional rates HCS+-He from Monteiro (1984).

To reproduce the line profiles more accurately, we changed the $v_{\rm LSR}$ of the compact ridge given in Table 2, adopting $v_{\rm LSR} = 9$ km s-1. The modeled lines are shown in Fig. A.3 (thin curves). We obtain the following column densities: $(5\pm 2)\times10^{13}$, $(5 \pm1)\times10^{13}$, $(8 \pm2)\times10^{13}$, and $(1.0 \pm 0.3) \times 10^{12}$ cm-2 for the hot core, plateau, compact ridge, and extended ridge, respectively. To reproduce the 3 mm line of HCS+, we had to significantly reduce the extended ridge column density with respect to the values of the other components. The HCS+ column density towards the hot core has to be considered with caution because of its weak line emission contribution.

Based on the observed values of $v_{\rm LSR}$ ($\simeq$9 km s-1) and $\Delta v$ ($\simeq$4 km s-1) and the reduced fractional ionization in the high density gas, Johansson et al. (1984), Blake et al. (1986), and Schilke et al. (1997) exclusively attributed the emission of this molecule to the extended ridge. These first two sets of authors reported beam-average column densities of  $4\times10^{13}$ (Johansson et al. 1984) and $1.6\times10^{13}$ cm-2 (Blake et al. 1986). Sutton et al. (1995) found emission of HCS+ from the five positions of their survey (extended ridge, hot core, compact ridge, northwest plateau, and southeast plateau); they obtained beam-averaged column densities of N(HCS $^+) = 6\times 10^{13}$ cm-2 for the extended ridge and N(HCS $^+) \simeq 10^{13}$ cm-2for the remaining positions. Schilke et al. (2001) found a questionable assignment of HCS+ J=16-15 ( $E_{\rm up} = 278.5$ K, emission coming from the hot core).

To compare the abundances of different molecular ions, we calculated the column density of H13CO+, assuming the same physical conditions we adopted for HCS+. As a total column density (sum of all components), we derive N(H13CO $^+) = 5.3\times 10^{13}$ cm-2; considering an isotopic abundance 12C/13C = 45 (see Sect. 6), we obtain N(HCO+)/N(HCS $^+) \simeq 13$. A similar value was given by Johansson et al. (1984) (in the extended ridge component), whereas Blake et al. (1986) obtained N(HCO+)/N(HCS $^+) \simeq 94$ (the H13CO+ line was strongly blended with HCOOCH3 and its $T_{\rm A}$* was estimated by subtracting the contribution of methyl formate from the overall emission). Assuming that the main production and destruction mechanisms for HCO+ and HCS+ are the reaction of H3+ with CO and CS and the dissociative recombination of HCO+ and HCS+ with electrons, we deduce that in chemical equilibrium N(CS)/N(CO $) = 1.5\times 10^{-3}\times[N$(HCS+)/N(HCO+) $] \simeq1.5\times10^{-4}$ (see Sect. 5.4 for the obtained CO/CS abundance ratio).

5.3 H2CS

Table 7:   Ortho/Para ratios - H2CS.

Owing to the lack of collisional rates for this molecule, we assumed LTE excitation in the H2CS column density calculations. Figures A.4-A.7 show the modeled line profiles (thin curves) for selected lines of H2CS, H2C34S, H213CS, and HDCS. Results are given in Table 6. The higher column densities correspond to the the compact ridge and the hot core component ( $1.5 \times 10^{15}$ and  $1.6 \times10^{15}$, respectively). The hot core is primarily responsible for the line emission from transitions with $K_{\rm a}>3$. Our column density results agree with those obtained in previous studies (Schilke et al. 1997; Sutton et al. 1995; Turner 1991; Blake et al. 1987; Sutton et al. 1985).

Since we derived the ortho- and para- H2CS column densities independently, we also computed the ortho-to-para ratios of this molecule for the different components (Table 7). The hottest, densest component (hot core) has an ortho-to-para ratio $\simeq$1.8 $\pm$ 0.7, whereas the extended ridge (the coldest, least dense component) has a ratio $\simeq$3 $\pm$ 1. Taking into account the uncertainties in these ratios, we conclude that the ratio is compatible with the statistical weight of 3.

Assuming the same hypothesis than for H2CS, we derived a H213CO column density of $\simeq$ $1.2 \times 10^{15}$ cm-2 (sum of all components). Adopting the isotopic abundance 12C/13C = 45 (see Sect. 6), we derive N(H2CO)/N(H2CS $) \simeq 12$, very close to the ratio N(HCO+)/N(HCS+) calculated in the previous section. Unlike H2CO, for which efficient gas-phase synthetic pathways have been studied in the laboratory, analogous reactions that might form thioformaldehyde do not occur. As an example, the chemical model of Nomura & Millar (2004) cannot reproduce, by several order of magnitudes, the observed N(H2CO)/N(H2CS) abundance ratio in hot cores.

5.4 CS

Table 8:   Column densities of CS, CS isotopologues, and CS vibrationally excited.

Our CS column densities were derived using collisional CS-H2 rates from Lique & Spielfiedel (2007). They are given in Table 8 and the modeled line profiles are shown in Fig. A.8.

The CS lines are optically thick and therefore the column density for each cloud component may be significantly underestimated. Lines from CS isotopologues are, however, optically thin so that we can estimate the column density of CS by assuming a value for the isotopic ratios. Assuming 32S/34S = 20 (see Sect. 6), the column density of CS in the hot core component is $1.4\times10^{16}$ cm-2. A value 2 times larger is obtained if we assume that 12C/13C = 45 (see Sect. 6). On average, we obtain N(CS) $_{\rm hot\;\;core}=2.1\times10^{16}$ cm-2. This CS column density is about 10-30 times larger than found in many previous studies (Lee et al. 2001; Blake et al. 1987; Schilke et al. 2001). In these earlier studies, the results were beam-averaged CS column densities derived from a LTE analysis. Sutton et al. (1995) obtained a corrected-source-averaged column density of  $1.5 \times 10^{16}$ cm-2 for the hot core, in agreement with both our result and the source-averaged CS column density obtained by Comito et al. (2005).

For the less abundant isotopologues (13C33S, C36S) and for CS vibrationally excited states, we can only derive upper limits due to the weakness of the lines and the large overlap with other features (see Fig. A.8, bottom panels. Among the three lines of CS v=1, only one seems to be detected).

The components with the largest CS column density are the hot core and the plateau, the latter having the larger value. However, in the emission of the CS isotopologues the hot core dominates (in agreement with Schilke et al. 2001).

To compare the CS and CO abundances, we calculated the column density of C18O in each component. We obtain N(C18O) of $1.5 \times 10^{16}$, $1.5 \times 10^{16}$, $1\times 10 ^{17}$, and $2\times10^{17}$ cm-2 for the extended ridge, compact ridge, plateau, and hot core, respectively. We have to include a high velocity plateau component with $v_{\rm LSR}=10$, $\Delta v=55$ km s-1, and a column density of $5 \times 10^{16}$ cm-2 to reproduce the line profiles. Assuming the isotopic abundance 16O/18O = 250 (see Sect. 6), we determine the column density of CO in each component to be $3.75 \times 10^{18}$, $3.75 \times 10^{18}$, $2.5 \times 10^{19}$, $5.0 \times 10^{19}$, and $1.25 \times10^{19}$for the extended ridge, compact ridge, plateau, hot core, and high velocity plateau, respectively. Therefore, the corresponding N(CS)/N(CO) ratio is $2.0\times10^{-4}$, $2.0\times10^{-3}$, $1.0\times10^{-4}$, and $4.1\times10^{-4}$ for the extended ridge, the compact ridge, the plateau, and the hot core, respectively. In all cases, this ratio is in good agreement with the N(CS)/N(CO $)\simeq1.5\times10^{-4}$, derived from N(HCS+)/N(HCO+).

When we fitted the line emission of CS, we found that it was difficult to distinguish the contribution of the high velocity plateau to the line profiles from those of the other components. Assuming N(CS)/N(CO $) = 1.5\times10^{-4}$, the column density of CS in the high velocity plateau would be $\simeq$ $2.0\times10^{15}$(peak  $T_{\rm A}\simeq 5$ K).

5.5 CCS

Collisional cross-sections of CCS-H2 were extrapolated from those of OCS (Green & Chapman 1978) using the IOS approximation for a $^3\Sigma$ molecule (see Corey 1984; Corey & McCourt 1984; Fuente et al. 1990). In this case, we changed the velocity parameters for the hot core component with respect to the parameters given in Table 2 to reproduce the line profiles more accurately. The new values are $v_{\rm LSR} = 5$ km s-1 and $\Delta v = 6$ km s-1.

The modeled lines are shown in Fig. 12 (thin lines). The values of the column densities are: $(5.0\pm 1.3) \times 10^{13}$, $(7.0\pm 1.8) \times 10^{12}$, $(2.0\pm0.5)\times10^{12}$, and $(2.0\pm0.5)\times10^{12}$ cm-2 for the hot core, the compact ridge, the extended ridge, and the plateau, respectively. We note that Turner (1991) reported the first tentative detection of CCS in this source with a beam-averaged column density of $4.8 \times 10^{12}$ cm-2.

5.6 C3S

For this molecule, we considered that only the hot core component is responsible for the emission, hence we assume LTE excitation. We chose the same physical conditions for this component as in the CCS analysis. Figure 13 shows the modeled line profiles for some selected lines, for N(C3S $) = (2.0\pm0.5)\times10^{13}$ cm-2. Taking into account the CCS column density, we derive the ratio CCS/C3S = 2.5 which is similar to the value of $\simeq$3.5 found in the dark cloud TMC-1 by Hirahara et al. (1992) and the value of $\simeq$3 found in the envelope of the C-rich star IRC+10216 by Cernicharo et al. (1987a) (note that we corrected this last value for the dipole moment of C3S adopted in this study, 3.7 versus 2.6 in Cernicharo et al. 1987a).

5.7 Non-detected CS-bearing molecules

OC3S.- The molecule OC3S has not yet been detected in space. The rotational constants used to derive the line frequencies were taken from Winnewisser et al. (2000). The dipole moment we used ($\mu=0$.63D) is quoted in Matthews et al. (1987). Assuming the same physical conditions as those derived for OCS, we obtain an upper limit to its column density of $2\times 10^{13}$ cm-2. This result provides an OCS/OC3S abundance ratio larger than 100.

H2CCS.- For this molecule, we derived its line frequencies with the rotational constants given in Winnewisser et al. (1980); some distortion constants were fixed to the value obtained from infrared data by McNaughton (1996). The dipole moment ($\mu=1$.02D) was taken from Georgiou et al. (1979). We derive an upper limit to the column density of thioketene of $2.4\times 10^{14}$ cm-2, which infers a H2CS/H2CCS abundance ratio near 20. This molecule has not yet been detected in space.

HNCS.- Isothiocyanic acid is a pseudolinear molecule with a large A rotational constant, similar to that of isocyanic acid, HNCO. Only transitions up to Ka = 1 have been observed in the interstellar medium (in SgrB2 by Frerking et al. 1979). However, this molecule has not yet been detected in Orion. Turner (1991) reported a tentative detection of HNCS in Orion and listed five transitions as detected, but three of them were not reliable. Turner derived an LTE column density of $9.3 \times 10^{12}$ cm-2 assuming $T_{\rm rot} = 50$ K based on a single transition. For frequency predictions, we used the rotational constants presented by Niedenhoff (1995). The a-dipole moment component ( $\mu_{\rm a}=1$.64D) was mentioned in Szalanski et al. (1978). We derive an upper limit to the column density of  $1.1 \times 10^{14}$ cm-2. Marcelino et al. (2009) calculated N(HNCO) towards Orion KL from this survey, to be N(HNCO $) \simeq 9.4 \times 10^{15}$ cm-2; these values imply a HNCO/HNCS ratio >85.

HOCS+.- Spectroscopic constants are taken from Ohshima & Endo (1996). The dipole moment ($\mu=1$.517D) was calculated by Wheeler et al. (2006). We obtain an upper limit to the column density of this cation of N(HOCS $^+) \la 3 \times 10^{13}$ cm-2. This result and the high column density of OCS may indicate that this ion is efficiently destroyed by dissociative recombination to produce OCS + H (Charnley 1997).

NCS.- Thiocyanogen has not yet been detected in space. The rotational constants used to derive the line frequencies were taken from CDMS Catalog. The dipole moment ($\mu=2$.45D) is from an ab initio calculation by H. S. P. Müller (unpublished). We derive here N(NCS $) \la 7 \times 10^{13}$ cm-2.

6 Isotopic abundances

From the derived column densities for OCS, H2CS, CS, and their isotopologues, we can now estimate the isotopic abundance ratios. They are given in Table B.9, which is only available online. The isotopic ratios that are not discussed in the following but given in Table B.9 are consistent with the solar values (taking into account a factor of 2 introduced by the 12C/13C solar abundance, see below).

Because of the large opacity of the OCS emission in the hot core and the compact ridge, we can only provide a lower limit to the OCS column density ratios in these components. In the same way, the column density ratios O13CS/O13C34S, OC34S/O13C34S, OCS/17OCS, OCS/OC36S, 13CS/13C34S, C34S/13C34S, 13CS/13C33S, C33S/13C33S represent lower limits due to the low intensity of the lines and the strong blending overlap with other molecular lines. From the remaining column density ratios of Table B.9, we estimated the following isotopic abundances:

12C/13C: From the OCS, lines we obtained a column density ratio of N(OCS)/N(O13CS $) = 33 \pm12$ and $25 \pm9$ for the extended ridge and the plateau, respectively. From H2CS (o- and p-), we obtained N(H2CS)/N(H213CS $) = 42 \pm16$, $50\pm20$, $47\pm18$, and $20 \pm 9$ for the extended ridge, compact ridge, plateau, and hot core, respectively. The values estimated with the H2CS lines are slightly higher (except the value for the hot core) than those derived from OCS, which is indicative of a low opacity in the OCS lines coming from the plateau and the extended ridge, and in the hot core emission of H2CS. We find an average value from our study of 12C/13C = $45\pm 20$. Previous studies found that N(OCS)/N(O13CS $) \simeq 30{-}40$ (Johansson et al. 1984) and 12C/13C $\simeq$ 30-40 (Blake et al. 1987, who used several molecules -CS, CO, HCN, HNC, OCS, H2CO, CH3OH- to achieve tighter constraints), N(CN)/N(13CN $) = 43\pm7$(Savage et al. 2002), and N(CH3OH)/N(13CH3OH $) = 57\pm 14$(Persson et al. 2007). The solar isotopic abundance of 12C/13C = 90 (Anders & Grevesse 1989) is approximately a factor 2 higher than the values obtained in Orion. This ratio is understood to be a sensitive indicator of the degree of galactic chemical evolution and the solar isotope value reflects conditions in the interstellar medium at an earlier epoch (Savage et al. 2002; Wyckoff et al. 2000).

32S/34S: From the values obtained of N(OCS)/N(OC34S) and p-/o- N(H2CS)/N(H2C34S), we estimate an average value 32S/34S = $20\pm6$, in agreement with the solar isotopic abundance and with previous studies (N(OCS)/N(OC34S $) \simeq 16$ by Johansson et al. 1984, 32S/34S $\simeq$ 13-16 by Blake et al. 1987, N(32SO)/N(34SO $) = 21\pm 6$, and N(32SO2)/N(34SO2 $) = 23\pm 7$ by Persson et al. 2007).

32S/33S: From N(OCS)/N(OC33S) in the extended ridge, we obtained a 32S/33S ratio three times lower than the solar abundance. It is possible that we overestimated the column density of OC33S in the extended ridge because we had only three blending-free transitions to compare to the model (see Sect. 5.1). For the plateau component, we obtained OCS/OC33S = $75\pm29$, in close agreement with the solar isotopic abundance. Persson et al. (2007) obtained 32S/33S $\simeq$ 103-113.

33S/34S: The 33S/34S abundance ratio is $\simeq$ $0.22 \pm 0.10$ and $\simeq$ $0.37\pm 0.10$ from OCS and CS respectively, i.e., very close to the solar values and in agreement with Persson et al. (2007).

16O/18O: This ratio was inferred from N(OCS)/N(18OCS). The ratio 16O/18O obtained (250 $\pm$ 135 for the plateau) is two times lower than the solar value for all the cloud components. However, taking into account the uncertainties in the column density of both the plateau and the extended ridge, we consider that the true values may be compatible with the solar one. Similar conclusions can be obtained from the observed 18OCS/OC34S and 18OCS/OC33S abundance ratios (see Table B.9).

D/H: We found a N(HDCS)/N(H2CS) column density ratio of $0.07 \pm 0.03$, $0.040 \pm 0.012$, $0.040 \pm 0.012$, and $0.05 \pm 0.02$ for the extended ridge, compact ridge, plateau, and hot core, respectively. Pardo et al. (2001) found a N(HDO)/N(H2O) abundance ratio in the range 0.004-0.01 in the plateau component, and Persson et al. (2007) derived 0.005, 0.001, and 0.03 for the large velocity plateau, the hot core, and the compact ridge, respectively. For N(HDCO)/N(H2CO), Persson et al. (2007) derived a value of 0.01 (for the compact ridge), whereas Turner (1991) found $\simeq$0.14 (note that this value is too high and is incompatible with the H2CO column density reported in this work and by several authors, see Sutton et al. 1995). Water and formaldehyde present its higher deuterium fractionation in the compact ridge component. Schilke et al. (1992) derived the DCN/HCN column density ratio of 0.001 and 0.01-0.06 for the hot core and the ridge region, respectively. Studies of hot core deuterium chemistry (Rodgers & Millar 1996) conclude that the D/H ratios of molecules injected from the dust mantles to the hot gaseous medium do not undergo significant modifications and should represent those of the original mantles for molecules that were efficiently deposited during the cold phase (such as water, methanol, and formaldehyde). However, H2CS is not considered to be a molecule deposited in the original mantles and its high deuteration may be caused by gas phase reactions. Very high deuterium fractionation has been also found in cold molecular clouds (Marcelino et al. 2005; Roberts et al. 2002).

7 Vibrational temperatures

We report the first space detection of rotational line emission from OCS $\nu_2 = 1$ and $\nu_3 = 1$ vibrational levels. Given the high energy of these vibrational levels, the emission is dominated by the hot core component. From the column density obtained for OCS in the ground and the vibrationally excited states, we can estimate a vibrational temperature taking into account that

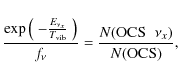
\begin{displaymath}\frac{\exp \left( \begin{array}{c} - \frac{E_{\nu_x}}{T_{\rm ... ...ht)}{f_{\nu}} = \frac{N ({\rm OCS}\;\;\nu_x)}{N ({\rm OCS})}, \end{displaymath} (1)

where $E_{\nu_x}$ is the energy of the vibrational state ( $E_{\nu_{2}} = 748.7$ K; $E_{\nu_{3}}= 1235.9$ K), $T_{\rm vib}$ is the vibrational temperature, f$_{\nu}$ is the vibrational partition function, N(OCS $\nu_x$) is the column density of the vibrational state, and N(OCS) is the column density of OCS in the ground state. The vibrational partition function can be approximated by
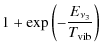
                          $\displaystyle f_{\nu}$ = $\displaystyle 1 + \exp \left(- \frac{E_{\nu_{3}}}{T_{\rm vib}} \right)$  
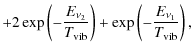
    $\displaystyle + 2 \exp \left( - \frac{E_{\nu_{2}}}{T_{\rm vib}} \right) + \exp \left( - \frac{E_{\nu_{1}}}{T_{\rm vib}} \right),$ (2)


which, for low $T_{\rm vib}$ leads to $f_{\nu} \simeq 1$.

From the observed lines, we obtain $T_{\rm vib} = 210 \pm 10$ K for OCS $\nu_2 = 1$, and $T_{\rm vib} =210\pm60$ K for OCS $\nu_3 = 1$. These values are similar to the averaged kinetic temperature we adopted for the hot core component (225 K). A direct comparison of the derived $T_{\rm vib}$ for OCS with the average Tk assumed for the gas in the hot core is difficult. Vibrational excitation is expected to depend strongly on temperature and density gradients in that region. It is also difficult to ascertain if either IR dust photons or molecular collisions dominate the vibrational excitation of OCS given the lack of collisional rates for that species. Nevertheless, assuming that ro-vibrational collisional rates for OCS are similar to those of SiO or SiS (Tobola et al. 2008), $\sigma$( $\nu_2=0\rightarrow1300$ K $) \simeq 10^{-14}$ cm3 s-1, we find that, even for H2 densities as high as 109 cm-3, the net collisional rate is well below the spontaneous de-excitation rates from $\nu _2$ and $\nu _3$ to the ground state. Hence, the population of these levels have to be mainly caused by IR photons from the dust. That the OCS rotational lines are narrower in vibrationally excited states than in $\nu=0$ may indicate that this IR pumping operates in a more compact region with a shallower velocity gradient. Higher angular resolution observations are necessary to resolve any possible excitation gradient and temperature profile in this component.

We also calculated the vibrational temperature for the first vibrationally excited state of CS ( $E_{\textit{v}=1} = 1830.4$ K). With the column density results of the CS hot core component ( $2.1 \times 10^{16}$ cm-2) and of CS $\textit{v} = 1~(\la 5\times10^{13}$ cm-2), we obtain an upper limit to the vibrational temperature of $\simeq$300 K, which agrees with the values obtained for vibrationally excited OCS. However, in this case we could claim an inner and hotter emitting region for vibrationally excited CS.

Nevertheless, since the vibrationally excited gas is not necessarily spatially coincident with the ground state gas, the derived vibrational temperatures have to be considered as lower limits.

Table 9:   Column density ratios.

8 Discussion and conclusions

The power of spectral line surveys at different mm and sub-mm wavelengths to search for new molecular species and derive the physical and chemical structure of molecular sources has been demonstrated (Blake et al. 1987; Sutton et al. 1995; Cernicharo et al. 2000; Schilke et al. 2001; Pardo & Cernicharo 2007). The main and final goal of our line survey is to provide a consistent set of molecular abundances derived from a systematic analysis of the molecular rotational transitions. Our line survey allows us to obtain with unprecedented sensitivity and completeness the census of the identified and unidentified molecules in Orion KL. These kinds of studies are necessary to understand the chemical evolution of this archetypal star-forming region. Moreover, that many rotational transitions of the same molecule have been observed in different frequency ranges (the 3 mm window illustrates more clearly the extended ridge component, whereas the 1.3 mm one identifies the warmest gas at the hot core and along the compact ridge), provide strong observational constraints on the source structure, gas temperature, gas density, and molecular column densities.

8.1 Molecular abundances

Molecular abundances were derived using the H2 column density calculated by means of the C18O column density provided in Sect. 5.4, assuming that CO is a robust tracer of H2 and therefore their abundance ratio is roughly constant, ranging from CO/H $_2 \simeq 5\times10^{-5}$ (for the ridge components) to $2\times10^{-4}$ (for the hot core and the plateau). In spite of the large uncertainty in this calculation, we include it as a more intuitive result for the molecules described in the paper. We obtained N(H $_2) = 7.5\times10^{22}$, $7.5\times10^{22}$, $2.1\times10^{23}$, and $4.2\times10^{23}$ cm-2 for the extended ridge, compact ridge, plateau, and hot core, respectively. In addition, we assume that the H2 column density spatially coincides with the emission from the species considered. Our estimated source average abundances for each Orion KL component are summarized in Table B.10 (only available online), together with comparison values from other authors (Sutton et al. 1995 and Persson et al. 2007). The differences between the abundances shown in Table B.10 are mostly due to the different H2 column density considered, to the assumed cloud component of the molecular emission and discrepancies in the sizes of these components.

8.2 Column density ratios

To compare the chemistry of the different spectral cloud components related to sulfur-bearing carbon chains molecules, we derived the column density ratios showed in Table 9. This table also shows the ratios found in chemical models of hot cores, other results found in the literature for Orion, and other sources (the dark cloud TMC-1 and the hot core G327.3-0.6). We found good agreement between our ratios and those derived by Persson et al. (2007), both set of values corresponding to Orion KL. For the other molecular hot core, we noted a large difference in the ratio CO/CS. This discrepancy also occurs with the chemical models computed by Nomura & Millar (2004). We note that the chemical models cannot provide realistic values for the H2CO/H2CS column density ratio, as we have discussed in Sect. 5.3. TMC-1 exhibits ratios very different by those of hot cores, as expected from their different chemical and physical conditions.

We find N(C34S/OC34S $)\simeq 0.3$, 0.6, 0.2, and 0.2 in the extended ridge, the compact ridge, the plateau, and the hot core, respectively. The chemical models for hot cores computed by Nomura & Millar (2004) infer that N(CS)/N(OCS) = 0.2 (at 104 years). The N(CS)/N(CCS) abundance ratio is 300, 1143, 1000, and 280 for the extended ridge, the compact ridge, the plateau, and the hot core, respectively. For the hot core, we also derive N(CS)/N(C3S) $_{\rm Hot\;\;Core}=700$. Both CCS and C3S have not been studied in the chemical models available for hot cores. As expected, these values are very different from those derived in the dark cloud TMC-1 for which N(CS)/N(CCS)=2.2 and N(CS)/N(C3S)=7.8(Hirahara et al. 1992). However, we obtain N(C2S)/N(C3S) = 2.5, very similar to the 3.4 value derived by Hirahara et al. (1992) in TMC-1 (cyanopolyyne peak) and the value of $\simeq$3 found in the envelope of the C-rich star IRC+10216 by Cernicharo et al. (1987a).

This is a surprising result because CCS is considered to be a typical molecule in cold dark clouds. Moreover, C3S is found only in the hot core, which is indicative of an enhancement in the production of CCS and C3S in the warm and dense gas. Although spectral confusion is large when observing weak lines such as those of C3S, thanks to our survey, we detected 17 lines. They cover from the J=14-13 ( $E_{\rm up}=29.1$ K with $v_{\rm LSR}=4.2$ km s-1) up to J=47-46 ( $E_{\rm up}=313$ K with $v_{\rm LSR}=4.7$ km s-1), thus, we are fully confident in its detection. In addition, the observed velocities correspond definitively to the hot core.

Our results indicate that C3S is efficiently formed in warm regions. That the C2S/C3S abundance ratio is similar to that of dark clouds or evolved stars may indicate that these species formed in the gas phase. Gas phase chemical models predict C2S/C3S $\simeq$ 2 and 0.3 in TMC-1 and IRC10216, respectively (Walsh et al. 2009; Cordiner & Millar 2009).

8.3 Orion KL cloud structure

We have analyzed and discussed the emission lines of the studied molecules in terms of the four well-known Orion KL cloud components (hot core, extended ridge, compact ridge, and plateau). However, low angular resolution does not enable us to detect any possible variation in the excitation temperature across the hot core and the other Orion components. A more complex physical structure has been observed with sensitive interferometers (Beuther et al. 2005; Wright et al. 1996; Plambeck et al. 2009; Zapata et al. 2009a). Further analysis of our survey indicates that at the position of IRc2, the lines of both SiS and the SiO maser emission show a velocity component at 15.5 km s-1, an additional cloud component to those described above. Owing to the high energies involved in some emission lines, Schilke et al. (2001) and Comito et al. (2005) claimed that a hotter component exists at the hot core $v_{\rm LSR}$ in their surveys at high frequency. In the same way, we detected the emission of vibrationally excited OCS and CS at the hot core LSR velocity. In spite of the low angular resolution of our data, the amount of molecules, the large number of transitions, and the different vibrationally excited states found in the survey permit us to derive realistic source-averaged physical and chemical parameters.

9 Summary

We have presented an IRAM 30-m line survey of Orion KL with the highest sensitivity achieved to date. Because of the wide frequency range covered and high data quality, we intent to present the line survey in a series of papers focused in different molecular families. In this paper, we have presented the study of the emission from OCS, its isotopologues, and its vibrationally excited states ($\nu_2 = 1$ and $\nu_3 = 1$), as well as HCS+, H2CS, CS, CCS, CCCS, and different isotopic substitutions of them. The four well known components of Orion (hot core, plateau, extended ridge and compact ridge) contribute to the observed emission from the main isotopologues of all these molecules except for C3S, which we only detected in the hot core component.

Column densities have been calculated with radiative transfer codes based on either the LVG or the LTE approximations, taking into account the physical structure of the source. Results are provided as source-averaged column densities. In this way, our column density for OCS are between 4 to 10 times higher than the beam-averaged ones provided in previous surveys. Our column density derived for the hot core component compares well with the values obtained by Sutton et al. (1995) and Comito et al. (2005). Among those studied in this paper in all the cloud components, OCS appears as the most abundant species.

We have also reported on the first detection in space of OCS in the vibrationally excited states $\nu_2 = 1$ and $\nu_3 = 1$. This emission arises mostly from the hot core component. The resulting vibrational temperature ($\simeq$210 K) is similar to the kinetic temperature of this component ($\simeq$225 K).

For HCS+, we have to significantly reduce the contribution of the extended ridge component to reproduce all lines arising in our survey. The derived N(HCS+)/N(HCO+) ratio is in agreement with the observed N(CS)/N(CO) ratio in terms of chemical equilibrium.

The statistical value of 3 for the ortho-to-para ratio has been confirmed by the study of the emission lines of H2CS and its isotopologues. We have derived an abundance ratio of H2CS/HDCS $\simeq$ 20.

For CS, we have analyzed the emission of 7 distinct isotopologues and the vibrational state v = 1. The lines of the main isotopologue are optically thick and therefore we have derived the column density by means of the isotopologues (assuming the derived isotopic abundances from this work). Our results are in agreement with those of Sutton et al. (1995) and Comito et al. (2005). The vibrational temperature calculated for CS v = 1 (tentative detection) is less than 300 K, in agreement with those values obtained for OCS $\nu_2 = 1$ and $\nu_3 = 1$. However, this result may indicate that there is an inner, hotter region of emission from vibrationally excited CS that is difficult to resolve with our low angular resolution observations.

Since the intensity of the C2S and C3S lines is already weak, we could not detect either their isotopologues or their vibrationally excited states. We derived column densities of $5\times10^{13}$ cm-2 and  $2\times 10^{13}$ cm-2, respectively in the hot core component from the detected lines. We have detected C3S for the first time in warm regions. Finally, we have derived upper limits to the column density of non-detected molecules (-CS bearing species), obtaining the maximum value for thioketene N(H2CCS $)\la 2.4\times 10^{14}$ cm-2.

From the column density results, we have derived several abundance ratios that permit us to provide the following average isotopic abundances: 12C/13C = $45\pm 20$, 32S/34S = $20\pm6$, 32S/33S = $75\pm29$, and 16O/18O =  $250 \pm 135$(all of them in agreement with the solar isotopic abundances, see Sect. 6 and Table B.9, only available online).

Orion KL has been observed and described by a large number of authors. Single-dish observations cannot provide details about the complex physical structure and true spatial distribution that interferometric observations do reveal. It is not possible, for example, to track the variation in the excitation temperature in the hot core region that appear to exist according to the vibrational temperature derived from vibrationally excited CS. The need from a large contribution from the extended ridge component before OCS can reproduce the line profiles towards the hot core, relative to the contribution of the ambient molecular cloud (far away IRc2), implies that at the border between the hot core and the extended ridge, there is a physical structure with density and temperature gradients that the single-dish telescopes cannot resolve. Higher angular resolution observations are necessary to describe this source in detail and to reveal its physical structure. Interferometric instruments such as Plateau de Bure, SMA, or the future ALMA are necessary to avoid spectral confusion related to varying physical conditions inside large beams and to resolve the source structure. Nevertheless, the 30 m line survey of Orion will provide a consistent determination of column densities of all species with emission above 0.1 K.

Acknowledgements
We thank the Spanish MEC for funding support through grants AYA2003-2785, AYA2006-14876, AYA2009-07304, ESP2004-665 and AP2003-4619 (M. A.), Consolider project CSD2009-00038 the DGU of the Madrid Community government for support under IV-PRICIT project S-0505/ESP-0237 (ASTROCAM). Javier R. Goicoechea was supported by a Ramón y Cajal research contract from the Spanish MICINN and co-financed by the European Social Fund.

References

  1. Ahrens, V., & Winnewisser, G. 1998, Z. Naturforsch, 54a, 131 [Google Scholar]
  2. Anders, E., & Grevesse, N. 1989, GeCoA, 53, 197 [Google Scholar]
  3. Bell, M. B., Avery, L. W., & Feldman, P. A. 1993, ApJ, 417, L40 [Google Scholar]
  4. Beuther, H., Zhang, Q., Greenhill, L. J., et al. 2004, ApJ, 616, L31 [Google Scholar]
  5. Beuther, H., Zhang, Q., Greenhill, L. J., et al. 2005, ApJ, 632, 355 [NASA ADS] [CrossRef] [Google Scholar]
  6. Beuther, H., & Nissen, H. D. 2008, ApJ, 679, L121 [NASA ADS] [CrossRef] [Google Scholar]
  7. Blake, G. A., Sutton, E. C., Masson, C. R., & Philips, T. H. 1986, ApJS, 60, 357 [NASA ADS] [CrossRef] [Google Scholar]
  8. Blake, G. A., Sutton, E. C., Masson, C. R., & Philips, T. H. 1987, ApJ, 315, 621 [NASA ADS] [CrossRef] [Google Scholar]
  9. Blake, G. A., Mundy, L. G., Carlstrom, J. E., et al. 1996, ApJ, 472, L49 [NASA ADS] [CrossRef] [Google Scholar]
  10. Botschwina, P., & Sebald, P. 1985, J. Mol. Spectrosc., 110, 1 [NASA ADS] [CrossRef] [Google Scholar]
  11. Brown, P. D., Charnley, S. B., & Millar, T. J. 1988, MNRAS, 231, 409 [NASA ADS] [CrossRef] [Google Scholar]
  12. Burenin, A. V., Val'Dov, A. N., Karyakin, E. N., Krupnov, A. F., & Shapin, S. M. 1981, JMoSp, 87, 312B [Google Scholar]
  13. Burenin, A. V., Karyakin, E. N., Krupnov, A. F., Shapin, S. M., & Val'Dov, A. N. 1981, JMoSp, 85, 1B [NASA ADS] [Google Scholar]
  14. Carvajal, M., Margulès, L., Tercero, B., et al. 2009, A&A, 500, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Cernicharo, 1985, Internal IRAM report (Granada: IRAM) [Google Scholar]
  16. Cernicharo, J., & Guèlin, M. 1987, A&A, 176, 299 [NASA ADS] [Google Scholar]
  17. Cernicharo, J., Guèlin, M., Hein, H., & Kahane, C. 1987a, A&A, 181, L9 [NASA ADS] [Google Scholar]
  18. Cernicharo, J., Guèlin, M., & Kahane, C. 2000, A&A, 142, 181 [NASA ADS] [Google Scholar]
  19. Charnley, S. B. 1997, ApJ, 481, 396 [NASA ADS] [CrossRef] [Google Scholar]
  20. Comito, C., Schilke, P., Philips, T. G., et al. 2005, ApJS, 165, 127 [NASA ADS] [CrossRef] [Google Scholar]
  21. Cordiner, M. A., & Millar, T. J. 2009, ApJ, 697, 68 [NASA ADS] [CrossRef] [Google Scholar]
  22. Corey, G. C. 1984, JChPh, 81, 2678 [Google Scholar]
  23. Corey, G. C. 1984, JChPh, 81, 2678 [Google Scholar]
  24. Demyk, K., Mäder, H., Tercero, B., et al. 2007, A&A, 466, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. de Vicente, P., Martín-Pintado, J., Neri, R., & Rodríguez-Franco, A. 2002, ApJ, 574, L163 [NASA ADS] [CrossRef] [Google Scholar]
  26. Dougados, C., Lena, P., Ridgway, S. T., Christou, J. C. & Probst, R. G. 1993 ApJ, 406, 112 [Google Scholar]
  27. Evans, II, N. J., Lacy, J. H., & Carr, J. S. 1991 ApJ, 383, 674 [Google Scholar]
  28. Fabricant, B., Krieger, D., & Muenter, J. S. 1977, J. Chem. Phys., 67, 1576 [NASA ADS] [CrossRef] [Google Scholar]
  29. Frerking, M. A., Linke, R. A., Thaddeus, P. 1979, ApJ, 234, 143 [Google Scholar]
  30. Friedel, D. N., Snyder, L. E., Remijan, A. J., & Turner, B. E. 2005, ApJ, 632, L95 [NASA ADS] [CrossRef] [Google Scholar]
  31. Fuente, A., Cernicharo, J., Barcia, A., & Gómez-González, J. 1990, A&A, 231, 151 [NASA ADS] [Google Scholar]
  32. Gardner, F. F., Hölglund, B., Shukre, C., Stark, A. A., & Wilson, T. L. 1985, A&A, 146, 303 [NASA ADS] [Google Scholar]
  33. Genzel, R., & Stutzki, J. 1989, ARA&A, 27, 41 [NASA ADS] [CrossRef] [Google Scholar]
  34. Georgiou, K., Kroto, H. W., & Landsberg, B. M. 1979, JMoSp., 77, 365 [NASA ADS] [Google Scholar]
  35. Gezari, D. Y., Backman, D. E., & Werner, M. W. 1998 ApJ, 509, 283 [Google Scholar]
  36. Gibb, E., Nummelin, A., Irvine, W. M., Whittet, D. C. B., & Bergman, P. 2000, ApJ, 545, 309 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  37. Goddi, C., Greenhill, L. J., Humphreys, E. M. L., et al. 2009a, ApJ, 691, 1254 [NASA ADS] [CrossRef] [Google Scholar]
  38. Goddi, C., Greenhill, L. J., Chandler, C. J., et al. 2009b, ApJ, 698, 1165 [NASA ADS] [CrossRef] [Google Scholar]
  39. Goldflam, R., Kouri, D. J., & Green, S. 1977, J. Chem. Phys., 67, 4149 [NASA ADS] [CrossRef] [Google Scholar]
  40. Goldsmith, P. F., & Linke, R. A. 1981, ApJ, 245, 482 [NASA ADS] [CrossRef] [Google Scholar]
  41. Golubiatnikov, G. Yu., Lapinov, A. V., Guarnieri, A., & Knöchel, R. 2005, JMoSp, 234, 190 [Google Scholar]
  42. Gómez, L., Rodríguez, L. F., Loinard, L., et al. 2005, ApJ, 635, 1166 [NASA ADS] [CrossRef] [Google Scholar]
  43. González-Alfonso, E., & Cernicharo, J. 1993, A&A, 279, 506 [NASA ADS] [Google Scholar]
  44. Gottlieb, C. A., Myers, P. C., & Thaddeus, P. 2003, ApJ, 588, 655 [NASA ADS] [CrossRef] [Google Scholar]
  45. Greaves, J. S., & White, G. J. 1991, A&ASS, 91, 237 [NASA ADS] [Google Scholar]
  46. Green, S., & Chapman, S. 1978, ApJS, 37, 169 [NASA ADS] [CrossRef] [Google Scholar]
  47. Greenhill, L. J., Gezari, D. Y., Danchi, et al. 2004, ApJ, 605, L57 [NASA ADS] [CrossRef] [Google Scholar]
  48. Hasegawa, T., Kaifu, N., Inatani, J., et al. 1984, ApJ, 283, 117 [NASA ADS] [CrossRef] [Google Scholar]
  49. Hirahara, Y., Suzuki, H., Yamamoto, S., et al. 1992, ApJ, 394, 539 [NASA ADS] [CrossRef] [Google Scholar]
  50. Jewell, P. R., Hollis, J. M., Lovas, F. J., & Snyder, L. E. 1989, ApJS, 70, 833 [NASA ADS] [CrossRef] [Google Scholar]
  51. Johansson, L. E. B., Andersson, C., Elldér, J., et al. 1984, A&A, 130, 227 [NASA ADS] [PubMed] [Google Scholar]
  52. Johnstone, D., Boonman, A. M. S., & van Dishoeck, E. F. 2003, A&A, 412, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Kaifu, N., Suzuki, H., Ohishi, M., et al. 1987, ApJ, 317, L111 [NASA ADS] [CrossRef] [Google Scholar]
  54. Kim, E., & Yamamoto, S. 2003, JMoSp, 219, 296 [Google Scholar]
  55. Lee, C. W., Cho, S. H., & Lee, S. M. 2001, ApJ, 551, 333 [NASA ADS] [CrossRef] [Google Scholar]
  56. Lee, C. W., & Cho, S. H. 2002, J. Korea Astron. Soc., 35, 187 [Google Scholar]
  57. Lee, S. 1997, Chem. Phys. Lett., 268, 69 [NASA ADS] [CrossRef] [Google Scholar]
  58. Lerate, M. R., Barlow, M. J., Swinyard, B. M., et al. 2006, MNRAS, 370, 597 [NASA ADS] [CrossRef] [Google Scholar]
  59. Lique, F., & Spielfiedel, A. 2007, A&A, 462, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Liu, S.-Y., Girart, J. M., Remijan, A., & Snyder, L. E. 2002, ApJ, 576, 255 [NASA ADS] [CrossRef] [Google Scholar]
  61. Maeda, A., Medvedev, I. R., Winnewisser, M., et al. 2008, ApJS, 176, 543 [NASA ADS] [CrossRef] [Google Scholar]
  62. Marcelino, N., Cernicharo, J., Roueff, E., Gerin, M., & Mauersberger, R. 2005, ApJ, 620, 308 [NASA ADS] [CrossRef] [Google Scholar]
  63. Marcelino, N., Cernicharo, J., Tercero, B., & Roueff, E. 2009, ApJ, 690, 27 [Google Scholar]
  64. Margulès, L., Lewen, F., Winnewisser, G., Botschwina, P., & Müller, H. S. P. 2003, Phys. Chem. Chem. Phys., 5, 2770 [CrossRef] [Google Scholar]
  65. Margulès, L., Motiyenko, R., Demyk, K., et al. 2009, A&A, 493, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Margulès, L., Huet, T. R., Demaison, J., et al. 2010, ApJ, 714, 1120 [NASA ADS] [CrossRef] [Google Scholar]
  67. Matthews, H. E., MacLeod, J. M., Broten, N. W., Madden, S. C., & Friberg, P. 1987, ApJ, 315, 646 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  68. McNaughton, D. 1996, JMoSp., 175, 377 [NASA ADS] [Google Scholar]
  69. Menten, K. M., & Reid, M. J. 1995, ApJ, 445, L157 [NASA ADS] [CrossRef] [Google Scholar]
  70. Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Minh, Y. C., Irvine, W. M., & Brewer, M. K. 1991, A&A, 244, 181 [NASA ADS] [PubMed] [Google Scholar]
  72. Minowa, H., Satake, M., Hirota, T., et al. 1997, ApJ, 491, L63 [NASA ADS] [CrossRef] [Google Scholar]
  73. Monteiro, T. 1984, MNRAS, 210, 1 [NASA ADS] [Google Scholar]
  74. Morino, I., Yamada, K. M. T., & Maki, A. G. 2000, JMoSp, 200, 145 [Google Scholar]
  75. Morris, M., Palmer, P., & Zuckerman, B. 1980, ApJ, 237, 1 [NASA ADS] [CrossRef] [Google Scholar]
  76. Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
  78. Murata, Y., Kawabe, R., Ishiguro, M., Hasegawa, T., & Hayashi, M. 1991, IAUS, 147, 357 [NASA ADS] [Google Scholar]
  79. Niedenhoff, M. 1995, JMoSp., 169, 224 [Google Scholar]
  80. Nomura, H., & Millar, T. J. 2004, A&A, 414, 409 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  81. Ohshima, Y., & Endo, Y. 1996, Chem. Phys. Lett., 256, 635 [NASA ADS] [CrossRef] [Google Scholar]
  82. Olofsson, A. O. H., Persson, C. M., Koning, N., et al. 2007, A&A, 476, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Pardo, J. R., Cernicharo, J., & Serabyn, E. 2001, IEEE Tras. Antennas and Propagation, 49, 12 [Google Scholar]
  84. Pardo, J. R., Cernicharo, J., Herpin, F., et al. 2001, ApJ, 562, 799 [NASA ADS] [CrossRef] [Google Scholar]
  85. Pardo, J. R., & Cernicharo, J. 2007, ApJ, 654, 978 [NASA ADS] [CrossRef] [Google Scholar]
  86. Persson, C. M., Olofsson, A. O. H., Koning, N., et al. 2007, A&A, 476, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Plambeck, R. L., & Wright, M. C. H. 1988, ApJ, 330, L61 [NASA ADS] [CrossRef] [Google Scholar]
  88. Plambeck, R. L., Wright, M. C. H., Friedel, D. N., et al. 2009, ApJ, 704, L25 [NASA ADS] [CrossRef] [Google Scholar]
  89. Roberts, H., Herbst, E., & Millar, T. J. 2002, MNRAS, 336, 283 [NASA ADS] [CrossRef] [Google Scholar]
  90. Rodgers, S. D., & Millar, T. J. 1996, MNRAS, 280, 1046 [NASA ADS] [CrossRef] [Google Scholar]
  91. Rodríguez, L. F., Zapata, L. A., & Ho, P. T. P. 2009, ApJ, 692, 162 [NASA ADS] [CrossRef] [Google Scholar]
  92. Savage, C., Apponi, A. J., Ziurys, L. M., & Wyckoff, S. 2002, ApJ, 578, 211 [NASA ADS] [CrossRef] [Google Scholar]
  93. Schilke, P., Walmsley, C. M., Pineau Des Forets, G., et al. 1992, A&A, 256, 595 [NASA ADS] [Google Scholar]
  94. Schilke, P., Groesbeck, T. D., Blake, G. A., & Philips, T. G. 1997, ApJS, 108, 301 [NASA ADS] [CrossRef] [Google Scholar]
  95. Schilke, P., Benford, C. J., Hunter, T. R., Lis, D. C., & Philips, T. G. 2001, ApJS, 132, 281 [NASA ADS] [CrossRef] [Google Scholar]
  96. Serabyn, E., & Weisstein, E. W. 1995, ApJ, 451, 238 [NASA ADS] [CrossRef] [Google Scholar]
  97. Shuping, R. Y., Morris, M., & Bally, J. 2004, AJ, 128, 363 [NASA ADS] [CrossRef] [Google Scholar]
  98. Sobolev, V. V. 1958, en Theorical Astrophysics, ed. Ambartsumyan, Pergamon Press Ltd. London Cap. 29 [Google Scholar]
  99. Sobolev, V. V. 1960, en Moving Envelopes of Stars (Hardvard University Press) [Google Scholar]
  100. Suenram, R. D., & Lovas, F. J. 1994, ApJ, 429, L89 [NASA ADS] [CrossRef] [Google Scholar]
  101. Sutton, E. C., Blake, G. A., Masson, C. R., & Philips, T. G. 1985, ApJS, 58, 341 [NASA ADS] [CrossRef] [Google Scholar]
  102. Sutton, E. C., Blake, G. A., Genzel, R., Masson, C. R., & Philips, T. G. 1986, ApJS, 311, 921 [NASA ADS] [CrossRef] [Google Scholar]
  103. Sutton, E. C., Peng, R., Danchi, W. C., et al. 1995, ApJS, 97, 455 [NASA ADS] [CrossRef] [Google Scholar]
  104. Szalanski, L. B., Gerry, M. C. L., Winnewisser, G., Yamada, K. M. T., & Winnewisser, M. 1978, Can. J. Phys., 56, 1297 [NASA ADS] [Google Scholar]
  105. Tanaka, K., Tanaka, T., & Suzuki, I. 1985, JChPhys., 82, 2835 [Google Scholar]
  106. Tobola, R., Lique, F., Klos, J., & Chalasinski, G. 2008, JPhB, 41, 155702 [NASA ADS] [Google Scholar]
  107. Turner, B. E. 1989, ApJS, 70, 539 [NASA ADS] [CrossRef] [Google Scholar]
  108. Turner, B. E. 1991, ApJS, 76, 617 [NASA ADS] [CrossRef] [Google Scholar]
  109. Walsh, C., Harada, N., Herbst, E., & Millar, T. J. 2009, ApJ, 700, 752 [NASA ADS] [CrossRef] [Google Scholar]
  110. Wheeler, S. E., Yamaguchi, Y., & Schaefer, H. F. 2006, JChPh, 124, 044322 [Google Scholar]
  111. White, G. J., Monteiro, T. S., Richardson, K. J., Griffin, M. J., & Rainey, R. 1986, A&A, 162, 253 [NASA ADS] [Google Scholar]
  112. White, G. J., Araki, M., Greaves, J. S., Ohishi, M., & Higginbottom, N. S. 2003, A&A, 407, 598 [Google Scholar]
  113. Winnewisser, G., & Cook, R. L. 1968, J. Mol. Spect., 28, 266 [CrossRef] [Google Scholar]
  114. Winnewisser, M., & Schäfer, E. 1980, Zeitschrift Naturforschung Teil A, 35, 483 [NASA ADS] [Google Scholar]
  115. Winnewisser, M., Lichau, H., & Wolf, F. 2000, J. Mol. Spect., 202, 155 [Google Scholar]
  116. Wright, M. C. H., Plambeck, R. L., & Wilner, D. J. 1996, ApJ, 469, 216 [NASA ADS] [CrossRef] [Google Scholar]
  117. Wyckoff, S., Kleine, M., Peterson, B. A., Wehinger, P. A., & Ziurys, L. M. 2000, ApJ, 535, 991 [NASA ADS] [CrossRef] [Google Scholar]
  118. Yamamoto, S., Saito, S., Kawaguchi, K., et al. 1987, ApJ, 317, L119 [NASA ADS] [CrossRef] [Google Scholar]
  119. Yamamoto, S., Saito, S., Kawaguchi, K., et al. 1990, ApJ, 361, 318 [NASA ADS] [CrossRef] [Google Scholar]
  120. Zapata, L. A., Menten, K., Reid, M., & Beuther, H. 2009a, ApJ, 691, 332 [NASA ADS] [CrossRef] [Google Scholar]
  121. Zapata, L. A., Schmid-Burgk, J., Ho, P. T. P., Rodríguez, L. F., & Menten, K. M. 2009b, ApJ, 704, L45 [NASA ADS] [CrossRef] [Google Scholar]
  122. Zeng, Q., & Pei, C. C. 1995, Ap&SS, 229, 301 [NASA ADS] [CrossRef] [Google Scholar]
  123. Ziurys, L. M., & McGonagle, D. 1993, ApJS, 89, 155 [NASA ADS] [CrossRef] [Google Scholar]

Online Material

Appendix A: Online Figures

\begin{figure} \par\includegraphics[width=14cm,clip]{13501fgA1n.eps} \end{figure} Figure A.1:

Observed lines (offseted histogram) and model (thin curves) of O13CS, 18OCS, O13C34S, 17OCS, and OC36S. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

\begin{figure} \par\includegraphics[width=14cm,clip]{13501fgA2n.eps} \end{figure} Figure A.2:

Left panelshows the OCS J = 18-17 line at different positions. The right panel map shows the total integrated intensity of this transition; the interval of contours is 10 K km s-1, and the minimum contour is 40 K km s-1.

Open with DEXTER

\begin{figure} \par\includegraphics[width=6cm,clip]{13501fgA3.eps} \end{figure} Figure A.3:

Observed lines (histogram) and model (thin curves) of HCS+. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

\begin{figure} \par\includegraphics[width=14cm,clip]{13501fgA4.eps} \end{figure} Figure A.4:

Observed lines (histogram) and model (thin curves) of H2CS. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

\begin{figure} \par\includegraphics[width=14cm,clip]{13501fgA5.eps} \end{figure} Figure A.5:

Observed lines (histogram) and model (thin curves) of H2C34S. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

\begin{figure} \par\includegraphics[width=14cm,clip]{13501fgA6.eps} \end{figure} Figure A.6:

H213CS observed (offseted histogram) and modeled (continuum curves) lines. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

\begin{figure} \par\includegraphics[width=14cm,clip]{13501fgA7.eps} \end{figure} Figure A.7:

HDCS observed (histogram) and modeled (thin curves) lines. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

\begin{figure} \par\includegraphics[width=14.5cm,clip]{13501fgA8.eps} \end{figure} Figure A.8:

Observed lines (offseted histogram) and modeled (thin curves) of CS, CS isotopologues, and CS $\textit {v} = 1$. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER

Appendix B: Online Tables

Table B.1:   OCS isotopologues and OCS vibrationally excited velocity components.

Table B.2:   HCS+ Observed line parameters.

Table B.3:   H2CS observed line parameters.

Table B.4:   H2CS and its isotopologues velocity components.

Table B.5:   CS observed line parameters.

Table B.6:   CS and CS isotopologues velocities.

Table B.7:   CCS observed lines parameters.

Table B.8:   CCCS observed lines parameters.

Table B.9:   Isotopologue ratios.

Table B.10:   Molecular abundances.

Footnotes

... chains[*]
Appendices A and B are only available in electronic form at http://www.aanda.org
... software[*]
http://www.iram.fr/IRAMFR/GILDAS
... Catalog[*]
Müller et al. (2001), Müller et al. (2005) http://www.astro.uni-koeln.de/site/vorhersagen/.
Copyright ESO 2010

All Tables

Table 1:   $\eta _{\rm MB}$ and HPBW along the covered frequency range.

Table 2:   The assumed Orion KL spectral components.

Table 3:   OCS observed line parameters.

Table 4:   OCS velocity components from Gaussian fits.

Table 5:   Column densities - OCS.

Table 6:   Column densities - H2CS.

Table 7:   Ortho/Para ratios - H2CS.

Table 8:   Column densities of CS, CS isotopologues, and CS vibrationally excited.

Table 9:   Column density ratios.

Table B.1:   OCS isotopologues and OCS vibrationally excited velocity components.

Table B.2:   HCS+ Observed line parameters.

Table B.3:   H2CS observed line parameters.

Table B.4:   H2CS and its isotopologues velocity components.

Table B.5:   CS observed line parameters.

Table B.6:   CS and CS isotopologues velocities.

Table B.7:   CCS observed lines parameters.

Table B.8:   CCCS observed lines parameters.

Table B.9:   Isotopologue ratios.

Table B.10:   Molecular abundances.

All Figures

  \begin{figure} \par\includegraphics[width=8cm,clip]{13501fg01.eps} \end{figure} Figure 1:

The top panel shows two superimposed spectra corresponding to different frequency settings (112 500 and 112 520 MHz). The 40 MHz displaced line is the 115.5 GHz CO line in the image side band. The bottom panel shows the final spectrum resulting from our procedure to eliminate the image side band (see text, Sect. 2). We are confident that all lines above 0.05 K have frequencies correctly assigned.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270, width=17cm,clip]{13501fg02.eps} \end{figure} Figure 2:

Molecular line survey of Orion KL at 3 mm. The top panel shows the total intensity scale; the middle and the bottom panels show a zoom of the total intensity. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16cm,clip]{13501fg03n.eps} \end{figure} Figure 3:

Example of Orion's KL survey at 3 mm with 1 GHz bandwidth. The top panel shows the total intensity scale; the middle and the bottom panels show a zoom of the total intensity. Detected molecules are marked with labels and some unidentified features are marked as U.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[% width=16cm,clip]{13501fg04n.eps} \end{figure} Figure 4:

Molecular line survey of Orion KL at 2 mm presented similarly to Fig. 2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=17cm,clip]{13501fg05.eps} \end{figure} Figure 5:

Example of Orion's KL survey at 2 mm with 1 GHz bandwidth. The top panel shows the total intensity scale; the middle and the bottom panels show a zoom of the total intensity. Detected molecules are marked with labels and some unidentified lines are marked as U.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{13501fg06n.eps} \end{figure} Figure 6:

Molecular line survey of Orion KL at 1.3 mm presented similarly to Fig. 2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{13501fg07n.eps} \end{figure} Figure 7:

Example of the Orion KL survey at 1.3 mm with 1 GHz bandwidth. The top panel shows the total intensity scale; the middle and the bottom panels show a zoom of the total intensity. Detected molecules are labeled and some unidentified lines are marked as U.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{13501fg08.eps} \end{figure} Figure 8:

Observed (offseted histogram) and model (thin curves) OCS, OC34S and OC33S lines. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{13501fg09.eps} \end{figure} Figure 9:

Observed lines (offseted histogram) and model (thin curves) of OCS $\nu _2$ = 1 and OCS $\nu _3$ = 1. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=18cm,clip]{13501fg10n.eps} \end{figure} Figure 10:

OCS J = 18-17 integrated line intensity maps at different velocity ranges (indicated at the top of each panel). The integrated intensity of the maps has been multiplied by a scale factor (indicated in the panels) to maintain the same color dynamics for all maps. The interval of contours is 10 K km s-1, the minimum contour is 30 K km s-1 for the maps with velocities between -1 and 11 km s-1 and 50 K km s-1 for the rest of the panels.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=11.5cm,clip]{13501fg11.eps} \end{figure} Figure 11:

Some lines of OCS, OC34S and O13CS observed at different positions which correspond with different components of Orion KL. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=13.5cm,clip]{13501fg12.eps}\vspace*{-2mm} \end{figure} Figure 12:

Observed lines (offseted histogram) and model (thin curves) of CCS. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{13501fg13.eps} \end{figure} Figure 13:

Observed lines (offseted histogram) and model (thin curves) of C3S. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{13501fgA1n.eps} \end{figure} Figure A.1:

Observed lines (offseted histogram) and model (thin curves) of O13CS, 18OCS, O13C34S, 17OCS, and OC36S. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{13501fgA2n.eps} \end{figure} Figure A.2:

Left panelshows the OCS J = 18-17 line at different positions. The right panel map shows the total integrated intensity of this transition; the interval of contours is 10 K km s-1, and the minimum contour is 40 K km s-1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6cm,clip]{13501fgA3.eps} \end{figure} Figure A.3:

Observed lines (histogram) and model (thin curves) of HCS+. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{13501fgA4.eps} \end{figure} Figure A.4:

Observed lines (histogram) and model (thin curves) of H2CS. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{13501fgA5.eps} \end{figure} Figure A.5:

Observed lines (histogram) and model (thin curves) of H2C34S. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{13501fgA6.eps} \end{figure} Figure A.6:

H213CS observed (offseted histogram) and modeled (continuum curves) lines. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{13501fgA7.eps} \end{figure} Figure A.7:

HDCS observed (histogram) and modeled (thin curves) lines. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14.5cm,clip]{13501fgA8.eps} \end{figure} Figure A.8:

Observed lines (offseted histogram) and modeled (thin curves) of CS, CS isotopologues, and CS $\textit {v} = 1$. A $v_{\rm LSR}$ of 9 km s-1 is assumed.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.