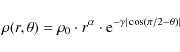| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A11 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913043 | |
| Published online | 23 July 2010 | |
The HELLAS2XMM survey
XIII. Multi-component analysis of the spectral energy distribution of obscured AGN
F. Pozzi1,2 - C. Vignali1,2 - A. Comastri2 - E. Bellocchi3 - J. Fritz4 - C. Gruppioni2 - M. Mignoli2 - R. Maiolino5 - L. Pozzetti2 - M. Brusa6 - F. Fiore5 - G. Zamorani2
1 - Dipartimento di Astronomia, Università degli Studi di Bologna, via Ranzani 1, 40127 Bologna, Italy
2 -
INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
3 -
Instituto de Estructura de la Materia (IEM/CSIC), C/ Serrano 121, 28006 Madrid, Spain
4 -
Sterrenkundig Observatorium, Vakgroep Fysica en Sterrenkunde, Universeit Gent, Krijgslaan 281, S9 9000 Gent, Belgium
5 -
INAF - Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Roma, Italy
6 -
Max Planck Institut für Extraterrestrische Physik (MPE), Giessenbachstrasse 1, 85748 Garching bei München, Germany
Received 31 July 2009 / Accepted 23 March 2010
Abstract
Aims. We combine near-to-mid-IR Spitzer data with
shorter wavelength observations (optical to X-rays) to get insight into
the properties of a sample of luminous, obscured active galactic nuclei
(AGN). We aim at modelling their broad-band spectral energy
distributions (SEDs) in order to estimate the main parameters related
to the dusty torus that is assumed to be responsible for the
reprocessed IR emission. Our final goal is to estimate the intrinsic
nuclear luminosities and the Eddington ratios for our luminous,
obscured AGN.
Methods. The sample comprises 16 obscured high-redshift (
![]() ), X-ray luminous quasars (
), X-ray luminous quasars (
![]() erg s-1)
selected from the HELLAS2XMM survey in the 2-10 keV band. The
optical-IR SEDs are described by a multi-component model that includes
a stellar component to account for the optical and near-IR emission, an
AGN component that dominates in the mid-IR (mainly emission from a
dusty torus heated by nuclear radiation), and a starburst to reproduce
the far-IR bump. A radiative transfer code to compute the spectrum and
intensity of dust reprocessed emission was extensively tested against
our multiwavelength data. While the torus parameters and the BH
accretion luminosities are a direct output of the SED-fitting
procedure, the BH masses were estimated indirectly by means of the
local
erg s-1)
selected from the HELLAS2XMM survey in the 2-10 keV band. The
optical-IR SEDs are described by a multi-component model that includes
a stellar component to account for the optical and near-IR emission, an
AGN component that dominates in the mid-IR (mainly emission from a
dusty torus heated by nuclear radiation), and a starburst to reproduce
the far-IR bump. A radiative transfer code to compute the spectrum and
intensity of dust reprocessed emission was extensively tested against
our multiwavelength data. While the torus parameters and the BH
accretion luminosities are a direct output of the SED-fitting
procedure, the BH masses were estimated indirectly by means of the
local
![]() -
-
![]() relation.
relation.
Results. The majority (![]() 80%) of the sources show moderate optical depth (
80%) of the sources show moderate optical depth (
![]() ), and the derived column densities
), and the derived column densities ![]() are consistent with the X-ray inferred values (
are consistent with the X-ray inferred values (
![]() cm-2)
for most of the objects, confirming that the sources are moderately
obscured Compton-thin AGN. Accretion luminosities in the range
cm-2)
for most of the objects, confirming that the sources are moderately
obscured Compton-thin AGN. Accretion luminosities in the range
![]() erg s-1
are inferred from the multiwavelength fitting procedure. We compare
model luminosities with those obtained by integrating the observed SED,
finding that the latter are lower by a factor of
erg s-1
are inferred from the multiwavelength fitting procedure. We compare
model luminosities with those obtained by integrating the observed SED,
finding that the latter are lower by a factor of ![]() 2 in the median. The discrepancy can be as high as an order of magnitude for models with high optical depth (
2 in the median. The discrepancy can be as high as an order of magnitude for models with high optical depth (
![]() ).
The ratio between the luminosities obtained by the fitting procedure
and from the observed SED suggest that, at least for type 2 AGN,
observed bolometric luminosities are likely to underestimate intrinsic
ones and the effect is more severe for highly obscured sources.
Bolometric corrections from the hard X-ray band are computed and have a
median value of
).
The ratio between the luminosities obtained by the fitting procedure
and from the observed SED suggest that, at least for type 2 AGN,
observed bolometric luminosities are likely to underestimate intrinsic
ones and the effect is more severe for highly obscured sources.
Bolometric corrections from the hard X-ray band are computed and have a
median value of
![]() .
The obscured AGN in our sample are characterized by relatively low Eddington ratios (median
.
The obscured AGN in our sample are characterized by relatively low Eddington ratios (median
![]() ). On average, they are consistent with the Eddington ratio increasing at increasing bolometric correction.
). On average, they are consistent with the Eddington ratio increasing at increasing bolometric correction.
Key words: quasars: general - galaxies: nuclei - galaxies: active
1 Introduction
A robust determination of active galactic nuclei (AGN) spectral energy distributions (SEDs) is of paramount importance to better understand the accretion processes onto supermassive black holes (SMBHs) and their cosmological evolution. According to our present knowledge, the bulk of accretion luminosity is emitted in the optical-UV range with a quasi-thermal spectrum originating in an optically thick, geometrically thin, accretion disk. Electrons with temperatures of a few hundreds of keV form a hot corona that upscatters disk photons to X-ray energies with a power-law spectrum and an exponential high-energy cut-off corresponding to the electron temperature (e.g., Haardt & Maraschi 1991). Dusty material, possibly with a toroidal geometry, intercepts a fraction of the primary continuum, which depends on the covering factor. The absorbed energy is re-emitted in the near-to-far infrared with a grey-body spectral shape.
The SED of optically bright, unobscured QSO is relatively well known. After
the seminal work of Elvis et al. (1994), fairly accurate measurements
were published by Richards et al. (2006) using Sloan Digital Sky Survey
(SDSS) data. The emission is characterized by a double bump.
In a
![]() diagram, the optical-UV spectrum rises steeply towards
the shortest accessible wavelengths. It is commonly referred to as the
Big Blue Bump and thought to be the accretion disk signature. The IR bump is
weaker and likely due to a dusty torus seen almost face-on.
The ratio between UV (at 2500 Å) and X-ray luminosity (at 2 keV),
parameterized by the slope
diagram, the optical-UV spectrum rises steeply towards
the shortest accessible wavelengths. It is commonly referred to as the
Big Blue Bump and thought to be the accretion disk signature. The IR bump is
weaker and likely due to a dusty torus seen almost face-on.
The ratio between UV (at 2500 Å) and X-ray luminosity (at 2 keV),
parameterized by the slope
![]()
![]() of the power law connecting the rest-frame luminosities,
increases with increasing UV luminosity
(e.g., Steffen et al. 2006).
of the power law connecting the rest-frame luminosities,
increases with increasing UV luminosity
(e.g., Steffen et al. 2006).
The average SEDs for radio-loud and radio-quiet type 1 AGN presented in
Elvis et al. (1994) allow estimation of bolometric corrections,
which are a key parameter in determining the bolometric luminosity from
observations at a given frequency, and the Eddington ratio, once the SMBH
mass is known.
By including the
![]() vs. UV luminosity dependence,
Hopkins et al. (2006)
have computed luminosity-dependent bolometric corrections and adopted
them for estimating the local SMBH mass density from the observed X-ray
luminosity functions.
vs. UV luminosity dependence,
Hopkins et al. (2006)
have computed luminosity-dependent bolometric corrections and adopted
them for estimating the local SMBH mass density from the observed X-ray
luminosity functions.
The luminosity dependence of bolometric corrections has recently been questioned by Vasudevan & Fabian (2009), who point out the importance of simultaneous optical-UV and X-ray observations and reddening corrections in the UV. They suggest that the bolometric correction correlates with the Eddington ratio rather than with the bolometric luminosity. Their observational results align with the predictions of accretion disk models (e.g., Witt et al. 1997) where higher blue-bump to X-ray ratios for sources with higher Eddington ratios are expected.
While significant progress has been made towards a better determination of type 1 AGN SEDs, our knowledge of type 2 broad-band spectra is much more limited even though most of the accretion-driven energy density in the Universe is expected to occur in obscured AGN (e.g., Gilli et al. 2007, and references therein). Therefore, a robust estimate of their bolometric luminosity is extremely important for properly addressing the issue of SMBH evolution over cosmic time.
Nuclear accretion luminosity in type 2 AGN is very faint in the optical-UV and soft X-rays. Moreover, the host galaxy stellar light often dominates in the optical, making it difficult to disentangle nuclear emission from starlight. Infrared emission is only marginally affected by dust obscuration and has proved to be a powerful indicator of dust-obscured AGN. In particular, the thermally reprocessed nuclear emission of obscured type 2 AGN is expected to peak around a few tens of microns (e.g., Fritz et al. 2006, hereafter F06, and references within).
Mid-IR (MIR) observations, especially those obtained in the past few years with the Spitzer satellite, are extremely efficient in studying obscured AGN (e.g. Rigby et al. 2005; Weedman et al. 2006; Fiore et al. 2008). In a previous paper (Pozzi et al. 2007), we presented the first analysis of the mid-IR data of a Spitzer programme devoted to systematic study of the broad-band properties of X-ray selected, luminous obscured quasars. In Pozzi et al. (2007), the SEDs were reproduced by means of SED templates from Silva et al. (2004).
Here we present the observational data for our final sample of 16
obscured quasars and the detailed modelling of their broad-band SED
using a more complete multi-component model, with goodness of fit estimated
via ![]() analysis.
analysis.
The outline of the paper is as follows. In Sect. 2 the X-ray selected quasar sample is presented, along with all the available multi-band (optical, near-IR (NIR) and sub-mm) and spectroscopic follow-up. The Spitzer data are presented in Sect. 3, with data reduction and analysis. In Sect. 4, the complete multi-component model is described. In Sect. 5, the best-fitting solutions are discussed, while in Sect. 6 we focus on the black hole physical properties that can be constrained from the best-fitting procedure. Finally, the main results are summarized in Sect. 7.
Hereafter, we adopt the concordance cosmology
(H0=70 km s-1 Mpc-1,
![]() ,
and
,
and
![]() ,
Spergel et al. 2003).
Magnitudes are expressed in the Vega system.
,
Spergel et al. 2003).
Magnitudes are expressed in the Vega system.
2 The sample
The sample presented in this work comprises 16 X-ray obscured quasars
detected in the HELLAS2XMM survey (Baldi et al. 2002)
and observed by Spitzer in 2006.
The HELLAS2XMM survey is a shallow, large-area, hard X-ray survey
(
![]()
![]() ) over a final area of 1.4 deg2.
The catalogue comprises 232 X-ray sources;
) over a final area of 1.4 deg2.
The catalogue comprises 232 X-ray sources; ![]() 92% of the sample is
optically identified down to
92% of the sample is
optically identified down to ![]() ,
while
,
while ![]() 70% of the sources
have a spectroscopic classification (Fiore et al. 2003;
Cocchia et al. 2007).
70% of the sources
have a spectroscopic classification (Fiore et al. 2003;
Cocchia et al. 2007).
The 16 sources were selected from the original survey to include
the most luminous obscured quasars. The selection was primarily based
on the X-ray-to-optical flux ratio (hereafter X/O)![]() ,
which has been proven to be an efficient way of selecting high-redshift
(
,
which has been proven to be an efficient way of selecting high-redshift
(![]() ), obscured quasars (see Fiore et al. 2003).
All but one of the sources were selected to have X/O greater
than 1 (see Fig. 1 and Table 1), with the only exception GD 158#19 (
), obscured quasars (see Fiore et al. 2003).
All but one of the sources were selected to have X/O greater
than 1 (see Fig. 1 and Table 1), with the only exception GD 158#19 (
![]() ), which was included in the sample
for its peculiar properties (see Vignali et al. 2009, hereafter V09). We note, however, that not all of the HELLAS2XMM sources
matching this selection criterion are present in this work.
), which was included in the sample
for its peculiar properties (see Vignali et al. 2009, hereafter V09). We note, however, that not all of the HELLAS2XMM sources
matching this selection criterion are present in this work.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13043fig1.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg47.png)
|
Figure 1:
R-band magnitudes vs. hard X-ray (2-10 keV) flux for the full
HELLAS2XMM sample (Cocchia et al. 2007). Blue triangles represent
the sources included in the present analysis: blue triangles inside
red symbols represent the sources with spectroscopic redshifts.
Other symbols: empty red squares = sources spectroscopically classified as
type 2 AGN; empty circles = sources spectroscopically classified as non-type 2
AGN (type 1 AGN, emission-line galaxies, early-type galaxies and
groups/clusters of galaxies); crosses: objects not observed spectroscopically;
upward arrows = lower limits. The dashed lines represent the
loci of constant X/O ratio (
|
| Open with DEXTER | |
Table 1: Properties of our luminous obscured quasars.
The selected sources are relatively faint in the optical band, with an R-band
magnitude in the range 21.8-25.1 (the brightest object being the peculiar source
GD 158#19).
By combining optical photometry with deep ![]() -band photometry
(obtained with the Infrared Spectrometer And Array Camera, ISAAC,
mounted on the ESO-VLT1 Telescope), almost all the objects are found to be
extremely red sources (EROs,
-band photometry
(obtained with the Infrared Spectrometer And Array Camera, ISAAC,
mounted on the ESO-VLT1 Telescope), almost all the objects are found to be
extremely red sources (EROs,
![]() ). The link between high X/O
ratios and optical-to-near colours was studied by e.g., Brusa et al. (2005). Considering different X-ray surveys at different
depths, they find a clear trend: the higher X/O, the redder the source.
). The link between high X/O
ratios and optical-to-near colours was studied by e.g., Brusa et al. (2005). Considering different X-ray surveys at different
depths, they find a clear trend: the higher X/O, the redder the source.
In Mignoli et al. (2004), detailed ![]() -band morphological
studies were presented for 8 objects of the sample selected from those sources
with the more
extreme
-band morphological
studies were presented for 8 objects of the sample selected from those sources
with the more
extreme
![]() colours: the majority of the sources
(6 over 8) have an extended
colours: the majority of the sources
(6 over 8) have an extended ![]() -band
morphology, consistent with an elliptical-type profile, without any
evidence of a nuclear point-like source (which would be expected to
trace the X-ray AGN). This suggests that the nuclear emission is
diluted and hidden by the host galaxy up to at least 2.2
-band
morphology, consistent with an elliptical-type profile, without any
evidence of a nuclear point-like source (which would be expected to
trace the X-ray AGN). This suggests that the nuclear emission is
diluted and hidden by the host galaxy up to at least 2.2 ![]() m. The R and
m. The R and
![]() -band magnitudes are reported in Table 1.
-band magnitudes are reported in Table 1.
Spectroscopic information for 11 sources is available thanks to optical
(8 sources, see Fiore et al. 2003; and
Cocchia et al. 2007) and near-IR spectroscopy (3 sources, see
Maiolino et al. 2006; and Sarria et al., in preparation).
All spectra but one are typical of optically obscured AGN, thus
confirming the X-ray classification (i.e., type 2). The only exception is source
PKS 0537#91, with emission line ratios typical of an HII region (Sarria
et al., in preparation).
One source, Abell 2690#29, shows the typical rest-frame spectrum of a
high-redshift, dust-reddened quasar, with a broad H![]() line and a type 1.9
classification (Maiolino et al. 2006).
Spectroscopic redshift z are in the range 0.9-2.08 and are reported in
Table 1. For the sources without redshift (5 out of 16), a photometric redshift was estimated in Pozzi et al. (2007), where the Spitzer data
reduction and a preliminary SED analysis were presented.
line and a type 1.9
classification (Maiolino et al. 2006).
Spectroscopic redshift z are in the range 0.9-2.08 and are reported in
Table 1. For the sources without redshift (5 out of 16), a photometric redshift was estimated in Pozzi et al. (2007), where the Spitzer data
reduction and a preliminary SED analysis were presented.
Finally, sub-mm observations were performed for four sources in
2004 October-November. Only one object, GD 158#19 (z=1.957), was
detected, while for the others upper limits were gained.
Because of its broad-band coverage (up to 850 ![]() m) with
good-quality photometric data, the source GD 158#19 was studied in a
dedicated work (see V09).
m) with
good-quality photometric data, the source GD 158#19 was studied in a
dedicated work (see V09).
In Table 1 we report source name, 2-10 keV flux, R, and ![]() photometry, X/O ratio,
the redshift z, the column densities
photometry, X/O ratio,
the redshift z, the column densities ![]() ,
and the absorption-corrected
(2-10 keV) X-ray luminosities of the sample. The source table order reflects
the Spitzer observation strategy (see Sect. 3).
The sub-mm flux densities are reported in Table 2 along with
the fluxes obtained in the IR bands (from 3.6
,
and the absorption-corrected
(2-10 keV) X-ray luminosities of the sample. The source table order reflects
the Spitzer observation strategy (see Sect. 3).
The sub-mm flux densities are reported in Table 2 along with
the fluxes obtained in the IR bands (from 3.6 ![]() m up to 160
m up to 160 ![]() m)
with the Spitzer satellite (see Sect. 3). Almost all the sources have column densities
m)
with the Spitzer satellite (see Sect. 3). Almost all the sources have column densities ![]() in the range
1022.0-1023.4 cm-2 and 2-10 keV rest-frame luminosities
in the range 1043.8-1044.7 erg s-1, placing them in the type 2 quasar population.
in the range
1022.0-1023.4 cm-2 and 2-10 keV rest-frame luminosities
in the range 1043.8-1044.7 erg s-1, placing them in the type 2 quasar population.
Table 2: Spitzer and SCUBA flux densities.
3 The Spitzer data
The targets were observed by Spitzer in 2006 with both IRAC and MIPS
instruments in photometry mode. All the sources were observed with the same
total integration time in the IRAC bands (480 s), while different strategies
were followed in the MIPS bands taking the different optical-NIR
properties into account. While all the
objects were observed at 24 ![]() m for a total integration time of 1400 s,
only a subsample of sources with relatively bright R-band magnitudes
(R< 24) and spectroscopic redshifts were observed at longer
wavelengths, with integration times of 300 s and
600 s at 70 and 160
m for a total integration time of 1400 s,
only a subsample of sources with relatively bright R-band magnitudes
(R< 24) and spectroscopic redshifts were observed at longer
wavelengths, with integration times of 300 s and
600 s at 70 and 160 ![]() m, respectively.
PKS 0537#91 (see Table 1) was not observed at 70 and
160
m, respectively.
PKS 0537#91 (see Table 1) was not observed at 70 and
160 ![]() m since it had no redshift at the epoch of the Spitzer
observations.
m since it had no redshift at the epoch of the Spitzer
observations.
The reduction method is described in detail in
Pozzi et al. (2007) and in V09 and it is briefly
summarized here. The IRAC flux densities of the sources were measured from the
post-basic calibrated data (post-BCD) images in the Spitzer archive. Aperture fluxes were measured on the background-subtracted
maps within a 2.45
![]() aperture radius using aperture
corrections of 1.21, 1.23,1.38, and 1.58 for the four IRAC bands
(following the IRAC Data Handbook). For the MIPS bands, we started the
analysis from the basic calibrated data (BCD) at 24
aperture radius using aperture
corrections of 1.21, 1.23,1.38, and 1.58 for the four IRAC bands
(following the IRAC Data Handbook). For the MIPS bands, we started the
analysis from the basic calibrated data (BCD) at 24 ![]() m and from
the median high-pass filtered BCD (fBCD) at 70 and 160
m and from
the median high-pass filtered BCD (fBCD) at 70 and 160 ![]() m, as
suggested for faint sources. At 24
m, as
suggested for faint sources. At 24 ![]() m, the BCD were corrected for a
residual flat-fielding dependent on the scan mirror position (see
Pozzi et al. 2007).
We then constructed our own mosaics using
the SSC MOPEX software (Makovoz & Marleau 2005).
Aperture fluxes were measured
within a 7
m, the BCD were corrected for a
residual flat-fielding dependent on the scan mirror position (see
Pozzi et al. 2007).
We then constructed our own mosaics using
the SSC MOPEX software (Makovoz & Marleau 2005).
Aperture fluxes were measured
within a 7
![]() aperture radius for the 24
aperture radius for the 24 ![]() m band and
16
m band and
16
![]() aperture radius for the 70 and 160
aperture radius for the 70 and 160 ![]() m bands. The aperture
corrections used were 1.61, 2.07, and 4.1 (see the
MIPS Data Handbook). A small aperture radius was used at longer
wavelengths (at 160
m bands. The aperture
corrections used were 1.61, 2.07, and 4.1 (see the
MIPS Data Handbook). A small aperture radius was used at longer
wavelengths (at 160 ![]() m the adopted radius is comparable to half of
the PSF FWHM) to exclude the contamination by nearby far-infrared
sources (see V09). At 24
m the adopted radius is comparable to half of
the PSF FWHM) to exclude the contamination by nearby far-infrared
sources (see V09). At 24 ![]() m, thanks to a
better PSF sampling, two sources (PKS 0312#36 and Abell 2690#29) were
deblended using a PSF deconvolution analysis.
m, thanks to a
better PSF sampling, two sources (PKS 0312#36 and Abell 2690#29) were
deblended using a PSF deconvolution analysis.
All 16 sources were clearly detected in the IRAC bands. At 24 ![]() m,
14 sources (out of 16) were detected above the 5
m,
14 sources (out of 16) were detected above the 5![]() level
and span almost two orders of magnitude in flux, from
level
and span almost two orders of magnitude in flux, from ![]() 7000
7000 ![]() Jy
down to the faintest source, close to the 5
Jy
down to the faintest source, close to the 5![]() detection
level (
detection
level (![]() 100
100 ![]() Jy). For the two sources without detection,
an upper limit (3
Jy). For the two sources without detection,
an upper limit (3![]() )
was estimated from the average noise of
the map, derived by making multiple aperture
measurements at random locations throughout the residual mosaic after
source extraction. The typical average noise (1
)
was estimated from the average noise of
the map, derived by making multiple aperture
measurements at random locations throughout the residual mosaic after
source extraction. The typical average noise (1![]() )
is 20
)
is 20 ![]() Jy. At 70 and 160
Jy. At 70 and 160 ![]() m, as said before, only the brightest
R-band sources were observed; among
them, only the two most luminous (in the optical band) were detected,
PKS 0537#43 and GD 158#19, where the latter is the source described in V09.
For the 6 remaining sources, an upper limit (3
m, as said before, only the brightest
R-band sources were observed; among
them, only the two most luminous (in the optical band) were detected,
PKS 0537#43 and GD 158#19, where the latter is the source described in V09.
For the 6 remaining sources, an upper limit (3![]() )
was estimated from the residual mosaic (see
also Frayer et al. 2006) after
source extraction, as done at 24
)
was estimated from the residual mosaic (see
also Frayer et al. 2006) after
source extraction, as done at 24 ![]() m. The typical average noise (1
m. The typical average noise (1![]() )
is 1.2 mJy at 70 and 8 mJy at 160
)
is 1.2 mJy at 70 and 8 mJy at 160 ![]() m (consistent with
the results obtained in the COSMOS field from Frayer et al. 2009,
taking the different integration times into account).
m (consistent with
the results obtained in the COSMOS field from Frayer et al. 2009,
taking the different integration times into account).
Table 2 reports the target flux densities provided by
Spitzer. To compute uncertainties, the noise map was added in
quadrature to the systematic uncertainties, assumed to be 10 per cent
in the IRAC and MIPS 24 ![]() m bands and 15 per cent at 70 and 160
m bands and 15 per cent at 70 and 160 ![]() m
(see IRAC and MIPS Data Handbook).
m
(see IRAC and MIPS Data Handbook).
4 Modelling the spectral energy distribution
The observed optical-to-MIR (or FIR/sub-mm) SEDs can be modelled as the sum of three distinct components: a stellar component, which emits most of its power in the optical/NIR; an AGN component, whose emission peaks in the MIR for obscured quasars and is caused by hot dust heated by UV/optical radiation from gas accreting onto the central SMBH; and a starburst component, which represents the major contribution to the FIR spectrum. In this work, we considered all the three components (see Sects. 4.1, 4.2; and Hatziminaoglou et al. 2008). Since the focus of the paper is on the AGN contribution to the SED, we discuss the hot dust modelling and its uncertainties in more detail.
The hot dust emission in AGN is reproduced using the F06 model. This model follows the formalism developed by different authors (e.g., Pier & Krolik 1992; Efstathiou & Rowan-Robinson 1995), where the IR emission in AGN originates in dusty gas around the SMBH with a smooth distribution. The dust grains are heated by high-energy photons coming from the accretion disk, and their thermal and scattering re-emission, mostly at IR wavelengths, is computed by means of the radiative transfer equations. For the dust distribution geometry, different possibilities (i.e. ``classical'' torus shape, tapered or flared disk) are explored in the literature.
More recently, models considering a clumpy distribution for the dust
have been developed (e.g., Nenkova et al. 2002;
Nenkova et al. 2008). These models
successfully explain many recent observations in the mid-IR, such as the strength
of absorption and emission features at 9.7 ![]() m and the X-ray variability
(Risaliti et al. 2002).
m and the X-ray variability
(Risaliti et al. 2002).
Another possibility for the torus models described above are the disk-wind models (see Elitzur & Shlosman 2006, and references therein), involving a completely different approach. The dusty clouds, responsible for the obscuration, are part of a hydro-magnetic wind coming from the accretion disk. On the one hand, these models are potentially capable of explaining disparate phenomena in AGN (from broad emission to absorption lines and obscuration), providing a hydro-dynamical justification for the persistence of the clouds around the SMBH. On the other hand, a parameterization that takes the observational constraints on the clumpy obscuration into account, thereby supplying a grid of synthetic IR SEDs, does not exist yet (see Elitzur 2008).
A detailed comparison between smooth and clumpy dust distribution models is discussed by Dullemond & van Bemmel (2005) who conclude that both models yield similar SEDs (see also Elitzur 2008; and Nenkova et al. 2008). The main difference is in the strength of the silicate feature observed in absorption in objects seen edge-on, which is, on average, weaker for clumpy models with the same global torus parameters. In clumpy models, in fact, clouds at different distances from the central source can be intercepted by the line of sight, including the innermost clouds, where the silicate feature is in emission given the higher temperature of the dust grains. A systematic comparison of the two model predictions is beyond the scope of the present paper and should be performed on high-quality IR data (i.e. a Spitzer IRS spectroscopic sample).
Notwithstanding these limitations, with the present work we aim at extracting the maximum information using the available photometric data. The F06 model adopted in this work is one of the models most tested against both broad-band photometry (F06; Rodighiero et al. 2007; Hatziminaoglou et al. 2009,2008; Agol et al. 2009; V09) and Spitzer mid-infrared spectra (F06). Moreover, the F06 model was the first one able to reproduce the quasar mid-IR spectra, considered a very strong constraint to characterize the dust properties in AGN and probe the unified model.
4.1 The AGN-torus component
The F06 code assumes a smooth dust distribution around the central source
consisting of a Galactic mixture of silicate and graphite grains.
The presence of silicate dust grains is clear from the absorption feature at
9.7 ![]() m seen in most type 2 AGN. The graphite grains are, instead, responsible
for the rapid decline in the emission at wavelengths shortwards
of a few microns, corresponding to a blackbody emission of about 1500 K, the
sublimation temperature of these grains (see F06).
m seen in most type 2 AGN. The graphite grains are, instead, responsible
for the rapid decline in the emission at wavelengths shortwards
of a few microns, corresponding to a blackbody emission of about 1500 K, the
sublimation temperature of these grains (see F06).
The assumed dust geometry is a flared disk
(see Efstathiou & Rowan-Robinson 1995), which is a sphere with the polar cones
removed. The internal radius of the dust distribution is defined by the
sublimation temperature of the dust itself. To simulate a more
realistic shape for the dust distribution, F06 assumes that the dust density
can vary both with the radial and the angular coordinates:
where
The dusty torus is heated by the emission of the inner accretion disk,
which represents the input energy to the radiative transfer code.
The assumed spectrum for the accretion disk is defined in the 10-3 to
20 ![]() m regime (from soft X-rays, i.e. 1.25 keV, to mid-IR) and is
parameterized by broken power laws in F06. The specific indices of the power laws are adapted from the Granato & Danese (1994)
and the Nenkova (2002) models and are consistent with the broad-band SEDs of a sample of type 1 AGN from the SDSS survey
(Hatziminaoglou et al. 2008, see their Figs. 8 and 9).
m regime (from soft X-rays, i.e. 1.25 keV, to mid-IR) and is
parameterized by broken power laws in F06. The specific indices of the power laws are adapted from the Granato & Danese (1994)
and the Nenkova (2002) models and are consistent with the broad-band SEDs of a sample of type 1 AGN from the SDSS survey
(Hatziminaoglou et al. 2008, see their Figs. 8 and 9).
Along with the thermally re-processed light, the F06 provides, as a function of the line-of-sight and optical depth, the fraction of the inner accretion disk light not intercepted by the torus and the scattered light. In the following, with the AGN component we will refer to the sum of all the three contributions.
4.2 The stellar and starburst components
The stellar component is modelled as the sum of simple stellar
populations (SSP) models of different ages, all assumed to have a common (solar)
metallicity. A Salpeter (1955)
initial mass function (IMF) with mass in the range (0.15-120 ![]() )
is assumed. The SSP spectra have
been weighted by a Schmidt-like law of star
formation (see Berta et al. 2004):
)
is assumed. The SSP spectra have
been weighted by a Schmidt-like law of star
formation (see Berta et al. 2004):
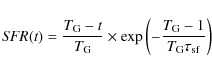
|
(2) |
where
To keep the number of free parameters
as low as possible, emission from cold dust, which dominates the bolometric emission at
wavelengths longer than 30 ![]() m rest-frame, is only included when far-IR/sub-mm data allow us to constrain that part of the SED
(two sources of the sample). For the same reason, additional components, such as the cold
absorber detached from the torus (i.e. Polletta et al. 2008),
which might improve the fit but would increase the complexity of the
overall modelling, is not included.
To reproduce the starburst component, a set of semi-empirical models of
well known and studied starburst galaxies is used, as in V09.
m rest-frame, is only included when far-IR/sub-mm data allow us to constrain that part of the SED
(two sources of the sample). For the same reason, additional components, such as the cold
absorber detached from the torus (i.e. Polletta et al. 2008),
which might improve the fit but would increase the complexity of the
overall modelling, is not included.
To reproduce the starburst component, a set of semi-empirical models of
well known and studied starburst galaxies is used, as in V09.
4.3 SED fitting procedure
The quality of the fitting solutions is measured using a
standard ![]() minimization technique (as in Hatziminaoglou et al. 2008), where the observed values are the
photometric flux densities (from optical-to-MIR/FIR) and the model values
are the ``synthetic'' flux densities obtained by convolving the sum of stars,
AGN, and starburst components through the filter response curves.
minimization technique (as in Hatziminaoglou et al. 2008), where the observed values are the
photometric flux densities (from optical-to-MIR/FIR) and the model values
are the ``synthetic'' flux densities obtained by convolving the sum of stars,
AGN, and starburst components through the filter response curves.
Before starting the general fitting procedure, we tested which torus parameters mainly influence the global model SED and are more sensitive to our data sets. Parameters that are not constrained by our data were then frozen.
The F06 torus model is described by six parameters: the ratio
![]() between
the outer and the inner radii of the
torus (the inner radius being defined by the sublimation temperature of the
dust grains); the torus full opening angle
between
the outer and the inner radii of the
torus (the inner radius being defined by the sublimation temperature of the
dust grains); the torus full opening angle ![]() ;
the optical depth
;
the optical depth
![]() at 9.7
at 9.7 ![]() m (
m (
![]() ;
the line of sight
;
the line of sight ![]() with
respect to the
equatorial plane, and two parameters,
with
respect to the
equatorial plane, and two parameters, ![]() and
and ![]() ,
describing the
law for the spatial distribution of the dust and gas density
,
describing the
law for the spatial distribution of the dust and gas density ![]() inside the torus (Eq. (1)).
inside the torus (Eq. (1)).
In our approach, we leave the following parameters free to vary inside the
pre-constructed grid of torus models: the torus full
opening angle ![]() ,
the optical depth
,
the optical depth
![]() ,
and the parameter
,
and the parameter ![]() describing the radial
dependence of the density. We fix
describing the radial
dependence of the density. We fix
![]() ,
which translates into compact tori of a few tens of
parsecs (given that
,
which translates into compact tori of a few tens of
parsecs (given that ![]() is directly connected to the sublimation
temperature and to the accretion luminosity of the central
BH).
Recent high-resolution IR observations support a compact dust distribution in nearby luminous AGN.
Using the interferometry at VLTI in the 8-13
is directly connected to the sublimation
temperature and to the accretion luminosity of the central
BH).
Recent high-resolution IR observations support a compact dust distribution in nearby luminous AGN.
Using the interferometry at VLTI in the 8-13 ![]() m band, a torus of size
m band, a torus of size ![]() 2-3 pc was detected in NGC 1068 (Jaffe et al. 2004). Similar compact tori were also found in
other local AGN, such as Circinus and NGC 4151 (see the review by
Elitzur 2008).
2-3 pc was detected in NGC 1068 (Jaffe et al. 2004). Similar compact tori were also found in
other local AGN, such as Circinus and NGC 4151 (see the review by
Elitzur 2008).
Regarding the density
distribution, we allow power-law profiles that decrease with the radius
with different coefficients ![]() .
We do not allow any dependence on the distance from the equatorial plane by fixing
.
We do not allow any dependence on the distance from the equatorial plane by fixing ![]() .
As a result, different angles for the lines of sight
.
As a result, different angles for the lines of sight ![]() (with respect
to the equatorial plane) give the same SED, once the torus is intercepted.
(with respect
to the equatorial plane) give the same SED, once the torus is intercepted.
Given the F06 grid of models, the discrete values, allowed for our free
parameters, are
![]() ,
,
![]() and
and
![]() ,
implying 72 different torus SEDs.
,
implying 72 different torus SEDs.
Considering the stellar component, we fix the redshift for the formation of the oldest SSPat z=4; i.e., given the observed redshift of the
sources, we consider galaxies with ages typical of early-type galaxies
(![]() 1-2 Gyr). This assumption is justified by the observed
1-2 Gyr). This assumption is justified by the observed
![]() colours and the brightness profiles typical of early-type galaxies as obtained
by a detailed morphological analysis in the
colours and the brightness profiles typical of early-type galaxies as obtained
by a detailed morphological analysis in the ![]() -band
(Mignoli et al. 2004). Concerning the star-formation history, we allow the
-band
(Mignoli et al. 2004). Concerning the star-formation history, we allow the
![]() parameter
of the Schmidt-like law and the value of the
extinction E(B-V) to vary. The latter is a key parameter, along with
the optical depth
parameter
of the Schmidt-like law and the value of the
extinction E(B-V) to vary. The latter is a key parameter, along with
the optical depth
![]() of the torus, in shaping the
optical-NIR continuum.
of the torus, in shaping the
optical-NIR continuum.
Overall, the SED-fitting procedure ends with 5 free parameters (6 when a starburst component is included).
Since the problem is
affected by some degeneracy, we consider, along with the best-fitting
solutions, all the acceptable solutions within
1![]() confidence level by considering, for
each source, all the solutions with
confidence level by considering, for
each source, all the solutions with
![]() or 7.04, when
the cold starburst component is added (see Lampton et al. 1976).
or 7.04, when
the cold starburst component is added (see Lampton et al. 1976).
Table 3: Best-fitting physical parameters and inferred rest-frame properties.
5 Results from SED fitting
In Fig. 2 we show the ![]() distribution.
The hatched histogram represents the distribution of
the best-fitting solutions for our 16 targets, while the empty histogram
shows the
distribution.
The hatched histogram represents the distribution of
the best-fitting solutions for our 16 targets, while the empty histogram
shows the ![]() distribution of all the solutions within 1
distribution of all the solutions within 1![]() ,
satisfying the criteria
,
satisfying the criteria
![]() .
Given our adopted grid
for the fitted parameters, the total number of
solutions at 1
.
Given our adopted grid
for the fitted parameters, the total number of
solutions at 1![]() (constructed by adding all the solutions at
1
(constructed by adding all the solutions at
1![]() of each object) is 137, or 8 solutions on average per source
(including the best-fitting one).
of each object) is 137, or 8 solutions on average per source
(including the best-fitting one).
![\begin{figure}
\par\includegraphics[angle=-270,width=7.5cm,clip]{13043fig2.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg110.png)
|
Figure 2:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13043fig3a.ps} \vspace*{2.3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg111.png)
|
Figure 3:
a) Observed-frame SEDs for 14 sources with data from the
R-band to the 24 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.8cm,clip]{13043fig3b.ps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg112.png)
|
Figure 3: b) As in Fig. 3a for sources with detections also at longer wavelengths (FIR/sub-mm). An additional starburst component (green dot-dashed line) is considered in the best-fit model. |
| Open with DEXTER | |
The two distributions do not show a significant difference, and this
reinforces our choice of considering all the solutions at 1![]() as a unique statistical
sample in the analysis of the
parameter space and degeneracy,
as a unique statistical
sample in the analysis of the
parameter space and degeneracy,
In terms of the absolute values of the ![]() ,
only 7 sources (out of
16) give a formally acceptable fit
(
,
only 7 sources (out of
16) give a formally acceptable fit
(
![]() ,
see Table 3); the remaining sources have a best-fit
model with large
,
see Table 3); the remaining sources have a best-fit
model with large
![]() .
While we use the
.
While we use the ![]() to assign
a relative goodness of different parameter combinations inside the parameter
grid, we will not take the absolute probabilities
at face value. Overestimated
to assign
a relative goodness of different parameter combinations inside the parameter
grid, we will not take the absolute probabilities
at face value. Overestimated ![]() is, in fact, a common
problem of most SED-fitting techniques, resulting from a combination of
two different reasons: the limited grid of models (72 torus
models with the adopted choice of parameters, see Sect. 4.3)
with no uncertainties associated, and the photometric measurements
with often underestimated uncertainties (see Gruppioni et al. 2008,
for a detailed description of this issue).
is, in fact, a common
problem of most SED-fitting techniques, resulting from a combination of
two different reasons: the limited grid of models (72 torus
models with the adopted choice of parameters, see Sect. 4.3)
with no uncertainties associated, and the photometric measurements
with often underestimated uncertainties (see Gruppioni et al. 2008,
for a detailed description of this issue).
In Fig. 3a,b the observed SEDs, from the R-band
to the IR (or sub-mm), are reported with the best-fitting models
overplotted. All the sources need a host galaxy component and an AGN
one. The stellar component
dominates in the R and ![]() bands, while the nuclear one does at 24
bands, while the nuclear one does at 24 ![]() m.
In the IRAC bands, both components contribute, with the fraction
depending on the properties of the individual sources. For PKS 0537_43 and
G158_19, where data points are available at longer wavelengths, an additional starburst component is needed
(Fig. 3b).
m.
In the IRAC bands, both components contribute, with the fraction
depending on the properties of the individual sources. For PKS 0537_43 and
G158_19, where data points are available at longer wavelengths, an additional starburst component is needed
(Fig. 3b).
In Fig. 4,
the relative contributions of the thermal, direct, and scattered light
to the total AGN light are shown for two sources characterized by a low
(
![]() ,
PKS 0537#123) and a high (
,
PKS 0537#123) and a high (
![]() ,
PKS 0537#111) optical depth.
While for
,
PKS 0537#111) optical depth.
While for
![]() ,
the AGN emission is dominated by the reprocessed emission
in all the UV/optical/IR bands, for
,
the AGN emission is dominated by the reprocessed emission
in all the UV/optical/IR bands, for
![]() the direct and scattered
components account for the optical/UV AGN emission. Nevertheless, the contribution
of the components mentioned above never exceeds the 20% of the observed flux
in the R-band.
For a sample of highly polarized red AGN selected from the 2MASS survey, a larger contribution of the scattered nuclear
component to the
optical and near-IR emission was found (Cutri et al. 2002;
Kuraszkiewicz et al. 2009). The different result obtained from our analysis is probably due to the different degrees of
obscuration of the two samples: the 2MASS sample is characterized by column
densities around 1022 cm-2, while the present sample has a median
column density of
the direct and scattered
components account for the optical/UV AGN emission. Nevertheless, the contribution
of the components mentioned above never exceeds the 20% of the observed flux
in the R-band.
For a sample of highly polarized red AGN selected from the 2MASS survey, a larger contribution of the scattered nuclear
component to the
optical and near-IR emission was found (Cutri et al. 2002;
Kuraszkiewicz et al. 2009). The different result obtained from our analysis is probably due to the different degrees of
obscuration of the two samples: the 2MASS sample is characterized by column
densities around 1022 cm-2, while the present sample has a median
column density of
![]() cm-2.
cm-2.
The negligible contribution of the AGN component, relative to the
stellar one, at short wavelengths, is consistent with the upper limits to the
AGN emission derived by
Mignoli et al. (2004) from the analysis of the ![]() -band images (shown
as downward-pointing arrows in Figs. 3 and 4). In Table 3, the
-band images (shown
as downward-pointing arrows in Figs. 3 and 4). In Table 3, the ![]() values (and the corresponding degree of
freedom) of the best-fitting solutions are reported for each source.
values (and the corresponding degree of
freedom) of the best-fitting solutions are reported for each source.
5.1 Torus parameters
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13043fig4.ps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg119.png)
|
Figure 4:
Observed-frame spectral energy distribution as in Figs. 3a,b for 2
sources characterized by extreme values of
the optical depth:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-270,width=7cm,clip]{13043fig5.ps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg120.png)
|
Figure 5:
Top panel: the fraction of solutions with flat density profile
( |
| Open with DEXTER | |
In the following section, we discuss how the model torus parameters are
constrained by our data set. As anticipated, we consider all the 137
solutions at the 1![]() level. First of all, the torus is seen almost edge-on in all the solutions
(i.e., the line of sight always intercepts the obscuring material),
in agreement with the type 2 X-ray and optical classification of our sources.
level. First of all, the torus is seen almost edge-on in all the solutions
(i.e., the line of sight always intercepts the obscuring material),
in agreement with the type 2 X-ray and optical classification of our sources.
The torus model parameters that are left free to vary within the grid of
models are the torus opening angle ![]() ,
the slope
,
the slope ![]() of the dust
density profile, and the optical depth
of the dust
density profile, and the optical depth
![]() .
By converting the torus opening angle into a covering factor (CF) representing
the fraction of solid angle covered by the dusty material, we find that
solutions with high and low CF are possible, with a slight preference for tori with large CF. The mean CF value is 0.65 (
.
By converting the torus opening angle into a covering factor (CF) representing
the fraction of solid angle covered by the dusty material, we find that
solutions with high and low CF are possible, with a slight preference for tori with large CF. The mean CF value is 0.65 (
![]() ),
corresponding to a torus opening angle of
),
corresponding to a torus opening angle of
![]() .
.
According to Maiolino et al. (2007), the covering factor of the
circum-nuclear dust decreases for increasing optical luminosity at 5100 Å (L5100). This relation is explained in terms of a
``receding-torus''. In Maiolino et al. (2007) the luminosities at 5100 Å were derived from optical spectroscopy and the CF values from the ratios
between the 6.7 ![]() m and the 5100 Å luminosities for a sample of type 1 quasars spanning five orders of
magnitude in optical luminosity. In our approach, L5100 is estimated for each solution from the input accretion-disk spectrum
(see Sect. 4.1), once the normalization is found
(see Sect. 6.1).
The average value of CF and L5100 for our sample lies within 1
m and the 5100 Å luminosities for a sample of type 1 quasars spanning five orders of
magnitude in optical luminosity. In our approach, L5100 is estimated for each solution from the input accretion-disk spectrum
(see Sect. 4.1), once the normalization is found
(see Sect. 6.1).
The average value of CF and L5100 for our sample lies within 1![]() on the relation found by Maiolino et al. (2007).
Unfortunately, given the limited range of
L5100, we cannot investigate the
validity of the CF vs. L5100 relation over the range probed by
Maiolino et al. (2007).
on the relation found by Maiolino et al. (2007).
Unfortunately, given the limited range of
L5100, we cannot investigate the
validity of the CF vs. L5100 relation over the range probed by
Maiolino et al. (2007).
Regarding the density profile, about ![]() of the solutions have
of the solutions have ![]() ,
while
,
while
![]() and
and
![]() represent
represent ![]() and
and
![]() of the solutions, respectively. This is also reflected in the 16
best-fitting solutions, where only 2 sources (Mrk 0509#1 and PKS 0537#111)
are fitted with
of the solutions, respectively. This is also reflected in the 16
best-fitting solutions, where only 2 sources (Mrk 0509#1 and PKS 0537#111)
are fitted with
![]() ,
one with
,
one with
![]() (PKS 0537#43) and the remaining ones with
(PKS 0537#43) and the remaining ones with ![]() (see Table 3).
(see Table 3).
Solutions with a moderate optical depth
![]() are favoured by the
SED-fitting analysis. As shown in Fig. 5
(bottom panel), there are few solutions with high optical
depths while the majority of the solutions (
are favoured by the
SED-fitting analysis. As shown in Fig. 5
(bottom panel), there are few solutions with high optical
depths while the majority of the solutions (
![]() )
are characterized
by ``moderate''
)
are characterized
by ``moderate''
![]() (
(
![]() )
and 50
)
and 50![]() by
low
by
low
![]() (
(
![]() ).
The median value for
).
The median value for
![]() is 2.
is 2.
The finding of a preferred range of optical depths by the SED-fitting,
even with relatively sparse photometric data, comes from the overall
shape of the NIR/MIR continuum. In fact, once the stellar component is
determined by the optical/NIR data, the slope of the torus component is
directly linked to the amount of absorption (i.e., to the optical
depth) and is relatively well constrained by the available data. As
shown in Fig. 3a,b, for the very low values of the optical depth
![]() (
(
![]() ), the
F06 model predicts spectra with a weak emission line at 9.7
), the
F06 model predicts spectra with a weak emission line at 9.7 ![]() m.
m.
We clearly find that the optical depth
![]() and the density profile
and the density profile
![]() are not independent parameters, since low optical depth solutions
mostly occur with flat density profile (
are not independent parameters, since low optical depth solutions
mostly occur with flat density profile (![]() ). This is shown in
Fig. 5 (top panel), where the fraction of solutions with
). This is shown in
Fig. 5 (top panel), where the fraction of solutions with
![]() is reported as a function of
is reported as a function of
![]() .
For the assumed flared
disk geometry, at high optical depth a flat density profile produces too much
IR emission because of the large amount of dust at high radii. Thus the two best-fitting
solutions with the highest
.
For the assumed flared
disk geometry, at high optical depth a flat density profile produces too much
IR emission because of the large amount of dust at high radii. Thus the two best-fitting
solutions with the highest
![]() found (
found (
![]() and 10
for Mrk 509#01 and PKS 0537#111 respectively,
see Fig. 5 and Table 3) have a density
profile decreasing with the distance from the central BH (
and 10
for Mrk 509#01 and PKS 0537#111 respectively,
see Fig. 5 and Table 3) have a density
profile decreasing with the distance from the central BH (
![]() ).
).
Recalling that in our procedure different lines of sight are equivalent
(having assumed ![]() in the radial density profile, Eq. (1)), we can convert the optical depths to column densities
in the radial density profile, Eq. (1)), we can convert the optical depths to column densities ![]() (adopting a Galactic
dust-to-gas ratio) to be compared with the
(adopting a Galactic
dust-to-gas ratio) to be compared with the ![]() derived from the X-ray
observations.
Despite the uncertainties affecting the derivation of
derived from the X-ray
observations.
Despite the uncertainties affecting the derivation of ![]() from the
dust's optical depths
(i.e., dust and gas spatial distributions could be different),
as well as those affecting the
from the
dust's optical depths
(i.e., dust and gas spatial distributions could be different),
as well as those affecting the ![]() values from X-rays
(see Perola et al. 2004, for details and Table 1), the two independent estimates
give a consistent picture for the
majority of the sources, once the 1
values from X-rays
(see Perola et al. 2004, for details and Table 1), the two independent estimates
give a consistent picture for the
majority of the sources, once the 1![]() uncertainties derived from the SED and X-ray fitting procedure are taken into
account. By excluding the two sources without a measured
uncertainties derived from the SED and X-ray fitting procedure are taken into
account. By excluding the two sources without a measured ![]() from
the X-rays analysis (see Table 1), the median values for
from
the X-rays analysis (see Table 1), the median values for ![]() are
are
![]() cm-2 from the X-rays analysis and
cm-2 from the X-rays analysis and
![]() cm-2 from the dust optical
depths. Therefore, the SED-fitting method confirms the
X-ray classification of the sources as moderately obscured Compton-thin AGN.
cm-2 from the dust optical
depths. Therefore, the SED-fitting method confirms the
X-ray classification of the sources as moderately obscured Compton-thin AGN.
Two sources have a significantly different ![]() (by an order of magnitude)
derived with the two methods, PKS 0537#111 and Mrk 509#01.
These objects are those characterized by the highest optical depths
(
(by an order of magnitude)
derived with the two methods, PKS 0537#111 and Mrk 509#01.
These objects are those characterized by the highest optical depths
(
![]() ,
which are converted into
,
which are converted into
![]() cm-2 and
cm-2 and
![]() cm-2, respectively).
Since Mrk 509#01 only has an upper limit for the
cm-2, respectively).
Since Mrk 509#01 only has an upper limit for the ![]() inferred from
X-ray analysis (
inferred from
X-ray analysis (
![]() cm-2, see Table 1),
the observed discrepancy for this object might be explained if the source is
Compton-thick (
cm-2, see Table 1),
the observed discrepancy for this object might be explained if the source is
Compton-thick (
![]() cm-2), and the observed X-ray
spectrum is due to a reflection component. However, we cannot draw any
firm conclusion on this issue.
cm-2), and the observed X-ray
spectrum is due to a reflection component. However, we cannot draw any
firm conclusion on this issue.
5.2 Host galaxy parameters
In the spectral procedure, the host galaxy accounts for the
optical/near-IR photometric data points, where the AGN contribution is
presumably low, given the obscured nature of our sources.
We use the SSP spectra weighted by a Schmidt-like law of star formation
(see Sect. 4.2). The extinction E(B-V) and
![]() are free parameters.
Once the best-fitting values for these two parameters are found, the stellar
mass (obtained by integrating the star formation history over the
galaxy age and subtracting the fraction due
to mass loss during stellar evolution,
are free parameters.
Once the best-fitting values for these two parameters are found, the stellar
mass (obtained by integrating the star formation history over the
galaxy age and subtracting the fraction due
to mass loss during stellar evolution, ![]() 30%, from it) is estimated from the SED
normalization.
At the end of the SED fitting procedure, stellar masses are well-constrained,
for a given pair of E(B-V) and
30%, from it) is estimated from the SED
normalization.
At the end of the SED fitting procedure, stellar masses are well-constrained,
for a given pair of E(B-V) and
![]() ,
with a typical 1
,
with a typical 1![]() uncertainty for the normalization of
uncertainty for the normalization of ![]() 20%.
20%.
All but one of the stellar masses derived in this work are within 30% from the values estimated by Pozzi et al. (2007; eight sources in common), where the same data were used but different stellar libraries and a simpler approach was adopted (see Sects. 4.1 and 5.2 of Pozzi et al. 2007).
The stellar masses found are in the range
![]() up to
up to
![]() with three very massive galaxies (
with three very massive galaxies (
![]() ,
see
Table 3), implying that our obscured AGN are
hosted by massive galaxies at high redshift. As said in Sect. 4.2, the masses are obtained using
a Salpeter (1955) initial mass function (IMF) with mass in the
range (0.15-120
,
see
Table 3), implying that our obscured AGN are
hosted by massive galaxies at high redshift. As said in Sect. 4.2, the masses are obtained using
a Salpeter (1955) initial mass function (IMF) with mass in the
range (0.15-120 ![]() ). The assumption of a Chabrier (2003)
IMF (see Renzini 2006) would produce a factor of
). The assumption of a Chabrier (2003)
IMF (see Renzini 2006) would produce a factor of
![]() lower stellar masses.
lower stellar masses.
In Table 3, the best-fitting value for the free host galaxy
parameters (
![]() and E(B-V)), and the stellar masses are reported for each source.
and E(B-V)), and the stellar masses are reported for each source.
6 Black hole physical properties
6.1 Black hole accretion luminosities
The accretion-disk luminosity
![]() is a direct output
of the fitting procedure and is obtained by integrating the code input energy
spectrum once the best-fitting torus components and its normalization are
found (see Sect. 4.3).
is a direct output
of the fitting procedure and is obtained by integrating the code input energy
spectrum once the best-fitting torus components and its normalization are
found (see Sect. 4.3).
The input spectrum is defined in the 10-3 to 20 ![]() m regime.
Although this wavelength range provides the largest contribution to the
nuclear AGN luminosity, we also included the hard X-ray luminosity (
m regime.
Although this wavelength range provides the largest contribution to the
nuclear AGN luminosity, we also included the hard X-ray luminosity (
![]() )
in the
)
in the
![]() computation. This luminosity is estimated from the de-absorbed, k-corrected
computation. This luminosity is estimated from the de-absorbed, k-corrected
![]() luminosity, assumping a photon index
luminosity, assumping a photon index
![]() (typical of
AGN emission) and an exponential cut-off at 200 keV
(e.g., Gilli et al. 2007).
A different choice for the energy cut-off (e.g., at 100 keV) would produce a
difference by
(typical of
AGN emission) and an exponential cut-off at 200 keV
(e.g., Gilli et al. 2007).
A different choice for the energy cut-off (e.g., at 100 keV) would produce a
difference by ![]() 20% in the total X-ray luminosity for
20% in the total X-ray luminosity for
![]() sources (see Vasudevan et al. 2010). Dust grains are almost transparent to hard X-ray photons,
therefore the output of the code is not affected by the accretion-disk model spectrum not extending above soft-X-ray energies.
sources (see Vasudevan et al. 2010). Dust grains are almost transparent to hard X-ray photons,
therefore the output of the code is not affected by the accretion-disk model spectrum not extending above soft-X-ray energies.
In Table 3
![]() ,
along with
,
along with
![]() and
and
![]() ,
are reported.
,
are reported.
![]() extends over two orders of
magnitudes (1044-1046 erg s-1), with the hard-X-ray luminosities (1.25-500 keV) contributing to the AGN power in the range 5-50
extends over two orders of
magnitudes (1044-1046 erg s-1), with the hard-X-ray luminosities (1.25-500 keV) contributing to the AGN power in the range 5-50![]() (see Table 3). The two
sources with the highest optical depths (
(see Table 3). The two
sources with the highest optical depths (
![]() ,
10) are among
the sources with the smallest hard-X-ray fraction
(Mrk 509#01 and PKS 0537#111). In Table 3 we also report the range of bolometric
luminosities as obtained by considering the full set of 1
,
10) are among
the sources with the smallest hard-X-ray fraction
(Mrk 509#01 and PKS 0537#111). In Table 3 we also report the range of bolometric
luminosities as obtained by considering the full set of 1![]() solutions.
The uncertainties are, on average, about 0.2 dex, but vary
significantly from source to source, ranging from about 5% to about a factor
3 (see also Fig. 7).
solutions.
The uncertainties are, on average, about 0.2 dex, but vary
significantly from source to source, ranging from about 5% to about a factor
3 (see also Fig. 7).
We compare the computed bolometric luminosities with the
luminosities derived by integrating the torus best-fitting templates
from 0.1-1000 ![]() m (plus adding the hard X-ray luminosity for self-consistency). The two methods assume the same
torus SED, so the comparison can give important
information on the systematics affecting the estimates of
m (plus adding the hard X-ray luminosity for self-consistency). The two methods assume the same
torus SED, so the comparison can give important
information on the systematics affecting the estimates of
![]() derived by integrating the observed SED, which is the widely used method. We refer to the first measures as the ``model''
luminosities and to the second as the ``observed'' luminosities.
derived by integrating the observed SED, which is the widely used method. We refer to the first measures as the ``model''
luminosities and to the second as the ``observed'' luminosities.
The ``observed''
![]() (see Fig. 6) are lower (up to an
order of magnitude) than the ``model'' ones for all the solutions and the median value of the ratio is
(see Fig. 6) are lower (up to an
order of magnitude) than the ``model'' ones for all the solutions and the median value of the ratio is ![]() .
An underestimate of the luminosity in type 2 sources is expected by
torus models (e.g., Pier & Krolik 1993;
Granato & Danese 1994); here, we quantify this effect and provide
an empirical factor to correct the `observed' luminosities, at least for
this class of sources.
.
An underestimate of the luminosity in type 2 sources is expected by
torus models (e.g., Pier & Krolik 1993;
Granato & Danese 1994); here, we quantify this effect and provide
an empirical factor to correct the `observed' luminosities, at least for
this class of sources.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13043fig6.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg149.png)
|
Figure 6:
``Model'' as a function of ``observed'' bolometric luminosities
for the sample of luminous obscured quasars at the 1 |
| Open with DEXTER | |
We underline how the observed discrepancy does not depend on the lack
of
observations at far-IR wavelengths. In fact, the two methods assume the
same torus SED for self-consistency (i.e., the integrated torus SED to
estimate the observed
IR luminosity is the output of the code); under this hypothesis, an
over(under)-estimate on one luminosity would introduce the same effect
on the
other. As a result, a poor sampling in the far-IR would have the same
impact on both (i.e. ``observed'' and ``model'' ) luminosities. Our
analysis takes this uncertainty into account by considering all the
solutions (i.e., all torus models) at the 1![]() confidence level.
By means of this procedure, a broad range of model SED is associated to each
source (on average, eight solutions; see Sect. 5),
characterized by different emission in the mid/far-IR region, as a result
of different torus geometry and absorption properties
(see Fig. 3).
confidence level.
By means of this procedure, a broad range of model SED is associated to each
source (on average, eight solutions; see Sect. 5),
characterized by different emission in the mid/far-IR region, as a result
of different torus geometry and absorption properties
(see Fig. 3).
As explained in Pier & Krolik (1992), the low values of the
``observed''
![]() depend on a combination of three factors: the torus
opening angle
depend on a combination of three factors: the torus
opening angle ![]() (geometrical factor), the observer viewing
angle
(geometrical factor), the observer viewing
angle ![]() ,
and the torus optical thickness
,
and the torus optical thickness
![]() .
By erroneously assuming isotropic torus emission (done to compute the
``observed''
.
By erroneously assuming isotropic torus emission (done to compute the
``observed''
![]() ), the primary flux that does not intercept the
obscuring material would not be included in the luminosity budget; moreover, as the
thickness of the torus increases, more and more primary high-energy photons
entering the torus are absorbed by the dust grains and re-emitted
isotropically (hence also in directions escaping the torus it self).
This effect is explained by the dust self-absorption,
i.e., thermal dust emission absorbed by the dust itself. For high
optical depth, the outer edges of the torus absorb the IR photons coming
from the warmer dust at smaller radii and re-emit them isotropically,
i.e., also in directions outside the line of sight.
To better visualize this effect, we report in
Fig. 6 the
``observed'' versus ``model'' luminosities, as predicted by Pier & Krolik (1992), as a function of
the viewing
angle
), the primary flux that does not intercept the
obscuring material would not be included in the luminosity budget; moreover, as the
thickness of the torus increases, more and more primary high-energy photons
entering the torus are absorbed by the dust grains and re-emitted
isotropically (hence also in directions escaping the torus it self).
This effect is explained by the dust self-absorption,
i.e., thermal dust emission absorbed by the dust itself. For high
optical depth, the outer edges of the torus absorb the IR photons coming
from the warmer dust at smaller radii and re-emit them isotropically,
i.e., also in directions outside the line of sight.
To better visualize this effect, we report in
Fig. 6 the
``observed'' versus ``model'' luminosities, as predicted by Pier & Krolik (1992), as a function of
the viewing
angle ![]() and the
torus optical thickness
and the
torus optical thickness
![]() for 4 sets of type 2
configurations (as described in the caption).
Although there are some slight differences between the F06 model
(adopted here) and the Pier & Krolik (1992) torus model
(where the optical depth varies independently along the
radial and the vertical axis), optically thinner models show less
anisotropy (red dotted lines in Fig. 6, corresponding to
two different viewing angles), than higher
for 4 sets of type 2
configurations (as described in the caption).
Although there are some slight differences between the F06 model
(adopted here) and the Pier & Krolik (1992) torus model
(where the optical depth varies independently along the
radial and the vertical axis), optically thinner models show less
anisotropy (red dotted lines in Fig. 6, corresponding to
two different viewing angles), than higher
![]() models
(blue dashed lines in Fig. 6, corresponding to the same
viewing angles considered for the thinner model). The cold outer edges of
the thicker models, in fact, radiate little and block the light coming from
the inner torus radii.
models
(blue dashed lines in Fig. 6, corresponding to the same
viewing angles considered for the thinner model). The cold outer edges of
the thicker models, in fact, radiate little and block the light coming from
the inner torus radii.
To investigate these issues further,
we apply a ``conservative'' correction to our ``observed''
luminosities, meant to correct only for the geometrical factor;
in other words, we divided each ``observed'' luminosity by the corresponding
covering factor CF (
![]() for
for
![]() and
and
![]() for
for
![]() ).
Although this correction increases the ``observed'' luminosities,
the ``model'' ones are still higher (
).
Although this correction increases the ``observed'' luminosities,
the ``model'' ones are still higher (
![]() ). The remaining discrepancy
is mostly found for solutions with high optical depth,
as expected (
). The remaining discrepancy
is mostly found for solutions with high optical depth,
as expected (![]() for models with
for models with
![]() ;
see
Fig. 6, where the squares mark the 52 solutions with
;
see
Fig. 6, where the squares mark the 52 solutions with
![]() ).
).
An independent and consistent analysis was also done by Pozzi et al. (2007, see their
Sect. 5.1) where a first-order correction of ![]() to the ``observed'' luminosities was estimated, accounting for geometrical and
anisotropy effects; in that work, however, the correction was estimated
using the ratio of obscured/unobscured quasars according to the Gilli et al. (2007) AGN synthesis
models of the X-ray background
and the different shape of type 2 vs. type 1 quasar
SEDs as a function of the column density. In Pozzi et al. (2007),
the SED fitting was done using the Silva et al. (2004) AGN templates. Since the template choice was based on
the X-ray
to the ``observed'' luminosities was estimated, accounting for geometrical and
anisotropy effects; in that work, however, the correction was estimated
using the ratio of obscured/unobscured quasars according to the Gilli et al. (2007) AGN synthesis
models of the X-ray background
and the different shape of type 2 vs. type 1 quasar
SEDs as a function of the column density. In Pozzi et al. (2007),
the SED fitting was done using the Silva et al. (2004) AGN templates. Since the template choice was based on
the X-ray ![]() (and not on the
(and not on the ![]() resulting from the torus modelling as
in the present analysis), the correction corresponding to the thicker models
(
resulting from the torus modelling as
in the present analysis), the correction corresponding to the thicker models
(
![]() cm-2)
was not included since no Compton-thick objects were revealed in X-rays.
cm-2)
was not included since no Compton-thick objects were revealed in X-rays.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13043fig7.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg159.png)
|
Figure 7:
2-10 keV bolometric corrections as a function of the ``model''
bolometric luminosities (filled circles). Filled circles inside empty red
squares represent the sources with a spectroscopic redshift. The red solid and dot-dashed
lines represent the predictions from the
Marconi et al. (2004) relation and its 1 |
| Open with DEXTER | |
6.2 Hard X-ray bolometric corrections
In Fig. 7 the bolometric-to-X-ray luminosity ratio
(
![]() )
is shown as a function of
)
is shown as a function of
![]() .
For the bolometric luminosities we assume the
model ones. The error bars on
.
For the bolometric luminosities we assume the
model ones. The error bars on
![]() are derived from the 1
are derived from the 1![]() dispersion on
dispersion on
![]() .
.
A wide spread in the
![]() is found
(
is found
(
![]() ), as also pointed out by the
pioneering work of Elvis et al. (1994) on type 1 QSOs, owing to the
large dispersion in the AGN spectral shape. Our median value
(
), as also pointed out by the
pioneering work of Elvis et al. (1994) on type 1 QSOs, owing to the
large dispersion in the AGN spectral shape. Our median value
(
![]() ,
estimated from the 137 solutions) is marginally consistent with the mean value of
Elvis et al. (1994),
,
estimated from the 137 solutions) is marginally consistent with the mean value of
Elvis et al. (1994), ![]() after removing the IR
contribution (in order not to double-count the fraction of the
nuclear emission absorbed by the circumnuclear dusty material seen
almost face-on). We confirm the trend to higher
after removing the IR
contribution (in order not to double-count the fraction of the
nuclear emission absorbed by the circumnuclear dusty material seen
almost face-on). We confirm the trend to higher
![]() for objects with
higher bolometric luminosities as predicted by
Marconi et al. (2004; see Fig. 7) but our
for objects with
higher bolometric luminosities as predicted by
Marconi et al. (2004; see Fig. 7) but our
![]() values are
significantly lower (at least a factor 2 in normalization). They derive
values are
significantly lower (at least a factor 2 in normalization). They derive
![]() by
constructing an AGN reference template taking into account how the
spectral index
by
constructing an AGN reference template taking into account how the
spectral index
![]() varies as a function of the
luminosity (Vignali et al. 2003). Predictions consistent with
Marconi et al. (2004) have been obtained more recently
by Hopkins et al. (2007, Fig. 7),
considering the most recent
determination of SED templates (i.e. Richards et al. 2006) and
varies as a function of the
luminosity (Vignali et al. 2003). Predictions consistent with
Marconi et al. (2004) have been obtained more recently
by Hopkins et al. (2007, Fig. 7),
considering the most recent
determination of SED templates (i.e. Richards et al. 2006) and
![]() (i.e. Steffen et al. 2006).
(i.e. Steffen et al. 2006).
Our low values for
![]() are consistent with our previous analysis
(median
are consistent with our previous analysis
(median
![]() ,
Pozzi et al. 2007) based on
a different method and on different AGN templates (Silva et al. 2004) and with other
estimates found in literature for hard X-ray-selected samples. Kuraszkiewicz et al. (2003) considered a sample
of X-ray-selected luminous AGN
(
,
Pozzi et al. 2007) based on
a different method and on different AGN templates (Silva et al. 2004) and with other
estimates found in literature for hard X-ray-selected samples. Kuraszkiewicz et al. (2003) considered a sample
of X-ray-selected luminous AGN
(
![]() erg s-1) and find a median
erg s-1) and find a median
![]() of 18. Ballo et al. (2007), analysed a sample of low-luminosity AGN
(
of 18. Ballo et al. (2007), analysed a sample of low-luminosity AGN
(
![]() erg s-1) and find a median
erg s-1) and find a median
![]() of 12.
Low bolometric-to-X-ray ratios, consistent with our estimate
(median
of 12.
Low bolometric-to-X-ray ratios, consistent with our estimate
(median
![]() ,
,
![]() )
have been found recently by Lusso et al. (2010),
where the statistical properties of a large (and complete) sample of 545
X-ray-selected type 1 QSO from
the XMM-COSMOS survey (Hasinger et al. 2007) are presented.
)
have been found recently by Lusso et al. (2010),
where the statistical properties of a large (and complete) sample of 545
X-ray-selected type 1 QSO from
the XMM-COSMOS survey (Hasinger et al. 2007) are presented.
The lower bolometric-to-X-ray luminosity ratios found in the present
work (and in the above mentioned samples), in
comparison to the Hopkins et al. (2007)
predictions, are probably caused by a
selection bias, since our sample (and most of the above cited ones) are
hard X-ray-selected samples (i.e., sources with high X-ray luminosity are
favoured). Moreover, as discussed in Sect. 2, our sources are
among the most extreme X-ray sources,
being characterized by red optical-to-NIR colours (
![]() )
and
high X-ray-to-optical ratio (
)
and
high X-ray-to-optical ratio (
![]() ). Our selection
is very likely the origin of the large deviation (at about the 5
). Our selection
is very likely the origin of the large deviation (at about the 5![]() level) for a large fraction of the present sample (see Fig. 7)
from the Marconi et al. (2004) relation. To further explore this issue,
a larger (and complete) sample of X-ray sources (with optical identification
up to the faintest X-ray fluxes) is needed, in order to correct for the
selection bias and to derive the properties of the parent AGN population
(see Lusso et al. 2010).
level) for a large fraction of the present sample (see Fig. 7)
from the Marconi et al. (2004) relation. To further explore this issue,
a larger (and complete) sample of X-ray sources (with optical identification
up to the faintest X-ray fluxes) is needed, in order to correct for the
selection bias and to derive the properties of the parent AGN population
(see Lusso et al. 2010).
6.3 Black hole masses
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13043fig8.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg168.png)
|
Figure 8:
|
| Open with DEXTER | |
The BH masses are not a direct output of the best-fitting
procedure and cannot be derived with ``standard methods'' (i.e. galaxy
stellar kinematics, nuclear gas motions, reverberation).
We estimate them indirectly using the
![]() relation
derived locally by Marconi & Hunt (2003) and by assuming as
relation
derived locally by Marconi & Hunt (2003) and by assuming as
![]() the stellar mass derived from our best-fitting procedure.
The main uncertainties affecting these estimates derive from the extrapolation
of the local relation to higher z, where the behaviour of this relation is
still a matter of debate (see discussion in Pozzi et al. 2007).
The stellar masses are constrained quite well by the SED-fitting procedure
inside the pre-constructed grid of galaxy models (see Sect. 5.2).
the stellar mass derived from our best-fitting procedure.
The main uncertainties affecting these estimates derive from the extrapolation
of the local relation to higher z, where the behaviour of this relation is
still a matter of debate (see discussion in Pozzi et al. 2007).
The stellar masses are constrained quite well by the SED-fitting procedure
inside the pre-constructed grid of galaxy models (see Sect. 5.2).
The inferred black hole masses are typically in the range
![]() ,
with three sources (PKS 0537
,
with three sources (PKS 0537![]() 43,
GD 158
43,
GD 158![]() 19, Abell 2690
19, Abell 2690![]() 29) with higher masses
(
29) with higher masses
(
![]() ). The range of BH masses is consistent with the values
reported by McLure & Dunlop (2004) for the SDSS quasars in the same
redshift interval (
). The range of BH masses is consistent with the values
reported by McLure & Dunlop (2004) for the SDSS quasars in the same
redshift interval (
![]() ,
see also
Shen et al. 2008, where new BH masses are derived).
,
see also
Shen et al. 2008, where new BH masses are derived).
In Fig. 8, the Eddington ratios
![]() ,
defined as
,
defined as
![]() (with
(with
![]() ), are reported as a
function of redshift. The values are compared
with those of the whole SDSS quasar sample
(McLure & Dunlop 2004) and those obtained by
Lusso et al. (2010) for the subsample of 150 X-ray selected type 1 AGN in
COSMOS with an accurate black hole mass determination.
), are reported as a
function of redshift. The values are compared
with those of the whole SDSS quasar sample
(McLure & Dunlop 2004) and those obtained by
Lusso et al. (2010) for the subsample of 150 X-ray selected type 1 AGN in
COSMOS with an accurate black hole mass determination.
The
![]() values of the present work cover slightly more
than an order of magnitude (0.01-0.3) with a median value of
values of the present work cover slightly more
than an order of magnitude (0.01-0.3) with a median value of
![]() (estimated considering all the 137 solutions at
1
(estimated considering all the 137 solutions at
1![]() level, see Sect. 5). The derived values are within the 3
level, see Sect. 5). The derived values are within the 3![]() confidence interval of the SDSS quasar
confidence interval of the SDSS quasar
![]() distribution, characterized by a median value
of
distribution, characterized by a median value
of ![]() and with a dispersion of 0.35 dex at the same redshift interval
sampled by our sources. However, almost
all our data points lie
towards the low
and with a dispersion of 0.35 dex at the same redshift interval
sampled by our sources. However, almost
all our data points lie
towards the low
![]() tail of the SDSS distribution (see
Fig. 8), suggesting
that X-ray selection is biased towards slightly lower
tail of the SDSS distribution (see
Fig. 8), suggesting
that X-ray selection is biased towards slightly lower
![]() than optical selection. Our data are fully consistent with the results
obtained from a much larger sample of X-ray-selected type 1 AGN in the COSMOS field (Lusso et al. 2010).
than optical selection. Our data are fully consistent with the results
obtained from a much larger sample of X-ray-selected type 1 AGN in the COSMOS field (Lusso et al. 2010).
The results are robust
against the uncertainties on the extrapolation, discussed above, of the
local
![]() relation, at the redshift of our
sample. In fact, allowing for positive evolution with
redshift of the
relation, at the redshift of our
sample. In fact, allowing for positive evolution with
redshift of the
![]() ratio by a factor of 2 (e.g., Merloni et al. 2010), the Eddington ratios
ratio by a factor of 2 (e.g., Merloni et al. 2010), the Eddington ratios
![]() would decrease further by the same factor.
would decrease further by the same factor.
Finally, in Fig. 9, the bolometric corrections
![]() are plotted against the Eddington ratios
are plotted against the Eddington ratios
![]() (following Vasudevan & Fabian 2009). The error bars representing
the
(following Vasudevan & Fabian 2009). The error bars representing
the ![]() confidence interval derived from the uncertainties on
confidence interval derived from the uncertainties on
![]() .
Along with our data we show the Vasudevan & Fabian (2009) results, where simultaneous optical, UV and X-ray
observations are included for the majority of the Peterson et al. (2004)
reverberation mapped sample of AGN. Our findings are in fairly good agreement with the trend towards increasing
.
Along with our data we show the Vasudevan & Fabian (2009) results, where simultaneous optical, UV and X-ray
observations are included for the majority of the Peterson et al. (2004)
reverberation mapped sample of AGN. Our findings are in fairly good agreement with the trend towards increasing
![]() for increasing
for increasing
![]() .
Vasudevan & Fabian (2009) interpret the observed trend as the result of different black hole SED shape as a function of
the Eddington ratio, with the high and low Eddington ratios
corresponding to different fractions of the ionizing UV
luminosity.
A similar trend has been recently found for a sample of 63
type 1 and type 2 AGN detected in the Swift/BAT 9-month catalogue (see Vasudevan & Fabian (2009), where the bolometric luminosities were
derived by integration over the observed optical/UV/X-ray SED,
in this work the authors consider the reprocessed IR emission, reproduced by
the empirical SEDs of Silva et al. (2004), as a proxy of the
intrinsic AGN bolometric luminosity, as first suggested by Pozzi et al. (2007).
.
Vasudevan & Fabian (2009) interpret the observed trend as the result of different black hole SED shape as a function of
the Eddington ratio, with the high and low Eddington ratios
corresponding to different fractions of the ionizing UV
luminosity.
A similar trend has been recently found for a sample of 63
type 1 and type 2 AGN detected in the Swift/BAT 9-month catalogue (see Vasudevan & Fabian (2009), where the bolometric luminosities were
derived by integration over the observed optical/UV/X-ray SED,
in this work the authors consider the reprocessed IR emission, reproduced by
the empirical SEDs of Silva et al. (2004), as a proxy of the
intrinsic AGN bolometric luminosity, as first suggested by Pozzi et al. (2007).
The dependence of bolometric corrections on Eddington ratios is expected by accretion-disk models, which predict an increasing hard X-ray bolometric corrections at increasing accretion rates (e.g. Witt et al. 1997). Recently also studying a large (156 sources) sample of type 1 X-ray AGN from the XMM-Newtonarchive, Bianchi et al. (2009) suggest that the bolometric correction must depend on the Eddington ratio to allow the intrinsic power of AGN to scale linearly with black hole masses.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13043fig9.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg178.png)
|
Figure 9:
|
| Open with DEXTER | |
7 Summary
We analysed the SEDs of a sample of 16 obscured quasars selected in the
hard X-ray band. Spitzer
mid/far-IR photometry (IRAC and MIPS), along with the data available in
the literature, is modelled using a multi-component model, where the
AGN re-processed emission is reproduced in the context of a flared disk
model, as described by F06. Within the context of a flared disk torus
model, the uncertainty in and
degeneracy between the various derived parameters are accounted for by
including all solutions within 1![]() of the best-fit in the subsequent
analysis.
of the best-fit in the subsequent
analysis.
The main results are summarized below.
- All the 16 quasars were detected up to 8
 m and
all but two sources were detected at 24
m and
all but two sources were detected at 24 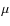 m with flux densities
in the range 100-7000
m with flux densities
in the range 100-7000 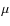 Jy at the 5
Jy at the 5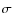 level.
The two most luminous sources of the sample were also detected at 70
and 160
level.
The two most luminous sources of the sample were also detected at 70
and 160 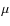 m.
m.
- The observed broad-band spectral energy distributions were reproduced well by a multi-component model comprising a stellar, an AGN, and a starburst component (when far-IR detections were available). The AGN component, modelled with the F06 radiative transfer code, accounts for the X-ray emission and for a fraction of the IR emission, mainly because of reprocessed emission from the putative dusty torus surrounding the central black hole.
- Solutions with a moderate optical depth
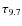 are favoured by the
SED-fitting, with the majority of the
sources having moderate optical depths (
are favoured by the
SED-fitting, with the majority of the
sources having moderate optical depths (
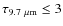 ).
The derived gas column densities (
).
The derived gas column densities (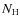 )
are consistent, for most of
the sources, with the values estimated from the X-ray analysis, both
indicating that the sources are Compton-thin AGN
(
)
are consistent, for most of
the sources, with the values estimated from the X-ray analysis, both
indicating that the sources are Compton-thin AGN
(
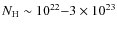 cm-2).
cm-2).
- The model nuclear bolometric luminosities are in the range
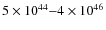 erg s-1. By comparing these values
with those obtained by integrating the nuclear observed SED, we
concluded that the latter underestimates the bolometric luminosities
by a factor of 2. The difference may be explained by anisotropic torus
emission and the effect of the torus optical depth
(e.g., Pier & Krolik 1992).
erg s-1. By comparing these values
with those obtained by integrating the nuclear observed SED, we
concluded that the latter underestimates the bolometric luminosities
by a factor of 2. The difference may be explained by anisotropic torus
emission and the effect of the torus optical depth
(e.g., Pier & Krolik 1992).
- From the model nuclear SEDs, we estimated the
bolometric-to-X-ray corrections (
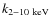 ). The median
). The median
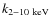 is
is
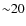 (
(
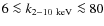 ). The value is lower than
assumed by some models of BH evolution (
). The value is lower than
assumed by some models of BH evolution (
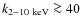 at the
median luminosity of our sample).
The discrepancy is significant at 5
at the
median luminosity of our sample).
The discrepancy is significant at 5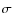 level at low bolometric
luminosity.
level at low bolometric
luminosity.
- By assuming the local
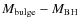 relation,
we estimate
relation,
we estimate
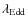 with a median value of 0.08
(
with a median value of 0.08
(
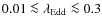 ). The whole SDSS quasar sample, at the same redshift interval sampled by our
objects, is characterized by a median value of 0.3. Our data are within the
). The whole SDSS quasar sample, at the same redshift interval sampled by our
objects, is characterized by a median value of 0.3. Our data are within the 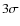 confidence level of the optically
selected quasar distribution; however, almost all our sources lie towards
the low
confidence level of the optically
selected quasar distribution; however, almost all our sources lie towards
the low
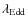 tail of the SDSS distribution, suggesting that our
X-ray selection is biased more towards lower Eddington efficiencies than optical
selection.
tail of the SDSS distribution, suggesting that our
X-ray selection is biased more towards lower Eddington efficiencies than optical
selection.
- The data are consistent with the correlation recently suggested
by Vasudevan & Fabian (2007, 2009) between
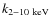 and
and
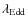 ,
where low bolometric corrections are found at low Eddington
ratios.
,
where low bolometric corrections are found at low Eddington
ratios.
The authors thank the anonymous referee for useful comments that helped improve the paper's content and presentation. The authors thank D. Fadda for suggestions about MIPS data reduction techniques, R. Gilli and F. La Franca for helpful discussions, and E. Lusso and E. Sarria for providing their results before publication. This work has benefited from partial support by the Italian Space Agency (contracts ASI/COFIS/WP3110 I/026/07/0 and ASI I/088/06/0), PRIN/MIUR (grant 2006-02-5203) and from research funding from the European Community's Sixth Framework Programme under RadioNet contract R113CT 2003 5158187. This work is based on observations with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under NASA contract 1407 and with the SCUBA camera, operating at the James Clerk Maxwell Telescope, a joint UK-Dutch-Canadian millimetre/sub-millimetre Telescope in Hawaii.
References
- Agol, E., Gogarten, S. M., Gorjian, V., & Kimball, A. 2009, ApJ, 697, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Baldi, A., Molendi, S., Comastri, A., et al. 2002, ApJ, 564, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Ballo, L., Cristiani, S., Fasano, G., et al. 2007, ApJ, 667, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, S., Fritz, J., Franceschini, A., Bressan, A., & Lonsdale, C. 2004, A&A, 418, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., Bonilla, N. F., Guainazzi, M., Matt, G., & Ponti, G. 2009, A&A, 501, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brusa, M., Comastri, A., Daddi, E., et al. 2005, A&A, 432, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Cocchia, F., Fiore, F., Vignali, C., et al. 2007, A&A, 466, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & van Bemmel, I. M. 2005, A&A, 436, 47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Efstathiou, A., & Rowan-Robinson, M. 1995, MNRAS, 273, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M. 2008, New Astron. Rev., 52, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M., & Shlosman, I. 2006, ApJ, 648, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Wilkes, B. J., McDowell, J. C., et al. 1994, ApJS, 95, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 1999, MNRAS, 308, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Fadda, D., Marleau, F. R., Storrie-Lombardi, L. J., et al. 2006, AJ, 131, 2859 [NASA ADS] [CrossRef] [Google Scholar]
- Fiore, F., Brusa, M., Cocchia, F., et al. 2003, A&A, 409, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiore, F., Grazian, A., Santini, P., et al. 2008, ApJ, 672, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Frayer, D. T., Huynh, M. T., Chary, R., et al. 2006, ApJ, 647, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Frayer, D. T., Sanders, D. B., Surace, J. A., et al. 2009, AJ, 138, 1261 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, J., Franceschini, A., & Hatziminaoglou, E. 2006, MNRAS, 366, 767 (F06) [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Granato, G. L., & Danese, L. 1994, MNRAS, 268, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Gruppioni, C., Pozzi, F., Polletta, M., et al. 2008, ApJ, 684, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G., Cappelluti, N., Brunner, H., et al. 2007, ApJS, 172, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Hatziminaoglou, E., Fritz, J., Franceschini, A., et al. 2008, MNRAS, 386, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Hatziminaoglou, E., Fritz, J., & Jarrett, T. H. 2009, MNRAS, 1247 [Google Scholar]
- Hönig, S. F., Beckert, T., Ohnaka, K., & Weigelt, G. 2006, A&A, 452, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Hopkins, P. F., Richards, G. T., & Hernquist, L. 2007, ApJ, 654, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, W., Meisenheimer, K., Röttgering, H. J. A., et al. 2004, Nature, 429, 47 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kuraszkiewicz, J. K., Wilkes, B. J., Hooper, E. J., et al. 2003, ApJ, 590, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Kuraszkiewicz, J., Wilkes, B. J., Schmidt, G., et al. 2009, ApJ, 692, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Lampton, M., Margon, B., & Bowyer, S. 1976, ApJ, 208, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., Comastri, A., Vignali, C., et al. 2010, A&A, 512, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Mignoli, M., Pozzetti, L., et al. 2006, A&A, 445, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Shemmer, O., Imanishi, M., et al. 2007, A&A, 468, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Makovoz, D., & Marleau, F. R. 2005, PASP, 117, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Sansigre, A., Rawlings, S., Lacy, M., et al. 2005, Nature, 436, 666 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., & Dunlop, J. S. 2004, MNRAS, 352, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Bongiorno, A., Bolzonella, M., et al. 2010, ApJ, 708, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Mignoli, M., Pozzetti, L., Comastri, A., et al. 2004, A&A, 418, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nenkova, M., Ivezic, Z., & Elitzur, M. 2002, ApJ, 570, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Nenkova, M., Sirocky, M. M., Ivezic, Z., & Elitzur, M. 2008, ApJ, 685, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Perola, G. C., Puccetti, S., Fiore, F., et al. 2004, A&A, 421, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Pier, E. A., & Krolik, J. H. 1992, ApJ, 401, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Pier, E. A., & Krolik, J. H. 1993, ApJ, 418, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Polletta, M., Weedman, D., Hönig, S., et al. 2008, ApJ, 675, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzi, F., Vignali, C., Comastri, A., et al. 2007, A&A, 468, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renzini, A. 2006, ARA&A, 44, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Rigby, J. R., Rieke, G. H., Pérez-González, P. G., et al. 2005, ApJ, 627, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Elvis, M., & Nicastro, F. 2002, ApJ, 571, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Gruppioni, C., Civano, F., et al. 2007, MNRAS, 376, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, Vistas in Astronomy, 1, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Greene, J. E., Strauss, M. A., Richards, G. T., & Schneider, D. P. 2008, ApJ, 680, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Shields, G. A., Salviander, S., & Bonning, E. W. 2006, New Astron. Rev., 50, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, L., Maiolino, R., & Granato, G. L. 2004, MNRAS, 355, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, A. A., Gammie, C. F., Wilson, R. W., et al. 1992, ApJS, 79, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, A. T., Strateva, I., Brandt, W. N., et al. 2006, AJ, 131, 2826 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., & Fabian, A. C. 2009, MNRAS, 392, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., Fabian, A. C., Gandhi, P., Winter, L. M., & Mushotzky, R. F. 2010, MNRAS, 402, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Brandt, W. N., & Schneider, D. P. 2003, AJ, 125, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Pozzi, F., Fritz, J., et al. 2009, MNRAS, 395, 2189 (V09) [NASA ADS] [CrossRef] [Google Scholar]
- Weedman, D., Polletta, M., Lonsdale, C. J., et al. 2006, ApJ, 653, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, H. J., Czerny, B., & Zycki, P. T. 1997, MNRAS, 286, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Zamorani, G., Henry, J. P., Maccacaro, T., et al. 1981, ApJ, 245, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Zombeck, M. V. 1990, Handbook of space astronomy and astrophysics (Cambridge University Press) [Google Scholar]
Footnotes
- ...
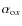
![[*]](/icons/foot_motif.png)
-
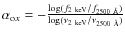 ,
Zamorani
et al. (1981).
,
Zamorani
et al. (1981).
- ... X/O)
![[*]](/icons/foot_motif.png)
- X/O is defined as
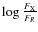 .
We used
.
We used 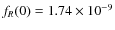 erg cm-2 s-1 Å-1
and
erg cm-2 s-1 Å-1
and 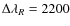 Å,
Zombeck (1990).
Å,
Zombeck (1990).
All Tables
Table 1: Properties of our luminous obscured quasars.
Table 2: Spitzer and SCUBA flux densities.
Table 3: Best-fitting physical parameters and inferred rest-frame properties.
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13043fig1.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg47.png)
|
Figure 1:
R-band magnitudes vs. hard X-ray (2-10 keV) flux for the full
HELLAS2XMM sample (Cocchia et al. 2007). Blue triangles represent
the sources included in the present analysis: blue triangles inside
red symbols represent the sources with spectroscopic redshifts.
Other symbols: empty red squares = sources spectroscopically classified as
type 2 AGN; empty circles = sources spectroscopically classified as non-type 2
AGN (type 1 AGN, emission-line galaxies, early-type galaxies and
groups/clusters of galaxies); crosses: objects not observed spectroscopically;
upward arrows = lower limits. The dashed lines represent the
loci of constant X/O ratio (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-270,width=7.5cm,clip]{13043fig2.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg110.png)
|
Figure 2:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13043fig3a.ps} \vspace*{2.3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg111.png)
|
Figure 3:
a) Observed-frame SEDs for 14 sources with data from the
R-band to the 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11.8cm,clip]{13043fig3b.ps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg112.png)
|
Figure 3: b) As in Fig. 3a for sources with detections also at longer wavelengths (FIR/sub-mm). An additional starburst component (green dot-dashed line) is considered in the best-fit model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13043fig4.ps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg119.png)
|
Figure 4:
Observed-frame spectral energy distribution as in Figs. 3a,b for 2
sources characterized by extreme values of
the optical depth:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-270,width=7cm,clip]{13043fig5.ps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg120.png)
|
Figure 5:
Top panel: the fraction of solutions with flat density profile
( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13043fig6.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg149.png)
|
Figure 6:
``Model'' as a function of ``observed'' bolometric luminosities
for the sample of luminous obscured quasars at the 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13043fig7.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg159.png)
|
Figure 7:
2-10 keV bolometric corrections as a function of the ``model''
bolometric luminosities (filled circles). Filled circles inside empty red
squares represent the sources with a spectroscopic redshift. The red solid and dot-dashed
lines represent the predictions from the
Marconi et al. (2004) relation and its 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13043fig8.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg168.png)
|
Figure 8:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13043fig9.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13043-09/Timg178.png)
|
Figure 9:
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.