Grain growth across protoplanetary discs: 10 μm silicate feature versus millimetre slope

D. J. P. Lommen; E. F. van Dishoeck; C. M. Wright; S. T. Maddison; M. Min; D. J. Wilner; D. M. Salter; H. J. van Langevelde; T. L. Bourke; R. F. J. van der Burg; G. A. Blake

doi:10.1051/0004-6361/200913150

Free Access

Issue		A&A Volume 515, June 2010


Article Number		A77
Number of page(s)		26
Section		Interstellar and circumstellar matter
DOI		https://doi.org/10.1051/0004-6361/200913150
Published online		11 June 2010

A&A 515, A77 (2010)

Grain growth across protoplanetary discs: 10 $\mu$ m silicate feature versus millimetre slope

D. J. P. Lommen¹ - E. F. van Dishoeck^1,2 - C. M. Wright³ - S. T. Maddison⁴ - M. Min^5,6 - D. J. Wilner⁷ - D. M. Salter¹ - H. J. van Langevelde^8,1 - T. L. Bourke⁷ - R. F. J. van der Burg¹ - G. A. Blake⁹

1 - Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
2 - Max-Planck-Institut für extraterrestrische Physik, Garching, Germany
3 - School of Physical, Environmental and Mathematical Sciences, UNSW@ADFA, Canberra ACT 2600, Australia
4 - Centre for Astrophysics and Supercomputing, Swinburne University of Technology, PO Box 218, Hawthorn, VIC 3122, Australia
5 - Astronomical Institute Utrecht, Princetonplein 5, 3584 CC Utrecht, The Netherlands
6 - Astronomical institute Anton Pannekoek, University of Amsterdam, Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
7 - Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, 02138 Cambridge, MA, USA
8 - Joint Institute for VLBI in Europe, PO Box 2, 7990 AA Dwingeloo, The Netherlands
9 - California Institute of Technology, Pasadena, CA 91125, USA

Received 19 August 2009 / Accepted 18 March 2010

Abstract
Context. Young stars are formed with dusty discs around them. The dust grains in the disc are originally of the same size as interstellar dust, i.e., of the order of 0.1 $\mu$ m. Models predict that these grains will grow in size through coagulation. Observations of the silicate features around 10 and 20 $\mu$ m are consistent with growth from submicron to micron sizes in selected sources whereas the slope of the spectral energy distribution (SED) at mm and cm wavelengths traces growth up to mm sizes and larger.
Aims. We here look for a correlation between these two grain growth indicators.
Methods. A large sample of T-Tauri and Herbig-Ae/Be stars, spread over the star-forming regions in Chamaeleon, Lupus, Serpens, Corona Australis, and the Gum nebula in Vela, was observed with the Spitzer Space Telescope at 5-13 $\mu$ m, and a subsample was observed with the SMA, ATCA, CARMA, and VLA at mm wavelengths. We complement this subsample with data from the literature to maximise the overlap between $\mu$ m and mm observations and search for correlations in the grain-growth signatures. Synthetic spectra are produced to determine which processes may produce the dust evolution observed in protoplanetary discs.
Results. Dust disc masses in the range <1 to 7 $\times$ $10^{-4}~M_\odot$ are obtained. The majority of the sources have a mm spectral slope consistent with grain growth. There is a tentative correlation between the strength and the shape of the 10- $\mu$ m silicate feature and the slope of the SED between 1 and 3 mm. The observed sources seem to be grouped per star-forming region in the 10- $\mu$ m-feature vs. mm-slope diagram. The modelling results show that, if only the maximum grain size is increased, first the 10- $\mu$ m feature becomes flatter and subsequently the mm slope becomes shallower. To explain the sources with the shallowest mm slopes, a grain size distribution shallower than that of the interstellar medium is required. Furthermore, the strongest 10- $\mu$ m features can only be explained with bright ( $L \sim 6~L_\odot$ ), hot ( $T_{\rm eff} = 4000$ K) central stars. Settling of larger grains towards the disc midplane results in a stronger 10- $\mu$ m feature, but has a very limited effect on the mm slope.
Conclusions. A tentative correlation between the strength of the 10- $\mu$ m feature and the mm slope is found, which would imply that the inner and outer disc evolve simultaneously. Dust with a mass dominated by large, $\sim$ mm-sized, grains is required to explain the shallowest mm slopes. Other processes besides grain growth, such as the clearing of an inner disc by binary interaction, may also be responsible for the removal of small grains. Observations with future telescopes with larger bandwidths or collecting areas are required to provide the necessary statistics to study these processes of disc and dust evolution.

Key words: accretion, accretion disks - circumstellar matter - stars: pre-main sequence - stars: formation

1 Introduction

A long-standing problem in planet formation is how tiny interstellar dust particles of less than a micron in size coagulate and grow to eventually form planets, thousands of kilometres in size. It is in the very nature of this field that it has to be studied at various levels, since different physical processes dominate during the various phases. The first steps, which lead to dust grains of about a decimetre in size, are studied both in the laboratory and with computer simulations (see Dominik et al. 2007; Blum & Wurm 2008 for detailed reviews). Local concentrations of boulders and subsequent gravitational collapse may then lead to the formation of planetesimals several hundreds of kilometres in size (e.g., Johansen et al. 2007). This paper focuses on the observational signatures of (sub)micron-sized grains up to centimetre-sized pebbles.

The InfraRed Spectrograph (IRS) on-board the Spitzer Space Telescope has provided a wealth of mid-infrared (5-40 $\mu$ m) spectra from discs around pre-main-sequence stars (e.g. Kessler-Silacci et al. 2006; Furlan et al. 2006). The spectra of these objects are often dominated by silicate emission features at 10 and 20 $\mu$ m. In young stellar objects, these features are formed in the upper atmosphere of the hot inner disc. The varying strength and the shape of these features can be naturally explained by different grain sizes in the upper layers of the inner disc, with strong, pointed features being representative of $\sim$ 0.1 $\mu$ m-sized grains and flatter features coming from dust grains of several $\mu$ m in size (Kessler-Silacci et al. 2006). These results confirm earlier results from the Infrared Space Observatory (Meeus et al. 2001; Bouwman et al. 2001) and from ground-based observations (e.g., Przygodda et al. 2003). It has been suggested that crystallisation has a similar effect on the 10- $\mu$ m feature as grain growth (e.g., Meeus et al. 2003; Honda et al. 2003). However, this effect is minimal and the dominating factor for the strength and shape of the 10- $\mu$ m feature is the characteristic grain size (Olofsson et al. 2009).

Because the 10- $\mu$ m feature only probes the surface layers of the inner disc, a stronger, more peaked feature could also be due to the settling of larger, micron-sized grains towards the mid-plane. As the larger grains settle and the small ones remain suspended in the upper layers, the surface becomes dominated by small grains, creating a strong silicate band. Dullemond & Dominik (2008) investigated this idea through theoretical models. They find that settling can in principle explain the different shapes of the 10- $\mu$ m feature, but only in quite specific cases, so that overall grain growth is still the most likely explanation for the flattening of these features. Recent interferometric observations of the 10- $\mu$ m spectral region in discs around $\sim$ 1 and 2-3- $M_\odot$ objects show that the grains closer to the central star are both larger and more crystalline than those further out in the disc (see, e.g., the recent review by van Boekel 2008). Hence, the evolution of the 10- $\mu$ m feature may be caused by a combination of grain growth and crystallisation and appears to progress from the inner disc outwards. On the other hand, analysis of the longer wavelenth mid-infrared crystalline features indicates significant growth and crystallisation in the outer disc as well (Olofsson et al. 2009).

Whereas the mid-infrared region potentially provides information on the growth of grains from interstellar, submicron sizes to sizes of several microns, the growth to larger sizes can only be probed by submillimetre (submm), millimetre (mm), and occasionally centimetre (cm) observations. Ground-breaking work was done by Beckwith et al. (1990) and Beckwith & Sargent (1991), both analytically studying the emission of dust grains and obtaining the first submm slopes by observing a large sample of young stellar objects at mm wavelengths. More recently, Andrews & Williams (2005) performed a sensitive single-dish submm continuum survey of 153 young stellar objects in the Taurus-Auriga star-formation region, including a large amount of archival and literature data. They found that the submm slope between 350 $\mu$ m and 1.3 mm could be well described by $\alpha = 2.0$ $\pm$ 0.5, where $F_\nu \propto \nu^{\alpha}$ , while the value for the interstellar medium is $\alpha \approx 3.7$ (cf. Draine 2006). Andrews & Williams (2005) interpreted this shallow slope as a combined effect of a contribution from optically thick regions in the disc and grain growth. It should be noted, however, that the sources in this study were spatially unresolved, and the (sub)mm emission may have a significant contribution from surrounding (envelope) material. More recently, interferometric studies of several dozen T-Tauri stars gave values of $\alpha \la 3.0$ (Lommen et al. 2007; Andrews & Williams 2007; Rodmann et al. 2006). Similar results were found for a number of more massive Herbig-Ae/Be stars (e.g., Natta et al. 2004). From this mm slope one can estimate the opacity index $\beta \approx (1 + \Delta)$ $\times$ $(\alpha - 2)$ , where $\Delta$ is found to be $\sim$ 0.20 (Lommen et al. 2007; Rodmann et al. 2006), and values of $\beta \approx 1.0$ for $\lambda \ga 1$ mm were found. Such a slope can be naturally explained by a significant fraction of grains at least several mm in size present in the discs (Draine 2006).

A subsample of the sources observed by Lommen et al. (2007) overlapped with the Spitzer Infrared Spectrograph (IRS) observations published by Kessler-Silacci et al. (2006) and Lommen et al. (2007) found a tentative correlation between the mm slope of the spectral energy distribution (SED) and the strength and shape of the 10- $\mu$ m silicate feature for these sources. Note that the 10- $\mu$ m feature primarily probes the hot surface layers of the inner disc, whereas the (sub)mm observations provide information of the cold mid-plane of the outer disc. A correlation between the two is therefore not obvious at all and a confirmation of this correlation would give very valuable information on the processes of dust growth in protoplanetary discs, as it would imply that grain growth from submicron to mm sizes is both fast and occurs simultaneously throughout the whole disc.

Acke et al. (2004) calculated the (sub)mm spectral indices of 26 Herbig-Ae/Be stars, for which the infrared SED could also be determined. They found a correlation between the strength of the ratio of the near- to mid-infrared excess and the slope of the (sub)mm energy distribution for these sources, which they attributed to a correlation between the disc geometry (flared versus self-shadowed) and the size of the grains in the disc. However, the authors did not find a correlation between the strength and the shape of the 10- $\mu$ m silicate feature and the (sub)mm spectral index (see also Acke & van den Ancker 2004).

The aim of this paper is to investigate the tentative correlation between the strength and shape of the 10- $\mu$ m silicate feature and the spectral slope in the (sub)mm regime, found by Lommen et al. (2007), for a larger sample. A subsample of sources studied with the Spitzer IRS were observed with mm and cm interferometers (Sect. 2). Interferometers were used to ascertain that the emission is dominated by disc emission, since extended emission from surrounding material will be filtered out. Also, spatially resolving the disc ensures that the emission is not optically thick (e.g., Natta et al. 2004). The results of the observations, including dust disc masses and mm slopes, are shown in Sect. 3, and in Sect. 4 we present model results for discs. The observations and models are compared and discussed in Sect. 5; conclusions are formulated in Sect. 6.

2 Observations

For this study, we compared Spitzer IRS observations covering the 10- $\mu$ m silicate feature with mm observations from the Very Large Array (VLA, operated by NRAO), the Combined Array for Research in Millimeter-wave Astronomy (CARMA), the Submillimeter Array (SMA), and the Australia Telescope Compact Array (ATCA). The sources for which new observations are obtained for this work are listed in Table 2. A full log of the newly obtained mm and cm observations is listed in Appendix A. A full log of the newly obtained mm and cm results is listed in Appendix B.

2.1 Source selection and Spitzer data

To look for possible environmental effects, sources in a total of five star-forming regions were observed, spread over the constellations Lupus, Chamaeleon, Corona Australis, Serpens, and the Gum nebula in Vela at distances of about 150-200, 160, 130, 260, and 400 pc, respectively. Furthermore, data from the literature for the Taurus-Auriga star-forming region at about 140 pc were included to improve the statistics further, see Table 1. The sources were pre-selected to have a large spread in the strengths and shapes of the 10- $\mu$ m features from Spitzer IRS data, mainly the ``From Molecular Cores to Planet-forming Discs'' programme (c2d, Evans et al. 2003, Program IDs 139 and 172-179), the ``The evolution of dust mineralogy in southern star forming clouds'' programme (C.M. Wright PI, Project ID 20611), and ``A complete IRS survey of the evolution of circumstellar disks within 3 Myr: New clusters of sequential star formation in Serpens'' (K.M. Pontoppidan PI, Project ID 30223). The spectra from the c2d project were previously published in Kessler-Silacci et al. (2006) and Olofsson et al. (2009). Program P20611 includes Spitzer IRS observations from embedded YSOs, T-Tauri stars, and Herbig/Vela-type stars. The results for the T-Tauri stars are presented in this work.

The data from Project ID 20611 are presented here for the first time. The data from the other programmes are re-reduced for this work using the updated c2d IRS reduction pipeline (Lahuis et al. 2006) for uniformity of the comparisons. Spectra were obtained both integrated over the full aperture of the instrument as well as convolved with the point spread function (PSF) at each wavelength. The spectra obtained using the Full-Aperture extraction method were used in here, unless the final spectrum quality of the PSF extraction method was considerably better. Furthermore, only data from the short-low module (SL, 5.2-14.5 $\mu$ m) were included, unless data from the short-high module (SH, 9.9-19.6 $\mu$ m) were present and of significantly higher quality.

Table 1: Distances to and ages of star-forming clouds.

In binary systems, it is possible that circumstellar discs get truncated due to binary interaction, affecting grain growth in the discs. To check for such effects, a number of binaries were included in the sample. Furthermore, the sources were selected to include so-called ``cold'' or ``transitional'' discs (e.g. Brown et al. 2007). The cold discs show a lower flux in the mid-infrared, which can be naturally explained by a lack of small warm dust close to the star. Several of the cold discs were recently found to be circumbinary discs, with a large hole or gap in the centre, e.g., CS Cha (Espaillat et al. 2007) and HH 30 (Guilloteau et al. 2008). However, some cold discs are supposedly single stars, requiring a different mechanism to clear the inner discs of small, hot grains (e.g., Pontoppidan et al. 2008). One such mechanism could be grain growth into larger particles. Another possibility would be that a planet has cleared the inner disc from most of the large grains, leaving behind a protoplanetary disc dominated by small, micron-sized grains. A number of cold discs of Brown et al. (2007) and Merín et al. (2008) were included in the sample with the aim to explore this possibility. A full list of the sources (35 single sources and five binaries) is given in Table 2. As will be shown in the next section, 33 of these turn out to have a detected 10- $\mu$ m feature and 13 yield a mm slope, more than doubling the sample of sources studied in Lommen et al. (2007).

Table 2: List of sources observed with the SMA, ATCA, CARMA, and VLA.

2.2 SMA observations

15 single sources and one binary were observed with the SMA for the project 2007B-S033. The observations were carried out on 14 March and 19 April 2008. The data of 14 March were unusable due to phase instabilities and the track was reobserved on 7 May 2009. On 19 April 2008, the phases were stable and the zenith optical depth at 225 GHz was around $\tau_{225} = 0.13$ all through the night. The synthesised beam was about 4.8 $\times$ 2.8 arcsec (natural weighting). On 7 May 2009, the phases were stable and $\tau_{225}$ was low with values ranging from 0.05 to 0.08. The synthesised beam was about 4.1 $\times$ 2.2 arcsec. The two sidebands were combined into one continuum channel to improve the signal-to-noise ratio, resulting in an effective wavelength of 1.33 mm.

The sources VV CrA (binary), S CrA (binary), and DG CrA (single source) were observed as part of the SMA ``filler'' project 2008A-S111 on 1 October 2008. Only six of the eight antennas were available for this track. However, $\tau_{225} \approx 0.1$ and the phases were stable, resulting in extremely good data. The synthesised beam of the resulting maps was about 5.0 $\times$ 2.1 arcsec (natural weighting). The correlator was tuned to 218 and 228 GHz. Combination of the two sidebands resulted in an effective wavelength of 1.35 mm.

The absolute flux calibration of the first track (19 April 2008) was carried out on Mars and the resulting fluxes are estimated to be accurate to about 20%. The second and third tracks (1 October 2008 and 7 May 2009) were flux calibrated on Callisto. The uncertainty in the absolute fluxes for those tracks is estimated to be 15% or better.

Hence, a total of 16 single sources and three binaries located in the Lupus star-forming region were observed with the SMA for this project. The sources are listed in Table 2, a detailed log of the observations is given in Table A.1, and detailed results are presented in Table B.1 and Fig. B.1.

2.3 ATCA observations

The data for the ATCA project C1794 were taken over the period July to August 2008 when the array was in the H214 configuration. A total of 15 sources were observed: 14 sources (including the binary IK Lup+Sz 66) were measured at 3 mm and 11 sources at 7 mm. The sources are listed in Table 2, a detailed log of the observations is given in Table A.2, and detailed results are presented in Table B.2 and Figs. B.3 and B.4. The weather changed considerably over the course of the observations. A short indication of the circumstances for each day is included in Appendix A. Physical baselines ranged from 82 to 247 m, resulting in synthesised beam sizes of about 2 arcsec at 3 mm and about 4 arcsec at 7 mm. Combining the two sidebands in the 3 mm band resulted in an effective wavelength of 3.17 mm, those taken in the 7 mm band in an effective wavelength of 6.82 mm.

The absolute flux calibration for the first track was carried out on Mars, whereas the flux calibration for the other tracks was carried out on Uranus. Only the shortest baselines were taken into account when determining the absolute gain offset so as to minimise the possible effect of the planets' being resolved. Furthermore, the planets were observed at elevations close to those at which the gain calibrators were observed. Overall, the uncertainty in the absolute fluxes is estimated to range from 15 to about 25%.

2.4 CARMA observations

For this work, eleven single sources and one binary located in Serpens were observed with CARMA at 1 and 3 mm in the period April to June 2008 for project c0165. The sources are listed in Table 2, a detailed log of the observations is given in Table A.3, and detailed results are presented in Table and Figs. B.5 and B.6. Weather conditions varied over the course of the observations, with a typical water path length of 3-6 mm.

The gain calibrator originally selected for the observations at 1 mm, QSO J1743-038, turned out to be too weak to perform a decent gain calibration, rendering most of the C-configuration observations unusable. For the second part of the observations the telescope was in the D configuration (baselines 11-148 m), yielding a synthesised beam of about 3 $\times$ 2 arcsec at 1 mm and about 6 $\times$ 4 arcsec at 3 mm. The effective wavelength of the 1 mm-band observations was 1.33 mm, that of the 3 mm-band observations 3.15 mm.

The absolute fluxes were calibrated on the quasars QSO J2253+161 (3c454.3), QSO J1229+020 (3c273), and QSO J1256-057 (3c279), whose fluxes were bootstrapped from planet observations on short baselines on dates as close as possible to the observation dates. The fluxes of these quasars vary considerably over the course of weeks to months at 1 and 3 mm, but day-to-day variations are usually less than 10%. Taking this into account, the effective uncertainty in the absolute fluxes for our target sources is estimated to be less than 30%.

2.5 VLA observations

Of the sources in the Serpens star-forming region observed with CARMA, seven single sources and the binary EC 90 were observed with the VLA at 7 mm and at 1.3, 3.6, and 6.3 cm under programme AL720. The sources are listed in Table 2, a detailed log of the observations is given in Table A.4, and detailed results are presented in Table B.4. The observations were carried out from 10-15 March 2008, when the array was in the C configuration, with baselines of up to 3.6 km and a synthesised beam of about 0.5 arcsec at 7 mm. All observations were performed in the default continuum mode in which, at each frequency, the full 100-MHz bandwidth was used in two adjacent 50 MHz bands. Although weather conditions were good in general, a few hours of observing time were lost at the end of the last two tracks due to high winds.

The VLA data were flux calibrated on the quasar QSO J1331+305 (3c286). The flux as a function of wavelength is modelled by the AIPS reduction package. The resulting uncertainty in the absolute flux calibration is estimated to be about 20% at 7 mm and 1.3 cm and better than 10% at 3.6 and 6.3 cm.

3 Results

3.1 Mm and cm source fluxes and dust disc masses

A full log of the results is listed in Appendix B. The results of the interferometric observations at 1, 3, and 7 mm are listed in Table 3.

Table 3: Fluxes from point-source fits in the (u, v) plane obtained from interferometric data and single-dish 1.20-1.27 mm SEST fluxes.

A total of 16 single sources and three binaries in Lupus are observed with the SMA. Nine of the single sources are detected and one of those, Sz 73, turned out to harbour two sources, with a projected separation of about 4 arcsec. It is possible that the detection of Sz 73 with SEST (Nürnberger et al. 1997) included both sources. The binaries VV CrA and S CrA are detected and unresolved. Of the binary system IK Lup (Sz 65) and Sz 66, only IK Lup is detected, although a second peak is detected at 2 arcsec from the 2MASS position of Sz 66. Sz 66 was previously detected with a S/N of almost four using the SEST bolometer. All sources in Lupus observed with the ATCA at 3.2 mm are detected; the binary system IK Lup and Sz 66 remained unresolved. Only one Lupus source, IM Lup, is detected at 6.8 mm. MY Lup would have been detected at 6.8 mm with a signal-to-noise ratio of about ten if it had a similar mm slope as IM Lup.

None of the three sources in the Gum nebula observed with the ATCA at 3.2 and at 6.8 mm are detected at either wavelength down to 3 $\sigma$ upper limits of $\sim$ 3 mJy at 3.2 mm and of $\sim$ 0.5 mJy at 6.8 mm. This can be attributed to the large distance between us and this star-forming region. If the sources in the Gum nebula had similar luminosities as those in the Lupus clouds, they would have had a flux of $\sim$ 0.7 mJy at 3.2 mm, which is below the noise level. Note that, although the Vela molecular ridge has been observed at mm wavelengths (Massi et al. 2007,1999), no published mm continuum data of the Gum nebula exist in the literature.

The source SZ Cha is detected at 2.3 mJy at 3.2 mm. Sz 32 is not detected down to a 3 $\sigma$ upper limit of 2.9 mJy at 3.2 mm. It is, however, detected with a flux of 0.77 mJy at 6.8 mm.

VV CrA and S CrA are clearly detected at 1.3 mm with the SMA, with fluxes of 376 and 303 mJy. DG CrA, however, is not detected, down to a 3 $\sigma$ upper limit of only 6.6 mJy. VV CrA and S CrA are also easily detected with the ATCA at 3 and 7 mm.

Of the sources in the Serpens star-forming region that were observed with the CARMA, only three are detected: the single sources SSTc2d J182900.88+002931.5 and GSC 00446-00153 and the binary system EC 90, which remained unresolved. This can in part be explained by the distance to the star-forming region in Serpens, which is larger than those in Chamaeleon, Lupus, and Corona Australis. Furthermore, some of the sources, of which six are new Spitzer sources, may have an intrinsically lower luminosity. None of the sources are detected at 6.8 mm using the VLA.

Table 4: Spectral slopes at mm wavelengths, dust disc masses, and properties of the 10- $\mu$ m silicate feature.

Four cold discs are observed at 1.3 and 3.2 mm for this work. Only one of those, Sz 111, is detected. Unfortunately, Sz 111 was not observed with the Spitzer IRS.

All four binaries that are observed at 1.3 and 3.2 mm are detected at both wavelengths. However, in the case of the binary consisting of the stars IK Lup and Sz 66, only the former is detected at 1.3 mm. EC 90 and S CrA remain unresolved. The binary IK Lup+Sz 66 is resolved with the ATCA at 3.2 mm. VV CrA is resolved with a binary separation of 2.0 arcsec with the ATCA at 3.2 mm if the source is imaged using uniform weighting (optimised for resolution). However, this binary remains unresolved with the SMA at 1.3 mm (beam size 4.7 $\times$ 1.9 arcsec) and with the ATCA at 6.8 mm (beam size 5.3 $\times$ 3.0 arcsec).

The detection rate of the sources observed in this study is rather low. This can in part be understood by the distance to the star-forming regions, with the Serpens star-forming region being almost twice as far away as the Taurus-Auriga star-forming region and the Gum nebula in Vela almost three times as far away. This reduces the observed flux for similar sources by a factor of about four to nine. The low detection rate for Lupus is largely a selection effect: most of the brightest sources had been observed before (Lommen et al. 2007). These previously detected sources were not reobserved for this work, but their published values will be included in the analysis below.

Dust disc masses are obtained from the fluxes at 3.2 mm under the rather crude assumptions of an isothermal disc and a fixed opacity. Assuming also optically thin mm emission, the dust disc mass is given by $M_{\rm disc} = F_\nu D^2 / \kappa_\nu B_\nu$ ( $T_{\rm dust}$ ), where D is the distance to the source, $\kappa_\nu$ the dust opacity (taken to be 0.9 cm² g^-1, cf. Beckwith et al. 1990), and $B_\nu$ ( $T_{\rm dust}$ ) the brightness at the frequency $\nu = 94$ GHz for a dust temperature $T_{\rm dust}$ , as given by the Planck function. We assume a dust temperature $T_{\rm dust} = 25$ K and find dust disc masses ranging from $\sim$ 0.4 to ${\sim}7$ $\times$ $10^{-4}~M_\odot$ . The dust disc masses are presented in Table 4.

3.2 Millimetre slopes

The fluxes at 1, 3, and 7 mm can be combined to obtain the spectral index $\alpha$ , where $F_\nu \propto \nu^{\alpha}$ . We are interested in the emission coming from the dusty disc. However, at 7 mm, other emission mechanisms may contribute significantly to the flux. Sources may include an ionised wind or chromospheric magnetic activity. Rodmann et al. (2006) compare their fluxes at 7 mm to those at 3 and 6 cm and claim that about 20% of the emission at 7 mm is due to free-free emission. On the other hand, Lommen et al. (2009) find that the emission at 7 mm can be entirely attributed to dust emission for a small sample of three sources. It is possible that the emission due to, e.g., an ionised wind, is independent of the disc mass and thus the relative contribution from such a wind will be larger for young stellar objects that are weaker at mm wavelengths. This could explain the findings of Lommen et al. (2009), who monitored some of the strongest pre-main-sequence mm emitters in the southern sky. However, a larger and more sensitive survey at mm to cm wavelengths is required before more quantitative statements on this subject can be made. Since we do not have fluxes at all three wavelengths for most sources, separate indices will be obtained between 1 and 3 mm and between 3 and 7 mm. The results are given in Table 4.

$\begin{figure} \par\includegraphics[width=16.5cm,clip]{13150fi1.eps} \end{figure}$	Figure 1: Spitzer IRS spectra from the T-Tauri stars observed for Spitzer project P20611 (C.M. Wright PI). Spectra with a maximum flux below 0.1 Jy were binned four times to improve the signal-to-noise ratio.
Open with DEXTER

The slopes between 1 and 3 mm lie between 2.38 $\pm$ 0.36 and 3.83 $\pm$ 0.46. The opacity index $\beta$ can be calculated from the mm slope $\alpha$ through $\beta \approx (1 + \Delta) \times (\alpha - 2)$ , where $\Delta$ is the ratio of optically thick to optically thin emission (Beckwith et al. 1990; Rodmann et al. 2006). Rodmann et al. (2006) and Lommen et al. (2007) found values of $\Delta \approx 0.2$ for the sources in their samples. Adopting this value, opacity indices $\beta$ of about 0.5 to 2.2 are found here. The Kolmogorov-Smirnov test gives a probability of 50% that the values from this sample and that of Lommen et al. (2007) are drawn from the same distribution. This rather low value is due to the steep slopes for the sources RY Lup (3.83 $\pm$ 0.46) and SZ Cha (3.78 $\pm$ 0.43). Note that the corresponding values for $\beta$ are ${\ga}2$ , whereas the value for the interstellar medium is $\beta_{\rm ISM} \approx 2.0$ (e.g., Draine & Lee 1984).

A mm slope between 3 and 7 mm could only be determined for three sources, whereas lower limits are found for four more sources and a strict upper limit of $\alpha_{3-7} < 1.8$ for Sz 32. Interestingly, a lower limit of $\alpha_{1-3} > 3.7$ is found for Sz 32 between 1 and 3 mm. Other emission mechanisms (due to, e.g., a wind or chromospheric activity) may contribute at 7 mm. Although it is found that for most sources this contribution is only of the order of 20% (Rodmann et al. 2006), it is possible that it is higher for Sz 32, causing the very shallow slope between 3 and 7 mm. The slopes of $\alpha_{3-7} = 2.4$ $\pm$ 0.5 and 2.5 $\pm$ 0.4 for VV CrA and S CrA are consistent with those of $\alpha_{1-3} = 2.5$ $\pm$ 0.5 and 2.9 $\pm$ 0.7 and also the slopes between 3 and 7 mm found for RY Lup (>2.0), Sz 111 (>2.9), RX J1615.3-3255 (>3.4), and MY Lup (>3.5) are consistent with the values between 1 and 3 mm. The slope between 3 and 7 mm for IM Lup, however, is very shallow compared to that between 1 and 3 mm: $\alpha_{3-7} = 1.8$ $\pm$ 0.3 vs. $\alpha_{1-3} = 3.6$ $\pm$ 0.4. Pinte et al. (2008) found a mm spectral index of 2.80 $\pm$ 0.25 and their modelling results suggested that IM Lup has grains of at least mm sizes in the disc. A shallowing of the slope beyond 3 mm may indicate the presence of at least cm-sized grains. A similar effect on the cm SED was found for TW Hya (Wilner et al. 2005).

3.3 Results from Spitzer infrared observations

The spectra of the T-Tauri stars observed for Spitzer project P20611, including sources in Lupus, Corona Australis, and the Gum nebula, are published for the first time here and shown in Fig. 1. The spectrum of VV CrA is saturated below 10 $\mu$ m and excluded from the sample. The spectrum of SSTc2d J161029.57-392214.7 (P30843, B. Merín PI) will be published in Merín et al., (2010, in prep.). The spectrum of SSTc2d J182944.11+003356.1 (P30223, K.M. Pontoppidan PI) will be published in Oliveira et al. (2010, in prep.).

The 10- $\mu$ m silicate features were analysed in the ways of both Furlan et al. (2006) and Kessler-Silacci et al. (2006). Furlan et al. (2006) fitted a third-order polynomial to the continuum around the 10- $\mu$ m feature and determined the integrated flux above and below the continuum. The strength of the 10- $\mu$ m feature was then defined as the ratio of the integrated flux due to the feature divided by the integrated flux due to the continuum, ( $F_{10}-F_{\rm cont}$ )/ $F_{\rm cont}$ , resulting in a strength larger than 0 for a feature in emission. Kessler-Silacci et al. (2006) determined the continuum in three different ways, depending on the full mid-infrared SED and which data were available for each source, and subsequently determined the normalised spectra $S_\nu$ according to

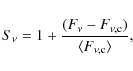
$\begin{displaymath}% S_\nu = 1 + \frac{(F_\nu - F_{\rm\nu, c})}{\langle F_{\rm\nu, c}\rangle}, \end{displaymath}$

(1)

where $F_\nu$ is the observed spectrum, $F_{\rm\nu, c}$ is the fitted continuum, and $\langle F_{\rm\nu, c} \rangle$ is the frequency-averaged continuum flux (see their paper for details). They defined the strength of the 10- $\mu$ m feature as the maximum value of $S_\nu$ between 5 and 13 $\mu$ m, $S^{10~\mu{\rm m}}_{\rm peak}$ , resulting in a value larger than 1 for a feature in emission. Furthermore, Kessler-Silacci et al. (2006) defined the shape of the 10- $\mu$ m feature as the ratio S_11.3/S_9.8.

For this work, the continuum was consistently chosen for all sources by fitting a third-order polynomial to data between 5.0 and 7.5 $\mu$ m and between 13.0 and 16.0 $\mu$ m (cf. Furlan et al. 2006). The regular continuum was used rather than the frequency-averaged continuum, resulting in the peak strength $F^{10~\mu{\rm m}}_{\rm peak}$ and the shape F_11.3/F_9.8. This does not change the results significantly (see Kessler-Silacci et al. 2006).

The results are listed in Table 4 and shown in Fig. 2. The upper panel of Fig. 2 gives ( $F_{10}-F_{\rm cont}$ )/ $F_{\rm cont}$ vs. $F^{10~\mu{\rm m}}_{\rm peak}$ , showing a clear correlation between the two definitions of the strength of the 10- $\mu$ m feature. The lower panel gives $F^{10~\mu{\rm m}}_{\rm peak}$ vs. F_11.3/F_9.8, also showing a correlation, confirming the results of Kessler-Silacci et al. (2006). This figure also confirms that our sample covers a large range in silicate-feature characteristics. It follows that the three methods to quantify the strength or shape of the 10- $\mu$ m feature give completely consistent results. When comparing the 10- $\mu$ m feature with the mm slope in Sect. 5 below, the strength defined as ( $F_{10}-F_{\rm cont}$ )/ $F_{\rm cont}$ will be used. The source that lies towards the top and to the right of the general trend in the lower panel is RX J1615.3-3255, an isolated source slightly to the north of the Lupus star-forming clouds.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{13150fi2.eps} \end{figure}$

Figure 2:

Upper panel: the peak strength of the 10- $\mu$ m, defined as the maximum of the normalised 10- $\mu$ m feature max( $1+(F_\nu - F_{\rm\nu , c})/(F_{\rm\nu , c})$ ), vs. the strength as defined in Furlan et al. (2006). Lower panel: the peak strength of the 10- $\mu$ m feature max( $1+(F_\nu - F_{\rm\nu , c})/(F_{\rm\nu , c})$ ) vs. the shape F_11.3/F_9.8. Included are the sources observed in this work for which the 10- $\mu$ m feature could be obtained. The object towards the top right off the general trend in the lower panel is the Lupus source RX J1615.3-3255, which is isolated from the Lupus clouds.

Open with DEXTER

3.4 10- $\mu$ m feature vs. mm slope

Figures 3 and 4 show the mm slope $\alpha$ , measured between 1 and 3 mm, as a function of the strength of the 10- $\mu$ m feature $(F_{10}-F_{\rm cont})/F_{\rm cont}$ . Only the slope between 1 and 3 mm is used, to make the sample as consistent as possible. However, as noted before, the slope between 3 and 7 mm is consistent with that between 1 and 3 mm for most sources. Included are the sources from this study, as well as eleven sources located in the Taurus-Auriga star-forming region discussed in Rodmann et al. (2006) and Andrews & Williams (2007) for which the spectral slope between 1 and 3 mm could be determined, and the sources located in Lupus and Chamaeleon discussed in Lommen et al. (2007). The total number of sources used is 31; the complete list is given in Table 5. In Fig. 4, the sources are sorted by their star-forming region. The smaller symbols designate single stars and the larger symbols binaries (or stars that are members of a multiple system). The open symbol to the left is T Cha, an evolved system that does not show any silicate emission and is not used in the analysis, and the open symbol in the centre designates the ``cold disc'' CS Cha.

Table 5: List of sources used in the analysis.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{13150fi3.eps} \end{figure}$

Figure 3:

The mm slope as measured between 1 and 3 mm as a function of the strength of the 10- $\mu$ m feature. The open symbols are for T Cha (to the left), which does not show any silicate emission and is not used in the analysis, and for CS Cha, a circumbinary disc. The dashed line shows a linear fit to all the data. The dotted line shows a linear fit to the data with RY Tau excluded. Included are the sources studied in this work, as well as those from Rodmann et al. (2006), Andrews & Williams (2007), and Lommen et al. (2007). The cross in the upper left shows typical uncertainties.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{13150fi4.eps} \end{figure}$

Figure 4:

Same as Fig. 3, with the different sources sorted by star-forming region: filled circles: Lupus, five-pointed stars: Chamaeleon, cross: Corona Australis, diamonds: Taurus-Auriga, and squares: Serpens. The ellipses show the concentrations of sources located in the Taurus-Auriga star-forming region (lower left), the Chamaeleon I cloud (top centre), and the Lupus 1 and Lupus 2 clouds (upper left). The remaining two Lupus sources in the upper right are an isolated source (RX J1615-.3-3255, right-most dot) and a source from the Lupus 3 cloud (RY Lup, upper-most dot). The small symbols designate the single stars and the large symbols designate multiple systems. The open five-pointed star to the left is for T Cha, an evolved cold disc which shows no silicate emission around 10 $\mu$ m. The open five-pointed star in the centre is CS Cha, a circumbinary disc.

Open with DEXTER

The sources in the sample shown in Fig. 3 lie in a broad band roughly running from the lower left (shallow mm slope and weak 10- $\mu$ m feature) to the upper right (steep mm slope and strong 10- $\mu$ m feature). The sole exception is the source RY Tau, which lies in the lower right corner. The mm slope and the strength of the 10- $\mu$ m feature correlate weakly for the full sample: the Spearman rank correlation coefficient is 0.50, with a 99.5% confidence level. However, if the point for RY Tau is excluded, the Spearman rank coefficient becomes 0.66, with a 99.99% confidence level. Note that RY Tau is a peculiar source: it is found to be a rapidly rotating UX Or-type star powering a microjet (e.g., Petrov et al. 1999; Agra-Amboage et al. 2009). A possible explanation for its location in the 10- $\mu$ m-feature vs mm-slope diagram is a rather evolved disc in which a recent collision event produced small grains. This may be similar to the effect recently observed in EX Lup, in which a significantly more crystalline 10- $\mu$ m feature was observed after an outburst (Ábrahám et al. 2009). RY Tau will not be included in the further discussion.

Figure 4 suggests a grouping in the $\mu$ m-vs.-mm diagram according to parental cloud, with the sources from the Taurus-Auriga star-forming region more concentrated in the lower left, the Lupus sources more to the upper left, and the Chamaeleon sources more to the centre right. Note that the six Lupus sources that are on the left part of the diagram (from top to bottom: IM Lup, Sz 66, Sz 65, RU Lup, GW Lup, and HT Lup) are all located in the Lupus 1 and Lupus 2 clouds, whereas the remaining two Lupus sources are located in Lupus 3 (top-most source, RY Lup) and off-cloud (RX J1615.3-3255). Larger-number statistics are needed to confirm this grouping by star-forming region in the $\mu$ m-vs.-mm diagram.

Kessler-Silacci et al. (2006) found a correlation between the spectral type of a source and the strength and shape of the 10- $\mu$ m silicate feature, brown dwarfs having predominantly flatter and Herbig-Ae/Be stars having more peaked features. It was found that this is most likely due to the location of the silicate emission region: Kessler-Silacci et al. (2007) showed that the radius of the 10- $\mu$ m silicate emission zone in the disc goes roughly as $(L_*/L_\odot)^{0.56}$ . Hence, the 10- $\mu$ m feature probes a radius further from the star for early-type stars than for late-type stars. In this context it is interesting to see whether a correlation with spectral type is found in the 10- $\mu$ m-feature vs. mm-slope diagram (Fig. 5). The M stars in the sample presented here are concentrated to the left, the F and G stars to the lower left, and the K stars are found both in the lower left and in the upper right. Hence, no clear correlation with spectral type is found here. It is interesting to note, though, that the F and G sources RY Tau and RY Lup show up isolated from the other F and G sources. This may indicate that these sources are indeed different from the other sources in the sample, justifying the choice not to include RY Tau in the analysis.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{13150fi5.eps} \end{figure}$	Figure 5: Same as Fig. 3, with the different sources sorted by spectral type: orange: F and G, blue: K, and green: M.
Open with DEXTER

4 Modelling

4.1 Disk model parameters and SEDs

Variations in the strength and shape of the 10- $\mu$ m feature (e.g., Kessler-Silacci et al. 2006) as well as in the (sub)mm slope (e.g., Beckwith et al. 1990) can be explained by variations in the dominating grain size in the circumstellar discs, so that one may expect a correlation between properties of the 10- $\mu$ m feature and the mm slope. Such a correlation is found for the sample as a whole (see previous section) and this may imply that grain growth occurs in the whole disc simultaneously, or that grains grow in the inner disc and the new grain size distribution is very efficiently spread to the outer disc through radial mixing. Both processes will have the effect of a shift of dust mass from small particles to larger grains. To study this more quantitatively, we ran a number of models with varying grain size distributions.

We use the axisymmetric radiative-transfer code RADMC, developed by Dullemond (2002) and Dullemond & Dominik (2004). The model consists of a flaring disc, heated passively by radiation from the central star, and includes a hot inner wall, which is directly irradiated by the central star (Natta et al. 2001; see also Dullemond et al. 2001). The surface density of the disc as a function of radius $\Sigma(r)$ is defined to be:

$\begin{displaymath}% \Sigma(r) = \Sigma_{\rm out} \left(r/R_{\rm out}\right)^n, \end{displaymath}$

(2)

with n = -1. The total gas+dust disc mass was fixed to $M_{\rm disc} = 5$ $\times$ $10^{-3}~M_\odot$ . The gas-to-dust mass ratio $\Psi$ was set to 100, which implies that the total mass in dust grains is also fixed, to a value of 5 $\times$ $10^{-5}~M_\odot$ . The inner radius is fixed to $R_{\rm in} = 0.1$ AU and the outer radius $R_{\rm out}$ is varied as outlined below. The photons, originating from the central star, are allowed to move in three dimensions within the axisymmetric grid. In the models, the geometry of the disc is determined by vertical thermal equilibrium. The temperature and luminosity of the central source are varied, as are the power-law slope of the grain size distribution, the disc outer radius, and the maximum grain size.

For the dust opacities, we use a mixture of 80% amorphous olivine and 20% armorphous carbon (percentages by mass). The opacities are calculated using a Distribution of Hollow Spheres (DHS, see Min et al. 2003). The total volume of the spheres occupied by the inclusion f is taken in the range f = [0, 0.8]. It was found (e.g. Dullemond & Dominik 2004; D'Alessio et al. 2001; Chiang et al. 2001) that the mm slope changes if one goes from a disc with only ``small'' particles to a disc that also contains some ``large'' grains. Dullemond & Dominik started with a disc in which the dust is made up of only 0.1- $\mu$ m-sized particles and subsequently replaced 90%, 99%, 99.9%, 99.99%, and 99.999% of the dust by large, 2-mm-sized grains. The mm slope changes considerably when the mass fraction in large grains is changed from 0 to 90%, but it does not change further if a larger fraction of the dust mass is put in large grains (see Fig. 7 in Dullemond & Dominik 2004). This is a result of the fact that at 1 mm the opacity is dominated by the large grains, virtually independent of the mass fraction (K. Pontoppidan, priv. comm.). Although it is possible that a more gradual change in the mm slope is seen when smaller mass fractions are put in large grains, it does seem to be more important what the largest grain size is, rather than which fraction of the dust is contained in such large grains. We therefore chose not to use a bimodal dust distribution, but a distribution in which the size of the grains ranges from a minimum value $a_{\rm min}$ to a maximum value $a_{\rm max}$ according to

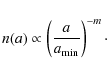
$\begin{displaymath}% n(a) \propto \left(\frac{a}{a_{\rm min}}\right)^{-m}\cdot \end{displaymath}$

(3)

This power-law distribution is expected on theoretical grounds whenever grain-grain collisions lead to shattering (Dohnanyi 1969). It should be noted that models which include grain growth may lead to different grain size distributions (e.g., Tanaka et al. 2005; Dullemond & Dominik 2005). The value $a_{\rm min}$ was fixed to 0.003 $\mu$ m. Note that $a_{\rm min}$ can still have a considerable effect on the 10- $\mu$ m feature, with large values for $a_{\rm min}$ giving significantly weaker features (Olofsson et al. 2009). This effect is strongest for steep grain size distributions, e.g., m = 4.0. The maximum grain size $a_{\rm max}$ was varied in steps of ten from 0.1 $\mu$ m to 1.0 cm. A value of m = 3.5 is representative of interstellar grains (Mathis et al. 1977). A shallower slope of m = 2.5 is expected when grains coagulate to larger sizes (Natta et al. 2007,2004), whereas a slope of m = 4.0 is expected when also fragmentation is taken into account (Dominik & Dullemond 2008; Brauer et al. 2008). The different model parameters are summarised in Table 6.

Table 6: Model parameters.

The resulting SEDs from six models, with $a_{\rm max}$ varying and the other parameters kept fixed, is shown in Fig. 6. In these models, $R_{\rm out}$ was fixed to 300 AU and the scale height was kept fixed at the same value in all models to show only the effect of varying $a_{\rm max}$ . Strong variations are seen in all wavelength regimes, from the near-infrared through the mm. At wavelengths $\lambda \la 2$ $\mu$ m, grain size distributions without grains larger than 1 $\mu$ m give such a high opacity that the central star is significantly reddened. In the mid- and far infrared, the flux drops with increasing maximum grain size. The (sub)mm part of the SED does not change appreciably unless grains with sizes of $\sim$ 100 $\mu$ m or larger are included. After that, the (sub)mm slope becomes shallower quite rapidly with increasing $a_{\rm max}$ . This figure also demonstrates that care must be taken when estimating the disc mass from the (sub)mm emission alone: even when the dust composition is kept the same, assuming a different grain size distribution may already change the opacity at 1 mm by an order of magnitude, which will give an equally large uncertainty in the mass estimate from an observed flux at that wavelength.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{13150fi6.eps} \end{figure}$

Figure 6:

Spectral energy distributions (SEDs) for models of a 5 $\times$ $10^{-3}~M_\odot$ disc with a varying grain size distribution, seen under an inclination $i = 45^\circ$ . The minimum grain size is 0.003 $\mu$ m for all models, and the maximum grain size varies from 0.1 $\mu$ m (black curve) to 1.0 cm in steps of ten (dark blue, light blue, green, yellow, red). The inset shows a blow-up of the 10- $\mu$ m features. Note that the SEDs for $a_{\rm max} = 0.1$ $\mu$ m, 1.0 $\mu$ m, and 10 $\mu$ m completely overlap in the mm part. The sharp drop in flux for $a_{\rm max} = 100$ $\mu$ m around 2000 $\mu$ m is due to a drop in opacity at about $\lambda = 2$ $\times$ $\pi$ $\times$ $a_{\rm max}$ .

Open with DEXTER

4.2 10- $\mu$ m feature vs. mm slope

In Fig. 7, we plot the strength of the 10- $\mu$ m feature vs. the mm slope for different models. The strength of the 10- $\mu$ m feature $(F_{10}-F_{\rm cont})/F_{\rm cont}$ is defined as in Furlan et al. (2006) and the mm slope $\alpha$ is determined between 1.0 and 3.0 mm. The main aim of this figure is to show the variation of the 10- $\mu$ m-feature strength and mm slope with various parameters. While the quantitative details will depend on the specific dust and disc parameters used, the qualitative trends found in these figures should be robust.

In each of the panels, the results for different maximum grain sizes are shown. The size of the triangles is an indication for the maximum grain size under consideration. A general trend is observed, in the sense that the models with only small grains end up in the upper right corner of the micron-vs.-mm diagram (strong 10- $\mu$ m feature and steep mm slope), the models which include grains of mm sizes or larger end up more to the lower left of the diagram (weak 10- $\mu$ m feature and shallower mm slope), and those with grain sizes of up to 10 or 100 $\mu$ m end up towards the upper left corner of the diagram (weak 10- $\mu$ m feature and steep mm slope). A possible evolutionary sequence, in which the maximum grain size in the disc gradually increases, is indicated by the arrows: first, the 10- $\mu$ m feature becomes weaker and later, the mm slope becomes shallower. A test to check whether radial variation of $a_{\rm max}$ - larger grains closer to the star, where the densities are higher - did not show any significant difference.

The models show the effect of the temperature and luminosity of the central star on the strength of the 10- $\mu$ m feature and the steepness of the mm slope. The left column shows the results for a central star with $T_{\rm eff} = 3000$ K and $L = 1~L_\odot$ and the right column for $T_{\rm eff} = 4000$ K and $L = 6~L_\odot$ . In Figs. 7a and b, the power-law slope of the grain size distribution is varied from m = 2.5 to 3.0, 3.5, and 4.0. It appears that only grain size distributions with m = 2.5 produce completely flat 10- $\mu$ m silicate features as well as mm slopes with $\alpha < 2.0$ , whereas grain size distributions with m = 4.0 never produce a mm slope with $\alpha < 3.0$ . Furthermore, the strongest 10- $\mu$ m features are only obtained with a central star of 4000 K and $L = 6~L_\odot$ .

$\begin{figure} \par\includegraphics[width=17cm,clip]{13150fi7.eps} \end{figure}$

Figure 7:

The mm slope $\alpha$ between 1 and 3 mm vs. the strength of the 10- $\mu$ m feature $(F_{10}-F_{\rm cont})/F_{\rm cont}$ . See text for disc parameters. The size of the triangles indicates the size of the largest dust grains $a_{\rm max}$ and the colour indicates the variation of the other parameters. The arrows indicate a possible evolution, that of increasing grain size. a): $T_{\rm eff} = 3000$ K and $L = 1~L_\odot$ . The power-law slope of the grain size distribution is varied from 2.5 (dark blue) to 3.0 (light blue), 3.5 (green), and 4.0 (yellow). b): $T_{\rm eff} = 4000$ K and $L = 6~L_\odot$ . The power-law slope of the grain size distribution is varied from 2.5 (dark blue) to 3.0 (light blue), 3.5 (green), and 4.0 (yellow). c): $T_{\rm eff} = 3000$ K and $L = 1~L_\odot$ . The disc radius is varied from 100 AU (dark blue) to 200 AU (light blue) to 300 AU (green). d): $T_{\rm eff} = 4000$ K and $L = 6~L_\odot$ . The disc radius is varied from 100 AU (dark blue) to 200 AU (light blue) to 300 AU (green). e): $T_{\rm eff} = 3000$ K and $L = 1~L_\odot$ . The inclination under which the disc is viewed is varied from 15 (dark blue) to 30 (light blue), 45 (green), 60 (yellow), and 75 (red) degrees. f): $T_{\rm eff} = 4000$ K and $L = 6~L_\odot$ . The inclination under which the disc is viewed is varied from 15 (dark blue) to 30 (light blue), 45 (green), 60 (yellow), and 75 (red) degrees.

Open with DEXTER

In Figs. 7c and d, the power-law slope of the grain size distribution is fixed to m = 3.5. The disc radius $R_{\rm out}$ is varied between 100, 200, and 300 AU. This has a small effect on the strength of the 10- $\mu$ m feature, particularly for $T_{\rm eff} = 3000$ K and $a_{\rm max} = 0.1$ $\mu$ m. This can be understood in the sense that for a smaller disc with the same dust mass, a larger amount of mass is closer to the star and thus radiates in the infrared. The mm slope of the SED is practically unaffected.

Figures 7e and f show the results for models in which the power-law slope of the grain size distribution was fixed to m = 3.5, the disc outer radius to $R_{\rm out} = 300$ AU, and for which the inclination i under which the disc is observed is varied. In most cases, the inclination has a limited effect on both the strength of the 10- $\mu$ m feature and the mm slope of the SED. Only under very high inclination (e.g., 75 $^\circ$ , where 90 $^\circ$ is edge-on) does the 10- $\mu$ m feature appear in absorption (not shown). A similar effect is seen if the discs are more flaring than found in vertical hydrostatic equilibrium: the 10- $\mu$ m feature is primarily weakened, because of the enhanced extinction under most inclinations.

A second set of models is run to investigate the effects of dust settling, i.e., the process in which larger grains fall to the disc midplane under the influence of gravity, while the smaller grains stay suspended in the disc atmosphere. As mentioned before, Dullemond & Dominik (2008) found that a bimodal grain size distribution can explain variations in the strength of the 10- $\mu$ m feature, but only under specific circumstances. They looked at grains that are mainly responsible for the 10- $\mu$ m feature, in particular grains of 3 $\mu$ m and of $\ll$ 1 $\mu$ m. To study the effect of the settling of larger grains, we ran a number of models with up to six different grain size distributions: grains with sizes between 0.003 and 0.1 $\mu$ m, between 0.1 and 1 $\mu$ m, 1 and 10, 10 and 100, 100 and 1000, and finally between 1000 and 10 000 $\mu$ m. The degree of settling is given by a parameter s, varying between 0.25, 0.50, 0.75, and 1.00, and is chosen to be different for each of the grain size distributions: the larger the grains, the larger the degree of settling. For example, if H denotes the self-consistent scale height, a settling parameter s = 0.75 indicates that:

: grains between 0.1 and 1 $\mu$ m are at $0.75 \times H$ ;
: grains between 1 and 10 $\mu$ m are at $0.75^2 \times H$ ;
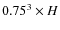: grains between 10 and 100 $\mu$ m are at $0.75^3 \times H$ ;
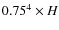: grains between 100 and 1000 $\mu$ m are at $0.75^4 \times H$ ;
: grains between 1000 and 10 000 $\mu$ m are at $0.75^5 \times H$ .

Hence, a larger number for s indicates a smaller degree of settling and s = 1.00 corresponds to no settling (all grains are at the self-consistent scale height).

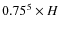These models are run using the radiative transfer code MCMax (Min et al. 2009). MCMax and RADMC were benchmarked against the results of Pascucci et al. (2004) and the differences in the resulting SEDs are minimal, with in particular the 10- $\mu$ m features being practically indistinguishable (see the Appendix in Min et al. 2009). The results for the settling are shown in Fig. 8. Note that the strength of the 10- $\mu$ m feature increases when settling is switched on, but does not increase significantly more when the value of s is decreased more (i.e., when the degree of settling is increased). The slope in the mm part of the SED is practically unaffected by the degree of settling.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{13150fi8.eps} \end{figure}$

Figure 8:

Strength of the 10- $\mu$ m feature as a function of the settling parameter s and the maximum grain size $a_{\rm max}$ . The size of the points indicates $a_{\rm max}$ , which varies from 1 to 10, 100, 1000, and 10 000 $\mu$ m. Note that a small value for s corresponds to a large degree of settling; s = 1.00 corresponds to no settling (all dust grains at the self-consistent scale height). All other disc parameters are as for the standard model in Table 6.

Open with DEXTER

It can be concluded that a variation of the maximum grain size $a_{\rm max}$ affects both the strength of the 10- $\mu$ m feature and the steepness of the mm slope $\alpha$ : a larger maximum grain size yields a weaker 10- $\mu$ m feature and a shallower mm slope. This effect is robust against variations in the degree of settling s, which only affects the strength of the 10- $\mu$ m feature. Only varying the maximum grain size is, however, not enough to explain the range in 10- $\mu$ m features and mm slopes that is observed. Variations in the power-law index of the grain size distribution and the temperature and luminosity of the central source are required as well to cover the full observed range. For example, only models with a central-star temperature of at least 4000 K yield a 10- $\mu$ m feature with a strength of $(F_{10}-F_{\rm cont})/F_{\rm cont} \approx 1.0$ ; models with relatively flat or shallow grain size distributions are required to get mm slopes of $\alpha \la 2.0$ (see also Ricci et al. 2010; Natta et al. 2007).

5 Discussion

A correlation between the strength of the 10- $\mu$ m silicate feature and the slope between 1 and 3 mm is observed in a sample of in total 31 T-Tauri stars. This seems to imply that, while in the upper layers of the hot inner disc small grains are still coagulating to a few microns in size, in the cold mid-plane of the outer disc large grains of at least several millimetres in size are already being formed. One should keep in mind, though, that the 10- $\mu$ m silicate feature only probes the hot surface layers of the inner disc. It is therefore possible, and even likely, that large grains or boulders exist in the mid-plane of the inner disc. The tentative correlation seen in our observations show, however, that the inner and outer discs of young stellar objects do not evolve independently from each other. Furthermore, the gradual decline of the 10- $\mu$ m feature as the mm slope becomes shallower implies that micron-sized grains remain present in the disc atmosphere as cm-sized pebbles are already forming in the mid-plane.

The radiative-transfer programmes RADMC and MCMax were used to run a number of models with varying disc parameters, stellar parameters, and power-law grain size distributions. The only parameter that affects the strength of the 10- $\mu$ m feature and the mm slope of the SED simultaneously is the maximum grain size $a_{\rm max}$ : a larger $a_{\rm max}$ gives both a weaker 10- $\mu$ m feature and a shallower mm slope. This result is very robust against variations of the other parameters. There are, however, a few striking results when the models are compared to the observations. Firstly, the strongest 10- $\mu$ m silicate features, with $(F_{10}-F_{\rm cont})/F_{\rm cont} \approx 1.0$ , can only be reproduced for a star with $T_{\rm eff} = 4000$ K and $L = 6~L_\odot$ , whereas a tempearature of 3000 K and a luminosity of 1 $L_\odot$ seem to be more common for observed T-Tauri stars (see Evans et al. 2009). This may in part be a selection effect: the sources with the hottest central stars are the most likely to have strong mm fluxes, making it more likely for them to provide a good mm slope. A subsample of the sources of Evans et al. (2009) which had enough data points in the SED to provide a decent model fit also gave on average a higher $T_{\rm eff}$ than would be expected from the near-infrared colours alone (B. Merín, priv. comm.). The physical reason for the increase in strength of the 10- $\mu$ m feature with temperature lies in the fact that the photosphere is still an important continuum source. When the temperature of the star is increased, the relative contribution from the photosphere becomes smaller and the peak/continuum ratio of the feature goes up.

Secondly, the sources with $(F_{10}-F_{\rm cont})/F_{\rm cont} \approx 0.0$ as well as those with a mm slope $\alpha \la 2.0$ can only be reproduced if the power-law slope of the grain size distribution is as low as m = 2.5. A slope m = 4.0 does not allow the mm slope to get below 3.0. The strength of the 10- $\mu$ m feature remains at least as large as 1.4, and even 1.6 in the case $T_{\rm eff} = 4000$ K. This appears to indicate that, as grains are growing to mm and cm sizes, the power-law slope of the grain size distribution becomes shallower. It is, however, more likely that a power-law grain size distribution with a mimimum grain size of $a_{\rm min} = 0.003$ $\mu$ m no longer applies. Either the effective minimum grain size increases, as suggested by the work of Olofsson et al. (2009), or a different grain size distribution is more applicable, such as naturally obtained from models including fragmentation (e.g., Dullemond & Dominik 2005).

It is important at this point to note once more that the 10- $\mu$ m feature originates entirely from the disc atmosphere; (sub)micron-sized dust grains that are closer to the midplane are not observable due to the optical thickness of the infrared emission. The emission at (sub)mm wavelengths, on the other hand, is predominantly optically thin; hence, it may originate from the whole disc. In fact, the bulk of the (sub)mm emission comes from the midplane, since the larger grains will settle to the midplane. To study the effect of the settling of larger (mm and cm-sized) grains, we ran a number of models with up to six different grain size distributions. The smallest grains ( 0.003 < a < 0.1 $\mu$ m) followed the gas, while the increasingly larger grains were located increasingly closer to the midplane. It turns out that the strength of the 10- $\mu$ m feature always increases when settling is switched on, but does not increase significantly more when the value of the settling parameter s is decreased more (i.e., when the degree of settling is increased). This can be understood from the fact that a small degree of settling already removes the larger grains from the disc atmosphere. Since the 10- $\mu$ m feature originates in the disc atmosphere, it does not matter where the larger grains reside, as long as they are not too close to the surface. The slope in the mm part of the SED is practically unaffected by the degree of settling. This is because the disc is optically thin at these long wavelengths and hence it does not matter where in the disc the large grains, which determine the brightness at long wavelengths, are located. While the absolute strength and slope depend on the detailed dust and disc model parameters, the trends found here should be robust. Further modelling and exploration of the large parameter space are left to a future paper.

The observations indicate a clustering of the sources per star-forming region. The T-Tauri stars in Chamaeleon show the strongest 10- $\mu$ m features, as well as the steepest mm slopes. The T-Tauri stars located in the Lupus 1 and Lupus 2 clouds have somewhat weaker 10- $\mu$ m features and mm slopes that are a bit shallower than the Chamaelon sources. The sources located in the Taurus-Auriga star-forming region, finally, have the weakest 10- $\mu$ m features and the shallowest mm slope. Although the number statistics are too low to draw strong conclusions from this grouping per star-forming region, it is intersesting to hypothesise as to what might be the origin of this grouping. It could in principle be due to a selection effect. To check for this, the strengths of the 10- $\mu$ m features of the eleven sources from Furlan et al. (2006) included in this work were compared with those of the 72 Taurus sources not included in this work and the two samples were found to be statistically indistinguishable. Furthermore, after this paper was submitted, Ricci et al. (2010) published mm slopes for a total of 21 sources in the Taurus-Auriga star-forming region. Ricci et al. found the slopes between 1 and 3 mm all to be $\alpha \leq 2.7$ ; the corresponding strengths of the 10- $\mu$ m features are $(F_{10}-F_{\rm cont})/F_{\rm cont} < 0.75$ for 17 of those 21 sources (Furlan et al. 2006). Thus, these sources mainly populate the lower left corner of the $\mu$ m-vs.-mm diagram. It is then tempting to attribute the clustering to an evolutionary sequence, with the Chamaeleon sources being the least evolved and the Taurus-Auriga sources the most evolved. If the evolution proceeds equally fast in each star-forming region, Taurus-Auriga would then be the oldest star-forming region and Chamaeleon the youngest. However, ages of pre-main-sequence stars are notoriously difficult to determine and there is a large spread of stellar ages within each region (see Table 1). Note that a chemical differentiation, with, e.g., Chamaeleon a region with more silicates than Taurus, would mainly have an effect on the strength of the 10- $\mu$ m feature, whereas the mm slope of the SED is largely determined by the sizes of the grains in the disc alone (Draine 2006). Also, sources are likely to go through their evolutionary stages at different rates, which may be determined by other parameters such as initial conditions of the core.

Our final sample only contained two cold discs for which the strength of the 10- $\mu$ m feature and the slope of the SED between 1 and 3 mm could be obtained. These are T Cha, an evolved disc with no silicates in the spectrum that is not included in the analysis, and CS Cha, a circumbinary disc. Several processes have been proposed which may cause the deficiency of hot dust in the inner disc, such as photo-evaporation, the clearing out of the inner disc by a planet, or grain growth up to mm sizes and larger. If grain growth were the dominating reason for the decrease in infrared flux, one would expect the cold disc to show up in the lower part of the 10- $\mu$ m-feature vs. mm-slope diagram. However, CS Cha is located rather in the centre of the diagram and it would appear that grain growth is not the main reason for the lack of infrared emission. Indeed, since CS Cha harbours a binary, it may be the case that the inner disc is cleared out due to binary interactions, with a ``normal'' outer disc remaining.

6 Conclusions

We observed five binary systems and 35 single T-Tauri stars (of which one turned out to harbour two sources as well) at infrared and mm wavelengths. New Spitzer IRS spectra of the wavelength region containing the 10- $\mu$ m silicate feature are presented for 13 sources and the slopes in the mm regime of the SED are obtained, also for 13 sources. Furthermore, dust disc masses are obtained for 21 new sources, including strict 3 $\sigma$ upper limits for nine of the sources. Combining our new observations with data from the literature, a tentative correlation between the strength of the 10- $\mu$ m feature and the mm slope is found for a sample of in total 31 T-Tauri stars. This seems to suggest that the inner and outer discs do not evolve independently.

Modelling protoplanetary discs with varying geometries and grain size distributions indicates that grain growth alone cannot explain the observed evolution in the strength of the 10- $\mu$ m feature and the mm slope of the SED. It would rather seem that as the maximum grain size increases, also the power-law slope of the grain size distribution becomes shallower. Ricci et al. (2010) also found that for the majority of the sources in their sample a grain size distribution flatter than that of the interstellar medium is required (see also Natta et al. 2007). This is an indication that a power-law grain size distribution with a fixed minimum grain size is too simple a representation of the dust in protoplanetary discs.

The sample contains only one cold or transitional disc for which the mm slope in the SED and the strength of the 10- $\mu$ m silicate feature could be obtained properly. This source, CS Cha, ends up rather in the centre of the 10- $\mu$ m vs. mm-slope diagram, indicating that grain growth is probably not the source of the removal of dust from the inner disc. Transitional discs are often relatively weak in the (sub)mm regime and a new generation of telescopes is required to determine the mm slope for more of these sources.

Although all 10- $\mu$ m features used in this work were obtained using the Spitzer Space Telescope, the mm fluxes and hence the mm slopes were determined with a large number of different telescopes. As this potentially leads to systematic effects, it will be necessary to observe a statistically large enough sample with only one or maybe two (sub)mm telescopes. Ideally, about a dozen sources per star-forming regions for at least four regions should be observed with the same telescope. However, due to the relative weakness of the sources under consideration, the scarcity of available telescope time, and the spread of young star-forming regions over the sky, this is currently hard to achieve. The Atacama Large Millimeter/submillimeter Array (ALMA) will, upon completion, be able to study an order of magnitude more sources than presented here, providing us with the statistics to study interesting relations such as the grouping of YSOs by star-forming region in the $\mu$ m-vs.-mm diagram. ALMA will also be able to resolve most of the sources studied here.

This work has mainly focused on observations at 1 and 3 mm, at which grains with sizes of the order of 1 cm can be studied (Draine 2006). The detection of larger grains, or pebbles, in protoplanetary discs, requires observations at cm wavelengths. However, there may be other sources of emission at cm wavelengths, such as magnetic fields or stellar winds, and it is necessary to monitor sources over extended periods of time to disentangle the different emission mechanisms (Lommen et al. 2009; Wilner et al. 2005). The maximum bandwidth of the ATCA was recently improved by a factor of 16 with the implementation of the Compact Array Broadband Backend (CABB). This will for the first time allow the survey of large samples of young stellar objects in the southern hemisphere at cm wavelengths.

Thus, in five to ten years from now we will not only be studying how grain growth occurs in protoplanetary discs, but we will actually be able to pinpoint the locations in the discs where the formation of pebbles and boulders, the precursors to planetesimals and planets, is taking place. Furthermore, on-going observations at cm wavelengths will give us a stronger handle on the processes taking place in and around the discs, affecting the growth of grains and the formation of planets.

Acknowledgements

We are indebted to Kees Dullemond for the use of his RADMC and RAYTRACE codes and to Stephen Bourke for help with AIPS. A special thanks to the ATNF and SMA staff for assistance with the observations. Ruud Visser's help on all things computer is greatly appreciated and Carsten Dominik is thanked for his useful comments. Partial support for this work was provided by a Netherlands Research School For Astronomy network 2 grant, and by a Netherlands Organisation for Scientific Research Spinoza grant. C.M.W. acknowledges financial support from an ARC Australian Research Fellowship, Discovery Project DP0345227. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.

References

Ábrahám, P., Juhász, A., Dullemond, C. P., et al. 2009, Nature, 459, 224 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Acke, B., & van den Ancker, M. E. 2004, A&A, 426, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Acke, B., van den Ancker, M. E., Dullemond, C. P., van Boekel, R., & Waters, L. B. F. M. 2004, A&A, 422, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Agra-Amboage, V., Dougados, C., Cabrit, S., Garcia, P. J. V., & Ferruit, P. 2009, A&A, 493, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Andrews, S. M., & Williams, J. P. 2005, ApJ, 631, 1134 [NASA ADS] [CrossRef] [Google Scholar]
Andrews, S. M., & Williams, J. P. 2007, ApJ, 659, 705 [NASA ADS] [CrossRef] [Google Scholar]
Beckwith, S. V. W., & Sargent, A. I. 1991, ApJ, 381, 250 [NASA ADS] [CrossRef] [Google Scholar]
Beckwith, S. V. W., Sargent, A. I., Chini, R. S., & Guesten, R. 1990, AJ, 99, 924 [NASA ADS] [CrossRef] [Google Scholar]
Bertout, C., Robichon, N., & Arenou, F. 1999, A&A, 352, 574 [NASA ADS] [Google Scholar]
Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bouwman, J., Meeus, G., de Koter, A., et al. 2001, A&A, 375, 950 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Brandt, J. C., Stecher, T. P., Crawford, D. L., & Maran, S. P. 1971, ApJ, 163, L99 [NASA ADS] [CrossRef] [Google Scholar]
Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Brown, J. M., Blake, G. A., Dullemond, C. P., et al. 2007, ApJ, 664, L107 [NASA ADS] [CrossRef] [Google Scholar]
Chiang, E. I., Joung, M. K., Creech-Eakman, M. J., et al. 2001, ApJ, 547, 1077 [NASA ADS] [CrossRef] [Google Scholar]
Chini, R., Kämpgen, K., Reipurth, B., et al. 2003, A&A, 409, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ciardi, D. R., Telesco, C. M., Packham, C., et al. 2005, ApJ, 629, 897 [NASA ADS] [CrossRef] [Google Scholar]
Comerón, F. 2008, in Handbook of Star Forming Regions, ed. B. Reipurth, ASP Monogr. Publ., 295 [Google Scholar]
Comerón, F., Fernández, M., Baraffe, I., Neuhäuser, R., & Kaas, A. A. 2003, A&A, 406, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Correia, S., Zinnecker, H., Ratzka, T., & Sterzik, M. F. 2006, A&A, 459, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
D'Alessio, P., Calvet, N., & Hartmann, L. 2001, ApJ, 553, 321 [NASA ADS] [CrossRef] [Google Scholar]
de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] [Google Scholar]
Dohnanyi, J. W. 1969, J. Geophys. Res., 74, 2531 [NASA ADS] [CrossRef] [Google Scholar]
Dominik, C., & Dullemond, C. P. 2008, A&A, 491, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dominik, C., Blum, J., Cuzzi, J. N., & Wurm, G. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 783-800 [Google Scholar]
Draine, B. T. 2006, ApJ, 636, 1114 [NASA ADS] [CrossRef] [Google Scholar]
Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [NASA ADS] [CrossRef] [Google Scholar]
Dullemond, C. P. 2002, A&A, 395, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dullemond, C. P., & Dominik, C. 2004, A&A, 417, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dullemond, C. P., & Dominik, C. 2008, A&A, 487, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
Espaillat, C., Calvet, N., D'Alessio, P., et al. 2007, ApJ, 664, L111 [NASA ADS] [CrossRef] [Google Scholar]
Evans, N. J., Allen, L. E., Blake, G. A., et al. 2003, PASP, 115, 965 [NASA ADS] [CrossRef] [Google Scholar]
Evans, II, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
Forbrich, J., Massi, M., Ros, E., Brunthaler, A., & Menten, K. M. 2007, A&A, 469, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Furlan, E., Hartmann, L., Calvet, N., et al. 2006, ApJS, 165, 568 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Guilloteau, S., Dutrey, A., Pety, J., & Gueth, F. 2008, A&A, 478, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Heiles, C. 1998, ApJ, 498, 689 [NASA ADS] [CrossRef] [Google Scholar]
Henning, T., Pfau, W., Zinnecker, H., & Prusti, T. 1993, A&A, 276, 129 [NASA ADS] [Google Scholar]
Henning, T., Launhardt, R., Steinacker, J., & Thamm, E. 1994, A&A, 291, 546 [NASA ADS] [Google Scholar]
Honda, M., Kataza, H., Okamoto, Y. K., et al. 2003, ApJ, 585, L59 [NASA ADS] [CrossRef] [Google Scholar]
James, D. J., Melo, C., Santos, N. C., & Bouvier, J. 2006, A&A, 446, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Johansen, A., Oishi, J. S., Low, M.-M. M., et al. 2007, Nature, 448, 1022 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Kenyon, S. J., Gomez, M., Marzke, R. O., & Hartmann, L. 1994, AJ, 108, 251 [NASA ADS] [CrossRef] [Google Scholar]
Kenyon, S. J., Gómez, M., & Whitney, B. A. 2008, Low Mass Star Formation in the Taurus-Auriga Clouds, ed. B. Reipurth, 405 [Google Scholar]
Kessler-Silacci, J., Augereau, J.-C., Dullemond, C. P., et al. 2006, ApJ, 639, 275 [NASA ADS] [CrossRef] [Google Scholar]
Kessler-Silacci, J. E., Dullemond, C. P., Augereau, J.-C., et al. 2007, ApJ, 659, 680 [NASA ADS] [CrossRef] [Google Scholar]
Lahuis, F., Kessler-Silacci, J. E., Evans, N. J., et al. 2006, c2d Spectroscopy Explanatory Suppl., Pasadena, Spitzer Science Center [Google Scholar]
Lommen, D., Wright, C. M., Maddison, S. T., et al. 2007, A&A, 462, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lommen, D., Maddison, S. T., Wright, C. M., et al. 2009, A&A, 495, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Luhman, K. L. 2007, ApJS, 173, 104 [NASA ADS] [CrossRef] [Google Scholar]
Massi, F., Giannini, T., Lorenzetti, D., et al. 1999, A&AS, 136, 471 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
Massi, F., de Luca, M., Elia, D., et al. 2007, A&A, 466, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
Meeus, G., Waters, L. B. F. M., Bouwman, J., et al. 2001, A&A, 365, 476 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Meeus, G., Sterzik, M., Bouwman, J., & Natta, A. 2003, A&A, 409, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Merín, B., Jørgensen, J., Spezzi, L., et al. 2008, ApJS, 177, 551 [NASA ADS] [CrossRef] [Google Scholar]
Min, M., Hovenier, J. W., & de Koter, A. 2003, A&A, 404, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Min, M., Dullemond, C. P., Dominik, C., de Koter, A., & Hovenier, J. W. 2009, A&A, 497, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Natta, A., Prusti, T., Neri, R., et al. 2001, A&A, 371, 186 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Natta, A., Testi, L., Neri, R., Shepherd, D. S., & Wilner, D. J. 2004, A&A, 416, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Natta, A., Testi, L., Calvet, N., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 767 [Google Scholar]
Neuhäuser, R., & Forbrich, J. 2008, The Corona Australis Star Forming Region, ed. B. Reipurth, 735 [Google Scholar]
Nürnberger, D., Chini, R., & Zinnecker, H. 1997, A&A, 324, 1036 [NASA ADS] [Google Scholar]
Oliveira, I., Merín, B., Pontoppidan, K. M., et al. 2009, ApJ, 691, 672 [NASA ADS] [CrossRef] [Google Scholar]
Olofsson, J., Augereau, J., van Dishoeck, E. F., et al. 2009, A&A, 507, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pascucci, I., Wolf, S., Steinacker, J., et al. 2004, A&A, 417, 793 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
Petrov, P. P., Zajtseva, G. V., Efimov, Y. S., et al. 1999, A&A, 341, 553 [NASA ADS] [Google Scholar]
Pinte, C., Padgett, D. L., Ménard, F., et al. 2008, A&A, 489, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pontoppidan, K. M., Blake, G. A., van Dishoeck, E. F., et al. 2008, ApJ, 684, 1323 [NASA ADS] [CrossRef] [Google Scholar]
Przygodda, F., van Boekel, R., Àbrahàm, P., et al. 2003, A&A, 412, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ricci, L., Testi, L., Natta, A., et al. 2010, A&A, 512, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Rodmann, J., Henning, T., Chandler, C. J., Mundy, L. G., & Wilner, D. J. 2006, A&A, 446, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Straizys, V., Cernis, K., & Bartasiute., S. 1996, Balt. Astron., 5, 125 [NASA ADS] [Google Scholar]
Tanaka, H., Himeno, Y., & Ida, S. 2005, ApJ, 625, 414 [NASA ADS] [CrossRef] [Google Scholar]
van Boekel, R. 2008, J. Phys. Conf. Ser., 131, 012023 [NASA ADS] [CrossRef] [Google Scholar]
Whittet, D. C. B., Prusti, T., Franco, G. A. P., et al. 1997, A&A, 327, 1194 [NASA ADS] [Google Scholar]
Wilner, D. J., D'Alessio, P., Calvet, N., Claussen, M. J., & Hartmann, L. 2005, ApJ, 626, L109 [NASA ADS] [CrossRef] [Google Scholar]

Online Material

Appendix A: Observations

In Lupus, 15 single sources and the binary IK Lup & Sz 66 were observed with the Submillimeter Array (SMA) at about 1 mm. Furthermore, the binaries VV CrA and S CrA and the single source DG CrA in Corona Australis were observed with the SMA at about 1 mm. A full log of the SMA observations is given in Table A.1. The results of these observations are shown in Table B.1 and Fig. B.1.

With the Australia Telescope Compact Array (ATCA), 15 sources spread over the constellations Lupus, Vela, Corona Australis, and Chamaeleon were observed at 3 and 7 mm. A log of the ATCA observations is given in Table A.2.

The Combined Array for Research in Millimeter-wave Astronomy (CARMA) was used to observe eleven single sources and one binary in Serpens at 1 and 3 mm. The log of these observations is presented in Table A.3; the full results are given in Table B.3.

Finally, eight sources in Serpens were observed with the (Very Large Array) VLA at 7 mm and at 1.3, 3.6, and 6 cm. A full log of those observations is given in Table A.4.

Table A.1: Overview of the SMA observations.

Table A.2: Overview of the ATCA observations.

Table A.3: Overview of the CARMA observations.

Table A.4: Overview of the VLA observations.

Appendix B: Results

The complete results of the SMA observations are shown in Table B.1. The amplitude as a function of (u, v) distance is plotted in Fig. B.1.

The complete results of the ATCA observations are shown in Table B.2. Several sources were observed at the same wavelength more than once. The data for those sources were co-added in the (u, v) plane to improve the signal-to-noise ratio. The resulting fluxes or 3 $\sigma$ upper limits are presented in Table 3 in the main text.

The binary VV CrA was not resolved with the ATCA at 3 or 7 mm using natural weighting, which is optimised for sensitivity. However, using uniform weighting, which is optimised for resolution, the binary could be resolved at 3 mm. The map is shown in Fig. B.2.

The amplitude as a function of (u, v) distance of the sources detected with the ATCA at 3 mm is plotted in Fig. B.3, that of the sources detected with the ATCA at 7 mm in Fig. B.4.

The complete results of the CARMA observations are shown in Table B.3. Data from tracks that could not be properly calibrated due to a weak gain calibrator are not included. Some sources were observed twice, once in the C and once in the D configuration. If good data were obtained in both occasions, they were co-added in the (u, v) plane to improve the signal-to-noise ratio. The resulting fluxes or 3 $\sigma$ upper limits are presented in Table 3 in the main text. The amplitude as a function of (u, v) distance of the sources detected with CARMA at 1 mm is plotted in Fig. B.5, that of the sources detected with CARMA at 3 mm in Fig. B.6.

The complete results of the VLA observations are shown in Table B.4.

Table B.1: Complete results of SMA observations at 1.3 mm.

Table B.2: Complete results of ATCA observations at 3 and 7 mm.

Table B.3: Complete results of CARMA observations at 1 and 3 mm.

Table B.4: Complete results of VLA observations at 6.9 mm and 1.3, 3.5, and 6.2 cm.

$\begin{figure} \par\mbox{\includegraphics[width=5cm,clip]{13150fi9.eps}\includeg... ...eps}\includegraphics[width=5cm,clip]{13150f19.eps}\hspace*{2.5cm}}\end{figure}$	Figure B.1: Amplitude as a function of (u, v) distance for sources detected with the SMA at 1 mm.
Open with DEXTER

$\begin{figure} \includegraphics[width=7.8cm,clip]{13150f20.eps} \end{figure}$	Figure B.2: Image of VV CrA, observed at 3.2 mm on 2 and 3 August 2008. The offsets are with respect to the phase centre, which is located at 19:03:06.7, -37:12:49.7. The contours are at 2, 4, 6, ... times the rms of 2.0 mJy/bm; negative contours are dashed.
Open with DEXTER

$\begin{figure} \par\mbox{\includegraphics[width=5cm]{13150f21.eps}\includegraphi... ...space{5cm}\includegraphics[width=5cm]{13150f27.eps}\hspace{5cm}}\end{figure}$	Figure B.3: Amplitude as a function of (u, v) distance for sources detected with the ATCA at 3 mm.
Open with DEXTER

$\begin{figure} \par\mbox{\includegraphics[width=5cm]{13150f28.eps}\includegraphi... ...space{5cm}\includegraphics[width=5cm]{13150f31.eps}\hspace{5cm}}\end{figure}$	Figure B.4: Amplitude as a function of (u, v) distance for sources detected with the ATCA at 7 mm.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=5cm]{13150f32.eps}\includegraphics[width=5cm]{13150f33.eps} \end{figure}$	Figure B.5: Amplitude as a function of (u, v) distance for sources detected with CARMA at 1 mm.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=5cm]{13150f34.eps}\includegraphics[width=5cm]{13150f35.eps}\includegraphics[width=5cm]{13150f36.eps} \end{figure}$	Figure B.6: Amplitude as a function of (u, v) distance for sources detected with CARMA at 3 mm.
Open with DEXTER

Footnotes

...: Appendices are only available in electronic form at http://www.aanda.org
... NRAO: The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
... (CARMA: Support for CARMA construction was derived from the Gordon and Betty Moore Foundation, the Kenneth T. and Eileen L. Norris Foundation, the Associates of the California Institute of Technology, the states of California, Maryland, and Illinois, and the National Science Foundation. Ongoing CARMA development and operations are supported by the National Science Foundation under a cooperative agreement, and by the CARMA partner universities.
... (SMA: The Submillimeter Array is a joint project between the Smithsonian Astrophysical Observatory and the Academia Sinica Institute of Astronomy and Astrophysics and is funded by the Smithsonian Institution and the Academia Sinica.
... (ATCA: The Australia Telescope Compact Array is part of the Australia Telescope which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO.

All Tables

Table 1: Distances to and ages of star-forming clouds.

Table 2: List of sources observed with the SMA, ATCA, CARMA, and VLA.

Table 3: Fluxes from point-source fits in the (u, v) plane obtained from interferometric data and single-dish 1.20-1.27 mm SEST fluxes.

Table 4: Spectral slopes at mm wavelengths, dust disc masses, and properties of the 10- $\mu$ m silicate feature.

Table 5: List of sources used in the analysis.

Table 6: Model parameters.

Table A.1: Overview of the SMA observations.

Table A.2: Overview of the ATCA observations.

Table A.3: Overview of the CARMA observations.

Table A.4: Overview of the VLA observations.

Table B.1: Complete results of SMA observations at 1.3 mm.

Table B.2: Complete results of ATCA observations at 3 and 7 mm.

Table B.3: Complete results of CARMA observations at 1 and 3 mm.

Table B.4: Complete results of VLA observations at 6.9 mm and 1.3, 3.5, and 6.2 cm.

All Figures

$\begin{figure} \par\includegraphics[width=16.5cm,clip]{13150fi1.eps} \end{figure}$	Figure 1: Spitzer IRS spectra from the T-Tauri stars observed for Spitzer project P20611 (C.M. Wright PI). Spectra with a maximum flux below 0.1 Jy were binned four times to improve the signal-to-noise ratio.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{13150fi2.eps} \end{figure}$	Figure 2: Upper panel: the peak strength of the 10- $\mu$ m, defined as the maximum of the normalised 10- $\mu$ m feature max( $1+(F_\nu - F_{\rm\nu , c})/(F_{\rm\nu , c})$ ), vs. the strength as defined in Furlan et al. (2006). Lower panel: the peak strength of the 10- $\mu$ m feature max( $1+(F_\nu - F_{\rm\nu , c})/(F_{\rm\nu , c})$ ) vs. the shape F_11.3/F_9.8. Included are the sources observed in this work for which the 10- $\mu$ m feature could be obtained. The object towards the top right off the general trend in the lower panel is the Lupus source RX J1615.3-3255, which is isolated from the Lupus clouds.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{13150fi3.eps} \end{figure}$	Figure 3: The mm slope as measured between 1 and 3 mm as a function of the strength of the 10- $\mu$ m feature. The open symbols are for T Cha (to the left), which does not show any silicate emission and is not used in the analysis, and for CS Cha, a circumbinary disc. The dashed line shows a linear fit to all the data. The dotted line shows a linear fit to the data with RY Tau excluded. Included are the sources studied in this work, as well as those from Rodmann et al. (2006), Andrews & Williams (2007), and Lommen et al. (2007). The cross in the upper left shows typical uncertainties.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{13150fi4.eps} \end{figure}$	Figure 4: Same as Fig. 3, with the different sources sorted by star-forming region: filled circles: Lupus, five-pointed stars: Chamaeleon, cross: Corona Australis, diamonds: Taurus-Auriga, and squares: Serpens. The ellipses show the concentrations of sources located in the Taurus-Auriga star-forming region (lower left), the Chamaeleon I cloud (top centre), and the Lupus 1 and Lupus 2 clouds (upper left). The remaining two Lupus sources in the upper right are an isolated source (RX J1615-.3-3255, right-most dot) and a source from the Lupus 3 cloud (RY Lup, upper-most dot). The small symbols designate the single stars and the large symbols designate multiple systems. The open five-pointed star to the left is for T Cha, an evolved cold disc which shows no silicate emission around 10 $\mu$ m. The open five-pointed star in the centre is CS Cha, a circumbinary disc.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{13150fi5.eps} \end{figure}$	Figure 5: Same as Fig. 3, with the different sources sorted by spectral type: orange: F and G, blue: K, and green: M.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{13150fi6.eps} \end{figure}$	Figure 6: Spectral energy distributions (SEDs) for models of a 5 $\times$ $10^{-3}~M_\odot$ disc with a varying grain size distribution, seen under an inclination $i = 45^\circ$ . The minimum grain size is 0.003 $\mu$ m for all models, and the maximum grain size varies from 0.1 $\mu$ m (black curve) to 1.0 cm in steps of ten (dark blue, light blue, green, yellow, red). The inset shows a blow-up of the 10- $\mu$ m features. Note that the SEDs for $a_{\rm max} = 0.1$ $\mu$ m, 1.0 $\mu$ m, and 10 $\mu$ m completely overlap in the mm part. The sharp drop in flux for $a_{\rm max} = 100$ $\mu$ m around 2000 $\mu$ m is due to a drop in opacity at about $\lambda = 2$ $\times$ $\pi$ $\times$ $a_{\rm max}$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=17cm,clip]{13150fi7.eps} \end{figure}$	Figure 7: The mm slope $\alpha$ between 1 and 3 mm vs. the strength of the 10- $\mu$ m feature $(F_{10}-F_{\rm cont})/F_{\rm cont}$ . See text for disc parameters. The size of the triangles indicates the size of the largest dust grains $a_{\rm max}$ and the colour indicates the variation of the other parameters. The arrows indicate a possible evolution, that of increasing grain size. a): $T_{\rm eff} = 3000$ K and $L = 1~L_\odot$ . The power-law slope of the grain size distribution is varied from 2.5 (dark blue) to 3.0 (light blue), 3.5 (green), and 4.0 (yellow). b): $T_{\rm eff} = 4000$ K and $L = 6~L_\odot$ . The power-law slope of the grain size distribution is varied from 2.5 (dark blue) to 3.0 (light blue), 3.5 (green), and 4.0 (yellow). c): $T_{\rm eff} = 3000$ K and $L = 1~L_\odot$ . The disc radius is varied from 100 AU (dark blue) to 200 AU (light blue) to 300 AU (green). d): $T_{\rm eff} = 4000$ K and $L = 6~L_\odot$ . The disc radius is varied from 100 AU (dark blue) to 200 AU (light blue) to 300 AU (green). e): $T_{\rm eff} = 3000$ K and $L = 1~L_\odot$ . The inclination under which the disc is viewed is varied from 15 (dark blue) to 30 (light blue), 45 (green), 60 (yellow), and 75 (red) degrees. f): $T_{\rm eff} = 4000$ K and $L = 6~L_\odot$ . The inclination under which the disc is viewed is varied from 15 (dark blue) to 30 (light blue), 45 (green), 60 (yellow), and 75 (red) degrees.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{13150fi8.eps} \end{figure}$	Figure 8: Strength of the 10- $\mu$ m feature as a function of the settling parameter s and the maximum grain size $a_{\rm max}$ . The size of the points indicates $a_{\rm max}$ , which varies from 1 to 10, 100, 1000, and 10 000 $\mu$ m. Note that a small value for s corresponds to a large degree of settling; s = 1.00 corresponds to no settling (all dust grains at the self-consistent scale height). All other disc parameters are as for the standard model in Table 6.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=5cm,clip]{13150fi9.eps}\includeg... ...eps}\includegraphics[width=5cm,clip]{13150f19.eps}\hspace*{2.5cm}}\end{figure}$	Figure B.1: Amplitude as a function of (u, v) distance for sources detected with the SMA at 1 mm.
Open with DEXTER
In the text

$\begin{figure} \includegraphics[width=7.8cm,clip]{13150f20.eps} \end{figure}$	Figure B.2: Image of VV CrA, observed at 3.2 mm on 2 and 3 August 2008. The offsets are with respect to the phase centre, which is located at 19:03:06.7, -37:12:49.7. The contours are at 2, 4, 6, ... times the rms of 2.0 mJy/bm; negative contours are dashed.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=5cm]{13150f21.eps}\includegraphi... ...space{5cm}\includegraphics[width=5cm]{13150f27.eps}\hspace{5cm}}\end{figure}$	Figure B.3: Amplitude as a function of (u, v) distance for sources detected with the ATCA at 3 mm.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=5cm]{13150f28.eps}\includegraphi... ...space{5cm}\includegraphics[width=5cm]{13150f31.eps}\hspace{5cm}}\end{figure}$	Figure B.4: Amplitude as a function of (u, v) distance for sources detected with the ATCA at 7 mm.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=5cm]{13150f32.eps}\includegraphics[width=5cm]{13150f33.eps} \end{figure}$	Figure B.5: Amplitude as a function of (u, v) distance for sources detected with CARMA at 1 mm.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=5cm]{13150f34.eps}\includegraphics[width=5cm]{13150f35.eps}\includegraphics[width=5cm]{13150f36.eps} \end{figure}$	Figure B.6: Amplitude as a function of (u, v) distance for sources detected with CARMA at 3 mm.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Grain growth across protoplanetary discs: 10 m silicate feature versus millimetre slope

1 Introduction

2 Observations

2.1 Source selection and Spitzer data

2.2 SMA observations

2.3 ATCA observations

2.4 CARMA observations

2.5 VLA observations

3 Results

3.1 Mm and cm source fluxes and dust disc masses

3.2 Millimetre slopes

3.3 Results from Spitzer infrared observations

3.4 10-m feature vs. mm slope

4 Modelling

4.1 Disk model parameters and SEDs

4.2 10-m feature vs. mm slope

5 Discussion

6 Conclusions

References

Online Material

Appendix A: Observations

Appendix B: Results

Footnotes

All Tables

All Figures

Grain growth across protoplanetary discs: 10 $\mu$ m silicate feature versus millimetre slope

3.4 10- $\mu$ m feature vs. mm slope

4.2 10- $\mu$ m feature vs. mm slope