EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 515 (June 2010) A&A, 515 (2010) L3 Full HTML
Free Access
Issue
A&A
Volume 515, June 2010
Article Number L3
Number of page(s) 7
Section Letters
DOI https://doi.org/10.1051/0004-6361/200913047
Published online 15 June 2010
A&A 515, L3 (2010)

LETTER TO THE EDITOR

Observational evidence for a broken Li Spite plateau and mass-dependent Li depletion[*],[*]

J. Meléndez1 - L. Casagrande2 - I. Ramírez2 - M. Asplund2 - W. J. Schuster3

1 - Centro de Astrofísica da Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
2 - Max Planck Institute for Astrophysics, Postfach 1317, 85741 Garching, Germany
3 - Observatorio Astronómico Nacional, Universidad Nacional Autónoma de México, Ensenada, B.C., CP 22800, Mexico

Received 31 July 2009 / Accepted 12 May 2010

Abstract
We present NLTE Li abundances for 88 stars in the metallicity range -3.5 < [Fe/H] < -1.0. The effective temperatures are based on the infrared flux method with improved E(B-V) values obtained mostly from interstellar Na I D lines. The Li abundances were derived through MARCS models and high-quality UVES+VLT, HIRES+Keck and FIES+NOT spectra, and complemented with reliable equivalent widths from the literature. The less-depleted stars with [Fe/H] < -2.5 and [Fe/H] > -2.5 fall into two well-defined plateaus of $A_{\rm Li}$ = $2.18 \; (\sigma =0.04)$ and $A_{\rm Li}$ = $2.27 \; (\sigma =0.05)$, respectively. We show that the two plateaus are flat, unlike previous claims for a steep monotonic decrease in Li abundances with decreasing metallicities. At all metallicities we uncover a fine-structure in the Li abundances of Spite plateau stars, which we trace to Li depletion that depends on both metallicity and mass. Models including atomic diffusion and turbulent mixing seem to reproduce the observed Li depletion assuming a primordial Li abundance $A_{\rm Li}$ = 2.64, which agrees well with current predictions ( $A_{\rm Li}$ = 2.72) from standard Big Bang nucleosynthesis. Adopting the Kurucz overshooting model atmospheres increases the Li abundance by +0.08 dex to $A_{\rm Li}$ = 2.72, which perfectly agrees with BBN+WMAP.

Key words: nuclear reactions, nucleosynthesis, abundances - cosmology: observations - stars: abundances - stars: Population II

1 Introduction

One of the most important discoveries in the study of the chemical composition of stars was made in 1982 by Monique and François Spite, who found an essentially constant Li abundance in warm metal-poor stars (Spite & Spite 1982), a result interpreted as a relic of primordial nucleosynthesis. Due to its cosmological significance, there have been many studies devoted to Li in metal-poor field stars (e.g., Ryan et al. 1999; Meléndez & Ramírez 2004, hereafter MR04; Boesgaard et al. 2005, hereafter B05; Charbonnel & Primas 2005; Asplund et al. 2006, hereafter A06; Shi et al. 2007, hereafter S07; Bonifacio et al. 2007, hereafter B07; Hosford et al. 2009; Aoki et al. 2009; Sbordone et al. 2010, hereafter S10), with observed Li abundances at the lowest metallicities ([Fe/H] $\sim $ -3) from $A_{\rm Li}$ = 1.94 (B07) to $A_{\rm Li}$ = 2.37 (MR04).

A primordial Li abundance of $A_{\rm Li}$ = 2.72 -0.06+0.05 is predicted (Cyburt et al. 2008; see also Steigman 2009; Coc & Vangioni 2010) with the theory of big bang nucleosynthesis (BBN) and the baryon density obtained from WMAP data (Dunkley et al. 2009), which is a factor of 2-6 times higher than the Li abundance inferred from halo stars. There have been many theoretical studies on non-standard BBN trying to explain the cosmological Li discrepancy by exploring the frontiers of new physics (e.g. Coc et al. 2009; Iocco et al. 2009; Jedamzik & Pospelov 2009; Kohri & Santoso 2009). Alternatively, the Li problem could be explained by a reduction of the original Li stellar abundance due to internal processes (i.e., by stellar depletion). In particular, stellar models including atomic diffusion and mixing can deplete a significant fraction of the initial Li content (Richard et al. 2005; Piau 2008), although such models depend on largely unconstrained free parameters. On the other hand, it is not easy to reconcile the lack of observed abundance scatter in the Spite plateau with substantial Li depletion (e.g. Ryan et al. 1999; A06). Due to the uncertainties in the Li abundances and to the small samples available, only limited comparisons of models of Li depletion with stars in a broad range of mass and metallicities have been performed (e.g., Pinsonneault et al. 2002; B05).

The observed scatter in derived Li abundances in previous studies of metal-poor stars can be as low as 0.03 dex (e.g. Ryan et al. 1999; A06), fully consistent with the expected observational errors. Yet, for faint stars observational errors as high as 0.2 dex have been reported (e.g., Aoki et al. 2009). In order to provide meaningful comparisons with stellar depletion models, precise Li abundances for a large sample of stars are needed. Here we present such a study for the first time for a large sample of metal-poor stars (-3.5 < [Fe/H] < -1.0) with masses in a relatively broad mass range (0.6-0.9 $M_\odot $).

2 Stellar sample and atmospheric parameters

The sample was initially based on the 62 stars analysed by MR04. We added stars with published equivalent width (EW) measurements based on high-quality observations (Sect. 3), and included also stars for which we could obtain EW Li measurements from UVES+VLT, HIRES+Keck and FIES+NOT spectra (either from our own observations or from the archives). The resolving power of the different instruments used ranges from $\sim $45 000 to 110 000, and the S/N is typically >100. Some measurements taken from the literature were obtained with lower resolving power ($\sim $35 000), or high resolving power (R $\sim $ 50 000) but lower S/N. When necessary we averaged several measurements in order to decrease the errors. The stars for which we could not obtain EW better than $\sim $5% were discarded, with a few exceptions (see Sect. 3). Our adopted log g values and metallicities [Fe/H] are mean values (after discarding outliers) taken from the compilation of stellar parameters by Meléndez (in preparation), who has updated the metallicity catalogue of Cayrel de Strobel et al. (2001) from 4918 entries to more than 14 000. We only keep stars with at least two previous spectroscopic analyses, so that their metallicities and surface gravities have been confirmed at least by one other study. The sample has 88 stars with stellar parameters $5250 < T_{\rm eff} < 6600$ K, $3.6 < \log g < 4.8$ and $-3.5 < {\rm [Fe/H]} < -1.0$.

We obtained effective temperatures ( $T_{\rm eff}$) by a new implementation (Casagrande et al. 2010, hereafter C10; see also Casagrande et al. 2006) of the infrared flux method (IRFM). In our previous work on Li abundances in metal-poor stars (MR04), $T_{\rm eff}$ was obtained from the IRFM implementation by Ramírez & Meléndez (2005), relying on the calibration of the bolometric correction by Alonso et al. (1995), which contains only a few low-metallicity stars; thus, for very metal-poor turn-off stars, it is not well defined and may introduce systematic errors. Indeed, C10 have found that below [Fe/H] $\simeq$ -2.5, the Ramírez & Meléndez (2005) $T_{\rm eff}$ go from being too cool by ${\simeq}100$ K at [Fe/H] = -2.5 to too hot by ${\simeq}100$ K at [Fe/H] = -3.5.

Our new IRFM implementation determines the bolometric flux from observed broad-band photometry (BVRIJHK), thus representing an important improvement over the $T_{\rm eff}$ obtained by Ramírez & Meléndez (2005). Furthermore, the zero point of our $T_{\rm eff}$ scale has been carefully checked for accuracy using solar twins (their average $T_{\rm eff}$ matching the solar one within a few K), spectral energy distributions measured with HST for a metal-rich star with planet and a metal-poor turn-off star, and stars with interferometric angular diameters (for which our IRFM $T_{\rm eff}$ and fluxes result in angular diameters only 0.6 $\pm$ 1.7% smaller, corresponding to 18 $\pm$ 50 K). Thus, contrary to most previous studies, the uncertainty of our absolute Li abundances is not dominated by the unknown zero point of the adopted $T_{\rm eff}$ scale.

In order to obtain $T_{\rm eff}$ values with IRFM, one needs good estimates of E(B-V) to properly correct the photometric data. In our previous work we used extinction maps (see Sect. 4 in Meléndez et al. 2006a, hereafter M06), but in order to achieve a very high precision ($\sim $0.005 mag), we must rely on other methods. Thanks to the large radial velocity of most metal-poor stars, the interstellar Na I D lines can be used to obtain this precision. We employed this technique (Alves-Brito et al. 2010) when high-resolution spectra were available ($\sim $72% of the cases), otherwise we used extinction maps (M06). Our adopted E(B-V) values are shown in Fig. 1 and have median errors of 0.003 $\pm$ 0.002 mag, implying errors in $T_{\rm eff}$ of ${\pm}15$ K. Adding in errors in photometry, bolometric flux, log g and [Fe/H], we estimate a typical total internal error in  $T_{\rm eff}$ of ${\pm}50$ K[*].

\begin{figure} \par\includegraphics[width=8cm,clip]{13047fg1.eps} % \vspace*{-1.5mm}\vspace*{-1.5mm} \end{figure} Figure 1:

Adopted E(B-V) values vs. [Fe/H]. Filled squares are values based on NaD lines and open squares on reddening maps.

Open with DEXTER

We obtained stellar masses from the $\alpha$-enhanced Y2 isochrones (Demarque et al. 2004). We interpolated a fine grid of models with a step $\Delta$[Fe/H] = 0.02 dex and adopting [$\alpha$/Fe] = 0 for [Fe/H] $\geq $ 0, [$\alpha$/Fe] = -0.3 $\times $ [Fe/H] for -1 < [Fe/H] < 0, and [$\alpha$/Fe] = +0.3 for [Fe/H] $\leq $ -1[*]. At a given metallicity, we searched for all solutions allowed by the error bars in  $T_{\rm eff}$, Hipparcos parallaxes (reliably available for 2/3 of the sample) and [Fe/H], adopting the median value in age and mass, and the standard deviation of the solutions is adopted as the error. We also used the mean log g values found in the literature to estimate another set of masses and ages. The masses obtained by both methods agree very well (median difference [Hipparcos - literature] of -0.001 $M_\odot $). The weighted averages of both results were adopted. We find typical ages of $\sim $11 Gyr and masses in the range of 0.6-0.9 $M_\odot $. In a few cases the adopted stellar parameters resulted in low ages (<6 Gyr), probably due to errors in log g. In those cases we estimated masses adopting an age = 11 Gyr, but the choice of age does not affect our conclusions (e.g., $\Delta$age = +1 Gyr results in $\Delta$mass = -0.007 $M_\odot $ for a dwarf with [Fe/H] = -2 and $T_{\rm eff}$ $\approx$ 6300 K).

3 Li abundance analysis

The LTE Li abundances were obtained with our code (A06) with MARCS (Gustafsson et al. 2008) models and the 2002 version of MOOG (Sneden 1973) with Kurucz overshooting (Castelli et al. 1997) models (which have improved overshooting with respect to earlier models that showed several problems described in van't Veer-Menneret & Megessier 1996). Both model atmospheres give similar Li abundances except for a zero-point difference of $\sim $0.08 dex (Kurucz overshooting - MARCS). According to MR04 the difference in  $A_{\rm Li}$ between Kurucz overshooting and no-overshooting models is also $\sim $0.08 dex, so Kurucz no-overshooting models give similar  $A_{\rm Li}$ as the MARCS models. The results presented herein will be based on the MARCS models, because the overshoot option implemented by Kurucz is not supported by 3D hydrodynamical model atmospheres (Asplund et al. 1999; see also Heiter et al. 2002); we will nevertheless mention the implication of using Kurucz overshooting models for completeness. We adopt the 1D non-LTE corrections by Lind et al. (2009a), which are based on the most recent radiative and collisional data (Barklem et al. 2003). The difference between LTE and non-LTE is relatively constant for our stars so that similar conclusions would have been obtained assuming LTE, yet, for an accurate analysis NLTE must be taken into account because it affects the absolute level of the Spite plateau. For metal-poor ([Fe/H] < -1) stars with $T_{\rm eff}$ > 6000 K the typical NLTE correction is -0.06 $\pm$ 0.01 dex.

We measured the EW of the Li feature at 6707.8 Å using UVES+VLT, HIRES+Keck and FIES+NOT high-resolution spectra, from which we obtain typical errors in EW of 0.7 mÅ, which includes uncertainties in continuum placement. We complemented our measurements with data from the literature (B05; A06; B07; S07; Asplund & Meléndez 2008, hereafter AM08; S10). An important improvement with respect to our previous work is that now we select stars with errors in EW below 5% (typically $\sim $2-3%), instead of the 10% limit adopted in MR04. The only exceptions are the cool dwarfs HD 64090 and BD+38 4955, which are severely depleted in Li and have EW errors of 8% and 10%, respectively, and the very metal-poor stars (B07) BPS CS29518-0020 (5.2%) and BPS CS29518-0043 (6.4%), which were kept due to their low metallicity.

The main sources of error are the uncertainties in equivalent widths and  $T_{\rm eff}$, which in our work have typical values of only 2.3% and 50 K, implying abundance errors of 0.010 dex and 0.034 dex, respectively, and a total error in $A_{\rm Li}$ of $\sim $0.035 dex. This low error in  $A_{\rm Li}$ is confirmed by the star-to-star scatter of the Li plateau stars, which have similar low values (e.g. $\sigma $ = 0.036 dex for [Fe/H] < -2.5, see below). Our Li abundances and stellar parameters are given in Table 1 (available in the online edition).

\begin{figure} \par\includegraphics[width=8.2cm,clip]{13047fg2.eps} % \vspace*{-1.5mm}\vspace*{-2mm} \end{figure} Figure 2:

Li abundances vs. $T_{\rm eff}$ for our sample stars in different metallicity ranges. A typical error bar is shown.

Open with DEXTER

4 Discussion

4.1 The Teff cutoff of the Spite plateau

Despite the fact that Li depletion depends on mass (e.g. Pinsonneault et al. 1992), this variable has been ignored by most previous studies. Usually a cutoff in  $T_{\rm eff}$ is imposed to exclude severely Li-depleted stars in the Spite plateau, with a wide range of adopted cutoffs, such as 5500 K (Spite & Spite 1982), 5700 K (B05), 6000 K (MR04; S07) and $\sim $6100 K for stars with [Fe/H] < -2.5 (Hosford et al. 2009).

At a given mass, the $T_{\rm eff}$ of metal-poor stars has a strong metallicity-dependence (e.g. Demarque et al. 2004). As shown in Figs. 11, 12 of M06, the  $T_{\rm eff}$ of turnoff stars increases for decreasing metallicities. Hence, a metallicity-independent cutoff in $T_{\rm eff}$ may be an inadequate way to exclude low-mass Li-depleted stars from the Spite plateau. As show in Fig. 2, where  $A_{\rm Li}$ in different metallicity bins is shown as a function of  $T_{\rm eff}$, stars with lower  $T_{\rm eff}$ in a given metallicity regime are typically the stars with the lowest Li abundances, an effect that can be seen even in the sample stars with the lowest metallicities ([Fe/H] $\sim $ -3). This is ultimately so because the coolest stars are typically the least massive, and therefore have been more depleted in Li (see Sect. 4.3).

\begin{figure} \par\includegraphics[width=7.8cm,clip]{13047fg3.eps} % \vspace*{-1.5mm}\vspace*{-2mm} \end{figure} Figure 3:

Li abundances for stars with $T_{\rm eff}$ > 5700 K (open circles), >6100 K (filled squares), >6350 K (filled triangles) and $\geq $5850-180 $\times $ [Fe/H] (stars). In the bottom panel stars above the cutoff in $T_{\rm eff}$ fall into two flat plateaus with $\sigma $ = 0.04 and 0.05 dex for [Fe/H] < -2.5 (dotted line) and [Fe/H] $\geq $ -2.5 (solid line), respectively.

Open with DEXTER

In Fig. 3 we show the Li abundance for cutoffs =5700 K (open circles), 6100 K (filled squares) and 6350 K (filled triangles). Using a hotter cutoff is useful to eliminate the most Li-depleted stars at low metallicities, but it removes from the Spite plateau stars with [Fe/H] > -2. Imposing a hotter $T_{\rm eff}$ cutoff at low metallicities and a cooler cutoff at high metallicities eliminates the most Li-depleted stars at low metallicities, but keeps the most metal-rich stars in the Spite plateau. We propose such a metallicity-dependent cutoff below.

4.2 Two flat Spite plateaus

Giving the shortcomings of a constant $T_{\rm eff}$ cutoff, we propose an empirical cutoff of $T_{\rm eff}$ = 5850-180 $\times $ [Fe/H]. The stars above this cutoff are shown as stars in the bottom panel of Fig. 3. Our empirical cutoff excludes only the most severely Li-depleted stars, i.e., the stars that remain in the Spite plateau may still be affected by depletion. The less Li-depleted stars in the bottom panel of Fig. 3 show two well-defined groups separated at [Fe/H] $\sim $ -2.5 (as shown below, this break represents a real discontinuity), which have essentially zero slopes (within the error bars) and very low star-to-star scatter in their Li abundances. The first group has -2.5 $\leq $ [Fe/H] < -1.0 and $\langle$ $A_{\rm Li}$ $\rangle _1$ = 2.272 ($\sigma $ = 0.051) dex and a slope of 0.018 $\pm$ 0.026, i.e., flat within the uncertainties. The second group is more metal poor ([Fe/H] < -2.5) and has $\langle$ $A_{\rm Li}$ $\rangle _2$ = 2.184 dex ( $\sigma = 0.036$) dex. The slope of this second group is also zero (-0.008 $\pm$ 0.037). Adopting a more conservative exponential cutoff obtained from Y2 isochrones (Demarque et al. 2004), which for a 0.79 $M_\odot $ star can be fit by $T_{\rm eff}$ = 6698-2173 $\times $ ${\rm e}^{\rm [Fe/H]/1.021}$, we would also recover a flat Spite plateau, although only stars with [Fe/H] > -2.5 are left using this more restrictive cut-off. Thus, the flatness of the Spite plateau is independent of applying a linear or an exponential cutoff.

Adopting a constant cutoff in $T_{\rm eff}$ we also find flat plateaus. For example adopting a cutoff of $T_{\rm eff}$ > 6100 K (filled squares in Fig. 3) we find in the most metal-rich plateau ([Fe/H] $\geq $ -2.5) no trend between Li and [Fe/H] (slope = 0.019 $\pm$ 0.025, Spearman rank correlation coefficient $r_{\rm Spearman}$ = 0.1 and a probability of 0.48 (i.e., 48%) of a correlation arising by pure chance for [Fe/H] $\geq $ -2.5), while for the most metal-poor plateau ([Fe/H] < -2.5) we also do not find any trend within the errors (slope = 0.058 $\pm$ 0.072, $r_{\rm Spearman}$ = 0.2 and 41% probability of a spurious correlation). Using a hotter cutoff ( $T_{\rm eff}$ > 6350 K, filled triangles in Fig. 3) we obtain also two flat plateaus with slope = -0.040 $\pm$ 0.063 ( $r_{\rm Spearman}$ = -0.2, probability =60%) for [Fe/H] $\geq $ -2.5 and slope = 0.008 $\pm$ 0.035 ( $r_{\rm Spearman}$ = 0.1, probability =68%) for [Fe/H] < -2.5.

\begin{figure} \par\includegraphics[width=7.8cm,clip]{13047fg4.eps} % \vspace*{-1mm}\vspace*{-2mm} \end{figure} Figure 4:

a) Filled circles show the slope/$\sigma $ of $A_{\rm Li}$ vs. [Fe/H] in the range $X_{\rm min}$ < [Fe/H] < -1.0, where $X_{\rm min}$ is in the interval [-3.5, -1.25]. For all values of $X_{\rm min}$ $\geq $ -2.5, the slope is insignificant ($\ll $3$\sigma $); only when stars with [Fe/H] < -2.5 are included, a slope is forced in $A_{\rm Li}$ vs. [Fe/H]. Open circles show the slope/$\sigma $ for the range -3.25 < [Fe/H] < $X_{\rm max}$, where -3.0 $\leq $ $X_{\rm max}$ $\leq $ -1.0. For  $X_{\rm max}$ < -2.5 the slope is negligible ( $\protect\ll$3$\sigma $), but when stars with [Fe/H] $\geq $ -2.5 are included, a slope is generated. b) The correlation coefficient  $r_{\rm Spearman}$ is shown by triangles, with filled and open symbols with similar meaning as in panel  a). The probabilities of a correlation between  $A_{\rm Li}$ and [Fe/H] by pure chance, associated to the filled and open triangles, are shown by solid and dashed lines, respectively. No meaningful correlation (probability  $\protect\ll$1) exists for either [Fe/H] < -2.5 or [Fe/H] $\geq $ -2.5.

Open with DEXTER

In Fig. 4 we demonstrate that the break at [Fe/H] $\sim $ -2.5 is statistically significant. In panel (a) the slope/$\sigma $ in the $A_{\rm Li}$ vs. [Fe/H] plot for the range $X_{\rm min}$ < [Fe/H] < -1.0 are shown as filled circles, where  $X_{\rm min}$ varies within [-3.50, -1.25]. For  $X_{\rm min}$ $\geq $ -2.5, the slope is insignificant ($\ll $3$\sigma $), and only when stars with [Fe/H] < -2.5 are included a measurable slope is forced in the $A_{\rm Li}$ vs. [Fe/H] relation. The opposite test is shown by open circles, where we show slope/$\sigma $ for the range -3.25 < [Fe/H] < $X_{\rm max}$, where  $X_{\rm max}$ changes from [-3.00, -1.00]. For  $X_{\rm max}$ < -2.5 the slope is negligible ($\ll $3$\sigma $), and only when stars with [Fe/H] $\geq $ -2.5 are included, a slope is produced between  $A_{\rm Li}$ and [Fe/H]. The correlation coefficient  $r_{\rm Spearman}$ and the probability of a correlation between  $A_{\rm Li}$ and [Fe/H] by pure chance are shown in panel (b). Again, this plot shows that no correlation between  $A_{\rm Li}$ and [Fe/H] exists within the two groups (-3.5 < [Fe/H] < -2.5 and -2.5 $\geq $ [Fe/H] $\geq $ -1.0), and that only when stars between the two groups are mixed, significant (probability $\sim $0) correlations of $A_{\rm Li}$ with [Fe/H] are generated. Systematically lower E(B-V) values (by $\sim $0.03 mag) in the most metal-poor plateau ([Fe/H] < -2.5) could produce a more Li-depleted plateau. However, those E(B-V) values (Fig. 1) are actually slightly higher ($\sim $0.007 mag, i.e., $\sim $33 K) than those for [Fe/H] $\geq $ -2.5 (mainly due to a high number of unreddened nearby more metal-rich stars), thus not explaining the existence of two different plateaus.

Previous claims of a steep monotonic decrease in Li abundance with decreasing metallicity (e.g. Ryan et al. 1999; A06; B07; Hosford et al. 2009) are probably due to the mix of stars from the two different groups, forcing a monotonic dependence with metallicity. Our large sample of homogeneous and precise Li abundances that covers a broad metallicity range (-3.5 < [Fe/H] < -1.0) does not support these claims. Nevertheless, a hint of two different groups in the Spite plateau was already found by A06, who found a change in the slope of the Spite plateau at [Fe/H] $\approx$ -2.2. Also, in the combined A06+B07 sample (Fig. 7 of B07), there are two different groups: stars with [Fe/H] $\ga$ -2.6 have $A_{\rm Li}$ > 2.2, while stars with [Fe/H] $\la$ -2.6 have $A_{\rm Li}$ < 2.2. Although in the study by MR04 a flat Spite plateau is found in the range -3.4 < [Fe/H] < -1, this is due to the overestimation of $T_{\rm eff}$ below [Fe/H] < -2.5, thus overestimating  $A_{\rm Li}$ at low metallicities and forcing a flat plateau from [Fe/H] = -3.4 to -1.

4.3 Correlation between Li and mass

Models of Li depletion predict that the least massive stars are the most depleted in Li, but due to the limitations of previous samples, these predictions have not been thoroughly tested at different metallicity regimes in metal-poor stars[*]. In Fig. 5 we show our Li abundances as a function of stellar mass for different metallicity ranges. As can be seen, the Li plateau stars have a clear dependence with mass for all metallicity regimes. Excluding stars with mass <0.7 $M_\odot $ (including those stars will result in even stronger correlations), linear fits result in slopes of 6, 3, 2, 2 dex  $M_\odot^{-1}$for stars in the metallicity ranges -1.3 < [Fe/H] < -1.0, -1.6 < [Fe/H] < -1.3, -2.5 < [Fe/H] < -1.6, and -3.5 < [Fe/H] < -2.5. The slopes are significant at the 8, 2, 5, 1$\sigma $ level, respectively. The correlation coefficient  $r_{\rm Spearman}$ is 0.9, 0.6, 0.6, 0.3, and the probability of a correlation between  $A_{\rm Li}$ and mass arising by pure chance is very small: 5 $\times $ 10-5, 3 $\times $ 10-2, 1 $\times $ 10-3, and 1.3 $\times $ 10-1, for stars in the same metallicity ranges as above. Thus, the correlations of  $A_{\rm Li}$ and mass in different metallicity regimes are very significant.

\begin{figure} \par\includegraphics[width=8cm,clip]{13047fg5.eps} % \vspace*{-1mm}\end{figure} Figure 5:

Li abundances as a function of stellar mass in different metallicity ranges. The metal-poor ([Fe/H] $\sim $ -3.5) binary BPS CS22876-032 (G08) is represented by open circles, nicely fitting the Li-mass trend. Models at [Fe/H] = -2.3 including diffusion and T6.0 (short dashed line), T6.09 (dotted line) and T6.25 (solid line) turbulence (Richard et al. 2005) are shown. The models were rescaled to an initial $A_{\rm Li}$ = 2.64 (long dashed line) and by $\Delta M = +0.05$ $M_\odot $.

Open with DEXTER

Recently, González Hernández et al. (2008, hereafter G08) have studied the metal-poor ([Fe/H] $\sim $ -3.5) double-lined spectroscopic binary BPS CS22876-032, providing thus crucial data to test our Li-mass trend. With our method and the stellar parameters of G08, we obtain a mass ratio of 0.89, very close to their value (0.911 $\pm$ 0.022) obtained from an orbital solution. For the primary we obtain MA = 0.776 $M_\odot $, and adopting the mass ratio of G08, MB = 0.707 $M_\odot $ is obtained for the secondary. The LTE Li abundances were taken from G08 and corrected for NLTE effects ($\sim $-0.05 dex). The components of the binary are shown as circles in Fig. 5, nicely following the trend of the most metal-poor stars. Including this binary in our sample would strengthen the Li-mass correlation of stars with [Fe/H] < -2.5. A slope =3 dex  $M_\odot^{-1}$ significant at the 3$\sigma $ level is obtained, with $r_{\rm Spearman}$ = 0.5 and a low probability (2 $\times $ 10-2) of the trend being spurious.

While mass-dependent Li depletion is expected from standard models of stellar evolution, this should only occur at significantly lower masses than considered here. These stellar models only predict very minor 7Li depletion (${\la}0.02$ dex) for metal-poor turn-off stars (e.g. Pinsonneault et al. 1992), which is far from sufficient to explain the $\sim $0.5 dex discrepancy between the observed Li abundance and predictions from BBN+WMAP. Bridging this gap would thus require invoking stellar models that include additional processes normally not accounted for, such as rotationally-induced mixing or diffusion. In Fig. 5 we confront the predictions of Richard et al. (2005) with our inferred stellar masses and Li abundances. The models include the effects of atomic diffusion, radiative acceleration, and gravitational settling, but moderated by a parameterized turbulent mixing (T6.0, T6.09, and T6.25, where higher numbers mean higher turbulence); so far only the predictions for [Fe/H] = -2.3 are available for different turbulent mixing models. The agreement is very good when adopting a turbulent model of T6.25 (see Richard et al., for the meaning of this notation) and an initial $A_{\rm Li} = 2.64$; had the Kurucz convective overshooting models been adopted, the required initial abundance to explain our observational data would correspond to $A_{\rm Li} = 2.72$. Two other weaker turbulence models that produce smaller overall Li depletions are also shown in Fig. 5, but they are less successful in reproducing the observed Li abundance pattern. Our best-fitting turbulence model (T6.25) is different from that (T6.0) required to explain the abundance pattern in the globular cluster NGC 6397 at similar metallicity (Korn et al. 2006; Lind et al. 2009b). Another problem with adopting this high turbulence is that the expected corresponding 6Li depletion would amount to >1.6 dex and thus imply an initial 6Li abundance at least as high as the primordial 7Li abundance if the claimed 6Li detections in some halo stars (A06; AM08) are real.

Our results imply that the Li abundances observed in Li plateau stars have been depleted from their original values and therefore do not represent the primordial Li abundance. It appears that the observed Li abundances in metal-poor stars can be reasonably well reconciled with the predictions from standard Big Bang nucleosynthesis (e.g. Cyburt et al. 2008) by means of stellar evolution models that include Li depletion through diffusion and turbulent mixing (Richard et al. 2005). We caution however that although encouraging, our results should not be viewed as proof of the Richard et al. models until the free parameters required for the stellar modelling are better understood from physical principles.

Acknowledgements
We thank the referee for valuable comments to strengthen the presentation of our results. We thank J. R. Shi for providing the EW measurements used in S07, O. Richard for providing tables with the Li depletion models, R. Collet, P. Nissen, A. García Peréz, D. Fabbian and L. Sbordone for providing data to estimate E(B-V) from interstellar Na I D lines, K.Lind for providing NLTE abundance corrections in electronic form. This work has been partially supported by FCT (project PTDC/CTE-AST/65971/2006, and Ciencia 2007 program).

References

  1. Alonso, A., Arribas, S., & Martinez-Roger, C. 1995, A&A, 297, 197 [NASA ADS] [Google Scholar]
  2. Alves-Brito, A., Meléndez, J., Asplund, M., Ramírez, I., & Yong, D. 2010, A&A, 513, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Aoki, W., Barklem, P. S., Beers, T. C., et al. 2009, ApJ, 698, 1803 [NASA ADS] [CrossRef] [Google Scholar]
  4. Asplund, M., & Meléndez, J. 2008, First Stars III, 990, 342 (AM08) [NASA ADS] [Google Scholar]
  5. Asplund, M., Nordlund, Å., Trampedach, R., & Stein, R. F. 1999, A&A, 346, L17 [NASA ADS] [Google Scholar]
  6. Asplund, M., Lambert, D. L., Nissen, P. E., Primas, F., & Smith, V. V. 2006, ApJ, 644, 229 (A06) [NASA ADS] [CrossRef] [Google Scholar]
  7. Barklem, P. S., Belyaev, A. K., & Asplund, M. 2003, A&A, 409, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Boesgaard, A. M., Stephens, A., & Deliyannis, C. P. 2005, ApJ, 633, 398 (B05) [NASA ADS] [CrossRef] [Google Scholar]
  9. Bonifacio, P., Molaro, P., Sivarani, T., et al. 2007, A&A, 462, 851 (B07) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Casagrande, L., Portinari, L., & Flynn, C. 2006, MNRAS, 373, 13 [NASA ADS] [CrossRef] [Google Scholar]
  11. Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 (C10) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 [NASA ADS] [Google Scholar]
  13. Cayrel de Strobel, G., Soubiran, C., & Ralite, N. 2001, A&A, 373, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Charbonnel, C., & Primas, F. 2005, A&A, 442, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Coc, A., & Vangioni, E. 2010, J. Phys. Conf. Ser., 202, 012001 [NASA ADS] [CrossRef] [Google Scholar]
  16. Coc, A., Olive, K. A., Uzan, J.-P., & Vangioni, E. 2009, Phys. Rev. D, 79, 103512 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cyburt, R. H., Fields, B. D., & Olive, K. A. 2008, J. Cosmol. Astro-Part. Phys., 11, 12 [Google Scholar]
  18. Demarque, P., Woo, J.-H., Kim, Y.-C., & Yi, S. K. 2004, ApJS, 155, 667 [NASA ADS] [CrossRef] [Google Scholar]
  19. Dunkley, J., Komatsu, E., Nolta, M. R., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef] [Google Scholar]
  20. González Hernández, J. I., Bonifacio, P., Ludwig, H.-G., et al. 2008, A&A, 480, 233 (G08) [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  21. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Heiter, U., Kupka, F., van't Veer-Menneret, C., et al. 2002, A&A, 392, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Hosford, A., Ryan, S. G., García Pérez, A. E., Norris, J. E., & Olive, K. A. 2009, A&A, 493, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Iocco, F., Mangano, G., Miele, G., Pisanti, O., & Serpico, P. D. 2009, Phys. Rep., 472, 1 [NASA ADS] [CrossRef] [Google Scholar]
  25. Jedamzik, K., & Pospelov, M. 2009, New J. Phys., 11, 105028 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kohri, K., & Santoso, Y. 2009, Phys. Rev. D, 79, 043514 [NASA ADS] [CrossRef] [Google Scholar]
  27. Korn, A. J., Grundahl, F., Richard, O., et al. 2006, Nature, 442, 657 [Google Scholar]
  28. Lind, K., Asplund, M., & Barklem, P. S. 2009a, A&A, 503, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Lind, K., Primas, F., Charbonnel, C., Grundahl, F., & Asplund, M. 2009b, A&A, 503, 545 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  30. Meléndez, J., & Ramírez, I. 2004, ApJ, 615, L33 (MR04) [NASA ADS] [CrossRef] [Google Scholar]
  31. Meléndez, J., Shchukina, N. G., Vasiljeva, I. E., & Ramírez, I. 2006, ApJ, 642, 1082 (M06) [NASA ADS] [CrossRef] [Google Scholar]
  32. Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 (NS10) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Piau, L. 2008, ApJ, 689, 1279 [NASA ADS] [CrossRef] [Google Scholar]
  34. Pinsonneault, M. H., Deliyannis, C. P., & Demarque, P. 1992, ApJS, 78, 179 [NASA ADS] [CrossRef] [Google Scholar]
  35. Pinsonneault, M. H., Steigman, G., Walker, T. P., & Narayanan, V. K. 2002, ApJ, 574, 398 [NASA ADS] [CrossRef] [Google Scholar]
  36. Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 465 [Google Scholar]
  37. Ramírez, I., Allende Prieto, C., & Lambert, D. L. 2007, A&A, 465, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Richard, O., Michaud, G., & Richer, J. 2005, ApJ, 619, 538 [NASA ADS] [CrossRef] [Google Scholar]
  39. Ryan, S. G., Norris, J. E., & Beers, T. C. 1999, ApJ, 523, 654 [NASA ADS] [CrossRef] [Google Scholar]
  40. Sbordone, L., Bonifacio, P., Caffau, E., et al. 2010, A&A, in press [arXiv:1003.4510] [Google Scholar]
  41. Shi, J. R., Gehren, T., Zhang, H. W., Zeng, J. L., & Zhao, G. 2007, A&A, 465, 587 (S07) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Sneden, C. A. 1973, Ph.D. Thesis, The University of Texas at Austin [Google Scholar]
  43. Spite, F., & Spite, M. 1982, A&A, 115, 357 [NASA ADS] [Google Scholar]
  44. Steigman, G. 2010, IAU Symp., 268, 19 [NASA ADS] [Google Scholar]
  45. van't Veer-Menneret, C., & Megessier, C. 1996, A&A, 309, 879 [NASA ADS] [Google Scholar]

Online Material

Table 1:   Parameters and Li abundances of our metal-poor stars.

Footnotes

... depletion[*]
Based in part on observations obtained at the W. M. Keck Observatory, the Nordic Optical Telescope on La Palma, and on data from the HIRES/Keck archive and the European Southern Observatory ESO/ST-ECF Science Archive Facility.
...[*]
Table 1 is only available in electronic form at http://www.aanda.org
...${\pm}50$ K[*]
In some cases the 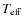$T_{\rm eff}$ given in Table 1 may be slightly different from the 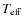$T_{\rm eff}$ given in C10 due to improved input parameters (e.g., better E(B-V) values) in the IRFM used here. The conclusions of C10 are unaffected by these minor changes.
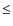...$\leq $ -1[*]
The adopted relation between [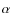$\alpha$/Fe] and [Fe/H] ignores the detailed abundance patterns of the two discs and halos (e.g., Ramírez et al. 2007; Nissen & Schuster 2010).
... stars[*]
Except for the work of B05, who provide comparisons at different metallicities but for cool severely Li-depleted dwarfs, i.e. probably of lower mass than most stars shown in Fig. 5

All Tables

Table 1:   Parameters and Li abundances of our metal-poor stars.

All Figures

  \begin{figure} \par\includegraphics[width=8cm,clip]{13047fg1.eps} % \vspace*{-1.5mm}\vspace*{-1.5mm} \end{figure} Figure 1:

Adopted E(B-V) values vs. [Fe/H]. Filled squares are values based on NaD lines and open squares on reddening maps.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.2cm,clip]{13047fg2.eps} % \vspace*{-1.5mm}\vspace*{-2mm} \end{figure} Figure 2:

Li abundances vs. $T_{\rm eff}$ for our sample stars in different metallicity ranges. A typical error bar is shown.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{13047fg3.eps} % \vspace*{-1.5mm}\vspace*{-2mm} \end{figure} Figure 3:

Li abundances for stars with $T_{\rm eff}$ > 5700 K (open circles), >6100 K (filled squares), >6350 K (filled triangles) and $\geq $5850-180 $\times $ [Fe/H] (stars). In the bottom panel stars above the cutoff in $T_{\rm eff}$ fall into two flat plateaus with $\sigma $ = 0.04 and 0.05 dex for [Fe/H] < -2.5 (dotted line) and [Fe/H] $\geq $ -2.5 (solid line), respectively.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{13047fg4.eps} % \vspace*{-1mm}\vspace*{-2mm} \end{figure} Figure 4:

a) Filled circles show the slope/$\sigma $ of $A_{\rm Li}$ vs. [Fe/H] in the range $X_{\rm min}$ < [Fe/H] < -1.0, where $X_{\rm min}$ is in the interval [-3.5, -1.25]. For all values of $X_{\rm min}$ $\geq $ -2.5, the slope is insignificant ($\ll $3$\sigma $); only when stars with [Fe/H] < -2.5 are included, a slope is forced in $A_{\rm Li}$ vs. [Fe/H]. Open circles show the slope/$\sigma $ for the range -3.25 < [Fe/H] < $X_{\rm max}$, where -3.0 $\leq $ $X_{\rm max}$ $\leq $ -1.0. For  $X_{\rm max}$ < -2.5 the slope is negligible ( $\protect\ll$3$\sigma $), but when stars with [Fe/H] $\geq $ -2.5 are included, a slope is generated. b) The correlation coefficient  $r_{\rm Spearman}$ is shown by triangles, with filled and open symbols with similar meaning as in panel  a). The probabilities of a correlation between  $A_{\rm Li}$ and [Fe/H] by pure chance, associated to the filled and open triangles, are shown by solid and dashed lines, respectively. No meaningful correlation (probability  $\protect\ll$1) exists for either [Fe/H] < -2.5 or [Fe/H] $\geq $ -2.5.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13047fg5.eps} % \vspace*{-1mm}\end{figure} Figure 5:

Li abundances as a function of stellar mass in different metallicity ranges. The metal-poor ([Fe/H] $\sim $ -3.5) binary BPS CS22876-032 (G08) is represented by open circles, nicely fitting the Li-mass trend. Models at [Fe/H] = -2.3 including diffusion and T6.0 (short dashed line), T6.09 (dotted line) and T6.25 (solid line) turbulence (Richard et al. 2005) are shown. The models were rescaled to an initial $A_{\rm Li}$ = 2.64 (long dashed line) and by $\Delta M = +0.05$ $M_\odot $.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.