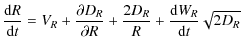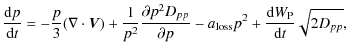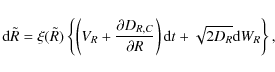| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913022 | |
| Published online | 15 June 2010 | |
Postshock turbulence and diffusive shock acceleration in young supernova remnants
A. Marcowith1 - F. Casse2
1 - Laboratoire de Physique Théorique et d'Astroparticules (LPTA), UMR
5207 CNRS, Université Montpellier II, 13 place E. Bataillon,
34095 Montpellier Cedex 5, France
2 - Laboratoire AstroParticule & Cosmologie (APC), UMR 7164
CNRS, Université Paris Diderot, 10 rue Alice Domon et Léonie Duquet,
75205 Paris Cedex 13, France
Received 30 July 2009 / Accepted 24 December 2009
Abstract
Context. Thin X-ray filaments are observed in the
vicinity of young supernova remnants (SNR) blast waves. Identifying the
process that creates these filaments would provide direct insight into
the particle acceleration occurring within SNR and in particular the
cosmic ray yield.
Aims. We investigate magnetic amplification in the
upstream medium of a SNR blast wave through both resonant and
non-resonant regimes of the streaming instability. We attempt to
understand more clearly of the diffusive shock acceleration (DSA)
efficiency by considering various relaxation processes of the magnetic
fluctuations in the downstream medium. Multiwavelength radiative
signatures originating in the SNR shock wave are used to test
various downstream turbulence relaxation models.
Methods. Analytical and numerical calculations that
couple stochastic differential equation schemes with
1D spherical magnetohydrodynamics simulations are used to
investigate, in the context of test particles, turbulence
evolution in both the forshock and post-shock regions. Stochastic
second-order Fermi acceleration induced by resonant modes, magnetic
field relaxation and amplification, and turbulence compression at the
shock front are considered to model the multiwavelength filaments
produced in SNRs. The ![]() -ray
emission is also considered in terms of inverse Compton mechanism.
-ray
emission is also considered in terms of inverse Compton mechanism.
Results. We confirm the result of Parizot and
collaborators that the maximum CR energies should not go well
beyond PeV energies in young SNRs where X-ray filaments are
observed. To reproduce observational data, we derive an upper
limit to the magnetic field amplitude and so ensure that stochastic
particle reacceleration remains inefficient. Considering various
magnetic relaxation processes, we then infer two necessary conditions
to achieve efficient acceleration and X-ray filaments in SNRs:
(1) the turbulence must fulfil the inequality
![]() ;
where
;
where ![]() is the turbulence spectral index and
is the turbulence spectral index and
![]() is the relaxation length
energy power-law index; (2) the
typical relaxation length must be of the order the X-ray rim size. We
find that Alvénic/fast magnetosonic mode damping fulfils all
conditions; while non-linear Kolmogorov damping does not.
By confronting previous relaxation processes with
observational data, we deducte that among our SNR sample, data
for the older ones (SN1006 and G347.3-0.5) does not comply with all
conditions, which means that their X-ray filaments are probably
controlled by radiative losses. The younger SNRs,
Cassiopeia A, Tycho, and Kepler pass all tests and we infer
that the downstream magnetic field amplitude is in the range of
200-300
is the relaxation length
energy power-law index; (2) the
typical relaxation length must be of the order the X-ray rim size. We
find that Alvénic/fast magnetosonic mode damping fulfils all
conditions; while non-linear Kolmogorov damping does not.
By confronting previous relaxation processes with
observational data, we deducte that among our SNR sample, data
for the older ones (SN1006 and G347.3-0.5) does not comply with all
conditions, which means that their X-ray filaments are probably
controlled by radiative losses. The younger SNRs,
Cassiopeia A, Tycho, and Kepler pass all tests and we infer
that the downstream magnetic field amplitude is in the range of
200-300 ![]() Gauss.
Gauss.
Key words: ISM: supernova remnants - acceleration of particles - magnetohydrodynamics (MHD) - shock waves
1 Introduction
Chandra high-angular resolution X-ray observations of young supernova remnants (SNR) such as Cassiopeia A, Kepler or Tycho, have detected very thin X-ray filaments, which are probably associated with the supernova (SN) forward shock expanding into the interstellar medium (ISM) (Uchiyama et al. 2003; Hwang et al. 2002; Cassam-Chenaï et al. 2004; Rho et al. 2002; Bamba et al. 2005b; Cassam-Chenaï et al. 2007; Gotthelf et al. 2001; Bamba et al. 2005a). The physical properties of these filaments were reviewed by Vink & Laming (2003), Vink (2004), Weisskopf & Hughes (2006), Ballet (2006), Parizot et al. (2006), Bamba et al. (2006), and Berezhko (2008). These filaments are believed to be produced by synchrotron radiation emitted by TeV electrons. Rim-like filaments are usually of a few arcsecond in angular size as reported in Parizot et al. (2006). Their true width, however has to be inferred from deprojection calculationsby taking into account the curvature of the remnant (Berezhko et al. 2003a; Ballet 2006). This size should depend on the magnetic field strength, local fluid properties (the shock velocity and compression ratio), and the relativistic electron diffusion regime.
Measurements of the X-ray rim size inferred a lower limit to
the magnetic field located downstream from the shock front. Typical
field strengths of two orders of magnitude above the standard ISM
values
![]() were reported by e.g., Berezhko
et al. (2003a), Vink
(2004), Völk
et al. (2005), Parizot
et al. (2006), and Berezhko
(2008). Vink (2004)
showed that advective and diffusive transport also contributes to the
filament extension at high energy close to the electron cut-off. The
aforementioned constraints infer a value of the electron spatial
diffusion coefficient that is a few times higher than the Bohm limit in
the downstream region from the shock
were reported by e.g., Berezhko
et al. (2003a), Vink
(2004), Völk
et al. (2005), Parizot
et al. (2006), and Berezhko
(2008). Vink (2004)
showed that advective and diffusive transport also contributes to the
filament extension at high energy close to the electron cut-off. The
aforementioned constraints infer a value of the electron spatial
diffusion coefficient that is a few times higher than the Bohm limit in
the downstream region from the shock![]() .
These results support the standard scenario of diffusive shock
acceleration (DSA) in SNRs and imply that strong magnetic field
amplification occurs at the shock precursor. However, Chandra
observations have been obtained for a limited frequency range. Thus,
diffusion regimes differing from that of the Bohm diffusion cannot be
ruled out by these sole observations (Marcowith
et al. 2006). For instance, alternative
diffusion regimes may affect high energy particle transport and modify
the way in which the synchrotron spectrum cut-off is reconstructed from
the extrapolation of the radio spectrum (Zirakashvili
& Aharonian 2007). However, the hard X-ray
detection of SNR RXJ 1713-3946.5 by Suzaku (Takahashi et al. 2008)
supports a cut-off spectrum in agreement with a Bohm-like
diffusion regime.
.
These results support the standard scenario of diffusive shock
acceleration (DSA) in SNRs and imply that strong magnetic field
amplification occurs at the shock precursor. However, Chandra
observations have been obtained for a limited frequency range. Thus,
diffusion regimes differing from that of the Bohm diffusion cannot be
ruled out by these sole observations (Marcowith
et al. 2006). For instance, alternative
diffusion regimes may affect high energy particle transport and modify
the way in which the synchrotron spectrum cut-off is reconstructed from
the extrapolation of the radio spectrum (Zirakashvili
& Aharonian 2007). However, the hard X-ray
detection of SNR RXJ 1713-3946.5 by Suzaku (Takahashi et al. 2008)
supports a cut-off spectrum in agreement with a Bohm-like
diffusion regime.
The origin of the magnetic fluctuations sustaining the
diffusive behavior of non-thermal particles remains widely debated. One
possibility is that the turbulent magnetic field is generated by the
relativistic particles themselves by means of their streaming motion
ahead of the shock front (Bell &
Lucek 2001). The field amplification has strong implications
for the physics of cosmic-ray (CR) acceleration at SNR shocks.
For instance, a calculation including the effect of
non-linear turbulence transfer concluded that proton acceleration is
possible up to the CR spectrum knee at ![]()
![]()
![]() .
This calculation was performed in the most extreme shock velocity
regimes, particularly for SNRs propagating in a hot interstellar medium
free of ion-neutral wave damping (Ptuskin
& Zirakashvili 2003). Bell
(2004) discussed a non-resonant regime of streaming
instability that can generate a very strong turbulent magnetic field
(and boost the CR maximum energy) readily at the very early
stage of the SNR free expansion phase. Diamond
& Malkov (2007) and Pelletier
et al. (2006) also highlighted the importance of
determining the saturation level of the magnetic fluctuations, which
was partially discarded in the previous work. Pelletier et al. (2006)
demonstrated that both resonant and non-resonant regimes of the
streaming instability have to be considered simultaneously to fix the
magnetic field spectrum and strength at the shock front.
In fast shocks, the non-resonant instability
dominates the magnetic field generation, the level of
fluctuation at the shock being found to be similar to the value derived
by Bell (2004). The resonant
instability dominates in slower shock regimes. The turbulence generated
upstream may then relax downstream from the shock front, limitating of
the spatial extent of the non-thermal particle journey (Pohl et al. 2005).
This possibility has not yet been completely taken into account in the
DSA process and the corresponding maximum energy reachable by
relativistic particles. This issue is investigated in a dedicated
section of the present article. We note that the problem of the maximum
CR energy was addressed by Zirakashvili
& Ptuskin (2008) using a semi-analytical approach to
the non-resonant streaming mode generation. The authors identified the
maximum CR energy, between the two confinement limits,
expected for a standard ISM medium or a completely amplified
magnetic field. One should keep in mind that several effects can
alterate these conclusions such as the propagation into a partially
ionised medium (Bykov
& Toptyghin 2005; Reville et al. 2007),
thermal effects in the dispersion relation of the non-resonant
instability (Reville et al.
2008), or a back reaction on the
CR current (Riquelme
& Spitkovsky 2009).
.
This calculation was performed in the most extreme shock velocity
regimes, particularly for SNRs propagating in a hot interstellar medium
free of ion-neutral wave damping (Ptuskin
& Zirakashvili 2003). Bell
(2004) discussed a non-resonant regime of streaming
instability that can generate a very strong turbulent magnetic field
(and boost the CR maximum energy) readily at the very early
stage of the SNR free expansion phase. Diamond
& Malkov (2007) and Pelletier
et al. (2006) also highlighted the importance of
determining the saturation level of the magnetic fluctuations, which
was partially discarded in the previous work. Pelletier et al. (2006)
demonstrated that both resonant and non-resonant regimes of the
streaming instability have to be considered simultaneously to fix the
magnetic field spectrum and strength at the shock front.
In fast shocks, the non-resonant instability
dominates the magnetic field generation, the level of
fluctuation at the shock being found to be similar to the value derived
by Bell (2004). The resonant
instability dominates in slower shock regimes. The turbulence generated
upstream may then relax downstream from the shock front, limitating of
the spatial extent of the non-thermal particle journey (Pohl et al. 2005).
This possibility has not yet been completely taken into account in the
DSA process and the corresponding maximum energy reachable by
relativistic particles. This issue is investigated in a dedicated
section of the present article. We note that the problem of the maximum
CR energy was addressed by Zirakashvili
& Ptuskin (2008) using a semi-analytical approach to
the non-resonant streaming mode generation. The authors identified the
maximum CR energy, between the two confinement limits,
expected for a standard ISM medium or a completely amplified
magnetic field. One should keep in mind that several effects can
alterate these conclusions such as the propagation into a partially
ionised medium (Bykov
& Toptyghin 2005; Reville et al. 2007),
thermal effects in the dispersion relation of the non-resonant
instability (Reville et al.
2008), or a back reaction on the
CR current (Riquelme
& Spitkovsky 2009).
Although disputed (see discussions in Katz
& Waxman 2008; Morlino
et al. 2009), the production of
relativistic hadrons in SNRs is consistent with detection of
a few TeV ![]() -ray emitting SNRs in the
Galactic plane by the HESS telescope. This
-ray emitting SNRs in the
Galactic plane by the HESS telescope. This ![]() -ray
emission may favor the interaction of relativistic hadrons with a dense
molecular cloud leading to the Compton upscattering of low energy
photons (Albert
et al. 2007; Aharonian et al. 2006,2004).
Nevertheless, more observations are mandatory before drawing any firm
conclusion about this important issue.
-ray
emission may favor the interaction of relativistic hadrons with a dense
molecular cloud leading to the Compton upscattering of low energy
photons (Albert
et al. 2007; Aharonian et al. 2006,2004).
Nevertheless, more observations are mandatory before drawing any firm
conclusion about this important issue.
The present article investigates DSA processes involving magnetic field amplification and relaxation. The paper considers the effect of shock acceleration, spatial variation in the magnetic field (and the corresponding diffusion coefficient), the possibility of finite diffusive extension zones, and the effect of stochastic Fermi acceleration by the electromagnetic fluctuations generated in the shock precursor. This modelling is performed by means of numerical calculations. The numerical scheme is based upon the stochastic differential equations (SDE) and is described in Appendix C. Section 2 presents the general framework adopted in this article. In particular, it investigates the conditions required to develop turbulence upstream from the shock, as expected from the non-linear evolution of the various regimes of the streaming instability. Sections 3 and 4 investigate the impact of post-shock turbulence upon particle acceleration. Section 3 dealing with advected downstream turbulence and Sect. 4 refering to a downstream relaxing turbulence. All calculations are then compared with those for a sample of young SNRs presented in Parizot et al. (2006) already.
Table 1 summarises the notations used in this article (the section where the parameter is reported at first is also indicated).
2 Upstream turbulence generation and accelerated particle diffusion
Highly turbulent supernova shocks involve several complex processes that modify the standard DSA model at some stage of the SNR evolution. In the upstream region, the properties of the turbulence are controlled by the fastest growing instability and its saturation mode (Pelletier et al. 2006). The diffusion regime strongly depends on the competition between the wave growth and the energy transfer to other scales provoked by non-linear cascades (Marcowith et al. 2006). The turbulence is then compressed at the shock-front, i.e., parallel modes (parallel to the shock normal) have wavelengths that are shorter by a factor equal to the (sub)shock compression ratio. In the downstream region, the turbulence can either be relaxed (Pohl et al. 2005) or amplified (Pelletier et al. 2006; Zirakashvili & Ptuskin 2008). The turbulent magnetic field coherence length may also vary with the distance to the shock, which can be modelled using self-similar solutions (Katz et al. 2007).Section 2.1 summarises the properties of the two regimes (both resonant and non-resonant) of the streaming instability as well as the magnetic field profiles inserted into the coupled SDE-magnetohydrodynamics (MHD) numerical calculations. In Sect. 2.3, we derive the general form of the diffusion coefficient. Finally, Sect. 2.4 displays the general expression of the particle distribution function, at the shock front, expected in the case of spatially varying diffusive zones. The various expressions derived in this section will be used in Sects. 3 and 4.
Table 1: Summary of the notations used in this article to denote the various physical quantities and parameters involved in our description of high energy particle yield in supernova remnants (SNR).
2.1 Cosmic-ray streaming instabilities
The streaming instability which is provoked by the superalfvenic motion of accelerated energetic particles, generates magnetic fluctuations over a large interval of wave numbers. The resonant instability involves wave-particle interaction on wave scales of the order of the particle gyro-radius2.1.1 The non-resonant regime
In the linear phase, the most rapidly growing waves have large wave
numbers (Bell 2004)
given by
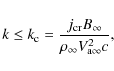
|
(1) |
where
The wave number corresponding to the maximal growth rate
![]() is
is
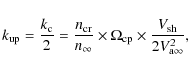
|
(2) |
where
MHD calculations (Bell
2004; Zirakashvili
& Ptuskin 2008) have shown that beyond an exponential
growth phase located on typical scale of
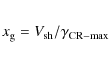
from the shock, the instability enters the non-linear regime. The magnetic fluctuations are redistributed on larger scales, while the turbulence level evolves in a linear way. Bell (2004) and Pelletier et al. (2006) discussed several saturation processes that all lead to an energy transfer from the dominant wavelength towards long wavelengths (see discussion in Riquelme & Spitkovsky 2009). One may then expect the coherence length of the turbulence to be transferred from a scale
Another important property of non-resonant modes is that they have non-vanishing helicity (Pelletier et al. 2006). These modes are mostly proton-induced and have a right-handed polarisation with respect to the mean magnetic field far upstream. This non-zero helicity may be the origin of additional amplification in the downstream medium, where the total magnetic field can eventually reach values close to the equipartition with the kinetic energy of the thermal gas.
2.1.2 The resonant regime
The resonant regime develops simultaneously with the non-resonant
regime (Pelletier
et al. 2006) and cannot be discarded.
The total amplification factor of the magnetic field
![]() at a distance x from the shock front is a
combinaition of both non-resonant and resonant contributions, namely
at a distance x from the shock front is a
combinaition of both non-resonant and resonant contributions, namely
![]() .
The exact spatial dependence of
.
The exact spatial dependence of
![]() is derived in
Appendix A
for completeness. It is found that a good approximation is
is derived in
Appendix A
for completeness. It is found that a good approximation is
![]() .
.
To quantify the previous assertion, we parametrise the
contribution of each instability regime. Pelletier
et al. (2006) argued that the shock velocity is the
main controlling factor of each contribution. This dependence can be
inferred from Eq. (A.2).
By comparing the respective saturation values of each regime,
one finds that
while
The level of magnetic fluctuations at the shock front given by Eqs. (3) and (4) is controlled by both
As a fiducial example, we assume that
![]() ,
,
![]() ,
and that the ion density as
,
and that the ion density as
![]() .
We then identify three distinct domains:
.
We then identify three distinct domains:
- 1.
-
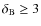 (corresponding
to
(corresponding
to 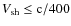 )
in which the magnetic field amplification provided by the streaming
instability is modest for slow shock velocities.
)
in which the magnetic field amplification provided by the streaming
instability is modest for slow shock velocities.
- 2.
- 1 <
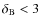 (corresponding to
(corresponding to
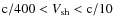 ):
for which we get the ordering
):
for which we get the ordering
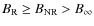 and, that the ratio
and, that the ratio
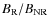 does not exceed a factor 2.
does not exceed a factor 2.
- 3.
-
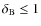 (corresponding
to
(corresponding
to 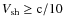 ):
for which the magnetic ordering becomes
):
for which the magnetic ordering becomes
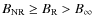 .
In that case, an upper limit velocity stands close
to c. Beyond that limit, the amplification
by the non-resonant instability is maximal. An accurate
analysis is then necessary to compare the saturation of the instability
induced by both advection and non-linear effects (Pelletier et al. 2009).
.
In that case, an upper limit velocity stands close
to c. Beyond that limit, the amplification
by the non-resonant instability is maximal. An accurate
analysis is then necessary to compare the saturation of the instability
induced by both advection and non-linear effects (Pelletier et al. 2009).
2.2 A note on the evolution of non-resonant modes
Non-resonant modes are purely growing modes of null frequency,
at least in the linear phase. They do not correspond to any
normal mode of the plasma as in the case of the resonant regime.
Consequently they are expected to be rapidly damped once the source
term is quenched, i.e., at the shock front. The damping length should
be of the order of a few plasma skin depths. However, these modes also
have a non-vanishing helicity (Pelletier et al. 2006;
Zirakashvili
& Ptuskin 2008) (as we see in Sect. 4.1.4).
So a fraction of the turbulent spectrum can grow
further downstream by means of dynamo action. At this point,
the downstream evolution of the non-resonant spectrum is
unclear. In some conditions the combinaition of magnetic field
compression and non-resonant mode damping at the shock front leads to a
downstream magnetic field that is weaker than the upstream field,
especially in the very fast shock regime (regime 3. discussed
in Sect. 2.1.2).
This is not the case for the SNR sample considered in this
work as the resonant modes tend to be dominant at the shock front.
A complete investigation of this difficult issue would require
a detailed investigation of the interstellar medium interaction with
shocks to fix the ratio
![]() .
For this reason, we assume hereafter that the downstream
behaviour of the turbulence is dominated by the resonant mode. However,
even if
.
For this reason, we assume hereafter that the downstream
behaviour of the turbulence is dominated by the resonant mode. However,
even if ![]() at the shock front, the fastest growing channel is the non-resonant
one, which is important for the complete setting of the magnetic field
turbulence in the upstream region. We acknowledge that this assumption
weakens the analysis presented in the following sections and consider
this first work to be an attempt to isolate the main properties of the
turbulence around a SNR shock.
at the shock front, the fastest growing channel is the non-resonant
one, which is important for the complete setting of the magnetic field
turbulence in the upstream region. We acknowledge that this assumption
weakens the analysis presented in the following sections and consider
this first work to be an attempt to isolate the main properties of the
turbulence around a SNR shock.
2.3 Upstream diffusion regimes
As previously discussed, the most energetic CRs generate fluctuations
at scales that are much smaller than
![]() .
These particles experience small-scale turbulence exclusively in the
unamplified magnetic field. Thus, the diffusion coefficient at
maximum energy scales as
.
These particles experience small-scale turbulence exclusively in the
unamplified magnetic field. Thus, the diffusion coefficient at
maximum energy scales as
![]() (see below). This allows us to compare
(see below). This allows us to compare ![]() and
and
![]() ,
the diffusive length of the most energetic
cosmic rays. One can then write (Pelletier
et al. 2006)
,
the diffusive length of the most energetic
cosmic rays. One can then write (Pelletier
et al. 2006)
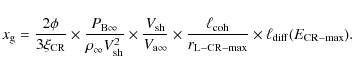
|
(5) |
We find that
CRs and electrons of energy lower than
![]() ,
diffuse by means of a large-scale turbulence, their transport
properties differing from those of most energetic CRs (Zirakashvili & Ptuskin 2008).
Whatever the turbulence level, the angular diffusion frequency
(for a relativistic particle in an amplified field)
can be estimated as (see Casse
et al. 2002, their Eq. (A22)):
,
diffuse by means of a large-scale turbulence, their transport
properties differing from those of most energetic CRs (Zirakashvili & Ptuskin 2008).
Whatever the turbulence level, the angular diffusion frequency
(for a relativistic particle in an amplified field)
can be estimated as (see Casse
et al. 2002, their Eq. (A22)):
where
The turbulence spectrum is assumed to spread over the range
In the non-linear phase (i.e., large-scale turbulence), we have
The results obtained by Casse et al. (2002) can be recovered using
We hereafter refer to ![]() as the normalization of the diffusion coefficient such that
as the normalization of the diffusion coefficient such that
It is noteworthy that the normalization of the diffusion coefficient is given by
Pelletier
et al. (2006) obtained a 1D stationary ![]() power-law
solution for the non-resonant wave spectrum. We can see from the above
analysis that the energetic particle transport properties around the
shock front depend on the possibility that non-resonant instability
will deeply enter in the non-linear regime. Verifying this condition
leads to a diffusion coefficient at
power-law
solution for the non-resonant wave spectrum. We can see from the above
analysis that the energetic particle transport properties around the
shock front depend on the possibility that non-resonant instability
will deeply enter in the non-linear regime. Verifying this condition
leads to a diffusion coefficient at
![]() given by Eq. (9),
the magnetic field profile being characterised by an
exponential growth over a scale
given by Eq. (9),
the magnetic field profile being characterised by an
exponential growth over a scale ![]() and a linear growth over a scale
and a linear growth over a scale
![]() .
.
This qualitative analysis confirms that the non-resonant
instability contributes to the turbulence level over a wide range of
parameters (once the non-linear regime of the instability is
established) and the control of the turbulence coherence length.
However, the analysis presented in Pelletier
et al. (2006) shows however that the resonant
instability at least in the domain 2 of our fiducial example
above also contributes to the magnetic fluctuation spectrum. The
resonant wave spectrum is found to be harder, i.e., for
a CR distribution spectrum scaling as p-4,
the 1D turbulence spectrum has an index ![]() .
In this work we assume that the turbulence index is in the
range
.
In this work we assume that the turbulence index is in the
range ![]() .
.
2.4 Shock particle distribution
Before discussing the effect of turbulence evolution in the downstream
region, we present the general solution for the particle distribution
at the shock front in the case of spatially varying diffusion
coefficients, where radiative losses are discarded. The complete
calculation is presented in Appendix B. We briefly
outline our result (see Eq. (B.5)) as follows.
We have assumed upstream and downstream magnetic fluctuations variation
lengths
![]() to be scale
(or energy) dependent (see Sect. 4). The slope of the
stationary particle distribution (neglecting any radiative loss) at the
shock front is
to be scale
(or energy) dependent (see Sect. 4). The slope of the
stationary particle distribution (neglecting any radiative loss) at the
shock front is
The value of the spectrum slope is controlled by the functions
If the shock wave is modified by the CR back-reaction, r will depend on the particle energy and the shock spectrum will not behave like power law. We note that provided functions
The present article investigates the effects of energy and
spatial dependencies of the ![]() functions in both
up- and downstream regions, by relying on a set of available
multiwavelength data of five SNR: Cassiopeia A, Tycho, Kepler,
SN1006, and G347.3-0.5 (also known as RXJ 1713-3946.5).
All of these remnants are of the case 2 discussed in
Sect. 2.1.2
and correspond to mildly fast shocks where both resonant and
non-resonant magnetic field amplification occur.
functions in both
up- and downstream regions, by relying on a set of available
multiwavelength data of five SNR: Cassiopeia A, Tycho, Kepler,
SN1006, and G347.3-0.5 (also known as RXJ 1713-3946.5).
All of these remnants are of the case 2 discussed in
Sect. 2.1.2
and correspond to mildly fast shocks where both resonant and
non-resonant magnetic field amplification occur.
3 Particle acceleration in the case of a downstream advected magnetic field
This section examines the DSA process for an efficient turbulence
amplification mechanism producing a strong magnetic field in the shock
precursor (see Sect. 2). In the
first Sect. 3.1,
we reconsider the calculations performed by Parizot
et al. (2006) but this time including the effect of
turbulent scale compression at the shock front. Section 3.2 then addresses
the usually overlooked aspect of stochastic particle acceleration in
the downstream flow. Finally, Sect. 3.3 deals with
tests involving the shock solutions obtained by Zirakashvili
& Aharonian (2007) for various turbulent spectrum
scalings. We then incorporate particle losses and Fermi stochastic
acceleration into the Fermi cycles and proceed with different numerical
experiments. We conclude with a comparison between X-ray and ![]() -ray
filaments produced by inverse Compton up-scattering of cosmic microwave
background photons.
-ray
filaments produced by inverse Compton up-scattering of cosmic microwave
background photons.
3.1 Downstream diffusion regimes and maximum particle energies
Downstream of the shock, the particle distribution was fully
isotropised (to an order of V/v)
and the streaming instability quenched. We insert the magnetic profiles
derived in the previous section into the diffusion coefficients
(see Eq. (9)).
To derive the downstream diffusion coefficients, we need to
specify properly how the transition occurs at the shock front. We only
consider here the case of a strong magnetic field amplification at the
shock precursor. The upstream magnetic field being highly disordered,
the magnetic compression ratio then becomes
![]() (with
(with ![]() )
)![]()
Parizot et al. (2006) only considered this final effect. But in the meantime, the maximum turbulence scale downstream is reduced by a factor
This scale compression induces an enhancement of the tangential magnetic field component and a reduction in the maximum turbulence length in the downstream region. The downstream turbulence is then anisotropic, displaying elongated eddies in the direction parallel to the shock front (Marcowith et al. 2006) unless other non-linear processes prevail (Zirakashvili & Ptuskin 2008). The coherence length of the turbulence is hereafter assumed to be a constant.
We can define the downstream diffusion coefficient according
to the definition of the upstream coefficient given in Eq. (9)
In the remaider of the article, we only consider the case where
Using Eq. (9)
evaluated at x=0 as well as Eqs. (13) and (14), we end up
linking up- and downstream diffusion coefficients at the shock front
(where we have assumed that
![]() ):
):
Once the up- and downstream diffusion coefficients are set, the magnetic field at the shock front can be inferred following the same procedure as that adopted in Parizot et al. (2006) (see the article for the detailed derivation). The balance between the electron acceleration rate and the mean synchrotron loss rate fixes the maximum electron energy to
Following DSA standard theory the acceleration rate is
Basic analytical relations can be derived when Bohm diffusion regime conditions prevail. In that case, electron and proton accelerations are no longer related because the diffusion coefficient no longer depends on
where we note that
Table 2:
Inferred values of the downstream magnetic field amplitude and
synchrotron
photon cut-off energy in the case of an advection-dominated
rim where Bohm diffusion regime prevails (![]() and
and ![]() ).
).
In Table 2,
we list the inferred values of the downstream magnetic field in the
context of an advection dominated X-ray rim, where a Bohm-type
turbulence is occurring. We have also provide the theoretical values
of
![]() required to verify
required to verify
![]() .
The similar to those in Table 1 of Parizot et al. (2006),
except for SN1006 where we used the value of shock velocity (
.
The similar to those in Table 1 of Parizot et al. (2006),
except for SN1006 where we used the value of shock velocity (
![]() )
given in Acero et al.
(2007). The results presented in this table were performed
using a diffusion coefficient normalization
)
given in Acero et al.
(2007). The results presented in this table were performed
using a diffusion coefficient normalization
![]() corresponding to predictions by the quasi-linear theory.
corresponding to predictions by the quasi-linear theory.
Based on the aforementioned assumptions, it appears that older
SNRs (
![]() )
should have a synchrotron cut-off energy that is much lower than the
observed value. However, as for instance in the case of
SN1006, the cut-off frequency depends on the observed region of the SNR
and 3 keV is probably an upper limit. On the other hand, young
SNRs (
)
should have a synchrotron cut-off energy that is much lower than the
observed value. However, as for instance in the case of
SN1006, the cut-off frequency depends on the observed region of the SNR
and 3 keV is probably an upper limit. On the other hand, young
SNRs (
![]() )
exhibit, in the same context, strong magnetic fields and
synchrotron energies cut-off close to the cut-off deduced from the
observations. The effect is even stronger in the case of modified
shocks. Parizot et al.
(2006) noted that the Bohm regime does not allow the
DSA theory to reproduce accurately the X-ray filaments unless
the diffusion coefficient normalization is replaced by a
factor k0
of a few. This is confirmed by the close agreement
between the two cut-off energies obtained for the young SNR.
)
exhibit, in the same context, strong magnetic fields and
synchrotron energies cut-off close to the cut-off deduced from the
observations. The effect is even stronger in the case of modified
shocks. Parizot et al.
(2006) noted that the Bohm regime does not allow the
DSA theory to reproduce accurately the X-ray filaments unless
the diffusion coefficient normalization is replaced by a
factor k0
of a few. This is confirmed by the close agreement
between the two cut-off energies obtained for the young SNR.
Several uncertainties may shift the value of the cut-off frequency from the extrapolation using the radio data. Zirakashvili & Aharonian (2007) pointed out that the electron particle distribution can be cut off in a smoother way than by a pure exponential cut-off. In that case, the true cut-off frequency is shifted towards higher energies. In the meantime, the observed synchrotron cut-off used previously is probably to be an upper limit because of the back-reaction of CR on the shock structure producing a curved shape of the spectrum. It seems justified to develop a detailed non-linear calculation to improve the estimate of the discrepancy between these solutions with a simple exponential cut-off. This aspect should also be an important issue for the next hard X-ray satellites generation such as nuStar or Next. We postpone its investigation to future work.
To summarise, we can say that scale compression has a very limited impact on the above calculation and that the results derived in Parizot et al. (2006) are quite robust.
3.2 Considering downstream stochastic Fermi acceleration
The downstream magnetic field amplitudes derived in Sect. 3 are lower limits, while the observed filament sizes are just upper limits because of the lack of resolution of X-ray instruments. If the downstream magnetic field reaches values close to mGauss and does not relax rapidly, then at some stage the Alfvén velocity will be of the order of the downstream fluid velocity. In that case, stochastic Fermi acceleration can no longer be neglected. Electrons will interact with turbulence modes generated by the resonant streaming instability since non-resonant modes are right-handed polarized and thus cannot interact with electrons. We included in our numerical calculations the so-called Fermi second-order process (in addition to the usual first-order acceleration) combined with energy losses, namely synchrotron losses for the electrons. We implicitly assume in the remainder of the paper that an efficient redistribution of forward and backward waves operates by means of non-linear interaction with magneto-sonic waves (Pelletier et al. 2006). In that case, forward and backward modes transmitted downstream are in balance (Vainio & Schlickeiser 1999). This assumption enables us to estimate the magnetic field amplitude when dominant stochastic Fermi acceleration occurs. Issues dealing with imbalanced magnetic turbulence are beyond the scope of this paper and will be investigated in future work.
The acceleration timescale characterising the stochastic Fermi
process for a relativistic particle can be written as
The conditions in which a stochastic acceleration less efficient than the usual shock acceleration can be transposed into a condition on the downstream magnetic field by writing
![\begin{displaymath}%
B_{\rm d-FII} \le [714~{\rm\mu Gauss}] \times {n_{\infty,-1...
...\bar{y}(r)^{1/2} (H(r_{\rm tot},\beta)
/r_{\rm tot}+1)^{1/2}},
\end{displaymath}](/articles/aa/full_html/2010/07/aa13022-09/img166.png)
|
(21) |
In this expression, we exceptionally use a shock velocity expressed in units of
In the case of young SNRs propagating into a standard ISM
medium with typical hydrogen densities
![]() ,
the previous limit leads to magnetic field strengths
,
the previous limit leads to magnetic field strengths
![]() mGauss
for a typical shock velocity of the order of 5
mGauss
for a typical shock velocity of the order of 5 ![]() 103 km s-1.
This is confirmed by the values of the limited magnetic field strengths
given Table 2
for each SNR. The surrounding gas density in most cases provides only a
crude estimate or is derived from averaged values over the entire
remnants. We have used for Cas A:
103 km s-1.
This is confirmed by the values of the limited magnetic field strengths
given Table 2
for each SNR. The surrounding gas density in most cases provides only a
crude estimate or is derived from averaged values over the entire
remnants. We have used for Cas A:
![]() (Berezhko et al. 2003b),
Kepler:
(Berezhko et al. 2003b),
Kepler: ![]() (Aharonian et al. 2008),
Tycho:
(Aharonian et al. 2008),
Tycho: ![]() (Hughes 2000), SN1006:
(Hughes 2000), SN1006:
![]() (SE rims see Acero
et al. 2007), G347.3-0.5:
(SE rims see Acero
et al. 2007), G347.3-0.5:
![]() (poorly constrained see Aharonian
et al. 2006).
(poorly constrained see Aharonian
et al. 2006).
The Fermi stochastic acceleration process produces an energy
gain in the downstream medium and a hardening of the particle
distribution at the shock front (see Eq. (15) in Marcowith et al. 2006,
and the simulations in Sect. 3.3.2).
As particles are continuously reaccelerated downstream, they
are expected to produce larger X-ray filaments. Both effects seem
clearly incompatible with the available data. The magnetic field
fluctuations in resonance with electrons are then expected to saturate
at the shock front with magnetic field amplitude
![]() ,
which is below the value for equipartition with thermal pressure of
the flow.
,
which is below the value for equipartition with thermal pressure of
the flow.
3.3 Numerical experiments
The SDE method presented in Appendix C does not account
for the back-reaction of CR over the fluid flow. This would require a
special smoothing and a difficult treatment of the
CR pressure
![]() .
The latter calculated from the particle distribution f(p,r)
at each grid point would produce unphysical fluctuations that develop
with time. Several numerical works have started to included wave
generation effects in CR modified shock hydrodynamics (Kang & Jones
2007; Vladimirov
et al. 2008,2006). Some
semi-analytical works has also started to investigate the effect of the
wave precursor heating on the CR back-reaction process (Caprioli et al. 2008).
Both approaches seem to reach a similar conclusion: the heating of the
precursor by the wave damping reduces the gas compressibility and thus
reduces the shock compression (Bykov
2004). Stationary solutions are found to be rather close to
the test particle case. Calculations performed in the test particle
framework using SDEs can then reproduce the main properties of the
particle acceleration process. SDE have several advantages: they are
simple to implement and rather simple to couple with
MHD equations. SDE schemes enable a fast and large
investigation of the parameter space of the DSA mechanism.
For instance, the inclusion of Fermi stochastic
acceleration is rather simple in both the SDE scheme and in the use of
various spatial diffusion coefficient regimes. Our results
can, for instance, be used as limiting tests for future
non-linear simulations.
.
The latter calculated from the particle distribution f(p,r)
at each grid point would produce unphysical fluctuations that develop
with time. Several numerical works have started to included wave
generation effects in CR modified shock hydrodynamics (Kang & Jones
2007; Vladimirov
et al. 2008,2006). Some
semi-analytical works has also started to investigate the effect of the
wave precursor heating on the CR back-reaction process (Caprioli et al. 2008).
Both approaches seem to reach a similar conclusion: the heating of the
precursor by the wave damping reduces the gas compressibility and thus
reduces the shock compression (Bykov
2004). Stationary solutions are found to be rather close to
the test particle case. Calculations performed in the test particle
framework using SDEs can then reproduce the main properties of the
particle acceleration process. SDE have several advantages: they are
simple to implement and rather simple to couple with
MHD equations. SDE schemes enable a fast and large
investigation of the parameter space of the DSA mechanism.
For instance, the inclusion of Fermi stochastic
acceleration is rather simple in both the SDE scheme and in the use of
various spatial diffusion coefficient regimes. Our results
can, for instance, be used as limiting tests for future
non-linear simulations.
3.3.1 Synchrotron spectrum solutions
We first validate the aforementioned numerical scheme by achieving
calculations in different configurations, such as reproducing
the analytical results of Zirakashvili
& Aharonian (2007). In this work,
the authors define the relativistic electron energy spectra at
the shock front in the presence of a discontinuous magnetic field
(the discontinuity is located at the shock). We performed
several
SDE-MHD simulations where constant upstream and downstream
magnetic fields prevail (
![]() ,
,
![]() is
set to 4) and where the shock velocity of the flow is set to
3000 km s-1. The various
presented simulations differ only in terms of their implemented spatial
diffusion coefficients, where
is
set to 4) and where the shock velocity of the flow is set to
3000 km s-1. The various
presented simulations differ only in terms of their implemented spatial
diffusion coefficients, where
![]() (the particles are injected at energy
(the particles are injected at energy
![]() TeV).
Zirakashvili & Aharonian (2007)
provided the shape of the electron energy spectra at the shock front
beyond the energy cut-off
TeV).
Zirakashvili & Aharonian (2007)
provided the shape of the electron energy spectra at the shock front
beyond the energy cut-off
![]() induced by synchrotron losses,
namely
induced by synchrotron losses,
namely
![]() .
Figure 1
displays three simulations with
.
Figure 1
displays three simulations with
![]() (Bohm diffusion),
(Bohm diffusion), ![]() (Kraichnan turbulence), and
(Kraichnan turbulence), and
![]() (constant coefficient). The result of the numerical calculations are
displayed using items, while analytical solutions of Zirakashvili & Aharonian (2007)
are displayed using solid lines. In the figure the following
parameters have been used: velocity of the downstream fluid
3000 km s-1, compression
factor
(constant coefficient). The result of the numerical calculations are
displayed using items, while analytical solutions of Zirakashvili & Aharonian (2007)
are displayed using solid lines. In the figure the following
parameters have been used: velocity of the downstream fluid
3000 km s-1, compression
factor ![]() )
and uniform upstream and downstream magnetic field are set (
)
and uniform upstream and downstream magnetic field are set (
![]() .
We have set various diffusion regime (
.
We have set various diffusion regime (
![]() )
while using our new numerical SDE scheme described in
Appendix C.
The agreement between numerical calculations and analytical profile is
good and proves that the skew SDE numerical scheme is valid for all
kinds of diffusion regimes and can handle magnetic discontinuities
properly (see Sect. C.2.1 for further
details).
)
while using our new numerical SDE scheme described in
Appendix C.
The agreement between numerical calculations and analytical profile is
good and proves that the skew SDE numerical scheme is valid for all
kinds of diffusion regimes and can handle magnetic discontinuities
properly (see Sect. C.2.1 for further
details).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13022fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13022-09/Timg186.png)
|
Figure 1: Shock front energy spectra of relativistic electrons provided by multi-scale simulations where the MHD part of the simulation mimics the behavior of a SNR blast wave. |
| Open with DEXTER | |
3.3.2 Shock particle distribution and second order Fermi process
Figures 2
and 3
show the shock particle distribution and synchrotron spectra for the
parameters corresponding to the conditions that prevail in the Kepler
and G347.3-0.5 SNRs, respectively. In the case of the
Kepler SNR, we use the parameters
![]()
![]() 103 km s-1,
103 km s-1,
![]() and,
and, ![]() .
Upstream density is
.
Upstream density is ![]() (Berezhko et al. 2006,
estimated the density to be
(Berezhko et al. 2006,
estimated the density to be
![]() ).
In the case of G347-0.5, we set parameters to be
).
In the case of G347-0.5, we set parameters to be
![]() km s-1,
km s-1,
![]() ,
,
![]() .
The averaged upstream density is
.
The averaged upstream density is
![]() (Aharonian et al. 2006).
In both cases, the magnetic profiles used in the simulations
are also presented. The dashed-line shows the stationary solution found
in Marcowith et al.
(2006), which includes particle re-acceleration in the Fermi
cycle. In the upper right panel, the acceleration
(with the sole regular Fermi acceleration), and both the diffusive and
downstream residence timescales are displayed. Diamonds are obtained
using a numerical calculation of the acceleration timescale. The slight
excess is produced by the stochastic Fermi acceleration process. We
also display the synchrotron spectrum and the magnetic profile around
the shock front at
(Aharonian et al. 2006).
In both cases, the magnetic profiles used in the simulations
are also presented. The dashed-line shows the stationary solution found
in Marcowith et al.
(2006), which includes particle re-acceleration in the Fermi
cycle. In the upper right panel, the acceleration
(with the sole regular Fermi acceleration), and both the diffusive and
downstream residence timescales are displayed. Diamonds are obtained
using a numerical calculation of the acceleration timescale. The slight
excess is produced by the stochastic Fermi acceleration process. We
also display the synchrotron spectrum and the magnetic profile around
the shock front at ![]() .
.
The maximum CR energy (and the aspect ratio
![]() )
corresponds to the maximum CR energy limited by either
particle escapes in the upstream medium or the SNR age limit.
At
)
corresponds to the maximum CR energy limited by either
particle escapes in the upstream medium or the SNR age limit.
At
![]() ,
the maximal upstream diffusion coefficient allowed by the
escaping limit is:
,
the maximal upstream diffusion coefficient allowed by the
escaping limit is:
The factor
It can be seen from Figs. 2 and 3 that stochastic
acceleration slightly modifies the shock particle spectrum in the case
of the Kepler SNR. The synchrotron losses create a bump close
to the maximum electron energies. In the Kepler remnant, the
synchrotron cut-off is found to be around 0.2 keV
(see Fig. 2),
while in the case of G347.3-0.5 it is around 0.5 keV
(see Fig. 3).
We verified that lowering the normalization factor ![]() of the diffusion coefficient from 16 to 3 produces a
cut-off around 1 keV (Kepler) and 2.5 keV
(G347.3-0.5), namely that a higher cut-off would require a
lower
of the diffusion coefficient from 16 to 3 produces a
cut-off around 1 keV (Kepler) and 2.5 keV
(G347.3-0.5), namely that a higher cut-off would require a
lower ![]() (see Eq. (19)).
The density around G347.3-0.5 is badly constrained and
(see Eq. (19)).
The density around G347.3-0.5 is badly constrained and
![]() would lead to similar effects. We note that the above simulations
maximize the incidence of the stochastic acceleration because we
assumed that the resonant field dominates the total field in the
downstream medium (see Eq. (3)).
would lead to similar effects. We note that the above simulations
maximize the incidence of the stochastic acceleration because we
assumed that the resonant field dominates the total field in the
downstream medium (see Eq. (3)).
To conclude it clearly appears that the downstream Alfvenic
Mach number
![]() cannot
be much less than unity otherwise: (1) the X-ray
filament would be too large with respect to the observed widths (see
next section); (2) the X-ray cut-off frequency would be far
larger than
cannot
be much less than unity otherwise: (1) the X-ray
filament would be too large with respect to the observed widths (see
next section); (2) the X-ray cut-off frequency would be far
larger than
![]() (see Fig. 2);
and (3) the radio spectrum would be harder than
(see Fig. 2);
and (3) the radio spectrum would be harder than
![]() (see Fig. 2).
Generally speaking, the maximum downstream resonant magnetic field
cannot be much stronger than a few mGauss downstream of the shock
front, otherwise regular acceleration process would be dominated by
stochastic Fermi acceleration. This places an important constraint on
the combined value of the magnetic field and the local
ISM density as well as the respective contribution of the
resonant and the non-resonant instability to the total magnetic field
at the shock front.
(see Fig. 2).
Generally speaking, the maximum downstream resonant magnetic field
cannot be much stronger than a few mGauss downstream of the shock
front, otherwise regular acceleration process would be dominated by
stochastic Fermi acceleration. This places an important constraint on
the combined value of the magnetic field and the local
ISM density as well as the respective contribution of the
resonant and the non-resonant instability to the total magnetic field
at the shock front.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13022fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13022-09/Timg203.png)
|
Figure 2: Energy spectrum of relativistic electrons at the shock front given by MHD-SDE simulations in the conditions of the Kepler SNR. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13022fg3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13022-09/Timg204.png)
|
Figure 3:
Same plots than in Fig. 2
but in the G347-0.5 SNR (velocity of the shock is 4 |
| Open with DEXTER | |
3.3.3
Comparisons between X- and  -ray filaments
-ray filaments
We end this section by a detailed comparison between X- and ![]() -ray
filaments produced by the relativistic electrons. The inclusion of
neutral pion decay caused by the hadronic interaction with the
interstellar fluid or with the shocked matter would require a complete
modelling of both the hadron spectrum and the ISM density
profile around the SNR. This study is postponed to future work.
-ray
filaments produced by the relativistic electrons. The inclusion of
neutral pion decay caused by the hadronic interaction with the
interstellar fluid or with the shocked matter would require a complete
modelling of both the hadron spectrum and the ISM density
profile around the SNR. This study is postponed to future work.
In our calculations, the leptonic ![]() -ray emission was integrated
into two characteristic wavebands 10-30 GeV and
1-3 TeV using the standard expression of the isotropic inverse
Compton emissivity (Blumenthal
& Gould 1970). The rims are produced by the
scattering off the cosmic microwave photons by relativistic electrons.
They are displayed in Figs. 4
and 5,
where they were obtained with parameters adapted to the dynamics of the
Kepler and the G347-0.5 SNR, respectively. We also displayed two X-ray
wavebands (4-6 keV and 0.5-1 keV, even if this later
wave band is usually dominated by the thermal emission).
In each case, both projected and deprojected filaments are
reproduced. The relative normalization between X-ray and
-ray emission was integrated
into two characteristic wavebands 10-30 GeV and
1-3 TeV using the standard expression of the isotropic inverse
Compton emissivity (Blumenthal
& Gould 1970). The rims are produced by the
scattering off the cosmic microwave photons by relativistic electrons.
They are displayed in Figs. 4
and 5,
where they were obtained with parameters adapted to the dynamics of the
Kepler and the G347-0.5 SNR, respectively. We also displayed two X-ray
wavebands (4-6 keV and 0.5-1 keV, even if this later
wave band is usually dominated by the thermal emission).
In each case, both projected and deprojected filaments are
reproduced. The relative normalization between X-ray and ![]() -ray
filaments depends mostly on the intensity of the magnetic field;
for the same particle energy domain, it is found to
scale as B2 as
expected. The width of the
-ray
filaments depends mostly on the intensity of the magnetic field;
for the same particle energy domain, it is found to
scale as B2 as
expected. The width of the ![]() -ray TeV rim is
usually the greatest because an important fraction of the
IC radiation is produced upstream. The 10-30 GeV
-ray TeV rim is
usually the greatest because an important fraction of the
IC radiation is produced upstream. The 10-30 GeV ![]() -rays are
produced closer to the shock upstream than 1-3 TeV
-rays are
produced closer to the shock upstream than 1-3 TeV ![]() -rays.
In the downstream region, the highest energetic electrons are
confined closer to the shock because of their shorter radiative loss
timescales. The projected rims indicate that only a slight difference
exists between the position of the peak of the gamma and X-ray
emission. As the size of the
-rays.
In the downstream region, the highest energetic electrons are
confined closer to the shock because of their shorter radiative loss
timescales. The projected rims indicate that only a slight difference
exists between the position of the peak of the gamma and X-ray
emission. As the size of the ![]() -ray rims is not much larger
than the X-ray filaments, it seems impossible for any
-ray rims is not much larger
than the X-ray filaments, it seems impossible for any ![]() -ray
instrument to separate both components. This will also be the case for
future instruments such as CTA unless the filaments are very large
(see the case of Vela Junior discussed in Bamba et al. 2005a).
-ray
instrument to separate both components. This will also be the case for
future instruments such as CTA unless the filaments are very large
(see the case of Vela Junior discussed in Bamba et al. 2005a).
4 Diffusive shock acceleration in the case of downstream spatially relaxing turbulence
We now consider a scenario where the downstream magnetic field
fluctuations vary over a length-scale much shorter than the
SNR shock radius
![]() .
This scale noted
.
This scale noted ![]() can depend on the wave number k of the
fluctuations. The damping of the turbulence in the downstream medium
and its compression at the shock front can modify the particle mean
residence time and the relativistic particle return probability to the
shock. Hence, this magnetic relaxation is expected to modify the
efficiency of the diffusive acceleration process itself.
can depend on the wave number k of the
fluctuations. The damping of the turbulence in the downstream medium
and its compression at the shock front can modify the particle mean
residence time and the relativistic particle return probability to the
shock. Hence, this magnetic relaxation is expected to modify the
efficiency of the diffusive acceleration process itself.
Equation (12)
shows that the particle energy spectrum at the shock front remains a
power law, provided that the quantities
(at a given energy E)
![]() are large compared to unity. For
are large compared to unity. For
![]() ,
the particle distribution will be strongly softened and the
acceleration timescale will shorten dramatically, the latter
being dominated by the particles experiencing the shortest residence
time. A softening effect induced by the upstream losses is
only expected at the highest energy close to
,
the particle distribution will be strongly softened and the
acceleration timescale will shorten dramatically, the latter
being dominated by the particles experiencing the shortest residence
time. A softening effect induced by the upstream losses is
only expected at the highest energy close to
![]() ,
namely as
,
namely as
![]()
![]() . The diffusive length of
particles with energy lower than
. The diffusive length of
particles with energy lower than
![]() is always smaller than the
variation scale of the magnetic
fluctuations
is always smaller than the
variation scale of the magnetic
fluctuations
![]() (controlled by the highest
energy), hence we have
(controlled by the highest
energy), hence we have
![]() ,
leading to a vanishing exponential factor in the above solution.
In contrast, the softening effect downstream can be
significant at energies much lower than
,
leading to a vanishing exponential factor in the above solution.
In contrast, the softening effect downstream can be
significant at energies much lower than
![]() as
as
![]() can be highly scale (and thus
energy) dependent. This is precisely the
main topic of this section, namely trying to identify the parameter
space that allows the Fermi acceleration process to be efficient in the
context of a relaxing downstream turbulence.
can be highly scale (and thus
energy) dependent. This is precisely the
main topic of this section, namely trying to identify the parameter
space that allows the Fermi acceleration process to be efficient in the
context of a relaxing downstream turbulence.
| Figure 4:
The unprojected and projected X-ray and |
|
| Open with DEXTER | |
Hereafter the downstream relaxation length
![]() is considered to be energy dependent and we normalize it with respect
to the maximum CR energy;
is considered to be energy dependent and we normalize it with respect
to the maximum CR energy;
![]() :
:
The scale
4.1 Downstream magnetic field relaxation
This work considers various turbulent magnetic field damped profiles:
the case of an energy-dependent Heaviside profile,
the profile produced by a non-linear Kolmogorov-type damping (Ptuskin & Zirakashvili 2003),
and the profile produced by the Alfvén or fast magnetosonic cascades (Pohl et al. 2005). We
also briefly discuss the case of a turbulent dynamo action downstream (Pelletier et al. 2006).
In this section, unless specified otherwise
![]() is implicitly assumed.
is implicitly assumed.
4.1.1 Heaviside profiles
Heaviside-type magnetic relaxation accounts for an idealized approach
to turbulence relaxation, where a given turbulence mode is assumed to
be uniform out a distance
![]() from the shock and to vanish
beyond that distance. This relaxation
model is probably unphysical but enables us to reproduce the basic
features of the turbulence relaxation effects upon particle
acceleration. Assuming this profile, we write the magnetic energy
turbulence spectrum as (the downstream medium is defined by x>0)
from the shock and to vanish
beyond that distance. This relaxation
model is probably unphysical but enables us to reproduce the basic
features of the turbulence relaxation effects upon particle
acceleration. Assuming this profile, we write the magnetic energy
turbulence spectrum as (the downstream medium is defined by x>0)
where
| Figure 5:
The unprojected and projected X-ray and |
|
| Open with DEXTER | |
The Heaviside profile, despite it crudely approximating the variation
in the magnetic energy density downstream, permits us to derive a basic
spatial profile of the total magnetic field
given by
which in the case of Bohm turbulence leads to (
At any given downstream location
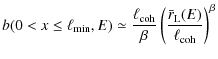
|
||
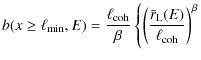
|
||
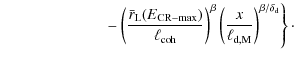
|
(27) |
Once both the total magnetic field and function b are known, it is easy to compute in our simulations both the spatial and energy diffusion coefficients of every test particle, which are mandatory to determine the particle motion and stationary particle distribution solutions in Eqs. (11) and (B.2). The procedure is repeated in the same way for any magnetic profile.
4.1.2 Non-linear Kolmogorov damping
In models of incompressible MHD turbulence described by the Kolmogorov
energy cascade towards large wave numbers, the non-linear damping
kernel scales as
k5/2
W(k)3/2.
Following Ptuskin &
Zirakashvili (2003), this kernel can be simplified
while still respecting the spatial relaxation
profile. We have
where
In the shock rest-frame, the turbulence relaxation downstream
(for x > 0) is described
by a stationary equation
and a boundary solution
An estimate of the scale x0 is (see Pohl et al. 2005)
We used
The relaxation scale is
![]() .
The factor
.
The factor
![]() is defined as the length over
which turbulence level has decreased
by 1/e compared to its value at the shock
front, i.e.,
is defined as the length over
which turbulence level has decreased
by 1/e compared to its value at the shock
front, i.e.,
![]() .
The spatial dependence of the total magnetic field and
function b were calculated using
Eqs. (25)
and (7).
These expressions, which are quite lengthy especially for the b function
in Eq. (6),
were implemented into the code but are not explicitly
given here.
.
The spatial dependence of the total magnetic field and
function b were calculated using
Eqs. (25)
and (7).
These expressions, which are quite lengthy especially for the b function
in Eq. (6),
were implemented into the code but are not explicitly
given here.
4.1.3 Exponential profiles
When turbulence damping rate does not depend on space but remains
dependent on wave number (
![]() ), the relaxation of
the downstream magnetic field follows an exponential cut-off on a scale
length
), the relaxation of
the downstream magnetic field follows an exponential cut-off on a scale
length
![]() .
The turbulent magnetic energy spectrum is then
.
The turbulent magnetic energy spectrum is then
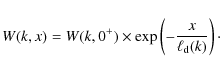
|
(32) |
The Alfvén and Magnetosonic waves cascades considered by Pohl et al. (2005) follow this scaling, the corresponding damping rates and expression for
The coherence scale of the downstream turbulence is
4.1.4 Turbulent dynamo downstream
Pelletier et al. (2006) (see also Zirakashvili & Ptuskin 2008) discussed the action of a turbulent dynamo in the downstream medium that would lead to additional amplification of the magnetic field. The magnetic field is expected to saturate at values close to equipartition with the dynamic gas pressure. The dynamo action is driven by the non-vanishing helicity of the non-resonant turbulent modes.
The corresponding scale of magnetic field variation is given
by the ratio of the magnetic turbulent diffusivity
![]() to the dynamo amplification
coefficient
to the dynamo amplification
coefficient
![]() .
The two coefficients can be expressed as (Pelletier
et al. 2006)
.
The two coefficients can be expressed as (Pelletier
et al. 2006)
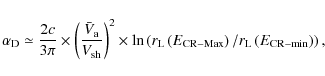
|
(34) |
and
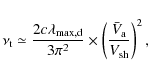
|
(35) |
where
4.2 Particle acceleration in a relaxed-compressed turbulence
In the next few paragraphs, we present some useful analytical estimations for the analysis of the numerical simulations presented in Sect. 4.3. These calculations used the Heaviside related profiles derived in Sect. 4.1.1. We note that the following characteristic timescales are strictly valid in the framework of infinitely extended diffusive zones but are used to discuss the effect of a spatially limited diffusive zones. However, we see in Sect. 4.3 that these approximations lead to correct energy spectrum features, except at the highest energies.
4.2.1 General statements about turbulence parameters
Pohl et al. (2005)
discussed various possible downstream relaxation processes. First,
the non-linear Kolmogorov damping produces a relaxation length
![]() .
Each turbulence mode k being in resonance
with relativistic particle whose Larmor radius verifies
.
Each turbulence mode k being in resonance
with relativistic particle whose Larmor radius verifies
![]() ,
we obtain
,
we obtain
![]() (between 1 and 1/2 for
(between 1 and 1/2 for
![]() ).
The two
other processes considered by Pohl
et al. (2005) scale as k-1/2,
namely
).
The two
other processes considered by Pohl
et al. (2005) scale as k-1/2,
namely ![]() .
A variation range of
.
A variation range of
![]() between 1/2
and 1 is then clearly identified. We
extend it to encompass the regime
between 1/2
and 1 is then clearly identified. We
extend it to encompass the regime
![]() ,
a limiting case where relaxation lengths are spatially
independent.
,
a limiting case where relaxation lengths are spatially
independent.
What if ![]() were negative? A strict lower limit to
were negative? A strict lower limit to
![]() is
given by the condition
is
given by the condition
![]() .
A non-relativistic minimum resonant energy
.
A non-relativistic minimum resonant energy
![]()
![]()
![]() seems
acceptable so that
seems
acceptable so that
![]() .
The lower limit
.
The lower limit
![]() has typical values of
between -0.3 and -0.2 when
identifying
has typical values of
between -0.3 and -0.2 when
identifying
![]() with the size of the X-ray
filament. Relaxation regimes with
with the size of the X-ray
filament. Relaxation regimes with
![]() do not necessary correspond to any known damping process but have some
interesting properties, in particular concerning the radio
filaments.
do not necessary correspond to any known damping process but have some
interesting properties, in particular concerning the radio
filaments.
4.2.2 The dominant loss mechanism
Comparing typical energy loss timescales is a useful tool for
determining whether or not diffusive particle losses can affect the
energy spectrum of relativistic particles. Assuming that turbulence
relaxation follows a Heaviside prescription, we can express these
timescales by assuming a constant downstream magnetic field on the
relaxation length
![]() relative to a particle of
energy E.
relative to a particle of
energy E.
Four timescales are relevant to set the maximum particle energy in a relaxed and compressed turbulence:
- 1.
- The acceleration timescale is given by
where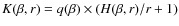 and the maximum wavelength of the downstream turbulence is expressed in
units of
and the maximum wavelength of the downstream turbulence is expressed in
units of
 .
.
- 2.
- The advection timescale, i.e., the time required for a
particle to travel over a distance
 while being advected with the
downstream flow, is given by
while being advected with the
downstream flow, is given by
- 3.
- The diffusive timescale, i.e., the time required for a
particle to travel over a distance
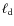 in a diffusive motion
in a diffusive motion![[*]](/icons/foot_motif.png) .
.
- 4.
- The synchrotron loss timescale
where the parameter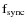 is represented by
is represented by
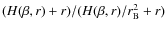 .
This expression takes into account the mean residence time both in the
upstream and downstream medium.
.
This expression takes into account the mean residence time both in the
upstream and downstream medium.
4.2.3 Conditions for an efficient particle acceleration
For relaxation-dominated filaments, the ratios of the acceleration
timescale (Eq. (36))
to either the diffusive (Eq. (38)) and to the
advective (Eq. (37))
timescales vary as
![]() and
and ![]() ,
respectively. Two different regimes are now discussed.
,
respectively. Two different regimes are now discussed.
Table 3: Analytical estimates of the downstream magnetic field value in the context of diffusive-loss-dominated SNRs rims.
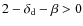 :
:
once where
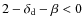 :
:
in this case, the
ratio of the diffusive to advective timescales is
always lower than unity, i.e., diffusive losses dominate at
all energies. Once Hence, efficient Fermi acceleration is only possible if
![]() .
For instance, an energy independent relaxation length
.
For instance, an energy independent relaxation length
![]() (as well
as
(as well
as ![]() )
verifies this criterion for all diffusion regimes. In the case
of a Kolmogorov type non-linear turbulence damping, the
supplementary relation
)
verifies this criterion for all diffusion regimes. In the case
of a Kolmogorov type non-linear turbulence damping, the
supplementary relation
![]() imposes
imposes ![]() ,
which means that only the Bohm regime can fulfil the previous condition
(we see in Sect. 4.3
that particle acceleration is inefficient in that case).
In the context of Alfvén and magnetosonic cascades, Kolmogorov
turbulence regime (
,
which means that only the Bohm regime can fulfil the previous condition
(we see in Sect. 4.3
that particle acceleration is inefficient in that case).
In the context of Alfvén and magnetosonic cascades, Kolmogorov
turbulence regime (![]() )
is the sole regime failing to verify the previous condition.
)
is the sole regime failing to verify the previous condition.
4.2.4 Magnetic field limits in a relaxed-compressed turbulence
In the context of X-ray filaments controlled by the downstream
turbulence damping, we can link the size of the filament,
noted
![]() ,
to the maximal relaxation length
,
to the maximal relaxation length
![]() as
as
![]()
![]() . The energy
. The energy
![]() is the energy of particles
emitting in the 4-6 keV band and
this value depends on the local value of the total magnetic field.
is the energy of particles
emitting in the 4-6 keV band and
this value depends on the local value of the total magnetic field.
A downstream magnetic field estimation
![]() can be obtained from the dynamics of the electrons by requiring that
can be obtained from the dynamics of the electrons by requiring that
![]() using the previous relation between
using the previous relation between
![]() and
and
![]() .
In the context of the Bohm diffusion, one obtains
.
In the context of the Bohm diffusion, one obtains
where
The determination of the SNR X-ray filaments are dominated
wether either by the relaxation of the downstream magnetic turbulence
or synchrotron losses is provided by the condition
![]() .
The corresponding limit value of the magnetic field is (again in case
of Bohm diffusion)
.
The corresponding limit value of the magnetic field is (again in case
of Bohm diffusion)
To ensure that SNR X-ray filaments dominated by the relaxation of the magnetic field, it is compulsory to have
Concerning cosmic rays of energy
![]() ,
the downstream diffusive losses will dominate if particles cannot
escape from the upstream region into the ISM. This imposes a constraint
on the magnetic field amplitude at the shock obtained from
Eq. (22).
Indeed, upstream escape losses are dominant if
,
the downstream diffusive losses will dominate if particles cannot
escape from the upstream region into the ISM. This imposes a constraint
on the magnetic field amplitude at the shock obtained from
Eq. (22).
Indeed, upstream escape losses are dominant if
![]() ,
when we assume that
,
when we assume that
![]() .
.
- In the case
 ,
downstream diffusive spatial escape downstream always controls the
maximum CR energy.
,
downstream diffusive spatial escape downstream always controls the
maximum CR energy.
- For
 ,
the previous condition leads to an upper limit to the downstream
magnetic field, noted
,
the previous condition leads to an upper limit to the downstream
magnetic field, noted
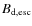 .
Hence if
.
Hence if 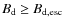 the CR maximum energy will be fixed by the upstream escape
losses and conversely if
the CR maximum energy will be fixed by the upstream escape
losses and conversely if
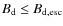 the CR maximum energy will be set by the downstream escape losses.
the CR maximum energy will be set by the downstream escape losses.
Table 3
displays the values of ![]() and
and ![]() related to our SNR sample. The Kolmogorov regime was discarded
as it does not produce any efficient acceleration as we see in
Sect. 4.3.
We show that for SN 1006 and G347.3-0.5, not much room is
effectively left for the case of magnetic relaxation-controlled
filaments. This result seems rather robust as a variation of the shock
velocity by a factor of
related to our SNR sample. The Kolmogorov regime was discarded
as it does not produce any efficient acceleration as we see in
Sect. 4.3.
We show that for SN 1006 and G347.3-0.5, not much room is
effectively left for the case of magnetic relaxation-controlled
filaments. This result seems rather robust as a variation of the shock
velocity by a factor of ![]() ,
or a variation in the synchrotron cut-off by a factor
of 2 does not lead to any variation in the magnetic field
greater than
,
or a variation in the synchrotron cut-off by a factor
of 2 does not lead to any variation in the magnetic field
greater than ![]() .
However, a variation in the filament width by a factor of 2
would imply a variation in the magnetic field by a factor of
.
However, a variation in the filament width by a factor of 2
would imply a variation in the magnetic field by a factor of ![]() ,
which may slightly modify the previous conclusion. Quite generally, the
maximum magnetic field amplitude is found to be in the range
,
which may slightly modify the previous conclusion. Quite generally, the
maximum magnetic field amplitude is found to be in the range
![]() .
.
To summarise we find that if downstream magnetic relaxation
controls the features of the SNRs X-ray filaments, a Bohm-like
diffusion regime is likely to occur and the particle diffusion
coefficient normalization factor
![]() has to be quite close to unity, i.e., the diffusion regime has
to be close to a genuine Bohm diffusion regime. In this context, we
show that only a fraction of our SNR sample to meet these
conditions, namely the young ones. Using the various observational
constraints related to the older SNRs (SN1006 and G347.3-0.5), we have
shown that the X-ray filaments existing in these objects are likely to
be ruled by radiative losses associated with synchrotron emission.
has to be quite close to unity, i.e., the diffusion regime has
to be close to a genuine Bohm diffusion regime. In this context, we
show that only a fraction of our SNR sample to meet these
conditions, namely the young ones. Using the various observational
constraints related to the older SNRs (SN1006 and G347.3-0.5), we have
shown that the X-ray filaments existing in these objects are likely to
be ruled by radiative losses associated with synchrotron emission.
4.2.5 Radio filaments
The energy of the radio electrons is typically four order of magnitude
below that of the X-ray emitting electrons, i.e.,
![\begin{eqnarray*}E_{\rm eobs,R} \simeq [1.5~{\rm GeV}] \ B_{\rm d,-4}^{-1/2} E_{\rm\gamma-obs-GHz}^{1/2},
\end{eqnarray*}](/articles/aa/full_html/2010/07/aa13022-09/img354.png)
where
4.3 Numerical simulations
We performed MHD-SDE simulations by taking into account all previous settings, namely the downstream magnetic field relaxation, the stochastic reacceleration, and the radiative losses for the electrons. In the following paragraphs, we discuss the physical agreement between assuming magnetic field relaxation to control the X-ray filaments and the actual results coming from the computation of relativistic electrons acceleration.
4.3.1 Downstream magnetic Kolmogorov damping
When non-linear Kolmogorov damping occurs in the downstream medium of
the shock, we have seen in the previous sections that two conditions
have to be fulfilled to reproduce both the appropriate energy cut-off
and the correct size of the observed X-ray filament. These two
conditions can be expressed as: having the correct downstream
magnetic field given by Eq. (41)
(to ensure that the electron energy cut-off is consistent with
the observations) and having the typical magnetic relaxation
length
![]() (see Eq. (31))
that is similar in the size of the X-ray filament. In the
non-linear Kolmogorov regime, the only diffusion regime able to provide
to an efficient particle acceleration is the Bohm diffusion regime,
where the relaxation energy index
(see Eq. (31))
that is similar in the size of the X-ray filament. In the
non-linear Kolmogorov regime, the only diffusion regime able to provide
to an efficient particle acceleration is the Bohm diffusion regime,
where the relaxation energy index
![]() .
Inserting, for the Kepler SNR, this value into Eq. (41) leads to a
downstream magnetic field of
.
Inserting, for the Kepler SNR, this value into Eq. (41) leads to a
downstream magnetic field of
![]() and a relaxation of
and a relaxation of ![]() pc.
The relaxation size is clearly too large to provide an X-ray filament,
whose thickness is inferred to be of the order of 10-2 pc
from X-ray observations. Applying the same reasoning to the other SNRs
leads to a similar conclusion: having both the appropriate electron
energy cut-off and X-ray filament size is incompatible with a
non-linear Kolmogorov occurring in the downstream medium of the
SNR shock. The only way to overcome this conclusion would be
to have the factor
pc.
The relaxation size is clearly too large to provide an X-ray filament,
whose thickness is inferred to be of the order of 10-2 pc
from X-ray observations. Applying the same reasoning to the other SNRs
leads to a similar conclusion: having both the appropriate electron
energy cut-off and X-ray filament size is incompatible with a
non-linear Kolmogorov occurring in the downstream medium of the
SNR shock. The only way to overcome this conclusion would be
to have the factor
![]() to be much smaller than expected (see Eq. (31)). Anyway,
having
to be much smaller than expected (see Eq. (31)). Anyway,
having ![]() so low would mean that the range of particle energy able to resonate
with turbulence mode would be so narrow that it would not be able to
provide any significant acceleration. This explains why our result
differs from the conclusion drawn by Pohl
et al. (2005). It seems then that it is
very unlikely that non-linear Kolmogorov damping, which is a slower
process than Alfvén/fast magnetosonic cascade, occurs in the downstream
medium of SNR shocks.
so low would mean that the range of particle energy able to resonate
with turbulence mode would be so narrow that it would not be able to
provide any significant acceleration. This explains why our result
differs from the conclusion drawn by Pohl
et al. (2005). It seems then that it is
very unlikely that non-linear Kolmogorov damping, which is a slower
process than Alfvén/fast magnetosonic cascade, occurs in the downstream
medium of SNR shocks.
4.3.2 Alfvènic-fast magnetosonic mode damping
In the context of Alfvénic-fast magnetosonic turbulence relaxation,
the typical relaxation length
![]() is shorter than
is shorter than
![]() .
Compiling the aforementioned necessary conditions to reproduce
accurately an X-ray filament in the SNR environment, we obtain
a typical
.
Compiling the aforementioned necessary conditions to reproduce
accurately an X-ray filament in the SNR environment, we obtain
a typical
![]() of the order of 10-2 pc
when using
magnetic field values provided by Table 2. This means that
the Alfvénic-fast magnetosonic modes damping is a plausible candidate
to explain the presence of SNRs X-ray filaments. To sustain
this conclusion, we performed, in the context of the
Kepler SNR, MHD-SDE simulations designed to reproduce the
dynamics of relativistic electrons and the associated X-ray and
of the order of 10-2 pc
when using
magnetic field values provided by Table 2. This means that
the Alfvénic-fast magnetosonic modes damping is a plausible candidate
to explain the presence of SNRs X-ray filaments. To sustain
this conclusion, we performed, in the context of the
Kepler SNR, MHD-SDE simulations designed to reproduce the
dynamics of relativistic electrons and the associated X-ray and ![]() -ray
emission maps. In Figs. 6
and 7,
we display the particle distribution at the shock front and the X- and
-ray
emission maps. In Figs. 6
and 7,
we display the particle distribution at the shock front and the X- and ![]() -ray
filaments respectively. All simulations were performed in the Bohm
regime. In that case,
-ray
filaments respectively. All simulations were performed in the Bohm
regime. In that case,
![]() .
In each cases the magnetic field is damped in the downstream
medium following an exponential relaxation as in Alfvènic-fast
magnetsonic modes damping. Bohm regime in downstream region has been
assumed. The dashed-line shows the stationary solution found in Marcowith et al. (2006),
which includes particle reacceleration in the Fermi cycle. In the upper
right panel the acceleration (only the regular Fermi
acceleration), and the diffusive and downstream residence timescales
are displayed using solid and dashed lines. Diamonds represent for our
numerical calculation of the acceleration timescale, which is in
agreement with the theoretical estimation. We also display in the two
lower panels the spatial dependence of the diffusion coefficient at the
maximum electron energy (lower left) and the magnetic profile in the
downstream medium at t=400 years (lower
right).
.
In each cases the magnetic field is damped in the downstream
medium following an exponential relaxation as in Alfvènic-fast
magnetsonic modes damping. Bohm regime in downstream region has been
assumed. The dashed-line shows the stationary solution found in Marcowith et al. (2006),
which includes particle reacceleration in the Fermi cycle. In the upper
right panel the acceleration (only the regular Fermi
acceleration), and the diffusive and downstream residence timescales
are displayed using solid and dashed lines. Diamonds represent for our
numerical calculation of the acceleration timescale, which is in
agreement with the theoretical estimation. We also display in the two
lower panels the spatial dependence of the diffusion coefficient at the
maximum electron energy (lower left) and the magnetic profile in the
downstream medium at t=400 years (lower
right).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13022fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13022-09/Timg365.png)
|
Figure 6: Energy spectrum of relativistic electrons at the shock front given by MHD-SDE simulations in the conditions of the Kepler SNR (see Fig. 2 for details). |
| Open with DEXTER | |
| Figure 7:
The unprojected and projected X-ray and |
|
| Open with DEXTER | |
Several obvious differences appear in both Figs. 6 and 7 with respect to
the simple advection case presented in Figs. 2 and 3. First, as stated
in Sect. 4.2
the normalization of the diffusion coefficient ![]() has to be close to one. Even in this case, the maximum
particle energy is limited to values close to ten TeV
(for parameters associated with the Kepler SNR). One
of the necessary conditions to fit the observed size of the X-ray rim,
namely
has to be close to one. Even in this case, the maximum
particle energy is limited to values close to ten TeV
(for parameters associated with the Kepler SNR). One
of the necessary conditions to fit the observed size of the X-ray rim,
namely ![]() ,
produces an increase in the diffusion coefficient by a factor of a few
tens above the typical diffusion length, and consequently low maximal
energies for both electrons and cosmic rays. The X- and
,
produces an increase in the diffusion coefficient by a factor of a few
tens above the typical diffusion length, and consequently low maximal
energies for both electrons and cosmic rays. The X- and ![]() -ray
filaments also exhibit some different features in the case of an
Alfvènic-like relaxed turbulence. The low energy particles producing
the synchrotron photons in the interval 0.5-1 keV and the
-ray
filaments also exhibit some different features in the case of an
Alfvènic-like relaxed turbulence. The low energy particles producing
the synchrotron photons in the interval 0.5-1 keV and the ![]() -ray photons
in the 10-30 GeV band, respectively, do extend to shorter
distances behind the shock (electrons having energy
-ray photons
in the 10-30 GeV band, respectively, do extend to shorter
distances behind the shock (electrons having energy ![]() TeV).
This can be understood by the effect of the resonant component of the
magnetic field b in Eq. (6).
At a given downstream location, particles with
energies
TeV).
This can be understood by the effect of the resonant component of the
magnetic field b in Eq. (6).
At a given downstream location, particles with
energies ![]() do interact with a lower number of modes than in the advected case.
This effect is caused by high wave number modes relaxing over shorter
distances than lower wave number modes within the same turbulence
spectrum. Compared to the advected case, more low energy particles
experiencing diffusive losses are lost than at highest energies (which
are also subject to diffusive losses). Particles of energy around a few
tens to hundreds of GeV are then confined to closer to the
shock and do not experience strong magnetic field variation: the
standard shock solution is then recovered in this domain. We verified
that the shock synchrotron spectrum cuts off at an energy close to
one keV.
do interact with a lower number of modes than in the advected case.
This effect is caused by high wave number modes relaxing over shorter
distances than lower wave number modes within the same turbulence
spectrum. Compared to the advected case, more low energy particles
experiencing diffusive losses are lost than at highest energies (which
are also subject to diffusive losses). Particles of energy around a few
tens to hundreds of GeV are then confined to closer to the
shock and do not experience strong magnetic field variation: the
standard shock solution is then recovered in this domain. We verified
that the shock synchrotron spectrum cuts off at an energy close to
one keV.
We also tested the solution in the case ![]() ,
i.e.,
,
i.e., ![]() .
No significant particle acceleration has been found as
diffusive losses dominate at low energy (see Fig. 8). The numerical
acceleration timescale is also found to be shorter than the theoretical
estimation which is consistent with particles only returning quickly to
the upstream medium after entering the downstream region, are able to
avoid massive diffusive losses. These simulations confirm the
conclusions drawn in Sect. 4.2.3.
.
No significant particle acceleration has been found as
diffusive losses dominate at low energy (see Fig. 8). The numerical
acceleration timescale is also found to be shorter than the theoretical
estimation which is consistent with particles only returning quickly to
the upstream medium after entering the downstream region, are able to
avoid massive diffusive losses. These simulations confirm the
conclusions drawn in Sect. 4.2.3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13022fg8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13022-09/Timg371.png)
|
Figure 8:
Same case as treated in Fig. 6 but with |
| Open with DEXTER | |
4.3.3 Solutions for turbulent dynamo amplification
The coherence length of the downstream turbulence entering the
evaluation of
![]() in Sect. 4.1.4
cannot be longer than the X-ray filament width, otherwise the condition
about the maximum CR diffusion coefficient upstream given by
Eq. (22)
would not be satisfied. This means that if a magnetic dynamo operates
downstream, then the growth scale length is
in Sect. 4.1.4
cannot be longer than the X-ray filament width, otherwise the condition
about the maximum CR diffusion coefficient upstream given by
Eq. (22)
would not be satisfied. This means that if a magnetic dynamo operates
downstream, then the growth scale length is
![]() .
The growing modes are restricted mostly to large scales,
i.e., to wave numbers close to
.
The growing modes are restricted mostly to large scales,
i.e., to wave numbers close to
![]() .
They are considered for the particles to contribute to the mean
magnetic field. The rapid increase in the magnetic field downstream to
values close to equipartition produces enhanced radiative losses and
thus much thinner filaments. We checked the effect by performing
simulations in which we added a mean magnetic field downstream of
values close to a few mGauss.
.
They are considered for the particles to contribute to the mean
magnetic field. The rapid increase in the magnetic field downstream to
values close to equipartition produces enhanced radiative losses and
thus much thinner filaments. We checked the effect by performing
simulations in which we added a mean magnetic field downstream of
values close to a few mGauss.
5 Discussion and summary
Young SNRs are strong particle accelerators, as illustrated by the
presence of thin X-ray filaments. In these astrophysical objects, the
X-ray emission is produced by synchrotron radiation, involving
particles whose maximal energy is higher than tens of TeV and magnetic
field strengths behind the shock of a few hundred ![]() Gauss (Parizot et al. 2006).
This work has extended the study undertaken by Parizot et al. (2006)
of the physical properties of both the turbulence and transport
coefficients in the same sample of five young SNR. We have
included the turbulence compression at the shock front, the possibility
of particle reacceleration in the downstream region of the shock, and
the relaxation of the magnetic fluctuations downstream (Pohl et al. 2005). We
have also described the generation of magnetic fluctuations in the
shock precursor for the two regimes of the streaming instability (Pelletier et al. 2006).
This work has been developed in the same framework as Lagage & Cesarsky (1983)
but adapted to the case of amplified magnetic fields around SNR,
although the maximum CR energy has not been fully investigated
here. We have developed a numerical scheme based on the coupling
between the equations of magnetohydrodynamics and a kinetic scheme
handling the calculation of the electron particle distribution
function. The scheme involves a set of stochastic differential
equations (SDE) described elsewhere (Casse & Marcowith 2003,2005). The
SDEs have been adapted to account for the discontinuity in the
diffusion coefficients properly using a skew Brownian motion (see also Zhang 2000). The following
conclusions can be made:
Gauss (Parizot et al. 2006).
This work has extended the study undertaken by Parizot et al. (2006)
of the physical properties of both the turbulence and transport
coefficients in the same sample of five young SNR. We have
included the turbulence compression at the shock front, the possibility
of particle reacceleration in the downstream region of the shock, and
the relaxation of the magnetic fluctuations downstream (Pohl et al. 2005). We
have also described the generation of magnetic fluctuations in the
shock precursor for the two regimes of the streaming instability (Pelletier et al. 2006).
This work has been developed in the same framework as Lagage & Cesarsky (1983)
but adapted to the case of amplified magnetic fields around SNR,
although the maximum CR energy has not been fully investigated
here. We have developed a numerical scheme based on the coupling
between the equations of magnetohydrodynamics and a kinetic scheme
handling the calculation of the electron particle distribution
function. The scheme involves a set of stochastic differential
equations (SDE) described elsewhere (Casse & Marcowith 2003,2005). The
SDEs have been adapted to account for the discontinuity in the
diffusion coefficients properly using a skew Brownian motion (see also Zhang 2000). The following
conclusions can be made:
- 1.
- The compression of turbulent scales at the shock front does not deeply modify the efficiency of shock acceleration. The conclusions addressed by Parizot et al. (2006) are found to be robust in the case of a downstream, advected, magnetic field, young SNRs exhibiting X-ray filaments do accelerate particles to at most PeV energies.
- 2.
- For the various regimes of streaming instability occurring
in the shock precursor, the SNRs contained in our sample are expected
to generate magnetic fields up to a few hundred
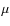 Gauss.
For shock velocities of a few hundred
thousand km s-1, the level of
fluctuations tends to be shared by the non-resonant and the resonant
regimes. The resonant modes may contribute to some particle
reacceleration downstream. However, the amount of reacceleration cannot
be too large, otherwise the shock particle spectrum would be harder and
the X-ray filament width would be larger than observed. This provides
an observational constraint of the number of resonant modes present
downstream of the shock front. The fate of non-resonant modes generated
upstream still requires consideration.
Gauss.
For shock velocities of a few hundred
thousand km s-1, the level of
fluctuations tends to be shared by the non-resonant and the resonant
regimes. The resonant modes may contribute to some particle
reacceleration downstream. However, the amount of reacceleration cannot
be too large, otherwise the shock particle spectrum would be harder and
the X-ray filament width would be larger than observed. This provides
an observational constraint of the number of resonant modes present
downstream of the shock front. The fate of non-resonant modes generated
upstream still requires consideration.
- 3.
- We have presented calculations of the projected and
deprojected X- and
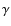 -ray
filaments, each one in two specific wavebands. For the separation
between the X and
-ray
filaments, each one in two specific wavebands. For the separation
between the X and 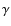 -ray peak emission is found to
be far below any
-ray peak emission is found to
be far below any 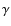 -ray
mission resolution capabilities when observing young SNR, some
detailed observations could be undertaken for more extended objects
such as Vela Junior.
-ray
mission resolution capabilities when observing young SNR, some
detailed observations could be undertaken for more extended objects
such as Vela Junior.
- 4.
- For relaxed turbulence occurring in the downstream region,
our conclusions are the following:
- When the magnetic relaxation scale varies as
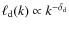 ,
a magnetic turbulence (whose power-law index is
,
a magnetic turbulence (whose power-law index is 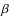 )
is able to provide suitable conditions giving rise to an efficient
particle acceleration if
)
is able to provide suitable conditions giving rise to an efficient
particle acceleration if
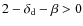 .
.
- We have tested several relaxation processes obtaining
various values of
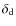 .
When Kolmogorov damping occurs in a Bohm diffusion regime,
it appears unlikely to produce strong acceleration in the
framework of relaxation limited filaments when accounting for the
complete dynamics of the turbulent spectrum. On the other hand, the
Alfvén and fast magneto-sonic cascades provide suitable conditions
giving birth to particle acceleration while being able to match all
observational features of X-ray filaments. In this context, we
have found that the maximum energy particle (both for electrons and
cosmic rays) cannot be much higher than
a few tens of TeV.
.
When Kolmogorov damping occurs in a Bohm diffusion regime,
it appears unlikely to produce strong acceleration in the
framework of relaxation limited filaments when accounting for the
complete dynamics of the turbulent spectrum. On the other hand, the
Alfvén and fast magneto-sonic cascades provide suitable conditions
giving birth to particle acceleration while being able to match all
observational features of X-ray filaments. In this context, we
have found that the maximum energy particle (both for electrons and
cosmic rays) cannot be much higher than
a few tens of TeV.
- The magnetic field strengths downstream of the shock
cannot be much higher than
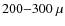 Gauss,
otherwise radiative losses would control the X-ray filament width.
Gauss,
otherwise radiative losses would control the X-ray filament width.
- For the supernova remnants SN1006 and
RXJ 1713-3946.5, none of the various turbulence relaxation
processes considered in the present paper have been able to provide
efficient particle acceleration and match the corresponding
observational features. It seems that only the youngest SNRs (
 yr) of our sample
may exhibit X-ray filaments controlled by downstream turbulence
relaxation.
yr) of our sample
may exhibit X-ray filaments controlled by downstream turbulence
relaxation.
- The normalization (i.e., factor
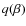 )
of the spatial diffusion coefficient should remain close to unity to
avoid massive particle diffusive losses, leading to a drop of the Fermi
acceleration efficiency. A genuine Bohm diffusion regime is
then required if magnetic turbulence relaxation is to occur in the
downstream region of the shock.
)
of the spatial diffusion coefficient should remain close to unity to
avoid massive particle diffusive losses, leading to a drop of the Fermi
acceleration efficiency. A genuine Bohm diffusion regime is
then required if magnetic turbulence relaxation is to occur in the
downstream region of the shock.
- When the magnetic relaxation scale varies as
The authors thank F. Acero, E. Parizot, G. Pelletier for their valuable comments. V. Tatischeff is thanked for his careful reading of the manuscript and many suggestions. This work work has been supported by the French National Research Agency project AccFermi.
Appendix A: Magnetic field profile produced by the resonant instability
The amplification factor related to the resonant instability
depends on the amplification factor produced by the non-resonant
instability (Pelletier
et al. 2006, Eq. (34)) and is
given by
where
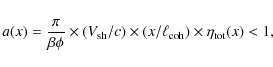
The exact integration of Eq. (A.1) involves a difference between two exponential integral:
The above equation is implicit because the total magnetic field is hidden in k* and
At distances
![]() where
where ![]() ,
we approximate
,
we approximate
![]() ,
,
![]() is
the Euler constant. At a first approximation, within
the precursor
is
the Euler constant. At a first approximation, within
the precursor ![]() scales
as
scales
as
![]() .
.
Appendix B: Derivation of the shock particle distribution function
The steady-state general 1D Fokker-Planck equation is given by
Where the upstream medium is defined by
where
The energy flux carried by the relativistic particle has to be conserved throughout the shock front, namely for
![\begin{displaymath}%
\left [D\frac{\partial f}{\partial x} + u\frac{\partial f}{\partial \ln{p^3}}
\right ]_{-\upsilon}^{\upsilon} = 0.
\end{displaymath}](/articles/aa/full_html/2010/07/aa13022-09/img404.png)
|
(B.4) |
The spatial derivatives of f are evaluated using Eq. (B.2), which produces a differential equation for
Appendix C: Particle acceleration and multi-scale simulations
This section presents the numerical framework used to simulate both the supernova thermal plasma evolution and the relativistic charged particles transport. As detailed in Casse & Marcowith (2003) and Casse & Marcowith (2005), the background fluid and large-scale magnetic field are calculated using the magnetohydrodynamics code VAC for Versatile Advection Code (Tóth 1996). The simulations are performed using a 1D spherical symmetry, where the evolution of the supra-thermal electrons and nuclei are calculated using the stochastic differential equations (SDE) formalism (Krülls & Achterberg 1994). The numerical description of supra-thermal particle transport is crucially dependent on the ability of the MHD code VAC to capture the shock structure. To obtain the sharpest shock front possible, we used the TVD-MUSCL scheme coupled with a Roe-type approximate Riemann solver (Tóth & Odstrcil 1996).
Section C.1 briefly reports on the MHD-SDE schemes used to model a 1D spherical SN remnant expansion. In particular, Sects. C.2 and C.2.1 discuss at length the stochastic differential Euler schemes with spatially dependent diffusion coefficients and their application to the diffusive shock acceleration problem. Section C.2.2 describes the shock capturing procedure that efficiently couple the MHD and SDE schemes.
C.1 Supernova remnant modelling
The time evolution of the thermal magnetised plasma is fully controlled by the MHD equations providing mass, momentum, and energy conservation as well as electromagnetic field induction, namely
The density
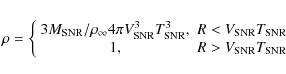
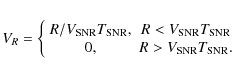
For each run, the physical quantities entering the problem are normalised by the known mass ejected
To test the ability of our simulation to model the propagation of
SNR shock, we simulated the long-term evolution of a
SNR blast wave corresponding to the previous initial set-up
where we defined the SNR parameter to
![]() ,
,
![]() ,
,
![]() and
and
![]() .
The results were found to reproduce the corresponding analytical
solution in Truelove & McKee
(1999) quite accurately. In particular, both the
free expansion and Sedov self-similar regimes were obtained, the
transition regime occurring at the expected Sedov time for this
simulation of
.
The results were found to reproduce the corresponding analytical
solution in Truelove & McKee
(1999) quite accurately. In particular, both the
free expansion and Sedov self-similar regimes were obtained, the
transition regime occurring at the expected Sedov time for this
simulation of ![]() .
.
C.2 Kinetic approach
The transport of relativistic particles (with velocities much larger
than the fluid speed) near the shock front is governed by a
Fokker-Planck equation when these particles resonate with the
turbulence and enter a diffusion regime. The related kinetic
equation is
where F=R2p2f is related to the distribution function f in terms of the spherical radius R and particle momentum
For electrons, the losses are produced by synchrotron cooling.
The cooling timescale
![]() is
is
For protons (or ions), the losses are produced by the generation of magnetic fluctuations and are a priori limited to the upstream medium (in the downstream flow the particle distribution is isotropic). The cooling timescale is adapted from Marcowith et al. (2006) their Eq. (13)
where P(p) is the rate of energy radiated by a relativistic particle
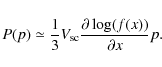
|
(C.5) |
The scattering centre velocity is close to the local Alfvén velocity, i.e.,
Stochastic particle acceleration is represented by the energy diffusion
coefficient ![]() ,
which is related to spatial diffusion (where
,
which is related to spatial diffusion (where ![]() is the local Alfvèn velocity).
is the local Alfvèn velocity).
C.2.1 Stochastic differential equations
As shown by Krülls & Achterberg (1994), this Fokker-Planck equation is equivalent to a set of two SDEs that can be written as
where Wi are Wiener processes for which
A shock discontinuity may lead, according to the MHD
Rankine-Hugoniot conservation laws,
to a discontinuous magnetic field at the shock front.
Depending on the diffusion regime affecting relativistic particles,
this may lead to discontinuous diffusion coefficients that can
be written DR=DR,C +
![]() ,
where the first term is a continuous function. In this case,
the usual Euler schemes are no longer valid, in contrast to the studies
of Krülls & Achterberg (1994),
Casse & Marcowith (2003),
van der Swaluw & Achterberg (2004),
and Casse & Marcowith (2005).
As shown by Zhang (2000),
it is possible to overcome this problem by employing a skew
Brownian motion where
an asymmetric shock crossing probability is considered.
In this framework, the spatial stochastic equation
becomes
,
where the first term is a continuous function. In this case,
the usual Euler schemes are no longer valid, in contrast to the studies
of Krülls & Achterberg (1994),
Casse & Marcowith (2003),
van der Swaluw & Achterberg (2004),
and Casse & Marcowith (2005).
As shown by Zhang (2000),
it is possible to overcome this problem by employing a skew
Brownian motion where
an asymmetric shock crossing probability is considered.
In this framework, the spatial stochastic equation
becomes
where
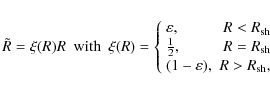
and where
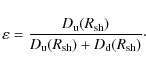
|
(C.7) |
Equation (C.6) can be solved using an Euler scheme where the stochastic variable WR is computed with Monte Carlo methods. In contrast to the study of Zhang (2000), realistic diffusion coefficients are likely to depend on particle energy. In this case, we have to consider the amount of energy
| (C.8) |
We note that this skew Brownian motion approach is valid only if shock curvature terms are negligible, i.e.,
The previous implicit calculation is valid for any diffusion regime provided that second-order Fermi acceleration is negligible. In the opposite case, we then have to step back into an explicit scheme to take into account the skew Brownian motion. Following Zhang (2000), the energy gained by a particle is
where
C.2.2 Kinetic description of MHD shock waves
The SDE formalism is useful for modelling the transport of relativistic
test particles a non-relativistic background fluid since it provides
both the spatial and energetic distribution of particles. Nevertheless
one drawback of this method does exist: the shock thickness.
The SDE algorithm is based on the use of fluid velocity
divergence to mimic particle acceleration. The MHD code
provides the velocity field at discrete locations on the grid so
that
![]() may
be obtained by means of linear interpolation. The most efficient
MHD code cannot reproduce shocks as sharp discontinuities but
rather displays velocity and density variations over two or three
cells. This is very important for kinetic computations since particles
with diffusion coefficients for which the diffusive step is small
compared to the MHD shock thickness will see the shock as
an adiabatic compression, leading to softer energy spectrum.
may
be obtained by means of linear interpolation. The most efficient
MHD code cannot reproduce shocks as sharp discontinuities but
rather displays velocity and density variations over two or three
cells. This is very important for kinetic computations since particles
with diffusion coefficients for which the diffusive step is small
compared to the MHD shock thickness will see the shock as
an adiabatic compression, leading to softer energy spectrum.
In previous work (see e.g., Casse & Marcowith 2003; Krülls &
Achterberg 1994), it was shown that the
SDE formalism was able to describe accurately the transport of
particles with diffusion coefficients greater than
![]() ,
where
,
where
![]() is typically the cell size in
the MHD code. This constraint
greatly reduced the range of applications of this method.
To overcome this problem, we designed a SDE algorithm
in which the
is typically the cell size in
the MHD code. This constraint
greatly reduced the range of applications of this method.
To overcome this problem, we designed a SDE algorithm
in which the
![]() is
no longer calculated locally but we instead integrate the term
is
no longer calculated locally but we instead integrate the term
![]() in Eq. (C.9),
where the velocity is given as
in Eq. (C.9),
where the velocity is given as ![]() or
or ![]() depending on the shock position. In our new approach,
the MHD code now provides the shock position and the
compression ratio r so that we deduce the
value of the fluid by considering the shock as
infinitely thin.
depending on the shock position. In our new approach,
the MHD code now provides the shock position and the
compression ratio r so that we deduce the
value of the fluid by considering the shock as
infinitely thin.
References
- Acero, F., Ballet, J., & Decourchelle, A. 2007, A&A, 475, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F. A., Akhperjanian, A. G., Aye, K.-M., et al. 2004, Nature, 432, 75 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F. A., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, Nature, 432, 75 [Google Scholar]
- Aharonian, F. A., Akhperjanian, A. G., Barres de Almeida, U., et al. 2008, A&A, 488, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 664, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Amato, E., & Blasi, P. 2009, MNRAS, 392, 1591 [NASA ADS] [CrossRef] [Google Scholar]
- Ballet, J. 2006, AdSpR, 37, 1902 [Google Scholar]
- Bamba, A., Yamazaki, R., & Hiraga, J. S. 2005a, ApJ, 632, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Bamba, A., Yamazaki, R., Yoshida, T., & Koyama, K. 2005b, ApJ, 621, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Bamba, A., Yamazaki, R., Yoshida, T., Terasawa, T., & Koyama, K. 2006, AdSpR, 37, 1439 [Google Scholar]
- Bell, A., & Lucek, S. 2001, MNRAS, 321, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 2004, MNRAS, 353, 550 [Google Scholar]
- Berezhko, E. G. 2008, Adv. Sp. Res., 41, 429 [Google Scholar]
- Berezhko, E. G., & Ellison, D. C. 1999, ApJ, 526, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Berezhko, E. G., Elshin, V. K., & Ksenofontov, L. T. 1996, JETP, 82, 1 [Google Scholar]
- Berezhko, E. G., Ksenofontov, L. T., & Völk, H. J. 2003a, A&A, 412, 11 [Google Scholar]
- Berezhko, E. G., Pühlhofer, G., & Völk, H. J. 2003b, A&A, 400, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berezhko, E. G., Ksenofontov, L. T., & Völk, H. J. 2006, A&A, 452, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, RMP, 42, 237 [Google Scholar]
- Bykov, A. 2001, SSR, 99, 321 [Google Scholar]
- Bykov, A. 2004, AdSpR, 33, 366 [Google Scholar]
- Bykov, A., & Toptyghin, I. N. 2005, AstL, 31, 748 [Google Scholar]
- Campeanu, A., & Schlickeiser, R. 1992, A&A, 263, 413 [NASA ADS] [Google Scholar]
- Candia, J., & Roulet, E. 2004, JCAP, 10, 007 [Google Scholar]
- Caprioli, D., Blasi, P., Amato, E., & Vietri, M. 2008, ApJ, 679, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D., Blasi, P., & Amato, E. 2009, MNRAS, 396, 2065 [NASA ADS] [CrossRef] [Google Scholar]
- Cassam-Chenaï, G., Decourchelle, A., Ballet, J., et al. 2004, A&A, 414, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassam-Chenaï, G., Hughes, J. P., Ballet, J., & Decourchelle, A. 2007, 665, 315 [Google Scholar]
- Casse, F., & Marcowith, A. 2003, A&A, 404, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casse, F., & Marcowith, A. 2005, Aph, 23, 31 [Google Scholar]
- Casse, F., Lemoine, M., & Pelletier, G. 2002, Phys. Rev. D, 65, 3002 [NASA ADS] [Google Scholar]
- Diamond, P. H., & Malkov, M. A. 2007, ApJ, 654, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O'C. 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., & Vladimirov, A. 2008, ApJ, 673, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Sridhar, S. 1995, ApJ, 438, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Giacalone, J., & Jokipii, J. R. 1999, ApJ, 520, 204 [Google Scholar]
- Gotthelf, E. V., Koralesky, B., Rudnick, L., et al. 2001, ApJ, 522, 39 [Google Scholar]
- Hughes, J. P. 2000, ApJ, 545, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang, U., Decourchelle, A., Holt, S. S., & Petre, R. 2002, ApJ, 581, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, H., & Jones, T. W. 2007, Aph, 28, 232 [Google Scholar]
- Katz, B., & Waxman, E. 2008, JCAP, 1, 18 [Google Scholar]
- Katz, B., Keshet, U., & Waxman, E. 2007, ApJ, 655, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Krülls, W. M., & Achterberg, A. 1994, A&A, 286, 314 [NASA ADS] [Google Scholar]
- Lagage, P.-O., & Cesarsky, C. J. 1983, A&A, 118, 223 [NASA ADS] [Google Scholar]
- Lucek, S., & Bell, A. R. 2000, MNRAS, 314, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Malkov, M. A., & Diamond, P. H. 2006, ApJ, 642, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Marcowith, A., & Kirk, J. G. 1999, A&A, 347, 291 [Google Scholar]
- Marcowith, A., Lemoine, M., & Pelletier, G. 2006, A&A, 453, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacKenzie, J. F., & Völk, H. J. 1982, A&A, 116, 191 [NASA ADS] [Google Scholar]
- Morlino, G., Amato, E., & Blasi, P. 2009, MNRAS, 392, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Niemiec, J., Pohl, M., Stroman, T., & Nishikawa, K.-I. 2008, ApJ, 684, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Ostrowski, M., & Schlickeiser, R. 1996, SoPh, 167, 3810 [Google Scholar]
- Parizot, E., Marcowith, A., Ballet, J., & Gallant, Y. A. 2006, A&A, 453, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pohl, M., Yan, H., & Lazarian, A. 2005, ApJ, 626, 101 [Google Scholar]
- Pelletier, G., Lemoine, M., & Marcowith, A. 2006, A&A, 453, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pelletier, G., Lemoine, M., & Marcowith, A. 2009, MNRAS, 393, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Ptuskin, V. S., & Zirakachvili, V. N. 2003, A&A, 403, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynolds, S. P. 1998, ApJ, 493, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Reville, B., Kirk, J. G., Duffy, P., & O'Sullivan, S. 2007, A&A, 475, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reville, B., O'Sullivan, S., Duffy, P., & Kirk, J. G. 2008, MNRAS, 386, 589 [Google Scholar]
- Riquelme, M. A., & Spitkovsky, A. 2009, ApJ, 694, 626 [Google Scholar]
- Rho, J., Dyer, K. K., Borkowski, K., & Reynolds, S. P. 2002, ApJ, 581, 1116 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A. 2009, Aph, 31, 273 [Google Scholar]
- Skilling, J. 1975, MNRAS, 172, 557 [NASA ADS] [CrossRef] [Google Scholar]
- van der Swaluw, E., & Achterberg, A. 2004, A&A, 421, 1021 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takahashi, T., Tanaka, T., Uchiyama, Y., et al. 2008, PASJ, 60, 131 [Google Scholar]
- Tóth, G. 1996, Astrophys. Lett. Commun., 34, 245 [NASA ADS] [Google Scholar]
- Tóth, G., & Odstrcil, D. 1996, J. Comp. Phys., 128, 82 [Google Scholar]
- Truelove, J. K., & McKee, C. F. 1999, ApJS, 120, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Uchiyama, Y., Aharonian, F. A., & Takahashi, T. 2003, A&A, 400, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vainio, R., & Schlickeiser, R. 1999, A&A, 343, 303 [NASA ADS] [Google Scholar]
- Vink, J. 2004, Nucl. Phys. B Proc. Supp., 132, 21 [Google Scholar]
- Vink, J., & Laming, J. M. 2003, ApJ, 584, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J., Berezhko, E. G., & Ksenofontov, L. T. 2005, A&A, 433, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vladimirov, A., Ellison, D. C., & Bykov, A. 2006, ApJ, 652, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Vladimirov, A., Ellison, D. C., & Bykov, A. 2008, ApJ, 688, 1094 [Google Scholar]
- Weisskopf, M. C., & Hughes, J. P. 2006, in Astrophysics update 2, ed. J. W. Mason (Springer Praxis Books) [Google Scholar]
- Zhang, M. 2000, ApJ, 541, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V. N., & Aharonian, F. 2007, A&A, 465, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zirakashvili, V. N., & Ptuskin, V. S. 2008, ApJ, 678, 939 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... shock
![[*]](/icons/foot_motif.png)
- The Bohm diffusion coefficient is obtained when the
particle mean free path is equal to its Larmor radius
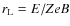 ,
i.e.,
,
i.e., 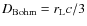 .
.
- ... ISM
![[*]](/icons/foot_motif.png)
- The density
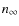 is usually the ion density, but when the coupling between ion and
neutrals is effective it must also involve the density of neutrals.
is usually the ion density, but when the coupling between ion and
neutrals is effective it must also involve the density of neutrals.
- ...
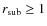 )
)![[*]](/icons/foot_motif.png)
- We make a distinction between the compression ratio at the
sub-shock (
 )
and the total shock compression ratio
)
and the total shock compression ratio 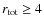 .
In the case of weakly modified shocks, we have
.
In the case of weakly modified shocks, we have 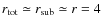 .
In the case of strongly CR modified shocks, one obtains
.
In the case of strongly CR modified shocks, one obtains 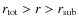 .
If the sole adiabatic heating of the precursor is
considered, values
.
If the sole adiabatic heating of the precursor is
considered, values  and
and 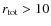 are possible (see e.g., Berezhko
& Ellison 1999). If a substantial
gas heating in the precursor is produced for instance by the absorption
of Alfvèn waves, the total compression ratio cannot
be much higher than 10, under ISM conditions considered above (Bykov 2004).
In a strongly modified shock, the most energetic
electrons producing the X-ray filaments have energy
are possible (see e.g., Berezhko
& Ellison 1999). If a substantial
gas heating in the precursor is produced for instance by the absorption
of Alfvèn waves, the total compression ratio cannot
be much higher than 10, under ISM conditions considered above (Bykov 2004).
In a strongly modified shock, the most energetic
electrons producing the X-ray filaments have energy 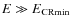 and do experience a compression ratio close to
and do experience a compression ratio close to
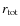 .
This value will be used in the following estimations. Values of
.
This value will be used in the following estimations. Values of 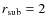 and
and 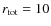 are accepted in this work in the case of strongly CR modified
shock.
are accepted in this work in the case of strongly CR modified
shock.
- ... anymore
![[*]](/icons/foot_motif.png)
- Excepted at the highest energies.
- ...
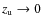
![[*]](/icons/foot_motif.png)
- Again, a correct way to handle this effect is to account properly for the particle back-reaction on the flow.
- ... energy
![[*]](/icons/foot_motif.png)
- All quantities with an index M are to be taken at the maximum particle energy.
- ... motion
![[*]](/icons/foot_motif.png)
- The factor 6 in the denominator of Eq. (38), which appears to be the random walk along the radius of a sphere is composed of 3 independent random walks along each cartesian coordinates.
- ...

![[*]](/icons/foot_motif.png)
- The dependence of
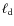 on the wavelength
on the wavelength 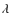 is a priori
valid only up to
is a priori
valid only up to 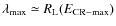 and, we should strictly not expect the scaling of
and, we should strictly not expect the scaling of
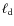 to extend beyond
to extend beyond
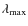 .
Above
.
Above 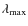 ,
the diffusion coefficient increases as
,
the diffusion coefficient increases as
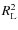 and particle acceleration continues to proceed beyond
and particle acceleration continues to proceed beyond
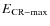 but the number of particle accelerated and the turbulence energy
density both rapidly drop. For this reason, we
consider
but the number of particle accelerated and the turbulence energy
density both rapidly drop. For this reason, we
consider
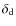 to be controlled by the kernel of the damping rate above
to be controlled by the kernel of the damping rate above
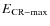 as,
e.g., in the case of the Kolmogorov damping
as,
e.g., in the case of the Kolmogorov damping 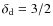 in this energy regime.
in this energy regime.
- ...
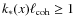
![[*]](/icons/foot_motif.png)
- As discussed in Sect. 2.1.1, we assume the same coherence length over the whole precursor.
All Tables
Table 1: Summary of the notations used in this article to denote the various physical quantities and parameters involved in our description of high energy particle yield in supernova remnants (SNR).
Table 2:
Inferred values of the downstream magnetic field amplitude and
synchrotron
photon cut-off energy in the case of an advection-dominated
rim where Bohm diffusion regime prevails (![]() and
and ![]() ).
).
Table 3: Analytical estimates of the downstream magnetic field value in the context of diffusive-loss-dominated SNRs rims.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13022fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13022-09/Timg186.png)
|
Figure 1: Shock front energy spectra of relativistic electrons provided by multi-scale simulations where the MHD part of the simulation mimics the behavior of a SNR blast wave. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13022fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13022-09/Timg203.png)
|
Figure 2: Energy spectrum of relativistic electrons at the shock front given by MHD-SDE simulations in the conditions of the Kepler SNR. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13022fg3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13022-09/Timg204.png)
|
Figure 3:
Same plots than in Fig. 2
but in the G347-0.5 SNR (velocity of the shock is 4 |
| Open with DEXTER | |
| In the text | |
| |
Figure 4:
The unprojected and projected X-ray and |
| Open with DEXTER | |
| In the text | |
| |
Figure 5:
The unprojected and projected X-ray and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13022fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13022-09/Timg365.png)
|
Figure 6: Energy spectrum of relativistic electrons at the shock front given by MHD-SDE simulations in the conditions of the Kepler SNR (see Fig. 2 for details). |
| Open with DEXTER | |
| In the text | |
| |
Figure 7:
The unprojected and projected X-ray and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13022fg8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13022-09/Timg371.png)
|
Figure 8:
Same case as treated in Fig. 6 but with |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



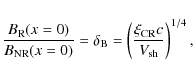
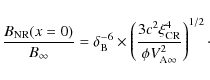
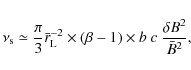
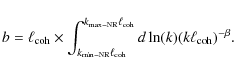
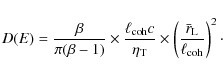
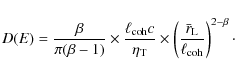
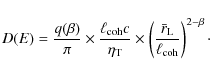
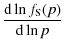
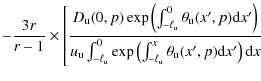
![$\displaystyle + \ \left.\frac{D_{\rm d}(0,p) \exp\left(-\int_0^{\rm\ell_{\rm d}...
...x^{\rm\ell_{\rm d}}\theta_{\rm d}(x',p) {\rm d}x'\right) {\rm d}x} \right]\cdot$](/articles/aa/full_html/2010/07/aa13022-09/img126.png)
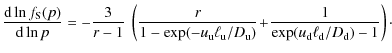
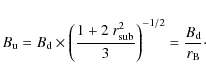
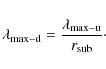
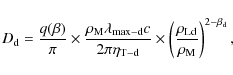
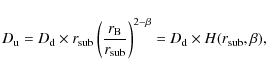
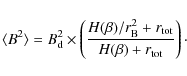
![\begin{displaymath}%
t_{\rm {acc}}(E) = {3 r^2 \over r-1} \ {D_{\rm d}(E) \over ...
...rm {sh}}^2}
\times \left[{H(r,\beta)\over r(E)} +1\right]\cdot
\end{displaymath}](/articles/aa/full_html/2010/07/aa13022-09/img150.png)
![\begin{displaymath}%
E_{\rm\gamma -cut} \simeq [0.875~{\rm\rm {keV}}] \times \fr...
...\bar{q} \bar{y}(r_{\rm tot}) (1 + H/r_{\rm tot} r^2_{\rm B})},
\end{displaymath}](/articles/aa/full_html/2010/07/aa13022-09/img151.png)
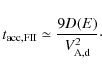
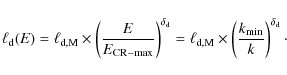
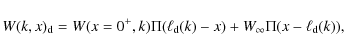
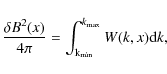
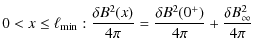
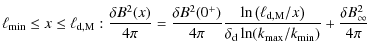
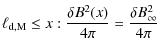
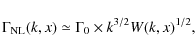
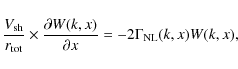
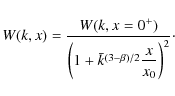
![\begin{displaymath}%
x_{\rm0-K} \simeq [300 \times \lambda_{\rm max,d}] \times {...
...igma}^{1/2} \over \bar{r}_{\rm tot}} \times B_{\rm d,-4}^{-1}.
\end{displaymath}](/articles/aa/full_html/2010/07/aa13022-09/img249.png)
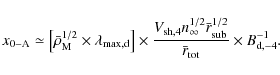
![\begin{displaymath}%
t_{\rm acc}(E)\! \simeq\! [7~\rm {yrs}] \times \bar{\rho}_{...
...s \left({\rho_{\rm d}(E) \over \rho_{\rm M}}\right)^{2-\beta},
\end{displaymath}](/articles/aa/full_html/2010/07/aa13022-09/img285.png)
![\begin{displaymath}%
t_{\rm adv}(E) = {\ell_{\rm d}(E) \over V_{\rm d}} \simeq [4~\rm {yrs}]\times \bar{r} \ V_{\rm sh,4}^{-1} \ell_{\rm d-2}(E).
\end{displaymath}](/articles/aa/full_html/2010/07/aa13022-09/img288.png)
![$\displaystyle {\ell_{\rm d}(E)^2 \over 6 D_{\rm d}(E)} \simeq [0.3~\rm {yrs}]$](/articles/aa/full_html/2010/07/aa13022-09/img290.png)
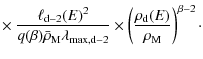
![\begin{displaymath}%
t_{\rm syn}(E) \simeq [1.25 \times 10^3~\rm {yrs}] \times E_{\rm TeV}^{-1} \times B_{\rm
d-4}^{-2} \times f_{\rm sync},
\end{displaymath}](/articles/aa/full_html/2010/07/aa13022-09/img292.png)
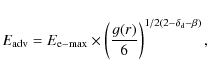
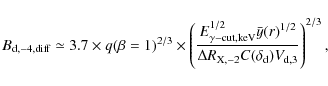
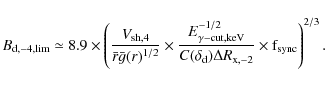
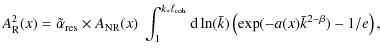
![$\displaystyle %
A_{\rm R}(x) \propto \left[A_{\rm NR}(x)
~ (-Ei(-a(x))/(2-\beta)-\ln(k_*(x))/\exp(1)) \right]^{1/2}.$](/articles/aa/full_html/2010/07/aa13022-09/img385.png)
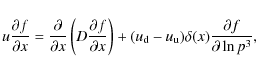
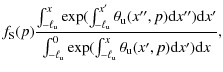
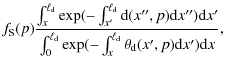
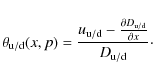
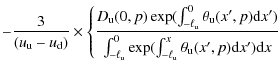
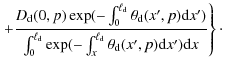
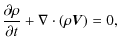
![$\displaystyle \frac{\partial (\rho {\vec V})}{\partial t} + \nabla \cdot [ \rho {\vec V}{\vec V}+ p_{\rm tot} I- {\vec B}{\vec B}/\mu_o]=0,$](/articles/aa/full_html/2010/07/aa13022-09/img408.png)