| Issue |
A&A
Volume 512, March-April 2010
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913403 | |
| Published online | 23 March 2010 | |
Dust properties of protoplanetary disks in the Taurus-Auriga star forming region from millimeter wavelengths
L. Ricci1 - L. Testi1,2 - A. Natta2 - R. Neri3 - S. Cabrit4 - G. J. Herczeg5
1 - European Southern Observatory,
Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
2 - INAF - Osservatorio Astrofisico di Arcetri, Largo Fermi 5, 50125 Firenze, Italy
3 - Institut de Radioastronomie Millimétrique, 300 rue de la Piscine, 38406 Saint Martin d'Hères, France
4 - LERMA, UMR 8112 du CNRS, Observatoire de Paris, 61 Av. de l'Observatoire, 75014 Paris, France
5 - Max Planck Institut fur Extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany
Received 4 October 2009 / Accepted 14 December 2009
Abstract
We present the most sensitive 3 mm-survey to date of protoplanetary
disks carried out in the Taurus-Auriga star forming region (average rms
of about 0.3 mJy), using the IRAM PdBI. With our high detection rate of
17/19 we provide the first detections at wavelengths longer than about
1 mm for 12 sources. This enables us to statistically study the mm SED
slopes and dust properties of faint disks and compare them to brighter
disks using a uniform analysis method.
With these new data and literature measurements at sub-millimeter and
millimeter wavelengths, we analyze the dust properties of a sample of
21 isolated
disks around T Tauri stars in the Taurus-Auriga star forming
region.
Together with the information about the disks' spatial extension from
sub/mm-mm interferometric studies, we derive from the observed
sub-mm/mm spectral energy distribution constraints on the dust opacity
law at these wavelengths, using two-layer flared disk models and a
self-consistent dust model that properly takes into account the
variation of the dust opacity with grain growth. We find evidence for
the presence of dust particles in the disk midplane that have grown to
sizes as large as at least 1 millimeter in all the disks of our sample,
confirming what was previously observed on smaller brighter objects.
This indicates that the dust coagulation from ISM dust to mm-sized
grains is a very fast process in protoplanetary disks, which appears to
occur before a young stellar object enters the class II evolutionary
stage. The amount of these large grains in the disk outer regions is
also found to be stationary throughout the whole class II evolutionary
stage, which indicates that mechanisms slowing down the dust inward
migration play an important role in the Taurus-Auriga protoplanetary
disks. Another result is that the spectral index between 1 and 3 mm for
the six faintest disks in our sample is on average smaller than for the
brighter disks, indicating either that these fainter yet unmapped disks
are spatially much less extended than the brighter spatially resolved
disks, or that fainter disks have typically larger dust grains in their
outer regions. Considering that these fainter disks are more
representative of the bulk of the disk population than the brighter
ones, this may have important consequences for the theories of
planetesimal formation and disk formation and evolution. Finally, we
investigate the relations between the derived dust properties, namely
dust mass and grain growth, and the properties of the central star,
like its mass, age and mass accretion rate.
Key words: protoplanetary disks - stars: pre-main sequence - planets and satellites: formation
1 Introduction
Circumstellar disks play a fundamental role in the physical processes involved in star and planet formation. In these systems part of the material (gas and dust) loses its angular momentum and accretes onto the central forming star, while another part of it may give birth to a planetary system. Although the content of dust is only a small fraction of the overall material in a circumstellar disk, dust grains are crucial elements in the early stages of planet formation. According to the core-accretion scenario (Safronov & Zvjagina 1969; Pollack et al. 1996), growth from an initial ISM population of submicrometer-sized dust grains to planetesimals of 1-100 km sizes is believed to be the key mechanism of early planet formation. These planetesimal ``embryos'' then continue to grow which leads to the formation of at least terrestrial-sized planets and possibly the cores of giant planets.
Observational evidence of grain growth from the ISM dust has
been obtained from a variety of techniques at different wavelengths.
Throop et al. (2001)
observed in the optical and near-infrared the translucent edge of the
114-426 protoplanetary disk in the Orion Nebula Cluster, and
derived from the extinction curve of the background nebular emission a
lower limit of a few microns for the dust grains in the far outer
regions of the disk, about 500 AU away from the central star.
Another method to probe the presence of large grains in the disk is
through the shape and intensity of the 10- and 20-![]() m
silicate features. The data indicate a broad variety of silicate
profiles, ranging from strongly peaked silicate bands and steeply
rising spectral energy distributions (SEDs) to ``boxy'' silicate
profiles and flatter SEDs (ISO, Malfait et al. 1998; Spitzer Space Telescope, Kessler-Silacci et al. 2006). The boxy features with low feature-to-continuum ratios are interpreted as grain growth to micron size (Bouwman et al. 2001).
m
silicate features. The data indicate a broad variety of silicate
profiles, ranging from strongly peaked silicate bands and steeply
rising spectral energy distributions (SEDs) to ``boxy'' silicate
profiles and flatter SEDs (ISO, Malfait et al. 1998; Spitzer Space Telescope, Kessler-Silacci et al. 2006). The boxy features with low feature-to-continuum ratios are interpreted as grain growth to micron size (Bouwman et al. 2001).
However, the techniques outlined so far can only probe dust grains as large as some ![]() m
in the disk surface layers. They are not sensitive to larger grains in
the disk midplane, the region in which planet formation is supposed to
occur. In order to probe larger grains in the midplane, observations at
millimeter wavelengths are needed.
Beckwith & Sargent (1991)
showed that T Tauri stars have shallow SEDs at sub-millimeter
wavelengths. Under the assumption of optically thin emission at these
frequencies, this implies a dust opacity dependence on wavelength (
m
in the disk surface layers. They are not sensitive to larger grains in
the disk midplane, the region in which planet formation is supposed to
occur. In order to probe larger grains in the midplane, observations at
millimeter wavelengths are needed.
Beckwith & Sargent (1991)
showed that T Tauri stars have shallow SEDs at sub-millimeter
wavelengths. Under the assumption of optically thin emission at these
frequencies, this implies a dust opacity dependence on wavelength (
![]() )
much flatter than in the ISM (
)
much flatter than in the ISM (
![]() ), which is naturally interpreted in terms of grain growth (see e.g. Draine 2006).
However, this interpretation of the disk SEDs is not unique, since the
same data can be explained by very small optically thick disks. To
break this degeneracy and sort out the effect of a potentially large
optical depth it is necessary to spatially resolve the disks to
determine their actual sizes. Furthermore, in this context observations
at millimeter wavelengths are very useful, since at these lower
frequencies the impact of optically thick disk inner regions to the
total emission is expected to be lower. Therefore, to actually probe
the dust properties in protoplanetary disks, one needs to combine the
determination of the sub-millimeter/millimeter SED with information on
the disk extension from high-angular resolution interferometric
observations (see e.g. Testi et al. 2001).
), which is naturally interpreted in terms of grain growth (see e.g. Draine 2006).
However, this interpretation of the disk SEDs is not unique, since the
same data can be explained by very small optically thick disks. To
break this degeneracy and sort out the effect of a potentially large
optical depth it is necessary to spatially resolve the disks to
determine their actual sizes. Furthermore, in this context observations
at millimeter wavelengths are very useful, since at these lower
frequencies the impact of optically thick disk inner regions to the
total emission is expected to be lower. Therefore, to actually probe
the dust properties in protoplanetary disks, one needs to combine the
determination of the sub-millimeter/millimeter SED with information on
the disk extension from high-angular resolution interferometric
observations (see e.g. Testi et al. 2001).
In the last years, several sub-mm/mm interferometric observations have
been carried out to investigate dust grain growth in protoplanetary
disks. Wilner et al. (2000)
resolved the disk around the TW Hya pre-main-sequence (PMS) star
at 7 mm using the Very Large Array (VLA). Extensive modeling
of the SED of this source has shown that the dust grains in the outer
parts of the TW Hya disk have grown to at least ![]() 1 cm (Calvet et al. 2002). An analogous result has been obtained for the disk around CQ Tau (Testi et al. 2003). More recently, Rodmann et al. (2006)
resolved ten disks in the Taurus-Auriga star forming region and found
clear evidence of grain growth in four of them. Lommen et al. (2007)
resolved one disk in Chamaeleon and four in Lupus with the
Submillimeter Array (SMA) at 1.4 mm and with the Australia
Telescope Compact Array (ATCA) at 3.3 mm, and found clear evidence
of dust grain growth to sizes of a few millimeters for four of them.
Finally Schaefer et al. (2009)
observed a sample of 23 low mass PMS stars (with spectral types of K7
and later) in Taurus-Auriga at 1.3 mm and 2.6 mm with the
Plateau de Bure Interferometer (PdBI); they detected only eight sources
at 1.3 mm and six at 2.6 mm, and found evidence of grain
growth for the three disks that they could spatially resolve.
1 cm (Calvet et al. 2002). An analogous result has been obtained for the disk around CQ Tau (Testi et al. 2003). More recently, Rodmann et al. (2006)
resolved ten disks in the Taurus-Auriga star forming region and found
clear evidence of grain growth in four of them. Lommen et al. (2007)
resolved one disk in Chamaeleon and four in Lupus with the
Submillimeter Array (SMA) at 1.4 mm and with the Australia
Telescope Compact Array (ATCA) at 3.3 mm, and found clear evidence
of dust grain growth to sizes of a few millimeters for four of them.
Finally Schaefer et al. (2009)
observed a sample of 23 low mass PMS stars (with spectral types of K7
and later) in Taurus-Auriga at 1.3 mm and 2.6 mm with the
Plateau de Bure Interferometer (PdBI); they detected only eight sources
at 1.3 mm and six at 2.6 mm, and found evidence of grain
growth for the three disks that they could spatially resolve.
In this paper we present our analysis on 21 protoplanetary
disks around T Tauri stars in the Taurus-Auriga
star forming region without stellar companions in the range of
0.05''-3.5''. For eleven of these objects, mainly faint disks with
![]() mJy, we have obtained new data at
mJy, we have obtained new data at ![]() 3 mm with the Plateau de Bure Interferometer
3 mm with the Plateau de Bure Interferometer![]() (hereafter PdBI) with an average rms
of about 0.3 mJy. Together with the data already present in the
literature at sub/mm- and mm-wavelengths, and with the information
obtained in the last years on the disks' spatial extension from
high-angular resolution interferometric observations at mm wavelengths,
we investigate the dust properties in the disks, namely grain growth
and dust mass, and their relation with the properties of the central
star.
(hereafter PdBI) with an average rms
of about 0.3 mJy. Together with the data already present in the
literature at sub/mm- and mm-wavelengths, and with the information
obtained in the last years on the disks' spatial extension from
high-angular resolution interferometric observations at mm wavelengths,
we investigate the dust properties in the disks, namely grain growth
and dust mass, and their relation with the properties of the central
star.
In Sect. 2 we present our new PdBI data, the properties of our sample, the method we used to estimate the main stellar physical quantities, and the data we used for our analysis. In Sect. 3 we describe the disk models adopted for the analysis of the disks sub-mm/mm SED. In Sect. 4 we show and discuss the results of our study in terms of dust grain growth and dust mass, whereas in Sect. 5 we summarize our main findings.
2 New 3 mm observations and sample properties
2.1 New PdBI observations
We observed a total list of 19 targets; 16 of them were selected to be relatively faint, with 15 mJy <
![]() <100 mJy and with no known detections beyond about 1 mm;
the other three (HL, DO and DR Tau) are brighter sources that were
observed for reference purposes. The observations were carried out with
PdBI between July and August 2007. Owing to antenna maintenance work,
all observations
were carried out in a subarray of the six-element interferometer. The
antennae were arranged in very compact configurations that provided
sensitive baselines from 15 m to 80 m. The dual-polarization
receivers,
which were observing in the 3 mm band, had typical receiver
temperatures of
about 35 K and were providing image sideband rejection values
better than
10 dB. To achieve maximum sensitivity in the continuum, the
spectral
correlator was adjusted to cover a total effective bandwidth of about
2 GHz.
<100 mJy and with no known detections beyond about 1 mm;
the other three (HL, DO and DR Tau) are brighter sources that were
observed for reference purposes. The observations were carried out with
PdBI between July and August 2007. Owing to antenna maintenance work,
all observations
were carried out in a subarray of the six-element interferometer. The
antennae were arranged in very compact configurations that provided
sensitive baselines from 15 m to 80 m. The dual-polarization
receivers,
which were observing in the 3 mm band, had typical receiver
temperatures of
about 35 K and were providing image sideband rejection values
better than
10 dB. To achieve maximum sensitivity in the continuum, the
spectral
correlator was adjusted to cover a total effective bandwidth of about
2 GHz.
The observing procedures were set up to fill in gaps in the scheduling
without any specific tuning wavelength within the 3 mm band. Visibilities
were obtained using on-source integration times of 22 min interspersed with
2 min calibrations on a nearby calibrator. Each star was observed on one or
more occasions for a minimum of 40 min and a maximum of 2 h on-source.
The atmospheric phase stability on the baselines was always better than
40![]() ,
consistent with seeing conditions of 1''-3'', typical for
summer. The absolute flux density scale was calibrated on 3C84,
0528+134, MWC349 and Mars, and was found to be accurate to 10%. The
receiver passband shape was determined with excellent precision on a strong
calibrator like 3C84.
,
consistent with seeing conditions of 1''-3'', typical for
summer. The absolute flux density scale was calibrated on 3C84,
0528+134, MWC349 and Mars, and was found to be accurate to 10%. The
receiver passband shape was determined with excellent precision on a strong
calibrator like 3C84.
We used the GILDAS package for the data reduction and analysis. The data were calibrated in the antenna based manner. The continuum visibilities were gridded with natural weighting and no taper to maximize the sensitivity. Since none of the target stars was found to be resolved in synthesized beams of 2''-4'', a point source model was fitted to the calibrated visibilities of each star to estimate the flux density of the continuum in the 3 mm band. The results are summarized in Table 1. Among the 19 targets, 17 were detected, including 14 of the 16 faint sources, thanks to our good sensitivity; 12 of these are first detections longward of about 1 mm, which strongly expands the available database of 3 mm data towards fainter disks. The 2.6 mm detections of LkHa 358 and GO Tau were recently published by Schaefer et al. (2009).
In Sects. 2.2, 2.3 and 2.4 we describe the final sample used for our analysis of dust properties, the adopted method to estimate the stellar properties and mass accretion rates summarized in Table 2, whereas in Sect. 2.5 we report the sub-mm/mm data that we collected from the literature for our analysis.
Table 1: Summary of the new PdBI observations.
2.2 Sample
Our final sample of 21 sources consists of all young stellar objects (YSO) in
Taurus-Auriga catalogued in Andrews & Williams (2005)
which fulfil the following
criteria: (1) a class II infrared SED, to avoid contamination of
sub-mm
fluxes by a residual envelope; (2) information on the central star
through optical-NIR spectroscopic/photometric data, necessary to
calculate self-consistent disk SED models; (3) one detection at ![]() 3 mm (either from our new PdBI observations or from the literature) and at least one detection in the 0.45 mm
3 mm (either from our new PdBI observations or from the literature) and at least one detection in the 0.45 mm
![]() mm
spectral region. This selection criterion was chosen to probe
a broad enough spectral window to efficiently constrain the optically
thin part of the sub-mm/mm spectral energy distribution (SED);
(4) no evidence of stellar companions in the 0.05-3.5'' range in angular separation.
This range corresponds to about 5-500 AU in projected physical
separation at the Taurus-Auriga star forming region distance, here
assumed to be 140 pc for all the sources of our sample (Bertout
et al. 1999).
The limit of 3.5 arcsec
ensures that mm interferometric flux measurements, of a typical
resolution of 1 arcsec, are not contaminated by the companion's
disk, while binaries closer
than 5 AU should have outer disk properties similar to those of
single stars on
the scales probed by (sub-)mm data.
mm
spectral region. This selection criterion was chosen to probe
a broad enough spectral window to efficiently constrain the optically
thin part of the sub-mm/mm spectral energy distribution (SED);
(4) no evidence of stellar companions in the 0.05-3.5'' range in angular separation.
This range corresponds to about 5-500 AU in projected physical
separation at the Taurus-Auriga star forming region distance, here
assumed to be 140 pc for all the sources of our sample (Bertout
et al. 1999).
The limit of 3.5 arcsec
ensures that mm interferometric flux measurements, of a typical
resolution of 1 arcsec, are not contaminated by the companion's
disk, while binaries closer
than 5 AU should have outer disk properties similar to those of
single stars on
the scales probed by (sub-)mm data.
Only 21 sources catalogued by Andrews & Williams (2005) fulfil the above four
criteria. They are listed in Table 2 and include eleven sources from our PdBI
sample![]() .
.
Table 2: Stellar properties.
Figure 1 reports histograms that describe the completeness level of our final
sample with respect to all Taurus-Auriga class II YSOs catalogued in Andrews &
Williams (2005), and fulfiling the ``isolation'' criterion (4). Our sample contains 63% of these ``isolated'' class II showing a flux at ![]() 0.85 mm
greater than 100 mJy, and 31% of the sources with lower
0.85 mm fluxes. Therefore our sample is not complete even for the
brightest YSOs at 0.85 mm. This is due to a lack of
observations at
0.85 mm
greater than 100 mJy, and 31% of the sources with lower
0.85 mm fluxes. Therefore our sample is not complete even for the
brightest YSOs at 0.85 mm. This is due to a lack of
observations at ![]() 3 mm for these sources. However, thanks to the high sensitivity of our new PdBI observations (see Sect. 2.1) our sample enables us to study
statistically the dust properties of faint disks (i.e. with
3 mm for these sources. However, thanks to the high sensitivity of our new PdBI observations (see Sect. 2.1) our sample enables us to study
statistically the dust properties of faint disks (i.e. with
![]() mJy,
mJy,
![]() mJy)
for the first time and compare them to the brighter ones using a uniform
analysis method.
In terms of the stellar properties,
it is important to note that the Andrews & Williams (2005) catalogue includes only a few very low mass PMS stars: only stars with an estimated
mass higher than about 0.2
mJy)
for the first time and compare them to the brighter ones using a uniform
analysis method.
In terms of the stellar properties,
it is important to note that the Andrews & Williams (2005) catalogue includes only a few very low mass PMS stars: only stars with an estimated
mass higher than about 0.2 ![]() have been detected because of
the sensitivity limits of the current facilities at sub-mm
and mm wavelengths that make the detection of disks
around very low mass YSOs very difficult. The sensitivity limitation is
even more severe at 3 mm, therefore our final sample
includes 58% of all the class II isolated sample of Andrews &
Williams (2005) with an estimated mass greater than 0.4
have been detected because of
the sensitivity limits of the current facilities at sub-mm
and mm wavelengths that make the detection of disks
around very low mass YSOs very difficult. The sensitivity limitation is
even more severe at 3 mm, therefore our final sample
includes 58% of all the class II isolated sample of Andrews &
Williams (2005) with an estimated mass greater than 0.4 ![]() ,
but only two sources with
,
but only two sources with
![]()
![]() (out of ten in Andrews & Williams 2005).
(out of ten in Andrews & Williams 2005).
![\begin{figure}
\par\includegraphics[scale=0.45]{06439f1a.eps}\par\includegraphic...
...45]{06439f1b.eps}\\
\par\includegraphics[scale=0.45]{06439f1c.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg41.png)
|
Figure 1:
Histograms higlighting some properties of our selected sample. In all
the histograms our sample is represented by black+grey columns, the
black columns represent the disks in our sample for which we obtained
new PdBI data at |
| Open with DEXTER | |
2.3 Stellar properties
Spectral types for all the sources in our sample are taken from the literature (Kenyon & Hartmann 1995, Briceño et al. 1998) and cover a range from G2 (SU Aur) to M2.5 (CX Tau).
Spectral types of M0 and earlier have been converted to effective
temperatures with the dwarf temperature scale of Schmidt-Kaler (1982),
whereas for types later than M0 we adopted the temperature scale
developed by Luhman 1999. Typical uncertainties for these sources
are ![]() 1-1.5 in spectral sub-types or
1-1.5 in spectral sub-types or ![]() 100-150 K in
temperature.
100-150 K in
temperature.
The stellar luminosities of all the pre-main-sequence (PMS) stars were computed from their J-band flux (2MASS All Sky Catalog of point sources, Cutri et al. 2003) to minimize contamination from UV and IR excess emission. For the bolometric corrections we adopted the dwarf values from Kenyon & Hartmann (1995) that are considered to be satisfactory approximations for these young sources in the J-band (Luhman 1999).
In order to estimate the amount of extinction toward these young
sources, we calculated the color excesses using intrinsic colors
provided by Kenyon & Hartmann (1995) for the G2-K7 spectral types and by Leggett (1992)
for the M0-M2.5 types. To ensure that the color excess reflects
only the effect of reddening, minimizing the emission due to accretion,
the typical selected colors
are between the R and H bands. Since for some of the objects
at later spectral types in our sample R-I measurements are
not available, we dereddened the J-H and H-Kscolors from the 2MASS All Sky Catalog of point
sources![]() to the locus observed for classical T Tauri stars (CTTS) by Meyer et al. (1997), following the method described in
Briceño et al. (2002). Extinctions are finally calculated adopting the extinction law of Rieke & Lebofsky (1985).
to the locus observed for classical T Tauri stars (CTTS) by Meyer et al. (1997), following the method described in
Briceño et al. (2002). Extinctions are finally calculated adopting the extinction law of Rieke & Lebofsky (1985).
The computed photospheric luminosities cover a range from
![]() (HO Tau) to
(HO Tau) to
![]() (SU Aur). Considering the uncertainties
in the photometry, reddenings, bolometric corrections and
distance, the typical errors in the bolometric luminosities are
(SU Aur). Considering the uncertainties
in the photometry, reddenings, bolometric corrections and
distance, the typical errors in the bolometric luminosities are
![]() 0.08-0.13 in
0.08-0.13 in
![]() .
Slight differences from the
values obtained by other authors are typically within the uncertainties and
are not significant for the purposes of this paper.
.
Slight differences from the
values obtained by other authors are typically within the uncertainties and
are not significant for the purposes of this paper.
Given the effective temperatures and photospheric luminosities, we
placed the PMS stars on the H-R diagram and derived stellar masses
and ages adopting the theoretical tracks and isocrones of
Palla & Stahler (1999) (see Fig. 2). One important source of
uncertainty for stellar masses and ages is given by the spread of
values obtainable by using different PMS evolutionary models. For
example, compared to the ones obtained with the Baraffe et al. (1998)
models, our adopted values of stellar masses and ages are
typically lower by a factor of ![]() 1.5 and
1.5 and ![]() 2
respectively. Our choice of using the Palla & Stahler (1999) models is
only due to the more complete coverage of the HR diagram
plane, which allows us to use the same evolutionary models for all the
sources of our sample. One should always bear in mind the high
uncertainty associated to these quantities, expecially to the
stellar age (see Sect. 4.1 for a more detailed discussion about the estimates of YSO ages). According to the Palla & Stahler (1999) models the ranges spanned by our sample go from about
2
respectively. Our choice of using the Palla & Stahler (1999) models is
only due to the more complete coverage of the HR diagram
plane, which allows us to use the same evolutionary models for all the
sources of our sample. One should always bear in mind the high
uncertainty associated to these quantities, expecially to the
stellar age (see Sect. 4.1 for a more detailed discussion about the estimates of YSO ages). According to the Palla & Stahler (1999) models the ranges spanned by our sample go from about
![]() (CX Tau) to
(CX Tau) to
![]() (RY Tau) in stellar masses and from
about 0.1 Myr (UZ Tau E) to 17 Myr (DS Tau) in stellar ages.
(RY Tau) in stellar masses and from
about 0.1 Myr (UZ Tau E) to 17 Myr (DS Tau) in stellar ages.
The main stellar quantities described here are summarized in Table 2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{06439fg2.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg48.png)
|
Figure 2:
H-R diagram for the sources of our sample. The dashed lines correspond
to the isochrones for ages in Myr as labeled at the right end of the
lines from the 1999
PMS evolutionary models, while the solid ones represent the
evolutionary tracks from the same models for PMS stars with masses as
labeled at the top of the evolutionary track lines. In this diagram the
evolutionary tracks start from an age of 0.1 Myr. The errorbars
for the (
|
| Open with DEXTER | |
2.4 Mass accretion rates
Given the stellar luminosities and effective temperatures we
calculated the stellar radii using the Stefan-Boltzmann law. Once
the stellar mass ![]() and radius
and radius ![]() are set, the
mass accretion rate
are set, the
mass accretion rate
![]() can be directly obtained
from an estimate of the accretion luminosity
can be directly obtained
from an estimate of the accretion luminosity
![]() by
by
where G is the gravitational constant and the factor of
The estimates of
![]() were obtained from spectroscopic detections of
excess Balmer continuum emission in the literature (see references in Table 2).
These estimates are obtained primarily from measuring the excess flux
in the Balmer continuum shortward of 3646 Å. The luminosity is then
obtained by applying a bolometric correction calculated from shock
models (Calvet & Gullbring 1998; Gullbring et al. 2000) or simplistic plane-parallel slabs (Valenti et al. 1993; Gullbring et al. 1998).
were obtained from spectroscopic detections of
excess Balmer continuum emission in the literature (see references in Table 2).
These estimates are obtained primarily from measuring the excess flux
in the Balmer continuum shortward of 3646 Å. The luminosity is then
obtained by applying a bolometric correction calculated from shock
models (Calvet & Gullbring 1998; Gullbring et al. 2000) or simplistic plane-parallel slabs (Valenti et al. 1993; Gullbring et al. 1998).
Two sources in our sample, FZ Tau and GO Tau, do not have literature estimates of accretion luminosity from the excess Balmer continuum emission. We obtained the accretion luminosity for these two sources from low-resolution spectra from 3200-8700 Å obtained with the double spectrograph at the 5m Hale Telescope at Palomar. The accretion luminosity was then calculated from the excess Balmer continuum emission, following the method described in Herczeg & Hillenbrand (2008).
2.5 Disks sub-mm and mm data from the literature
Table 3: Literature sources for the sub-mm/mm data.
In order to probe the sub-millimetre and millimeter SED we collected data of
the dust continuum emission between ![]() 0.450 to
0.450 to ![]() 7 mm from several works in the literature, listed in Table 3. These data, except for 7 mm measurements, have been used together with the new PdBI observations at
7 mm from several works in the literature, listed in Table 3. These data, except for 7 mm measurements, have been used together with the new PdBI observations at ![]() 3 mm to constrain the
disk properties by fitting the sub-mm/mm SED with the models
described in Sect. 3.
The 7-mm data are excluded because free-free emission from ionized gas
contaminates disk emission, with free-free emission typically
contributing
3 mm to constrain the
disk properties by fitting the sub-mm/mm SED with the models
described in Sect. 3.
The 7-mm data are excluded because free-free emission from ionized gas
contaminates disk emission, with free-free emission typically
contributing ![]() 20% of the 7 mm flux (Rodmann et al. 2006).
Simultaneous cm observations are required to constrain the free-free
emission at 7 mm, which is variable on short timescales (
20% of the 7 mm flux (Rodmann et al. 2006).
Simultaneous cm observations are required to constrain the free-free
emission at 7 mm, which is variable on short timescales (![]() a few days, see Lommen et al. 2009).
Only two disks in our sample (RY Tau and UZ Tau E) have been observed
nearly simultaneously at centimeter and millimeter wavelengths (Rodmann
et al. 2006), without which
the 7 mm fluxes should be considered only as upper limits for the
dust emission. We therefore did not include the 7 mm data in our
analysis, although we included the available 7 mm data from the
literature in Fig. 4
and verified a posteriori that the fluxes of our disk models for all
sources are equal or less than the measured flux at 7 mm.
Simultaneous 7 mm and cm-wavelength observations with the EVLA
will extend the coverage of the disk SED to longer wavelengths to
better constrain the millimeter-wavelengths dust opacity and to provide
information on dust grains larger than
a few days, see Lommen et al. 2009).
Only two disks in our sample (RY Tau and UZ Tau E) have been observed
nearly simultaneously at centimeter and millimeter wavelengths (Rodmann
et al. 2006), without which
the 7 mm fluxes should be considered only as upper limits for the
dust emission. We therefore did not include the 7 mm data in our
analysis, although we included the available 7 mm data from the
literature in Fig. 4
and verified a posteriori that the fluxes of our disk models for all
sources are equal or less than the measured flux at 7 mm.
Simultaneous 7 mm and cm-wavelength observations with the EVLA
will extend the coverage of the disk SED to longer wavelengths to
better constrain the millimeter-wavelengths dust opacity and to provide
information on dust grains larger than ![]() 1 cm.
1 cm.
![\begin{figure}
\par\includegraphics[scale=0.54]{06439f3a.eps}\includegraphics[scale=0.45]{06439f3b.eps}\\\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg53.png)
|
Figure 3:
Millimeter dust opacity for the adopted dust model. Left top panel: dust opacity at 1 mm as a function of
|
| Open with DEXTER | |
3 Disk models
We compare the observational sub-mm/mm data with the two-layer models of flared disks (i.e. in hydrostatic equilibrium) heated by the stellar radiation as developed by Dullemond et al. (2001), following the schematization of Chiang & Goldreich (1997). These models have been used in the analysis of CQ Tau by Testi et al. (2003) and of a sample of nine Herbig Ae stars by Natta et al. (2004) and we refer the interested reader to these papers for a more detailed description.
To completely characterize a model of the disk, we need to specify
the stellar properties (i.e. the luminosity ![]() ,
effective
temperature
,
effective
temperature
![]() ,
mass
,
mass ![]() and distance d,
assumed to
be 140 pc for all the sources in our sample), some characteristics
of the disk structure, namely the inner and outer radius (
and distance d,
assumed to
be 140 pc for all the sources in our sample), some characteristics
of the disk structure, namely the inner and outer radius (
![]() and
and
![]() ,
respectively), the parameters
,
respectively), the parameters
![]() and pwhich define the radial profile of the dust surface density assumed to
be a power-law
and pwhich define the radial profile of the dust surface density assumed to
be a power-law![]()
![]() AU)-p, the disk inclination angle i (90
AU)-p, the disk inclination angle i (90![]() for an
edge-on disk) and, lastly, the dust opacity.
The millimeter SED is almost completely insensitive to some of the disk
parameters, which consequently cannot be constrained by our analysis.
For example, the inner radius of the disk,
for an
edge-on disk) and, lastly, the dust opacity.
The millimeter SED is almost completely insensitive to some of the disk
parameters, which consequently cannot be constrained by our analysis.
For example, the inner radius of the disk,
![]() ,
affects the
emission only at near and mid-infrared wavelengths.
,
affects the
emission only at near and mid-infrared wavelengths.
The outer radius
![]() is a parameter that can be probed
by high-angular resolution interferometric observations. In our
sample 13 disks have been spatially resolved, yielding
an estimate for
is a parameter that can be probed
by high-angular resolution interferometric observations. In our
sample 13 disks have been spatially resolved, yielding
an estimate for
![]() .
It is important to note that
different interferometric observations performed on the same disk
can lead to very different values of
.
It is important to note that
different interferometric observations performed on the same disk
can lead to very different values of
![]() (
(![]() 100 AU) because of differences in the observations' angular resolution, sensitivity,
and methods for deriving the radius. Given these uncertainties in the determination of
100 AU) because of differences in the observations' angular resolution, sensitivity,
and methods for deriving the radius. Given these uncertainties in the determination of
![]() ,
we consider a range of possible values for
,
we consider a range of possible values for
![]() rather than a single-value estimate, as listed in Table 4.
For the eight objects in our sample that have not yet been mapped with
angular resolutions smaller than a few arcseconds which may potentially
resolve the disk, a fiducial interval of 100-300 AU has been
assumed
rather than a single-value estimate, as listed in Table 4.
For the eight objects in our sample that have not yet been mapped with
angular resolutions smaller than a few arcseconds which may potentially
resolve the disk, a fiducial interval of 100-300 AU has been
assumed![]() . This adopted range for
. This adopted range for
![]() comprises the vast majority of the disk outer radii distribution function as derived by Andrews & Williams (2007) through
comprises the vast majority of the disk outer radii distribution function as derived by Andrews & Williams (2007) through ![]() 1'' angular resolution sub-millimeter observations of 24 disks in Taurus-Auriga and
1'' angular resolution sub-millimeter observations of 24 disks in Taurus-Auriga and ![]() -Ophiucus. We will discuss the impact of the outer disk uncertainty on the results of our analysis in Sect. 4. Here we wish to note that with these values of
-Ophiucus. We will discuss the impact of the outer disk uncertainty on the results of our analysis in Sect. 4. Here we wish to note that with these values of
![]() the disk emission at sub-mm/mm wavelengths is dominated by the outer disk regions (R
> 30 AU) which are optically thin to their own radiation. An
effect of this is that the millimeter SED does not depend on the disk
inclination angle i (for
the disk emission at sub-mm/mm wavelengths is dominated by the outer disk regions (R
> 30 AU) which are optically thin to their own radiation. An
effect of this is that the millimeter SED does not depend on the disk
inclination angle i (for
![]() ), thus decreasing the number of the model parameters used to fit the observational SED. This is
certainly true for the spatially resolved disks for which we have an
estimate for
), thus decreasing the number of the model parameters used to fit the observational SED. This is
certainly true for the spatially resolved disks for which we have an
estimate for
![]() .
The eight unmapped objects could have optically thick inner disks that contribute significantly to the
sub-mm/mm emission. Since the disk outer radius cannot be
constrained by the SED alone, interferometric imaging that
spatially resolves these disks is the only way to get information
on the exact value of
.
The eight unmapped objects could have optically thick inner disks that contribute significantly to the
sub-mm/mm emission. Since the disk outer radius cannot be
constrained by the SED alone, interferometric imaging that
spatially resolves these disks is the only way to get information
on the exact value of
![]() .
Nevertheless, since the
disks that have been spatially resolved so far show outer radii
typically in the range 100-300 AU, we consider it to be highly
unlikely that a significant fraction of the unmapped disks have a
.
Nevertheless, since the
disks that have been spatially resolved so far show outer radii
typically in the range 100-300 AU, we consider it to be highly
unlikely that a significant fraction of the unmapped disks have a
![]() AU, which would make the
disk optically thick even at mm wavelengths.
AU, which would make the
disk optically thick even at mm wavelengths.
3.1 Dust opacity
The last quantity that defines the disk model is the dust opacity, which depends on grain sizes, chemical compositions, and shapes (e.g. Miyake & Nakagawa 1993; Pollack et al. 1994; Draine et al. 2006). In order to extract quantitative estimates from the sub-mm/mm SED for the dust grain sizes and the dust mass in the disks, assumptions on the chemical composition and shape of the dust grains have to be made.
For our discussion we considered porous composite spherical grains
made of astronomical silicates, carbonaceous materials
and water ice (optical constants for the individual components from Weingartner & Draine 2001; Zubko et al. 1996; Warren 1984 respectively) and adopted the fractional abundances used by Pollack et al. (1994) (see caption of Fig. 3). We considered a population of grains with a
power-law size distribution
![]() between a
minimum and a maximum size,
between a
minimum and a maximum size,
![]() and
and
![]() ,
respectively. In the ISM,
,
respectively. In the ISM,
![]() is a few tens of Å,
is a few tens of Å,
![]() m, and q = 3.5 (Mathis et al. 1977, Draine & Lee 1984, by analyzing extinction and scattering of starlinght from the interstellar dust). As discussed e.g. in
Natta et al. (2004), in a protoplanetary disk one expects much higher values of
m, and q = 3.5 (Mathis et al. 1977, Draine & Lee 1984, by analyzing extinction and scattering of starlinght from the interstellar dust). As discussed e.g. in
Natta et al. (2004), in a protoplanetary disk one expects much higher values of
![]() than in the ISM because of grain
processing, and a variety of possible q values, depending on the processes of
grain coagulation and fragmentation that occur in the disk.
Experimental studies of fragmentation from a single target have found values of q ranging from
than in the ISM because of grain
processing, and a variety of possible q values, depending on the processes of
grain coagulation and fragmentation that occur in the disk.
Experimental studies of fragmentation from a single target have found values of q ranging from ![]() 1.9 for low-velocity collisions to
1.9 for low-velocity collisions to ![]() 4 for catastrophic impacts (Davies & Ryan 1990),
but the power-law index for fragments from shattering events integrated
over a range of target masses need not be necessarily the same as in
the case of a single target. In the disk, if the coagulation processes
from the initial ISM-grains population dominate over the fragmentation,
a value for q that is lower than the ISM one is expected (the opposite should occur in the case of fragmentation playing the major role).
4 for catastrophic impacts (Davies & Ryan 1990),
but the power-law index for fragments from shattering events integrated
over a range of target masses need not be necessarily the same as in
the case of a single target. In the disk, if the coagulation processes
from the initial ISM-grains population dominate over the fragmentation,
a value for q that is lower than the ISM one is expected (the opposite should occur in the case of fragmentation playing the major role).
![\begin{figure}
\par\includegraphics[scale=0.75]{figures/06439fg4.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg64.png)
|
Figure 4:
Fits of the sub-mm/mm SEDs with the two-layer flared disk models (solid
lines). Note that even if the data at 7 mm, available for only
eight disks in our sample, are present in the plots, they have not been
used in the fitting procedure (see Sect. 2.5).
The errorbars in the plots take into account an uncertainty of 10% on
the absolute flux scale, typical for flux measurements at these
wavelengths. The circled data come from the new PdBI observations. The
fitting values of the spectral index |
| Open with DEXTER | |
In the adopted two-layer disk model, the disk is divided into the surface and midplane regions, and therefore two different opacity laws are considered. Because of the assumed vertical hydrodynamical equilibrium and dust settling, the content of mass in the midplane in a protoplanetary disk is much higher than in the surface. At millimeter wavelengths, where the disk is mostly optically thin to its own radiation, the midplane total emission dominates over that of the surface (although the surface dust plays a crucial role for the heating of the disk). As a consequence, we can extract information from our analysis only on the dust opacity of the midplane, and so when we consider the dust opacity we will refer only to the midplane component for the rest of the paper.
For the dust grains in the disk surface we assumed the same
chemical composition and shape as for the midplane grains, while we
assumed for their size distribution for
![]() and
and
![]() values around
values around ![]() m (the sub-mm SED is insensitive to these values as long as
m (the sub-mm SED is insensitive to these values as long as
![]() in the surface is much lower than
in the surface is much lower than
![]() in the midplane, as expected if dust settling is important).
in the midplane, as expected if dust settling is important).
Once the chemical composition and
shape of the dust grains in the midplane are set, the dust opacity law depends on
![]() ,
,
![]() and q.
Considering a value of
and q.
Considering a value of ![]() m for
m for
![]() (the dependence of the millimeter dust opacity from this parameter
turns out to be very weak), the model parameters for our analysis are
the stellar parameters (
(the dependence of the millimeter dust opacity from this parameter
turns out to be very weak), the model parameters for our analysis are
the stellar parameters (![]() ,
,
![]() ,
,
![]() ), which have been set and listed in Table 2, plus those of the disk (
), which have been set and listed in Table 2, plus those of the disk (
![]() ,
p,
,
p,
![]() ,
q,
,
q,
![]() ), or
equivalently (
), or
equivalently (
![]() ,
p, q,
,
p, q,
![]() ,
,
![]() )
where
)
where
![]() is the mass of dust in the disk.
is the mass of dust in the disk.
For reasons described in Sect. 4 it is convenient to
approximate the millimeter dust opacity law discussed so far in terms of a power-law at millimeter wavelengths
![]() (
(![]() 1 mm)
1 mm)![]() ,
with
,
with
![]() in
units of cm2 per gram of dust. At a fixed value of q the relations between
in
units of cm2 per gram of dust. At a fixed value of q the relations between
![]() ,
,
![]() and
and
![]() can be determined. These are shown in Fig. 3 for
q=2.5,3,3.5,4.
can be determined. These are shown in Fig. 3 for
q=2.5,3,3.5,4.
4 Results
The sub-mm/mm SED fits for all the objects in our sample are
reported in Fig. 4![]() . As discussed in
Testi et al. (2003) and Natta et al. (2004), the only quantities that can be
constrained by the sub-mm/mm SED are the millimeter dust opacity spectral
index
. As discussed in
Testi et al. (2003) and Natta et al. (2004), the only quantities that can be
constrained by the sub-mm/mm SED are the millimeter dust opacity spectral
index ![]() (in this paper calculated between 1 and 3 mm) and the
(in this paper calculated between 1 and 3 mm) and the
![]() product
product![]() . From the SED alone it is impossible to constrain the value of the surface density exponent p, since
it is generally possible to fit the SED data with either very flat
(p = 0.5) or very steep (p = 2) surface density profiles.
However, all available high angular resolution observations
performed so far suggest that
. From the SED alone it is impossible to constrain the value of the surface density exponent p, since
it is generally possible to fit the SED data with either very flat
(p = 0.5) or very steep (p = 2) surface density profiles.
However, all available high angular resolution observations
performed so far suggest that
![]() (e.g. Dutrey et al. 1996;
Wilner et al. 2000; Kitamura et al. 2002; Testi et al. 2003; Andrews & Williams 2007; Isella et al. 2009; Andrews et al. 2009).
(e.g. Dutrey et al. 1996;
Wilner et al. 2000; Kitamura et al. 2002; Testi et al. 2003; Andrews & Williams 2007; Isella et al. 2009; Andrews et al. 2009).
The degeneracy of the SED on p and
![]() has an impact onto the derived uncertainties for
has an impact onto the derived uncertainties for ![]() and
and
![]() .
Considering both this degeneracy and uncertainties of the observational data, the total absolute uncertainties are
approximately 0.2-0.3 for
.
Considering both this degeneracy and uncertainties of the observational data, the total absolute uncertainties are
approximately 0.2-0.3 for ![]() and a factor of
and a factor of ![]() three
and
three
and ![]() four for
four for
![]() for the spatially resolved and unmapped disks respectively. These uncertainties are mainly due to the adopted ranges for
for the spatially resolved and unmapped disks respectively. These uncertainties are mainly due to the adopted ranges for
![]() (listed in Table 4) and p
between 0.5 and 1.5, whose values determine the impact of the
optically thick regions of the disk to the total emission, as explained
in Sect. 3.
(listed in Table 4) and p
between 0.5 and 1.5, whose values determine the impact of the
optically thick regions of the disk to the total emission, as explained
in Sect. 3.
The estimates for ![]() and
and
![]() obtained by our analysis are reported in Table 5.
obtained by our analysis are reported in Table 5.
4.1 Spectral slopes and dust opacity index
Table 4: Adopted disk outer radii.
Before analysing the values of ![]() ,
which provide information on the level of grain growth in the outer
disk regions, it is important to check whether our results could be
affected by detection biases: indeed, for a given flux at
,
which provide information on the level of grain growth in the outer
disk regions, it is important to check whether our results could be
affected by detection biases: indeed, for a given flux at ![]() 1 mm, a disk with large dust grains in the outer parts will produce a stronger emission at
1 mm, a disk with large dust grains in the outer parts will produce a stronger emission at ![]() 3 mm than a disk with a population of smaller-sized grains and it would be easier to detect. In Fig. 5 the grey region of the plot indicates the area in the (
3 mm than a disk with a population of smaller-sized grains and it would be easier to detect. In Fig. 5 the grey region of the plot indicates the area in the (
![]() ,
,
![]() )
plane in which the observations carried out so far are not sensitive,
due to the sensitivity limits obtained at 1 and 3 mm. While
we could investigate the dust properties for four disks with
)
plane in which the observations carried out so far are not sensitive,
due to the sensitivity limits obtained at 1 and 3 mm. While
we could investigate the dust properties for four disks with
![]() ,
the plot shows that a disk with a 1 mm flux in this same range, but with a spectral index
,
the plot shows that a disk with a 1 mm flux in this same range, but with a spectral index
![]() ,
which is consistent with a disk model with ISM-like dust and an outer radius of
,
which is consistent with a disk model with ISM-like dust and an outer radius of ![]() 100 AU, would not be detected at 3 mm. Nevertheless, we want to point out that only two of our 16 targets with
100 AU, would not be detected at 3 mm. Nevertheless, we want to point out that only two of our 16 targets with
![]() mJy were not detected at 3 mm, and both have very weak
mJy were not detected at 3 mm, and both have very weak
![]() fluxes (upper limits of 27 mJy and 21 mJy for DP Tau and GK Tau respectively, Andrews & Williams 2005), therefore the lack of disks with
fluxes (upper limits of 27 mJy and 21 mJy for DP Tau and GK Tau respectively, Andrews & Williams 2005), therefore the lack of disks with
![]() 3.2 at
3.2 at
![]() mJy
does not seem to be due to our sensitivity limit, but is most likely
real. Furthermore, as is evident from the same plot, the six faintest
disks with
mJy
does not seem to be due to our sensitivity limit, but is most likely
real. Furthermore, as is evident from the same plot, the six faintest
disks with
![]() show a spectral index between 1 and 3 mm that is lower on average (
show a spectral index between 1 and 3 mm that is lower on average (
![]() )
than for the brighter disks (
)
than for the brighter disks (
![]() ). This is the reason for the discrepancy of the average value of the dust opacity spectral index
). This is the reason for the discrepancy of the average value of the dust opacity spectral index
![]() between unmapped and resolved disks (see discussion below).
between unmapped and resolved disks (see discussion below).
In Fig. 3 we plot
![]() and
and ![]() as functions of
as functions of
![]() for different values of q. One interesting result is
that the values of
for different values of q. One interesting result is
that the values of ![]() obtained for the objects in our sample by the SED-fitting
procedure are all less than or equal to 1, which can be explained only if
dust grains with sizes larger than 1 mm are present in the disk.
For the nine sources with
obtained for the objects in our sample by the SED-fitting
procedure are all less than or equal to 1, which can be explained only if
dust grains with sizes larger than 1 mm are present in the disk.
For the nine sources with
![]() ,
the largest dust grains
must have grown to sizes
,
the largest dust grains
must have grown to sizes ![]() 1 cm according to our dust model.
If we let q assume values lower than 2.5, thus increasing the
fractional number of the larger grains, the maximum grain size
decreases, but
1 cm according to our dust model.
If we let q assume values lower than 2.5, thus increasing the
fractional number of the larger grains, the maximum grain size
decreases, but
![]() mm for
mm for
![]() is still needed.
is still needed.
The estimates of the maximum grain sizes
![]() depend on
the adopted dust model. If we consider for example the
dust model adopted in Natta et al. (2004) (5% olivine, 15% organic
materials, 35% water ice and 50% vacuum), the estimates for
depend on
the adopted dust model. If we consider for example the
dust model adopted in Natta et al. (2004) (5% olivine, 15% organic
materials, 35% water ice and 50% vacuum), the estimates for
![]() are greater by about an order of magnitude than the
ones obtained with our dust model. In general, no realistic dust
grain models result in
are greater by about an order of magnitude than the
ones obtained with our dust model. In general, no realistic dust
grain models result in ![]() for
for
![]() mm.
mm.
Here it is worthwhile to remember that whereas for the 13 resolved disks in our sample ![]() is well determined, for the eight disks for which we do not have information on their spatial extension,
the optically thick parts of a possible compact disk could
significantly contribute to the emission. If that is the case,
no conclusions on the dust grain properties could be drawn. In
particular, for the six unmapped disks with
is well determined, for the eight disks for which we do not have information on their spatial extension,
the optically thick parts of a possible compact disk could
significantly contribute to the emission. If that is the case,
no conclusions on the dust grain properties could be drawn. In
particular, for the six unmapped disks with
![]() 1.9-2.2 (CX Tau, DS Tau, FM Tau, FZ Tau, HO Tau, SU Aur)
a very compact disk with
1.9-2.2 (CX Tau, DS Tau, FM Tau, FZ Tau, HO Tau, SU Aur)
a very compact disk with
![]() AU, a relative
high inclination
AU, a relative
high inclination
![]() ,
and with ISM-like dust grains
would fit the sub-mm/mm SED. For the other two unmapped sources, DE
Tau (
,
and with ISM-like dust grains
would fit the sub-mm/mm SED. For the other two unmapped sources, DE
Tau (
![]() )
and CW Tau (
)
and CW Tau (
![]() ), ISM-like dust grains are
consistent with the sub-mm/mm data using a disk model with
), ISM-like dust grains are
consistent with the sub-mm/mm data using a disk model with
![]() and
and
![]() ,
40 AU
respectively. For the faintest disks the outer
radius has to be small, because if the disks were larger they
would also need to be more massive to keep being
optically thick, thus producing an
,
40 AU
respectively. For the faintest disks the outer
radius has to be small, because if the disks were larger they
would also need to be more massive to keep being
optically thick, thus producing an ![]() value close to 2 with
all the possible dust properties. In that case, they would emit more
sub-mm/mm-wave radiation than observed. Since for an optically
thick disk decreasing the inclination angle has the effect of
making the SED steeper (because the central, hotter parts are less
obscured), for disks with
value close to 2 with
all the possible dust properties. In that case, they would emit more
sub-mm/mm-wave radiation than observed. Since for an optically
thick disk decreasing the inclination angle has the effect of
making the SED steeper (because the central, hotter parts are less
obscured), for disks with
![]() the outer radii would need
to be even smaller to fit the SED. As these disk outer radii
are lower by factors of 2-4 than the smallest disks that have
been spatially resolved so far, and since for all the 13 resolved
disks the values of
the outer radii would need
to be even smaller to fit the SED. As these disk outer radii
are lower by factors of 2-4 than the smallest disks that have
been spatially resolved so far, and since for all the 13 resolved
disks the values of ![]() have been found always much lower than
in the ISM (
have been found always much lower than
in the ISM (
![]() ,
see Fig. 6), thus showing clear evidence of grain growth,
we consider it to be very unlikely that many of the unmmapped
sources are compact, optically-thick disks with unprocessed ISM
grains. For AA Tau, which is the faintest of the mapped sources (
,
see Fig. 6), thus showing clear evidence of grain growth,
we consider it to be very unlikely that many of the unmmapped
sources are compact, optically-thick disks with unprocessed ISM
grains. For AA Tau, which is the faintest of the mapped sources (
![]() mJy) and which has a low spectral index of
mJy) and which has a low spectral index of
![]() typical of fainter sources, the maps indicate a disk radius of
200-400 AU, ruling out the possibility of optically thick disk
regions that dominate the total emission, and require a low
typical of fainter sources, the maps indicate a disk radius of
200-400 AU, ruling out the possibility of optically thick disk
regions that dominate the total emission, and require a low ![]() of 0.3 to explain the shallow slope.
of 0.3 to explain the shallow slope.
Also, only for the disks with
![]() ,
values of
,
values of
![]() are consistent with the data (see right panel in Fig. 3), in which case
are consistent with the data (see right panel in Fig. 3), in which case
![]() cm. This agrees well with the following consideration using the approximated asymptotic formula
cm. This agrees well with the following consideration using the approximated asymptotic formula
![]() ,
derived by Draine (2006), where
,
derived by Draine (2006), where
![]() is the opacity spectral index of the solid
material in the Rayleigh limit and is valid for a population of
grains with 3 < q < 4 and
is the opacity spectral index of the solid
material in the Rayleigh limit and is valid for a population of
grains with 3 < q < 4 and
![]() ,
with ac a function of the real and
imaginary parts of the complex dielectric function and wavelength
(at millimeter wavelengths
,
with ac a function of the real and
imaginary parts of the complex dielectric function and wavelength
(at millimeter wavelengths
![]() mm). Since at a fixed
q the function
mm). Since at a fixed
q the function
![]() decreases when
decreases when
![]() mm (see Fig. 3), it follows
that the approximated asymptotic value
mm (see Fig. 3), it follows
that the approximated asymptotic value
![]() gives a lower limit for
gives a lower limit for ![]() at a finite
at a finite
![]() .
Adopting
.
Adopting
![]() from the small dust grains in the
ISM, we derive
from the small dust grains in the
ISM, we derive
![]() for
for
![]() ,
i.e.
dust grain populations with
,
i.e.
dust grain populations with
![]() cannot explain
cannot explain
![]() -values lower than
-values lower than ![]() 0.85
0.85![]() .
.
In Fig. 6 we report the histogram of the ![]() -values derived by our analysis. The average value in our sample considering both unmapped and resolved disks,
-values derived by our analysis. The average value in our sample considering both unmapped and resolved disks,
![]() ,
is not consistent with dust populations with q-values of 3.5, like for the ISM, or greater. Values of q lower than 3.5 have been obtained by e.g. Tanaka et al. (2005) from simulations of grain growth in stratified protoplanetary disks, which give vertically integrated size distributions with
,
is not consistent with dust populations with q-values of 3.5, like for the ISM, or greater. Values of q lower than 3.5 have been obtained by e.g. Tanaka et al. (2005) from simulations of grain growth in stratified protoplanetary disks, which give vertically integrated size distributions with
![]() plus a population of much larger bodies, to which however our observations would not be sensitive.
plus a population of much larger bodies, to which however our observations would not be sensitive.
These considerations clearly suggest that the process of dust grain growth to mm-sizes has played a fundamental role in most, if not all, of the Taurus-Auriga protoplanetary disks whose sub-mm/mm SED has been sufficiently investigated.
From Fig. 6 it is also evident that the two sub-samples made of unmapped and resolved disks separately have different averaged ![]() values, with the
values, with the ![]() values being on average lower for the unmapped disks than for the resolved ones (
values being on average lower for the unmapped disks than for the resolved ones (
![]() ,
,
![]() for the unmapped and resolved disks respectively). Since the unmapped sample nearly coincides with the fainter disks with
for the unmapped and resolved disks respectively). Since the unmapped sample nearly coincides with the fainter disks with
![]() mJy, and since
mJy, and since ![]() is correlated with the spectral index
is correlated with the spectral index ![]() ,
this is due to the trend already presented in Fig. 5 between
,
this is due to the trend already presented in Fig. 5 between
![]() and
and
![]() .
This trend agrees with simple expectations for grain growth: as the maximum grain size
.
This trend agrees with simple expectations for grain growth: as the maximum grain size
![]() increases, both
increases, both ![]() and
and
![]() decrease, so disks with the same dust mass should become fainter as
decrease, so disks with the same dust mass should become fainter as ![]() gets smaller. Alternatively, the
gets smaller. Alternatively, the
![]() -
-
![]() trend
could arise if the fainter disks are smaller, and then more optically
thick, than the brighter resolved ones, while their ``true''
trend
could arise if the fainter disks are smaller, and then more optically
thick, than the brighter resolved ones, while their ``true'' ![]() would be nearly the same.
would be nearly the same.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{06439fg5.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg140.png)
|
Figure 5:
Spectral index |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{06439fg6.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg141.png)
|
Figure 6:
Distribution of the dust opacity spectral index |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{06439fg7.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg142.png)
|
Figure 7:
Beta versus age: relationship between the dust opacity spectral index |
| Open with DEXTER | |
In Fig. 7 we show the ![]() vs. stellar age plot. No evidence of an evolutionary trend is present
over the broader range of stellar ages spanned by our sample. As
already discussed the determination of the individual ages of PMS stars
is very uncertain. Hartmann (2001)
has shown that the large age spread deduced for T Tauri stars in
Taurus may just be the result of uncertainties in the measurements
towards individual members of a population with a very narrow age
spread. Our most solid conclusion, not affected by the age
determination uncertainties, is that most (if not all) of the
class II YSO in our sample show evidence of evolved grains in the
disk outer regions.
vs. stellar age plot. No evidence of an evolutionary trend is present
over the broader range of stellar ages spanned by our sample. As
already discussed the determination of the individual ages of PMS stars
is very uncertain. Hartmann (2001)
has shown that the large age spread deduced for T Tauri stars in
Taurus may just be the result of uncertainties in the measurements
towards individual members of a population with a very narrow age
spread. Our most solid conclusion, not affected by the age
determination uncertainties, is that most (if not all) of the
class II YSO in our sample show evidence of evolved grains in the
disk outer regions.
4.2 Grain growth
These results confirm two statements that have been addressed in the last years. The first one is that the dust coagulation from ISM dust to mm/cm-sized grains is a fast process, which appears to occur before a YSO enters in the class II evolutionary stage, i.e. when a dense envelope still surrounds the protostar+disk system. This is also consistent with the recent results by Kwon et al. (2009) who have found evidence of grain growth in three class 0 YSOs in Perseus and Cepheus through CARMA observations at 1.3 and 2.7 mm.
The second statement is that the mm/cm-sized dust grains appear
to stay longer in the outer disk if compared with their expected inward
drift timescale due to the interaction with the gas component. In a
circumstellar disk the gas experiences a pressure gradient force which
cancels a part of the central star's gravity and induces a rotation
slower than the Keplerian velocity. Dust grains, whose orbits are
hardly affected by gas pressure, are assumed to be rotating with
Keplerian velocity and thus experience a headwind. They lose angular
momentum and spiral inward to the central star (Adachi et al. 1976; Weidenschilling 1977).
Takeuchi & Lin (2005)
proposed as possible solutions to the drift problem that either the
grain growth process from mm-sized to cm-sized grains is very long in
the outer regions of the disk (timescales greater than 1 Myr, e.g.
given by grains' sticking probability as low as 0.1) or that grains
have already grown to 10 m or larger and do not migrate rapidly
anymore, while mm-sized particles are continuosly replenished through
collisions of these large bodies. However, our analysis suggests that
unless the grain size distribution index is very low, i.e. q < 2.5, disks with
![]() show evidence of grains as large as
show evidence of grains as large as ![]() 1 cm in the outer regions. Also, as already pointed out in Natta et al. (2004) and Brauer et al. (2007),
a considerable amount of larger bodies, which would not contribute to
the disk emission because of their negligibly small opacity
coefficient, could significantly increase the disk masses. Since the
typical orbital decay time for a cm-sized grain with a density of
0.1 g cm-3 at 50 AU is
1 cm in the outer regions. Also, as already pointed out in Natta et al. (2004) and Brauer et al. (2007),
a considerable amount of larger bodies, which would not contribute to
the disk emission because of their negligibly small opacity
coefficient, could significantly increase the disk masses. Since the
typical orbital decay time for a cm-sized grain with a density of
0.1 g cm-3 at 50 AU is ![]() 105 yr (104 yr for a more compact grain with a 1 g cm-3 density), to explain the presence of cm-sized grains in the older disks in our sample (with ages of few Myrs and up to
105 yr (104 yr for a more compact grain with a 1 g cm-3 density), to explain the presence of cm-sized grains in the older disks in our sample (with ages of few Myrs and up to ![]() 107 yr)
the reservoir of larger bodies would have to contain at least 100 times
more mass than the observed dust mass. The total disk mass would then
be comparable to or would even exceed the estimated stellar mass (using
a standard gas-to-dust mass ratio of 100, see Sect. 4.3).
107 yr)
the reservoir of larger bodies would have to contain at least 100 times
more mass than the observed dust mass. The total disk mass would then
be comparable to or would even exceed the estimated stellar mass (using
a standard gas-to-dust mass ratio of 100, see Sect. 4.3).
To solve the drift problem for very low and very high disk masses Brauer et al. (2007)
proposed a significant reduction of the drag experienced by the dust
due to a reduction of the gas-to-dust ratio in the disk from the
canonical value of 100, and to possible collective effects of dust
gathering in a thin midplane layer in the case of very low-turbulence
disks. For example, using a low value for the turbulence parameter
![]() and a gas-to-dust ratio of 5, they find that cm-sized dust grains
remain in the outer parts of the disk for more than 2 Myr if disk
masses <
and a gas-to-dust ratio of 5, they find that cm-sized dust grains
remain in the outer parts of the disk for more than 2 Myr if disk
masses <
![]() or >
or >
![]() are considered. In the range of
are considered. In the range of
![]() the
collective effects of dust are not efficient enough to retain cm-sized
grains in the disk outer regions. If the disk is more turbulent, then
more gas has to be removed to keep the particles in the outer parts for
a longer period of time. To justify such small gas-to-dust ratios the
authors suggest the process of photoevaporation as the main driver of
gas removal. However, in this case, since photoevaporation is expected
to manifest only in the later stages of disk evolution, we would expect
a strong evolutionary trend of
the
collective effects of dust are not efficient enough to retain cm-sized
grains in the disk outer regions. If the disk is more turbulent, then
more gas has to be removed to keep the particles in the outer parts for
a longer period of time. To justify such small gas-to-dust ratios the
authors suggest the process of photoevaporation as the main driver of
gas removal. However, in this case, since photoevaporation is expected
to manifest only in the later stages of disk evolution, we would expect
a strong evolutionary trend of ![]() ,
which is not found by our analysis though.
,
which is not found by our analysis though.
Another possibility is the presence in the disk of local gas pressure maxima that would block the inward drift of the dust grains. As shown by the dynamics calculation of Barge & Sommeria (1995) and Klahr & Henning (1997), this mechanism may provide a solution also to the relative velocity fragmentation barrier that prevents meter-sized bodies to further grow in size in the inner regions of the disk.
4.3 Dust mass
From the sub-mm/mm SED fitting procedure we derived the quantity
![]() .
To obtain the dust mass in the disks, an
estimate of
.
To obtain the dust mass in the disks, an
estimate of
![]() is needed. The choice of the dust
opacity at 1 mm creates the highest uncertainty in the
derivation of (dust) disk masses from millimeter observations.
Estimates of
is needed. The choice of the dust
opacity at 1 mm creates the highest uncertainty in the
derivation of (dust) disk masses from millimeter observations.
Estimates of
![]() from different dust models in
the literature span a range of a factor greater than ten. The most
commonly used value in the literature is
from different dust models in
the literature span a range of a factor greater than ten. The most
commonly used value in the literature is
![]() cm2 per gram of dust (Beckwith et al. 1990) that, for
simplicity, is supposed to be constant, i.e. independent of the
dust grain properties, for all the disks. As noted in Natta et al. (2004)
this is not realistic as grain growth affects both the frequency
dependence of the dust opacity and its absolute value (e.g.
Miyake & Nakagawa 1993).
cm2 per gram of dust (Beckwith et al. 1990) that, for
simplicity, is supposed to be constant, i.e. independent of the
dust grain properties, for all the disks. As noted in Natta et al. (2004)
this is not realistic as grain growth affects both the frequency
dependence of the dust opacity and its absolute value (e.g.
Miyake & Nakagawa 1993).
In this paper we use the dust model described in Sect. 3.1 to get an estimate of
![]() that takes into account the dust physical properties, expecially grain growth. As
shown in the left top panel of Fig. 3, at a fixed value
of the grain size distribution index q, the value of
that takes into account the dust physical properties, expecially grain growth. As
shown in the left top panel of Fig. 3, at a fixed value
of the grain size distribution index q, the value of
![]() can be inferred from
can be inferred from
![]() which in
turn can be derived from
which in
turn can be derived from ![]() through the relation plotted in
the left bottom panel of the same figure. The relation between
through the relation plotted in
the left bottom panel of the same figure. The relation between
![]() and
and ![]() is shown in the right panel. Therefore, from an estimate
of
is shown in the right panel. Therefore, from an estimate
of ![]() and
and
![]() obtained by the sub-mm/mm
SED fitting procedure we can get an estimate for
obtained by the sub-mm/mm
SED fitting procedure we can get an estimate for
![]() and then the dust mass
and then the dust mass
![]() for our dust
model, after fixing the q parameter. In Table 5 we report the values of
for our dust
model, after fixing the q parameter. In Table 5 we report the values of
![]() as
obtained with this method for q = 2.5, 3.0, 3.5. It is important to bear in mind that, as for the estimate of the maximum grain size, so also for
as
obtained with this method for q = 2.5, 3.0, 3.5. It is important to bear in mind that, as for the estimate of the maximum grain size, so also for
![]() and for the dust mass, the estimates depend on the specific dust model that one adopts (see discussion in Natta et al. 2004). However, following Isella et al. (2009), we take into account the variation of the dust opacity with
and for the dust mass, the estimates depend on the specific dust model that one adopts (see discussion in Natta et al. 2004). However, following Isella et al. (2009), we take into account the variation of the dust opacity with ![]() using a well defined dust model to infer dust masses, and this approach is more accurate than considering a fixed
using a well defined dust model to infer dust masses, and this approach is more accurate than considering a fixed
![]() ,
as is often done in previous studies.
,
as is often done in previous studies.
Table 5: Disk properties.
In general for our specific dust model, when ![]() then
then
![]() ,
and the amount of variation of
,
and the amount of variation of
![]() for the different q values is dependent
on
for the different q values is dependent
on ![]() .
This is particularly the case when
.
This is particularly the case when
![]()
![]() and
and
![]() are nearly
coincident, and
are nearly
coincident, and
![]() is greater than
is greater than
![]() by factors of
by factors of ![]() 2-4. For
2-4. For
![]() a grain size distribution with q = 3.5 cannot
explain the observational data, and the discrepancy between
a grain size distribution with q = 3.5 cannot
explain the observational data, and the discrepancy between
![]() and
and
![]() increases to
a factor of
increases to
a factor of ![]() 15 when
15 when
![]() .
This is due to the increase of the distance between the
.
This is due to the increase of the distance between the
![]() (
(![]() )
curves at fixed q-values when
)
curves at fixed q-values when ![]() decreases, as shown in the right panel of Fig. 3.
decreases, as shown in the right panel of Fig. 3.
As already mentioned in Sect. 4.1, from the value of ![]() it is impossible to disentangle
it is impossible to disentangle
![]() and q.
Nevertheless, only the disks showing
and q.
Nevertheless, only the disks showing
![]() can be
explained by a grain size distribution index q
= 3.5. Consequently, we will separately consider for the rest of our
analysis only those cases where the dust grain size distribution is
characterized by q = 2.5 or 3. The value of q in
protoplanetary disks is unknown and it is not observationally
constrainable, and so it is in principle possible that it can vary
substantially from one disk to the other. For our discussion we
will use the assumption that q is the same for all the disks.
can be
explained by a grain size distribution index q
= 3.5. Consequently, we will separately consider for the rest of our
analysis only those cases where the dust grain size distribution is
characterized by q = 2.5 or 3. The value of q in
protoplanetary disks is unknown and it is not observationally
constrainable, and so it is in principle possible that it can vary
substantially from one disk to the other. For our discussion we
will use the assumption that q is the same for all the disks.
Once the dust mass is estimated, this is commonly converted into an estimate of the total disk mass (dust+gas) using the standard ISM gas-to-dust ratio of 100. However, if the dust and gas components have different evolutionary timescales, this ratio is a function of time, and the standard ISM value would be inappropriate to estimate the disk mass at the present time. Physical processes that are likely to alter this ratio during the evolution of a protoplanetary disk are gas photo-evaporation, which would lead to a decrease of the gas-to-dust ratio (unless a significant amount of dust is dragged away by the gas flow), and dust inward migration, which instead would increase it. Natta et al. (2004) suggested that the standard ISM ratio provides a correct estimate of the ``original'' disk mass when the disk composition reflects that of the parent cloud. This is only true however if a negligible amount of dust has migrated with respect to the gas and accreted onto the central star, otherwise the ISM ratio would provide only a lower limit to the original disk mass. Because of our ignorance on the gas-to-dust ratio evolution we will not convert the dust mass into a total disk mass. It is also important to note that since millimeter observations are insensitive to the emission of bodies much larger than 1 cm, including planetesimals and planets, the dust mass we are referring to in this paper does not include the contribution from these larger objects. The dust mass is intended to be the mass in ``small grains'' only, and is a lower limit to the total mass in dust.
![\begin{figure}
\par\mbox{\includegraphics[scale=0.45]{06439f8a.eps}\hspace{3mm}
\includegraphics[scale=0.45]{06439f8b.eps} } \\\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg214.png)
|
Figure 8:
Dust opacity spectral index |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[scale=0.45]{06439f9a.eps}\hspace{4mm}
\includegraphics[scale=0.45]{06439f9b.eps} }\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg215.png)
|
Figure 9: Disk mass in dust plotted against the stellar mass for the sources in our sample. In the left and right panels the dust mass has been obtained adopting a value of 2.5 and 3 respectively for the power index q of the dust grain size distribution. The stellar mass has been estimated as described in Sect. 2.3, and the errorbars take into account the range of values given by different PMS stars evolutionary models. Open blue points represent the spatially resolved disks, whereas the filled red points are for the unmapped ones. The errorbars in the dust mass estimates do not take into account our uncertainty on the real value of q. |
| Open with DEXTER | |
Figure 8 shows the ![]() vs.
vs.
![]() plots for q equal to 2.5 and 3. The plot with q = 2.5 does not show any significant relation. In the q
= 3 case an anticorrelation between these two quantities may be
present, with the more massive dust disks associated to the ones
showing today the largest grains in their outer parts, with
plots for q equal to 2.5 and 3. The plot with q = 2.5 does not show any significant relation. In the q
= 3 case an anticorrelation between these two quantities may be
present, with the more massive dust disks associated to the ones
showing today the largest grains in their outer parts, with
![]() up to
up to ![]() 10 cm.
This possible anticorrelation is clearly an effect of the choice of a
physical model for the dust that takes into account the variation of
the dust opacity normalization factor with the size-distribution of the
dust grains (Sect. 3.1).
If we had made the unrealistic assumption of a constant value for the
dust opacity at, say, 1 mm, we would have found an opposite result,
i.e. disks with less mass in dust would have shown on average larger grains, as can be derived from Fig. 5, since
10 cm.
This possible anticorrelation is clearly an effect of the choice of a
physical model for the dust that takes into account the variation of
the dust opacity normalization factor with the size-distribution of the
dust grains (Sect. 3.1).
If we had made the unrealistic assumption of a constant value for the
dust opacity at, say, 1 mm, we would have found an opposite result,
i.e. disks with less mass in dust would have shown on average larger grains, as can be derived from Fig. 5, since ![]() is approximately proportional to
is approximately proportional to ![]() and
and
![]() would be approximately proportional to the dust mass in the constant
would be approximately proportional to the dust mass in the constant
![]() case. More realistically, lower values of
case. More realistically, lower values of ![]() imply low absolute values of the dust millimeter opacity (see right panel of Fig. 3),
so that for a fixed observed flux and disk temperature, the
corresponding dust mass must be larger. The reason why the plot with q = 2.5 does not show signs of anticorrelation is that at a fixed
imply low absolute values of the dust millimeter opacity (see right panel of Fig. 3),
so that for a fixed observed flux and disk temperature, the
corresponding dust mass must be larger. The reason why the plot with q = 2.5 does not show signs of anticorrelation is that at a fixed ![]() a lower q value is associated to a smaller dust grain maximum size. The
a lower q value is associated to a smaller dust grain maximum size. The ![]() range spanned by the disks in our sample translates into a range in
range spanned by the disks in our sample translates into a range in
![]() that is narrower for q = 2.5 than it is for q = 3 (see right panel of Fig. 3), thus leading to smaller correction factors with respect to the constant
that is narrower for q = 2.5 than it is for q = 3 (see right panel of Fig. 3), thus leading to smaller correction factors with respect to the constant
![]() case. Note that among the five disks showing the smallest
case. Note that among the five disks showing the smallest ![]() (
(![]() 0.2-0.3) and the highest dust masses (about
0.2-0.3) and the highest dust masses (about
![]() for q
= 3) only one (AA Tau) has been mapped and spatially resolved.
High angular resolution and high sensitivity imaging of these disks
together with other ones are needed to test the robustness of the
for q
= 3) only one (AA Tau) has been mapped and spatially resolved.
High angular resolution and high sensitivity imaging of these disks
together with other ones are needed to test the robustness of the
![]() anticorrelation in the q = 3 case.
anticorrelation in the q = 3 case.
Figures 9 and 10 plot the disk mass in dust against the estimated mass of the central star (dust mass obtained with q-values of 2.5 and 3) and mass accretion rate (dust mass with q = 3 and stellar ages smaller and greater than 2 Myr) respectively. In the
![]() range in stellar mass the dust mass does not show any trend (for q = 2.5:
range in stellar mass the dust mass does not show any trend (for q = 2.5:
![]() ;
for q = 2.5:
;
for q = 2.5:
![]() ). The two YSOs with
). The two YSOs with
![]() have lower dust masses than all the other YSOs for both q
= 2.5 and 3. However, the range in stellar mass spanned by our
sample is rather limited and particularly biased toward YSOs with
late-K and early-M spectral types. From the upper limits obtained at
1.3 mm by Schaefer et al. (2009) for 14 T-Tauri stars with spectral types later than
have lower dust masses than all the other YSOs for both q
= 2.5 and 3. However, the range in stellar mass spanned by our
sample is rather limited and particularly biased toward YSOs with
late-K and early-M spectral types. From the upper limits obtained at
1.3 mm by Schaefer et al. (2009) for 14 T-Tauri stars with spectral types later than ![]() M2 (
M2 (
![]() mJy) and from the detection of very low disk masses around sub-stellar objects in Taurus-Auriga (Klein et al. 2003, Scholz et al. 2006),
it is likely that a correlation between the disk mass in dust and the
mass of the central star exists. High sensitivity millimeter
observations are needed to constrain the disk masses in dust around
very low mass PMS stars. In Fig. 10
a trend of higher mass accretion rates for the more massive disks in
dust may be present in the data, but the scatter is still very
significant (a similar result is obtained for the case of q = 2.5).
Other relations between the dust properties (
mJy) and from the detection of very low disk masses around sub-stellar objects in Taurus-Auriga (Klein et al. 2003, Scholz et al. 2006),
it is likely that a correlation between the disk mass in dust and the
mass of the central star exists. High sensitivity millimeter
observations are needed to constrain the disk masses in dust around
very low mass PMS stars. In Fig. 10
a trend of higher mass accretion rates for the more massive disks in
dust may be present in the data, but the scatter is still very
significant (a similar result is obtained for the case of q = 2.5).
Other relations between the dust properties (![]() ,
dust mass) and the stellar ones (e.g. stellar luminosity, effective
temperature) have been investigated, but no significant correlations
were found.
,
dust mass) and the stellar ones (e.g. stellar luminosity, effective
temperature) have been investigated, but no significant correlations
were found.
![\begin{figure}
\par\mbox{\includegraphics[scale=0.45]{6439f10a.eps}\hspace{4mm}
\includegraphics[scale=0.45]{6439f10b.eps} }\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg223.png)
|
Figure 10: Disk mass in dust plotted against the mass accretion rate for the sources in our sample. In the left and right panels we included the objects with estimated ages of less and more than 2 Myr respectively. The dust mass has been obtained adopting a value of 3 for the power index q of the dust grain size distribution. The stellar mass accretion rate has been estimated following the method described in Sect. 2.4. Open blue points represent the spatially resolved disks, whereas the filled red points are for the unmapped ones. The errorbars in the mass accretion rate take into account the typical intrinsic time-variability of the accretion rates. The errorbars in the dust mass estimates do not include our uncertainty on the actual value of q. |
| Open with DEXTER | |
Finally, we have compared the values of ![]() obtained in this paper with those derived in Natta et al. (2004)
for a sample of six intermediate mass Herbig Ae stars and three lower
mass T Tauri stars. From the two-sided Kolmogorov-Smirnov test,
the probability that the
obtained in this paper with those derived in Natta et al. (2004)
for a sample of six intermediate mass Herbig Ae stars and three lower
mass T Tauri stars. From the two-sided Kolmogorov-Smirnov test,
the probability that the ![]() values from the two samples come from the same distribution is
about 88%, indicating that the disks in the two samples have
similar dust properties in terms of grain growth (in the Natta
et al. 2004 sample only one object, the Herbig Ae star HD150193, has a relatively high
values from the two samples come from the same distribution is
about 88%, indicating that the disks in the two samples have
similar dust properties in terms of grain growth (in the Natta
et al. 2004 sample only one object, the Herbig Ae star HD150193, has a relatively high
![]() ,
compatible with non-evolved ISM-like dust grains).
,
compatible with non-evolved ISM-like dust grains).
5 Summary
We have analysed the sub-mm/mm SED out to 3 mm of a sample of
21 class II T-Tauri stars in the Taurus-Auriga star forming
region. This sample comprises about the 60% of the ``isolated'' class
II YSOs with an estimated stellar mass greater than ![]()
![]() .
It also comprises approximately 1/3 of the isolated class II wich have
been observed at 0.85 mm to have a flux less than 100 mJy, for
which we provide the first 3 mm detections thanks to sensitive
PdBI observations. Our main findings are summarized below:
.
It also comprises approximately 1/3 of the isolated class II wich have
been observed at 0.85 mm to have a flux less than 100 mJy, for
which we provide the first 3 mm detections thanks to sensitive
PdBI observations. Our main findings are summarized below:
- 1.
- For all the sources in our sample the millimeter opacity spectral index
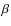 is
significantly lower than the value obtained for the dust in the ISM.
For the 13 spatially resolved disks this is a clear evidence of
the presence in the outer disk regions of dust grains as large as at
least 1 mm. For the eight unmapped sources, assuming disk outer radii
comparable to the resolved sources, low
is
significantly lower than the value obtained for the dust in the ISM.
For the 13 spatially resolved disks this is a clear evidence of
the presence in the outer disk regions of dust grains as large as at
least 1 mm. For the eight unmapped sources, assuming disk outer radii
comparable to the resolved sources, low 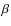 values are found as well, which suggests that even for these fainter
sources 1 mm-sized grains are in the disk outer regions. This confirms
over a larger sample and less massive disks the results obtained by
past observations on T-Tauri stars (e.g. Rodmann et al. 2006 and references therein).
values are found as well, which suggests that even for these fainter
sources 1 mm-sized grains are in the disk outer regions. This confirms
over a larger sample and less massive disks the results obtained by
past observations on T-Tauri stars (e.g. Rodmann et al. 2006 and references therein).
- 2.
- No significant evidence of an evolutionary trend for the millimeter opacity spectral index
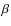 has been found. This indicates that the dust grain growth to
has been found. This indicates that the dust grain growth to  1 mm-sizes
is a very fast process in a protoplanetary disk, which appears to occur
before a YSO enters into the class II evolutionary stage. Also,
the amount of these large grains in the disk outer regions does not
appear to decline throughout all the class II evolutionary stage.
1 mm-sizes
is a very fast process in a protoplanetary disk, which appears to occur
before a YSO enters into the class II evolutionary stage. Also,
the amount of these large grains in the disk outer regions does not
appear to decline throughout all the class II evolutionary stage.
- 3.
- Only for nine sources in our sample a power law index for the grain size distribution of the ISM,
 ,
is consistent with the sub/mm-mm SED. Instead, most of the disks show evidence of a smaller q-value.
,
is consistent with the sub/mm-mm SED. Instead, most of the disks show evidence of a smaller q-value.
- 4.
- We have not found any significant correlation between the dust properties, namely grain growth and dust mass in the disk outer regions, and the properties of the central star, including the mass accretion rate onto the stellar surface. However, our sample contains mostly YSOs with a narrow range in spectral types, namely between late-K and early-M, and it is possible that a correlation between the disk mass in dust and the stellar mass will become apparent if one also considers disks around late-M spectral types.
- 5.
- The six faintest sources in our sample with
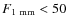 mJy
show a spectral index between 1 and 3 mm that is on average lower
than the spectral index of the brighter sources. This may indicate
either that for these fainter, yet unmapped disks the emission from the
optically thick inner disk is much more significant than for the
brighter sources or that the dust grains in the outer regions of these
fainter disks are even larger than in the brighter YSOs, possibly up to
10 cm if q = 3. The latter hypothesis would imply on
average a lower absolute value for the millimeter opacity coefficient
for these fainter disks. Taking into account this effect through a
physical model for the dust properties, we found in the case of a value
for the power index of the grain size distribution q = 3 an anticorrelation between
mJy
show a spectral index between 1 and 3 mm that is on average lower
than the spectral index of the brighter sources. This may indicate
either that for these fainter, yet unmapped disks the emission from the
optically thick inner disk is much more significant than for the
brighter sources or that the dust grains in the outer regions of these
fainter disks are even larger than in the brighter YSOs, possibly up to
10 cm if q = 3. The latter hypothesis would imply on
average a lower absolute value for the millimeter opacity coefficient
for these fainter disks. Taking into account this effect through a
physical model for the dust properties, we found in the case of a value
for the power index of the grain size distribution q = 3 an anticorrelation between 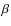 and the disk dust mass, which would indicate that larger dust grains
are found in the outer parts of the more massive disks (in dust).
and the disk dust mass, which would indicate that larger dust grains
are found in the outer parts of the more massive disks (in dust).
We thank the anonymous referee for his/her comments that greatly improved the manuscript. L.R. acknowledges the PhD fellowship of the International Max-Planck-Research School.
References
- Adachi, I., Hayashi, C., & Nakazawa, K. 1976, Prog. Theor. Phys., 56, 1756 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, F. C., Emerson, J. P., & Fuller, G. A. 1990, ApJ, 357, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Altenhoff, W. J., Thum, C., & Wendker, H. J. 1994, A&A, 281, 161 [NASA ADS] [Google Scholar]
- Andrews, S. M., & Williams, J. P. 2005, ApJ, 631, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., & Williams, J. P. 2007, ApJ, 659, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., et al. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Barge, P., & Sommeria, J. 1995, A&A, 295, L1 [NASA ADS] [Google Scholar]
- Beckwith, S. V. W., & Sargent, A. I. 1991, ApJ, 381, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, S. V. W., Sargent, A. I., Chini, R. S., et al. 1990, AJ, 99, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Bertout, C., Robichon, N., & Arenou, F. 1999, A&A, 352, 574 [NASA ADS] [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Brauer, F., Dullemond, C. P., Johansen, A., et al. 2007, A&A, 469, 1169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwman, J., Meeus, G., de Koter, A., et al. 2001, A&A, 375, 950 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Briceño, C., Hartmann, L., Stauffer, J. R., et al. 1998, AJ, 115, 2074 [NASA ADS] [CrossRef] [Google Scholar]
- Briceño, C., Luhman, K. L., Hartmann L., Stauffer, J. R., & Kirkpatrick, J. D. 2002, ApJ, 580, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., & Gullbring, E. 1998, ApJ, 509, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., D'Alessio, P., Hartmann, L., et al. 2002, ApJ, 568, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., Muzerolle, J., Briceño, C., et al. 2004, AJ, 128, 1294 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M. 2001, AJ, 121, 2851 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., et al. 2003, 2MASS All Sky Catalog of point sources [Google Scholar]
- Davies, D. R., & Ryan, E. V. 1990, Icarus, 83, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2006, ApJ, 636, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H.-M. 1984, ApJ, 285, 89 [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Dutrey, A., Guilloteau, S., Duvert, G., et al. 1996, A&A, 309, 493 [NASA ADS] [Google Scholar]
- Gullbring, E., Calvet, N., Muzerolle, J., et al. 2000, ApJ, 544, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Gullbring, E., Hartmann, L., Briceño, C. 1998, ApJ, 492, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., & Kenyon, S. J. 2003, ApJ, 583, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L. 2001, AJ, 121, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, C. J., & Hillenbrand, L. A. 2008, ApJ, 681, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, M. A., Wilner, D. J., Qi, C., et al. 2008, ApJ, 678, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Carpenter, J. M., & Sargent, A. F. 2009, ApJ, 701, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, Y., Hayashi, M., Tamura, M., et al. 2005, ApJ, 620, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, E. L. N., Koerner, D. W., & Mathieu, R. D. 1996, AJ, 111, 2431 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, E. L. N., Dhital, S., Stassun, K. G., et al. 2007, AJ, 134, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler-Silacci, J., Augereau, J. C., Dullemond, C. P., Geers, V., Lahuis, F., et al. 2006, ApJ, 639, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Kitamura, Y., Momose, M., Yokogawa, S., et al. 2002, ApJ, 581, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H. H., & Henning, T. 1997, Icarus, 128, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, R., Apai, D., Pascucci, I., Henning, Th., & Waters, L. B. F. M. 2003, ApJ, 593, 57 [Google Scholar]
- Koerner, D. W., Chandler, C. J., & Sargent, A. I. 1995, ApJ, 452, 69 [Google Scholar]
- Kwon, W., Looney, L. W., Mundy, L. G., Chiang, H., & Kemball, A. 2009, ApJ, 696, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Leggett, S. K. 1992, ApJS, 82, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., Zinnecker, H., Weitzel, N., et al. 1993, A&A, 278, 129 [NASA ADS] [Google Scholar]
- Lommen, D., Wright, C. M., Maddison, S. T., et al. 2007, A&A, 462, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lommen, D., Maddison, S. T., Wright, C. M., 2009, A&A, 495, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luhman, K. L. 1999, ApJ, 525, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Malfait, K., Waelkens, C., Waters, L. B. F. M., et al. 1998, A&A, 332, 25 [Google Scholar]
- Mannings, V., & Emerson, J. P. 1994, MNRAS, 267, 361 [NASA ADS] [Google Scholar]
- Mathieu, R. D. 1994, ARA&A, 32, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, M. R., Calvet, N., & Hillenbrand, L. A. 1997, AJ 114, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Miyake, K., & Nakagawa, Y. 1993, Icarus, 106, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Mundy, L. G., Looney, L. W., Erickson, W., et al. 1996, ApJ, 464, L169 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Testi, L., Neri, R., Shepherd, D. S., & Wilner, D. J. 2004, A&A, 416, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohashi, N., Hayashi, M., Kawabe, R., et al. 1996, ApJ, 466, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Padgett, D. L., Brandner, W., Stapelfeldt, K. R., et al. 1999, AJ, 117, 1490 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 1999, ApJ, 525, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Pinte, C., Fouchet, L., Ménard, F., Gonzalez, J.-F., & Duchêne, G. 2007, A&A, 469, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, J. B., Hollenbach, D., Beckwith, S. 1994, ApJ, 421, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 Hollenbach, D., Beckwith, S., Simonelli, D. P., Roush, T., & Fong, W. 1994, ApJ, 421, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Reipurth, B., & Zinnecker, H. 1993, A&A, 278, 81 [NASA ADS] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Rodmann, J., Henning, T., Chandler, C. J., Mundy, L. G., & Wilner, D. J. 2006, A&A, 446, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Safronov, V. S., & Zvjagina, E. V. 1969, Icarus, 10, 109 [Google Scholar]
- Schaefer, G. H., Dutrey, A., Guilloteau, S., Simon, M., & White, R. J. 2009, ApJ, 710, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt-Kaler, T. 1982, in Landolt-BornsteinGroup VI, 2, ed. K.-H. Hellwege (Berlin: Springer), 454 [Google Scholar]
- Scholz, A., Jayawardhana, R., & Wood, K. 2006, ApJ, 645, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, M., & Prato, L. 1995, ApJ, 450, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, M., Chen, W.-P., Howell, R. R., Benson, J. A., & Slowick, D. 1992, ApJ, 384, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T., & Lin, D. N. C. 2005, ApJ, 623, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Himeno, Y., & Ida, S. 2005, ApJ, 625, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Natta, A., Shepherd, D. S., & Wilner, D. J. 2001, ApJ, 554, 1087 [Google Scholar]
- Testi, L., Natta, A., Shepherd, D. S., et al. 2003, A&A, 403, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Throop, H. B., Bally, J., Esposito, L. W., et al. 2001, Science, 292, 1686 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Valenti, J. A., Basri, G., & Johns, C. M. 1993, AJ, 106, 2024 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, S. G. 1984, ApOpt 23, 1206 [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Wilner, D. J., Ho, P. T. P., Kastner, J. H., et al. 2000, ApJ, 534, L101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., et al. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... Interferometer
![[*]](/icons/foot_motif.png)
- The Plateau de Bure Interferometer at IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain).
- ...
sample
![[*]](/icons/foot_motif.png)
- The eight sources dropped from the PdBI sample are HL Tau (a flat spectrum source that retains an envelope; Padgett et al. 1999); DP Tau, FP Tau, FY Tau and LkHa 358 that have no available submm detections for SED fitting; and DK Tau, GK Tau and Haro 6-28 which are binary systems with angular separations of 2.5'' (Simon et al. 1992), 2.5''(Reipurth & Zinnecker 1993) and 0.7'' (Leinert et al. 1993) respectively. We keep in our sample the wide binaries DS Tau and HO Tau (angular separations of 7.1''and 6.9'' respectively, Mathieu et al. 1994); they do not show any emission from the companions from our new 3 mm interferometric observations. The other dropped multiple systems from the AW05 catalog are DH Tau (2.3'' binary, Itoh et al. 2005), GG Tau (quadruple system with a circumbinary ring of inner and outer radii of 180 and 260 AU respectively, Pinte et al. 2007), and UY Aur (0.9'' binary, Leinert et al. 1993).
- ...
sources
![[*]](/icons/foot_motif.png)
- For this analysis the JHKs magnitudes have been transformed from the 2MASS photometric system to the Johnson-Glass one using the color transformations reported in Carpenter (2001) and Bessell & Brett (1988).
- ... power-law
![[*]](/icons/foot_motif.png)
- As shown by Hughes et al. (2008) and Isella et al. (2009),
a tapered exponential edge in the surface density profile, physically
motivated by the viscous evolution of the disk, is able to explain the
apparent discrepancy between gas and dust outer radii derived from
millimeter observations of protoplanetary disks. Here we wish to note
that when fitting the sub/mm-mm SED with an exponential tail instead of
a truncated power-law, the dust opacity spectral index
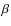 (defined in Sect. 3.1)
is unchanged, and disk masses vary by less than a factor of two, even
if the outer disk radius becomes much bigger (see, e.g., Table 4
in Kitamura et al. 2002). So the simpler truncated power-law model is a justified approximation for the purposes of this paper.
(defined in Sect. 3.1)
is unchanged, and disk masses vary by less than a factor of two, even
if the outer disk radius becomes much bigger (see, e.g., Table 4
in Kitamura et al. 2002). So the simpler truncated power-law model is a justified approximation for the purposes of this paper.
- ... assumed
![[*]](/icons/foot_motif.png)
- We will refer to these sources (CW, CX, DE, DS, FM, FZ,
HO Tau, and SU Aur) as ``unmapped'' for the rest of the paper. Note
that they are all faint with
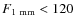 mJy.
This probably explains why for these objects no observations at
high-angular resolution have been attempted yet: the sensitivity of the
current (sub-)mm interferometers would be not high enough to detect the
low surface brightness of the outer disk regions.
mJy.
This probably explains why for these objects no observations at
high-angular resolution have been attempted yet: the sensitivity of the
current (sub-)mm interferometers would be not high enough to detect the
low surface brightness of the outer disk regions.
- ...
![[*]](/icons/foot_motif.png)
- We did not include existing NIR and mid-IR data in our analysis because at these shorter wavelengths the disk emission is optically thick and thus depends on the properties of the dust grains located in the surface layers of the inner disk regions. The aim of our analysis is instead to probe the optically thin disk emission to investigate the dust properties in the disk midplane.
- ... product
![[*]](/icons/foot_motif.png)
- Note that according to the adopted disk model the midplane temperature is well constrained after fixing the stellar parameters and these two quantities from the observed SED.
- ...
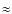 0.85
0.85![[*]](/icons/foot_motif.png)
- Note that
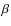 -values greater than
-values greater than 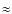 0.85 can be explained by
both
0.85 can be explained by
both
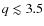 and
and
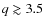 .
.
All Tables
Table 1: Summary of the new PdBI observations.
Table 2: Stellar properties.
Table 3: Literature sources for the sub-mm/mm data.
Table 4: Adopted disk outer radii.
Table 5: Disk properties.
All Figures
![\begin{figure}
\par\includegraphics[scale=0.45]{06439f1a.eps}\par\includegraphic...
...45]{06439f1b.eps}\\
\par\includegraphics[scale=0.45]{06439f1c.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg41.png)
|
Figure 1:
Histograms higlighting some properties of our selected sample. In all
the histograms our sample is represented by black+grey columns, the
black columns represent the disks in our sample for which we obtained
new PdBI data at |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{06439fg2.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg48.png)
|
Figure 2:
H-R diagram for the sources of our sample. The dashed lines correspond
to the isochrones for ages in Myr as labeled at the right end of the
lines from the 1999
PMS evolutionary models, while the solid ones represent the
evolutionary tracks from the same models for PMS stars with masses as
labeled at the top of the evolutionary track lines. In this diagram the
evolutionary tracks start from an age of 0.1 Myr. The errorbars
for the (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.54]{06439f3a.eps}\includegraphics[scale=0.45]{06439f3b.eps}\\\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg53.png)
|
Figure 3:
Millimeter dust opacity for the adopted dust model. Left top panel: dust opacity at 1 mm as a function of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.75]{figures/06439fg4.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg64.png)
|
Figure 4:
Fits of the sub-mm/mm SEDs with the two-layer flared disk models (solid
lines). Note that even if the data at 7 mm, available for only
eight disks in our sample, are present in the plots, they have not been
used in the fitting procedure (see Sect. 2.5).
The errorbars in the plots take into account an uncertainty of 10% on
the absolute flux scale, typical for flux measurements at these
wavelengths. The circled data come from the new PdBI observations. The
fitting values of the spectral index |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{06439fg5.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg140.png)
|
Figure 5:
Spectral index |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{06439fg6.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg141.png)
|
Figure 6:
Distribution of the dust opacity spectral index |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{06439fg7.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg142.png)
|
Figure 7:
Beta versus age: relationship between the dust opacity spectral index |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[scale=0.45]{06439f8a.eps}\hspace{3mm}
\includegraphics[scale=0.45]{06439f8b.eps} } \\\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg214.png)
|
Figure 8:
Dust opacity spectral index |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[scale=0.45]{06439f9a.eps}\hspace{4mm}
\includegraphics[scale=0.45]{06439f9b.eps} }\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg215.png)
|
Figure 9: Disk mass in dust plotted against the stellar mass for the sources in our sample. In the left and right panels the dust mass has been obtained adopting a value of 2.5 and 3 respectively for the power index q of the dust grain size distribution. The stellar mass has been estimated as described in Sect. 2.3, and the errorbars take into account the range of values given by different PMS stars evolutionary models. Open blue points represent the spatially resolved disks, whereas the filled red points are for the unmapped ones. The errorbars in the dust mass estimates do not take into account our uncertainty on the real value of q. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[scale=0.45]{6439f10a.eps}\hspace{4mm}
\includegraphics[scale=0.45]{6439f10b.eps} }\end{figure}](/articles/aa/full_html/2010/04/aa13403-09/Timg223.png)
|
Figure 10: Disk mass in dust plotted against the mass accretion rate for the sources in our sample. In the left and right panels we included the objects with estimated ages of less and more than 2 Myr respectively. The dust mass has been obtained adopting a value of 3 for the power index q of the dust grain size distribution. The stellar mass accretion rate has been estimated following the method described in Sect. 2.4. Open blue points represent the spatially resolved disks, whereas the filled red points are for the unmapped ones. The errorbars in the mass accretion rate take into account the typical intrinsic time-variability of the accretion rates. The errorbars in the dust mass estimates do not include our uncertainty on the actual value of q. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



