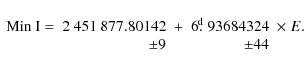EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 511 (February 2010) A&A, 511 (2010) A22 Full HTML
Free Access
Issue
A&A
Volume 511, February 2010
Article Number A22
Number of page(s) 10
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200913698
Published online 25 February 2010
A&A 511, A22 (2010)

Absolute dimensions of solar-type eclipsing binaries

III. EW Orionis: stellar evolutionary models tested by a G0 V system[*],[*]

J. V. Clausen1 - H. Bruntt2,3 - E. H. Olsen1 - B. E. Helt1 - A. Claret4

1 - Niels Bohr Institute, Copenhagen University, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
2 - Sydney Institute for Astronomy, School of Physics, University of Sydney, NSW 2006, Australia
3 - Observatoire de Paris, LESIA, 5 Place Jules Janssen, 95195 Meudon, France
4 - Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain

Received 19 November 2009 / Accepted 14 December 2009

Abstract
Context. Recent studies of inactive and active solar-type binaries suggest that chromospheric activity, and its effect on envelope convection, is likely to cause significant radius and temperature discrepancies. Accurate mass, radius, and abundance determinations from additional solar-type binaries exhibiting various levels of activity are needed for a better insight into the structure and evolution of these stars.
Aims. We aim to determine absolute dimensions and abundances for the G0 V detached eclipsing binary EW Ori, and to perform a detailed comparison with results from recent stellar evolutionary models.
Methods. ${\it uvby}$ light curves and ${\it uvby}\beta$ standard photometry were obtained with the Strömgren Automatic Telescope, published radial velocity observations from the CORAVEL spectrometer were reanalysed, and high-resolution spectra were observed at the FEROS spectrograph; all are/were ESO, La Silla facilities. State-of-the-art methods were applied for the photometric and spectroscopic analyses.
Results. Masses and radii that are precise to 0.9% and 0.5%, respectively, have been established for both components of EW Ori. The 1.12 $M_{\odot}$ secondary component reveals weak Ca   II H and K emission and is probably mildly active; no signs of activity are seen for the 1.17 $M_{\odot}$ primary. We derive an $[{\rm Fe/H}]$ abundance of +0.05 $\pm$ 0.09 and similar abundances for Si, Ca, Sc, Ti, Cr, and Ni. Yonsai-Yale and Granada solar-scaled evolutionary models for the observed metal abundance reproduce the components fairly well at an age of $\approx$2 Gyr. Perfect agreement is, however, obtained at an age of 2.3 Gyr for a combination of a) a slight downwards adjustment of the envelope mixing length parameter for the secondary, as seen for other active solar-type stars; and b) a slightly lower helium content than prescribed by the Y-Z relations adopted for the standard model grids. The orbit is eccentric ( e = 0.0758 $\pm$ 0.0020), and apsidal motion with a 62% relativistic contribution has been detected. The apsidal motion period is U = 16 300 $\pm$ 3900 yr, and the inferred mean central density concentration coefficient, log(k2) = -1.66 $\pm$ 0.30, agrees marginally with model predictions. The measured rotational velocities, 9.0 $\pm$ 0.7 (primary) and 8.8 $\pm$ 0.6 (secondary) km s-1, are in agreement with both the synchronous velocities and the theoretically predicted pseudo-synchronous velocities. Finally, the distance (175 $\pm$ 7 pc), age, and center-of mass velocity (6 km s-1) exclude suggested membership of the open cluster Collinder 70.
Conclusions. EW Ori now belongs to the small group of solar-type eclipsing binaries with well-established astrophysical properties.

Key words: stars: evolution - stars: fundamental parameters - stars: abundances - binaries: eclipsing - techniques: photometric - techniques: spectroscopic

1 Introduction

Recent studies of inactive and active solar-type binaries suggest that chromospheric activity, and its effect on envelope convection, is likely to cause significant radius and temperature discrepancies, which can be removed by adjusting the model mixing length parameter downwards (Clausen et al. 2009, hereafter CBC09, and references herein). In a study of the F8/G0 V eclipsing binary V636 Cen, CBC09 compared the properties of 11 solar-type binaries (at least one component in the 0.80-1.10 $M_{\odot}$ mass interval) with well-established dimensions, which - with one exception - fall in two groups: four long period, slowly rotating inactive systems, which seem to be fitted reasonably well by solar-scaled models. And six systems, which exhibit intrinsic variation, have short orbital periods and high rotational velocities, and which can not be reproduced by solar-scaled models. In addition, the authors found that the sample lends support to theoretical 2D radiation hydrodynamics studies, which predict a slight decrease of the mixing length parameter with increasing temperature/mass for $\it inactive$ main sequence stars. More binaries are, however, needed for a calibration in terms of physical parameters and level of activity.

We are presently undertaking analyses of several eclipsing binaries with solar-type components; see CBC09. In order to make critical tests of stellar evolutionary models, abundance determinations are in general included. In this paper we present results for the well-known system EW Ori based on new observations.

Table 1:   Photometric data for EW Ori and the comparison stars.

2 EW Ori

EW Ori (HD 287727, mV = 9.90, Sp. type G0V, P = 6 $.\!\!^{\rm d}$94), is a well detached, double-lined eclipsing binary with 1.17 and 1.12 $M_{\odot}$ main-sequence components in a slightly eccentric (e = 0.0758) orbit. The eclipsing nature of EW Ori was discovered by Hoffmeister (1930), and Lause (1937) established the first ephemeris. Much later, EW Ori was found to be double-lined (Lacy 1984). Several times of minima, back to 1937, have been published, as well as photometric indices. Popper et al. (1986) obtained photoelectric (V,R) light curves and spectrographic material, and they determined absolute dimensions. Improved spectroscopic elements, based on CORAVEL radial velocities, were later published by Imbert (2002).

EW Ori has been included in samples of eclipsing binaries used for tests of stellar evolutionary models (Pols et al. 1997; Lastennet & Valls-Gabaud 2002), determination of the helium-to-metal enrichment ratio (Ribas et al. 2000), and as a (possible) test of general relativity through apsidal motion (Giménez 1985; Wolf et al. 1997,2010). It is listed as a possible member of the open cluster Collinder 70 by Sahade & Davila (1963) and Giménez & Clausen (1996).

Although EW Ori is already well-studied, there is still room for significant improvements. In this paper we present analyses of new ${\it uvby}$ light curves, leading to much more accurate radii, we derive chemical abundances from high-resolution spectra, and we perform a detailed comparison with current stellar evolutionary models. We refer to the more massive, larger component as the primary (p) component, which, for the ephemeris we adopt (Eq. (1)), is eclipsed at phase 0.0.

3 Photometry

Below, we present the new photometric material for EW Ori and refer to Clausen et al. (2001; hereafter CHO01) for further details on observation and reduction procedures, and determination of times of minima.

\begin{figure} \par\includegraphics[width=17cm,clip]{13698f1.ps} \end{figure} Figure 1:

y light curve and b-y and u-b colour curves (instrumental system) for EW Ori.

Open with DEXTER

3.1 Light curves

The differential ${\it uvby}$ light curves of EW Ori were observed at the Strömgren Automatic Telescope (SAT) at ESO, La Silla and its 6-channel ${\it uvby}\beta$ photometer on 70 nights between November 2000 and December 2002 (JD 2 451 854-2 452 609). They contain 624 points per band with most phases covered at least twice. The observations were done through an 18 arcsec diameter circular diaphragm at airmasses between 1.2 and 2.0. HD 34658 (HR 1746, NSV 1922), HD 34745, and HD 35638 - all within a few degrees from EW Ori on the sky - were used as comparison stars and were all found to be constant within a few mmag; see Table 1. The light curves are calculated relative to HD 34745, but all comparison star observations were used, shifting them first to the same light level. The average accuracy per point is about 6 mmag ($\it ybv$) and 7 mmag (u).

As seen from Fig. 1, EW Ori is well detached with y eclipse depths of about 0.8 and 0.6 mag, respectively. The secondary eclipse is total (duration of totality about 10 min) and occurs at phase 0.5305. The light curves (Table 11) will only be available in electronic form.

3.2 Standard photometry

Standard ${\it uvby}\beta$ indices for EW Ori and the three comparison stars, observed and derived as described by CHO01, are presented in Table 1. As seen, the indices are based on many observations and their precision is high. For comparison, we have included published photometry from other sources. In general, the agreement is good, but individual differences larger than the quoted errors occur; we have used the new results for the analysis of EW Ori.

3.3 Times of minima, ephemeris, and apsidal motion

Table 2:   Times of primary (P) and secondary (S) minima of EW Ori determined from the ${\it uvby}$ observations.

Three times of the primary minimum and four of the secondary have been determined from the ${\it uvby}$ light curve observations; see Table 2. A complete list of earlier times of minima was kindly provided by Kreiner and has been included in the ephemeris and apsidal motion analyses; see Kreiner et al. (2001) and Kreiner (2004)[*].

Separate weighted linear least squares fits to the times of primary and secondary minima lead to slightly different orbital periods of $6\hbox{$.\!\!^{\rm d}$ }93684324$ $\pm$ 0.00000044 and $6\hbox{$.\!\!^{\rm d}$ }93684514$ $\pm$ 0.00000018, respectively, and nearly identical results are obtained if only photoelectric and CCD data are used. Whereas this difference indicates a slow apsidal motion, we have adopted the result from the primary minima for the analyses of the ${\it uvby}$ light curves and radial velocities in this paper:

\begin{displaymath}% \begin{array}{r r c r r} {\rm Min ~ I} = & 2~451~877.80142 ... ...93684324 & \times\; E. \\ & \pm 9& & \pm 44 & \\ \end{array}\end{displaymath} (1)

Within uncertainties, the same ephemeris is obtained from the analyses of the ${\it uvby}$ light curves (Sect. 4) if the period and the epoch are included as adjustable parameters.

From a weighted least squares analysis, following the formalism by Giménez & Garcia-Pelayo (1983) and Giménez & Bastero (1995), we obtain the apsidal motion parameters presented in Table 3. The orbital inclination i and eccentricity e were fixed at the values derived from the photometric analysis (Table 5). As seen, a slow but significant motion has been detected, but the apsidal motion period is still very uncertain. Our results agree with those published by Wolf et al. (1997); recently, Wolf et al. (2010) obtained $\omega_1 = 0.00057$ $\pm$ 0.00004 $^\circ$/cycle. We note that the sidereal period is equal to the mean of the periods determined above from primary and secondary eclipses, respectively, and that the longitude of periastron, $\omega$, derived for the epoch of the ${\it uvby}$ observations is identical to the result obtained from the light curve analyses (Sect. 4). The contribution from general relativity (Giménez 1985, Eqs. (3), (4)) is 0.00026 $^\circ$/cycle, or about 62% of the observed rate. Within the rather large uncertainties, the derived mean central density concentration coefficient[*] log(k2) = -1.66 $\pm$ 0.30 marginally agrees with predictions from evolutionary models, -1.91 (Table 10, model set #3).

Table 3:   Apsidal motion parameters for EW Ori derived from all available times of minima.

4 Photometric elements

Since EW Ori is well detached, the photometric elements have been determined from JKTEBOP analyses (Southworth et al. 2004a,b) of the ${\it uvby}$ light curves. The underlying Nelson-Davis-Etzel binary model (Nelson & Davis 1972; Etzel 1981; Martynov 1973) represents the deformed stars as biaxial ellipsoids and applies a simple bolometric reflection model. We refer to Clausen et al. (2008, hereafter CTB08) for details on the binary model and code, and on the general approach applied. In tables and text, we use the following symbols: i orbital inclination; e eccentricity of orbit; $\omega$ longitude of periastron; r relative radius (in units of the semi-major axis); $k = r_{\rm s}/r_{\rm p}$; u linear limb darkening coefficient; y gravity darkening coefficient; J central surface brightness; L luminosity; $T_{\rm eff}$ effective temperature.

The mass ratio between the components was kept at the spectroscopic value; see Sect. 5. The simple built-in bolometric reflection model was used, linear limb darkening coefficients by Van Hamme (1993) and Claret (2000) were applied, or included as free parameters, and gravity darkening coefficients corresponding to convective atmospheres were adopted.

Solutions for EW Ori are presented in Table 4, and as seen, the results from the four bands agree well. Changing from Van Hamme to Claret limb darkening coefficients, which are 0.06-0.10 higher, does not change the orbital and stellar parameters significantly. Coefficients determined from the light curves reproduce those by Van Hamme slightly better than those by Claret; they have formal uncertainties of about ${\pm}0.05$. Including non-linear limb darkening (logarithmic or square-root law) also has no significant effect on the photometric elements.

Table 4:   Photometric solutions for EW Ori from the JKTEBOP code.

The adopted photometric elements listed in Table 5 are the weighted mean values of the JKTEBOP solutions adopting the linear limb darkening coefficients by Van Hamme. Realistic errors, based on 1000 Monte Carlo simulations in each band and on comparison between the ${\it uvby}$ solutions, have been assigned. The Monte Carlo simulations include random variations within ${\pm}0.07$ of the linear limb darkening coefficients. As seen, the relative radii have been established to better than 0.5%. Due to the accurate light curves with about 265 points within eclipses - coupled to the fact that secondary eclipse is total - we obtain a reliable photometric determination of k, and the corresponding luminosity ratios are exactly identical to those derived directly from the depths of the total secondary eclipse. Also, e and $\omega$ are much better constrained than from the radial velocity analyses; see Sect. 5. At phase 0.0, about 90% of the y light from the primary component is eclipsed.

For comparison, Popper et al. (1986) obtained $r_{\rm p} = 0.0561$ $\pm$ 0.005 and k = 0.955 $\pm$ 0.030, an orbital inclination of $i = 89\hbox{$.\!\!^\circ$ }65$ $\pm$ $0\hbox{$.\!\!^\circ$ }1$, and a V luminosity ratio of $L_{\rm s}/L_{\rm p} = 0.745$ $\pm$ 0.037. Inside eclipses, only 69 V,R points from two nights were available, and to constrain k they adopted a fixed $e\sin\omega = -0.0486$, based on e = 0.068 $\pm$ 0.004 from the spectroscopic orbit and $e\cos \omega$determined separately from the light curve analysis.

In conclusion, the new photometric elements differ somewhat from those by Popper et al. and are significantly more accurate.

Table 5:   Adopted photometric elements for EW Ori.

\begin{figure} \par\includegraphics[width=8cm,clip]{13698f2.ps} \end{figure} Figure 2:

($\rm O{-}C$) residuals of the EW Ori y-band observations from the theoretical light curve computed for the photometric elements given in Table 4.

Open with DEXTER

5 Spectroscopic elements

Spectroscopic orbits have been derived from re-analyses of the radial velocities by Popper et al. (1986) and Imbert (2002). We have used the method of Lehman-Filhés implemented in the SBOP[*] program (Etzel 2004), which is a modified and expanded version of an earlier code by Wolfe et al. (1967). The orbital period P was fixed at the ephemeris value (Eq. (1)), and the eccentricity e and longitude of periastron $\omega$ at the better constrained results from the photometric analysis (Table 5). Equal weights were assigned to the radial velocities of Popper et al., whereas the CORAVEL velocities by Imbert were weighted according to the inverse square of their internal errors.

The spectroscopic elements are presented in Table 6. The radial velocities of the components were analysed independently (SB1 solutions), but we note that SB2 solutions lead to nearly identical results. Within errors, the semiamplitudes agree with the published results, which are, however, based on different orbital periods and treatments of e and $\omega$. For the secondary component, the semiamplitudes of our two solutions agree well, whereas they differ by almost 1 km s-1 for the primary. We adopt the elements determined from the CORAVEL velocities, which are more accurate and have a better phase coverage; see Fig. 3.

Table 6:   Spectroscopic orbital solutions for EW Ori determined from re-analyses of the radial velocity observations by Popper et al. (1986) and Imbert (2002).

\begin{figure} \par\includegraphics[width=8cm,clip]{13698f3.ps} \end{figure} Figure 3:

Adopted spectroscopic orbital solution for EW Ori (solid line: primary; dashed line: secondary) and radial velocities (filled circles: primary; open circles: secondary). The dotted line ( upper panel) represents the center-of-mass velocity of the system. Phase 0.0 corresponds to central primary eclipse.

Open with DEXTER

6 Chemical abundances

To determine the chemical composition of EW Ori, we have obtained two high-resolution spectra. They were observed at different phases and opposite line shifts with the FEROS fiber echelle spectrograph at ESO, La Silla January-February 1999; see Table 7. Details on the spectrograph, the reduction of the spectra, and the basic approach followed in the abundance analyses is described by CTB08.

The versatile VWA tool, now extended to analyses of double-lined spectra, was used. We refer to Bruntt et al. (2004,2008) and Bruntt (2009) for detailed descriptions of VWA. It uses the SYNTH software (Valenti & Piskunov 1996) to generate the synthetic spectra. Atmosphere models were interpolated from the recent grid of MARCS model atmospheres (Gustafsson et al. 2008), which adopt the solar composition by Grevesse et al. (2007). Line information was taken from the Vienna Atomic Line Database (VALD; Kupka et al. 1999), but in order to derive abundances relative to the Sun, log(gf) values have been adjusted in such a way that each measured line in the Wallace et al. (1998) solar atlas reproduces the atmospheric abundances by Grevesse et al. (2007). Analyses of a FEROS sky spectrum reproduce these adjustments closely.

The abundance results derived from all useful lines in both spectra are presented in Table 8. We have only included lines with measured equivalent widths above 10 mÅ and below 50 mÅ (primary) and 40 mÅ (secondary). The lines are diluted by a factor of about 1.8 (primary) and 2.3 (secondary), meaning that lines with intrinsic strengths above 90 mÅ are excluded. Comparing the results from the two spectra, we find no significant differences. The effective temperatures, surface gravities and rotational velocities listed in Table 9 were adopted. Microturbulence velocities were tuned until Fe   I abundances were independent of line equivalent widths, and the resulting values are 1.22 $\pm$ 0.16 (primary) and 1.45 $\pm$ 0.30 (secondary) km s-1. The calibration by Edvardsson et al. (1993) predicts 1.48 $\pm$ 0.31 km s-1 (primary) and 1.30 $\pm$ 0.31 (secondary). For the adopted effective temperatures we see no dependency of the abundance on excitation potential, which, however, occurs if they are changed by more than about ${\pm}150$ K.

As seen, a robust $[{\rm Fe/H}]$ is obtained, with identical results from Fe   I and Fe   II lines of both components. Changing the model temperatures by ${\pm}100$ K modifies $[{\rm Fe/H}]$ from the Fe   I lines by about ${\pm}0.06$ dex whereas almost no effect is seen for Fe   II lines. If 0.25 km s-1 higher microturbulence velocities are adopted, $[{\rm Fe/H}]$ decreases by about 0.06 dex for both neutral and ionized lines. Taking these contributions to the uncertainties into account, we adopt $[{\rm Fe/H}]$ = +0.05 $\pm$ 0.09 for EW Ori.

We also find relative abundances close to +0.05 dex for the other ions listed in Table 8, including the $\alpha$-elements Si, Ca, and Ti.

As a supplement to the spectroscopic abundance analyses, we have derived metal abundances from the de-reddened ${\it uvby}$ indices for the individual components (Table 9) and the calibration by Holmberg et al. (2007). The results are: $[{\rm Fe/H}]$ = 0.03 $\pm$ 0.12 (primary) and $[{\rm Fe/H}]$ = -0.05 $\pm$ 0.12 (secondary). Within errors they agree with those from the spectroscopic analysis; the quoted $[{\rm Fe/H}]$ errors include the uncertainties of the photometric indices and the published spread of the calibration.

Table 7:   Log of the FEROS observations of EW Ori.

Table 8:   Abundances ( $[{\rm El./H}]$) for the primary and secondary components of EW Ori determined from the two FEROS spectra.

7 Absolute dimensions

Absolute dimensions for EW Ori are presented in Table 9, as calculated from the photometric and spectroscopic elements given in Tables 5 and 6. As seen, masses and radii accurate to 0.9% and 0.5%, respectively, have been established for the binary components. For the radii, this is a clear improvement compared to the 1-3% different results listed in the new review on masses and radii by Torres et al. (2009), which are based on the work by Popper et al. (1986) and Imbert (2002).

Table 9:   Astrophysical data for EW Ori.

The V magnitudes and ${\it uvby}$ indices for the components included in Table 9 were calculated from the combined magnitudes and indices of the system outside eclipses (Table 1) and the luminosity ratios between the components (Table 5). The V magnitude and the ${\it uvby}$ indices obtained for the primary component agree very well with those measured during the total part of central secondary eclipse (Table 1).

The E(b-y) interstellar reddening, also given in Table 9, was determined from the calibration by Olsen (1988), using the ${\it uvby}\beta$standard photometry for the combined light outside eclipses. For comparison, Popper et al. (1986) estimated E(b-y) = 0.010 $\pm$ 0.009, equivalent to the reddening listed by Torres et al. (2009), E(B-V) = 0.014 $\pm$ 0.012. The model by Hakkila et al. (1997) yields a negative reddening in the direction of and at the distance of EW Ori, whereas the maps by Burstein & Heiles (1982) and Schlegel et al. (1998) give high total E(B-V) reddenings of 0.09 and 0.16, respectively. Knude (private communication) finds that EW Ori is located in or in front of a tiny cloud in the outskirts of the Orion OB Ia association.

From the individual indices and the calibration by Holmberg et al. (2007), we derive effective temperatures of 6070 $\pm$ 95 and 5870 $\pm$ 95 K for the primary and secondary components, respectively, assuming the final $[{\rm Fe/H}]$ abundance. The temperature uncertainties include those of the ${\it uvby}$ indices, E(b-y), $[{\rm Fe/H}]$, and the calibration itself. Temperatures based on the calibrations by Alonso et al. (1996) and Ramírez & Meléndez (2005) are slightly lower but agree within errors. 2MASS photometry of the combined light at phase 0.58 and the $V-K_{\rm s}$ calibration by Masana et al. (2006) gives an ``average'' temperature of 6100 K compared to about 6000 K obtained from the combined ${\it uvby}$ indices. Finally, the empirical flux scale by Popper (1980) and the y flux ratio between the components (Table 5) yield a well-established temperature difference between the components of 170 $\pm$ 30 K (excluding possible errors of the scale itself). Consequently, we assign temperatures of 6070 and 5900 K. They are about 100 K higher than adopted by Popper et al. (1986) and Torres et al. (2009).

The projected rotational velocities listed in Table 9 were determined from broadening function analyses (e.g. Kaluzny et al. 2006) of several orders of the two FEROS spectra (Table 7). Within errors they agree with the synchronous and the pseudo-synchronous values (Hut 1981, Eq. (42)). The turbulent dissipation and radiative damping formalism of Zahn (1977,1989) predicts synchronization time scales of 3.4 $\times$ 108 yr (primary) and 3.6 $\times$ 108 yr (secondary), and a time scale for circularization of 7.4 $\times$ 109 yr, compared to the predicted age of EW Ori of about 2 $\times$ 109 yr (Sect. 9).

The distance to EW Ori was calculated from the ``classical'' relation (see e.g. CTB08), adopting the solar values and bolometric corrections given in Table 9, and AV/E(b-y) = 4.28 (Crawford & Mandwewala 1976). As seen, identical values are obtained for the two components, and the distance has been established to 4%, accounting for all error sources and including the use of other BC scales (e.g. Code et al. 1976; Bessell et al. 1998; Girardi et al. 2002). The empirical K surface brightness - $T_{\rm eff}$ relation by Kervella et al. (2004) leads to nearly identical and perhaps even more precise distances (about $\pm 3$ pc); see Southworth et al. (2005) for details.

As mentioned in Sect. 2, EW Ori has been considered as a possible member of Collinder 70. According to Kharchenko et al. (2005) the distance to this open cluster is 391 pc, its radial velocity is +19.49 km s-1, and its age is 5.1 Gyr. This rules out that EW Ori is a member; see Tables 9, 6, and Sect. 9.

8 Stellar activity

Popper et al. (1986) reported weak evidence for intrinsic variability in their V,R light curves. We see no clear signs of periodic and/or yearly variations, e.g. due to spots, in the ${\it uvby}$ light curves, but on the other hand the rms of the $\rm O{-}C$ residuals of the ${\it uvby}$ observations from the theoretical light curves (Table 4) are marginally higher than expected from the average accuracy per point (Sect. 3.1). The Rossby[*] numbers for the primary and secondary components are approximately 0.90 and 0.42, respectively. This places the secondary in the range where other stars tend to show spot activity (Hall 1994). Also, the FEROS spectra (see Sect. 6) reveal weak Ca   II H and K emission from the secondary component[*]. The secondary component is therefore likely to be active, but at a rather low level. There is no information on X-ray emission from ROSAT (Voges et al. 1999).

9 Discussion

In the following, we compare the absolute dimensions obtained for EW Ori with properties of recent theoretical stellar evolutionary models. A detailed comparison with other similar, well-studied eclipsing binaries will be included in a forthcoming paper.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13698f4.ps} \end{figure} Figure 4:

EW Ori compared with Y2 models for $[{\rm Fe/H}]$ = +0.05. Tracks for the component masses (solid lines, thick) and isochrones for 0.5 and 1.0-4.0 Gyr (dashed; step 1.0 Gyr) are shown. The uncertainty in the location of the tracks coming from the mass errors are indicated (solid lines, thin). Tracks (dotted, blue) and the 2 Gyr isochrone (dash-dot, thin, blue) for $[{\rm Fe/H}]$ = +0.14 are included.

Open with DEXTER

Table 10:   Information on the Claret models and ages inferred from the observed radii; see Figs. 7 and 8.

Figures 4-6 illustrate the results from comparisons with the Yonsei-Yale (Y2) evolutionary tracks and isochrones by Demarque et al. (2004)[*]. The mixing length parameter in convective envelopes is calibrated using the Sun, and is held fixed at $l/H_{\rm p} = 1.7432$. The enrichment law Y = 0.23 + 2Z is adopted, together with the solar mixture by Grevesse et al. (1996), leading to (X, Y, Z)$_{\odot}$ = (0.71564, 0.26624, 0.01812). Only models for $[{\rm\alpha/Fe}]$ = 0.0 have been considered. We refer to CTB08 for a brief description of other aspects of their up-to-date input physics.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13698f5.ps} \end{figure} Figure 5:

EW Ori compared with Y2 models for $[{\rm Fe/H}]$ = +0.05 (solid lines) and $[{\rm Fe/H}]$ = +0.14 (dotted). Isochrones for 0.5 and 1.0-4.0 Gyr (step 1.0 Gyr) are shown.

Open with DEXTER

As seen from Fig. 4, models for the observed masses and abundance, $[{\rm Fe/H}]$ = +0.05, equivalent to (X, Y, Z) = (0.70955, 0.27030, 0.02015), are hotter than observed. Also, the well-established temperature difference between the components, 170 $\pm$ 30 K, is slightly larger than between the corresponding models, although this is partly covered by the uncertainty in the track positions coming from the small 0.9% mass errors. The uncertainty of  $[{\rm Fe/H}]$is ${\pm}0.09$ dex, and models for $[{\rm Fe/H}]$ = +0.14, equivalent to (X, Y, Z) = (0.69695, 0.27870, 0.02435), fit the components better. However, for EW Ori, the correlation between $[{\rm Fe/H}]$and $T_{\rm eff}$is such, that a 0.09 dex higher metal abundance corresponds to 150 K higher temperatures (see Sect. 6), meaning that $[{\rm Fe/H}]$ = +0.14 models actually tend to become a bit too cool. The best match is obtained for the combination of 75 K higher temperatures, e.g. coming from a 0.01 mag higher interstellar reddening, and a 0.04 dex higher  $[{\rm Fe/H}]$.

Turning to the scale-independent masses and radii, Fig. 5 shows that the models predict nearly identical ages, close to 2 Gyr for the components, perhaps with a slight tendency of a higher value for the secondary. From the observed masses and luminosities, the models predict identical but less precise ages of about 1 Gyr ( $[{\rm Fe/H}]$ = +0.05) and 2 Gyr ( $[{\rm Fe/H}]$ = +0.14); see Fig. 6. Comparisons with solar-scaled (VRSS) Victoria-Regina models (VandenBerg et al. 2006) lead to nearly identical results.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13698f6.ps} \end{figure} Figure 6:

EW Ori compared with Y2 models for $[{\rm Fe/H}]$ = +0.05 (solid lines) and $[{\rm Fe/H}]$ = +0.14 (dotted). Isochrones for 0.5 and 1.0-4.0 Gyr (step 1.0 Gyr) are shown.

Open with DEXTER

In conclusion, solar-scaled models provide fairly acceptable fits to the observed properties of EW Ori within their uncertainties. It is, however, of interest to see if specific model tunings can lead to perfect reproduction of EW Ori. To that end, we have calculated dedicated models for the observed $[{\rm Fe/H}]$ using the Granada code by Claret (2004), which assumes an enrichment law of Y = 0.24 + 2.0Z together with the solar mixture by Grevesse & Sauval (1998). The observed $[{\rm Fe/H}]$ = +0.05 then corresponds to (X, Y, Z) = (0.70, 0.28, 0.02). The envelope mixing length parameter needed to reproduce the Sun is $l/H_{\rm p} = 1.68$, and the adopted amount of core overshooting is $\alpha_{\rm ov}$ = 0.20 (in units of the pressure scale height)[*].

Table 10 lists the few models we have investigated, and they are compared to EW Ori in Figs. 7 and 8. The model set #1, which is closest to the Y2 models for $[{\rm Fe/H}]$ = +0.05, show the same temperature and age differences as discussed above, although the track shapes are somewhat different. By decreasing  $l/H_{\rm p}$by 0.14 (primary) and 0.18 (secondary), the models (set #2) match EW Ori perfectly at an age of 1.45 Gyr. Alternatively, keeping the solar  $l/H_{\rm p}$for the primary and decreasing it slightly by 0.08 for the secondary (model set #3) also gives a good fit, provided the helium content is lowered to $Y \approx0.27$, i.e. close to the Y2 value. The predicted age is 2.3 Gyr. For the secondary, which exhibits signs of activity at a mild level (see Sect. 3.1), a lower  $l/H_{\rm p}$ - and thereby larger model radius and lower model temperature - is consistent with findings for other active solar-type binary components (CBC09). On the other hand, for the primary there is no observational background for a lower  $l/H_{\rm p}$, and besides, 2D radiation hydrodynamics calculations (Ludwig et al. 1999) predict mixing length parameters close to the solar value for inactive stars with temperatures and surface gravities like those of the EW Ori components. So, the model set #3 is our preferred fit.

Indications of a need for a slight downwards revision of the helium content, compared to the Y-Z relations adopted for the model grids, has been seen in a few other cases (e.g. VZ Hya, CTB08; V1130 Tau, Clausen et al. 2010). It is, however, still too early to drawn any firm conclusions. We will return to this issue in forthcoming papers on analyses of several new solar-type binaries; see the list in CBC09.

10 Summary and conclusions

From state-of-the-art observations and analyses, precise (0.5-0.9%) absolute dimensions have been established for the components of the totally eclipsing G0 V system EW Ori. A detailed spectroscopic analysis yields an iron abundance relative to the Sun of $[{\rm Fe/H}]$ = +0.05 $\pm$ 0.09 and similar relative abundances for Si, Ca, Sc, Cr, and Ni.

The 1.12 $M_{\odot}$ secondary component reveals weak Ca   II H and K emission and is probably mildly active; we see no signs of activity for the 1.17 $M_{\odot}$ primary. Apsidal motion ( U = 16 300 $\pm$ 3900 yr) with a 62% relativistic contribution has been detected for the eccentric orbit ( e = 0.0758 $\pm$ 0.0020), and the inferred mean central density concentration coefficient, log(k2) = -1.66 $\pm$ 0.30, agrees marginally with model predictions. The measured rotational velocities, 9.0 $\pm$ 0.7 (primary) and 8.8 $\pm$ 0.6 (secondary) km s-1, are in agreement with both synchronous rotation and the theoretically predicted pseudo-synchronous velocities.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13698f7.ps} \end{figure} Figure 7:

EW Ori compared to Claret models for the observed masses and $[{\rm Fe/H}]$ abundance. See Table 10 for details and linestyles/colours.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13698f8.ps} \end{figure} Figure 8:

EW Ori compared to Claret models for the observed masses and $[{\rm Fe/H}]$ abundance. See Table 10 for details. The curves illustrate model radii as function of age for the components (upper: primary; lower: secondary). The horizontal full drawn lines mark the observed radii of the components with errors (dotted lines). The vertical lines mark the ages predicted for the primary component.

Open with DEXTER

Stellar models with solar-scaled envelope mixing length parameters reproduce the observed properties of EW Ori fairly well at an age of $\approx$2 Gyr. We demonstrate, however, that perfect agreement can be obtained by a) a slight downwards adjustment of the envelope mixing length parameter for the secondary, as seen for other active solar-type stars; and b) a slightly lower helium content than prescribed by the Y-Z relations adopted for the various standard model grids.

This study is part of a larger project on solar-type eclipsing binaries; see e.g. CBC09.



Acknowledgements

It is a great pleasure to thank the many colleagues and students, who have shown interest in our project and have participated in the extensive (semi)automatic observations of EW Ori at the SAT: Gwillerm Berard, Vanessa Doublier, Mathias P. Egholm, Anders Johansen, Erling Johnsen, Helene Jørgensen, Raslan Leguet, Gilbert Mahoux, and John D. Pritchard. Excellent technical support was received from the staffs of Copenhagen University and ESO, La Silla. We thank J. M. Kreiner for providing a complete list of published times of eclipses for EW Ori and J. Southworth for access to his JKTEBOP code. G. Torres and J. Knude kindly made independent interstellar reddening information available. The projects ``Stellar structure and evolution - new challenges from ground and space observations'' and ``Stars: Central engines of the evolution of the Universe'', carried out at Copenhagen University and Aarhus University, are supported by the Danish National Science Research Council. The following internet-based resources were used in research for this paper: the NASA Astrophysics Data System; the SIMBAD database and the VizieR service operated by CDS, Strasbourg, France; the ar$\chi$iv scientific paper preprint service operated by Cornell University; the VALD database made available through the Institute of Astronomy, Vienna, Austria; the MARCS stellar model atmosphere library. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/ California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.

References

  1. Alonso, A., Arribas, S., & Martínez-Roger, C. 1996, A&A, 313, 873 [NASA ADS] [Google Scholar]
  2. Arrelano Ferro, A., Parrao, L., Schuster, W., et al. 1990, A&AS, 83, 225 [Google Scholar]
  3. Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
  4. Bruntt, H. 2009, A&A, 506, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bruntt, H., Bikmaev, I. F., Catala, C., et al. 2004, A&A, 425, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bruntt, H., De Cat, P., & Aerts, C. 2008, A&A, 478, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Burstein, D., & Heiles, C. 1982, AJ, 87, 1165 [NASA ADS] [CrossRef] [Google Scholar]
  8. Claret, A. 1995, A&AS, 109, 441 [NASA ADS] [Google Scholar]
  9. Claret, A. 1997, A&AS, 125, 439 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
  10. Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
  11. Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Clausen, J. V., Helt, B. E., & Olsen, E. H. 2001, A&A, 374, 980 (CHO01) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Clausen, J. V., Torres, G., Bruntt, H., et al. 2008, A&A, 487, 1095 (CTB08) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Clausen, J. V., Bruntt, H., Claret, A., et al. 2009, A&A, 502, 253 (CBC09) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Clausen, J. V., Olsen, E. H., Helt, B. E., & Claret, A. 2010, A&A, 510, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Code, A. D., Bless, R. C., Davis, J., & Brown, R. H. 1976, ApJ, 203, 417 [NASA ADS] [CrossRef] [Google Scholar]
  17. Crawford, D. L., & Mandwewala, N. 1976, PASP, 88, 917 [NASA ADS] [CrossRef] [Google Scholar]
  18. Crawford, D. L., Barnes, J. V., Faure, B. Q., Golson, J. C., & Perry, C. 1966, AJ, 71, 709 [NASA ADS] [CrossRef] [Google Scholar]
  19. Demarque, P., Woo, J.-H., Kim, Y.-C., & Yi, S. K. 2004, ApJS, 155, 667 [NASA ADS] [CrossRef] [Google Scholar]
  20. Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
  21. Etzel P. B. 1981, in Photometric and Spectroscopic Binary Systems, ed. E. B. Carling, & Z. Kopal (NATO), 111 [Google Scholar]
  22. Etzel, P. B. 2004, SBOP: Spectroscopic Binary Orbit Program, San Diego State University [Google Scholar]
  23. Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
  24. Giménez, A. 1985, ApJ, 297, 405 [NASA ADS] [CrossRef] [Google Scholar]
  25. Giménez, A., & Garcia-Pelayo, J. 1983, Ap&SS, 92, 203 [NASA ADS] [CrossRef] [Google Scholar]
  26. Giménez, A., & Bastero, M. 1995, Ap&SS, 226, 99 [NASA ADS] [CrossRef] [Google Scholar]
  27. Giménez, A., & Clausen, J. V. 1996, in The Origins, Evolution, and Destinies of Binary Stars in Clusters, ed. E. F. Milone, & J.-C. Mermilliod, ASP Conf. Ser., 90, 44 [Google Scholar]
  28. Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
  30. Grevesse, N., Noels, A., & Sauval, A. J. 1996, in Cosmic Abundances, ed. S. S. Holt, & G. Sonneborn (San Francisco: ASP), 117 [Google Scholar]
  31. Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
  32. Grønbech, B., & Olsen, E. H. 1976, A&AS, 25, 213 [NASA ADS] [Google Scholar]
  33. Grønbech, B., & Olsen, E. H. 1977, A&AS, 27, 443 [NASA ADS] [Google Scholar]
  34. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Hakkila, J., Myers, J. M., Stidham, B. J., & Hartmann, D. H. 1997, AJ, 114, 2043 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hall, D. S. 1994, Mem. Soc. Astron. Italiana, 65, 73 [NASA ADS] [Google Scholar]
  37. Hilditch, R. W., & Hill, G. 1975, MmRAS, 79, 101 [Google Scholar]
  38. Hoffmeister, C. 1930, Astron. Nachr., 238, 190 [NASA ADS] [Google Scholar]
  39. Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  40. Houk, N., & Swift, C. 1999, Michigan Catalogue of two-dimensional spectraltypes for HD stars, Dep. Astron., Univ. Michigan, Ann Arbor, Michigan, USA, 5 [Google Scholar]
  41. Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
  42. Imbert, M. 2002, A&A, 387, 850 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Kaluzny, J., Pych, W., Rucinski, S. M., & Thompson, I. B. 2006, , 56, 237 [Google Scholar]
  44. Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R.-D. 2005, A&A, 438, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  46. Kreiner, J. M. 2004, , 54, 207 [Google Scholar]
  47. Kreiner, J. M., Kim, C. H., & Nha, I. S. 2001, an Atlas of O-C Diagrams of Eclipsing Binary Stars (Krakow: Wydawnictwo Naukowe Akad. Pedagogicznej) [Google Scholar]
  48. Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  49. Lacy, C. H. 1984, Inf. Bull. Var. Stars, 2489 [Google Scholar]
  50. Lacy, C. H. S. 2002, AJ, 124, 1162 [NASA ADS] [CrossRef] [Google Scholar]
  51. Lastennet, E., & Vals-Gabaud, D. 2002, A&A, 396, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Lause, F. 1937, Astron. Nachr., 263, 115 [NASA ADS] [CrossRef] [Google Scholar]
  53. Ludwig, H.-G., Freytag, B., & Steffen, M. 1999, A&A, 346, 111 [NASA ADS] [Google Scholar]
  54. Martynov, D. Ya. 1973, in Eclipsing Variable Stars, ed. V. P. Tsesevich, Israel Program for Scientific Translation, Jerusalem [Google Scholar]
  55. Masana, E., Jordi, C., & Ribas, I. 2006, A&A, 450, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Nelson B., & Davis, W. 1972, ApJ, 174, 617 [NASA ADS] [CrossRef] [Google Scholar]
  57. Olsen, E. H. 1983, A&AS, 54, 55 [Google Scholar]
  58. Olsen, E. H. 1988, A&A, 189, 173 [NASA ADS] [Google Scholar]
  59. Olsen, E. H. 1994, A&AS, 106, 257 [Google Scholar]
  60. Pols, O. R., Tout, C. A., Schröder, K.-P., Eggleton, P. P., & Manners, J. 1997, MNRAS, 289, 869 [NASA ADS] [CrossRef] [Google Scholar]
  61. Popper, D. M. 1980, ARA&A, 18, 115 [NASA ADS] [CrossRef] [Google Scholar]
  62. Popper, D. M., Lacy, C. H., Frueh, M. L., & Turner, A. E. 1986, AJ, 91, 383 [NASA ADS] [CrossRef] [Google Scholar]
  63. Ramírez, I., & Meléndez, J. 2005, AJ, 626, 465 [Google Scholar]
  64. Ribas, I., Jordi, C., Torra, J., & Giménez, A. 2000, MNRAS, 313, 99 [NASA ADS] [CrossRef] [Google Scholar]
  65. Sahade, J., & Dávila, F. B. 1963, AnAp, 26, 153 [Google Scholar]
  66. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  67. Southworth, J., Maxted, P. F. L., & Smalley, B. 2004a, MNRAS, 351, 1277 [NASA ADS] [CrossRef] [Google Scholar]
  68. Southworth, J., Zucker, S., Maxted, P. F. L., & Smalley, B. 2004b, MNRAS, 355, 986 [NASA ADS] [CrossRef] [Google Scholar]
  69. Southworth, J., Maxted, P. F. L., & Smalley, B. 2005, A&A, 429, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
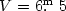  70. Strömgren, B., & Perry, C. 1965, Photoelectric Photometry for 1217 Stars Brighter thanFormula , mostly of spectral classes A, F and G, Inst. Advanced Study, Princeton, New Jersey, preprint [Google Scholar]
  71. Torres, G., Andersen, J., & Giménez, A. 2009, A&ARv, in press [Google Scholar]
  72. Valenti, J., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. VandenBerg, D. A., Bergbusch, P. A., & Dowler, P. D. 2006, ApJS, 162, 375 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  74. Van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] [Google Scholar]
  75. Voges, W., Aschenbach, B., Boller, T., et al. 1999 [Google Scholar]
  76. Wallace, L., Hinkle, K., & Livingston, W. 1998, an atlas of the spectrum of the solar photosphere from 13 500 to 28 000 cm-1 (3570 to 7405 A) (Tucon, AZ: NOAO) [Google Scholar]
  77. Wolf, M., Sarounova, L., Kozyreva, V. S., & Pogrocheva, T. 1997, Inf. Bull. Var. Stars, 4542 [Google Scholar]
  78. Wolf, M., Claret, A., Kotková, L., et al. 2010, A&A, 509, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Wolfe, R. H., Horak, H. G., & Storer, N. W. 1967, in Modern Astrophysics: A Memorial to Otto Struve, ed. M. Hack, 251 [Google Scholar]
  80. Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
  81. Zahn, J.-P. 1989, A&A, 220, 112 [NASA ADS] [Google Scholar]

Footnotes

... system[*]
Based on observations carried out at the Strömgren Automatic Telescope (SAT) and the 1.5 m telescope (62.L-0284) at ESO, La Silla.
...[*]
Table 11 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/511/A22
...2004)[*]
http://www.as.ap.krakow.pl/ephem
... coefficient[*]
See e.g. Giménez (1985) for the definition of k2 and for references to the ``classical'' papers.
... SBOP[*]
Spectroscopic Binary Orbit Program, http://mintaka.sdsu.edu/faculty/etzel/
... Rossby[*]
Defined as the ratio of the rotation period to the convective turnover time.
... component[*]
Popper et al. (1986) saw no emission, probably due to inadequate resolution.
...2004)[*]
http://www.astro.yale.edu/demarque/yystar.html
... height)[*]
Models without core overshooting are very similar at the age of EW Ori.

All Tables

Table 1:   Photometric data for EW Ori and the comparison stars.

Table 2:   Times of primary (P) and secondary (S) minima of EW Ori determined from the ${\it uvby}$ observations.

Table 3:   Apsidal motion parameters for EW Ori derived from all available times of minima.

Table 4:   Photometric solutions for EW Ori from the JKTEBOP code.

Table 5:   Adopted photometric elements for EW Ori.

Table 6:   Spectroscopic orbital solutions for EW Ori determined from re-analyses of the radial velocity observations by Popper et al. (1986) and Imbert (2002).

Table 7:   Log of the FEROS observations of EW Ori.

Table 8:   Abundances ( $[{\rm El./H}]$) for the primary and secondary components of EW Ori determined from the two FEROS spectra.

Table 9:   Astrophysical data for EW Ori.

Table 10:   Information on the Claret models and ages inferred from the observed radii; see Figs. 7 and 8.

All Figures

  \begin{figure} \par\includegraphics[width=17cm,clip]{13698f1.ps} \end{figure} Figure 1:

y light curve and b-y and u-b colour curves (instrumental system) for EW Ori.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13698f2.ps} \end{figure} Figure 2:

($\rm O{-}C$) residuals of the EW Ori y-band observations from the theoretical light curve computed for the photometric elements given in Table 4.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13698f3.ps} \end{figure} Figure 3:

Adopted spectroscopic orbital solution for EW Ori (solid line: primary; dashed line: secondary) and radial velocities (filled circles: primary; open circles: secondary). The dotted line ( upper panel) represents the center-of-mass velocity of the system. Phase 0.0 corresponds to central primary eclipse.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13698f4.ps} \end{figure} Figure 4:

EW Ori compared with Y2 models for $[{\rm Fe/H}]$ = +0.05. Tracks for the component masses (solid lines, thick) and isochrones for 0.5 and 1.0-4.0 Gyr (dashed; step 1.0 Gyr) are shown. The uncertainty in the location of the tracks coming from the mass errors are indicated (solid lines, thin). Tracks (dotted, blue) and the 2 Gyr isochrone (dash-dot, thin, blue) for $[{\rm Fe/H}]$ = +0.14 are included.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13698f5.ps} \end{figure} Figure 5:

EW Ori compared with Y2 models for $[{\rm Fe/H}]$ = +0.05 (solid lines) and $[{\rm Fe/H}]$ = +0.14 (dotted). Isochrones for 0.5 and 1.0-4.0 Gyr (step 1.0 Gyr) are shown.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13698f6.ps} \end{figure} Figure 6:

EW Ori compared with Y2 models for $[{\rm Fe/H}]$ = +0.05 (solid lines) and $[{\rm Fe/H}]$ = +0.14 (dotted). Isochrones for 0.5 and 1.0-4.0 Gyr (step 1.0 Gyr) are shown.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13698f7.ps} \end{figure} Figure 7:

EW Ori compared to Claret models for the observed masses and $[{\rm Fe/H}]$ abundance. See Table 10 for details and linestyles/colours.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13698f8.ps} \end{figure} Figure 8:

EW Ori compared to Claret models for the observed masses and $[{\rm Fe/H}]$ abundance. See Table 10 for details. The curves illustrate model radii as function of age for the components (upper: primary; lower: secondary). The horizontal full drawn lines mark the observed radii of the components with errors (dotted lines). The vertical lines mark the ages predicted for the primary component.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.