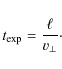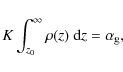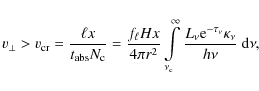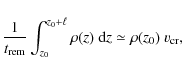| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 8 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200912035 | |
| Published online | 19 February 2010 | |
The destruction and survival of polycyclic aromatic hydrocarbons in the disks of T Tauri stars
R. Siebenmorgen1 - E. Krügel2
1 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748
Garching b. München, Germany
2 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, Postfach
2024, 53010 Bonn, Germany
Received 10 March 2009 / Accepted 4 December 2009
Abstract
In Spitzer observations of Tauri stars and their disks, features of
polycyclic aromatic hydrocarbons (PAHs) are detected in less than 10%
of the objects, although the stellar photosphere is sufficiently hot to
excite PAHs. To explain the deficiency, we discuss
PAH destruction by photons, assuming that the star has beside
its photospheric emission also a far ultraviolet (FUV), an extreme
ultraviolet (EUV) and an X-ray component with a fractional luminosity
of 1%, 0.1% and 0.025%, respectively. We consider as a PAH destruction
process unimolecular dissociation and present a simplified scheme to
estimate the location from the star at which the molecules become
photo-stable. We find that soft photons with energies below ![]() 20 eV
dissociate PAHs only up to short distances from the star (r
< 1 AU); whereas dissociation by hard photons (EUV and
X-ray) is so efficient that it would destroy all PAHs (from regions in
the disk where they could be excited). As a possible path for
PAH-survival we suggest turbulent motions in the disk. They can
replenish or remove PAHs from the reach of hard photons. For standard
disk models, where the surface density changes like r-1
and the mid plane temperature like r-0.5,
the critical vertical velocity for PAH survival is proportional to r-3/4
and equals
20 eV
dissociate PAHs only up to short distances from the star (r
< 1 AU); whereas dissociation by hard photons (EUV and
X-ray) is so efficient that it would destroy all PAHs (from regions in
the disk where they could be excited). As a possible path for
PAH-survival we suggest turbulent motions in the disk. They can
replenish or remove PAHs from the reach of hard photons. For standard
disk models, where the surface density changes like r-1
and the mid plane temperature like r-0.5,
the critical vertical velocity for PAH survival is proportional to r-3/4
and equals ![]() 5 m/s
at 10 AU, which is in the range of expected velocities in the
surface layer. The uncertainty in the parameters is large enough to
explain both detection and non-detection of PAHs. Our approximate
treatment also takes into account the presence of gas which is ionized
at the top of the disk and neutral at lower levels.
5 m/s
at 10 AU, which is in the range of expected velocities in the
surface layer. The uncertainty in the parameters is large enough to
explain both detection and non-detection of PAHs. Our approximate
treatment also takes into account the presence of gas which is ionized
at the top of the disk and neutral at lower levels.
Key words: protoplanetary disks - dust, extinction - infrared: stars - X-rays: stars - X-rays: ISM - radiation mechanisms: general
1 Introduction
Infrared emission bands of PAHs can be used as a probe of the UV environment. They are commonly seen in the interstellar medium (ISM), but also in young stellar objects such as Herbig Ae/Be stars (Waelkens et al. 1996; Siebenmorgen et al. 2000; Meeus et al. 2001; Peeters et al. 2002; van Boekel et al. 2004). The observed emission can be explained in models of an irradiated disk (Habart et al. 2004; Visser et al. 2007; Dullemond et al. 2007a).
The infrared space observatory (ISO) looked at a few of the
much
fainter T Tauri stars, but without a clear PAH detection
(Siebenmorgen
et al. 2000).
In the Evans et al. (2003) legacy
program, which
employs the more sensitive Spitzer Space Telescope (SST), three out of
38 T Tauri stars show PAH features (Geers
et al. 2006).
This
corresponds to a detection rate of only 8% in contrast to almost 60%
found in Herbig Ae/Be stars (Acke &
van den Ancker 2004).
Similarly
low rates for T Tauri stars are found by Furlan
et al. (2006)
who
present 111 SST spectra in the Taurus-Auriga star forming region and
speculate that the absence of PAH resonances is due to the much weaker
UV field compared to Herbig Ae/Be stars. Geers
et al. (2009),
on the
other hand, argue that the PAHs are simply under-abundant relative to
the ISM. They also find that variations of the disk geometry, such as
flaring or gaps, have only a small effect on the strength of the PAH
bands. Clearing out gas and dust by planet formation inside the disk
could effectively remove PAHs. Indeed, inner gaps in disks are
observed at radii between 40-60 AU and at wavelengths between
20-1000 ![]() m,
where the emission is dominated by large grains (Brown
et al. 2008;
Geers et al. 2007b).
But in cases where PAH emission is
resolved, it is extended up to 15-60 AU without sub-structure
and
inside the inner gap region (Geers et al. 2007a). The
spatial extent
of the PAH emission is similar for T Tauri as well as Herbig
Ae/Be
stars. We therefore suggest that PAH removal by radiative destruction
is dominant.
m,
where the emission is dominated by large grains (Brown
et al. 2008;
Geers et al. 2007b).
But in cases where PAH emission is
resolved, it is extended up to 15-60 AU without sub-structure
and
inside the inner gap region (Geers et al. 2007a). The
spatial extent
of the PAH emission is similar for T Tauri as well as Herbig
Ae/Be
stars. We therefore suggest that PAH removal by radiative destruction
is dominant.
Present radiative transfer models of the PAH emission from dusty disks consider only the stellar radiation field and no additional EUV or X-ray component (Habart et al. 2004; Geers et al. 2006; Visser et al. 2007; Dullemond et al. 2007a). Their hard photons could, according to laboratory experiments (Ruhl et al. 1989; Leach et al. 1989a,b; Jochims et al. 1994) and theory (Omont 1986; Tielens 2005; Rapacioli et al. 2006; Micelotta et al. 2010a,b), destroy PAHs. We discuss below their impact on the PAH abundance in the disks of T Tauri stars.
Table 1: The four radiation components of our T Tauri model star.
2 Radiation components of T Tauri stars
Our T Tauri model star has a total luminosity L*=2 ![]() .
Its
radiation consists of a photospheric, a FUV, an EUV and an X-ray
component. Their parameters are listed in Table 1 and
are very similar to those proposed by Gorti & Hollenbach (2008). The
total spectrum is displayed in Fig. 1. We point out that
the FUV and EUV radiation are observationally poorly constrained.
.
Its
radiation consists of a photospheric, a FUV, an EUV and an X-ray
component. Their parameters are listed in Table 1 and
are very similar to those proposed by Gorti & Hollenbach (2008). The
total spectrum is displayed in Fig. 1. We point out that
the FUV and EUV radiation are observationally poorly constrained.
![\begin{figure}
\par\includegraphics[angle=0,width=6.8cm,clip]{AA200912035Fig1.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12035-09/Timg32.png)
|
Figure 1: The spectral energy distribution of our T Tauri model star at 1 AU without foreground extinction (Eq. (1)). The absolute luminosities of the components are given in Table 1. |
| Open with DEXTER | |
The photosphere supplies most of the luminosity, whereas the FUV, EUV
and X-ray radiation are much weaker and believed to originate from
accretion onto the star as well as from chromospheric and coronal
activity. The photosphere, the FUV and EUV component are approximated
by blackbodies. We assume 4000 K for the photosphere and,
following
Stahler et al. (1980) and
Calvet & Gullbring (1998),
15 000 K for the
FUV (pre-shock) and ![]()
![]() K for the EUV
emission
(post-shock region).
K for the EUV
emission
(post-shock region).
The strength of the FUV and EUV radiation is determined by the
accretion luminosity, which we approximate by
![]() .
If R* = 2
.
If R* = 2 ![]() and M* = 1
and M* = 1 ![]() are the
radius and mass of the star, an accretion rate
are the
radius and mass of the star, an accretion rate
![]()
![]() yr-1 (Akeson et al. 2005) yields
yr-1 (Akeson et al. 2005) yields
![]() .
Higher values (
.
Higher values (
![]() ),
but with a
large spread, are derived by Muzerolle et al. (1998, 2003) from
hydrogen emission lines. However, as we show in Sect. 5,
such stronger fluxes have little influence on the stability analysis
of PAHs.
),
but with a
large spread, are derived by Muzerolle et al. (1998, 2003) from
hydrogen emission lines. However, as we show in Sect. 5,
such stronger fluxes have little influence on the stability analysis
of PAHs.
Preibisch et al. (2006)
establish from Chandra observations
(0.5-8 keV) a relation between the X-ray luminosity ![]() and
the total luminosity L*,
confirming the ROSAT results of Sterzik &
Schmitt (1997).
The ratio
and
the total luminosity L*,
confirming the ROSAT results of Sterzik &
Schmitt (1997).
The ratio ![]() is similar in rapidly rotating
main-sequence stars and non-accreting T Tauri stars (
is similar in rapidly rotating
main-sequence stars and non-accreting T Tauri stars (![]() 10-3),
but systematically lower by a factor of about four in accreting T
Tauri stars (Preibisch et al. 2006).
Interestingly,
10-3),
but systematically lower by a factor of about four in accreting T
Tauri stars (Preibisch et al. 2006).
Interestingly, ![]() is much
smaller (
is much
smaller (![]()
![]() ,
Stelzer et al. 2006) in
Herbig Ae/Be stars, with values comparable to those of the
Sun. The
solar X-ray luminosity in the 0.1-2.4 keV ROSAT passband lies
in
the range of
,
Stelzer et al. 2006) in
Herbig Ae/Be stars, with values comparable to those of the
Sun. The
solar X-ray luminosity in the 0.1-2.4 keV ROSAT passband lies
in
the range of
![]() during a
solar cycle and is typical for G stars (Judge et al. 2003).
during a
solar cycle and is typical for G stars (Judge et al. 2003).
X-ray fluxes are generally variable on timescales of hours to
weeks
and weaken during the evolution of the T Tauri star. For
example,
half of the sources in the Taurus molecular cloud detected by
XMM/Newton (0.3-7.8 keV) show variations, more often at hard
(>0.5 keV) than at soft energies, and a quarter of them
display
flares (Stelzer et al. 2007) about
once a week and lasting for a few
hours. In a strong flare, more than 1035 erg
are emitted, and
![]() can reach 1%
of the total luminosity. We assume up to 2 keV a
power law spectrum
can reach 1%
of the total luminosity. We assume up to 2 keV a
power law spectrum ![]()
![]() (Güdel et al. 2007)
and neglect
harder radiation, because the emission then steeply declines (
(Güdel et al. 2007)
and neglect
harder radiation, because the emission then steeply declines (![]()
![]() ).
).
Let Li
be the frequency-integrated luminosity of the radiation
component i (see Table 1) and ![]() its spectral
luminosity, so that
its spectral
luminosity, so that
![]() .
Dropping the index
i for convenience, the flux (of the component i )
at a distance
r is
.
Dropping the index
i for convenience, the flux (of the component i )
at a distance
r is
We include a screening factor
photons of total energy
The inverse of
The mean photon energy equals
3 Cross sections
As the light from the star enters the disk, it is attenuated by gas and dust. The absorption cross section of gas depends on the ionization stage of the atoms, which is determined by the balance between recombination and photo-ionization. By far the most important atoms are, of course, hydrogen and helium with ionization potentials of 13.6 eV and 24.6 eV, respectively. Because the recombination rate is proportional to the square of the gas density, which is high in the disk (Sect. 5), the gas is ionized only in a thin surface layer ( AV < 0.001 mag, Sect. 2.6 of Gorti & Hollenbach 2008). We use the atomic cross sections of Morrison & McCommon (1982) and Balucinska-Church & McCommon (1992) as well as solar element abundances.
The dust cross sections are taken from the model of Krügel (2006),
which describes standard dust. The absorption efficiency calculated
from the Mie theory must be corrected downwards for X-rays. Hard
photons can eject electrons from the grain, and as these conduct
kinetic energy, only part of the photon energy is deposited in the
dust particle. The threshold ![]() ,
above which such a
correction is necessary, depends on the grain size; details are given
in Dwek & Smith (1996).
For a 10 Å graphite particle,
,
above which such a
correction is necessary, depends on the grain size; details are given
in Dwek & Smith (1996).
For a 10 Å graphite particle,
![]() eV,
and the reduction factor is roughly proportional to
eV,
and the reduction factor is roughly proportional to ![]() .
.
The absorption coefficient of dust
![]() and of neutral
gas plus dust
and of neutral
gas plus dust
![]() ,
both per gram of disk material, are plotted in Fig. 2 for
a dust-to-gas mass ratio of 1:130. Note that at the ionization
threshold of hydrogen,
,
both per gram of disk material, are plotted in Fig. 2 for
a dust-to-gas mass ratio of 1:130. Note that at the ionization
threshold of hydrogen, ![]() is almost 104 times greater
than
is almost 104 times greater
than ![]() .
.
| Figure 2: The mass extinction coefficient per gram disk material when the gas is neutral (Morrison & McCommon 1983); the gas-to-dust mass ratio equals 130. |
|
| Open with DEXTER | |
With respect to the absorption cross section of PAHs, we assume
![]() cm2
per carbon atom when
cm2
per carbon atom when ![]() eV,
and scale
eV,
and scale ![]() at higher energies to follow the
values of a graphite sphere of 10 Å radius (Dwek &
Smith 1996).
The maximum wavelength (in Å) for the PAH excitation is
at higher energies to follow the
values of a graphite sphere of 10 Å radius (Dwek &
Smith 1996).
The maximum wavelength (in Å) for the PAH excitation is
![]() (Schutte
et al. 1993),
resulting in a minimum photon energy of 2.3 eV for a PAH with
(Schutte
et al. 1993),
resulting in a minimum photon energy of 2.3 eV for a PAH with
![]() carbon atoms.
carbon atoms.
3.1 PAH emission
As the PAHs are transiently heated, their excitation is usually
treated statistically. For the computation we follow the method of
Guhathakurta & Draine (1989) who
consider a large ensemble of PAHs in
a steady state. Let ![]() be the probability of finding an
arbitrary PAH in the temperature interval
be the probability of finding an
arbitrary PAH in the temperature interval
![]() .
The temperature
distribution P(T) is calculated
in this method from a transition
matrix
.
The temperature
distribution P(T) is calculated
in this method from a transition
matrix ![]() .
The PAH absorption cross section is denoted by
.
The PAH absorption cross section is denoted by
![]() .
The matrix element
.
The matrix element ![]() refers to dust heating from an
initial enthalpy bin centered at
refers to dust heating from an
initial enthalpy bin centered at ![]() to a final one centered at
to a final one centered at
![]() .
The final enthalpy bin is of a width of
.
The final enthalpy bin is of a width of
![]() .
For a
mono-chromatic flux, the transition matrix equals to
.
For a
mono-chromatic flux, the transition matrix equals to
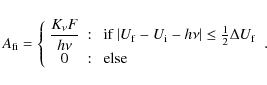
|
Examples of P(T) are displayed in Fig. 3 for mono-chromatic fluxes, which cover almost the entire range encountered anywhere in the disk in terms of intensity, the flux is varied from F=10 to 107 erg s-1 cm-2, and also the hardness, the photon energy is between
![\begin{figure}
\par\includegraphics[angle=0,width=7cm,clip]{AA200912035Fig3.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12035-09/Timg81.png)
|
Figure 3:
The temperature distribution P(T)
of a PAH with 100 C atoms exposed to mono-chromatic radiation
with |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=0,width=6.8cm,clip]{AA200912035Fig4.ps}
\vspace*{8mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12035-09/Timg82.png)
|
Figure 4:
The power |
| Open with DEXTER | |
4 PAH destruction
The abundance of PAHs is determined by the competition between the formation and destruction processes under the specific environmental conditions. Underlying processes are discussed, for example, by Omont (1986), Voit (1992), or recently by Micelotta et al. (2010a). Here we only consider PAH destruction by photons and generally assume that PAH formation is negligible. After photon absorption, a highly vibrationally excited PAH may relax through emission of IR photons or, if sufficiently excited, lose atoms. The latter process is called unimolecular dissociation and is discussed for interstellar PAHs by Allamandola (1989), Leger et al. (1989), Le Page et al. (2003), Rapacioli et al. (2006), and Micelotta et al. (2010b). Laboratory studies of PAH dissociation which can be applied to astrophysical situations are rare (Jochims et al. 1994). The photo-chemistry of PAHs is reviewed by Tielens (2005, 2008).
4.1 Procedure
In the disks of T Tau stars, the PAH abundance obviously depends on
place and on time as the disk evolves. There is no general solution
to the problem, and to extract numbers, we have to radically simplify
it. We wish to find some estimate of the location where PAHs become
stable against photo-destruction. To derive a procedure, we recall
that although after absorption of an energetic photon its energy is
immediately distributed over all available vibrational modes
(Allamandola et al. 1989), the
excitation of a particular atom
fluctuates, and it is occasionally pushed into the continuum and
leaves the PAH. Quantitatively, the unimolecular dissociation can be
written in the Arrhenius form. In a classical description, an atom of
a critical (Arrhenius) energy ![]() detaches from a PAH of a
peak temperature
detaches from a PAH of a
peak temperature ![]() if the dissociation time
if the dissociation time
is shorter than the cooling time
The exponential term
![]() in Eq. (7)
increases very rapidly as T falls, and meaningful
values (i.e. not
too large ones) of
in Eq. (7)
increases very rapidly as T falls, and meaningful
values (i.e. not
too large ones) of ![]() are obtained only if
are obtained only if ![]() K.
Atoms will only detach when
K.
Atoms will only detach when
![]() .
As the cooling time at these temperatures is for astrophysical
applications on the order of 1 s, independent of the PAH size,
the
dissociation criterion reads
.
As the cooling time at these temperatures is for astrophysical
applications on the order of 1 s, independent of the PAH size,
the
dissociation criterion reads
It leads to a minimum temperature for destruction
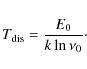
|
(8) |
Assuming
or when the number of carbon atoms
Micelotta et al. (2010b) find that a PAH with
The minimum energy input required for dissociation can either
be
delivered by absorption of i) many soft photons
with a total
energy ![]() (Eq. (3));
or ii) by a single hard photon, with an
energy
(Eq. (3));
or ii) by a single hard photon, with an
energy ![]() .
If a
photon heats the PAH to a peak temperature much above
.
If a
photon heats the PAH to a peak temperature much above
![]() ,
more than one atom will detach. The first expulsion occurs
momentarily (
,
more than one atom will detach. The first expulsion occurs
momentarily (
![]() s). It consumes the
energy
s). It consumes the
energy ![]() plus some kinetic energy
plus some kinetic energy ![]() for the liberated atom.
The new PAH temperature follows from
for the liberated atom.
The new PAH temperature follows from
| (11) |
This happens x times until T has dropped to
| (12) |
With
For
Table 2: Quantities relevant to PAH survival.
4.2 Disruption by Coulomb forces
For completeness we also mention the possible disruption of PAHs by
Coulomb forces. Double or multiple ionization of a PAH loosens the
binding of the peripheral H atoms as well as that of the skeleton of
carbon atoms. The ejection of K-shell electrons by X-ray photons
(
![]() eV) in combination
with Auger electrons will amplify
the process. Coulomb explosion is relevant mainly for small PAHs and
is neglected here.
eV) in combination
with Auger electrons will amplify
the process. Coulomb explosion is relevant mainly for small PAHs and
is neglected here.
5 Conditions for PAH survival
According to Eq. (10),
PAHs are destroyed if the source
emits photons of an energy
![]() ,
irrespective of the distance to the star or its luminosity. For
,
irrespective of the distance to the star or its luminosity. For
![]() ,
the critical photon energy is only 50 eV (Eq. (10)).
As T Tauri stars (or their jets) also radiate at X-rays and in
the
EUV, the surface of the disk should be devoid of PAHs unless a) the
period over which hard photons are emitted is too short to destroy
all PAHs; b) the PAHs are removed by
vertical motions from the
hard radiation before they are destroyed and there is an influx of
PAHs from below; or c) PAH destruction is
compensated by PAH
formation in the surface layer. The last effect should be prevented
by Coulomb repulsion (Voit 1992)
in a hard photon environment where
PAHs and carbon atoms are ionized.
,
the critical photon energy is only 50 eV (Eq. (10)).
As T Tauri stars (or their jets) also radiate at X-rays and in
the
EUV, the surface of the disk should be devoid of PAHs unless a) the
period over which hard photons are emitted is too short to destroy
all PAHs; b) the PAHs are removed by
vertical motions from the
hard radiation before they are destroyed and there is an influx of
PAHs from below; or c) PAH destruction is
compensated by PAH
formation in the surface layer. The last effect should be prevented
by Coulomb repulsion (Voit 1992)
in a hard photon environment where
PAHs and carbon atoms are ionized.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{AA200912035Fig5.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12035-09/Timg124.png)
|
Figure 5:
Of each radiation component, |
| Open with DEXTER | |
5.1 Destruction time
The above PAH survival condition under a) can
easily be
dismissed. To estimate the time for PAH removal
![]() by
the radiation component i, we note that most of the
radiation is
absorbed on the disk surface in a sheet of vertical optical depth
by
the radiation component i, we note that most of the
radiation is
absorbed on the disk surface in a sheet of vertical optical depth
![]() equal to the grazing angle
equal to the grazing angle
![]() of the
incident light. We call this sheet the extinction layer
(of
the radiation component i) and denote its
geometrical thickness
of the
incident light. We call this sheet the extinction layer
(of
the radiation component i) and denote its
geometrical thickness ![]() (see
Fig. 5).
To first order, the PAHs in the extinction
layer receive the stellar flux of Eq. (1) with
(see
Fig. 5).
To first order, the PAHs in the extinction
layer receive the stellar flux of Eq. (1) with
![]() .
If the instability criterion of Eq. (10) is
fulfilled,
.
If the instability criterion of Eq. (10) is
fulfilled, ![]() follows from
follows from
![]() ,
where x is from Eq. (14), therefore
,
where x is from Eq. (14), therefore
With
5.2 Exposure time and vertical mixing
Next we consider the possibility that vertical motions in the disk lead to a continuous exchange between matter in the extinction layers, where almost all photons are absorbed and the PAHs are destroyed as well as the layers below where the PAHs are shielded and damaged ones are possibly rebuilt (Fig. 5). We assume that gas and dust are perfectly mixed in a mass ratio of 130:1.
In a Keplerian disk that is isothermal in z-direction
and in
hydrostatic equilibrium, the gas density changes like
Here
and
is the scale height,
For the radial variation of the gas temperature in the opaque
mid
plane, T(r), we also adopt a
power law,
The mid plane is roughly isothermal in z because the optical depth is high and the net flux zero. It is much colder than the extinction layers because it is not exposed to direct stellar heating. The radiative transfer in the disk, including the energy equation, can be solved to any desired accuracy even when the disk is very opaque (see Sect. 11.3.2 of Krügel 2006). As long as the dust in the mid plane is optically thick to its own emission, the results for T(r)can be well approximated by putting in Eq. (19)
Each extinction layer extends vertically from some value z0
upwards
to infinity (Fig. 5).
We give it a finite thickness
![]() by demanding
that for instance 90% of the photons are absorbed
between z0 and
by demanding
that for instance 90% of the photons are absorbed
between z0 and ![]() .
If
.
If ![]() denotes the typical
vertical velocity, for example, as a result of turbulence, PAHs are
exposed to radiation for a time
denotes the typical
vertical velocity, for example, as a result of turbulence, PAHs are
exposed to radiation for a time
This is also the mean residence time of a PAH in the extinction layer. For PAHs to survive,
and
K is the mass absorption coefficient of gas and dust at the characteristic frequency of the particular radiation component (see Table 2). Because
| Figure 6:
The height, z0, of the
bottom of the extinction layer and its thickness |
|
| Open with DEXTER | |
| Figure 7:
The critical vertical velocity for PAH survival
|
|
| Open with DEXTER | |
From Eqs. (4), (15) and (20), one finds that
vertical motions safeguard PAHs against destruction if
with
One expects the disk also to be turbulent. Turbulence may be
driven by various processes such as shear flows in the disk (Lin
& Bodenheimer 1982),
magneto-rotational instabilities (Balbus & Harley 1991) or
velocity discontinuities at places where in-falling matter (Cassen
& Mossman 1981)
or outflows (Elmegreen 1978)
strike the disk surface. As yet it is unclear which type of turbulence
dominates. We assume that for the size of the largest eddies
![]() the average turbulent velocity
the average turbulent velocity ![]() grows linearly with the sound speed
grows linearly with the sound speed ![]() .
Various three dimensional hydrodynamical calculations support this view
(Cabot 1996;
Boss 2004;
Johansen & Klahr 2005;
Fromang & Papaloizou 2006).
The favored parametrization is
.
Various three dimensional hydrodynamical calculations support this view
(Cabot 1996;
Boss 2004;
Johansen & Klahr 2005;
Fromang & Papaloizou 2006).
The favored parametrization is
![]() with q = 0.5. This choice has consequences on the
eddy scale
with q = 0.5. This choice has consequences on the
eddy scale
![]() and the turnover time
and the turnover time
![]() ,
with the Kepler frequency
,
with the Kepler frequency
![]() (e.g. Dullemond & Domink 2004).
Weidenschilling & Cuzzi (1993)
use q = 1 so that the eddy scale is about the
pressure scale height,
(e.g. Dullemond & Domink 2004).
Weidenschilling & Cuzzi (1993)
use q = 1 so that the eddy scale is about the
pressure scale height,
![]() and larger than the thickness of the extinction layer,
and larger than the thickness of the extinction layer,
![]() .
Estimated values for
.
Estimated values for ![]() are in the range from 0.0001 up to 0.1 (Dullemond
& Dominik 2004;
Schräpler & Henning 2004;
Youdin & Lithwick 2007).
Taking
are in the range from 0.0001 up to 0.1 (Dullemond
& Dominik 2004;
Schräpler & Henning 2004;
Youdin & Lithwick 2007).
Taking ![]() ,
the eddy scale is ten times smaller for q = 0.5
than for q = 1, and in addition larger turbulent
velocities are obtained with
,
the eddy scale is ten times smaller for q = 0.5
than for q = 1, and in addition larger turbulent
velocities are obtained with
![]() ,
supporting a faster transport of the PAH. Identifying
,
supporting a faster transport of the PAH. Identifying
![]() in
Eq. (23)
with the turbulent velocity
in
Eq. (23)
with the turbulent velocity ![]() and assuming a temperature
dependence as in Eq. (19),
we
plot in Fig. 7
the vertical velocity
and assuming a temperature
dependence as in Eq. (19),
we
plot in Fig. 7
the vertical velocity ![]() as a
function of radius. The figure also shows the critical velocity for
PAH survival
as a
function of radius. The figure also shows the critical velocity for
PAH survival ![]() with respect to X-rays. Note that the critical velocity for the X-ray
radiation component is insensitive to the particular choice of E0
and
with respect to X-rays. Note that the critical velocity for the X-ray
radiation component is insensitive to the particular choice of E0
and ![]() (Eqs. (10), (23)). When
(Eqs. (10), (23)). When
![]() ,
PAHs can
survive at distances r > 10 AU;
when
,
PAHs can
survive at distances r > 10 AU;
when ![]() is considerably
smaller than
is considerably
smaller than
![]() ,
they cannot.
,
they cannot.
Critical velocities for PAH survival are much higher for EUV than for X-ray photons (Table 2). EUV radiation will therefore always destroy PAHs, but as depicted in Fig. 6, the EUV extinction layer is the topmost, and below it, PAHs may survive and be excited.
If PAHs are removed from the extinction layer before they are
destroyed, they must be injected at the same rate from below to be
detected at all. Therefore, the critical velocity can alternatively
be expressed through
which leads to similar values. We note that the mass reservoir below the extinction layer is sufficient to sustain the required mass influx
5.3 PAH dissociation by soft versus hard photons
The energy ![]() (Eq. (3)),
which is absorbed by a PAH of
(Eq. (3)),
which is absorbed by a PAH of
![]() carbon atoms, is shown in Fig. 8 as a function of
distance from the star. The PAH is exposed to the photospheric and FUV
radiation component described in Table 1, and the results
are shown for the top (
carbon atoms, is shown in Fig. 8 as a function of
distance from the star. The PAH is exposed to the photospheric and FUV
radiation component described in Table 1, and the results
are shown for the top (![]() )
and the bottom (
)
and the bottom (![]() )
of the extinction layer. The minimum energy input
)
of the extinction layer. The minimum energy input ![]() (Eq. (10))
for PAH dissociation depends on the choice of the Arrhenius energy E0
and is indicated for E0= 5,
7 and 10 eV, respectively. In this picture, for E0=
5 eV and at the bottom of the extinction layer, PAHs are
dissociated by soft photons up to 1 AU. For X-rays,
however, we find that PAH destruction occurs typically at distances up
to
(Eq. (10))
for PAH dissociation depends on the choice of the Arrhenius energy E0
and is indicated for E0= 5,
7 and 10 eV, respectively. In this picture, for E0=
5 eV and at the bottom of the extinction layer, PAHs are
dissociated by soft photons up to 1 AU. For X-rays,
however, we find that PAH destruction occurs typically at distances up
to ![]() 10 AU
or greater (Fig. 7).
Dissociation of PAH acts for soft (photospheric and FUV) photons on
much shorter distances than for hard photons (X-ray component).
10 AU
or greater (Fig. 7).
Dissociation of PAH acts for soft (photospheric and FUV) photons on
much shorter distances than for hard photons (X-ray component).
| Figure 8:
The energy |
|
| Open with DEXTER | |
6 Large grains
Observations of T Tauri stars at millimeter wavelengths (Testi et al. 2003; Lommen et al. 2007) and in the mid-infrared (van Boekel et al. 2003; Przygodda et al. 2003; Kessler-Silacci et al. 2006; Bouwman et al. 2008; Watson et al. 2009) suggest that grains in T Tauri disks are at least ten times larger than those in the ISM. As such large grains may also be present in the top disk layer, we estimate how this would affect the stability analysis of PAHs. We first note that in case of homogeneous mixing an increase in particle size would not alter the dust-to-gas mass ratio.
Should the grains be much larger than the wavelength, the
absorption
coefficient per gram of dust
![]() would decrease
roughly like 1/a, with grain size a,
whereas the ratio
would decrease
roughly like 1/a, with grain size a,
whereas the ratio
![]() would still roughly be given by the values in
Table 2.
For hard X-rays, on the other hand,
would still roughly be given by the values in
Table 2.
For hard X-rays, on the other hand,
![]() is not sensitive to the grain size.
is not sensitive to the grain size.
Therefore, if disk grains are on average ten times bigger and
thus
103 more massive than interstellar ones, we
expect that the height
z0 to which the stellar
radiation components can penetrate (see
Fig. 6)
stays the same for X-ray and also for EUV radiation,
because EUV absorption is due to gas, not dust. However, optical and
FUV photons will reach farther down, about half a scale height, so
that there may be a thin disk layer (![]() H/4) where
PAHs are
shielded from X-rays and EUV photo-destruction and are excited by
optical or FUV radiation.
H/4) where
PAHs are
shielded from X-rays and EUV photo-destruction and are excited by
optical or FUV radiation.
7 Conclusion
Why most T Tauri stars do not exhibit PAH features while a few do, we investigate the processes which can remove PAHs from the surface layer of T Tauri disks and find out under which conditions PAHs should be present. Clearing of PAH through interaction with planets seems not an efficient process (Geers et al. 2007b), and we show that PAH under-abundance can be caused by radiative destruction. We use a fiducial model for the photon emission of the T Tauri star that includes beside the photosphere also FUV and EUV radiation and an X-ray component.
- 1.
- We introduce for each stellar radiation component the
notion of
an extinction layer as the place where
 90% of the
photons are absorbed. EUV photons are mainly absorbed by gas, X-rays by
gas and dust alike, and the photospheric and FUV component are only
attenuated by dust. The extinction layers of all four components have a
similar geometrical thickness, and their bottom is at a similar
elevation z0, except for the
EUV extinction layer, which is situated higher up (Fig. 6).
90% of the
photons are absorbed. EUV photons are mainly absorbed by gas, X-rays by
gas and dust alike, and the photospheric and FUV component are only
attenuated by dust. The extinction layers of all four components have a
similar geometrical thickness, and their bottom is at a similar
elevation z0, except for the
EUV extinction layer, which is situated higher up (Fig. 6).
- 2.
- PAH may be radiatively destroyed by unimolecular dissociation where one or several atoms are expelled after photon absorption.
- 3.
- Destruction by the photospheric and FUV radiation component (soft photons) increases with the strength of the radiation field and is very efficient below 1 AU.
- 4.
- Hard photons can dissociate PAHs at all distances, and their efficiency grows with the hardness of the photons. Without some counter process, all PAHs (in layers where they can be excited) would be destroyed within a time that is short compared to the lifetime of the disk.
- 5.
- Although grains in the disk surface are presumably larger than interstellar ones, the stability analysis of PAHs would not change significantly.
- 6.
- Therefore there must be some survival channel in disks where PAHs are detected. Because creation of PAHs in the extinction layer is too slow to compete with PAH destruction (Voit 1992), we suggest vertical mixing as a result of turbulence. It can replenish PAHs or remove them from the reach of hard photons.
- 7.
- For standard disk models, the minimum velocity for PAH
survival is proportional to r-3/4
and equals
 5 m/s
at 10 AU. If turbulent velocities are proportional to the
sound speed, a velocity
5 m/s
at 10 AU. If turbulent velocities are proportional to the
sound speed, a velocity 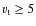 m/s
would imply
m/s
would imply
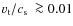 as a PAH survival condition. Theoretical predictions for this ratio
have a large spread, but in accordance with the observational fact that
PAH features are usually absent, it seems that generally the condition
is not fulfilled.
as a PAH survival condition. Theoretical predictions for this ratio
have a large spread, but in accordance with the observational fact that
PAH features are usually absent, it seems that generally the condition
is not fulfilled.
- 8.
- A higher PAH detection rate is found in Herbig Ae/Be stars.
In our picture this is explained, as their destructive hard radiation
component is relatively weak (
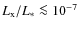 ,
Preibisch et al. 2006) and
also because the intensity of the PAH emission from a large distance
from the star is higher given their brighter optical luminosities.
,
Preibisch et al. 2006) and
also because the intensity of the PAH emission from a large distance
from the star is higher given their brighter optical luminosities.
We thank an anonymous referee for constructive comments on PAH processing.
References
- Akeson, R. L., Walker, C. H., Wood, K., et al. 2005, ApJ, 622, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Allamandola, L. J., Tielens, A. G. G. M., & Barker, J. R. 1989, ApJS, 71, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Acke, B., & van den Ancker, M. E. 2004, A&A, 426, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Boss, A. P. 2004, ApJ, 610, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Blake, G. A., Qt, C., Dullemond, C. P., & Wilner, D. J. 2008, ApJ, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Balucinska-Church, M., & McCommon, D. 1992, ApJ, 400, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Bertout, C., Siess, L., & Cabrit, S. 2007, A&A, 473, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwman, J., Henning, Th., & Hillenbrand, L. A. 2008, ApJ, 683, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Cabot, W. 1996, ApJ, 465, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., & Gullbring, E. 1998, ApJ, 509, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Cassen, P. M., & Mossman, A. 1981, Icarus, 48, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Cieza, L., Padgettt, D. L., Stapelfeldt, K. R., et al. 2007, ApJ, 667, 328 [NASA ADS] [Google Scholar]
- CRC Handbook of Chemsitry & Physics 2005 (Taylor & Francis), 6ff [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, A&A, 421, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., van Zadelhoff, G. J., & Natta, A. 2002, A&A, 389, 464 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., Henning, Th., Visser, R., et al. 2007a, A&A, 473, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., Hollenbach, D., Kamp, I., & D'Alessio, P. 2007b, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 555 [Google Scholar]
- Dwek, E., & Smith, R. K. 1996, ApJ, 459, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G. 1978, Moon and Planets, 19, 21 [Google Scholar]
- Evans, N. J., Allen, L. E., Blake, G. A., et al. 2003, PASP, 115, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Fromang, S., & Papaloizou, J. 2006, A&A, 452, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Furlan, E., Hartmann, L., Calvet, N., et al. 2006, ApJS, 156, 568 [CrossRef] [Google Scholar]
- Geers, V. C., Augereau, J.-C., Pontoppidan, K. M., et al. 2006, A&A, 459, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geers, V. C., van Dishoeck, E. F., Pontoppidan, K. M., et al. 2007a, A&A, 476, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geers, V. C., Pontoppidan, K. M., van Dishoeck, E. F., et al. 2007b, A&A, 469, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geers, V. C., van Dishoeck, E. F., Pontoppidan, K. M., et al. 2009, A&A, 495, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güdel, M., Skinner, S. L., & Mel'Nikov, S. Yu. 2007, A&A, 468, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guhathakurta, P., & Draine, B. T. 1989, ApJ, 345, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Gorti, U., & Hollenbach, D. 2008, ApJ, 683, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler-Silacci, J., Augereau, J.-C., Dullemond, C., et al. 2006, ApJ, 639, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Kitamura, Y., Momose, M., Yokogawa, S., et al. 2002, ApJ, 581, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Krügel, E. 2006, An introduction to the Physics of Interstellar Dust (IoP), Sects. 5.4 and 10.2 [Google Scholar]
- Johansen, A., & Klahr, H. 2005, ApJ, 634, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Judge, P. G., Solomon, S. C., & Ayres, T. R. 2003, ApJ, 593, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Leach, S., Eland, J. H. D., & Price, S. D. 1989a, J. Phys. Chem., 93, 7575 [CrossRef] [Google Scholar]
- Leach, S., Eland, J. H. D., & Price, S. D. 1989b, J. Phys. Chem., 93, 7583 [CrossRef] [Google Scholar]
- Leger, A., D'Hendecourt, L., Boissel, P., & Desert, F. X. 1989, A&A, 213, 351 [NASA ADS] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2003, ApJ, 584, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Bodenheimer, P. 1982, ApJ, 262, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Lommen, D., Wright, C. M., Maddison, S. T., et al. 2007, A&A, 462, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meeus, G., Waters, L. B. F. M., Bouwman, J., et al. 2001, A&A, 365, 476 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010a, A&A, 510, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010b, A&A, 510, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morrison, R., & McCommon, D. 1983, ApJ, 270, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Hartmann, L., & Calvet, N. 1998, AJ, 116, 2965 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Calvet, N., Hartmann, L., & D'Alessio, P. 2003, ApJ, 597, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Omont, A. 1986, A&A, 166, 159 [NASA ADS] [Google Scholar]
- Peeters, E., Hony, S., van Kerckhoven, C., et al. 2002, A&A, 390, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preibisch, T., Kim, Y.-C., Favata, F., et al. 2006, ApJSS, 160, 401 [Google Scholar]
- Przygodda, F., van Boekel, R., Abraham, P., et al. 2003, A&A, 412, 43 [Google Scholar]
- Rafikov, R. R., & de Colle, F. 2006, ApJ, 646, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Rapacioli, M., Calvo, F., Joblin, C., et al. 2006, A&A, 460, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruhl, E., Price, S. D., & Leach, S. 1989, J. Phys. Chem., 93, 6312 [CrossRef] [Google Scholar]
- Salpeter, E. E. 1977, ARA&A, 15, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Schräpler, R., & Henning, Th. 2004, ApJ, 614, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Schutte, W. A., Tielens, A. G. G. M., & Allamandola, L. J. 1993, ApJ, 415, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Siebenmorgen, R., Prusti, T., Natta, A., & Müller, T. G. 2000, A&A, 361, 258 [NASA ADS] [Google Scholar]
- Stahler, S. W., Shu, F. H., & Taam, R. E. 1980, ApJ, 242, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Stelzer, B., Micela, G., Hamaguchi, K., & Schmitt, J. H. M. M. 2006, A&A, 457, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stelzer, B., Flaccomio, E., & Briggs, K. 2007, A&A, 468, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sterzik, M. F., & Schmitt, H. M. M. 1997, AJ, 114 (4), 1673 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Natta, A., Shepherd, D. S., & Wilner, D. J. 2003, A&A, 403, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge University Press), Sect. 6.4 [Google Scholar]
- Tielens, A. G. G. M. 2008, ARA&A, 46, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visser, R., Geers, V. C., Dullemond, C. P., et al. 2007, A&A, 466, 229 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Voit, G. M. 1992, MNRAS, 258, 841 [NASA ADS] [CrossRef] [Google Scholar]
- van Boekel, R., Waters, L. B. F. M., Dominik, C., et al. 2003, A&A, 400, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Boekel, R., Min, M., Leinert, C., et al. 2004, Nature, 432, 479 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Waelkens, C., Waters, L. B. F. M., de Graauw, M. S., et al. 1996, A&A, 315, L245 [NASA ADS] [Google Scholar]
- Watson, D. M., Leisenring, J. M., Furlan, E., et al. 2009, ApJS, 180, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J., & Cuzzi, J. N. 1993, Protostars and Planets III (A93-42937 17-90), 1031 [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icar, 192, 588 [CrossRef] [Google Scholar]
All Tables
Table 1: The four radiation components of our T Tauri model star.
Table 2: Quantities relevant to PAH survival.
All Figures
![\begin{figure}
\par\includegraphics[angle=0,width=6.8cm,clip]{AA200912035Fig1.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12035-09/Timg32.png)
|
Figure 1: The spectral energy distribution of our T Tauri model star at 1 AU without foreground extinction (Eq. (1)). The absolute luminosities of the components are given in Table 1. |
| Open with DEXTER | |
| In the text | |
| |
Figure 2: The mass extinction coefficient per gram disk material when the gas is neutral (Morrison & McCommon 1983); the gas-to-dust mass ratio equals 130. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=7cm,clip]{AA200912035Fig3.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12035-09/Timg81.png)
|
Figure 3:
The temperature distribution P(T)
of a PAH with 100 C atoms exposed to mono-chromatic radiation
with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=6.8cm,clip]{AA200912035Fig4.ps}
\vspace*{8mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12035-09/Timg82.png)
|
Figure 4:
The power |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{AA200912035Fig5.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12035-09/Timg124.png)
|
Figure 5:
Of each radiation component, |
| Open with DEXTER | |
| In the text | |
| |
Figure 6:
The height, z0, of the
bottom of the extinction layer and its thickness |
| Open with DEXTER | |
| In the text | |
| |
Figure 7:
The critical vertical velocity for PAH survival
|
| Open with DEXTER | |
| In the text | |
| |
Figure 8:
The energy |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



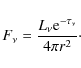
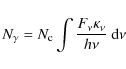
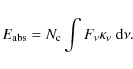
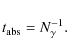
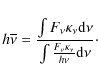
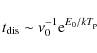
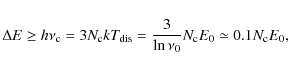
![\begin{displaymath}
N_{\rm c} \ \le \ {2 \Delta E\over {\rm [eV]}}\cdot
\end{displaymath}](/articles/aa/full_html/2010/03/aa12035-09/img99.png)
![\begin{displaymath}
x = {h\nu - 3N_{\rm c}kT_{\rm dis}\over E_{\rm0} + E_{\rm ki...
...\simeq {h\nu \over 5~ {\rm [eV]}} - {N_{\rm c} \over 10} \cdot
\end{displaymath}](/articles/aa/full_html/2010/03/aa12035-09/img109.png)
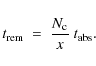
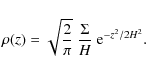
![\begin{displaymath}
\Sigma(r) = \int\limits_{0}^\infty \rho(z)~{\rm d}z = \Sigma_0
\bigg[{r\over {\rm AU}} \bigg]^{-\gamma} ,
\end{displaymath}](/articles/aa/full_html/2010/03/aa12035-09/img133.png)
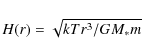
![\begin{displaymath}
T(r) = T_0 \bigg[{r\over {\rm AU}} \bigg]^{-\beta}\cdot
\end{displaymath}](/articles/aa/full_html/2010/03/aa12035-09/img138.png)