EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 510 (February 2010) A&A, 510 (2010) A87 Full HTML
Free Access
Issue
A&A
Volume 510, February 2010
Article Number A87
Number of page(s) 12
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200913077
Published online 16 February 2010
A&A 510, A87 (2010)

CHAMP+ observations of warm gas in M 17 SW

J. P. Pérez-Beaupuits1 - M. Spaans1 - M. R. Hogerheijde2 - R. Güsten3 - A. Baryshev4 - W. Boland2,5

1 - Kapteyn Astronomical Institute, Rijksuniversiteit Groningen, 9747 AV Groningen, The Netherlands
2 - Leiden Observatory, Leiden University, PO Box 9513, 2300 RA, Leiden, The Netherlands
3 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
4 - SRON Netherlands Institute for Space Research , PO Box 800, 9700 AV Groningen, The Netherlands
5 - Nederlandse Onderzoeksschool Voor Astronomie (NOVA), PO Box 9513, 2300 RA Leiden, The Netherlands

Received 6 August 2009 / Accepted 26 October 2009

Abstract
Context. Sub-millimeter and Far-IR observations have shown the presence of a significant amount of warm (few hundred K) and dense ( $n(\rm H_2)\ge10^4~\rm {cm^{-3}}$) gas in sources ranging from active star-forming regions to the vicinity of the Galactic center. Since the main cooling lines of the gas phase are important tracers of the interstellar medium in Galactic and extragalactic sources, proper and detailed understanding of their emission and the ambient conditions of the emitting gas, is necessary for a robust interpretation of the observations.
Aims. With high resolution (7''-9'') maps ($\sim$$3\times3$ pc2) of mid-J molecular lines we aim to probe the physical conditions and spatial distribution of the warm (50 to several hundred K) and dense gas ( $n(\rm H_2)>10^5~\rm {cm^{-3}}$) across the interface region of the nearly edge-on M 17 SW nebula.
Methods. We have used the dual color multiple pixel receiver CHAMP+ on the APEX telescope to obtain a $5\hbox{$.\mkern-4mu^\prime$ }3\times4\hbox{$.\mkern-4mu^\prime$ }7$map of the $J = 6\rightarrow 5$ and $J = 7\rightarrow 6$ transitions of 12CO, the 13CO  $J = 6\rightarrow 5$line, and the $^3{\rm P}_2\rightarrow{^3{\rm P}_1}$ 370 $\mu$m fine-structure transition of [C I] in M 17 SW. LTE and non-LTE radiative transfer models are used to constrain the ambient conditions.
Results. The warm gas extends up to a distance of $\sim$2.2 pc from the M 17 SW ridge. The 13CO  $J = 6\rightarrow 5$ and [C I]  370 $\mu$m lines have a narrower spatial extent of about 1.3 pc along a strip line at $\rm PA=63^{\circ }$. The structure and distribution of the [C I]  $^3{\rm P}_2\rightarrow{^3{\rm P}_1}$ 370 $\mu$m map indicate that its emission arises from the interclump medium with densities on the order of $10^3~\rm {cm^{-3}}$.
Conclusions. The warmest gas is located along the ridge of the cloud, close to the ionization front. An LTE approximation indicates that the excitation temperature of the embedded clumps reaches $\sim$120 K. The non-LTE model suggests that the kinetic temperature at four selected positions cannot exceed 230 K in clumps of a density of $n(\rm H_2)\sim5\times10^5~\rm {cm^{-3}}$and that the warm ( $T_{\rm k}>100$ K) and dense ( $n(\rm H_2)\ge10^4~\rm {cm^{-3}}$) gas traced by the mid-J 12CO lines represents just about 2% of the bulk of the molecular gas. The clump volume-filling factor ranges between 0.04 and 0.11 at these positions.

Key words: ISM: general - ISM: atoms - ISM: molecules

1 Introduction

The heating and cooling balance in photon-dominated regions (PDRs) remains an active study of research. The comprehensive understanding of PDRs requires observations of large areas close to radiation sources and of a wide wavelength range covering various emissions of atoms, molecules, and grains. In particular, mid-J CO lines have been detected in almost all known massive Galactic star forming regions (e.g. Orion Nebula, W51, Cepheus A, NGC 2024). This indicates that warm ( $T_{\rm K}\ge50$ K) and dense ( $n(\rm H_2)\ge10^4~\rm {cm^{-3}}$) gas is common and probably of importance in most OB star forming regions. The mid-J CO lines detected in regions like e.g. M 17, Cepheus A and W51 have relatively narrow line widths of 5-10  ${\rm km~s}^{-1}$, although not as narrow as the line widths observed in cold quiescent cloud cores.

Observations of the $J = 6\rightarrow 5$and $J = 7\rightarrow 6$ transitions of 12CO in several massive star forming regions indicate that the warm emitting gas is confined to narrow (<1 pc) zones close to the ionization front. These observations favor photoelectric heating of the warm gas by UV radiation fields outside the HII regions (e.g. Harris et al. 1987; Graf et al. 1993; Yamamoto et al. 2001; Kramer et al. 2004 and 2008). Nevertheless, shocks may also be an important source of heating in high velocity wing sources like Orion, W51 and W49 (Jaffe et al. 1987).

Because of its nearly edge-on geometry and the large amount of observational data available in the literature, M 17 SW is one of the best Galactic regions to study the entire structure of PDRs from the exciting sources to the ionization front, and the succession (or not) of H2, [C I] and CO emissions, as predicted by PDR models (Icke et al. 1980; Felli et al. 1984; Meixner et al. 1992; Meijerink & Spaans 2005). M 17 SW is also one of the few star-forming regions for which the magnetic field strength can be measured in the PDR interface and where the structure of the neutral and molecular gas seems to be dominated by magnetic pressure rather than by gas pressure (Pellegrini et al. 2007).

M 17 SW is a giant molecular cloud at a distance of 2.2 kpc, illuminated by a highly obscured ( $A_{\rm v}>10$ mag) cluster of several OB stars (among $\ga$100 stars) at about 1 pc to the east (Beetz et al. 1976; Hanson et al. 1997). It also harbours a number of candidate young stellar objects that have recently been found (Povich et al. 2009). Several studies of molecular emission, excitation and line profiles (e.g. Snell et al. 1984; Martin et al. 1984; Stutzki & Güsten 1990) from the M 17 SW core indicate that the structure of the gas is highly clumped rather than homogeneous. Emission of [C I] and [C II] was detected more than a parsec into the molecular cloud along cuts through the interface region (Keene et al. 1985; Genzel et al. 1988; Stutzki et al. 1988). These results, as well as those found in other star-forming regions like S106, the Orion Molecular Cloud, and the NGC 7023 Nebula (e.g. Gerin & Phillips 1998; Yamamoto et al. 2001; Schneider et al. 2002, 2003; Mookerjea et al. 2003) do not agree with the atomic and molecular stratification predicted by standard steady-state PDR models. However, the extended [C I]  $^3{\rm P}_1\rightarrow{^3{\rm P}_0}$and 13CO  $J = 2\rightarrow 1$emissions in S140 have been successfully explained by a stationary but clumpy PDR model (Spaans 1996; Spaans & van Dishoeck 1997). Hence, the lack of stratification in [C I] , [C II] and CO is a result that can be expected for inhomogeneous clouds, where each clump acts as an individual PDR. On the other hand, a partial face-on illumination of the molecular clouds would also suppress stratification.

Based on analysis of low-J lines of 12CO, 13CO and CH3CCH data, the temperature towards the M 17 SW cloud core has been estimated as 50-60 K, whereas the mean cloud temperature has been found to be about 30-35 K (e.g. Güsten & Fiebig 1988; Bergin et al. 1994; Wilson et al. 1999; Howe et al. 2000; Snell et al. 2000). Temperatures of $\sim$275 K have been estimated from NH3 observations (Güsten & Fiebig 1988) towards the VLA continuum arc, which agrees with estimates from highly excited 12CO transitions (Harris et al. 1987). Multitransition CS and HC3N observations indicate that the density at the core region of M 17 SW is about $6\times10^5~\rm {cm^{-3}}$(e.g., Snell et al. 1984; Wang et al. 1993; Bergin et al. 1996). On the other hand, densities up to $3\times10^6~\rm {cm^{-3}}$have been estimated towards the north rim with multitransition observations of NH3, which indicates that ammonia is coexistent with high density material traced in CS and HCN (Güsten & Fiebig 1988). The UV radiation field G0 has been estimated to be on the order of 104 in units of the ambient interstellar radiation field ( $1.2\times10^{-4}~\rm erg~s^{-1}~cm^{-1}~sr^{-1}$, Habing 1968; Meixner et al. 1992).

However, most of the millimeter-wave molecular observations in M 17 SW are sensitive only to low temperatures (<100 K), and the few available data of mid-J CO and [C I] lines (consisting mostly of cuts across the ionization front and observations at a few selected positions) are limited in spatial resolution and extent (e.g. Harris et al. 1987; Stutzki et al. 1988; Genzel et al. 1988; Stutzki & Güsten 1990; Meixner et al. 1992; Graf et al. 1993; Howe et al. 2000). Therefore, in this work we present maps ($\sim$$3\times3$ pc2) of mid-J molecular (12CO and 13CO $\!\!$) and atomic ([C I] $\!\!$) gas with an excellent high resolution ( 9.4''-7.7''), which advances existing work in M 17 SW.

The observations were done with CHAMP+ (Carbon Heterodyne Array of the MPIfR) on the Atacama Pathfinder EXperiment (APEX[*]) (Güsten et al. 2006). The multiple pixels at two submm frequencies of CHAMP+ allow the efficient mapping of $\sim$arcmin regions, and provide the ability to observe simultaneously the emission from the $J = 6\rightarrow 5$ and $J = 7\rightarrow 6$ rotational transitions of 12CO at 691.473 GHz and 806.652 GHz, respectively. We also observed the $J = 6\rightarrow 5$ transition of 13CO at 661.067 GHz and the $^3{\rm P}_2\rightarrow~^3{\rm P}_1$370 $\mu$m (hereafter: $2\rightarrow1$) fine-structure transition of [C I] at 809.342 GHz.

Since the gas phase cools mainly via the atomic fine structure lines of [O I] $\!\!$, [C II] $\!\!$, [C I] and the rotational CO lines (e.g. Kaufman et al. 1999; Meijerink & Spaans 2005), these carbon bearing species presented here are very important coolants in the interstellar medium (ISM) of a variety of sources in the Universe, from Galactic star forming regions, the Milky Way as a galaxy, and external galaxies up to high redshifts (e.g. Fixsen et al. 1999; Weiss et al. 2003; Kramer et al. 2005; Bayet et al. 2006; Jakob et al. 2007).

The case of M 17 SW can be considered as a proxy for extra galactic star forming regions. M 17 SW is not special, nor does it need to be, compared to other massive star-forming regions like Orion, W49, Cepheus A, or W51. Still, it does allow feedback effects, expected to be important for starburst and active galaxies, to be studied in great spatial detail. A comparison of the local line ratios to the extra-galactic regions can then shed light on the properties of massive star-forming regions that drive the energetics of active galaxies. Our results will be of great use for future high resolution observations, since molecular clouds of the size of the maps we present will be resolved by ALMA at the distance ($\sim$14 Mpc) of galaxies like NGC 1068.

The main purpose of this work is to explore the actual spatial distribution of the mid-J 12CO  and [C I] lines in M 17 SW and to test the ambient conditions of the warm gas. A simple LTE model based on the ratio between the 12CO and 13CO  $J = 6\rightarrow 5$ lines is used to probe the temperature of the warm ( $T_{\rm K}\sim100$ K) and dense ( $n_{\rm H}>10^5~\rm {cm^{-3}}$) molecular gas. Then a non-LTE model is used to test the ambient conditions at four selected positions. In a follow-up work we will present an elaborate model of these high resolution data.

The most frequent references to Stutzki et al. (1988), Stutzki & Güsten (1990) and Meixner et al. (1992) will be cited as S88, SG90 and M92, respectively. The organization of this article is as follows. In Sect. 2 we describe the observations. The maps of the four lines observed are presented in Sect. 3. The modeling and analysis of the ambient conditions are presented in Sect. 4, and the conclusions and final remarks are presented in Sect. 5.

2 Observations

We have used the dual color heterodyne array receiver CHAMP+ (Kasemann et al. 2006; Güsten et al. 2008), providing $2\times7$ pixels, on the APEX telescope during July 2008 to map the $J = 6\rightarrow 5$and $J = 7\rightarrow 6$ lines of 12CO simultaneously, and - in a second coverage - the 13CO  $J = 6\rightarrow 5$and [C I]  $J = 2\rightarrow 1$. We observed a region of about $5\hbox{$.\mkern-4mu^\prime$ }3\times4\hbox{$.\mkern-4mu^\prime$ }7$(3.4 pc $\times$3.0 pc) in on-the-fly (OTF) slews in RA ($\sim$320 arcsec long), subsequent scans spaced by 4'' in declination. The observations were done in total power mode, nodding the antenna prior to each OTF slew to a reference position 180'' east of the SAO star 161357. The latter is used as a reference throughout the paper, with RA(J2000)=18:20:27.64 and Dec(J2000)=-16:12:00.90. We used Sgr B2(N) as a reference for continuum poiting. Calibration measurements were performed regularly every $\sim$10 min with a cold liquid nitrogen (LN2) load and an ambient temperature load. The data were processed with the APEX real-time calibration software (Muders et al. 2006), assuming an image sideband suppression of 10 dB.

We used the Fast Fourier Transform Spectrometer (FFTS) as backend with a fixed bandwidth of 1.5 GHz and 1024 channels. We used the two IF groups of the FFTS with an offset of $\pm $460 MHz between them. The spectral resolution was smoothed to about 1  ${\rm km~s}^{-1}$, while the line widths are between 4  ${\rm km~s}^{-1}$and 9  ${\rm km~s}^{-1}$, so they are well resolved. The on-source integration time per dump and pixel was 1 s only. However, oversampling with 4'' spacing, all the seven pixels of CHAMP+ covered a given grid position at least once. So, after adding all the subscans from both IF channels, and after convolving the maps with the corresponding beam size, the total integration time in the central $5'\times4'$ region of the maps varied between about 50 and 80 s per grid cell.

The SSB system temperatures are typically about 2000 K and 6000 K respectively for the low and high frequency bands. The spatial resolution varies between 9.4'' for the 13CO  $J = 6\rightarrow 5$transition in the low frequency band (at 661 GHz - the nominal beam at 691 GHz is 8.4'') and 7.7'' for the high frequency band (809  GHz). All data in the paper were converted to the line brightness temperature $T_{\rm B}=\eta_{\rm f}\times T_{\rm A}^{*}/\eta_{\rm c}$, using a forward efficiency ( $\eta_{\rm f}$) of 0.95 and beam coupling efficiencies ( $\eta_{\rm c}$) of 0.45 and 0.43 (at 661 GHz and 809 GHz, respectively) as determined towards Jupiter[*] (Güsten et al. 2008). We assumed brightness temperatures of 150 K (at 660 GHz) and 145 (at 815 GHz) for Jupiter (Griffin et al. 1986). This coupling efficiency was chosen because in velocity-space (velocity channels) the size of the M 17 clumps is Jupiter-like, which had a size $\sim$38.7'' at the time of the observations. The calibrated data were reduced with the GILDAS[*] package CLASS90.

3 Results

3.1 Integrated line temperature maps

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13077f1a-cmjn.eps}\par\vspace*{2mm} \includegraphics[width=8.5cm,clip]{13077f1b-cmjn.eps} \end{figure} Figure 1:

Top - Color map of the integrated temperature of 12CO  $J = 6\rightarrow 5$in M 17 SW. The contour lines correspond to the 12CO  $J = 7\rightarrow 6$, which has a peak emission of 925 K  ${\rm km~s}^{-1}$. The countour levels are the 25%, 50%, 75% and 90% of the peak emission. Dashed lines correspond to the E-W and NE-SW strip lines at $\rm PA=90^{\circ }$and $\rm PA=63^{\circ }$, respectively. Bottom - Color map of the integrated temperature of 13CO  $J = 6\rightarrow 5$and the contour levels (as described before) of [C I]  $J = 2\rightarrow 1$with a peak emission of 282 K  ${\rm km~s}^{-1}$. The filled triangle and square mark selected positions where ambient conditions are estimated from. The reference position ( $\Delta \alpha =0$, $\Delta \delta =0$), marked with a cross, corresponds to the SAO star 161357 at $\rm RA(J2000)=18$:20:27.6483 and Dec(J2000)=-16:12:00.9077.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13077f2a-cmjn.eps} \end{figure} Figure 2:

Color map of the 21 cm continuum emission (Jy beam-1) in M 17 SW with a $10''\times 7''$resolution by Brogan & Troland (2001). The white contour lines correspond to the 12CO  $J = 6\rightarrow 5$with a peak emission of 830 K  ${\rm km~s}^{-1}$, while the green contour lines correspond to the [C I]  $J = 2\rightarrow 1$with a peak emission of 260 K  ${\rm km~s}^{-1}$. The countour levels (from thin to thick) are the 25%, 50%, 75% and 90% of the peak emission. The red stars indicate the O and B ionizing stars (Beetz et al. 1976; Hanson et al. 1997). The reference position ( $\Delta \alpha =0$, $\Delta \delta =0$) is the same as in Fig. 1. These 12CO and [C I] maps have a slightly lower integrated temperature than in Fig. 1 because they were convolved with a 20'' beam to smooth the contour lines.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.5cm,clip]{13077f3a-cmjn.eps}\par\vspace*{2mm} \includegraphics[width=7.5cm,clip]{13077f3b-cmjn.eps} \end{figure} Figure 3:

Top panel - strip lines of the velocity integrated intensities of 12CO J=7-6 (black), 12CO J=6-5 (red), 12CO J=2-1 (green) (adapted from S88), 13CO  J=6-5 (blue) and [C I]  J=2-1 (cyan) at $\Delta \delta =30''$(PA $90^{\circ }$) across the ionization front of M 17 SW. Bottom panel - strip lines at PA $63^{\circ }$ ( $\Delta \delta =\Delta \alpha /2$). The X-axis corresponds to the actual offset in RA of the maps shown in Fig. 1. Hence, $\Delta \alpha =0''$is the RA of the reference illuminating star SAO 161357.

Open with DEXTER

Figure 1 shows the maps of the temperatures, integrated between 5  ${\rm km~s}^{-1}$and 35  ${\rm km~s}^{-1}$, of 12CO  $J = 6\rightarrow 5$(top) with the contour lines of 12CO  $J = 7\rightarrow 6$, and the velocity integrated temperature of 13CO  $J = 6\rightarrow 5$(bottom) with the contour lines corresponding to [C I]  $J = 2\rightarrow 1$. All the maps were convolved to the largest beam size (9.4'') of the 13CO  $J = 6\rightarrow 5$line, obtaining a grid size of about $4.7''\times4.7''$. The peak integrated temperatures of the 12CO  $J = 6\rightarrow 5$and $J = 7\rightarrow 6$lines are 852 K  ${\rm km~s}^{-1}$and 925 K  ${\rm km~s}^{-1}$  respectively. These lines follow a similar spatial distribution. The peak integrated temperatures of 13CO  $J = 6\rightarrow 5$and [C I]  $J = 2\rightarrow 1$are 420 K and 282 K. respectively, and the peak of [C I] is shifted towards the inner side of the interface region at about 0.55 pc ($\sim$50''). The ionization front traced by the high resolution ( $10''\times 7''$) map of the 21 cm continuum emission (Brogan & Troland 2001) as well as the ionizing stars identified by Beetz et al. (1976) and Hanson et al. (1997) are shown in Fig. 2, with 12CO  $J = 6\rightarrow 5$(white contour lines) and [C I]  $J = 2\rightarrow 1$(green contour lines) overlaid. The transition between the hot ( $T_{\rm k}>300$ K) atomic gas and the warm ( $T_{\rm k}>100$ K) molecular gas can be seen due to the almost edge-on geometry of M 17 SW.

The top panel of Fig. 3 shows the variation of the integrated temperature of all the lines across the ionization front (strip line at $\rm PA=90^{\circ }$in Fig. 1). Due to the limited S/N the 12CO  $J = 7\rightarrow 6$and [C I]  $J = 2\rightarrow 1$strip lines have been smoothed spatially with respect to the strip direction. The [C I]  $J = 2\rightarrow 1$line starts peaking up at about 0.1 pc ($\sim$10'') after the molecular lines and presents a smooth transition towards the inner part of the cloud, forming a plateau at about $\Delta\alpha=-100''$, from where it increases its emission until the peak is reached at about $\Delta\alpha=-120''$. The peak of [C I]  correlates with a secondary peak seen in 13CO. However, the main peak emission of the latter correlates with the peak of the 12CO  lines along this strip line.

The strip line at $\rm PA=63^{\circ }$(bottom panel of Fig. 3) can be compared with Fig. 5 in M92, and Fig. 2 in S88. At this position angle, there is no marked plateau in the [C I]  emission, and the peak of the [C I]  line is closer to the peaks of the 12CO  and 13CO  lines. The dip in 12CO  $J = 2\rightarrow 1$at about $\Delta\alpha=-120''$ is an artifact. The integrated temperature of the 12CO  $J = 2\rightarrow 1$, $J = 6\rightarrow 5$and $J = 7\rightarrow 6$ lines have a comparable strength deep ( $\Delta\alpha>-160''$) into the M 17 SW complex.

3.2 The complex internal structure of M 17 SW

Figure 4 shows the spectra at selected positions along the NE-SW strip line at PA  $63^{\circ }$. The main-beam temperature of the spectra is shifted by 70 K at each offset position. This set of spectra can be compared with the 12CO  and C18O  $J = 2\rightarrow 1$spectra along the same strip line of Fig. 8 in S88. The warm gas ( $T_{\rm K}>50$ K), traced by the mid-J 12CO  lines, is as extended as the cold gas ( $T_{\rm K}<50$ K) traced by the 12CO  $J = 2\rightarrow 1$line deeper into the cloud. On the other hand, the 13CO  $J = 6\rightarrow 5$ and [C I]  $J = 2\rightarrow 1$lines are strongly detected in a narrower spatial extent of about 1.3 pc, similar to the extent of the C18O  $J = 2\rightarrow 1$ emission.

\begin{figure} \par\mbox{\includegraphics[height=14cm,angle=0]{13077f4a.eps}\hsp... ...ce{-0.2cm} \includegraphics[height=14cm,angle=0]{13077f4d.eps} } \end{figure} Figure 4:

Selected spectra of 12CO  $J = 6\rightarrow 5$, 12CO  $J = 7\rightarrow 6$, 13CO  $J = 6\rightarrow 5$and [C I]  $J = 2\rightarrow 1$along the NE-SW strip line (see Fig. 1). The positions in arcsecs are the offsets with respect to the reference position at RA(J2000)=18:20:27.6483 and Dec(J2000)=-16:12:00.9077. The spectra are the average spectra within $\pm $2'' of the indicated offset positions and smoothed to 1  ${\rm km~s}^{-1}$velocity resolution.

Open with DEXTER

Multilevel molecular line observations in CS, 12CO, 13CO and C18O and in several fine structure lines ([C I], [C II], [Si II], [O I]) indicate that M 17 SW consists of numerous high density clumps ( $n(\rm H_2)>10^4~\rm {cm^{-3}}$) from which the [O I], [Si II] and mid-J CO lines emanate. This dense gas is found within a relatively warm ($\sim$50 K) and less dense ( $n(\rm H_2)\sim3\times10^3~\rm {cm^{-3}}$) molecular gas (interclump medium), which in turn is surrounded by a diffuse halo ( $n(\rm H_2)\sim300~\rm {cm^{-3}}$) which is the source of the very extended [C I] and [C II] emission (Snell et al. 1984, 1986; Evans et al. 1987; S88; SG90; M92).

From the C18O  observations in M 17 SW a beam-averaged (13'') column density of $\sim$ $8\times10^{23}~\rm {cm^{-2}}$has been estimated for the cloud core and masses in the range $\sim$ $10{-}2000~M_{\odot}$for the CO clumps (SG90). A comparable mass range ($\sim$ $10{-}120~M_{\odot}$) was lately estimated from submillimeter continuum observations in the northern part of M 17 (Reid & Wilson 2006), although the region mapped by Reid & Wilson (2006) adjoins, but does not overlap with M 17 SW.

Figure 5 shows representative velocity channel maps of the 12CO  $J = 6\rightarrow 5$(top left) and $J = 7\rightarrow 6$ (top right) lines in M 17 SW. These are the main-beam brightness temperatures averaged over two and three velocity channels between 18.2  ${\rm km~s}^{-1}$and 19.9  ${\rm km~s}^{-1}$. These are similar to the velocity channels shown in Fig. 3 by SG90. The fact that the C18O  $J = 2\rightarrow 1$line traces colder ( $T_{\rm K}<50$ K) and less dense ( $n_H\sim3\times10^3~\rm {cm^{-3}}$) gas than the 12CO lines is reflected in the different velocity integrated maps (Fig. 1) and in the channel maps of these lines. In theory the critical densities (at $T_{\rm K}=100$ K) of the 12CO  $J = 6\rightarrow 5$and $J = 7\rightarrow 6$lines are $n_{\rm crit}\sim2.7\times10^5~\rm {cm^{-3}}$and $n_{\rm crit}\sim4.4\times10^5~\rm {cm^{-3}}$, respectively, which corresponds to a difference of a factor $\sim$1.6. However, this difference is not directly translated into a different clumpyness. This is reflected in the similar clumpy structure seen in the channel maps of these mid-J 12CO lines.

Even though the critical density of the 13CO  $J = 6\rightarrow 5$ line is similar to that of the 12CO ( $n_{\rm crit}\sim2.4\times10^5~\rm {cm^{-3}}$) the south-east region of its channel map (bottom left) differs from that seen with the 12CO lines. This could be due to a change in the temperature of the gas, or to a variation in the 13CO column density in that region. Since 13CO is much more optically thin than 12CO (abundance ratio of about 50-70), this difference in the map can be expected. In Sects. 4.2 and 4.3 we discuss the optical depths.

On the other hand, the [C I]  $J = 2\rightarrow 1$channel map (bottom right) shows a completely different structure and distribution than the 12CO and the isotope lines. Since the critical density of this line is about $2.8\times10^3~\rm {cm^{-3}}$, its emission is likely emerging partly from the interclump medium mentioned above.

\begin{figure} \par\mbox{\includegraphics[width=4.1cm]{13077f5a-cmjn.eps} \hspac... ...\hspace*{6mm}\includegraphics[width=4.1cm]{13077f5d-cmjn.eps} } \end{figure} Figure 5:

Top panel - Channel maps of the main-beam brightness temperature of 12CO  $J = 6\rightarrow 5$(left) and $J = 7\rightarrow 6$(right) averaged over two and three velocity channels, between 18.2-19.9  ${\rm km~s}^{-1}$, respectively. The contour lines are as described in Fig. 1, with peak-integrated line temperatures of 54.5  ${\rm~K}~{\rm km}^{-1}~{\rm s}$and 55.7  ${\rm~K}~{\rm km}^{-1}~{\rm s}$for the $J = 6\rightarrow 5$ and $J = 7\rightarrow 6$ lines, respectively. Bottom panel - Channel maps of 13CO  $J = 6\rightarrow 5$(left) and [C I]  $J = 2\rightarrow 1$(right), averaged over two velocity channels between 18.4-19.7  ${\rm km~s}^{-1}$. Contours are as in the top panel, and the peak-integrated line temperatures are 37.0  ${\rm~K}~{\rm km}^{-1}~{\rm s}$and 23.9  ${\rm~K}~{\rm km}^{-1}~{\rm s}$ .

Open with DEXTER

4 Discussion

4.1 Self-absorption in the mid-J 12CO lines?

The complex structure of the 12CO  $J = 1\rightarrow0$, $J = 2\rightarrow 1$, and $J = 3\rightarrow2$ line profiles has been attributed to strong self-absorption effects (e.g. Rainey et al. 1987; Stutzki et al. 1988). Martin et al. (1984) also reported a flat topped spectrum of 12CO  $J = 3\rightarrow2$, attributed to self-absorption or saturation at velocities near the line center and gave details about the effects of macroturbulent clumpy medium in the line profiles.

A double peaked structure in the 13CO  $J = 1\rightarrow0$line was also reported by Lada (1976). Rainey et al. considered that this double peaked structure in 13CO suggests that either this line is optically thick or that the double peaked structure is due to more than one cloud component. The latter is the interpretation favored by Rainey et al. in view of the available data at that time.

Phillips et al. (1981) presented a self-absorption LTE model that considers a 12CO  cloud of uniform temperature $T_{\rm k}$ in front of a hot background source of a temperature $T_{\rm bg}$, at the same central velocity. The velocity dispersion of the background cloud is considered to be larger than that of the foreground cloud, so the self-absorption effect is seen mostly at the line center. This model indicates that, depending on the total column density of 12CO, the self-absorption effect will be stronger in the $J = 2\rightarrow 1$and $J = 3\rightarrow2$ lines than in the $J = 1\rightarrow0$ line, with decreasing intensity as the transition number J increases. This is indeed observed in Fig. 12 of S88 for the 12CO  $J = 4\rightarrow3$, $J = 3\rightarrow2$, $J = 2\rightarrow 1$, and $J = 1\rightarrow0$ lines.

We reproduced the model by Phillips et al.  including the higher-J lines of 12CO. The top panel of Fig. 6 shows the model with the same background and foreground temperatures used by Phillips et al.This model implies that, for a background temperature $T_{\rm bg}=64$ K and a foreground kinetic temperature $T_{\rm k}=15$ K, the lower-J lines (J=1, 2, 3, 4) of the background cloud start showing self-absorption at the line center for lower column densities ( $N/\Delta V = 10^{14}{-}10^{15}$ cm-2 km s-1). Instead, the higher-J lines (J=5, 6, 7) need larger columns ( $N/\Delta V = 10^{15}{-}10^{17}$ cm-2 km s-1) in order to be affected by self-absorption. For a velocity dispersion of $\Delta V=5$  ${\rm km~s}^{-1}$, the upper limits of these 12CO  columns would correspond to extinctions $A_{\rm v}$ of $\sim$0.1 mag and $\sim$10 mag, respectively.

The bottom panel of of Fig. 6 shows the model for a background temperature $T_{\rm bg}=150$ K and a foreground temperature $T_{\rm k}=30$ K (from S88). In this case the lower-J lines show self-absorption at the same range of columns as before, while the higher-J lines start showing self-absorption at a narrower range of columns ( $N/\Delta V=10^{15}{-}10^{16}$ cm-2 km s-1). A remarkable characteristic of these models (top and bottom panels of Fig. 6) is that all the J lines are expected to be strongly self-absorbed at columns larger than 1018 cm-2 km s-1, which is similar to the column density estimated by S88. Another characteristic is that the 12CO emission of the higher-J lines are also expected to decrease with the transition number J, and be weaker than the low-J lines. However, the 12CO  $J = 7\rightarrow 6$line seems to break this rule, as can be seen in Fig. 12 of S88. The high peak temperature observed in the 12CO  $J = 7\rightarrow 6$line is missing in the lower-J lines. Even considering a calibration uncertainty of 20%, the 12CO  $J = 7\rightarrow 6$line (observed at offset position (-100'',0''), bottom panel of Fig. 12 in S88) will be as strong as the $J = 4\rightarrow3$ line (at least at the peak intensity) but still stronger than the $J = 2\rightarrow 1$line.

\begin{figure} \par\includegraphics[width=7cm]{13077f6a-cmjn.eps}\par\vspace{2mm} \includegraphics[width=7cm]{13077f6b-cmjn.eps} \end{figure} Figure 6:

Top panel - expected brightness temperature at the center of the 12CO  lines for a warm background cloud with a temperature $T_{\rm bg}=64$ K and a colder foreground-absorbing cloud with a temperature $T_{\rm k}=15$ K. Bottom panel - same as in the top panel, but for a background temperature $T_{\rm bg}=100$ K and a foreground temperature of $T_{\rm k}=30$ K.

Open with DEXTER

On the other hand, the 12CO  $J = 7\rightarrow 6$line seems to be asymmetric, with a left shoulder weaker than the right shoulder, which may be due to self-absorption produced by a colder foreground cloud with slightly lower center velocity than the warmer clump traced by the $J = 7\rightarrow 6$line. However, that weaker left shoulder of the mid-J line is still brighter than the corresponding shoulder of the lower-J lines, in most of the velocity range and in both positions (-100'',0'') and (-60'',-30'') - assuming a low (<10%) uncertainty in the calibration of the data. This is not what would be expected in the self-absorption scenario proposed by Phillips et al. (1981).

Figure 4 shows that the 13CO  $J = 6\rightarrow 5$line has a similar asymmetry as the 12CO lines, at positions (-45'',-23'') and (-60'',-30''). But it shows only one component at the other positions. This difference may be related to a gradient in the temperature (or total column density) of the foreground cloud that produces self-absorption in the first two positions, but not in the others. Instead, [C I]  $J = 2\rightarrow 1$shows similar asymmetry as 12CO  at positions (-45'',-23''), (-150'',-75'') and (-180'',-90''), and an opposite asymmetry at position (-75'',-38''). Given that there is no strong evidence for self-absorption in neither the 13CO  lines nor in the [C I]  lines and that the 13CO lines are mostly optically thin, it is unlikely that the observed asymmetries of the 13CO and [C I] lines are produced by self-absorption. Hence, we agree with Rainey et al. (1987) in that this complex structure is more likely due to more than one kinematical component along the line of sight. And this could also be the case for the mid-J 12CO lines.

Therefore, the observational facts and the models suggest that the self absorption effect, if present, should have little impact on the mid-J lines, and a few cloud components at different central velocities could also explain the complex structure of the line profiles. The asymmetry of the profiles suggests that self-absorption affects mostly one wing of the line profile, while the peak temperatures seems to be the least affected velocity channel in the mid-J lines. Hence, in the following sections we test the ambient conditions of the warm gas based on the ratios between the peak main-beam temperatures of the 12CO and 13CO  $J = 6\rightarrow 5$and $J = 7\rightarrow 6$ lines.

4.2 Optical depth and excitation temperature (LTE)

Since we have the maps of the 12CO and the 13CO  $J = 6\rightarrow 5$lines, we can estimate the optical depth and the excitation temperature of these lines, assuming local thermal equilibrium (LTE), from the ratio between their peak main-beam temperature $T_{\rm mb}$observed between the 5  ${\rm km~s}^{-1}$and 35  ${\rm km~s}^{-1}$velocity channels. This will provide at least a lower limit for the kinetic temperature in M 17 SW. Then we will estimate the ambient conditions at two selected positions based on a non-LTE model of the ratio between the peak $T_{\rm mb}$ temperatures of the 12CO  $J = 6\rightarrow 5$and $J = 7\rightarrow 6$lines (hereafter referred as 12CO  $\frac{7-6}{6-5}$line ratio). The temperature and densities obtained in this way will be compared to those values estimated in previous work.

In LTE the radiation temperature can be approximated (e.g. Kutner 1984; Bergin et al. 1994) by the expression:

\begin{displaymath}T_{\rm R}=[J_{\nu}(T_{\rm ex})-J_{\rm bg}][1-{\rm e}^{-\tau_{\nu}}] , \end{displaymath} (1)

where the term $J_{\nu}(T)$ is the Planck's function evaluated at a frequency $\nu$ and temperature T, and multiplied by the factor $\frac{\lambda^2}{2k}$ to obtain the intensity in K. So it is defined as:

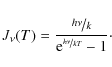
\begin{displaymath}J_{\nu}(T)=\frac{\nicefrac{h\nu}{k}}{{\rm e}^{\nicefrac{h\nu}{kT}}-1}\cdot \end{displaymath} (2)

We use the full $J_{\nu}(T)$ function since the Rayleigh-Jeans (R-J) approximation (commonly applied when $h\nu\ll kT$) does not hold for the high frequency lines studied in this work. For the R-J approximation to be true, we require $T\gg300$ K, which is a much higher temperature than what we expect to trace with our observations.

The background radiation $J_{\rm bg}$is a composite between the cosmic microwave background radiation (CMB), as a blackbody function at 2.73 K, and the diluted infrared radiation remitted by dust. That is:

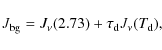
\begin{displaymath}J_{\rm bg}=J_{\nu}(2.73)+\tau_{\rm d}J_{\nu}(T_{\rm d}), \end{displaymath} (3)

where $\tau_{\rm d}$ is the effective optical depth of the warm surface layer, adopted from Hollenbach et al. (1991), and it is defined as $\tau_{\rm d}=\tau_{100~\mu{\rm m}}(100~\mu{\rm m}/\lambda)$. For M 17 SW we adopted an emission optical depth at 100 $\mu$m of $\tau_{100~\mu {\rm m}}=0.106$ and the average dust temperature $T_{\rm d}=50$ K from M92. We tried both, with and without the dust contribution to the background radiation, and we found that the contribution of the radiation by dust continuum emission is negligible at frequencies on the order of 690 GHz and 810 GHz. Nevertheless, all the following analysis includes the dust contribution for completeness.

For extended (resolved) sources like the clumps in M 17 SW, the radiation temperature is well estimated by the observed main-beam brightness temperature $T_{\rm mb}$. Hence, we use that quantity in the following analysis. From the LTE approximation we can assume that the excitation temperatures $T_{\rm ex}$of 12CO and 13CO  $J = 6\rightarrow 5$are the same, although the terms $J_{\nu}(T_{\rm ex})$are not exactly the same because of the slightly ($\sim$4%) different frequencies of the 12CO and 13CO lines. So, from Eq. (1) the ratio between 12CO and 13CO can be approximated as:

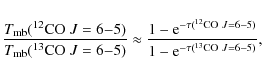
\begin{displaymath}\frac{T_{\rm mb}(^{12}{\rm CO}~J=6{-}5)}{T_{\rm mb}(^{13}{\rm... ...{\rm CO}~J=6{-}5)}}{1-{\rm e}^{-\tau(^{13}{\rm CO}~J=6{-}5)}}, \end{displaymath} (4)

Following the work by Wilson et al. (1999), we adopt a constant [12CO /13CO $\!\!$] abundance ratio of 50 for M 17 SW, which is approximately the value measured at a similar Galactic radius towards the W51 region (Langer & Penzias 1990). Assuming that the optical depth is proportional to the total column density of the molecules and, hence, to the abundance ratio between them, we can estimate that $\tau(^{12}{\rm CO})\approx50\tau(^{13}{\rm CO})$. The 13CO line is usually optically thin, so $\tau(^{13}{\rm CO})$ could be taken out of the exponential in Eq. (3) and estimated directly. However, we do not really know if this holds true for the entire M 17 SW region, so we do not apply further approximations and we solve Eq. (3) for $\tau(^{13}{\rm CO})$ with a numerical method (Newton-Raphson).

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13077f7a-cmjn.eps}\par\vspace*{2mm} \includegraphics[width=8.5cm,clip]{13077f7b-cmjn.eps} \end{figure} Figure 7:

LTE approximation of the optical depth (top) of the 13CO   $J = 6\rightarrow 5$and the excitation temperature (bottom) of the 13CO and 12CO  $J = 6\rightarrow 5$lines in M 17 SW. Contours are the 10%, 25%, 50%, 75% and 90% of the peak value, which is 1.9 for $\tau(\rm ^{13}CO~6{-}5)$and 120 K for $T_{\rm ex}$.

Open with DEXTER

The top panel in Fig. 7 shows the $\tau(^{13}{\rm CO})$map. The 13CO  line is optically thin in most of the region, with some optically thick spots (e.g., $\Delta\alpha=-30, \Delta\delta=-110$). Knowing $\tau(^{13}{\rm CO})$ we can estimate $T_{\rm ex}$ from Eq. (2) using either tracer, considering that the $T_{\rm ex}$estimated using 12CO is just $\sim$0.6% higher than that estimated using 13CO. The $T_{\rm ex}$map is shown in the bottom panel of Fig. 7. This map indicates that the warmest gas is located along the ridge of the cloud, close to the ionization front. The temperature in this region ranges between 40 and 120 K, and the peak temperature is located at around ( $\Delta\alpha=-60, \Delta\delta=10$). If we consider only the gas with temperatures $\ge$80 K, the warm gas would be confined to a zone of about 40'' ($\sim$0.44 pc) next to, and along, the HII region, which agrees with previous results found by Graf et al. (1993). If the gas were thermalized, this could be the actual map of the kinetic temperature of the gas. Otherwise, the $T_{\rm ex}$map can be considered as a lower limit of $T_{\rm K}$. Since in velocity space the clumps cover the whole beam, this would imply that the 12CO and 13CO molecules are subthermal in the $J = 6\rightarrow 5$ transition. That is, the density of the gas and the column density of 12CO and 13CO may be insufficient to thermalize these transitions. A more detailed analysis is presented in the next section.

\begin{figure} \par\includegraphics[width=8cm]{13077f8a-cmjn.eps}\par\vspace*{1m... ...\par\vspace*{1mm} \includegraphics[width=8cm]{13077f8d-cmjn.eps} \end{figure} Figure 8:

Top - spectra of the four lines observed in M 17 SW at position A ( $\Delta \alpha =-70'', \Delta \delta =+32''$), close to the peak emission in the 12CO and 13CO maps. Middle top - spectra observed at position B ( $\Delta \alpha =-70'', \Delta \delta =-82''$), where the integrated line temperatures are about 50% of the peak emission. Middle bottom - spectra observed at position C ( $\Delta \alpha =-60'', \Delta \delta =-30''$), the peak of the NE-SW strip scan. Bottom - spectra observed at position D ( $\Delta \alpha =-100'', \Delta \delta =0''$), close to the continuum far-IR peak.

Open with DEXTER

4.3 Ambient condition at selected positions (non-LTE)

Figure 8 shows the spectra of all the observed lines extracted at four different positions in the map. The top panel shows the spectra observed at position A ( $\Delta \alpha =-70'', \Delta \delta =+32''$), close to the peak emission of the 12CO lines. All the lines show a double component structure with the secondary component peaking at $\sim$25  ${\rm km~s}^{-1}$. The middle top panel shows the spectra at position B ( $\Delta \alpha =-70'', \Delta \delta =-82''$), where the velocity-integrated temperature corresponds to about 50% of the peak emission. Here only the 12CO  $J = 7\rightarrow 6$line seems to have a dip at the line center. However, because of the low S/N in the high frequency band, this dip may be likely due to noise. The middle bottom panel shows the spectra at position C ( $\Delta \alpha =-60'', \Delta \delta =-30''$), which corresponds to the peak of the NE-SW strip scan reported in S88 and Graf et al. (1993), with beams of 40'' and 8'', respectively. The bottom panel shows the spectra at position D ( $\Delta \alpha =-100'', \Delta \delta =0''$), which is close to the continuum far-IR peak, also reported in S88. Since we do not have dedicated observations at these positions, we extracted the spectra from the nearest pixels in our maps, convolved to the largest beam (9.4'') of the 13CO  $J = 6\rightarrow 5$line. So the spectra shown in Fig. 8 are the convolved spectra centered within $\pm $1'' of the indicated coordinates. This is justified because we have oversampled data.

Table 1 shows the Gaussian fits of the spectra obtained at the four selected positions. Two Gaussian components were needed to fit the lines, except at position B, where only one component was used. The main components of the 12CO lines have a line width that is about 8-9  ${\rm km~s}^{-1}$at position A, while the 13CO has a line width of about 3  ${\rm km~s}^{-1}$narrower. The [C I] line is the narrowest line, with a line width of $\sim$4  ${\rm km~s}^{-1}$. At position B, the 12CO lines are the widest of the four lines with about 8  ${\rm km~s}^{-1}$  and the 13CO and [C I] lines have about half the line width of the 12CO lines. At position C and D the Gaussian parameters of the 12CO  $J = 7\rightarrow 6$presented uncertainties of $\sim$$50\%$ when let free in the fitting. However, because the line shape of the 12CO  $J = 7\rightarrow 6$and $J = 6\rightarrow 5$ transitions are very similar, we set the line width of the $J = 7\rightarrow 6$transition to the value found for the $J = 6\rightarrow 5$line. The line width of the main components of the 12CO lines at position C and D are $\sim$6  ${\rm km~s}^{-1}$, that is about 2  ${\rm km~s}^{-1}$narrower than the lines observed at positions A and B. This difference can be due to a higher optical depth towards the latter positions or to the contribution of a few fast-moving cloudlets (Martin et al. 1984; Graf et al. 1993).

The 12CO  $\frac{7-6}{6-5}$line ratio between the peak main-beam temperatures $T_{\rm mb}$ obtained from the Gaussian fit of the main components is $1.02\pm0.05$at position A, $0.95\pm0.05$ at position B, $1.00\pm0.05$ at position C, and $0.99\pm0.07$ at position D. From these line ratios we can estimate the ambient conditions for these particular positions. We have used the non-LTE radiative transfer code RADEX[*] (Van der Tak et al. 2007) to estimate the average ambient conditions (kinetic temperature, density and column density) of the molecular gas. We assumed collisional excitation by molecular hydrogen. We also assumed an homogeneous spherical symmetry in the clumps for the escape-probability formalism. The collision rates between 12CO and ortho- and para-H2 are taken from Wernli et al. (2006), and can be found in the LAMDA database (Schöier et al. 2005). As in the LTE case, we used the cosmic microwave background radiation at 2.73 K, and we also tested the non-LTE model with and without the infrared radiation remitted by dust (Eq. (3)) as the background source. It was found also for this case that the dust continuum emission produces a negligible effect in the non-LTE model at the frequencies of the 12CO  $J = 6\rightarrow 5$and $J = 7\rightarrow 6$lines. We explored molecular hydrogen densities between $10^4~\rm {cm^{-3}}$and $10^7~\rm {cm^{-3}}$, temperatures between 5 K and 500 K, and 12CO column densities between $10^{10}~\rm {cm^{-2}}$ and $10^{18}~\rm {cm^{-2}}$.

Figure 9 shows the possible ambient conditions required to reproduce the 12CO  $\frac{7-6}{6-5}$line ratios, and the peak $T_{\rm mb}$ of the 12CO   $J = 6\rightarrow 5$line observed at position A (top panel) and B (bottom panel). A wide range of temperatures (100-450 K) and densities (> $3\times10^4~\rm {cm^{-3}}$) are possible solutions for a 12CO column density per line width $N({\rm ^{12}CO})/\Delta V\sim5\times10^{16}$${\rm cm}^{-2}~{\rm km}^{-1}~{\rm s} $.

Table 1:   M 17 SW line parameters derived from Gaussian fits, at four selected positions.

\begin{figure} \par\includegraphics[width=8cm,clip]{13077f9a.eps}\par\vspace*{2mm} \includegraphics[width=8cm,clip]{13077f9b.eps} \end{figure} Figure 9:

Top - the gray scale and contours represent the average ($\log_{10}$ scale) column density per line width ( ${\rm cm}^{-2}~{\rm km}^{-1}~{\rm s} $) required to reproduce the observed 12CO   $\frac{7-6}{6-5}$line ratio between the peak main-beam temperatures $T_{\rm mb}$and the the peak $T_{\rm mb}$ of the 12CO   $J = 6\rightarrow 5$line observed at position A ( $\Delta \alpha =-70'', \Delta \delta =+32''$), for different kinetic temperatures $T_{\rm K}$ and densities $n(\rm H_2)$. Bottom - same as top, but at position B ( $\Delta \alpha =-70'', \Delta \delta =-82''$).

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13077f9c.eps}\par\vspace*{2mm} \includegraphics[width=8cm,clip]{13077f9d.eps} \end{figure} Figure 10:

Top - the gray scale and contours represent the average ($\log_{10}$ scale) column density per line width ( ${\rm cm}^{-2}~{\rm km}^{-1}~{\rm s} $) required to reproduce the observed 12CO   $\frac{7-6}{6-5}$line ratio between the peak main-beam temperatures $T_{\rm mb}$and the the peak $T_{\rm mb}$ of the 12CO   $J = 6\rightarrow 5$line observed at position C ( $\Delta \alpha =-60'', \Delta \delta =-30''$), for different kinetic temperatures $T_{\rm K}$ and densities $n(\rm H_2)$. Bottom - same as top, but at position D ( $\Delta \alpha =-100'', \Delta \delta =0''$).

Open with DEXTER

Figure 10 shows the possible ambient conditions estimated for position C (top panel) and D (bottom panel). The combinations of temperatures and densities required to reproduce the line ratios and peak temperatures are similar to those found for position A and B, although the range of possible temperatures (for a given density) at position D is larger than at the other positions. The column densities differ due to the different line strengths observed at the four positions (Table 1).

In order to constrain the range of solutions we can adopt the average $5\times10^5~\rm {cm^{-3}}$ density estimated by M92, which is also similar to the mean density of the clumps estimated by SG90. This is a sensitive assumption for a collision dominated scenario since this density is larger than the critical density of both 12CO lines for $T_{\rm K}\ge20$ K. However, at this density ( $5\times10^5~\rm {cm^{-3}}$) the temperature cannot be higher than 230 K in order to reproduce the line ratio and the peak $T_{\rm mb}$of the 12CO  $J = 6\rightarrow 5$line observed at position A. And it cannot be higher than 150 K at position B. At position C the limit is about 220 K, and at position D it is about 200 K. These are lower kinetic temperatures than the 1000 K estimated for the dense clumps in the three-component model proposed by M92. Our upper limits for the kinetic temperature agree with the results reported in previous work (e.g Harris et al. 1987; S88; SG90). From the map of the excitation temperature $T_{\rm ex}$estimated from the LTE model (Fig. 7), the lower limits for $T_{\rm K}$ would be $\sim$110 K and $\sim$80 K at position A & C and B & D, respectively. These are similar (within 30%) to the lowest temperatures obtained with the non-LTE models (Figs. 9 and 10).

According to the radiative transfer model, temperatures up to 400 K and higher are also possible, but they require densities of < $10^5~\rm {cm^{-3}}$in order to reproduce the observed line ratios and peak temperatures. These densities and temperatures are consistent with the estimates made based on previous observations of the 12CO  $J = 7\rightarrow 6$and $J = 14\rightarrow13$ lines (Harris et al. 1987; SG90). On the other hand, clumps with densities of > $10^6~\rm {cm^{-3}}$could also reproduce the observed ratios and peak $T_{\rm mb}$ in all the positions at temperatures $\le$200 K. However, these would be at the lower limit of the temperature range estimated in Harris et al. (1987) and SG90. The densities and temperatures found for M 17 SW are similar to those found in W3 Main (Kramer et al. 2004), but higher (although compatible) than the kinetic temperatures found in Carina, where lower limits between 30 K and 50 K were estimated (Kramer et al. 2008).

4.3.1 Column densities at selected positions

The column density per line width $N({\rm ^{12}CO})/\Delta V$at position A varies over a small range of $4{-}6\times10^{16}~\hbox{${\rm cm}^{-2}~{\rm km}^{-1}~{\rm s} $ }$. If we consider an average line width of 8.7  ${\rm km~s}^{-1}$estimated for the 12CO  $J = 6\rightarrow 5$ and $J = 7\rightarrow 6$ lines (Table 1) and the average $N({\rm CO})/\Delta V=5\times10^{16}~\hbox{${\rm cm}^{-2}~{\rm km}^{-1}~{\rm s} $ }$, we have a total column density of $N({\rm ^{12}CO})\approx4\times10^{17}~\rm {cm^{-2}}$.

The model indicates that at position B the 12CO column density per line width would be $\sim$ $4\times10^{16}~\hbox{${\rm cm}^{-2}~{\rm km}^{-1}~{\rm s} $ }$. The average line width of the lines at position B is $\sim$7.7  ${\rm km~s}^{-1}$(Table 1), which gives a total column density of $N({\rm ^{12}CO})\approx3\times10^{17}~\rm {cm^{-2}}$, similar to the column found at position A. At positions C and D the average column densities per line width are $\sim$ $8\times10^{16}~\hbox{${\rm cm}^{-2}~{\rm km}^{-1}~{\rm s} $ }$and $\sim$$5\times10^{16}~\hbox{${\rm cm}^{-2}~{\rm km}^{-1}~{\rm s} $ }$, respectively. Considering a line width of $\sim$6  ${\rm km~s}^{-1}$we obtain similar column densities as in the previous two positions. That is $N({\rm ^{12}CO})\approx5\times10^{17}~\rm {cm^{-2}}$and $N({\rm ^{12}CO})\approx3\times10^{17}~\rm {cm^{-2}}$for positions C and D, respectively. At positions A and C the lines are optically thin, with $\tau$ ranging from about 0.6 to 1 for $T_{\rm K}\ge150$ K. At temperatures of $\le150$ K, the lines become optically thick ( $1\le\tau\le3$). The optically thin limit at positions B and D is reached at $T_{\rm K}\sim120$ K, with about the same ranges of optical depths as before, for temperatures higher or lower than 120 K.

Assuming a density of $5\times10^5~\rm {cm^{-3}}$and average temperatures of 200 K at position A and 150 K at position B, the non-LTE model indicates that 13CO column densities of $\sim$ $1.5\times10^{17}~\rm {cm^{-2}}$and $\sim$$7.4\times10^{16}~\rm {cm^{-2}}$ would be required to reproduce the observed strength (Table 1) of the 13CO  $J = 6\rightarrow 5$line at these positions, respectively. For a temperature of 200 K, the 13CO column density at position C and D would be $\sim$ $5.6\times10^{16}~\rm {cm^{-2}}$. And the excitation temperatures would be $\sim$180 K at position A, C and D, and $\sim$140 K at position B, which are higher temperatures than estimated with the LTE approximation. However, these excitation temperatures are just between 10 and 20 K lower than the assumed kinetic temperatures, which indicates that these lines are close (within 10%) to the thermal equilibrium.

From their C18O  $J = 2\rightarrow 1$observations, S88 estimated a 12CO beam-averaged column density of $\sim$ $2\times10^{19}~\rm {cm^{-2}}$, considering a [12CO]/[C18O] abundance ratio of 500. Hence, the column densities found for the four selected positions in M 17 SW suggest that the warm ( $T_{\rm k}>100$ K) and dense ( $n(\rm H_2)\ge10^4~\rm {cm^{-3}}$) gas traced by the mid-J 12CO lines represent $\la$2% of the bulk of the cold ( $T_{\rm k}<50$ K) and less dense ( $n(\rm H_2)\sim10^3~\rm {cm^{-3}}$) gas traced by the low-J 12CO lines.

4.3.2 Volume-filling factors

The clump volume-filling factor $\Phi_{\rm V}$can be estimated from the ratio between the average volume density $n_{\rm av}$per beam and the average clump density $n_{\rm clump}\sim5\times10^5~\rm {cm^{-3}}$derived from the non-LTE model (e.g. Kramer et al. 2004). The average volume density per beam can be estimated from the total column density of the gas and the line of sight extent of the cloud ( $D_{\rm cloud}$). That is $n_{\rm av}\sim N({\rm H}_2)/D_{\rm cloud}$. Following the work by Howe et al. (2000) we can assume a 13CO abundance ratio of $1.5\times10^{-6}$relative to H2, and estimate the hydrogen column densities of $N_{\rm A}(\rm H_2)\sim2.3\times10^{23}~\rm {cm^{-2}}$, $N_{\rm B}(\rm H_2)\sim1.1\times10^{23}~\rm {cm^{-2}}$, and $N_{\rm C,D}(\rm H_2)\sim8.4\times10^{22}~\rm {cm^{-2}}$, for the four selected positions.

The line of sight extent of the cloud is a difficult parameter to estimate. From a 13'' ($\sim$0.14 pc) beam-averaged column density of $N(\rm H_2)\sim8\times10^{23}~\rm {cm^{-2}}$, a volume-filling factor of 0.13 was estimated by SG90. While Howe et al. (2000) reported a $\Phi_{\rm V}$ of $\sim$0.002 from the total column density of $N(\rm H_2)\sim4\times10^{22}~\rm {cm^{-2}}$estimated at the peak column density of their 13CO   $J = 1\rightarrow0$map, and assuming a cloud extent of 3 pc, which was deconvolved from the 4' beam of the SWAS space telescope. The line of sight extent should be larger than the smallest possible clump size ($\sim$0.1 pc) that we can deconvolve from our 9.4'' beam. But we do not think it can be as large as 3 pc, which is about the size of the maps we present here. This holds true at least for the region of bright 12CO and 13CO emission close to the ionization front, where our four selected positions are taken from. If we take the average between the upper (3 pc) and lower (0.1 pc) limits of the cloud extent, we would obtain a cloud size of $\sim$1.6 pc. This line of size extent of the cloud is uncertain, but perhaps more realistic given the geometry of M 17 SW and the high resolution of our maps. Besides, it is similar to the diameter of the [C I] emitting region ($\approx$1 pc) estimated by Genzel et al. (1988), and the narrow spatial extension ($\sim$1.3 pc) of the 13CO  $J = 6\rightarrow 5$ and [C I]  370 $\mu$m lines along the strip line at $\rm PA=63^{\circ }$(Figs. 3 and 4).

Using the total column densities estimated for the four selected positions and $D_{\rm cloud}=1.6$ pc, the average volume densities at position A and B would be $\sim$ $5.3\times10^4~\rm {cm^{-3}}$and $\sim$$2.5\times10^4~\rm {cm^{-3}}$, respectively, and $\sim$ $1.9\times10^4~\rm {cm^{-3}}$at position C and D. This in turn yields volume-filling factors $\Phi_{\rm V}=n_{\rm av}/n_{\rm clump}$of $\sim$0.106, $\sim$0.050 and 0.038 at positions A, B and C/D respectively. These volume-filling factors, as well as the total hydrogen densities estimated here, are larger than those estimated by Howe et al. (2000), but smaller than the ones reported in SG90. This is an expected and reasonable result since the 13CO  $J = 6\rightarrow 5$line traces only the warm and dense clumps and not the interclump medium. Besides, the volume-filling factors estimated at the four selected positions agree closely with those estimated in other star-forming regions using clumpy PDR models (e.g. S140, W3 Main; Spaans & van Dishoeck 1997; Kramer et al. 2004).

4.3.3 Jeans stability of the clumps

With an average density of $5\times10^5~\rm {cm^{-3}}$and an average clump size of 0.2 pc in diameter, which gives a typical total clump mass of $\sim$100 $M_{\odot}$ in molecular hydrogen, M92 estimated that these clumps are not in pressure equilibrium with the interclump gas (with average density $3\times10^3~\rm {cm^{-3}}$and temperature of 200 K), but rather that they are self-gravitating. With these parameters and a temperature of about 1000 K, the Jeans mass and radius should be about $1500~M_{\odot}$and 0.3 pc, respectively. Hence these clumps are not near the collapsing regime. Even with our upper limits for the temperatures of the clumps of 230 K and 150 K at position A and B, and 220 K and 200 K at position C and D, respectively, the Jeans mass and radius of these clumps would still be larger than those estimated with the average density of $5\times10^5~\rm {cm^{-3}}$. Temperatures of <170 K would be required to break the Jeans stability at that density. This means that the clumps at position B should have a slightly lower density of $\sim$ $3\times10^5~\rm {cm^{-3}}$(or lower) to be Jeans-stable at a temperature of about 150 K (or higher).

4.4 Follow-up work

A higher resolution map of the 609 $\mu$m (492 GHz) $^3{\rm P}_1\rightarrow{^3{\rm P}_0}$fine-structure transition of [C I] will be obtained with FLASH on APEX, in order to constrain the ambient conditions of the interclump medium and the halo in M 17 SW. More complex radiative transfer codes like RATRAN (Hogerheijde & van der Tak 2000) and $\beta 3D$ (Poelman & Spaans 2005), will be used to model the internal dynamics, temperature and density structure of individual clouds. The models will also allow us to explore in detail the effect of absorbing foreground clouds, or multiple cloud components, in the line profiles. Our PDR code (Meijerink & Spaans 2005) will provide the abundances of the molecular and atomic species, according to the UV flux estimated from historical data and our mid-J lines data. All together, these models will aid to test and constrain the heating and cooling of the irradiated gas.

5 Conclusions

We have used the dual-color heterodyne receiver array of 7 pixels CHAMP+ on the APEX telescope to map a region of about 3.4 pc $\times$ 3.0 pc in the $J = 6\rightarrow 5$ and $J = 7\rightarrow 6$ lines of 12CO, the 13CO  $J = 6\rightarrow 5$and the $^3{\rm P}_2\rightarrow{^3{\rm P}_1}$ 370 $\mu$m ( $J = 2\rightarrow 1$) fine-structure transition of [C I] in M 17 SW nebula.

The completely different structure and distribution of the $^3{\rm P}_2\rightarrow{^3{\rm P}_1}$370 $\mu$m emission and its critical density indicate that this emission arises from the interclump medium ($\sim$ $3\times10^3~\rm {cm^{-3}}$). On the other hand, the mid-J lines of 12CO and the isotope emissions arise from the high density ($\sim$ $5\times10^5~\rm {cm^{-3}}$) and clumpy region.

The spatial extent of the warm gas (40-230 K) traced by the 12CO  $J = 7\rightarrow 6$line is about 2.2 pc from the ridge of the M 17 SW complex, which is smaller than the extent observed in the low-J 12CO and C18O lines reported in previous work. The 13CO  $J = 6\rightarrow 5$ and [C I]  370 $\mu$m lines, have a narrower spatial extent of about 1.3 pc along a strip line at $\rm PA=63^{\circ }$.

An LTE approximation of the excitation temperature provides lower limits for the kinetic temperature. The warmest gas is located along the ridge of the cloud, close to the ionization front. In this region the excitation temperatures range between 40 and 120 K. A non-LTE estimate of the ambient conditions at four selected positions of M 17 SW indicates that the high density clumps ($\sim$ $5\times10^5~\rm {cm^{-3}}$) cannot have temperatures higher than 230 K. The warm ( $T_{\rm k}>100$ K) and dense ( $n(\rm H_2)\ge10^4~\rm {cm^{-3}}$) gas traced at the four selected positions by the mid-J 12CO lines represents $\sim2$% of the bulk of the molecular gas traced by the low-J 12CO lines. Volume-filling factors of the warm gas ranging from 0.04 to 0.11 were found at these positions.

Acknowledgements
We are grateful to the MPfIR team and the APEX staff for their help and support during and after the observations. We are grateful to J. Stutzki for providing the low-J 12CO data and to C. Brogan for providing the 21 cm map. We thank the referee for the careful reading of the manuscript and constructive comments. Molecular Databases that have been helpful include the NASA/JPL, LAMDA and NIST. The construction of CHAMP+ is a collaboration between the Max-Planck-Institut für Radioastronomie Bonn, SRON Groningen, the Netherlands Research School for Astronomy (NOVA), and the Kavli Institute of Nanoscience at Delft University of Technology, with support from the Netherlands Organization for Scientific Research (NWO) grant 600.063.310.10.

References

  1. Bayet, E., Gerin, M., Phillips, T. G., & Contursi, A. 2006, A&A, 460, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Beetz, M., Elsaesser, H., Weinberger, R., & Poulakos, C. 1976, A&A, 50, 41 [NASA ADS] [Google Scholar]
  3. Bergin, E. A., Goldsmith, P. F., Snell, R. L., & Ungerechts, H. 1994, ApJ, 431, 674 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bergin, E. A., Snell, R. L., & Goldsmith, P. F. 1996, ApJ, 460, 343 [NASA ADS] [CrossRef] [Google Scholar]
  5. Brogan, C. L., & Troland, T. H. 2001, ApJ, 560, 821 [NASA ADS] [CrossRef] [Google Scholar]
  6. Evans, N. J., II, Davis, J. H., Mundy, L. G., & Vanden Bout, P. 1987, ApJ, 312, 344 [NASA ADS] [CrossRef] [Google Scholar]
  7. Felli, M., Churchwell, E., & Massi, M. 1984, A&A, 136, 53 [NASA ADS] [Google Scholar]
  8. Fixsen, D. J., Bennett, C. L., & Mather, J. C. 1999, ApJ, 526, 207 [NASA ADS] [CrossRef] [Google Scholar]
  9. Genzel, R., Harris, A. I., Stutzki, J., & Jaffe, D. T. 1988, ApJ, 332, 1049 [NASA ADS] [CrossRef] [Google Scholar]
  10. Gerin, M., & Phillips, T. G. 1998, ApJ, 509, L17 [NASA ADS] [CrossRef] [Google Scholar]
  11. Graf, U. U., Eckart, A., Genzel, R., et al. 1993, ApJ, 405, 249 [NASA ADS] [CrossRef] [Google Scholar]
  12. Griffin, M. J., Ade, P. A. R., Orton, G. S., et al. 1986, Icarus, 65, 244 [NASA ADS] [CrossRef] [Google Scholar]
  13. Güsten, R., & Fiebig, D. 1988, A&A, 204, 253 [NASA ADS] [Google Scholar]
  14. Güsten, R., Nyman, L. A., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Güsten, R., Baryshev, A., Bell, A., et al. 2008, Proc. SPIE, 7020, 25 [Google Scholar]
  16. Habing, H. J. 1968, Bull. Astr. Inst. Netherlands, 19, 421 [Google Scholar]
  17. Hogerheijde, M. R., & van der Tak, F. F. S. 2000, A&A, 362, 697 [NASA ADS] [Google Scholar]
  18. Hanson, M. M., Howarth, I. D., & Conti, P. S. 1997, ApJ, 489, 698 [NASA ADS] [CrossRef] [Google Scholar]
  19. Harris, A. I., Stutzki, J., Genzel, R., et al. 1987, ApJ, 322L, 49 [Google Scholar]
  20. Howe, J. E., Ashby, M. L. N., Bergin, E. A., et al. 2000, ApJ, 539, L137 [NASA ADS] [CrossRef] [Google Scholar]
  21. Icke, V., Gatley, I., & Israel, F. P. 1980, ApJ, 236, 808 [NASA ADS] [CrossRef] [Google Scholar]
  22. Jaffe, D. T., Harris, A. I., & Genzel, R. 1987, ApJ, 316, 231 [NASA ADS] [CrossRef] [Google Scholar]
  23. Jakob, H., Kramer, C., Simon, R., et al. 2007, A&A, 461, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Kasemann, C., Güsten, R., Heyminck, S., et al. 2006, Proc. of the SPIE, 6275, 19 [NASA ADS] [Google Scholar]
  25. Kaufman, M., Wolfire, M., Hollenbach, D., & Luhman, M. 1999, ApJ, 527, 795 [NASA ADS] [CrossRef] [Google Scholar]
  26. Keene, J., Blake, G. A., Phillips, T. G., Huggins, P. J., & Beichman, C. A. 1985, ApJ, 299, 967 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kramer, C., Stutzki, J., Rohrig, R., & Corneliussen, U. 1998, A&A, 329, 249 [NASA ADS] [Google Scholar]
  28. Kramer, C., Jakob, H., Mookerjea, B., et al. 2004, A&A, 424, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Kramer, C., Mookerjea, B., Bayet, E., et al. 2005, A&A, 441, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Kramer, C., Cubick, M., Röllig, M., et al. 2008, A&A, 477, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Kutner, M. L. 1984, Fund. Cosmic Phys., 9, 233 [NASA ADS] [Google Scholar]
  32. Lada, C. J. 1976, ApJS, 32, 603 [NASA ADS] [CrossRef] [Google Scholar]
  33. Langer, W. D., & Penzias, A. A. 1990, ApJ, 357, 477 [NASA ADS] [CrossRef] [Google Scholar]
  34. Martin, H. M., Sanders, D. B., & Hills, R. E. 1984, MNRAS, 208, 35 [NASA ADS] [CrossRef] [Google Scholar]
  35. Meixner, M., Haas, M. R., Tielens, A. G. G. M., Erickson, E. F., & Werner, M. 1992, ApJ, 390, 499 (M92) [NASA ADS] [CrossRef] [Google Scholar]
  36. Meijerink, R., & Spaans, M. 2005, A&A, 436, 397 (MS05) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Meijerink, R., Spaans, M., & Israel, F. P. 2007, A&A, 461, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Mookerjea, B., Ghosh, S., Kaneda, H., et al. 2003, A&A, 404, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Muders, D., Hafok, H., Wyrowski, F., et al. 2006, A&A, 454, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Pellegrini, E. W., Baldwin, J. A., Brogan, C. L., et al. 2007, ApJ, 658, 1119 [NASA ADS] [CrossRef] [Google Scholar]
  41. Phillips, T. G., Knapp, G. R., Wannier, P. G., et al. 1981, ApJ, 245, 512 [NASA ADS] [CrossRef] [Google Scholar]
  42. Poelman, D. R., & Spaans, M. 2005, A&A, 440, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Povich, M. S., Churchwell, Ed., Bieging, J. H., et al. 2009, ApJ, 696, 1278 [NASA ADS] [CrossRef] [Google Scholar]
  44. Rainey, R., White, G. J., Gatley, I., et al. 1987, A&A, 171, 252 [NASA ADS] [Google Scholar]
  45. Reid, M. A., & Wilson, C. D. 2006, ApJ, 644, 990 [NASA ADS] [CrossRef] [Google Scholar]
  46. Schilke, P., Walmsley, C. M., Pineau de Forêst, G., et al. 1992, A&A, 256, 595 (S92) [NASA ADS] [Google Scholar]
  47. Schneider, N., Simon, R., Kramer, C., Stutzki, J., & Bontemps, S. 2002, A&A, 384, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Schneider, N., Simon, R., Kramer, C., et al. 2003, A&A, 406, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Snell, R. L., Goldsmith, P. F., Erickson, N. R., Mundy, L. G., & Evans, N. J., II 1984, ApJ, 276, 625 [NASA ADS] [CrossRef] [Google Scholar]
  51. Snell, R. L., Erickson, N. R., Goldsmith, P. F., et al. 1986, ApJ, 304, 780 [NASA ADS] [CrossRef] [Google Scholar]
  52. Snell, R. L., Howe, J. E., Ashby, M. L. N., et al. 2000, ApJ, 539, L97 [NASA ADS] [CrossRef] [Google Scholar]
  53. Spaans, M., & van Dishoeck, E. F. 1997, A&A, 323, 953 [NASA ADS] [Google Scholar]
  54. Stutzki, J., & Güsten, R. 1990, ApJ, 356, 513 (SG90) [NASA ADS] [CrossRef] [Google Scholar]
  55. Stutzki, J., Stacey, G. J., Genzel, R., et al. 1988, ApJ, 332, 379 (S88) [NASA ADS] [CrossRef] [Google Scholar]
  56. Van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Wang, Y., Jaffe, D. T., Evans, N. J., II, et al. 1993, ApJ, 419, 707 [NASA ADS] [CrossRef] [Google Scholar]
  58. Weiss, A., Henkel, C., Downes, D., & Walter, F. 2003, A&A, 409, 41 [Google Scholar]
  59. Wernli, M., Valiron, P., Faure, A., et al. 2006, A&A, 446, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Wilson, C. D., Howe, J. E., & Balogh, M. L. 1999, ApJ, 517, 174 [NASA ADS] [CrossRef] [Google Scholar]
  61. Yamamoto, S., Maezawa, H., Ikeda, M., et al. 2001, ApJ, 547, L165 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... (APEX[*]
This publication is based on data acquired with the Atacama Pathfinder Experiment (APEX). APEX is a collaboration between the Max-Planck-Institut fur Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory.
... Jupiter[*]
http://www.mpifr.de/div/submmtech/heterodyne/champplus/ champmain.html
... GILDAS[*]
http://www.iram.fr/IRAMFR/GILDAS
... RADEX[*]
http://www.sron.rug.nl/ vdtak/radex/radex_manual.pdf

All Tables

Table 1:   M 17 SW line parameters derived from Gaussian fits, at four selected positions.

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13077f1a-cmjn.eps}\par\vspace*{2mm} \includegraphics[width=8.5cm,clip]{13077f1b-cmjn.eps} \end{figure} Figure 1:

Top - Color map of the integrated temperature of 12CO  $J = 6\rightarrow 5$in M 17 SW. The contour lines correspond to the 12CO  $J = 7\rightarrow 6$, which has a peak emission of 925 K  ${\rm km~s}^{-1}$. The countour levels are the 25%, 50%, 75% and 90% of the peak emission. Dashed lines correspond to the E-W and NE-SW strip lines at $\rm PA=90^{\circ }$and $\rm PA=63^{\circ }$, respectively. Bottom - Color map of the integrated temperature of 13CO  $J = 6\rightarrow 5$and the contour levels (as described before) of [C I]  $J = 2\rightarrow 1$with a peak emission of 282 K  ${\rm km~s}^{-1}$. The filled triangle and square mark selected positions where ambient conditions are estimated from. The reference position ( $\Delta \alpha =0$, $\Delta \delta =0$), marked with a cross, corresponds to the SAO star 161357 at $\rm RA(J2000)=18$:20:27.6483 and Dec(J2000)=-16:12:00.9077.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13077f2a-cmjn.eps} \end{figure} Figure 2:

Color map of the 21 cm continuum emission (Jy beam-1) in M 17 SW with a $10''\times 7''$resolution by Brogan & Troland (2001). The white contour lines correspond to the 12CO  $J = 6\rightarrow 5$with a peak emission of 830 K  ${\rm km~s}^{-1}$, while the green contour lines correspond to the [C I]  $J = 2\rightarrow 1$with a peak emission of 260 K  ${\rm km~s}^{-1}$. The countour levels (from thin to thick) are the 25%, 50%, 75% and 90% of the peak emission. The red stars indicate the O and B ionizing stars (Beetz et al. 1976; Hanson et al. 1997). The reference position ( $\Delta \alpha =0$, $\Delta \delta =0$) is the same as in Fig. 1. These 12CO and [C I] maps have a slightly lower integrated temperature than in Fig. 1 because they were convolved with a 20'' beam to smooth the contour lines.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{13077f3a-cmjn.eps}\par\vspace*{2mm} \includegraphics[width=7.5cm,clip]{13077f3b-cmjn.eps} \end{figure} Figure 3:

Top panel - strip lines of the velocity integrated intensities of 12CO J=7-6 (black), 12CO J=6-5 (red), 12CO J=2-1 (green) (adapted from S88), 13CO  J=6-5 (blue) and [C I]  J=2-1 (cyan) at $\Delta \delta =30''$(PA $90^{\circ }$) across the ionization front of M 17 SW. Bottom panel - strip lines at PA $63^{\circ }$ ( $\Delta \delta =\Delta \alpha /2$). The X-axis corresponds to the actual offset in RA of the maps shown in Fig. 1. Hence, $\Delta \alpha =0''$is the RA of the reference illuminating star SAO 161357.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[height=14cm,angle=0]{13077f4a.eps}\hsp... ...ce{-0.2cm} \includegraphics[height=14cm,angle=0]{13077f4d.eps} } \end{figure} Figure 4:

Selected spectra of 12CO  $J = 6\rightarrow 5$, 12CO  $J = 7\rightarrow 6$, 13CO  $J = 6\rightarrow 5$and [C I]  $J = 2\rightarrow 1$along the NE-SW strip line (see Fig. 1). The positions in arcsecs are the offsets with respect to the reference position at RA(J2000)=18:20:27.6483 and Dec(J2000)=-16:12:00.9077. The spectra are the average spectra within $\pm $2'' of the indicated offset positions and smoothed to 1  ${\rm km~s}^{-1}$velocity resolution.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=4.1cm]{13077f5a-cmjn.eps} \hspac... ...\hspace*{6mm}\includegraphics[width=4.1cm]{13077f5d-cmjn.eps} } \end{figure} Figure 5:

Top panel - Channel maps of the main-beam brightness temperature of 12CO  $J = 6\rightarrow 5$(left) and $J = 7\rightarrow 6$(right) averaged over two and three velocity channels, between 18.2-19.9  ${\rm km~s}^{-1}$, respectively. The contour lines are as described in Fig. 1, with peak-integrated line temperatures of 54.5  ${\rm~K}~{\rm km}^{-1}~{\rm s}$and 55.7  ${\rm~K}~{\rm km}^{-1}~{\rm s}$for the $J = 6\rightarrow 5$ and $J = 7\rightarrow 6$ lines, respectively. Bottom panel - Channel maps of 13CO  $J = 6\rightarrow 5$(left) and [C I]  $J = 2\rightarrow 1$(right), averaged over two velocity channels between 18.4-19.7  ${\rm km~s}^{-1}$. Contours are as in the top panel, and the peak-integrated line temperatures are 37.0  ${\rm~K}~{\rm km}^{-1}~{\rm s}$and 23.9  ${\rm~K}~{\rm km}^{-1}~{\rm s}$ .

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm]{13077f6a-cmjn.eps}\par\vspace{2mm} \includegraphics[width=7cm]{13077f6b-cmjn.eps} \end{figure} Figure 6:

Top panel - expected brightness temperature at the center of the 12CO  lines for a warm background cloud with a temperature $T_{\rm bg}=64$ K and a colder foreground-absorbing cloud with a temperature $T_{\rm k}=15$ K. Bottom panel - same as in the top panel, but for a background temperature $T_{\rm bg}=100$ K and a foreground temperature of $T_{\rm k}=30$ K.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13077f7a-cmjn.eps}\par\vspace*{2mm} \includegraphics[width=8.5cm,clip]{13077f7b-cmjn.eps} \end{figure} Figure 7:

LTE approximation of the optical depth (top) of the 13CO   $J = 6\rightarrow 5$and the excitation temperature (bottom) of the 13CO and 12CO  $J = 6\rightarrow 5$lines in M 17 SW. Contours are the 10%, 25%, 50%, 75% and 90% of the peak value, which is 1.9 for $\tau(\rm ^{13}CO~6{-}5)$and 120 K for $T_{\rm ex}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm]{13077f8a-cmjn.eps}\par\vspace*{1m... ...\par\vspace*{1mm} \includegraphics[width=8cm]{13077f8d-cmjn.eps} \end{figure} Figure 8:

Top - spectra of the four lines observed in M 17 SW at position A ( $\Delta \alpha =-70'', \Delta \delta =+32''$), close to the peak emission in the 12CO and 13CO maps. Middle top - spectra observed at position B ( $\Delta \alpha =-70'', \Delta \delta =-82''$), where the integrated line temperatures are about 50% of the peak emission. Middle bottom - spectra observed at position C ( $\Delta \alpha =-60'', \Delta \delta =-30''$), the peak of the NE-SW strip scan. Bottom - spectra observed at position D ( $\Delta \alpha =-100'', \Delta \delta =0''$), close to the continuum far-IR peak.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13077f9a.eps}\par\vspace*{2mm} \includegraphics[width=8cm,clip]{13077f9b.eps} \end{figure} Figure 9:

Top - the gray scale and contours represent the average ($\log_{10}$ scale) column density per line width ( ${\rm cm}^{-2}~{\rm km}^{-1}~{\rm s} $) required to reproduce the observed 12CO   $\frac{7-6}{6-5}$line ratio between the peak main-beam temperatures $T_{\rm mb}$and the the peak $T_{\rm mb}$ of the 12CO   $J = 6\rightarrow 5$line observed at position A ( $\Delta \alpha =-70'', \Delta \delta =+32''$), for different kinetic temperatures $T_{\rm K}$ and densities $n(\rm H_2)$. Bottom - same as top, but at position B ( $\Delta \alpha =-70'', \Delta \delta =-82''$).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13077f9c.eps}\par\vspace*{2mm} \includegraphics[width=8cm,clip]{13077f9d.eps} \end{figure} Figure 10:

Top - the gray scale and contours represent the average ($\log_{10}$ scale) column density per line width ( ${\rm cm}^{-2}~{\rm km}^{-1}~{\rm s} $) required to reproduce the observed 12CO   $\frac{7-6}{6-5}$line ratio between the peak main-beam temperatures $T_{\rm mb}$and the the peak $T_{\rm mb}$ of the 12CO   $J = 6\rightarrow 5$line observed at position C ( $\Delta \alpha =-60'', \Delta \delta =-30''$), for different kinetic temperatures $T_{\rm K}$ and densities $n(\rm H_2)$. Bottom - same as top, but at position D ( $\Delta \alpha =-100'', \Delta \delta =0''$).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.