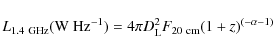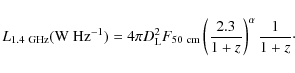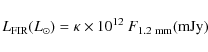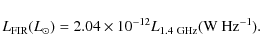| Issue |
A&A
Volume 508, Number 1, December II 2009
|
|
|---|---|---|
| Page(s) | 117 - 132 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200912742 | |
| Published online | 15 October 2009 | |
A&A 508, 117-132 (2009)
Multi-wavelength properties of Spitzer selected starbursts at
z  2
2![[*]](/icons/foot_motif.png)
N. Fiolet1,2 - A. Omont1,2 - M. Polletta1,2,3 - F. Owen4 - S. Berta5 - D. Shupe6 - B. Siana7 - C. Lonsdale8 - V. Strazzullo4 - M. Pannella4 - A. J. Baker9 - A. Beelen10 - A. Biggs11,12 - C. De Breuck12 - D. Farrah13 - R. Ivison11, 14 - G. Lagache10 - D. Lutz5 - L. J. Tacconi5 - R. Zylka15
1 - UPMC Univ Paris 06, UMR7095, Institut d'Astrophysique de Paris, 75014 Paris, France
2 - CNRS, UMR7095, Institut d'Astrophysique de Paris, 75014 Paris, France
3 - INAF-IASF Milano, via E. Bassini 15, 20133 Milan, Italy
4 - National Radio Astronomy Observatory, PO Box 0, Socorro, NM 87801, USA
5 - Max-Planck Institut für extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany
6 - Herschel Science Center, California Institute of Technology, 100-22, Pasadena, CA 91125, USA
7 - Astronomy Department, California Institute of Technology, MC
105-24, 1200 East California Boulevard, Pasadena, CA 91125, USA
8 - North American ALMA Science Center, NRAO, Charlottesville, USA
9 - Department of Physics and Astronomy, Rutgers, the State
University of New Jersey, 136 Frelinghuysen Road, Piscataway,
NJ 08854, USA
10 - Institut d'Astrophysique Spatiale, Université de Paris XI, 91405 Orsay Cedex, France
11 - UK Astronomy Technology Centre, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
12 - European Southern Observatory, Karl-Schwarzschild Strasse, 85748 Garching bei München, Germany
13 - Department of Physics & Astronomy, University of Sussex, Falmer, Brighton, BN1 9RH, UK
14 - Institute for Astronomy, University of Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK
15 - Institut de Radioastronomie Millimétrique, 300 rue de la Piscine, 38406 St.-Martin-d'Hères, France
Received 22 June 2009 / Accepetd 1 September 2009
Abstract
Context. Wide-field Spitzer surveys allow identification of thousands of potentially high-z submillimeter galaxies (SMGs) through their bright 24 ![]() m emission and their mid-IR colors.
m emission and their mid-IR colors.
Aims. We want to determine the average properties of such ![]() Spitzer-selected SMGs by combining millimeter, radio, and infrared photometry for a representative IR-flux (
Spitzer-selected SMGs by combining millimeter, radio, and infrared photometry for a representative IR-flux (
![]() m) limited sample of SMG candidates.
m) limited sample of SMG candidates.
Methods. A complete sample of 33 sources believed to be starbursts (``5.8 ![]() m-peakers'') was selected in the (0.5 deg2) J1046+56 field with selection criteria
m-peakers'') was selected in the (0.5 deg2) J1046+56 field with selection criteria
![]() 400
400 ![]() Jy, the presence of a redshifted stellar emission peak at 5.8
Jy, the presence of a redshifted stellar emission peak at 5.8 ![]() m, and
m, and
![]() 23.
The field, part of the SWIRE Lockman Hole field, benefits from very
deep VLA/GMRT 20 cm, 50 cm, and 90 cm radio data (all 33
sources are detected at 50 cm), and deep 160
23.
The field, part of the SWIRE Lockman Hole field, benefits from very
deep VLA/GMRT 20 cm, 50 cm, and 90 cm radio data (all 33
sources are detected at 50 cm), and deep 160 ![]() m and 70
m and 70 ![]() m Spitzer data. The 33 sources, with photometric redshifts
m Spitzer data. The 33 sources, with photometric redshifts ![]() 1.5-2.5, were observed at 1.2 mm with IRAM-30m/MAMBO to an rms
1.5-2.5, were observed at 1.2 mm with IRAM-30m/MAMBO to an rms ![]() 0.7-0.8 mJy in most cases. Their millimeter, radio, 7-band Spitzer, and near-IR properties were jointly analyzed.
0.7-0.8 mJy in most cases. Their millimeter, radio, 7-band Spitzer, and near-IR properties were jointly analyzed.
Results. The entire sample of 33 sources has an average 1.2 mm flux density of
![]() mJy and a median of 1.61 mJy, so the majority of the sources can be considered SMGs. Four sources have confirmed 4
mJy and a median of 1.61 mJy, so the majority of the sources can be considered SMGs. Four sources have confirmed 4![]() detections, and nine were tentatively detected at the 3
detections, and nine were tentatively detected at the 3![]() level. Because of its 24
level. Because of its 24 ![]() m selection, our sample shows systematically lower
m selection, our sample shows systematically lower
![]() flux ratios than classical SMGs, probably because of enhanced PAH
emission. A median FIR SED was built by stacking images at the
positions of 21 sources in the region of deepest Spitzer coverage. Its parameters are
flux ratios than classical SMGs, probably because of enhanced PAH
emission. A median FIR SED was built by stacking images at the
positions of 21 sources in the region of deepest Spitzer coverage. Its parameters are
![]() K,
K,
![]() ,
and SFR = 450
,
and SFR = 450 ![]() yr-1. The FIR-radio correlation provides another estimate of
yr-1. The FIR-radio correlation provides another estimate of
![]() for each source, with an average value of
for each source, with an average value of
![]() ;
however, this value may be overestimated because of some AGN contribution. Most of our targets are also luminous star-forming BzK galaxies which constitute a significant fraction of weak SMGs at
;
however, this value may be overestimated because of some AGN contribution. Most of our targets are also luminous star-forming BzK galaxies which constitute a significant fraction of weak SMGs at
![]()
Conclusions. Spitzer 24 ![]() m-selected starbursts and AGN-dominated ULIRGs can be reliably distinguished using IRAC-24
m-selected starbursts and AGN-dominated ULIRGs can be reliably distinguished using IRAC-24 ![]() m SEDs. Such ``5.8
m SEDs. Such ``5.8 ![]() m-peakers'' with
m-peakers'' with
![]() 400
400 ![]() Jy have
Jy have
![]() .
They are thus
.
They are thus ![]() ULIRGs, and the majority may be considered SMGs. However, they have systematically lower 1.2 mm/24
ULIRGs, and the majority may be considered SMGs. However, they have systematically lower 1.2 mm/24 ![]() m
flux density ratios than classical SMGs, warmer dust, comparable or
lower IR/mm luminosities, and higher stellar masses. About 2000-3000
``5.8
m
flux density ratios than classical SMGs, warmer dust, comparable or
lower IR/mm luminosities, and higher stellar masses. About 2000-3000
``5.8 ![]() m-peakers'' may be easily identifiable within SWIRE catalogues over 49 deg2.
m-peakers'' may be easily identifiable within SWIRE catalogues over 49 deg2.
Key words: galaxies: high-redshift - galaxies: starburst - galaxies: active - infrared: galaxies - submillimeter - radio continuum: galaxies
1 Introduction
Ultra-Luminous InfraRed Galaxies (ULIRGs, with
![]() )
are the most powerful class of star-forming galaxies. For
25 years, these prominent sources and their intense starbursts have been the
target of many comprehensive studies, both locally
(e.g., Sanders & Mirabel 1996; Lonsdale et al. 2006; Veilleux et al. 2009) and at high redshift
(e.g., Solomon & Vanden Bout 2005; Blain et al. 2004). While local ULIRGs are relatively rare,
submm/mm surveys with large bolometer arrays such as JCMT/SCUBA
(James Clerk Maxwell Telescope/Submillimetre Common User Bolometer Array, Holland et al. 1999),
APEX/LABOCA (Atacama Pathfinder Experiment/Large Apex Bolometer Camera, Siringo et al. 2009)
or IRAM/MAMBO (Institut de Radioastronomie Millimétrique/Max-Planck Bolometer Array, Kreysa et al. 1998)
have shown that the comoving density of submillimetre galaxies (SMGs), which
represent a significant class of high-redshift (
)
are the most powerful class of star-forming galaxies. For
25 years, these prominent sources and their intense starbursts have been the
target of many comprehensive studies, both locally
(e.g., Sanders & Mirabel 1996; Lonsdale et al. 2006; Veilleux et al. 2009) and at high redshift
(e.g., Solomon & Vanden Bout 2005; Blain et al. 2004). While local ULIRGs are relatively rare,
submm/mm surveys with large bolometer arrays such as JCMT/SCUBA
(James Clerk Maxwell Telescope/Submillimetre Common User Bolometer Array, Holland et al. 1999),
APEX/LABOCA (Atacama Pathfinder Experiment/Large Apex Bolometer Camera, Siringo et al. 2009)
or IRAM/MAMBO (Institut de Radioastronomie Millimétrique/Max-Planck Bolometer Array, Kreysa et al. 1998)
have shown that the comoving density of submillimetre galaxies (SMGs), which
represent a significant class of high-redshift (
![]() )
ULIRGs,
is about a thousand times greater than that of ULIRGs in the local Universe
(e.g., Chapman et al. 2005; Le Floc'h et al. 2005).
They represent a major phase of star formation at early epochs and are also
characterized by high stellar masses (e.g., Borys et al. 2005).
They are thus ideal candidates to be the precursors of local massive
elliptical galaxies (e.g., Blain et al. 2002; Lonsdale et al. 2009; Dye et al. 2008, hereafter Lo09, and references
therein). Nearly all of the enormous UV energy produced
by their massive young stars is absorbed
by interstellar dust and re-emitted at far-infrared wavelengths, with their far-infrared
luminosity (
)
ULIRGs,
is about a thousand times greater than that of ULIRGs in the local Universe
(e.g., Chapman et al. 2005; Le Floc'h et al. 2005).
They represent a major phase of star formation at early epochs and are also
characterized by high stellar masses (e.g., Borys et al. 2005).
They are thus ideal candidates to be the precursors of local massive
elliptical galaxies (e.g., Blain et al. 2002; Lonsdale et al. 2009; Dye et al. 2008, hereafter Lo09, and references
therein). Nearly all of the enormous UV energy produced
by their massive young stars is absorbed
by interstellar dust and re-emitted at far-infrared wavelengths, with their far-infrared
luminosity (
![]() )
able to reach
)
able to reach
![]() .
However, despite the considerable efforts invested in mm/submm surveys, the
total number of known SMGs remains limited to several hundred, and current
observational capabilities are still somewhat marginal at many wavelengths.
We thus still lack comprehensive studies of SMGs and their various subclasses
at all wavelengths and redshifts and in various environments.
Even their star formation rates (SFRs) remain uncertain in most cases because
of a lack of direct observations at the FIR/submm wavelengths of their maximum
emission.
The identification of large samples of SMGs is important for investigating
the properties of these galaxies (SFR, luminosity, spectral energy
distribution [SED],
stellar mass, AGN content, spatial structure, radio and X-ray parameters,
clustering, etc.) on a statistical basis, as a function of their various
subclasses, redshift, and environment. This is the main goal of the wide-field submm
surveys planned with SCUBA2 and Herschel.
.
However, despite the considerable efforts invested in mm/submm surveys, the
total number of known SMGs remains limited to several hundred, and current
observational capabilities are still somewhat marginal at many wavelengths.
We thus still lack comprehensive studies of SMGs and their various subclasses
at all wavelengths and redshifts and in various environments.
Even their star formation rates (SFRs) remain uncertain in most cases because
of a lack of direct observations at the FIR/submm wavelengths of their maximum
emission.
The identification of large samples of SMGs is important for investigating
the properties of these galaxies (SFR, luminosity, spectral energy
distribution [SED],
stellar mass, AGN content, spatial structure, radio and X-ray parameters,
clustering, etc.) on a statistical basis, as a function of their various
subclasses, redshift, and environment. This is the main goal of the wide-field submm
surveys planned with SCUBA2 and Herschel.
Although Spitzer generally lacks the sensitivity to detect SMGs in
the far-IR, its very good sensitivity in the mid-IR allows the efficient
detection of a significant fraction of SMGs in the very large area observed
by its wide-field surveys, and in particular the ![]()
![]() Spitzer
Wide-area Infrared Extragalactic (SWIRE) survey (Lonsdale et al. 2003).
From an analysis of a sample of
Spitzer
Wide-area Infrared Extragalactic (SWIRE) survey (Lonsdale et al. 2003).
From an analysis of a sample of ![]() 100 SMGs observed with
Spitzer, Lo09 have estimated that SWIRE has detected
more than 180 SMGs with
100 SMGs observed with
Spitzer, Lo09 have estimated that SWIRE has detected
more than 180 SMGs with
![]() mJy per square degree at
24
mJy per square degree at
24 ![]() m and in several IRAC bands from 3.6 to 8.0
m and in several IRAC bands from 3.6 to 8.0 ![]() m. However, the
identification of SMGs among SWIRE sources is not straightforward, since it
requires inferring FIR emission from mid-IR photometry in objects with various
SEDs, especially as regards AGN versus starburst emission, and various
redshifts.
m. However, the
identification of SMGs among SWIRE sources is not straightforward, since it
requires inferring FIR emission from mid-IR photometry in objects with various
SEDs, especially as regards AGN versus starburst emission, and various
redshifts.
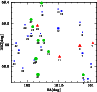
|
Figure 1:
Positions of the 33 sources of our sample (
|
| Open with DEXTER | |
We have therefore undertaken a systematic study of the 1.2 mm emission from the
best SMG candidates among Spitzer bright 24 ![]() m sources, focusing
on
m sources, focusing
on ![]() 2 starburst candidates. In Lonsdale et al. (2006) and Lo09 (see
also Farrah et al. 2008; Weedman et al. 2006), it is shown that selecting sources with a secondary
maximum emission in one of the intermediate IRAC bands at 4.5 or 5.8
2 starburst candidates. In Lonsdale et al. (2006) and Lo09 (see
also Farrah et al. 2008; Weedman et al. 2006), it is shown that selecting sources with a secondary
maximum emission in one of the intermediate IRAC bands at 4.5 or 5.8 ![]() m
provides an efficient discrimination against AGN power-law SEDs. In
particular, 24
m
provides an efficient discrimination against AGN power-law SEDs. In
particular, 24 ![]() m bright ``5.8
m bright ``5.8 ![]() m-peakers'' have a high probability
of being dominated by a strong starburst at
m-peakers'' have a high probability
of being dominated by a strong starburst at ![]() ,
whose intense 7.7
,
whose intense 7.7 ![]() m
feature is redshifted into the 24
m
feature is redshifted into the 24 ![]() m band. A first 1.2 mm MAMBO study of a
sample of
m band. A first 1.2 mm MAMBO study of a
sample of ![]() 60 bright SWIRE sources (Lo09) has confirmed that such a
selection yields a high detection rate at 1.2 mm and a significant average
1.2 mm flux density, showing that the majority of such sources are high-z
ULIRGs, probably at
60 bright SWIRE sources (Lo09) has confirmed that such a
selection yields a high detection rate at 1.2 mm and a significant average
1.2 mm flux density, showing that the majority of such sources are high-z
ULIRGs, probably at ![]() .
However, as described in Lo09, this sample was
selected with the aim of trying to observe the ``5.8
.
However, as described in Lo09, this sample was
selected with the aim of trying to observe the ``5.8 ![]() m-peakers''
with the strongest mm flux over more than 10 deg2. This was achieved by
deriving photometric redshifts, estimating the expected 1.2 mm flux densities
by fitting templates of various local starbursts and ULIRGs to the optical and
infrared (3.6-24
m-peakers''
with the strongest mm flux over more than 10 deg2. This was achieved by
deriving photometric redshifts, estimating the expected 1.2 mm flux densities
by fitting templates of various local starbursts and ULIRGs to the optical and
infrared (3.6-24 ![]() m) bands, and selecting the candidates predicted to
give the strongest mm emission. Therefore, the selection criteria of this
sample were biased, especially toward the strongest 24
m) bands, and selecting the candidates predicted to
give the strongest mm emission. Therefore, the selection criteria of this
sample were biased, especially toward the strongest 24 ![]() m sources and
those in clean environments. We report here the results of an analogous MAMBO
study, but of a complete 24
m sources and
those in clean environments. We report here the results of an analogous MAMBO
study, but of a complete 24 ![]() m-flux limited sample of all SWIRE
``5.8
m-flux limited sample of all SWIRE
``5.8 ![]() m-peakers'' in a 0.5 deg2 region within the SWIRE Lockman
Hole field, with
m-peakers'' in a 0.5 deg2 region within the SWIRE Lockman
Hole field, with
![]() Jy and
Jy and
![]() (see Sect. 2 for a precise definition of ``5.8
(see Sect. 2 for a precise definition of ``5.8 ![]() m-peakers'', which of
course depends on the actual SWIRE data and limits of sensitivity and
accuracy).
This region was selected because of the richness in multi-wavelength data, in
particular the exceptionally deep radio data at 20 cm (VLA, Owen & Morrison 2008),
50 cm (GMRT, Owen et al. in prep.), and 90 cm (VLA, Owen et al. 2009). Our
study aims at characterizing the average multi-wavelength properties of these
sources, their dominant emission processes (starburst or AGN), their stellar
masses, and their star formation rates.
We adopt a standard flat cosmology: H0=71 km s-1 Mpc-1,
m-peakers'', which of
course depends on the actual SWIRE data and limits of sensitivity and
accuracy).
This region was selected because of the richness in multi-wavelength data, in
particular the exceptionally deep radio data at 20 cm (VLA, Owen & Morrison 2008),
50 cm (GMRT, Owen et al. in prep.), and 90 cm (VLA, Owen et al. 2009). Our
study aims at characterizing the average multi-wavelength properties of these
sources, their dominant emission processes (starburst or AGN), their stellar
masses, and their star formation rates.
We adopt a standard flat cosmology: H0=71 km s-1 Mpc-1,
![]() and
and
![]() (Spergel et al. 2003).
(Spergel et al. 2003).
2 Sample selection and ancillary data
We selected all Spitzer/SWIRE ``5.8 ![]() m-peakers'' with
m-peakers'' with
![]() Jy in the
Jy in the
![]() (0.49 deg2)
J1046+59 field in the SWIRE Lockman
Hole, centered at
(0.49 deg2)
J1046+59 field in the SWIRE Lockman
Hole, centered at
![]() h46m00s,
h46m00s,
![]() (Fig. 1). A source is
considered to be a ``5.8
(Fig. 1). A source is
considered to be a ``5.8 ![]() m-peaker'' if it satisfies the following
conditions:
m-peaker'' if it satisfies the following
conditions:
![]() ,
without consideration of uncertainties. 13 sources
have no detection in the 8.0
,
without consideration of uncertainties. 13 sources
have no detection in the 8.0 ![]() m band. We assume that these sources are
also ``5.8
m band. We assume that these sources are
also ``5.8 ![]() m-peakers'' because their fluxes at 5.8
m-peakers'' because their fluxes at 5.8 ![]() m are greater
than the detection limits at 8.0
m are greater
than the detection limits at 8.0 ![]() m ( 40
m ( 40 ![]() Jy). We also
require that the sources are optically faint, i.e.,
Jy). We also
require that the sources are optically faint, i.e.,
![]() ,
to remove low redshift interlopers
(Lonsdale et al. 2006). The selected sample contains 33 sources, which represent 6% of all sources with
,
to remove low redshift interlopers
(Lonsdale et al. 2006). The selected sample contains 33 sources, which represent 6% of all sources with
![]() Jy and
Jy and
![]() in the field.
in the field.
We use the SWIRE internal catalogue available at the time of definition of the project, September 2006. Details on the SWIRE observations and data are available in Surace et al. (2005). The 2006 SWIRE internal catalogue has been superseded by the current version, dated 2007. Since our selection, MAMBO observations, and analysis were based on the 2006 catalogue, but there are no significant changes for our sources in the 2007 catalogue, and the numbers of sources selected in the two versions of the catalogue do not vary significantly, for this work we will use the selection from 2006 data. Based on the analysis of the sources that would have been missed or included applying our selection criteria to the two versions of the catalogues, we find that the original sample selected from the 2006 SWIRE catalogue remains representative of a sample strictly meeting our selection criteria.
We have reported in Table 1 the fluxes from the 2006 SWIRE catalogue. The optical magnitudes have been obtained with the MOSAIC camera on the 4-m Mayall Telescope at Kitt Peak National Observatory (e.g., Muller et al. 1998). However, for a few sources, the optical data differ slightly from those available in the SWIRE catalogue because a measurement at each source position was performed for all non-detections in the catalogue. The revised optical magnitudes are listed in Table 1.
Table 1: Optical, Near-IR and Spitzer mid-IR data of the selected sample.
Table 2:
Related Spitzer-selected ![]() ULIRGs samples.
ULIRGs samples.
Table 2 compares the selection criteria for our sample to those for similar
samples of bright 24 ![]() m sources. The sample of Lo09 is based on the
same criteria, but is biased toward sources brighter at 24
m sources. The sample of Lo09 is based on the
same criteria, but is biased toward sources brighter at 24 ![]() m, with
819
m, with
819 ![]() Jy on average vs. 566
Jy on average vs. 566 ![]() Jy for the present
sample. The sample of Farrah et al. (2008) is similar but aimed at
``4.5
Jy for the present
sample. The sample of Farrah et al. (2008) is similar but aimed at
``4.5 ![]() m-peakers''; the sample of Huang et al. (2009) and
Younger et al. (2009)
is based on different IRAC criteria, but they indeed select
almost exclusively ``5.8
m-peakers''; the sample of Huang et al. (2009) and
Younger et al. (2009)
is based on different IRAC criteria, but they indeed select
almost exclusively ``5.8 ![]() m-peakers'' (Sect. 5.1). On the other hand, the
selection criteria of Magliocchetti et al. (2007) and Yan et al. (2005), which do not use the
IRAC flux densities, do not discriminate against AGN and yield a large
proportion of AGN.
m-peakers'' (Sect. 5.1). On the other hand, the
selection criteria of Magliocchetti et al. (2007) and Yan et al. (2005), which do not use the
IRAC flux densities, do not discriminate against AGN and yield a large
proportion of AGN.
Compared to the twin starburst sample of Lo09, the present sample is
complete down to a 24 ![]() m flux density of 400
m flux density of 400 ![]() Jy. It thus includes
weaker 24
Jy. It thus includes
weaker 24 ![]() m sources on average, but it should be free from the
selection biases present in the Lo09 sample that resulted from the
effort to maximize the number of detections at 1.2 mm. In addition, our sample
benefits from very deep radio data at 1400, 610, and 324 MHz (Sect. 4.3).
The positions of the sources in the field are shown in Fig. 1. The radio flux densities are listed in Table 4.
m sources on average, but it should be free from the
selection biases present in the Lo09 sample that resulted from the
effort to maximize the number of detections at 1.2 mm. In addition, our sample
benefits from very deep radio data at 1400, 610, and 324 MHz (Sect. 4.3).
The positions of the sources in the field are shown in Fig. 1. The radio flux densities are listed in Table 4.
3 MAMBO observations and results
Observations were made during the winter 2006/2007 MAMBO observing pool
between December 2006 and March 2007 at the IRAM 30 m telescope,
located at Pico Veleta, Spain, using the 117-element version of the MAMBO
array (Kreysa et al. 1998) operating at 1.2 mm (250 GHz).
We used a standard ``on-off'' photometry observing mode with a secondary
mirror wobbling at a frequency of 0.5 Hz between the source
and a blank sky position offset in azimuth by ![]()
![]() .
Periodically, the telescope was nodded so that the sky position lay on
the other side of the source position. Pointing and focus were updated
regularly on standard sources. Nearly every hour, the atmospheric
opacity was measured by observing the sky at six elevations. Our
observations are divided in 16 or 20 ``subscans'' of
60 s each. In this operating mode, the integration time is
.
Periodically, the telescope was nodded so that the sky position lay on
the other side of the source position. Pointing and focus were updated
regularly on standard sources. Nearly every hour, the atmospheric
opacity was measured by observing the sky at six elevations. Our
observations are divided in 16 or 20 ``subscans'' of
60 s each. In this operating mode, the integration time is ![]() 40 s
(20 s on source and 20 s on sky) per subscan. Observations of
each source were never concentrated in a single night, but distributed
over several nights in order to reduce the risks of systematic effects.
The initial aim was to observe the 32 sources (L-12 was observed
in the project described by Lo09, under the name ``LH-11'') with an rms
40 s
(20 s on source and 20 s on sky) per subscan. Observations of
each source were never concentrated in a single night, but distributed
over several nights in order to reduce the risks of systematic effects.
The initial aim was to observe the 32 sources (L-12 was observed
in the project described by Lo09, under the name ``LH-11'') with an rms
![]() 0.8 mJy,
which corresponds to
0.8 mJy,
which corresponds to ![]() 0.6 h of integration for the system sensitivity
0.6 h of integration for the system sensitivity ![]() 35-40 mJy s-1/2 in average weather conditions.
As seen in Table 4, this was achieved for most of the sources. However, for
35-40 mJy s-1/2 in average weather conditions.
As seen in Table 4, this was achieved for most of the sources. However, for ![]() 20% of the sources the rms was instead
20% of the sources the rms was instead ![]() 0.9-1.1 mJy,
while a similar number of sources were observed somewhat longer to reach an rms
0.9-1.1 mJy,
while a similar number of sources were observed somewhat longer to reach an rms ![]() 0.5-0.6 mJy in order to confirm their detection.
0.5-0.6 mJy in order to confirm their detection.
The data reduction is straightforward thanks to the MOPSIC software
package![]() , which is regularly updated on the MAMBO pool page.
This program reduces the noise due to the sky emission if
it is sufficiently correlated between the different bolometers. This process is generally sufficient for the majority of
observations. However, in a few cases, some scans may present faults due, e.g.,
to lack of helium in the cryostat or problems of acquisition. These
scans are validated or rejected after close inspection.
, which is regularly updated on the MAMBO pool page.
This program reduces the noise due to the sky emission if
it is sufficiently correlated between the different bolometers. This process is generally sufficient for the majority of
observations. However, in a few cases, some scans may present faults due, e.g.,
to lack of helium in the cryostat or problems of acquisition. These
scans are validated or rejected after close inspection.
The results of our observations at 1.2 mm are reported in Table 4.
The average flux density (with equal weight) of the entire sample is
![]() mJy, very comparable to Lo09 (
mJy, very comparable to Lo09 (
![]() mJy) and
Younger et al. (2009) (
mJy) and
Younger et al. (2009) (
![]() mJy), but greater than obtained
by Lutz et al. (2005) for a Spitzer-selected sample of high-z starbursts
and (mostly) AGNs (
mJy), but greater than obtained
by Lutz et al. (2005) for a Spitzer-selected sample of high-z starbursts
and (mostly) AGNs (
![]() mJy).
The median for our sample is 1.61 mJy. This confirms that on average
the majority of these sources are
SMGs (at
mJy).
The median for our sample is 1.61 mJy. This confirms that on average
the majority of these sources are
SMGs (at ![]() ,
1.6 mJy corresponds to
,
1.6 mJy corresponds to ![]() 4 mJy at
850
4 mJy at
850 ![]() m: Greve et al. 2004). Because of the limited integration time, only
four sources were solidly detected at >4
m: Greve et al. 2004). Because of the limited integration time, only
four sources were solidly detected at >4![]() .
However, the fraction
of sources at least tentatively detected
at >3
.
However, the fraction
of sources at least tentatively detected
at >3![]() is 39% (13/33 sources). It is worth stressing that the reliability of such
is 39% (13/33 sources). It is worth stressing that the reliability of such ![]() tentative detections in careful ``on-off''
MAMBO observations is much higher than those detected in a mm/submm map amongst
hundreds of possible resolution elements, where flux boosting is inevitable.
tentative detections in careful ``on-off''
MAMBO observations is much higher than those detected in a mm/submm map amongst
hundreds of possible resolution elements, where flux boosting is inevitable.
This on-off ![]() ``detection'' rate is similar to what was obtained by Lo09 for a similar sample,
higher than obtained by Lutz et al. (2005) for their
Spitzer-selected sample of starbursts and (mostly) AGNs (18%), and
lower than obtained by Younger et al. (2009) with deeper observation of a
similar sample of Spitzer-selected
``detection'' rate is similar to what was obtained by Lo09 for a similar sample,
higher than obtained by Lutz et al. (2005) for their
Spitzer-selected sample of starbursts and (mostly) AGNs (18%), and
lower than obtained by Younger et al. (2009) with deeper observation of a
similar sample of Spitzer-selected ![]() starbursts (75%).
starbursts (75%).
4 Source properties
4.1 Spectral energy distributions and redshifts
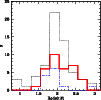
|
Figure 2: Histogram of redshifts for our sample (photometric, thick solid red line), the full sample from Lo09 (photometric and spectroscopic, dotted black line), and the sample from Younger et al. (2009) (spectroscopic, long-short-dashed blue line). |
| Open with DEXTER | |
In order to estimate photometric redshifts, we fit the spectral energy
distributions (SEDs), including optical and IR (![]()
![]() m) data for each
source, with a library of galaxy templates following the method described in
Lo09 and Polletta et al. (2007). The SEDs are fitted using the Hyper-zcode (Bolzonella et al. 2000), and the effects of dust extinction are taken into
account. As discussed in Lo09, such photometric redshifts are limited in
accuracy and have uncertainties of
m) data for each
source, with a library of galaxy templates following the method described in
Lo09 and Polletta et al. (2007). The SEDs are fitted using the Hyper-zcode (Bolzonella et al. 2000), and the effects of dust extinction are taken into
account. As discussed in Lo09, such photometric redshifts are limited in
accuracy and have uncertainties of ![]() 0.5.
0.5.
SED fits for all the sources in the sample are shown in the Appendix (only in the electronic edition), and the
photometric redshifts are listed in Table 4. The photometric
redshift distribution of the sample is shown in Fig. 2. All
redshifts but four are within the range
![]() .
The
average
redshift from these SEDs is
.
The
average
redshift from these SEDs is
![]() (median = 2.04, scatter = 0.32, and semi-inter-quartile range = 0.26). This result is consistent
with our selection criteria, which assume that the 7.7
(median = 2.04, scatter = 0.32, and semi-inter-quartile range = 0.26). This result is consistent
with our selection criteria, which assume that the 7.7 ![]() m PAH band is
redshifted into the 24
m PAH band is
redshifted into the 24 ![]() m MIPS band and the 1.6
m MIPS band and the 1.6 ![]() m stellar band into
the 5.8
m stellar band into
the 5.8 ![]() m IRAC band. The redshift distribution of our sample is similar
to the one measured in Lo09 (
m IRAC band. The redshift distribution of our sample is similar
to the one measured in Lo09 (
![]() ), which is mostly based on
photometric redshifts, and the one measured
in Younger et al. (2009) (
), which is mostly based on
photometric redshifts, and the one measured
in Younger et al. (2009) (
![]() ), which is based on spectroscopic
redshifts (Fig. 2).
Thus, all these works select sources in a similar redshift range.
Indeed, the actual redshift distribution of our sample might be similar to that of Huang et al. (2009) and Younger et al. (2009)
and concentrated within a rather narrow redshift range around
), which is based on spectroscopic
redshifts (Fig. 2).
Thus, all these works select sources in a similar redshift range.
Indeed, the actual redshift distribution of our sample might be similar to that of Huang et al. (2009) and Younger et al. (2009)
and concentrated within a rather narrow redshift range around ![]() -2.3 as shown by the few spectroscopic redshifts
reported for the sample of Lo09.
-2.3 as shown by the few spectroscopic redshifts
reported for the sample of Lo09.
Twelve sources from our sample have redshifts from the catalogue of SWIRE photometric redshifts of Rowan-Robinson et al. (2008).
For ten of these sources, our photometric redshifts determined by the SED fitting show a good (![]()
![]() )
agreement with the determinations from Rowan-Robinson et al. (2008).
)
agreement with the determinations from Rowan-Robinson et al. (2008).
4.2 Comparison between 1.2 mm and 24  m flux densities
m flux densities
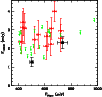
|
Figure 3:
Observed MAMBO 1.2 mm flux density as a function of 24 |
| Open with DEXTER | |
In order to investigate whether there is a correlation between mid-IR and mm
emission, we compare the flux densities at 1.2 mm and at 24 ![]() m
(
m
(
![]() and
and
![]() )
in Fig. 3. Because of the limited
sensitivity of the 1.2 mm data, we have stacked the data for the first
)
in Fig. 3. Because of the limited
sensitivity of the 1.2 mm data, we have stacked the data for the first
![]() quartile (8 sources), and independently for the 25 other sources.
These stacked values have been computed with the observed
quartile (8 sources), and independently for the 25 other sources.
These stacked values have been computed with the observed
![]() values.
Figure 3 shows that it is impossible to see whether there
is a correlation between mid-IR and mm emission with this sensitivity. However, the average
for the highest
values.
Figure 3 shows that it is impossible to see whether there
is a correlation between mid-IR and mm emission with this sensitivity. However, the average
for the highest
![]() quartile seems
quartile seems ![]() 1.5-2 times larger than the average for all the other sources.
1.5-2 times larger than the average for all the other sources.
Because of the 24 ![]() m selection, the
m selection, the
![]() ratio of our sources is relatively low compared to that submm selected
SMGs, as in the case of Lo09.
The ratio of the average
ratio of our sources is relatively low compared to that submm selected
SMGs, as in the case of Lo09.
The ratio of the average
![]() to the average
to the average
![]() is
is
![]() for
the entire sample of 33 sources (and
for
the entire sample of 33 sources (and
![]() for 13 sources with
1.2 mm S/N > 3, see Table 3).
As seen in Fig. 8, these ratios of averages are a factor
for 13 sources with
1.2 mm S/N > 3, see Table 3).
As seen in Fig. 8, these ratios of averages are a factor
![]() 4 (
4 (![]() 2) smaller
than that of a sample of literature SMGs (Sect. 5.2),
and a factor
2) smaller
than that of a sample of literature SMGs (Sect. 5.2),
and a factor ![]() 6 (
6 (![]() 10) larger than one of the (AGN dominated)
sample of bright 24
10) larger than one of the (AGN dominated)
sample of bright 24 ![]() m sources of Lutz et al. (2005).
They are a factor
m sources of Lutz et al. (2005).
They are a factor ![]() 10 (
10 (![]() 5) smaller than that of the extreme SMG
template Arp 220 at z=2,
but comparable to those of starburst templates (M 82 or NGC 6090) and
AGN-starburst composites (IRAS19254-7245 South).
5) smaller than that of the extreme SMG
template Arp 220 at z=2,
but comparable to those of starburst templates (M 82 or NGC 6090) and
AGN-starburst composites (IRAS19254-7245 South).
4.3 Radio properties and the nature of the sources
The studied sources benefit from exceptionally deep VLA data at 1.4 GHz
(rms = 2.7 ![]() Jy in the center of the field, 12-15
Jy in the center of the field, 12-15 ![]() Jy in
most of the 0.5 deg2 field; Owen & Morrison 2008). Such a depth yields
radio detections for almost the entire sample. 8 of 33 sources
are not detected due to a loss of radio sensitivity in the
outer parts of the field, largely due to the decrease in primary beam sensitivity and bandwidth smearing.
The GMRT 610 MHz observations are also very deep (rms = 10
Jy in
most of the 0.5 deg2 field; Owen & Morrison 2008). Such a depth yields
radio detections for almost the entire sample. 8 of 33 sources
are not detected due to a loss of radio sensitivity in the
outer parts of the field, largely due to the decrease in primary beam sensitivity and bandwidth smearing.
The GMRT 610 MHz observations are also very deep (rms = 10 ![]() Jy),
cover almost the entire field, and detect all 33 sources.
The VLA 324 MHz observations reach a depth of rms = 70
Jy),
cover almost the entire field, and detect all 33 sources.
The VLA 324 MHz observations reach a depth of rms = 70 ![]() Jy and cover the
entire field (Owen et al. 2009). They yield detections for 17 sources. The radio flux densities are listed in
Table 4. The cross identification was made by comparing the radio
and the SWIRE positions. Following the method of Ivison et al. (2007) and Downes et al. (1986), we have verified that all our sources have very reliable radio
associations,
with an average probability of spurious association in 2
Jy and cover the
entire field (Owen et al. 2009). They yield detections for 17 sources. The radio flux densities are listed in
Table 4. The cross identification was made by comparing the radio
and the SWIRE positions. Following the method of Ivison et al. (2007) and Downes et al. (1986), we have verified that all our sources have very reliable radio
associations,
with an average probability of spurious association in 2
![]() of
of
![]() = 0.001. For Ivison et al. (2007), the association
is reliable if
= 0.001. For Ivison et al. (2007), the association
is reliable if
![]() .
.
Based on the correlation between
![]() and the radio
luminosity in star-forming regions and in local starburst galaxies
(Sanders & Mirabel 1996; Crawford et al. 1996; Helou et al. 1985; Condon 1992), the radio and FIR luminosities are
expected to be linked as well at
and the radio
luminosity in star-forming regions and in local starburst galaxies
(Sanders & Mirabel 1996; Crawford et al. 1996; Helou et al. 1985; Condon 1992), the radio and FIR luminosities are
expected to be linked as well at ![]() (Ibar et al. 2008). We discuss this in Sect. 4.4, together with the derivation of
(Ibar et al. 2008). We discuss this in Sect. 4.4, together with the derivation of
![]() .
However, if this correlation is verified at
.
However, if this correlation is verified at ![]() ,
one may expect a straightforward relation between the radio and 1.2 mm flux densities for starbursts with similar SEDs.
To check that, we plot the 1.2 mm flux density as a function of the
radio flux density at 20 cm in Fig. 4.
Because of the limited sensitivity at 1.2 mm, we consider average
values of 1.2 mm flux density and radio flux density, for the
entire sample, for the 13 sources with 1.2 mm S/N > 3, and for the 20 sources with 1.2 mm S/N < 3 (Table 3).
In Fig. 4, we also
report the ratio of the average flux densities and
,
one may expect a straightforward relation between the radio and 1.2 mm flux densities for starbursts with similar SEDs.
To check that, we plot the 1.2 mm flux density as a function of the
radio flux density at 20 cm in Fig. 4.
Because of the limited sensitivity at 1.2 mm, we consider average
values of 1.2 mm flux density and radio flux density, for the
entire sample, for the 13 sources with 1.2 mm S/N > 3, and for the 20 sources with 1.2 mm S/N < 3 (Table 3).
In Fig. 4, we also
report the ratio of the average flux densities and ![]() dispersion
found by Chapman et al. (2005) (see also e.g. Smail et al. 2002; Yun & Carilli 2002; Condon 1992; Ivison et al. 2002) for
a sample of radio-detected sub-millimeter galaxies at
dispersion
found by Chapman et al. (2005) (see also e.g. Smail et al. 2002; Yun & Carilli 2002; Condon 1992; Ivison et al. 2002) for
a sample of radio-detected sub-millimeter galaxies at ![]() .
The mm/radio ratios for both the whole sample and the S/N > 3 sources are reasonably compatible with the correlation between
mm/submm and
radio fluxes found for
.
The mm/radio ratios for both the whole sample and the S/N > 3 sources are reasonably compatible with the correlation between
mm/submm and
radio fluxes found for ![]() starbursts (Chapman et al. 2005).
However, the ratio between average values of 1.2 mm flux density
and radio flux density, for the entire sample and especially for the
20 sources with 1.2 mm S/N < 3,
might be slightly smaller compared to submm selected galaxies. This
could be explained as an effect of the 24
starbursts (Chapman et al. 2005).
However, the ratio between average values of 1.2 mm flux density
and radio flux density, for the entire sample and especially for the
20 sources with 1.2 mm S/N < 3,
might be slightly smaller compared to submm selected galaxies. This
could be explained as an effect of the 24 ![]() m selection,
and by a greater AGN contribution and/or hotter dust (see Sects. 5.3 and 5.4 for a complete discussion).
m selection,
and by a greater AGN contribution and/or hotter dust (see Sects. 5.3 and 5.4 for a complete discussion).
In order to assess whether the radio emission observed in our sources
is associated with AGN or with star-forming regions, one may also
consider the radio spectral shape, the rest-frame radio luminosity, and
the radio morphology (see e.g. Seymour et al. 2008; Biggs & Ivison 2008). The
radio spectral index ![]() ,
where
,
where
![]() ,
is first calculated from the flux densities at 20 cm, 50 cm,
and 90 cm, when they are available, using the best power law fit
between these three wavelengths, and is
reported in Table 4. When only
two radio fluxes are available, the index is just derived from the flux
density ratio. Seven sources have no determined spectral radio index
because of a lack of radio detections at 1.4 GHz and 324 MHz.
,
is first calculated from the flux densities at 20 cm, 50 cm,
and 90 cm, when they are available, using the best power law fit
between these three wavelengths, and is
reported in Table 4. When only
two radio fluxes are available, the index is just derived from the flux
density ratio. Seven sources have no determined spectral radio index
because of a lack of radio detections at 1.4 GHz and 324 MHz.
Most of our sources have a radio spectral index in the range ![]() -0.4 to -1.2 (average
-0.4 to -1.2 (average
![]() ;
median = -0.74). This is not very discriminating since,
considering the uncertainties, such values of
;
median = -0.74). This is not very discriminating since,
considering the uncertainties, such values of ![]() are typical for star-forming galaxies, type II AGN, and many radio galaxies
(e.g., De Breuck et al. 2000; Ciliegi et al. 2003; Polletta et al. 2000; De Breuck et al. 2001; Condon 1992).
About 20% of the sources, mostly among those with some radio excess, could either be in the same range or have
are typical for star-forming galaxies, type II AGN, and many radio galaxies
(e.g., De Breuck et al. 2000; Ciliegi et al. 2003; Polletta et al. 2000; De Breuck et al. 2001; Condon 1992).
About 20% of the sources, mostly among those with some radio excess, could either be in the same range or have ![]()
![]() -0.5 typical of flat spectrum sources.
-0.5 typical of flat spectrum sources.
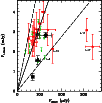
|
Figure 4: Observed MAMBO
1.2 mm flux density as a function of 20 cm flux density. The
large black symbols show different stacked values: the entire sample
(filled triangle), all sources with > |
| Open with DEXTER | |
Table 3: Derived values from the stacked flux densitiesa.
Table 4: 1.2 mm and radio data.
Table 5: Luminosities and star formation rates.
The radio luminosity and the FIR-radio correlation
are most often expressed in term of the rest-frame luminosity at 1.4 GHz,
![]() .
With the same assumptions as for the SMG sample of
Kovács et al. (2006), we can rewrite their Eq. (7) as
.
With the same assumptions as for the SMG sample of
Kovács et al. (2006), we can rewrite their Eq. (7) as
where
Using the flux at 610 MHz, this equation becomes
Finally, we examine the radio sizes of our sources. A large size (
4.4 Far-infrared luminosity
Estimates of
![]() for our individual
sources are
quite uncertain due to the lack of data between 24
for our individual
sources are
quite uncertain due to the lack of data between 24 ![]() m and 1.2 mm, where
most of the far-infrared energy is emitted. None of our
sources are detected at 70
m and 1.2 mm, where
most of the far-infrared energy is emitted. None of our
sources are detected at 70 ![]() m or 160
m or 160 ![]() m at the SWIRE sensitivities
(the 3
m at the SWIRE sensitivities
(the 3![]() limits at 70 and 160
limits at 70 and 160 ![]() m are 18 and 108 mJy, respectively).
There are not even detections in the
m are 18 and 108 mJy, respectively).
There are not even detections in the ![]() 2.5 times
deeper MIPS images available from GO Program 30391 (PI: Owen) in
the center of the field, which is well observed at 20 cm. We thus
make use of these deep MIPS data only for stacking the 70 and
160
2.5 times
deeper MIPS images available from GO Program 30391 (PI: Owen) in
the center of the field, which is well observed at 20 cm. We thus
make use of these deep MIPS data only for stacking the 70 and
160 ![]() m images to
constrain the average
m images to
constrain the average
![]() of our sample.
of our sample.
We estimate average flux densities from the stacked MIPS images at 24, 70, and
160 ![]() m, following the method described in Lo09. An initial stack based
on the SWIRE MIPS images was made for the entire sample of 33 sources, but
it yields only a marginally significant (
m, following the method described in Lo09. An initial stack based
on the SWIRE MIPS images was made for the entire sample of 33 sources, but
it yields only a marginally significant (![]() 2-3
2-3 ![]() )
detection at 160
)
detection at 160 ![]() m. The average flux densities at 70
m. The average flux densities at 70 ![]() m and 160
m and 160 ![]() m are almost 5
times lower than the SWIRE 3
m are almost 5
times lower than the SWIRE 3![]() limits (Table 6).
We thus use stacks made with the GO-30391 images of the 21 sources
covered by these deeper MIPS observations. The results from stacks are
reported in Table 6.
In addition to the stacked flux densities for the
entire sample, we also report
stacked flux densities for two subsamples apiece: 10 sources
with 1.2 mm SNR > 3, and 11 sources with SNR < 3.
limits (Table 6).
We thus use stacks made with the GO-30391 images of the 21 sources
covered by these deeper MIPS observations. The results from stacks are
reported in Table 6.
In addition to the stacked flux densities for the
entire sample, we also report
stacked flux densities for two subsamples apiece: 10 sources
with 1.2 mm SNR > 3, and 11 sources with SNR < 3.
The median stacked flux densities at 70 ![]() m and 160
m and 160 ![]() m
for the entire sample are
quite faint, about 3 mJy and 13 mJy respectively. We use
these median stacked flux densities in the following analysis. There is
no appreciable
difference in
m
for the entire sample are
quite faint, about 3 mJy and 13 mJy respectively. We use
these median stacked flux densities in the following analysis. There is
no appreciable
difference in
![]() and
and
![]() between sources tentatively detected (>3
between sources tentatively detected (>3![]() )
and
undetected (<3
)
and
undetected (<3![]() )
at 1.2 mm. The median 160
)
at 1.2 mm. The median 160 ![]() m and 70
m and 70 ![]() m flux densities seem smaller
than for the previous similar sample of Younger et al. (2009), which has higher average 24
m flux densities seem smaller
than for the previous similar sample of Younger et al. (2009), which has higher average 24 ![]() m flux density (Table 6).
m flux density (Table 6).
We combine the median flux densities at 70 ![]() m, 160
m, 160 ![]() m, and 1.2 mm to
build a median far-IR SED for our sample. We fit the median FIR SED
assuming the average redshift of the sample (z = 2.08) with a ``graybody''
model with a fixed value of the emissivity index (
m, and 1.2 mm to
build a median far-IR SED for our sample. We fit the median FIR SED
assuming the average redshift of the sample (z = 2.08) with a ``graybody''
model with a fixed value of the emissivity index (
![]() ,
see e.g. Kovács et al. 2006; Beelen et al. 2006) to derive
the temperature,
,
see e.g. Kovács et al. 2006; Beelen et al. 2006) to derive
the temperature,
![]() ,
of a single dust component. The best-fit value for
the whole sample is
,
of a single dust component. The best-fit value for
the whole sample is
![]() K. This model yields
K. This model yields
![]() ,
which is well in the ULIRG
range and may be considered the average value for ``5.8
,
which is well in the ULIRG
range and may be considered the average value for ``5.8 ![]() m-peakers''
with
m-peakers''
with
![]() Jy and r > 23. Note that these values for
Jy and r > 23. Note that these values for
![]() and
and
![]() are slightly smaller than the values of
Lo09,
are slightly smaller than the values of
Lo09,
![]() K and
K and
![]() and of Younger et al. (2009),
and of Younger et al. (2009),
![]() K and
K and
![]() .
.
The actual
![]() of our sources will span some range around this
value. Although it is not possible to derive accurate values of
of our sources will span some range around this
value. Although it is not possible to derive accurate values of
![]() for each source in the absence of individual detections at 160
for each source in the absence of individual detections at 160 ![]() m or at
another wavelength close to the FIR maximum of the SED, several alternative
approaches are possible for estimating individual
m or at
another wavelength close to the FIR maximum of the SED, several alternative
approaches are possible for estimating individual
![]() .
.
One can simply infer
![]() from the flux density at 1.2 mm,
from the flux density at 1.2 mm,
![]() .
The value of
.
The value of
![]() can place strong constraints on
can place strong constraints on
![]() if we
assume that the whole
if we
assume that the whole
![]() and the radiation detected at 1.2 mm
are produced by dust heated by the same mechanism. The relation between
and the radiation detected at 1.2 mm
are produced by dust heated by the same mechanism. The relation between
![]() and
and
![]() can be derived assuming a thermal spectral
model. A ``graybody'' model, with a single dust component and emissivity
index, e.g.
can be derived assuming a thermal spectral
model. A ``graybody'' model, with a single dust component and emissivity
index, e.g.
![]() (Beelen et al. 2006), yields:
(Beelen et al. 2006), yields:
where the proportionality factor,
We also estimate
![]() of each source using the available radio
data and the well-known FIR-radio relation for local
starbursts (Condon 1992). The original definition is based on the 60
of each source using the available radio
data and the well-known FIR-radio relation for local
starbursts (Condon 1992). The original definition is based on the 60 ![]() m and 100
m and 100 ![]() m flux densities, but following Sajina et al. (2008), we have adopted the definition:
m flux densities, but following Sajina et al. (2008), we have adopted the definition:
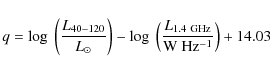
|
(4) |
where L40-120 is the integrated IR luminosity between 40
|
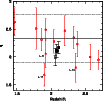
Figure 5:
The radio-FIR q
factor (FIR-to-radio ratio) (Eq. (4)). The large black symbols
show the stacked values of different samples: the entire sample
(33 sources, filled circle), the 13 sources with S/N > 3 at 1.2 mm (filled square), and the 20 sources with S/N < 3 (open square).
The solid black line shows the typical value q = 2.34 for local starbursts. The dotted black lines are the |
| Open with DEXTER | |
Although Eq. (4) has been found to hold for local
sources, its validity seems to be confirmed also at the redshifts of our
sources (Kovács et al. 2006; Younger et al. 2009). The relation between
![]() and the 20 cm
or
50 cm flux density
is thus straightforward, if we assume the typical value q = 2.34 and
and the 20 cm
or
50 cm flux density
is thus straightforward, if we assume the typical value q = 2.34 and
![]()
However, this method is valid only if the radio emission is not significantly affected by an AGN. This expression will give an upper limit to the star-formation related
The values of these two estimates of
![]() are within a factor of 3
for most of the sample. They range from
are within a factor of 3
for most of the sample. They range from ![]() 0.5 to
0.5 to
![]()
![]() ,
confirming that almost all our
sources are ULIRGs with luminosities greater than
,
confirming that almost all our
sources are ULIRGs with luminosities greater than
![]() .
The
average
.
The
average
![]() derived from the radio flux densities is
derived from the radio flux densities is
![]() .
Since this value may be slightly overestimated because of AGN, it is consistent with
.
Since this value may be slightly overestimated because of AGN, it is consistent with
![]() derived from fitting the median
FIR SED,
derived from fitting the median
FIR SED,
![]() .
.
Alternatively, the radio-FIR relation (Eq. (5)) can be applied to
identify or test for the presence of AGN-driven radio activity in our
sample (similarly to Sect. 4.3 but slightly more rigorously). The
agreement or deviation from this correlation can be easily
expressed by the value of the q-factor, as reported in Table 5.
We obtain an
average value
![]() for the whole sample.
for the whole sample.
This is
not very different from the average value
![]() found for local
star-forming galaxies (Yun et al. 2001). As shown in Fig. 5, the q-factors
of the three sources identified as having the highest
20 cm/1.2 mm flux density ratios seem to be, on average,
lower than those of most other sources. This is not surprising, since
the q factor is another way to quantify the radio excess.
found for local
star-forming galaxies (Yun et al. 2001). As shown in Fig. 5, the q-factors
of the three sources identified as having the highest
20 cm/1.2 mm flux density ratios seem to be, on average,
lower than those of most other sources. This is not surprising, since
the q factor is another way to quantify the radio excess.
4.5 Stellar mass
The IRAC-based selection of our sample corresponds to a rest-frame NIR selection; therefore, if we ignore a possibly significant AGN contribution at these wavelengths, we are directly sampling the stellar component (Lo09). Applying the method developed by Berta et al. (2004), we have derived an estimation of the stellar mass for our sources. As summarized in Lo09, this derivation uses not only the IRAC data, but also optical and 24
As discussed in Lo09, these values may be somewhat overestimated
for several reasons: our models may not fully take into account the TP-AGB
contribution to infrared light (Maraston 2005); they assume a Salpeter-like IMF,
which yields higher
masses than other IMFs; and although the near-IR SED is dominated by stellar
emission, it is possible that an AGN component is also present. Therefore,
these estimates should be considered as upper limits to the true stellar
masses, and may be overestimated by a small factor up to ![]() 2.
2.
Using the same method, Lo09
found a median stellar mass
![]() =
=
![]()
![]() and an average value
and an average value
![]()
![]() ,
about 30% larger than for our
sample. This is consistent with the comparison of the average values of the
5.8
,
about 30% larger than for our
sample. This is consistent with the comparison of the average values of the
5.8 ![]() m flux density of both samples, which reflects the rest-frame luminosity at
1.6
m flux density of both samples, which reflects the rest-frame luminosity at
1.6 ![]() m: 53
m: 53 ![]() Jy for our sample and 77
Jy for our sample and 77 ![]() Jy for that of Lo09.
Indeed, as discussed by Lo09, the direct comparison of the NIR rest-frame
luminosity at 1.6
Jy for that of Lo09.
Indeed, as discussed by Lo09, the direct comparison of the NIR rest-frame
luminosity at 1.6 ![]() m is probably the most consistent way to compare
stellar masses in different samples, in order to avoid the dependence on the various
methods applied to infer stellar masses from infrared fluxes. We have thus
estimated the rest-frame luminosities at 1.6
m is probably the most consistent way to compare
stellar masses in different samples, in order to avoid the dependence on the various
methods applied to infer stellar masses from infrared fluxes. We have thus
estimated the rest-frame luminosities at 1.6 ![]() m,
m,
![]() (1.6
(1.6 ![]() m)
(Table 5), by interpolating the
observed IRAC fluxes as in Lo09. As expected, the average rest-frame
luminosity at 1.6
m)
(Table 5), by interpolating the
observed IRAC fluxes as in Lo09. As expected, the average rest-frame
luminosity at 1.6 ![]() m in Lo09,
m in Lo09,
![]()
![]() ,
is a factor of 1.6 larger than for our sample,
,
is a factor of 1.6 larger than for our sample,
![]()
![]() (Table 5).
The sources in our sample are as luminous as, or slightly more luminous at 1.6
(Table 5).
The sources in our sample are as luminous as, or slightly more luminous at 1.6 ![]() m by a factor
m by a factor ![]() 1.5
than, submm selected SMGs, and should also be
1.5
than, submm selected SMGs, and should also be ![]() 1.5 times more massive than classical SMGs assuming the same mass-to-light ratio of Lo09.
Our sample also shows a mass-to-light ratio consistent with the radio galaxy sample detected at 24
1.5 times more massive than classical SMGs assuming the same mass-to-light ratio of Lo09.
Our sample also shows a mass-to-light ratio consistent with the radio galaxy sample detected at 24 ![]() m by Seymour et al. (2007), who computed stellar
masses directly from the luminosity at 1.6
m by Seymour et al. (2007), who computed stellar
masses directly from the luminosity at 1.6 ![]() m in the rest-frame.
m in the rest-frame.
4.6 Star formation rate
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12742f6.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2009/46/aa12742-09/Timg142.png)
|
Figure 6:
(Adapted from Fig. 14 of Daddi et al. 2007). Star formation rate vs. stellar mass. Values of SFR deduced from radio data for the
sources of our sample are represented by the red triangles (see Sects. 4.4, 4.6 and Table 5). The arrows are 2 |
| Open with DEXTER | |
From the estimated
![]() ,
we derive the star formation
rate (SFR) of our sources assuming the relation from Kennicutt (1998) using a
0.10-100
,
we derive the star formation
rate (SFR) of our sources assuming the relation from Kennicutt (1998) using a
0.10-100 ![]() Salpeter IMF:
Salpeter IMF:
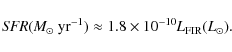
|
(6) |
The SFR values derived from
To estimate the contribution of ``5.8 ![]() m-peakers'' with
m-peakers'' with
![]() > 400
> 400 ![]() Jy to the star formation rate density (SFRD) of the
universe, we consider the space density and average SFR of our sources.
Assuming a redshift interval of 1.5<z<2.5, and an average SFR of
450
Jy to the star formation rate density (SFRD) of the
universe, we consider the space density and average SFR of our sources.
Assuming a redshift interval of 1.5<z<2.5, and an average SFR of
450 ![]() yr-1, we derive the contribution of our sample to the
(comoving) SFRD to be
yr-1, we derive the contribution of our sample to the
(comoving) SFRD to be ![]() 1.5-
1.5-
![]()
![]() yr-1 Mpc-3. This
value corresponds to
yr-1 Mpc-3. This
value corresponds to ![]() 5% of the SFRD of all classical SMGs
(Chapman et al. 2005; Aretxaga et al. 2007), i.e., to
5% of the SFRD of all classical SMGs
(Chapman et al. 2005; Aretxaga et al. 2007), i.e., to ![]() 10% of the SFRD of SMGs in the
interval 1.5 <z< 2.5, and up to
10% of the SFRD of SMGs in the
interval 1.5 <z< 2.5, and up to ![]() 15% in the interval of 1.7<z<2.3where ``5.8
15% in the interval of 1.7<z<2.3where ``5.8 ![]() m-peakers'' are mostly confined.
m-peakers'' are mostly confined.
The specific star formation rate (SSFR), defined as SFR/![]() ,
ranges from
,
ranges from ![]() 10-8 yr-1 to
10-8 yr-1 to ![]() 10-9 yr-1 for our sample.
There is a tendency for the sources with the lowest stellar masses to have the highest SSFRs.
This result is consistent with, e.g., Noeske et al. (2007).
However, it is seen in Fig. 6 that ``5.8
10-9 yr-1 for our sample.
There is a tendency for the sources with the lowest stellar masses to have the highest SSFRs.
This result is consistent with, e.g., Noeske et al. (2007).
However, it is seen in Fig. 6 that ``5.8 ![]() m-peakers'' have significantly higher SSFRs than classical sBzK galaxies of comparable masses on average (Sect. 5.3).
m-peakers'' have significantly higher SSFRs than classical sBzK galaxies of comparable masses on average (Sect. 5.3).
5 Discussion
5.1 Comparison with other samples: 1) Spitzer selection (see Table 2)
|
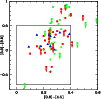
Figure 7:
IRAC color-color diagram for several samples. The sample of Huang et al. (2009) and Younger et al. (2009) is represented by the solid blue triangles. The red circles show our sample.
The open green stars are the sample of Lonsdale et al. (2009). The arrows are 3 |
| Open with DEXTER | |
|
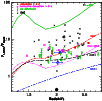
Figure 8:
Observed flux density ratio,
|
| Open with DEXTER | |
The present work is an extension of the study presented in Lo09 on a sample
of 61 sources selected in four SWIRE fields. The sources in Lo09 meet the same
selection criteria and span the same redshift range, 1.4
![]() 2.7, as our sample. However, their selection is biased
toward brighter sources at 24
2.7, as our sample. However, their selection is biased
toward brighter sources at 24 ![]() m, while the present sample is complete
to a 24
m, while the present sample is complete
to a 24 ![]() m flux density limit of 400
m flux density limit of 400 ![]() Jy. This bias results in an average
24
Jy. This bias results in an average
24 ![]() m flux density a factor 1.5 greater than in our sample,
m flux density a factor 1.5 greater than in our sample,
![]() = 819
= 819 ![]() Jy vs. 566
Jy vs. 566 ![]() Jy (see Sect. 2).
Nevertheless, the 1.2 mm properties of the two samples are comparable. The
average flux densities at 1.2 mm are similar:
Jy (see Sect. 2).
Nevertheless, the 1.2 mm properties of the two samples are comparable. The
average flux densities at 1.2 mm are similar:
![]() mJy for our
entire sample, against
mJy for our
entire sample, against
![]() mJy for the sample in Lo09.
mJy for the sample in Lo09.
Although the source selection in Lo09 was optimized
to favor 1.2 mm bright sources, their detection rate is slightly lower than
what we achieve with our complete sample, only 26% (31% in their best observed
field with a sensitivity similar to ours) with
![]()
![]() compared to 39% in our sample. Both samples are characterized by a similar average
compared to 39% in our sample. Both samples are characterized by a similar average
![]() determined using a thermal spectral model (see Sect. 4.4 and Eq. (3)),
determined using a thermal spectral model (see Sect. 4.4 and Eq. (3)),
![]() =
=
![]()
![]() in this work
vs. (
in this work
vs. (
![]() )
) ![]() 1012
1012 ![]() in Lo09 (restricted to the Lockman Hole
field). Thus, in spite of the refinement implemented by Lo09 in
their sample selection to increase the chance of finding mm bright sources
among ``5.8
in Lo09 (restricted to the Lockman Hole
field). Thus, in spite of the refinement implemented by Lo09 in
their sample selection to increase the chance of finding mm bright sources
among ``5.8 ![]() m peakers'', the average mm properties of their sample and our
complete sample are consistent.
m peakers'', the average mm properties of their sample and our
complete sample are consistent.
Younger et al. (2009) have studied the FIR properties of a similar Spitzer-selected sample, based on MIPS 70 and 160 ![]() m detections and MAMBO 1.2 mm observations.
This sample (see also Huang et al. 2009) is selected based on IRAC colors, and
24
m detections and MAMBO 1.2 mm observations.
This sample (see also Huang et al. 2009) is selected based on IRAC colors, and
24 ![]() m flux densities (see Fig. 7, Table 2 and Sect. 2), yielding 12 starburst galaxies with overall properties (redshifts, IRAC colors, 1.2 mm
flux densities) similar to those in Lo09 and in this work. Consequently, the
m flux densities (see Fig. 7, Table 2 and Sect. 2), yielding 12 starburst galaxies with overall properties (redshifts, IRAC colors, 1.2 mm
flux densities) similar to those in Lo09 and in this work. Consequently, the
![]() and derived star formation rates are also similar in all these samples.
and derived star formation rates are also similar in all these samples.
Finally, Lutz et al. (2005) studied the mm properties of a Spitzer sample
selected based on faint R band magnitudes, relatively bright 24 ![]() m
flux densities (
m
flux densities (
![]() 1 mJy), and high
1 mJy), and high
![]() /
/
![]() ratios (Yan et al. 2007,2005; Sajina et al. 2008). This sample contains
40 sources at
ratios (Yan et al. 2007,2005; Sajina et al. 2008). This sample contains
40 sources at ![]() exhibiting both starburst and AGN properties. They are
on average fainter 1.2 mm emitters than our sources and they show
significantly lower
exhibiting both starburst and AGN properties. They are
on average fainter 1.2 mm emitters than our sources and they show
significantly lower
![]() /
/
![]() flux density ratios, with
flux density ratios, with
![]() mJy (simple average) and
mJy (simple average) and
![]() (simple averages), compared to
(simple averages), compared to
![]() mJy and
mJy and
![]() for our sample
(Table 3; see also Fig. 8). These differences are
due to the fact that in the majority of these objects, the main source of
power is an AGN rather than the powerful starburst required to produce bright mm
flux, with the AGN dominating their 24
for our sample
(Table 3; see also Fig. 8). These differences are
due to the fact that in the majority of these objects, the main source of
power is an AGN rather than the powerful starburst required to produce bright mm
flux, with the AGN dominating their 24 ![]() m
emission.
m
emission.
5.2 Comparison with other samples: 2) Submillimetre selection
In order to characterize more quantitatively the difference in
![]() /
/
![]() flux density ratios between our sample of ``5.8
flux density ratios between our sample of ``5.8 ![]() m-peakers'' and classical
SMGs, we show them as a function of redshift in
Fig. 8. The sample of classical SMGs is the sub-set of the
sample used in Lo09 completed by the SHADES SMG sample from Coppin et al. (2006) and Ivison et al. (2007) detected at 24
m-peakers'' and classical
SMGs, we show them as a function of redshift in
Fig. 8. The sample of classical SMGs is the sub-set of the
sample used in Lo09 completed by the SHADES SMG sample from Coppin et al. (2006) and Ivison et al. (2007) detected at 24 ![]() m with 1.5 < z < 2.5. We also display a sub-set of ``5.8
m with 1.5 < z < 2.5. We also display a sub-set of ``5.8 ![]() m-peakers'' from Lo09.
Note that most of the redshifts available for the Lo09 and the
SHADES samples are photometric (Aretxaga et al. 2007). We also show in
Fig. 8 the expected flux ratios for representative starburst
and AGN templates. To facilitate the comparison, we also show the ratio of the average flux densities for the samples
of ``5.8
m-peakers'' from Lo09.
Note that most of the redshifts available for the Lo09 and the
SHADES samples are photometric (Aretxaga et al. 2007). We also show in
Fig. 8 the expected flux ratios for representative starburst
and AGN templates. To facilitate the comparison, we also show the ratio of the average flux densities for the samples
of ``5.8 ![]() m-peakers''
from this work and from Lo09, and for a sample of classical SMGs (the
SMG sample of Lo09 augmented by those of SHADES: Ivison et al. 2007; Coppin et al. 2006).
Our complete sample
of ``5.8
m-peakers''
from this work and from Lo09, and for a sample of classical SMGs (the
SMG sample of Lo09 augmented by those of SHADES: Ivison et al. 2007; Coppin et al. 2006).
Our complete sample
of ``5.8 ![]() m-peakers'' confirms that the ratio of the average
1.2 mm and 24
m-peakers'' confirms that the ratio of the average
1.2 mm and 24 ![]() m flux densities for this class of sources is
smaller than for SMGs. However, the difference is slightly smaller than in
Lo09 because of our lower mean 24
m flux densities for this class of sources is
smaller than for SMGs. However, the difference is slightly smaller than in
Lo09 because of our lower mean 24 ![]() m flux density. The
m flux density. The
![]() /
/
![]() flux density ratios of our sample are also similar to one for
the lensed LBG cB58, despite the fact that this lensed
LBG is an order of magnitude less luminous than the average of our sample (Siana et al. 2008).
flux density ratios of our sample are also similar to one for
the lensed LBG cB58, despite the fact that this lensed
LBG is an order of magnitude less luminous than the average of our sample (Siana et al. 2008).
We have shown that ``5.8 ![]() m-peakers'' are
m-peakers'' are ![]() ULIRGs and that about 40%
of them are bright mm sources. Thus,
ULIRGs and that about 40%
of them are bright mm sources. Thus, ![]() of them also belong to the class
of SMGs (Table 5), one of the main classes of high-z ULIRGs. A detailed comparison
between the MIR and FIR properties of a large sample of
SMGs (Hainline et al. 2009; Chapman et al. 2005; Borys et al. 2005; Frayer et al. 2004; Pope et al. 2005; Greve et al. 2004) and ``5.8
of them also belong to the class
of SMGs (Table 5), one of the main classes of high-z ULIRGs. A detailed comparison
between the MIR and FIR properties of a large sample of
SMGs (Hainline et al. 2009; Chapman et al. 2005; Borys et al. 2005; Frayer et al. 2004; Pope et al. 2005; Greve et al. 2004) and ``5.8 ![]() m-peakers''
is presented in Lo09. In this study, Lo09 find that most
``5.8
m-peakers''
is presented in Lo09. In this study, Lo09 find that most
``5.8 ![]() m-peakers''
represent a sub-class of SMGs. The differences found by Lo09 with respect to
classical SMGs are mainly related to the selection criteria for the
``5.8
m-peakers''
represent a sub-class of SMGs. The differences found by Lo09 with respect to
classical SMGs are mainly related to the selection criteria for the
``5.8 ![]() m-peakers''. More specifically, the Spitzer selection
favours sources with redshifts mostly concentrated in the range
m-peakers''. More specifically, the Spitzer selection
favours sources with redshifts mostly concentrated in the range
![]() -2.3, rather higher stellar masses than classical SMGs at
similar redshifts, brighter 24
-2.3, rather higher stellar masses than classical SMGs at
similar redshifts, brighter 24 ![]() m flux densities, and thus higher
m flux densities, and thus higher
![]() /
/
![]() flux density ratios (see Fig. 9 in Lo09 and
Fig. 8), and likely warmer dust temperatures. The
mm-detected ``5.8
flux density ratios (see Fig. 9 in Lo09 and
Fig. 8), and likely warmer dust temperatures. The
mm-detected ``5.8 ![]() m-peakers'' and classical SMGs show similar mm/submm flux
densities, implying that the main difference in the 1.2 mm/24
m-peakers'' and classical SMGs show similar mm/submm flux
densities, implying that the main difference in the 1.2 mm/24 ![]() m ratio
comes from the 24
m ratio
comes from the 24 ![]() m rather than the 1.2 mm intensity. This
result implies that a high 24
m rather than the 1.2 mm intensity. This
result implies that a high 24 ![]() m flux density does not directly translate into
a high 1.2 mm flux density, and thus into high
m flux density does not directly translate into
a high 1.2 mm flux density, and thus into high
![]() and SFR, in starburst galaxies
at
and SFR, in starburst galaxies
at ![]() (see also Rieke et al. 2009; Pope et al. 2008a).
(see also Rieke et al. 2009; Pope et al. 2008a).
5.3 Nature of the sources: 1. Powerful starburst activity
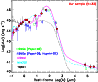
|
Figure 9:
Median optical through radio SED of all 33 ``5.8 |
| Open with DEXTER | |
As discussed in Sec. 2, our selection criteria are devised to distinguish
starburst ULIRGs from AGN through the presence of the redshifted
1.6 ![]() m stellar ``bump'' which dominates over a strong AGN continuum in
the near infrared. As shown by similar studies such as Weedman et al. (2006),
Farrah et al. (2008), Huang et al. (2009), and Lo09, such criteria are very successful in
selecting a majority of starbursts with strong mid-IR PAH features, and we
have good evidence that this is also the case for the present sample from the
combination of millimetre and radio data.
m stellar ``bump'' which dominates over a strong AGN continuum in
the near infrared. As shown by similar studies such as Weedman et al. (2006),
Farrah et al. (2008), Huang et al. (2009), and Lo09, such criteria are very successful in
selecting a majority of starbursts with strong mid-IR PAH features, and we
have good evidence that this is also the case for the present sample from the
combination of millimetre and radio data.
Although there might be some fraction of ``5.8 ![]() m-peakers'' that
host a certain level of AGN activity, in the majority of these sources, the
optical to far-IR light is likely dominated by starburst emission. This is
confirmed by 1) the high detection rate at 1.2 mm and the high average
value
m-peakers'' that
host a certain level of AGN activity, in the majority of these sources, the
optical to far-IR light is likely dominated by starburst emission. This is
confirmed by 1) the high detection rate at 1.2 mm and the high average
value
![]() = 1.56 mJy;
and 2) the correlation between the mm and radio emission for the
majority of the sources.
With star formation rates ranging from a few 102
= 1.56 mJy;
and 2) the correlation between the mm and radio emission for the
majority of the sources.
With star formation rates ranging from a few 102 ![]() yr-1to
yr-1to ![]() 103
103 ![]() yr-1 and a mean
yr-1 and a mean
![]()
![]() 450-750
450-750 ![]() yr-1, they are powerful ULIRGs
with starburst strengths similar to those of SMGs.
yr-1, they are powerful ULIRGs
with starburst strengths similar to those of SMGs.
Significant emission in the mid-IR bands of PAHs is a common feature in
starbursts (see, e.g., Desai et al. 2007; Rigopoulou et al. 1999; Farrah et al. 2009; Veilleux et al. 2009, for local galaxies). Although we are still lacking mid-IR spectroscopy for our ![]() sample to infer the precise strength of the objects' PAH emission, there are very good
reasons for thinking that it is strong and comparable to that observed in other
24
sample to infer the precise strength of the objects' PAH emission, there are very good
reasons for thinking that it is strong and comparable to that observed in other
24 ![]() m-bright starburst galaxies at
m-bright starburst galaxies at
![]() satisfying similar
criteria for selection of ``4.5
satisfying similar
criteria for selection of ``4.5 ![]() m-'' or ``5.8
m-'' or ``5.8 ![]() m-peakers'' (Huang et al. 2009; Yan et al. 2007; Weedman et al. 2006; Murphy et al. 2009, Lonsdale et al. in prep.) or in about 30 ``4.5
m-peakers'' (Huang et al. 2009; Yan et al. 2007; Weedman et al. 2006; Murphy et al. 2009, Lonsdale et al. in prep.) or in about 30 ``4.5 ![]() m-peakers''
(Farrah et al. 2008). The strong PAH emission displayed in these objects
accounts for the major part of the mid-IR emission in the range
m-peakers''
(Farrah et al. 2008). The strong PAH emission displayed in these objects
accounts for the major part of the mid-IR emission in the range
![]() 6-12
6-12 ![]() m. It is thus clear that the PAHs generally contribute much of
the flux detected in the Spitzer/MIPS broad 24
m. It is thus clear that the PAHs generally contribute much of
the flux detected in the Spitzer/MIPS broad 24 ![]() m band in such
``5.8
m band in such
``5.8 ![]() m-'' or ``4.5
m-'' or ``4.5 ![]() m-peakers''. As noted, most SMGs have a much weaker 24
m-peakers''. As noted, most SMGs have a much weaker 24 ![]() m intensity than our sources.
It is not yet well understood why ``5.8
m intensity than our sources.
It is not yet well understood why ``5.8 ![]() m-'' and ``4.5
m-'' and ``4.5 ![]() m-peakers'' happen to have stronger PAH
emission without a parallel enhancement of the observed mm/submm flux
density, resulting in a higher 24
m-peakers'' happen to have stronger PAH
emission without a parallel enhancement of the observed mm/submm flux
density, resulting in a higher 24 ![]() m/1.2 mm ratio than the bulk of the
SMGs (Lo09). Farrah et al. (2008) suggest the
possibility that star formation is extended on spatial scales of 1-4 kpc
in such galaxies.
m/1.2 mm ratio than the bulk of the
SMGs (Lo09). Farrah et al. (2008) suggest the
possibility that star formation is extended on spatial scales of 1-4 kpc
in such galaxies.
In Fig. 9, we show the median SED of our
sample of ``5.8 ![]() m-peakers'', compared to the templates of a starburst, an obscured
AGN, and an unobscured AGN.
It is clear that the median observed SED is much better
matched by the starburst template than by the obscured AGN SED, where the 5.8
m-peakers'', compared to the templates of a starburst, an obscured
AGN, and an unobscured AGN.
It is clear that the median observed SED is much better
matched by the starburst template than by the obscured AGN SED, where the 5.8 ![]() m bump is absent.
m bump is absent.
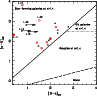
|
Figure 10:
BzK color-color plot for our sample. B magnitude is extrapolated from u
and
|
| Open with DEXTER | |
``5.8 ![]() m-peakers'' (and ``4.5
m-peakers'' (and ``4.5 ![]() m-peakers'') also have some relationship with other broader classes of infrared selected high-z
star-forming galaxies,
as judged by 24
m-peakers'') also have some relationship with other broader classes of infrared selected high-z
star-forming galaxies,
as judged by 24 ![]() m intensity. As already discussed (e.g., Table 3), there are various samples (e.g. Yan et al. 2005; Houck et al. 2005; Magliocchetti et al. 2007; Murphy et al. 2009)
just selected as relatively strong at 24
m intensity. As already discussed (e.g., Table 3), there are various samples (e.g. Yan et al. 2005; Houck et al. 2005; Magliocchetti et al. 2007; Murphy et al. 2009)
just selected as relatively strong at 24 ![]() m and weak in the optical, especially for the purpose of IRS mid-IR spectroscopy.
One recent example is the so called ``Dust-Obscured Galaxies'' (DOGs) defined as having
m and weak in the optical, especially for the purpose of IRS mid-IR spectroscopy.
One recent example is the so called ``Dust-Obscured Galaxies'' (DOGs) defined as having
![]() /
/
![]() > 1000,
with various limits for
> 1000,
with various limits for
![]() such as 300
such as 300 ![]() Jy by Dey & The Ndwfs/MIPS Collaboration (2009); Dey et al. (2008), or 100
Jy by Dey & The Ndwfs/MIPS Collaboration (2009); Dey et al. (2008), or 100 ![]() Jy by Pope et al. (2008a).
However, such broad criteria select a mixture of starbursts and AGN, especially those with power-law IRAC SEDs.
As seeing from Table 1, practically all sources of our sample satisfy or are close to the
Jy by Pope et al. (2008a).
However, such broad criteria select a mixture of starbursts and AGN, especially those with power-law IRAC SEDs.
As seeing from Table 1, practically all sources of our sample satisfy or are close to the
![]() /
/
![]() > 1000 flux density
ratio defining DOGs.
> 1000 flux density
ratio defining DOGs.
A better established class of high-z galaxies partially selected from optical-NIR colors is the ``BzK'' galaxies (Daddi et al. 2004).
This includes an ``sBzK'' sub-class of star-forming galaxies and a ``pBzK'' sub-class of passively evolving proto-ellipticals.
Figure 10 shows that all sources in our sample with B, z, and
K information are sBzK galaxies.
``5.8 ![]() m-peakers'' share the same redshift range as the bulk of BzKs (see e.g. Fig. 2 of Daddi et al. 2007).
However, they are at the very top of the BzK luminosity function. This is clearly shown in Fig. 11 where we have put our sample of
``5.8
m-peakers'' share the same redshift range as the bulk of BzKs (see e.g. Fig. 2 of Daddi et al. 2007).
However, they are at the very top of the BzK luminosity function. This is clearly shown in Fig. 11 where we have put our sample of
``5.8 ![]() m-peakers''
on top of Fig. 7 of Daddi et al. (2007), which displays the rest luminosity
m-peakers''
on top of Fig. 7 of Daddi et al. (2007), which displays the rest luminosity ![]() (8
(8![]() m) (roughly proportional to the bulk of
m) (roughly proportional to the bulk of
![]() )
and
)
and
![]() (deduced from
(deduced from
![]() )
for all BzKs in the GOODS-N field.
)
for all BzKs in the GOODS-N field.
We note that the two ![]() BzKs where CO was recently detected by Daddi et al. (2008)
are ``4.5
BzKs where CO was recently detected by Daddi et al. (2008)
are ``4.5 ![]() m-peakers'' with
m-peakers'' with
![]() = 140 and 400
= 140 and 400 ![]() Jy and
Jy and
![]() close to 1012
close to 1012 ![]() ,
i.e., comparable to or below
the lower end of the luminosity distribution of our sample (Fig. 11). This probably means that CO should be easily detectable in most of our ``5.8
,
i.e., comparable to or below
the lower end of the luminosity distribution of our sample (Fig. 11). This probably means that CO should be easily detectable in most of our ``5.8 ![]() m-peakers''
with the current sensitivity of the IRAM Plateau de Bure Interferometer
(PdBI), as shown by Yan et al. (in prep.), who detected strong CO
emission in two ``5.8
m-peakers''
with the current sensitivity of the IRAM Plateau de Bure Interferometer
(PdBI), as shown by Yan et al. (in prep.), who detected strong CO
emission in two ``5.8 ![]() m-peakers'' of Sajina et al. (2008).
m-peakers'' of Sajina et al. (2008).
Since sBzK sources are major contributors to star formation at ![]() ,
it is interesting to compare their star formation properties with those of our ``5.8
,
it is interesting to compare their star formation properties with those of our ``5.8 ![]() m-peakers''.
Figure 6 shows that the average SFR of ``5.8
m-peakers''.
Figure 6 shows that the average SFR of ``5.8 ![]() m-peakers'' is significantly greater than the average for sBzKs at
m-peakers'' is significantly greater than the average for sBzKs at ![]() (Daddi et al. 2007).
Even their SSFRs are significantly higher than those of sBzKs with comparable masses. This figure confirms that our ``5.8
(Daddi et al. 2007).
Even their SSFRs are significantly higher than those of sBzKs with comparable masses. This figure confirms that our ``5.8 ![]() m-peakers'' represent as significant a fraction
of the most massive and star-forming sBzKs as Fig. 11 implies.
On the other hand, as the average SFR of ``5.8
m-peakers'' represent as significant a fraction
of the most massive and star-forming sBzKs as Fig. 11 implies.
On the other hand, as the average SFR of ``5.8 ![]() m-peakers'' is significantly lower than those of the bulk of classical SMGs, and their stellar mass slightly higher,
it is not surprising that the mean SSFR of ``5.8
m-peakers'' is significantly lower than those of the bulk of classical SMGs, and their stellar mass slightly higher,
it is not surprising that the mean SSFR of ``5.8 ![]() m-peakers'' is markedly smaller than one of SMGs (Fig. 6).
m-peakers'' is markedly smaller than one of SMGs (Fig. 6).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12742f11.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12742-09/Timg168.png)
|
Figure 11:
(Adapted from Fig. 7 of Daddi et al. 2007). Luminosity at 1.4 GHz rest frame vs. luminosity at 8 |
| Open with DEXTER | |
Another class of powerful starburst galaxies are the so called ``submillimetre faint radio galaxies'' (SFRGs; Chapman et al. 2008,2004; Blain et al. 2004).
They are defined as radio sources with radio fluxes similar to those of
SMGs which are not detected in typical SCUBA surveys. In addition to
AGN, this class of sources
may contain star-forming galaxies characterized by slightly hotter
temperatures
than typically observed in submillimetre galaxies. It is also possible
that
the radio properties and the hotter dust temperatures in these sources
might
be due to the presence of AGN activity, but clear evidence is still
lacking for the relative fractions of AGN and hotter starbursts (Chapman et al. 2008; Casey et al. 2008,2009).
It is thus interesting to consider whether our sources undetected at
1.2 mm and lying outside or at the outskirts of the
radio-1.2 mm correlation might belong to the class of SFRG. More
precisely, Chapman et al. (2008) propose to reserve the name of SFRG for radio sources with
![]() > 1024 W Hz-1.
As SFRGs must also not be detected in 850
> 1024 W Hz-1.
As SFRGs must also not be detected in 850 ![]() m surveys with typical sensitivity 4 mJy, we assume that SFRGs in our sample may be defined
by
m surveys with typical sensitivity 4 mJy, we assume that SFRGs in our sample may be defined
by
![]() > 1024 W Hz-1 and
> 1024 W Hz-1 and
![]() < 1.6 mJy. SFRGs are identified with these criteria in Table 5.
There are 3 confirmed SFRGs and 3 tentative SFRGs (together with 4 confirmed SMGs and
9 tentative SMGs defined as satisfying the limit
< 1.6 mJy. SFRGs are identified with these criteria in Table 5.
There are 3 confirmed SFRGs and 3 tentative SFRGs (together with 4 confirmed SMGs and
9 tentative SMGs defined as satisfying the limit
![]() > 1.6 mJy,
and 7 sources too weak in radio to be SFRG and at 1.2 mm to be SMG). We may thus estimate that among ``5.8
> 1.6 mJy,
and 7 sources too weak in radio to be SFRG and at 1.2 mm to be SMG). We may thus estimate that among ``5.8 ![]() m-peakers'',
at least
m-peakers'',
at least ![]() 40% are SMGs,
40% are SMGs, ![]() 10-20% may be SFRGs, and
10-20% may be SFRGs, and ![]() 15-20% are weak radio and mm sources.
15-20% are weak radio and mm sources.
5.4 Nature of the sources: 2. Weak AGN activity
Our selection criteria were designed to select
starburst ULIRGs over AGN through the presence of the redshifted
1.6 ![]() m stellar ``bump''. However, similar studies have shown that the discrimination against AGN with such
criteria is not perfect and that a small fraction
has a weak but significant AGN contribution in
their mid-IR SED. Since AGNs are powerful NIR emitters due to their ability
to heat dust up to its sublimation temperature, we expect that such emission may
smear out the
1.6
m stellar ``bump''. However, similar studies have shown that the discrimination against AGN with such
criteria is not perfect and that a small fraction
has a weak but significant AGN contribution in
their mid-IR SED. Since AGNs are powerful NIR emitters due to their ability
to heat dust up to its sublimation temperature, we expect that such emission may
smear out the
1.6 ![]() m stellar ``bump'', flatten it, or move to longer observed wavelengths (Daddi et al. 2007; Berta et al. 2007a). However, some AGNs can satisfy our selection criteria. Indeed, about
8 radio-galaxies
from the sample of Seymour et al. (2007) follow our criteria. But these sources show a significant radio excess (Archibald et al. 2001; Reuland et al. 2004) due to the AGN.
m stellar ``bump'', flatten it, or move to longer observed wavelengths (Daddi et al. 2007; Berta et al. 2007a). However, some AGNs can satisfy our selection criteria. Indeed, about
8 radio-galaxies
from the sample of Seymour et al. (2007) follow our criteria. But these sources show a significant radio excess (Archibald et al. 2001; Reuland et al. 2004) due to the AGN.
To identify, quantify, and characterize any AGN activity which might be present in our sample it would be useful to have mid-IR spectroscopic data (see, e.g., Farrah et al. 2008; Weedman et al. 2006), optical/NIR spectroscopic data (Berta et al. 2007b; Chapman et al. 2005), morphological data from high angular resolution radio observations (see, e.g., Richards et al. 2007; Muxlow et al. 2005; Biggs & Ivison 2008), or deep X-ray data (see, e.g., Alexander et al. 2005). Only limited observations of this kind are available for our sample. A spectroscopic observation from Keck/LRIS is available for source L-25 (LH_574364 in Berta et al. 2007b). Based on one emission line identified as MgII, this source is classified as a type 2 AGN, although its radio/1.2 mm flux density ratio is not one of the highest and its radio spectral index instead point to a starburst-dominated IR SED (Table 4).
X-ray data of moderate depth (70 ks exposures)
from Chandra are also available for all our sources (Polletta et al. 2006).
None of them is detected by Chandra to a 0.3-8 keV flux
limit of
![]() erg cm-2 s-1. We stacked the X-ray
images of all 33 sources, but no significant detection was obtained. We can
only set an upper limit to the average 0.3-8 keV flux of
10-16 erg cm-2 s-1 which corresponds to an average X-ray
luminosity of 2
erg cm-2 s-1. We stacked the X-ray
images of all 33 sources, but no significant detection was obtained. We can
only set an upper limit to the average 0.3-8 keV flux of
10-16 erg cm-2 s-1 which corresponds to an average X-ray
luminosity of 2 ![]() 1042 erg s-1. Such a low signal does not
allow us to make any claim about the AGN contribution and X-ray properties of
our sample.
1042 erg s-1. Such a low signal does not
allow us to make any claim about the AGN contribution and X-ray properties of
our sample.
The multi-frequency radio observations available for the majority of our sources may also allow us to investigate the AGN contribution. As discussed in Sect. 4.3, we can find some indication of AGN activity based on the 1.2 mm/radio flux density ratio complemented by the spectral index and the radio size; however, an extension may as easily reflect well an extended starburst as an AGN lobe.
Two 20 cm radio sources, L-17 and L-11, are specially strong
(
![]()
![]() Jy).
The 20 cm flux density of L-17 is slightly greater than 300
Jy).
The 20 cm flux density of L-17 is slightly greater than 300 ![]() Jy,
implying a 1.4 GHz luminosity close to 1025 W Hz-1 (see Fig. 12) which is close to the
radio loudness limit at
Jy,
implying a 1.4 GHz luminosity close to 1025 W Hz-1 (see Fig. 12) which is close to the
radio loudness limit at ![]() (Jiang et al. 2007; Sajina et al. 2007). L-11, despite
its high 20 cm flux, is not strictly radio loud according to this
definition. Neither source is resolved in the radio; however, this
might be not very meaningful, since both sources are in regions with limited
sensitivity at 20 cm. Their spectral indices are -0.76 and
-0.45, respectively, which is not very discriminating.
Interestingly, both sources are rather strong and well
detected at 1.2 mm (S/N = 3.5 and 5.3 respectively), implying that, if they are AGN, they might experience both
starburst and accretion activity.
(Jiang et al. 2007; Sajina et al. 2007). L-11, despite
its high 20 cm flux, is not strictly radio loud according to this
definition. Neither source is resolved in the radio; however, this
might be not very meaningful, since both sources are in regions with limited
sensitivity at 20 cm. Their spectral indices are -0.76 and
-0.45, respectively, which is not very discriminating.
Interestingly, both sources are rather strong and well
detected at 1.2 mm (S/N = 3.5 and 5.3 respectively), implying that, if they are AGN, they might experience both
starburst and accretion activity.
The two other sources with evidence of possible AGN-driven radio activity based on a high 20 cm/1.2 mm flux density ratio, L-8 and L-14, are not detected at 1.2 mm (S/N < 1 and S/N = 3, respectively), L-8 could be an SFRG, and L-14 either an SMG or an SFRG. L-8 is also extended in its radio image.
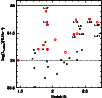
|
Figure 12: 1.4 GHz luminosity as function of redshift. Same symbols as Figs. 3 and 10. The solid black line shows the radio loudness limit for 1.4 GHz luminosity (Sajina et al. 2007). |
| Open with DEXTER | |
Table 6: Results from the co-added MIPS images.
6 Summary and conclusion
The aim of this project was to determine the average properties of a
complete 24 ![]() m flux limited sample of bright Spitzer sources selected
to be starburst dominated at
m flux limited sample of bright Spitzer sources selected
to be starburst dominated at ![]() ,
using multi-wavelength data.
The sample of 33
,
using multi-wavelength data.
The sample of 33 ![]() SMG candidates was built with all the optically faint sources in a
SMG candidates was built with all the optically faint sources in a ![]() 0.5 deg2 area
of the Lockman Hole SWIRE field meeting selection criteria based on
MIPS/IRAC fluxes. These criteria are
0.5 deg2 area
of the Lockman Hole SWIRE field meeting selection criteria based on
MIPS/IRAC fluxes. These criteria are
![]() 400 mJy, a peak in the 5.8
400 mJy, a peak in the 5.8 ![]() m IRAC band due
to redshifted 1.6
m IRAC band due
to redshifted 1.6 ![]() m stellar emission, and
m stellar emission, and
![]() > 23. The
J1046+59 field was selected because of the availability of very deep radio observations at
20 cm and 90 cm with the VLA and at 50 cm with the GMRT.
All sources in our sample are detected at 50 cm.
> 23. The
J1046+59 field was selected because of the availability of very deep radio observations at
20 cm and 90 cm with the VLA and at 50 cm with the GMRT.
All sources in our sample are detected at 50 cm.
The entire
sample has an average 1.2 mm flux density of 1.56 ![]() 0.22 mJy. However, the limited sensitivity allowed only four confirmed 4
0.22 mJy. However, the limited sensitivity allowed only four confirmed 4![]() detections, plus nine tentative 3
detections, plus nine tentative 3![]() detections.
Since the average 1.2 mm flux density, 1.56 mJy, corresponds to a 850
detections.
Since the average 1.2 mm flux density, 1.56 mJy, corresponds to a 850 ![]() m flux density close to 4 mJy, about half of the sources
may be considered SMGs. However, their redshifts range from
m flux density close to 4 mJy, about half of the sources
may be considered SMGs. However, their redshifts range from ![]() -2.3, similarly to the sample in Huang et al. (2009), but smaller than the redshift range covered by SMGs.
The sample selected here is characterized by brighter
24
-2.3, similarly to the sample in Huang et al. (2009), but smaller than the redshift range covered by SMGs.
The sample selected here is characterized by brighter
24 ![]() m flux densities, on average, than those of SMGs, and consequently shows
systematically lower
m flux densities, on average, than those of SMGs, and consequently shows
systematically lower
![]() /
/
![]() ratios than classical
SMGs. It is quite likely that our selection favours the SMGs with the
brightest 24
ratios than classical
SMGs. It is quite likely that our selection favours the SMGs with the
brightest 24 ![]() m flux densities, due probably to enhanced PAH emission.
m flux densities, due probably to enhanced PAH emission.
From stacking individual images of the sources, we are able to build the
median FIR SED of our sample and estimate the corresponding
![]() ,
SFR and
,
SFR and
![]() assuming a single temperature ``greybody'' model. The inferred values
are
assuming a single temperature ``greybody'' model. The inferred values
are
![]() = 37
= 37![]() 8 K,
8 K,
![]() = 2.5
= 2.5 ![]() 1012
1012 ![]() ,
and SFR = 450
,
and SFR = 450 ![]() yr-1. These estimates indicate that most of the
sources are ULIRGs. However, estimates of
yr-1. These estimates indicate that most of the
sources are ULIRGs. However, estimates of
![]() for individual sources deduced
from the IR-mm SED are highly uncertain due to the lack of flux measurements
between 100
for individual sources deduced
from the IR-mm SED are highly uncertain due to the lack of flux measurements
between 100 ![]() m and 500
m and 500 ![]() m. The high quality radio data provide
important complementary information on
m. The high quality radio data provide
important complementary information on
![]() and the star
formation rate, since the 1.2 mm/radio flux density ratio of the majority of
individual sources is consistent with the FIR/radio correlation, which allows a
derivation of
and the star
formation rate, since the 1.2 mm/radio flux density ratio of the majority of
individual sources is consistent with the FIR/radio correlation, which allows a
derivation of
![]() and SFR from the radio flux, providing further
confirmation that most of the selected sources are ULIRGs. The average value of
and SFR from the radio flux, providing further
confirmation that most of the selected sources are ULIRGs. The average value of
![]() inferred from the FIR-radio correlation is
inferred from the FIR-radio correlation is
![]()
![]() ;
however, this value may be overestimated because of an AGN contribution.
;
however, this value may be overestimated because of an AGN contribution.
Stellar masses are estimated by modelling the optical-IR SED with stellar
population synthesis models. They are of order a few 1011 ![]() .
Roughly scaling with the observed 5.8
.
Roughly scaling with the observed 5.8 ![]() m fluxes, they are similar to those of
other samples of 24
m fluxes, they are similar to those of
other samples of 24 ![]() m-bright,
m-bright, ![]() Spitzer starbursts, and
slightly higher than those of classical SMGs.
Spitzer starbursts, and
slightly higher than those of classical SMGs.
Overall, this sample appears similar to other samples of
Spitzer ![]() SMGs (Lo09; Younger et al. 2009) in terms of
millimetre emission,
SMGs (Lo09; Younger et al. 2009) in terms of
millimetre emission,
![]() ,
and SFR.
,
and SFR.
The complete radio detection of
all sources provides a good estimate of the total star formation rate
of such sources. They represent a significant fraction of all SMGs in the
redshift range ![]() -2.3 (
-2.3 (![]() 10-15%).
Most of these ``5.8
10-15%).
Most of these ``5.8 ![]() m-peakers'' are star-forming BzK galaxies with luminosities at the top of the luminosity distribution of sBzKs.
m-peakers'' are star-forming BzK galaxies with luminosities at the top of the luminosity distribution of sBzKs.
The surface density of ``5.8 ![]() m-peakers'' has been found to be 61 deg-2 by Farrah et al. (2006).
This is consistent with 33 sources in the 0.49 deg2 of our field. We may thus estimate that 40-60 similar ``5.8
m-peakers'' has been found to be 61 deg-2 by Farrah et al. (2006).
This is consistent with 33 sources in the 0.49 deg2 of our field. We may thus estimate that 40-60 similar ``5.8 ![]() m-peakers'' per square degree
could be identified in the full SWIRE survey (49 deg2).
Most of them should be
m-peakers'' per square degree
could be identified in the full SWIRE survey (49 deg2).
Most of them should be ![]() starburst ULIRGs. At least half of them may be considered to be SMGs,
including a small fraction of composite obscured AGN/starburst objects.
Another significant fraction may be considered as SFRGs.
starburst ULIRGs. At least half of them may be considered to be SMGs,
including a small fraction of composite obscured AGN/starburst objects.
Another significant fraction may be considered as SFRGs.
These results illustrate the power of deep multi-![]() studies, especially with complete radio data, for analysing populations of powerful high-z
IR and submm sources. Such deep radio data are essential for
disentangling starbursts and infrared-bright AGN, and for easily
providing estimates of their star formation rates. We note especially
the impressive complete detection of relatively weak
studies, especially with complete radio data, for analysing populations of powerful high-z
IR and submm sources. Such deep radio data are essential for
disentangling starbursts and infrared-bright AGN, and for easily
providing estimates of their star formation rates. We note especially
the impressive complete detection of relatively weak ![]() SMGs over 0.5 deg2 in a single pointing of the GMRT at 610 MHz.
As already proved by the analysis of SCUBA sources (e.g., Ivison et al. 2002), radio data are essential for identifying optical/near-IR counterparts and analysing submm surveys.
This will be even more crucial for future surveys at the confusion limits of instruments like Herschel at 300-500
SMGs over 0.5 deg2 in a single pointing of the GMRT at 610 MHz.
As already proved by the analysis of SCUBA sources (e.g., Ivison et al. 2002), radio data are essential for identifying optical/near-IR counterparts and analysing submm surveys.
This will be even more crucial for future surveys at the confusion limits of instruments like Herschel at 300-500 ![]() m and SCUBA2 at 850
m and SCUBA2 at 850 ![]() m.
Even as we wait for EVLA and the new generation of SKA precursors, our
results show that the GMRT at 610 MHz and even 325 MHz can
already currently provide sensitivity well matched to wide Herschel surveys.
m.
Even as we wait for EVLA and the new generation of SKA precursors, our
results show that the GMRT at 610 MHz and even 325 MHz can
already currently provide sensitivity well matched to wide Herschel surveys.
It would be interesting to explore further whether the main properties which characterize this sample, i.e. strong MIR emission, radio activity, and high stellar mass, are related. Some of these properties are likely the result of biases introduced by our selection; however, this is unlikely to be the case for all of them, especially for the radio properties. In particular, a comparison between the starburst morphology (traced by young stars, dust, PAHs or CO emission, as measured by ALMA or JWST) and the radio size would probe whether the radio emission is produced by the starburst or by an AGN, and whether the parameters of the starburst are different from those of most classical SMGs and reveal a different star formation regime.
We have several multi-wavelength observations planned or in progress for this sample to obtain better estimates of redshifts, dust temperatures, star formation rates, PAH luminosities, and AGN contributions, and thus constrain the dominant emission processes, and investigate the evolution and clustering properties of these sources.
AcknowledgementsWe thank Roy Kilgard, Jacqueline Bergeron, Attila Kovács and Helmut Dannerbauer for their helpful contribution. This work includes observations made with IRAM, which is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). Thanks to the staff of IRAM for their support and the anonymous observers of the MAMBO pool for observations presented here. This work is based in part on observations made within the context of SWIRE survey with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. The VLA is operated by NRAO, the National Radio Astronomy Observatory, a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. We thank the staff of the GMRT who have made these observations possible. GMRT is run by the National Centre for Radio Astrophysics of the Tata Institute of Fundamental Research. The optical data come from KPNO (Kitt Peak National Observatory), National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under cooperative agreement with the National Science Foundation. This work includes observations made with WFCAM/UKIRT. The UKIRT is operated by the Joint Astronomy Centre on behalf of the UK's Science and Technology Facilities Council.
References
- Alexander, D. M., Bauer, F. E., Chapman, S. C., et al. 2005, ApJ, 632, 736 [NASA ADS] [CrossRef]
- Archibald, E. N., Dunlop, J. S., Hughes, D. H., et al. 2001, MNRAS, 323, 417 [NASA ADS] [CrossRef]
- Aretxaga, I., Hughes, D. H., Coppin, K., et al. 2007, MNRAS, 379, 1571 [NASA ADS] [CrossRef]
- Beelen, A., Cox, P., Benford, D. J., et al. 2006, ApJ, 642, 694 [NASA ADS] [CrossRef]
- Berta, S., Fritz, J., Franceschini, A., Bressan, A., & Pernechele, C. 2003, A&A, 403, 119 [NASA ADS] [CrossRef] [EDP Sciences]
- Berta, S., Fritz, J., Franceschini, A., Bressan, A., & Lonsdale, C. 2004, A&A, 418, 913 [NASA ADS] [CrossRef] [EDP Sciences]
- Berta, S., Lonsdale, C. J., Polletta, M., et al. 2007a, A&A, 476, 151 [NASA ADS] [CrossRef] [EDP Sciences]
- Berta, S., Lonsdale, C. J., Siana, B., et al. 2007b, A&A, 467, 565 [NASA ADS] [CrossRef] [EDP Sciences]
- Biggs, A. D., & Ivison, R. J. 2008, MNRAS, 385, 893 [NASA ADS] [CrossRef]
- Blain, A. W., Smail, I., Ivison, R. J., Kneib, J.-P., & Frayer, D. T. 2002, Phys. Rep., 369, 111 [NASA ADS] [CrossRef]
- Blain, A. W., Chapman, S. C., Smail, I., & Ivison, R. 2004, ApJ, 611, 52 [NASA ADS] [CrossRef]
- Bolzonella, M., Miralles, J.-M., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS]
- Borys, C., Smail, I., Chapman, S. C., et al. 2005, ApJ, 635, 853 [NASA ADS] [CrossRef]
- Casey, C. M., Impey, C. D., Trump, J. R., et al. 2008, ApJS, 177, 131 [NASA ADS] [CrossRef]
- Casey, C. M., Chapman, S. C., Beswick, R. J., et al. 2009, MNRAS, 1097
- Chapman, S. C., Smail, I., Windhorst, R., Muxlow, T., & Ivison, R. J. 2004, ApJ, 611, 732 [NASA ADS] [CrossRef]
- Chapman, S. C., Blain, A. W., Smail, I., & Ivison, R. J. 2005, ApJ, 622, 772 [NASA ADS] [CrossRef]
- Chapman, S. C., Neri, R., Bertoldi, F., et al. 2008, ApJ, 689, 889 [NASA ADS] [CrossRef]
- Ciliegi, P., Vignali, C., Comastri, A., et al. 2003, MNRAS, 342, 575 [NASA ADS] [CrossRef]
- Condon, J. J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef]
- Coppin, K., Chapin, E. L., Mortier, A. M. J., et al. 2006, MNRAS, 372, 1621 [NASA ADS] [CrossRef]
- Crawford, T., Marr, J., Partridge, B., & Strauss, M. A. 1996, ApJ, 460, 225 [NASA ADS] [CrossRef]
- Daddi, E., Cimatti, A., Renzini, A., et al. 2004, ApJ, 617, 746 [NASA ADS] [CrossRef]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef]
- Daddi, E., Dannerbauer, H., Elbaz, D., et al. 2008, ApJ, 673, L21 [NASA ADS] [CrossRef]
- De Breuck, C., van Breugel, W., Röttgering, H. J. A., & Miley, G. 2000, A&AS, 143, 303 [NASA ADS] [CrossRef] [EDP Sciences]
- De Breuck, C., van Breugel, W., Röttgering, H., et al. 2001, AJ, 121, 1241 [NASA ADS] [CrossRef]
- Desai, V., Armus, L., Spoon, H. W. W., et al. 2007, ApJ, 669, 810 [NASA ADS] [CrossRef]
- Dey, A., Soifer, B. T., Desai, V., et al. 2008, ApJ, 677, 943 [NASA ADS] [CrossRef]
- Dey, A., & The Ndwfs/MIPS Collaboration 2009, ed. W. Wang, Z. Yang, Z. Luo, & Z. Chen, ASP Conf. Ser., 408, 411
- Downes, A. J. B., Peacock, J. A., Savage, A., & Carrie, D. R. 1986, MNRAS, 218, 31 [NASA ADS]
- Dye, S., Eales, S. A., Aretxaga, I., et al. 2008, MNRAS, 386, 1107 [NASA ADS] [CrossRef]
- Farrah, D., Lonsdale, C. J., Borys, C., et al. 2006, ApJ, 641, L17 [NASA ADS] [CrossRef]
- Farrah, D., Lonsdale, C. J., Weedman, D. W., et al. 2008, ApJ, 677, 957 [NASA ADS] [CrossRef]
- Farrah, D., Connolly, B., Connolly, N., et al. 2009, ApJ, 700, 395 [NASA ADS] [CrossRef]
- Frayer, D. T., Chapman, S. C., Yan, L., et al. 2004, ApJS, 154, 137 [NASA ADS] [CrossRef]
- Greve, T. R., Ivison, R. J., Bertoldi, F., et al. 2004, MNRAS, 354, 779 [NASA ADS] [CrossRef]
- Hainline, L. J., Blain, A. W., Smail, I., et al. 2009, ApJ, 699, 1610 [NASA ADS] [CrossRef]
- Hambly, N. C., Collins, R. S., Cross, N. J. G., et al. 2008, MNRAS, 384, 637 [NASA ADS] [CrossRef]
- Helou, G., Soifer, B. T., & Rowan-Robinson, M. 1985, ApJ, 298, L7 [NASA ADS] [CrossRef]
- Henry, D. M., Atad-Ettedgui, E., Casali, M. M., et al. 2000, in SPIE Conf. Ser., ed. M. Iye, & A. F. Moorwood, 4008, 1325
- Holland, W. S., Robson, E. I., Gear, W. K., et al. 1999, MNRAS, 303, 659 [NASA ADS] [CrossRef]
- Houck, J. R., Soifer, B. T., Weedman, D., et al. 2005, ApJ, 622, L105 [NASA ADS] [CrossRef]
- Huang, J., Faber, S. M., Daddi, E., et al. 2009, ApJ, 700, 183 [NASA ADS] [CrossRef]
- Huynh, M. T., Pope, A., Frayer, D. T., & Scott, D. 2007, ApJ, 659, 305 [NASA ADS] [CrossRef]
- Ibar, E., Cirasuolo, M., Ivison, R., et al. 2008, MNRAS, 386, 953 [NASA ADS] [CrossRef]
- Ivison, R. J., Greve, T. R., Smail, I., et al. 2002, MNRAS, 337, 1 [NASA ADS] [CrossRef]
- Ivison, R. J., Greve, T. R., Dunlop, J. S., et al. 2007, MNRAS, 380, 199 [NASA ADS] [CrossRef]
- Jiang, L., Fan, X., Ivezic, Z., et al. 2007, ApJ, 656, 680 [NASA ADS] [CrossRef]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [NASA ADS] [CrossRef]
- Kovács, A., Chapman, S. C., Dowell, C. D., et al. 2006, ApJ, 650, 592 [NASA ADS] [CrossRef]
- Kreysa, E., Gemuend, H.-P., Gromke, J., et al. 1998, in Advanced Technology MMW, Radio, and Terahertz Telescopes, Presented at the SPIE Conf. Ser., ed. T. G. Phillips, Proc. SPIE, 3357, 319
- Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef]
- Le Floc'h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [NASA ADS] [CrossRef]
- Lonsdale, C. J., Smith, H. E., Rowan-Robinson, M., et al. 2003, PASP, 115, 897 [NASA ADS] [CrossRef]
- Lonsdale, C. J., Omont, A., Polletta, M. D. C., et al. 2006, BAAS, 38, 1171 [NASA ADS]
- Lonsdale, C. J., Polletta, M. D. C., Omont, A., et al. 2009, ApJ, 692, 422 [NASA ADS] [CrossRef] [Lo09]
- Lutz, D., Yan, L., Armus, L., et al. 2005, ApJ, 632, L13 [NASA ADS] [CrossRef]
- Magliocchetti, M., Silva, L., Lapi, A., et al. 2007, MNRAS, 375, 1121 [NASA ADS] [CrossRef]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef]
- Muller, G. P., Reed, R., Armandroff, T., Boroson, T. A., & Jacoby, G. H. 1998, in SPIE Conf. Ser., 3355, 577
- Murphy, E. J., Chary, R.-R., Alexander, D. M., et al. 2009, ApJ, 698, 1380 [NASA ADS] [CrossRef]
- Murphy, Jr., T. W., Soifer, B. T., Matthews, K., & Armus, L. 2001, ApJ, 559, 201 [NASA ADS] [CrossRef]
- Muxlow, T. W. B., Richards, A. M. S., Garrington, S. T., et al. 2005, MNRAS, 358, 1159 [NASA ADS] [CrossRef]
- Noeske, K. G., Faber, S. M., Weiner, B. J., et al. 2007, ApJ, 660, L47 [NASA ADS] [CrossRef]
- Owen, F. N., & Morrison, G. E. 2008, AJ, 136, 1889 [NASA ADS] [CrossRef]
- Owen, F. N., Morrison, G. E., Klimek, M. D., & Greisen, E. W. 2009, AJ, 137
- Polletta, M., Courvoisier, T. J.-L., Hooper, E. J., & Wilkes, B. J. 2000, A&A, 362, 75 [NASA ADS]
- Polletta, M., Wilkes, B. J., Siana, B., et al. 2006, ApJ, 642, 673 [NASA ADS] [CrossRef]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef]
- Pope, A., Borys, C., Scott, D., et al. 2005, MNRAS, 358, 149 [NASA ADS] [CrossRef]
- Pope, A., Scott, D., Dickinson, M., et al. 2006, MNRAS, 370, 1185 [NASA ADS] [CrossRef]
- Pope, A., Bussmann, R. S., Dey, A., et al. 2008a, ApJ, 689, 127 [NASA ADS] [CrossRef]
- Pope, A., Chary, R.-R., Alexander, D. M., et al. 2008b, ApJ, 675, 1171 [NASA ADS] [CrossRef]
- Reuland, M., Röttgering, H., van Breugel, W., & De Breuck, C. 2004, MNRAS, 353, 377 [NASA ADS] [CrossRef]
- Richards, A. M. S., Muxlow, T. W. B., Beswick, R., et al. 2007, A&A, 472, 805 [NASA ADS] [CrossRef] [EDP Sciences]
- Rieke, G. H., Alonso-Herrero, A., Weiner, B. J., et al. 2009, ApJ, 692, 556 [NASA ADS] [CrossRef]
- Rigopoulou, D., Spoon, H. W. W., Genzel, R., et al. 1999, AJ, 118, 2625 [NASA ADS] [CrossRef]
- Rowan-Robinson, M., Babbedge, T., Oliver, S., et al. 2008, MNRAS, 386, 697 [NASA ADS] [CrossRef]
- Sajina, A., Yan, L., Armus, L., et al. 2007, ApJ, 664, 713 [NASA ADS] [CrossRef]
- Sajina, A., Yan, L., Lutz, D., et al. 2008, ApJ, 683, 659 [NASA ADS] [CrossRef]
- Salpeter, E. E. 1955, ApJ, 121, 161 [NASA ADS] [CrossRef]
- Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef]
- Seymour, N., Stern, D., De Breuck, C., et al. 2007, ApJS, 171, 353 [NASA ADS] [CrossRef]
- Seymour, N., Dwelly, T., Moss, D., et al. 2008, MNRAS, 386, 1695 [NASA ADS] [CrossRef]
- Siana, B., Teplitz, H. I., Chary, R.-R., Colbert, J., & Frayer, D. T. 2008, ApJ, 689, 59 [NASA ADS] [CrossRef]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences]
- Smail, I., Ivison, R. J., Blain, A. W., & Kneib, J.-P. 2002, MNRAS, 331, 495 [NASA ADS] [CrossRef]
- Solomon, P. M., & Vanden Bout, P. A. 2005, ARA&A, 43, 677 [NASA ADS] [CrossRef]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef]
- Surace, J. A., Shupe, D. L., Fang, F., et al. 2005, Data Delivery Document (Spitzer Science Center, California Institute of Technology, Pasadena, CA)
- Veilleux, S., Rupke, D. S. N., Kim, D.-C., et al. 2009, ApJS, 182, 628 [NASA ADS] [CrossRef]
- Warren, S. J., Hambly, N. C., Dye, S., et al. 2007, MNRAS, 375, 213 [NASA ADS] [CrossRef]
- Weedman, D., Polletta, M., Lonsdale, C. J., et al. 2006, ApJ, 653, 101 [NASA ADS] [CrossRef]
- Wilson, J. C., Eikenberry, S. S., Henderson, C. P., et al. 2003, in SPIE Conf. Ser., ed. M. Iye, & A. F. M. Moorwood, 4841, 451
- Yan, L., Chary, R., Armus, L., et al. 2005, ApJ, 628, 604 [NASA ADS] [CrossRef]
- Yan, L., Sajina, A., Fadda, D., et al. 2007, ApJ, 658, 778 [NASA ADS] [CrossRef]
- Younger, J. D., Omont, A., Fiolet, N., et al. 2009, MNRAS, 394, 1685 [NASA ADS] [CrossRef]
- Yun, M. S., & Carilli, C. L. 2002, ApJ, 568, 88 [NASA ADS] [CrossRef]
- Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803 [NASA ADS] [CrossRef]
Online Material
Appendix A: SED fits and photometric redshifts
The optical (Ugriz), NIR (JHK), and MIR (3.6-24 ![]() m) SEDs of each
source have been fitted with a library of 18 star-forming galaxy
templates (Polletta et al. 2007) using the H YPER-Z
code (Bolzonella et al. 2000) and the same procedure described
in Lonsdale et al. (2009). In Fig. A.1, we show the optical-IR SED and the best-fit template and
corresponding photometric redshift of each source. In seven cases we also
report a secondary solution corresponding to a second minimum in the
m) SEDs of each
source have been fitted with a library of 18 star-forming galaxy
templates (Polletta et al. 2007) using the H YPER-Z
code (Bolzonella et al. 2000) and the same procedure described
in Lonsdale et al. (2009). In Fig. A.1, we show the optical-IR SED and the best-fit template and
corresponding photometric redshift of each source. In seven cases we also
report a secondary solution corresponding to a second minimum in the ![]() distribution if associated with a different template than the
primary solution. In case a spectroscopic redshift is available
(source L-25), the best-fit template at the spectroscopic redshift
is also reported.
distribution if associated with a different template than the
primary solution. In case a spectroscopic redshift is available
(source L-25), the best-fit template at the spectroscopic redshift
is also reported.
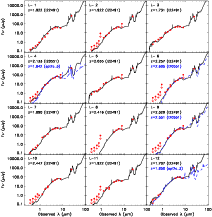
|
Figure A.1:
Optical-IR SEDs of our sources. The
solid curves represent the best-fit template of the optical-MIR data (up to
24 |
| Open with DEXTER | |
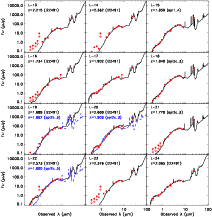
|
Figure A.1: continued. |
| Open with DEXTER | |
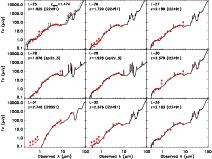
|
Figure A.1: continued. |
| Open with DEXTER | |
Footnotes
- ...z
 2
2![[*]](/icons/foot_motif.png)
- Color figures and the Appendix A are only available in the electronic form via http://www.aanda.org
- ...
package
![[*]](/icons/foot_motif.png)
- Documentation by Zylka is available at http://www.iram.es/IRAMES/mainWiki/CookbookMopsic
- ... CA)
![[*]](/icons/foot_motif.png)
- http://swire.irac.caltech.edu/swire/astronomers/publications/SWIRE2_doc_083105.pdf
All Tables
Table 1: Optical, Near-IR and Spitzer mid-IR data of the selected sample.
Table 2:
Related Spitzer-selected ![]() ULIRGs samples.
ULIRGs samples.
Table 3: Derived values from the stacked flux densitiesa.
Table 4: 1.2 mm and radio data.
Table 5: Luminosities and star formation rates.
Table 6: Results from the co-added MIPS images.
All Figures

|
Figure 1:
Positions of the 33 sources of our sample (
|
| Open with DEXTER | |
| In the text | |

|
Figure 2: Histogram of redshifts for our sample (photometric, thick solid red line), the full sample from Lo09 (photometric and spectroscopic, dotted black line), and the sample from Younger et al. (2009) (spectroscopic, long-short-dashed blue line). |
| Open with DEXTER | |
| In the text | |

|
Figure 3:
Observed MAMBO 1.2 mm flux density as a function of 24 |
| Open with DEXTER | |
| In the text | |

|
Figure 4: Observed MAMBO
1.2 mm flux density as a function of 20 cm flux density. The
large black symbols show different stacked values: the entire sample
(filled triangle), all sources with > |
| Open with DEXTER | |
| In the text | |

|
Figure 5:
The radio-FIR q
factor (FIR-to-radio ratio) (Eq. (4)). The large black symbols
show the stacked values of different samples: the entire sample
(33 sources, filled circle), the 13 sources with S/N > 3 at 1.2 mm (filled square), and the 20 sources with S/N < 3 (open square).
The solid black line shows the typical value q = 2.34 for local starbursts. The dotted black lines are the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12742f6.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2009/46/aa12742-09/Timg142.png)
|
Figure 6:
(Adapted from Fig. 14 of Daddi et al. 2007). Star formation rate vs. stellar mass. Values of SFR deduced from radio data for the
sources of our sample are represented by the red triangles (see Sects. 4.4, 4.6 and Table 5). The arrows are 2 |
| Open with DEXTER | |
| In the text | |

|
Figure 7:
IRAC color-color diagram for several samples. The sample of Huang et al. (2009) and Younger et al. (2009) is represented by the solid blue triangles. The red circles show our sample.
The open green stars are the sample of Lonsdale et al. (2009). The arrows are 3 |
| Open with DEXTER | |
| In the text | |

|
Figure 8:
Observed flux density ratio,
|
| Open with DEXTER | |
| In the text | |

|
Figure 9:
Median optical through radio SED of all 33 ``5.8 |
| Open with DEXTER | |
| In the text | |

|
Figure 10:
BzK color-color plot for our sample. B magnitude is extrapolated from u
and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12742f11.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12742-09/Timg168.png)
|
Figure 11:
(Adapted from Fig. 7 of Daddi et al. 2007). Luminosity at 1.4 GHz rest frame vs. luminosity at 8 |
| Open with DEXTER | |
| In the text | |

|
Figure 12: 1.4 GHz luminosity as function of redshift. Same symbols as Figs. 3 and 10. The solid black line shows the radio loudness limit for 1.4 GHz luminosity (Sajina et al. 2007). |
| Open with DEXTER | |
| In the text | |

|
Figure A.1:
Optical-IR SEDs of our sources. The
solid curves represent the best-fit template of the optical-MIR data (up to
24 |
| Open with DEXTER | |
| In the text | |

|
Figure A.1: continued. |
| Open with DEXTER | |
| In the text | |

|
Figure A.1: continued. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.