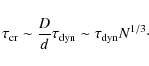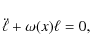| Issue |
A&A
Volume 505, Number 2, October II 2009
|
|
|---|---|---|
| Page(s) | 625 - 627 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200912218 | |
| Published online | 03 September 2009 | |
Collective relaxation of stellar systems revisited
(Research Note)
V. G. Gurzadyan1 - A. A. Kocharyan1,2
1 - Yerevan Physics Institute and Yerevan State University, Yerevan,
Armenia
2 - School of Mathematical Sciences, Monash University, Clayton, Australia
Received 27 March 2009 / Accepted 30 July 2009
Abstract
The chaos in stellar systems is studied using the
theory of dynamical systems and the Van Kampen stochastic differential equation approach. The exponential instability (chaos) of spherical N-body gravitating systems, already known previously, is confirmed. The characteristic timescale of that instability is estimated confirming the collective relaxation time obtained by means of the Maupertuis principle.
Key words: Galaxy: kinematics and dynamics
1 Introduction
Stellar dynamics, a well established discipline, continues to be an active field of research due to its complex dynamics. Newly developed sophisticated tools on nonlinear dynamics or ever increasing numerical capacities are readily applied to N-body gravitating systems.
The problem of relaxation of gravitating systems is among the key ones in stellar dynamics since it can be directly constrained by observations, especially, of well-relaxed globular clusters and elliptical galaxies.
Historically, plasma methods were among the first to be applied to gravitating systems (Chandrasekhar 1942), neglecting, however, a drastic difference between plasma and long-range gravity. In retrospect, it can seem strange how easily were ignored the challenges in theory and observations, and later also in numerical simulations: (a) the Coulomb logarithmic cut-off and hence the canceling of the N-body effects was applied at the absence of Debye screening; (b) the result contradicted observations, i.e. the plasma two-body relaxation timescale exceeds the age of elliptical galaxies by several orders of magnitude; (c) the two-body timescale could never be identified in numerical studies.
Then comes the epoch of realization of importance of chaos, occasionally in unexpected forms, for nonlinear systems. Chaos caused by small perturbations appears crucial even to nearly integrable problems, such as the dynamics of planetary system, (see Laskar & Robutel 1993; Morbidelli 2002 and references therein); for non-integrable N-body systems the situation is far more complex. The Fermi-Pasta-Ulam problem is another example of apparently simple, but still not well understood system (Fermi et al. 1955).
Do chaos, chance and randomness have significant role also in the evolution of stellar systems, or the two-body plasma approach is the whole story? Although it has been generally agreed that chaos must affect N-body dynamics (see Gurzadyan & Pfenniger 1994; Contopoulos 2002; Regev 2008), proper treatments require well-founded approaches![]() . Application of ergodic theory methods enabled us to prove a notable result: the spherical systems are exponentially unstable and that chaoticity drives their dynamics (Gurzadyan & Savvidy 1984, 1986). An exponential law defines an intrinsic timescale, the collective relaxation time, which for real stellar systems has a value intermediate between the dynamical (crossing) and the two-body timescales. This was obtained by estimating the divergence of the trajectories of the system in a Riemannian space defined by the potential of the interaction (Maupertuis principle), i.e. by a method known in theory of dynamical systems (Arnold 1989).
Importantly, the derived collective (N-body) relaxation timescale fits the observational data (Vesperini 1992). The three timescales, i.e., the dynamical
. Application of ergodic theory methods enabled us to prove a notable result: the spherical systems are exponentially unstable and that chaoticity drives their dynamics (Gurzadyan & Savvidy 1984, 1986). An exponential law defines an intrinsic timescale, the collective relaxation time, which for real stellar systems has a value intermediate between the dynamical (crossing) and the two-body timescales. This was obtained by estimating the divergence of the trajectories of the system in a Riemannian space defined by the potential of the interaction (Maupertuis principle), i.e. by a method known in theory of dynamical systems (Arnold 1989).
Importantly, the derived collective (N-body) relaxation timescale fits the observational data (Vesperini 1992). The three timescales, i.e., the dynamical
![]() ,
collective
,
collective
![]() ,
and two-body
,
and two-body
![]() timescales, correspond to the 3 distance scales of the system, specifically, its size D, mean inter-particle distance d, and radius of gravitational influence of particles
timescales, correspond to the 3 distance scales of the system, specifically, its size D, mean inter-particle distance d, and radius of gravitational influence of particles ![]() ,
in particular (Gurzadyan & Savvidy 1984, 1986) (see also Lang 1999),
,
in particular (Gurzadyan & Savvidy 1984, 1986) (see also Lang 1999),
When the role of complex N-body dynamics was finally recognized, another confusion did appear, namely, in assigning of the dynamical time as the relaxation timescale, i.e., for reaching fine-grained equilibrium. However, this again contradicts observations: globular clusters would then have already disappeared because of the evaporation of stars (Ambartsumian 1938) within 100 crossing times, i.e., within around 100 mln years
Numerical studies possess their own difficulties, starting from the choice of descriptors up to the interpretation of the results, e.g., as shown in Gurzadyan & Kocharyan (1994),
the computer image of the Lyapunov exponents is non-equivalent to their definition.
So, the importance of further searches of strict methods to study the chaos in stellar systems is doubtless. We revisit the problem of both N-body relaxation and its time scale using both geometric (Kocharyan 1993) and Van Kampen stochastic differential equation approaches (Van Kampen 1976). The results confirm those of the Maupertuis principle for the collective relaxation timescale of collisionless spherical systems![]() .
.
2 Stochastic instability
We consider an N-body system described by the Lagrangian
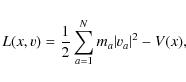 |
(2) |
where
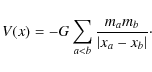 |
(3) |
Hereafter we use units G = 1 and ma =1, and
are the coordinates and velocities of stars, respectively,
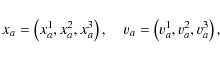
where
According to the theory of dynamical systems, the statistical properties of the systems can be studied from the behaviour of close trajectories (Arnold 1989). It is shown (Kocharyan 1993), that the evolution of the distance between two nearby trajectories, denoted by ![]() ,
is described by a generalized Jacobi equation, which can be written in the form
,
is described by a generalized Jacobi equation, which can be written in the form
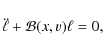 |
(4) |
where
![\begin{eqnarray*}\mathcal{B}({x},{v})&=&-\frac{1}{3N-1}\left[\Delta V({x})
+\fra...
...limits_{a=1}^NF_a({x})\cdot\v_a\right)^2}{4(E-V({x}))^2}\right],
\end{eqnarray*}](/articles/aa/full_html/2009/38/aa12218-09/img13.png)
E is the total energy of the system
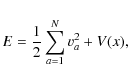 |
(5) |
and
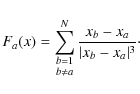 |
(6) |
As in Gurzadyan & Savvidy (1984, 1986), we assume that the system is collisionless
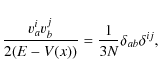 |
(7) |
to obtain
where
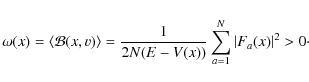 |
(9) |
One observes that E-V(x) is the total kinetic energy of the system
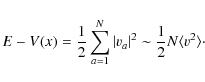 |
(10) |
Thus,
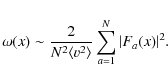 |
(11) |
For spherically symmetric systems, we can replace |Fa(x)|2 with |F(x)|2 (see Chandrasekhar 1942; Cohen 1975), where
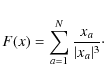 |
(12) |
We then replace
| (13) |
approaches the normal distribution
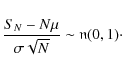 |
(14) |
In our case, we have X=|F(x)|2,
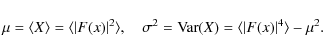 |
(15) |
Thus,
| (16) |
where
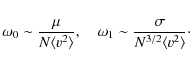 |
(17) |
We investigate Eq. (8) by means of a technique developed by Van Kampen (cf. Van Kampen 1976; Casetti et al. 2000). One can derive the second moments of
where (Casetti et al. 2000)
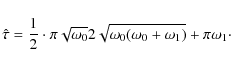 |
(19) |
The system given by Eq. (18) has a positive Lyapunov exponent
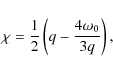 |
(20) |
where
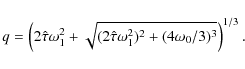 |
(21) |
We now estimate
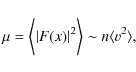 |
(22) |
where n is the mean concentration of stars in the system, then
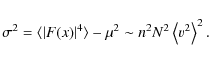 |
(23) |
Therefore,
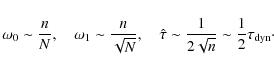 |
(24) |
And finally we derive the relaxation time
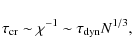 |
(25) |
confirming the result of Eq. (1) derived in (Gurzadyan & Savvidy 1984, 1986).
3 Conclusion
The stochastic equation approach used above complements the probabilistic approach of Chandrasekhar & von Neumann (1943). Both are supported by the fact of decay of the time correlation function due to the exponential instability
and the Holtsmark distribution of the fluctuating force![]() .
.
Thus, the stochastic equation method confirms the purely geometric derivation of the collective relaxation time given by Eq. (1). Although that formula is also supported also by alternative numerical analyses (Antoni et al. 1999), the present derivation avoids any approximations in numerical simulations.
Chaotic effects could be useful in constraining observationally modified gravity theories in the Solar system and galaxies (see Capozziello & Tsujikawa 2008).
References
- Ambartsumian, V. A. 1938, Commun. Leningrad Univ., 22, 19 (In the text)
- Antoni, M., Ruffo, S., & Torcini, A. 1999, in The Chaotic Universe, 467 (World Scientific) cond-mat/9908336 (In the text)
- Arnold, V. I. 1989, Mathematical Methods of Classical Mechanics (Springer-Verlag) (In the text)
- Capozziello, S., & Tsujikawa, S. 2008, Phys. Rev. D, 77, 107501 [NASA ADS] [CrossRef] (In the text)
- Casetti, L., Pettini, M., & Cohen, E. G. D. 2000, Phys. Rep., 337, 237 [NASA ADS] [CrossRef] (In the text)
- Chandrasekhar, S. 1942, Principles of Stellar Dynamics (Chicago Univ. Press) (In the text)
- Chandrasekhar, S. 1943, Rev. Mod. Phys., 15, 1 [NASA ADS] [CrossRef] (In the text)
- Chandrasekhar, S., & von Neumann, J. 1943, ApJ, 97, 1 [NASA ADS] [CrossRef]
- Cohen, L. 1975, in Dynamics of Stellar Systems, Proc. dd. A. Hayli, 33 (Reidel-Dordrecht), IAU Symp. 69 (In the text)
- Contopoulos G. 2002, Order in Chaos in Dynamical Astronomy (Springer-Verlag)
- El-Zant, A. 1997, A&A, 326, 113 [NASA ADS]
- Fermi, E., Pasta, J., & Ulam, S. M. 1955, LA-1940, in Fermi, E., Collected Papers, II, 978, Acad. Lincei and Univ. (Chicago Press), 1965 (In the text)
- Gurzadyan, V. G., & Kocharyan, A. A. 1988, A&A, 205, 93 [NASA ADS]
- Gurzadyan, V. G., & Kocharyan, A. A. 1994, J. Phys. A, 27, 2879 [NASA ADS] [CrossRef]
- Gurzadyan, V. G., & Pfenniger, D. 1994, Ergodic Concepts in Stellar Dynamics (Springer-Verlag) (In the text)
- Gurzadyan, V. G., Savvidy, G. K. 1984, Doklady AN SSSR, 277, 69 [NASA ADS] (In the text)
- Gurzadyan, V. G., Savvidy, G. K. 1986, A&A, 160, 203 [NASA ADS]
- Kocharyan, A. A. 1993, in Proc. Fourth Monash General Relativity Workshop, ed. A. Lun, L. Brewin, E. Chow, p. 38 [arXiv:astro-ph/0411595] (In the text)
- Lang, K. 1999, Astrophysical Formulae, II, 94 (Springer-Verlag) (In the text)
- Laskar, J., & Robutel, P. 1993, Nature, 361, 608 [NASA ADS] [CrossRef] (In the text)
- Lynden-Bell, D. 1967, MNRAS, 136, 101 [NASA ADS] (In the text)
- Miller, R.H. 1964, ApJ, 140, 250 [NASA ADS] [CrossRef]
- Morbidelli, A. 2002, Modern Celestial Mechanics: Aspects of Solar System Dynamics (Taylor & Francis) (In the text)
- Regev, O. 2008, in Encyclopedia of Complexity and System Science (Springer-Verlag) (In the text)
- Ruelle, D. 1993, Chance and Chaos (Princeton Univ. Press)
- Van Kampen, N. G. 1976, Phys. Rep., 24, 171 [NASA ADS] [CrossRef] (In the text)
- Vesperini E. 1992, A&A, 266, 215 [NASA ADS] (In the text)
Footnotes
- ... approaches
![[*]](/icons/foot_motif.png)
- Ruelle mentions the appearance of numerous incorrect papers about chaos when chaos became a fashion (Ruelle 1993).
- ... years
![[*]](/icons/foot_motif.png)
- One of the motivations for concluding that the dynamical time equals the relaxation time were the numerical experiments on the apparent divergence in real space first observed in (Miller 1964) for systems of between N = 8 and 32 particles, for which obviously no relaxation process has any sense. Properly performed numerical experiments (El-Zant 1997) confirmed the timescale obtained in (Gurzadyan & Savvidy 1984, 1986) via Maupertuis principle.
- ... systems
![[*]](/icons/foot_motif.png)
- For a study of systems with rotational momentum (spiral galaxies) with quite different dynamics, see e.g., (Gurzadyan & Kocharyan 1988).
- ... collisionless
![[*]](/icons/foot_motif.png)
- By collisionless systems, we understand, as usual, systems in which the direct impact of two stars have no role in their dynamics, and not the neglect of gravitational encounters (scattering) of two stars. In this sense, collisionless are even the dense cores of star clusters and galaxies.
- ... force
![[*]](/icons/foot_motif.png)
- At distances of the order of the radius of gravitational influence
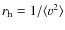 the Holtsmark distribution diverges and should be cut off, as done in (Chandrasekhar 1943; Gurzadyan & Savvidy 1984, 1986). For real stellar systems however, this cutoff is insensitive to the precise value of
the Holtsmark distribution diverges and should be cut off, as done in (Chandrasekhar 1943; Gurzadyan & Savvidy 1984, 1986). For real stellar systems however, this cutoff is insensitive to the precise value of 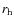 ,
since for them
,
since for them 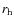 is far smaller than the mean interstellar distance d and hence the Holtsmark law vanishes far earlier.
is far smaller than the mean interstellar distance d and hence the Holtsmark law vanishes far earlier.
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.