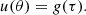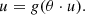| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 7 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202348933 | |
| Published online | 28 May 2024 | |
Evolution of a stellar system in the context of the virial equation
Crimean Astrophysical Observatory, Nauchny 298409, Crimea
e-mail: valery@terebizh.ru
Received:
13
December
2023
Accepted:
26
February
2024
The virial equation is used to clarify the nature of the dynamic evolution of a stellar system. The methods used are based on analytical and numerical modeling of evolution, as well as on an approach long used in the nonlinear theory of oscillations. It is shown that the mean harmonic radius of a system with negative total energy never exceeds two times the equilibrium value. The time to reach the virial equlibrium state Tv is about two to three dozen dynamic time periods Td. For systems not in close proximity to virial equilibrium, the virial ratio, the mean harmonic radius, and the root mean square radius of the system fluctuate during Tv; then the virial ratio and mean harmonic radius stabilize near their equilibrium values, while the root mean square radius continues to increase (possibly ad infinitum). Thus, the moment of inertia of the system relative to the center of gravity and its potential energy have significantly different behavior, which leads to the formation of a relatively small quasi-equilibrium core and an extended halo.
Key words: galaxies: kinematics and dynamics
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Theoretical considerations, reinforced in recent years by extensive numerical simulations, show that the dynamical evolution of a stellar system in its own gravitational field is characterized by three basic timescales.
The shortest of them, the dynamic time Td ∼ (Gρ)−1/2, where G is the gravitational constant and ρ is the mass-average density of the system, is associated with large-scale motions of matter in the early stages of system evolution. This parameter is also called the crossing time, as the return time of a body that has fallen from the surface of a homogeneous ball of density ρ into a hole passing along its diameter is equal to (3π/Gρ)1/2.
According to Jeans (1915, 1919), the subsequent relaxation of the system to a quasi-stationary state in the smoothed, so-called regular gravitational field (see Hénon 1982; Binney & Tremaine 2008) is described by the collisionless Boltzmann equation for the distribution function f(r, v, t) in six-dimensional phase space,
supplemented by the Poisson equation for the conjoint potential Φ(r, t). The definition of a quasi-stationary state is often associated with the virial equation, which is valid for any set of N gravitating points in the center of mass coordinate system:
where
respectively, are the moment of inertia of the system and its kinetic and potential energies, whereas mi, ri(t), and vi(t) are the mass, radius-vector, and the speed of the i-th star1. The total mass of the star system M = ∑mi and its total energy E are assumed to be given. If the motions occur in a limited region of space, then averaging Eq. (2) over time, we obtain the equality 2⟨K⟩+⟨W⟩ = 0, called the virial theorem (Landau & Lifshitz 1976). It seems reasonable to distinguish between the terms virial equation and virial theorem, since the former is strictly true at any stage of the evolution of a gravitating system, while the latter is only approximately valid under certain conditions.
Star clusters are not closed in space, but observations show that, over time, a state close to a quasi-stationary one is reached, for which the virial theorem is approximately satisfied. By marking the parameters of such a system with asterisks, we can accept
Within the framework of the approach discussed here, we should understand the quasi-stationary state as the virial equilibrium state (VES). The characteristic time interval for reaching VES is denoted as Tv. Some models for subsequent restructuring of the system have been described by Binney & Tremaine (2008, Chapt. 8) and further explored by Levin et al. (2008) and Benetti et al. (2014).
Finally, the third stage, the relaxation of the system’s core towards the Maxwell-Boltzmann state, takes even more time Tr. For half a century it was believed that this process is due solely to the irregular gravitational field of the system, which is defined as the difference between the real and smoothed fields (Ambartsumian 1938; Chandrasekhar 1942; Spitzer 1987). Since the spatial density of stars in galaxies is low, the main contribution to the process is made by pair collisions (close passages) of stars; it is taken into account by the non-zero collisional term on the right-hand side of Eq. (1). An explicit representation of this term for systems with Coulomb or gravitational interaction was given by Landau (1937). Research in recent decades has associated relaxation to a more efficient process of dynamic chaos (Gurzadyan & Savvidy 1984, 1986); the corresponding relaxation time Tr ≃ N1/3Td (according to Rastorguev & Sementsov 2006, the exponent is 1/5). Thermodynamic equilibrium is never reached already due to the long-range nature of the gravitational force (Lynden-Bell 1967; Levin et al. 2008, 2014; Benetti et al. 2014); in addition, the openness of the system manifests itself in its external parts.
With regard to the evolution at the second of the stages mentioned above, the nature of the observed fast ‘Maxwellization’ of star systems in a regular field remained unclear for a long time. The revival of research in this direction was initiated by Hénon (1964) and Lynden-Bell (1967); the latter proposed an appropriate stochastic mechanism, as he called it, violent relaxation. In the current understanding, this implies the importance of collective processes in systems with long-range interaction (Shu 1978; Levin et al. 2008, 2014; Gurzadyan & Kocharyan 2009; Giachetti & Casetti 2019). On the other hand, numerical simulations, starting with van Albada (1982) studies and up to Halle et al. (2019) and Sylos Labini & Capuzzo-Dolcetta (2020) recent calculations, gradually clarify the commensurate role of radial instabilities and initial density fluctuations that lead to the formation of local substructures of increasing size. Unlike Td and Tr, no explicit representation of Tv in terms of the integral parameters of the system has been found so far, especially since it depends on the initial state. Quantification is hindered by the extreme complexity of combining the kinetic and Poisson equations.
In this connection, the virial equation merits more attention. It should be taken to a deeper level of description compared to the kinetic equation in one its form or another because the latter is inevitably formulated with finite accuracy, while the virial equation is due only to the fundamental fact that the potential energy in the gravitational interaction of a pair of point-like bodies is inversely proportional to the distance between them; in other words, it is a homogeneous function coordinates of degree −1. Among other things, the virial equation is valid for any, small or large, number of interacting points, while the accuracy of Eq. (1) drops as N decreases. For N ≫ 1, the collisionless Boltzmann equation is consistent with the virial equation in the sense that Eq. (2), in its continuous version, can be derived from Eq. (1).
Since the total energy of an isolated system E = K(t)+W(t) is conserved in time, Eq. (2) is usually written as
For a gravitationally bound system, a necessary (but insufficient) stability condition is E < 0 (Chandrasekhar 1942, Sect. 5.1); here, we assume that this condition is satisfied. This picture of evolution is illustrated in Fig. 1 (see also Fig. 6.1 in Ciotti 2021). Equation (5) includes two unknown functions of time, and therefore, by itself, does not allow complete description of even the integral properties of the system. However, we can anticipate that it shall provide some information about the character of evolution and the corresponding time intervals. Lynden-Bell (1967) and Chandrasekhar & Elbert (1972) looked at this equation from a dynamical point of view under simple assumptions (see Sect. 3 below). The purpose of this investigation is to clarify the character of evolution under more general conditions.
 |
Fig. 1. Representation of the dynamic evolution of a system on a diagram connecting kinetic, K, and potential energy, W. Evolution occurs along the straight line K(t)+W(t) = E, approaching on average a virial equilibrium state (VES). The thin lines correspond to fixed values of the virial ratio V given by Eq. (6). The letters C and H denote cold and hot configurations, which are characterized by the values K < |E| and K > |E|, respectively. |
2. Signs of different behavior of two characteristic radii of the system
Usually, the degree of proximity to the state of virial equilibrium is given by the value of the virial ratio
In view of Eq. (4), the values of the kinetic and potential energies in VES are:
so the equilibrium virial ratio V* = 1. As the timescale in VES, we take T* ≡ ℜ*/v* – the time of intersection of the mean harmonic radius ℜ* of the system with the characteristic velocity v*. The values of the last two follow from Eq. (7) and the definitions
In this way we get:
The literature uses similar definitions with minor differences in numerical coefficients; the values adopted here are convenient for the following discussion. Notice that all these parameters are determined by the values of M and E. We can write the last part of Eq. (9) as T* = (3/2πGρ*)1/2, where the characteristic density 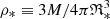 . As expected, the timescale T* turns out to be on the order of dynamic time Td. For a system supposedly in virial equilibrium, v* and ℜ* can be estimated directly from observations, and then the first two of formulas (9) allow us to find the total mass and energy of the system (Bahcall & Tremaine 1981; Binney & Tremaine 2008).
. As expected, the timescale T* turns out to be on the order of dynamic time Td. For a system supposedly in virial equilibrium, v* and ℜ* can be estimated directly from observations, and then the first two of formulas (9) allow us to find the total mass and energy of the system (Bahcall & Tremaine 1981; Binney & Tremaine 2008).
It is convenient to go in Eq. (5) to the requered quantities of a single physical nature, namely, the root mean square radius R(t) and the mean harmonic radius ℜ(t), which are defined as follows:
so that
and Eq. (5) takes the form:
Finally, the parameters specified in Eq. (9) allow us to form dimensionless variables
and bring the virial equation to a dimensionless form with all unit coefficients:
while the definition (6) for the virial ratio becomes
It is worth emphasizing an important fact that has not been discussed previously: Throughout the entire evolutionary process, the mean harmonic radius of a system with a negative total energy does not exceed twice the equilibrium value. The assertion follows from the definition ℜ/ℜ* ≡ 2|E|/|W| and the inequalities K > 0, |E|< |W|. A clear evidence is that the lines V = constant in Fig. 1 do not intersect with the line corresponding to the given value E when the constant is greater than or equal to 2.
In view of the above, the approximation to virial equilibrium over time means that the harmonic radius of the system ℜ(t), changing in a relatively narrow range of values (0, 2ℜ*), tends to its equilibrium value (Eq. (9)), that is X(τ)→1, the second derivative of R2(t) tends to zero, while the rms radius R(t) tends to a finite or, which is more likely, infinite value.
To demonstrate the theoretical possibility of the described scenario, and anticipating the discussion in the next section, we present in Fig. 2 the evolution of the harmonic and rms radii for a given behavior of the first radius, while the change in the second radius is calculated according to the virial Eq. (14). When solving this equation, we should take into account the interdependence of the initial values of X0 and Y0. Indeed, the initial system is a certain physical configuration with a specific value g0 ≡ Y0/X0. As a given parameter, it is convenient to choose the initial value of the virial ratio V0, and then X0 = 2 − V0 and Y0 = g0 ⋅ X0. The choice of 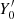 is more complicated; we do not dwell on this, since only a representative example is considered. Specifically, it was assumed that X(τ) tends to 1, experiencing an exponential decay and oscillations with a period 2πT* (see Eq. (23) below). It is noteworthy that Y2(τ) grows linearly as τ → ∞.
is more complicated; we do not dwell on this, since only a representative example is considered. Specifically, it was assumed that X(τ) tends to 1, experiencing an exponential decay and oscillations with a period 2πT* (see Eq. (23) below). It is noteworthy that Y2(τ) grows linearly as τ → ∞.
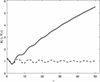 |
Fig. 2. Change in the system rms radius Y(τ) over time (solid line) for a given behavior of the harmonic radius X(τ) (dashed line). The initial system is a homogeneous sphere with Y0/X0 = g0 given in Table 1; the initial virial ratio and speed are V0 = 0.75 and |
A. Rastorguev (priv. comm.) drew our attention to the fact that the practical constancy in time of the half-mass radius Rh in the Spitzer (1987) calculations of the evolution of stellar systems can be considered as a consequence of the above conclusion regarding the value of the harmonic radius. This is because the mean harmonic radius ℜ ≃ 2.5Rh within the framework of King’s models, which describe well the internal structure of the globular clusters.
Thus, the ratio of radii
can vary within wide limits, as opposed to the usual assumption of their equality or proportionality. In this regard, it is useful to estimate the parameter g for several continuous, for simplicity, density distributions that differ significantly from each other. Table 1 lists the corresponding data for systems with central symmetry. These distributions can be conditionally considered as instantaneous (but not sequential) states of a star cluster evolving in accordance with the kinetic and Poisson equations. To calculate the values given in the table, note that for a continuous distribution, the mass M(r) inside a sphere of radius r and the potential energy W are defined by the formulas
Characteristics of systems with central symmetry for various spatial density distributions ρ(r).
so the analogs of Eqs. (10) are reduced, using Eq. (11), to
As Table 1 shows, for the first three, relatively homogeneous distributions, the values of g are close to 1. Apparently, these density distributions are adequate only at the initial stage of evolution. The values of g remain of the same order for fairly significant deviations from the spherical symmetry of the density distribution, for example, towards ellipsoidality. A more important point is the density distribution in the outer region of the system. Still early theoretical research by von Hoerner (1957) indicate the formation of a power-law density distribution ρ(r)∝r−α with exponent α ∼ 4 in the halo. This is supported by the thorough numerical modeling by Hénon (1964) and van Albada (1982), reinforced by the physical arguments of Trenti et al. (2005), along with further simulations of cluster evolution by Yangurazova & Bisnovatyi-Kogan (1984), Levin et al. (2008, 2014), Joyce et al. (2010), Sylos Labini (2013), Halle et al. (2019), and Sylos Labini & Capuzzo-Dolcetta (2020). The last two examples of Table 1 are just that. Example 4 is the system of Schuster (1883) and Plummer (1911), which was repeatedly used in connection with studies of globular star clusters. With density distributions as flat as in examples 4 and 5, the integrals for R diverge, so the g-factor is infinitely large.
The above models assume a more or less gradual change in density with distance from the center. An idea of the reverse behavior is given by a two-layer model with radii R1, R2 and densities ρ1, ρ2 in the central and outer zones, respectively. We do not present the corresponding formulas because of their cumbersomeness. The general conclusion is that at moderate values of the ratio ρ1/ρ2, the g-factor is still close to 1, and it is only when ρ1/ρ2 ≫ 1 and R1/R2 < 0.1 that a g value of more than 10 can be achieved.
Thus, it seems likely that relatively homogeneous systems at the initial stage of evolution are characterized by g(τ) on the order of 1, while the g-factor increases significantly during evolution as the dense core and extended halo of the system are formed.
3. Solutions for a given ratio of radii
In addition to the formal reason for the studying in Eq. (12) the dimensionless ratio of two unknown radii R(t) and ℜ(t), the function g(τ) plays an important role by setting the systematic behavior of the rms radius averaged over fast oscillations with a period on the order of dynamic time Td (see the appendix for details).
In order to verify the oscillatory nature of the solutions of the virial equation, we write down Eq. (14) as
and assume first that the ratio of the radii does not change with time. Lynden-Bell (1967) additionally linearized the corresponding equation; Chandrasekhar & Elbert (1972) found a rather complicated analytical solution to a nonlinear equation. Written in parametric form, the exact solution of Eq. (19) at g(τ)≡g0 describes a classical cycloid:
whereas the mean harmonic radius of the system
oscillates around the equilibrium value X* = 1. The constants a and b are determined by the initial state:
It is convenient to proceed from three initial values, namely, the pair 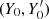 and the virial ratio V0; then, according to Eqs. (15) and (16), we have X0 = 2 − V0 and g0 = Y0/X0.
and the virial ratio V0; then, according to Eqs. (15) and (16), we have X0 = 2 − V0 and g0 = Y0/X0.
Equation (6) shows that values of the kinetic energy less or greater than |E| correspond to virial ratio values less or greater than 1 (see Fig. 1); how it is accepted, we call the respective states of the system either cold or hot. The mean harmonic radius ℜ of the former state exceeds the equilibrium value ℜ*, while we have ℜ < ℜ* for the latter state. For example, the virial ratio of an isothermal sphere, regardless of its radius, is 3/2, so it should be classified as a hot unstable system.
A particular solution for V0 = 0.20 (cold system) is shown in Fig. 3. The period of oscillations of the cycloid in real time is equal to g0P*, where
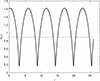 |
Fig. 3. Changing the rms radius Y(τ) in a model with constant ratio Y/X ≡ g0 at initial values Y0 = 1.60, |
and 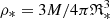 is the characteristic density of the cluster.
is the characteristic density of the cluster.
It is clear that the undamped, so-called homologous oscillations give only a preliminary description of the early evolution of a self-gravitating system. As noted at the end of the previous section, to estimate the characteristic time to reach virial equilibrium, it is necessary to take into account a progressive macroscopic inhomogeneity of the system. Accordingly, we must turn to a model with a time-varying ratio of radii R/ℜ. The appendix to this paper shows that the approximate solution of Eq. (19) with an arbitrary function g(τ), on which only the condition of its slow change on the timescale T* is imposed, is a generalization of the classical cycloid, namely:
Here, the base function u(θ) is given by the implicit equation u = g(θ ⋅ u) and the variable coefficients a(θ) and b(θ) depend on u(θ), that is, they are also given by the function g(τ). In the case of g(τ)≡g0, we get u = g0, the coefficients a, b become constant, and we return to the homologous model considered above. The physical meaning of representation in Eq. (24) is that the functions u(θ),a(θ) and b(θ) change relatively slowly, following g(τ), while their trigonometric factors precisely reflect these rapid variations of the rms radius around g(τ); the mean harmonic radius and virial ratio fluctuate around an equilibrium value 1. Our numerical examples show that in the immediate vicinity of the VES, the oscillation period slightly increases.
A more accurate approach, albeit not as informative as the analytical one, is the direct numerical solution of Eq. (19) for a given g(τ). Figure 4 gives an idea of a typical evolutionary pattern, in this case a hot system. The behavior of the mean harmonic radius X(τ) is not shown because, in view of Eq. (15), it is a reflection of V(τ) relative to the equilibrium level. We see several rapid initial fluctuations in both the rms radius and the virial ratio, however, later Y(τ) follows the given function g(τ), while V(τ) and X(τ) practically stabilize around the equilibrium level X* = 1. This means that, over a period of two to three dozen of dynamic time intervals T*, an almost equilibrium core with radius ℜ* is formed in the system, while the surrounding halo, which determines the rms radius R(t), continues to expand.
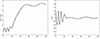 |
Fig. 4. Solution of Eq. (19) with initial data V0 = 1.40, Y0 = 0.60, |
The pattern of virial oscillations seen in the right Fig. 4 has the same character as that obtained by numerical simulation of the dynamics of a multiparticle system (see, e.g., Fig. 6 in Trenti et al. 2005). Fast oscillations are just a ringing against the backdrop of a slower reorganization of the system. Eventually, it is possible that after two dozen dynamic time periods T* the harmonic radius of the system X(τ) will become close to 1; then, as the virial Eq. (14) shows, the further evolution of the root mean square radius of the system is described by simple law R(t)/ℜ* = g(τ)≃(c1τ + c2)1/2, where τ = t/T* and c1, c2 are some dimensionless constants.
For control, it is also necessary to check the evolution of the system, which was initially in a virial equilibrium state. As can be seen in Fig. 5, the rapid oscillations of the radii and the virial ratio have disappeared, the rms radius Y(τ) still follows g(τ), while the quasi-equilibrium nucleus experiences only long-term weak oscillations. This result is expected.
 |
Fig. 5. Solution of Eq. (19) with initial data V0 = 1.0, Y0 = 1.0, |
The difference in the behavior of the system core and halo seems quite plausible, but we should not forget that in the context considered here it is partly determined by the specification of the g(τ) function. This prompted us to consider models with different types of g(τ); all cases, except for extremely hot systems, show the same behavior.
4. Concluding remarks
Since the time of H. Poincaré it has been known that motion in a system of several gravitating bodies is unstable; under certain initial conditions it becomes chaotic (Hénon & Heiles 1964). The virial equation contains only integral characteristics of a system of gravitating bodies, and the stability of its solutions remains to be studied. As for the dependence on the initial data, firstly on the virial ratio V0, it manifests itself in a quite obvious way. Figures 4 and 5 show this when V0 ≥ 1. On the other hand, we would generally expect that if V0 is small, or even if V0 = 0 when the system is completely cold and big in size, the initial oscillations in the virial ratio and both radii are relatively large, and the time to reach virial equilibrium increases. This behavior is confirmed both by extensive numerical simulations, in particular van Albada (1982), Trenti et al. (2005), and by our calculations. However, despite all the differences in the details, the general character of the evolution towards virial equilibrium of the system’s core remains unchanged.
The above consideration implies two features. First, the integral characteristics of the system fluctuate during two to three tens of dynamic time T* until the virial ratio stabilizes near the equilibrium value V* = 1. Secondly, the root mean square and mean harmonic radii vary differenly over time, so the common assumption that the radii are approximately equal or proportional is far from realistic. As already noted, the first conclusion agrees with the results of numerical simulation of self-gravitating systems at N ≫ 1. The second conclusion means a fundamentally different behavior of the moment of inertia of the system relative to the center of gravity and its potential energy.
Further details of the process of approaching the virial equilibrium state remain hidden when only the virial equation is analyzed. Additional data are desirable, at least in the form of approximate relationships between the integral characteristics of the system. On the other hand, the difference between evolutionary paths of the root mean square and the mean harmonic radii can be easily elucidated on the basis of both already performed and future numerical simulations.
The virial equation as presented here follows from Eq. (5.133) and the Lagrange-Jacobi identity (5.136) of Chandrasekhar (1942) monograph.
Acknowledgments
The author is grateful to A.S. Rastorguev and the anonymous referee for useful comments. No new data were generated or analysed in support of this research.
References
- Ambartsumian, V. A. 1938, Ann. Leningrad St. Univ., 22, 19 [Google Scholar]
- Bahcall, J., & Tremaine, S. 1981, ApJ, 244, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Benetti, F. P. C., Ribeiro-Teixeira, A. C., Pakter, R., & Levin, Y. 2014, Phys. Rev. Lett., 113, 100602 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics (Princeton: Princeton Univ. Press) [Google Scholar]
- Chandrasekhar, S. 1942, Principles of Stellar Dynamics (Chicago: Univ. of Chicago Press) [Google Scholar]
- Chandrasekhar, S., & Elbert, D. D. 1972, MNRAS, 155, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L. 2021, Introduction to Stellar Dynamics (Cambridge: Cambridge Univ. Press) [CrossRef] [Google Scholar]
- Giachetti, G., & Casetti, L. 2019, J. Stat. Mech., 1, 043201 [CrossRef] [Google Scholar]
- Gurzadyan, V. G., & Savvidy, G. K. 1984, Doklady AN SSSR, 277, 69 [NASA ADS] [Google Scholar]
- Gurzadyan, V. G., & Savvidy, G. K. 1986, A&A, 160, 203 [NASA ADS] [Google Scholar]
- Gurzadyan, V. G., & Kocharyan, A. A. 2009, A&A, 505, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeans, J. H. 1915, MNRAS, 76, 71 [Google Scholar]
- Jeans, J. H. 1919, Problems of Cosmogony and Stellar Dynamics (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Joyce, M., Marcos, B., & Sylos Labini, F. 2010, AIP Conf. Proc., 1245, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Halle, A., Colombi, S., & Peirani, S. 2019, A&A, 621, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hénon, M. 1964, Ann. Astrophys., 27, 83 [Google Scholar]
- Hénon, M. 1982, A&A., 114, 211 [Google Scholar]
- Hénon, M., & Heiles, C. 1964, AJ, 69, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. D. 1937, J. Exper. Theor. Phys., 7, 203 [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1976, Theoretical Physics. vol. I, Mechanics, 3rd ed. (Elsevier) [Google Scholar]
- Levin, Y., Pakter, R., & Rizzato, F. B. 2008, Phys. Rev. E, 78, 021130 [CrossRef] [Google Scholar]
- Levin, Y., Pakter, R., Rizzato, F. B., Teles, T. N., & Benetti, F. P. C. 2014, Phys. Rep., 535, 1 [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1967, MNRAS, 136, 101 [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [Google Scholar]
- Rastorguev, A. S., & Sementsov, V. N. 2006, Astron. Lett., 32, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Schuster, A. 1883, Br. Assoc. Rep., 470, 427 [Google Scholar]
- Shu, F. H. 1978, ApJ, 225, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L., Jr. 1987, Dynamical Evolution of Globular Clusters (Princeton: Princeton Univ. Press) [Google Scholar]
- Sylos Labini, F. 2013, MNRAS, 429, 679 [Google Scholar]
- Sylos Labini, F., & Capuzzo-Dolcetta, R. 2020, A&A, 643, A118 [EDP Sciences] [Google Scholar]
- Trenti, M., Bertin, G., & van Albada, T. S. 2005, A&A, 433, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Albada, T. S. 1982, MNRAS, 201, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Van der Pol, B. 1927, Lond. Edinb. Dublin Philos. Mag. J. Sci., 2, 978 [Google Scholar]
- von Hoerner, S. 1957, ApJ, 125, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Yangurazova, L. R., & Bisnovatyi-Kogan, G. S. 1984, Astrophys. Space Sci., 100, 319 [CrossRef] [Google Scholar]
Appendix A: Approximate analytical solution of the virial equation
A nonlinear differential equation of the second order
is considered in the domain τ ≥ 0 for a given non-negative function g(τ). The approach presented below, which goes back to the method of Van der Pol (1927), is widely used in the theory of oscillations.
We look for a solution in a parametric form:
where u(θ), a(θ) and b(θ) are some unknown functions slowly varying over an interval of length 2π. In particular, they can be constant. Specifically, we assume that |u′(θ)/u(θ)| ≪ 1, and similar inequalities hold for the coefficients a and b. Under this condition, the solution averaged over an interval of length 2π is
which determines the physical meaning of the function u(θ).
We have from Eqs. (A.2):
According to the above condition, we can neglect here terms with derivatives, i.e. put
so that Eqs. (A.4) take the form:
Dividing the top of Eqs. (A.6) by the bottom gives:
Moreover, Eqs. (A.6) shows that the derivatives with respect to τ and with respect to θ are connected by the relation
Applying this operator to Eq. (A.7), taking into account the first of Eqs. (A.2) and the condition of smallness of derivatives, we find:
Thus,
which coincides with Eq. (A.1) provided that
Here it suffices to restrict ourselves to the first term in the representation of τ from Eqs. (A.2), so that the function u(θ) is found from the implicit equation
Finally, given the known function u(θ), one can find coefficients a(θ) and b(θ) by solving the system of linear Eqs. (A.5) with respect to a′ and b′, and then integrating the results. Further technical details are quite obvious.
All Tables
Characteristics of systems with central symmetry for various spatial density distributions ρ(r).
All Figures
 |
Fig. 1. Representation of the dynamic evolution of a system on a diagram connecting kinetic, K, and potential energy, W. Evolution occurs along the straight line K(t)+W(t) = E, approaching on average a virial equilibrium state (VES). The thin lines correspond to fixed values of the virial ratio V given by Eq. (6). The letters C and H denote cold and hot configurations, which are characterized by the values K < |E| and K > |E|, respectively. |
| In the text | |
 |
Fig. 2. Change in the system rms radius Y(τ) over time (solid line) for a given behavior of the harmonic radius X(τ) (dashed line). The initial system is a homogeneous sphere with Y0/X0 = g0 given in Table 1; the initial virial ratio and speed are V0 = 0.75 and |
| In the text | |
 |
Fig. 3. Changing the rms radius Y(τ) in a model with constant ratio Y/X ≡ g0 at initial values Y0 = 1.60, |
| In the text | |
 |
Fig. 4. Solution of Eq. (19) with initial data V0 = 1.40, Y0 = 0.60, |
| In the text | |
 |
Fig. 5. Solution of Eq. (19) with initial data V0 = 1.0, Y0 = 1.0, |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



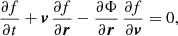
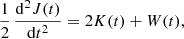
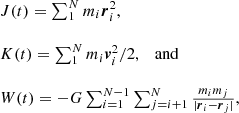
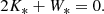
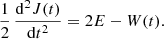
![$$ \begin{aligned} V(t) \equiv \frac{2K(t)}{|W(t)|} = 2\left[ 1-\frac{E}{W(t)} \right], \qquad 0 \le V < 2. \end{aligned} $$](/articles/aa/full_html/2024/06/aa48933-23/aa48933-23-eq6.gif)

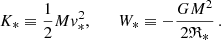
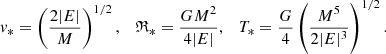
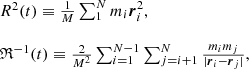
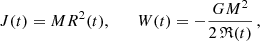
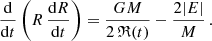
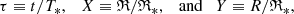
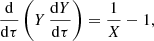
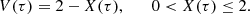
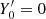
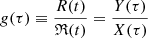
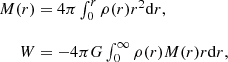
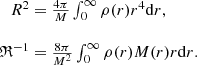
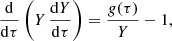
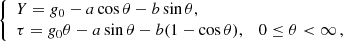
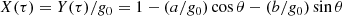

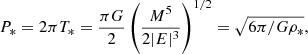
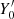
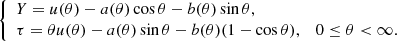
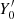
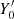
![$$ \begin{aligned} Y \left[ \frac{d}{d\tau } \left( Y\,\frac{dY}{d\tau }\right) + 1 \right] = g(\tau ) \end{aligned} $$](/articles/aa/full_html/2024/06/aa48933-23/aa48933-23-eq42.gif)
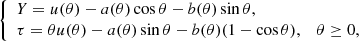
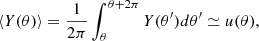
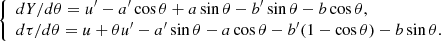
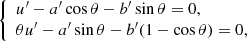
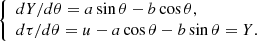
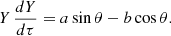
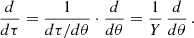
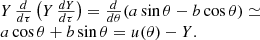
![$$ \begin{aligned} Y \left[ \frac{d}{d\tau } \left( Y\,\frac{dY}{d\tau }\right) + 1 \right] = u(\theta ), \end{aligned} $$](/articles/aa/full_html/2024/06/aa48933-23/aa48933-23-eq51.gif)