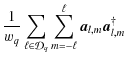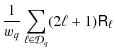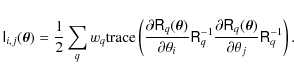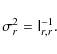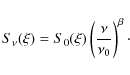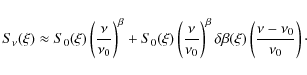| Issue |
A&A
Volume 503, Number 3, September I 2009
|
|
|---|---|---|
| Page(s) | 691 - 706 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200911624 | |
| Published online | 27 May 2009 | |
Measuring the tensor to scalar ratio from CMB B-modes in the presence of foregrounds![[*]](/icons/foot_motif.png)
M. Betoule1 - E. Pierpaoli2 - J. Delabrouille1 - M. Le Jeune1 - J.-F. Cardoso1
1 - AstroParticule et Cosmologie (APC), CNRS: UMR 7164, Université Denis Diderot, Paris 7, Observatoire de Paris, France
2 - University of Southern California, Los Angeles, CA 90089-0484, USA
Received 7 January 2009 / Accepted 7 May 2009
Abstract
Aims. We investigate the impact of polarised foreground emission on the performances of future CMB experiments aiming to detect primordial tensor fluctuations in the early universe. In particular, we study the accuracy that can be achieved in measuring the tensor-to-scalar ratio r in the presence of foregrounds.
Methods. We designed a component separation pipeline, based on the SMICA method, aimed at estimating r and the foreground contamination from the data with no prior assumption on the frequency dependence or spatial distribution of the foregrounds. We derived error bars accounting for the uncertainty on foreground contribution. We used the current knowledge of galactic and extra-galactic foregrounds as implemented in the Planck sky model (PSM) to build simulations of the sky emission. We applied the method to simulated observations of this modelled sky emission, for various experimental setups. Instrumental systematics are not considered in this study.
Results. Our method, with Planck data, permits us to detect r=0.1 from B-modes only at more than 3![]() .
With a future dedicated space experiment, such as EPIC, we can measure r=0.001 at
.
With a future dedicated space experiment, such as EPIC, we can measure r=0.001 at ![]()
![]() for the most ambitious mission designs. Most of the sensitivity to r comes from scales
for the most ambitious mission designs. Most of the sensitivity to r comes from scales
![]() for high r values, shifting to lower
for high r values, shifting to lower ![]() 's for progressively smaller r. This shows that large-scale foreground emission does not prevent proper measurement of the reionisation bump for full sky experiments. We also investigate the observation of a small but clean part of the sky. We show that diffuse foregrounds remain a concern for a sensitive ground-based experiment with a limited frequency coverage when measuring r < 0.1. Using the Planck data as additional frequency channels to constrain the foregrounds in such ground-based observations reduces the error by a factor two but does not allow detection of r=0.01. An alternate strategy, based on a deep field space mission with a wide frequency coverage, would allow us to deal with diffuse foregrounds efficiently, but is in return quite sensitive to lensing contamination. In contrast, we show that all-sky missions are nearly insensitive to small-scale contamination (point sources and lensing) if the statistical contribution of such foregrounds can be modelled accurately. Our results do not significantly depend on the overall level and frequency dependence of the diffused foreground model, when varied within the limits allowed by current observations.
's for progressively smaller r. This shows that large-scale foreground emission does not prevent proper measurement of the reionisation bump for full sky experiments. We also investigate the observation of a small but clean part of the sky. We show that diffuse foregrounds remain a concern for a sensitive ground-based experiment with a limited frequency coverage when measuring r < 0.1. Using the Planck data as additional frequency channels to constrain the foregrounds in such ground-based observations reduces the error by a factor two but does not allow detection of r=0.01. An alternate strategy, based on a deep field space mission with a wide frequency coverage, would allow us to deal with diffuse foregrounds efficiently, but is in return quite sensitive to lensing contamination. In contrast, we show that all-sky missions are nearly insensitive to small-scale contamination (point sources and lensing) if the statistical contribution of such foregrounds can be modelled accurately. Our results do not significantly depend on the overall level and frequency dependence of the diffused foreground model, when varied within the limits allowed by current observations.
Key words: cosmology: cosmic microwave background - cosmology: cosmological parameters - cosmology: observations
1 Introduction
After the success of the WMAP space mission in mapping the cosmic microwave background (CMB) temperature anisotropies, much attention now turns towards the challenge of measuring CMB polarisation, in particular pseudo-scalar polarisation modes (the B-modes) of primordial origin. These B-modes offer one of the best options for constraining inflationary models (Hu & White 1997; Kamionkowski & Kosowsky 1998; Baumann & Peiris 2008; Kamionkowski et al. 1997; Seljak & Zaldarriaga 1997).
First polarisation measurements have already been obtained by a number of instruments (Page et al. 2007; Kovac et al. 2002; Sievers & CBI Collaboration 2005), but no detection of B-modes has been claimed yet. While several ground-based and balloon-borne experiments are already operational, or under construction, no CMB-dedicated space-mission is planned after Planck at the present time: whether there should be one for CMB B-modes, and how it should be designed, are still open questions.
As CMB polarisation anisotropies are expected to be significantly smaller than temperature anisotropies (a few per cent at most), improving detector sensitivities is the first major challenge towards measuring CMB polarisation B-modes. It is not, however, the only one. Foreground emissions from the galactic interstellar medium (ISM) and from extra-galactic objects (galaxies and clusters of galaxies) superimpose to the CMB. Most foregrounds are expected to emit polarised light, with a polarisation fraction typically comparable to or larger than that of the CMB. Component separation (disentangling CMB emission from all these foregrounds) is needed to extract cosmological information from observed frequency maps. The situation is particularly severe for the B-modes of CMB polarisation, which will be, if measurable, subdominant on every scale and at every frequency.
The main objective of this paper is to evaluate the accuracy with which various upcoming or planned experiments can measure the tensor-scalar ratio r (see Peiris et al. (2003) for a precise definition) in the presence of foregrounds. This problem has been addressed before: Tucci et al. (2005) investigate the lower bound for r that can be achieved considering a simple foreground cleaning technique, based on the extrapolation of foreground templates and subtraction from a channel dedicated to CMB measurement; Verde et al. (2006) assume foreground residuals at a known level in a cleaned map, treat them as additional Gaussian noise, and compute the error on r due to such excess noise; Amblard et al. (2007) investigate how best to select the frequency bands of an instrument and how to distribute a fixed number of detectors among them, to maximally reject galactic foreground contamination. This analysis is based on an internal linear combination cleaning technique similar to the one of Tegmark et al. (2003) on WMAP temperature anisotropy data. The last two studies assume somehow that the residual contamination level is perfectly known - information that is used to derive error bars on r.
In this paper, we relax this assumption and propose a method for estimating the uncertainty on residual contamination from the data themselves, as would be the case for real data analysis. We test our method on semi-realistic simulated data sets, including CMB and realistic foreground emission, as well as simple instrumental noise. We study a variety of experimental designs and foreground mixtures. Alternative approaches to the same question are also presented in Dunkley et al. (2008a) and Baumann et al. (2008).
This paper is organised as follows: the next section (Sect. 2) deals with polarised foregrounds and presents the galactic emission model used in this work. In Sect. 3, we propose a method, using the most recent version of the SMICA component separation framework (Cardoso et al. 2008), for providing measurements of the tensor to scalar ratio in the presence of foregrounds. In Sect. 4, we present the results obtained by applying the method to various experimental designs. Section 5 discusses the reliability of the method (and of our conclusions) against various issues, in particular modelling uncertainty. Main results are summarised in Sect. 6.
2 Modelling polarised sky emission
Several processes contribute to the total sky emission in the frequency range of interest for CMB observation (typically between 30 and 300 GHz). Foreground emission arises from the galactic interstellar medium (ISM), from extra-galactic objects, and from distortions of the CMB itself through its interaction with structures in the nearby universe. Although the physical processes involved and the general emission mechanisms are mostly understood, specifics of these polarised emissions in the millimetre range remain poorly known as few actual observations, on a significant enough part of the sky, have been made.
Diffuse emission from the ISM arises through synchrotron emission from energetic electrons, through free-free emission, and through grey-body emission of a population of dust grains. Small spinning dust grains with a dipole electric moment may also emit significantly in the radio domain (Draine & Lazarian 1998). Among those processes, dust and synchrotron emissions are thought to be significantly polarised. Galactic emission also includes contributions from compact regions such as supernovae remnants and molecular clouds, which have specific emission properties.
Extra-galactic objects emit via a number of different mechanisms, each of them having its own spectral energy distribution and polarisation properties.
 |
Figure 1:
Respective emission levels of the various components as predicted by the PSM.
Left: predicted power spectra of the various components at 100 GHz, compared to CMB and lensing level for standard cosmology and various values of r (
|
| Open with DEXTER | |
Finally, the CMB polarisation spectra are modified by the interactions
of the CMB photons on their way from the last scattering
surface. Reionisation, in particular, re-injects power in polarisation
on large scales by late-time scattering of CMB photons. This produces
a distinctive feature, the reionisation bump, in the CMB B-mode spectrum at low ![]() .
Other interactions with the latter universe,
and in particular lensing, contribute to hinder the measurement of the
primordial signal. The lensing effect is particularly important on
smaller scales as it converts a part of the dominant E-mode power into
B-mode.
.
Other interactions with the latter universe,
and in particular lensing, contribute to hinder the measurement of the
primordial signal. The lensing effect is particularly important on
smaller scales as it converts a part of the dominant E-mode power into
B-mode.
In the following, we review the identified polarisation processes and detail the model used for the present work, with a special emphasis on B-modes. We also discuss main sources of uncertainty in the model, as a basis for evaluating their impact on the conclusions of this paper.
Our simulations![]() are
based on the PSM, a sky emission simulation tool developed by the
Planck collaboration for pre-launch preparation of Planck data
analysis (Delabrouille et al. 2009). Figure 1 gives an
overview of foregrounds as included in our baseline model. Diffuse
galactic emission from synchrotron and dust dominates at all
frequencies and on all scales, with a minimum (relative to CMB)
between 60 and 80 GHz, depending on the galactic cut. Contaminations
by lensing and a point source background are lower than primordial CMB
for r > 0.01 and for
are
based on the PSM, a sky emission simulation tool developed by the
Planck collaboration for pre-launch preparation of Planck data
analysis (Delabrouille et al. 2009). Figure 1 gives an
overview of foregrounds as included in our baseline model. Diffuse
galactic emission from synchrotron and dust dominates at all
frequencies and on all scales, with a minimum (relative to CMB)
between 60 and 80 GHz, depending on the galactic cut. Contaminations
by lensing and a point source background are lower than primordial CMB
for r > 0.01 and for
![]() ,
but should clearly be taken into
account in attempts to measure r < 0.01.
,
but should clearly be taken into
account in attempts to measure r < 0.01.
2.1 Synchrotron
Cosmic ray electrons spiralling in the galactic magnetic field produce
highly polarised synchrotron emission
(e.g. Rybicki & Lightman 1979). This is the dominant contaminant
of the polarised CMB signal at low frequency
(![]()
![]() ), as can be seen in the right panel of
Fig. 1. In the
frequency range of interest for CMB observations, measurements of this
emission have been provided, both in temperature and polarisation, by
WMAP (Page et al. 2007; Gold et al. 2008). The intensity of
the synchrotron emission depends on the cosmic ray density
ne, and on the strength of the magnetic field perpendicularly to the
line of sight. Its frequency scaling and its intrinsic polarisation
fraction fs depend on the energy distribution of the cosmic
rays.
), as can be seen in the right panel of
Fig. 1. In the
frequency range of interest for CMB observations, measurements of this
emission have been provided, both in temperature and polarisation, by
WMAP (Page et al. 2007; Gold et al. 2008). The intensity of
the synchrotron emission depends on the cosmic ray density
ne, and on the strength of the magnetic field perpendicularly to the
line of sight. Its frequency scaling and its intrinsic polarisation
fraction fs depend on the energy distribution of the cosmic
rays.
2.1.1 Synchrotron emission law
For electron density following a power law of index p,
![]() ,
the synchrotron frequency dependence is also a
power law, of index
,
the synchrotron frequency dependence is also a
power law, of index
![]() .
So, given the intensity
of the synchrotron emission at a reference frequency
.
So, given the intensity
of the synchrotron emission at a reference frequency ![]() ,
the
intensity at the frequency
,
the
intensity at the frequency ![]() reads:
reads:
where the spectral index,
The synchrotron spectral index depends significantly on cosmic ray properties. It varies with the direction of the sky, and possibly, with the frequency of observation (see e.g. Strong et al. 2007, for a review of propagation and interaction processes of cosmic rays in the galaxy). For a multi-channel experiment, the consequence of this is a decrease of the coherence of the synchrotron emission across channels, i.e. the correlation between the synchrotron emission in the various frequency bands of observation will be below unity.
Observational constraints have been put on the synchrotron emission
law. A template of synchrotron emission intensity at 408 MHz has been
provided by Haslam et al. (1982). Combining this map with sky
surveys at 1.4 GHz (Reich & Reich 1986) and 2.3 GHz
(Jonas et al. 1998), Giardino et al. (2002) and
Platania et al. (2003) have derived nearly full sky spectral
index maps. Using the measurement from WMAP,
Bennett et al. (2003) derived the spectral index between 408 MHz
and 23 GHz. Compared to the former results, it showed a significant
steepening toward
![]() around 20 GHz, and a strong
galactic plane feature with flatter spectral index. This feature was
first interpreted as a flatter cosmic ray distribution in star forming
regions. Recently, however, taking into account the presence, at 23 GHz, of additional contribution from a possible anomalous emission
correlated with the dust column density, Miville-Deschênes et al. (2008)
found no such pronounced galactic feature, in better agreement with
lower frequency results. The spectral index map obtained in this way
is consistent with
around 20 GHz, and a strong
galactic plane feature with flatter spectral index. This feature was
first interpreted as a flatter cosmic ray distribution in star forming
regions. Recently, however, taking into account the presence, at 23 GHz, of additional contribution from a possible anomalous emission
correlated with the dust column density, Miville-Deschênes et al. (2008)
found no such pronounced galactic feature, in better agreement with
lower frequency results. The spectral index map obtained in this way
is consistent with
![]() .
There is, hence, still
significant uncertainty on the exact variability of the synchrotron
spectral index, and in the amplitude of the steepening if any.
.
There is, hence, still
significant uncertainty on the exact variability of the synchrotron
spectral index, and in the amplitude of the steepening if any.
2.1.2 Synchrotron polarisation
If the electron density follows a power law of index p,
the synchrotron polarisation fraction reads:
For p = 3, we get fs = 0.75, a polarisation fraction which varies slowly for small variations of p. Consequently, the intrinsic synchrotron polarisation fraction should be close to constant on the sky. However, geometric depolarisation arises due to variations of the polarisation angle along the line of sight, partial cancellation of polarisation occurring for superposition of emission with orthogonal polarisation directions. Current measurements show variations of the observed polarisation value from about 10% near the galactic plane, to 30-50% at intermediate to high galactic latitudes (Macellari et al. 2008).
2.1.3 Our model of synchrotron
In summary, the B-mode intensity of the synchrotron emission is modulated by the density of cosmic rays, the slope of their spectra, the intensity of the magnetic field, its orientation, and the coherence of the orientation along the line of sight. This makes the amplitude and frequency scaling of the polarised synchrotron signal dependant on the sky position in a rather complex way.
For the purpose of the present work, we use the synchrotron model
proposed in Miville-Deschênes et al. (2008) (model 4). It relies on the
synchrotron polarised template at 23 GHz measured by WMAP, and the
computation of a spectral index map
![]() used to
extrapolate the template to other frequency following
Eq. (1). This model also defines a pixel-dependent
geometric depolarisation factor
used to
extrapolate the template to other frequency following
Eq. (1). This model also defines a pixel-dependent
geometric depolarisation factor ![]() ,
computed as the ratio
between the polarisation expected theoretically from
Eq. (2), and the polarisation actually observed. This
depolarisation, assumed to be due to varying orientations of the
galactic magnetic field along the line of sight, is used also for
modelling polarised dust emission (see below).
,
computed as the ratio
between the polarisation expected theoretically from
Eq. (2), and the polarisation actually observed. This
depolarisation, assumed to be due to varying orientations of the
galactic magnetic field along the line of sight, is used also for
modelling polarised dust emission (see below).
As an additional refinement, we also investigate the impact of a
slightly modified frequency dependence with a running spectral index
in Sect. 5. For this purpose, the synchrotron
emission Stokes parameters (
![]() for
for
![]() ), at frequency
), at frequency ![]() and in direction
and in direction ![]() on the sky,
will be modelled instead as:
on the sky,
will be modelled instead as:
where
The reconstructed B-modes map of the synchrotron-dominated sky emission at 30 GHz is shown in Fig. 2 (synthesis of B-mode maps from Q/U maps is described further along with the pipeline presentation in Sect. 4.1).
2.2 Dust
The thermal emission from heated dust grains is the dominant galactic signal at frequencies higher than 100 GHz (Fig. 1). Polarisation of starlight by dust grains indicates partial alignment of elongated grains with the galactic magnetic field (see Lazarian (2007) for a review of possible alignment mechanisms). Partial alignment of grains should also result in polarisation of the far infrared dust emission.
Contributions from a wide range of grain sizes and compositions are
required to explain the infrared spectrum of dust emission from 3 to
1000 ![]() (Li & Draine 2001; Désert et al. 1990). At
long wavelengths of interest for CMB
observations (above 100
(Li & Draine 2001; Désert et al. 1990). At
long wavelengths of interest for CMB
observations (above 100 ![]() ), the emission from big grains, at equilibrium with the
interstellar radiation field, should
dominate.
), the emission from big grains, at equilibrium with the
interstellar radiation field, should
dominate.
2.2.1 Dust thermal emission law
There is no single theoretical emission law for dust, which is
composed of many different populations of particles of matter. On
average, an emission law can be fit to observational data. In the
frequency range of interest for CMB observations,
Finkbeiner et al. (1999) have shown that the dust emission in
intensity is well modelled by emission from a two components mixture
of silicate and carbon grains. For both components, the thermal
emission spectrum is modelled as a modified grey-body emission,
![]() ,
with different emissivity spectral
index
,
with different emissivity spectral
index ![]() and different equilibrium temperature T.
and different equilibrium temperature T.
2.2.2 Dust polarisation
So far, dust polarisation measurements have been mostly concentrated on specific regions of emission, with the exception of the Archeops balloon-borne experiment (Benoît et al. 2004), which has mapped the emission at 353 GHz on a significant part of the sky, showing a polarisation fraction around 4-5% and up to 10% in some clouds. This is in rough agreement with what could be expected from polarisation of starlight (Draine & Fraisse 2008; Fosalba et al. 2002). Macellari et al. (2008) show that dust fractional polarisation in WMAP5 data depends on both frequency and latitude, but is typically about 3% and anyway below 7%.
Draine & Fraisse (2008) have shown that for particular mixtures of dust grains, the intrinsic polarisation of the dust emission could vary significantly with frequency in the 100-800 GHz range. Geometrical depolarisation caused by integration along the line of sight also lowers the observed polarisation fraction.
2.2.3 Our model of dust
To summarise, dust produces polarised light depending on grains shape, size, composition, temperature and environment. The polarised light is then observed after integration along a line of sight. Hence, the observed polarisation fraction of dust depends on its three-dimensional distribution, and of the geometry of the galactic magnetic field. This produces a complex pattern which is likely to be only partially coherent from one channel to another.
Making use of the available data, the PSM models polarised thermal
dust emission by extrapolating dust intensity to polarisation
intensity assuming an intrinsic polarisation fraction fd constant
across frequencies. This value is set to
fd = 0.12 to be
consistent with maximum values observed by Archeops
(Benoît et al. 2004) and is in good agreement with the WMAP
94 GHz measurement. The dust intensity (![]() ), traced by the
template map at 100
), traced by the
template map at 100 ![]() from Schlegel et al. (1998), is
extrapolated using Finkbeiner et al. (1999, model )7# to
frequencies of interest. The stokes Q and U parameters
(respectively DQ and DU) are then obtained as:
from Schlegel et al. (1998), is
extrapolated using Finkbeiner et al. (1999, model )7# to
frequencies of interest. The stokes Q and U parameters
(respectively DQ and DU) are then obtained as:
| (4) | |||
| (5) |
The geometric ``depolarisation'' factor g is a modified version of the synchrotron depolarisation factor (computed from WMAP measurements). Modifications account for differences of spatial distribution between dust grains and energetic electrons, and are computed using the magnetic field model presented in Miville-Deschênes et al. (2008). The polarisation angle
![\begin{figure}
\par\includegraphics[angle=90]{11624f2}\par\includegraphics[angle=90]{11624f3} \end{figure}](/articles/aa/full_html/2009/33/aa11624-09/Timg37.png) |
Figure 2: B-modes of the galactic foreground maps (synchrotron + dust) as simulated using v1.6.4 of the PSM. Top: synchrotron-dominated emission at 30 GHz, Bottom: dust-dominated emission at 340 GHz. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90]{11624f4}\par\includegraphics[angle=90]{11624f5}\par
\end{figure}](/articles/aa/full_html/2009/33/aa11624-09/Timg38.png) |
Figure 3:
Maps of the depolarisation factor g ( upper panel) and
polarisation angle |
| Open with DEXTER | |
2.2.4 Anomalous dust
If the anomalous dust emission, which may account for a significant part of the intensity emission in the range 10-30 GHz (Finkbeiner 2004; Miville-Deschênes et al. 2008; de Oliveira-Costa et al. 2004), can be interpreted as spinning dust grains emission (Draine & Lazarian 1998), it should be slightly polarised under 35 GHz (Battistelli et al. 2006), and only marginally polarised at higher frequencies (Lazarian & Finkbeiner 2003). For this reason, it is neglected (and not modelled) here. However, we should keep in mind that there exist other possible emission processes for dust, like the magneto-dipole mechanism, which can produce highly polarised radiation, and could thus contribute significantly to dust polarisation at low frequencies, even if subdominant in intensity (Lazarian & Finkbeiner 2003).
2.3 Other processes
The left panel in Fig. 1 presents the respective contribution from the various foregrounds as predicted by the PSM at 100 GHz. Synchrotron and dust polarised emission, being by far the strongest contaminants on large scales, are expected to be the main foregrounds for the measurement of primordial B-modes. In this work, we thus mainly focus on the separation from these two diffuse contaminants. However, other processes yielding polarised signals at levels comparable with either the signal of interest, or with the sensitivity of the instrument used for B-mode observation, have to be taken into account.
2.3.1 Free-free
Free-free emission is assumed unpolarised to first order (the emission process is not intrinsically linearly polarised), even if, in principle, low level polarisation by Compton scattering could exist at the edge of dense ionised regions. In WMAP data analysis, Macellari et al. (2008) find an upper limit of 1% for free-free polarisation. At this level, free-free would have to be taken into account for measuring CMB B-modes for low values of r. As this is just an upper limit however, no polarised free-free is considered for the present work.
2.3.2 Extra-galactic sources
Polarised emission from extra-galactic sources is expected to be faint below the degree scale. Tucci et al. (2005), however, estimate that radio sources become the major contaminant after subtraction of the galactic foregrounds. It is, hence, an important foreground at high galactic latitudes. In addition, the point source contribution involves a wide range of emission processes and superposition of emissions from several sources, which makes this foreground poorly coherent across frequencies, and hence difficult to subtract using methods relying on the extrapolation of template emission maps.
The PSM provides estimates of the point source polarised
emission. Source counts are in agreement with the prediction of
de Zotti et al. (2005), and with WMAP data. For radio-sources,
the degree of polarisation for each source is randomly drawn from the
observed distribution at 20 GHz (Ricci et al. 2004). For
infrared sources, a distribution with mean polarisation degree of 0.01
is assumed. For both populations, polarisation angles are uniformly
drawn in ![]() .
The emission of a number of known galactic point
sources is also included in PSM simulations.
.
The emission of a number of known galactic point
sources is also included in PSM simulations.
2.3.3 Lensing
The last main contaminant to the primordial B-mode signal is
lensing-induced B-type polarisation, the level of which should be of
the same order as that of point sources (left panel of
Fig. 1). For the present work, no sophisticated lensing
cleaning method is used. Lensing effects are modelled and taken into
account only at the power spectrum level and computed using the CAMB
software package![]() , based itself on the
CMBFAST software (Zaldarriaga & Seljak 2000; Zaldarriaga et al. 1998).
, based itself on the
CMBFAST software (Zaldarriaga & Seljak 2000; Zaldarriaga et al. 1998).
2.3.4 Polarised Sunyaev-Zel'dovich effect
The polarised Sunyaev Zel'dovich effect (Seto & Pierpaoli 2005; Sazonov & Sunyaev 1999; Audit & Simmons 1999), is expected to be very subdominant and is neglected here.
2.4 Uncertainties on the foreground model
Due to the relative lack of experimental constraints from observation at millimetre wavelengths, uncertainties on the foreground model are large. The situation will not drastically improve before the Planck mission provides new observations of polarised foregrounds. It is thus very important to evaluate, at least qualitatively, the impact of such uncertainties on component separation errors for B-mode measurements.We may distinguish two types of uncertainties, which impact differently the separation of CMB from foregrounds. One concerns the level of foreground emission, the other its complexity. Quite reliable constraints on the emission level of polarised synchrotron at 23 GHz are available with the WMAP measurement, up to the few degrees scale. Extrapolation to other frequencies and smaller angular scales may be somewhat insecure, but uncertainties take place where this emission becomes weak and subdominant. The situation is worse for the polarised dust emission, which is only weakly constrained from WMAP and Archeops at 94 and 353 GHz. The overall level of polarisation is constrained only in the galactic plane, and its angular spectrum is only roughly estimated. In addition, variations of the polarisation fraction (Draine & Fraisse 2008) may introduce significant deviations to the frequency scaling of dust B-modes.
Several processes make the spectral indexes of dust and synchrotron vary both in space and frequency. Some of this complexity is included in our baseline model, but some aspects, like the dependence of the dust polarisation fraction with frequency and the steepening of the synchrotron spectral index, remain poorly known and are not modelled in our main set of simulations. In addition, uncharacterised emission processes have been neglected. This is the case for anomalous dust, or polarisation of the free-free emission through Compton scattering. If such additional processes for polarised emission exist, even at a low level, they would decrease the coherence of galactic foreground emission between frequency channels, and hence our ability to predict the emission in one channel knowing it in the others - a point of much importance for any component separation method based on the combination of multi-frequency observations.
The component separation as performed in this paper, hence, is obviously sensitive to these hypotheses. We will dedicate a part of the discussion to assess the impact of such modelling errors on our conclusions.
3 Estimating r with contaminants
Let us now turn to a presentation of the component separation (and parameter estimation) method used to derive forecasts on the tensor to scalar ratio measurements. Note that in principle, the best analysis of CMB observations should simultaneously exploit measurements of all fields (T, E, and B), as investigated already by Aumont & Macías-Pérez (2007). Their work, however, addresses an idealised problem. For component separation of temperature and polarisation together, the best approach is likely to depend on the detailed properties of the foregrounds (in particular on any differences, even small, between foreground emissions laws in temperature and in polarisation) and of the instrument (in particular noise correlations, and instrumental systematics). None of this is available for the present study. For this reason, we perform component separation in B-mode maps only. Additional issues such as disentangling E from B in cases of partial sky coverage for instance, or in the presence of instrumental systematic effects, are not investigated here either. Relevant work can be found in Kaplan & Delabrouille (2002); Smith & Zaldarriaga (2007); Hu et al. (2003); Rosset et al. (2007); Challinor et al. (2003).
For low values of tensor fluctuations, the constraint on r is expected to come primarily from the B-mode polarisation. B-modes indeed are not affected by the cosmic variance of the scalar perturbations, contrarily to E-modes and temperature anisotropies. In return, B-mode signal would be low and should bring little constraint on cosmological parameters other than r (and, possibly, the tensor spectral index nt, although this additional parameter is not considered here). Decoupling the estimation of r (from B-modes only) from the estimation of other cosmological parameters (from temperature anisotropies, from E-modes, and from additional cosmological probes) thus becomes a reasonable hypothesis for small values of r. As we are primarily interested in accurate handling of the foreground emission, we will make the assumption that all cosmological parameters but r are perfectly known. Further investigation of the coupling between cosmological parameters can be found in Colombo et al. (2008) and Verde et al. (2006), and this question is discussed a bit further in Sect. 5.4.
3.1 Simplified approaches
3.1.1 Single noisy map
The first obstacle driving the performance of an experiment being the
instrumental noise, it is interesting to recall the limit on rachievable in absence of foreground contamination in the observations.
We thus consider first a single frequency observation of the CMB,
contaminated by a noise term n:
where
where
The smallest achievable variance
For a detector (or a set of detectors at the same frequency) of noise equivalent temperature s (in
A similar approach to estimating ![]() is used in Verde et al. (2006) where a
single ``cleaned'' map is considered. This map is obtained by optimal
combination of the detectors with respect to the noise and cleaned
from foregrounds up to a certain level of residuals, which are accounted for as an
extra Gaussian noise.
is used in Verde et al. (2006) where a
single ``cleaned'' map is considered. This map is obtained by optimal
combination of the detectors with respect to the noise and cleaned
from foregrounds up to a certain level of residuals, which are accounted for as an
extra Gaussian noise.
3.1.2 Multi-map estimation
Alternatively, we may consider observations in F frequency bands,
and form the
![]() vector of data
vector of data
![]() ,
assuming
that each frequency is contaminated by
,
assuming
that each frequency is contaminated by
![]() .
This
term includes all contaminations (foregrounds, noise, etc.). In the
harmonic domain, denoting
.
This
term includes all contaminations (foregrounds, noise, etc.). In the
harmonic domain, denoting
![]() the emission law of the
CMB (the unit vector when working in thermodynamic units):
the emission law of the
CMB (the unit vector when working in thermodynamic units):
We then consider the
with the CMB contribution modelled as
and all contaminations contributing a term
In the approximation that contaminants are Gaussian (and, here,
stationary) but correlated, all the relevant information about the CMB
is preserved by combining all the channels into a single filtered
map. In the harmonic domain, the filtering operation reads:
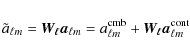
with
We are back to the case of a single map contaminated by a characterised noise of spectrum:
If the residual
The same filter is used by Amblard et al. (2007). Assuming that
the foreground contribution is perfectly known, the contaminant terms
![]() can be modelled as
can be modelled as
![]() .
This approach thus permits to derive the actual level of
contamination of the map in the presence of known foregrounds,
i.e. assuming that the covariance matrix of the foregrounds is known.
.
This approach thus permits to derive the actual level of
contamination of the map in the presence of known foregrounds,
i.e. assuming that the covariance matrix of the foregrounds is known.
3.2 Estimating r in the presence of unknown foregrounds with SMICA
The two simplified approaches of Sects. 3.1.1
and 3.1.2 offer a way to estimate the impact of foregrounds
in a given mission, by comparing the sensitivity on r obtained in
absence of foregrounds (from Eq. (8) when
![]() contains instrumental noise only), and the sensitivity achievable with
known foregrounds (when
contains instrumental noise only), and the sensitivity achievable with
known foregrounds (when
![]() contains the contribution of residual
contaminants as well, as obtained from Eq. (13) assuming
that the foreground correlation matrix is known).
contains the contribution of residual
contaminants as well, as obtained from Eq. (13) assuming
that the foreground correlation matrix is known).
A key issue, however, is that the solution and the error bar
require the covariance matrix of foregrounds and noise to be
known![]() . Whereas the instrumental noise can be estimated accurately,
assuming prior knowledge of the covariance of the foregrounds to the
required precision is optimistic.
. Whereas the instrumental noise can be estimated accurately,
assuming prior knowledge of the covariance of the foregrounds to the
required precision is optimistic.
To deal with unknown foregrounds, we thus follow a different route
which considers a multi-map likelihood (Delabrouille et al. 2003). If
all processes are modelled as Gaussian isotropic, then standard
computations yield:
where
and where
Expression (14) is nothing but the multi-map extension of (7).
If
![]() is known and fixed, then the
likelihood (Eq. (14)) depends only on the CMB angular
spectrum and can be shown to be equal (up to a constant) to
expression 7 with
is known and fixed, then the
likelihood (Eq. (14)) depends only on the CMB angular
spectrum and can be shown to be equal (up to a constant) to
expression 7 with
![]() and
and
![]() given by Eq. (13).
Thus this approach encompasses both the single map and filtered map approaches.
given by Eq. (13).
Thus this approach encompasses both the single map and filtered map approaches.
Unknown foreground contribution can be modelled as the mixed
contribution of D correlated sources:
where

We then maximise the likelihood (14) of the model with respect to r,
We note that the foreground parameterisation in Eq. (17) is
redundant, as an invertible matrix can be exchanged between
![]() and
and
![]() ,
without modifying the actual value
of
,
without modifying the actual value
of
![]() .
The physical meaning of this is that the various
foregrounds are not identified and extracted individually, only their
mixed contribution is characterised. If we are interested in
disentangling the foregrounds as well, e.g. to separate synchrotron
emission from dust emission, this degeneracy can be lifted by making
use of prior information to constrain, for example, the mixing
matrix. Our multi-dimensional model offers, however, greater
flexibility. Its main advantage is that no assumption is made about
the foreground physics. It is not specifically tailored to perfectly
match the model used in the simulation. Because of this, it is generic
enough to absorb variations in the properties of the foregrounds, as
will be seen later-on, but specific enough to preserve identifiability
in the separation of CMB from foreground emission. A more complete
discussion of the SMICA method with flexible components can be found
in Cardoso et al. (2008).
.
The physical meaning of this is that the various
foregrounds are not identified and extracted individually, only their
mixed contribution is characterised. If we are interested in
disentangling the foregrounds as well, e.g. to separate synchrotron
emission from dust emission, this degeneracy can be lifted by making
use of prior information to constrain, for example, the mixing
matrix. Our multi-dimensional model offers, however, greater
flexibility. Its main advantage is that no assumption is made about
the foreground physics. It is not specifically tailored to perfectly
match the model used in the simulation. Because of this, it is generic
enough to absorb variations in the properties of the foregrounds, as
will be seen later-on, but specific enough to preserve identifiability
in the separation of CMB from foreground emission. A more complete
discussion of the SMICA method with flexible components can be found
in Cardoso et al. (2008).
A couple last details on SMICA and its practical implementation are
of interest here. For numerical purposes, we actually divide the
whole ![]() range into Q frequency bins
range into Q frequency bins
![]() ,
and form the
binned versions of the empirical and true cross power-spectra:
,
and form the
binned versions of the empirical and true cross power-spectra:
where wq is the number of modes in
Finally, we compute the Fisher information matrix
![]() deriving
from the maximised likelihood (14) for the
parameter set
deriving
from the maximised likelihood (14) for the
parameter set
![]() :
:
The lowest achievable variance of the r estimate is obtained as the entry of the inverse of the FIM corresponding to the parameter r:
4 Predicted results for various experimental designs
We now turn to the numerical investigation of the impact of galactic foregrounds on the measurements of r with the following experimental designs:
- the P LANCK space mission, due for launch early 2009, which, although not originally planned for B-mode physics, could provide a first detection if the tensor to scalar ratio r is around 0.1;
- various versions of the EPIC space mission, either low cost and low resolution (EPIC-LC), or more ambitious versions (EPIC-CS and EPIC-2m);
- an ambitious (fictitious) ground-based experiment, based on the extrapolation of an existing design (the C
 over experiment);
over experiment);
- an alternative space mission, with sensitivity performances similar to the EPIC-CS space mission, but mapping only a small (and clean) patch of the sky, and referred as the ``deep field mission''.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11624f6}
\end{figure}](/articles/aa/full_html/2009/33/aa11624-09/Timg94.png) |
Figure 4: Noise spectra of various experimental designs compared to B-modes levels for r = 0.1, 0.01 and 0.001. When computing the equivalent multipole noise level for an experiment, we assume that only the central frequency channels contribute to the CMB measurement and that external channels are dedicated to foreground characterisation. |
| Open with DEXTER | |
4.1 Pipeline
For each of these experiments, we set up one or more simulation and analysis pipelines, which include, for each of them, the following main steps:- simulation of the sky emission for a given value of r and a given foreground model, at the central frequencies and the resolution of the experiment;
- simulation of the experimental noise, assumed to be white, Gaussian and stationary;
- computation, for each of the resulting maps, of the coefficients of the spherical harmonic expansion of the B-modes
 ;
;
- synthesis from those coefficients of maps of B-type signal only;
- for each experiment, a mask based on the B-modes level of the foregrounds is built to blank out the brightest features of the galactic emission (see Fig. 5). This mask is built with smooth edges to reduce mode-mixing in the pseudo-spectrum;
- statistics described in Eq. (18) are built from the masked B maps;
- the free parameters of the model described in Sect. 3.2 are adjusted to fit these statistics. The shape of the CMB pseudo-spectrum that enters in the model, is computed using the mode-mixing matrix of the mask (Hivon et al. 2002);
- Error bars are derived from the Fisher information matrix of the model.
| |
Figure 5:
Analysis mask for EPIC B maps, smoothed with a |
| Open with DEXTER | |
Table 1: Summary of experimental designs.
In practice we choose
![]() according to the sky coverage
and
according to the sky coverage
and
![]() according to the beam and the sensitivity. The
value of D is selected by iterative increments until the goodness of
fit (as measured from the SMICA criterion on the data themselves,
without knowledge of the input CMB and foregrounds) reaches its
expectation. The mask is chosen in accordance to maximise the sky
coverage for the picked value of D (see Appendix A for
further discussion of the procedure). The
according to the beam and the sensitivity. The
value of D is selected by iterative increments until the goodness of
fit (as measured from the SMICA criterion on the data themselves,
without knowledge of the input CMB and foregrounds) reaches its
expectation. The mask is chosen in accordance to maximise the sky
coverage for the picked value of D (see Appendix A for
further discussion of the procedure). The
![]() mask in
Fig. 5, used for EPIC analysis, is based on a 10 degrees
cut of the galactic plane. An additional cut of brightest region on
the B-modes map is built by applying a threshold on the emission level
at the central frequency of the instrument. The threshold can be
adjusted to obtain the suitable sky coverage. These two masks are
combined and edges are smoothed by a 1-degree transition
window
mask in
Fig. 5, used for EPIC analysis, is based on a 10 degrees
cut of the galactic plane. An additional cut of brightest region on
the B-modes map is built by applying a threshold on the emission level
at the central frequency of the instrument. The threshold can be
adjusted to obtain the suitable sky coverage. These two masks are
combined and edges are smoothed by a 1-degree transition
window![]() .
For the Planck data analysis, the galactic plane cut is not necessary,
and the emission level mask is used alone.
.
For the Planck data analysis, the galactic plane cut is not necessary,
and the emission level mask is used alone.
For each experimental design and fiducial value of r we compute three kinds of error estimates which are recalled in Table 2:
- knowing the noise level and resolution of the instrument, we
first derive from Eq. (8) the error
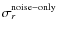 set by the instrument sensitivity
assuming no foreground contamination in the covered part of the
sky. The global noise level of the instrument is given by
set by the instrument sensitivity
assuming no foreground contamination in the covered part of the
sky. The global noise level of the instrument is given by
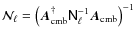 ,
where the only
contribution to
,
where the only
contribution to
 comes from the instrumental noise:
comes from the instrumental noise:
 ;
;
- in the same way, we also compute the error
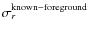 that would be obtained if
foreground contribution
that would be obtained if
foreground contribution
 to the covariance of the
observations was perfectly known, using
to the covariance of the
observations was perfectly known, using
 .
Here we assume that
.
Here we assume that
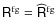 where
where
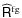 is the sample estimate of
is the sample estimate of
 computed from the simulated
foreground maps;
computed from the simulated
foreground maps;
- finally, we compute the error
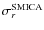 given by
the Fisher information matrix of the model
(Eq. (20)).
given by
the Fisher information matrix of the model
(Eq. (20)).
We may notice that in some favourable cases (at low ![]() ,
where the
foregrounds dominate), the error estimate given by SMICA can be
slightly more optimistic than the estimate obtained using the actual empirical value of
the correlation matrix
,
where the
foregrounds dominate), the error estimate given by SMICA can be
slightly more optimistic than the estimate obtained using the actual empirical value of
the correlation matrix
![]() .
This reflects the fact that our
modelling hypothesis, which imposes to
.
This reflects the fact that our
modelling hypothesis, which imposes to
![]() to be of rank smaller
than D, is not perfectly verified in practice (see Appendix A for further discussion of this hypothesis). The (small) difference (an error on the estimation of
to be of rank smaller
than D, is not perfectly verified in practice (see Appendix A for further discussion of this hypothesis). The (small) difference (an error on the estimation of ![]() when foregrounds are approximated by our model) has negligible impact on the conclusions of this work.
when foregrounds are approximated by our model) has negligible impact on the conclusions of this work.
Table 2: Error prediction for various experimental designs, assumptions about foregrounds, and fiducial r values.
4.2 Planck
The Planck space mission will be the first all-sky experiment to give
sensitive measurements of the polarised sky in seven bands between 30
and 353 GHz. The noise level of this experiment being somewhat too
high for precise measurement of low values of r, we run our pipeline
for r = 0.1 and 0.3. We predict a possible 3-sigma measurement
for r = 0.1 using SMICA (first lines in Table 2). A comparison of the errors obtained from SMICA,
with the prediction in absence of foreground contamination, and with
perfectly known foreground contribution, indicates that the error is
dominated by cosmic variance and noise, foregrounds contributing to a
degradation of the error of ![]()
![]() and uncertainties on
foregrounds for another increase around
and uncertainties on
foregrounds for another increase around ![]() (for r=0.1).
(for r=0.1).
Figure 4 hints that a good strategy to detect primordial
B-modes with Planck consists in detecting the reionisation bump below
![]() ,
which requires the largest possible sky coverage. Even at
high latitude, a model using D=2 fails to fit the galactic
emission, especially on large scales where the galactic signal is
above the noise. Setting D = 3, however, gives a satisfactory fit
(as measured by the mismatch criterion) on 95 percent of the sky. It
is therefore our choice for Planck.
,
which requires the largest possible sky coverage. Even at
high latitude, a model using D=2 fails to fit the galactic
emission, especially on large scales where the galactic signal is
above the noise. Setting D = 3, however, gives a satisfactory fit
(as measured by the mismatch criterion) on 95 percent of the sky. It
is therefore our choice for Planck.
We also note that a significant part of the information is coming from
the reionisation bump (
![]() ). The relative importance of the
bump increases for decreasing value of r, as a consequence of the
cosmic variance reduction. For a signal-to-noise ratio corresponding
roughly to the detection limit (r = 0.1), the stronger constraint is
given by the bump (Appendix B gives further illustration of
the relative contribution of each multipole). This has two direct
consequences: the result is sensitive to the actual value of the
reionisation optical depth and to reionisation history (as
investigated by Colombo & Pierpaoli 2008), and the actual
capability of Planck to measure r will depend on the level (and the
knowledge of) instrumental systematics on large scales. Note that
this numerical experiment estimates how well Planck can measure r in
the presence of foregrounds from B-modes only.
). The relative importance of the
bump increases for decreasing value of r, as a consequence of the
cosmic variance reduction. For a signal-to-noise ratio corresponding
roughly to the detection limit (r = 0.1), the stronger constraint is
given by the bump (Appendix B gives further illustration of
the relative contribution of each multipole). This has two direct
consequences: the result is sensitive to the actual value of the
reionisation optical depth and to reionisation history (as
investigated by Colombo & Pierpaoli 2008), and the actual
capability of Planck to measure r will depend on the level (and the
knowledge of) instrumental systematics on large scales. Note that
this numerical experiment estimates how well Planck can measure r in
the presence of foregrounds from B-modes only.
4.3 EPIC
We perform a similar analysis for three possible designs of the EPIC probe (Bock et al. 2008). EPIC-LC and EPIC-CS correspond respectively to the low cost and comprehensive solutions. EPIC-2m is an alternate design which contains one extra high-frequency channel (not considered in this study) dedicated to additional scientific purposes besides CMB polarisation. We consider two values of r, 0.01 and 0.001. For all these three experiments, the analysis requires D = 4 for a reasonable fit, which is obtained using about 87% of the sky.
The two high resolution experiments provide measurements of
r =
10-3 with a precision better than five sigma. For the lower
values of r, the error is dominated by foregrounds and their
presence degrades the sensitivity by a factor of 3, as witnessed by
the difference between
![]() and
and
![]() .
However, while the difference between the
noise-only and the SMICA result is a factor 4-6 for EPIC-LC, it is
only a factor about 2-3 for EPIC-CS and EPIC-2m. Increased
instrumental performance (in terms of frequency channels and
resolution) thus also allows for better subtraction of foreground
contamination.
.
However, while the difference between the
noise-only and the SMICA result is a factor 4-6 for EPIC-LC, it is
only a factor about 2-3 for EPIC-CS and EPIC-2m. Increased
instrumental performance (in terms of frequency channels and
resolution) thus also allows for better subtraction of foreground
contamination.
For all experiments considered, the constraining power moves from
small scales to larger scale when r decreases down to the detection
limit of the instrument. In all cases, no information for the CMB is
coming from
![]() .
Higher multipoles, however, are still giving
constraints on the foreground parameters, effectively improving the
component separation also on large scales.
.
Higher multipoles, however, are still giving
constraints on the foreground parameters, effectively improving the
component separation also on large scales.
4.4 Small area experiments
4.4.1 Ground-based
A different observation strategy for the measurement of B-modes is
adopted for ground-based experiments that cannot benefit from the
frequency and sky coverage of a space mission. Such experiments target
the detection of the first peak around
![]() ,
by observing a
small but clean area (typically 1000 square-degrees) in few frequency
bands (2 or 3).
,
by observing a
small but clean area (typically 1000 square-degrees) in few frequency
bands (2 or 3).
The test case we propose here is inspired from the announced
performances of C![]() over (North et al. 2008). The
selected sky coverage is a 10 degree radius area centred on
over (North et al. 2008). The
selected sky coverage is a 10 degree radius area centred on
![]() ,
,
![]() in galactic
coordinates. The region has been retained by the C
in galactic
coordinates. The region has been retained by the C![]() over team as
a tradeoff between several issues including, in particular, foreground and
atmospheric contamination. According to our polarised galactic
foreground model, this also correspond to a reasonably clean part of
the sky (within 30% of the cleanest).
over team as
a tradeoff between several issues including, in particular, foreground and
atmospheric contamination. According to our polarised galactic
foreground model, this also correspond to a reasonably clean part of
the sky (within 30% of the cleanest).
The most interesting conclusion is that for r =0.01, although the raw instrumental sensitivity (neglecting issues like E-B mixing due to partial sky coverage) would allow a more than five sigma detection, galactic foregrounds cannot be satisfactorily removed with the scheme adopted here.
An interesting option would be to complement the measurement obtained
from the ground, with additional data such as that of Planck, and
extract r in a joint analysis of the two data sets. To simply test this
possibility here, we complement the ground data set with a simulation
of the Planck measurements on the same area. This is equivalent to
extend the frequency range of the ground experiment with less
sensitive channels. We find a significant improvement of the error-bar
from
![]() to
to
![]() ,
showing that a joint
analysis can lead to improved component separation. The degradation of
sensitivity due to foreground remains however higher than for a fully
sensitive space mission (as witnessed by the following section). This
last result is slightly pessimistic as we do not make use of the full
Planck data set but use it only to constrain foregrounds in the small
patch. However considering the ratio of sensitivity between the two
experiments, it is likely that there is little to gain by pushing the
joint analysis further.
,
showing that a joint
analysis can lead to improved component separation. The degradation of
sensitivity due to foreground remains however higher than for a fully
sensitive space mission (as witnessed by the following section). This
last result is slightly pessimistic as we do not make use of the full
Planck data set but use it only to constrain foregrounds in the small
patch. However considering the ratio of sensitivity between the two
experiments, it is likely that there is little to gain by pushing the
joint analysis further.
4.4.2 Deep field space mission
We may also question the usefulness of a full-sky observation strategy for space-missions, and consider the possibility to spend the whole observation time mapping deeper a small but clean region. We investigate this alternative using an hypothetical experiment sharing the sensitivity and frequency coverage of the EPIC-CS design, and the sky coverage of the ground-based experiment. Although the absence of strong foreground emission may permit a design with a reduced frequency coverage, we keep a design similar to EPIC-CS to allow comparisons. In addition, the relative failure of the ground-based design to disentangle foregrounds indicates that the frequency coverage cannot be freely cut even when looking in the cleanest part of the sky. In the same way, to allow straightforward comparison with the ground-based case we stick to the same sky coverage, although in principle, without atmospheric constraints, slightly better sky areas could be selected.In spite of the increased cosmic variance due to the small sky coverage, the smaller foreground contribution allows our harmonic-based foreground separation with SMICA to achieve better results with the ``deep field'' mission than with the full sky experiment, when considering only diffuse galactic foreground. However, this conclusion does not hold if lensing is considered as will be seen in the following section.
We may also notice that, despite the lower level of foregrounds, the higher precision of the measurement requires the same model complexity (D = 4) as for the full sky experiment to obtain a good fit. We also recall that our processing pipeline does not exploit the spatial variation of foreground intensity, and is, in this sense, suboptimal, in particular for all-sky experiments. Thus, the results presented for the full-sky experiment are bound to be slightly pessimistic which tempers further the results of this comparison between deep field and full sky mission. This is further discussed below. Finally, note that here we also neglect issues related to partial sky coverage that would be unavoidable in this scheme.
4.5 Comparisons
4.5.1 Impact of foregrounds: the ideal case
As a first step, the impact of foregrounds on the capability to measure r with a given experiment, if foreground covariances are known, is a measure of the adequacy of the experiment to deal with foreground contamination. Figures for this comparison are computed using Eqs. (8) and (13), and are given in Table 2 (first two sets of three columns).
The comparison shows that for some experiments,
![]() in the
``noise-only'' and the ``known foregrounds'' cases are very close. This is
the case for Planck and for the deep field mission. For these
experiments, if the second order statistics of the foregrounds are
known, galactic emission does not impact much the measurement. For
other experiments, the ``known foregrounds'' case is considerably worse
than the ``noise-only'' case. This happens, in particular, for a ground
based experiment when r=0.01, and for EPIC-LC.
in the
``noise-only'' and the ``known foregrounds'' cases are very close. This is
the case for Planck and for the deep field mission. For these
experiments, if the second order statistics of the foregrounds are
known, galactic emission does not impact much the measurement. For
other experiments, the ``known foregrounds'' case is considerably worse
than the ``noise-only'' case. This happens, in particular, for a ground
based experiment when r=0.01, and for EPIC-LC.
If foreground contamination was Gaussian and stationary, and in
absence of priors on the CMB power spectrum, the linear filter of
Eq. (12) would be the optimal filter for CMB
reconstruction. The difference between ![]() in the ``noise-only''
and the ``known foregrounds'' cases would be a good measure of how much
the foregrounds hinder the measurement of r with the experiment
considered. A large difference would indicate that the experimental
design (number of frequency channels and sensitivity in each of them)
is inadequate for ``component separation''.
in the ``noise-only''
and the ``known foregrounds'' cases would be a good measure of how much
the foregrounds hinder the measurement of r with the experiment
considered. A large difference would indicate that the experimental
design (number of frequency channels and sensitivity in each of them)
is inadequate for ``component separation''.
However, since foregrounds are neither Gaussian nor stationary, the
linear filter of Eq. (12) is not optimal. Even if
we restrict ourselves to linear solutions, the linear weights given to
the various channels should obviously depend on the local properties
of the foregrounds. Hence, nothing guarantees that we can not deal
better with the foregrounds than using a linear filter in harmonic
space. Assuming that the covariance matrix of the foregrounds is
known, the error in Eq. (8) with
![]() from Eq. (13) is a pessimistic
bound on the error on r. The only conclusion that can be drawn is
that the experiment does not allow effective component separation with
the implementation of a linear filter in harmonic space. There is,
however, no guarantee either that an other approach to component
separation would yield better results. Hence, the comparison of the
noise-only and known foregrounds cases shown here gives an upper limit
of the impact of foregrounds, if they were known.
from Eq. (13) is a pessimistic
bound on the error on r. The only conclusion that can be drawn is
that the experiment does not allow effective component separation with
the implementation of a linear filter in harmonic space. There is,
however, no guarantee either that an other approach to component
separation would yield better results. Hence, the comparison of the
noise-only and known foregrounds cases shown here gives an upper limit
of the impact of foregrounds, if they were known.
4.5.2 Effectiveness of the blind approach
Even if in some cases the linear filter of Eq. (12) may not be fully optimal, it is for each mode ![]() the best linear combination of observations in a set of
frequency channels, to reject maximally contamination from foregrounds
and noise, and minimise the error on r. Other popular methods as
decorrelation in direct space, such as the so-called
``internal linear combination'', and other linear combinations cannot do better,
unless they are implemented locally in both pixel and harmonic space
simultaneously, using for instance spherical needlets as in
Delabrouille et al. (2008). Such localisation is not considered in
the present work.
the best linear combination of observations in a set of
frequency channels, to reject maximally contamination from foregrounds
and noise, and minimise the error on r. Other popular methods as
decorrelation in direct space, such as the so-called
``internal linear combination'', and other linear combinations cannot do better,
unless they are implemented locally in both pixel and harmonic space
simultaneously, using for instance spherical needlets as in
Delabrouille et al. (2008). Such localisation is not considered in
the present work.
Given this, the next question that arises is how well the spectral covariance of the foreground contamination can be actually constrained from the data, and how this uncertainty impact the measurement of r. The answer to this question is obtained by comparing the second and third sets of columns of Table 2.
In all cases, the difference between the results obtained assuming perfect knowledge of the foreground residuals, and those obtained after the blind estimation of the foreground covariances with SMICA, are within a factor of 2. For EPIC-2m and the deep field mission, the difference between the two is small, which means that SMICA allows for component separation very effectively. For a ground based experiment with three frequency channels, the difference is very significant, which means that the data does not allow a good blind component separation with SMICA.
Comparing column set 1 (noise-only) and 3 (blind approach with SMICA) gives the overall impact of unknown galactic foregrounds on the measurement of r from B-modes with the various instruments considered. For Planck, EPIC-2m, or a deep field mission with 8 frequency channels, the final error bar on r is within a factor of 2 of what would be achievable without foregrounds. For EPIC-LC, or even worse for a ground-based experiment, foregrounds are likely to impact the outcome of the experiment quite significantly. For this reason, EPIC-2m and the deep field mission seem to offer better perspectives for measuring r in the presence of foregrounds.
4.5.3 Full sky or deep field
The numerical investigations performed here allow -to some extent- to compare what can be achieved with our approach in two cases of sky observation strategies with the same instrument. For EPIC-CS, it has been assumed that the integration time is evenly spread on the entire sky, and that 87% of the sky is used to measure r. For the ``deep field'' mission, 1% of the sky only is observed with the same instrument, with much better sensitivity per pixel (by a factor of 10).
Comparing
![]() between the two in the noise-only case shows
that the full sky mission should perform better (by a factor 1.4) if
the impact of the foregrounds could be made to be negligible. This is
to be expected, as the cosmic or ``sample'' variance of the measurement
is smaller for larger sky coverage. After component separation
however, the comparison is in favour of the deep field mission, which
seems to perform better by a factor 1.4 also. The present work,
however, does not permit to conclude on what is the best strategy for
two reasons. First, this study concentrates on the impact of diffuse
galactic foregrounds which are not expected to be the limiting issue
of the deep field design.
And secondly, in the case of a deep field, the properties of the
(simulated) foreground emission are more homogeneous in the observed
area, and thus the harmonic filter of Eq. (12) is
close to optimal everywhere. For the full sky mission, however, the
filter is obtained as a compromise minimising the overall error
between the two in the noise-only case shows
that the full sky mission should perform better (by a factor 1.4) if
the impact of the foregrounds could be made to be negligible. This is
to be expected, as the cosmic or ``sample'' variance of the measurement
is smaller for larger sky coverage. After component separation
however, the comparison is in favour of the deep field mission, which
seems to perform better by a factor 1.4 also. The present work,
however, does not permit to conclude on what is the best strategy for
two reasons. First, this study concentrates on the impact of diffuse
galactic foregrounds which are not expected to be the limiting issue
of the deep field design.
And secondly, in the case of a deep field, the properties of the
(simulated) foreground emission are more homogeneous in the observed
area, and thus the harmonic filter of Eq. (12) is
close to optimal everywhere. For the full sky mission, however, the
filter is obtained as a compromise minimising the overall error ![]() by
by ![]() ,
which is not likely to be the best everywhere on the
sky. Further work on component separation, making use of a localised
version of SMICA, is needed to conclude on this issue. A preliminary
version of SMICA in wavelet space is described in
Moudden et al. (2004), but applications to CMB polarisation and
full sky observations require specific developments.
,
which is not likely to be the best everywhere on the
sky. Further work on component separation, making use of a localised
version of SMICA, is needed to conclude on this issue. A preliminary
version of SMICA in wavelet space is described in
Moudden et al. (2004), but applications to CMB polarisation and
full sky observations require specific developments.
5 Discussion
The results presented in the previous section have been obtained using a number of simplifying assumptions. First of all, only galactic foregrounds (synchrotron and dust) are considered. It has been assumed that other foregrounds (point sources, lensing) can be dealt with independently, and thus will not impact much the overall results. Second, it is quite clear that the results may depend on details of the galactic emission, which might be more complex than what has been used in our simulations. Third, most of our conclusions depend on the accuracy of the determination of the error bars from the Fisher information matrix. This method, however, only provides an approximation, strictly valid only in the case of Gaussian processes and noise. Finally, the measurement of r as performed here assumes a perfect prediction (from other sources of information) of the shape of the BB spectrum. In this section, we discuss and quantify the impact of these assumptions, in order to assess the robustness of our conclusions.
5.1 Small-scale contamination
5.1.1 Impact of lensing
Limitations on tensor mode detection due to lensing have been widely investigated in the literature, and cleaning methods, based on the reconstruction of the lensed B-modes from estimation of the lens potential and unlensed CMB E-modes, have been proposed (Knox & Song 2002; Kesden et al. 2003; Lewis & Challinor 2006; Hirata & Seljak 2003). However, limits on r achievable after such ``delensing'' (if any) are typically significantly lower than limits derived in Sect. 4, for which foregrounds and noise dominate the error.
In order to check whether the presence of lensing can significantly
alter the detection limit, we proceed as follows: assuming no specific
reconstruction of the lens potential, we include lensing effects in
the simulation of the CMB (at the power spectrum level). The impact of
this on the second order statistics of the CMB is an additional
contribution to the CMB power spectrum. This extra term is taken into
account on the CMB model used in SMICA. For this, we de-bias the CMB
SMICA component from the (expectation value of) the lensing
contribution to the power-spectrum. The cosmic variance of the lensed
modes thus contributes as an extra ``noise'' which lowers the
sensitivity to the primordial signal, and reduces the range of
multipoles contributing significantly to the measurement. We run this
lensing test case for the EPIC-CS and deep field mission. Table 3 shows a comparison of the constraints obtained with
and without lensing in the simulation for a fiducial value of r =
0.001. On large scales for EPIC-CS, lensing has negligible impact on
the measurement of r (the difference between the two cases is not
significant on one single run of the component separation). On small
scales, the difference becomes significant. Overall,
![]() changes from 0.18 to 0.21, which is not a very
significant degradation of the measurement: lensing produces a 15%
increase in the overall error estimate, the small-scale error (for
changes from 0.18 to 0.21, which is not a very
significant degradation of the measurement: lensing produces a 15%
increase in the overall error estimate, the small-scale error (for
![]() )
being most impacted. For the small coverage mission,
however, the large cosmic variance of the lensing modes considerably
hinder the detection.
)
being most impacted. For the small coverage mission,
however, the large cosmic variance of the lensing modes considerably
hinder the detection.
Table 3: Comparison of the constraints on r with and without lensing (here r=0.001).
Thus, at this level of r, if the reionisation bump is satisfactorily measured, the difference is perceptible but not very significant. Hence, lensing is not the major source of error for a full-sky experiment measuring r. It becomes however a potential problem for a small coverage experiment targeting the measurement of the recombination bump. Such a strategy would thus require efficient ``delensing''. Indications that ``delensing'' can be performed even in the presence of foregrounds in the case of a low noise and high resolution experiment can be found in Smith et al. (2008). However, a complete investigation of this case, accounting for all the complexity (diffuse foregrounds, point sources, lensing, modes-mixing effects), would be needed to conclude on the validity of a deep-field strategy.
5.1.2 Impact of extra-galactic sources
Although largely subdominant on scales larger than 1 degree, extra-galactic sources, in particular radio-sources, are expected to be the worst contaminant on small scales (see e.g. Pierpaoli & Perna 2004; Tucci et al. 2004). Obviously, the strongest point sources are known, or (for most of them) will be detected by Planck. Their polarisation can be measured either by the B-mode experiment itself, or by dedicated follow-up. We make the assumption that point sources brighter than 500 mJy in temperature (around 6000 sources) are detected, and that their polarised emission is subtracted from the polarisation observations. We stress that 500 mJy is a conservative assumption as Planck is expected to have better detection thresholds.
The present level of knowledge about point sources does not allow a very accurate modelling of the contribution to the power spectra of the remaining point sources (those not subtracted by the 500 mJy cut). For this reason we investigate their impact in two extreme cases: perfect modelling of their contribution to the power-spectra (``ideal'' case), and no specific modelling at all (``no-model'' case). Results of a SMICA run for both assumptions are compared to what is obtained in total absence of point sources (``no-ps'' case), and are summarised in Table 4.
Table 4: EPIC-CS measurement for three point sources cases.
 |
Figure 6: Goodness-of-fit for the three point sources cases. For the reference case ``no-ps'', point sources have neither been including in the simulation, nor taken into account in the modelling. The mismatch criterion wander around its expectation value (horizontal dashed line). The ``no-model'' case is a pessimistic situation where no effort has been made to model the point sources contribution, yielding a net increase of the mismatch criterion. The ``ideal'' case presents an optimistic situation where the exact contribution of the simulated point sources has been used to build the model. |
| Open with DEXTER | |
The bottom line of this investigation is that modelling properly the
point sources statistical contribution is necessary to measure
r=0.001. An insufficient model results in a biased estimator: for
EPIC-CS the estimated r is two times larger than expected, with a
difference incompatible with the error bar, in spite of an increased
standard deviation (![]() increased by +30% for r=0.001). An
ideal model restores the goodness of fit of the no-ps case and
suppresses the bias of the estimator. Still, the presence of point
sources increases the variance of the measurement of r. In our
experiment, the effect is not truly significant (
increased by +30% for r=0.001). An
ideal model restores the goodness of fit of the no-ps case and
suppresses the bias of the estimator. Still, the presence of point
sources increases the variance of the measurement of r. In our
experiment, the effect is not truly significant (![]() shifting
from 1.84 to
shifting
from 1.84 to
![]() ).
).
Figure 6 shows the mismatch criterion (from
Eq. (16), using covariance matrixes binned in ![]() )
in
the three cases. When no specific model of the point source
contribution is used, some of their emission is nonetheless absorbed
by the SMICA ``galactic'' component, which adjusts itself (via the
values of its maximum likelihood parameters) to represent best the
total foreground emission. The remaining part is responsible for the
increase of the mismatch at high
)
in
the three cases. When no specific model of the point source
contribution is used, some of their emission is nonetheless absorbed
by the SMICA ``galactic'' component, which adjusts itself (via the
values of its maximum likelihood parameters) to represent best the
total foreground emission. The remaining part is responsible for the
increase of the mismatch at high ![]() .
At the same time, the
galactic estimation is twisted by the presence of point sources. This
slightly increases the mismatch on large scales.
.
At the same time, the
galactic estimation is twisted by the presence of point sources. This
slightly increases the mismatch on large scales.
5.2 Galactic foregrounds uncertainties
We now investigate the impact on the above results of modifying somewhat the galactic emission. In particular, we check whether a space dependant curvature of the synchrotron spectral index, and modifications of the dust angular power spectrum, significantly change the error bars on r obtained in the previous section. Those two modifications reflect two of the main uncertainties on diffuse foregrounds modelling discussed in Sect. 2.4. Although it is quite expectable that substantial variations of dust emission law can occur, modifications of the model in this sense would remain purely speculative and we choose to stick with simple modification of the (poorly constrained) dust emission level. Those two points are also representative of two different kinds of modelling errors: the first modification impacts the coherence of the emission across channels, while the second one illustrates the effect of an overall increase of the contamination level.
5.2.1 Impact of synchrotron curvature
As mentioned earlier on, the synchrotron emission law may not be
perfectly described as a single power law per pixel, with a constant
spectral index across frequencies. Steepening of the spectral index is
expected in the frequency range of interest. As this variation is
related to the aging of cosmic rays, it should vary on the sky.
Hence, the next level of sophistication in modelling synchrotron
emission makes use of a (random) template map ![]() to model
the curvature of the synchrotron spectral index. We then produce
simulated synchrotron maps as:
to model
the curvature of the synchrotron spectral index. We then produce
simulated synchrotron maps as:
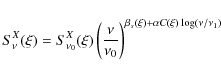 |
(21) |
where
We now investigate whether such a modified synchrotron changes the accuracy with which r can be measured. We decide, for illustrative purposes, to perform the comparison for EPIC-2m, and for r=0.001. Everything else, regarding the other emissions and the foreground model in SMICA, remains unchanged. Table 5 shows the results of this study in terms of goodness of fit and influence on the r estimate. We observe no significant effect, which indicates that the foreground emission model of Eq. (17) is flexible enough to accommodate the variation of the synchrotron modelling. Even if we cannot test all possible deviation from the baseline PSM model, robustness against running of the spectral index remains a good indication that results are not overly model dependent.
Table 5: Influence of the running of the synchrotron spectral index on component separation in term of goodness of fit and r estimates for the EPIC-2m design.
 |
Figure 7: Variations of the galactic foregrounds model. The left panel shows the dispersion of the synchrotron spectral index for the PSM model (in black) and the curved model (in gray). Solid lines present the frequency scaling for the mean values of the spectral index and dotted lines for its extremal values. The right panel shows the difference between the default power spectrum of dust polarisation B-modes at 150 GHz as modelled by the PSM (solid curve) and a model assuming pessimistic values for the overall level and power spectrum index (dotted curve). |
| Open with DEXTER | |
5.2.2 Level and power spectrum of dust emission
Similarly, we now vary the model of dust emission and check how the main results of Sect. 4 are modified. Measurements give some constraints on dust emission on large scales, but smaller scales remain mostly unconstrained. Hence, we consider here a pessimistic extreme in which we multiply the large-scale level of the dust by a factor of two, and flatten the power spectrum from a nominal index of -2.5 to -1.9. The power spectra corresponding to these two cases are shown in Fig. 7 (right panel).
Table 6: Influence of dust polarisation level on component separation.
Running the same component separation pipeline for the ground based and the EPIC-2m experiments at their detection limit, we find only marginal changes in the measured values of r (see Table 6). This result can be interpreted in the following way: as the noise of the experiment remains unchanged, the increased signal-to-noise ratio allows for a better constraint of the dust parameters. Component separation effectiveness depends mainly on the coherence of the component, rather than on its overall level.
5.3 Error bar accuracy
Estimates of the error derived from the FIM (Eq. (20)) are expected to be meaningful only if the model leading to the likelihood (Eq. (14)) holds. In particular we assume that processes can be modelled as Gaussian.
We first note that the FIM errors are reasonably compatible with the
difference between input and measured r values, which gives
confidence that these error estimates are not obviously wrong.
Nonetheless, we investigate this issue further, using Monte-Carlo
studies to obtain comparative estimates of errors, with the EPIC-CS
design. Table 7 gives, for two values of r and for 100 runs of the SMICA pipeline in each case, the average recovered value
of r, the average error as estimated from the Fisher matrix
![]() ,
and the standard deviation
,
and the standard deviation
![]() of the measured values of r. For each of the
Monte-Carlo runs, a new realisation of CMB and noise is
generated. Simulated galactic foregrounds, however, remain unchanged.
of the measured values of r. For each of the
Monte-Carlo runs, a new realisation of CMB and noise is
generated. Simulated galactic foregrounds, however, remain unchanged.
Results show that the FIM approximation give estimates of the error in very good agreement with the MC result. Hence, the FIM estimate looks good enough for the purpose of the present paper, given the number of other potential sources of error and the computational cost of Monte-Carlo studies.
The Monte-Carlo study also allows to investigate the existence of a
bias. For an input tensor to scalar ratio of 0.01, we observe that
the measured value of r seems to be systematically low, with an
average of
![]() .
This we interpret as resulting from
a slight over-fitting of the data. Still this small bias does not
dominate the error and we are more interested in noise dominated
regime. The overall conclusion of this investigation of error bars is
that the errors estimated by the FIM are reasonably representative of
the measurement error.
.
This we interpret as resulting from
a slight over-fitting of the data. Still this small bias does not
dominate the error and we are more interested in noise dominated
regime. The overall conclusion of this investigation of error bars is
that the errors estimated by the FIM are reasonably representative of
the measurement error.
Table 7: Comparaison of the predicted error bar and the root mean squared error measured on 100 Monte Carlo realisations of EPIC-CS observation.
5.4 Other cosmological parameters
The main conclusions of this study are mostly independent of the value
of all cosmological parameters except ![]() .
Within present
uncertainties indeed, only the value of the reionisation optical depth
.
Within present
uncertainties indeed, only the value of the reionisation optical depth
![]() ,
which drives the amplitude and position of the reionisation
bump, is critical for our estimations (Colombo et al. 2008). Lower
,
which drives the amplitude and position of the reionisation
bump, is critical for our estimations (Colombo et al. 2008). Lower ![]() means less accurate measurement of r, and higher
means less accurate measurement of r, and higher ![]() better measurement of r. Here we choose a rather conservative value
of
better measurement of r. Here we choose a rather conservative value
of
![]() in agreement with the last measurements from WMAP
(Dunkley et al. 2008c,b). The value of
in agreement with the last measurements from WMAP
(Dunkley et al. 2008c,b). The value of ![]() ,
however, should affect mainly low resolution and noisy experiments,
for which most of the information comes from the lowest frequency
``reionisation'' bump in the B-mode spectrum.
,
however, should affect mainly low resolution and noisy experiments,
for which most of the information comes from the lowest frequency
``reionisation'' bump in the B-mode spectrum.
Another issue is that we assume the value of ![]() and nt (and, to
a less extent, the value of all other cosmological parameters) to be
perfectly known (setting the shape of the B-mode power spectrum). In
fact, uncertainties on all cosmological parameters imply that the
shape will be known only approximately, and within a certain
framework. Such uncertainties will have to be taken into account in
the analysis of a real-life data set. Our SMICA pipeline can be
adapted to do this, provided we know the uncertainties on the
cosmological parameter set. A Monte-Carlo approach, in which we
assume, for each SMICA run, a B-mode power spectrum from one of the
possible cosmological parameter sets, will permit to propagate the
uncertainties onto the measurement of r. We expect, however, that
this additional error will be significantly smaller than that due to
the experimental noise.
and nt (and, to
a less extent, the value of all other cosmological parameters) to be
perfectly known (setting the shape of the B-mode power spectrum). In
fact, uncertainties on all cosmological parameters imply that the
shape will be known only approximately, and within a certain
framework. Such uncertainties will have to be taken into account in
the analysis of a real-life data set. Our SMICA pipeline can be
adapted to do this, provided we know the uncertainties on the
cosmological parameter set. A Monte-Carlo approach, in which we
assume, for each SMICA run, a B-mode power spectrum from one of the
possible cosmological parameter sets, will permit to propagate the
uncertainties onto the measurement of r. We expect, however, that
this additional error will be significantly smaller than that due to
the experimental noise.
6 Conclusion
In this paper, we presented an investigation of the impact of
foregrounds on the measurement of the tensor to scalar ratio of
primordial perturbations. The measurement of r is based on the
(simulated) observation of the B-mode polarisation of the cosmic
microwave background by various instruments, either in preparation or
planned for the future: the Planck space mission, a ground-based
experiment of the type of C![]() over, and several versions of a
possible dedicated space mission.
over, and several versions of a
possible dedicated space mission.
Foreground contamination is modelled and simulated using the present development version (v1.6.4) of the PSM. Our main analysis considers the contribution from diffuse polarised emission (from the galactic interstellar medium modelled as a mixture of synchrotron emission and thermal emission from dust) and from instrumental noise. The impact of more complicated galactic foreground emission, and of point sources and lensing, is investigated in a second step.
Our approach uses the SMICA component separation method on maps of B-modes alone. The method is robust with respect to specifics of foreground emission, because it does not rely on an accurate representation of foreground properties. That last point is demonstrated by varying the input foreground sky, and comparing results obtained with different inputs, without changing the analysis pipeline.
It is shown that for r at the level of
![]() ,
Planck could
make a meaningful (
,
Planck could
make a meaningful (![]() )
detection from B-modes alone. The
final sensitivity of Planck for measuring r may be better than what
is achieved here, as a significant part of the constraining power on r should also come from EE/TE for high r. This has not been
investigated in the present paper, which is more focussed on the
measurement of low values of r (not achievable with Planck). With
the various EPIC mission designs, one could achieve detections at
levels of 4-8
)
detection from B-modes alone. The
final sensitivity of Planck for measuring r may be better than what
is achieved here, as a significant part of the constraining power on r should also come from EE/TE for high r. This has not been
investigated in the present paper, which is more focussed on the
measurement of low values of r (not achievable with Planck). With
the various EPIC mission designs, one could achieve detections at
levels of 4-8![]() for r=10-3.
for r=10-3.
For full-sky, multi-frequency space missions, dealing with foregrounds in harmonic space results in a loss of sensitivity by a factor 3 to 4, as compared to what would be achievable without foregrounds, even if the covariance of foreground contaminants is known. The SMICA pipeline allows to achieve performances almost as good (within a factor 1.5), which demonstrates the effectiveness of the blind approach, but is still significantly worse (factor 3-5) than if there were no foregrounds at all. The loss of sensitivity is probably due in part to insufficient localisation in pixel space, which results in suboptimality of the estimator. This could (at least in principle) be improved with a localised processing.
For the most ambitious EPIC space mission, we find that our main conclusions are not modified significantly when taking into account the contamination of primordial B-modes by extra-galactic point sources, by gravitational lensing, or when simulating a more complicated galactic emission. In contrast, we find that the measurement of r from the ground with few frequency channels can be severely compromised by foregrounds, even in clean sky regions.
The joint analysis of such ground-based data together with those from less sensitive experiments covering a wider frequency range, such as the Planck data, permits to improve the constraints on r. Still, the result from a combined analysis of Planck and of a small patch observed from the ground at few frequencies cannot match what is obtained using sensitive measurements on the whole frequency range.
This makes a strong case for sensitive multi-frequency observations, and thus probably also for a space mission, as observations from the ground are severely limited (in frequency coverage) by atmospheric absorption and emission. This conclusion is further supported by the fact that a space mission mapping the same clean region (about 1% of the sky), but with the full frequency range allowed by the absence of atmosphere, makes it possible to deal with diffuse foregrounds very efficiently.
Such a deep field mission would, in that respect, outperform a comparable full-sky experiment. The results obtained in the present study, however, do not permit to conclude whether a full sky or a deep field mission would ultimately perform better. A strategy based on the observation of a small patch seems to offer better prospects for measuring r with an harmonic-space based version of SMICA, but also seems to be more impacted by small-scale contamination than all-sky experiments, and is in particular quite sensitive to the lensing effect. Further developments of the component separation pipeline could improve the processing of both types of datasets.
As a final comment, we would like to emphasise that the present study
designs, implements effectively, and tests thoroughly on numerous
simulations a component separation method for measuring r with CMB
B-modes which do not rely on a physical model of foreground
emission. The method is shown to be robust against complicated
foregrounds (pixel-dependent and running synchrotron spectral index,
multi-template dust emission, polarised point sources and lensing). It
is also shown to provide reliable errors bars on r by comparing
analytical error bars (from the FIM) to estimates obtained from
Monte-Carlo simulations. Although more work is needed for the optimal
design of the next B-mode experiment, our results demonstrate that
foregrounds can be handled quite effectively, making possible the
measurement of r down to values of 0.001 or better, at the
5-6![]() level.
level.
Certainly, next steps will require fully taking into account small-scale contaminants, partial sky coverage effects, and probably some instrumental effects in addition to diffuse foregrounds. For this level of detail, however, it would be mandatory to refine as well the diffuse foreground model, using upcoming sensitive observations of the sky in the frequency range of interest and on both large and small scales. Such data will become available soon with the forthcoming Planck mission.
Acknowledgements
The authors acknowledge the use of the PSM, developed by the Component Separation Working Group (WG2) of the Planck Collaboration. The HEALPix package (Górski et al. 2005) was used for the derivation of some of the results presented in this paper. M.B. would like to thank USC for hospitality during the Spring 2008 and Marc-Antoine Miville-Deschênes for sharing his expertise on galactic foreground modelling. EP is an NSF-ADVANCE fellow (AST-0649899) also supported by NASA grant NNX07AH59G and Planck subcontract 1290790. J.D., J.F.C. and M.L.J. were partially supported by the ACI ``Astro-Map'' grant of the French ministry of research to develop the SMICA component separation package used here.Partial support for EP and MB in carrying out this research was provided by the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration and funded through the Director's Research and Development Fund Program. (SURP award 1314616)''.
References
- Amblard, A., Cooray, A., & Kaplinghat, M. 2007, Phys. Rev. D, 75, 083508 [NASA ADS] [CrossRef] (In the text)
- Audit, E., & Simmons, J. F. L. 1999, MNRAS, 305, L27 [NASA ADS] [CrossRef]
- Aumont, J., & Macías-Pérez, J. F. 2007, MNRAS, 376, 739 [NASA ADS] [CrossRef] (In the text)
- Battistelli, E. S., Rebolo, R., Rubiño-Martín, J. A., et al. 2006, ApJ, 645, L141 [NASA ADS] [CrossRef] (In the text)
- Baumann, D., & Peiris, H. V. 2008, ArXiv e-prints
- Baumann, D., Jackson, M. G., Adshead, P., et al. 2008, ArXiv e-prints (In the text)
- Bennett, C. L., Hill, R. S., Hinshaw, G., et al. 2003, ApJS, 148, 97 [NASA ADS] [CrossRef] (In the text)
- Benoît, A., Ade, P., Amblard, A., et al. 2004, A&A, 424, 571 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bock, J., Cooray, A., Hanany, S., et al. 2008, ArXiv e-prints (In the text)
- Cardoso, J.-F., Le Jeune, M., Delabrouille, J., Betoule, M., & Patanchon, G. 2008, ArXiv e-prints, 803 (In the text)
- Challinor, A., Chon, G., Hivon, E., Prunet, S., & Szapudi, I. 2003, New Astron. Rev., 47, 995 [NASA ADS] [CrossRef]
- Colombo, L. P. L., & Pierpaoli, E. 2008, ArXiv e-prints (In the text)
- Colombo, L. P. L., Pierpaoli, E., & Pritchard, J. R. 2008, ArXiv e-prints (In the text)
- de Oliveira-Costa, A., Tegmark, M., Davies, R. D., et al. 2004, ApJ, 606, L89 [NASA ADS] [CrossRef]
- de Zotti, G., Ricci, R., Mesa, D., et al. 2005, A&A, 431, 893 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Delabrouille, J., Cardoso, J.-F., & Patanchon, G. 2003, MNRAS, 346, 1089 [NASA ADS] [CrossRef] (In the text)
- Delabrouille, J., Cardoso, J., Le Jeune, M., et al. 2008, ArXiv e-prints (In the text)
- Delabrouille, et al. 2009, in preparation (In the text)
- Désert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS]
- Draine, B. T., & Fraisse, A. A. 2008, ArXiv e-prints
- Draine, B. T., & Lazarian, A. 1998, ApJ, 508, 157 [NASA ADS] [CrossRef] (In the text)
- Dunkley, J., Amblard, A., Baccigalupi, C., et al. 2008a, ArXiv e-prints (In the text)
- Dunkley, J., Komatsu, E., Nolta, M. R., et al. 2008b, ArXiv e-prints, 803 (In the text)
- Dunkley, J., Spergel, D. N., Komatsu, E., et al. 2008c, ArXiv e-prints
- Finkbeiner, D. P. 2004, ApJ, 614, 186 [NASA ADS] [CrossRef]
- Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] (In the text)
- Fosalba, P., Lazarian, A., Prunet, S., & Tauber, J. A. 2002, ApJ, 564, 762 [NASA ADS] [CrossRef]
- Giardino, G., Banday, A. J., Górski, K. M., et al. 2002, A&A, 387, 82 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gold, B., Bennett, C. L., Hill, R. S., et al. 2008, ArXiv e-prints, 803
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] (In the text)
- Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] (In the text)
- Hirata, C. M., & Seljak, U. 2003, Phys. Rev. D, 67, 043001 [NASA ADS] [CrossRef]
- Hivon, E., Górski, K. M., Netterfield, C. B., et al. 2002, ApJ, 567, 2 [NASA ADS] [CrossRef] (In the text)
- Hu, W., & White, M. 1997, New Astron., 2, 323 [NASA ADS] [CrossRef]
- Hu, W., Hedman, M. M., & Zaldarriaga, M. 2003, Phys. Rev. D, 67, 043004 [NASA ADS] [CrossRef]
- Jonas, J. L., Baart, E. E., & Nicolson, G. D. 1998, MNRAS, 297, 977 [NASA ADS] [CrossRef] (In the text)
- Kamionkowski, M., & Kosowsky, A. 1998, Phys. Rev. D, 57, 685 [NASA ADS] [CrossRef]
- Kamionkowski, M., Kosowsky, A., & Stebbins, A. 1997, Phys. Rev. Lett., 78, 2058 [NASA ADS] [CrossRef]
- Kaplan, J., & Delabrouille, J. 2002, in Astrophysical Polarized Backgrounds, ed. S. Cecchini, S. Cortiglioni, R. Sault, & C. Sbarra, AIP Conf. Ser., 609, 209
- Kesden, M., Cooray, A., & Kamionkowski, M. 2003, Phys. Rev. D, 67, 123507 [NASA ADS] [CrossRef]
- Knox, L., & Song, Y.-S. 2002, Phys. Rev. Lett., 89, 011303 [NASA ADS] [CrossRef]
- Kovac, J. M., Leitch, E. M., Pryke, C., et al. 2002, Nature, 420, 772 [NASA ADS] [CrossRef]
- Lazarian, A. 2007, J. Quant. Spec. Rad. Trans., 106, 225 [NASA ADS] [CrossRef] (In the text)
- Lazarian, A., & Finkbeiner, D. 2003, New Astron. Rev., 47, 1107 [NASA ADS] [CrossRef] (In the text)
- Lewis, A., & Challinor, A. 2006, Phys. Rep., 429, 1 [NASA ADS] [CrossRef]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [NASA ADS] [CrossRef]
- Macellari, N., Pierpaoli, E., Dickinson, C., & Vaillancourt, J. 2008, in prep. (In the text)
- Miville-Deschênes, M., Ysard, N., Lavabre, A., et al. 2008, ArXiv e-prints, 802 (In the text)
- Moudden, Y., Cardoso, J., Starck, J., & Delabrouille, J. 2004, ArXiv Astrophysics e-prints (In the text)
- North, C. E., Johnson, B. R., Ade, P. A. R., et al. 2008, ArXiv e-prints (In the text)
- Page, L., Hinshaw, G., Komatsu, E., et al. 2007, ApJS, 170, 335 [NASA ADS] [CrossRef]
- Peiris, H. V., Komatsu, E., Verde, L., et al. 2003, ApJS, 148, 213 [NASA ADS] [CrossRef] (In the text)
- Pierpaoli, E., & Perna, R. 2004, MNRAS, 354, 1005 [NASA ADS] [CrossRef]
- Platania, P., Burigana, C., Maino, D., et al. 2003, A&A, 410, 847 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Reich, P., & Reich, W. 1986, A&AS, 63, 205 [NASA ADS] (In the text)
- Ricci, R., Prandoni, I., Gruppioni, C., Sault, R. J., & De Zotti, G. 2004, A&A, 415, 549 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rosset, C., Yurchenko, V. B., Delabrouille, J., et al. 2007, A&A, 464, 405 [NASA ADS] [CrossRef] [EDP Sciences]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative processes in astrophysics (New York: Wiley-Interscience), 393 (In the text)
- Sazonov, S. Y., & Sunyaev, R. A. 1999, MNRAS, 310, 765 [NASA ADS] [CrossRef]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] (In the text)
- Seljak, U., & Zaldarriaga, M. 1997, Phys. Rev. Lett., 78, 2054 [NASA ADS] [CrossRef]
- Seto, N., & Pierpaoli, E. 2005, Phys. Rev. Lett., 95, 101302 [NASA ADS] [CrossRef]
- Sievers, J., & CBI Collaboration. 2005, in BAAS, 37, 1329
- Smith, K. M., & Zaldarriaga, M. 2007, Phys. Rev. D, 76, 043001 [NASA ADS] [CrossRef]
- Smith, K. M., Cooray, A., Das, S., et al. 2008, ArXiv e-prints (In the text)
- Strong, A. W., Moskalenko, I. V., & Ptuskin, V. S. 2007, Ann. Rev. Nucl. Part. Sci., 57, 285 [NASA ADS] [CrossRef] (In the text)
- Tegmark, M., de Oliveira-Costa, A., & Hamilton, A. J. 2003, Phys. Rev. D, 68, 123523 [NASA ADS] [CrossRef] (In the text)
- Tucci, M., Martínez-González, E., Toffolatti, L., González-Nuevo, J., & De Zotti, G. 2004, MNRAS, 349, 1267 [NASA ADS] [CrossRef]
- Tucci, M., Martínez-González, E., Vielva, P., & Delabrouille, J. 2005, MNRAS, 360, 935 [NASA ADS] [CrossRef] (In the text)
- Verde, L., Peiris, H. V., & Jimenez, R. 2006, J. Cosmol. Astro-Part. Phys., 1, 19 [NASA ADS] [CrossRef] (In the text)
- Zaldarriaga, M., & Seljak, U. 2000, ApJS, 129, 431 [NASA ADS] [CrossRef]
- Zaldarriaga, M., Seljak, U., & Bertschinger, E. 1998, ApJ, 494, 491 [NASA ADS] [CrossRef]
Online Material
Appendix A: Parameterisation the foreground component and choice of a mask
In this appendix, we discuss in more detail the dimension D of matrix used to represent the covariance of the total galactic emission, and the choice of a mask to hide regions of strong galactic emission for the estimation of r with SMICA.
A.1 Dimension D of the foreground component
First, we explain on a few examples the mechanisms which set the rank
of the foreground covariance matrix, to give an intuitive
understanding of how the dimension D of the foregrounds component
used in SMICA to obtain a good model of the data. Let us consider
the case of a ``perfectly coherent'' physical process, for which the
total emission, as a function of sky direction ![]() and frequency
and frequency ![]() ,
is well described by a spatial template multiplied by a
pixel-independent power law frequency scaling:
,
is well described by a spatial template multiplied by a
pixel-independent power law frequency scaling:
The covariance matrix of this foreground will be of rank one and
This is not necessarily the best linear approximation of the emission, but supposing it holds, the covariance matrix of the foreground will be of rank two (as the sum of two correlated rank 1 processes). If the noise level is sufficiently low, the variation introduced by the first order term of Eq. (A.2) becomes truly significant, we can't model the emission by a mono-dimensional component as in Eq. (A.1).
In this work, we consider two processes, synchrotron and dust, which are expected to be correlated (at least by the galactic magnetic field and the general shape of the galaxy). Moreover, significant spatial variation of their emission law arises (due to cosmic aging, dust temperature variation ...), which makes their emission only partially coherent from one channel to another. Consequently, we expect that the required dimension D of the galactic foreground component will be at least 4 as soon as the noise level of the instrument is low enough.
The selection of the model can also be made on the basis of a statistical criterion. For example, Table A.1 shows the Bayesian information criterion (BIC) in the case of the EPIC-2m experiment (r = 0.01) for 3 consecutive values of D. The BIC is a decreasing function of the likelihood and of the number of parameter. Hence, lower BIC implies either fewer explanatory variables, better fit, or both. In our case the criterion reads:
where k is the number of estimated parameters and wq the effective number of modes in bin q. Taking into account the redundancy in the parameterisation, the actual number of free parameters in the model is
Table A.1: Bayesian information criterion of 3 models with increasing dimension of the galactic component for the EPIC-2m mission.
A.2 Masking influence
The noise level and the scanning strategy remaining fixed in the full-sky experiments, a larger coverage gives more information and should result in tighter constraints on both foreground and CMB. In practice, it is only the case up to a certain point, due to the non stationarity of the foreground emission. In the galactic plane, the emission is too strong and too complex to fit in the proposed model, and this region must be discarded to avoid contamination of the results. The main points governing the choice of an appropriate mask are the following:
- the covariance of the total galactic emission (synchrotron and dust polarised emissions), because of the variation of emission laws as a function of the direction on the sky, is never exactly modelled by a rank D matrix. However it is satisfactorily modelled in this way if the difference between the actual second order statistics of the foregrounds, and those of the rank D matrix model, are indistinguishable because of the noise level (or because of cosmic variance in the empirical statistics). The deviation from the model is more obvious in regions of strong galactic emission, hence the need for a galactic mask. The higher the noise, the smaller the required mask;
- SMICA provides a built-in measure of the adequacy of the model, which is the value of the spectral mismatch. If too high, the model under-fits the data, and the dimension of the foreground model (or the size of the mask) should be increased. If too low, the model over-fits the data, and D should be decreased;
- near full sky coverage is better for measuring adequately the reionisation bump;
- the dimension of the foreground component must be smaller than the number of channels.
If, on the other hand, the error seems dominated by the contribution of foregrounds, which is, for example, the case of the EPIC-2m experiment for r = 0.001, the tradeoff is unclear and it may happen that a better estimator is obtained with a stronger masking of the foreground contamination. We found that it is not the case. Table A.2 illustrates the case of the EPIC-2m experiment with the galactic cut used in Sect. 4 and a bigger cut. Although the reduction of sensitivity is slower in the presence of foreground than for the noise dominated case, the smaller mask still give the better results.
Table A.2: Estimation of the tensor to scalar ratio with two different galactic cuts in the EPIC-2m experiment.
We may also recall that the expression (7) of the likelihood is an approximation for partial sky coverage. The scheme presented here thus may not give fully reliable results when masking effects become important.
Appendix B: Spectral mismatch
Computed for each bin q of ![]() ,
the mismatch criterion,
,
the mismatch criterion,
![]() ,
between the best-fit model
,
between the best-fit model
![]() at the point of convergence
at the point of convergence ![]() ,
and the data
,
and the data
![]() ,
gives a picture of the goodness of fit as a function of the
scale. Black curves in Figs. B.1 and B.2 show the mismatch criterion of the best fits for
Planck and EPIC designs respectively. When the model holds, the value
of the mismatch is expected to be around the number of degrees of
freedom (horizontal black lines in the figures). We can also compute
the mismatch for a model in which we discard the CMB contribution
,
gives a picture of the goodness of fit as a function of the
scale. Black curves in Figs. B.1 and B.2 show the mismatch criterion of the best fits for
Planck and EPIC designs respectively. When the model holds, the value
of the mismatch is expected to be around the number of degrees of
freedom (horizontal black lines in the figures). We can also compute
the mismatch for a model in which we discard the CMB contribution
![]() .
Gray curves in
Figs. B.1 and B.2 show the mismatch
for this modified model. The difference between the two curves
illustrates the ``weight'' of the CMB component in the fit, as a
function of the scale.
.
Gray curves in
Figs. B.1 and B.2 show the mismatch
for this modified model. The difference between the two curves
illustrates the ``weight'' of the CMB component in the fit, as a
function of the scale.
 |
Figure B.1:
Those plots present the distribution in |
| Open with DEXTER | |
Figure B.1 shows the results for Planck for
r=0.3 and 0.1. The curves of the difference plotted in inclusion
illustrate the predominance of the reionisation bump. In
Fig. B.2, we plot the difference curve on the bottom
panels for the three experiments for r=0.01 and r=0.001. They
illustrate clearly the difference of sensitivity to the peak between
the EPIC-LC design and the higher resolution experiments. In general
it can be seen that no significant contribution to the CMB is coming
from scales smaller than
![]() .
.
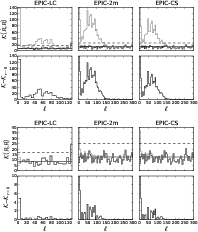 |
Figure B.2:
Mismatch criterion for r = 0.01 ( top) and r = 0.001
( bottom). In each plot, the top panel shows the mismatch criterion between the best fit model and the data (black curve) and the best fit model deprived from the CMB contribution and the data (gray curve). Solid and dashed horizontal lines show respectively the mismatch expectation and 2 times the mismatch expectation. The difference between the gray and the black curve is plotted in the bottom panel and gives an idea of the significance of the CMB signal in each bin of |
| Open with DEXTER | |
Footnotes
- ... foregrounds
![[*]](/icons/foot_motif.png)
- Appendices are only available in electronic form at http://www.aanda.org
- ... simulations
![[*]](/icons/foot_motif.png)
- Foreground maps used specifically for this work are available at http://www.apc.univ-paris7.fr/~betoule/doku.php?id=bmodes
- ... package
![[*]](/icons/foot_motif.png)
- http://camb.info
- ...
known
![[*]](/icons/foot_motif.png)
- The actual knowledge of the contaminant term is not strictly required to build the filter. It is required, however, to derive the contamination level of the filtered map.
- ...
window
![[*]](/icons/foot_motif.png)
- The mask apodisation code can be downloaded from http://www.apc.univ-paris7.fr/~betoule/doku.php?id=software
All Tables
Table 1: Summary of experimental designs.
Table 2: Error prediction for various experimental designs, assumptions about foregrounds, and fiducial r values.
Table 3: Comparison of the constraints on r with and without lensing (here r=0.001).
Table 4: EPIC-CS measurement for three point sources cases.
Table 5: Influence of the running of the synchrotron spectral index on component separation in term of goodness of fit and r estimates for the EPIC-2m design.
Table 6: Influence of dust polarisation level on component separation.
Table 7: Comparaison of the predicted error bar and the root mean squared error measured on 100 Monte Carlo realisations of EPIC-CS observation.
Table A.1: Bayesian information criterion of 3 models with increasing dimension of the galactic component for the EPIC-2m mission.
Table A.2: Estimation of the tensor to scalar ratio with two different galactic cuts in the EPIC-2m experiment.
All Figures
 |
Figure 1:
Respective emission levels of the various components as predicted by the PSM.
Left: predicted power spectra of the various components at 100 GHz, compared to CMB and lensing level for standard cosmology and various values of r (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90]{11624f2}\par\includegraphics[angle=90]{11624f3} \end{figure}](/articles/aa/full_html/2009/33/aa11624-09/Timg37.png) |
Figure 2: B-modes of the galactic foreground maps (synchrotron + dust) as simulated using v1.6.4 of the PSM. Top: synchrotron-dominated emission at 30 GHz, Bottom: dust-dominated emission at 340 GHz. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90]{11624f4}\par\includegraphics[angle=90]{11624f5}\par
\end{figure}](/articles/aa/full_html/2009/33/aa11624-09/Timg38.png) |
Figure 3:
Maps of the depolarisation factor g ( upper panel) and
polarisation angle |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11624f6}
\end{figure}](/articles/aa/full_html/2009/33/aa11624-09/Timg94.png) |
Figure 4: Noise spectra of various experimental designs compared to B-modes levels for r = 0.1, 0.01 and 0.001. When computing the equivalent multipole noise level for an experiment, we assume that only the central frequency channels contribute to the CMB measurement and that external channels are dedicated to foreground characterisation. |
| Open with DEXTER | |
| In the text | |
| |
Figure 5:
Analysis mask for EPIC B maps, smoothed with a |
| Open with DEXTER | |
| In the text | |
 |
Figure 6: Goodness-of-fit for the three point sources cases. For the reference case ``no-ps'', point sources have neither been including in the simulation, nor taken into account in the modelling. The mismatch criterion wander around its expectation value (horizontal dashed line). The ``no-model'' case is a pessimistic situation where no effort has been made to model the point sources contribution, yielding a net increase of the mismatch criterion. The ``ideal'' case presents an optimistic situation where the exact contribution of the simulated point sources has been used to build the model. |
| Open with DEXTER | |
| In the text | |
 |
Figure 7: Variations of the galactic foregrounds model. The left panel shows the dispersion of the synchrotron spectral index for the PSM model (in black) and the curved model (in gray). Solid lines present the frequency scaling for the mean values of the spectral index and dotted lines for its extremal values. The right panel shows the difference between the default power spectrum of dust polarisation B-modes at 150 GHz as modelled by the PSM (solid curve) and a model assuming pessimistic values for the overall level and power spectrum index (dotted curve). |
| Open with DEXTER | |
| In the text | |
 |
Figure B.1:
Those plots present the distribution in |
| Open with DEXTER | |
| In the text | |
 |
Figure B.2:
Mismatch criterion for r = 0.01 ( top) and r = 0.001
( bottom). In each plot, the top panel shows the mismatch criterion between the best fit model and the data (black curve) and the best fit model deprived from the CMB contribution and the data (gray curve). Solid and dashed horizontal lines show respectively the mismatch expectation and 2 times the mismatch expectation. The difference between the gray and the black curve is plotted in the bottom panel and gives an idea of the significance of the CMB signal in each bin of |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




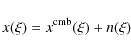
![\begin{displaymath}
-2 \ln \mathcal{L}
=
\sum_\ell (2\ell+1) \ensuremath{f_{\...
...ell}\right)+\frac{\hat{C}_\ell}{C_\ell}\right]
+{\rm const.}
\end{displaymath}](/articles/aa/full_html/2009/33/aa11624-09/img44.png)
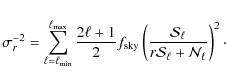
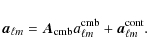
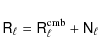

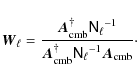


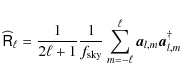
![\begin{displaymath}
\ensuremath{K \left( \ensuremath{\widehat{\tens{R}}}, \ensu...
...tens{R}} }^{-1} \ensuremath{\widehat{\tens{R}}} ) - F \right].
\end{displaymath}](/articles/aa/full_html/2009/33/aa11624-09/img72.png)