| Issue |
A&A
Volume 695, March 2025
|
|
|---|---|---|
| Article Number | A157 | |
| Number of page(s) | 11 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202451570 | |
| Published online | 19 March 2025 | |
Biases induced by retardance and diattenuation in the measurements of long-baseline interferometers
LIRA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université Paris Cité,
5 place Jules Janssen,
92195,
Meudon, France
★★ Corresponding author; guy.perrin@obspm.fr
Received:
19
July
2024
Accepted:
16
December
2024
Context. The coherence of long-baseline interferometers is affected by the polarization properties of the instrument. This is a possible source of biases, which would need to be calibrated.
Aims. The goal of this paper is to study the biases due to retardance and diattenuation in long-baseline interferometers. In principle, the results can be applied to both optical and radio interferometers.
Methods. We derived theoretical expressions for biases on fringe contrast and fringe visibility phase for interferometers whose polarizing properties can be described by beam rotation, retardance, and diattenuation. The nature of these biases are discussed for natural light, circular and linear polarization, and partially polarized light. Expansions were obtained for small degrees of polarization, small differential retardance, and small diattenuation.
Results. The biases on fringe contrasts were already known. It is shown in this paper that retardance and diattenuation are also sources of bias on the visibility phases and derived quantities. In some cases, the bias is zero (for non-polarizing interferometers with natural or partially circulary polarized light.) If the retardance is achromatic, differential phases are not affected. Closure phases are not affected to the second order for an interferometer with weak diattenuation and weak differential retardance and for moderately polarized sources whatever the type of light. Otherwise, a calibration procedure is required. It has been shown that astrometric measurements are biased in the general case. The bias depends on both the polarization properties of the interferometer and on the (u, v) sampling. In the extreme case where the samples are aligned on a line crossing the origin of the spatial frequency plane, the bias is undetermined and can be arbitrarily large. In all other cases, it can be calibrated if the polarizing characteristics of the interferometer are known. In the case of a low differential retardance and low degree of polarization, the bias lies on a straight line, crossing the astrometric reference point. If the degree of linear polarization varies during the observations, then the astrometric bias has a remarkable signature, which describes a section of the line. For slightly polarizing interferometers, a fixed offset is added without changing the shape of the bias.
Conclusions. A polarizing interferometer does generate bias on visibility contrast and visibility phase. The bias depends on the polarization characteristics of the source. In any case, the bias can be computed if the polarization characteristics of the interferometer are known. Astrometric biases can also be corrected and depend on the (u, v) sampling achieved for the measurements.
Key words: instrumentation: interferometers / methods: analytical / techniques: polarimetric
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Long baseline interferometers measure the spatial coherence of light. The degree of coherence measured on a baseline is the normalized scalar product of the waves collected by two telescopes averaged over time. Thus, the polarization characteristics of the waves (i.e., a characteristic of the source or of the interferometer) play a role in the obtained result. It is a well-known fact that polarization axes cannot be crossed; otherwise the fringe contrast will be canceled for incoherent linear polarizations or a π differential birefringence phase will lead to a zero contrast if polarizations are not split. This was experienced by Labeyrie before the first detection of long-baseline fringes at visible wavelengths (Labeyrie 1975). Futhermore, Rousselet-Perraut et al. (1996) investigated the effects of differential phases between interference patterns and of differential rotation between polarization planes on fringe contrast applied to the REcombinateur pour GrAnd INterféromètre (REGAIN) beamcombiner of the Grand Interféromètre à 2 Télescopes (GI2T) interferometer, a descendant of Labeyrie’s first interferometer.
Optical interferometers have complex trains of mirrors and include delay lines. Accurately modeling their polarization properties is quite complex. The Jones calculus for fully polarized light and the Mueller calculus for partially polarized light are the usual methods applied to deduce the effect of the interferometer on input light waves. Elias (2001) and Elias (2004) proposed a general formalism to deal with polarization in interferometers by describing the optical train with Jones and Mueller matrices to propagate polarization states and Stokes parameters across the interferometer. This method has been used by GRAVITY Collaboration (2024) to study polarization characteristics of the Very Large Telescope Interferometer (VLTI) and their effects. This method is accurate, but it does not allow for an analytical study of the effects of diattenuation and retardance on visibility data. I have investigated the possibility of modeling complex trains of mirrors using a simple Jones matrix with generalized neutral axes in Perrin (2024). I have shown that the VLTI train can be modeled with a quasi-unitary Jones matrix with a very good accuracy because of the large set of optical elements. This method greatly simplifies the problem and the polarization properties of the optical train can then be described by a rotation, a retardance, and a polarizing transmission applied to two orthogonal linear polarizations. I use this formalism in this paper to derive the biases on fringe contrast (visibility modulus), visibility phase, and astrometric quantities.
The interferometric formalism is described in Sect. 2, the impact of the polarization characteristics on the interferograms is given in Sect. 3. The bias on phases is derived in Sect. 4 and discussed for visibility phases and derivations in Sect. 5. In Sect. 6, the astrometric bias induced by retardance and diattenuation is discussed. Our conclusions are presented in Sect. 7.
2 Interferometric formalism
2.1 General expression of the waves
The complex notation is chosen to describe the instantaneous wave 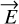 in the general case:
in the general case:
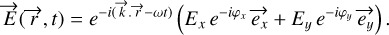 (1)
(1)
Here, 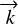 is the wave vector and ω the pulsation of the wave. It describes the direction of propagation of the wave and depends on the wavelength. Then, (x, y) defines a plane perpendicular to
is the wave vector and ω the pulsation of the wave. It describes the direction of propagation of the wave and depends on the wavelength. Then, (x, y) defines a plane perpendicular to 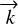 . Based on the assumption that a monochromatic wave is a good description of the wave, it is possible to drop the integration over the wavelength that is necessary to describe a quasi-monochromatic wave, as done in Goodman (2000). The full expressions can be recovered with an integration. In the following,
. Based on the assumption that a monochromatic wave is a good description of the wave, it is possible to drop the integration over the wavelength that is necessary to describe a quasi-monochromatic wave, as done in Goodman (2000). The full expressions can be recovered with an integration. In the following, 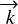 defines an axis whose coordinate is noted z. The equation above can be written:
defines an axis whose coordinate is noted z. The equation above can be written:
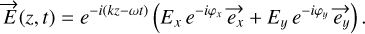 (2)
(2)
This expression holds as well if the z axis is along a curved waveguide, with the (x, y) plane being locally perpendicular to the z axis.
Here, φx and φy are constant for polarized light: φx = φy for linearly polarized light and 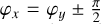 , for circularly polarized light (+ for left-handed circular polarization and − for right-handed). Ex and Ey are also constant for polarized light: they can be written Ex = E0 cos α and Ey = E0 sin α where, in the case of linearly polarized light, α is the electric vector position angle (EVPA) and
, for circularly polarized light (+ for left-handed circular polarization and − for right-handed). Ex and Ey are also constant for polarized light: they can be written Ex = E0 cos α and Ey = E0 sin α where, in the case of linearly polarized light, α is the electric vector position angle (EVPA) and 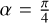 for circularly polarized light. For the general case of elliptically polarized light, φx, φy, Ex, and Ey can take any value. In the case of unpolarized light,
for circularly polarized light. For the general case of elliptically polarized light, φx, φy, Ex, and Ey can take any value. In the case of unpolarized light, 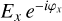 and
and 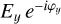 take random values as the direction of polarization is random and as the wave components on the two axes are not coherent, with
take random values as the direction of polarization is random and as the wave components on the two axes are not coherent, with 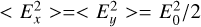 . In all cases, the intensity carried by the wave is
. In all cases, the intensity carried by the wave is 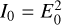 .
.
2.2 Polarization properties of the beam path
During propagation, the wave may experience various effects such as retardance, which will build phase differences between different polarization axes, or diattenuation with a differential transmission depending on the polarization axis. I also consider beam rotation in addition to these effects in this work. I assume that the whole system can be described as a non-depolarizing system and that two perpendicular neutral axes x and y can be defined with a good approximation, as in Perrin (2024). This allows for an analytical study the effects of retardance and diattenuation. Retardance could be the consequence of differential phases at reflections on optical surfaces or through thin layers, or of birefringence because of propagation in birefringent media induced by the dependence of optical index with polarization axes. Equation (2) is then updated taking into account two phases ψx and ψy, whose difference leads to the retardance:
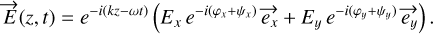 (3)
(3)
In addition, the optical system may be polarizing with a differential throughput on the x and y axes with transmissions τx and τy leading to a new general expression for the wave:
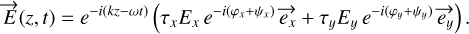 (4)
(4)
Finally, the beams may be rotated in the interferometer by an angle, θ, thereby mixing the neutral axes of polarization according to:
![$\vec E(z,t) = {e^{ - i(kz - \omega t)}}\left[ {\matrix{ {{\tau _x}\cos \theta {E_x}{e^{ - i\left( {{\varphi _x} + {\psi _x}} \right)}} - {\tau _y}\sin \theta {E_y}{e^{ - i\left( {{\varphi _y} + {\psi _y}} \right)}}} \hfill \cr {{\tau _x}\sin \theta {E_x}{e^{ - i\left( {{\varphi _x} + {\psi _x}} \right)}} + {\tau _y}\cos \theta {E_y}{e^{ - i\left( {{\varphi _y} + {\psi _y}} \right)}}} \hfill \cr } } \right].$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq15.png) (5)
(5)
This general expression is the one described in Perrin (2024), where the Jones matrix describing the effect of the optical system on polarizations is a quasi-unitary matrix; however, there is no frame rotation of the neutral axes here with respect to the x and y axes.
2.3 Case of partially polarized waves
For partially polarized waves, the non-polarized and polarized components of the instantaneous wave are noted 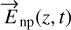 and
and 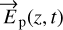 . The instantaneous components on the x and y axes in Eq. (2) are noted as Enp,x and Enp,y for the non-polarized wave and Ep,x and Ep,y for the polarized wave.
. The instantaneous components on the x and y axes in Eq. (2) are noted as Enp,x and Enp,y for the non-polarized wave and Ep,x and Ep,y for the polarized wave.
The degree of polarization is defined as:
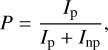 (6)
(6)
where the average intensities of the beams are expressed as:
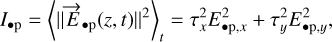 (7)
(7)
with the •p index being either the np index for non-polarized light or the p index for polarized light. For the non-polarized component, 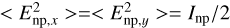 for a 100% throughput. For a polarized wave, Ep,x = Ep cos α and Ep,y = Ep sin α where α is the position angle of the linearly polarized wave and
for a 100% throughput. For a polarized wave, Ep,x = Ep cos α and Ep,y = Ep sin α where α is the position angle of the linearly polarized wave and 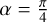 for a circularly polarized wave. In either case,
for a circularly polarized wave. In either case, 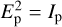
2.4 Interferometric equations
The interferometric equations are derived for a two-beam interferometer. The beams are labeled 1 and 2. The equations just need to be replicated per baseline for a larger number of beams. The interferogram is denoted as I and expressed as:
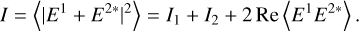 (8)
(8)
In the following, I assume that the intensities I1 and I2 are equal (it is the case after photometric calibration in single-mode interferometers, an imbalance parameter needs to be introduced otherwise) and noted as I0 . The modulated part of the interferogram is noted 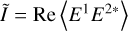 With these notations, the interferogram is:
With these notations, the interferogram is:
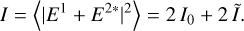 (9)
(9)
The Poynting vector of the sum of the waves of two neutral axes is the sum of their respective Poynting vectors. As a consequence, the interferogram of the two orthogonal axes of polarization is the sum of the interferograms on each polarization axis. The polarization axes can therefore be studied independently and summed a posteriori. In addition, unpolarized light cannot interfere with polarized light as they are mutually incoherent (as a matter of fact, the cross terms like for example 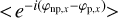 are equal to zero as phase φnp,x is a random variable, while φp,x takes a constant value) so that the polarized and unpolarized interferograms can be summed as well. Such conclusions are not necessarily valid for different polarization states and, in the following, the polarized part of the radiation is considered to be of one type only: either linear or circular. Two interferograms, Ix and Iy, are defined, one per neutral axis. Each interferogram is the sum of the polarized and of the unpolarized interferograms and consequently:
are equal to zero as phase φnp,x is a random variable, while φp,x takes a constant value) so that the polarized and unpolarized interferograms can be summed as well. Such conclusions are not necessarily valid for different polarization states and, in the following, the polarized part of the radiation is considered to be of one type only: either linear or circular. Two interferograms, Ix and Iy, are defined, one per neutral axis. Each interferogram is the sum of the polarized and of the unpolarized interferograms and consequently:
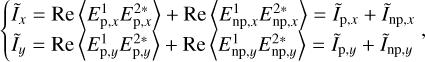 (10)
(10)
The object is supposed to be a point source, so that no other spatial coherence effect is taken into account in this paper. For the case of extended sources, we refer the remarks at the end of Sect. 4.
3 The impact of the polarization properties of the optical system on the interferograms
We first define a series of phase differences and averages where the prefix A is for an average and Δ for a difference to ease the expression of the equations:
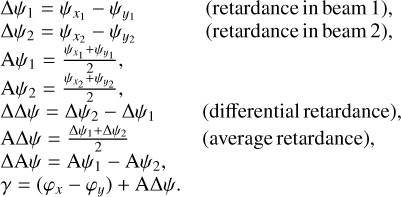 (11)
(11)
The two waves of Eq. (5) collected by telescopes 1 and 2 are noted as 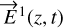 and
and 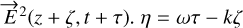 is defined where τ and ζ are respectively the time and optical path differences between the waves collected by telescopes 1 and 2. Then, η is equal to zero at the zero optical path difference, which is the origin of the visibility phase. The two waves are injected in Eq. (10), yielding the following expression for the x axis:
is defined where τ and ζ are respectively the time and optical path differences between the waves collected by telescopes 1 and 2. Then, η is equal to zero at the zero optical path difference, which is the origin of the visibility phase. The two waves are injected in Eq. (10), yielding the following expression for the x axis:
![$\eqalign{ & {{\tilde I}_{ \bullet {\bf{p}},x}} = {\mathop{\rm Re}\nolimits} \left[ {{e^{ - i{\eta _1}}}} \right.\left\langle {{\tau _{{x_1}}}{\tau _{{x_2}}}} \right.E_x^2\cos {\theta _1}\cos {\theta _2}{e^{ - i\left( {{\psi _{{x_1}}} - {\psi _{{x_2}}}} \right)}} + {\tau _{{y_1}}}{\tau _{{y_2}}}E_y^2\sin {\theta _1}\sin {\theta _2}{e^{ - i\left( {{\psi _{{y_1}}} - {\psi _{{y_2}}}} \right)}} \cr & \left. { - {\tau _{{x_1}}}{\tau _{{y_2}}}{E_x}{E_y}\cos {\theta _1}\sin {\theta _2}{e^{ - i\left( {{\varphi _x} - {\varphi _y} + {\psi _{{x_1}}} - {\psi _{{y_2}}}} \right)}} - {\tau _{{x_2}}}{\tau _{{y_1}}}{E_x}{E_y}\cos {\theta _2}\sin {\theta _1}e\left. {^{ - i\left( {{\varphi _y} - {\varphi _x} + {\psi _{{y_1}}} - {\psi _{{x_2}}}} \right)}} \right\rangle } \right], \cr}$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq31.png) (12)
(12)
I then classically define ρ and ϕ to help identify trigonometric relations in the above equation and its derivations:
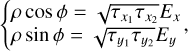 (13)
(13)
and rewrite the previous equation as (see Appendix A.1 for the details of the derivation):
![$\eqalign{ & 2{{\tilde I}_{ \bullet {\rm{p}},x}} = {\mathop{\rm Re}\nolimits} \left[ {{e^{ - i(\eta + \Delta {\rm{A}}\psi )}}{\rho ^2}\left[ {\left[ {\cos \left( {{\theta _1} + {\theta _2}} \right)\cos 2\phi + \cos \left( {{\theta _1} - {\theta _2}} \right)} \right]\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) + i\left[ {\cos \left( {{\theta _1} + {\theta _2}} \right) + \cos \left( {{\theta _1} - {\theta _2}} \right)\cos 2\phi } \right]\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \right]} \right. \cr & - {E_x}{E_y}\left[ {\cos \gamma \left[ {\left( {{\tau _{{x_1}}}{\tau _{{y_2}}} + {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \left( {{\theta _1} + {\theta _2}} \right) - \left( {{\tau _{{x_1}}}{\tau _{{y_2}}} - {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \left( {{\theta _1} - {\theta _2}} \right)} \right]} \right. \cr & \left. {\left. {\left. { + i\sin \gamma \left[ { - \left( {{\tau _{{x_1}}}{\tau _{{y_2}}} - {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \left( {{\theta _1} + {\theta _2}} \right) + \left( {{\tau _{{x_1}}}{\tau _{{y_2}}} + {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \left( {{\theta _1} - {\theta _2}} \right)} \right]} \right]} \right\rangle } \right], \cr} $](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq33.png) (14)
(14)
The expression for 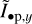 can be easily deduced by adding
can be easily deduced by adding 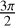 to θ1 and θ2:
to θ1 and θ2:
![$\eqalign{ & 2{{\tilde I}_{ \bullet {\rm{p}},y}} = {\mathop{\rm Re}\nolimits} \left[ {{e^{ - i(\eta + \Delta {\rm{A}}\psi )}}\left\langle {{\rho ^2}} \right.\left[ {\left[ { - \cos \left( {{\theta _1} + {\theta _2}} \right)\cos 2\phi + \cos \left( {{\theta _1} - {\theta _2}} \right)} \right]\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) + i\left[ { - \cos \left( {{\theta _1} + {\theta _2}} \right) + \cos \left( {{\theta _1} - {\theta _2}} \right)\cos 2\phi } \right]\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \right]} \right. \cr & \matrix{ { + {E_x}{E_y}\left[ {\cos \gamma \left[ {\left( {{\tau _{{x_1}}}{\tau _{{y_2}}} + {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \left( {{\theta _1} + {\theta _2}} \right) + \left( {{\tau _{{x_1}}}{\tau _{{y_2}}} - {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \left( {{\theta _1} - {\theta _2}} \right)} \right]} \right.} \cr {\left. {\left. { - i\sin \gamma \left. {\left[ {\left( {{\tau _{{x_1}}}{\tau _{{y_2}}} - {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \left( {{\theta _1} + {\theta _2}} \right) + \left( {{\tau _{{x_1}}}{\tau _{{y_2}}} + {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \left( {{\theta _1} - {\theta _2}} \right)} \right]} \right\rangle } \right]} \right]} \cr } \cr}$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq36.png) (15)
(15)
In the total intensity 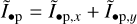 , all θ1 + θ2 terms disappear while the θ1 - θ2 terms are doubled, yielding:
, all θ1 + θ2 terms disappear while the θ1 - θ2 terms are doubled, yielding:
![$\matrix{ {{{\mathop I\limits^ }_{ \bullet p}} = {\mathop{\rm Re}\nolimits} [{e^{ - i(\eta + {\rm{\Delta A}}\psi )}}{\rho ^2}\cos \left( {{\theta _1} - {\theta _2}} \right)\left[ {\cos \left( {{1 \over 2}{\rm{\Delta \Delta }}\psi } \right) + i\cos 2\phi \sin \left( {{1 \over 2}{\rm{\Delta \Delta }}\psi } \right)} \right]} \cr { + {E_x}{E_y}\sin \left( {{\theta _1} - {\theta _2}} \right)\left[ {\left( {{\tau _{{x_1}}}{\tau _{{y_2}}} - {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\cos \gamma - i\left( {{\tau _{{x_1}}}{\tau _{{y_2}}} + {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \gamma } \right]\rangle ].} \cr }$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq38.png) (16)
(16)
4 Symmetric interferometer
Interferometers are designed to be symmetric to minimize polarization effects in instruments. It means that for any characteristic χ value of the instrument, χ1 = χ2. As a consequence, θ1 = θ2, which is natural for maximizing the fringe contrast, and 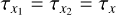 ,
, 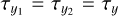 . This also applies to the retardance induced by optical reflections or thin layers, which can be considered the same in all arms of the interferometer. In the following, we still consider a source of retardance, namely: the birefringence of propagation media like fibers. As a consequence, the ΔΔψ term is essentially due to the propagation media, while the AΔψ term is due to both optical surfaces or thin layers and to propagation media. The interferometer is polarizing in the general case but is non-polarizing when, in addition, τx = τy = τ.
. This also applies to the retardance induced by optical reflections or thin layers, which can be considered the same in all arms of the interferometer. In the following, we still consider a source of retardance, namely: the birefringence of propagation media like fibers. As a consequence, the ΔΔψ term is essentially due to the propagation media, while the AΔψ term is due to both optical surfaces or thin layers and to propagation media. The interferometer is polarizing in the general case but is non-polarizing when, in addition, τx = τy = τ.
4.1 Basic expressions
With these hypotheses, Eqs. (14), (15), and (16) become:
![$\matrix{ {2{{\mathop I\limits^ }_{ \bullet {\rm{p}},x}} = {\mathop{\rm Re}\nolimits} [{e^{ - i(\eta + {\rm{\Delta A}}\psi )}}\langle {\rho ^2}\left[ {[1 + \cos 2\theta \cos 2\phi ]\cos \left( {{1 \over 2}{\rm{\Delta \Delta }}\psi } \right) + i[\cos 2\theta + \cos 2\phi ]\sin \left( {{1 \over 2}{\rm{\Delta \Delta }}\psi } \right)} \right]} \cr { - {E_x}{E_y}\sin 2\theta \left[ {\left( {{\tau _{{x_1}}}{\tau _{{y_2}}} + {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\cos \gamma - i\left( {{\tau _{{x_1}}}{\tau _{{y_2}}} - {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \gamma } \right]\rangle ],} \cr }$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq41.png) (17)
(17)
![$\matrix{ {2{I_{ \bullet {\rm{p}},y}} = {\mathop{\rm Re}\nolimits} [{e^{ - i(\eta + {\rm{\Delta A}}\psi )}}\langle {\rho ^2}\left[ {[1 - \cos 2\theta \cos 2\phi ]\cos \left( {{1 \over 2}{\rm{\Delta \Delta }}\psi } \right) + i[ - \cos 2\theta + \cos 2\phi ]\sin \left( {{1 \over 2}{\rm{\Delta \Delta }}\psi } \right)} \right]} \cr { - {E_x}{E_y}\sin 2\theta \left[ { - \left( {{\tau _{{x_1}}}{\tau _{{y_2}}} + {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\cos \gamma + i\left( {{\tau _{{x_1}}}{\tau _{{y_2}}} - {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \gamma } \right]\rangle ],} \cr }$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq42.png) (18)
(18)
![${\mathop I\limits^ _{ \bullet {\rm{p}}}} = {\mathop{\rm Re}\nolimits} [e - i(\eta + {\rm{A}}\psi )\langle {\rho ^2}\cos ({1 \over 2}\psi ) + i\cos 2\phi \sin ({1 \over 2}\psi )\rangle ].$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq43.png) (19)
(19)
Equation (13) is now written as:
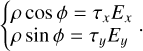 (20)
(20)
Then 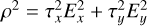 and ρ2 cos
and ρ2 cos 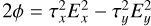 with the special cases:
with the special cases:
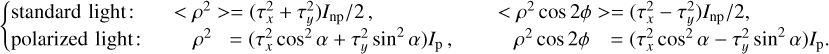 (21)
(21)
The expressions of the interferograms can now be derived for the two kinds of light from Eqs. (17), (18), and (19). For standard light:
![$\left\{ {\matrix{ {4{{\tilde I}_{{\rm{np}},x}} = {I_{{\rm{np}}}}\left[ {\cos (\eta + \Delta {\rm{A}}\psi )\left[ {\left( {\tau _x^2 + \tau _y^2} \right) + \left( {\tau _x^2 - \tau _y^2} \right)\cos 2\theta } \right]\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) + \sin (\eta + \Delta {\rm{A}}\psi )\left[ {\left( {\tau _x^2 - \tau _y^2} \right) + \left( {\tau _x^2 + \tau _y^2} \right)\cos 2\theta } \right]\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \right],} \hfill \cr {4{{\tilde I}_{{\rm{np}},y}} = {I_{{\rm{np}}}}\left[ {\cos (\eta + \Delta {\rm{A}}\psi )\left[ {\left( {\tau _x^2 + \tau _y^2} \right) - \left( {\tau _x^2 - \tau _y^2} \right)\cos 2\theta } \right]\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) + \sin (\eta + \Delta {\rm{A}}\psi )\left[ {\left( {\tau _x^2 - \tau _y^2} \right) - \left( {\tau _x^2 + \tau _y^2} \right)\cos 2\theta } \right]\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \right],} \hfill \cr {2{{\tilde I}_{{\rm{np}}}} = {I_{{\rm{np}}}}\left[ {\cos (\eta + \Delta {\rm{A}}\psi )\left( {\tau _x^2 + \tau _y^2} \right)\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) + \sin (\eta + \Delta {\rm{A}}\psi )\left( {\tau _x^2 - \tau _y^2} \right)\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \right].} \hfill \cr } } \right.$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq48.png) (22)
(22)
In the case of a non-polarizing interferometer, namely, for τx = τy = τ, and for unpolarized light, we would get the traditional result that the effect of retardance is to reduce the fringe contrast (see e.g., Rousselet-Perraut et al. (1996) with τ = 1), so that the fringe contrasts goes down to to 0 when ΔΔψ is half a fringe or π, meaning a bright fringe on one polarization axis exactly coincides with a dark fringe on the other one:
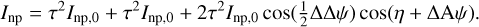 (23)
(23)
with 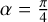 and
and 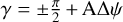 for circular polarization and γ = AΔψ for linear polarization. I remark that the phase shift term, ΔAψ, is independent of the degree of polarization of the source and is therefore not considered as a source of phase shift in what follows. This is because this phase shift is the same, no matter the characteristics of the source, and is compensated for all sources by a simple delay. Some first conclusions can be drawn from these equations. First of all, all fringe patterns on the x and y axes are shifted by retardance with respect to the position of the central fringe in absence of retardance because of the presence of the sin(η + ΔAψ) term. The shifts are opposite on the x and y axes for standard light for a non-polarizing interferometer (i.e., with τx = τy) as the sin(η + ΔAψ) terms have opposite signs, while the signs of the cos(η + ΔAψ) term are the same. For both standard and circularly polarized light (cos 2α = 0), the fringes of the combined x and y polarization axes are not shifted for the same type of interferometer, as the sin(η + ΔAψ) term vanishes. In both cases, the only consequence of retardance on the total light interferogram is a decrease in the fringe contrast, as in the example of Eq. (23). For linearly polarized light, the combined light interferogram is phase shifted in the general case because of retardance.
for circular polarization and γ = AΔψ for linear polarization. I remark that the phase shift term, ΔAψ, is independent of the degree of polarization of the source and is therefore not considered as a source of phase shift in what follows. This is because this phase shift is the same, no matter the characteristics of the source, and is compensated for all sources by a simple delay. Some first conclusions can be drawn from these equations. First of all, all fringe patterns on the x and y axes are shifted by retardance with respect to the position of the central fringe in absence of retardance because of the presence of the sin(η + ΔAψ) term. The shifts are opposite on the x and y axes for standard light for a non-polarizing interferometer (i.e., with τx = τy) as the sin(η + ΔAψ) terms have opposite signs, while the signs of the cos(η + ΔAψ) term are the same. For both standard and circularly polarized light (cos 2α = 0), the fringes of the combined x and y polarization axes are not shifted for the same type of interferometer, as the sin(η + ΔAψ) term vanishes. In both cases, the only consequence of retardance on the total light interferogram is a decrease in the fringe contrast, as in the example of Eq. (23). For linearly polarized light, the combined light interferogram is phase shifted in the general case because of retardance.
4.2 Partially polarized interferograms
Equations (22) and (24) are combined to derive the expressions of the interferograms in partially polarized light conditions:
![$\left\{ \matrix{ 2{{\tilde I}_x} = {I_0}\left[ {\cos (\eta + \Delta {\rm{A}}\psi )\left[ {{1 \over 2}\left[ {\left( {\tau _x^2 + \tau _y^2} \right)(1 + P\cos 2\theta \cos 2\alpha ) + \left( {\tau _x^2 - \tau _y^2} \right)(P\cos 2\alpha + \cos 2\theta )} \right]\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) - P{\tau _x}{\tau _y}\sin 2\theta \sin 2\alpha \cos \gamma } \right]} \right. \hfill \cr \left. { + \sin (\eta + \Delta {\rm{A}}\psi ){1 \over 2}\left[ {\left( {\tau _x^2 - \tau _u^2} \right)(1 + P\cos 2\theta \cos 2\alpha ) + \left( {\tau _x^2 + \tau _u^2} \right)(P\cos 2\alpha + \cos 2\theta )} \right]\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \right], \hfill \cr 2{{\tilde I}_y} = {I_0}\left[ {\cos (\eta + \Delta {\rm{A}}\psi )\left[ {{1 \over 2}\left[ {\left( {\tau _x^2 + \tau _y^2} \right)(1 - P\cos 2\theta \cos 2\alpha ) + \left( {\tau _x^2 - \tau _y^2} \right)(P\cos 2\alpha - \cos 2\theta )} \right]\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) + P{\tau _x}{\tau _y}\sin 2\theta \sin 2\alpha \cos \gamma } \right]} \right. \hfill \cr \left. { + \sin (\eta + \Delta {\rm{A}}\psi ){1 \over 2}\left[ {\left( {\tau _x^2 - \tau _y^2} \right)(1 - P\cos 2\theta \cos 2\alpha ) + \left( {\tau _x^2 + \tau _y^2} \right)(P\cos 2\alpha - \cos 2\theta )} \right]\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \right] \hfill \cr \tilde I = {I_0}\left[ {\cos (\eta + \Delta {\rm{A}}\psi ){1 \over 2}\left[ {\left( {\tau _x^2 + \tau _y^2} \right) + \left( {\tau _x^2 - \tau _y^2} \right)P\cos 2\alpha } \right]\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) + \sin (\eta + \Delta {\rm{A}}\psi ){1 \over 2}\left[ {\left( {\tau _x^2 - \tau _y^2} \right) + \left( {\tau _x^2 + \tau _y^2} \right)P\cos 2\alpha } \right]\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \right]. \hfill \cr} \right.$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq53.png) (25)
(25)
All interferograms can be written as:
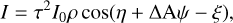 (26)
(26)
where ξ is the phase shift due to retardance (both ρ and ξ depend on the polarization characteristics of the instrument and on the degree of polarization of the source), yielding:
![$\left\{ {\matrix{ {{2^{|\varepsilon |}}\rho \cos \xi = {1 \over 2}\left[ {\left( {\tau _x^2 + \tau _y^2} \right)(1 + \varepsilon P\cos 2\theta \cos 2\alpha ) + \left( {\tau _x^2 - \tau _y^2} \right)(P\cos 2\alpha + \varepsilon \cos 2\theta )} \right]\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) - \varepsilon P{\tau _x}{\tau _y}\sin 2\theta \sin 2\alpha \cos \gamma } \hfill \cr {{2^{|\varepsilon |}}\rho \sin \xi = {1 \over 2}\left[ {\left( {\tau _x^2 - \tau _y^2} \right)(1 + \varepsilon P\cos 2\theta \cos 2\alpha ) + \left( {\tau _x^2 + \tau _y^2} \right)(P\cos 2\alpha + \varepsilon \cos 2\theta )} \right]\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \hfill \cr } } \right.$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq55.png) (27)
(27)
with ε = +1 for the x axis, ε = −1 for the y axis and ε = 0 for combined polarizations.
Some conclusions can be drawn from these expressions. The general conclusion is that differential retardance induces a shift, even in the case of natural light, since sin ξ is not zero. In addition, the amount of differential retardance depends on various parameters: the rotation of the beams, the degree and nature of polarization, and the orientation of linear polarization. All cases are summarized in Table 1 with some other particular cases. The phase shift is always proportional to retardance if retardance is small since 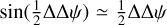 to the first order in this case. The rotation of the beams plays a particular role: if the beams are aligned with the polarization axes
to the first order in this case. The rotation of the beams plays a particular role: if the beams are aligned with the polarization axes 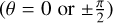 , then the tangent of the phase shift is always proportional to
, then the tangent of the phase shift is always proportional to 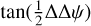 . If the beams are rotated by
. If the beams are rotated by 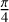 with respect to the (x, y) frame, then there is no phase shift for a non-polarizing interferometer (or equivalently with 0 diattenuation, i.e., with τx = τy) and with natural or partially circularly polarized light (cos 2α = 0) since sin ξ = 0 in this case. The phase shift is never 0 if diattenuation is present and shifts on the x and y axes are never opposite in the general case. However, the tangent of the phase shift is proportional to
with respect to the (x, y) frame, then there is no phase shift for a non-polarizing interferometer (or equivalently with 0 diattenuation, i.e., with τx = τy) and with natural or partially circularly polarized light (cos 2α = 0) since sin ξ = 0 in this case. The phase shift is never 0 if diattenuation is present and shifts on the x and y axes are never opposite in the general case. However, the tangent of the phase shift is proportional to 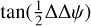 for a non-polarized source or in combined mode; this means that the phase shift is proportional to retardance to the first order in these cases. Finally, the phase shifts are opposite on the x and y axes for natural light for a non-polarizing interferometer, with a zero phase shift in combined mode.
for a non-polarized source or in combined mode; this means that the phase shift is proportional to retardance to the first order in these cases. Finally, the phase shifts are opposite on the x and y axes for natural light for a non-polarizing interferometer, with a zero phase shift in combined mode.
Remark: In the case of extended sources, the interferograms from individual point-like sources of Eq. (26) need to be integrated over the sky coordinates α and Δ with a component of η being the phase term −2π(αu + Δv), where u and v are the spatial frequency coordinates conjugated to the sky coordinates. As a consequence, the visibilities need to be calculated with a modified version of the Zernike-van Cittert theorem where the phase shift due to retardance ξ is added to the classical phase term 2π(αu + Δv). In the particular case of sources whose degree of polarization is independent of location, the visibility phase is simply shifted by ξ and a calibration is required.
Visibility phase shifts.
5 Biases of the visibility phase and derived quantities
I have shown (see Sect. 4) that in the general case, the phase of the visibility is biased in presence of retardance whatever the polarization characteristics of the source; however, in some cases, the phase bias is strictly zero (as shown in Table 1). Here, the biases on differential and closure phases are discussed in the general case.
Differential phase. If the chromaticity of the phase shift ξ in Eq. (27) is negligible, then the differential phase can be considered to be unbiased by the polarization properties of the interferometer.
Closure phase. The closure phase can be immune to retardance as well under some circumstances. We can introduce, τ, which is the average transmission on the two polarization axes and Δτ = τx − τy is the difference in transmission between the two axes. For weak diattenuation and differential retardance, as well as for moderately polarized sources (i.e., assuming the degree of polarization is a few tens of percent at most, which is quite standard for polarized astronomical sources), the Eq. (27) system can be expanded to the second order in P, ΔΔψ and Δτ yielding for each baseline i:
![${\xi _i} \approx {1 \over 4}\left[ {2\varepsilon \cos 2\theta + 2\left( {P\cos 2\alpha + {{\delta \tau } \over \tau }} \right)\left( {1 - {\varepsilon ^2}{{\cos }^2}2\theta } \right) + {\varepsilon ^2}P\sin 4\theta \sin 2\alpha \cos {\gamma _i}} \right]{\psi _i}.$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq77.png) (28)
(28)
If the differential retardances ΔΔψi are first order quantities then the average retardances AΔψi are a same constant plus first order quantities linearly linked to the ΔΔψi so that 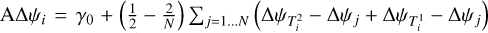 , where
, where 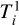 and
and 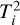 are, respectively, the first and second telescopes of baseline i,
are, respectively, the first and second telescopes of baseline i, 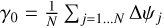 , N being the number of baselines. As a consequence, γi ≈ γ = (φx − φy) + γ0 to zero order. That means that the phase bias writes to the second order:
, N being the number of baselines. As a consequence, γi ≈ γ = (φx − φy) + γ0 to zero order. That means that the phase bias writes to the second order:
![${\xi _i} \approx {1 \over 4}\left[ {2\varepsilon \cos 2\theta + 2\left( {P\cos 2\alpha + {{\delta \tau } \over \tau }} \right)\left( {1 - {\varepsilon ^2}{{\cos }^2}2\theta } \right) + {\varepsilon ^2}P\sin 4\theta \sin 2\alpha \cos \gamma } \right]{\psi _i}.$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq82.png) (29)
(29)
Since the ΔΔψi are closing quantities and the term between brackets is independent of the baseline, the ξi values are also closing quantities to the second order. Here, the consequence is that the bias on closure phases is zero to this order.
6 Astrometric bias
6.1 Theoretical derivation
We considered a phase-referenced interferometer for which the phase of the visibility of a point source is equal to 0 at the center of the coordinate frame. In such a case, the visibility of a point source located at 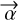 writes
writes 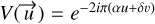 The position of the point source is deduced from the visibility phases measured by the interferometer. One way to deduce one from the other is to find the optimum phase model
The position of the point source is deduced from the visibility phases measured by the interferometer. One way to deduce one from the other is to find the optimum phase model 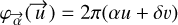 that minimizes the quantity:
that minimizes the quantity:
![${\chi ^2}(\vec \alpha ) = \mathop \sum \limits_{i = 1}^N {\left[ {{\xi _i} - 2\pi \left( {\alpha {u_i} + \delta {v_i}} \right)} \right]^2},$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq86.png) (30)
(30)
where N is the number of baselines or the number of visibility points available if they can be combined over time. Since the phase model is linear, there is a linear relation between the interferogram phases and the optimum position:
![$\left[ {\matrix{ \alpha \hfill \cr \delta \hfill \cr } } \right] = {M^{ - 1}}\left[ {\matrix{ {\mathop \sum \limits_{i = 1}^N {\xi _i}{u_i}} \cr {\mathop \sum \limits_{i = 1}^N {\xi _i}{\upsilon _i}} \cr } } \right],$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq87.png) (31)
(31)
with det ![$M = 4{\pi ^2}\left[ {\left( {\sum\limits_{i = 1}^N {u_i^2} } \right)\left( {\sum\limits_{i = 1}^N {\upsilon _i^2} } \right) - {{\left( {\sum\limits_{i = 1}^N {{u_i}} {\upsilon _i}} \right)}^2}} \right]$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq90.png) . When det M ≠ 0, the general solution of the linear system is:
. When det M ≠ 0, the general solution of the linear system is:
![$\left[ {\matrix{ \alpha \hfill \cr \delta \hfill \cr } } \right] = {{2\pi } \over {\det M}}\left[ {\matrix{ {\left( {\sum\nolimits_{i = 1}^N {\upsilon _i^2} } \right)\left( {\sum\nolimits_{i = 1}^N {} \sum\limits_{i = 1}^N {{\xi _i}} {u_i}} \right) - \left( {\sum\nolimits_{i = 1}^N {{u_i}} {\upsilon _i}} \right)\left( {\sum\nolimits_{i = 1}^N {{\xi _i}} {\upsilon _i}} \right)} \hfill \cr {\left( {\sum\nolimits_{i = 1}^N {u_i^2} } \right)\left( {\sum\nolimits_{i = 1}^N {{\xi _i}} {\upsilon _i}} \right) - \left( {\sum\nolimits_{i = 1}^N {{u_i}} {\upsilon _i}} \right)\left( {\sum\nolimits_{i = 1}^N {{\xi _i}} {u_i}} \right)} \hfill \cr } } \right].$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq91.png) (34)
(34)
Let us note 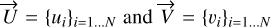 then det
then det ![$M = 4{\pi ^2}\left[ {\vec U{^2}\vec V{^2} - {{(\vec U \cdot \vec V)}^2}} \right]$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq93.png) . According to the Cauchy-Schwartz theorem, the determinant is always positive and is zero if and only if
. According to the Cauchy-Schwartz theorem, the determinant is always positive and is zero if and only if 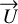 and
and 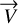 are colinear meaning there exists a constant κ such that
are colinear meaning there exists a constant κ such that 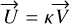 In the general case, we can write
In the general case, we can write 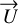 as the sum of its projection on
as the sum of its projection on 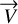 and of a vector perpendicular to
and of a vector perpendicular to 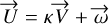 . This yields:
. This yields: 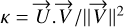 , where
, where 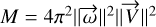 . The determinant is therefore expressed as: det
. The determinant is therefore expressed as: det 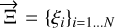 and coupled with Eq. (34), we have:
and coupled with Eq. (34), we have:
![$\left[ {\matrix{ \alpha \hfill \cr \delta \hfill \cr } } \right] = {{2\pi } \over {\det M}}\left[ {\matrix{ {\vec V{^2}(\vec \omega \cdot \vec \Xi )} \cr { - \kappa \vec V{^2}(\vec \omega \cdot \vec \Xi ) + \vec \omega {^2}(\vec V \cdot \vec \Xi )} \cr } } \right] = {{\vec \omega \cdot \vec \Xi } \over {2\pi \vec \omega {^2}}}\left[ {\matrix{ \hfill 1 \cr \hfill { - \kappa } \cr } } \right] + {{\vec V \cdot \vec \Xi } \over {2\pi \vec V{^2}}}\left[ {\matrix{ 0 \hfill \cr 1 \hfill \cr } } \right]$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq103.png) (35)
(35)
with 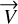 . Equivalent expressions are obtained if
. Equivalent expressions are obtained if 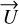 is projected onto
is projected onto 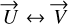 swapping α ↔ δ and
swapping α ↔ δ and 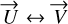 .In the case where det M is close to 0,
.In the case where det M is close to 0, 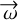 is a negligible quantity. The terms of the third side of the equation are ordered so that the second half is of zero order in
is a negligible quantity. The terms of the third side of the equation are ordered so that the second half is of zero order in 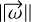 and the first half of the vector is of the order of
and the first half of the vector is of the order of 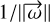 and dominates except in the particular case where
and dominates except in the particular case where 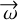 is perpendicular to
is perpendicular to 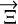 for which only the last term remains. Except in this particular case, for a small
for which only the last term remains. Except in this particular case, for a small 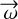 , the astrometric bias is approximately colinear to [1, –κ]T and can take arbitrarily large values (it becomes infinite for
, the astrometric bias is approximately colinear to [1, –κ]T and can take arbitrarily large values (it becomes infinite for 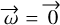 meaning the astrometry cannot be constrained in this case).
meaning the astrometry cannot be constrained in this case).
For det M ≠ 0, for weak diattenuation and differential retardance and for moderately polarized sources, the expansion of ξi to the second order of Eq. (29) can be used and injected into Eq. (31) to get the astrometric bias expansion to the second order:
![$\left[ {\matrix{ \alpha \hfill \cr \delta \hfill \cr } } \right] \approx {1 \over 4}\left[ {2\varepsilon \cos 2\theta + 2\left( {P\cos 2\alpha + {{\delta \tau } \over \tau }} \right)\left( {1 - {\varepsilon ^2}{{\cos }^2}2\theta } \right) + {\varepsilon ^2}P\sin 4\theta \sin 2\alpha \cos \gamma } \right]\left[ {\matrix{ {{\alpha _0}} \hfill \cr {{\delta _0}} \hfill \cr } } \right],$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq115.png) (36)
(36)
The only terms that depend on the characteristics of the source in Eq. (36) are the scalar terms. The vector 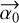 in the second member of the equation only depends on the points in the (u, v) plane and on the retardance (differential and average) of the arms of the interferometer. The astrometric bias is therefore proportional to
in the second member of the equation only depends on the points in the (u, v) plane and on the retardance (differential and average) of the arms of the interferometer. The astrometric bias is therefore proportional to 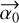 to the first order with coefficients depending on the polarization properties of the source, on the (u, v) sampling, and on the polarizing properties of the interferometer. All cases are summarized in Table 2. For a non-polarizing interferometer (δτ = 0), there is no astrometric bias for partially circularly polarized light (cos 2α = 0) when the two polarizations are combined (ɛ = 0). For linearly polarized light, the astrometric bias is proportional to the degree of polarization P and to cos 2α for combined polarizations. If the orientation of the EVPA α varies, then the bias describes a line segment whose inclination is given by
to the first order with coefficients depending on the polarization properties of the source, on the (u, v) sampling, and on the polarizing properties of the interferometer. All cases are summarized in Table 2. For a non-polarizing interferometer (δτ = 0), there is no astrometric bias for partially circularly polarized light (cos 2α = 0) when the two polarizations are combined (ɛ = 0). For linearly polarized light, the astrometric bias is proportional to the degree of polarization P and to cos 2α for combined polarizations. If the orientation of the EVPA α varies, then the bias describes a line segment whose inclination is given by 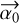 . The astrometries of both split polarizations (ɛ = −1 and +1) are biased for both types of polarizations. The biases vary linearly with the degree P of polarization and are shifted symmetrically by
. The astrometries of both split polarizations (ɛ = −1 and +1) are biased for both types of polarizations. The biases vary linearly with the degree P of polarization and are shifted symmetrically by 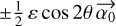 on the x and y axes. For a linear polarization, the biases also vary linearly with P and if the EVPA varies by at least an amplitude of π or –π, then the x and y biases cover opposite ranges of values. In this case, the biases also describe line segments whose inclination is given by
on the x and y axes. For a linear polarization, the biases also vary linearly with P and if the EVPA varies by at least an amplitude of π or –π, then the x and y biases cover opposite ranges of values. In this case, the biases also describe line segments whose inclination is given by 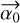 . If the interferometer is slightly polarizing
. If the interferometer is slightly polarizing 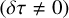 , the general shape of the biases do not change but an extra source of bias appears because of the
, the general shape of the biases do not change but an extra source of bias appears because of the 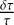 term. In all cases, the biases can be calibrated knowing the amount of retardance (differential and average) in the arms of the interferometer and the (u, v) plane samples.
term. In all cases, the biases can be calibrated knowing the amount of retardance (differential and average) in the arms of the interferometer and the (u, v) plane samples.
Astrometric bias.
6.2 Simulation
An example of astrometric bias assuming a partially linearly polarized source and a non-polarizing interferometer is simulated in this section. Aspro2 from the JMMC has been used to simulate the (u, v) points for a fictitious source at the same location as α Cru. The (u, v) tracks are given in Fig. 1. (u, v) points are selected for three different hour angles labeled with a square, a circle, and a star to compute the astrometric biases. Computations are made using the birefringence measurements of the GRAVITY science channel fibers (Perrin et al. 2024) and organizing the signs to maximize the effect of differential birefringence:
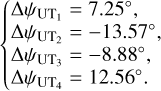 (38)
(38)
At this point, we chose a wavelength of λ = 2 µm. A value of 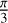 is assumed for θ as it is intermediate between 0 and
is assumed for θ as it is intermediate between 0 and 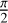 and does not set cos 2θ nor sin 2θ to 0. The amount of differential birefringence is indicated for the values of Eq. (38) (green) and for 2.5 times (orange) and 5 times (blue) that ground level. For each subset, the degree of polarization is varied from 0 to 50% and the EVPA covers the 0–2π range. The computed biases are plotted in Fig. 2 for the two polarization axes x and y and in combined mode for each of the three selected hour angles. The immediate conclusion one can draw from these graphs is that the bias is very much stretched in a single direction as anticipated with the first-order analysis. For moderate differential birefringence, the bias is a line segment. For the lowest level of differential birefringence, a 50% linear polarization leads to a maximum bias on the order of 100 µas. The second conclusion is that the effect of differential birefringence combined with source polarization is easily detectable given the characteristic signatures on the x and y axis that makes these biases simple to calibrate a priori.
and does not set cos 2θ nor sin 2θ to 0. The amount of differential birefringence is indicated for the values of Eq. (38) (green) and for 2.5 times (orange) and 5 times (blue) that ground level. For each subset, the degree of polarization is varied from 0 to 50% and the EVPA covers the 0–2π range. The computed biases are plotted in Fig. 2 for the two polarization axes x and y and in combined mode for each of the three selected hour angles. The immediate conclusion one can draw from these graphs is that the bias is very much stretched in a single direction as anticipated with the first-order analysis. For moderate differential birefringence, the bias is a line segment. For the lowest level of differential birefringence, a 50% linear polarization leads to a maximum bias on the order of 100 µas. The second conclusion is that the effect of differential birefringence combined with source polarization is easily detectable given the characteristic signatures on the x and y axis that makes these biases simple to calibrate a priori.
 |
Fig. 2 Computation of the astrometric bias with multiples (×1, 2.5,5) of a ground level (G) of differential birefringence based on fiber measurements in the case of α Cru and with a degree of linear polarization varying between 0 and 50% and polarization angles in the 0–2π range for different hour angles. The instantaneous (u, v) coverage with the four Unit Telescopes is displayed as an inset in the bottom right of each plot. The full (u, v) coverage is presented in Fig. 1. |
7 Conclusions
The theoretical expressions of the biases of long-baseline interferometer observables established in this paper are aimed at interferometers whose polarimetric characteristics can be exactly or approximately described by a diattenuation and a retardance. The bias on the fringe contrast was already well known prior to this sudy. General expressions were derived for the interferograms with split or combined polarization axes for natural, polarized, and partially polarized light (only linear and circular polarization are studied here, but our conclusions can easily be extended to elliptical polarization). These biases were studied for the particular case of symmetric interferometers, as this is how interferometers are built to maximize coherence.
Theoretical expressions of the bias on the visibility phase have been established for both polarizing and non-polarizing interferometers. It is remarkable that in combined mode for a non-polarizing interferometer, the visibility phase measurements are unbiased for natural light and for partially circularly polarized light. Analytical expressions are given for the other cases. It is shown that for weak diattenuation and retardance, as well as for moderately polarized sources, closure phases are immune to biases to the second order (no matter the type of light). If retardance is achromatic, then the differential phase is also immune to differential retardance. Finally, we investigated the bias on astrometry. It is shown that the bias depends on the (u, v) sampling with an extreme case when the (u, v) points are aligned on a line crossing the origin, in which case the bias can be arbitrarily large. In any other case, the bias can be computed if the retardance of the interferometer is known for each beam. The astrometric bias is expanded for small polarization degrees and small differential retardance. It is shown that in this case, the astrometric bias lies on a straight line crossing the astrometric reference point for non-polarizing interferometers. If the degree of linear polarization varies during the observations, then the astrometric bias has a remarkable signature as it describes a section of the line. If the interferometer is slightly polarizing, then a fixed offset is to be added without changing the general shape of the bias.
Acknowledgements
This research has made use of the Jean-Marie Mariotti Center Aspro service1 .
Appendix A Equation details
A.1 Derivation of Equation 14
This section describes how Eq.14 is derived from Eq. 12, which is recalled here:
![$\eqalign{ & {{\tilde I}_{ \bullet {\rm{p}},x}} = {\mathop{\rm Re}\nolimits} \left[ {{e^{ - i\eta }}\left\langle {{\tau _{{x_1}}}} \right.{\tau _{{x_2}}}E_x^2\cos {\theta _1}\cos {\theta _2}{e^{ - i\left( {{\psi _{{x_1}}} - {\psi _{{x_2}}}} \right)}} + {\tau _{{y_1}}}{\tau _{{y_2}}}E_y^2\sin {\theta _1}\sin {\theta _2}{e^{ - i\left( {{\psi _{{y_1}}} - {\psi _{{y_2}}}} \right)}}} \right. \cr & \left. {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - {\tau _{{x_1}}}{\tau _{{y_2}}}{E_x}{E_y}\cos {\theta _1}\sin {\theta _2}{e^{ - i\left( {{\varphi _x} - {\varphi _y} + {\psi _{{x_1}}} - {\psi _{{y_2}}}} \right)}} - {\tau _{{x_2}}}{\tau _{{y_1}}}{E_x}{E_y}\cos {\theta _2}\sin {\theta _1}{e^{ - i\left( {{\varphi _y} - {\varphi _x} + {\psi _{{y_1}}} - {\psi _{{x_2}}}} \right)}}} \right\rangle } \right]. \cr}$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq133.png) (A.1)
(A.1)
Given the notations defined in Eq. 11, we can write:
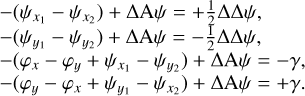 (A.2)
(A.2)
Now, using the definition ofρ and ϕ (given in Eq. 13), Eq. 12 becomes
![$\eqalign{ & {{\tilde I}_{ \bullet {\bf{p}},x}} = {\mathop{\rm Re}\nolimits} \left[ {{e^{ - i(\eta + \Delta {\rm{A}}\psi )}}\left\langle {{\rho ^2}{{\cos }^2}\phi \cos {\theta _1}} \right.\cos {\theta _2}{e^{{i \over 2}\Delta \Delta \psi }} + {\rho ^2}{{\sin }^2}\phi \sin {\theta _1}\sin {\theta _2}{e^{ - {i \over 2}\Delta \Delta \psi }}} \right. \cr & {\left. {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - {\tau _{{x_1}}}{\tau _{{y_2}}}{E_x}{E_y}\cos {\theta _1}\sin {\theta _2}{e^{ - i\gamma }} - {\tau _{{x_2}}}{\tau _{{y_1}}}{E_x}{E_y}\cos {\theta _2}\sin {\theta _1}{e^{i\gamma }}} \right\rangle } \right]^ \cdot } \cr}$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq135.png) (A.3)
(A.3)
Using the trigonometric formulae for cos θi cos θj, sin θi sin θj and cos θi sin θj, we get the result of Eq. 14:
![$\eqalign{ & 2{{\tilde I}_{ \bullet {\bf{p}},x}} = {\mathop{\rm Re}\nolimits} \left[ {{e^{ - i(\eta + \Delta {\rm{A}}\psi )}}\left\langle {{\rho ^2}\left[ {\left[ {\cos \left( {{\theta _1} + {\theta _2}} \right)\cos 2\phi + \cos \left( {{\theta _1} - {\theta _2}} \right)} \right]\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) + i\left[ {\cos \left( {{\theta _1} + {\theta _2}} \right) + \cos \left( {{\theta _1} - {\theta _2}} \right)\cos 2\phi } \right]\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \right]} \right.} \right. \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - {E_x}{E_y}\left[ {\cos \gamma \left[ {\left( {{\tau _{{x_1}}}{\tau _{{y_2}}} + {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \left( {{\theta _1} + {\theta _2}} \right) - \left( {{\tau _{{x_1}}}{\tau _{{y_2}}} - {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \left( {{\theta _1} - {\theta _2}} \right)} \right]} \right. \cr & \left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. {\left. { + i\sin \gamma \left[ { - \left( {{\tau _{{x_1}}}{\tau _{{y_2}}} - {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \left( {{\theta _1} + {\theta _2}} \right) + \left( {{\tau _{{x_1}}}{\tau _{{y_2}}} + {\tau _{{x_2}}}{\tau _{{y_1}}}} \right)\sin \left( {{\theta _1} - {\theta _2}} \right)} \right]} \right]} \right\rangle } \right]. \cr}$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq136.png) (A.4)
(A.4)
A.2 Derivation of Equation 28
This section describes how Eq. 28 is derived from Eq. 27. Weak diattenuation (δτ = τx − τy) and weak differential retardance (∆∆ψ) are assumed meaning δτ and ∆∆ψ are considered first-order quantities. A moderate degree of polarization of the source is also assumed meaning P is also considered as a first order quantity. In what follows, “xth order” means “xth order in δτ, ∆∆ψ or P.” The idea is to derive ξ from tan ξ by taking the ratio of the two lines of Eq. 27. Since sin ξ is proportional to sin 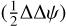 in this equation, it is at most of order of 1 as well as ξ since sin ξ ≃ ξ to first order. As a consequence, the tangent can be expanded to first order as tan ξ ≃ ξ, which indeed is also an expansion to second order since the second order term of the tangent is equal to 0. In addition, to get an expansion of ξ to the second order and since the zeroth order term of sin ξ is null, the expression of cos ξ only needs to be expanded to first order.
in this equation, it is at most of order of 1 as well as ξ since sin ξ ≃ ξ to first order. As a consequence, the tangent can be expanded to first order as tan ξ ≃ ξ, which indeed is also an expansion to second order since the second order term of the tangent is equal to 0. In addition, to get an expansion of ξ to the second order and since the zeroth order term of sin ξ is null, the expression of cos ξ only needs to be expanded to first order.
With these assumptions and these considerations, Eq. 27 can be expanded according to
![$\left\{ {\matrix{ {{2^{|\varepsilon |}}\rho \cos \xi \simeq {\tau ^2}\left[ {1 + \varepsilon P(\cos 2\theta \cos 2\alpha - \sin 2\theta \sin 2\alpha \cos \gamma ) + {{\delta \tau } \over \tau }\varepsilon \cos 2\theta } \right],} \hfill & {{\rm{ to first order, }}} \hfill \cr {{2^{|\varepsilon |}}\rho \sin \xi \simeq {1 \over 4}{\tau ^2}\Delta \Delta \psi \left[ {2\varepsilon \cos 2\theta + 2{{\delta \tau } \over \tau } + 2P\cos 2\alpha } \right],} \hfill & {{\rm{ to second order}}{\rm{. }}} \hfill \cr } } \right.$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq138.png) (A.5)
(A.5)
As a consequence, the expansion of tan ξ ≃ ξ to second order is equal to
![$\tan \xi \simeq \xi \simeq {1 \over 4}\Delta \Delta \psi \left[ {2\varepsilon \cos 2\theta + 2{{\delta \tau } \over \tau } + 2P\cos 2\alpha } \right] \times \left[ {1 - \varepsilon P(\cos 2\theta \cos 2\alpha - \sin 2\theta \sin 2\alpha \cos \gamma ) - {{\delta \tau } \over \tau }\varepsilon \cos 2\theta } \right].$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq139.png) (A.6)
(A.6)
Keeping second order terms only in the product and grouping terms leads to
![$\left. {\xi \simeq {1 \over 4}\Delta \Delta \psi \left[ {2\varepsilon \cos 2\theta + 2\left( {P\cos 2\alpha + {{\delta \tau } \over \tau }} \right)\left( {1 - {\varepsilon ^2}{{\cos }^2}\theta } \right) + {\varepsilon ^2}P\sin 4\theta \sin 2\alpha \cos \gamma } \right)} \right].$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq140.png) (A.7)
(A.7)
Hence, the result of Eq. 28 when applied to baseline i, as noted in Sect. 5.
References
- Elias, N. M. I. 2001, ApJ, 549, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Elias, N. M. I. 2004, ApJ, 611, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J. W. 2000, Statistical Optics (Wiley-VCH) [Google Scholar]
- GRAVITY Collaboration (Widmann, F., et al.) 2024, A&A, 681, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labeyrie, A. 1975, ApJ, 196, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, G. 2024, J. Opt. Soc. Am. A, 41, 708 [Google Scholar]
- Perrin, G., Jocou, L., Perraut, K., et al. 2024, A&A, 681, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rousselet-Perraut, K., Vakili, F., & Mourard, D. 1996, Opt. Eng., 35, 2943 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 (u, v) plane coverage for α Cru with symbols for samples used for Fig. 2. |
| In the text | |
 |
Fig. 2 Computation of the astrometric bias with multiples (×1, 2.5,5) of a ground level (G) of differential birefringence based on fiber measurements in the case of α Cru and with a degree of linear polarization varying between 0 and 50% and polarization angles in the 0–2π range for different hour angles. The instantaneous (u, v) coverage with the four Unit Telescopes is displayed as an inset in the bottom right of each plot. The full (u, v) coverage is presented in Fig. 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\left\{ \matrix{ 4{{\tilde I}_x} = {I_{\rm{p}}}\left[ {\cos (\eta + \Delta {\rm{A}}\psi )\left[ {\left[ {\left( {\tau _x^2 + \tau _y^2} \right)(1 + \cos 2\theta \cos 2\alpha ) + \left( {\tau _x^2 - \tau _y^2} \right)(\cos 2\alpha + \cos 2\theta )} \right]\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) - 2{\tau _x}{\tau _y}\sin 2\theta \sin 2\alpha \cos \gamma } \right]} \right. \hfill \cr \left. { + \sin (\eta + \Delta {\rm{A}}\psi )\left[ {\left( {\tau _x^2 - \tau _y^2} \right)(1 + \cos 2\theta \cos 2\alpha ) + \left( {\tau _x^2 + \tau _y^2} \right)(\cos 2\alpha + \cos 2\theta )} \right]\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \right] \hfill \cr 4{{\tilde I}_y} = {I_{\rm{p}}}\left[ {\cos (\eta + \Delta {\rm{A}}\psi )\left[ {\left[ {\left( {\tau _x^2 + \tau _y^2} \right)(1 - \cos 2\theta \cos 2\alpha ) + \left( {\tau _x^2 - \tau _y^2} \right)(\cos 2\alpha - \cos 2\theta )} \right]\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) + 2{\tau _x}{\tau _y}\sin 2\theta \sin 2\alpha \cos \gamma } \right]} \right. \hfill \cr \left. { + \sin (\eta + \Delta {\rm{A}}\psi )\left[ {\left( {\tau _x^2 - \tau _y^2} \right)(1 - \cos 2\theta \cos 2\alpha ) + \left( {\tau _x^2 + \tau _y^2} \right)(\cos 2\alpha - \cos 2\theta )} \right]\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \right], \hfill \cr 2\tilde I = {I_{\rm{p}}}\left[ {\cos (\eta + \Delta {\rm{A}}\psi )\left[ {\left( {\tau _x^2 + \tau _y^2} \right) + \left( {\tau _x^2 - \tau _y^2} \right)\cos 2\alpha } \right]\cos \left( {{1 \over 2}\Delta \Delta \psi } \right) + \sin (\eta + \Delta {\rm{A}}\psi )\left[ {\left( {\tau _x^2 - \tau _y^2} \right) + \left( {\tau _x^2 + \tau _y^2} \right)\cos 2\alpha } \right]\sin \left( {{1 \over 2}\Delta \Delta \psi } \right)} \right]. \hfill \cr} \right.$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq50.png)
![$M = 2\pi \left[ {\matrix{ {\mathop \sum \limits_{i = 1}^N u_i^2} \hfill & {\mathop \sum \limits_{i = 1}^N {u_i}{\upsilon _i}} \hfill \cr {\mathop \sum \limits_{i = 1}^N {u_i}{\upsilon _i}} \hfill & {\mathop \sum \limits_{i = 1}^N \upsilon _i^2} \hfill \cr } } \right],$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq88.png)
![${M^{ - 1}} = {{2\pi } \over {\det M}}\left[ {\matrix{ {\sum\nolimits_{i = 1}^N {\upsilon _i^2} } & { - \sum\nolimits_{i = 1}^N {{u_i}} {\upsilon _i}} \cr { - \sum\nolimits_{i = 1}^N {{u_i}} {\upsilon _i}} & {\sum\nolimits_{i = 1}^N {u_i^2} } \cr } } \right]{\rm{, }}$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq89.png)
![$\overrightarrow {{\alpha _0}} = {M^{ - 1}}\left[ {\matrix{ {\sum\nolimits_{i = 1}^N \Delta \Delta {\psi _i}{u_i}} \hfill \cr {\sum\nolimits_{i = 1}^N \Delta \Delta {\psi _i}{\upsilon _i}} \hfill \cr } } \right].$](/articles/aa/full_html/2025/03/aa51570-24/aa51570-24-eq116.png)