| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 18 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202348218 | |
| Published online | 02 February 2024 | |
Formation-flying interferometry in geocentric orbits
Institute of Space and Astronautical Science,
3-1-1 Yoshinodai, Chuo-ward, Sagamihara,
Kanagawa
252-0222,
Japan
e-mail: ito.takahiro@jaxa.jp
Received:
10
October
2023
Accepted:
16
November
2023
Context. Spacecraft formation flying serves as a method of astronomical instrumentation that enables the construction of large virtual structures in space. The formation-flying interferometry generally requires very high control accuracy, and extraterrestrial orbits are typically selected. To pave the way for comprehensive missions, proposals have been made for preliminary space missions, involving nano- or small satellites, to demonstrate formation-flying interferometry technologies, especially in low Earth orbits. From a theoretical perspective, however, it is unknown where and to what extent feasible regions for formation-flying interferometry should exist in geocentric orbits.
Aims. This study aims to demonstrate the feasibility of formation-flying interferometry in geocentric orbits in which various perturbation sources exist. Geocentric orbits offer the advantage of economic accessibility and the availability of proven formation-flying technologies tailored for Earth orbits. Its feasibility depends on the existence of specific orbits that satisfy a small-disturbance environment with good observation conditions.
Methods. Spacecraft motions in Earth orbits subjected to perturbations are analytically modeled based on celestial mechanics. The magnitudes of the accelerations required to counteract these perturbations are characterized by parameters such as the semimajor axis and the size of the formation.
Results. Small-perturbation regions tend to appear in higher-altitude and shorter-separation regions in geocentric orbits. Candidate orbits are identified in high Earth orbits for the triangular laser-interferometric gravitational-wave telescope, which is 100 km in size, and in medium Earth orbits for the linear astronomical interferometer, which is 0.5 km in size. A low Earth orbit with a separation of approximately 0.1 km may be suitable for experimental purposes.
Conclusions. Geocentric orbits are potentially applicable for various types of formation-flying interferometry.
Key words: gravitation / gravitational waves / instrumentation: interferometers / space vehicles / telescopes / celestial mechanics
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Spacecraft formation flying represents a crucial method in astronomical instrumentation, with the potential to revolutionize modern astronomy by creating large virtual structures in space. Some space-based astronomical missions under conceptual study require rigid and continuous formation while maintaining a very high control accuracy of less than 1 μm and/or μrad, and interferometric techniques are typically used. The Deci-hertz Interferometer Gravitational Wave Observatory (DECIGO; Kawamura et al. 2021) is a laser-interferometric, space-based gravitational-wave observatory used to measure coalescing binary neutron stars, the acceleration of the universe, and stochastic gravitational waves predicted by inflation. Each cluster comprises three spacecraft that are 1000 km apart and form an equilateral triangle, and four clusters are placed in a near-circular heliocentric orbit. Fabry-Pérot cavities are employed in DECIGO, each comprising two mirrors to measure the arm-length changes. The Large Interferometer For Exoplanets (LIFE; Quanz et al. 2022) is a space-based midinfrared nulling interferometer that detects and characterizes the thermal emissions of exoplanets. LIFE is based on earlier mission concepts, such as Darwin (Cockell et al. 2009) and the Terrestrial Planet Finder Interferometer (Lawson & Dooley 2005), and its primary orbital selection is an orbit around the Sun-Earth Lagrange second (L2) point. The current design for LIFE assumes four collector spacecrafts and one beam-combiner spacecraft, and their formation size is controlled to remain between tens and hundreds of meters. The common features of DECIGO and LIFE are that precise control is necessary to maintain the optical path length or difference between satellites and that their candidate orbits are beyond Earth’s orbit.
Flight-proven examples in formation flying have been shown in geocentric orbits, and coarse formation control on the order of submeters to meters was typically sufficient to satisfy mission objectives. The Japanese Engineering Test Satellite-VII (Kawano et al. 2001) demonstrated autonomous formation flying, rendezvous, and docking in the late 1990s in a circular low Earth orbit (LEO). In the 2000s and 2010s, autonomous formation-flying technology advanced for circular LEOs through leading space missions such as Prototype Research Instruments and Space Mission technology Advancement (PRISMA; Gill et al. 2007) and TerraSAR-X/TanDEM-X (TerraSAR-X addon for Digital Elevation Measurement; Kahle et al. 2014) for technological demonstration and Earth observation. Their accuracy during formation flying reached the centimeter to meter level based on the navigation accuracy provided by the global navigation satellite system (GNSS). In the 2020s, Project for OnBoard Autonomy-3 (PROBA-3) will demonstrate several formation activities, including coarse-to-fine control, autonomy, and safety management, to observe the solar coronagraph in a highly elliptical orbit. Its formation-flying precision is capable of submillimeter relative displacement and arcsecond-order pointing accuracy. This accuracy will be achieved using state-of-the-art metrology sensors and millinewton-class thrusters (Penin et al. 2020). As seen in these examples, formation flight technologies are gradually maturing; however, a technological gap still exists in the development of future formation-flying interferometry.
System-level, end-to-end, in-space verification for the pathfinder may be necessary to mature formation-flying interferometry before full-scale missions, as suggested in Monnier et al. (2019). However, the use of extraterrestrial orbits may be an inherent bottleneck for this purpose. The major benefits of using extraterrestrial orbits are the small-disturbance environment and good observation conditions. However, its major limitations are the high transportation cost to the desired orbit and that GNSS cannot be used for formation-flying autonomy, safety, and management. Such drawbacks may lead to formationflying interferometry becoming a larger and longer-term project.
An alternative is to use a geocentric orbit in which various perturbation sources exist. The expected advantages of using Earth orbits are the economic accessibility and availability of flight-proven technologies for formation flying autonomy, safety, and management with GNSS. Furthermore, state-of-the-art technologies are extending the use of GNSS from LEO to high Earth orbit (Ashman et al. 2018). However, few studies have applied Earth orbits to formation-flying interferometry. Representative and state-of-the-art research in this context conducted by Hansen & Ireland (2020) involved a linear astronomical interferometer in a near-circular LEO, and Earth’s J2 gravity potential and atmospheric drag were considered to be major perturbations. The necessary ΔV (the time integral of the thrust acceleration) to maintain the strict formation requirements was at an acceptable level of a few tens of m s−1 per year, as calculated based on the numerical integration of the equations of motion. However, the numerical approach tends to rely on trial and error to determine feasible Earth-orbit regions. From a theoretical perspective, understanding where and to what extent feasible regions should exist is difficult. The characterization of orbital perturbations is as crucial for formation-flying interferometry as site characterization is for the deployment of ground-based telescopes.
This study investigates the feasibility of formation-flying interferometry in geocentric orbits based on a celestialmechanics approach. This study makes four major contributions to the literature. The first contribution is the analytical modeling of the perturbed orbital motion to attain precise formation flying. We identify four types of absolute and relative perturbations that need to be mitigated. The second contribution is to offer a propellant-efficient control strategy for correcting the absolute and/or relative perturbing accelerations. Secular and long-period perturbations of the eccentricity vector play key roles in determining the control strategy. The third contribution enables a complete and explicit calculation of major perturbing accelerations. Using the proposed method, the disturbance environments for different formations can be analytically evaluated in various Earth orbits. By integrating these three contributions, the perturbation magnitudes can be characterized by the semimajor axis and size of the formation, and this information can be used as a guideline for finding candidate orbits. The final contribution is the provision of detailed examples of orbital selection and control approaches for formation-flying interferometry. The proposed approach as well as methods for satisfying the observation conditions will be useful for future applications.
This study considers only a near-circular Earth orbit because such is sufficient for various potential applications in formationflying interferometry. In terms of terminology, this study uses the chief-deputy expression to describe formation-flying satellites. A chief does not necessarily represent the actual chief satellite, but rather the virtual origin of formation-flying satellites. By contrast, a deputy denotes a real spacecraft flying in proximity to the chief. These terms are used throughout the paper without any notation. Lastly, this study uses numerous symbols owing to the thorough analysis of perturbed motion. The major symbols, particularly those used in the theoretical development, are listed in Appendix A.
The remainder of this paper is organized as follows. Section 2 presents a review of unperturbed relative motion for a circular orbit. Section 3 presents the development of a perturbed relative-motion model for a near-circular orbit against arbitrary perturbations and explains the four types of resultant perturbing accelerations. Section 4 first presents an analysis of the relationship between the perturbation periods and their contributions to perturbing acceleration magnitudes. Then, it presents analytical models of the perturbed orbital motions and perturbing accelerations as well as an effective approach for orbital selection and control. Section 5 presents numerical examples of the proposed approach to formation-flying interferometry. The concluding remarks are presented in Sect. 6.
2 Unperturbed relative motion
The relative equation of motion of the deputy with respect to the chief in the Earth-centered inertial (ECI) frame is
 (1)
(1)
where μe is the Earth gravitational constant, rI is the relative position vector of the deputy  and
and  are the position vectors of the chief and deputy, respectively,
are the position vectors of the chief and deputy, respectively,  is the disturbance acceleration vector of the deputy relative to the chief
is the disturbance acceleration vector of the deputy relative to the chief  and
and  are the disturbance acceleration vectors for the chief and deputy, respectively,
are the disturbance acceleration vectors for the chief and deputy, respectively,  and
and  are the control acceleration vectors applied to the chief and deputy, respectively,
are the control acceleration vectors applied to the chief and deputy, respectively,  and
and  . The superscript 1 indicates the position, velocity, or acceleration in the ECI frame.
. The superscript 1 indicates the position, velocity, or acceleration in the ECI frame.
By assuming the unperturbed motion of both the chief and deputy  and the uncontrolled motion of the chief
and the uncontrolled motion of the chief  , Eq. (1) in the ECI frame is transformed into the local-verticallocal-horizontal (LVLH) frame:
, Eq. (1) in the ECI frame is transformed into the local-verticallocal-horizontal (LVLH) frame:
 (2)
(2)
where r = [x, y, z]T denotes the position vector of the deputy relative to the chief in the LVLH frame, θ is the argument of latitude of the chief, and ud = [ux, uy, uz]T is the control acceleration vector applied to the deputy in the LVLH frame. The position, velocity, or acceleration in the LVLH frame are written without superscript notations, unlike those in the ECI frame. The LVLH frame is defined such that the x direction is directed radially outward from the chief, the z direction is normal to the orbital plane and positive in the direction of the (instantaneous) angular momentum, and the y direction in the right-hand frame completes the setup. Assuming r ≪ Rc (r = ||r||), the first term on the right-hand side of Eq. (2) can be linearized as follows:
 (3)
(3)
For a circular orbit,  , and Rc = a, where n and a are the mean motion and semimajor axis of the chief, respectively. In addition, using Eqs. (2) and (3) and the relationship
, and Rc = a, where n and a are the mean motion and semimajor axis of the chief, respectively. In addition, using Eqs. (2) and (3) and the relationship  , the unperturbed and linear relative dynamics model for a circular orbit is obtained as follows:
, the unperturbed and linear relative dynamics model for a circular orbit is obtained as follows:
 (4)
(4)
where Au1 and Au2 are matrices defined as follows:
![${A_{u1}} = \left[ {\matrix{ {3{n^2}} & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & { - {n^2}} \cr } } \right],\quad {A_{u2}} = \left[ {\matrix{ 0 & {2n} & 0 \cr { - 2n} & 0 & 0 \cr 0 & 0 & 0 \cr } } \right]$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq17.png) (5)
(5)
Equation (4) is known as the Clohessy-Wiltshire (CW) equation (Clohessy & Wiltshire 1960).
A possible approach for realizing formation flying under the orbital dynamics in Eq. (4) is to cancel the relative accelerations Au1 r and  with the control accelerations. However, the control acceleration requirement tends to become large, which is inefficient and unrealistic for formation-flying applications. Therefore, the reference formation orbit is typically selected using the natural solution of Eq. (4) when ud = 0. The bounded CW solution (the solution without an along-track drift) is
with the control accelerations. However, the control acceleration requirement tends to become large, which is inefficient and unrealistic for formation-flying applications. Therefore, the reference formation orbit is typically selected using the natural solution of Eq. (4) when ud = 0. The bounded CW solution (the solution without an along-track drift) is
![${r_r} = \left[ {\matrix{ {{\rho _x}\sin \left( {\theta + {\alpha _x}} \right)} \cr {{\rho _y} + 2{\rho _x}\cos \left( {\theta + {\alpha _x}} \right)} \cr {{\rho _z}\sin \left( {\theta + {\alpha _z}} \right)} \cr } } \right]$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq19.png) (6)
(6)
where ρx, ρy, ρz, αx, and αz denote the design parameters of the relative orbit (Clohessy & Wiltshire 1960). Clearly, θ is a linear function of time because  for the unperturbed circular orbit; therefore, rr is also a function of time.
for the unperturbed circular orbit; therefore, rr is also a function of time.
3 Perturbed relative motion
In contrast to Keplerian dynamics, oscillating and drifting orbital motion can arise in the presence of orbital perturbations. The reference formation described in the previous section was obtained using unperturbed, circular, and linearized assumptions. Therefore, elliptical and nonlinear effects may disturb the actual formation. This section analyzes how orbital perturbations and un-modeled dynamics can affect the rigid and continuous formation control.
The perturbed relative equation of motion of the deputy in the LVLH frame is expressed as follows (Izzo et al. 2003):
 (7)
(7)
where ω = [ωx,ωy,ωz]T is the orbital angular velocity vector of the chief in the LVLH frame, f2B is the linearized gravity gradient acceleration owing to the two-body gravitational field  is the sum of the relative and physical perturbing accelerations applied to the deputy, and uc and ud are the control acceleration vectors applied to the chief and deputy in the LVLH frame, respectively. The elements of ω are (Alfriend et al. 2010)
is the sum of the relative and physical perturbing accelerations applied to the deputy, and uc and ud are the control acceleration vectors applied to the chief and deputy in the LVLH frame, respectively. The elements of ω are (Alfriend et al. 2010)
 (8)
(8)
where Ω and I are the right ascension of the ascending node (RAAN) and inclination of the chief, respectively. We can verify ωy = 0 by substituting I and ![$\left( {{f_{g2B}} = - \left( {{\mu _e}/R_c^3} \right){{[ - 2x,y,z]}^T}} \right),{f_p}$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq24.png) from Gauss’s variational equations into Eq. (8) (Alfriend et al. 2010).
from Gauss’s variational equations into Eq. (8) (Alfriend et al. 2010).
Next, Eq. (7) is transformed into
 (9)
(9)
We note that At1 and At2 are (3 × 3) matrices, where the elements of Au1 and Au2 in Eq. (5) are replaced by n → ωt, where ωt is the user-defined target angular velocity. In Eq. (9), fo takes the following form:
 (10)
(10)
where Ap1 and Ap2 are (3 × 3) matrices corresponding to the first four terms in Eq. (7). It should be noted that fo is the relative fictitious acceleration owing to the perturbed orbital motion of the chief, and it remains zero if the chief orbit is unperturbed and circular. Equation (10) suggests that the selection of the ωt profile is important for minimizing fo. Choosing ωt close to ωz is one of the best solutions, and Eq. (10) can be approximated further. Hereafter, ωt is selected as ωz throughout this study. First, under the near-circular-orbit assumption, the argument of latitude can be approximated as follows:
 (11)
(11)
where ϕ is the mean argument of latitude defined as ϕ = (l + ω), ω is the argument of perigee, l is the mean anomaly, ex and ey are the elements of the eccentricity vector defined as [ex, ey]T = [e cos ω, e sin ω]T, and e is the eccentricity of the chief. Then, let the time derivative of ϕ be expressed as  . More over, the time derivatives
. More over, the time derivatives  , and
, and  are assumed sufficiently small with respect to n. By neglecting the second- and higher- order terms of the small variables, (Ap1 – At1) and (Ap2 – At2) in Eq. (10) can be expressed as follows:
are assumed sufficiently small with respect to n. By neglecting the second- and higher- order terms of the small variables, (Ap1 – At1) and (Ap2 – At2) in Eq. (10) can be expressed as follows:
![$\matrix{ {\left( {{A_{p1}} - {A_{t1}}} \right) = \left[ {\matrix{ {a_{A1}^{(11)}} & {a_{A1}^{(12)}} & {a_{A1}^{(13)}} \cr { - a_{A1}^{(12)}} & {a_{A1}^{(22)}} & {a_{A1}^{(23)}} \cr {a_{A1}^{(13)}} & { - a_{A1}^{(23)}} & {a_{A1}^{(13)}} \cr } } \right],} \cr {\left( {{A_{p2}} - {A_{t2}}} \right) = \left[ {\matrix{ 0 & 0 & 0 \cr 0 & 0 & {a_{A2}^{(23)}} \cr {0 - a_{A2}^{(23)}} & 0 & {} \cr } } \right],} \cr } $](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq31.png) (12)
(12)
The following relationships are used to obtain Eqs. (12) and (13):
 (14)
(14)
Then, the desired reference formation is selected as the natural solution of Eq. (6):
![${r_r} = \left[ {\matrix{ {{\rho _x}\sin {{\rm{\Theta }}_x}} \cr {{\rho _y} + 2{\rho _x}\cos {{\rm{\Theta }}_x}} \cr {{\rho _z}\sin {{\rm{\Theta }}_z}} \cr } } \right]$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq34.png) (15)
(15)
where Θx and Θz are the new variables satisfying Θx = (θ + αx),  , and
, and  , and the parameters of (ρx, ρy, ρz) can be time-variant. The relationships between
, and the parameters of (ρx, ρy, ρz) can be time-variant. The relationships between  , and
, and  can be written as follows:
can be written as follows:
 (16)
(16)
![$\eqalign{ & {f_f} = {A_{t2}}\left[ {\matrix{ {{{\dot \rho }_x}\sin {{\rm{\Theta }}_x}} \cr {{{\dot \rho }_y} + 2{{\dot \rho }_x}\cos {{\rm{\Theta }}_x}} \cr {{{\dot \rho }_z}\sin {{\rm{\Theta }}_z}} \cr } } \right] - {{\dot \omega }_t}\left[ {\matrix{ {{\rho _x}\cos {{\rm{\Theta }}_x}} \cr { - 2{\rho _x}\sin {{\rm{\Theta }}_x}} \cr {{\rho _z}\cos {{\rm{\Theta }}_z}} \cr } } \right] \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 2{\omega _t}\left[ {\matrix{ {{{\dot \rho }_x}\cos {{\rm{\Theta }}_x}} \cr { - 2{{\dot \rho }_x}\sin {{\rm{\Theta }}_x}} \cr {{{\dot \rho }_z}\cos {{\rm{\Theta }}_z}} \cr } } \right] - \left[ {\matrix{ {{{\mathop \rho \limits^ }_x}\sin {{\rm{\Theta }}_x}} \cr {{{\mathop \rho \limits^ }_y} + 2{{\mathop \rho \limits^ }_x}\cos {{\rm{\Theta }}_x}} \cr {{{\mathop \rho \limits^ }_z}\sin {{\rm{\Theta }}_z}} \cr } } \right]. \cr} $](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq40.png) (17)
(17)
We note that ff is the relative fictitious acceleration owing to the perturbed motion of the reference formation.
Finally, by subtracting Eq. (16) from Eq. (9), we obtain the following:
 (18)
(18)
where ϵ = (r – rr) is the relative positional error with respect to the reference formation. By setting the control command of the deputy to
 (19)
(19)
where ur is the control acceleration to compensate for all relative disturbances, and by assuming that the current relative position and velocity are on the desired formation  , the relative acceleration error
, the relative acceleration error  becomes zero; thus, tracking on the reference formation is expected for the deputy.
becomes zero; thus, tracking on the reference formation is expected for the deputy.
Table 1 summarizes the four categories of perturbing accelerations that can be mitigated by the control. The simplest way to nullify the perturbation effects is to compensate for all absolute and relative perturbing accelerations (i.e., Fc, which is the expression of  in the LVLH frame, fp , fo , and ff ) using the control ud . However, compensation for absolute perturbing accelerations typically leads to a significant waste of propellant. In such cases, another possible approach is to maintain most of the absolute perturbing accelerations, except for the small ones, and compensate for all the relative perturbations with respect to the chief. The feasibility of such a control strategy depends on whether the control acceleration ud , and eventually Fc , fp , fo , and ff are sufficiently small for the reference formation. Determining the differential disturbances of the deputy with respect to the chief is necessary to evaluate fp . Moreover, determining the perturbed orbital motions of (ex, ey) as well as the first and second time derivatives of (ex, ey, I, Ω, ϕ) is necessary to evaluate fo. The ωt(= ωz) profile affects fo and ff, and understanding the perturbed motions of ωz and ωz, which are functions of (ex, ey , I, Ω, ϕ), is essential. Furthermore, the control-effort trade-off between compensating for or maintaining Fc remains unknown. Such concerns motivate the development of analytical models of perturbed orbital motions and perturbing accelerations, as described in the next section.
in the LVLH frame, fp , fo , and ff ) using the control ud . However, compensation for absolute perturbing accelerations typically leads to a significant waste of propellant. In such cases, another possible approach is to maintain most of the absolute perturbing accelerations, except for the small ones, and compensate for all the relative perturbations with respect to the chief. The feasibility of such a control strategy depends on whether the control acceleration ud , and eventually Fc , fp , fo , and ff are sufficiently small for the reference formation. Determining the differential disturbances of the deputy with respect to the chief is necessary to evaluate fp . Moreover, determining the perturbed orbital motions of (ex, ey) as well as the first and second time derivatives of (ex, ey, I, Ω, ϕ) is necessary to evaluate fo. The ωt(= ωz) profile affects fo and ff, and understanding the perturbed motions of ωz and ωz, which are functions of (ex, ey , I, Ω, ϕ), is essential. Furthermore, the control-effort trade-off between compensating for or maintaining Fc remains unknown. Such concerns motivate the development of analytical models of perturbed orbital motions and perturbing accelerations, as described in the next section.
Categories of perturbing accelerations that can be mitigated by the control.
4 Perturbation mitigation methods
4.1 Perturbation periods and acceleration magnitudes
The physical perturbing accelerations (i.e., Fc and fp) are determined simply from the positions and velocities of the chief and deputy, in addition to spacecraft and environmental parameters at a certain moment. In contrast, to calculate the fictitious perturbing accelerations (i.e., fo and ff), it is necessary to understand the perturbed orbital motion of the chief, as presented in the previous section. In addition, the control accelerations to compensate for the absolute physical perturbations (Fc) can be divided into the secular, long-period, and short-period parts through Gauss’s variational equations. Whereas compensation for all parts of Fc could lead to a significant waste of propellant, compensation for small parts of Fc may be comparable to the relative fictitious perturbations. Therefore, before developing the perturbation models for each perturbing source, we show an analysis to understand how the perturbed orbital motion of the chief can affect the control accelerations to compensate for the relative fictitious perturbations, and how the relative fictitious perturbations are compared to the absolute physical ones with respect to the perturbation periods.
Equations (10), (12), and (13) suggest that the osculating orbital motion produces the relative fictitious acceleration of fo , whose magnitude comprises the following terms: (·)n2rr for (ex, ey), and  and
and  for (ex, ey, I, Ω, ϕ), where (·) expresses the osculating orbital element and ||rr|| = rr. From Gauss’s variational equations, the control accelerations to compensate for the absolute perturbations comprise the following terms:
for (ex, ey, I, Ω, ϕ), where (·) expresses the osculating orbital element and ||rr|| = rr. From Gauss’s variational equations, the control accelerations to compensate for the absolute perturbations comprise the following terms:  for (ex, ey, I, Ω, ϕ). At this point, the osculating orbital elements are modeled as follows:
for (ex, ey, I, Ω, ϕ). At this point, the osculating orbital elements are modeled as follows:
 (20)
(20)
where (·)(s) is the secular term that is a linear function of time, δ(·)(lp) is the long-period term for which the angular frequency has an order of nl(≪ n), δ(·)(sp) is the short-period term for which the angular frequency has an order of n,  is the initial value of the secular term, and
is the initial value of the secular term, and  is the drift rate of the secular term. By substituting Eq. (20) into relevant terms, the effects of the secular, long-period, and short-period terms can be analyzed. The same discussion holds for the relative fictitious acceleration of ff, provided that ρx, ρy, and ρz are derived from the natural solution in Eq. (6).
is the drift rate of the secular term. By substituting Eq. (20) into relevant terms, the effects of the secular, long-period, and short-period terms can be analyzed. The same discussion holds for the relative fictitious acceleration of ff, provided that ρx, ρy, and ρz are derived from the natural solution in Eq. (6).
Table 2 summarizes the orders of the control acceleration magnitudes required to compensate for the relative fictitious perturbations (fo and ff) for the secular, long-period, and shortperiod terms in comparison with those of the absolute physical perturbations (Fc). Table 2 suggests that most terms to compensate for the relative fictitious perturbations include the common terms of the absolute physical ones multiplied by (rr/a) and/or (nl/n), both of which are sufficiently smaller than 1. Therefore, the best approach is to compensate for the relative fictitious perturbations to gain less control acceleration. However, two exceptional cases appear in the secular and long-period parts of the term with (·)n2rr. They have common terms of the absolute physical perturbations multiplied by not only (rr/a) (≪ 1), but also (nt), which can be considerably larger than 1 when t is large, or (nl/n)−1, which is significantly larger than 1. This result implies that the secular and long-period motions of the eccentricity vector (ex, ey) must be compared to determine whether to compensate for the absolute or relative perturbations to attain more efficient control. This insight is used to determine the orbit and formation control approach in Sect. 4.3.
Orders of the control acceleration magnitudes to compensate for the relative fictitious perturbations (fo and ff) for the secular, long-period, and short-period terms, in comparison to those of the absolute physical perturbations (Fc).
4.2 Analytical perturbation models
The perturbation sources considered in this study are CW nonlinearity, Earth J2 gravity potential, Earth J3 gravity potential, lunisolar gravity, atmospheric drag, and SRP. Their analytical models are explained in the following.
4.2.1 CW nonlinearity
The relative acceleration owing to CW nonlinearity is produced by nonlinear terms that are neglected in the CW equation (Eq. (4)). This can be computed by subtracting the first term on the right-hand side of Eq. (3) from the left-hand side. The CW nonlinearity can contribute to a part of fp .
4.2.2 Earth J2 gravity potential
The J2 gravity potential of Earth’s gravity is known to be one of the major perturbation sources for satellites, particularly in low-to-medium Earth orbit. By considering only zonal effects, the J2 -perturbed absolute acceleration vector acting on the chief ( , as a part of Fc) is given by (Alfriend et al. 2010)
, as a part of Fc) is given by (Alfriend et al. 2010)
![${F_{{J_2}}} = - {{3{J_2}{\mu _e}R_e^2} \over {2R_c^4}}\left[ {\matrix{ {1 - 3{{\sin }^2}I{{\sin }^2}\theta } \cr {{{\sin }^2}I\sin 2\theta } \cr {\sin 2I\sin \theta } \cr } } \right]{\rm{,}}$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq58.png) (21)
(21)
where Re is the mean equatorial radius of Earth. The linearized J2 differential acceleration vector ( , as a part of fp) has the following form (Izzo et al. 2003):
, as a part of fp) has the following form (Izzo et al. 2003):
![${f_{{J_2}}} = {{6{J_2}{\mu _e}R_e^2} \over {R_c^5}}\left[ {\matrix{ {a_{{J_2}}^{(11)}a_{{J_2}}^{(12)}a_{{J_2}}^{(13)}} \cr {a_{{J_2}}^{(21)}a_{{J_2}}^{(22)}a_{{J_2}}^{(23)}} \cr {a_{{J_2}}^{(31)}a_{{J_2}}^{(32)}a_{{J_2}}^{(33)}} \cr } } \right]r,$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq60.png) (22)
(22)
A comparison of Eqs. (21) and (22) shows that  is always less than
is always less than  under the assumption that r ≪ Rc.
under the assumption that r ≪ Rc.
The J2-perturbed motion of the chief can also yield the relative fictitious accelerations of fo and ff . The osculating orbital elements owing to the J2 potential for the near-circular orbit are obtained by substituting e → 0 into the known analytical solutions (e.g., see Kozai 1959; Brouwer 1959), as given in Appendix B. Notably, the J2 perturbation produces a secular drift in the RAAN. This drift may be useful for the mission orbit to scan the visible sky area, as discussed in detail in Sect. 5.
4.2.3 Earth J3 gravity potential
The Earth J3 gravitational potential represents asymmetry with respect to the equatorial plane. Its coefficient is on the order of 10−6 , which is thee orders of magnitude smaller than that for the J2 term; therefore, most effects on the J3 term can be neglected in comparison to the J2-perturbed effects. The only effect to be considered is the long-period J3 perturbation of the eccentricity vector in the presence of the J2 perturbation.
Assuming a small eccentricity and neglecting longitudedependent effects, Lagrange’s equations relating to the eccentricity vector for the long-period J3 perturbation are as follows (Kozai 1959):
 (24)
(24)
where  is the J2-perturbed secular drift rate of the argument of perigee given by
is the J2-perturbed secular drift rate of the argument of perigee given by  for the near-circular orbit. By applying the equilibrium condition of the eccentricity vector to an arbitrary inclination, the equilibrium eccentricity vector, known as a frozen eccentricity vector (ef), is given as follows (Kozai 1959):
for the near-circular orbit. By applying the equilibrium condition of the eccentricity vector to an arbitrary inclination, the equilibrium eccentricity vector, known as a frozen eccentricity vector (ef), is given as follows (Kozai 1959):
![${e_f} = \left[ {\matrix{ 0 \cr { - {{{J_3}{R_e}} \over {2{J_2}a}}\sin I} \cr } } \right]$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq67.png) (25)
(25)
Equation (25) implies that the mean eccentricity vector cannot be maintained at zero under the existence of Earth’s J2 and J3 gravity potentials, and its effect can be significant, particularly in LEO. For example, for a satellite in a near-circular LEO at an altitude of 500 km and inclination of 100°, the frozen eccentricity becomes ef = [0, 0.0011]T. Such a nonzero eccentricity vector can contribute to the relative fictitious accelerations of fo and ff.
4.2.4 Lunisolar gravity
The absolute lunisolar gravity acceleration vector of the chief with respect to the Earth (F3rd, as a part of Fc) is approximated as (Montenbruck & Gill 2000)
![${F_{3rd}} = C_I^L\left[ {{{{\mu _b}} \over {R_b^3}}\left\{ { - R_c^I + 3\left( {{{R_c^I \cdot R_b^I} \over {R_b^2}}} \right)R_b^I} \right\}} \right],$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq68.png) (26)
(26)
where  is the position vector of the third body in the ECI frame, μb denotes the gravity constant of the third body,
is the position vector of the third body in the ECI frame, μb denotes the gravity constant of the third body,  is the rotation matrix from the ECI frame to the rotational (LVLH) frame of the chief, and
is the rotation matrix from the ECI frame to the rotational (LVLH) frame of the chief, and  .
.
The linearized gravity gradient acceleration vector owing to the third body (f3rd , as a part of fp) is
![${f_{3rd}} = C_I^L\left[ {{{{\mu _b}} \over {R_b^3}}\left\{ { - {r^I} + 3\left( {{{{r^I} \cdot R_b^I} \over {R_b^2}}} \right)R_b^I} \right\}} \right].$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq72.png) (27)
(27)
Assume that r ≪ a; then, ||f3rd|| is always less than ||F3rd||.
The perturbed motion of the chief by lunisolar gravity can also yield the relative fictitious accelerations of fo and ff; therefore, understanding its osculating motion is important. To the best of our knowledge, however, no appropriate analytical expressions describing the secular, long-periodic, and short-period motions in a near-circular geocentric orbit due to lunisolar gravity have been proposed with reasonable accuracy for a relatively short timescale. Early work (Cook 1962) analytically calculated the secular and long-period satellite motion due to lunisolar perturbations up to the second degree of Legendre polynomials, but short-period motions were not analyzed. Subsequent work (Kozai 1973) analytically proposed the calculation of short-period satellite motion caused by lunisolar perturbations, but secular and long-period motions were calculated numerically. Recent work (Roscoe et al. 2013) developed secular and periodic motion models owing to third-body perturbations using a single- and double-averaged disturbing function. Analytical models were developed based on the assumption of a circular-restricted three-body problem; however, this may be problematic, particularly when long-term orbital motion on the eccentricity vector is a major concern. It is known that the parallactic term (third harmonic) of the lunar disturbing function can change the eccentricity of a circular geocentric orbit (e.g., see the Introduction in Allan & Cook 1964) through the nonzero eccentricity of the lunar orbit. To capture this effect, the disturbing function of the third body is considered up to the third degree of the Legendre polynomials. Taking these points into account, this study analytically developed a relatively simple, near-circular satellite motion model based on to lunisolar gravity, and the results are given in Appendix C.
In addition, the long-term effects of the lunisolar gravitational field and J2 term of the Earth’s oblateness may be comparable for a medium-to-high Earth orbit. For this gravity field, equilibrium solutions exist in which the averaged chief orbits may be frozen. This plane is known as the classical Laplace plane, which is between the Earth’s equator and that of the ecliptic, passing the vernal equinox (Allan & Cook 1964; Tremaine et al. 2009; Rosengren et al. 2014). Assuming that the chief orbit is circular, the lunar orbit lies in the ecliptic, and the direction of the angular momentum for the chief lies on the principal plane defined by the Earth polar axis and normal direction of the Earth orbit (such that Ω = 0° or 180°), the frozen orbit condition is (Allan & Cook 1964)
 (28)
(28)
where ϵe is the obliquity of the ecliptic (ϵe = 23.4°), Φ is the azimuth angle, and  , ωm, and ωs are defined as
, ωm, and ωs are defined as
 (29)
(29)
The subscripts m and s indicate the Moon or the Sun, respectively, and a and e with these subscripts represent the semimajor axis and eccentricity for the Moon or the Sun. For example, for a chief satellite at an altitude of 35 800 km (geosynchronous) with Ω = 0°, one can find that I = Φ = 7.4° is one of the solutions for the frozen orbits in Eq. (28). If the circular orbit does not lie in the classical Laplace plane, the orbital orientation will oscillate around the frozen point with a period of up to several tens of years. The frozen orbit lying in the classical Laplace plane may be useful particularly for the gravitational-wave detector, for obtaining the long-term stability on the orbital orientation with respect to the Sun, as discussed in Sect. 5.1.
4.2.5 Atmospheric drag
Atmospheric drag is a small force for most orbits, but it can be a major perturbation source for relative motion in LEOs. The atmospheric-drag acceleration vector acting on the chief spacecraft in the LVLH frame (FD, as a part of Fc) is as follows:
 (30)
(30)
where V is the velocity vector of the chief for the unperturbed and circular assumption in the LVLH frame (V = ||V||= na), ρ is atmospheric density, BD(= S CD/m) is the coefficient for drag, S is the cross-sectional area, CD is the drag coefficient, and m is the spacecraft mass. Equation (30) is obtained by assuming that the atmosphere co-rotates with the Earth (Montenbruck & Gill 2000) and V is approximately one order of magnitude higher than that of the Earth-fixed atmosphere; thus, atmospheric velocity is neglected.
In general, the atmospheric density has a large uncertainty, mainly owing to diurnal variation, periodic solar activity, and sudden solar activity (Montenbruck & Gill 2000). However, the most evident dependence of atmospheric density is that it decreases with increasing altitude. The Harris-Priester density model (Harris & Priester 1962) is relatively simple and is widely used as a standard atmospheric model. The model is given as follows:
![$\rho (h) = {\rho _m}(h) + \left[ {{\rho _M}(h) - {\rho _m}(h)} \right]{\cos ^N}\left( {{{\rm{\Psi }} \over 2}} \right),$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq77.png) (31)
(31)
where h is the height above Earth’s reference ellipsoid, Ψ is the angle between the satellite position vector and the apex of the diurnal bulge, N is a numerical value set to 2 for low- inclination orbits and 6 for polar orbits, and ρM(h) and ρm(h) are the apex and antapex densities, respectively. It should be noted that ρ(h) can be directly computed from the table of Harris- Priester atmospheric-density coefficients for mean solar activity (Long et al. 1989). When assuming a spherical Earth, height is given by h = (a − Re); thus, ρ is written as a function of the semimajor axis.
Assuming that the two satellites are flying in proximity formation, such that V and ρ are the same for both spacecraft, the relative acceleration vector for the deputy caused by atmospheric drag ( fD , as a part of fp) can be modeled as follows:
 (32)
(32)
where δ BD is the difference between the coefficients BD of the two spacecraft for atmospheric drag.
In contrast to Earth J2 and lunisolar gravity, ||FD|| and || fD|| can be of the same order. In addition, drag is a small force in most Earth orbits. Therefore, we assumed that both FD and fD are compensated for by the control accelerations, and we neglected the effects of fo and ff.
4.2.6 Solar radiation pressure
Solar radiation pressure (SRP) can be regarded as a function of the Sun-to-spacecraft distance, such that its magnitude is almost identical for spacecraft orbiting the Earth. A cannonball model was used, in which the satellite shape was assumed to be a uniform sphere. When the shade effect of the Earth and the small eccentricity of the Earth’s orbit are neglected, the acceleration vector by SRP acting on the chief spacecraft in the LVLH frame (Fs, as a part of Fc) is expressed as follows (Montenbruck & Gill 2000):
 (33)
(33)
where Ps is the SRP, Cs is the radiation pressure coefficient, Bs is the coefficient for SRP, and s is the unit vector pointing to the Sun in the LVLH frame. Assuming that two spacecraft are flying in proximity formation (Ps is the same for both spacecraft), the relative acceleration vector for the deputy caused by SRP (fs, as a part of fp) can be modeled as follows (Koenig et al. 2017):
 (34)
(34)
where δBs is the difference between the coefficients Bs of the two spacecraft for SRP. Similar to atmospheric drag, ||Fs|| and ||fs|| can be of the same order and their acceleration magnitudes are small. Therefore, we assumed that both Fs and fs are compensated for by the control accelerations and neglected and the effects of fo and ff.
4.3 Control approach
The orbit and formation control approach used in this study is determined based on the characteristics of each perturbation. Table 3 summarizes the control approach used to mitigate each perturbation. The check mark in Table 3 indicates that all marked perturbations are compensated for by the control, and the check mark with an asterisk indicates that either the absolute or relative perturbations are compensated for. As summarized in Table 3, the CW nonlinearity must be nullified by the control to maintain the rigid formation; compensating for the relative perturbations for the Earth J2 gravity potential and lunisolar gravity is economical (except for the secular and long-period effects on the eccentricity vector); the control strategy against the secular and long-period changes on the eccentricity vector owing to the lunisolar and Earth J3 gravity potential are compared to decide whether to compensate for the absolute or relative perturbations; the absolute and relative accelerations for the atmospheric drag and SRP, both of which are small in most Earth orbits, are corrected by the control (although the compensation of the absolute accelerations may be unnecessary for certain applications).
We propose three possible methods for mitigating the secular and long-period effects on the eccentricity vector, as shown in Fig. 1. The first approach is to maintain the eccentricity vector at zero by nullifying secular and/or long-period drifts using continuous control. For a near-circular orbit, the radial control force (ux) is sensitive to the eccentricity vector and mean argument of latitude; the tangential force (uy) is sensitive to the eccentricity vector and semimajor axis; and the normal force (uz) is sensitive to the inclination and RAAN. Therefore, when ux and uy are used to compensate for the eccentricity vector drift, Gauss’s variational equations for the eccentricity vector are as follows:
 (35)
(35)
where  and
and  denote the change rates of the eccentricity vector by the control. Terms with e and e2 are neglected in these equations. Setting ux and uy as
denote the change rates of the eccentricity vector by the control. Terms with e and e2 are neglected in these equations. Setting ux and uy as
 (36)
(36)
provides the necessary control to compensate for the eccentricity vector drift, where  , and
, and  . In this context,
. In this context,  and
and  are considered as the time derivatives of the secular and long-period variations on the eccentricity vector without control. This control law does not yield the secular and long-period changes in a and ϕ. The second approach is to accept the small eccentricity and compensate for its relative perturbing acceleration using continuous control. As previously mentioned, the control acceleration can be calculated using Eqs. (10) and (17). The third approach combines the previous two methods: the eccentricity vector drift is left as long as it remains within an acceptable level, and the accumulated eccentricity is periodically nullified by impulsive or continuous control. A benefit of the third approach is that the propellant for the observation may be saved by using another propulsion system for the satellite bus system (if available) because the objective of this control is only to reconfigure the orbit of the chief, whereas the previous two methods must realize the formation maintenance for the observation and orbit control of the chief simultaneously; thus, the propellant for the observation cannot be saved.
are considered as the time derivatives of the secular and long-period variations on the eccentricity vector without control. This control law does not yield the secular and long-period changes in a and ϕ. The second approach is to accept the small eccentricity and compensate for its relative perturbing acceleration using continuous control. As previously mentioned, the control acceleration can be calculated using Eqs. (10) and (17). The third approach combines the previous two methods: the eccentricity vector drift is left as long as it remains within an acceptable level, and the accumulated eccentricity is periodically nullified by impulsive or continuous control. A benefit of the third approach is that the propellant for the observation may be saved by using another propulsion system for the satellite bus system (if available) because the objective of this control is only to reconfigure the orbit of the chief, whereas the previous two methods must realize the formation maintenance for the observation and orbit control of the chief simultaneously; thus, the propellant for the observation cannot be saved.
For long-period perturbations owing to J3 and lunisolar gravity, the eccentricity vector can remain around the frozen point. Thus, the first and second methods are compared. For secular perturbations due to lunisolar gravity, the eccentricity can increase linearly with time; thus, the secular drift of the eccentricity vector may not be acceptable. Thus, the first and third methods are compared.
 |
Fig. 1 Three methods for mitigating the secular and long-period eccentricity vector drift. The panels on the left ((a) e-drift compensation) show the approach for compensating for the eccentricity vector drift of the chief using continuous control. The center panels ((b) e-error compensation) show the method that accepts the small eccentricity error and compensates for the relative perturbing acceleration of the deputy via continuous control. The panels on the right ((c) e-drift and e-error compensation) show the hybrid approach. The top and bottom panels for each approach show the time histories of the eccentricity and control accelerations, respectively. |
Control approach for mitigating each perturbation in this study.
4.4 Orbit selection approach
By analyzing the factors that contribute the most to the control magnitudes, further insight is attained regarding the orbit selection approach. The developed perturbation models suggest that the semimajor axis (a) characterizes the absolute perturbations, whereas the semimajor axis and formation size (rr) characterize the relative perturbations. Therefore, the orders of the control magnitudes for Fc and fp can be evaluated by an explicit analysis of their accelerations as a function of a and/or rr . Similarly, the control magnitudes for fo and ff can be evaluated using a two- step analysis to first evaluate the factors for the perturbed orbital elements of the chief and then calculate the orders of their perturbing accelerations as a function of a and rr . The three types of relative perturbations ( fp , fo , ff , if available) have the same order against each perturbation source provided that ρx, ρy, and ρz are derived from the natural solution in Eq. (6).
Table 4 summarizes the factors that contribute the most to the control magnitudes for mitigating the absolute and relative perturbations, characterized by a, rr, and other important parameters. The control magnitudes against the absolute perturbations relating to Earth’s J2 gravity, the long-period drift of the eccentricity vector owing to Earth’s J3 gravity, and atmospheric drag decrease with an increase in a, whereas those of the luniso- lar gravity increase, and that of the SRP remains constant. The control magnitudes against the relative perturbations for Earth’s J2 gravity, long-period drift of the eccentricity vector owing to Earth’s J3 gravity, atmospheric drag, and SRP maintain the same trend as that for the absolute perturbations. Interestingly, those of the lunisolar gravity (except for the long-term drift of the eccentricity vector) remain constant, and their secular and long- period effects on the eccentricity even decrease with an increase in a. Regarding the relationship with rr, the control magnitudes against the relative perturbations increase linearly with rr for Earth’s J2 gravity, the long-period drift of the eccentricity vector owing to Earth’s J3 gravity, and lunisolar gravity, and are squared with rr for the CW nonlinearity. In contrast, those for the atmospheric drag and SRP remain constant with respect to rr.
To mitigate the long-term drift on the eccentricity vector, a more propellant-saving approach for Earth’s J3 gravity is the compensation for the absolute perturbations (with a factor of a−5) in the larger semimajor axis and size of formation, and the relative perturbations (with a factor of a−4 rr) for smaller a and rr . However, a better approach for the lunisolar gravity is to compensate for the absolute perturbations in the smaller a and larger rr as well as the relative perturbations in the larger a and smaller rr.
Overall, small-perturbation regions tend to appear in the higher-altitude and shorter-separation regions. Thus, a reasonable approach for orbit selection is to search for the candidates of the semimajor axis that satisfy the small-disturbance conditions under the desired formation size. However, the orbital orientation parameters (I and Ω) are selected to satisfy the observation conditions, considering the long-term perturbations. Because the observation conditions are highly mission-oriented, the orbit selection approach is verified through case studies in the next section.
5 Results and discussion
Numerical examples of control acceleration magnitudes, observabilities, and visibilities are provided to verify the proposed approach to formation-flying interferometry. The selected case studies were a laser-interferometric gravitational-wave telescope and an astronomical interferometer.
The analytical perturbation models developed in this study were used to analyze the control acceleration magnitudes and observation conditions. In addition, the control acceleration magnitudes were evaluated by averaging each perturbing acceleration per orbital revolution from the initial time and then calculating their root-sum-square (Rss). Table 5 lists the common numerical conditions for all formation configurations. The area-to-mass ratio was assumed for a small class of satellites (e.g., M ≈ 500 kg and S ≈ 2.3 m2), and its value was used to calculate atmospheric drag and SRP effects. To calculate the control acceleration by method (c) in Fig. 1, the secular drift of the eccentricity vector owing to lunisolar gravity was assumed to be periodically corrected to zero each year. The propellant consumption for this correction did not consider the control acceleration; the consumption to mitigate the relative acceleration due to the mean (nonzero) eccentricity vector accumulated over one year was considered only. The study did not account for propellant consumption related to formation reconfiguration maneuvers, such as altering observation directions or the size of the formation.
In the heliocentric orbit or halo orbit around the Sun-Earth L2 point, SRP is the dominant disturbance. Using the values in Table 5, the sum of the absolute and relative perturbing accelerations owing to SRP was calculated as approximately 4.5 × 10−8 m s−2 (1.4 m s−1 per year). Therefore, this study aims to find a small disturbance environment in geocentric orbits of less than 1.0 × 10−7 m s−2 (3.0 m s−1 per year) that maintains a magnitude only a few times larger than that in the heliocentric or Sun-Earth L2 orbits.
Largest contributing factors to the control magnitudes.
Typical numerical conditions for control-acceleration analysis.
 |
Fig. 2 Reference formation orbit for the laser-interferometric gravitational-wave observatory. The distance between each spacecraft is given by |
5.1 Gravitational-wave telescope
The assumed laser-interferometric gravitational-wave telescope in this study is B-DECIGO (Kawamura et al. 2021), which is a precursor to DECIGO. B-DECIGO has three pairs of Fabry-Pérot cavities, and one cluster of three satellites is placed equidistantly, 100 km apart, in a triangular formation.
The triangular reference formation for B-DECIGO uses a general circular orbit (GCO; Alfriend et al. 2010), which is achieved by setting the parameters in Eq. (6) as ρy = 0,  , and αz = αx. The GCO is always inclined by 60° with respect to the orbital plane of the chief, because
, and αz = αx. The GCO is always inclined by 60° with respect to the orbital plane of the chief, because  where rr = [xr, yr, zr]T. The reference formation can be configured by placing the three spacecraft in a GCO with orbit phase angles of 2π/3 from each other. The radius of the GCO (rr) and the distance between each spacecraft (L12, L23, L31) remain constant such that
where rr = [xr, yr, zr]T. The reference formation can be configured by placing the three spacecraft in a GCO with orbit phase angles of 2π/3 from each other. The radius of the GCO (rr) and the distance between each spacecraft (L12, L23, L31) remain constant such that  and
and  . The control requirement for B-DECIGO is imposed on the stability of each optical path length between the mirrors comprising the Fabry–Pérot cavity (e.g.,
. The control requirement for B-DECIGO is imposed on the stability of each optical path length between the mirrors comprising the Fabry–Pérot cavity (e.g.,  ) within the order of nanometers. Based on the B-DECIGO requirements, the sizing parameter was selected as
) within the order of nanometers. Based on the B-DECIGO requirements, the sizing parameter was selected as  . Spacecraft 1 (SC1), 2 (SC2), and 3 (SC3) were assigned αx = 0, 2π/3, and 4π/3, respectively. Figure 2 illustrates the triangular formation of the GCO. For this reference formation, the first and second time derivatives of ρx, ρy, and ρz are zero, but
. Spacecraft 1 (SC1), 2 (SC2), and 3 (SC3) were assigned αx = 0, 2π/3, and 4π/3, respectively. Figure 2 illustrates the triangular formation of the GCO. For this reference formation, the first and second time derivatives of ρx, ρy, and ρz are zero, but  is nonzero. Therefore, only the second term in Eq. (17) is nonzero, and the other terms are zero.
is nonzero. Therefore, only the second term in Eq. (17) is nonzero, and the other terms are zero.
The most important observation requirement for the orbital orientation of B-DECIGO is sunlight avoidance of the optical paths. The minimum avoidance angle was set to 15° in this study. This requirement can always be satisfied in a heliocentric orbit, whereas it can be violated in Earth orbits; therefore, a careful choice of orbital orientation parameters is necessary. To satisfy the sunlight-avoidance requirement, the parameters were selected as  in a high Earth orbit for the following reasons.
in a high Earth orbit for the following reasons.
The target attitude frame is illustrated in Figs. 2 and 3 such that the two laser beams of each spacecraft point to [xt, yt, zt]T = [1, 0, 0]T and ![${\left[ {1/2,\,\,\sqrt 3 /2,\,\,0} \right]^T}$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq102.png) and the zt, axis is selected in the right-hand frame. In addition, by approximating the inclination as the same as the obliquity of the ecliptic, the direction of the Sun is constrained within the x-y plane in the LVLH frame. Then, the Sun vector in the target attitude frame (st = [stx, sty, stz]T) is expressed as follows:
and the zt, axis is selected in the right-hand frame. In addition, by approximating the inclination as the same as the obliquity of the ecliptic, the direction of the Sun is constrained within the x-y plane in the LVLH frame. Then, the Sun vector in the target attitude frame (st = [stx, sty, stz]T) is expressed as follows:
![${s^t} = {1 \over 4}\left[ {\matrix{ {\sin (2P + Q) - 3\sin Q} \cr { - \cos (2P + Q) + 3\cos Q} \cr { - 2\sqrt 3 \cos P} \cr } } \right]{\rm{, }}$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq103.png) (37)
(37)
and θS is the argument of latitude of the Sun, changing by 2π over one year. By defining the azimuth angle (ψ) and elevation angle (γ) with respect to the Sun vector as ψ = arctm2(sty, stx) and γ = sin−1 (stz), respectively (see Fig. 3), a pair of (ψ, γ) follows the locus similar to a “figure of eight” per orbit revolution of satellites passing the cross-point (ψ, γ) = (Q + π/2, 0) twice, as shown in Fig. 4. In addition, angle Q drifts by 2π annually. Because the angle between the Sun vector and laser direction approaches zero when (ψ, γ) → (0, 0) or (π/3, 0) (see Fig. 3), each of the two laser axes in a single satellite is subject to interference by sunlight only once per year. Hence, excellent observability is expected. Furthermore, as the selected orbital plane approximately corresponds to the classical Laplace plane, long-term stability of the orbital orientation is expected, and this stability will maintain excellent observability.
To comprehensively understand the nature of geocentric orbit regions, the control acceleration magnitudes were computed over a wider range of spacecraft separations than the assumed value for B-DECIGO. The left panel of Fig. 5 shows a contour map of the control acceleration magnitudes with respect to separation and altitude. The right panel shows the control acceleration magnitudes for each perturbing source at the desired separation  for B-DECIGO with respect to the semimajor axis.
for B-DECIGO with respect to the semimajor axis.
The first feature is shown in Fig. 5 left, indicating that the smaller control acceleration magnitudes appeared in the shorter-separation and higher-altitude region. Therefore, a small-disturbance region of less than 10−7 m s−2 was identified in high Earth orbit. The second feature is observed at the borderlines in Fig. 5 left to attain more propellant-efficient control. In particular, the control approach to the secular drift of the eccentricity vector owing to lunar gravity switched from the mitigation of the absolute perturbing acceleration (in Fig. la with a factor of a2) at an altitude lower than 51000 km to that of the relative perturbing acceleration (in Fig. 1c with a factor of a−1/2rt). Consequently, the total control acceleration magnitudes were maintained as low for 105 km along the semimajor axis, as shown in Fig. 5 right.
By selecting the candidate Earth orbit for B-DECIGO at an altitude of 80000 km  , the magnitude of the control acceleration was 7 × 10−8 m s−2. This acceleration can be further broken down to compensate for the absolute and relative perturbations, which account for 17 % of the total acceleration (||Fc||), 20 % (||fp||), 33 % (||fo||), and 30 % (||ff||). This result suggests that these four types of perturbed acceleration may contribute in the same order, and all of them must be considered in the control approach. The eccentricity (initially zero) in the selected orbital environment can increase to 0.0012 in a one year duration owing to the Moon’s gravity, based on the satellite motion model in Appendix C. Thus, the eccentricity error must be corrected periodically.
, the magnitude of the control acceleration was 7 × 10−8 m s−2. This acceleration can be further broken down to compensate for the absolute and relative perturbations, which account for 17 % of the total acceleration (||Fc||), 20 % (||fp||), 33 % (||fo||), and 30 % (||ff||). This result suggests that these four types of perturbed acceleration may contribute in the same order, and all of them must be considered in the control approach. The eccentricity (initially zero) in the selected orbital environment can increase to 0.0012 in a one year duration owing to the Moon’s gravity, based on the satellite motion model in Appendix C. Thus, the eccentricity error must be corrected periodically.
Then, the observation conditions were analyzed at an altitude of 80000 km. Figure 6 shows the rate of sunlight avoidance per orbit for one year. Each of the three laser cavities interfered twice per year, and the interference season lasted for approximately 40 days. The minimum satisfaction rate was 83% per orbit, which is approximately equivalent to 10 h of the 50 h (one orbital period) subject to interference by sunlight. One of the three cavities cannot be used during these periods. Nonetheless, sunlight interference might be avoided by taking appropriate measures, such as changing the target attitudes of the satellites while one of the three cavities suspends scientific observations.
It is important to note that an Earth eclipse can occur once per orbit. This is primarily because the orientation of the selected orbit is closely aligned with the ecliptic plane. As depicted in Fig. D.1, the duration of these eclipses can extend up to approximately 100 min during both the vernal and autumnal equinoxes. Such eclipse events may limit the observation time owing to potential thermal instability in the satellite or constraints on the electrical power system. While this factor should be considered in the design of satellites, a detailed exploration of its implications is beyond the scope of this study.
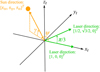 |
Fig. 3 Sun and laser directions in the target attitude frame. The azimuth and elevation angles (ψ, γ) of the Sun vector are also depicted. |
 |
Fig. 4 Sunlight-avoidance area and Sun-vector locus per orbit with respect to the azimuth and elevation. The sunlight-avoidance areas for the two laser axes of each spacecraft are depicted as gray circles. Equation (37) indicates that the Sun-vector locus per orbit has azimuth and elevation amplitudes of nearly π/9 and π/3, respectively. The angle Q drifts by 2π over one year. |
 |
Fig. 5 Control acceleration magnitudes for the laser-interferometric gravitational-wave observatory. The left panel shows the contour map of the control acceleration magnitudes (ud = ||ud||) with respect to the separation (defined as rr) and altitude. The gray lines show the borderlines that indicate when to change the mitigation methods for the secular and long-period drifts of the eccentricity vector. For the secular and long-period eccentricity drift owing to lunar gravity, the more propellant-saving approach appeared above the lines (specified by e(s)(Moon) and e(lp)(Moon)) when applying method (c) for the secular one and (b) for the long-period one in Fig. 1, while it appeared below the lines when applying method (a) in Fig. 1. For the long-period eccentricity drift owing to Earth’s J3 gravity, the more propellant-saving approach appeared above the line (specified by e(lp)(J3)) when applying method (a) in Fig. 1, while it appeared below the line when applying method (b) in Fig. 1. The borderlines for the secular and long-period drifts of the eccentricity vector owing to solar gravity were abbreviated because their magnitudes were sufficiently smaller than 10−9 m s−2 in the plotted region. The right panel shows the control acceleration magnitudes at the desired separation |
 |
Fig. 6 Rate of sunlight avoidance per orbit during one year (January 1 – December 31, 2024). The six lines indicate the rates for the six laser-target directions: from SC1 to SC2, from SC2 to SC3, from SC3 to SC1, and their opposite directions. Each laser direction is subject to interference by the Sun once per year; thus, each cavity is interfered twice per year. |
5.2 Astronomical interferometer
The astronomical interferometer assumed in this study uses a linear formation under orthogonal inertial pointing, similar to nanosatellite astronomical interferometers (Hansen & Ireland 2020; Matsuo et al. 2022). The target observation direction in the ECI frame is given by dI = [cos δ cos α, cos δ sin α, sin δ]T, where α and δ denote the right ascension and declination of the target observation direction, respectively. The reference formation can be configured by placing one spacecraft at the origin and the other two spacecraft symmetrically in the (y − z) plane in the LVLH frame (Hansen & Ireland 2020). A symmetrical spacecraft is placed by setting the parameters in Eq. (6) as ρx = 0, pz = ρy tan p (−π/2 < p < π/2), and αz = q (0 ≤ q ≤ 2π), and the other is placed symmetrically. Angles p and q are defined to satisfy the following relationships:
 (39)
(39)
where ∆Ωα = (Ω − α). The distances between spacecraft 1 (origin) and spacecrafts 2 and 3 are not necessarily constant; however, their optical path difference must be sufficiently small to attain the interference signals from the target directions. Although specific missions were not assumed in this study, the selected sizing parameter was ρy = 0.25 km, similar to that in Hansen & Ireland (2020) as the typical mission. Figure 7 illustrates the linear formation under orthogonal inertial pointing in Earth’s orbit. For this reference, the first and second time derivatives of ρx and ρy are zero, but  are nonzero; therefore, all four terms in Eq. (17) are nonzero. The first and second time derivatives of ρz are given by
are nonzero; therefore, all four terms in Eq. (17) are nonzero. The first and second time derivatives of ρz are given by  and
and ![${\ddot \rho _z} = \left[ {\left( {\ddot p + 2{{\dot p}^2}\tan p} \right){\rho _y}/{{\cos }^2}p} \right]$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq111.png) , respectively, and ṗ and
, respectively, and ṗ and  can be calculated from Eq. (39).
can be calculated from Eq. (39).
The most important observation condition for the orbital orientation of an astronomical interferometer is the coverage of the visible sky area. The key factors applied in this study are that the maximum angle between the observation target (star) and the Sun’s directions is less than π/3 (condition 1) to maintain the solar arrays of each spacecraft facing to the Sun and keep the sunlight from interfering with the optical paths of the science instruments; and the clearance to the target star occultation by the Earth and its atmospheric thickness during one orbit (condition 2). These factors are derived from the same ideas as those in previous research (Hansen & Ireland 2020); however, condition 2 is a stricter rule because temporal occultation during one orbit is allowed in Hansen & Ireland (2020), but not allowed in this study so that better observation conditions may be attained. In addition, this study imposes a further requirement that the angle |p| be less than π/3 to regulate the formation size up to  (condition 3). The albedo effects of the Earth and Moon and the lunar occultation of the target stars were neglected in this study. Conditions 1–3 are given as follows:
(condition 3). The albedo effects of the Earth and Moon and the lunar occultation of the target stars were neglected in this study. Conditions 1–3 are given as follows:
 (40)
(40)
where sI is the unit Sun vector in the ECI frame, and ht is the Earth’s atmospheric thickness, assuming ht = 100 km. A spherical Earth is assumed to derive condition 2. Finally, the secular drift of Ω owing to Earth’s J2 perturbation is actively used to increase the visible sky area during several years, so that the orbital inclination should be taken away from ±90° (see Eq. (B.2) for  ). Considering these conditions, the orbital orientation parameters were selected as
). Considering these conditions, the orbital orientation parameters were selected as  .
.
Lastly, the observation direction was set to α = 19h 20m and δ = 20° for the perturbing acceleration analysis. This selection was mainly aimed at understanding the typical acceleration magnitudes by taking the typical value of p as approximately 20°, and was not intended at particular observations of astronomical objects.
The left panel of Fig. 8 shows a contour map of the control acceleration magnitudes with respect to the separation and altitude of the astronomical interferometer. The right panel shows the control acceleration magnitude at the desired separation (0.25 km) with respect to the semimajor axis. A trend similar to that of B-DECIGO is shown in the left panel of Fig. 8: smaller control acceleration magnitudes appeared in the shorter-separation and higher-altitude region, and a small-disturbance region of less than 10−7 m s−2 was identified in medium Earth orbit. The control approach to the long-period drift of the eccentricity vector owing to Earth’s J3 gravity was to compensate for the relative perturbing acceleration (in Fig. 1b) for the lower altitude and shorter separation and the absolute perturbing acceleration (in Fig. 1a) for the higher altitude and longer separation.
By selecting the candidate Earth orbit for the astronomical interferometer at an altitude of 8000 km  , the control acceleration magnitude was determined to be approximately 6 × 10−8 m s−2. This acceleration can be further broken down to compensate for the absolute and relative perturbations, each accounting for 31% (||Fc||), 31% (||fp||), 26% (||fo||), and 12% (||ff||).
, the control acceleration magnitude was determined to be approximately 6 × 10−8 m s−2. This acceleration can be further broken down to compensate for the absolute and relative perturbations, each accounting for 31% (||Fc||), 31% (||fp||), 26% (||fo||), and 12% (||ff||).
Figure 9 shows the visible sky area for an astronomical interferometer at an altitude of 8000 km. The mission duration was assumed to be 5 years, where Ω drifted by 2π owing to the J2 perturbation. The visible area ranged for any possible α within approximately −75° < δ < 75° (depending on α), and the maximum visibility was approximately 25 %. In particular, good visibility appeared within the area of −30° < δ < 30°. Although Earth eclipses do occur in the selected orbit for the astronomical interferometer, they are not a constant phenomenon in each orbit. The maximum duration of these eclipses is approximately 40 min, as illustrated in Fig. D.l.
 |
Fig. 7 Reference formation orbit for the astronomical interferometer. The two purple arrows are parallel and point in the same direction. |
 |
Fig. 8 Control acceleration magnitudes for the linear astronomical interferometer. The left panel shows the contour map of the control acceleration magnitudes with respect to the separation (defined as ρy) and altitude. For the long-period eccentricity drift owing to Earth’s J3 gravity, the more propellant-saving approach appeared above the line (specified by e(lp) (J3)) when applying method (a) in Fig. 1, while it appeared below the line when applying method (b) in Fig. 1. The borderlines for the secular and long-period drifts of the eccentricity vector owing to lunisolar gravity were abbreviated because their magnitudes were sufficiently smaller than 10−9 m s−2 in the plotted region. The right panel shows the control acceleration magnitudes at the desired separation (0.25 km) with respect to the semimajor axis. The atmospheric drag, lunisolar gravity, and secular and long-period drifts of the eccentricity vector owing to the lunisolar gravity were removed from the figure because their magnitudes were sufficiently smaller than 10−9 m s−2. |
 |
Fig. 9 Visible sky area for the astronomical interferometer at an altitude of 8000 km and |
5.3 LEO environment
The use of LEOs has been considered in some formation-flying interferometry missions, particularly for astronomical interferometers (Hansen & Ireland 2020; Matsuo et al. 2022). However, their disturbance characteristics tended to be analyzed within mission-specific baseline lengths and orbits. Therefore, it remains unclear where and to what extent a small-disturbance environment can exist in LEO. Therefore, the LEO environment was assessed based on a perturbing acceleration analysis, assuming linear astronomical interferometers as potential applications. The Sun synchronous orbit was selected, where the RAAN drifts by 2π per year, and daylight is ensured in most seasons. The initial RAAN and inclination were set to  and
and  , respectively. The same observation direction in Sect. 5.2 was used for the perturbing acceleration analysis.
, respectively. The same observation direction in Sect. 5.2 was used for the perturbing acceleration analysis.
The left panel of Fig. 10 shows a contour map of the control acceleration magnitudes with respect to separation (up to 1 km) and altitude (up to 1000 km). The right panel shows the control acceleration magnitude at a specific separation (0.1 km) with respect to the semimajor axis. In contrast to the high and medium Earth orbits, the LEO has few small-disturbance regions of less than 10−7 m s−2. The largest perturbing acceleration sources were dominated by atmospheric drag (below approximately 600 km in altitude and 0.2 km in separation) and the Earth J2 gravity potential for the other regions in Fig. 10 left. However, a relatively small acceleration of 10−65 to 10−6m s−2 (considering ∆V: 10–30 m s−1 per year) can be attained in LEO at an altitude > 500 km, with a separation of approximately 0.1 km. For example, the control acceleration magnitude at an altitude of 600 km  was approximately 5 × 10−7 m s−2. This acceleration can be further broken down to compensate for the absolute and relative perturbations, each accounting for 9% (||Fc||), 52% (||fp,||), 29% (||fo||), and 10% (||ff||). In the plotted region in Fig. 10 left, the better mitigation approach to the J3-perturbed long-period drift of the eccentricity vector was to compensate for the relative perturbing acceleration (in Fig. 1b).
was approximately 5 × 10−7 m s−2. This acceleration can be further broken down to compensate for the absolute and relative perturbations, each accounting for 9% (||Fc||), 52% (||fp,||), 29% (||fo||), and 10% (||ff||). In the plotted region in Fig. 10 left, the better mitigation approach to the J3-perturbed long-period drift of the eccentricity vector was to compensate for the relative perturbing acceleration (in Fig. 1b).
Figure 11 shows the visible sky area for an astronomical interferometer at an altitude of 600 km. The mission duration was assumed to be one year, where Ω drifted by 2π owing to the J2 perturbation. In comparison to the results in Fig. 9 and Hansen & Ireland (2020), the visible area reduced within approximately −14° < δ < 30° for any possible α, and the maximum visibility decreased to approximately 12 %. This reduction in visibility is attributed to condition 2 in Eq. (40). When condition 2 is omitted, the visibility returns to levels similar to those found in Fig. 9 and the work of Hansen & Ireland (2020). Earth eclipses also occur, but they are seasonally limited. Their maximum duration is approximately 20 min, as detailed in Fig. D.1.
A negative aspect of using LEO for formation-flying interferometry is that the mission lifetime may be significantly shortened in comparison with those at higher geocentric orbits, owing to the limitation of the maximum load capability of the propellant. Another limitation is that precise formation control becomes more difficult with stronger perturbation effects. However, using LEO may outweigh these limitations from a benefit-to-cost perspective, particularly for small-class, experimental, and/or pathfinder missions. Moreover, using the latest low-thrust electrical propulsion with a high specific impulse can further improve the lifetime problem, as indicated in Hansen & Ireland (2020). The last point to discuss is safe autonomous formation flying in proximity. In particular, proximity formation flying at 0.1 km or less is considered high-risk for collisions (Monnier et al. 2019). In addition, the linear formation for the astronomical interferometer cannot apply the passively safe formation orbit known as the “eccentricity/inclination vector separation” technique (D’Amico & Montenbruck 2006). Therefore, active safety for collision-hazard detection and avoidance must be ensured using autonomous formation-flying functions. However, if this technical bottleneck is resolved, the LEO environment will become an ideal platform for demonstrating various technologies for future space interferometry.
 |
Fig. 10 Control acceleration magnitudes for the linear astronomical interferometer in LEO. The left panel shows the contour map of the control acceleration magnitudes with respect to the separation (defined as ρy) and altitude. The control magnitudes against the secular and long-period drifts of the eccentricity vector owing to lunisolar gravity were sufficiently smaller than 10−9 m s−2 in the plotted region. The right panel shows the control acceleration magnitudes at the desired separation (0.1 km) with respect to the semimajor axis. The lunisolar gravity and the secular and long-period drifts of the eccentricity vector owing to lunisolar gravity were removed from the figure because their magnitudes were sufficiently smaller than 10−9 m s−2. |
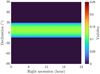 |
Fig. 11 Visible sky area for the astronomical interferometer at an altitude of 600 km and |
6 Conclusions
This study demonstrates the feasibility of formation-flying interferometry in geocentric orbits based on celestial mechanics. The perturbing accelerations to be mitigated by precise control can be categorized into four types: (1) absolute physical acceleration, (2) relative physical acceleration, (3) relative fictitious acceleration owing to the perturbed orbital motion of the chief, and (4) relative fictitious acceleration owing to the perturbed motion of the reference formation. In addition, the secular and/or long-period perturbations on the eccentricity vector owing to Earth J3 and lunisolar gravity were unique because an efficient control approach could be changed to correct the absolute or relative perturbing accelerations. These results led to the characterization of the magnitude of each disturbance by the semimajor axis and the size of the formation. Consequently, small-perturbation conditions tended to appear in the higher-altitude and shorter-separation regions. Candidate orbits with a disturbance of less than 10−7 m s−2 were observed in the high Earth orbit for a laser-interferometric gravitational-wave telescope with a size of 100 km and in the medium Earth orbit for a linear astronomical interferometer with a size of 0.5 km. The LEO tended to have larger disturbance magnitudes; however, a LEO at a separation of approximately 0.1 km may be suitable for experimental purposes. These examples support the idea that the Earth’s orbit can be used for various types of formation-flying interferometry.
Acknowledgements
This study was supported by JSPS KAKENHI Grant Number JP23K13501. We would like to thank Dr. Shuichi Sato of Hosei University and Dr. Taro Matsuo of Nagoya University for their valuable advice on the formation control requirements for the space-based gravitational-wave observatory and astronomical interferometer.
Appendix A Nomenclature
Table A.1 lists the major symbols particularly used in the theoretical development of this study.
Nomenclature.
Appendix B J2-perturbed orbital elements
For a mean circular orbit, the J2-perturbed orbital motion of the chief up to the first order is given as follows:
![$\left\{ {\matrix{ {a = a_0^{(s)}\left( {1 + {{3J} \over 2}{{\sin }^2}I_0^{(s)}\cos 2{\phi ^{(s)}}} \right),} \hfill \cr {{e_x} = {J \over {16}}\left[ {14{{\sin }^2}I_0^{(s)}\cos 3{\phi ^{(s)}} + 3\left( {3 + 5\cos 2I_0^{(s)}} \right)\cos {\phi ^{(s)}}} \right],} \hfill \cr {{e_y} = {J \over {16}}\left[ {14{{\sin }^2}I_0^{(s)}\sin 3{\phi ^{(s)}} + 3\left( {1 + 7\cos 2I_0^{(s)}} \right)\sin {\phi ^{(s)}}} \right],} \hfill \cr {I = I_0^{(s)} + {{3J} \over 8}\sin 2I_0^{(s)}\cos 2{\phi ^{(s)}},} \hfill \cr {\Omega = \Omega _0^{(s)} + \dot \bar \Omega t + {{3J} \over 4}\cos I_0^{(s)}\sin 2{\phi ^{(s)}},} \hfill \cr {\phi = \phi _0^{(s)} + \dot \bar \phi t - {{3J} \over 8}\left( {2 - 5{{\sin }^2}I_0^{(s)}} \right)\sin 2{\phi ^{(s)}},} \hfill \cr } } \right.$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq124.png) (B.1)
(B.1)
Appendix C Third-body-perturbed orbital elements
The disturbing function owing to the third body can be written as follows (Kozai 1973):
![${\cal R} = n_b^2R_c^2\beta {\left( {{{{a_b}} \over {{R_b}}}} \right)^3}\left[ {{P_2}\left( {\cos {S_b}} \right) + \left( {{{{R_c}} \over {{R_b}}}} \right){P_3}\left( {\cos {S_b}} \right) + \cdots } \right], $](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq126.png) (C.1)
(C.1)
where ab, Rb, and nb are the semimajor axis, radius, and mean motion of the disturbing body, respectively; P2, P3, and ⋯ are Legendre polynomials; cos Sb is the direction cosine between the radius to the spacecraft and that to the disturbing body; β = mb/(m + mb); and m and mb are the masses of the Earth and disturbing body, respectively. The single-averaged disturbing function 〈𝓡〉 was derived by obtaining the average with respect to the mean anomaly l of the chief. The double-averaged disturbing function 〈〈𝓡〉〉 is derived by averaging 〈𝓡〉 with respect to the mean anomaly lb of the disturbing body. The long-period and short-period terms of the disturbing function are calculated using 𝓡(lp) = (〈𝓡〉 − 〈〈𝓡〉〉) and 𝓡(sp) = (𝓡 − 〈𝓡〉), respectively. By replacing 𝓡 with 〈〈𝓡〉〉, 𝓡(lp), and 𝓡(sp) in Lagrange’s equations, the orbital equations for the secular, long-period, and short-period motions are obtained, and the orbital elements can be calculated analytically by integrating the orbital equations with respect to time.
If the terms with e2 and higher are neglected, the single-averaged disturbing function up to P3(cos Sb) of the Legendre polynomials is written as follows (Kozai 1973):
![$\eqalign{ & {{\langle {\cal R}\rangle } \over {n_b^2{a^2}\beta }} = {1 \over 4}{\left( {{{{a_b}} \over {{R_b}}}} \right)^3}\left[ {3\left( {{A^2} + {B^2}} \right) - 2} \right] - {{15} \over {16}}e{\left( {{{{a_b}} \over {{R_b}}}} \right)^4}\left( {{a \over {{a_b}}}} \right) \times \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ {5\left( {{A^2} + {B^2}} \right) - 4} \right](A\cos \omega + B\sin \omega ). \cr} $](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq127.png) (C.2)
(C.2)
The A and B are defined as follows:
 (C.3)
(C.3)
where αb and δb denote the right ascension and declination of the disturbing body in the ECI frame, respectively. Assuming that the eccentricity of the third body (eb) is small, the following approximations are applied: (ab/Rb)3 ≈ (1 + 3eb cos lb) and (ab/Rb)4 ≈ (1 + 4eb cos lb). This approximation is used to calculate 〈〈𝓡〉〉. By contrast, a further approximation of eb = 0 (the circular-orbit assumption for the third body) is used to calculate 𝓡(lp). The double-averaged disturbing function is calculated as follows:
![$\eqalign{ & {{\langle \langle {\cal R}\rangle \rangle } \over {n_b^2{a^2}\beta }} = {1 \over 8}\left[ { - 4 + 3\left( {k_1^2 + k_2^2 + k_3^2 + k_4^2} \right)} \right] \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - {{15} \over {64}}e{e_b}\left( {{a \over {{a_b}}}} \right)\left( {{K_1}\cos \omega + {K_2}\sin \omega } \right), \cr} $](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq129.png) (C.4)
(C.4)
The constants K1 and K2 are introduced to obtain compact expressions:
![$\eqalign{ & {K_1} = - 16{k_1} + 5{k_1}\left[ {3\left( {k_1^2 + k_2^2 + k_3^2} \right) + k_4^2} \right] + 10{k_2}{k_3}{k_4}, \cr & {K_2} = - 16{k_2} + 5{k_2}\left[ {3\left( {k_1^2 + k_2^2 + k_4^2} \right) + k_3^2} \right] + 10{k_1}{k_3}{k_4}. \cr} $](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq131.png) (C.6)
(C.6)
Subsequently, the orbital elements for the near-circular satellite motion are provided. The secular parts are
 (C.7)
(C.7)
The long-period parts are as follows:
 (C.9)
(C.9)
The short-period parts are as follows:
 (C.11)
(C.11)
To calculate the osculating orbital elements, the secular orbital elements are first computed. Then, the long-period variation δ(·)(lp) is calculated using the secular orbital elements, and the short-period variation δ(·)(sp) is calculated using the secular and long-period orbital elements.
Appendix D Eclipse effects of the Earth
Figure D.1 illustrates the Earth’s eclipse effects spanning from January 1, 2024, 00:00:00 UT to December 31, 2024, 24:00:00 UT for the orbits selected in Sect. 5. The three lines in Fig. D.1 represent the annual duration of eclipses per orbit for the orbits discussed in Sects. 5.1 (depicted in blue), 5.2 (in orange), and 5.3 (in yellow). These durations were computed under the assumption of circular orbits. For low and medium Earth orbits, (J2)-perturbed secular motion was considered, whereas high Earth orbits were assumed to exhibit unperturbed motion. Furthermore, only the effects of the umbra were taken into account.
 |
Fig. D.1 Eclipse effects of the Earth in various selected orbits. |
References
- Alfriend, K. T., Vadali, S. R., Gurfil, P., How, J., & Breger, L. S. 2010, Spacecraft Formation Flying: Dynamics, Control and Navigation, Elsevier Astrodynamics Series (Elsevier) [Google Scholar]
- Allan, R. R., & Cook, G. E. 1964, Proc. R. Soc. London Ser. A Math. Phys. Sci., 280, 97 [NASA ADS] [Google Scholar]
- Ashman, B., Bauer, F. H., Parker, J., & Donaldson, J. 2018, in 2018 SpaceOps Conference, https://arc.aiaa.org/doi/abs/10.2514/6.2018-2568 [Google Scholar]
- Brouwer, D. 1959, AJ, 64, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Clohessy, W. H., & Wiltshire, R. S. 1960, J. Aerospace Sci., 27, 653 [CrossRef] [Google Scholar]
- Cockell, C. S., Herbst, T., & Léger, A. 2009, Exp. Astron., 23, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, G. E. 1962, Geophys. J. Int., 6, 271 [NASA ADS] [CrossRef] [Google Scholar]
- D’Amico, S., & Montenbruck, O. 2006, J. Guidance Control Dyn., 29, 554 [CrossRef] [Google Scholar]
- Gill, E., D’Amico, S., & Montenbruck, O. 2007, J. Spacecraft Rockets, 44, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, J. T., & Ireland, M. J. 2020, PASA, 37, e019 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, I., & Priester, W. 1962, J. Atmos. Sci., 19, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Izzo, D., Sabatini, M., & Valente, C. 2003, in Proceedings of the 17th AIDAA National Congress, 1, 493 [Google Scholar]
- Kahle, R., Runge, H., Ardaens, J. S., et al. 2014, Acta Astron., 99, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Kawamura, S., Ando, M., Seto, N., et al. 2021, Progr. Theoret. Exp. Phys., 2021, 05A105 [CrossRef] [Google Scholar]
- Kawano, I., Mokuno, M., Kasai, T., & Suzuki, T. 2001, J. Spacecraft Rockets, 38, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Koenig, A. W., Guffanti, T., & D’Amico, S. 2017, J. Guidance Control Dyn., 40, 1749 [NASA ADS] [CrossRef] [Google Scholar]
- Kozai, Y. 1959, AJ, 64, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Kozai, Y. 1973, A New Method to Compute Lunisolar Perturbations in Satellite Motions, Tech. rep., Smithsonian Astrophysical Observatory [Google Scholar]
- Lawson, P. R., & Dooley, J. A. 2005, Technology Plan for the Terrestrial Planet Finder Interferometer, Tech. rep., Jet Propulsion Laboratory [Google Scholar]
- Long, A., Cappellari, J., Velez, C., & Fuchs, A. 1989, Goddard Trajectory Determination System (GTDS) – Mathematical Theory – Revision 1, Tech. rep., Goddard Space Flight Center [Google Scholar]
- Matsuo, T., Ikari, S., Kondo, H., et al. 2022, J. Astron. Telesc. Instrum. Syst., 8, 015001 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J., Aarnio, A., Absil, O., et al. 2019, A realistic roadmap to formation flying space interferometry, Tech. rep., Astro2020 APC White Paper [Google Scholar]
- Montenbruck, O., & Gill, E. 2000, Satellite Orbits: Models, Methods, and Applications (Springer) [CrossRef] [Google Scholar]
- Peñin, L. F., Scoarnec, Y., Fernández-Ibarz, J. M., et al. 2020, in 34th Annual Small Satellite Conference, Logan, Utah [Google Scholar]
- Quanz, S. P., Ottiger, M., Fontanet, E., et al. 2022, A&A, 664, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roscoe, C., Vadali, S. R., & Alfriend, K. T. 2013, J. Astronaut. Sci., 60, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Rosengren, A. J., Scheeres, D. J., & McMahon, J. W. 2014, Adv. Space Res., 53, 1219 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S., Touma, J., & Namouni, F. 2009, AJ, 137, 3706 [Google Scholar]
All Tables
Orders of the control acceleration magnitudes to compensate for the relative fictitious perturbations (fo and ff) for the secular, long-period, and short-period terms, in comparison to those of the absolute physical perturbations (Fc).
All Figures
 |
Fig. 1 Three methods for mitigating the secular and long-period eccentricity vector drift. The panels on the left ((a) e-drift compensation) show the approach for compensating for the eccentricity vector drift of the chief using continuous control. The center panels ((b) e-error compensation) show the method that accepts the small eccentricity error and compensates for the relative perturbing acceleration of the deputy via continuous control. The panels on the right ((c) e-drift and e-error compensation) show the hybrid approach. The top and bottom panels for each approach show the time histories of the eccentricity and control accelerations, respectively. |
| In the text | |
 |
Fig. 2 Reference formation orbit for the laser-interferometric gravitational-wave observatory. The distance between each spacecraft is given by |
| In the text | |
 |
Fig. 3 Sun and laser directions in the target attitude frame. The azimuth and elevation angles (ψ, γ) of the Sun vector are also depicted. |
| In the text | |
 |
Fig. 4 Sunlight-avoidance area and Sun-vector locus per orbit with respect to the azimuth and elevation. The sunlight-avoidance areas for the two laser axes of each spacecraft are depicted as gray circles. Equation (37) indicates that the Sun-vector locus per orbit has azimuth and elevation amplitudes of nearly π/9 and π/3, respectively. The angle Q drifts by 2π over one year. |
| In the text | |
 |
Fig. 5 Control acceleration magnitudes for the laser-interferometric gravitational-wave observatory. The left panel shows the contour map of the control acceleration magnitudes (ud = ||ud||) with respect to the separation (defined as rr) and altitude. The gray lines show the borderlines that indicate when to change the mitigation methods for the secular and long-period drifts of the eccentricity vector. For the secular and long-period eccentricity drift owing to lunar gravity, the more propellant-saving approach appeared above the lines (specified by e(s)(Moon) and e(lp)(Moon)) when applying method (c) for the secular one and (b) for the long-period one in Fig. 1, while it appeared below the lines when applying method (a) in Fig. 1. For the long-period eccentricity drift owing to Earth’s J3 gravity, the more propellant-saving approach appeared above the line (specified by e(lp)(J3)) when applying method (a) in Fig. 1, while it appeared below the line when applying method (b) in Fig. 1. The borderlines for the secular and long-period drifts of the eccentricity vector owing to solar gravity were abbreviated because their magnitudes were sufficiently smaller than 10−9 m s−2 in the plotted region. The right panel shows the control acceleration magnitudes at the desired separation |
| In the text | |
 |
Fig. 6 Rate of sunlight avoidance per orbit during one year (January 1 – December 31, 2024). The six lines indicate the rates for the six laser-target directions: from SC1 to SC2, from SC2 to SC3, from SC3 to SC1, and their opposite directions. Each laser direction is subject to interference by the Sun once per year; thus, each cavity is interfered twice per year. |
| In the text | |
 |
Fig. 7 Reference formation orbit for the astronomical interferometer. The two purple arrows are parallel and point in the same direction. |
| In the text | |
 |
Fig. 8 Control acceleration magnitudes for the linear astronomical interferometer. The left panel shows the contour map of the control acceleration magnitudes with respect to the separation (defined as ρy) and altitude. For the long-period eccentricity drift owing to Earth’s J3 gravity, the more propellant-saving approach appeared above the line (specified by e(lp) (J3)) when applying method (a) in Fig. 1, while it appeared below the line when applying method (b) in Fig. 1. The borderlines for the secular and long-period drifts of the eccentricity vector owing to lunisolar gravity were abbreviated because their magnitudes were sufficiently smaller than 10−9 m s−2 in the plotted region. The right panel shows the control acceleration magnitudes at the desired separation (0.25 km) with respect to the semimajor axis. The atmospheric drag, lunisolar gravity, and secular and long-period drifts of the eccentricity vector owing to the lunisolar gravity were removed from the figure because their magnitudes were sufficiently smaller than 10−9 m s−2. |
| In the text | |
 |
Fig. 9 Visible sky area for the astronomical interferometer at an altitude of 8000 km and |
| In the text | |
 |
Fig. 10 Control acceleration magnitudes for the linear astronomical interferometer in LEO. The left panel shows the contour map of the control acceleration magnitudes with respect to the separation (defined as ρy) and altitude. The control magnitudes against the secular and long-period drifts of the eccentricity vector owing to lunisolar gravity were sufficiently smaller than 10−9 m s−2 in the plotted region. The right panel shows the control acceleration magnitudes at the desired separation (0.1 km) with respect to the semimajor axis. The lunisolar gravity and the secular and long-period drifts of the eccentricity vector owing to lunisolar gravity were removed from the figure because their magnitudes were sufficiently smaller than 10−9 m s−2. |
| In the text | |
 |
Fig. 11 Visible sky area for the astronomical interferometer at an altitude of 600 km and |
| In the text | |
 |
Fig. D.1 Eclipse effects of the Earth in various selected orbits. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\eqalign{ & \matrix{ {a_{A1}^{(11)} = - 4n\left( {{\rm{\dot \Omega }}\cos I + {\rm{\Delta }}\dot \phi + 2{{\dot e}_x}\sin \phi - 2{{\dot e}_y}\cos \phi } \right)} \cr { - 2{n^2}\left( {{e_x}\cos \phi + {e_y}\sin \phi } \right),} \cr {a_{A1}^{(12)} = \mathop {\rm{\Omega }}\limits^ \cos I + \mathop \phi \limits^ + 2\left[ {\left( {{{\mathop e\limits^ }_x} + 2n{{\dot e}_y} - {n^2}{e_x}} \right)\sin \phi } \right.} \cr {\left. { - \left( {{{\mathop e\limits^ }_y} - 2n{{\dot e}_x} - {n^2}{e_y}} \right)\cos \phi } \right],} \cr } \cr & \matrix{ {a_{A1}^{(13)} = - n({\rm{\dot \Omega }}\sin I\sin \phi + \dot I\cos \phi ),\quad a_{A1}^{(22)} = a_{A1}^{(33)} = - {1 \over 2}a_{A1}^{(11)},} \cr {a_{A1}^{(23)} = (\mathop {\rm{\Omega }}\limits^ \sin I - n\dot I)\sin \phi + (\mathop I\limits^ + n{\rm{\dot \Omega }}\sin I)\cos \phi ,} \cr {a_{A2}^{(23)} = 2({\rm{\dot \Omega }}\sin I\sin \phi + \dot I\cos \phi ).} \cr } \cr} $](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq32.png)









![$\eqalign{ & {\Gamma ^{(lp)}} = {{{n_b}\beta } \over n}, \cr & {K_3} = - 16{k_3} + 5{k_3}\left[ {3\left( {k_1^2 + k_3^2 + k_4^2} \right) + k_2^2} \right] + 10{k_1}{k_2}{k_4}, \cr & {K_4} = - 16{k_4} + 5{k_4}\left[ {3\left( {k_2^2 + k_3^2 + k_4^2} \right) + k_1^2} \right] + 10{k_1}{k_2}{k_3}, \cr & {K_5} = {k_1}\left( {k_1^2 + k_2^2 - 3k_3^2 - k_4^2} \right) - 2{k_2}{k_3}{k_4}, \cr & {K_6} = {k_2}\left( {k_1^2 + k_2^2 - k_3^2 - 3k_4^2} \right) - 2{k_1}{k_3}{k_4}, \cr & {K_7} = {k_3}\left( { - 3k_1^2 - k_2^2 + k_3^2 + k_4^2} \right) - 2{k_1}{k_2}{k_4}, \cr & {K_8} = {k_4}\left( { - k_1^2 - 3k_2^2 + k_3^2 + k_4^2} \right) - 2{k_1}{k_2}{k_3}. \cr} $](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq135.png)
![$\left\{ \matrix{ \delta {a^{(sp2)}} = {3 \over 2}a{\Gamma ^{(sp2)}}\left[ {\left( {{A^2} - {B^2}} \right)\cos 2\phi + 2AB\sin 2\phi } \right], \hfill \cr \delta e_x^{(sp2)} = {1 \over 4}{\Gamma ^{(sp2)}} \times \hfill \cr \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\{ {\matrix{ {\left( {{A^2} - {B^2}} \right)\cos 3\phi + 2AB\sin 3\phi } \hfill \cr { + \left[ {4 + 3\left( {{A^2} - 5{B^2}} \right)} \right]\cos \phi + 18AB\sin \phi } \hfill \cr } } \right\}, \hfill \cr \delta e_y^{(sp2)} = {1 \over 4}{\Gamma ^{(sp2)}} \times \hfill \cr \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\{ {\matrix{ { - 2AB\cos 3\phi + \left( {{A^2} - {B^2}} \right)\sin 3\phi } \hfill \cr { + 18AB\cos \phi + \left[ {4 + 3\left( { - 5{A^2} + {B^2}} \right)} \right]\sin \phi } \hfill \cr } } \right\}, \hfill \cr \delta {I^{(sp2)}} = {3 \over {4\sin I}}{\Gamma ^{(sp2)}} \times \hfill \cr \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\{ {\matrix{ {\left[ {A{k_{12}} + B{k_{11}} + \left( {{A^2} - {B^2}} \right)\cos I} \right]\cos 2\phi } \hfill \cr { + \left( { - A{k_{11}} + B{k_{12}} + 2AB\cos I} \right)\sin 2\phi } \hfill \cr } } \right\}, \hfill \cr \delta {\Omega ^{(sp2)}} = - {3 \over {4\sin I}}{\Gamma ^{(sp2)}}{k_{13}}(A\cos 2\phi + B\sin 2\phi ), \hfill \cr \delta {\phi ^{(sp2)}} = {{21} \over 8}{\Gamma ^{(sp2)}}\left[ {2AB\cos 2\phi + \left( { - {A^2} + {B^2}} \right)\sin 2\phi } \right] \hfill \cr \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \delta {\Omega ^{(sp2)}}\cos I, \hfill \cr} \right.$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq137.png)
![$\left\{ \matrix{ \delta {a^{(sp3)}} = {1 \over 4}a{\Gamma ^{(sp3)}} \times \left\{ {\matrix{ {5A\left( {{A^2} - 3{B^2}} \right)\cos 3\phi } \hfill \cr {\, + 5B\left( {3{A^2} - {B^2}} \right)\sin 3\phi } \hfill \cr {\, + 3A\left[ { - 4 + 5\left( {{A^2} + {B^2}} \right)} \right]\cos \phi } \hfill \cr {\, + 3B\left[ { - 4 + 5\left( {{A^2} + {B^2}} \right)} \right]\sin \phi } \hfill \cr } } \right\}, \hfill \cr \delta e_x^{(sp3)} = {3 \over {64}}{\Gamma ^{(sp3)}} \times \left\{ {\matrix{ {5A\left( {{A^2} - 3{B^2}} \right)\cos 4\phi } \hfill \cr {\, + 5B\left( {3{A^2} - {B^2}} \right)\sin 4\phi } \hfill \cr {\, + 4A\left[ {2 + 5\left( {{A^2} - 5{B^2}} \right)} \right]\cos 2\phi } \hfill \cr {\, + 8B\left[ {1 + 5\left( {2{A^2} - {B^2}} \right)} \right]\sin 2\phi } \hfill \cr } } \right\}, \hfill \cr \delta e_y^{(sp3)} = {3 \over {64}}{\Gamma ^{(sp3)}} \times \left\{ {\matrix{ {5B\left( { - 3{A^2} + {B^2}} \right)\cos 4\phi } \hfill \cr {\, + 5A\left( {{A^2} - 3{B^2}} \right)\sin 4\phi } \hfill \cr {\, - 4B\left[ {2 - 5\left( {5{A^2} - {B^2}} \right)} \right]\cos 2\phi } \hfill \cr {\, + 8A\left[ {1 - 5\left( {{A^2} - 2{B^2}} \right)} \right]\sin 2\phi } \hfill \cr } } \right\}, \hfill \cr \delta {I^{(sp3)}} = {1 \over {8\sin I}}{\Gamma ^{(sp3)}} \times \left\{ {\matrix{ {5{K_9}\cos 3\phi + 5{K_{10}}\sin 3\phi } \hfill \cr { + 3{K_{11}}\cos \phi - 3{K_{12}}\sin \phi } \hfill \cr } } \right\}, \hfill \cr \delta {\Omega ^{(sp3)}} = - {1 \over {8\sin I}}{\Gamma ^{(sp3)}} \times \hfill \cr \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{k_{13}}\left\{ {\matrix{ {5\left( {{A^2} - {B^2}} \right)\cos 3\phi } \hfill \cr {\, + 10AB\sin 3\phi } \hfill \cr {\, + 3\left[ { - 4 + 5\left( {{A^2} + 3{B^2}} \right)} \right]\cos \phi } \hfill \cr {\, - 30AB\sin \phi } \hfill \cr } } \right\}, \hfill \cr \delta {\phi ^{(sp3)}} = {3 \over 8}{\Gamma ^{(sp3)}} \times \left\{ {\matrix{ {5B\left( {3{A^2} - {B^2}} \right)\cos 3\phi } \hfill \cr {\, - 5A\left( {{A^2} - 3{B^2}} \right)\sin 3\phi } \hfill \cr {\, + 9B\left[ { - 4 + 5\left( {{A^2} + {B^2}} \right)} \right]\cos \phi } \hfill \cr {\, - 9A\left[ { - 4 + 5\left( {{A^2} + {B^2}} \right)} \right]\sin \phi } \hfill \cr } } \right\}, \hfill \cr \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \delta {\Omega ^{(sp3)}}\cos I{\rm{ }} \hfill \cr} \right.$](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq138.png)
![$\eqalign{ & {\Gamma ^{(sp2)}} = {\left( {{{{n_b}} \over n}} \right)^2}{\left( {{{{a_b}} \over {{R_b}}}} \right)^3}\beta ,\quad {\Gamma ^{(sp3)}} = \left( {{a \over {{R_b}}}} \right){\Gamma ^{(sp2)}}, \cr & \,\,\,\,\,\,{k_{11}} = {{\partial A} \over {\partial \Omega }},\quad {k_{12}} = {{\partial B} \over {\partial \Omega }},\quad {k_{13}} = {{\partial B} \over {\partial I}}, \cr & \,\,\,\,{K_9} = 2AB{k_{11}} + \left( {{A^2} - {B^2}} \right){k_{12}} + A\left( {{A^2} - 3{B^2}} \right)\cos I{\rm{, }} \cr & {K_{10}} = 2AB{k_{12}} - \left( {{A^2} - {B^2}} \right){k_{11}} + B\left( {3{A^2} - {B^2}} \right)\cos I, \cr & {K_{11}} = 10AB{k_{11}} + \left[ { - 4 + 5\left( {{A^2} + 3{B^2}} \right)} \right]{k_{12}} \cr & \,\,\,\,\,\,\,\,\,\, - A\left[ {4 - 5\left( {{A^2} + {B^2}} \right)} \right]\cos I, \cr & {K_{12}} = 10AB{k_{12}} + \left[ { - 4 + 5\left( {3{A^2} + {B^2}} \right)} \right]{k_{11}} \cr & \,\,\,\,\,\,\,\,\,\,\,\, + B\left[ {4 - 5\left( {{A^2} + {B^2}} \right)} \right]\cos I. \cr} $](/articles/aa/full_html/2024/02/aa48218-23/aa48218-23-eq139.png)