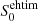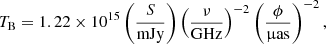EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 687 (July 2024) A&A, 687 (2024) L6 Full HTML
Open Access
Issue
A&A
Volume 687, July 2024
Article Number L6
Number of page(s) 4
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202450590
Published online 26 June 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open Access funding provided by Max Planck Society.

1. Introduction

Relativistic astrophysical jets emanating from the centres of galaxies are a telltale sign of highly energetic activity connected to the central supermassive black hole (SMBH) that they harbour. Specifically, radio galaxies with an active galactic nucleus (AGN) are a ubiquitous target of jet studies since they are generally nearby and therefore provide more insights into jet formation and launching. At larger scales, jet interactions with the ambient medium can give clues about AGN feedback, star formation, and galactic evolution (e.g. Fabian et al. 2000; García-Burillo et al. 2014; Fotopoulou et al. 2019; Dasyra et al. 2022). On the other hand, at smaller scales, the ultimate vicinity of SMBHs can be explored using very long baseline interferometry (VLBI), with which the shrouding medium around them can be peered through. Such studies have been carried out for M 87 (Event Horizon Telescope Collaboration 2019; Lu et al. 2023), Sgr A* (Event Horizon Telescope Collaboration 2022), Cygnus A (Boccardi et al. 2016), 3C 84 (Nagai et al. 2014; Paraschos et al. 2021, 2022), NGC 1052 (Baczko et al. 2016), and Centaurus A (Müller et al. 2011, 2014; Kim et al. 2018; Janssen et al. 2021), among others.

Fornax A (NGC 1316, J0322-3712) is another such radio galaxy whose radio emission is very prominent, providing clues about its central engine. It is located in the Fornax cluster and is one of the nearest (DL = 18.8 Mpc; Hatt et al. 2018) and brightest (e.g. Cantiello et al. 2013) radio galaxies, harbouring a SMBH of ∼1.3 × 108 M⊙ (Nowak et al. 2008). This system is thought to be the result of more than one merger event (Schweizer 1980; Mackie & Fabbiano 1998; Lanz et al. 2010; Richtler et al. 2012a,b). Consequently, it has been the target of numerous studies, covering a wide frequency spectrum (see Stanley & Slee 1950; Schweizer 1980; Geldzahler & Fomalont 1984; Horellou et al. 2001; Lanz et al. 2010; Richtler et al. 2012a; Maccagni et al. 2020, among others). The most prominent morphological characteristic of Fornax A are two extended radio jets (the centres of the two lobes are ∼30 arcmin apart, with total edge-to-edge size of ≤50 arcmin; see e.g. Ekers et al. 1983) emanating from the central AGN and encased in a dense interstellar medium. Their larger-scale physical characteristics have been studied with radio and X-ray observations, revealing variability in the orientation of the inner jets (Geldzahler & Fomalont 1984) and associated X-ray cavities (Lanz et al. 2010). Recent MeerKat data show that the radio lobes of Fornax A have a double shell morphology and that its core is rapidly flickering (Maccagni et al. 2020). The complexity of its structure has been connected to past merger events (Lanz et al. 2010; Richtler et al. 2012a,b), which are possibly associated with its numerous occurrences of intermittent radio activity (Maccagni et al. 2020).

Nevertheless, Fornax A had until now not been detected with VLBI (Slee et al. 1990; Fomalont et al. 2000; Angioni et al. 2019). This is because VLBI monitoring of the southern sky is limited and this source exhibits a faint nuclear region. With our exploratory observations, we aimed to study the core region of Fornax A, peering as far as possible into the vicinity of the central engine. Here we report the first VLBI detection of this compact region of Fornax A, with which we were able to constrain the size and structure of its core. This work is structured as follows: In Sect. 2 we present the observational setup, our data analysis methodology, and our results. In Sect. 3 we discuss constraints of the core structure and polarisation, and in Sect. 4 we conclude with a summary of this work.

2. Observations, data analysis, and results

Fornax A was observed in the X band (8.4 GHz) on February 11, 2023, for a total of one hour as a test source, as part of the VLBI monitoring programme Tracking Active Galactic Nuclei with Austral Milliarcsecond Interferometry (TANAMI; see Ojha et al. 2010). The participating antennas were ATCA (AT; 5 × 22 m), Ceduna (CD; 30 m), Hobart (HO; 26 m), Katherine (KE; 12 m), Mopra (MP; 22 m), Parkes (PA; 64 m), DSS36 (TD; 34 m), and DSS43 (TI; 70 m) in Australia, Warkworth (WW; 12 m) in New Zealand, and Hartebeesthoek (HH; 26 m) in South Africa. Further details about them can be found in Benke et al. (2024). In Fig. 1 we display the (u, v) coverage corresponding to observations of Fornax A with the TANAMI array.

thumbnail Fig. 1.

Illustration of the TANAMI (u, v) coverage of the target source, Fornax A. Two point clouds can be identified in the (u, v) coverage, corresponding to the shorter distance Intra-Australian/New Zealand baselines and to the ones between Australia/New Zealand and South Africa. The outer dashed circle corresponds to a (u, v) radius of 700 μas and the inner one to 1300 μas.

We conducted the data calibration with the software package AIPS (Greisen 2003). The standard VLBI procedure was followed (described in more detail in Benke et al. 2024), in which digital sampling and parallactic angle corrections were applied to the data, and fringe fitting and amplitude calibration were performed. A fringe fitting signal-to-noise ratio (S/N) detection threshold of 5σ was imposed. Phase-referenced calibration was also performed; however, this approach did not yield an increase in the number of detections and the final data products did not exhibit any discernible difference. Finally, the data were averaged in frequency (to output a single channel per sub-band) and coherently in time (into 90-second bins), and then written out for image reconstruction. The final S/N in the range of ∼5 − 30 provided a solid basis for our subsequent analysis.

The challenges of the analysis of the Fornax A dataset are caused by the sparse (u, v) coverage, with a large gap between approximately 0.1 and 0.2 Gλ (see Fig. 1) related to the geographic spread of the antennas that comprise TANAMI and uncertainties of the amplitude gain calibration in the absence of strongly constraining interferometric closure information. To leverage the relatively high S/N and to mitigate potential spurious instrumental effects or artefacts in our data, we employed two methods for the source morphology reconstruction. Our first approach was to use the CLEAN algorithm within the difmap software package (Shepherd et al. 1994). The image is shown in the left panel of Fig. 2; the structure is consistent with a compact point source. As a second step we modelled the flux density with a circular Gaussian component. 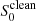The best-fit parameters for the flux density ( S 0 clean $ S_0^{\rm clean} $) and diameter ( D 0 clean $ D_0^{\rm clean} $) were S 0 clean $ S_0^{\rm clean} $ = 62.3 ± 6.2 mJy and 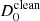D 0 clean $ D_0^{\rm clean} $ = 96.0 μas.

thumbnail Fig. 2.

Geometrical model of Fornax A using CLEAN, geometrical modelling image reconstruction, and the flux density versus (u, v) distance plot. Left: CLEAN image of Fornax A. The structure is consistent with that of a point source, convolved with an elliptical beam of size 580 × 1420 μas (indicated with a dashed black ellipse in the bottom-left corner). The contour levels are 1, 5, 30, 50, 75, and 95% of the intensity maximum of 1.7 × 109 K, and the colour scale corresponds to the measured TB. Right: eht-imaging model of Fornax A. The point source structure is confirmed. The higher values recovered here stem from the fact that, in the geometrical modelling framework, beam convolution is not required and thus the small diameter of the Gaussian component plugged into Eq. (1) increases the corresponding TB. Notice here that the axes are zoomed in by a factor of ten compared to the left panel. Bottom: Data and their uncertainties (black dots) with the best-fit model overlaid (grey crosses). The preferred flux density level of the single Gaussian component of the model at S 0 ehtim $ S^{\rm ehtim}_0 $ = 47.5 ± 4.8 mJy is clearly visible.

Our second approach was to use geometrical modelling within the eht-imaging framework (Chael et al. 2016; Roelofs et al. 2023). The advantage of this forward-modelling technique lies in the fact that best-fit solutions are leveraged from the data without the necessity of convolving the solution afterwards with the point-spread function. Thus, more fine structure can be recovered and information can be extracted even from sparse datasets (see e.g. Paraschos et al. 2024) without performing full-fledged imaging. The right panel of Fig. 2 presents our best-fit model to the visibility amplitudes and closure phases as a function of the (u, v) distance. In this case the input model used was an elliptical Gaussian component. However, the best fit was achieved when the major axis of the ellipse equalled the minor one, resulting again in a circular Gaussian component, characterised by a flux density of 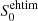S 0 ehtim $ S^{\rm ehtim}_0 $ = 47.5 ± 4.8 mJy and a diameter of 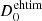D 0 ehtim $ D^{\rm ehtim}_0 $ = 10.0 μas. We note that here 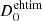D 0 ehtim $ D^{\rm ehtim}_0 $ corresponds to the lower limit of the allowed parameter extent.

Using the formalism described in Lobanov (2005), we then calculated the minimum resolvable scale of our observations, which corresponds to Dlim = 70 μas. Since from our two approaches we constrained the diameter of the compact source to a lower value on average, this implies that the compact source is consistent with an unresolved point source (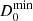 D 0 min $ D_0^{\rm min} $ ≤ 70 μas). The bottom panel of Fig. 2 showcases the fitted data and the geometrical model used. The measurements at longer baselines correspond to robust detections, with a S/N of ≥5, indicative of a very compact structure.

We also constrained the flux density of the source’s core to be S0 = 47.5 − 62.3 mJy. To transform this into the observed brightness temperature, TB, we used the formula

T B = 1.22 × 10 15 ( S mJy ) ( ν GHz ) − 2 ( ϕ μ as ) − 2 , $$ \begin{aligned} T_{\rm B} = 1.22\times 10^{15}\left(\frac{S}{\mathrm{mJy}}\right)\left(\frac{\nu }{\mathrm{GHz}}\right)^{-2}\left(\frac{\phi }{\upmu \mathrm{as}}\right)^{-2}, \end{aligned} $$(1)

where ν is the observing frequency and ϕ is the source size (or a corresponding upper limit for an unresolved source). For the CLEAN reconstruction (using 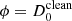ϕ= D 0 clean $ \phi=D_0^{\rm clean} $), this corresponds to TB = (3.4 ± 0.3)×1011 K. A more realistic value can be obtained instead by plugging in ϕ = Dlim, which provides a robust lower limit of TB = (1.5 ± 0.2)×1011 K. Finally, for the geometrical modelling reconstruction, where no convolution takes place, setting 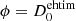ϕ= D 0 ehtim $ \phi=D_0^{\rm ehtim} $ yields TB = (8.1 ± 0.8)×1012 K; this result indicates that even higher TB are feasible for Fornax A. Overall, the magnitude of TB suggests that the radiation is non-thermal and associated with synchrotron processes, and thus likely connected to its AGN launching the jets of Fornax A.

3. Discussion

3.1. Core structure

Given the complexity of the large-scale radio lobes connected to the jet emission, it is reasonable to assume that the compact region could be fitted with a core-jet structure. To test this, we added a second Gaussian component to the geometrical model fit and allowed its position to vary within the entire field of view. This approach serves two purposes: Firstly, it provides a constraint on the core structure. Secondly, as is the case with wide field imaging, it ensures that no other source is present in the data, thus confirming that our detection corresponds to the radio core of Fornax A. We find no significant improvement over our fiducial model of one elliptical Gaussian component. The second Gaussian component was also preferably placed at the centre of the image, and its corresponding flux density tends to the minimum prior value.

Finally, we examined the structure encoded in the closure phases; any discernible structure present in them would be suggestive of the existence of asymmetry in the source morphology. To quantify this, we examined the mean deviation of the closure phases per triangle from zero degrees. By time-averaging the closure phases under a constant value assumption, we found that the triangle formed by CD-TD-WW exhibits a deviation of 3.1σ from zero degrees. To assess the significance of this detection, we performed a simple Monte Carlo experiment, modelling closure phases on all independent triangles as normal random variables with zero mean and a standard deviation of one. We then determined how often the largest measured deviation from zero is larger than 3.1σ, obtaining a frequency of 8.3%. Thus, we conclude with 91.7% confidence that the CD-TD-WW triangle closure phase deviates from zero, and hence a faint source structure on scales of ∼4000 μas, probed by that triangle, is present.

3.2. Polarisation

The observations discussed in this work were conducted in full Stokes. However, due to the faintness of the source, the absence of suitable calibrators, and the heterogeneous nature of the array, extracting polarisation information is challenging (albeit possible, as demonstrated in, for example, Dodson 2008). Nevertheless, conclusions can be drawn regarding the presence of circular polarisation in the signal. We imaged both parallel hand polarisations in order to investigate whether or not we could detect a mismatch in their respective flux densities. A significant discrepancy would indicate the detection of a circular polarisation signature in the data (Event Horizon Telescope Collaboration 2023). We find that the difference in flux density between the two parallel hands is of the order of ∼4%. We note, however, that this value corresponds to a very conservative upper limit given that the S/N is not significant enough to draw a robust conclusion. Therefore, the fractional circular polarisation (mcirc) of the core of Fornax A is consistent with zero, or at most mcirc ≤ 4%.

4. Conclusions

In this Letter we have presented the first detection of the radio core of Fornax A with VLBI. Our findings can be summarised as follows:

  • The core of Fornax A is best approximated by an unresolved point source.

  • The best-fit model is that of a circular Gaussian component with an upper limit size of 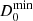D 0 min $ D_0^{\rm min} $ ≤ 70 μas and a flux density of S0 = 47.5 − 62.3 mJy.

  • We constrained TB ≳ 1011 K, which is suggestive of a non-thermal origin for the measured radiation, possibly originating from the central SMBH of Fornax A.

  • While through geometrical modelling no additional flux density was recovered, information from closure phases implies the existence of a more extended structure, with a size of ∼4000 μas, at a confidence level of 91.7%.

  • The fractional circular polarisation of the core region is consistent with zero. A conservative upper limit is of the order of mcirc ≤ 4%.

Our first successful detection of Fornax A serves as a proof of concept for the detectability of this source with VLBI. Future VLBI observations that include more sensitive arrays, such as the next-generation Very Large Array, the Square Kilometre Array, or the Atacama Large Millimeter Array, will provide further insight into the compact region of Fornax A.

Acknowledgments

This research is supported by the European Research Council advanced grant “M2FINDERS – Mapping Magnetic Fields with INterferometry Down to Event hoRizon Scales” (Grant No. 101018682). The Long Baseline Array is part of the Australia Telescope National Facility (https://ror.org/05qajvd42) which is funded by the Australian Government for operation as a National Facility managed by CSIRO. From the 2023 July 1, operation of Warkworth was transferred from Auckland University of Technology (AUT) to Space Operations New Zealand Ltd. Hartebeesthoek is a facility of the National Research Foundation, South Africa. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has also made use of NASA’s Astrophysics Data System Bibliographic Services. Finally, this research made use of the following python packages: numpy (Harris et al. 2020), scipy (Virtanen et al. 2020), matplotlib (Hunter 2007), astropy (Astropy Collaboration 2013, 2018), and Uncertainties: a Python package for calculations with uncertainties.

References

  1. Angioni, R., Ros, E., Kadler, M., et al. 2019, A&A, 627, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  4. Baczko, A. K., Schulz, R., Kadler, M., et al. 2016, A&A, 593, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Benke, P., Rösch, F., Ros, E., et al. 2024, A&A, 681, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Boccardi, B., Krichbaum, T. P., Bach, U., et al. 2016, A&A, 585, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Cantiello, M., Grado, A., Blakeslee, J. P., et al. 2013, A&A, 552, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Chael, A. A., Johnson, M. D., Narayan, R., et al. 2016, ApJ, 829, 11 [Google Scholar]
  9. Dasyra, K. M., Paraschos, G. F., Bisbas, T. G., Combes, F., & Fernández-Ontiveros, J. A. 2022, Nat. Astron., 6, 1077 [Google Scholar]
  10. Dodson, R. 2008, A&A, 480, 767 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Event Horizon Telescope Collaboration (Akiyama, K., et al. 2019, ApJ, 875, L1 [Google Scholar]
  12. Event Horizon Telescope Collaboration (Akiyama, K., et al. 2022, ApJ, 930, L12 [NASA ADS] [CrossRef] [Google Scholar]
  13. Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2023, ApJ, 957, L20 [NASA ADS] [CrossRef] [Google Scholar]
  14. Ekers, R. D., Goss, W. M., Wellington, K. J., et al. 1983, A&A, 127, 361 [NASA ADS] [Google Scholar]
  15. Fabian, A. C., Sanders, J. S., Ettori, S., et al. 2000, MNRAS, 318, L65 [Google Scholar]
  16. Fomalont, E. B., Frey, S., Paragi, Z., et al. 2000, ApJS, 131, 95 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fotopoulou, C. M., Dasyra, K. M., Combes, F., Salomé, P., & Papachristou, M. 2019, A&A, 629, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. García-Burillo, S., Combes, F., Usero, A., et al. 2014, A&A, 567, A125 [Google Scholar]
  19. Geldzahler, B. J., & Fomalont, E. B. 1984, AJ, 89, 1650 [NASA ADS] [CrossRef] [Google Scholar]
  20. Greisen, E. W. 2003, Astrophys. Space Sci. Libr., 285, 109 [NASA ADS] [Google Scholar]
  21. Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hatt, D., Freedman, W. L., Madore, B. F., et al. 2018, ApJ, 866, 145 [NASA ADS] [CrossRef] [Google Scholar]
  23. Horellou, C., Black, J. H., van Gorkom, J. H., et al. 2001, A&A, 376, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
  25. Janssen, M., Falcke, H., Kadler, M., et al. 2021, Nat. Astron., 5, 1017 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kim, J., Marrone, D. P., Roy, A. L., et al. 2018, ApJ, 861, 129 [NASA ADS] [CrossRef] [Google Scholar]
  27. Lanz, L., Jones, C., Forman, W. R., et al. 2010, ApJ, 721, 1702 [NASA ADS] [CrossRef] [Google Scholar]
  28. Lobanov, A. P. 2005, ArXiv e-prints [arXiv:astroph/0503225] [Google Scholar]
  29. Lu, R.-S., Asada, K., Krichbaum, T. P., et al. 2023, Nature, 616, 686 [CrossRef] [Google Scholar]
  30. Maccagni, F. M., Murgia, M., Serra, P., et al. 2020, A&A, 634, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Mackie, G., & Fabbiano, G. 1998, AJ, 115, 514 [NASA ADS] [CrossRef] [Google Scholar]
  32. Müller, C., Kadler, M., Ojha, R., et al. 2011, A&A, 530, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Müller, C., Kadler, M., Ojha, R., et al. 2014, A&A, 569, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Nagai, H., Haga, T., Giovannini, G., et al. 2014, ApJ, 785, 53 [Google Scholar]
  35. Nowak, N., Saglia, R. P., Thomas, J., et al. 2008, MNRAS, 391, 1629 [NASA ADS] [CrossRef] [Google Scholar]
  36. Ojha, R., Kadler, M., Böck, M., et al. 2010, A&A, 519, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Paraschos, G. F., Kim, J. Y., Krichbaum, T. P., & Zensus, J. A. 2021, A&A, 650, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Paraschos, G. F., Krichbaum, T. P., Kim, J. Y., et al. 2022, A&A, 665, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Paraschos, G. F., Kim, J. Y., Wielgus, M., et al. 2024, A&A, 682, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Richtler, T., Bassino, L. P., Dirsch, B., & Kumar, B. 2012a, A&A, 543, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Richtler, T., Kumar, B., Bassino, L. P., Dirsch, B., & Romanowsky, A. J. 2012b, A&A, 543, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Roelofs, F., Johnson, M. D., Chael, A., et al. 2023, ApJ, 957, L21 [NASA ADS] [CrossRef] [Google Scholar]
  43. Schweizer, F. 1980, ApJ, 237, 303 [Google Scholar]
  44. Shepherd, M. C., Pearson, T. J., & Taylor, G. B. 1994, in Bull. Am. Astron. Soc., 26, 987 [Google Scholar]
  45. Slee, O. B., White, G. L., Reynolds, J. E., & Caganoff, S. 1990, Astrophys. Lett. Commun., 27, 361 [NASA ADS] [Google Scholar]
  46. Stanley, G. J., & Slee, O. B. 1950, Aust. J. Sci. Res. A Phys. Sci., 3, 234 [NASA ADS] [Google Scholar]
  47. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]

All Figures

thumbnail Fig. 1.

Illustration of the TANAMI (u, v) coverage of the target source, Fornax A. Two point clouds can be identified in the (u, v) coverage, corresponding to the shorter distance Intra-Australian/New Zealand baselines and to the ones between Australia/New Zealand and South Africa. The outer dashed circle corresponds to a (u, v) radius of 700 μas and the inner one to 1300 μas.
In the text
thumbnail Fig. 2.

Geometrical model of Fornax A using CLEAN, geometrical modelling image reconstruction, and the flux density versus (u, v) distance plot. Left: CLEAN image of Fornax A. The structure is consistent with that of a point source, convolved with an elliptical beam of size 580 × 1420 μas (indicated with a dashed black ellipse in the bottom-left corner). The contour levels are 1, 5, 30, 50, 75, and 95% of the intensity maximum of 1.7 × 109 K, and the colour scale corresponds to the measured TB. Right: eht-imaging model of Fornax A. The point source structure is confirmed. The higher values recovered here stem from the fact that, in the geometrical modelling framework, beam convolution is not required and thus the small diameter of the Gaussian component plugged into Eq. (1) increases the corresponding TB. Notice here that the axes are zoomed in by a factor of ten compared to the left panel. Bottom: Data and their uncertainties (black dots) with the best-fit model overlaid (grey crosses). The preferred flux density level of the single Gaussian component of the model at S 0 ehtim $ S^{\rm ehtim}_0 $ = 47.5 ± 4.8 mJy is clearly visible.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.