| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202348228 | |
| Published online | 01 February 2024 | |
Light curves and spectra for theoretical models of high-velocity red-giant star collisions
1
Institut d’Astrophysique de Paris, CNRS-Sorbonne Université, 98 bis boulevard Arago, 75014 Paris, France
e-mail: dessart@iap.fr
2
The Max Planck Institute for Astrophysics, Karl-Schwarzschild-Str. 1, Garching 85748, Germany
3
Physics and Astronomy Department, Johns Hopkins University, Baltimore, MD 21218, USA
4
Universitad Politècnica de València, Valencia, Spain
5
Max Planck Institute for Extraterrestrial Physics, Garching, Germany
6
Higgs Centre for Theoretical Physics, Edinburgh, UK
7
Kavli Institute for Astronomy and Astrophysics, Beijing 100871, PR China
8
DESY, Zeuthen, Germany
Received:
10
October
2023
Accepted:
21
November
2023
High-velocity stellar collisions driven by a supermassive black hole (BH) or BH-driven disruptive collisions in dense, nuclear clusters can rival the energetics of supergiant star explosions following the gravitational collapse of their iron core. Starting from a sample of red-giant star collisions simulated with the hydrodynamics code AREPO, we generated photometric and spectroscopic observables using the nonlocal thermodynamic equilibrium time-dependent radiative transfer code CMFGEN. Collisions from more extended giants or more violent collisions (with higher velocities or smaller impact parameters) yield bolometric luminosities on the order of 1043 erg s−1 at 1 d, evolving on a timescale of a week to a bright plateau at ∼1041 erg s−1 before plunging precipitously after 20–40 d at the end of the optically thick phase. This luminosity falls primarily in the UV in the first few days, thus when it is at its maximum, and shifts to the optical thereafter. Collisions at lower velocities or from less extended stars produce ejecta that are fainter but can remain optically thick for up to 40 d if they have a low expansion rate. This collision debris shows a similar spectral evolution as that observed or modeled for Type II supernovae from blue-supergiant star explosions, differing only in the more rapid transition to the nebular phase. Such BH-driven disruptive collisions should be detectable by high-cadence surveys in the UV such as ULTRASAT.
Key words: hydrodynamics / radiative transfer
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
In astrophysical environments that have a sufficiently high stellar density, such as globular clusters or the central regions of galaxies (also known as nuclear clusters), stars can collide with each other (Hills & Day 1976; Dale & Davies 2006). Such collisions can be significantly more destructive in nuclear clusters than in globular clusters, primarily because of the greater velocity of stars in the former. In globular clusters, the collision velocity is on the order of the velocity dispersion, which is about 10–15 km s−1 (Cohen 1983). In nuclear clusters, this collision velocity is, in contrast, much higher. It is determined by the local Keplerian speed around the central supermassive black hole (BH), thus on the order of 1000 km s−1 (MBH/107 M⊙)1/2(r/0.05 pc)−1/2, where MBH is the mass of the BH and r is the distance from the BH. In such cases, the kinetic energy of the collision exceeds the binding energy of each star, resulting in their nearly complete destruction, the formation of homologously expanding debris, and a burst of radiation analogous to what is routinely observed in supernovae (SNe; Ryu et al. 2023). The rate of such BH-driven destructive collisions (BDCs) has been estimated to range from 10−4 to 10−9 yr−1 galaxy−1 for main-sequence stars (Rose et al. 2020, 2023; Amaro Seoane 2023a; Balberg & Yassur 2023). This rate depends on various factors, including the distance from the supermassive BH, the influx of stars into the nuclear center, and the core’s depletion rate (the latter refers to the rate at which the stellar density in the core decreases because of tidal disruption events, stellar collisions, and stellar ejections via multi-body interactions). However, Amaro Seoane (2023a) recently showed that the event rate must be dominated by high-velocity events, both for main-sequence and red-giant stars. In the case of red-giant stars, due to their larger cross-section, this estimated event rate is even higher, reaching tens of such collisions per year within a volume of radius 100 Mpc. In the case of main-sequence stars, this number is estimated to be a few per year in the same volume.
Despite the potential for detecting such events, the observables of BDCs have not been extensively studied. Recently, using the moving-mesh hydrodynamics code AREPO (Springel 2010; Weinberger et al. 2020; Pakmor et al. 2016), Ryu et al. (2023) conducted simulations of collisions between 1 M⊙ giants with a surface radius, R⋆, in the range 10–100 R⊙ and collision (or relative) velocities, vrel, of 2500 up to 10 000 km s−1. Their simulations revealed that for vrel ≳ 2500 km s−1 and impact parameters b ≤ 0.8 R⋆, the collisions produce quasi-spherical, supersonic, and homologously expanding debris. Additionally, by considering the radiation energy stored in that ejecta and the local cooling time, they estimate that the peak luminosity occurs essentially at the moment of collision, reaching values as high as 1042–1044 erg s−1 depending on the collision parameters. The luminosity subsequently decreases by an order of magnitude during the first week after the collision and stays relatively constant thereafter. The maximum photospheric temperature can reach 105 K, which corresponds to a spectral energy distribution (SED) that peaks in the far-UV, and gradually declines over the course of a month down to several 103 K, which corresponds to an SED that peaks at optical wavelengths. Such properties are in agreement with the analytical work of Amaro Seoane (2023a), which was further expanded in Amaro Seoane (2023b) to address the additional observables investigated in the numerical simulations of Ryu et al. (2023). The results from this second, analytical work show a good agreement with the numerical predictions. The high luminosity of BDCs suggests that they should be detectable by optical/UV transient surveys such as ZTF (Bellm et al. 2019)1, ASAS-SN (Kochanek et al. 2017)2, LSST (Ivezić et al. 2019)3, or ULTRASAT (Shvartzvald et al. 2023)4.
The radiative signatures of BDCs inferred from hydrodynamic simulations in Ryu et al. (2023) are only rough estimates. A fixed ionization level was assumed, which ignores the expected recombination of the gas as it cools from 105 down to several 103 K. The adopted fixed ionization level overestimates the duration of the optically thick, photospheric phase, and consequently underestimates the luminosity at the corresponding epochs. Finally, the color evolution and the spectral properties of BDCs are not provided. Here, we improve the robustness of these predictions by performing 1D nonlocal thermodynamic equilibrium (NLTE) time-dependent radiative-transfer calculations for the BDC simulations of Ryu et al. (2023) using CMFGEN (Hillier & Dessart 2012). The rapid transition to a homologous flow and the quasi-spherical material distribution of the debris obtained in the hydrodynamic simulations supports the approach with CMFGEN, which ignores dynamics and assumes spherical symmetry. The benefit is, however, the state-of-the-art treatment of the radiative transfer, at the same level of sophistication as employed for SNe (see, for example, Hillier & Dessart 2019).
In the next section, we present the numerical approach with CMFGEN, including a description of the mapping procedure from the 3D AREPO simulations to the 1D ejecta we start with at 1 d after the collision of the two stars. Section 3 describes the results from the CMFGEN simulations, with a description of the photometric, spectroscopic, and gas properties for our model set. In Sect. 4 we present our conclusions. The model light curves and spectra presented in this work are available online5.
2. Numerical approach
The simulations presented in this work are analogous to those performed for Type II SN ejecta with the code CMFGEN (Hillier & Dessart 2012). The main difference is in the preparation of the initial models for the CMFGEN computations. When modeling the radiative transfer for SNe, we need massive star models evolved from the main sequence until iron-core collapse together with a computation of the explosion using radiation hydrodynamics. Here, our initial conditions were taken from the simulations of high-velocity collisions of red-giant stars performed by Ryu et al. (2023). Two stars in the vicinity of a supermassive BH and with a high relative velocity come into collision, leading to the formation of a double-shock structure crossing each stellar envelope while the denser He-core of each component continues on its trajectory largely unimpeded. The huge dissipation of energy during the collision produces debris that expands quasi-spherically at supersonic speeds, very much like what is produced in SN explosions. Once the dynamical phase is over, which takes less than a day for red-giant star collisions, all mass shells have essentially the same radius-to-velocity ratio R/V = t, where t is the time since the onset of the collision; all mass shells move ballistically and the expansion is homologous (any interaction that may take place with the interstellar medium (ISM) was ignored in this work). The remapping into CMFGEN is then straightforward and practically equivalent to the approach used for SNe II (see, for example, Hillier & Dessart 2019).
Our sample is composed of eight models from the red-giant star collisions presented in Ryu et al. (2023). We took the AREPO simulations at about 1 d and built angular averages at all radii for the density and the temperature. In all models, the total ejecta mass is 60–80% of the sum of the mass of each colliding star because their denser He-core remains unaffected by the collision – only the lower density stellar envelopes are shocked and modeled in this work while the two He-core traveling within the ejecta in opposite directions have a negligible impact on the observables. The composition of the material that makes up the ejecta is essentially primordial and uniform. For simplicity, we adopted a solar composition in this work. We forced the velocity to exactly match R/t, where t is the average value of R/V in the original, 1D model. In Fig. 1 we show the initial spherical-averaged ejecta density and temperature profiles for our model set (we truncated the outer part interacting with the ambient medium in the AREPO simulations). The density structure is similar in the four models with the highest collision velocity (i.e., 10 000 km s−1) and the smallest impact parameter (i.e., 0.04 R⋆). In those four models ejecta masses cover the range 1.19–1.59 M⊙ but the kinetic energy per unit mass is the same within a few percent. In contrast, the temperature in those four models is greater in the more extended progenitors (i.e., rs100 versus rs10). This temperature offset arises from the greater cooling from expansion in more compact progenitors (see, e.g., Sect. 4.1 of Dessart & Hillier 2010), which is the primary effect at the origin of the light curve contrast between blue-supergiant (BSG) and red-supergiant (RSG) star explosions (i.e., SNe II-pec such as SN 1987A and SNe II-Plateau). The other four models with a greater impact parameter (i.e., 0.4 or 0.8 R⋆) or smaller collision velocity (i.e., vrel of 2500 or 5000 km s−1) yield weaker energetics and have more complicated density and temperature profiles. For example, the maximum density and temperature in model rs10/v1e4/b0p8 occurs well above the inner ejecta layers. In the weakest collision rs10/v2p5e3/b0p04, the kinetic energy is only 2.6 × 1049 erg, which is a factor of ten smaller than in model rs100/v1e4/b0p04 and its radiative energy content is 100 times smaller. This different radiative energy content at 1 d is the root cause of the differences in radiative properties throughout the photospheric phase (i.e., at times when the ejecta are optically thick). Our model nomenclature is such that model rs100/v1e4/b0p04 stands for the collision model of two stars with a surface radius of 100 R⊙ colliding at a relative velocity of 10 000 km s−1 and with an impact parameter of 0.04 R⋆. A summary of the properties of our model set is provided in Table 1.
 |
Fig. 1. Initial ejecta properties for our model set of high-velocity collisions of red giants. We show the density (top) and the temperature (bottom) for the models at the time of remapping from AREPO to CMFGEN, which is at about 1 d in all cases. Additional properties are given in Table 1. |
Properties of our model set at the start of the CMFGEN simulations at about 1 d after collision.
At 1 d, these models are remapped into the NLTE time-dependent radiative transfer code CMFGEN (Hillier & Dessart 2012) and evolved until they become optically thin at 20–40 d. A solar-metallicity composition is assumed for all species. Specifically, we treated H, He, C, N, O, Ne, Na, Mg, Al, Si, S, Ar, Ca, Sc, Ti, Cr, Fe, Co, and Ni. We used the updated atomic data described in Blondin et al. (2023) and include the following ions for the above species: H I, He I– II, C I– IV, N I– V, O I– VI, Ne II– V, Na I, Mg II– V, Al II– III, Si II– V, S II– V, Ar I– III, Ca II– V, Sc II– III, Ti II– III, Cr II– VI, Fe I– VI, Co II– VI, and Ni I– VI. With our model atom, we treated 24 000 levels and a total of 1.8 million bound-bound transitions. These are mostly coming from iron-group elements, in particular Fe, Co, and Ni (and of these three elements, Fe is the most important followed by Ni). We assumed all isotopes are stable and thus ignore any radioactive decay and associated nonthermal processes. The grid employs 80 grid points uniformly spaced on a logarithmic optical-depth scale. Remapping the grid is necessary at the start of every timestep as well as during the calculation in order to track recombination fronts, if present. To cover the full evolution, a total of about 35 timesteps were computed in all models except for the weaker collisions. The main CMFGEN output of interest for this study is the emergent flux, which is calculated at each time step in the observer’s frame from the far-UV to the far-IR. This spectrum can be shown directly or used to compute the bolometric luminosity Lbol or the absolute magnitude in various filters. We selected the Swift UVW2 and UVW1 filters and the optical U and V filters. The UVW1 filter is a close analog of the near-UV filter that will be on board ULTRASAT (Shvartzvald et al. 2023).
For the weaker collisions, the models had to be stopped at 5–10 d because of convergence difficulties associated with a steep recombination front, high densities, and low temperatures. Hence, for the three models rs10/v1e4/b0p8, rs10/v5e3/b0p04, and rs10/v2p5e3/b0p04, the full evolution computed by CMFGEN is truncated (i.e., stopped before the ejecta are optically thin). In order to provide complete bolometric light curves for the full set of models, these three models were computed with the gray radiation-hydrodynamics code V1D (Livne 1993; Dessart et al. 2010a,b), and in that case the simulation proceeded successfully until 50 d.
Since the present calculations share similarities with core-collapse SNe, we included comparisons to the Type II-Plateau SN model X of Bostroem et al. (2023, named RSG here) and the Type II-peculiar SN model a4 of Dessart & Hillier (2019, named BSG here). Model RSG (BSG) provides a close match to SN 2022acko (SN 1987A; photometric data from Hamuy et al. 1988 is used for this SN in Sect. 3). We chose this Type II-Plateau SN model because it is one of the few of its type that have been calculated with CMFGEN at times prior to 10 d; hence, it is better suited for comparison to these fast evolving stellar collisions. The RSG model corresponds to an ejecta of 8.16 M⊙ with a kinetic energy of 0.6 × 1051 erg. The BSG model corresponds to an ejecta of 13.22 M⊙ and kinetic energy 1.26 × 1051 erg. The same color coding is used for all models throughout the paper (spectra are shown in black when there is no ambiguity about the corresponding model).
3. Results
Figure 2 shows the bolometric light curve computed with CMFGEN for our set of eight red-giant star collisions (as discussed above, the bolometric light curves for the three faintest models is completed after 5–10 d using the results obtained with the gray radiation hydrodynamics code V1D). All simulations show a steeply declining luminosity at 1 d (approximately following t−1.4 to t−2.2) for a maximum value that was probably well in excess of 1043 erg s−1 (the peak is expected to occur at the time of collision; Ryu et al. 2023). The decline rate is greater for more compact giants (rs10 versus rs100), larger impact parameters (b0p8 versus b0p04) and weaker collision velocities (v2p5e3 versus v1e4). After about 5 d, the bolometric light curves flatten and enter a plateau phase that is less luminous as we progress to weaker collisions or more compact progenitors (the range covers from about 1041.7 down to 1040 erg s−1). The plateau in brightness occurs during the recombination phase, when the photospheric temperature is around 6000 K, and arises from a rough balance between the radial expansion of the ejecta and the recession in mass space of the photosphere. The duration of the plateau phase is set by a combination of factors, including the amount of stored radiative energy (see Table 1), the rate at which this stored energy is released through the receding photosphere, and the optical depth of the ejecta (which depends on mass, expansion rate, temperature, composition, or progenitor radius) – all these quantities are not independent. The duration of this plateau phase, which ends at the same time as the optically thick phase (Fig. 3), is shorter for more compact progenitors for the same collision parameters (impact parameter and velocity; models rs100/, rs50/, rs20/, and rs10/v1e4/b0p04). The main reason is the reduced stored radiative energy at 1 d in collisions of more compact giants. In the weaker collisions, the expansion rate of the debris is lower and contributes to lengthening the optically thick phase, although the model is underluminous throughout that photospheric phase. For example, models rs100/v1e4/b0p04 and rs10/v2p5e3/b0p04 have roughly the same optically thick phase duration, but over that time the former radiates 50 times more energy (it started at 1 d with 140 times more stored radiative energy). Unlike core-collapse SNe, there are no unstable isotopes to provide a persistent power source so once the debris from stellar collisions turns optically thin, the power drops precipitously. In practice, the ejecta would reprocess the radiation from the two He-cores of the colliding stars, which are embedded within the ejecta, and the luminosity would level off at a rate of 1035 − 1037 erg s−1 (progenitors rs10 or rs100). When comparing with the BSG and RSG explosion models, the main ingredient causing the change in bolometric luminosity is the change in progenitor radius because of the impact it has on expansion cooling (see, for example, the correlations established in the context of SNe by Popov 1993). Another ingredient is radioactive decay, which is at the origin of the steady slow brightening in the BSG explosion model.
 |
Fig. 2. Bolometric light curves of red-giant star collisions computed with CMFGEN. We include results for our set of eight models as well as those for the BSG explosion model a4 from Dessart & Hillier (2019) and the RSG explosion model X from Bostroem et al. (2023). We add the inferred values for SN 1987A (Hamuy et al. 1988). For the three faintest models, the CMFGEN light curve (thick line) is completed with the V1D results (thin line of the same color). |
 |
Fig. 3. Same as Fig. 2 but now showing the evolution of the total electron-scattering optical depth. The thin dashed black line indicates the 1/t2 slope expected for constant ionization. |
Figure 4 shows the photometric properties computed with CMFGEN for our model set. In the UV (filters UVW2 and UVW1), all light curves show a similar behavior as obtained for the bolometric luminosity, with a decline from a maximum of −18 to −19 mag down to −8 to −10 mag at 5–15 d. The UV plateau lasts until the debris turns optically thin. At that time the UV brightness plunges again. In contrast, in the BSG explosion model, radioactive decay maintains the UV brightness on a faint plateau. In the RSG explosion model, the much larger progenitor radius (i.e., ∼500 R⊙) causes the UV luminosity to remain large for much longer as a result of the reduced cooling from expansion. It is clear, however, that all models are UV luminous for at least a few days after the collision.
 |
Fig. 4. Same as Fig. 2, but now showing the photometric properties for the filters UVW2, UVW1, U, and V (data for SN 1987A are shown for the optical filters). The light curves for the three models corresponding to weaker collisions are truncated because of convergence difficulties with CMFGEN during the recombination phase. |
In the U band, all light curves show a continuous drop without any obvious plateau, while in the V band, the light curves are essentially a continuous plateau throughout the optically thick phase until they plunge when the debris becomes optically thin. This behavior of the U band, also shared by UV filters, is caused by the low temperature (which systematically drops, although more slowly after the onset of the recombination phase) and the enhanced metal-line blanketing in the blue part of the optical and in the UV – see below. The U and V-band light curves for the high-velocity collisions (models rs10/, rs20/, and rs50/v1e4/b0p04) are at the same brightness level as obtained for the BSG explosion model and observed for SN 1987A but differ in shape due to the lack of radioactive decay. The difference is in part associated with the lower ejecta mass (on the order of 1–2 M⊙) compared to ≳10 M⊙ for the BSG model and SN 1987A (Dessart & Hillier 2019).
Figure 5 shows the photospheric properties of our model set. Photospheric radii cover from about 0.1 to a maximum of 0.5 − 0.9 × 1015 cm, the greater for the bigger progenitors or more energetic collisions. The photospheric velocity follows the same evolution for the four violent collisions (i.e., vvel = 10 000 km s−1) with maximum values of 20 000 km s−1 at 1 d followed by a rapid and steady decline. A steeper drop occurs after about a week; it is more pronounced in the more compact progenitors because of the earlier recombination, causing the photosphere to recede faster in mass, and therefore in velocity space. In the weaker collisions, the reduced kinetic energy in the ejecta leads to maximum velocities at 1 d of about 7000 to 17 000 km s−1. Although the CMFGEN calculations are truncated, the evolution of the photospheric velocity is expected to follow that of other models. The photospheric temperatures cover the range 18–23 kK at 1 d, dropping steadily until reaching the H-recombination temperature between 4 to 12 d. The onset of the recombination phase occurs earlier in weaker explosion and more compact progenitors. During that recombination phase, all models have exactly the same photospheric temperature of 5000–6000 K.
 |
Fig. 5. Evolution of the photospheric radius (top), velocity (middle), and gas temperature (bottom) for our model set. For comparison, we also show the results for the BSG and RSG explosion models. The photosphere is taken at the location where the inward-integrated electron scattering optical depth is 2/3. |
Figure 6 illustrates the spectral evolution for stellar-collisions models rs100/v1e4/b0p04 and rs10/v1e4/b0p04 (a presentation of spectra for the entire model set is given in Figs. A.1 and A.2). The spectra, which are shown from 100 Å to 1 μm, are normalized to the maximum flux within that range. The luminosity and photometric properties can be gathered from Figs. 2 and 4. The spectral evolution reflects the color evolution from UV bright to optically bright, with a transition that occurs later in the rs100 model. Because of the high expansion rate of these ejecta (and by extension of their photospheres and spectral-formation regions), the spectra exhibit only a few strong lines – isolated ones from the H I Balmer series (in particular Hα and Hβ), resonance transitions such as Na I λλ 5896,5890, or blends of numerous transitions associated with metal ions such as Ti II or Fe II. Strong lines are also predicted in the rapidly changing UV range such as Mg II λλ 2795, 2802 and a forest of Fe III lines, though mostly prior the recombination phase (see, for example, the discussion in Bostroem et al. 2023). Metals such as Ti II or Fe II contribute significant blanketing in the optical band during the recombination phase (i.e., once Tph drops to 5000–6000 K; Fig. 5). These are responsible for the broad peaks and valleys between 4000 and 7000 Å. Apparent in the evolution is also the fact that the main qualitative distinction in the two sequences is the rate at which the SED shifts to the red. For the same color, the two models are nearly identical (e.g., model rs10/v1e4/b0p04 at 4.6 d appears nearly identical to model rs100/v1e4/b0p04 at the earlier time of 9.9 d). By extension, the similarity would extend also to the BSG explosion model or the observations of SN 1987A. At early times, they would appear analogous to the present predictions for model rs50/v1e4/b0p04.
 |
Fig. 6. Spectral evolution for models rs100/v1e4/b0p04 (left) and rs10/v1e4/b0p04 (right). Although the time step adopted in our CMFGEN simulations is 10% of the current time, we show spectra here with an increment of about 30% of the current time (i.e., epochs shown are 1, 1.3, 1.8 d etc.). At each epoch, the spectra are normalized to a maximum flux of unity. |
Figure 7 gives a more direct comparison between the spectra of our model set at a given time of 5.1 d. The top four models in the figure mostly differ in that their photospheric temperature has not dropped as much (rs100 is still hot and ionized while rs10 is entering the recombination phase). The bottom four panel show much less contrast because they correspond to models in the recombination phase. The most obvious difference is the presence of narrower lines in model rs10/v2p5e3/b0p04, which arise from the lower expansion rate of the ejecta, itself caused by the much weaker collision relative to other models in our set. In this ejecta from a weak collision, both absorption and emission components of all lines are reduced in extent (most visibly in strong lines like Hα), and the associated reduction in the line overlap makes individual line features appear sharper.
 |
Fig. 7. Spectral comparison covering the UV and the optical for our model set at 5.1 d after collision. All spectra are normalized to a maximum flux of unity (the difference in luminosity between models is shown in Fig. 2). |
4. Conclusion
We have presented NLTE time-dependent radiative transfer calculations carried out with CMFGEN for the debris resulting from the high-velocity collisions of 1 M⊙ red-giant stars expected to occur in dense, nuclear clusters. These calculations complement the earlier estimates of Ryu et al. (2023) and Amaro Seoane (2023a,b). The CMFGEN calculations are based on the hydrodynamic simulations performed with AREPO by Ryu et al. (2023). The remapping from AREPO to CMFGEN is taken at 1 d after collision, when the quasi-spherical ejecta are essentially in homologous expansion. This shocked stellar gas is reminiscent of supergiant star explosions following gravitational collapse, and thus the results from our CMFGEN calculations are qualitatively similar to those obtained for Type II SNe, either from BSG (Dessart & Hillier 2019) or RSG star progenitors (Hillier & Dessart 2019). Our sample includes eight models that vary in terms of progenitor radius (10–100 R⊙), collision velocity (2500, 5000, and 10 000 km s−1), and impact parameter (0.04, 0.4, 0.8 R⋆). In all cases, the two colliding stars have identical properties. These collisions yield ejecta with masses, Mej, in the range 1.19–1.60 M⊙, kinetic energies, Ekin, in the range 0.26 − 4.0 × 1050 erg, and stored radiative energies at 1 d in the range 0.01 − 1.6 × 1049 erg.
In our model set, the ratio Ekin/Mej is in the range 0.16 − 2.5 × 1050 erg 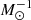 . This brackets the value of our BSG explosion model, which has an Ekin/Mej of ∼1050 erg
. This brackets the value of our BSG explosion model, which has an Ekin/Mej of ∼1050 erg 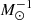 . Together with the comparable progenitor radius (10–100 R⊙ compared to 50 R⊙ for the BSG model), this explains to a large extent the very similar bolometric light curve, multi-band light curves, and spectral evolution. The reduced ejecta mass implies a much shallower ejecta optical depth and therefore a shorter photospheric phase. This is aggravated by the absence of unstable isotopes and associated radioactive decay heating. Stellar collisions never re-brighten significantly (in contrast to BSG explosions such as SN 1987A) and eventually plunge precipitously into oblivion. More specifically, our stellar collisions have bolometric luminosities on the order of 1042 − 1043 erg s−1 at 1 d, dropping to a plateau brightness of 1040 − 1041.7 erg s−1 after 5–10 d, and fading suddenly at the end of the optically thick phase at 15–40 d, depending on the progenitor radius and the strength of the collision. All simulations are UV bright (magnitude on the order of −18 to −19 mag) for a few days and should be detectable by UV transient surveys such as ULTRASAT (Shvartzvald et al. 2023) or UVEX (Kulkarni et al. 2021).
. Together with the comparable progenitor radius (10–100 R⊙ compared to 50 R⊙ for the BSG model), this explains to a large extent the very similar bolometric light curve, multi-band light curves, and spectral evolution. The reduced ejecta mass implies a much shallower ejecta optical depth and therefore a shorter photospheric phase. This is aggravated by the absence of unstable isotopes and associated radioactive decay heating. Stellar collisions never re-brighten significantly (in contrast to BSG explosions such as SN 1987A) and eventually plunge precipitously into oblivion. More specifically, our stellar collisions have bolometric luminosities on the order of 1042 − 1043 erg s−1 at 1 d, dropping to a plateau brightness of 1040 − 1041.7 erg s−1 after 5–10 d, and fading suddenly at the end of the optically thick phase at 15–40 d, depending on the progenitor radius and the strength of the collision. All simulations are UV bright (magnitude on the order of −18 to −19 mag) for a few days and should be detectable by UV transient surveys such as ULTRASAT (Shvartzvald et al. 2023) or UVEX (Kulkarni et al. 2021).
The spectral evolution is also reminiscent of that observed for SN 1987A or obtained for the BSG model (Dessart & Hillier 2019). Our energetic stellar collisions span a similar range in photospheric velocity, radius, and temperature but evolve much faster owing to the much smaller ejecta mass. Weaker collisions yield results that are analogous to under-energetic BSG explosions (Dessart & Hillier 2019; see, for example, their model a3), and are characterized by lower luminosities and narrower lines at all times.
In this work we have neglected the potential power injection from interaction with the ISM and fallback accretion into the supermassive BH. Interaction with the ISM would yield a sustained bolometric luminosity until very late times, perhaps for years, depending on the ISM density and extent, although this power would most likely emerge in the UV (Dessart & Hillier 2022; Dessart et al. 2023). In addition, it would produce peculiar profiles. During the photospheric phase, broad boxy emission would be present on top of the strongest lines, such as Hα, and would thus modify the spectral properties at all times. Fallback accretion could also produce a sustained or delayed re-brightening depending on the history of this accretion (see, for example, Dexter & Kasen 2013). It may produce super-luminous events, such as the peculiar Type II SNe OGLE14-073 (Terreran et al. 2017) or iPTF14hls (Arcavi et al. 2017; Dessart 2018).
In this work we have assumed a solar metallicity. Stars in dense nuclear clusters may form there and exhibit a solar or supra-solar metallicity. If they were formed outside the nuclear center, as may occur from globular cluster infall, they would likely have a subsolar metallicity (see, e.g., Do et al. 2015; Schultheis et al. 2020). Variations in metallicity would not alter the bolometric light curve, but they would modulate the colors (the higher the metallicity, the greater the impact of metal-line blanketing at < 5500 Å) and the spectra (they would exhibit varying strengths in metal lines, both from the forests of lines due to iron-group elements and from isolated transitions associated with Na I or Ca II). A discussion of these effects is presented in Dessart et al. (2014).
Considering their peak luminosity, which rivals that of tidal disruption events (see Gezari 2021, for a review) or Type II SNe, BDCs can appear as nuclear transients. It is possible that BDCs have already been detected by ongoing surveys such as ASAS-SN or ZTF and will be detected by upcoming surveys such as ULTRASAT or LSST. The light curves and spectra presented in this paper will be instrumental in distinguishing BDCs from other types of nuclear transients observed in these surveys. While we focused on the observables of BDCs involving giant stars, in principle BDCs involving stars of different types (e.g., main-sequence stars) can generate a luminous electromagnetic display as long as a significant portion of collision kinetic energy is converted into radiation. Investigations into the detection rate of such events and their observable characteristics for stars of various types will be pursued in follow-up projects.
Acknowledgments
This research was supported by the Munich Institute for Astro-, Particle and BioPhysics (MIAPbP) which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311. P.A.S. acknowledges the funds from the “European Union NextGenerationEU/PRTR”, Programa de Planes Complementarios I+D+I (ref. ASFAE/2022/014). This work was granted access to the HPC resources of TGCC under the allocation 2022 – A0130410554 made by GENCI, France. This research has made use of NASA’s Astrophysics Data System Bibliographic Services.
References
- Amaro Seoane, P. 2023a, ApJ, 947, 8 [CrossRef] [Google Scholar]
- Amaro Seoane, P. 2023b, arXiv e-prints [arXiv:2307.10330] [Google Scholar]
- Arcavi, I., Howell, D. A., Kasen, D., et al. 2017, Nature, 551, 210 [Google Scholar]
- Balberg, S., & Yassur, G. 2023, ApJ, 952, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019, PASP, 131, 018002 [Google Scholar]
- Blondin, S., Dessart, L., Hillier, D. J., Ramsbottom, C. A., & Storey, P. J. 2023, A&A, 678, A170 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bostroem, K. A., Dessart, L., Hillier, D. J., et al. 2023, ApJ, 953, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G. 1983, ApJ, 270, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., & Davies, M. B. 2006, MNRAS, 366, 1424 [NASA ADS] [Google Scholar]
- Dessart, L. 2018, A&A, 610, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dessart, L., & Hillier, D. J. 2010, MNRAS, 405, 2141 [NASA ADS] [Google Scholar]
- Dessart, L., & Hillier, D. J. 2019, A&A, 622, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dessart, L., & Hillier, D. J. 2022, A&A, 660, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dessart, L., Livne, E., & Waldman, R. 2010a, MNRAS, 405, 2113 [NASA ADS] [Google Scholar]
- Dessart, L., Livne, E., & Waldman, R. 2010b, MNRAS, 408, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Gutierrez, C. P., Hamuy, M., et al. 2014, MNRAS, 440, 1856 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Gutiérrez, C. P., Kuncarayakti, H., Fox, O. D., & Filippenko, A. V. 2023, A&A, 675, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dexter, J., & Kasen, D. 2013, ApJ, 772, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Do, T., Kerzendorf, W., Winsor, N., et al. 2015, ApJ, 809, 143 [Google Scholar]
- Gezari, S. 2021, ARA&A, 59, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Suntzeff, N. B., Gonzalez, R., & Martin, G. 1988, AJ, 95, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Hillier, D. J., & Dessart, L. 2012, MNRAS, 424, 252 [CrossRef] [Google Scholar]
- Hillier, D. J., & Dessart, L. 2019, A&A, 631, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hills, J. G., & Day, C. A. 1976, Astrophys. Lett., 17, 87 [NASA ADS] [Google Scholar]
- Ivezić, Z., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S., Shappee, B. J., Stanek, K. Z., et al. 2017, PASP, 129, 104502 [Google Scholar]
- Kulkarni, S. R., Harrison, F. A., Grefenstette, B. W., et al. 2021, PASP, submitted [arXiv:2111.15608] [Google Scholar]
- Livne, E. 1993, ApJ, 412, 634 [Google Scholar]
- Pakmor, R., Springel, V., Bauer, A., et al. 2016, MNRAS, 455, 1134 [Google Scholar]
- Popov, D. V. 1993, ApJ, 414, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Rose, S. C., Naoz, S., Gautam, A. K., et al. 2020, ApJ, 904, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Rose, S. C., Naoz, S., Sari, R., & Linial, I. 2023, ApJ, 955, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Ryu, T., Amaro Seoane, P., Taylor, A. M., & Ohlmann, S. T. 2023, MNRAS, submitted [arXiv:2307.07338] [Google Scholar]
- Schultheis, M., Rojas-Arriagada, A., Cunha, K., et al. 2020, A&A, 642, A81 [EDP Sciences] [Google Scholar]
- Shvartzvald, Y., Waxman, E., Gal-Yam, A., et al. 2023, AAS J., submitted [arXiv:2304.14482] [Google Scholar]
- Springel, V. 2010, MNRAS, 401, 791 [Google Scholar]
- Terreran, G., Pumo, M. L., Chen, T.-W., et al. 2017, Nat. Astron., 1, 228 [Google Scholar]
- Weinberger, R., Springel, V., & Pakmor, R. 2020, ApJS, 248, 32 [Google Scholar]
Appendix A: Additional figures for all models
In Figs. A.1 and A.2, we illustrate the full spectral evolution for all eight models in our set. The corresponding photometric evolution is shown in the main text, in Figs. 2 and 4.
 |
Fig. A.1. Spectral evolution for models rs100/v1e4/b0p04 (top left), rs50/v1e4/b0p04 (top right), rs20/v1e4/b0p04 (bottom left), and rs10/v1e4/b0p04 (bottom right). The main difference between these models is the red-giant star radius (100, 50, 20, and 10 R⊙, given in the same order). |
 |
Fig. A.2. Spectral evolution for models rs10/v1e4/b0p4 (top left), rs10/v1e4/b0p8 (top right), rs10/v5e3/b0p04 (bottom left), and rs10/v2p5e3/b0p04 (bottom right). The main difference between these models is the impact parameter (0.4 or 0.8 R⋆; top row) or the velocity of the collision (5000 or 2500 km s−1; bottom row). For the last three models, the CMFGEN calculation is truncated at 5–10 d; convergence difficulties prevented the calculations from being carried out until the ejecta were fully optically thin (see Fig. 3). |
All Tables
Properties of our model set at the start of the CMFGEN simulations at about 1 d after collision.
All Figures
 |
Fig. 1. Initial ejecta properties for our model set of high-velocity collisions of red giants. We show the density (top) and the temperature (bottom) for the models at the time of remapping from AREPO to CMFGEN, which is at about 1 d in all cases. Additional properties are given in Table 1. |
| In the text | |
 |
Fig. 2. Bolometric light curves of red-giant star collisions computed with CMFGEN. We include results for our set of eight models as well as those for the BSG explosion model a4 from Dessart & Hillier (2019) and the RSG explosion model X from Bostroem et al. (2023). We add the inferred values for SN 1987A (Hamuy et al. 1988). For the three faintest models, the CMFGEN light curve (thick line) is completed with the V1D results (thin line of the same color). |
| In the text | |
 |
Fig. 3. Same as Fig. 2 but now showing the evolution of the total electron-scattering optical depth. The thin dashed black line indicates the 1/t2 slope expected for constant ionization. |
| In the text | |
 |
Fig. 4. Same as Fig. 2, but now showing the photometric properties for the filters UVW2, UVW1, U, and V (data for SN 1987A are shown for the optical filters). The light curves for the three models corresponding to weaker collisions are truncated because of convergence difficulties with CMFGEN during the recombination phase. |
| In the text | |
 |
Fig. 5. Evolution of the photospheric radius (top), velocity (middle), and gas temperature (bottom) for our model set. For comparison, we also show the results for the BSG and RSG explosion models. The photosphere is taken at the location where the inward-integrated electron scattering optical depth is 2/3. |
| In the text | |
 |
Fig. 6. Spectral evolution for models rs100/v1e4/b0p04 (left) and rs10/v1e4/b0p04 (right). Although the time step adopted in our CMFGEN simulations is 10% of the current time, we show spectra here with an increment of about 30% of the current time (i.e., epochs shown are 1, 1.3, 1.8 d etc.). At each epoch, the spectra are normalized to a maximum flux of unity. |
| In the text | |
 |
Fig. 7. Spectral comparison covering the UV and the optical for our model set at 5.1 d after collision. All spectra are normalized to a maximum flux of unity (the difference in luminosity between models is shown in Fig. 2). |
| In the text | |
 |
Fig. A.1. Spectral evolution for models rs100/v1e4/b0p04 (top left), rs50/v1e4/b0p04 (top right), rs20/v1e4/b0p04 (bottom left), and rs10/v1e4/b0p04 (bottom right). The main difference between these models is the red-giant star radius (100, 50, 20, and 10 R⊙, given in the same order). |
| In the text | |
 |
Fig. A.2. Spectral evolution for models rs10/v1e4/b0p4 (top left), rs10/v1e4/b0p8 (top right), rs10/v5e3/b0p04 (bottom left), and rs10/v2p5e3/b0p04 (bottom right). The main difference between these models is the impact parameter (0.4 or 0.8 R⋆; top row) or the velocity of the collision (5000 or 2500 km s−1; bottom row). For the last three models, the CMFGEN calculation is truncated at 5–10 d; convergence difficulties prevented the calculations from being carried out until the ejecta were fully optically thin (see Fig. 3). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


