| Issue |
A&A
Volume 663, July 2022
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 10 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202142930 | |
| Published online | 21 July 2022 | |
Stellar mass and radius estimation using artificial intelligence
1
Departament d’Astronomia i Astrofísica, Universitat de València,
C. Dr. Moliner 50,
46100
Burjassot, Spain
e-mail: andres.moya-bedon@uv.es
2
Electrical Engineering, Electronics, Automation and Applied Physics Department, E.T.S.I.D.I, Polytechnic University of Madrid (UPM),
Madrid
28012,
Spain
3
GRAM Research Group, Department of Signal Theory and Communications, University of Alcalá,
Alcalá de Henares,
28805, Spain
e-mail: robertoj.lopez@uah.es
Received:
16
December
2021
Accepted:
11
March
2022
Context. Estimating stellar masses and radii for most stars is a challenge, but it is critical to know them for many different astrophysical fields, such as exoplanet characterization or stellar structure and evolution. One of the most extended techniques for estimating these variables is the so-called empirical relations.
Aims. We propose a group of frontier artificial intelligence (AI) regression models, with the aim of studying their proficiency in estimating stellar masses and radii. We select the model that provides the best accuracy with the least possible bias. Some of these AI techniques do not treat uncertainties properly, but in the current context, in which statistical analyses of massive databases in different fields are conducted, the most accurate estimate possible of stellar masses and radii can provide valuable information. We publicly release the database, the AI models, and an online tool for stellar mass and radius estimation to the community.
Methods. We used a sample of 726 MS stars from the literature with accurate M, R, Teff, L, log ɡ, and [Fe/H]. We split our data sample into training and testing sets and then analyzed the different AI techniques with them. In particular, we experimentally evaluated the accuracy of the following models: linear regression, Bayesian regression, regression trees, random forest, support-vector regression (SVR), neural networks, K-nearest neighbour, and stacking. We propose a series of experiments designed to evaluate the accuracy of the estimates, and also the generalization capability of AI models. We also analyzed the impact of reducing the number of input parameters and compared our results with those from current empirical relations in the literature.
Results. We have found that stacking several regression models is the most suitable technique for estimating masses and radii. In the case of the mass, neural networks also provide precise results, and for the radius, SVR and neural networks work as well. Compared with other currently used empirical relation-based models, our stacking improves the accuracy by a factor of two for both variables. In addition, bias is reduced to one order of magnitude in the case of stellar mass. Finally, we found that using our stacking and only Teff and L as input features, the accuracies obtained are slightly higher than 5%, with a bias of ≈1.5%. In the case of the mass, including [Fe/H] significantly improves the results. For the radius, including log ɡ yields better results. Finally, the proposed AI models exhibit an interesting generalization capability: they are able to perform estimations for masses and radii that were never observed during the training step.
Key words: astronomical databases: miscellaneous / methods: data analysis / stars: fundamental parameters / stars: statistics
© ESO 2022
1 Introduction
Of all different stellar parameters, stellar mass (M) and radius (R) are two variables that have a larger impact for understanding different stellar physical processes. Unfortunately, they can only be estimated indirectly for most of the stars. In the literature, only two observational methods provide reliable estimates of stellar masses: detached eclipsing binaries (EBs), and asteroseismology (Ast). In the case of radii, we must add interferometry to the list. When these methods are applied, almost all the isolated stars are out of their focus for physical or technical reasons. Nevertheless, in addition to these techniques, a large number of other techniques for estimating these parameters have been proposed or used (see Serenelli et al. 2021, for a complete review for the case of stellar masses).
One of the most frequently used techniques for accomplishing these estimations is the so-called empirical relations of M or R and other stellar parameters, such as the effective temperature (Teff), stellar metallicity ([Fe/H]), (logarithm of) the surface gravity (log ɡ), and stellar luminosity (L). The history of these empirical relations starts in the early twentieth century with Hertzsprung (1923), Russell et al. (1923), and Eddington (1926). Many works have been published since then, offering different empirical relations for these estimations or using them for different purposes (Torres et al. 2010; Gafeira et al. 2012; Eker et al. 2015, 2018, 2021; Benedict et al. 2016; Mann et al. 2019; Fernandes et al. 2021). All of them used EB data as the training set for their relations.
Recently, Moya et al. (2018) constructed a comprehensive dataset that included masses and radii obtained from EB and Ast (and only a few interferometric radii). This set consisted of a total of more than 700 main-sequence stars with accurate M, R, Teff, L, log ɡ, and [Fe/H]. It was the basis of a complete analysis of all the empirical relations possible for estimating M and R as a linear combination of any of the remaining observables. The authors presented a total of 38 empirical relations with the best accuracy and precision possible, using classic linear regressions. In addition, they also presented results obtained with a random forest model as a demonstration of the benefits of using machine-learning techniques for this problem.
This paper follows that work. Taking advantage of the exceptional database gathered by Moya et al. (2018), we used the most recent artificial intelligence (AI) techniques for getting the most of them to estimate the most accurate stellar masses and radii possible from empirical data. These techniques have the exceptional advantage of extracting the most from the training data and in some cases minimize possible biases. We must take into account that because the regression models are trained with inputs from EB, Ast, and interferometry (in a few cases), their estimates mimic the results that should be obtained using these techniques. On the other hand, not all of them offer an appropriate treatment and propagation of uncertainties. That is, they use as input information only the observed values and not their uncertainties. In any case, the exercise and model we propose is important and provides valuable information because accurate estimates of stellar masses and radii, regardless of their uncertainties, are an important intermediate step for the statistical analysis of other astrophysical properties, especially in an era when thousands or tens of thousands of observations are analyzed at the same time.
2 Data Sample
The data sample was presented and described in detail in Moya et al. (2018). Here we offer a summary of its main characteristics with an impact on our new results. We refer to the original work for additional details about the different sources, data quality, and so on.
The data sample consists of 726 main-sequence stars covering spectral types from B to K; most of them are F-G stars (80%). All of them have precise estimates of M, R, Teff, L, log ɡ, [Fe/H], and stellar mean density (ρ, not used in this work). Sixty-seven percent of these stars have been characterized using asteroseismology, 31% of them belong to EB systems, and the rest (2%) has been studied using interferometry. Asteroseismic stars are mainly solar-like pulsators, explaining the large presence of F- and G-type stars in the sample. EB stars are more homogeneously distributed along the Hertzsprung-Russell (HR) diagram (see Fig. 1 in Moya et al. 2018 for a detailed distribution of the different subsamples).
Although the sample was gathered from many different sources, masses and radii were estimated with uncertainties lower than 7%, and the luminosity has an uncertainty of about 10%. The uncertainties of Teff, log ɡ, and [Fe/H] are more heterogeneous, but always within the standard values for these observables, that is, about 100 K or lower for Teff, 0.05 dex or lower for log ɡ, and 0.15 dex or lower for [Fe/H]. Despite the different HR distribution of the asteroseismic and EB subsets, we have not identified other biases in this data sample.
During the learning step of the AI models we describe in the next section, we took advantage of the error bounds provided in the data sample for each feature. Basically, we proceeded to artificially increase the training data with a uniform sampling in the intervals defined by the error bounds, hence generating more samples. For the experiments, we generated ten additional samples per original sample. We observed that generating more samples than this has almost no influence on the results and slows the training process down. Only neural networks and stacking, the techniques that need a large data sample, would benefit from a larger sample, but this is not true for the remaining models in terms of accuracy.
The inclusion of these additional samples did not change the distribution of the original sample. We followed a simple uniform distribution within the error bounds provided in the original data sample to generate additional possible values. This was a conservative choice because we assumed that samples are distributed equiprobably over the entire range defined by the uncertainties. We chose not to use a Gaussian distribution to generate the samples because it would concentrate most of the samples on the currently provided sample. The asymmetric error bounds mean that a uniform model is more appropriate.
3 Artificial Intelligence Models
Estimating the mass or radius of stars is primarily a regression problem. Traditionally, the problem has been approached by trying to define empirical relations that take the observables of the stars as input to estimate the mass and radius (see Moya et al. 2018). We here propose to approach the problem from a different perspective and replace this manual search for empirical relations with an approach based on AI models. The idea is simple: considering the observables of the stars as the input features, we let the AI solutions learn the best regression models for estimating M and R.
To the best of our knowledge, no similar previous study has been performed with a data sample of this type. For this reason, we did not restrict ourselves to a particular AI model, but analyzed a battery of AI solutions that represent the currently best models. Our goal is to provide a comparative study to elucidate the AI models that are most appropriate for addressing the regression of the mass and radius of stars. In this section, we describe each of the AI regression approaches we used in the experiments.
3.1 Mathematical Notation
We include the mathematical notation we used to describe the AI models we propose. Based on the data sample described in Sect. 2, we considered a set of training star feature vectors {(x1, t1)…, (xN, tN)}, such that 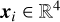 encodes the stellar properties provided in the sample (i.e., Teff, L, log ɡ, [Fe/H]), and
encodes the stellar properties provided in the sample (i.e., Teff, L, log ɡ, [Fe/H]), and 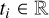 is the corresponding target value we wish to estimate. In our case, t can be either the mass (M) of the star or its radius (R).
is the corresponding target value we wish to estimate. In our case, t can be either the mass (M) of the star or its radius (R).
3.2 Linear Regression
We first propose to learn a linear regression (LR). Technically, LR assumes that the target (M or R) can be estimated by employing a linear combination of the features provided in the data sample. Let 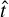 be the predicted target value, then
be the predicted target value, then
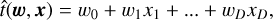 (1)
(1)
where vectors x and w encode the input feature vector (directly taken from the data sample) and the coefficients of the linear regressor, respectively. We followed the least-squares approach (Bishop 2006) for learning the model, where the objective consists of minimizing the residual sum of squares between the observed targets in the dataset and the targets predicted by the linear approximation. This is done by solving a problem of the form minw 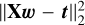 . X is a matrix containing all the training vectors, and t encodes the target vectors. Similar regression models have been used before, for instance, by Moya et al. (2018). We therefore included this machine-learning technique for validation and comparison purposes.
. X is a matrix containing all the training vectors, and t encodes the target vectors. Similar regression models have been used before, for instance, by Moya et al. (2018). We therefore included this machine-learning technique for validation and comparison purposes.
3.3 Bayesian Regression
We implemented a Bayesian regression model to estimate a probabilistic model for the stellar targets. In particular, we followed a Bayesian ridge regression (BRR) (Bishop 2006) of the form
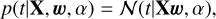 (2)
(2)
where the target t was assumed to be a Gaussian distribution over Xw. α was estimated directly from data and was treated as a random variable. The regularization parameter was tuned to the available data, introducing over the hyperparameters of the model, that is, w, the following spherical Gaussian prior 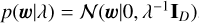 .
.
During model fitting, we jointly estimated parameters w, α, and λ. Regularization parameters α and λ were estimated to maximize the log marginal likelihood following Tipping (2001).
3.4 Regression Trees and Random Forest
We used decision trees (Breiman et al. 1984) as a nonparametric supervised learning model for the regression of our targets. As described by Breiman et al. (1984), a regression tree (RT) estimates a target variable t using a decision tree where a regression model is fitted to each node of the tree to cast the predictions. Different functions can be used to measure the quality of every split performed by the tree nodes (mean squared error, mean absolute error, etc.).
We also used the AI model known as random forest (RF) (Breiman 2001). A RF for regression is a meta estimator that fits various RTs on different subsamples of the dataset and uses averaging to increase the predicted accuracy and control overfitting. Specifically, this AI ensemble model was implemented in our work following the original approach of Breiman (2001), where the regression trees were built from data samples drawn with replacements from the training set. The mean predicted regression targets of the trees in the forest were used to calculate the predicted regression target of an input sample.
During the learning of RT, we let our model optimize its internal hyperparameters via a grid search process with cross validation. For RT, we adjusted the strategy of choosing the split at each tree node (best or random), the minimum number of samples required to be at a leaf node (5, 10, 50, and 100), and the function with which the split quality is measured (mean squared error, mean squared error with Friedman’s improvement score for potential splits, and mean absolute error or reduction in Poisson deviance to find splits). In the case of RF, we used the following hyperparameters: number of trees (100), minimum number of samples required to be at a leaf node (1), and the function for measuring the quality of the split (mean squared error).
3.5 Support-vector Regression
In machine-learning, support-vector machines (SVMs) (Boser et al. 1992) are one of the most robust supervised-learning models. They were originally formulated for classification purposes and were later extended to solve regression problems by Drucker et al. (1996), defined as support-vector regression (SVR). We used the SVR AI model for our regression problems. Technically, we followed the ϵ-SVR approach using the LibSVM implementation for regression (Chang & Lin 2011).
Given a set of training vectors, {(x1, t1),…, (xN, tN)}, the goal of ϵ-SVR consists of finding a function that deviates ϵ > 0 at most from the obtained targets ti for all our training data, and at the same time, is as flat as possible. In other words, the regression errors can be smaller than ϵ, but any variation greater than this is unacceptable.
Therefore, the main task in training an SVR is to solve the following optimization problem:
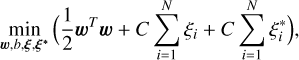 (3)
(3)
subject to wT ϕ(xi) + b − ti ≤ ϵ + ξi,
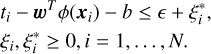
w defines the hyperplane that fits the training samples best. Flatness for w means to seek small w, as is done in Eq. (3). The function we searched for is 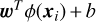 , where b is the bias. ϕ(хi) is a function that maps the training vector xi into a higher dimensional space. C > 0 is the penalty parameter of the error term. The higher this parameter, the fewer regression errors we tolerate. Finally, ξi and
, where b is the bias. ϕ(хi) is a function that maps the training vector xi into a higher dimensional space. C > 0 is the penalty parameter of the error term. The higher this parameter, the fewer regression errors we tolerate. Finally, ξi and 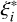 are known as the slack variables. They cope with otherwise infeasible constraints of the optimizaiont problem. That is, thanks to them, we allow for some errors (higher than e).
are known as the slack variables. They cope with otherwise infeasible constraints of the optimizaiont problem. That is, thanks to them, we allow for some errors (higher than e).
The following dual problem due to the high dimensionality of the vector variable w is commonly solved,
![$_{\alpha ,\alpha *}^{\min }\left[ {{1 \over 2}{{(\alpha - \alpha *)}^T}Q(\alpha - \alpha *) + \in \,\sum\limits_{i = 1}^N {({\alpha _i} + \alpha _i^*) + \sum\limits_{i = 1}^N {{t_i}({\alpha _i} - \alpha _i^*)} } } \right],\,$](/articles/aa/full_html/2022/07/aa42930-21/aa42930-21-eq12.png) (4)
(4)
where e = [1,…, 1]T is a vector of all ones, Q is an N × N positive semi-definite matrix, and 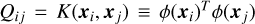 . is known as the kernel function. We employed the radial basis function (RBF) kernel because it leads to the best results. The RBF kernel is defined as follows:
. is known as the kernel function. We employed the radial basis function (RBF) kernel because it leads to the best results. The RBF kernel is defined as follows:
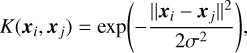 (5)
(5)
where σ is a free parameter of the kernel. For our experiments, ϵ was fixed to 0.1, and we performed a grid search with cross-validation to adjust the regularization parameter C (1, 10, 100, 1000) and 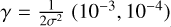 . The best values were (i) for the estimation of the stellar mass, C = 10 and γ = 0.001, and (ii) for the radius estimation, C = 1000 and γ = 0.001.
. The best values were (i) for the estimation of the stellar mass, C = 10 and γ = 0.001, and (ii) for the radius estimation, C = 1000 and γ = 0.001.
3.6 K-nearest Neighbor
As an interesting baseline, we also included the k-nearest neighbor (kNN) regression model. The output of a kNN regression model is obtained as the average of values of the targets of the k-nearest neighbours for the test input. Technically, given a test sample xi, our model first identifies the kNNs in the training set. This is done employing the Euclidean distance. Then, the estimation for the test xi is obtained as the mean of the targets of its kNNs. For our experiments, we tested the following k parameter values: 1, 5, 10, 15, 20, and 50. Of these, k = 5 led to the best results on average for all the experiments and targets. Therefore, we fixed the parameter k to 5. The type of weight function we used to scale the contribution of each neighbor was uniform, which means that all points in each neighborhood were weighted equally.
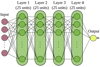 |
Fig. 1 Architecture of the feedforward neural network. Four hidden layers have been used with 25 units, each followed by a ReLU. The output layer has no activation function to directly perform the star parameter regression. |
3.7 Neural Networks
We analyzed the performance of neural networks (NNs) for our problem. Due to the size of the database we handled and the type of input data, we decided to use deep feedforward network models (Goodfellow et al. 2016). Technically, we implemented a multilayer perceptron to learn a mapping of the form t = f (x, w), where w encodes the model parameters. Our NN is able to learn the values for w that result in the best function approximation in the form of a feedforward network.
The architecture implemented in our work is depicted in Fig. 1. It consists of a multilayer perceptron with an input layer, a set of four hidden fully connected layers with 25 units each, and the output layer in charge of the regression of the target variable. Every hidden unit is followed by a rectified linear unit (ReLU) activation function. We used the square error as the loss function,
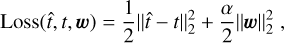 (6)
(6)
where  is the prediction of the NN, and α is the regularization parameter. Backpropagation (LeCun et al. 2012) was used to learn the model with stochastic gradient descent (SGD) (Robbins & Monro 1951) optimizer. During the learning, we fixed α = 0.01 and used an adaptive learning-rate policy. To estimate R and M, the initial learning rate was fixed to 0.09 and 0.2, respectively, because they provided the best results.
is the prediction of the NN, and α is the regularization parameter. Backpropagation (LeCun et al. 2012) was used to learn the model with stochastic gradient descent (SGD) (Robbins & Monro 1951) optimizer. During the learning, we fixed α = 0.01 and used an adaptive learning-rate policy. To estimate R and M, the initial learning rate was fixed to 0.09 and 0.2, respectively, because they provided the best results.
3.8 Stacking
Finally, we used a machine-learning ensemble method known as a stacked generalization (or stacking) (Wolpert 1992). Stacked generalization involves stacking the output of a set of individual estimators (level 0) to learn a final estimator (level 1); see Fig. 2. In a regression problem like ours, the predictions of each individual level 0 regression model, that is, (t1, t2,…,tn) in Fig. 2, are stacked and fed into a final level 1 estimator that calculates the final prediction for our targets. Overall, stacking is an ensemble strategy in which the model at level 1 learns how to combine the predictions from multiple existing models in the most effective way. This strategy is different from other ensemble methods such as bagging or boosting. Unlike bagging, the models in stacking are usually distinct (e.g., not all decision trees as in a random forest) and fit on the same dataset (e.g., instead of samples of the training dataset). Different from boosting, stacking uses a single model at level 1 to learn how to integrate the predictions from the contributing level 0 models in the most effective way (e.g., instead of a sequence of models that correct the predictions of prior models). The use of stacking allows us to explore and combine a variety of heterogeneous regression models.
We employed a specific stacking architecture for each stellar target variable, where at level 0 we simply integrated its corresponding best regression models. At level 1, both architectures used a linear BRR. Typically, the stacking meta-model at level 1 should be simple, allowing for a smooth interpretation of the prediction of the base models. In this way, the final prediction works as a weighted average or blending of the predictions given by the base models. Worse results are obtained for level 1 when more complex models are used (e.g., an NN). Moreover, we are aware that a proper uncertainty propagation is one of the main requirements for any astrophysical study, and not all the proposed AI techniques are able to naturally provide this. Using a BRR at level 1 allows us to provide a model that can associate the corresponding uncertainty with each regression. Therefore, we decided to build this approach with the aim of a consistent error propagation pipeline, and for this, a Bayesian regression is the best choice for stacking.
During training and to avoid overfitting, this final BRR estimator of level 1 was trained on out-of-samples. That is, data that were used to train the models in level 0 were fed to these n models. Then, predictions (t1, t2,…, tn) at level 0 were made and were used along with the expected target values as training pairs to fit the level 1 model. To prepare the training data for the level 1 model, we followed a standard five-fold cross validation (Hastie et al. 2009) of the models at level 0, where the out-of-fold predictions were used to train the level 1 model.
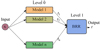 |
Fig. 2 Architecture of the stacked generalization model. We used a specific architecture for each stellar property, where we integrate its best regression models at level 0. At level 1, both models use a BRR, which is trained on out-samples (taken from the training set), following a cross-validation method. |
3.9 Evaluation Metrics
To evaluate the performance of the different AI regression models, we used the following three metrics. For all our experiments, the main evaluation metric was the mean absolute error (MAE),
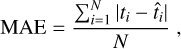 (7)
(7)
where ti and 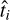 are the target (mass or radius) provided in our dataset, and the corresponding value estimated by a regression model, respectively. When we compare the estimated mass (or radius)
are the target (mass or radius) provided in our dataset, and the corresponding value estimated by a regression model, respectively. When we compare the estimated mass (or radius) 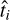 using our AI models with the real mass (or radius) ti for the testing sample, it is also interesting to measure the dispersion of the estimates with respect to the real values. For a numerical estimation of this dispersion, we calculated the mean relative difference (MRD) and mean absolute relative difference (MARD), defined as
using our AI models with the real mass (or radius) ti for the testing sample, it is also interesting to measure the dispersion of the estimates with respect to the real values. For a numerical estimation of this dispersion, we calculated the mean relative difference (MRD) and mean absolute relative difference (MARD), defined as
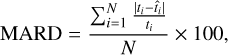 (8)
(8)
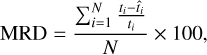 (9)
(9)
where MRD measures the bias of our estimates, and MARD focuses on their accuracy.
We assumed that the dataset provides real masses and radii for the stars in the sample. These features were determined with any of the techniques described in Sect. 2: asteroseismology, EBs, and interferometry in a few cases. We thus tried to mimic these techniques with machine-learning models fed with training data.
4 Results and Discussion
The problem of stellar mass and radius estimation is considered here as a regression problem. With the following experiments, we analyze the suitability of the set of AI models described in the previous section for this particular problem.
In order to reproduce all the results of our study, we release all codes and data we used in a repository1. In addition to the dataset we used in the experiments, we publicly release the different AI models that have been employed in this study. We built all the regression models in Python, using the free software machine-learning library scikit-learn (version 1.0) (Pedregosa et al. 2011), which requires a Python version ≥3.7. Our AI models are also available2 for the online estimation of stellar masses and radii. In this last service, the linear regressions of Moya et al. (2018) are also provided.
4.1 AI for Estimating Stellar Mass and Radius
We split the data sample of Moya et al. (2018) into a training and a testing set, the same for all the experiments. We randomly selected 80% of the samples for the training set, and the rest of stars, that is, 20% of the sample, were used for testing purposes. Figures 3 and 4 show the histograms for masses and radii, respectively, of the training and testing sets. We artificially incremented the density curve fitting the testing set to facilitate visual comparison with the training set. They show the statistical coherence of the split, since the testing set covers the training set population properly. Our first experiment analyzed the effectiveness of different AI techniques in predicting these test values using the training set to learn them.
In Table 1 we show the MAE on the test set for all the AI models detailed in Sect. 3. If no stacked generalization is used, the best models for both target variables are the neural networks we designed. They lead to an MAE of 0.05 and 0.049 for the mass and radius, respectively. The stacking architectures, which combine the best models at level 0 for every target variable, lead to the lowest errors. In particular, the stacking architecture for the mass integrates the following models at level 0: NN, kNN, and RF. We did not include the SVR at level 0, although it reports a better MAE than the kNN. In our tests, including the SVR did not yield better results, and it also slowed the training down. For the radius, our stacking architecture simply integrates the NN and the SVR at level 0. We offer a detailed comparison of our two stacking models with currently used models in Sect. 4.4, but we report here in advance that they have improved the performance of classical techniques based on empirical relations.
Figures 5 and 6 show the detailed estimates for every test sample for its mass or radius, respectively. The best estimates for the stellar mass are clearly offered by the NN and the stacking models. For the radius estimations, SVR, the NN, and their stacking perform best.
 |
Fig. 3 Histogram of the masses of the stars included in the training (red) and the testing (blue) splits. |
 |
Fig. 4 Histogram of the radii of the stars included in the training (red) and the testing (blue) splits. |
 |
Fig. 5 Detailed estimates of the stellar mass for every test sample of all the AI models proposed in this paper. The orange line shows the masses estimated by the AI techniques, and the blue line shows the corresponding test value. The red line represents the absolute error between these two previous quantities. The X-axis shows the identifier of each test star when they have been sorted in increasing order of mass. |
 |
Fig. 6 Detailed estimates of the stellar radius for every test sample of all the AI models. The orange line shows the radii estimated by the AI techniques, and the blue line shows the corresponding test value. The red line represents the absolute error between these two previous quantities. The X-axis shows the identifier of each test star when they have been sorted in increasing order of radius. |
4.2 Generalization Experiment
The range of masses and radii covered by the data sample is limited and not equally covered by the data sample. For a detailed analysis of the strengths and weaknesses of this data sample, we refer to Moya et al. (2018). In summary, some spectral types are statistically well covered by the data sample, especially FGK stars, but beyond theses types, the data sample is not that robust. In the near future, large facility surveys and space missions will populate these regions, but in the meantime it is important to analyse whether AI models are able to generalize their estimates to ranges little or not observed during training. Technically, we used the data sample as follows in this second experiment. We first sorted the star samples in the dataset in ascending order according to their masses (or radii). Then we trained the AI models with 90% of the stars with the lowest masses (or radii). The test set was compared with the remaining stars (10%), whose masses (or radii) were not observed during training. Specifically, the training and test intervals for the radii were [0.64, 2.98] and [3.00, 8.35], respectively. For the masses, we used the interval [0.66, 1.49] for training, and [1.50, 2.31] was the interval of the test set. Overall, we are able to evaluate how the AI models are able to offer estimations for the masses and radii of stars with unobserved characteristics during training with these splits.
Table 2 shows the MAE for all the AI models and every target stellar property. The results are less precise than in the previous experiment. This is an indicator of the degree of difficulty offered by the proposed generalization setting. While the previous best result was an MAE of approximately 0.04, the errors are now shifted to a higher order of magnitude, which is 0.16 and 0.19 for the mass and radius, respectively. Interestingly, generalization results again confirm that a stacking approach is the best option. This improvement is remarkable in the case of the radius. Our stacking integrates the two best regression models for every target at level 0, that is, (a) for the mass, we used LR and NN, (b) for the radius, we employed SVR and NN. We show in Fig. 7 the detailed estimates performed by our stacking model. The figure shows that even for masses or radii that were not observed during training, the model shows a tendency to adjust the estimates toward the real value of each sample. For the mass, the stacking tends to overestimate the values, especially for masses higher than 2 M⊙. For radius estimations, we observe the excellent generalization capability of the stacking model, which offers accurate predictions up to 6 R⊙. For the last sample of 8.35 R⊙, the model reports an absolute error of ≈2 R⊙.
Generalization experiment. MAE for every AI model.
4.3 Reducing the Number of Input Variables
As described in Sect. 2, the input independent variables we used to estimate stellar masses and radii were Teff, L, log ɡ, and [Fe/H]. That is, we assumed that the AI model has all these input data at its disposal. Nevertheless, real life is usually not that good, and for a given star, we sometimes lack information about all these values. In this section, we seek to measure the importance of each of these input variables with respect to the ability of the model to perform good predictions, and we finally construct models using a reduced set of inputs. Technically, we used our best machine-learning model for the study: the stacking. Given these four input features, we removed some of them during the AI model learning. We started training the stacking model with the simplest and most common combinations of input features: (Teff + L). We then incrementally incorporated different features and measured the impact on the model performance. Figure 8 shows our analysis for all these input feature combinations.
The estimates of the stellar mass become progressively more accurate, as expected, as more features are incorporated into the model: see Figs. 8a,c,e,g. This effect is even more remarkable in the case of stellar radius, shown in Figs. 8b,f,d,h. The influence of the logarithm of the surface gravity (i.e., log ɡ) is clear for the estimation of the radii, also as expected, since log ɡ explicitly includes information about R.
In Table 3 we list the MRD and MARD we obtained when estimating M and R on the testing set and the models using Teff + L, Teff + L + [Fe/H], Teff + L + log ɡ, and Teff + L + [Fe/H] + log ɡ as input variables. Here we can see more explicitly what is shown in Fig 8. For example, the most accurate and unbiased results are obtained when all input variables are used. We also see that including the metallicity when the mass is to be estimated remarkably improves the results. log ɡ is not that important if Teff and L are known. However, when only Teff and L are available, our model provides a notable accuracy of 6.6% and a slight tendency to underestimate. Finally we note that including log ɡ when the radii are to be estimated significantly improves results. Using only Teff and L also provides remarkable results with an accuracy of 5.3% and again a slight tendency to underestimate. The inclusion of metallicity worsens the results. This is an unexpected result, but the quality is only slightly poorer, can it be regarded as an effect of increasing variability when adding a new variable without including additional information. That is, according to these results, metallicity is not relevant when stellar radii are to be estimated.
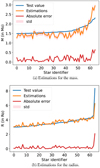 |
Fig. 7 Generalization experiment. Detailed estimate for the stacking model. The figure is similar to Figs. 5 and 6. |
4.4 Comparison with Current Models
Finally, we compare our results with the corresponding model based on classical empirical relations between stellar variables published by Moya et al. (2018), considering this work as the most recent models for the problem. The authors compared the performance of their linear regressions with other models in the literature, showing that their proposal provided the best balance between accuracy and precision at that time. Technically, for each star in our testing set, we chose from Moya et al. (2018) the best linear empirical relation for all the features provided in the data sample. This selection was made by finding the empirical relation with the best combination of accuracy and precision.
In Figs 9a,b we overplot the estimates of our best machine-learning model, i.e. the stacking, and the best empirical relation of Moya et al. (2018) for the mass and radius, respectively. Graphically, the dispersion for both variables is slightly higher when the empirical relations are used. Table 4 shows the MRD and MARD metrics for our AI approach and the traditional empirical relations.
Using the empirical relations for the mass, we obtain an MARD of 8.4% and an MRD of 4.3%, that is, an accuracy better than 10% (this result is remarkable for the empirical relations) and a bias of 4.3%, which is lower than the accuracy. However, our AI model based on stacking reduces the bias by a factor of ten and improves the accuracy by a factor of two. Similar results can be observed for the radius. This time, the empirical relations report an MARD = 5.3% and an MRD = −0.25%, that is, an accuracy of about 5% (again a remarkable result for an empirical relation) and a negligible bias. Moya et al. (2018) already highlighted this finding in their previous work, that is, for the radius, the empirical relations provide better results than for the mass. Compared with our AI model, the bias remains negligible and the accuracy is improved again by a factor of two. We can therefore conclude that the alternative proposed in this work, using AI models, is able to provide better results for the estimation of stellar masses and radii than any of the previous empirical relations in Moya et al. (2018). Thus, our work improves the currently best model and provides a clear experimental evaluation, which will allow future comparisons with new methods.
 |
Fig. 8 “Testing” vs. estimated masses and radii using the stacking model and the following input feature combinations: (Teff + L) in a and b; (Teff + L + [Fe/H]) in c and d; (Teff + L + log ɡ) in e and f; and (Teff + L + [Fe/H] + logg) in ɡ and h. |
MRD and MARD using the stacking model and different input variables to estimate the masses and radii of the testing sample.
Comparison between our best AI model, i.e., stacking, and the best emprirical relation in Moya et al. (2018).
 |
Fig. 9 Comparison of the estimates performed by best machine-learning model, i.e., the stacking, and the best empirical relation in Moya et al. (2018). |
5 Conclusions
We have analyzed the effectiveness of different AI techniques for the estimation of stellar masses and radii. To achieve this goal, we need a high-quality data sample with the most accurate masses and radii. We used the sample of Moya et al. (2018) in our experiments, which is currently the most adequate database for this purpose in the literature. It consists of a total of 726 main-sequence stars covering spectral types from B to K, most of which are F-G stars (80%). All of them have precise estimates of M, R, Teff, L, log ɡ, and [Fe/H].
We trained and tested a number of AI techniques to estimate masses and radii using the detailed dataset. Specifically, we evaluated the regression capability of the following AI techniques: linear regression, Bayesian regression, regression trees, random forest, SVR, kNN, NN, and stacking. We designed a series of experiments to study the effectiveness of these techniques for stellar radius and mass estimates.
We first divided our data sample into a training set (80% of the total sample) and a test set (the remaining 20%) and analyzed the accuracy of the AI models with them. This first experiment consisted of analyzing the accuracy that can be reached when the testing masses and radii were estimated. In both cases, the stacking technique showed the best results, with an MAE of 0.049 for the mass and 0.048 for the radius. We found that to estimate stellar masses, the NN provides precise results (MAE = 0.05), and to estimate stellar radii, NN and SVR are two good choices, with an MAE of 0.049 and 0.05, respectively.
In a second experiment, we explored the generalization capacity of these AI techniques. That is, we explored the ability of these models to make estimates of radii and masses that were not observed during training. The interest of this experiment lies in the fact that the data sample covers a certain region of the HR diagram, and we would like to quantify how well masses and radii are estimated in the boundary HR regions defined by the data sample or even beyond them. Our results confirmed that models based on neural networks and stacking are able to generalize adequately. In particular, they yield an MAE for mass and radius estimates above the upper bound of the training set of 0.16 and 0.19, respectively.
The simultaneous knowledge of Teff, L, log ɡ, and [Fe/H] for every target of which we wish to estimate mass and radius is rare. We analyzed how the best AI technique (stacking) works when only some of these independent variables are known. We trained models using only Teff and L, and Teff, L, and [Fe/H], and we compared them with estimates obtained using all the variables. For the stellar mass, our results show that when only Teff and L are known, we report an MRD = 1.5 and an MARD = 6.6, which are remarkable results. The inclusion of [Fe/H] significantly improves the estimations, but the addition of log ɡ is not that important. In the case of the stellar radius, again using only Teff and L provides an MRD = 1.3 and an MARD = 5.3. In this case, including log ɡ notably improves the results, whereas [Fe/H] has a null impact on the results.
We finally compared our best AI model results with the corresponding estimates using the empirical relation of Moya et al. (2018). These authors provided a complete comparison with other empirical relations in the literature. In estimating stellar masses, stacking improves the results compared with classical linear regressions. It reduces the bias (MRD) by one order of magnitude and improves the accuracy (MARD) a factor two. In terms of the stellar radius, the bias is almost unaltered, but the accuracy is again improved by the same factor.
One of the main benefits of using these AI-based techniques is the accuracy. On the other hand, the treatment, propagation, and estimation of uncertainties are still one of the limitations of some of these AI models. Some of them have been improved in recent years in this sense, but additional efforts are needed. However, massive statistical studies, where an accurate estimate of the mass and radius of thousands or more stars is needed, will greatly benefit from the methods and tools we propose in this paper.
The data sample and codes to reproduce all the experiments are available in a repository3. Additionally, we offer an online tool for the estimation of stellar masses and radii using our best AI technique (stacking) and the linear regressions of Moya et al. (2018)4. This online facility is also offered as an R package5.
Acknowledgements
The authors acknowledge the referee for his/her very useful and constructive comments. A.M. acknowledges funding support from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No 749962 (project THOT), from Grant PID2019-107061GB-C65 funded by MCIN/AEI/10.13039/501100011033, and from Generalitat Valenciana in the frame of the GenT Project CIDE-GENT/2020/036. R.J.L.S. acknowledges partial funding support from project AIRPLANE, with reference PID2019-104323RB-C31, of Spain’s Ministry of Science and Innovation. This research has made use of the Spanish Virtual Observatory (http://svo.cab.inta-csic.es) supported from Ministerio de Ciencia e Innovación through grant PID2020-112949GB-I00. In memoriam of Federico Zuccarino.
References
- Benedict, G. F., Henry, T. J., Franz, O. G., et al. 2016, AJ, 152 141 [Google Scholar]
- Bishop, C. M. 2006, Pattern Recognition and Machine Learning, Information Science and Statistics (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Boser, B. E., Guyon, I. M., & Vapnik, V. N. 1992, in Proceedings of the Fifth Annual Workshop on Computational Learning Theory, COLT ‘92 (New York, NY, USA: Association for Computing Machinery), 144 [CrossRef] [Google Scholar]
- Breiman, L. 2001, Mach. Learn., 45 5 [Google Scholar]
- Breiman, L., Friedman, J. H., Olshen, R. A., & Stone, C. J. 1984, Classification and Regression Trees (Monterey, CA: Wadsworth and Brooks) [Google Scholar]
- Chang, C.-C., & Lin, C.-J. 2011, ACM Trans. Intell. Syst. Technol., 2 27 [CrossRef] [Google Scholar]
- Drucker, H., Burges, C. J. C., Kaufman, L., Smola, A., & Vapnik, V. 1996, in Proceedings of the 9th International Conference on Neural Information Processing Systems, NIPS’96 (Cambridge, MA, USA: MIT Press), 155 [Google Scholar]
- Eddington, A. S. 1926, The Internal Constitution of the Stars / by A.S. Eddington (Cambridge: University Press Cambridge), 8 407 [Google Scholar]
- Eker, Z., Soydugan, F., Soydugan, E., et al. 2015, AJ, 149 131 [Google Scholar]
- Eker, Z., Bakış, V., Bilir, S., et al. 2018, MNRAS, 479 5491 [NASA ADS] [CrossRef] [Google Scholar]
- Eker, Z., Soydugan, F., Bilir, S., & Bakış, V. 2021, MNRAS, 507 3583 [NASA ADS] [CrossRef] [Google Scholar]
- Fernandes, J., Gafeira, R., & Andersen, J. 2021, A&A, 647, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gafeira, R., Patacas, C., & Fernandes, J. 2012, Ap&SS, 341 405 [Google Scholar]
- Goodfellow, I., Bengio, Y., & Courville, A. 2016, Deep Learning (Cambridge: MIT Press) [Google Scholar]
- Hastie, T., Tibshirani, R., & Friedman, J. 2009, The Elements of Statistical Learning (Berlin: Springer-Verlag) [Google Scholar]
- Hertzsprung, E. 1923, Bull. Astron. Inst. Netherlands, 2 15 [NASA ADS] [Google Scholar]
- LeCun, Y., Bottou, L., Orr, G., & Müller, K.-R. 2012, Efficient BackProp (Berlin, Heidelberg: Springer), 9 [Google Scholar]
- Mann, A. W., Dupuy, T., Kraus, A. L., et al. 2019, ApJ, 871 63 [Google Scholar]
- Moya, A., Zuccarino, F., Chaplin, W. J., & Davies, G. R. 2018, ApJS, 237 21 [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12 2825 [Google Scholar]
- Robbins, H., & Monro, S. 1951, Annal. Math. Stat., 22 400 [CrossRef] [Google Scholar]
- Russell, H. N., Adams, W. S., & Joy, A. H. 1923, PASP, 35 189 [NASA ADS] [CrossRef] [Google Scholar]
- Serenelli, A., Weiss, A., Aerts, C., et al. 2021, A&ARv, 29 4 [Google Scholar]
- Tipping, M. E. 2001, J. Mach. Learn. Res., 1 211 [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18 67 [Google Scholar]
- Wolpert, D. H. 1992, Neural Netw., 5 241 [CrossRef] [Google Scholar]
All Tables
MRD and MARD using the stacking model and different input variables to estimate the masses and radii of the testing sample.
Comparison between our best AI model, i.e., stacking, and the best emprirical relation in Moya et al. (2018).
All Figures
 |
Fig. 1 Architecture of the feedforward neural network. Four hidden layers have been used with 25 units, each followed by a ReLU. The output layer has no activation function to directly perform the star parameter regression. |
| In the text | |
 |
Fig. 2 Architecture of the stacked generalization model. We used a specific architecture for each stellar property, where we integrate its best regression models at level 0. At level 1, both models use a BRR, which is trained on out-samples (taken from the training set), following a cross-validation method. |
| In the text | |
 |
Fig. 3 Histogram of the masses of the stars included in the training (red) and the testing (blue) splits. |
| In the text | |
 |
Fig. 4 Histogram of the radii of the stars included in the training (red) and the testing (blue) splits. |
| In the text | |
 |
Fig. 5 Detailed estimates of the stellar mass for every test sample of all the AI models proposed in this paper. The orange line shows the masses estimated by the AI techniques, and the blue line shows the corresponding test value. The red line represents the absolute error between these two previous quantities. The X-axis shows the identifier of each test star when they have been sorted in increasing order of mass. |
| In the text | |
 |
Fig. 6 Detailed estimates of the stellar radius for every test sample of all the AI models. The orange line shows the radii estimated by the AI techniques, and the blue line shows the corresponding test value. The red line represents the absolute error between these two previous quantities. The X-axis shows the identifier of each test star when they have been sorted in increasing order of radius. |
| In the text | |
 |
Fig. 7 Generalization experiment. Detailed estimate for the stacking model. The figure is similar to Figs. 5 and 6. |
| In the text | |
 |
Fig. 8 “Testing” vs. estimated masses and radii using the stacking model and the following input feature combinations: (Teff + L) in a and b; (Teff + L + [Fe/H]) in c and d; (Teff + L + log ɡ) in e and f; and (Teff + L + [Fe/H] + logg) in ɡ and h. |
| In the text | |
 |
Fig. 9 Comparison of the estimates performed by best machine-learning model, i.e., the stacking, and the best empirical relation in Moya et al. (2018). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.