| Issue |
A&A
Volume 656, December 2021
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202141809 | |
| Published online | 07 December 2021 | |
Search for pairs and groups in the 2006 Geminid meteor shower
1
Astronomical Institute, CAS,
Fričova 298,
25165
Ondřejov,
Czech Republic
e-mail: koten@asu.cas.cz
2
Faculty of Electrical Engineering, Czech Technical University,
Prague,
Czech Republic
Received:
16
July
2021
Accepted:
1
October
2021
Context. The existence of pairs and groups of meteors during meteor showers has been an open question for a long time. The double-station video observation of the 2006 Geminid meteor shower, one of the most active annual showers, is used for the search of such events.
Aims. The goal of the paper is to determine whether the observed pairs of Geminid meteors are real events or cases of random coincidence.
Methods. The atmospheric trajectories of the observed meteors, photometric masses, and both time and spatial distances of meteoroids in the atmosphere were determined using a double-station video observation. The time gaps between them were analysed statistically. The Monte Carlo simulation was used for the determination of the probability of random pairings.
Results. A higher than expected number of candidates for pairs was found among 2006 Geminids. An evaluation of the Poisson distribution shows that a significant fraction of them may be real cases. However, the Monte Carlo simulation did not confirm this result and provided a different view. Analysis of geometrical positions of candidate pairs also did not support the presence of real pairs and groups. Although we cannot exclude that some of them may be physically connected pairs, all the observed cases can be explained as the coincidental appearance of unrelated meteors.
Key words: meteorites, meteors, meteoroids
© ESO 2021
1 Introduction
Visual and telescopic observers have repeatedly reported that meteors appear in pairs or even groups. As these observational methods are rather subjective, more reliable results can be provided by instrumental observations. Earlier studies of the major meteor showers and sporadic meteors usually lead to contradictory results. Porubčan (1968) investigated the radar records of six meteor showers, including the Geminids, using several statistical methods and found an excellent agreement with a random time distribution. A comprehensive overview of earlier studies is provided by Porubčan et al. (2002). Their paper analysed recent Leonid storms observed in 1966, 1969, and 1999, as well as April Lyrid activity observed by radar in 1982. The authors found positive results for younger streams. In the case of older showers, no grouping of meteoroids above the random level was found. Similarly, clustering analysis of the arrival times of the 1999 Leonids did not show any clustering on the timescales of the video frame rate (Gural & Jenniskens 2000). The authors conclude that meteoroids do not tend to fragment in the vicinity of the Earth. Ofek (1999) found a very small excess of clustering on 5-s intervals when analysing 1998 Leonid visual and video observations, but did not suppose the results to be conclusive.
On the other hand, several papers have reported observations of the meteor clusters. Hapgood & Rothwell (1981) analysed double-station television observations of three Perseid meteors arriving within 1.3 s on August 12, 1977, and interpreted this event as a result of the fragmentation that occurred at least 1700 km from the Earth’s surface. Five nearly simultaneous meteors were observed within only 0.1 s on October 18, 1985 (Piers & Hawkes 1993). Their radiants were not consistent with any major meteor shower. Moreover, each main object seemed to be composed of several smaller fragments. Huge clusters were observed several times during recent Leonid meteor storms at the turn of the century. Kinoshita et al. (1999) reported 100–150 Leonid meteors observed within 2 s during the 1997 return, and Watanabe et al. (2002) at least 15 meteors within 4 s in 2002. Both events were only single-station observations. In another paper Watanabe et al. (2003) provided results of 38 double-station Leonids, observed again in 2002, that occurred within 2 s. They analysed all three Leonid events, assumed that they were meteor clusters, and discussed possible scenarios of their origin.
Another interesting event occurred above the Czech Republic on September 9, 2016 (Koten et al. 2017). It consisted of a bright fireball and eight faint meteors, all of them following parallel trajectories. All the meteors were recorded within 1.5 s. The double-station observation provided their atmospheric trajectories; the spatial separation among them was between 14 and 105 km. The small meteoroids were supposed to be fragments separated from the main body no earlier than two or three days before entering the atmosphere at distances smaller than 0.08 AU. The meteor cluster belonged to the September ϵ Perseid meteor shower.
Here, we investigate the possibility of the existence of the meteor pairs and groups within the Geminid meteor shower. This is one of the most intensive annual showers (004 GEM1). It is usually active in the first half of December with a peak around December 14. In recent years, the zenith hourly rate reached values of about 120–140 meteors. Plavec (1950) was the first who noted that the observability of the Geminid meteor shower from the Earth is limited to a few centuries. The first observation of the Geminid meteor was found to be recorded in 1077 in the Chinese chronicles (Hasegawa 1999). The age of the stream is no longer a few thousand years. Its activity has been increasing in the last few decades (Ryabova & Rendtel 2018). Jenniskens (2006) suggests that it will reach its maximum in around 2050. The model of Ryabova (2016) implies the cometary origin of the meteor stream. On the other hand, the observations of the meteors in the atmosphere did not support such an origin. For example, fireballs reported by Spurný (1993) exclusively belonged to the fireball group I called asteroidal meteors.
Asteroid (3200) Phaeton is supposed to be a parent body of the meteor shower as was first suggested by Whipple (1983). It is probably a dormant comet that has already lost all its volatiles and does not replenish the meteoroid stream anymore. Only weak and very short perihelion activity was observed in 2009 and 2012 (Li & Jewitt 2013), but this cannot contribute to the current activity of the meteor shower (Ryabova 2018).
Traditionally, statistical methods were used for the analyses of possible groupings among the meteors (Porubčan 1968). They rely mainly on the Poisson distribution, which shows the number of expected random appearances of the meteor pairs or groups. Another way is a comparison of interval distribution between consecutive meteors compared with exponential distribution. Nevertheless, doubts were cast on these methods by Sampson (2007) who found that there is a significant discrepancy between the Poisson statistics and numerical models. The Poisson distribution uses fixed time intervals, which is not the case of typical meteor observations. The author found that the Poisson distribution underestimates the number of coincidental meteor groupings. He recommended further testing on the Perseid and Geminid meteor showers as they show consistent activity profiles. Therefore, we provide a comparison of the two approaches to the solution of the problem based on the 2006 Geminid meteor shower observations.
The paper is organized as follows. Section 2 describes the observations, instrumentation, data processing, and observed data regarding the meteor pair candidates. Section 3 provides a comparison between the statistical analyses of the pairs and the Monte Carlo simulation, as well as the geometrical properties of potential pairs. Section 4 summarizes the results.
2 Data acquisition, processing, and overview
Double-station video observations have been carried out at the Ondřejov Observatory since 1998. The analogue recording was switched to digital in 2008. Recently, the archive videotapes were digitalized and each meteor record was stored in the form of an AVI video sequence. When checking this process, some pairs were recognized, which initiated the idea to investigate whether the pairs are real events or random coincidences.
The S-VHS cameras connected with Mullard XX1332 image intensifiers and 50 mm lenses were used for the observations during the era of the analogue recording. As usual, the cameras were deployed at the Ondřejov (14° 46′ 48.5″ E, 49° 54′ 36.1″ N, 524 m) and Kunžak (15° 12′ 1.1″ E, 49° 6′ 27.3″ N, 650 m) stations. The distance between them is 92.5 km, the azimuth of the southern station is 340° (Koten et al. 2004). The data was stored on S-VHS videotapes, which were searched using the automatic meteor detection software MetRec (Molau 1999). Meteor records were digitalized with a resolution of 25 images per second and 768 × 576 pixels.
The shower membership was determined using MetRec. For the whole night the time gap between consecutive Geminid meteors was computed. When this gap was shorter than 2 s, both meteors were listed as candidates for a pair. These cases were measured manually using the MAIAMetPho software (Koten et al. 2016) and their atmospheric trajectories and heliocentric orbits calculated using the method of Borovicka (1990). In some cases, one or both members of the possible pair were recorded only at one station. For the single-station meteors, their atmospheric trajectories were computed under the assumption that the velocity was the same as the Geminid shower velocity. The meteor radiant was compared with Geminid nominal radiant. If the distance between them was smaller than 5°, the meteor was considered a Geminid meteor, and thus a member of a pair candidate. Although the precision of the atmospheric trajectory determination in such cases is lower in comparison with the double-station meteors, in this kind of study it is not so important. If the meteor had a greater distance, it was not considered a Geminid and the pair was dismissed from the list. The average radiant and velocity (αG = 113°, δG = 33.3°, vG = 34.3 km s−1) based on the values posted for the Geminids on the IAU Meteor Data Center web page2 were used as nominal radiant and velocity for the single-station meteors.
2.1 Recorded data
According to the International Meteor Organization (IMO)3 Visual Meteor Database (VMDB), the maximum activity of the 2006 Geminid meteor shower occurred in the morning hours of December 14. The peak was measured to occur at around 8:38 UT with a zenith hourly rate (ZHR) of ~130 meteors. Visual inspection of the video records showed a higher number of potential meteor pairs during the night before the maximum. Therefore, this night as well as the night following the maximum were searched for the potential pairs. Conditions were cloudy at the beginning of the first night, thus the observation started later. In the morning hours of December 14 the conditions were also not ideal. Nevertheless, during the 8 h of observations a total of 720 single- and double-station meteors were recorded, of which 524 were Geminid meteors: 251 were recorded at both stations and 273 at one of them. During the night following visual maximum the observational conditions were better, but the number of Geminid meteors had already started to decline. Although the observational period was 50% longer, the total number of 730 observed meteors was similar to the previous night and the number of Geminids decreased to 320.
2.2 Geminid activity
For the statistical analyses of the existence of the meteor pairs, it is necessary to know the shower activity. Ryabova & Rendtel (2018) showed that the activity of the Geminid meteor shower has been increasing for the last 30 yr. According to their Fig. 3, the visual ZHR was between 130 and 140 in 2006.
We did not use those values because they are based on visual observations. The activity reported by visual observers is not directly comparable with the video rates. The two methods offer different sensitivity values and fields of view (FOVs), which can cause the absolute numbers of the meteors to be different. For our observations with limited FOV (⊘ = 44°) we calculated the corrected hourly rate cHR, which is the hourly rate corrected on the zenith distance of the radiant. It is called corrected to distinguish it from the ZHR, although they are both computed in the same way. Details can be found in Koten et al. (2020).
The activity profile recorded by the video cameras is shown in Fig. 1. The rates reached a maximum value of about 120 meteors per hour during the first night. The initial increase was slow as one of the stations started observation later due to the cloudy sky. A small dip after midnight was again caused by an interval of cloudy weather at the second site. The same was true for the morning hours. Excluding the small dip in the middle of the night and averaging the five highest values we got cHR = 115. For comparison, measurements by the IMO Video Meteor Network were added for the first night4. Although the absolute values are different, probably due to the different sensitivities of the cameras, there is good agreement with our profile. Both data sets show the peak around midnight. The IMO profile did not fall to zero in the morning as the network covers a broader range of the geographical longitudes.
The number of observed Geminid meteors per hour is significantly lower for the second night. It seems that the value of cHR is slowly decreasing during the night. We adopt cHR = 40 for this night.
 |
Fig. 1 Activity of the 2006 Geminid meteor shower determined using the video cameras from December 13 to December 15. The dashed violet line represents the peak determined by IMO VMDB, the thin black lines the time (UT). The red line shows the activity profile derived by the IMO Video Meteor Network. |
2.3 Candidates for pairs
Based on the September ϵ Perseid observation (Koten et al. 2017) when all the meteors occurred within 1.5 s, we chose a 2-s separation as an initial threshold for the definition of the meteor pair. During the 8 h of observations on the night of maximum activity we detected 18 such pairs. Just seven of them were separated more than 1 s.
This sample contains only meteors with a complete light curve. A whole luminous trajectory is recorded and the information about the photometric mass is complete. The time gap Δt between twometeors is defined as the difference in the time of the first appearance of each of them. The minimum distance ΔD was measured asthe distance between the two meteoroids. If the first meteor disappeared before the beginning of the second, its trajectory was prolonged, the position at the beginning of the second meteor estimated, and the distance between the meteoroids computed. The typical duration of observed meteors was several tenths of a second, the average time interval between them Δt =0.79 s, and the average minimum distance ΔD = 61.0 km. The list of all possible pairs with a time interval and spatial distance between the two meteors, the photometric mass of the heavier meteoroid, and the mass ratios is given in Table 1. The mass ratio is defined as the photometric mass of the heavier meteoroid to the photometric mass of the lighter one within one pair.
We now look at the meteors 06C13069 and 06C13070 as an example. Both meteors were recorded as double-station cases. Meteor 069 appeared first at 23:03:03.72 UT. A calculation shows that its beginning height was 105.1 km. Five frames later (i.e. Δt =0.2 s) meteor 070 became visible at a height of 101.6 km. As both meteors were seen simultaneously, we were able to directly determine their distance: ΔD = 22.6 km. A composite image shows that 069 was brighter (Fig. 2). Its photometric mass was 2.1 ×10−3 g, whereas for 070 we obtained a value of 5.5 × 10−4 g (mass ratio = 3.75). Projected on the ground, the two trajectories are within a small area of 23.25× 17.7 km, which is about 295 km2. A 3D view of the atmospheric trajectories of this pair is shown as plot A in Fig. 3.
Similar calculations and visualizations were done for all pairs. Moreover, an unusual event was found occurring at 0:30:22 UT.Firstly, a single-station meteor 06C13260A was recorded with a double-station 06C13260B following 0.6 s later. The spatial distance between them was 38.5 km. After only 0.3 s another single-station Geminid meteor 06C13261 was detected at a distance of 91.0 km from the second meteor. The gap between the first and third meteors was0.9 s and the distance 81.4 km. When projected on the ground, all three meteors cover an area of 4000 km2. A 3D view of all three meteors is shown as plot B in Fig. 3.
Potential meteor pairs.
 |
Fig. 2 Composite image of two Geminid meteors 06C13069 (upper) and 06C13070 (lower) showing one of the closest pairs observed in this study. |
3 Results
Even if two meteors are observed simultaneously, it does not automatically mean that they form a physically connected pair. Their concurrent appearance can still be coincidental. This behaviour was analysed using statistical distributions in the past. Later on, it was shown that such an approach can provide an overestimated number of linked pairs. Therefore, we applied both approaches and provide a comparison of the results.
3.1 Poisson distribution
Porubčan (1968) and Porubčan et al. (2002) used several statistical methods to decide whether any pairing or grouping was seen among several meteor showers observed by radar or by television cameras. Here, we apply this method to our video data. We note that the number of meteors in our sample is several times lower than the numbers available to Porubčan (1968). For example, he investigated six different samples of the Geminid shower containing between 800 and 2200 meteors. Another difference is that we concentrate only on very short gaps between meteors (1 and 2 s) as we are interested in very close pairs.
Traditionally, the number of observed meteors with a given time separation is compared with the expected Poisson distribution. The expected number of random appearances N is given by the equation (Porubčan 1968)
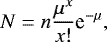 (1)
(1)
where n is the number of intervals, μ is the number of meteors per interval, and x is the number of meteors within the cluster. For example, if the interval is 2 s, the number of intervals per hour is 1800. Having cHR = 115, μ = 0.064. We note that using cHR means that the number N is also corrected to the zenith distance of the radiant.
The activity was not constant for the whole night, as Fig. 1 shows. Therefore, we calculated the expected number of pairs using Eq. (1) for each time the cHR is determined, summed all the cases, and compared the total with the observed numbers. For example, for a 1 s interval between two consecutive meteors, we would expect 14.8 ± 0.2 random pairs during an 8-h observation period. Results for three different intervals are shown in Table 2. We note that the observed numbers were also corrected for the zenith distance of the radiant. The excess of the number of actually observed pairs is seen in each of the selected intervals. If we look at the interval of 1 s, we can see that at least half of the observed pairs may be real, not random cases. On the other hand, the difference between the expected and observed number of pairs during the night following the maximum of activity is significantly smaller for all the intervals.
It should be noted that according to Eq. (1), the probability that three Geminid meteors are observed within 1 s is only 0.02 cases per hour (i.e. 0.16 cases per whole observing period).
3.2 Monte Carlo simulation
Although the results of this statistical test are promising, we are aware of the Sampson (2007) warning that this method underestimates the number of random pairings and groupings. Therefore, we conducted additional tests.
The observed meteor pairs may be a result of chance. An alternative hypothesis is that some of them are physically related (i.e. they are produced by the recent disruption of a parent meteoroid). To assess these hypotheses a Monte Carlo simulation was used. As a level of significance we assumed the commonly used value of 5%, and 100 000 artificial random Geminid meteor showers that follow the activity profile of the observed 2006 Geminid shower were generated inthe following way.
We divided the observation time between t1 = Dec. 13, 21:18:53 UT and t2 = Dec. 14, 5:45:02 UT into 16 intervals (1898 s each) and computed the number of meteors inside these intervals 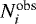 with i = 1, …, 16. Next, a random number N1 ∈⟨t1, t2⟩ with uniform distribution was generated and index j of corresponding time interval was determined. Then another random number N2 with uniform distribution was generated inside interval
with i = 1, …, 16. Next, a random number N1 ∈⟨t1, t2⟩ with uniform distribution was generated and index j of corresponding time interval was determined. Then another random number N2 with uniform distribution was generated inside interval 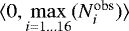 . If
. If 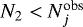 , then N1 is accepted as the time of the artificial meteor, otherwise it is rejected. This was repeated until we obtained a total number of 524 artificial meteor times. Finally, we counted the occurrence of pairs in this set of 100 000 artificial random Geminid meteor showers and derived corresponding probabilities.
, then N1 is accepted as the time of the artificial meteor, otherwise it is rejected. This was repeated until we obtained a total number of 524 artificial meteor times. Finally, we counted the occurrence of pairs in this set of 100 000 artificial random Geminid meteor showers and derived corresponding probabilities.
We found that 81 595 out of 100 000 artificial random Geminid meteor showers contain at least one pair with Δt ≤0.14 s. In other words, there is ~ 82% probability that such a pair is a result of chance. For a pair with Δt ≤ 0.2 s the corresponding probability is ~91%. With the increasing value of Δt, the probability that the pair is a result of chance increases. In the case of a specific observed pair it is therefore not possible to distinguish whether it was formed by fragmentation or only by chance.
The presence of physically related pairs would result in excess over the number of expected pairs for random distribution. We also tested this hypothesis. Figure 4 shows a slight excess of observed pairs above expected counts according to the Monte Carlo simulation. However, all the points are still inside the 95% interval of coincidence. To be statistically significant they should lie outside the blue area. Therefore, again, we cannot rule out that all these pairs are only the result of chance.
Let us focus on the triplet that was observed within 0.9 s. The Monte Carlo simulation shows that at least one triplet with Δt ≤ 0.9 s occurs in 11% of cases of artificial random Geminid meteor showers. This probability is lower than those of observed meteor pairs, but it is still higher than the assumed level of significance. Therefore, we cannot rule out that the triplet is only a result of chance.
 |
Fig. 3 Three-dimensional map of the atmospheric trajectories (red dots) of a close pair 069–070 (plot A, meteor 069 on the right and 070 on the left) and a triplet 06C13260A, 06C13260B, and 06C13261 (plot B, meteor 260A on the right, 260B in the middle, 261 on the left) and their horizontal and vertical projections (blue lines). The x-axis represents the geographic longitude, the y-axis the geographic latitude, and the z-axis the height. Each red dot shows the position of the meteor at a given video frame. The time between one dot and the next is 0.04 s. |
Expected and observed numbers of pairs.
3.3 Geometry of pairs
Despite the negative results of the Monte Carlo simulations, let us suppose that at least some of the observed pairs are real. If the fragmentation occurs in the interplanetary space days before the encounter with the Earth, we may expect that lighter particles are affected more by the solar radiation pressure and are pushed in the direction opposite to the Sun. If the ejection velocity of the lighter particle in the Sun direction is non-negligible, there should be less time to push this particle far away from the Sun than for the heavier one. We note that the Poyinting–Robertson effect is negligible in this case.
The acceleration depends on the particle’s diameter d and its density ρ, and can be estimated as (Finson & Probstein 1968)
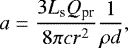 (2)
(2)
where Ls is the solar luminosity, Qpr = 1 is the radiation pressure efficiency factor, c is the speed of light, and r is the heliocentric distance.
The position of each meteor point is given by its geographic longitude, latitude, and height above the ground. A rectangular coordinate system (X, Y, Z) was defined for each pair with an origin at the first point of the heavier particle. The azimuth and elevation of the Sun from this point were calculated. The original coordinates were transformed into the new system with a direction vector to the Sun to be the same as the X-axis. The position of the lighter particle at the same time was calculated according to its movement. An angle θ between the direction to the Sun and the direction to the lighter particle is visible in this representation. Figure 5 shows the case of the pair 360A, 360B.
The value θ = 100.7° was found for the pair 360A, 360B. It means that the heavier particle is closer to the Sun than the lighter one. The mass ratio is 62.0. The absolute distance between particles is ΔD ~ 53 km and the radial component is DR ~ 10 km. Using Eq. (2) and assuming a density of Geminids to be 2600 kg m−3 (Borovička et al. 2010), the acceleration of the ith particle can be computed from 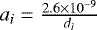 , where di is the particle diameter. The radial distance of 10 km is reached within 38.5 h in the case of zero ejection velocity. Because the velocity of Geminid meteoroids is about 35 km s−1, the fragmentation can occur at a distance of 4.9 million km from the Earth. As the zero ejection velocity is improbable, we set two extreme limits on the determination of the ejection time. Let us suppose the ejection velocity to be ± 1 m s−1. That this assumption is realistic is shown for example in the paper of Hapgood & Rothwell (1981), which supposed velocities between 0.6 and 6.6 m s−1. A negative value means ejection towards the Sun, a positive value in the opposite direction. Depending on the direction, the observed radial distance is reached in the time range between 3 h and 22 days.
, where di is the particle diameter. The radial distance of 10 km is reached within 38.5 h in the case of zero ejection velocity. Because the velocity of Geminid meteoroids is about 35 km s−1, the fragmentation can occur at a distance of 4.9 million km from the Earth. As the zero ejection velocity is improbable, we set two extreme limits on the determination of the ejection time. Let us suppose the ejection velocity to be ± 1 m s−1. That this assumption is realistic is shown for example in the paper of Hapgood & Rothwell (1981), which supposed velocities between 0.6 and 6.6 m s−1. A negative value means ejection towards the Sun, a positive value in the opposite direction. Depending on the direction, the observed radial distance is reached in the time range between 3 h and 22 days.
We determined the mutual positions of potential pairs and calculated θ angle for all the candidates. The results are summarized in Fig. 6. There are two segments in this plot. The pairs having the heavier member closer to the Sun than the lighter one can be found in the area represented by the blue rectangle. Only 6 out of 21 candidates (the triplet is counted as three pairs in this analysis) are plotted within this segment. Their geometrical properties, time from possible fragmentation, and distances are listed in Table 3. The majority of the candidates have θ < 90°, although few of them are very close to the threshold. More than half of the cases represent a situation where the lower mass particle is closer to the Sun.
To understand what this result means we extended the Monte Carlo test explained in Sect. 3.2. The times of the meteors were generated in the same way. For each meteor a mass was generated randomly from the range of the observed masses. Moreover, the position of each meteor was also randomly determined inside the cube of a size of 80 km. The size of the cube was determined by the diameter of the field of view of the video camera at the distance of the observed meteors. Then the pairs with a time gap shorter than 2 s were identified. For such a pair, the relative position between the two components was determined. Finally, the Sun-heavier particle-lighter particle angle was determined. This simulation was run 100 000 times.
The results of the simulation are shown in Fig. 7. For each run we found 23.6 pairs within 2 s. The observed number of 21 pairs fitted well inside the 2σ interval (σ = 4.7). Again, we cannot exclude that all the observed pairs were actually random appearances of physically unconnected meteors. The simulation shows that in 11.8 of such cases (50%) the lighter particle is at a greaterdistance than the heavier one. The observed number of such cases is again inside the 2σ interval (σ = 3.4). Therefore, the arrangement of the particles inside the pair tells us nothing about their origin except the unknown ejection velocity during hypothetical fragmentation event; we cannot rule out their coincidental origin.
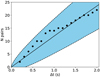 |
Fig. 4 Total number of pairs with delay smaller than Δt. The solid line corresponds to the mean value from the Monte Carlo simulation and the blue area with dashed margins defines the 95% interval of coincidence. The black dots represent the observed count of pairs. The hypothesis that the excess of observed pair counts is a result of chance cannot be ruled out. |
 |
Fig. 5 Positions of the meteors (red dots) belonging to the pair candidate 360A (lower right), 360B (upper left) in a rectangular coordinated system with an origin connected with the first position of the heavier particle 360B (green circle). Also shown is the theoretical position of the particle 360A at the same time extrapolated according to its motion (smaller blue circle). The blue vector illustrates the relative position of particle 360A against 360B. The x-axis is oriented in the direction of the Sun, as the green vector shows. The vectors represent an angle between the lighter particle, the heavier particle, and the Sun. |
 |
Fig. 6 Mass ratio and angle between the fragments and the Sun. The light blue rectangle represents an area where the fragments separated from the same original body would be expected. |
4 Conclusions
The visual inspection of the 2006 Geminid archive data during its digitalization shows a higher than usual number of meteor pairs appearing within less than 2 s of each other. It looked like a promising sample of interesting data for the study of themeteor pairing. The traditional way of the analyses using Poisson statistics supported this suspicion. It showed that there is a significant excess of the pairs in comparison with the randomly expected number of cases.
The atmospheric trajectory computation shows that the potential pairs were very close not only temporally, but also spatially. The closest pairs were separated only by a few tens of kilometers. The distances were comparable or even smaller than separations among the fragments of the well-documented September epsilon Perseid meteor cluster, which was proven to be a real case of meteor grouping (Koten et al. 2017).
However, the Monte Carlo simulations made on the sample of 100 000 artificial Geminid showers with similar activity profiles showed that even the most promising cases may be still result from the random appearance of two meteoroids without any physical connection. A comparison of the observed and expected number of pairs showed a small excess of the observed cases, but it was still within a 95% interval of coincidence. Therefore, we cannot rule out that all the cases are random appearances. The results of this study confirmed the suspicion of Sampson (2007) that the Poisson statistics using fixed intervals cannot be used for this kind of analyses as it underestimates the numbers of randomly observed pairs.
If the fragmentation of the meteoroid in the interplanetary space occurred before the encounter with Earth we would expect the smaller meteoroid to be pushed more in the anti-Sun direction than the bigger one. This behaviour was observed, for example, in the case of the September epsilon Perseid cluster (Koten et al. 2017). An extension of the Monte Carlo simulation shows that the observed data are in agreement with the randomly generated population of Geminid meteors according to the meteor shower activity. Therefore, it is not possible to prove whether the observed pair is a real pair or if it represents a coincidental appearance of two independent meteors.
It was mentioned above that Porubčan et al. (2002) identified non-random groups of the meteoroids within the core of young streams. These streams were 1969 and 1999 Leonids, which were caused by one and three revolutions old filaments (McNaught & Asher 1999). As the Geminid meteor stream is a few thousand years old, it is not young from this point of view. It may be a case similar to that of the Lyrid shower in the Porubčan paper for which no evidence of groupings was found. Moreover, as Plavec (1953) already noted, the dispersion of the pairs is relatively fast. The only exceptions are pairs with components of equal masses. He compared several meteor showers and found that the relative rate of disintegration is about eight times higher for Lyrids or Geminids in comparison with Leonids. Finally, the strength of Geminid meteoroids may be another reason for the low abundance of the pairs within the stream. Due to high strength, there could not be a sufficient number of fragmentation events in the vicinity of the Earth to create a detectable number of pairs. As a lesson from this work, there are a few recommendations for future observation campaigns that can increase the probability of successful detections of the pairs and groups. The wider FOV cameras can be useful. The wider field allows the detection of a higher number of meteors and among them the pairs may be present. Even more spatially distant meteors can be still considered as pairs and they can be missed using very narrow FOV cameras. On the other hand, using very wide FOV and even all-sky cameras can usually eliminate many fainter meteors. In addition, the selection of the target meteor shower can improve the chances of detection for pairs and groups. Using a relative rate of disintegration defined by Plavec (1953) shows that Perseid, Taurids, Leonids, or Draconids are better candidates than Geminids.
In summary, we conclude that we did not find firm evidence for the existence of the pairs and groups within the Geminid meteor shower, at least for its 2006 appearance.
Properties of candidates with θ > 90°.
 |
Fig. 7 Random numbers of all pairs and pairs with θ > 90° among the 524 observed meteors. |
Acknowledgements
This work was supported by the Grant Agency of the Czech Republic grants 20-10907S and the institutional project RVO:67985815. We thank to an anonymous referee, who helped us to improve the paper.
References
- Borovicka, J. 1990, Bull. Astron. Inst. Czech., 41, 391 [NASA ADS] [Google Scholar]
- Borovička, J., Koten, P., Spurný, P., et al. 2010, in Icy Bodies of the Solar System, 263, ed. J. A. Fernandez, D. Lazzaro, D. Prialnik, & R. Schulz, 218 [Google Scholar]
- Finson, M. J., & Probstein, R. F. 1968, ApJ, 154, 327 [Google Scholar]
- Gural, P. S., & Jenniskens, P. 2000, Earth Moon Planets, 82, 221 [Google Scholar]
- Hapgood, M. A., & Rothwell, P. 1981, Nature, 290, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, I. 1999, in Meteroids 1998, eds. W. J. Baggaley, & V. Porubcan, 177 [Google Scholar]
- Jenniskens, P. 2006, Meteor Showers and their Parent Comets (Cambridge, UK: Cambridge University Press) [CrossRef] [Google Scholar]
- Kinoshita, M., Maruyama, T., & Sagayama, T. 1999, Geophys. Res. Lett., 26, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Koten, P., Borovička, J., Spurný, P., Betlem, H., & Evans, S. 2004, A&A, 428, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koten, P., Štork, R., Páta, P., Fliegel, K., & Vítek, S. 2016, in International Meteor Conference Egmond, the Netherlands, 2–5 June 2016, eds. A. Roggemans, & P. Roggemans, 133 [Google Scholar]
- Koten, P., Čapek, D., Spurný, P., et al. 2017, A&A, 600, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koten, P., Borovička, J., Vojáček, V., et al. 2020, Planet. Space Sci., 184, 104871 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J., & Jewitt, D. 2013, AJ, 145, 154 [NASA ADS] [CrossRef] [Google Scholar]
- McNaught, R. H., & Asher, D. J. 1999, WGN, J. Int. Meteor Organ., 27, 85 [Google Scholar]
- Molau, S. 1999, in Proceedings of the International Meteor Conference, 17th IMC, Stara Lesna, Slovakia, 1998, 9 [Google Scholar]
- Ofek, E. 1999, WGN, J. Int. Meteor Organ., 27, 172 [NASA ADS] [Google Scholar]
- Piers, P. A., & Hawkes, R. L. 1993, WGN, J. Int. Meteor Organ., 21, 168 [NASA ADS] [Google Scholar]
- Plavec, M. 1950, Nature, 165, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Plavec, M. 1953, Bull. Astron. Inst. Czech., 4, 60 [NASA ADS] [Google Scholar]
- Porubčan, V. 1968, Bull. Astron. Inst. Czech., 19, 316 [Google Scholar]
- Porubčan, V., Tóth, J., & Yano, H. 2002, Contrib. Astron. Observ. Skalnate Pleso, 32, 132 [Google Scholar]
- Ryabova, G. O. 2016, MNRAS, 456, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabova, G. O. 2018, MNRAS, 479, 1017 [NASA ADS] [Google Scholar]
- Ryabova, G. O., & Rendtel, J. 2018, MNRAS, 475, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Sampson, R. D. 2007, JRASC, 101, 57 [NASA ADS] [Google Scholar]
- Spurný, P. 1993, in Meteoroids and their Parent Bodies, eds. J. Stohl, & I. P. Williams, 193 [Google Scholar]
- Watanabe, J.-I., Sekiguchi, T., Shikura, M., Naito, S., & Abe, S. 2002, PASJ, 54, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, J.-I., Tabe, I., Hasegawa, H., et al. 2003, PASJ, 55, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Whipple, F. L. 1983, IAU Circ., 3881, 1 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Activity of the 2006 Geminid meteor shower determined using the video cameras from December 13 to December 15. The dashed violet line represents the peak determined by IMO VMDB, the thin black lines the time (UT). The red line shows the activity profile derived by the IMO Video Meteor Network. |
| In the text | |
 |
Fig. 2 Composite image of two Geminid meteors 06C13069 (upper) and 06C13070 (lower) showing one of the closest pairs observed in this study. |
| In the text | |
 |
Fig. 3 Three-dimensional map of the atmospheric trajectories (red dots) of a close pair 069–070 (plot A, meteor 069 on the right and 070 on the left) and a triplet 06C13260A, 06C13260B, and 06C13261 (plot B, meteor 260A on the right, 260B in the middle, 261 on the left) and their horizontal and vertical projections (blue lines). The x-axis represents the geographic longitude, the y-axis the geographic latitude, and the z-axis the height. Each red dot shows the position of the meteor at a given video frame. The time between one dot and the next is 0.04 s. |
| In the text | |
 |
Fig. 4 Total number of pairs with delay smaller than Δt. The solid line corresponds to the mean value from the Monte Carlo simulation and the blue area with dashed margins defines the 95% interval of coincidence. The black dots represent the observed count of pairs. The hypothesis that the excess of observed pair counts is a result of chance cannot be ruled out. |
| In the text | |
 |
Fig. 5 Positions of the meteors (red dots) belonging to the pair candidate 360A (lower right), 360B (upper left) in a rectangular coordinated system with an origin connected with the first position of the heavier particle 360B (green circle). Also shown is the theoretical position of the particle 360A at the same time extrapolated according to its motion (smaller blue circle). The blue vector illustrates the relative position of particle 360A against 360B. The x-axis is oriented in the direction of the Sun, as the green vector shows. The vectors represent an angle between the lighter particle, the heavier particle, and the Sun. |
| In the text | |
 |
Fig. 6 Mass ratio and angle between the fragments and the Sun. The light blue rectangle represents an area where the fragments separated from the same original body would be expected. |
| In the text | |
 |
Fig. 7 Random numbers of all pairs and pairs with θ > 90° among the 524 observed meteors. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


