| Issue |
A&A
Volume 645, January 2021
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202038590 | |
| Published online | 19 January 2021 | |
Accretion-to-jet energy conversion efficiency in GW170817
1
INAF – Osservatorio Astronomico di Brera, Via E. Bianchi 46, 23807 Merate (LC), Italy
e-mail: omsharan.salafia@gmail.com
2
INFN – Sezione di Milano-Bicocca, Piazza della Scienza 3, 20126 Milano (MI), Italy
3
Università degli Studi di Milano-Bicocca, Dip. di Fisica “G. Occhialini”, Piazza della Scienza 3, 20126 Milano, Italy
Received:
5
June
2020
Accepted:
20
October
2020
Gamma-ray bursts (GRBs) are thought to be produced by short-lived, supercritical accretion onto a newborn compact object. Some process is believed to tap energy from the compact object, or the accretion disc, powering the launch of a relativistic jet. For the first time, we can construct independent estimates of the GRB jet energy and of the mass in the accretion disc in its central engine; this is thanks to gravitational wave observations of the GW170817 binary neutron star merger by the Laser Interferometer Gravitational wave Observatory (LIGO) and Virgo interferometers, as well as a global effort to monitor the afterglow of the associated short gamma-ray burst GRB 170817A on a long-term, high-cadence, multi-wavelength basis. In this work, we estimate the accretion-to-jet energy conversion efficiency in GW170817, that is, the ratio of the jet total energy to the accretion disc rest mass energy, and we compare this quantity with theoretical expectations from the Blandford-Znajek and neutrino-antineutrino annihilation (νν̄) jet-launching mechanisms in binary neutron star mergers. Based on previously published multi-wavelength modelling of the GRB 170817A jet afterglow, we construct the posterior probability density distribution of the total energy in the bipolar jets launched by the GW170817 merger remnant. By applying a new numerical-relativity-informed fitting formula for the accretion disc mass, we construct the posterior probability density distribution of the GW170817 remnant disc mass. Combining the two, we estimate the accretion-to-jet energy conversion efficiency in this system, carefully accounting for uncertainties. The accretion-to-jet energy conversion efficiency in GW170817 is η ∼ 10−3, with an uncertainty of slightly less than two orders of magnitude. This low efficiency is in agreement with expectations from the 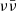 mechanism, which therefore cannot be excluded by this measurement alone. The low efficiency also agrees with that anticipated for the Blandford-Znajek mechanism, provided that the magnetic field in the disc right after the merger is predominantly toroidal (which is expected as a result of the merger dynamics). This is the first estimate of the accretion-to-jet energy conversion efficiency in a GRB that combines independent estimates of the jet energy and accretion disc mass. Future applications of this method to a larger number of systems will reduce the uncertainties in the efficiency and reveal whether or not it is universal. This, in turn, will provide new insights into the jet-launching conditions in neutron star mergers.
mechanism, which therefore cannot be excluded by this measurement alone. The low efficiency also agrees with that anticipated for the Blandford-Znajek mechanism, provided that the magnetic field in the disc right after the merger is predominantly toroidal (which is expected as a result of the merger dynamics). This is the first estimate of the accretion-to-jet energy conversion efficiency in a GRB that combines independent estimates of the jet energy and accretion disc mass. Future applications of this method to a larger number of systems will reduce the uncertainties in the efficiency and reveal whether or not it is universal. This, in turn, will provide new insights into the jet-launching conditions in neutron star mergers.
Key words: relativistic processes / gamma-ray burst: individual: GRB 170817A / stars: neutron / gravitational waves
© ESO 2021
1. Introduction
It has been long established that the outflows that produce gamma-ray bursts (GRBs) must expand at relativistic speeds (e.g. Ruderman et al. 1975; Goodman 1986, 1997; Paczynski 1986; Fenimore et al. 1993; Woods & Loeb 1994, 1995; Frail et al. 1997; Taylor et al. 2004) and be collimated (e.g. Rhoads 1997, 1999; Mészáros et al. 1999; Sari et al. 1999; Ghisellini & Lazzati 1999; Frail et al. 2001), that is, they must be relativistic jets. The widely accepted site for the production of such jets is an accreting stellar-mass compact object (Piran 2004), either a black hole (BH) or a neutron star (Usov 1994; Bucciantini et al. 2008). The first association of a supernova with a long GRB (Galama et al. 1998) strongly supported this link, pointing to the gravitational collapse of a massive star as the progenitor. More recently, the association (Abbott et al. 2017; LIGO Scientific Collaboration et al. 2017) of the gravitational wave event GW170817 (LIGO Scientific Collaboration & Virgo Collaboration 2017a), interpreted as having been produced by the merger of a binary of neutron stars (BNS hereafter, LIGO Scientific Collaboration & Virgo Collaboration 2017a; The LIGO Scientific Collaboration & The Virgo Collaboration 2019) with the short gamma-ray burst (SGRB) GRB 170817A (Goldstein et al. 2017; Savchenko et al. 2017), confirmed the long-held expectation (Bisnovatyi-Kogan et al. 1975; Paczynski 1986; Eichler et al. 1989) that some GRBs are produced in compact binary mergers. The identification of an optical counterpart to GW170817 (Coulter et al. 2017; Valenti et al. 2017), later spectroscopically classified (Pian et al. 2017; Smartt et al. 2017) as a kilonova (Li & Paczyński 1998; Metzger 2017), pinpointed the host galaxy of the event, allowing for a long-term, multi-wavelength monitoring of its location. This uncovered an additional non-thermal counterpart (e.g. Hallinan et al. 2017; Margutti et al. 2017, 2018; Troja et al. 2017; Alexander et al. 2017, 2018; D’Avanzo et al. 2018; Dobie et al. 2018; Lyman et al. 2018; Lamb et al. 2019; Hajela et al. 2019) that was eventually established (Mooley et al. 2018a,b; Ghirlanda et al. 2019, thanks to very-long-baseline interferometry imaging) as being the afterglow (i.e. synchrotron emission from the external shock in the interstellar medium) of an off-axis relativistic jet.
The large amount of lanthanide-rich ejecta inferred from kilonova observations (≳10−2 M⊙, e.g. Shibata et al. 2017; Nicholl et al. 2017; Cowperthwaite et al. 2017; Villar et al. 2017; Perego et al. 2017a) has been interpreted (Margalit & Metzger 2017) as being the result of strong winds from the accretion disc around the merger remnant. Since these winds are expected to unbind a few tens of percent of the accretion disc mass (e.g. Siegel & Metzger 2017), this in turn requires the disc to be rather massive, of the order of Mdisc ∼ 10−1 M⊙ (Radice & Dai 2019).
The kinetic energy in the GRB 170817A jet has been constrained by several groups, based on multi-wavelength modelling of the non-thermal afterglow and on the VLBI centroid motion (see Sect. 3 and Fig. 2). All estimates essentially agree within the uncertainties, clustering slightly below EK, jet ∼ 1050 erg.
We therefore have, for the first time, two independent estimates of the energy in a GRB jet and of the mass of the accretion disc around the compact object that produced it, which enables us to estimate the accretion-to-jet energy conversion efficiency. By simply using the gross estimates above, one finds that this efficiency is of the order of η ∼ EK, jet/Mdiscc2 ∼ 10−3. While this number may appear surprisingly low, this level of efficiency was anticipated in previous studies that attempted to connect the energy in SGRB jets with the underlying disc masses (e.g. Giacomazzo et al. 2013; Ascenzi et al. 2019; Barbieri et al. 2019).
In this work, we assume the remnant of GW170817 to be a BH surrounded by an accretion disc1; the actual nature of the remnant could not be identified based on GW observations alone (LIGO Scientific Collaboration & Virgo Collaboration 2017b, 2019), but the collapse to a BH after a short hyper-massive neutron star (HMNS) phase seems the most likely outcome for this system (see for example Gill et al. 2019 for a thorough discussion). We carefully constructed a posterior probability distribution for this efficiency in order to account for the (large) uncertainties in both the disc mass and the jet energy, and we compared the result with expectations based on the two main candidate jet-launching processes, namely the Blandford & Znajek (1977) and the neutrino-antineutrino annihilation mechanisms (Eichler et al. 1989; Meszaros & Rees 1992). We show that such a low efficiency is expected in SGRBs for both mechanisms and (unfortunately) cannot be used to distinguish between the two.
2. Disc mass in GW170817
Several mechanisms are thought to cause dynamical mass ejection during the merger of two neutron stars (Shibata & Hotokezaka 2019; Radice et al. 2018; Bauswein et al. 2013; Hotokezaka et al. 2013; Rosswog et al. 1999; Davies et al. 1994), such as tidal interactions between the two stars, shocks that form as a consequence of the collision, and violent oscillations of the highly oblate remnant shortly after the two stars have merged. Numerical simulations show that such matter is typically ejected with a broad range of (mostly non-relativistic) velocities and internal energies, but a large fraction generally remain gravitationally bound and form an accretion disc around the merger remnant. The amount of disc mass ultimately depends on the intrinsic properties of the binary prior to the merger, namely the equation of state (EoS) of neutron star matter, the component masses, spins, orbit eccentricity, and possibly the magnetic fields. The pre-merger magnetic field hardly affects the dynamics of the inspiral2. On the other hand, the magnetic field intensity in the post-merger can influence the lifetime of a meta-stable HMNS remnant (Giacomazzo et al. 2011) and the intensity of its winds (e.g. Ciolfi 2020b; Ciolfi & Kalinani 2020; Mösta et al. 2020), which can in turn affect the disc mass before the HMNS collapses to a BH. Nevertheless, the magnetic field amplification by Kelvin-Helmholtz instabilities during the merger (Kiuchi et al. 2014, 2018) likely erases any memory of the initial magnetic field; therefore, we neglect here any dependence on the pre-merger magnetic field for the sake of simplicity as it is, in any case, most likely well below our uncertainties. While their effect on the dynamics and mass ejection could be relevant (East et al. 2019), spins are usually expected to be low at merger, based on observations of Galactic double neutron star systems (Lorimer 2008) and their decay due to spin-down prior to merger (Stovall et al. 2018); we will therefore assume spins to be negligible in this work. The orbit eccentricity prior to the merger is expected to be low in most realistic cases (Kowalska et al. 2011) unless the merger happens soon after a dynamical interaction in a dense stellar environment, though the associated rates are expected to be low (e.g. Ye et al. 2020) due to circularisation caused by GW emission. We are therefore left with the neutron star masses and the EoS as the only parameters upon which the disc mass can depend.
2.1. Disc mass posterior probability
Based on a large suite of general relativistic hydrodynamical simulations, Radice et al. (2018, R18 hereafter) devised a fitting formula for the disc mass that depends solely on the binary effective dimensionless tidal deformability  , which is a combination of the masses and tidal deformabilities (which are in turn determined by the EoS) of the binary components. This quantity is of particular interest because it appears in the leading post-Newtonian term that describes tidal effects on the GW waveform (Flanagan & Hinderer 2008) and is therefore the best constrained combination of EoS-related parameters from GW analysis. The fitting formula is accurate to ∼50% when compared to most of the simulations in the suite of R18, but these are based on a limited number of different EoSs, and, most importantly, they do not comprise significantly unequal-mass binaries3. Kiuchi et al. (2019) later showed that, at fixed
, which is a combination of the masses and tidal deformabilities (which are in turn determined by the EoS) of the binary components. This quantity is of particular interest because it appears in the leading post-Newtonian term that describes tidal effects on the GW waveform (Flanagan & Hinderer 2008) and is therefore the best constrained combination of EoS-related parameters from GW analysis. The fitting formula is accurate to ∼50% when compared to most of the simulations in the suite of R18, but these are based on a limited number of different EoSs, and, most importantly, they do not comprise significantly unequal-mass binaries3. Kiuchi et al. (2019) later showed that, at fixed  , unequal-mass systems can yield a larger disc mass due to the increased tidal deformation of the lighter star. Barbieri et al. (2020) presented a new, simple fitting formula based on a toy model of the mass ejection in a neutron star binary merger. The formula depends on
, unequal-mass systems can yield a larger disc mass due to the increased tidal deformation of the lighter star. Barbieri et al. (2020) presented a new, simple fitting formula based on a toy model of the mass ejection in a neutron star binary merger. The formula depends on 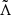 and on the masses of the primary (M1) and secondary (M2) components of the binary. After fitting the free parameters to the results of numerical simulations collected from R18, Kiuchi et al. (2019), Vincent et al. (2020), and Bernuzzi et al. (2020), they find that such a formula predicts the correct disc mass for both equal- and unequal-mass systems, with an error that is comparable to that of the original R18 formula for equal-mass binaries. We applied this formula4 to the posterior samples from the GW parameter estimation of GW170817 (The LIGO Scientific Collaboration & The Virgo Collaboration 2019) for low-spin priors (following our assumption of negligible spins). Following Radice & Dai (2019), we accounted for the uncertainty in the disc mass fitting formula as follows: For each GW posterior sample, we computed the disc mass using the fitting formula from Barbieri et al. (2020), and then we extracted 100 samples from a log-normal distribution centred at that value, with a dispersion σ = 0.5 dex. The resulting disc mass posterior distributions are shown in Fig. 1. The most probable disc mass value is around Mdisc ∼ 0.1 M⊙, with a tail of smaller probability that extends down to ∼10−3 M⊙. Compared to the predictions obtained using the formula from Radice et al. (2018; dashed blue line), the bimodality in the predicted disc masses is essentially suppressed, in agreement with the argument by Kiuchi et al. (2019). This indicates that the most compact configurations compatible with GW170817 – those with
and on the masses of the primary (M1) and secondary (M2) components of the binary. After fitting the free parameters to the results of numerical simulations collected from R18, Kiuchi et al. (2019), Vincent et al. (2020), and Bernuzzi et al. (2020), they find that such a formula predicts the correct disc mass for both equal- and unequal-mass systems, with an error that is comparable to that of the original R18 formula for equal-mass binaries. We applied this formula4 to the posterior samples from the GW parameter estimation of GW170817 (The LIGO Scientific Collaboration & The Virgo Collaboration 2019) for low-spin priors (following our assumption of negligible spins). Following Radice & Dai (2019), we accounted for the uncertainty in the disc mass fitting formula as follows: For each GW posterior sample, we computed the disc mass using the fitting formula from Barbieri et al. (2020), and then we extracted 100 samples from a log-normal distribution centred at that value, with a dispersion σ = 0.5 dex. The resulting disc mass posterior distributions are shown in Fig. 1. The most probable disc mass value is around Mdisc ∼ 0.1 M⊙, with a tail of smaller probability that extends down to ∼10−3 M⊙. Compared to the predictions obtained using the formula from Radice et al. (2018; dashed blue line), the bimodality in the predicted disc masses is essentially suppressed, in agreement with the argument by Kiuchi et al. (2019). This indicates that the most compact configurations compatible with GW170817 – those with 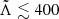 , which produce the low-disc-mass peak in the Radice et al. 2018 distribution – also have consistently lower mass ratios q = M2/M1 on average.
, which produce the low-disc-mass peak in the Radice et al. 2018 distribution – also have consistently lower mass ratios q = M2/M1 on average.
 |
Fig. 1. GW170817 accretion disc mass posterior distributions. The solid red line shows the posterior probability distribution of the logarithm of the accretion disc mass (in solar masses) for the low-spin LVC priors. The dashed blue line shows the corresponding result that would have been obtained using the disc mass fitting formula from Radice et al. (2018). |
2.2. Accreted disc mass
Long-term numerical simulations of merger remnant accretion discs (e.g. Fujibayashi et al. 2020; Christie et al. 2019, Fernández et al. 2019; Siegel & Metzger 2018, 2017; Just et al. 2015; Fernández & Metzger 2013) indicate that a significant fraction (fw = 0.1 to 0.5) of the disc mass can be lost in the form of winds in these systems, therefore lowering the actual accretion rate and the final accreted mass. The majority of such mass loss takes place as the disc spreads viscously and transitions to the advection-dominated accretion flow (ADAF) phase, during which it inflates due to viscous heating and convective motions (Metzger et al. 2009; Fernández & Metzger 2013; Just et al. 2015). Observations of AT2017gfo, the kilonova associated with GW170817, and the subsequent modelling indeed seem to indicate that a significant fraction of the kilonova ejecta mass did originate in disc winds (Margalit & Metzger 2017, see the introduction for additional references). We therefore defined Ma = (1 − fw)Mdisc as the accreted mass, and we adopted the fiducial value fw = 0.3. The exact value of this parameter does not significantly affect our conclusions.
3. Jet energy in GRB 170817A
Inferring the true energy of a GRB jet is not straightforward in general, even in cases where both the prompt and afterglow emissions have been extensively observed. The understanding of the prompt emission phase is hampered by theoretical uncertainties on several aspects, regarding both the dominant form of energy in the jet (either magnetic or bulk kinetic) and the way this energy is transformed into the radiation we observe. Moreover, during the prompt emission, the emitting material is thought to be in highly relativistic motion, which essentially renders it impossible to infer the jet opening angle – and therefore derive the jet true energy – from observations of this emission phase alone.
Observations of the afterglow provide, in principle, a better tool for inferring the true jet energy. As the jet material collides with the interstellar medium (ISM), it drives a shock that heats up particles, which can then radiate (Paczynski & Rhoads 1993; Mészáros & Rees 1997). Moreover, as the shock sweeps the ISM, the shocked fluid slows down and relativistic beaming is reduced, thus allowing the observer to infer the actual jet opening angle (Rhoads 1997).
In the case of GRB 170817A, the jet kinetic energy has been estimated by several groups based on the multi-wavelength modelling of the afterglow emission. Despite the modelling uncertainties, the various estimates (see Fig. 2, where we show estimates from Ghirlanda et al. 2019; Lamb et al. 2019; Lyman et al. 2018; Troja et al. 2019; Lazzati et al. 2018; Margutti et al. 2018; D’Avanzo et al. 2018; Granot et al. 2018) essentially agree within their uncertainties, clustering around EK, jet ∼ 1050 erg (see also the recent pre-print by Lamb et al. 2020, who find a similar energy under significantly different assumptions). This is the total kinetic energy contained in the jet material that caused the relativistic shock that produced the observed (X-ray, optical, and radio) afterglow of GRB 170817A. This is not, in principle, the same as the jet energy actually produced by the merger remnant since a fraction, fbk, is spent to break out of the kilonova ejecta and another fraction, fγ, is lost in the prompt emission. Duffell et al. (2018) have shown, though, that the jet energy spent in breaking out of the ejecta is roughly 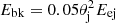 , where θj is the opening angle of the jet at launch and Eej is the total kinetic energy in the ejecta. Even assuming ejecta as massive as Mej = 0.1 M⊙ with an average velocity vej ∼ 0.1c and a relatively large jet opening angle at launch θj = 0.3 rad (the jet is then collimated by the ejecta prior to breakout), the energy Ebk barely reaches 5 × 1048 erg and can therefore be safely neglected (i.e. we set fbk = 0). As for fγ, this value can generally be estimated by comparing the jet kinetic energy inferred from early X-ray afterglow observations to the energy radiated in the prompt emission5 (e.g. Zhang et al. 2007). This leads to a variety of values for the efficiency, which in some cases are as high as 90%. Recently, though, Beniamini et al. (2015, 2016) found that these values were typically overestimated as Compton cooling was overlooked in the modelling of these afterglows in part due to a bias in the adopted post-shock magnetic field equipartition parameter ϵB. Removing this bias, they showed that the typical prompt emission efficiency in GRBs is fγ ∼ 0.15, which is the value we adopt here. Therefore, our estimate of the actual jet energy produced by the merger remnant is Ej = 2 × EK, jet/(1 − fγ)≈2.36EK, jet (here the factor of 2 is inserted to account for the counterjet, which is assumed to be identical to the jet that produced the observed emission), but we note that our uncertainties make us essentially insensitive to the precise value of fγ as long as it is significantly less than unity.
, where θj is the opening angle of the jet at launch and Eej is the total kinetic energy in the ejecta. Even assuming ejecta as massive as Mej = 0.1 M⊙ with an average velocity vej ∼ 0.1c and a relatively large jet opening angle at launch θj = 0.3 rad (the jet is then collimated by the ejecta prior to breakout), the energy Ebk barely reaches 5 × 1048 erg and can therefore be safely neglected (i.e. we set fbk = 0). As for fγ, this value can generally be estimated by comparing the jet kinetic energy inferred from early X-ray afterglow observations to the energy radiated in the prompt emission5 (e.g. Zhang et al. 2007). This leads to a variety of values for the efficiency, which in some cases are as high as 90%. Recently, though, Beniamini et al. (2015, 2016) found that these values were typically overestimated as Compton cooling was overlooked in the modelling of these afterglows in part due to a bias in the adopted post-shock magnetic field equipartition parameter ϵB. Removing this bias, they showed that the typical prompt emission efficiency in GRBs is fγ ∼ 0.15, which is the value we adopt here. Therefore, our estimate of the actual jet energy produced by the merger remnant is Ej = 2 × EK, jet/(1 − fγ)≈2.36EK, jet (here the factor of 2 is inserted to account for the counterjet, which is assumed to be identical to the jet that produced the observed emission), but we note that our uncertainties make us essentially insensitive to the precise value of fγ as long as it is significantly less than unity.
 |
Fig. 2. Kinetic energy in the GRB 1790817A jet during the afterglow phase. The solid red line shows the posterior distribution constructed by fitting a structured jet afterglow model to the multi-wavelength afterglow and VLBI centroid motion by Ghirlanda et al. (2019). Black dots with error bars represent the estimates presented in several other papers, all based on afterglow fitting. All estimates essentially agree within the uncertainties. |
For our fiducial estimate of EK, jet, we used the posterior from Ghirlanda et al. (2019), which accounts for the uncertainty on all parameters and is based on multi-wavelength afterglow fitting, including the very-long-baseline interferometry (VLBI) centroid motion. The posterior is shown by the red line in Fig. 2, which compares it to several estimates from other authors.
4. Accretion-to-jet energy conversion efficiency in GW170817
Combining the posterior distributions of the accreted disc mass Ma = (1 − fw)Mdisc (Sect. 2) and the posterior distributions of the total jet energy Ej = 2 × EK, jet/(1 − fγ) (Sect. 3), we can derive the posterior distribution of the accretion-to-jet energy conversion efficiency η = Ej/Mac2 = 2EK, jet/(1 − fγ)(1 − fw)Mdiscc2. Figure 3 shows the resulting posterior probability distribution for η (solid red line), assuming fw = 0.3 and fγ = 0.15, as discussed in the previous sections. The 1 sigma confidence interval is 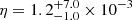 . If we require the GW170817 disc mass to be Mdisc > 0.04 M⊙, based on the constraint from kilonova observations (Radice & Dai 2019; Margalit & Metzger 2017), the posterior (dashed orange line) is pushed further towards low efficiencies; the 1 sigma confidence interval in this case is
. If we require the GW170817 disc mass to be Mdisc > 0.04 M⊙, based on the constraint from kilonova observations (Radice & Dai 2019; Margalit & Metzger 2017), the posterior (dashed orange line) is pushed further towards low efficiencies; the 1 sigma confidence interval in this case is 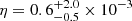 . These efficiencies are summarised, along with theoretically expected values (discussed in the following sections), in Table 1.
. These efficiencies are summarised, along with theoretically expected values (discussed in the following sections), in Table 1.
 |
Fig. 3. Posterior probability density distribution of the accretion-to-jet energy conversion efficiency η = Ej/Mac2 in GW170817 (solid red line), assuming fw = 0.3 and fγ = 0.15. The dashed orange line shows the same quantity, but with the disc mass in GW170817 required to be equal or greater than 0.04 M⊙ (Radice & Dai 2019). Black error bars show the expected efficiency for the Blandford & Znajek (1977) and |
Summary of the accretion-to-jet energy conversion efficiencies discussed in the text.
5. Comparison with theoretical expectations
It is informative to compare the GW170817 accretion-to-jet energy conversion efficiency estimate derived in the previous section with theoretical expectations based on the two main jet launching mechanism candidates, namely the Blandford & Znajek (1977) magneto-hydrodynamical (MHD) mechanism and the neutrino energy deposition mechanism (Eichler et al. 1989).
5.1. Blandford-Znajek mechanism
The Blandford & Znajek (1977, BZ hereafter) mechanism can produce efficient energy extraction from a BH threaded by a large-scale magnetic field in relative rotation with respect to the BH. The mechanism operates in force-free regions (i.e. regions where the matter contribution to the stress energy tensor is negligible with respect to the electromagnetic contribution) close to the BH horizon (e.g. Komissarov 2004; McKinney & Gammie 2004; McKinney 2005; De Villiers et al. 2005; Hawley & Krolik 2006; Hawley et al. 2007; Tchekhovskoy et al. 2010). In the case of a Kerr BH with dimensionless spin parameter aBH, the extracted power depends on the strength of the radial component Br of the magnetic field at the horizon, as well as on the spin parameter (Blandford & Znajek 1977; Komissarov 2004; Tchekhovskoy et al. 2010). The magnetic field is most naturally brought to the BH horizon by an accretion disc, where it can be amplified by means of the magneto-rotational instability (MRI, Balbus & Hawley 1991; Hawley & Balbus 1991). In stationary accretion conditions, it is plausible to expect the MRI to saturate to a definite disc magnetisation that does not depend on the seed magnetic field strength. Indeed, based on a series of axisymmetric general-relativistic magneto-hydrodynamical (GRMHD) simulations of Kerr BHs surrounded by thick accretion discs seeded with a dipole magnetic field (described in McKinney & Gammie 2004), McKinney (2005) found that, after an initial transient phase, the disc magnetisation saturates and the accretion-to-jet energy conversion efficiency of the BZ process stabilises depending solely on the BH spin, which is well described by the simple relation 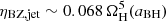 for a > 0.5. Here,
for a > 0.5. Here, 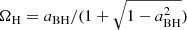 is the dimensionless angular frequency at the BH horizon. The full set of their simulations (see Fig. 4), including those with a < 0.5, can be fitted by the function
is the dimensionless angular frequency at the BH horizon. The full set of their simulations (see Fig. 4), including those with a < 0.5, can be fitted by the function
 |
Fig. 4. Accretion-to-jet energy conversion efficiency of the Blandford & Znajek (1977) mechanism as a function of the BH spin parameter aBH from the GRMHD simulations of McKinney (2005, black squares) and Hawley et al. (2007, orange stars). The red and blue curves are fitting functions Eqs. (1) and (2), respectively. |
Three-dimensional simulations by a different group, described in De Villiers et al. (2005), Hawley & Krolik (2006), and Hawley et al. (2007), find a somewhat different saturation efficiency, which can be described (see again Fig. 4) by the simple expression
This efficiency is obtained in simulations where the seed magnetic field is poloidal, and the authors note that the efficiency of jet launching critically depends on the seed magnetic field configuration, with purely toroidal initial fields leading to weak or absent jets. On the other hand, Liska et al. (2020) more recently found that even an initially purely toroidal magnetic field can lead to a strong jet, provided that the simulation is run for long enough (several ×104 dynamical times) for an MHD dynamo-like process (Moffatt 1978) to convert part of the magnetic field into a large-scale poloidal component (see the discussion in Liska et al. 2020). In other words, the expectation that the disc magnetisation eventually saturates regardless of its initial strength and configuration seems fulfilled, provided that the accretion lasts long enough and that the accretion conditions remain otherwise unchanged in the meantime.
The above arguments assume the seed magnetic field to be initially sub-dominant. At the other extreme end, the highest BZ efficiency is reached (e.g. Narayan et al. 2003; Tchekhovskoy et al. 2011; McKinney et al. 2012) when accretion takes the form of a magnetically arrested disc (MAD, Bisnovatyi-Kogan & Ruzmaikin 1976). In this case, the magnetic field energy density is so high that it dominates the disc dynamics, and the magnetic flux through the BH horizon is maximised, leading to efficiencies that can exceed 100% (we note that the ultimate energy source of the process is BH rotation rather than accretion power). The jet efficiency can also be expressed in this case as a function of the BH spin (Tchekhovskoy & Giannios 2015), namely6
5.1.1. Expected Blandford-Znajek efficiency in GW170817
A first simple (but naive – see next section) estimate of the expected BZ efficiency in GW170817 can be obtained by evaluating the fitting formulae from the previous section at the GW170817 BH remnant spin (computed as described in Appendix A). Doing so, we obtained the theoretical efficiency estimates shown in Fig. 3, namely 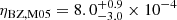 ,
, 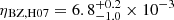 , and
, and 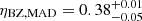 . While the MAD case is clearly excluded, the estimates based on McKinney (2005) and Hawley et al. (2007) are both in good agreement with our ‘measured’ efficiency in GW170817, given the large uncertainties. If we assume the disc mass constraint Mdisc > 0.04 M⊙ (Radice & Dai 2019; Margalit & Metzger 2017), then the efficiency from Hawley et al. (2007) falls outside of the 1 sigma confidence interval.
. While the MAD case is clearly excluded, the estimates based on McKinney (2005) and Hawley et al. (2007) are both in good agreement with our ‘measured’ efficiency in GW170817, given the large uncertainties. If we assume the disc mass constraint Mdisc > 0.04 M⊙ (Radice & Dai 2019; Margalit & Metzger 2017), then the efficiency from Hawley et al. (2007) falls outside of the 1 sigma confidence interval.
5.1.2. Efficiency found in GRMHD simulations of generic BNS mergers
One thing to keep in mind when considering the efficiencies calculated in the previous section is that the simulations on which they are based are actually more relevant to BH-accretion disc systems hosted by active galactic nuclei, in which accretion is thought to take place on sufficiently long time scales to settle on a definite state with a constant accretion rate (on the time scales of interest). Accretion on the remnant of a BNS merger, on the other hand, is essentially transient, with a declining accretion rate (see Sect. 5.2). Under typical circumstances, it most likely evolves over four stages (e.g. Just et al. 2015; Christie et al. 2019): (1) Initially, the accretion rate is high enough for the disc to be optically thick to neutrinos, so that a strong and fast neutrino-driven wind is produced by the inner part of the disc. During this short phase, jet launching is likely hampered by baryon pollution in the funnel above the BH. (2) As the accretion rate decreases, the disc transitions to a neutrino-dominated accretion flow (NDAF) state, where it efficiently cools by neutrino emission, and the density in the polar region drops, allowing for the formation of a force-free region. This is a requirement for the BZ process to take place. (3) The decreasing accretion rate eventually renders neutrino cooling inefficient again, leading to an ADAF phase during which viscous heating inflates and expands the disc, leading to strong disc winds. (4) Finally, the accretion rate becomes low enough for the magnetic field energy density to overcome that of the accreting matter, leading to an MAD (Tchekhovskoy & Giannios 2015). During this evolution, the BZ efficiency increases (Christie et al. 2019), but this is compensated for by the decreasing accretion rate so that, in the end, the average efficiency typically falls well below the MAD case.
A recent well-suited example is the set of high-resolution, long-term GRMHD simulations, described in Christie et al. (2019), of a BH surrounded by an accretion disc with initial conditions that represent those that immediately follow a BNS merger, with a BH mass MBH = 3 M⊙, a spin parameter aBH = 0.8, and a disc (torus) of mass Mdisc = 0.033 M⊙. The simulations were designed to investigate the impact of magnetic field geometry on the properties of the outflows (both relativistic and non-relativistic) produced by such a system. Two simulations, called BPS and BPW, were initialised with a poloidal magnetic field within the disc, differing only in the degree of magnetisation (BPS had a stronger magnetisation than BPW). The third simulation, BT, was seeded with a toroidal magnetic field within the disc7 In all cases, the system was able to launch a relativistic jet, but with differing efficiencies: The BPS simulation produced bipolar jets with Ej ∼ 1051 erg, and the fraction of disc mass lost in winds was fw = 0.4, leading to ηBZ ∼ 2.8 × 10−2. For the BPW simulation, Ej ∼ 3.9 × 1050 erg and fw = 0.3, yielding ηBZ ∼ 9.4 × 10−3. Finally, simulation BT resulted in significantly weaker jets with Ej ∼ 2 × 1049 erg. Strong disc winds were still present, with fw = 0.27, so that ηBZ ∼ 4.6 × 10−4. Our maximum posterior estimate of the efficiency falls in between the BT and BPW cases, which seems reasonable since the expected magnetic field configuration right after the merger is predominantly toroidal, but a weak poloidal component is expected.
Another set of recent GRMHD simulations of BNS mergers that resolve the relativistic jet launching by the Blandford & Znajek (1977) mechanism in the post-merger phase are those described in Ruiz et al. (2019, 2020). These simulations start a few orbits before the merger, so that, in this case, the magnetic field configuration in the torus is self-consistently determined by the merger dynamics8. Essentially, regardless of the initial configuration, the authors find BZ efficiencies9ηBZ ∼ 2 − 3 × 10−3 in all jet-producing simulations, in good agreement with our results.
We therefore conclude that the accretion-to-jet energy conversion efficiency in GW170817 is consistent with theoretical expectations for the BZ mechanism in the presence of an initial magnetic field whose energy density does not dominate over that of the accreting matter (i.e. the disc is not in the MAD state) during most of the accretion, and whose configuration is predominantly toroidal right after the merger.
5.2. Neutrino mechanism
While the Blandford & Znajek (1977) process today is widely regarded as the most likely jet-launching mechanism in GRBs, the first works to propose neutron star mergers as potential progenitors of GRBs (Eichler et al. 1989; Meszaros & Rees 1992; Mochkovitch et al. 1993, 1995) actually envisioned energy deposition by the annihilation of neutrino-antineutrino pairs in the vicinity of the merger remnant (‘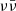 mechanism’ hereafter) as the process responsible for powering the jet. Whether such a scenario can realistically power GRB jets (including long GRBs, e.g. Popham et al. 1999; Kohri et al. 2005; Lee & Ramirez-Ruiz 2006) has long been a subject of debate. Several works have studied the detailed structure and stability of accretion discs in NDAF conditions (e.g. Popham et al. 1999; Asano & Fukuyama 2001; Narayan et al. 2001; Di Matteo et al. 2002; Kohri & Mineshige 2002; Kohri et al. 2005; Lee & Ramirez-Ruiz 2006; Chen & Beloborodov 2007; Birkl et al. 2007; Kawanaka & Mineshige 2007; Janiuk et al. 2007, 2013; Rossi et al. 2007; Zhang & Dai 2009; Janiuk & Yuan 2010; Kawanaka & Kohri 2012; Pan & Yuan 2012; Kawanaka et al. 2013a,b; Liu et al. 2014, 2015a,b; Liu et al. 2018; Janiuk 2017; Kawanaka & Masada 2019); others attempted to directly simulate the neutron star merger (or its remnant) and the formation of a jet by the
mechanism’ hereafter) as the process responsible for powering the jet. Whether such a scenario can realistically power GRB jets (including long GRBs, e.g. Popham et al. 1999; Kohri et al. 2005; Lee & Ramirez-Ruiz 2006) has long been a subject of debate. Several works have studied the detailed structure and stability of accretion discs in NDAF conditions (e.g. Popham et al. 1999; Asano & Fukuyama 2001; Narayan et al. 2001; Di Matteo et al. 2002; Kohri & Mineshige 2002; Kohri et al. 2005; Lee & Ramirez-Ruiz 2006; Chen & Beloborodov 2007; Birkl et al. 2007; Kawanaka & Mineshige 2007; Janiuk et al. 2007, 2013; Rossi et al. 2007; Zhang & Dai 2009; Janiuk & Yuan 2010; Kawanaka & Kohri 2012; Pan & Yuan 2012; Kawanaka et al. 2013a,b; Liu et al. 2014, 2015a,b; Liu et al. 2018; Janiuk 2017; Kawanaka & Masada 2019); others attempted to directly simulate the neutron star merger (or its remnant) and the formation of a jet by the 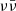 mechanism (e.g. Ruffert et al. 1997; Ruffert & Janka 1999; Rosswog et al. 2003; Shibata et al. 2007; Dessart et al. 2009; Just et al. 2015, 2016; Perego et al. 2017b; Siegel & Metzger 2017). While most works on the former aspect find promising neutrino luminosities and energy deposition rates, the latter investigations mostly indicate that the
mechanism (e.g. Ruffert et al. 1997; Ruffert & Janka 1999; Rosswog et al. 2003; Shibata et al. 2007; Dessart et al. 2009; Just et al. 2015, 2016; Perego et al. 2017b; Siegel & Metzger 2017). While most works on the former aspect find promising neutrino luminosities and energy deposition rates, the latter investigations mostly indicate that the 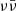 mechanism faces some apparently serious difficulties. In particular (Just et al. 2016), the typical BNS post-merger environment could be sufficiently dense as to prevent a
mechanism faces some apparently serious difficulties. In particular (Just et al. 2016), the typical BNS post-merger environment could be sufficiently dense as to prevent a 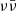 -powered jet to successfully break out, in part due to the short duration of the high neutrino luminosity phase.
-powered jet to successfully break out, in part due to the short duration of the high neutrino luminosity phase.
In what follows, we aim to test whether, in principle, the 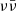 mechanism accretion-to-jet energy conversion efficiency is compatible with our measured one. In order to estimate the expected efficiency, we adopted the parameterisation of the jet power given in Leng & Giannios (2014), which relies on energy deposition rates computed by Zalamea & Beloborodov (2011) based on the relativistic model of a neutrino-cooled accretion disc around a Kerr BH described in Chen & Beloborodov (2007), as well as on general-relativistic ray tracing of the neutrino trajectories.
mechanism accretion-to-jet energy conversion efficiency is compatible with our measured one. In order to estimate the expected efficiency, we adopted the parameterisation of the jet power given in Leng & Giannios (2014), which relies on energy deposition rates computed by Zalamea & Beloborodov (2011) based on the relativistic model of a neutrino-cooled accretion disc around a Kerr BH described in Chen & Beloborodov (2007), as well as on general-relativistic ray tracing of the neutrino trajectories.
We assume the disc accretion rate to evolve with time as a power law, namely
for t > t0, while Ṁ = 0 for t < t0. When 1.5 ≲ α ≲ 2.5, this simple prescription is a fair description of the actual output of detailed numerical simulations (e.g. Fernández et al. 2019; Just et al. 2016). Time here is measured from the formation of the central BH, and t0 is the time to the onset of accretion, which is of the order of a few dynamical times. This allows us, following Leng & Giannios (2014), to write the jet power as a function of the accretion rate Ṁ and BH spin parameter aBH as follows
where
Here, Rg = GMBH/c2 is the gravitational radius, MBH is the central BH mass, RISCO = RISCO(aBH) is the innermost stable circular orbit, Msat = 1.8 M⊙ s−1 is the saturation accretion rate (above which the jet power is assumed to saturate), and Ṁign = 0.021 M⊙ s−1 is the accretion rate below which neutrino cooling becomes inefficient.
Assuming this description holds true at all times during the evolution of Ṁ(t), and neglecting the small change (in the SGRB case) in the BH mass and spin due to accretion (and jet production), the jet energy can be obtained by integrating Eq. (5) over time analytically. For that purpose, it is useful to identify two dimensionless transition times:
and
Setting δ = (9/4)α − 1, one can then write the final jet energy produced by neutrino-antineutrino annihilation as
The ratio 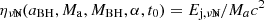 then represents the accretion-to-jet energy conversion efficiency of the neutrino-antineutrino annihilation mechanism.
then represents the accretion-to-jet energy conversion efficiency of the neutrino-antineutrino annihilation mechanism.
Figure 5 shows the resulting efficiency contours on the (Ma, aBH) plane, assuming α = 2, t0 = 10 ms, and MBH = 2.6 M⊙. Overlaid cyan contours show the joint posterior probability density P(Ma, aBH) for GW170817 assuming fw = 0.3, obtained after marginalising over the BH mass (see Appendix A for the computation of the remnant BH mass and spin). The corresponding prediction for the neutrino mechanism efficiency in GW170817, adopting uniform priors on α in the range (1.5, 2.5) and on t0/ms in the range (5, 30), amounts to 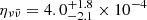 , which is shown in Fig. 3. This efficiency is only slightly lower than that of the BZ mechanism as predicted by the McKinney (2005) fitting formula, and it is compatible with the measured one (see Table 1). We therefore cannot exclude, on the basis of our determination of the accretion-to-jet energy conversion efficiency in GW170817 alone, that the neutrino mechanism was responsible for the launching of the relativistic jet identified by Mooley et al. (2018a,b) and Ghirlanda et al. (2019).
, which is shown in Fig. 3. This efficiency is only slightly lower than that of the BZ mechanism as predicted by the McKinney (2005) fitting formula, and it is compatible with the measured one (see Table 1). We therefore cannot exclude, on the basis of our determination of the accretion-to-jet energy conversion efficiency in GW170817 alone, that the neutrino mechanism was responsible for the launching of the relativistic jet identified by Mooley et al. (2018a,b) and Ghirlanda et al. (2019).
 |
Fig. 5. Accretion-to-jet energy conversion efficiency of the |
6. Discussion
In Table 1, we summarise the values and confidence ranges of our estimates of the accretion-to-jet energy conversion efficiency in GW170817, as well as the theoretically expected values for the Blandford & Znajek (1977) and 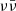 jet-launching mechanisms. Our estimates are based on a comparison of the jet energy obtained by fitting the GRB 170817 afterglow and VLBI centroid motion by Ghirlanda et al. (2019) with the GW170817 disc mass obtained by applying the fitting formula by Barbieri et al. (2020) to the publicly available posterior samples from GW parameter estimation (The LIGO Scientific Collaboration & The Virgo Collaboration 2019). We list two estimates that were obtained either requiring the accretion disc mass to be at least 0.04 M⊙ (Margalit & Metzger 2017; Radice & Dai 2019, based on the large ejecta mass inferred from observations of the AT2017gfo kilonova, interpreted as being produced by disc winds) or imposing no constraints on the disc mass. These estimates point to a rather low efficiency of ∼10−3, which is not unexpected: Owing to the predominantly toroidal magnetic field configuration in the disc right after the merger (Kiuchi et al. 2014) and to the relatively short duration of the accretion, the Blandford & Znajek (1977) process in the BNS post-merger is expected to be rather inefficient (Christie et al. 2019; Ruiz et al. 2019, 2020). Such a low efficiency is also compatible, in principle, with that of the neutrino-antineutrino annihilation mechanism, even though direct simulations of BNS mergers (Ruffert & Janka 1999; Just et al. 2016) seem to indicate that the baryon pollution in the polar region of the post-merger system, at the time when most of the
jet-launching mechanisms. Our estimates are based on a comparison of the jet energy obtained by fitting the GRB 170817 afterglow and VLBI centroid motion by Ghirlanda et al. (2019) with the GW170817 disc mass obtained by applying the fitting formula by Barbieri et al. (2020) to the publicly available posterior samples from GW parameter estimation (The LIGO Scientific Collaboration & The Virgo Collaboration 2019). We list two estimates that were obtained either requiring the accretion disc mass to be at least 0.04 M⊙ (Margalit & Metzger 2017; Radice & Dai 2019, based on the large ejecta mass inferred from observations of the AT2017gfo kilonova, interpreted as being produced by disc winds) or imposing no constraints on the disc mass. These estimates point to a rather low efficiency of ∼10−3, which is not unexpected: Owing to the predominantly toroidal magnetic field configuration in the disc right after the merger (Kiuchi et al. 2014) and to the relatively short duration of the accretion, the Blandford & Znajek (1977) process in the BNS post-merger is expected to be rather inefficient (Christie et al. 2019; Ruiz et al. 2019, 2020). Such a low efficiency is also compatible, in principle, with that of the neutrino-antineutrino annihilation mechanism, even though direct simulations of BNS mergers (Ruffert & Janka 1999; Just et al. 2016) seem to indicate that the baryon pollution in the polar region of the post-merger system, at the time when most of the 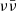 energy is deposited, is too high for the jet to successfully propagate and break out.
energy is deposited, is too high for the jet to successfully propagate and break out.
Such a low accretion-to-jet energy conversion efficiency contrasts with the much higher values derived for flat-spectrum radio quasars and blazars by several authors (e.g. Rawlings & Saunders 1991; Ghisellini et al. 2014; Pjanka et al. 2017; Soares & Nemmen 2020). This could be explained by a nearly maximal BH spin in these systems (e.g. Soares & Nemmen 2020, while in binary neutron star merger remnants, typically aBH ∼ 0.7, see Appendix A), given the steep dependence of the efficiency on this parameter found in simulations of the BZ process (McKinney 2005; Hawley et al. 2007; Tchekhovskoy et al. 2010; McKinney et al. 2012). Another difference that may play a role is the accretion rate: While GRB central engines accrete at extremely super-Eddington rates, supermassive BHs in quasars are thought to typically accrete at or near the Eddington limit (e.g. Maraschi & Tavecchio 2003). Clearly, the large difference could instead be due to two different jet-launching mechanisms at play. Last, but not least, we note that the efficiency found in this work represents an average value over the entire duration of the accretion and that the instantaneous efficiency likely varies significantly over time (see Sect. 5.1), which makes the comparison with quasars more difficult.
Our efficiency estimate is in principle model-dependent as it relies on afterglow modelling as a means to measure the jet energy, as well as on a fitting formula based on a limited number of general-relativistic numerical simulations (which in turn suffer from limited resolution, uncertainty on the EoS at supra-nuclear densities, and the difficulty in accounting for the effects of neutrinos and magnetic fields at the same time) as a means to estimate the disc mass. Nevertheless, as noted before, the disc mass cannot be much less than the ∼0.1 M⊙ most probable value derived using the Barbieri et al. (2020) fitting formula, given the constraints imposed by the large kilonova mass (Margalit & Metzger 2017). Moreover, we account to some extent for systematic uncertainties by introducing a relatively large dispersion in the values of the disc mass predicted by the fitting formula (Sect. 2), and we properly account for statistical uncertainties – including those arising from intrinsic afterglow model degeneracies (such as those pointed out by Nakar & Piran 2020) – in the jet energy by taking the full posterior from Ghirlanda et al. (2019). We note, moreover, that our adopted jet energy estimate is in agreement with essentially all others in the literature (see Fig. 2), some of which are based on significantly different models (e.g. in terms of the adopted jet structure). We are therefore confident that our conclusions are not heavily affected by systematics.
7. Conclusions
In this work we obtained, for the first time, an estimate of the accretion-to-jet energy conversion efficiency in a GRB by combining independent measurements of the jet energy (from multi-wavelength afterglow modelling) and of the disc mass (by applying a fitting formula based on a large suite of numerical simulations to the binary parameters inferred from gravitational wave parameter estimations). The resulting efficiency is rather low, η ∼ 10−3 (with large error bars), in agreement with expectations from both the Blandford & Znajek (1977) jet-launching mechanism, in the presence of a predominantly toroidal magnetic field configuration in the disc right after the merger, and the 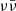 annihilation mechanism; the efficiency therefore does not allow us to distinguish between the two. Future applications of this method to a larger number of systems with well-measured gravitational wave parameters and well-sampled jet afterglows, together with improved disc mass predictions from numerical relativity simulations of binary neutron star mergers, will reduce the uncertainty in the efficiency and reveal its distribution among different systems. Such a distribution could be the key to distinguishing between the two candidate jet-launching mechanisms due to the likely different dependencies on the disc and BH remnant properties: While the efficiency in both mechanisms increases with the BH spin, the dependence on the disc mass is likely different in the two scenarios. In the
annihilation mechanism; the efficiency therefore does not allow us to distinguish between the two. Future applications of this method to a larger number of systems with well-measured gravitational wave parameters and well-sampled jet afterglows, together with improved disc mass predictions from numerical relativity simulations of binary neutron star mergers, will reduce the uncertainty in the efficiency and reveal its distribution among different systems. Such a distribution could be the key to distinguishing between the two candidate jet-launching mechanisms due to the likely different dependencies on the disc and BH remnant properties: While the efficiency in both mechanisms increases with the BH spin, the dependence on the disc mass is likely different in the two scenarios. In the 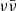 case, a higher disc mass favours a higher initial accretion rate, which extends the duration of the high neutrino luminosity phase (Sect. 5.2). In the BZ case, on the other hand, the role of disc mass is less clear: depending on the origin of the material that forms the disc – either resulting from the tidal disruption of one or both the neutron stars, or from other processes that take place during and immediately after the merger – the seed magnetic field configuration in the disc could be different, potentially affecting the efficiency (Christie et al. 2019). While a detailed investigation of such a dependence is beyond the scope of this work, we expect it to differ significantly from the
case, a higher disc mass favours a higher initial accretion rate, which extends the duration of the high neutrino luminosity phase (Sect. 5.2). In the BZ case, on the other hand, the role of disc mass is less clear: depending on the origin of the material that forms the disc – either resulting from the tidal disruption of one or both the neutron stars, or from other processes that take place during and immediately after the merger – the seed magnetic field configuration in the disc could be different, potentially affecting the efficiency (Christie et al. 2019). While a detailed investigation of such a dependence is beyond the scope of this work, we expect it to differ significantly from the 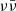 case. This could therefore constitute the basis to distinguish the two mechanisms from each other through the application of the method described in this work to a large sample of events. Independently of this, polarimetric observations of the SGRB prompt emission and, potentially, of the reverse shock in the early afterglow phase (Lamb & Kobayashi 2019) could reveal the degree of magnetisation in the jet, which can provide further insights into the jet-launching mechanism.
case. This could therefore constitute the basis to distinguish the two mechanisms from each other through the application of the method described in this work to a large sample of events. Independently of this, polarimetric observations of the SGRB prompt emission and, potentially, of the reverse shock in the early afterglow phase (Lamb & Kobayashi 2019) could reveal the degree of magnetisation in the jet, which can provide further insights into the jet-launching mechanism.
Once the accretion-to-jet energy conversion efficiency in SGRBs (and its possible dependence on the progenitor binary parameters) is established, it will be possible to infer the distribution of disc masses in jet-launching binary neutron star mergers by converting SGRB energies, even in the absence of a GW detection. The disc mass distribution, in turn, can shed light on the distribution of properties of the progenitor binaries (e.g. Giacomazzo et al. 2013) A similar approach can also be applied to BH-neutron star mergers if they are also found to produce GRBs. In that case, the information on the accretion-to-jet energy conversion efficiency could be used to constrain the EoS of matter at supra-nuclear densities (Ascenzi et al. 2019).
Jet launching is still possible (e.g. Thompson 1994; Bucciantini et al. 2008; Metzger et al. 2011; Mösta et al. 2020) in the case of a long-lived neutron star remnant, though it seems disfavored by recent simulations (e.g. Ciolfi 2020a). In this case, the launch of the jet would be powered by the rotation of the magnetised neutron star remnant, so that our definition of efficiency would not be applicable.
Unless it is of extreme intensity, B ≳ 1017 G – Giacomazzo et al. 2009 – but it is unclear how such a high magnetic field could survive during the neutron star lifetime before the merger.
These simulations also do not include magnetic fields, which could affect the disc mass around the BH remnant by their effects on pressure and viscosity, especially during a possible HMNS transient phase. This is mitigated, though, by their implementation of an effective ‘large-eddy’ simulation method (Radice 2017) that partly reproduces the effects of small-scale magneto-hydrodynamical turbulence. Such a method requires fixing an effective mixing length parameter: the Barbieri et al. (2020) fitting formula was calibrated on all their models, which include a range of mixing lengths, in order to effectively account for the systematic uncertainty that stems from the uncertainty on this parameter.
During the preparation of this work, two different pre-prints with two alternative fitting formulae for the disc mass were circulated (Krüger & Foucart 2020; Dietrich et al. 2020). We verified that our conclusions remained unchanged when employing either of these alternative fitting formulae to compute the disc mass.
This approach may be questioned since there are indications (e.g. Ghisellini et al. 2007; D’Avanzo et al. 2012) that the early X-ray afterglow of a relevant fraction of GRBs is dominated by a component that is linked to central engine activity. Nevertheless, focusing on late-time X-ray observations, D’Avanzo et al. (2012) still find typical efficiencies below 10 percent. See also Nemmen et al. (2012), who find indications that 15 percent is a typical radiative efficiency in all astrophysical jets.
We omit here, for the sake of simplicity, a linear scaling with the height-to-radius (H/R) ratio, which is set to 0.2 as in Tchekhovskoy & Giannios (2015), as this does not affect our conclusions.
A predominantly toroidal configuration is expected in neutron star mergers, due to the stretching of neutron star material undergoing tidal disruption, and to flux freezing, see e.g. Kiuchi et al. (2014), Kawamura et al. (2016).
The formula was reported incorrectly in Coughlin et al. (2019), but a comparison with the BH remnant mass formula allows one to figure out the missing pieces.
Acknowledgments
We thank the anonymous referee for insightful comments that helped to improve the quality and presentation of this work. We thank A. Celotti, G. Ghisellini, G. Ghirlanda, G. Oganesyan, S. Ascenzi, C. Barbieri, R. Ciolfi, A. Perego, D. Lazzati and G. Lamb for useful discussions and comments. O. S. acknowledges the INAF-Prin 2017 (1.05.01.88.06) and the Italian Ministry for University and Research grant “FIGARO” (1.05.06.13) for support.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, ApJ, 848, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, K. D., Berger, E., Fong, W., et al. 2017, ApJ, 848, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, K. D., Margutti, R., Blanchard, P. K., et al. 2018, ApJ, 863, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Asano, K., & Fukuyama, T. 2001, ApJ, 546, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Ascenzi, S., De Lillo, N., Haster, C.-J., Ohme, F., & Pannarale, F. 2019, ApJ, 877, 94 [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Barbieri, C., Salafia, O. S., Perego, A., Colpi, M., & Ghirlanda, G. 2019, A&A, 625, A152 [CrossRef] [EDP Sciences] [Google Scholar]
- Barbieri, C., Salafia, O. S., Colpi, M., Ghirlanda, G., & Perego, A. 2020, A&A, submitted [arXiv:2002.09395] [Google Scholar]
- Bauswein, A., Goriely, S., & Janka, H. T. 2013, ApJ, 773, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., Nava, L., Duran, R. B., & Piran, T. 2015, MNRAS, 454, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., Nava, L., & Piran, T. 2016, MNRAS, 461, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Bernuzzi, S., Breschi, M., Daszuta, B., et al. 2020, MNRAS, 497, 1488 [CrossRef] [Google Scholar]
- Birkl, R., Aloy, M. A., Janka, H. T., & Müller, E. 2007, A&A, 463, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisnovatyi-Kogan, G. S., & Ruzmaikin, A. A. 1976, Ap&SS, 42, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Bisnovatyi-Kogan, G. S., Imshennik, V. S., Nadyozhin, D. K., & Chechetkin, V. M. 1975, Ap&SS, 35, 23 [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Bucciantini, N., Quataert, E., Arons, J., Metzger, B. D., & Thompson, T. A. 2008, MNRAS, 383, L25 [NASA ADS] [Google Scholar]
- Chen, W.-X., & Beloborodov, A. M. 2007, ApJ, 657, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Christie, I. M., Lalakos, A., Tchekhovskoy, A., et al. 2019, MNRAS, 490, 4811 [NASA ADS] [CrossRef] [Google Scholar]
- Ciolfi, R. 2020a, MNRAS, 495, L66 [CrossRef] [Google Scholar]
- Ciolfi, R. 2020b, Gen. Rel. Grav., 52, 59 [CrossRef] [Google Scholar]
- Ciolfi, R., & Kalinani, J. V. 2020, ApJ, 900, L35 [CrossRef] [Google Scholar]
- Coughlin, M. W., Dietrich, T., Margalit, B., & Metzger, B. D. 2019, MNRAS, 489, L91 [CrossRef] [Google Scholar]
- Coulter, D. A., Foley, R. J., Kilpatrick, C. D., et al. 2017, Science, 358, 1556 [NASA ADS] [CrossRef] [Google Scholar]
- Cowperthwaite, P. S., Berger, E., Villar, V. A., et al. 2017, ApJ, 848, L17 [NASA ADS] [CrossRef] [Google Scholar]
- D’Avanzo, P., Salvaterra, R., Sbarufatti, B., et al. 2012, MNRAS, 425, 506 [NASA ADS] [CrossRef] [Google Scholar]
- D’Avanzo, P., Campana, S., Salafia, O. S., et al. 2018, A&A, 613, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, M. B., Benz, W., Piran, T., & Thielemann, F. K. 1994, ApJ, 431, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Ott, C. D., Burrows, A., Rosswog, S., & Livne, E. 2009, ApJ, 690, 1681 [NASA ADS] [CrossRef] [Google Scholar]
- De Villiers, J.-P., Hawley, J. F., Krolik, J. H., & Hirose, S. 2005, ApJ, 620, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, T., Coughlin, M. W., Pang, P. T. H., et al. 2020, Science, 370, 1450 [Google Scholar]
- Di Matteo, T., Perna, R., & Narayan, R. 2002, ApJ, 579, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Dobie, D., Kaplan, D. L., Murphy, T., et al. 2018, ApJ, 858, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Duffell, P. C., Quataert, E., Kasen, D., & Klion, H. 2018, ApJ, 866, 3 [NASA ADS] [CrossRef] [Google Scholar]
- East, W. E., Paschalidis, V., Pretorius, F., & Tsokaros, A. 2019, Phys. Rev. D, 100, 124042 [CrossRef] [Google Scholar]
- Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Fenimore, E. E., Epstein, R. I., & Ho, C. 1993, A&AS, 97, 59 [NASA ADS] [Google Scholar]
- Fernández, R., & Metzger, B. D. 2013, MNRAS, 435, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, R., Tchekhovskoy, A., Quataert, E., Foucart, F., & Kasen, D. 2019, MNRAS, 482, 3373 [CrossRef] [Google Scholar]
- Flanagan, É., & Hinderer, T. 2008, Phys. Rev. D, 77, 021502 [NASA ADS] [CrossRef] [Google Scholar]
- Frail, D. A., Kulkarni, S. R., Nicastro, L., Feroci, M., & Taylor, G. B. 1997, Nature, 389, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Frail, D. A., Kulkarni, S. R., Sari, R., et al. 2001, ApJ, 562, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Fujibayashi, S., Shibata, M., Wanajo, S., et al. 2020, Phys. Rev. D, 101, 083029 [CrossRef] [Google Scholar]
- Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature, 395, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Salafia, O. S., Paragi, Z., et al. 2019, Science, 363, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Lazzati, D. 1999, MNRAS, 309, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Ghirlanda, G., Nava, L., & Firmani, C. 2007, ApJ, 658, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Maraschi, L., Celotti, A., & Sbarrato, T. 2014, Nature, 515, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Giacomazzo, B., Rezzolla, L., & Baiotti, L. 2009, MNRAS, 399, L164 [NASA ADS] [Google Scholar]
- Giacomazzo, B., Rezzolla, L., & Baiotti, L. 2011, Phys. Rev. D, 83, 044014 [NASA ADS] [CrossRef] [Google Scholar]
- Giacomazzo, B., Perna, R., Rezzolla, L., Troja, E., & Lazzati, D. 2013, ApJ, 762, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Gill, R., Nathanail, A., & Rezzolla, L. 2019, ApJ, 876, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, A., Veres, P., Burns, E., et al. 2017, ApJ, 848, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J. 1986, ApJ, 308, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J. 1997, New Astron., 2, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., Gill, R., Guetta, D., & De Colle, F. 2018, MNRAS, 481, 1597 [CrossRef] [Google Scholar]
- Hajela, A., Margutti, R., Alexander, K. D., et al. 2019, ApJ, 886, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Hallinan, G., Corsi, A., Mooley, K. P., et al. 2017, Science, 358, 1579 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., & Balbus, S. A. 1991, ApJ, 376, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., & Krolik, J. H. 2006, ApJ, 641, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Beckwith, K., & Krolik, J. H. 2007, Ap&SS, 311, 117 [CrossRef] [Google Scholar]
- Hotokezaka, K., Kiuchi, K., Kyutoku, K., et al. 2013, Phys. Rev. D, 87, 024001 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A. 2017, ApJ, 837, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., & Yuan, Y. F. 2010, A&A, 509, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janiuk, A., Yuan, Y., Perna, R., & Di Matteo, T. 2007, ApJ, 664, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., Mioduszewski, P., & Moscibrodzka, M. 2013, ApJ, 776, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Just, O., Bauswein, A., Ardevol Pulpillo, R., Goriely, S., & Janka, H. T. 2015, MNRAS, 448, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Just, O., Obergaulinger, M., Janka, H. T., Bauswein, A., & Schwarz, N. 2016, ApJ, 816, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Kawamura, T., Giacomazzo, B., Kastaun, W., et al. 2016, Phys. Rev. D, 94, 064012 [NASA ADS] [CrossRef] [Google Scholar]
- Kawanaka, N., & Kohri, K. 2012, MNRAS, 419, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Kawanaka, N., & Masada, Y. 2019, ApJ, 881, 138 [CrossRef] [Google Scholar]
- Kawanaka, N., & Mineshige, S. 2007, ApJ, 662, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- Kawanaka, N., Piran, T., & Krolik, J. H. 2013a, ApJ, 766, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Kawanaka, N., Mineshige, S., & Piran, T. 2013b, ApJ, 777, L15 [CrossRef] [Google Scholar]
- Kiuchi, K., Kyutoku, K., Sekiguchi, Y., Shibata, M., & Wada, T. 2014, Phys. Rev. D, 90, 041502 [CrossRef] [Google Scholar]
- Kiuchi, K., Kyutoku, K., Sekiguchi, Y., & Shibata, M. 2018, Phys. Rev. D, 97, 124039 [NASA ADS] [CrossRef] [Google Scholar]
- Kiuchi, K., Kyutoku, K., Shibata, M., & Taniguchi, K. 2019, ApJ, 876, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Kohri, K., & Mineshige, S. 2002, ApJ, 577, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Kohri, K., Narayan, R., & Piran, T. 2005, ApJ, 629, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S. 2004, MNRAS, 350, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Kowalska, I., Bulik, T., Belczynski, K., Dominik, M., & Gondek-Rosinska, D. 2011, A&A, 527, A70 [CrossRef] [EDP Sciences] [Google Scholar]
- Krüger, C. J., & Foucart, F. 2020, Phys. Rev. D, 101, 103002 [CrossRef] [Google Scholar]
- Lamb, G. P., & Kobayashi, S. 2019, MNRAS, 489, 1820 [CrossRef] [Google Scholar]
- Lamb, G. P., Lyman, J. D., Levan, A. J., et al. 2019, ApJ, 870, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Lamb, G. P., Levan, A. J., & Tanvir, N. R. 2020, ApJ, 899, 105 [CrossRef] [Google Scholar]
- Lazzati, D., Perna, R., Morsony, B. J., et al. 2018, Phys. Rev. Lett., 120, 241103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lee, W. H., & Ramirez-Ruiz, E. 2006, ApJ, 641, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Leng, M., & Giannios, D. 2014, MNRAS, 445, L1 [CrossRef] [Google Scholar]
- Li, L.-X., & Paczyński, B. 1998, ApJ, 507, L59 [Google Scholar]
- LIGO Scientific Collaboration& Virgo Collaboration 2017a, Phys. Rev. Lett., 119, 161101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- LIGO Scientific Collaboration& Virgo Collaboration 2017b, ApJ, 851, L16 [NASA ADS] [CrossRef] [Google Scholar]
- LIGO Scientific Collaboration& Virgo Collaboration 2019, ApJ, 875, 160 [CrossRef] [Google Scholar]
- LIGO Scientific Collaboration, Virgo Collaboration, Fermi GBM, et al. 2017, ApJ, 848, L12 [Google Scholar]
- Liska, M., Tchekhovskoy, A., & Quataert, E. 2020, MNRAS, 494, 3656 [CrossRef] [Google Scholar]
- Liu, T., Yu, X.-F., Gu, W.-M., & Lu, J.-F. 2014, ApJ, 791, 69 [CrossRef] [Google Scholar]
- Liu, T., Hou, S.-J., Xue, L., & Gu, W.-M. 2015a, ApJ, 218, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, T., Lin, Y.-Q., Hou, S.-J., & Gu, W.-M. 2015b, ApJ, 806, 58 [CrossRef] [Google Scholar]
- Liu, T., Song, C.-Y., Zhang, B., Gu, W.-M., & Heger, A. 2018, ApJ, 852, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R. 2008, Liv. Rev. Rel., 11, 8 [Google Scholar]
- Lyman, J. D., Lamb, G. P., Levan, A. J., et al. 2018, Nat. Astron., 2, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Maraschi, L., & Tavecchio, F. 2003, ApJ, 593, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Margalit, B., & Metzger, B. D. 2017, ApJ, 850, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Berger, E., Fong, W., et al. 2017, ApJ, 848, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Alexander, K. D., Xie, X., et al. 2018, ApJ, 856, L18 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C. 2005, ApJ, 630, L5 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., & Gammie, C. F. 2004, ApJ, 611, 977 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., Tchekhovskoy, A., & Bland ford, R. D. 2012, MNRAS, 423, 3083 [NASA ADS] [CrossRef] [Google Scholar]
- Meszaros, P., & Rees, M. J. 1992, MNRAS, 257, 29P [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P., & Rees, M. J. 1997, ApJ, 476, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P., Rees, M. J., & Wijers, R. A. M. J. 1999, New Astron., 4, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D. 2017, Liv. Rev. Relat., 20, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Piro, A. L., & Quataert, E. 2009, MNRAS, 396, 304 [CrossRef] [Google Scholar]
- Metzger, B. D., Giannios, D., Thompson, T. A., Bucciantini, N., & Quataert, E. 2011, MNRAS, 413, 2031 [NASA ADS] [CrossRef] [Google Scholar]
- Mochkovitch, R., Hernanz, M., Isern, J., & Martin, X. 1993, Nature, 361, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Mochkovitch, R., Hernanz, M., Isern, J., & Loiseau, S. 1995, A&A, 293, 803 [Google Scholar]
- Moffatt, H. K. 1978, Magnetic Field Generation in Electrically Conducting Fluids [Google Scholar]
- Mooley, K. P., Deller, A. T., Gottlieb, O., et al. 2018a, Nature, 561, 355 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mooley, K. P., Frail, D. A., Dobie, D., et al. 2018b, ApJ, 868, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Mösta, P., Radice, D., Haas, R., Schnetter, E., & Bernuzzi, S. 2020, ApJ, 901, L37 [CrossRef] [Google Scholar]
- Nakar, E., & Piran, T. 2020, ApJ, submitted [arXiv:2005.01754] [Google Scholar]
- Narayan, R., Piran, T., & Kumar, P. 2001, ApJ, 557, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., Igumenshchev, I. V., & Abramowicz, M. A. 2003, PASJ, 55, L69 [NASA ADS] [Google Scholar]
- Nemmen, R. S., Georganopoulos, M., Guiriec, S., et al. 2012, Science, 338, 1445 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nicholl, M., Berger, E., Kasen, D., et al. 2017, ApJ, 848, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1986, ApJ, 308, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B., & Rhoads, J. E. 1993, ApJ, 418, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, Z., & Yuan, Y.-F. 2012, ApJ, 759, 82 [CrossRef] [Google Scholar]
- Perego, A., Radice, D., & Bernuzzi, S. 2017a, ApJ, 850, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Perego, A., Yasin, H., & Arcones, A. 2017b, J. Phys. G Nucl. Phys., 44, 084007 [CrossRef] [Google Scholar]
- Pian, E., D’Avanzo, P., Benetti, S., et al. 2017, Nature, 551, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Piran, T. 2004, Rev. Mod. Phys., 76, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Pjanka, P., Zdziarski, A. A., & Sikora, M. 2017, MNRAS, 465, 3506 [CrossRef] [Google Scholar]
- Popham, R., Woosley, S. E., & Fryer, C. 1999, ApJ, 518, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Radice, D. 2017, ApJ, 838, L2 [CrossRef] [Google Scholar]
- Radice, D., & Dai, L. 2019, Eur. Phys. J. A, 55, 50 [CrossRef] [EDP Sciences] [Google Scholar]
- Radice, D., Perego, A., Hotokezaka, K., et al. 2018, ApJ, 869, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Rawlings, S., & Saunders, R. 1991, Nature, 349, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Rhoads, J. E. 1997, ApJ, 487, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Rhoads, J. E. 1999, ApJ, 525, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Rossi, E. M., Armitage, P. J., & Di Matteo, T. 2007, Ap&SS, 311, 185 [CrossRef] [Google Scholar]
- Rosswog, S., Liebendörfer, M., Thielemann, F. K., et al. 1999, A&A, 341, 499 [NASA ADS] [Google Scholar]
- Rosswog, S., Ramirez-Ruiz, E., & Davies, M. B. 2003, MNRAS, 345, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. 1975, in Seventh Texas Symposium on Relativistic Astrophysics, eds. P. G. Bergman, E. J. Fenyves, & L. Motz, 262, 164 [Google Scholar]
- Ruffert, M., & Janka, H. T. 1999, A&A, 344, 573 [Google Scholar]
- Ruffert, M., Janka, H. T., Takahashi, K., & Schaefer, G. 1997, A&A, 319, 122 [Google Scholar]
- Ruiz, M., Tsokaros, A., Paschalidis, V., & Shapiro, S. L. 2019, Phys. Rev. D, 99, 084032 [CrossRef] [Google Scholar]
- Ruiz, M., Tsokaros, A., & Shapiro, S. L. 2020, Phys. Rev. D, 101, 064042 [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Halpern, J. P. 1999, ApJ, 519, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Savchenko, V., Ferrigno, C., Bozzo, E., et al. 2017, ApJ, 846, L23 [CrossRef] [Google Scholar]
- Shibata, M., & Hotokezaka, K. 2019, Ann. Rev. Nucl. Part. Sci., 69, 41 [CrossRef] [Google Scholar]
- Shibata, M., Sekiguchi, Y.-I., & Takahashi, R. 2007, Prog. Theor. Phys., 118, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, M., Fujibayashi, S., Hotokezaka, K., et al. 2017, Phys. Rev. D, 96, 123012 [NASA ADS] [CrossRef] [Google Scholar]
- Siegel, D. M., & Metzger, B. D. 2017, Phys. Rev. Lett., 119, 231102 [CrossRef] [Google Scholar]
- Siegel, D. M., & Metzger, B. D. 2018, ApJ, 858, 52 [CrossRef] [Google Scholar]
- Smartt, S. J., Chen, T.-W., Jerkstrand, A., et al. 2017, Nature, 551, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Soares, G., & Nemmen, R. 2020, MNRAS, 495, 981 [CrossRef] [Google Scholar]
- Stovall, K., Freire, P. C. C., Chatterjee, S., et al. 2018, ApJ, 854, L22 [CrossRef] [Google Scholar]
- Taylor, G. B., Frail, D. A., Berger, E., & Kulkarni, S. R. 2004, ApJ, 609, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Tchekhovskoy, A., & Giannios, D. 2015, MNRAS, 447, 327 [CrossRef] [Google Scholar]
- Tchekhovskoy, A., Narayan, R., & McKinney, J. C. 2010, ApJ, 711, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Tchekhovskoy, A., Narayan, R., & McKinney, J. C. 2011, MNRAS, 418, L79 [NASA ADS] [CrossRef] [Google Scholar]
- The LIGO Scientific Collaboration& The Virgo Collaboration 2019, Phys. Rev. X, 9, 011001 [Google Scholar]
- Thompson, C. 1994, MNRAS, 270, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Troja, E., Piro, L., van Eerten, H., et al. 2017, Nature, 551, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Troja, E., van Eerten, H., Ryan, G., et al. 2019, MNRAS, 489, 1919 [NASA ADS] [Google Scholar]
- Usov, V. V. 1994, MNRAS, 267, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, S., Sand, D. J., Yang, S., et al. 2017, ApJ, 848, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Villar, V. A., Guillochon, J., Berger, E., et al. 2017, ApJ, 851, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Vincent, T., Foucart, F., Duez, M. D., et al. 2020, Phys. Rev. D, 101, 044053 [CrossRef] [Google Scholar]
- Woods, E., & Loeb, A. 1994, ApJ, 425, L63 [CrossRef] [Google Scholar]
- Woods, E., & Loeb, A. 1995, ApJ, 453, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Ye, C. S., Fong, W.-F., Kremer, K., et al. 2020, ApJ, 888, L10 [CrossRef] [Google Scholar]
- Zalamea, I., & Beloborodov, A. M. 2011, MNRAS, 410, 2302 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, D., & Dai, Z. G. 2009, ApJ, 703, 461 [CrossRef] [Google Scholar]
- Zhang, B., Liang, E., Page, K. L., et al. 2007, ApJ, 655, 989 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Black hole mass and spin
A crucial parameter that regulates the efficiency of both the neutrino and Blandford & Znajek (1977) mechanisms is the BH spin. In neutron star mergers, the spin of the final remnant is set by angular momentum conservation: The simplest estimate is obtained by equating the angular momentum of the remnant BH to the orbital angular momentum of the binary prior to merger, which suggests a typical value around aBH ∼ 0.7. A more accurate estimate requires that the angular momentum lost in gravitational waves and stored in bound and unbound matter that does not immediately accrete onto the BH be taken into account. Based on a series of general relativistic numerical simulations, Coughlin et al. (2019) provide a fitting formula for the spin of the remnant BH in neutron star mergers, which depends on the component masses and on the dimensionless tidal deformability of the binary. The formula reads10
where ν = M1M2/(M1 + M2)2 and M = M1 + M2. Based on the same suite of simulations, they also provide a fitting formula for the remnant BH mass, which reads
Applying these formulae to the LVC posterior samples for the low spin prior, we obtain the posterior distributions shown in Fig. A.1, which we then used as inputs to our Blandford & Znajek (1977) and 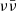 annihilation efficiency calculations in Sects. 5.1 and 5.2.
annihilation efficiency calculations in Sects. 5.1 and 5.2.
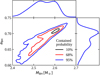 |
Fig. A.1. GW170817 remnant BH mass and spin posterior distributions, based on The LIGO Scientific Collaboration & The Virgo Collaboration (2019) posterior samples from the GW parameter estimation and on the Coughlin et al. (2019) fitting formulae. |
All Tables
Summary of the accretion-to-jet energy conversion efficiencies discussed in the text.
All Figures
 |
Fig. 1. GW170817 accretion disc mass posterior distributions. The solid red line shows the posterior probability distribution of the logarithm of the accretion disc mass (in solar masses) for the low-spin LVC priors. The dashed blue line shows the corresponding result that would have been obtained using the disc mass fitting formula from Radice et al. (2018). |
| In the text | |
 |
Fig. 2. Kinetic energy in the GRB 1790817A jet during the afterglow phase. The solid red line shows the posterior distribution constructed by fitting a structured jet afterglow model to the multi-wavelength afterglow and VLBI centroid motion by Ghirlanda et al. (2019). Black dots with error bars represent the estimates presented in several other papers, all based on afterglow fitting. All estimates essentially agree within the uncertainties. |
| In the text | |
 |
Fig. 3. Posterior probability density distribution of the accretion-to-jet energy conversion efficiency η = Ej/Mac2 in GW170817 (solid red line), assuming fw = 0.3 and fγ = 0.15. The dashed orange line shows the same quantity, but with the disc mass in GW170817 required to be equal or greater than 0.04 M⊙ (Radice & Dai 2019). Black error bars show the expected efficiency for the Blandford & Znajek (1977) and |
| In the text | |
 |
Fig. 4. Accretion-to-jet energy conversion efficiency of the Blandford & Znajek (1977) mechanism as a function of the BH spin parameter aBH from the GRMHD simulations of McKinney (2005, black squares) and Hawley et al. (2007, orange stars). The red and blue curves are fitting functions Eqs. (1) and (2), respectively. |
| In the text | |
 |
Fig. 5. Accretion-to-jet energy conversion efficiency of the |
| In the text | |
 |
Fig. A.1. GW170817 remnant BH mass and spin posterior distributions, based on The LIGO Scientific Collaboration & The Virgo Collaboration (2019) posterior samples from the GW parameter estimation and on the Coughlin et al. (2019) fitting formulae. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



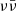
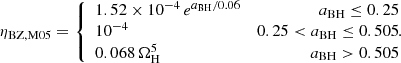
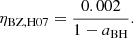
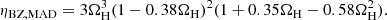
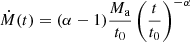
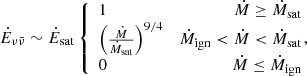
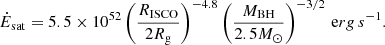
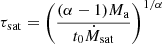
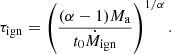
![$$ \begin{aligned} E_\mathrm j,\nu \bar{\nu } \sim \dot{E}_\mathrm{sat} t_0 \tau _\mathrm{sat} \left[\max \left(1-\tau _\mathrm{sat} ^{-1},0\right) + \frac{1}{\delta }\left(1-\left(\frac{\tau _\mathrm{sat} }{\tau _\mathrm{ign} }\right)^{\delta }\right) \right] .\end{aligned} $$](/articles/aa/full_html/2021/01/aa38590-20/aa38590-20-eq31.gif)
![$$ \begin{aligned} a_\mathrm{BH} = \tanh \left[0.537 (4 \nu )^2 \left(\frac{M}{{M_\odot }}-0.185\frac{\tilde{\Lambda }}{400}\right)-0.514\right] ,\end{aligned} $$](/articles/aa/full_html/2021/01/aa38590-20/aa38590-20-eq40.gif)