| Issue |
A&A
Volume 640, August 2020
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 18 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201937207 | |
| Published online | 07 August 2020 | |
Radio and X-ray connection in radio mini-halos: Implications for hadronic models
1
Dipartimento di Fisica e Astronomia, Università di Bologna, via Gobetti 93/2, 40129 Bologna, Italy
e-mail: alessandro.ignesti2@unibo.it
2
INAF, Istituto di Radioastronomia di Bologna, via Gobetti 101, 40129 Bologna, Italy
3
Naval Research Laboratory, 4555 Overlook Avenue SW, Code 7213, Washington, DC 20375, USA
Received:
28
November
2019
Accepted:
15
June
2020
Context. A large fraction of cool-core clusters are known to host diffuse, steep-spectrum radio sources, called radio mini-halos, in their cores. Mini-halos reveal the presence of relativistic particles on scales of hundreds of kiloparsecs, beyond the scales directly influenced by the central active galactic nucleus (AGN), but the nature of the mechanism that produces such a population of radio-emitting, relativistic electrons is still debated. It is also unclear to what extent the AGN plays a role in the formation of mini-halos by providing the seeds of the relativistic population.
Aims. In this work we explore the connection between thermal and non-thermal components of the intra-cluster medium in a sample of radio mini-halos and we study the implications within the framework of a hadronic model for the origin of the emitting electrons.
Methods. For the first time, we studied the thermal and non-thermal connection by carrying out a point-to-point comparison of the radio and the X-ray surface brightness in a sample of radio mini-halos. We extended the method generally applied to giant radio halos by considering the effects of a grid randomly generated through a Monte Carlo chain. Then we used the radio and X-ray correlation to constrain the physical parameters of a hadronic model and we compared the model predictions with current observations.
Results. Contrary to what is generally reported in the literature for giant radio halos, we find that the mini-halos in our sample have super-linear scaling between radio and X-rays, which suggests a peaked distribution of relativistic electrons and magnetic field. We explore the consequences of our findings on models of mini-halos. We use the four mini-halos in the sample that have a roundish brightness distribution to constrain model parameters in the case of a hadronic origin of the mini-halos. Specifically, we focus on a model where cosmic rays are injected by the central AGN and they generate secondaries in the intra-cluster medium, and we assume that the role of turbulent re-acceleration is negligible. This simple model allows us to constrain the AGN cosmic ray luminosity in the range ∼1044−46 erg s−1 and the central magnetic field in the range 10–40 μG. The resulting γ-ray fluxes calculated assuming these model parameters do not violate the upper limits on γ-ray diffuse emission set by the Fermi-LAT telescope. Further studies are now required to explore the consistency of these large magnetic fields with Faraday rotation studies and to study the interplay between the secondary electrons and the intra-cluster medium turbulence.
Key words: galaxies: clusters: intracluster medium / radiation mechanisms: non-thermal / radiation mechanisms: thermal / methods: observational / X-rays: galaxies: clusters
© ESO 2020
1. Introduction
Cluster scale radio emission probes magnetic field and relativistic particles in the intra-cluster medium (ICM) on hundred-kiloparsec to megaparsec scales, thus posing fundamental questions on the micro-physics of the ICM (e.g., Brunetti & Jones 2014, for review). In particular, in the past decades radio observations have revealed the presence of diffuse radio emission with a steep spectrum (α > 1 with synchrotron flux at the frequency νS ∝ ν−α) at the center of massive, relaxed clusters, the so-called radio mini-halos (MHs). The radio emission, whose emissivity is generally higher than that of giant radio halos (e.g., Cassano et al. 2008; Murgia et al. 2009), has been observed surrounding the central radio galaxy and extending up to 300 kpc (e.g., van Weeren et al. 2019, and the references therein). The radio emission is often confined within the cool cores of the clusters, thus suggesting a connection between the non-thermal ICM components and the thermal plasma (e.g., Mazzotta & Giacintucci 2008; Giacintucci et al. 2014a). This intrinsic connection is supported by the correlations observed between global radio and X-ray luminosities (Bravi et al. 2016; Gitti et al. 2015, 2018; Giacintucci et al. 2019). At the present time, we know 23 MHs, observed in almost all the massive cool-core clusters (the incidence is ∼80% for M500 > 6 ⋅ 1014 M⊙, Giacintucci et al. 2017), but current and future facilities, like the Low-Frequency Array (LOFAR) and the Square Kilometre Array (SKA), may have the potential to discover up to 104 new MHs (Gitti et al. 2018).
The origin of radio-emitting, cosmic-ray electrons (CRe) in the MH volume is still debated. Two possible scenarios have been proposed. One is the leptonic scenario, where the CRe, possibly injected by the active galactic nucleus (AGN) of the central radio galaxy, are re-accelerated by ICM turbulence. In this scenario the turbulence in the cool cores may be injected by the cooling flow of the ICM onto the central galaxy (e.g., Gitti et al. 2002), by the AGN itself during so-called “radio-mode” AGN feedback (e.g., McNamara & Nulsen 2012; Gitti et al. 2012, for a review), or by the gas dynamics driven by the cold fronts (e.g., ZuHone et al. 2013). The other scenario is the hadronic one, where CRe are produced by collisions between cosmic-ray protons (CRp) and the thermal protons of the ICM (e.g., Pfrommer & Enßlin 2004). Once the CRp are released into the cluster, most likely by the central AGN, they can diffuse on the scale of the observed radio emission due to their longer radiative times (τCRp ≃ 1010 yr ≫τCRe ≃ 108 years, e.g. Brunetti & Jones 2014).
The two scenarios share two common aspects: the possible role played by the AGN as the source of relativistic particles and the physical connection between the CRe and thermal plasma (as background medium for the turbulence or targets for CRp collisions). This connection would induce a spatial correlation between the radio, IR, and X-ray, IX, surface brightness. The importance of this correlation has been discussed in the case of giant radio halos (e.g., Govoni et al. 2001; Brunetti et al. 2004; Pfrommer 2008; Donnert et al. 2010; Brunetti & Jones 2014). In re-acceleration models the IR − IX correlation is sensitive to the way turbulence is generated in the thermal background plasma and relativistic particles are accelerated and transported in that turbulence. The correlation is particularly straightforward in the case of secondary models, where the thermal plasma, which generates the X-ray emission, also provides the targets for the inelastic collisions with the CRp that produce the secondary electrons emitting in the radio band. In this latter case, a super-linear scaling between radio and X-ray brightness is generally expected.
Similar considerations apply to the case of MHs, and thus following this idea, in this work for the first time we study the connection between IR and IX surface brightness for a sample of MHs. Our results enable us to place constraints on the dynamics of CR and magnetic fields in the emitting region. In particular, we explore the case of a hadronic model assuming that CRp are generated only by the central AGN and we show that is possible to obtain constraints on the magnetic field in the MH and CRp luminosity of the AGN.
The paper is structured as follows. In Sect. 2 we present the sample of MHs, the Chandra data reduction, and we introduce a new tool to evaluate the IR − IX connection. The results are presented in Sect. 3. In Sect. 4 we present a pure hadronic model, based on the diffusion of CRp from a central source, and we derive the physical conditions that allow the model to reproduce the observed radio emission for a sub-sample of MHs in the pure hadronic framework. The results are discussed and summarized in Sect. 5. In Appendix A we report a brief, morphological description of each cluster analyzed in this work, whereas the radio and X-ray maps that we used are presented in Appendix B, and the role of central sources is briefly discussed in Appendix C. In Appendix D we present our considerations on the diffusion coefficient that we adopted in Sect. 4. We adopted ΛCDM cosmology, with H0 = 73 km s−1 Mpc−1, Ωm = 1 − ΩΛ = 0.27.
2. Data analysis
Radio and X-ray correlations can be studied through the point-to-point connection between radio and X-ray surface brightness. For giant radio halos, these studies generally found a sub-linear scaling between the two quantities, as 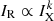 , with k ≤ 1 (Govoni et al. 2001; Feretti et al. 2001; Giacintucci et al. 2005; Vacca et al. 2010; Hoang et al. 2019). Here we extend the analysis of the IR − IX connection to the case of radio MHs. Exploring these correlations potentially provides important information on the origin of these sources and their connection with the central AGN. However, these studies are difficult for MHs because of their limited extent, which may affect the spatial sampling, and the presence of bright radio galaxies at their center, which may contaminate the diffuse emission. For these reasons, we selected a sample of targets with deep and well-resolved radio images in the literature. Our sample consists of seven MHs (Table 1). We then produced the X-ray images of each cluster from archival Chandra observations. We report in Appendix A a brief, morphological description of the clusters of our sample.
, with k ≤ 1 (Govoni et al. 2001; Feretti et al. 2001; Giacintucci et al. 2005; Vacca et al. 2010; Hoang et al. 2019). Here we extend the analysis of the IR − IX connection to the case of radio MHs. Exploring these correlations potentially provides important information on the origin of these sources and their connection with the central AGN. However, these studies are difficult for MHs because of their limited extent, which may affect the spatial sampling, and the presence of bright radio galaxies at their center, which may contaminate the diffuse emission. For these reasons, we selected a sample of targets with deep and well-resolved radio images in the literature. Our sample consists of seven MHs (Table 1). We then produced the X-ray images of each cluster from archival Chandra observations. We report in Appendix A a brief, morphological description of the clusters of our sample.
Physical properties of the clusters analyzed in this work.
2.1. Data preparation
The radio images used in this paper have been presented in previous works (see list of references in Table 2). The images were obtained from high-sensitivity, pointed radio observations with the Very Large Array (VLA) at 1.4 and 5.5 GHz and the Giant Metrewave Radio Telescope (GMRT) at 0.3 and 0.6 GHz. To enhance the diffuse emission, a weighting scheme close to natural weighting was typically adopted during the data imaging. Higher resolution images, showing the smaller scale emission associated with the central galaxy, are also presented in the previous works. All observations used to produce our MH images have a good sampling of the uv plane at short antenna spacings, which ensures the detection of large-scale emission (above the image sensitivity) on scales significantly larger than the measured extent of the MH (for details see Giacintucci et al. 2017, Table 10 and Fig. 12). Furthermore, the MH sizes do not appear to correlate with the signal-to-noise ratio of the radio images (Giacintucci et al. 2017, Appendix B), thus ensuring that the measured extent is not biased by the image sensitivity. Besides a good uv coverage at short spacings, the observations also have a sufficiently high resolution to disentangle the central radio galaxy from the surrounding diffuse emission. Nevertheless, to avoid any possible contamination of the radio galaxy emission into the diffuse MH, we masked the central region of each MH using an appropriate mask with a size larger than the radio beam. We report the mask of each cluster in Appendix B, whereas in Appendix C we briefly discuss the comparison between masked and source-subtracted images and we show that the two approaches are equivalent for the purpose of the study of the IR − IX spatial correlation.
Archival radio and X-ray observations used in this work.
Concerning the X-ray images, we retrieved the Chandra observations of the clusters from the archive1 to produce the X-ray images and to derive the physical quantities of the thermal ICM. When it was possible, we collected multiple observations to improve the sensitivity of our analysis. The datasets were reprocessed with CIAO v.4.9 and corrected for known time-dependent gain and charge transfer inefficiency problems following techniques similar to those described in the Chandra analysis threads2. To filter out strong background flares, we also applied screening of the event files. We used CALDB v.4.7.8 blank-sky background files normalized to the count rate of the source image in the 9–12 keV band to produce the appropriate background image for each observation. We produced the exposure-corrected, background-subtracted brightness maps in the energy range 0.5–2.0 keV. We used this energy band because it is where the thermal ICM emission and Chandra sensitivity are at their maximum, thus it assures an optimal count statistic for the analysis using our data. We checked for the presence of X-ray point sources embedded in the cluster emission and, if we found any, we masked them. We report the details of the radio images and archival X-ray observations in Table 2, while the X-ray images with the radio contours are presented in Appendix B.
2.2. Monte Carlo point-to-point analysis
Govoni et al. (2001) performed a point-to-point analysis of the radio and X-ray emission for a sample of clusters. In their work they adopted a single grid of cells to sample the diffuse radio emission. Here we extend the single-mesh point-to-point (SMptp) analysis introduced in Govoni et al. (2001). The case of MHs is more complex than that of giant, well-resolved, radio halos, because of the small number of independent beams sampling the surface brightness. Furthermore, the sampling scale that allows the maximum number of cells is the angular resolution of the image itself. However, using grids with cells as large as the beam of the image could generate biases in the analysis of the spatial correlations, because contiguous cells are not statistically independent. For these reasons, we carried out a Monte Carlo point-to-point (MCptp) analysis. We performed several cycles of SMptp analysis with a randomly generated mesh tailored to the diffuse radio emission for each one. Each cycle produced a different estimate of the k index (kSM) that we combined to obtain a more reliable estimate of the real scaling.
We have developed the MCptp analysis as follow:
-
Each cycle begins with the generation of the sampling mesh (Fig. 1, top panel). The grid is generated starting from a random point close to the center of the MH within a radius of ∼1/4 the radius of the MH. The size of the cells of the grid matches the resolution of the radio image to maximize the number of sampling points. The grid starts as a rectangle covering the whole MH, then its final shape is tailored by a given lower threshold on the radio surface brightness level and a mask provided by the user. The mask is produced by identifying the regions that are meant to be excluded from the analysis of the diffuse emission (emission related to the central galaxy or field sources). The IR is obtained from the total flux measured in every cell and, then, all those cells that cover a region of the sky previously masked or with an IR below the threshold are rejected;
-
IR and IX are measured in the cells of the final sampling grid obtained in step 1. When several Chandra observations of the same cluster are involved, we compute the total IX of a cell as
where
is the flux measured for the ith Chandra observation, Ωc is the angular area of the cell in units of arcsec2, and Ncnt, i, Nbkg, i (in units of counts), and qexp, i (in units of counts cm2 s photons−1) are, respectively, the values measured on the counts, the background, and the exposure map of the ith Chandra observation. We also compute the associated error on each measure. For the IR, we obtain the value of the uncertainties as the root mean square of the contribution from the noise of the map and the calibration error. We assume a calibration error of 5% of the amplitude, which is a value acceptable for both VLA and GMRT observations (e.g., Chandra et al. 2004). On the other hand, we derive the associated errors on SX, i by assuming a Poisson error for Ncnt, i and Nbkg, i and computing the error propagation of Eq. (1). The cells measuring upper limits for IR or IX are excluded from the following steps;
-
We estimate the value of kSM with the BCES (Bivariate Correlated Errors and intrinsic Scatter) estimator proposed by Akritas & Bershady (1996). We adopted this tool over the ordinary least squares estimator adopted in Govoni et al. (2001) because it takes into account the possible intrinsic scatter of the data with respect to the power-law fit and the errors associated to each measure. BCES estimates both the (IR ∣ IX) and (IX ∣ IR) slopes and then it estimates kSM, with the associated error σSM, as an index of the bisector slope between them (Fig. 1, bottom-left panel).
-
At the end of each cycle, we bootstrap a value of k from a normal distribution centered at kSM with a dispersion equal to σSM. This procedure enables us to transpose the error of the fit in the following step;
-
Finally, the result of the MCptp analysis, k, is
where
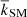 and σkSM are the mean and the standard deviation of the distribution of bootstrapped k obtained at the end of each cycle (Fig. 1, bottom-right panel).
and σkSM are the mean and the standard deviation of the distribution of bootstrapped k obtained at the end of each cycle (Fig. 1, bottom-right panel).
 |
Fig. 1. Top: Chandra image of the RBS 797 cluster with the contours at the −3, 3, 24, 96σ levels of the radio emission at 1.4 GHz (Doria et al. 2012). The resolution of the radio maps is 3″ × 3″ and 1σ = 10 μJy beam−1. Shown in green is the final mesh that samples the emission above the 3σ level with cells of 4″ × 4″ size. The central cavities and the external sources were masked (gray) and, therefore they were excluded from the sampling. Bottom-left: IR vs. IX plot where each point corresponds to a cell of the sampling mesh. The red and green lines are, respectively, the best-fit power law estimated for (IR ∣ IX) and (IX ∣ IR). The blue line is their bisector power law. The value of kSM is reported in the legend. Bottom-right: histogram of the distribution of values of kSM produced by the Monte Carlo point-to-point analysis with 1000 cycles. The best estimate of k is reported in the legend with the associated 1σ error. |
We developed a Python script to perform the steps of the MCptp analysis. The code handles the radio and X-ray maps through the National Radio Astronomy Observatory (NRAO) radio analysis package CASA (Common Astronomy Software Applications). The results presented here were obtained by using CASA v4.7.
3. Results
We performed the MCptp analysis with 1000 cycles on each MH of the sample. For each cluster, we set the size of the cells to match the resolution of the radio map and we set the IR minimum threshold for the brightness measured in each cell (flux/cell area) to 3σ. We excluded the region of the radio-filled cavities from the analysis for 2A0335+096, RBS 797 and RX J1532.9+3021. In Appendix B we report an example of a random SMptp analysis for each cluster (with the exception of RBS 797, which is shown in Fig. 1).
We found clear evidence of a spatial correlation between radio and X-ray emission. To further corroborate this result, we ran the Spearman test for each cluster, finding statistical dependence ρs > 0.6 and two-sided significance levels of deviation from zero Pc < 2 ⋅ 10−2. We also tested if the sampling size may affect the results of the MCptp. We tried to vary the size of the cells from the 1 × beam size to 1.5 × beam size, finding that the increment of the cell size does not produce significant differences in the results. We limit our analysis to the band 0.5–2 keV (Sect. 2.1). We could not test the presence of the correlation at higher energies because the low count statistics limit the quality of the brightness maps.
For the whole sample we estimate k ≥ 1 and for the two cases with radio observations at two frequencies we do not find a significant variation of k with frequency (Table 3). This is different from the sub-linear or linear scalings that are reported in the literature for giant radio halos (Govoni et al. 2001; Feretti et al. 2001; Giacintucci et al. 2005; Vacca et al. 2010; Hoang et al. 2019; Xie et al. 2020)3.
Results of the MCptp analysis.
4. Implications for hadronic models
The study of radio and X-ray brightness distribution provides important information on the origin of diffuse radio sources and on the model parameters (e.g., Govoni et al. 2001; Brunetti et al. 2004; Pfrommer 2008; Brunetti & Jones 2014). In this paper we focus on the hadronic model. The super-linear scaling between IR and IX for MHs suggests that the number density of emitting electrons rapidly declines from the center to the external regions. One possibility is that CRp propagate from the central AGN and generate secondary particles, from inelastic collisions with thermal protons in the ICM, which emit the observed radio emission. As we will show in the following, in this scenario the observed radio and X-ray spatial correlation can constrain the model parameters, including the CRp luminosity of the AGN and the magnetic fields in the MH volume. We note, however, that steep IR profiles can also be explained by pure leptonic models (e.g., Gitti et al. 2002, for the MH in the Perseus cluster).
4.1. Model
In the context of a pure hadronic scenario, we assume the central AGN as the primary source of CRp, which are injected with a rate of
where p is the proton momentum for which we assumed a power-law distribution in momentum as typically assumed for CR sources in the ICM (Brunetti & Jones 2014, for a theoretical discussion). We assume a diffusive propagation of CR on scales much larger than the coherent scale of the magnetic field in the ICM, (≫10 kpc, e.g., Brunetti & Jones 2014). In this case, the time required for a particle to diffuse up to the observed MH radius, RMH, is 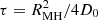 , where D0 is the spatial diffusion coefficient. In this work we assumed a diffusion coefficient D0 that does not depend on CRp energy. The resulting spectrum of CRp as a function of momentum, distance, and time is
, where D0 is the spatial diffusion coefficient. In this work we assumed a diffusion coefficient D0 that does not depend on CRp energy. The resulting spectrum of CRp as a function of momentum, distance, and time is
where r is the distance from the source and 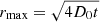 is the distance reached by CRp in an interval of time t (e.g., Blasi & Colafrancesco 1999). In this paper we assume the simplified case where stationary conditions for CRp distribution are established. These conditions are generated by the interplay of diffusion and injection from the central AGN and are valid under the following assumptions:
is the distance reached by CRp in an interval of time t (e.g., Blasi & Colafrancesco 1999). In this paper we assume the simplified case where stationary conditions for CRp distribution are established. These conditions are generated by the interplay of diffusion and injection from the central AGN and are valid under the following assumptions:
-
CRp diffuse on a MH scale on a timescale that is considerably smaller than the timescale of the energy losses of CRp with energy ∼100 GeV (∼1010 yr, e.g., Brunetti & Jones 2014); this condition selects a minimum value of the spatial diffusion coefficient (see Appendix D for details);
-
The CRp injection rate from the AGN, LCRp, is fairly constant when averaged and sampled on a sufficiently long timescale (smaller than the diffusion time) of about 100 Myr or longer. We note that this also includes the possibility of an AGN duty-cycle, provided that its timescale is considerably smaller than the diffusion time.
Assuming stationary conditions, Eq. (5) gives the stationary solution
While they are diffusing over the cluster volume, CRp with kinetic energy above 300 MeV (e.g., Brunetti et al. 2017) interact with the ICM thermal protons in the cool core, for which we assumed a β-model distribution
where n0 is the central proton density, rc is the core radius, and β describes the ratio between thermal and gravitational energy of the plasma (e.g., Cavaliere & Fusco-Femiano 1976). As a result of these interactions, secondary particles, that is, π0, positrons, and electrons, are continuously injected into the cluster volume (e.g., Blasi & Colafrancesco 1999; Pfrommer & Enßlin 2004; Brunetti & Blasi 2005).
We follow the procedures in Brunetti et al. (2017, Sect. 3.4) to calculate the injection spectrum of secondary electrons and positrons, 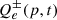 , and calculate the spectrum of electrons and positrons,
, and calculate the spectrum of electrons and positrons, 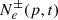 , assuming the stationary conditions
, assuming the stationary conditions
where |dp/dt|rad, i are the radiative and Coulomb losses, and
where Fe(Ee,Eπ) is given in Brunetti & Blasi (2005) (Eqs. (36) and (37)), 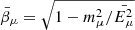 ,
, 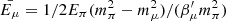 ,
, 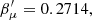 and dσ±, 0/dE is the differential inclusive cross-section for the production of charged and neutral pions (we assume the cross-section in Brunetti et al. 2017). The secondary CRe injected into the ICM magnetic field, B(r), can generate, in turn, synchrotron radio emission with an emissivity
and dσ±, 0/dE is the differential inclusive cross-section for the production of charged and neutral pions (we assume the cross-section in Brunetti et al. 2017). The secondary CRe injected into the ICM magnetic field, B(r), can generate, in turn, synchrotron radio emission with an emissivity
where 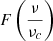 is the synchrotron kernel (e.g., Rybicki & Lightman 1979), BCMB = 3.25(1 + z)2μG is the cosmic microwave background (CMB) equivalent magnetic field and the spectral index is α ≃ δ/2 (Brunetti et al. 2017, and references therein). We assumed that the ICM magnetic field radial profile scaled with the gas density profile, nth(r), as
is the synchrotron kernel (e.g., Rybicki & Lightman 1979), BCMB = 3.25(1 + z)2μG is the cosmic microwave background (CMB) equivalent magnetic field and the spectral index is α ≃ δ/2 (Brunetti et al. 2017, and references therein). We assumed that the ICM magnetic field radial profile scaled with the gas density profile, nth(r), as
where η is the parameter that describes the scaling and n0 is the central gas density (Eq. (7)).
We follow the procedures in Brunetti et al. (2017) to calculate the injection spectrum of neutral pions:
Then the γ-ray emissivity produced by the π0 decay is
which produces a large-scale γ-ray halo surrounding the AGN.
Finally, due to the spherical symmetry of our model, radio and γ-ray emissivities can be straightforwardly converted into a surface brightness profile with the Abel transformation
where IR, γ(b) is the surface brightness at the projected distance b obtained by integrating the emissivity jR, γ(r) along the line of sight. In this pure, hadronic framework, from the ratio of Eqs. (10) and (13) we can derive a relation between radio and γ-ray emission as
where A(α) is function of the spectral index and the quantities are averaged in the emitting volume. Equation (15) shows that for a source with an observed LR, which is assumed to be generated only by secondary electrons, a larger (smaller) γ-ray luminosity is predicted for weaker (stronger) magnetic fields. This is simply because for weaker (stronger) magnetic fields a larger (smaller) number of secondary electrons is necessary to explain the observed radio luminosity, which also implies a larger (smaller) number of CR that generate the neutral pions and the γ-rays.
4.2. Application to a sample of MHs
The model presented in Sect. 4.1 is based on spherical symmetry. For this reason we select only the most roundish MHs of our sample, namely RBS 797, RXC J1504.1−0248, RX J1532.9+3021, and Abell 3444, for which we could extend our assumption of spherical symmetry. Specifically, our model depends on a set of physical parameters:
-
CRp injection spectrum;
-
Number density of thermal targets;
-
ICM magnetic field;
-
AGN CRp luminosity.
In the hadronic framework the spectrum of CRp can be constrained from the radio spectrum of MHs as δ ≃ α/2. We infer the parameters that describe the distribution of thermal plasma inside the MHs (n0, β and rc, see Table 4) from the observed IX profile as (e.g., Sarazin 1986)
Parameters of the nth profile estimated within RMH.
where Λ(T) is the cooling function that describes the emissivity of a plasma with a temperature T that we measured from the X-ray spectra (Sutherland & Dopita 1993). The remaining model parameters to constrain are, thus, the AGN CRp luminosity and the magnetic field in the ICM. In the following we describe in detail the steps of our analysis. We report the results of this analysis in Table 5.
Parameters of the hadronic model.
4.2.1. ICM magnetic field implied by the IR − IX correlation
In the case of spherical symmetry, the radial profile of the ratio IR/IX depends on the magnetic field model (Eqs. (10), (11), (14), and (15)). Specifically, the values of the index k in Sect. 3 constrain a range of values for the couples B0 − η. Therefore, for each cluster, we calculated numerically the IR within the MH radius (Table 1) by testing a wide range of combinations B0 − η, then we compared them with the observed IX to estimate the corresponding k-index. In Fig. 2 we report the numerical estimates compared with the observed k for each cluster. For RBS 797 the spectral index of the diffuse emission was not measured unambiguously (Doria et al. 2012), therefore we tested two extreme possibilities, α = 1.1 (δ = 2.2) and α = 1.5 (δ = 3.0).
 |
Fig. 2. Parameter spaces of k-index for the spherical MHs. The red lines locate the 1-σ confidence interval for k measured for each MH. For RBS 797 we report the result obtained with α = 1.1. For Abell 3444 we report in red the result at 610 MHz and in green the result at 1.4 GHz. The horizontal, dashed line points out the level η = 0.5 that reproduces the equilibrium between thermal and non-thermal energy. For RXC J1504.1−0248 we report the η = 1 level with the black dash-dotted line and the lower limit derived from the Fermi-LAT observation presented in Dutson et al. (2013). The lower limits for B0 for the other clusters are below 1 μG and they are reported in Table 6. |
We found that for a given value of k, larger values of B0 are obtained for larger values of η. As a reference value, we assumed η = 0.5, which is the case where magnetic field energy scales linearly with thermal energy for isothermal ICM. Under this assumption, we constrain central values of the magnetic field of 11.8 ± 4.8 and 18.5 ± 5.5 μG for RBS 797 assuming α=1.1 and α = 1.5, 18.8 ± 5.5 μG for Abell 3444, and we derive a lower limit of 14.5 μG for RX J1532.9+3021 (see Figs. B.1 and B.2).
A value of η = 0.5 is inconsistent with the case of RXC J1504.1−0248, whose steep scaling (k ≃ 2) is reproduced only by a peaked spatial distribution of the magnetic field (0.6 < η < 1.3). On the one hand, by assuming a steeper profile for the magnetic field (η = 1), we estimate a central magnetic field B0 = 20.0 ± 18.5 μG. On the other hand, assuming η = 0.5 would require a CRp density radial profile steeper than the ∝1/r profile of the stationary solution (Eq. (6)) to produce a final IR as peaked in the center as the observed one. This case would imply a more complicated situation, including (1) a non-constant CRp luminosity of the central AGN showing a significant enhancement across the duty cycle, or (2) that the diffusion time that is necessary for CRp to cover the MH scale is longer than (i) the AGN activity timescale, and/or (ii) the energy losses of CRp.
Fermi lower limits for the central magnetic field B0.
4.2.2. AGN CRp luminosity
Once the scaling between the magnetic field and the thermal density is constrained by the observed scaling between IR and IX, we can derive the CRp luminosity of the central AGN that is required to substain the observed radio luminosity of MHs. The AGN luminosity, LCRp, is
where mp is the proton mass and p0.2GeV is the momentum for which the kinetic energy, pc, is 0.2 GeV. We note that for δ < 3 the exact choice of the minimum energy is not relevant for the final result.
In order to obtain the value of Q0 to compute LCRp (Eq. (17)) we matched the observations with the IR profiles predicted by our model. We estimated the synchrotron emissivity numerically with Eq. (10) by following the formalism presented in Sect. 4.1 and by assuming the B(r) configurations that we constrained in Sect. 4.2.1. The radio emission depends on the ratio Q0/D0 (Eq. (10)), therefore we estimated Q0, and thus LCRp, by assuming a diffusion coefficient 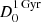 for which the diffusion time of CRp in the MH is
for which the diffusion time of CRp in the MH is 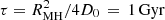 . This implies an optimistic diffusion coefficient and consequently a upper bound to the LCRp that is required by the model. In Appendix D we discuss the consequences of different assumptions, including the scenario of total dissipation of CRp within RMH, which entails the lower bound for LCRp in our model. Finally we compared them with the observed IR profiles measured in circular bins with the same resolution of the radio maps. We report in Table 5 the parameters adopted and the results obtained. We estimate that the AGN LCRp required in our model to reproduce the observed radio emission is 1044–1046 erg s−1 (see Appendix D). In Figs. 3–5 for each cluster we report the integrated radio luminosity and the surface brightness radial profiles, predicted and observed, at the observed frequency.
. This implies an optimistic diffusion coefficient and consequently a upper bound to the LCRp that is required by the model. In Appendix D we discuss the consequences of different assumptions, including the scenario of total dissipation of CRp within RMH, which entails the lower bound for LCRp in our model. Finally we compared them with the observed IR profiles measured in circular bins with the same resolution of the radio maps. We report in Table 5 the parameters adopted and the results obtained. We estimate that the AGN LCRp required in our model to reproduce the observed radio emission is 1044–1046 erg s−1 (see Appendix D). In Figs. 3–5 for each cluster we report the integrated radio luminosity and the surface brightness radial profiles, predicted and observed, at the observed frequency.
 |
Fig. 3. Results for RBS 797 for δ = 2.2 (top) and δ = 3.0 (bottom). Left: integrated radio and γ-ray luminosity. Right: radio and γ-ray surface brightness. We report the observed IR profile and the 3σ level of the observation (dashed red line). |
 |
Fig. 4. Results for Abell 3444 at 1.4 GHz (top) and RX J1532.9+3021 (bottom). For the latter, we report reference values of LR and Lγ derived from the upper limit of the magnetic field (Table 5). Left: integrated radio and γ-ray luminosity. Right: radio and γ-ray surface brightness. We report the observed IR profile and the 3σ level of the observation (dashed red line). |
 |
Fig. 5. Results for RXC J1504.1−0248 with B0 = 1 μG (top), B0 = 10 μG (middle), and B0 = 20 μG (bottom). Left: integrated radio and γ-ray luminosity. Right: radio and γ-ray surface brightness. We report the observed IR profile and the 3σ level of the observation (dashed red line). We limited the profile up to RMH to avoid possible contamination by field sources (see Fig. B.3). |
4.3. Resulting γ-rays emission and comparison with current and future observations
In the previous sections we used the IR − IX scaling to derive constraints on the model parameters. In this section we check if the γ-ray fluxes are consistent with current observational limits. We calculated numerically the γ-ray emission produced by the π0 decay described in Sect. 4.1 within the same physical boundaries adopted in Sect. 4.2.2 by implementing numerically Eq. (13). However, the approximation of thermal density adopted to reproduce the MH volume (Eq. (7)) could extrapolate incorrectly the thermal density beyond RMH. Therefore, to calculate the total γ-ray luminosity we used a double β-model to better describe the radial decline of the thermal gas density beyond RMH.
In Table 5 we report the radius containing 85% of the γ-ray emission and the γ-ray flux. Figures 3–5 report the integrated γ-ray luminosity and surface brightness radial profiles at 1 GeV. The radio and γ-ray halos differ in terms of size, because the jR (Eq. (10)) declines faster than jγ (Eq. (13)). According to our results, the γ-ray halos extend beyond the cooling region, which contains instead almost the totality of the radio emission. In the case of RXC J1504.1−0248, the value of B0 is poorly constrained from the analysis presented in Sect. 4.2.1 (B0 = 20.0 ± 18.5 μG). Therefore, for this cluster we compute LCRp and the γ-ray emission assuming three values of the central magnetic field, namely B0 = 1.0, 10.0, 20.0 μG. We note that assuming B0 > 20 μG would produce results close to the case B0 = 20.0 μG (Eq. (15)).
Diffuse γ-ray emission from galaxy clusters has never been firmly detected, so we tested the consistency of our model with the observational constraints. This is shown in Fig. 6, where we compare the expected γ-ray emission, computed with the parameters reported in Table 5, with the Fermi-LAT detection limit after 15 years. In general, we find that the γ-ray fluxes predicted for the four MHs are below the Fermi-LAT detection limit, hence our model constrained from the IR − IX scaling does not violate the current non-detection of diffuse γ-ray emission. The Fermi-LAT detection limits can also be used to infer complementary limits to the central magnetic field B0 in our model, because in our model a fainter magnetic field will result in stronger γ-ray emission (Eq. (15)). For RBS 797, Abell 3444, and RX J1532.9+3021 we used the results of the Fermi-LAT 15yr observations as constraints, whereas for RXC J1504.1−0248 we used the limit obtained by Dutson et al. (2013) with the Fermi-LAT. In Table 6 we report the limits inferred for the configurations of ICM magnetic field and LCRp constrained by our results. The Fermi-LAT detection limit provides lower limits below 1 μG for RBS 797, Abell 3444, and RX J1532.9+3021. On the contrary, for RXC J1504.1−0248 the lower limit is 5.9 μG, due to the higher γ-ray emissivity predicted by our model.
 |
Fig. 6. Predicted γ-rays spectrum for the MHs for parameters reported in Table 5 compared with the Fermi-LAT 15 yr detection limit. |
5. Discussion and summary
In this work, for the first time, we have carried out a systematic study of the spatial connection between thermal and non-thermal ICM components in relaxed clusters. Here we summarize and discuss our results.
5.1. New scaling relation for MHs
The most important result of our paper comes from the study of the spatial correlation between non-thermal radio and thermal X-ray brightness for a sample of seven MHs. We extended the strategy based on a single grid, which has been applied to giant radio halos, by including a Monte Carlo approach in the generation of the grid. This approach allows us to avoid the biases generated by the relatively small (∼20–30) number of independent radio beams that cover the emission of MHs (after excluding the regions contaminated by discrete sources). We found evidence of a spatial correlation between IR and IX, where the radio emission is generally more peaked than the thermal emission, thus indicating that the ICM non-thermal components are more concentrated around the central AGN. Our result further confirms the connection between thermal and non-thermal ICM components in MHs, which has already been claimed by previous works that studied the correlations between radio and X-ray luminosity (Gitti et al. 2015, 2018; Bravi et al. 2016; Giacintucci et al. 2019) and the morphological connection between cold fronts and MHs (Mazzotta & Giacintucci 2008). Furthermore, the values of k that we measure for MHs differ from the case of radio halos reported in the literature, where a sub-linear or linear scaling is generally found (Govoni et al. 2001; Feretti et al. 2001; Giacintucci et al. 2005; Vacca et al. 2010; Hoang et al. 2019). This may suggest an intrinsic difference in the nature of these radio sources. The steep decline of the radio emission in MHs also suggests that secondary particles injected at the center by the AGN play a role, both directly or as seed particles re-accelerated by other mechanisms.
5.2. Comparison with hadronic models
We consider a simple, reference hadronic model based on the injection of CRp by the central AGN. The model is a pure hadronic scenario without including the effect of re-acceleration. Furthermore, we assume that the combination of CRp injection and diffusion generates stationary conditions in the ICM. We note that this simple scenario connecting the AGN activity and the MH has already been proposed to explain the origin of the Perseus MH (e.g., Boehringer & Morfill 1988; Pfrommer & Enßlin 2004) and, in general, to evaluate the effect of CRp-driven streaming instability on the heating of the cool cores and the connection with the formation of MHs (e.g., Fujita & Ohira 2013; Jacob & Pfrommer 2017; Ehlert et al. 2018). We compare the observed scalings between IR and IX with our simple model to infer combined constraints on the AGN CRp luminosity and the ICM magnetic field. We selected the four MHs of our sample with a roundish shape for which it is possible to assume spherical symmetry in 3D. In this case, constraints deriving from point-to-point correlations are similar to those deriving from the azimuthally averaged brightness profile. Specifically, we derive B0 in the range 10-40 μG assuming η = 0.5, where smaller values of B0 would require smaller values of η, and a 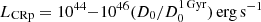 , where we assumed a
, where we assumed a 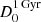 that allows the diffusion of CRp in the MH volume in 1 Gyr. We stress that, although these results are based on the assumption of stationary conditions, they are obtained by sampling spatial scales of a few 100 kpc and consequently they do not depend significantly on local variations. As a consequence, we expect that only a strong violation of stationary conditions can affect our conclusions.
that allows the diffusion of CRp in the MH volume in 1 Gyr. We stress that, although these results are based on the assumption of stationary conditions, they are obtained by sampling spatial scales of a few 100 kpc and consequently they do not depend significantly on local variations. As a consequence, we expect that only a strong violation of stationary conditions can affect our conclusions.
The values of B0 that we found are consistent, although slightly larger than the values reported by Carilli & Taylor (2002) for relaxed clusters. An independent observational test of pure hadronic models, where the AGN plays the main role in the injection of the primary CRp, would thus result from detailed studies of the Faraday rotation measure and depolarization of the discrete radio sources embedded in the cluster core or in background (e.g., Bonafede et al. 2011).
5.2.1. γ-ray emission
The unavoidable consequence of a hadronic scenario is the production of γ-rays with a luminosity that is close to the CRp luminosity of the AGN, where the γ-ray luminosity depends on the model parameters. In Sect. 4.3 we calculated the γ-ray emission under the assumption of the parameters reported in Table 5. The expectations do not violate Fermi upper limits (Fig. 6). We found that smaller B0 produce a larger γ-ray luminosity, whereas larger D0 entail larger LCRp and fulfill the stationary conditions for the CRp distribution in shorter timescales. The Fermi-LAT detection limit allowed us to provide a lower limit for the central magnetic field, which we report in Table 6. The Iγ profile is broader than the IR profile (Figs. 3–5), although for the parameters used in Sect. 4.2 we find that the radius where 85% of the emission is produced is larger than the core radius of the cluster.
5.2.2. Observation tests and limitations
The size of the MH predicted by our model depends on our assumptions on the diffusion coefficient (see Appendix D). Large diffusion coefficients produce MHs that extend beyond the radius measured by current observations (Figs. 3–5). Deeper observations of the MHs of our sample will allow us to test whether the emission can extend on larger scales or is more confined, for example within the region defined by cold fronts (Mazzotta & Giacintucci 2008). These tests will allow us to understand whether additional mechanisms, such as turbulent re-acceleration, are necessary to explain observations (ZuHone et al. 2013).
One of the main caveats in our analysis is the assumption of stationary conditions. On the one hand, these are justified by the fact that in a cooling time the CRp can diffuse on scales similar to or larger than that of MHs. On the other hand, the duty cycles of AGN last for 107−108 years (Morganti 2017) and, consequently, the MHs would be powered by numerous bursts of injection of CRp, whose diffusion scale is 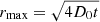 , with t being the look-back time for the single burst. Consequently, stationary conditions also imply that the phase of the interplay between the AGN and MH is much longer than a single burst of activity of the AGN and, thus, that the MH results from the integrated effect of many bursts and AGN active phases. However, if the system has recently experienced unusually powerful AGN activity (injection of CRp), the resulting spatial distribution of CRp would be steeper than in our approximation. This would also result from a scenario where the LCRp of the AGN active phases decreases with look-back time. The case of RX1504 where a very steep trend between radio and X-ray brightness is found, might suggest that the system had very strong CRp activity in the last 100 Myr or so.
, with t being the look-back time for the single burst. Consequently, stationary conditions also imply that the phase of the interplay between the AGN and MH is much longer than a single burst of activity of the AGN and, thus, that the MH results from the integrated effect of many bursts and AGN active phases. However, if the system has recently experienced unusually powerful AGN activity (injection of CRp), the resulting spatial distribution of CRp would be steeper than in our approximation. This would also result from a scenario where the LCRp of the AGN active phases decreases with look-back time. The case of RX1504 where a very steep trend between radio and X-ray brightness is found, might suggest that the system had very strong CRp activity in the last 100 Myr or so.
5.3. Future prospects
The Monte Carlo point-to-point analysis and BCES fitting procedure presented in this work can be extended to a larger sample of targets, including both mini and giant radio halos, to confirm the different behavior that we observe. Moreover, the estimates provided by our model could work as constraints for future theoretical work aimed at addressing the connection between AGN feedback and cooling flow quenching. Our results suggest that simple hadronic models can still match the main observations of MHs. Further studies are now required to address the implications of secondary production of electrons in the presence of ICM turbulence, and the implications of interplay with the leptonic models in general in the origin of the diffuse radio emission. The incoming Athena X-ray observatory will play a crucial role in these studies by providing an unprecedented spectral resolution. In particular, by combining radio images and Athena X-ray Integral Field Unit (X-IFU, Barcons et al. 2017) observations in a point-to-point analysis, we will be able to explore the spatial connection between the energy of CRe and the ICM turbulence.
The study of radio emission in galaxy clusters will greatly benefit from the present and new radio observatories, such as LOFAR and SKA, that could potentially observe thousands of new sources. Interestingly, LOFAR observations are already showing that relaxed clusters can host diffuse, ultra-steep spectrum emission extending far beyond the sloshing region, suggesting a more complex scenario involving “gentle” CRe re-acceleration due to ICM turbulence on large scales (Savini et al. 2018, 2019). In this case, follow-up studies of point-to-point brightness distribution based on our approach open up the possibility of discriminating the contribution of hadronic collisions (pure hadronic or re-accelerated secondaries) from that of turbulent re-acceleration of primary seeds, because the two regimes should produce different scalings. By probing the steep spectrum emission on larger scales at lower frequencies, we may expect to observe a flattening of the radio and X-ray scaling, similar to what is observed in giant radio halos.
The only exception is 1RXS J0603.3+4214 (Rajpurohit et al. 2018). This difference may suggest an intrinsic difference in the origin and dynamics of the CRs in MHs and giant radio halos, although a re-analysis of the case of giant radio halos adopting our procedure is required for a more quantitative statement.
Acknowledgments
We thank the Referee for their comments that improved the presentation of the work. AI thanks M. Sereno for the useful discussion. Basic research in radio astronomy at the Naval Research Laboratory is supported by 6.1 Base funding. This research made use of APLpy, an open-source plotting package for Python (Robitaille & Bressert 2012).
References
- Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Barcons, X., Barret, D., Decourchelle, A., et al. 2017, Astron. Nachr., 338, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., & Colafrancesco, S. 1999, Astropart. Phys., 12, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Boehringer, H., & Morfill, G. E. 1988, ApJ, 330, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Bonafede, A., Govoni, F., Feretti, L., et al. 2011, A&A, 530, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bravi, L., Gitti, M., & Brunetti, G. 2016, MNRAS, 455, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G. 2004, in 195: Outskirts of Galaxy Clusters: Intense Life in the Suburbs, ed. A. Diaferio, IAU Colloq., 148 [Google Scholar]
- Brunetti, G., & Blasi, P. 2005, MNRAS, 363, 1173 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., & Jones, T. W. 2014, Int. J. Mod. Phys. D, 23, 30007 [Google Scholar]
- Brunetti, G., Zimmer, S., & Zandanel, F. 2017, MNRAS, 472, 1506 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., & Taylor, G. B. 2002, ARA&A, 40, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., Gitti, M., & Brunetti, G. 2008, A&A, 486, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS] [Google Scholar]
- Chandra, P., Ray, A., & Bhatnagar, S. 2004, ApJ, 612, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Donnert, J., Dolag, K., Brunetti, G., Cassano, R., & Bonafede, A. 2010, MNRAS, 401, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Doria, A., Gitti, M., Ettori, S., et al. 2012, ApJ, 753, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Dutson, K. L., White, R. J., Edge, A. C., Hinton, J. A., & Hogan, M. T. 2013, MNRAS, 429, 2069 [NASA ADS] [CrossRef] [Google Scholar]
- Ehlert, K., Weinberger, R., Pfrommer, C., Pakmor, R., & Springel, V. 2018, MNRAS, 481, 2878 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L., Fusco-Femiano, R., Giovannini, G., & Govoni, F. 2001, A&A, 373, 106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fujita, Y., & Ohira, Y. 2013, MNRAS, 428, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Giacintucci, S., Markevitch, M., Brunetti, G., Cassano, R., & Venturi, T. 2011, A&A, 525, L10+ [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giacintucci, S., Venturi, T., Brunetti, G., et al. 2005, A&A, 440, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giacintucci, S., Markevitch, M., Brunetti, G., et al. 2014a, ApJ, 795, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Giacintucci, S., Markevitch, M., Venturi, T., et al. 2014b, ApJ, 781, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Giacintucci, S., Markevitch, M., Cassano, R., et al. 2017, ApJ, 841, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Giacintucci, S., Markevitch, M., Cassano, R., et al. 2019, ApJ, 880, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Gitti, M., Brunetti, G., & Setti, G. 2002, A&A, 386, 456 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gitti, M., Feretti, L., & Schindler, S. 2006, A&A, 448, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gitti, M., Brighenti, F., & McNamara, B. R. 2012, Adv. Astron., 2012, [CrossRef] [Google Scholar]
- Gitti, M., Giroletti, M., Giovannini, G., Feretti, L., & Liuzzo, E. 2013, A&A, 557, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gitti, M., Tozzi, P., Brunetti, G., et al. 2015, Proceedings of Advancing Astrophysics with the Square Kilometre Array, PoS(AASKA14)076, 76 [Google Scholar]
- Gitti, M., Brunetti, G., Cassano, R., & Ettori, S. 2018, A&A, 617, A11 [CrossRef] [EDP Sciences] [Google Scholar]
- Govoni, F., Enßlin, T. A., Feretti, L., & Giovannini, G. 2001, A&A, 369, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hlavacek-Larrondo, J., Allen, S. W., Taylor, G. B., et al. 2013, ApJ, 777 [Google Scholar]
- Hoang, D. N., Shimwell, T. W., van Weeren, R. J., et al. 2019, A&A, 622, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jacob, S., & Pfrommer, C. 2017, MNRAS, 467, 1449 [Google Scholar]
- Mazzotta, P., & Giacintucci, S. 2008, ApJ, 675, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzotta, P., Markevitch, M., Vikhlinin, A., et al. 2001, ApJ, 555, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzotta, P., Edge, A. C., & Markevitch, M. 2003, ApJ, 596, 190 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2012, New J. Phys., 14, 055023 [NASA ADS] [CrossRef] [Google Scholar]
- Morganti, R. 2017, Nat. Astron., 1, 596 [Google Scholar]
- Murgia, M., Govoni, F., Markevitch, M., et al. 2009, A&A, 499, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfrommer, C. 2008, MNRAS, 385, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Pfrommer, C., & Enßlin, T. A. 2004, A&A, 413, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rajpurohit, K., Hoeft, M., van Weeren, R. J., et al. 2018, ApJ, 852, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T., & Bressert, E. 2012, APLpy: Astronomical Plotting Library in Python [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics, ed (Rybicki: G. B. & Lightman, A. P) [Google Scholar]
- Sanders, J. S., Fabian, A. C., & Taylor, G. B. 2009, MNRAS, 396, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1986, Rev. Mod. Phys., 58, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L., Baum, S. A., & O’Dea, C. P. 1995, ApJ, 451, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Savini, F., Bonafede, A., Brüggen, M., et al. 2018, MNRAS, 478, 2234 [NASA ADS] [CrossRef] [Google Scholar]
- Savini, F., Bonafede, A., Brüggen, M., et al. 2019, A&A, 622, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Vacca, V., Murgia, M., Govoni, F., et al. 2010, A&A, 514, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., de Gasperin, F., Akamatsu, H., et al. 2019, Space Sci. Rev., 215, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Venturi, T., Giacintucci, S., Brunetti, G., et al. 2007, A&A, 463, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xie, C., van Weeren, R. J., Lovisari, L., et al. 2020, A&A, 636, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ZuHone, J. A., Markevitch, M., Brunetti, G., & Giacintucci, S. 2013, ApJ, 762, 78 [NASA ADS] [CrossRef] [Google Scholar]
- ZuHone, J. A., Brunetti, G., Giacintucci, S., & Markevitch, M. 2015, ApJ, 801, 146 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Cluster sample
Here we present a brief morphological description of each cluster of the sample.
2A0335+096. The MH was first imaged at 1.4 GHz and 5.5 GHz by Sarazin et al. (1995). The MH morphology in our images, obtained from the same radio data (see Giacintucci et al. 2019, for details), is consistent with the structure previously mapped. The central radio galaxy is a core-dominated, double-lobe source and another patch of extended emission, which is interpreted as a fossil lobe from an older AGN outburst, is detected at ∼25″(∼18 kpc) from the cluster center. The MH surrounds this structure extending for ∼100″ (∼70 kpc). In the X-ray band we observe two cavities, which coincide with the radio lobes, and a cold front located at ∼40 kpc from the center. The region inside the cold front shows a number of small, dense gas blobs that may be the shred of a cooling core disturbed by either Kelvin-Helmotz instabilities or intermittent AGN activity. All of these properties relate to processes that may act to disrupt or destroy any cooling flow (Mazzotta et al. 2003; Sanders et al. 2009). The cluster hosts a head-tail radio galaxy whose radio tail is close to the MH with a projected distance of ∼90 kpc. This suggests the possibility that the close-by passage of the galaxy may have played a role in the injection of both CRe and turbulence in the ICM;
RBS 797. This cluster shows radio emission on three different scales. VLA observations at 4.8 GHz at high resolutions (∼0.4″) revealed the presence of a pair of jets connected to the central galaxy, oriented in the north-south direction and extended for ∼15 kpc. On the larger scale, the radio emission observed at 1.4 GHz coincides with a striking system of cavities extending for ∼26 kpc in the east-west direction observed by Chandra in the X-ray band. The misalignment of the cavities with respect to the inner jet system suggests that the central AGN had different cycles of activity with the jets oriented in different directions (Gitti et al. 2006). Finally, the cluster shows diffuse radio emission with a roughly spherical morphology and a radius of ∼100 kpc (Gitti et al. 2006; Doria et al. 2012). We excluded the region of the cavities from the analysis of the MH;
Abell 3444. The MH was reported first by Venturi et al. (2007) and then confirmed in Giacintucci et al. (2019). The BCG at the center of the low-entropy cool core does not show jets (Giacintucci et al., in prep.). The morphology of the radio emission seems orthogonal to the X-ray emission, with the IR decreasing rapidly eastward;
MS 1455.0+2232. The MH is composed of a central region and a tail located at the southeast. The northern part of the MH is delimited by a cold front. The cluster, along with RX J1720.1+2637, has been reported by Mazzotta & Giacintucci (2008) as a first evidence of the connection between cold fronts and MHs;
RXC J1504.1−0248. This cluster is characterized by an extreme X-ray luminosity (Lbol = 4.3 × 1045
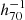 erg s−1), of which more the 70% is radiated inside the cool core region.
erg s−1), of which more the 70% is radiated inside the cool core region.
The exceptional X-ray luminosity suggests that we are observing AGN-ICM interactions taking place in extreme conditions. The MH surrounds the BCG, extending for ∼140 kpc, and it has a spectral index of α = 1.2. The cluster also shows a pair of cold fronts located inside the radio emitting region that highlight the presence of ongoing sloshing processes (Giacintucci et al. 2011);
RX J1532.9+3021. The Chandra observation shows a pair of cavities associated with the BCG and a cold front located at ∼65 kpc from the center, partially associated with one of the cavities (Hlavacek-Larrondo et al. 2013). The MH appears more extended toward the northeast, with a radius of ∼180 kpc, following the morphology of the X-ray surface brightness. Giacintucci et al. (2014b) estimated the total spectral index of the diffuse radio emission α = 1.2 by combining observations at 325 MHz, 610 MHz, 1.4 GHz, and 4.9 GHz;
RX J1720.1+2637. This cluster was the first relaxed system in which sloshing cold fronts were revealed by Chandra (Mazzotta et al. 2001) as well as one of the first two clusters in which a connection between MH and cold fronts was reported (Mazzotta & Giacintucci 2008). The MH consists of a bright central region that contains most of its flux density, and a fainter, arc-shaped tail elongated for ∼230 kpc, and it is delimited by the cold front. Giacintucci et al. (2014a) combined several radio observations spanning from 0.317 to 8.44 GHz to obtain a detailed spectral index map of the MH. They observed that the spectral index varies within the MH. The central region shows α≃1, whereas the tail shows α≃2–2.5. ZuHone et al. (2015) demonstrated via numerical simulations that the CRe in the tail could be efficiently re-accelerated by the turbulence injected at the edge of the cold front.
Appendix B: Sampling of the diffuse radio emission
For each cluster of the sample, we report here the contours of the radio emission and the mask used for the analysis overlapped on the X-ray image. We also present a random mesh generated during the MCptp analysis, the corresponding SMptp analysis, and the distribution of k produced by the MCptp analysis. The resolution and the noise of each map are reported in Table 2. For each object we report:
Left. X-ray surface brightness map smoothed with a 1.5″ gaussian, with the contours of the radio map at the −3, 3, 24, 96σ levels (white), the mask used in the analysis (gray), and a random sampling mash (green). The cell size matches the angular resolution of the radio image;
Center.IR versus IX obtained from the presented mesh. The red, green, and blue lines are, respectively, the best-fit slopes obtained with the BCES for (IX ∣ IR), (IR ∣ IX), and the bisector. The estimated value of kSM is reported in the label;
Right. Distribution of indexes k produced after 1000 iterations of MCptp analysis.
 |
Fig. B.1. RXJ1720.1+2637. |
 |
Fig. B.2. MS 1455.0+2232. |
 |
Fig. B.3. RXC J1504.1−0248. |
 |
Fig. B.4. RX J1532.9+3021. |
 |
Fig. B.5. Abell 3444 at 610 MHz (top) and 1.4 GHz (bottom). |
 |
Fig. B.6. 2A03335+096 at 1.4 GHz (top) and 5.5 GHz (bottom). |
Appendix C: Considerations on the role of the central source in SMptp analysis
In order to test that the adopted masking is sufficient to contain the contamination of the central radio source in our analysis, we present here a comparison of the SMptp analysis for two of our objects after the subtraction of the central source, namely clusters RX J1532.9+3021 and RXC J1504.1−0248. We selected RXC J1504.1−0248 because it hosts the most luminous radio sources of our sample, therefore it should be the most sensitive to possible contaminations. In the two observations, the central sources were first imaged by selecting only baselines longer than, respectively, 10 and 15 kλ. The clean components were then subtracted from the uv-data to obtain images of the diffuse emission alone. In Fig. C.1 we present the images before and after the subtraction with the same color-scale and surface brightness levels and the same resolution reported in Table 2, and the corresponding SMptp analysis performed on the subtracted images by using the same grids presented in Appendix B (Figs. B.4 and B.3). We found that, for each cluster, the two estimates of k obtained with the two different approaches are consistent within the errors and, thus, that for the aims of this work the central source can be masked instead of subtracted.
 |
Fig. C.1. Top: RX J1532.9+3021, before (left) and after the subtractions (center). The contours are at 2, 4, 8, 16, 32, and 64 × 22 μJy beam−1. The plot (right) is the result of the SMptp analysis performed on the subtracted image with the same grid presented in B.3. bottom: RXC J1504.1−0248, before (left) and after the subtractions (center). The contours are at 2, 4, 8, 16, 32, and 64 × 0.9 mJy beam−1. The plot (right) is the result of the SMptp analysis performed on the subtracted image with the same grid presented in Fig. B.3. |
Appendix D: Considerations on the diffusion coefficient D0
In our model the luminosity of the radio emission depends on the value of the ratio Q0/D0, and thus also on assuming that the value of D0 has consequences on the estimate of CRp injection amplitude, Q0, and, ultimately, on the AGN CRp luminosity necessary to reproduce the observed radio emission. Specifically, higher values of D0 result in a higher Q0 and LCRp. We assumed that CRp can diffuse on the MH scale on timescales that are shorter than the CRp cooling time. This cooling time is dominated by CRp-p collisions and is on the order of several gigayears (Brunetti & Jones 2014). More quantitatively, the condition is that the optical depth due to CRp-thermal proton collision calculated on a MH scale is τ ≃ σppnthL, where σpp = 32 mBarn is the cross-section of the collision and L is the spatial scale. As the CRp diffuse in the ICM, they move within different thermal densities, which contribute to the total optical depth as dτ = σppnth(r(t))cdt, where 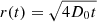 . Therefore, the time tmax required to dissipate all the injected CRp in the thermal plasma within RMH can be derived by imposing that the total optical depth is
. Therefore, the time tmax required to dissipate all the injected CRp in the thermal plasma within RMH can be derived by imposing that the total optical depth is
where n0, rc, and β are the parameters that describe the β-model for each cluster. For a given tmax, the associated diffusion coefficient is 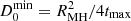 . In Table D.1 we report the diffusion coefficients that we estimated for each MH.
. In Table D.1 we report the diffusion coefficients that we estimated for each MH.
Diffusion coefficients.
This gives a lower limit to the CRp luminosity and an upper limit to the timescale for diffusion, which is shown to be longer than the timescale of cosmological cluster evolution. Assuming a larger value of the diffusion coefficient allows the diffusion of CRp on the MH scale on shorter timescales, thus establishing the stationary CRp distribution faster, and entails that a higher LCRp is required to reproduce the observed radio emission. Therefore, as a reference value, we assumed a coefficient that allows the diffusion of CRp over the MH radius in 1 Gyr (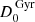 ), which we report in Tables D.1 and 5 with the corresponding LCRp. We note that adopting
), which we report in Tables D.1 and 5 with the corresponding LCRp. We note that adopting 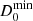 , instead of
, instead of 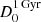 , results in values of LCRp that are a factor of
, results in values of LCRp that are a factor of 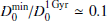 lower that the values that we report. The γ-ray luminosity does not change, because it depends, instead, on the ratio Q0/D0, which is constrained by the observed radio luminosity (Figs. B.5 and B.6).
lower that the values that we report. The γ-ray luminosity does not change, because it depends, instead, on the ratio Q0/D0, which is constrained by the observed radio luminosity (Figs. B.5 and B.6).
All Tables
All Figures
 |
Fig. 1. Top: Chandra image of the RBS 797 cluster with the contours at the −3, 3, 24, 96σ levels of the radio emission at 1.4 GHz (Doria et al. 2012). The resolution of the radio maps is 3″ × 3″ and 1σ = 10 μJy beam−1. Shown in green is the final mesh that samples the emission above the 3σ level with cells of 4″ × 4″ size. The central cavities and the external sources were masked (gray) and, therefore they were excluded from the sampling. Bottom-left: IR vs. IX plot where each point corresponds to a cell of the sampling mesh. The red and green lines are, respectively, the best-fit power law estimated for (IR ∣ IX) and (IX ∣ IR). The blue line is their bisector power law. The value of kSM is reported in the legend. Bottom-right: histogram of the distribution of values of kSM produced by the Monte Carlo point-to-point analysis with 1000 cycles. The best estimate of k is reported in the legend with the associated 1σ error. |
| In the text | |
 |
Fig. 2. Parameter spaces of k-index for the spherical MHs. The red lines locate the 1-σ confidence interval for k measured for each MH. For RBS 797 we report the result obtained with α = 1.1. For Abell 3444 we report in red the result at 610 MHz and in green the result at 1.4 GHz. The horizontal, dashed line points out the level η = 0.5 that reproduces the equilibrium between thermal and non-thermal energy. For RXC J1504.1−0248 we report the η = 1 level with the black dash-dotted line and the lower limit derived from the Fermi-LAT observation presented in Dutson et al. (2013). The lower limits for B0 for the other clusters are below 1 μG and they are reported in Table 6. |
| In the text | |
 |
Fig. 3. Results for RBS 797 for δ = 2.2 (top) and δ = 3.0 (bottom). Left: integrated radio and γ-ray luminosity. Right: radio and γ-ray surface brightness. We report the observed IR profile and the 3σ level of the observation (dashed red line). |
| In the text | |
 |
Fig. 4. Results for Abell 3444 at 1.4 GHz (top) and RX J1532.9+3021 (bottom). For the latter, we report reference values of LR and Lγ derived from the upper limit of the magnetic field (Table 5). Left: integrated radio and γ-ray luminosity. Right: radio and γ-ray surface brightness. We report the observed IR profile and the 3σ level of the observation (dashed red line). |
| In the text | |
 |
Fig. 5. Results for RXC J1504.1−0248 with B0 = 1 μG (top), B0 = 10 μG (middle), and B0 = 20 μG (bottom). Left: integrated radio and γ-ray luminosity. Right: radio and γ-ray surface brightness. We report the observed IR profile and the 3σ level of the observation (dashed red line). We limited the profile up to RMH to avoid possible contamination by field sources (see Fig. B.3). |
| In the text | |
 |
Fig. 6. Predicted γ-rays spectrum for the MHs for parameters reported in Table 5 compared with the Fermi-LAT 15 yr detection limit. |
| In the text | |
 |
Fig. B.1. RXJ1720.1+2637. |
| In the text | |
 |
Fig. B.2. MS 1455.0+2232. |
| In the text | |
 |
Fig. B.3. RXC J1504.1−0248. |
| In the text | |
 |
Fig. B.4. RX J1532.9+3021. |
| In the text | |
 |
Fig. B.5. Abell 3444 at 610 MHz (top) and 1.4 GHz (bottom). |
| In the text | |
 |
Fig. B.6. 2A03335+096 at 1.4 GHz (top) and 5.5 GHz (bottom). |
| In the text | |
 |
Fig. C.1. Top: RX J1532.9+3021, before (left) and after the subtractions (center). The contours are at 2, 4, 8, 16, 32, and 64 × 22 μJy beam−1. The plot (right) is the result of the SMptp analysis performed on the subtracted image with the same grid presented in B.3. bottom: RXC J1504.1−0248, before (left) and after the subtractions (center). The contours are at 2, 4, 8, 16, 32, and 64 × 0.9 mJy beam−1. The plot (right) is the result of the SMptp analysis performed on the subtracted image with the same grid presented in Fig. B.3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



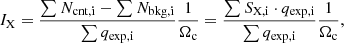
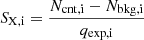
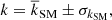
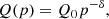
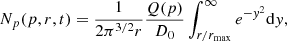
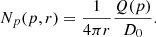
![$$ \begin{aligned} n_{\rm th}(r)=n_{\rm 0}\left[1+\left(\frac{r}{r_{\rm c}}\right)^{2}\right]^{-\frac{3}{2}\beta } ,\end{aligned} $$](/articles/aa/full_html/2020/08/aa37207-19/aa37207-19-eq25.gif)
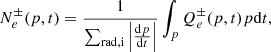
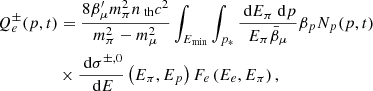
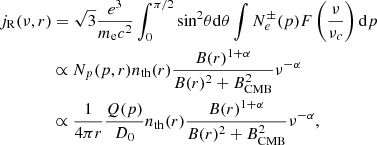
![$$ \begin{aligned} B(r)=B_{\rm 0}\left[\frac{n_{\rm th}(r)}{n_0}\right]^{\eta } ,\end{aligned} $$](/articles/aa/full_html/2020/08/aa37207-19/aa37207-19-eq35.gif)
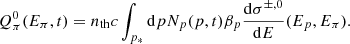
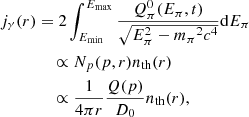
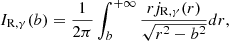
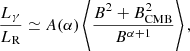
![$$ \begin{aligned} I_{\rm x}(r)=\sqrt{\pi }n_{\rm 0}^{2}r_{\rm c}\Lambda (T)\frac{\Gamma (3\beta -0.5)}{\Gamma (3\beta )}\left[1+\left(\frac{r}{r_{\rm c}}\right)^{2}\right]^{\frac{1}{2}-3\beta } ,\end{aligned} $$](/articles/aa/full_html/2020/08/aa37207-19/aa37207-19-eq40.gif)
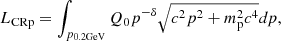
![$$ \begin{aligned} \tau =c\sigma _{\rm pp}n_0\int _0^{t_{\rm max}}\left[1+ \left( \frac{R_{\rm MH}}{r_c}\sqrt{\frac{t}{t_{\rm max}}}\right)^2\right]^{-\frac{3}{2}\beta }\mathrm{d}t=1, \end{aligned} $$](/articles/aa/full_html/2020/08/aa37207-19/aa37207-19-eq53.gif)