© ESO, 2013

1. Introduction

For over two centuries, astronomers have been able to detect and analyse orbital motions for objects beyond the solar system. From measured positions (visual binaries) or radial velocities (spectroscopic binaries, exoplanets), orbital elements and their standard errors are typically obtained by least-squares. Accordingly, at this late date, when orbital motion is detected, prior information concerning similar objects is available and can be incorporated into the analysis.

An example is the Lucy-Sweeney (1971; LS) test for the statistical significance of small measured eccentricities e for spectroscopic binaries (SB’s). The prior information that provided support for the LS test was as follows:

• 1)

  The small e’s (typically ≲0.05) of numerous catalogued SB’s were ~E(e | 0), the expected value of e due to measurement errors when the true value is ε = 0.

• 2)

  Savedoff’s (1951) investigation of ecosω, where ω is the longitude of periastron. If an SB is also an eclipsing binary (EB), ecosω can be determined from the velocity curve (sp) and independently from the light curve (ph). For EB’s with secondary eclipses midway between consecutive primary eclipses, (ecosω)_ph = 0, but the values of (ecosω)_sp are scattered over the interval (–0.05, 0.05), confirming that non-zero e’s ≲0.05 are often spurious.

• 3)

  Tidal dissipation gives ε → 0 as t → ∞ since, for two point masses, ε = 0 is the state of minimum orbital energy for fixed orbital angular momentum. Thus, if the time constant for this decay is short enough, the system is likely to be observed when ε ≪ E(e | 0) – i.e., well below the measurement threshold.

In view of this prior information, LS adopted ε = 0 as the preferred (null) hypothesis (H₀) and imposed a moderately demanding level of significance before rejecting H₀ and accepting an elliptical orbit.

Given that secular evolution due to tidal dissipation was already well established in 1971 and is not less so now, there is merit in explicitly incorporating this mechanism into the analysis rather than implicitly via the LS preference for ε = 0. This can be achieved by replacing the frequentist approach of LS by one based on Bayes’ theorem.

2. Estimating the true eccentricity ε

We suppose that radial velocities of a single-lined spectoscopic binary (SB1) have been analysed to estimate the orbital elements and their standard errors. We ask: what can be inferred about the error-free elements when orbital evolution due to tidal dissipation is taken into account?

2.1. Posterior probability

We adopt the notation used in Lucy (1974; L74). The vectors of the estimated and the error-free elements are denoted by x and ξ, respectively; and the distribution of probability in x-space for given ξ is denoted by Π(x | ξ)dx. Integrating over ξ-space, we find that the distribution of probability in x-space is φ(x)dx, where 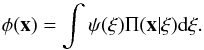$\mathit{\phi }\mathrm{\left(}{x}\mathrm{\right)}\mathrm{=}\mathrm{\int }\mathit{\psi }\mathrm{\left(}\mathit{\xi }\mathrm{\right)}\mathrm{\Pi }\mathrm{\left(}{x}\mathrm{\right|}\mathit{\xi }\mathrm{)}\mathrm{d}\mathit{\xi }\mathit{.}$(1)Here ψ is the probability density function (pdf) that represents our prior knowledge about ψ(ξ)dξ, the distribution of probability in ξ-space for the SB1’s true elements.

Since SB1’s with small e’s are of interest, we suppose that Sterne’s (1941) elements have been chosen, as in LS. The six elements are then: P, the orbital period; γ, the systemic velocity; K, the semi-amplitude of the velocity curve; T₀, an epoch at which the mean longitude is zero; and the pair ecosω,esinω. In terms of these parameters, the radial velocity curve of an SB1 is given by Eq. (1) in LS.

With this choice and the assumption e² ≪ 1, the off-diagonal elements of the least-squares matrix have zero expectation values when observational weight is uniformly distributed in phase (LS). Since observers strive to meet this condition, we assume it to be true; and this then implies negligible correlations between the elements. Accordingly, to a good approximation, the error-broadening kernel Π(x | ξ) is simply the product of the six Gaussians giving the independent error distributions of the six elements.

Next consider the pdf ψ(ξ), which is convolved in Eq. (1) with the kernel Π(x | ξ). It follows that ψ is only relevant if it varies significantly within the error bars of an individual orbital element. This is not true for P,γ,K, and T₀. However, when orbit circularisation is taken into account, ψ(ξ) may vary significantly within the domain (ecosω ± σ_ecosω,esinω ± σ_esinω). Accordingly, we now integrate Eq. (1) with respect to the (P,γ,K,T₀)-components of x and use the normalization of Π(x | ξ)dx with respect to each of these four elements. The result is 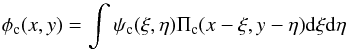${\mathit{\phi }}_{\mathrm{c}}\mathrm{\left(}\mathit{x,y}\mathrm{\right)}\mathrm{=}\mathrm{\int }{\mathit{\psi }}_{\mathrm{c}}\mathrm{\left(}\mathit{\xi ,\eta }\mathrm{\right)}{\mathrm{\Pi }}_{\mathrm{c}}\mathrm{(}\mathit{x}\mathrm{-}\mathit{\xi ,y}\mathrm{-}\mathit{\eta }\mathrm{)}\mathrm{d}\mathit{\xi }\mathrm{d}\mathit{\eta }$(2)where x = ecosω and y = esinω are the two surviving estimated quantities, whose error-free values are ξ = εcosϖ and η = εsinϖ, respectively, and the subscript c indicates that the pdf’s are defined on a Cartesian grid.

We now assume that the standard errors of ecosω and esinω are equal, which is true of their expectation values when observational weight is uniformly distributed in phase (LS). The broadening kernel is then the circular normal distribution ${\mathrm{\Pi }}_{\mathrm{c}}\mathrm{(}\mathit{x}\mathrm{-}\mathit{\xi ,y}\mathrm{-}\mathit{\eta }\mathrm{)}\mathrm{=}\frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }{\mathit{\mu }}^{\mathrm{2}}}\exp \left[\mathrm{-}\frac{\mathrm{(}\mathit{x}\mathrm{-}\mathit{\xi }{\mathrm{)}}^{\mathrm{2}}\mathrm{+}\mathrm{(}\mathit{y}\mathrm{-}\mathit{\eta }{\mathrm{)}}^{\mathrm{2}}}{\mathrm{2}{\mathit{\mu }}^{\mathrm{2}}}\right]$(3)where μ = σ_ecosω = σ_esinω.

Bayes’ theorem can now be invoked to derive – see Eq. (10) in L74 – the posterior probability 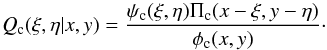${\mathit{Q}}_{\mathrm{c}}\mathrm{\left(}\mathit{\xi ,\eta }\mathrm{\right|}\mathit{x,y}\mathrm{)}\mathrm{=}\frac{{\mathit{\psi }}_{\mathrm{c}}\mathrm{\left(}\mathit{\xi ,\eta }\mathrm{\right)}{\mathrm{\Pi }}_{\mathrm{c}}\mathrm{(}\mathit{x}\mathrm{-}\mathit{\xi ,y}\mathrm{-}\mathit{\eta }\mathrm{)}}{{\mathit{\phi }}_{\mathrm{c}}\mathrm{\left(}\mathit{x,y}\mathrm{\right)}}\mathrm{·}$(4)Thus, if the least-square solution is 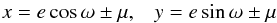$\mathit{x}\mathrm{=}\mathit{e}\cos \mathit{\omega }\mathrm{\pm }\mathit{\mu ,y}\mathrm{=}\mathit{e}\sin \mathit{\omega }\mathrm{\pm }\mathit{\mu }$(5)the distribution of probability in (εcosϖ,εsinϖ)-space is given by Q_c(ξ,η | x,y)dξdη. To evaluate this posterior distribution, we must specify what our expectations were for ψ_c(ξ,η)dξdη, the prior distribution of probability in (εcosϖ,εsinϖ)-space.

For the problem at hand, polar (p) coordinates (ε,ϖ) are more convenient than the Cartesian coordinates (ξ,η) in the above formulae. The Jacobian of the transformation is J = ε, so that, by conservation of probability, 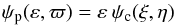${\mathit{\psi }}_{\mathrm{p}}\mathrm{\left(}\mathit{\epsilon ,\varpi }\mathrm{\right)}\mathrm{=}\mathit{\epsilon }{\mathit{\psi }}_{\mathrm{c}}\mathrm{\left(}\mathit{\xi ,\eta }\mathrm{\right)}$(6)and 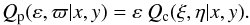${\mathit{Q}}_{\mathrm{p}}\mathrm{\left(}\mathit{\epsilon ,\varpi }\mathrm{\right|}\mathit{x,y}\mathrm{)}\mathrm{=}\mathit{\epsilon }{\mathit{Q}}_{\mathrm{c}}\mathrm{(}\mathit{\xi ,\eta }\mathrm{\left|}\mathit{x,y}\mathrm{\right)}\mathit{.}$(7)

2.2. A physical model for ψ_p

Given P, there is a 2D family of binaries that match the measured K at some inclination. For simplicity, a representative example is chosen to avoid integrating over all possibilities.

Now consider an ensemble of such binaries that form at a uniform rate in the solar neighbourhood and have lifetime t_∗. We further suppose that all have ε = ε₀ at t = 0 and that thereafter ε decays exponentially with fixed e-folding time t_∗/ν, so that 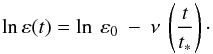$\ln \mathit{\epsilon }\mathrm{\left(}\mathit{t}\mathrm{\right)}\mathrm{=}\ln {\mathit{\epsilon }}_{\mathrm{0}}\mathrm{-}\mathit{\nu }\left(\frac{\mathit{t}}{{\mathit{t}}_{\mathrm{\ast }}}\right)\mathrm{·}$(8)It follows that lnε is uniformly distributed in the interval (lnε_∗,lnε₀), where ε_∗ = ε₀exp( − ν). The probability that ε ∈ (ε,ε + dε) is therefore dε/νε.

If we now assume randomly oriented orbits, the probability that ϖ ∈ (ϖ,ϖ + dϖ) is dϖ/2π. Accordingly, the prior probability that a binary is in the element dεdϖ at (ε,ϖ) is ψ_pdεdϖ, where 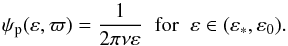${\mathit{\psi }}_{\mathrm{p}}\mathrm{\left(}\mathit{\epsilon ,\varpi }\mathrm{\right)}\mathrm{=}\frac{\mathrm{1}}{\mathrm{2}\mathit{\pi \nu \epsilon }}\mathrm{for}\mathit{\epsilon }\mathrm{\in }\mathrm{\left(}{\mathit{\epsilon }}_{\mathrm{\ast }}\mathit{,}{\mathit{\epsilon }}_{\mathrm{0}}\mathrm{\right)}\mathit{.}$(9)Note that ψ_p decreases with increasing ν = ln   (ε₀/ε_∗). Nevertheless, normalization of this pdf is maintained by the corresponding decrease in ε_∗, the lower limit for integrations over ε.

In introducing this physical model, we in effect adopt an informative prior. The following quote is apt: “The real power of Bayesian inference lies in its ability to incorporate “informative” prior information, not “ignorance”” (Feldman & Cousins 1998).

2.3. Distribition of ε

For numerical calculations, it is convenient to transform the integral in Eq. (2) into an integration with respect to the polar coordinates ε and ϖ, so that 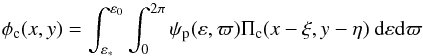${\mathit{\phi }}_{\mathrm{c}}\mathrm{\left(}\mathit{x,y}\mathrm{\right)}\mathrm{=}{\mathrm{\int }}_{{\mathit{\epsilon }}_{\mathrm{\ast }}}^{{\mathit{\epsilon }}_{\mathrm{0}}}{\mathrm{\int }}_{\mathrm{0}}^{\mathrm{2}\mathit{\pi }}{\mathit{\psi }}_{\mathrm{p}}\mathrm{\left(}\mathit{\epsilon ,\varpi }\mathrm{\right)}{\mathrm{\Pi }}_{\mathrm{c}}\mathrm{(}\mathit{x}\mathrm{-}\mathit{\xi ,y}\mathrm{-}\mathit{\eta }\mathrm{)}\mathrm{d}\mathit{\epsilon }\mathrm{d}\mathit{\varpi }$(10)and to use logarithmic spacing in ε in order to accurately evaluate the contribution near ε_∗. Note that φ_c is independent of ω when ψ_p is independent of ϖ, as in Eq. (9).

With φ_c evaluated, the distribution of probability in (ε,ϖ)-space is given by Q_p(ε,ϖ | x,y)dεdϖ, with Q_p = εQ_c from Eq. (4). This 2D pdf, which in general is not independent of ϖ, may be of interest when analysing a particular SB1. But here our interest is in ε, so we integrate over ϖ to obtain 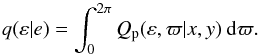$\mathit{q}\mathrm{\left(}\mathit{\epsilon }\mathrm{\right|}\mathit{e}\mathrm{)}\mathrm{=}{\mathrm{\int }}_{\mathrm{0}}^{\mathrm{2}\mathit{\pi }}{\mathit{Q}}_{\mathrm{p}}\mathrm{(}\mathit{\epsilon ,\varpi }\mathrm{\left|}\mathit{x,y}\mathrm{\right)}\mathrm{d}\mathit{\varpi }\mathit{.}$(11)Note that q(ε | e) is independent of ω because of the absence of a correlation term in Π_c – see Eq. (3). This in turn follows from the assumptions (Sect. 2.1) that e² ≪ 1 and that observational weight is uniformly distributed in phase.

The posterior probability that the true eccentricity ∈ (ε,ε + dε) is therefore q(ε | e)dε, with mean value 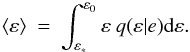$\mathrm{⟨}\mathit{\epsilon }\mathrm{⟩}\mathrm{=}{\mathrm{\int }}_{{\mathit{\epsilon }}_{\mathrm{\ast }}}^{{\mathit{\epsilon }}_{\mathrm{0}}}\mathit{\epsilon q}\mathrm{\left(}\mathit{\epsilon }\mathrm{\right|}\mathit{e}\mathrm{)}\mathrm{d}\mathit{\epsilon }\mathit{.}$(12)

2.4. Bayesian terminology

In the above, notation and terminology is from L74. To modern Bayesians, Π_c(x − ξ,y − η) is the likelihood and φ_c(x,y) is the Bayes’ factor. Elsewhere, modern usage is followed with respect to the terms prior pdf, posterior pdf and credible intervals.

3. Numerical results

The theory of Sect. 2 is now illustrated by computing a particular case in detail.

3.1. Parameters

There are two basic parameters, e/μ and ν, the number of e-folding decay times in t_∗.

Note that ϵ₀ is not a consequential parameter provided that e ≪ ϵ₀. In effect, we assume that an SB1 with e ≈ 0 has reached this configuration due to secular evolution and not due to the formation mechanism. In these calculations, ϵ₀ = 0.5.

We choose ν = 8.52, so that ε_∗ = 10^-4. Then, with μ = 0.01, ε(t) < 2.45μ, the LS threshold, when t > 0.35t_∗. Thus, from our ensemble of SB1’s, ≈65% would be assigned ε = 0 by the LS test.

3.2. The posterior pdf χ(log ε |e)

Because of the concentration of probability towards ε_∗, plots are more informative if the abscissa is log ε rather than ε. Accordingly, we define 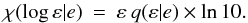$\mathit{\chi }\mathrm{\left(}\log \mathit{\epsilon }\mathrm{\right|}\mathit{e}\mathrm{)}\mathrm{=}\mathit{\epsilon q}\mathrm{(}\mathit{\epsilon }\mathrm{\left|}\mathit{e}\mathrm{\right)}\mathrm{\times }\ln \mathrm{10.}$(13)In Fig. 1, this pdf is plotted for e/μ = 1.0,2.45,3.03 and 3.72, values selected as follows: if ε = 0, LS showed that the probability p_e of exceeding e is given by 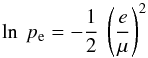$\ln {\mathit{p}}_{\mathrm{e}}\mathrm{=}\mathrm{-}\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathit{e}}{\mathit{\mu }}\right)2$(14)provided that μ ≪ 1. Therefore, when testing H₀, the above values of e/μ correspond to levels of significance 61, 5, 1 and 0.1%, respectively. The criterion e/μ > 1 was proposed and implemented by Luyten (1936); the 5% level by LS.

For e/μ = 3.72, χ is an asymmetric bell-shaped function peaking at ≈e, but with a tail extending down to log ε_∗ =  −4.0. As e/μ decreases, the peak weakens and the tail strengthens. At e/μ = 1.0, the peak is absent and all the probability is in the tail, which derives from the physical model. Intermediate calculations show that the peak first appears at e/μ = 1.42. Thus, for e/μ < 1.42, χ is a monotonically decreasing function of ε. For e/μ > 1.42, χ is unimodal.

The pdf χ for e/μ = 3.72 and μ = 0.01 in Fig. 1 is computed with ε₀/μ = 50. Repeating this calculation shows that χ is independent of the upper limit ε₀ provided that ε₀/μ ≳ 10.

3.3. Percentiles

The posterior pdf’s in Fig. 1 imply asymmetric and rapidly changing credible (or Bayesian confidence) intervals as e/μ varies. These are plotted in Fig. 2 for the indicated values of the probability that the true eccentricity is <ε. For the normal distribution, the values 0.159,0.500,0.841 and 0.977 correspond to displacements of − 1,0, + 1 and + 2σ, respectively.

Figure 2 reveals a dramatic switch in solution regime at e_†/μ ≈ 3.6. For e ≳ e_†, the measured value e is close to the 50% percentile and is tightly enclosed by the ±1σ intervals. In this regime, inferences are dominated by the actual measurement e ± μ. But this ceases to be so for e ≲ e_†. Thus, for e/μ < 2.65, the “solution” ε = e falls outside the ± 1σ intervals. Evidently, for e ≲ e_†, inferences are increasingly dominated by the model of Sect. 2.2.

3.4. Highest posterior density intervals

For e/μ < 1.42, χ is a monotonically decreasing function of ε (Sect. 3.2). It follows that traditional, equal-tail credible intervals exclude the point (ε = ε_∗) with greatest probability density (pd). This undesirable feature is avoided by instead computing highest posterior density intervals (HPDI; Box & Tiao 1973). These intervals are such that every point included has a higher pd than every point excluded.

In general, the calculation of HPDIs is non-trivial. But here the pdf’s χ are not pathological (Fig. 1), and so the following clipping algorithm finds the HPDI for specified e and designated enclosed probability (1 − α).

Let log ε_kL,...,log ε_kU be consecutive grid points that belong to and define the HPDI (ε_kL,ε_kU). Then an HPDI with smaller included probability is obtained by eliminating the grid point log ε_kL if χ_kL < χ_kU or the grid point log ε_kU if χ_kU < χ_kL. This is repeated until the included probability = (1 − α).

The 95% HPDIs thus obtained for χ(log ε | e) are plotted for e = 0.000(0.001)0.080 in Fig. 3. For e < 0.018, the HPDIs are effectively one-tail intervals since the lower bound is ε_L = ε_∗ = 10^-4. Accordingly, for this problem, HPDIs provide a seamless transition from upper limits for non-detected to two-sided intervals for detected eccentricities (cf. Feldman & Cousins 1998). This is an appealing aspect of HDPIs for interpreting measured e’s and their uncertainties.

For e < 0.0142, the interval excluded from an HPDI is a single-tail because of the aforementioned monotonicity. For e > 0.0142, the pdf χ is unimodal (Fig. 1), with a maximum whose location → e as e/μ increases. This emerging, measurement-driven maximum eventually brings about the transition from one- to two-tailed intervals. For e > 0.018, the excluded probability is contained in two tails, with the upper tail’s probability being initially 5%, but this decreases to ≈2.5% when e/μ ≫ 1 because of χ’s increasing symmetry – see Fig. 1.

Note that for the normal distribution, 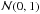, the 95% HPDI is the familiar equal tail interval (− 1.96, + 1.96) and the width of this interval is the narrowest that ecloses 95% of the probability. For non-symmetric pdf’s, HPDIs are the narrowest intervals enclosing probability (1 − α) and as such are a natural generalization of the conventional equal-tail intervals for symmetric, bell-shaped pdf’s.

Confidence intervals are an economical means of conveying the compactness or otherwise of a variate’s distribution. The resulting loss of information, if of concern, can be avoided by plotting the pdf’s, as in Figs. 1 and A.2.

3.5. Detection threshold

The transition from one- to two-tailed HPDIs is a natural definition of the detection threshold e_th for non-zero eccentricity – i.e., the measured value e above which attribution purely to measurement errors is implausible. However, Fig. 3 shows that ε_L remains ≪e for a considerable interval beyond e_th = 0.018, which in any case depends on ν, a parameter likely to be only crudely estimated.

If detection is crucial for a subsequent investigation – e.g., an observing program – then a threshold closer to e_† should be adopted (Figs. 2 and 3).

3.6. Simulation

The role that HPDIs can play in reporting eccentricities is best illustrated by sampling experiments. Accordingly, synthetic data for the model of Sect. 2.2 are created as follows: if z₁,z₂ are random numbers in (0,1), a random ensemble member in (ε,ϖ)-space is at 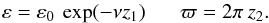$\mathit{\epsilon }\mathrm{=}{\mathit{\epsilon }}_{\mathrm{0}}\exp \mathrm{(}\mathrm{-}\mathit{\nu }{\mathit{z}}_{\mathrm{1}}\mathrm{)}\mathit{\varpi }\mathrm{=}\mathrm{2}\mathit{\pi }{\mathit{z}}_{\mathrm{2}}\mathit{.}$(15)Then, if ζ₁,ζ₂ are random Gaussian variates, this ensemble member is observed at the point $\mathit{e}\cos \mathit{\omega }\mathrm{=}\mathit{\epsilon }\cos \mathit{\varpi }\mathrm{+}\mathit{\mu }{\mathit{\zeta }}_{\mathrm{1}}\mathit{e}\sin \mathit{\omega }\mathrm{=}\mathit{\epsilon }\sin \mathit{\varpi }\mathrm{+}\mathit{\mu }{\mathit{\zeta }}_{\mathrm{2}}\mathit{.}$(16)Repeated N times, the resulting e’s comprise a simulated observing campaign of N random ensemble members whose exact eccentricities ε are known.

With ε_∗ = 10^-4, a sample of N = 1000 SB1’s are plotted in Fig. 4. As expected, the large majority of the points fall within the 95% HPDIs (ε_L,ε_U). With Luyten’s criterion e > μ, 79.5% of this sample would have their elliptical orbits accepted. But Fig. 4 clearly shows that most systems with e ∈ (0.01,0.03) have ε < 0.01 and so exceed Luyten’s criterion because of the bias of the non-negative estimator e (LS). With the LS criterion e > 2.45μ, the accepted percentage drops to 40.5, and most of the systems with e ∈ (0.01,0.03) would now be assigned ε = 0, a marked improvement.

The further improvement provided by the HPDIs is that the assignment ε = 0 can now be replaced by an upper limit. Thus, for example, with this choice of prior, an SB1 with e = 0.01 ± 0.01 is preferably reported as ε < ε₉₅ = 0.014. From the standpoint of testing theories of tidal dissipation, an upper limit is more informative than ε = 0.

The sampling procedure can also be used to validate the upper limits. A sample with N = 10⁶ has 161, 521 systems with log e ∈ (−2.1, −1.9) and 8,317 of these have ε > ε₉₅. Thus 94.85% lie below the upper limit, closely agreeing with the designated 95%.

3.7. Upper limits

Upper limits ε_U when e < e_th are the most useful products of this Bayesian machinery. With their validity confirmed above, their dependence on the orbital decay rate is now explored.

Consider the representative measurement e = 0.01 ± 0.01, so that e/μ = 1.0, well below the detection threshold. In Table 1, the HPDI 95% upper limits ε₉₅ are given for this e/μ as a function of ε_∗. The decrease of ε₉₅ with increasing ν reflects statistical reality: if the e-folding time t_∗/ν ≪ t_∗, most systems will have ε ≪ e and a correspondingly small ε₉₅. Note that ε₉₅ even drops below e when ν ≳ 13.

In analysing an observed system without a good estimate of ν or, equivalently, of ε_∗, the conservative approach is to suppose that ε_∗ is no more than a factor ~10 below the measured e, thus avoiding claiming too low an upper limit ε_U. An even more conservative approach is to adopt a uniform prior – see Appendix.

4. Conclusion

In this paper, by incorporating a model of an SB1’s secular evolution, Bayes’ theorem is used to infer bounds on its exact eccentricity ε given its measured value e ± μ. Because the system’s lifetime t_∗ is finite, the asymptote ε = 0 is never reached. Thus, in contrast to Luyten (1936) and LS, the statistical problem is not one of model selection. Systems assigned ε = 0 by these earlier tests should preferably have upper limits ε_U computed.

As Fig. 4 shows, the Bayesian upper limits contain the systems for which e is significantly larger than ε due to measurement errors and bias. Thus, a major historical cause of spurious e’s is eliminated. But physical causes remain, such as those due to proximity effects or to additional line absorption by gas streams. An example is ζ TrA, for which Skuljan et al. (2004) improved the precision of the radial velocities by a remarkable factor of 100 and reported a small but highly significant e = 0.0140 ± 0.0002. However, the significant non-detection of the Keplerian third harmonic (Lucy 2005) invalidated this claim¹. As precision improves, similar testing for the third and higher Keplerian harmonics is essential for confirming that an orbit is truly eccentric. In addition, an update of Savedoff’s (1951) work would provide numerous examples of spurious e’s for investigation into physical causes other than measurement bias.

---

Acknowledgments

I am grateful to the referee for pointing out an error in statistical terminology.

References

Appendix A: Uniform prior

The model of Sect. 2.2 is not appropriate if the SB or star-planet system has additional components causing significant gravitational perturbations. In this circumstance, a sensible option is to assume a uniform prior for ε, as is already common practice for exoplanets (e.g., Ford 2006; Eastman et al. 2013). Together with the assumption of randomly oriented orbits, the prior probability of the system being in dεdϖ is then ψ_pdεdϖ, where 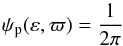${\mathit{\psi }}_{\mathrm{p}}\mathrm{\left(}\mathit{\epsilon ,\varpi }\mathrm{\right)}\mathrm{=}\frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }}$(A.1)which now replaces Eq. (9) in Sects. 2.3 and 3.

From the resulting posterior pdf q(ε | e), the 95% HPDIs and means ⟨ ε ⟩ are plotted in Fig. A.1 for e ∈ (0.00,0.08). Comparison with Fig. 3 shows that the HPDIs are nearly identical for e/μ ≳ 5. However, for e/μ ≲ 2 – i.e., in the non-detection domain – the upper limits ε_U in Fig. 3 are markedly lower, reflecting the effect of tidal circularisation in creating systems with ε ≪ e.

In contrast with Fig. 3, Fig. A.1 shows that a uniform prior results in a sharply defined detection threshold e_th/μ = 2.49, which is gratifyingly close to the (frequentist) LS value e_LS/μ = 2.45 given by Eq. (14) for p_e = 0.05. The thresholds for other critical levels are given in Table A.1, with the corresponding upper limits (bounds) ε_U in Table A.2.

For the representative measurement e/μ = 1.0 of Sect. 3.7, the 95% upper limit from Table A.2 is 2.41μ. This exceeds the corresponding values in Table 1, confirming that the uniform prior is the more conservative option.

A.1: A revised Lucy-Sweeney test

Even without evidence of additional components, an investigator may be reluctant to base an analysis of orbital elements on uncertain estimates of tidal decay. If so, the assumption of a uniform prior for ε should be attractive. Physically, this corresponds to no secular evolution of εand a formation mechanism that uniformly populates the interval 0 < ε < 1. Accordingly, a system with e ≈ 0 is assumed to have formed as such (cf. Sect. 3.1).

This neutral standpoint is an attractive basis for a revised version of the LS test in which the previous acceptance of a circular orbit (H₀) is now replaced by an upper limit.

The revised LS test with 1 − α = 0.95 proceeds as follows:

1): The eccentricitye ± μ is derived from the least squares solution.

2): If e/μ > 2.49, this measured value e ± μ is accepted.

3): However, if e/μ < 2.49, the measured value is replaced by the upper limit ε₉₅ obtained by interpolation in Col. 4 of Table A.2.

To illustrate this revised test, upper limits are given in Table A.3 for six SB1’s for which circular orbits are reported on the first page of Table 1 in LS. Thus for YZ Cas, the least squares value e = 0.004 was rejected by the LS test and ε = 0 accepted. We now compute the 95% upper limit as follows: the estimate μ = 0.0037 is derived from Eq. (13) and Table 1 of LS. Linear interpolation in Table A.2 at e/μ = 1.1 then gives ε₉₅/μ = 2.50, whence ε < ε₉₅ = 0.009. Table A.3. shows that upper limits can differ by large factors, reinforcing the earlier remark (Sect. 3.6) that upper limits are to be preferred in testing theories of tidal dissipation. A critical data base of detections and upper limits would facilitate progress in this field.

All Tables

All Figures