| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 23 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913909 | |
| Published online | 27 September 2010 | |
C2D Spitzer-IRS spectra of disks around T Tauri stars
V. Spectral decomposition![[*]](/icons/foot_motif.png)
J. Olofsson1,2 - J.-C. Augereau1 - E. F. van Dishoeck3,4 - B. Merín5 - N. Grosso6,7 - F. Ménard1 - G. A. Blake8 - J.-L. Monin1
1 - Université Joseph Fourier/CNRS, Laboratoire
d'Astrophysique de Grenoble, UMR 5571, BP 53, 38041 Grenoble Cedex 09,
France
2 - Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
3 - Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
4 -
Max Planck Institut für Extraterrestrische Physik,
Giessenbachstrasse 1, 85748 Garching, Germany
5 -
Herschel Science Centre, SRE-SDH, ESA PO Box 78, 28691
Villanueva de la Cañada, Madrid, Spain
6 -
Université de Strasbourg, Observatoire Astronomique de
Strasbourg, 11 rue de l'université, 67000 Strasbourg, France
7 -
CNRS, UMR 7550, 11 rue de l'université, 67000 Strasbourg, France
8 -
Division of Geological and Planetary Sciences 150-21, California
Institute of Technology, Pasadena, CA 91125, USA
Received 18 December 2009 / Accepted 1 July 2010
Abstract
Context. Dust particles evolve in size and lattice structure
in protoplanetary disks, due to coagulation, fragmentation and
crystallization, and are radially and vertically mixed in disks due to
turbulent diffusion and wind/radiation pressure forces.
Aims. This paper aims at determining the mineralogical
composition and size distribution of the dust grains in planet forming
regions of disks around a statistical sample of 58 T Tauri stars
observed with Spitzer/IRS as part of the Cores to Disks (c2d) Legacy
Program.
Methods. We present a spectral decomposition model, named
``B2C'', that reproduces the IRS spectra over the full spectral range
(5-35 ![]() m). The model assumes two dust populations: a warm component responsible for the 10
m). The model assumes two dust populations: a warm component responsible for the 10 ![]() m emission arising from the disk inner regions (
m emission arising from the disk inner regions (![]() 1 AU) and a colder component responsible for the 20-30
1 AU) and a colder component responsible for the 20-30 ![]() m emission, arising from more distant regions (
m emission, arising from more distant regions (![]() 10 AU). The fitting strategy relies on a random exploration of parameter space coupled with a Bayesian inference method.
10 AU). The fitting strategy relies on a random exploration of parameter space coupled with a Bayesian inference method.
Results. We show evidence for a significant size distribution flattening
in the atmospheres of disks compared to the typical MRN distribution,
providing an explanation for the usual flat, boxy 10 ![]() m feature profile generally observed in T Tauri star spectra. We reexamine the crystallinity paradox,
observationally identified by Olofsson et al. (2009, A&A, 507,
327), and we find a simultaneous enrichment of the crystallinity in
both the warm and cold regions, while grain sizes in both components
are uncorrelated. We show that flat disks tend to have larger grains
than flared disk. Finally our modeling results do not show evidence for
any correlations between the crystallinity and either the star spectral
type, or the X-ray luminosity (for a subset of the sample).
m feature profile generally observed in T Tauri star spectra. We reexamine the crystallinity paradox,
observationally identified by Olofsson et al. (2009, A&A, 507,
327), and we find a simultaneous enrichment of the crystallinity in
both the warm and cold regions, while grain sizes in both components
are uncorrelated. We show that flat disks tend to have larger grains
than flared disk. Finally our modeling results do not show evidence for
any correlations between the crystallinity and either the star spectral
type, or the X-ray luminosity (for a subset of the sample).
Conclusions. The size distribution flattening may
suggests that grain coagulation is a slightly more effective process
than fragmentation (helped by turbulent diffusion) in disk atmospheres,
and that this imbalance may last over most of the T Tauri phase.
This result may also point toward small grain depletion via strong
stellar winds or radiation pressure in the upper layers of disk. The
non negligible cold crystallinity fractions suggests efficient radial
mixing processes in order to distribute crystalline grains at large
distances from the central object, along with possible nebular shocks
in outer regions of disks that can thermally anneal amorphous grains.
Key words: stars: pre-main sequence - protoplanetary disks - circumstellar matter - infrared: stars - methods: statistical - techniques: spectroscopic
1 Introduction
The mid-infrared spectral regime probes the warm dust grains located in the planet forming region (typically 1-10 AU for a classical T Tauri disk). At these wavelengths, the young disks are optically opaque to the stellar light, and the thermal emission arises from the disk surface, well above the disk midplane. Single-aperture imaging of disks in the mid-IR suffers from both a relatively low spatial resolution compared to optical/near-IR telescopes, and from poorly extended emission zones. On the other hand, silicates have features due to stretching and bending resonance modes which make spectroscopy at mid-IR wavelengths of very high interest and feasible with current instrumentation. Silicates are indeed the most abundant sort of solids in disks, and therefore constitute a very important ingredient in any planet formation theory.
The dust grains that are originally incorporated into protoplanetary
circumstellar disks are essentially of interstellar nature. They are
thought to be particles much smaller than ![]() m, and mostly composed of silicates or organic refractories. Kemper et al. (R2005)
placed an upper limit of 2.2% on the amount of crystalline silicates in
the interstellar medium (hereafter ISM), which suggests an amorphous
lattice structure for the pristine silicates in forming protoplanetary
disks. In the very early stages of the disk evolution, the tiny dust
grains are so coupled with the gas that grain-grain collisions occur at
sufficiently low relative velocity to allow the grains to coagulate and
grow. This results in fractal aggregates that will tend to settle
toward the disk midplane as their mass increases. From simple
theoretical arguments, considering only the gravitational and drag
forces on the grains in a laminar disk, one can show that
m, and mostly composed of silicates or organic refractories. Kemper et al. (R2005)
placed an upper limit of 2.2% on the amount of crystalline silicates in
the interstellar medium (hereafter ISM), which suggests an amorphous
lattice structure for the pristine silicates in forming protoplanetary
disks. In the very early stages of the disk evolution, the tiny dust
grains are so coupled with the gas that grain-grain collisions occur at
sufficiently low relative velocity to allow the grains to coagulate and
grow. This results in fractal aggregates that will tend to settle
toward the disk midplane as their mass increases. From simple
theoretical arguments, considering only the gravitational and drag
forces on the grains in a laminar disk, one can show that ![]() m-sized grains at 1 AU should settle in the midplane in less than 105 years in a classical T Tauri disk (Weidenschilling 1980).
In fact, the grains are expected to settle even faster as their mass
increases in the course of their journey to the disk midplane. Because
the T Tauri disks are a few million years old, this would suggest
that the inner disk upper layers should be devoided of
m-sized grains at 1 AU should settle in the midplane in less than 105 years in a classical T Tauri disk (Weidenschilling 1980).
In fact, the grains are expected to settle even faster as their mass
increases in the course of their journey to the disk midplane. Because
the T Tauri disks are a few million years old, this would suggest
that the inner disk upper layers should be devoided of ![]() m-sized
or larger grains in the absence of turbulence and grain fragmentation.
This is a prediction that can be tested observationnaly, especially in
the infrared where spectroscopic signatures of silicate grains are
present.
m-sized
or larger grains in the absence of turbulence and grain fragmentation.
This is a prediction that can be tested observationnaly, especially in
the infrared where spectroscopic signatures of silicate grains are
present.
The Spitzer Space Telescope, launched in August 2003, had a sensitivity that surpassed previous mid-IR space missions by orders of magnitudes until the cryogenic mission ended in May 2009. As part of the ``Core to Disks'' (c2d) Legacy survey (Evans et al. 2003), more than a hundred T Tauri stars were spectroscopically observed, to confirm or invalidate some of the predictions concerning dust processing and grain dynamics in protoplanetary disks. In Kessler-Silacci et al. (2006,2007), and Olofsson et al. (2009), we showed that most of the objects display silicate emission features arising from within 10 AU from the star. This allowed both a classical study of grain coagulation and a comprehensive statistical analysis of dust crystallization in planet forming regions of disks around young solar analogs.
In Olofsson et al. (2009),
we showed that not only the warm amorphous silicates had grown, but so
had the colder crystalline silicates as probed by their ![]() m
emission feature. In fact, the emission features in IRS spectra are
very much dominated by micron-sized grains in the upper layers of
disks, pointing toward vertical (turbulent?) mixing of the dust grains
to compensate for gravitational settling, together with grain-grain
destructive fragmentation in the innermost regions of most
protoplanetary disks to compensate for grain growth. This equilibrium
seems to last over several millions of years and be to independent of
the specific star forming region (Oliveira et al. 2010).
Winds and/or radiation pressure, in complement to these processes, can
act to remove a fraction of the submicron-sized grains from disk
atmospheres, and may thus contribute to the transport of crystalline
silicate grains toward the outermost disk regions (see discussion in Olofsson et al. 2009).
m
emission feature. In fact, the emission features in IRS spectra are
very much dominated by micron-sized grains in the upper layers of
disks, pointing toward vertical (turbulent?) mixing of the dust grains
to compensate for gravitational settling, together with grain-grain
destructive fragmentation in the innermost regions of most
protoplanetary disks to compensate for grain growth. This equilibrium
seems to last over several millions of years and be to independent of
the specific star forming region (Oliveira et al. 2010).
Winds and/or radiation pressure, in complement to these processes, can
act to remove a fraction of the submicron-sized grains from disk
atmospheres, and may thus contribute to the transport of crystalline
silicate grains toward the outermost disk regions (see discussion in Olofsson et al. 2009).
Crystalline silicates appear to be very frequent in disks around
T Tauri disks and in regions much colder than their presumed
formation regions, suggesting efficient outward radial transport
mechanisms in disks (Bouwman et al. 2008; Watson et al. 2009a; Olofsson et al. 2009).
Therefore, the determination of the composition and size distribution
of the dust grains in circumstellar disks is one of the keys in
understanding the first steps of planet formation as it can trace the
dust fluxes in planet-forming disks. Detailed modeling of the ![]() m silicate emission feature has already been performed for HAEBE disks by Bouwman et al. (2001) and van Boekel et al. (R2005). Mineralogical studies of dust in disks around very low mass stars and brown dwarfs were also led by Apai et al. (R2005), Riaz (2009), Merín et al. (2007) and Bouy et al. (2009).
The two last studies introduced a novel method to fit the spectra over
the entire IRS spectral range, which allows to decompose the spectra
into two main contributions at different temperatures. This in turn
allowed to compare the degrees of crystallinity and the grain sizes in
two different disk regions. The latter compositional fitting approach
is further supported by the analysis by Olofsson et al. (2009) who showed that the energy and frequencies at which crystalline silicate features are seen at wavelengths larger than
m silicate emission feature has already been performed for HAEBE disks by Bouwman et al. (2001) and van Boekel et al. (R2005). Mineralogical studies of dust in disks around very low mass stars and brown dwarfs were also led by Apai et al. (R2005), Riaz (2009), Merín et al. (2007) and Bouy et al. (2009).
The two last studies introduced a novel method to fit the spectra over
the entire IRS spectral range, which allows to decompose the spectra
into two main contributions at different temperatures. This in turn
allowed to compare the degrees of crystallinity and the grain sizes in
two different disk regions. The latter compositional fitting approach
is further supported by the analysis by Olofsson et al. (2009) who showed that the energy and frequencies at which crystalline silicate features are seen at wavelengths larger than ![]() m are largely uncorrelated to the amorphous
m are largely uncorrelated to the amorphous ![]() m feature observational properties.
m feature observational properties.
We present in this paper an improved version of the compositional fitting method used in Merín et al. (2007) and Bouy et al. (2009). We apply the model to a subsample (58 stars) of high SNR spectra presented in Olofsson et al. (2009)
to derive the dust content in disks about young solar analogs. The
method relies on the fact that the IRS spectral range is sufficiently
broad so that the regions probed at around 10 ![]() m and between 20 and 30
m and between 20 and 30 ![]() m do overlap only partially. This is illustrated for instance in Kessler-Silacci et al. (2006) who show that for a typical T Tauri star, a factor of 2 increase in wavelength (10
m do overlap only partially. This is illustrated for instance in Kessler-Silacci et al. (2006) who show that for a typical T Tauri star, a factor of 2 increase in wavelength (10 ![]() m
m
![]()
![]() m), translates into a factor of 10 (1 AU
m), translates into a factor of 10 (1 AU
![]() 10 AU)
into the regions from which most of the observed emission arises. An
additional goal of our model is therefore to search for differential
effects in crystallinity and grain sizes between the warm and slightly
cooler disks regions which may be indicative of radial and/or vertical
dependent chemical composition and grain size, due for instance to
differential grain evolution and/or grain transport.
10 AU)
into the regions from which most of the observed emission arises. An
additional goal of our model is therefore to search for differential
effects in crystallinity and grain sizes between the warm and slightly
cooler disks regions which may be indicative of radial and/or vertical
dependent chemical composition and grain size, due for instance to
differential grain evolution and/or grain transport.
We develop in Sect. 2
our procedure to model IRS spectra of Class II objects, and
present the tests for robustness of this procedure in Appendix A. The results for 58 objects are presented in Sect. 3, and they are discussed in terms of dust coagulation and dust crystallization in Sect. 4. Section 5
summarizes the implications of our results on disks dynamics at this
stage of evolution and critically discuss the use of the shape and
strength of the amorphous 10 ![]() m silicate feature as a grain size proxy.
m silicate feature as a grain size proxy.
2 Spectral decomposition with the B2C method
We elaborate in this section a modeling procedure whose goal is to
reproduce the observed IRS spectra, from about 5 to ![]() m, in
order to infer the composition and size of the emitting dust
grains. This is achevied by using two dust grain populations at two
different temperatures. We will refer to these two populations as two
different ``components''. The first component aims at reproducing the
features at around
m, in
order to infer the composition and size of the emitting dust
grains. This is achevied by using two dust grain populations at two
different temperatures. We will refer to these two populations as two
different ``components''. The first component aims at reproducing the
features at around ![]() m, its temperature is generally around
m, its temperature is generally around
![]() K (warm component hereafter). The second
component aims at reproducing the residuals, over the full spectral
range and its temperature is colder,
K (warm component hereafter). The second
component aims at reproducing the residuals, over the full spectral
range and its temperature is colder,
![]() K
(cold component hereafter). Each of these two components is described
by several grain compositions, including amorphous and crystalline
silicates, and sizes as detailed below. Bayesian inference is used to
best fit the IRS spectra and to derive uncertainties on the
parameters, hence the name of the procedure, ``B2C'', which stands for
Bayesian inference with 2 Components.
K
(cold component hereafter). Each of these two components is described
by several grain compositions, including amorphous and crystalline
silicates, and sizes as detailed below. Bayesian inference is used to
best fit the IRS spectra and to derive uncertainties on the
parameters, hence the name of the procedure, ``B2C'', which stands for
Bayesian inference with 2 Components.
2.1 Theoretical opacities and grain sizes
To reproduce the observed spectra, we consider five different dust species. The amorphous species include silicates of olivine stoichiometry (glassy MgFeSiO4, density of 3.71 g cm-3, optical indexes from Dorschner et al. 1995), silicates of pyroxene stoichiometry (glassy MgFeSiO6, density of 3.2 g cm-3, Dorschner et al. 1995), and silica (amorphous quartz, density of 3.33 g cm-3, Henning & Mutschke 1997). For the Mg-rich (see Olofsson et al. 2009) crystalline species, we consider enstatite (MgSiO3, density of 2.8 g cm-3, Jaeger et al. 1998) and forsterite (Mg2SiO4, density of 2.6 g cm-3, Servoin & Piriou 1973).
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13909_f01.ps}\par {\hspace*...
...ics[width=13cm,clip]{13909_f02.ps}\hspace*{1.5cm}}\vspace*{-4mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg20.png)
|
Figure 1:
Blowup of the opacities (in units of cm2 g-1) used to model the IRS spectra. The solid line is for
0.1 |
| Open with DEXTER | |
Following previous papers (e.g. Bouwman et al. 2001; Bouwman et al. 2008;
Juhász et al. 2009), the theoretical opacities
![]() of amorphous species are computed assuming homogeneous sphere (Mie
theory), while the DHS theory (Distribution of Hollow Spheres,
Min et al. R2005) is employed for the crystalline silicates in order
to simulate irregularly-shaped dust particles. To limit the number of
free parameters in the model, we consider three spectroscopically
representative grain sizes radii, which are 0.1
of amorphous species are computed assuming homogeneous sphere (Mie
theory), while the DHS theory (Distribution of Hollow Spheres,
Min et al. R2005) is employed for the crystalline silicates in order
to simulate irregularly-shaped dust particles. To limit the number of
free parameters in the model, we consider three spectroscopically
representative grain sizes radii, which are 0.1 ![]() m, 1.5
m, 1.5 ![]() m
and 6.0
m
and 6.0 ![]() m. These three grain sizes are supposed to best mimic
the behaviour of very small grains, intermediate-sized grains and
large grains (e.g. Bouwman et al. 2001,2008). We limit
ourselves to the two smallest sizes, 0.1 and 1.5
m. These three grain sizes are supposed to best mimic
the behaviour of very small grains, intermediate-sized grains and
large grains (e.g. Bouwman et al. 2001,2008). We limit
ourselves to the two smallest sizes, 0.1 and 1.5 ![]() m, for the
crystalline species. The first reason for this choice is that large
crystalline grains present a high degeneracy with large amorphous
grains, as 6.0
m, for the
crystalline species. The first reason for this choice is that large
crystalline grains present a high degeneracy with large amorphous
grains, as 6.0 ![]() m-sized grains are mostly featureless. Therefore
large crystals can be used by the procedure instead of large amorphous
grains, thereby introducing a bias toward high crystallinity
fractions. The second reason is that, according to crystallisation
models (e.g. Gail 2004), one does not expect to produce such
large pure crystals via thermal annealing. Grains more likely grow via
collisional aggregation of both small crystalline and amorphous
material (e.g. Min et al. 2008). Following these two
considerations, we decided not to include 6.0
m-sized grains are mostly featureless. Therefore
large crystals can be used by the procedure instead of large amorphous
grains, thereby introducing a bias toward high crystallinity
fractions. The second reason is that, according to crystallisation
models (e.g. Gail 2004), one does not expect to produce such
large pure crystals via thermal annealing. Grains more likely grow via
collisional aggregation of both small crystalline and amorphous
material (e.g. Min et al. 2008). Following these two
considerations, we decided not to include 6.0 ![]() m-sized
crystals. This choice is in line with previous works from
Sargent et al. (2009) or Riaz (2009). The fifteen opacity curves
(5 grain compositions, 3 grain sizes) used in this paper are displayed
in Fig. 1, including 6.0
m-sized
crystals. This choice is in line with previous works from
Sargent et al. (2009) or Riaz (2009). The fifteen opacity curves
(5 grain compositions, 3 grain sizes) used in this paper are displayed
in Fig. 1, including 6.0 ![]() m-sized crystals to show
the degeneracy with large amorphous grains.
m-sized crystals to show
the degeneracy with large amorphous grains.
2.2 The B2C model
The B2C model elaborated in this paper assumes that the IRS spectrum
can be fitted by considering a continuum emission, and two main
components, a warm and a cold one, essentially responsible for the
10![]() m and 20-30
m and 20-30 ![]() m emissions, respectively. The two
component approach is supported by the work of Olofsson et al. (2009)
who show that disks usually have inhomogeneous compositions with
respect to the dust temperature (crystalline features being more
frequently detected at long than at short wavelengths, the
so-called crystallinity paradox), and that the emission features
at around 10
m emissions, respectively. The two
component approach is supported by the work of Olofsson et al. (2009)
who show that disks usually have inhomogeneous compositions with
respect to the dust temperature (crystalline features being more
frequently detected at long than at short wavelengths, the
so-called crystallinity paradox), and that the emission features
at around 10![]() m are essentially uncorrelated with those
appearing at wavelengths larger than 20
m are essentially uncorrelated with those
appearing at wavelengths larger than 20![]() m. This approach is
also supported by the T Tauri model described in
Kessler-Silacci et al. (2006) where they show that the emission at
10
m. This approach is
also supported by the T Tauri model described in
Kessler-Silacci et al. (2006) where they show that the emission at
10 ![]() m is arising from regions within
m is arising from regions within ![]() 1 AU while the flux
at 20
1 AU while the flux
at 20 ![]() m is arising from within
m is arising from within ![]() 10 AU. Furthermore, we
first used the simpliest solution, with only one component, without
successful results. Any compositional method that aims at fitting IRS
spectra over the full spectral range should therefore be able to
handle inhomogeneous disk compositions. The two component approach
developed in this paper is a simple attempt to go in that
direction. This modeling strategy has already proven sufficient to
provide adequate fits to IRS spectra, from 5 to 35
10 AU. Furthermore, we
first used the simpliest solution, with only one component, without
successful results. Any compositional method that aims at fitting IRS
spectra over the full spectral range should therefore be able to
handle inhomogeneous disk compositions. The two component approach
developed in this paper is a simple attempt to go in that
direction. This modeling strategy has already proven sufficient to
provide adequate fits to IRS spectra, from 5 to 35![]() m
(Merín et al. 2007; Bouy et al. 2009). In this paper, we improve both the model
and the fitting strategy originally developed in Merín et al. (2007)
and Bouy et al. (2009) in order to apply the decompositional method to a
large number of objects.
m
(Merín et al. 2007; Bouy et al. 2009). In this paper, we improve both the model
and the fitting strategy originally developed in Merín et al. (2007)
and Bouy et al. (2009) in order to apply the decompositional method to a
large number of objects.
The first step of the modeling approach is the estimate of the
continuum to be subtracted to the observed IRS spectrum before
performing a compositional fit. This could be done using a radiative
transfer code (e.g. Merín et al. 2007; Bouy et al. 2009), but given the
number of objects (58) to be analyzed, and given the objectives of the
paper which is oriented toward searching for trends thanks to the
analysis of a large sample, obtaining a satisfying model for every
object is not a manageable task. We instead adopt a continuum built by
using a power-law (
![]() )
plus a black-body at
temperature
)
plus a black-body at
temperature
![]() ,
to make our problem more tractable:
,
to make our problem more tractable:
| (2) |
where
In our fitting approach, only two free parameters characterize the
continuum: the black-body temperature
![]() and a
normalization offset
and a
normalization offset ![]() at
at
![]() m. The implementation of a variable offset comes from the
fact that the 10 and 18
m. The implementation of a variable offset comes from the
fact that the 10 and 18![]() m amorphous features partly overlap at
m amorphous features partly overlap at
![]() 13-15
13-15 ![]() m (Fig. 1), and any realistic
continuum should therefore pass below the observed flux at these
wavelengths. For a given set of
m (Fig. 1), and any realistic
continuum should therefore pass below the observed flux at these
wavelengths. For a given set of ![]() ,
,
![]() and offset
value
and offset
value ![]() ,
the synthetic continuum is obtained by solving the
following two-equation system with respect to the normalization
coefficients
,
the synthetic continuum is obtained by solving the
following two-equation system with respect to the normalization
coefficients
![]() and
and
![]() :
:
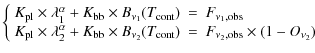
|
(3) |
where
The fit to the continuum-subtracted IRS spectrum is performed in two
steps. First, a fit to the 10 ![]() m feature is obtained between
m feature is obtained between
![]() and
and
![]() (warm component), then a second fit to
the residual spectrum is obtained for wavelengths between
(warm component), then a second fit to
the residual spectrum is obtained for wavelengths between ![]() and
and
![]() 35
35 ![]() m (cold component). The
continuum-substracted IRS spectrum (
m (cold component). The
continuum-substracted IRS spectrum (
![]() )
around
)
around ![]() m is reproduced within the range
[
m is reproduced within the range
[
![]() ,
,
![]() ], by summing up the thirteen mass
absorption coefficients
], by summing up the thirteen mass
absorption coefficients
![]() (
(
![]() dust
species, i index, and
dust
species, i index, and
![]() or 2 grain sizes, j index
depending on the lattice structure), multiplied by a blackbody
or 2 grain sizes, j index
depending on the lattice structure), multiplied by a blackbody
![]() )
at a given warm temperature
)
at a given warm temperature
![]() ,
and weighted with relative masses
,
and weighted with relative masses
![]() :
:
The residuals (
The final synthetic spectrum, obtained in two steps, then reads:
| (6) |
It depends on
|
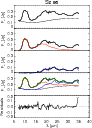
Figure 2: Detailed example of B2C modeling steps for the object Sz 96. From top to bottom: the original spectrum and the estimated continuum (top panel), the continuum substracted spectrum and the fit to the warm component (in orange, 2nd panel), the residuals from the fit to the warm component and the fit to this cold component (in blue, 3rd panel), the final fit to the entire spectrum (in green) and the various contributions (4th panel), the relative residuals between the original spectrum and the final fit (last panel). |
| Open with DEXTER | |
2.3 Fitting process
![\begin{figure}
\par\includegraphics[angle=0,width=16cm,origin=bl]{13909_f04.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg65.png)
|
Figure 3:
Examples of probabilities distributions for
the fit to the Sz 96 spectrum. From the top left panel, clockwise,
are displayed the probability distributions for the warm olivine,
pyroxene, enstatite and forsterite grains. On each panel are
represented 0.1 |
| Open with DEXTER | |
The parameter space has a high dimensionality in our problem and imposes a specific fitting approach to appreciate the reliability of the results. We develop in this paper a method based on a Bayesian analysis, combined with a Monte Carlo Markov chain (MCMC)-like approach to explore the parameter space.
Our procedure is built in order to randomly explore the space of free
parameters (
![]() dust compositions, 2 dust temperatures and 2 parameters for the continuum). We start with a randomly chosen initial
set of parameters, then one of these parameters is randomly modified,
while all the others remain unchanged. When the chosen parameter is
related to the abundance of a grain species (the
dust compositions, 2 dust temperatures and 2 parameters for the continuum). We start with a randomly chosen initial
set of parameters, then one of these parameters is randomly modified,
while all the others remain unchanged. When the chosen parameter is
related to the abundance of a grain species (the
![]() and
and
![]() ), the maximal value for the increment is 1%
of the previous total mass for the considered component (warm or
cold). When the chosen parameter is a temperature or the offset
), the maximal value for the increment is 1%
of the previous total mass for the considered component (warm or
cold). When the chosen parameter is a temperature or the offset
![]() ,
we allow increments of at most 4% of the previous
temperature or the previous offset, respectively. These maximum values
were chosen to obtain small enough increments and therefore explore
continuously the parameter space.
,
we allow increments of at most 4% of the previous
temperature or the previous offset, respectively. These maximum values
were chosen to obtain small enough increments and therefore explore
continuously the parameter space.
For each set of parameters, a synthetic spectrum
![]() is calculated and the goodness of the fit to the observed spectrum is
evalutated with a reduced
is calculated and the goodness of the fit to the observed spectrum is
evalutated with a reduced
![]() .
The parameter space
exploration is therefore very much alike a MCMC approach, with two
specificities: we only perform jumps for one parameter at a time, and
second, the jumps are always accepted
.
The parameter space
exploration is therefore very much alike a MCMC approach, with two
specificities: we only perform jumps for one parameter at a time, and
second, the jumps are always accepted![]() . After niterations (typically n = 800), we set all the parameters to those
that gave the lowest
. After niterations (typically n = 800), we set all the parameters to those
that gave the lowest
![]() among the n previous
iterations. This loop is done m times (usually m is also set to
800) and all the compositions, temperatures, offset and their
associated
among the n previous
iterations. This loop is done m times (usually m is also set to
800) and all the compositions, temperatures, offset and their
associated
![]() values are stored.
values are stored.
![\begin{figure}
\par\mbox{ \includegraphics[width=7cm]{13909_f05.ps} \includegrap...
...th=7cm]{13909_f07.ps} \includegraphics[width=7cm]{13909_f08.ps} }
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg67.png)
|
Figure 4:
Examples of B2C fits over the entire IRS
spectral range for four objects: IRS 60,
Hn 9, SSTc2d J161159.8-382338 and
Sz 96. The warm component is displayed in dotted
orange line, the cold component in dashed blue line, and final
fit to the entire spectrum in green. The dot-dashed grey line
represents the continuum. The light grey enveloppe represents
the 3- |
| Open with DEXTER | |
The
![]() reduced
reduced
![]() values are
transformed into probabilities assuming a Gaussian likelihood function
(
values are
transformed into probabilities assuming a Gaussian likelihood function
(
![]() )
for Bayesian
analysis. Marginalized probability distribution for each free
parameter are then obtained by projection of theseprobabilities onto
each dimension of the parameter space. The best fit to the observed
spectrum among all the simulations (i.e., the one with the lowest
)
for Bayesian
analysis. Marginalized probability distribution for each free
parameter are then obtained by projection of theseprobabilities onto
each dimension of the parameter space. The best fit to the observed
spectrum among all the simulations (i.e., the one with the lowest
![]() value), yields relative masses for all the dust
species and grain sizes (
value), yields relative masses for all the dust
species and grain sizes (
![]() and
and
![]() parameters in Eqs. (3) and (4)) for both
the warm and cold components, as well as best temperatures
parameters in Eqs. (3) and (4)) for both
the warm and cold components, as well as best temperatures
![]() and
and
![]() ,
which typically range between
200 K and 300 K for the warm component, and between 70 K and
150 K for the cold one. The 1-
,
which typically range between
200 K and 300 K for the warm component, and between 70 K and
150 K for the cold one. The 1-![]() uncertainties on the
parameters are derived from the probability distributions for each
parameter. We over-sample each probability distribution to compute
half-width at half maximum for both sides of the distribution, and
derive minimum and maximum 1-
uncertainties on the
parameters are derived from the probability distributions for each
parameter. We over-sample each probability distribution to compute
half-width at half maximum for both sides of the distribution, and
derive minimum and maximum 1-![]() uncertainties. Figure 3 displays ten examples of
well-peaked probability distributions, with their respective
over-sampled distributions overplotted, for some parameters of the fit
to the Sz 96 spectrum, indicating the parameters are
constrained by the B2C fitting approach. Figure 4
displays four example spectra with their best fits (and residuals)
over the entire IRS spectral range, showing that good fits can be
obtained for spectra with different shapes. Spectral regions with high
residuals mostly correspond to regions with low signal-to-noise ratio.
uncertainties. Figure 3 displays ten examples of
well-peaked probability distributions, with their respective
over-sampled distributions overplotted, for some parameters of the fit
to the Sz 96 spectrum, indicating the parameters are
constrained by the B2C fitting approach. Figure 4
displays four example spectra with their best fits (and residuals)
over the entire IRS spectral range, showing that good fits can be
obtained for spectra with different shapes. Spectral regions with high
residuals mostly correspond to regions with low signal-to-noise ratio.
The robustness of the B2C procedure has been intensively tested and this work is reported in Appendix A. Using theoretical spectra we search for any possible deviations to the input dust mineralogy, that could either affect the inferred grain sizes or crystallinity fractions. The main result is that even if there is a slight deviation for a few individual cases, in a statistical point of view for a large sample, the B2C procedure is robust when determining the dust mineralogy.
3 Spectral decomposition of 58 T Tauri IRS spectra with the B2C model
We run the B2C compositional fitting procedure on 58 different stars
(most of them being T Tauri stars, except BD+31 634 which is
an Herbig Ae star), for which we obtained Spitzer/IRS spectra as part
of the c2d Legacy program. The spectra are presented in
Olofsson et al. (2009) and we refer to that paper for details about data
reduction. The selection of the 58 objects out of 96 in
Olofsson et al. (2009) is based on several criteria. First, some objects
do not have Short-Low data therefore the amorphous 10 ![]() m feature
is not complete. Second, as the goal is to determine the dust
mineralogy, we do not run the procedure for objects that do not show
clear silicate emission features, or with peculiar spectra
(e.g. cold disks like LkHa 330 or
CoKu Tau /4, Brown et al. 2007). Finally, objects for which
continuum estimation in the 5-7.5
m feature
is not complete. Second, as the goal is to determine the dust
mineralogy, we do not run the procedure for objects that do not show
clear silicate emission features, or with peculiar spectra
(e.g. cold disks like LkHa 330 or
CoKu Tau /4, Brown et al. 2007). Finally, objects for which
continuum estimation in the 5-7.5 ![]() m spectral region was not
possible using a power-law were eliminated.
m spectral region was not
possible using a power-law were eliminated.
The spectral range used for the fits is always limited to a maximum
wavelength of 35 ![]() m. The first reason of this choice is that the
products of the c2d extraction pipeline are, for our sample, in
average limited to 36.6
m. The first reason of this choice is that the
products of the c2d extraction pipeline are, for our sample, in
average limited to 36.6 ![]() m. In addition to this, the degrading
quality of the end of the spectra, likely caused by the quality of the
relative spectral response function used at these wavelengths, may
lead to an over-prediction of the crystalline content, for the cold
component. In a few cases, the spectra are rising for wavelengths
larger than 35
m. In addition to this, the degrading
quality of the end of the spectra, likely caused by the quality of the
relative spectral response function used at these wavelengths, may
lead to an over-prediction of the crystalline content, for the cold
component. In a few cases, the spectra are rising for wavelengths
larger than 35 ![]() m, and the fitting procedure tries to match this
rise with crystalline features (which are the only features strong
enough in this spectral range). Finally, longer wavelengths may probe
an even colder dust content and this would require the implementation
of a third dust component in order to reproduce the entire spectral
range. For all these reasons, we choose to limit the modeling to
wavelengths smaller than 35
m, and the fitting procedure tries to match this
rise with crystalline features (which are the only features strong
enough in this spectral range). Finally, longer wavelengths may probe
an even colder dust content and this would require the implementation
of a third dust component in order to reproduce the entire spectral
range. For all these reasons, we choose to limit the modeling to
wavelengths smaller than 35 ![]() m.
m.
The source list and relative abundances for every object can be found in Table A.1. Because of some degeneracy between amorphous olivine and pyroxene opacities, we sum their respective abundances to a single amorphous component. The final fits to the 58 IRS spectra are displayed in Figs. A.6.
3.1 Grain size properties
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,origin=bl]{13909_f09.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg71.png)
|
Figure 5: Mean grain sizes for the cold component as a function of the mean grain size for the warm component |
| Open with DEXTER | |
3.1.1 Mean mass-averaged grain sizes
With the outputs of the ``B2C'' procedure for the 58 objects processed
we have statistical trends on typical grain sizes necessary to
reproduce the spectra. The mean mass-averaged grain sizes for the warm
and cold components,
![]() and
and
![]() ,
respectively, are calculated as follows:
,
respectively, are calculated as follows:
where
We obtain a mean mass-averaged size of
![]() m for the warm component, and a comparable value of
m for the warm component, and a comparable value of
![]() m for the cold
component. Figure 5 shows that mass-averaged grain sizes
for both components are uncorrelated with each other. In order to
quantify the strength of the correlation, we compute the Kendall
m for the cold
component. Figure 5 shows that mass-averaged grain sizes
for both components are uncorrelated with each other. In order to
quantify the strength of the correlation, we compute the Kendall
![]() correlation coefficient and its associated probability P. The
correlation coefficient and its associated probability P. The
![]() value denotes if there is any correlation or anti-correlation
(
value denotes if there is any correlation or anti-correlation
(![]() or -1, respectively), and the P probability
corresponds to the significance probability (from 0 to 1, from the
most to the less significant). Regarding the latter two quantities we
obtain a Kendall
or -1, respectively), and the P probability
corresponds to the significance probability (from 0 to 1, from the
most to the less significant). Regarding the latter two quantities we
obtain a Kendall ![]() value of 0.007 and a significance probability
P = 0.941. This overall suggests that the warm and cold disk regions
considered in this study are independent, as both components show
uncorrelated grain sizes in the inner and outer regions. This
suggests that differential grain growth is not the sole process
explaining the observed variations from object to object. This result
is in line with the conclusions of Olofsson et al. (2009) and supporting
the B2C model assumptions. In their study of 65 T Tauri stars,
Sargent et al. (2009) find that grains are larger in the inner regions
compared to outer regions, and argue this difference can be explained
by faster grain coagulation in the inner regions, where dynamical
timescales are shorter. In our study, we find no strong evidence of
such a difference (2.28 versus 2.02
value of 0.007 and a significance probability
P = 0.941. This overall suggests that the warm and cold disk regions
considered in this study are independent, as both components show
uncorrelated grain sizes in the inner and outer regions. This
suggests that differential grain growth is not the sole process
explaining the observed variations from object to object. This result
is in line with the conclusions of Olofsson et al. (2009) and supporting
the B2C model assumptions. In their study of 65 T Tauri stars,
Sargent et al. (2009) find that grains are larger in the inner regions
compared to outer regions, and argue this difference can be explained
by faster grain coagulation in the inner regions, where dynamical
timescales are shorter. In our study, we find no strong evidence of
such a difference (2.28 versus 2.02 ![]() m). However
Fig. 5 shows a larger dispersion in grain sizes for the
warm component compared to the cold component. This could be a
consequence of shorter dynamical timescales in the inner regions where
grains are not frozen and will be strongly submitted to both
coagulation and fragmentation processes, compared to the outer
regions.
m). However
Fig. 5 shows a larger dispersion in grain sizes for the
warm component compared to the cold component. This could be a
consequence of shorter dynamical timescales in the inner regions where
grains are not frozen and will be strongly submitted to both
coagulation and fragmentation processes, compared to the outer
regions.
Additionally, we investigate the different mass-averaged grain sizes,
for both the crystalline and amorphous grains. For the warm component,
crystalline grains have a mean mass-averaged grain size of
![]() m while amorphous grains
have
m while amorphous grains
have
![]() m. For the
cold component, we find
m. For the
cold component, we find
![]() m and
m and
![]() m. As we did not include large crystalline grains in the
fitting process, it is not surprising to obtain smaller mass-averaged
sizes for the crystalline grains compared to amorphous grains. However
this trend is supported by the results from Bouwman et al. (2008), for
seven T Tauri stars.
m. As we did not include large crystalline grains in the
fitting process, it is not surprising to obtain smaller mass-averaged
sizes for the crystalline grains compared to amorphous grains. However
this trend is supported by the results from Bouwman et al. (2008), for
seven T Tauri stars.
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,origin=bl]{13909_f10.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg88.png)
|
Figure 6: Flaring indices F30/F13 as a function of the warm mass-averaged mean grain size. |
| Open with DEXTER | |
3.1.2 Mass-averaged grain size versus disk flaring
As in Olofsson et al. (2009), we find a trend between
![]() and disk flaring as measured by the flux ratio
F30/F13 (fluxes in Jy integrated between
and disk flaring as measured by the flux ratio
F30/F13 (fluxes in Jy integrated between
![]() m
for F13, and
m
for F13, and
![]() m for F30). As illustrated in
Fig. 6, we find that large grains in the warm
component are mostly present in flat disks, while smaller grains can
be found in both flared or flat disks. This anti-correlation for
the warm component has a Kendall correlation coefficient
m for F30). As illustrated in
Fig. 6, we find that large grains in the warm
component are mostly present in flat disks, while smaller grains can
be found in both flared or flat disks. This anti-correlation for
the warm component has a Kendall correlation coefficient ![]() of
-0.32 with a significance probability of
of
-0.32 with a significance probability of
![]() .
This anti-correlation is still present, when considering
only the warm amorphous grain sizes (
.
This anti-correlation is still present, when considering
only the warm amorphous grain sizes (
![]() with
with
![]() ). A similar anti-correlation has also been
found by Bouwman et al. (2008), and by Watson et al. (2009a) in their
Taurus-Auriga association sample.
). A similar anti-correlation has also been
found by Bouwman et al. (2008), and by Watson et al. (2009a) in their
Taurus-Auriga association sample.
Considering
![]() as a function of
the flaring degree (
F30/F13), we search for a similar result
as in Olofsson et al. (2009) where we found that small crystalline
grains are preferentially seen in flattened disks, while large
crystalline grains can be found in a variety of flat or flared
disks. We did not find a similar trend from the outputs of the
modeling, the correlation coefficient being
as a function of
the flaring degree (
F30/F13), we search for a similar result
as in Olofsson et al. (2009) where we found that small crystalline
grains are preferentially seen in flattened disks, while large
crystalline grains can be found in a variety of flat or flared
disks. We did not find a similar trend from the outputs of the
modeling, the correlation coefficient being
![]() ,
with a
significance probability of 0.66. According to this model, the size of
the cold crystalline material seems to be strongly unrelated with the
flaring degree of disks.
,
with a
significance probability of 0.66. According to this model, the size of
the cold crystalline material seems to be strongly unrelated with the
flaring degree of disks.
3.1.3 Flattened grain size distributions
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,origin=bl]{13909_f11.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg96.png)
|
Figure 7: Grain sizes distribution, for warm (red circles and dotted line) and cold (blue squares and dashed line) component. The MRN reference distribution (-3.5 index) is the black plain line. |
| Open with DEXTER | |
Since our spectral decomposition includes three grain sizes, for the
amorphous species, we can evaluate the shape of the size distribution
in the atmospheres of disks. Assuming a differential size distribution
![]() where Ka is a normalization
constant, we approximate the number Na of grains of size a with:
where Ka is a normalization
constant, we approximate the number Na of grains of size a with:
after a Taylor expansion to the first order of Eq. (7) about a assuming
Figure 7 shows the mean differential grain size distribution
in normalized number of grains obtained following this procedure. In
Fig. 7, the warm component is represented in open
circles, the cold component in open squares, and a reference MRN
differential size distribution (p=-3.5) with a plain line. Assuming
power-law size distributions, we find p indexes of
![]() and
and
![]() for the warm and cold
components, respectively, indicating much flatter size distributions
compared to the MRN size distribution. Two additional runs of the B2C
procedure for the 58 objects allowed to confirm this trend, and to
estimate uncertainties on the slopes. For the warm component, we
typically find
for the warm and cold
components, respectively, indicating much flatter size distributions
compared to the MRN size distribution. Two additional runs of the B2C
procedure for the 58 objects allowed to confirm this trend, and to
estimate uncertainties on the slopes. For the warm component, we
typically find
![]() ,
and
,
and
![]() for the
cold component.
for the
cold component.
Because the p indexes are larger or close to -3, an immediate
consequence of this result is that the emission in disk upper layers
is statistically dominated by the ![]() m-sized grains in our stellar
sample, especially for the warm component, and is largely independent
of the minimum grain size of the size distribution as long as its
value is small enough (submicronic, see discussion in Sect. 5.3 of
Olofsson et al. 2009). This suggests that the flat, boxy 10
m-sized grains in our stellar
sample, especially for the warm component, and is largely independent
of the minimum grain size of the size distribution as long as its
value is small enough (submicronic, see discussion in Sect. 5.3 of
Olofsson et al. 2009). This suggests that the flat, boxy 10 ![]() m
feature profile for most T Tauri stars discussed in terms of a
depletion of small grains in Olofsson et al. (2009), is more precisely
revealing a significant flattening of the size distribution,
i.e. a relative lack of submicron-sized grains with respect to
micron-sized grains, but not a complete depletion. This size
distribution flattening is further discussed in
Sect. 4.
m
feature profile for most T Tauri stars discussed in terms of a
depletion of small grains in Olofsson et al. (2009), is more precisely
revealing a significant flattening of the size distribution,
i.e. a relative lack of submicron-sized grains with respect to
micron-sized grains, but not a complete depletion. This size
distribution flattening is further discussed in
Sect. 4.
3.2 Silicate crystals
3.2.1 The crystallinity paradox reexamined
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,origin=bl]{13909_f12.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg108.png)
|
Figure 8:
Crystalline fraction of the cold component (
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=8.8cm,origin=bl]{13909_f...
...ps}\includegraphics[angle=0,width=8.8cm,origin=bl]{13909_f14.ps} }\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg109.png)
|
Figure 9:
Left panel: crystalline distributions for warm component (
|
| Open with DEXTER | |
Figure 8 shows the correlation between the warm and
cold crystalline fractions (which we denote as
![]() and
and
![]() ,
respectively, in the following), with Kendall's
,
respectively, in the following), with Kendall's
![]() and a significance probability
and a significance probability
![]() .
While slightly dispersed, there is a tendency for a
simultaneous increase of the crystallinity in both the warm and cold
components. The crystalline distributions for the warm and cold
components are displayed on the left panel of Fig. 9.
For the warm component, the mean crystalline fraction is
.
While slightly dispersed, there is a tendency for a
simultaneous increase of the crystallinity in both the warm and cold
components. The crystalline distributions for the warm and cold
components are displayed on the left panel of Fig. 9.
For the warm component, the mean crystalline fraction is
![]() %, while this fraction shifts up to
%, while this fraction shifts up to
![]() % for the cold
component. Overall, these results show no significant difference
between the crystalline fractions in both components.
% for the cold
component. Overall, these results show no significant difference
between the crystalline fractions in both components.
These modeling results give us new insights concerning the
crystallinity paradox identified observationally in
Olofsson et al. (2009). The crystallinity paradox expresses the fact
that crystalline features at long wavelengths are ![]() 3.5 times
more frequently detected than those at shorter wavelengths. Using
simple models of dust opacities, we concluded that a contrast effect
(i.e. the strong 10
3.5 times
more frequently detected than those at shorter wavelengths. Using
simple models of dust opacities, we concluded that a contrast effect
(i.e. the strong 10 ![]() m amorphous feature masking smaller
crystalline features) could not be accounted for the low detection
frequency of crystalline features in the 10
m amorphous feature masking smaller
crystalline features) could not be accounted for the low detection
frequency of crystalline features in the 10 ![]() m range, a result
valid for crystallinity fraction larger than 15% for 1.5
m range, a result
valid for crystallinity fraction larger than 15% for 1.5 ![]() m
grains (Olofsson et al. 2009). For lower crystallinity values, we
indeed showed that the synthetic spectra computed in
Olofsson et al. (2009) were not representative of the observations. This
contrast effect could therefore not be constrained for
low-crystallinity fractions, where most of our objects lie for
the warm component, according to Fig. 9. With the
outputs of the modeling procedure, we can investigate this issue with
a new look. Right panel of Fig. 9 shows the cumulative
fractions as a function of the crystallinity fractions. Even if there
are a few differences between the warm (red dotted) and cold (blue
dashed) components, the two cumulative fractions display a very
similar behavior that cannot solely explain the crystallinity paradox
that we derived from the observations. This therefore means that, with
this modeling procedure, a contrast issue around 10
m
grains (Olofsson et al. 2009). For lower crystallinity values, we
indeed showed that the synthetic spectra computed in
Olofsson et al. (2009) were not representative of the observations. This
contrast effect could therefore not be constrained for
low-crystallinity fractions, where most of our objects lie for
the warm component, according to Fig. 9. With the
outputs of the modeling procedure, we can investigate this issue with
a new look. Right panel of Fig. 9 shows the cumulative
fractions as a function of the crystallinity fractions. Even if there
are a few differences between the warm (red dotted) and cold (blue
dashed) components, the two cumulative fractions display a very
similar behavior that cannot solely explain the crystallinity paradox
that we derived from the observations. This therefore means that, with
this modeling procedure, a contrast issue around 10 ![]() m is
required to match the observations described in
Olofsson et al. (2009). In other words, for some objects, few
crystalline grains are required to reproduce the 10
m is
required to match the observations described in
Olofsson et al. (2009). In other words, for some objects, few
crystalline grains are required to reproduce the 10 ![]() m feature,
but these grains do not produce strong features (on top of the
amorphous feature) that can easily be detected in the spectra. Still,
the left panel of Fig. 9 shows that the cold
crystalline distribution is wider than the warm distribution. For the
warm component, 3.5% of the objects have a crystallinity fractions
larger than 40%, while this fraction shifts up to 13.8% for the cold
component. This overall means that in a few cases, we see more
crystalline grains in the cold component compared to the warm
component, as result also found by Sargent et al. (2009)
m feature,
but these grains do not produce strong features (on top of the
amorphous feature) that can easily be detected in the spectra. Still,
the left panel of Fig. 9 shows that the cold
crystalline distribution is wider than the warm distribution. For the
warm component, 3.5% of the objects have a crystallinity fractions
larger than 40%, while this fraction shifts up to 13.8% for the cold
component. This overall means that in a few cases, we see more
crystalline grains in the cold component compared to the warm
component, as result also found by Sargent et al. (2009)
3.2.2 Crystallinity versus disk and stellar properties
We also search for correlations between disk flaring proxies and
crystallinity. We find no striking correlations regarding the disk
flaring indexes
F30/F13 and warm crystalline fraction
![]() with a significance probability P =
0.25). Flared or flat disks present a wide range of crystalline
fractions, with a strong dispersion. We find similar results, with an
important dispersion, for the flaring index versus cold crystalline
fraction
with a significance probability P =
0.25). Flared or flat disks present a wide range of crystalline
fractions, with a strong dispersion. We find similar results, with an
important dispersion, for the flaring index versus cold crystalline
fraction
![]() (
(
![]() with a significance
probability P = 0.12), meaning that crystallinity fraction of the
cold component does not strongly depend on the disk flaring.
with a significance
probability P = 0.12), meaning that crystallinity fraction of the
cold component does not strongly depend on the disk flaring.
![\begin{figure}
\includegraphics[angle=0,width=9cm,origin=bl]{13909_f15.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg116.png)
|
Figure 10:
Crystalline fraction for the warm (
|
| Open with DEXTER | |
Figure 10 displays the dependence of crystalline
fractions for both the warm (
![]() ,
red open circles) and
cold components (
,
red open circles) and
cold components (
![]() ,
blue open squares) as a function of
the spectral type, for stars between K0 and M5. We find no correlation
for the warm component with the spectral type (
,
blue open squares) as a function of
the spectral type, for stars between K0 and M5. We find no correlation
for the warm component with the spectral type (
![]() with P
= 0.60), suggesting that the degree of crystallization does not
depend upon the spectral type (in the explored range), and that
crystallization processes are very general for TTs. This result is in
good agreement with Watson et al. (2009a), who find no correlation
between crystallinity and stellar luminosity or stellar mass. On the
other hand, Watson et al. (2009a) only studied the cold disk regions
crystallinity via the presence of the 33.6
with P
= 0.60), suggesting that the degree of crystallization does not
depend upon the spectral type (in the explored range), and that
crystallization processes are very general for TTs. This result is in
good agreement with Watson et al. (2009a), who find no correlation
between crystallinity and stellar luminosity or stellar mass. On the
other hand, Watson et al. (2009a) only studied the cold disk regions
crystallinity via the presence of the 33.6 ![]() m forsterite
feature. Using the outputs of our B2C procedure, we are able to better
quantify the crystalline fraction of the cold component, and we do not
find any correlation of
m forsterite
feature. Using the outputs of our B2C procedure, we are able to better
quantify the crystalline fraction of the cold component, and we do not
find any correlation of
![]() with spectral type, the
dispersion being too large (
with spectral type, the
dispersion being too large (
![]() with P = 0.59), thereby
confirming the result by Watson et al. (2009a).
with P = 0.59), thereby
confirming the result by Watson et al. (2009a).
3.2.3 Dust evolution: coagulation versus crystallization
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,origin=bl]{13909_f16.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg119.png)
|
Figure 11:
Warm crystalline fraction
|
| Open with DEXTER | |
Dust is evolving inside circumstellar disks, either in size or in
lattice structure, in particular through coagulation and
crystallization. To investigate possible links between these two
phenomena, we search for correlations between grain sizes, for
amorphous and crystalline dust contents (
![]() ), as a function of crystalline fractions, in both
the warm and cold components (
), as a function of crystalline fractions, in both
the warm and cold components (
![]() ).
).
We find no evidence that grains are growing and crystallizing at the
same time in the warm component. Considering
![]() and
and
![]() values, we obtain the following
coefficients:
values, we obtain the following
coefficients:
![]() ,
with a significance probability equal to
0.67. This result is displayed in Fig. 11. We obtain an
even less favorable correlation coefficients for the cold component
(
,
with a significance probability equal to
0.67. This result is displayed in Fig. 11. We obtain an
even less favorable correlation coefficients for the cold component
(
![]() with P = 0.92). This overall indicates that the
processes that govern the mean size of the grains and their
crystallinity are independent phenomena in disks.
with P = 0.92). This overall indicates that the
processes that govern the mean size of the grains and their
crystallinity are independent phenomena in disks.
We also search for correlations between the amorphous and crystalline dust contents for the two components, to see how they evolve with respect to each others. Based on our B2C spectral decomposition, we find no significant correlations between the several amorphous or crystalline dust populations.
3.2.4 Enstatite, forsterite and silica
|
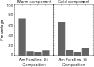
Figure 12: Mean composition for warm and cold components according to the results of the 58 objects processed. |
| Open with DEXTER | |
Bouwman et al. (2008) find that enstatite dominates in the innermost warm regions over forsterite, and on the other side that forsterite is the dominant silicate crystal in the cooler outer regions. Figure 12 shows the mean composition we obtain for the 58 objects, for both components (warm and cold). As amorphous pyroxene and amorphous olivine spectral signatures are very similar, we merge together their relative contributions. Regarding the crystalline content, even if there is no clear predominance of forsterite or enstatite masses for the warm component (8.7% vs. 7.4% respectively), for the cold component forsterite appears more abundant than enstatite (11.4% vs. 7.4% in mass). In order to have more details on the presence or absence of these two crystals, Fig. 13 shows the distribution for the enstatite and forsterite abundances (left and right panel, respectively), for the warm and cold components (open circles and open squares, respectively). No predominance of either enstatite or forsterite is found in the warm component, while forsterite seems to be more frequent than enstatite in the cold component. Similar distributions are found by Sargent et al. (2009) regarding the warm and cold forsterite and enstatite.
We search for correlations between the masses of the warm or cold
enstatite populations, and warm or cold forsterite populations. We
find a correlation between warm enstatite and warm forsterite grains,
with a Kendall's ![]() value of 0.33 and with a significance
probability P equal to
value of 0.33 and with a significance
probability P equal to
![]() .
This trend tends to
confirm the results displayed in Fig. 12: the
crystallisation processes in the warm component do not favor the
formation of one or the other crystals. We also find a correlation
between the relative masses of warm enstatite grains and cold
forsterite grains, with
.
This trend tends to
confirm the results displayed in Fig. 12: the
crystallisation processes in the warm component do not favor the
formation of one or the other crystals. We also find a correlation
between the relative masses of warm enstatite grains and cold
forsterite grains, with
![]() and P equal to
and P equal to
![]() .
This tends to indicate that the enrichment in
crystalline grains in the disk is global within
.
This tends to indicate that the enrichment in
crystalline grains in the disk is global within ![]() 10 AU, and
not local.
10 AU, and
not local.
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=8cm,origin=bl]{13909_f18...
...phics[angle=0,width=8cm,origin=bl]{13909_f19.ps} }\vspace*{-2mm} \end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg128.png)
|
Figure 13: Distribution for the warm (red circles and dotted histogram), cold (blue squares and dashed histogram) for enstatite ( left panel) and forsterite (right panel) crystalline abundances. |
| Open with DEXTER | |
Knowing that forsterite and silica can interact with each other to
form enstatite (
![]() ), we search for correlations between the relatives
masses of forsterite, enstatite and silica in both components. We may
expect to find an anti-correlation between the presence of enstatite
and silica, as silica disappears from the disk medium in the above
reaction. We did not find any striking trend between all the masses,
even when considering only small and intermediate-sized grains (0.1
and 1.5
), we search for correlations between the relatives
masses of forsterite, enstatite and silica in both components. We may
expect to find an anti-correlation between the presence of enstatite
and silica, as silica disappears from the disk medium in the above
reaction. We did not find any striking trend between all the masses,
even when considering only small and intermediate-sized grains (0.1
and 1.5 ![]() m). This suggests that the reaction between
forsterite and silica is not the main path for enstatite
production.
m). This suggests that the reaction between
forsterite and silica is not the main path for enstatite
production.
3.3 Sample homogeneity
The studied stellar sample is drawn from several star forming regions. It may therefore be interesting to see if any cloud-to-cloud variations can be observed. The 58 Class II objects are distributed among 6 different clouds: Chamaleon, Ophiuchus, Lupus, Perseus, Serpens and Taurus (except for IRAS 08267-3336 which is an isolated star). Table 1 shows several results as a function of the corresponding clouds: the number of objects, the grain-size distribution slopes for the warm and cold components, and both the warm and cold crystallinity fractions. The results for the Perseus, Serpens and Taurus clouds are not statistically significant, given the low-statistics number of stars for these regions. On the other side, the three other clouds show very similar behavior for all the considered results. The grain size distributions and crystallinity fractions are very close to each other (with a number of objects between 13 and 16 per cloud).
Recently, Oliveira et al. (2010) studied the amorphous silicate features
in a large sample of 147 sources in the Serpens, and compared their
results with the Taurus young stars. That study, along with the
results from Olofsson et al. (2009), show that the 10 ![]() m feature
appears to have a similar distribution of shape and strength,
regardless of the star forming region or stellar ages. In terms of
silicate features, the stellar sample analyzed in this study is
therefore representative of a typical population of T Tauri stars.
m feature
appears to have a similar distribution of shape and strength,
regardless of the star forming region or stellar ages. In terms of
silicate features, the stellar sample analyzed in this study is
therefore representative of a typical population of T Tauri stars.
4 Discussion
4.1 Implications for the dust dynamics in the atmospheres of young disks
In Olofsson et al. (2009), we discussed the impact of a size
distribution on the shape of the 10 ![]() m feature, and could not
disentangle between two possibilities to explain the flat, boxy
m feature, and could not
disentangle between two possibilities to explain the flat, boxy
![]() m feature profile that is characteristic of micron-sized
grains. One possibility was that the grain size distribution is close
to a MRN-like distribution (p = -3.5), extending down to sizes of at
least several micrometers, with the consequence that the Spitzer/IRS
observations would then probe a truncation of the size distribution at
the minimum grain size (of the order of a micrometer). A second
possibility implied a differential size distribution
m feature profile that is characteristic of micron-sized
grains. One possibility was that the grain size distribution is close
to a MRN-like distribution (p = -3.5), extending down to sizes of at
least several micrometers, with the consequence that the Spitzer/IRS
observations would then probe a truncation of the size distribution at
the minimum grain size (of the order of a micrometer). A second
possibility implied a differential size distribution
![]() that departs from a MRN-like
distribution, being much flatter and with an index p close to, or
larger than -3 to get the dust absorption/emission cross sections
dominated by grains with size parameters
that departs from a MRN-like
distribution, being much flatter and with an index p close to, or
larger than -3 to get the dust absorption/emission cross sections
dominated by grains with size parameters
![]() close to
unity.
close to
unity.
By model fitting 58 IRS spectra of T Tauri stars, we find a general
flattening of the grain size distribution (
![]()
![]() )
in the atmospheres of disks around
T Tauri stars with respect to the grain size distribution in the ISM
up to about 10 AU (this effect being stronger for the inner regions
of disks). Our results suggest that the frequently observed boxy shape
of the 10
)
in the atmospheres of disks around
T Tauri stars with respect to the grain size distribution in the ISM
up to about 10 AU (this effect being stronger for the inner regions
of disks). Our results suggest that the frequently observed boxy shape
of the 10 ![]() m feature is rather due to the slope of the size
distribution, than to a minimum grain size in the disk atmospheres
close to a micrometer. This finding very much relaxes the need for a
sharp, and quite generic truncation of the size distribution at around
one micrometer as proposed in Olofsson et al. (2009). Nevertheless,
radiation pressure and/or stellar winds which had been proposed to
explain such a cut-off are likely to operate anyway, and may thus
contribute to the flattening of the size distribution by removing a
fraction of the submicron-sized grains. This would furthermore help
transporting crystalline grains outwards.
m feature is rather due to the slope of the size
distribution, than to a minimum grain size in the disk atmospheres
close to a micrometer. This finding very much relaxes the need for a
sharp, and quite generic truncation of the size distribution at around
one micrometer as proposed in Olofsson et al. (2009). Nevertheless,
radiation pressure and/or stellar winds which had been proposed to
explain such a cut-off are likely to operate anyway, and may thus
contribute to the flattening of the size distribution by removing a
fraction of the submicron-sized grains. This would furthermore help
transporting crystalline grains outwards.
An alternative explanation for the size distribution flattening involves an overabundance of micrometer-sized grains with respect to the submicron-sized grains. At first glance, this situation may sound counterintuitive as micrometer-sized grains are more prone to settle toward the disk midplane which would, in turn, tend to steepen the size distribution in disk atmospheres. This ignores that both turbulent diffusion and collisions between pebbles may complicate this picture, and may even possibly revert this trend by supplying the disk atmospheres with micrometer-sized (and larger) grains. Therefore, the IRS observations may in fact indicate that coagulation and vertical mixing are slightly more efficient processes to supply grains in disk atmospheres than fragmentation, resulting in an overabundance of micrometer-sized grains compared to an ISM-like distribution. This situation may last over most of the T Tauri phase.
Interestingly, Lommen et al. (2010) also found a flattening of the grain
size distributions for T Tauri stars, probed by the millimeter slope
of the SED. They found a tentative correlation between the shape of
the 10 ![]() m feature and the mm slope for a large sample of sources,
with flatter 10
m feature and the mm slope for a large sample of sources,
with flatter 10 ![]() m feature being associated with shallower mm
slopes. Similarly, Ricci et al. (2010) also find grain size
distributions flatter than in the ISM, with 3 mm PdBI observations of
T Tauri stars in the Taurus-Auriga star forming region. Therefore, the
size distribution flattening in disk atmospheres may extend to deeper
and more distant regions, and to larger grains sizes than those probed
by mid-IR spectroscopy.
m feature being associated with shallower mm
slopes. Similarly, Ricci et al. (2010) also find grain size
distributions flatter than in the ISM, with 3 mm PdBI observations of
T Tauri stars in the Taurus-Auriga star forming region. Therefore, the
size distribution flattening in disk atmospheres may extend to deeper
and more distant regions, and to larger grains sizes than those probed
by mid-IR spectroscopy.
Table 1: Cloud-to-cloud variations for several parameters from the spectral decomposition.
4.2 Silicate crystallization and amorphization
In this study, we have been able to quantify the fraction of crystals
for both the warm and cold components. In Olofsson et al. (2009), we
identify a crystallinity paradox expressing the fact that
crystalline features are much more frequently detected at long
wavelengths compared to short wavelengths. By building crystallinity
distributions with the results from the spectral decomposition, we
find that even if the cold crystalline distribution is slightly
broader than the warm distribution, they both show a similar behavior
(see right panel of Fig. 9). Therefore, this may suggest
that the observational crystallinity paradox could be the
consequence of a combined effect: relatively low crystalline fractions
(![]() 15-20%) for a great number of the T Tauri stars, and a contrast
issue at short wavelengths preventing the direct identification of
weak crystalline features on top of the 10
15-20%) for a great number of the T Tauri stars, and a contrast
issue at short wavelengths preventing the direct identification of
weak crystalline features on top of the 10 ![]() m amorphous
feature. Nevertheless, it is noteworthy that correcting for the
contrast issue through B2C spectral decomposition does not revert the
trend, but instead makes the distribution of crystals in the warm and
cold disk regions quite similar.
m amorphous
feature. Nevertheless, it is noteworthy that correcting for the
contrast issue through B2C spectral decomposition does not revert the
trend, but instead makes the distribution of crystals in the warm and
cold disk regions quite similar.
Table 2: X-ray luminosities for a subset of our stellar sample.
In order to explain the non negligible crystallinity fractions
obtained for the cold component (up to 70% in a few cases,
e.g. Fig. 8), there is a strong need for radial outward
transport, assuming that the only source of production of crystals is
thermal annealing or gas-phase condensation/annealing, taking place in
the inner regions of disks. Several models have shown that such
mechanism is likely to happen in circumstellar disks around active
stars (see Keller & Gail 2004 or Ciesla 2009). According to
Ciesla (2009), for an accretion rate larger than
10
![]() /yr, grains can be transported to distances out
to 20 AU in about
/yr, grains can be transported to distances out
to 20 AU in about ![]() 105 years. A result in line with the 2D
time-dependent disk model described in Visser & Dullemond (2010). However
given the relatively young ages of our stellar sample (
105 years. A result in line with the 2D
time-dependent disk model described in Visser & Dullemond (2010). However
given the relatively young ages of our stellar sample (![]() few
Myrs), and the rather high accretion rate required
(10
few
Myrs), and the rather high accretion rate required
(10
![]() /yr), we cannot assess that radial transport is
the only mechanism responsible for the strong similarity of both warm
and cold crystallinity distributions. This instead suggests that other
crystallization processes are necessary, that must take place in the
outer regions of disks. A theoretical model, detailed in
Tanaka et al. (2010), shows that depending on the gas density,
crystallization can take place with typical temperature of a few
hundred Kelvin. Such process can be triggered in the outer regions by
nebular shocks (Desch & Connolly 2002) which lead to graphitization of
the carbon mantle providing the latent heat for silicate
crystallization.
/yr), we cannot assess that radial transport is
the only mechanism responsible for the strong similarity of both warm
and cold crystallinity distributions. This instead suggests that other
crystallization processes are necessary, that must take place in the
outer regions of disks. A theoretical model, detailed in
Tanaka et al. (2010), shows that depending on the gas density,
crystallization can take place with typical temperature of a few
hundred Kelvin. Such process can be triggered in the outer regions by
nebular shocks (Desch & Connolly 2002) which lead to graphitization of
the carbon mantle providing the latent heat for silicate
crystallization.
However, crystallization by thermal annealing is likely to happen on
very short timescales (few hours at
![]() K, according to
laboratory measurements, see Hallenbeck et al. 1998). Therefore, one
can expect to observe higher crystallinity fractions in the inner warm
regions compared to the outer cold regions. One possible explanation
to this issue may rely on the importance of accretion activity and on
amorphization processes of crystals that are preferentially taking
place in the inner regions of disks, as tentatively proposed by
Kessler-Silacci et al. (2006) and Olofsson et al. (2009), and recently
discussed in more detail in Glauser et al. (2009). This possibility is
further supported by the results of Ábrahám et al. (2009) who studied
the T Tauri star EX Lup with IRS, at two different epochs separated by
a three-year time span, first in a quiescent phase (see spectrum in
Kessler-Silacci et al. 2006), and then two months after an optical
outburst driven by an increase of the mass accretion rate. They find
an increase of crystallinity caused by this outburst in the inner disk
regions, supposedly due to thermal annealing of amorphous silicates.
The authors did not find any colder crystals in the outer component
after the outburst, and therefore excluded shock heating at larger
distances. This study shows that, obviously, the accretion activity
may have a strong impact on the dust chemistry in circumstellar
disks. Recently, Glauser et al. (2009) identified an anti-correlation
between X-ray luminosity of the stars and crystalline fraction for the
warm disk component (
K, according to
laboratory measurements, see Hallenbeck et al. 1998). Therefore, one
can expect to observe higher crystallinity fractions in the inner warm
regions compared to the outer cold regions. One possible explanation
to this issue may rely on the importance of accretion activity and on
amorphization processes of crystals that are preferentially taking
place in the inner regions of disks, as tentatively proposed by
Kessler-Silacci et al. (2006) and Olofsson et al. (2009), and recently
discussed in more detail in Glauser et al. (2009). This possibility is
further supported by the results of Ábrahám et al. (2009) who studied
the T Tauri star EX Lup with IRS, at two different epochs separated by
a three-year time span, first in a quiescent phase (see spectrum in
Kessler-Silacci et al. 2006), and then two months after an optical
outburst driven by an increase of the mass accretion rate. They find
an increase of crystallinity caused by this outburst in the inner disk
regions, supposedly due to thermal annealing of amorphous silicates.
The authors did not find any colder crystals in the outer component
after the outburst, and therefore excluded shock heating at larger
distances. This study shows that, obviously, the accretion activity
may have a strong impact on the dust chemistry in circumstellar
disks. Recently, Glauser et al. (2009) identified an anti-correlation
between X-ray luminosity of the stars and crystalline fraction for the
warm disk component (
![]() in Sect. 3.2). The
authors performed a decomposition fit to the
in Sect. 3.2). The
authors performed a decomposition fit to the ![]() m feature for a
stellar sample of 42 T Tauri stars, and find an anti-correlation
between
m feature for a
stellar sample of 42 T Tauri stars, and find an anti-correlation
between
![]() and X-ray luminosities for a subsample of 20 objects with ages between 1 and 4.5 Myr. This anti-correlation
suggests that the stellar activity and energetic ions from stellar
winds, traced by X-ray flux, can amorphize crystalline grains in disk
atmospheres due to high-energy particles.
and X-ray luminosities for a subsample of 20 objects with ages between 1 and 4.5 Myr. This anti-correlation
suggests that the stellar activity and energetic ions from stellar
winds, traced by X-ray flux, can amorphize crystalline grains in disk
atmospheres due to high-energy particles.
In a similar approach as Glauser et al. (2009), we attempt to
investigate the impact of high-energy particles, assumed to be traced
by X-ray luminosity, on the disk mineralogy. Table 2
displays the X-ray luminosities (in units of erg s-1) available
in the literature or obtained by fitting the spectra from the Second
XMM-Newton serendipitous source catalogue
(Watson et al. 2009b) with the X-ray emission from one or
two-temperature plasma combined with photoelectric absorption, for a
subset of 17 objects among our stellar sample analyzed with the B2C
compositional fitting model. The low overlap between X-ray
observations with the c2d sample can be explained by the different
observation strategies: X-ray campaigns are mostly targetting dense
cores while our observations are located at the periphery of the
clouds. Figure 14 displays the crystalline fraction
![]() for the warm component inferred with the B2C procedure, as a
function of the X-ray luminosity. The associated Kendall
for the warm component inferred with the B2C procedure, as a
function of the X-ray luminosity. The associated Kendall ![]() value
is 0.16 with a significance probability P = 0.36, suggesting a
dispersed weak trend, if any. To confirm any weak trend, we would need
to have more measurements below about
value
is 0.16 with a significance probability P = 0.36, suggesting a
dispersed weak trend, if any. To confirm any weak trend, we would need
to have more measurements below about
![]() erg s-1. Above this luminosity value no trend is visible. Still,
we observe that objects with high X-ray luminosities seem to have
higher crystalline fractions, which seems at first in contradiction
with the conclusion by Glauser et al. (2009). Given the limited number
of objects for which we have X-ray data in our sample, however, we
were not able to perform any age selection as in Glauser et al. (2009).
erg s-1. Above this luminosity value no trend is visible. Still,
we observe that objects with high X-ray luminosities seem to have
higher crystalline fractions, which seems at first in contradiction
with the conclusion by Glauser et al. (2009). Given the limited number
of objects for which we have X-ray data in our sample, however, we
were not able to perform any age selection as in Glauser et al. (2009).
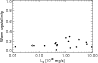
|
Figure 14:
Crystalline fraction for the warm component
(
|
| Open with DEXTER | |
4.3 Strength of the 10 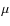 m feature, a proxy for grain size?
m feature, a proxy for grain size?
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=8cm,origin=bl]{13909_f21...
...raphics[angle=0,width=8cm,origin=bl]{13909_f22.ps} }\vspace*{-2mm}\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg162.png)
|
Figure 15:
Left panel: mass-averaged grain sizes for the warm component, as a function of the strength of the 10 |
| Open with DEXTER | |
The strength
![]() of the 10
of the 10 ![]() m feature
has been commonly used in previous studies (e.g. van Boekel et al. R2005;
Kessler-Silacci et al. 2006; Olofsson et al. 2009) as a proxy for
grain size, small
m feature
has been commonly used in previous studies (e.g. van Boekel et al. R2005;
Kessler-Silacci et al. 2006; Olofsson et al. 2009) as a proxy for
grain size, small
![]() values tracing large
(micrometer-sized) grains, while larger
values tracing large
(micrometer-sized) grains, while larger
![]() would be tracing smaller (submicron-sized) grains. In a recent paper,
Watson et al. (2009a) instead attribute the diversity of strengths of the
10
would be tracing smaller (submicron-sized) grains. In a recent paper,
Watson et al. (2009a) instead attribute the diversity of strengths of the
10 ![]() m feature to a combination of sedimentation and an increase
of the crystallinity degree (as in Sargent et al. 2009). With the
outputs of our B2C spectral decompositional procedure, we revisit the
interpretation of the strength of the 10
m feature to a combination of sedimentation and an increase
of the crystallinity degree (as in Sargent et al. 2009). With the
outputs of our B2C spectral decompositional procedure, we revisit the
interpretation of the strength of the 10 ![]() m feature as a proxy
for grain size.
m feature as a proxy
for grain size.
The left panel of Fig. 15 displays the correlation
between the mass-averaged grain size for the warm grains (
![]() )
and the strength of the 10
)
and the strength of the 10 ![]() m feature
(
m feature
(
![]() ). We find a Kendall
). We find a Kendall ![]() correlation
coefficient of about -0.30 with a significance P probability smaller
than
correlation
coefficient of about -0.30 with a significance P probability smaller
than
![]() ,
showing that grain size is well traced by
the strength of the feature. It is noteworthy to point out that
Sargent et al. (2009) find a different result regarding these two
quantities, in their spectral decomposition analysis of 65 T Tauri
stars. As shown in the review by Watson (2009), based on
Sargent et al. (2009) results, they find a correlation coefficient of
0.08 with a significant probability of 0.55. This means, according to
their model, that the strength of the 10
,
showing that grain size is well traced by
the strength of the feature. It is noteworthy to point out that
Sargent et al. (2009) find a different result regarding these two
quantities, in their spectral decomposition analysis of 65 T Tauri
stars. As shown in the review by Watson (2009), based on
Sargent et al. (2009) results, they find a correlation coefficient of
0.08 with a significant probability of 0.55. This means, according to
their model, that the strength of the 10 ![]() m feature is not
correlated with the presence of large grains. More precisely, they
find that seven objects among their sample with the smallest
10
m feature is not
correlated with the presence of large grains. More precisely, they
find that seven objects among their sample with the smallest
10 ![]() m feature strength, can be reproduced with low abundances of
large grains. However, our opposite result is supported by several
points: we successfully checked for all dependencies that could lead
to a possible overestimate of the grain sizes (e.g. the continuum
offset
m feature strength, can be reproduced with low abundances of
large grains. However, our opposite result is supported by several
points: we successfully checked for all dependencies that could lead
to a possible overestimate of the grain sizes (e.g. the continuum
offset ![]() )
and we show in Appendix A.1, based on the
analysis of synthetic spectra, that we may eventually underestimate
the grain sizes in the warm component rather than over-estimate it
(underestimated by
)
and we show in Appendix A.1, based on the
analysis of synthetic spectra, that we may eventually underestimate
the grain sizes in the warm component rather than over-estimate it
(underestimated by ![]() % with respect to the input value). This
deviation (
% with respect to the input value). This
deviation (
![]() )
is
furthermore independent of the strength of the 10
)
is
furthermore independent of the strength of the 10 ![]() m feature
(
m feature
(
![]() ), with a
), with a ![]() value of
-0.06 and a significance probability of 0.52.
value of
-0.06 and a significance probability of 0.52.
We also search for a correlation between the warm crystalline fraction
![]() and the strength of the 10
and the strength of the 10 ![]() m feature
(
m feature
(
![]() ), and find a highly dispersed relation
between the two quantities. Figure 16 shows that the
distribution is flat (
), and find a highly dispersed relation
between the two quantities. Figure 16 shows that the
distribution is flat (
![]() with a significance probability
of 0.10), which suggests that crystallization cannot be the sole
explanation for the diversity of 10
with a significance probability
of 0.10), which suggests that crystallization cannot be the sole
explanation for the diversity of 10![]() m feature strengths. This is
in line with the results by Bouwman et al. (2008) who do not find any
correlation between these two quantities in their seven T Tauri star
sample.
m feature strengths. This is
in line with the results by Bouwman et al. (2008) who do not find any
correlation between these two quantities in their seven T Tauri star
sample.
As mentioned in Olofsson et al. (2009) and in this paper, the grain size
distribution in the upper layers of disks has a strong impact on the
10 ![]() m feature strength. The right panel of Fig. 15
shows the power-law indexes p of the size distributions (calculated
as in Sect. 3.1.3), as a function of the
m feature strength. The right panel of Fig. 15
shows the power-law indexes p of the size distributions (calculated
as in Sect. 3.1.3), as a function of the
![]() values. We find an anti-correlation
(
values. We find an anti-correlation
(
![]() with
with
![]() ), indicating the shape
of the 10
), indicating the shape
of the 10![]() m feature is indeed related to the slope of the grain
size distribution. In fact we see two different regimes appearing: the
small
m feature is indeed related to the slope of the grain
size distribution. In fact we see two different regimes appearing: the
small
![]() values mostly correspond to
objects with slopes p larger than -3 (dashed horizontal line on
the figure), while objects with large
values mostly correspond to
objects with slopes p larger than -3 (dashed horizontal line on
the figure), while objects with large
![]() values essentially have slopes p smaller than -3. This points in
the same direction as previously discussed, namely that the variation
in
values essentially have slopes p smaller than -3. This points in
the same direction as previously discussed, namely that the variation
in
![]() may to a large extent trace the
variation in the slope of the size distribution. Not surprisingly, we
find a very strong correlation between the mean mass-averaged grain
size and the slope of the grain size distribution, with
may to a large extent trace the
variation in the slope of the size distribution. Not surprisingly, we
find a very strong correlation between the mean mass-averaged grain
size and the slope of the grain size distribution, with
![]() and a significance probability below 10-38.
and a significance probability below 10-38.
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,origin=bl]{13909_f23.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg171.png)
|
Figure 16:
Crystalline fraction for the warm component (
|
| Open with DEXTER | |
5 Summary and conclusion
In this paper, we present a large statistical study of the dust
mineralogy in 58 proto-planetary (Class II) disks around young solar
analogs. We develop a robust routine that reproduces IRS spectra over
their entire spectral range (5-35 ![]() m), with a MCMC-like approach
coupled with a Bayesian inference method. This procedure explores
randomly the parameter space and reproduces IRS spectra using two
independent dust populations: a warm and a cold component, arising
from inner and outer regions from disks, respectively. This
2-component approach is supported by our previous statistical analysis
of the silicate features in Olofsson et al. (2009).
This B2C procedure
has been tested over synthetic spectra giving, statistically speaking,
coherent and reproducible results. In its current form, the B2C model
allows to derive relative abundances for 5 different dust species,
3 different grain sizes for the amorphous grains, 2 sizes for
the
crystalline grains, for both inner regions (
m), with a MCMC-like approach
coupled with a Bayesian inference method. This procedure explores
randomly the parameter space and reproduces IRS spectra using two
independent dust populations: a warm and a cold component, arising
from inner and outer regions from disks, respectively. This
2-component approach is supported by our previous statistical analysis
of the silicate features in Olofsson et al. (2009).
This B2C procedure
has been tested over synthetic spectra giving, statistically speaking,
coherent and reproducible results. In its current form, the B2C model
allows to derive relative abundances for 5 different dust species,
3 different grain sizes for the amorphous grains, 2 sizes for
the
crystalline grains, for both inner regions (![]() 1 AU) and outer
regions (
1 AU) and outer
regions (![]() 10 AU) of disks. Based on the modeling of the 58 IRS
spectra of T Tauris stars, we find the following results:
10 AU) of disks. Based on the modeling of the 58 IRS
spectra of T Tauris stars, we find the following results:
- 1.
- The grain sizes in the inner and outer regions of disks are found to be uncorrelated, reinforcing the idea of two independent components probed by IRS. However, crystallinity fractions in warm and cold components are correlated to each other, indicative of a simultaneous enrichment of crystals within the first 10 AU of disks. This suggests that dynamical processes affecting the size distribution are essentially local rather than global, while crystallization may rather trace larger scale phenomena (e.g. radial diffusion). Finally, we find that grain size and crystallinity fraction are two independent quantities with respect to each other in both the warm and cold components.
- 2.
- We quantify the growth of grains compared to the ISM. We find a
significant size distribution flattening in the upper
atmospheres of disks probed by IRS, compared to the MRN grain size
distribution. While the MRN size distribution has a power law index
p = -3.5, we find flatter distributions for both the inner regions
(
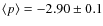 ), and the outer regions (
), and the outer regions (
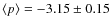 ). This explains why the IR emission of
T Tauri stars studied using Spitzer-IRS is dominated by
). This explains why the IR emission of
T Tauri stars studied using Spitzer-IRS is dominated by
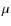 m-sized grains, despite the possible presence of significant
amounts of submicron-sized grains. The
m-sized grains, despite the possible presence of significant
amounts of submicron-sized grains. The
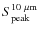 value turns out to be a proxy of the slope of the grain size
distribution. This finding, combined with recent similar results
from observations at millimeter wavelengths, suggests that the size
distribution flattening is not confined to the disk upper layers but
may extend to deeper and more distance disk regions, and larger
grains.
value turns out to be a proxy of the slope of the grain size
distribution. This finding, combined with recent similar results
from observations at millimeter wavelengths, suggests that the size
distribution flattening is not confined to the disk upper layers but
may extend to deeper and more distance disk regions, and larger
grains.
- 3.
- We reexamined the crystallinity paradox identified in
Olofsson et al. (2009), by building crystallinity distributions for
the warm and cold components. The mean crystallinity fractions are
16 and 19% for the warm and cold components, respectively. Even if
the crystalline distribution for the cold component is slightly
wider compared to the warm component, both distributions show a very
similar behavior, suggesting the silicate crystals are well mixed
within the first 10 AU of disks around T Tauri stars. According to
the B2C model, the 3.5 times more frequently detected crystalline
features at long (20-30
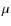 m) than at short (
m) than at short (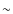 10
10 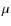 m)
wavelengths arises from the combination of rather low crystalline
fractions (
m)
wavelengths arises from the combination of rather low crystalline
fractions (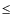 15-20%) for many T Tauri stars, and a contrast
effect that makes the crystalline features more difficult to
identify at around 10
15-20%) for many T Tauri stars, and a contrast
effect that makes the crystalline features more difficult to
identify at around 10 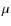 m where the strong amorphous feature can
hide smaller crystalline features.
m where the strong amorphous feature can
hide smaller crystalline features.
- 4.
- We see a trend where flared disks (high F30/F13 values) tend to preferentially show small warm grains while flat disks (small F30/F13) show a large diversity of grain sizes. We do not find any correlations between the disk flaring and the crystallinity, meaning that the presence of such crystals is not related to the shape of the disks.
- 5.
- We find no predominance of any crystal species in the warm component, while forsterite seems to be more frequent compared to enstatite in the cold component. Regarding the different dust compositions, we find no evidence of correlations between them, except for the warm enstatite and forsterite grains, suggesting that the crystallisation processes in the inner regions of disks do not favor any of the two crystals. We find no link between silica and enstatite as one may expect if the main path for enstatite production would be the reaction between silica plus forsterite.
- 6.
- We do not find any striking correlation between spectral type and warm or cold crystallinity fraction. We do not either find any correlation between X-ray activity and crystallinity. As suggested by Watson et al. (2009a), the time variability in young objects may be responsible for erasing most of the correlations regarding dust mineralogy.
The authors thank Christophe Pinte for his help on the bayesian study to derive uncertainties on the output parameters of the compositionnal fitting procedure. We thank the referee, Dan M. Watson, for his very constructive comments, that helped improving both the modeling procedure, especially on the question of large 6.0m crystalline grains, and the general quality of the paper. We also thank N. J. Evans II for his very useful comments that helped improving this study. We finally thank the Programme National de Physique Stellaire (PNPS) and ANR (contract ANR-07-BLAN-0221) for supporting part of this research. This research is also based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA.
References
- Ábrahám, P., Juhász, A., Dullemond, C. P., et al. 2009, Nature, 459, 224 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Apai, D., Pascucci, I., Bouwman, J., et al. 2005, Science, 310, 834 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bouwman, J., Meeus, G., de Koter, A., et al. 2001, A&A, 375, 950 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwman, J., Henning, T., Hillenbrand, L. A., et al. 2008, ApJ, 683, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Bouy, H., Huelamo, N., Pinte, C., et al. 2009, A&A, 493, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, J. M., Blake, G. A., Dullemond, C. P., et al. 2007, ApJ, 664, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Casanova, S., Montmerle, T., Feigelson, E. D., & Andre, P. 1995, ApJ, 439, 752 [Google Scholar]
- Ciesla, F. J. 2009, Icarus, 200, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Desch, S. J., & Connolly, Jr., H. C. 2002, Meteorit. Planet. Sci., 37, 183 [CrossRef] [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS] [Google Scholar]
- Feigelson, E. D., Casanova, S., Montmerle, T., & Guibert, J. 1993, ApJ, 416, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Gail, H. 2004, A&A, 413, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Getman, K. V., Feigelson, E. D., Townsley, L., et al. 2002, ApJ, 575, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Giardino, G., Favata, F., Micela, G., Sciortino, S., & Winston, E. 2007, A&A, 463, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glauser, A. M., Guedel, M., Watson, D. M., et al. 2009, A&A, 508, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güdel, M., Skinner, S. L., Mel'Nikov, S. Y., et al. 2007, A&A, 468, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hallenbeck, S. L., Nuth, J. A., & Daukantas, P. L. 1998, Icarus, 131, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., & Meeus, G. 2009 [arXiv:0911.1010] [Google Scholar]
- Henning, T., & Mutschke, H. 1997, A&A, 327, 743 [NASA ADS] [Google Scholar]
- Jaeger, C., Molster, F. J., Dorschner, J., et al. 1998, A&A, 339, 904 [NASA ADS] [Google Scholar]
- Juhász, A., Henning, T., Bouwman, J., et al. 2009, ApJ, 695, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, C., & Gail, H.-P. 2004, A&A, 415, 1177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kemper, F., Vriend, W. J., & Tielens, A. G. G. M. 2005, ApJ, 633, 534 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kessler-Silacci, J., Augereau, J.-C., Dullemond, C. P., et al. 2006, ApJ, 639, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler-Silacci, J. E., Dullemond, C. P., Augereau, J.-C., et al. 2007, ApJ, 659, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Lommen, D. J. P., van Dishoeck, E. F., Wright, C. M., et al. 2010, A&A, 515, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merín, B., Augereau, J.-C., van Dishoeck, E. F., et al. 2007, ApJ, 661, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Min, M., Hovenier, J. W., & de Koter, A. 2005, A&A, 432, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Hovenier, J. W., Waters, L. B. F. M., & de Koter, A. 2008, A&A, 489, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliveira, I., Pontoppidan, K. M., Merin, B., et al. 2010, ApJ, 714, 778 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, J., Augereau, J., van Dishoeck, E. F., et al. 2009, A&A, 507, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ozawa, H., Grosso, N., & Montmerle, T. 2005, A&A, 429, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riaz, B. 2009, ApJ, 701, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., et al. 2010, A&A, 512, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robrade, J., & Schmitt, J. H. M. M. 2007, A&A, 461, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sargent, B. A., Forrest, W. J., Tayrien, C., et al. 2009, ApJS, 182, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Servoin, J., & Piriou, B. 1973, Phys. Stat. Sol. (b), 55, 677 [Google Scholar]
- Stelzer, B., Micela, G., & Neuhäuser, R. 2004, A&A, 423, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, K. K., Yamamoto, T., & Kimura, H. 2010, ApJ, 717, 586 [NASA ADS] [CrossRef] [Google Scholar]
- van Boekel, R., Min, M., Waters, L. B. F. M., et al. 2005, A&A, 437, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visser, R., & Dullemond, C. P. 2010, A&A, 519, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, D. 2009, in ASP Conf. Ser., ed. T. Henning, E. Grün, & J. Steinacker, 414, 77 [Google Scholar]
- Watson, D. M., Leisenring, J. M., Furlan, E., et al. 2009a, ApJS, 180, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, M. G., Schröder, A. C., Fyfe, D., et al. 2009b, A&A, 493, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidenschilling, S. J. 1980, Icarus, 44, 172 [NASA ADS] [CrossRef] [Google Scholar]
Online Material
Appendix A: Validation
A.1 Procedure validation
We evaluate the robustness of our procedure by fitting synthetic spectra with known abundances, temperatures and continua. This allows to check whether these quantities could be recovered when the spectra are processed with the B2C procedure. To this end, we used the best fit, synthetic spectra for the 58 objects analyzed in this paper (and presented in Sect. 3), as fake, but representative observations for serving as inputs to our B2C procedure. We reconstructed these synthetic spectra using the outputs of the fitting process on the original data. Namely, the same continuum emission, the same relative abundances for the dust species and their corresponding temperatures. The uncertainties chosen for the synthetic spectra are those of the original observed spectra.
Figure A.1 shows the ratio between the output and input crystallinity, as a function of the ratio between the output and input grain sizes, for both the warm and cold components. The plot shows ratios of about 1 on both axis, especially for the cold component (blue squares on the figure), suggesting some best fits obtained with the procedure may not be unique. But from a statistical point view, the B2C procedure produces reproducible results as the mean ratios between output and input quantities remain close to 1 (vertical and horizontal bars on the figure).
More precisely, the warm component crystallinity is slightly
overestimated by 22% with a dispersion (i.e. the standard deviation)
about this value of 30%. The inferred cold component crystallinity
is satisfactorily reproduced at the 2% level with respect to the
input value, and the dispersion, 35%, is rather similar to that for
the crystallinity of the warm grains. The mean mass-averaged size of
the warm grains is slightly underestimated by ![]() % with respect
to the input value, while the mean mass-averaged size of the cold
grains is well reproduced but with a larger dispersion (
% with respect
to the input value, while the mean mass-averaged size of the cold
grains is well reproduced but with a larger dispersion (![]() %).
%).
A closer look at the dispersion of the calculated crystalline fraction
as a function of the input crystallinity is shown in
Fig. A.2 for the 58 fits to synthetic spectra, for
both the warm (red open circles) and cold (blue open squares)
components. The over-estimation of the warm component crystalline
fractions seen in Fig. A.1 is mostly visible for objects with
low-crystalline fractions (below 20%). For the cold component, it
actually tends to be rather underestimated for large crystalline
fractions (above ![]() 40%). The overall trend for both the warm and
cold components is that the dispersion raises with the decreasing
crystallinity. This finds an explanation in the fact that objects
showing high crystalline fractions display strong, high-contrast
crystalline features that are less ambiguously matched by theoretical
opacities than objects with lower crystalline fractions.
40%). The overall trend for both the warm and
cold components is that the dispersion raises with the decreasing
crystallinity. This finds an explanation in the fact that objects
showing high crystalline fractions display strong, high-contrast
crystalline features that are less ambiguously matched by theoretical
opacities than objects with lower crystalline fractions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13909_f24.ps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg176.png)
|
Figure A.1: Results for the fits to the 58 synthetic spectra to test our ``B2C'' procedure. The x-axis shows the dispersion in grain size (ratio of inferred over input mean mass-averaged grain sizes) and the y-axis the ratio between inferred and input crystallinity. Red open circles correspond to the warm component, and blue open squares to the cold component. The filled circles are mean values, with error bars corresponding to standard deviations. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13909_f25.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg177.png)
|
Figure A.2: Ratios between output over input crystallinity fractions as a function of the input crystallinity fractions, for the fits to the 58 synthetic spectra. Red open circles are results for the warm component and blue open squares are for the cold component. |
| Open with DEXTER | |
A.2 Influence of the continuum on the cold component
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=9cm,origin=bl]{13909_f26.ps}\includegraphics[angle=0,width=9cm,origin=bl]{13909_f27.ps} }
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg178.png)
|
Figure A.3:
Left panel: crystalline fraction for the cold
component as a function of the integrated continuum substracted
flux in the range 22-35 |
| Open with DEXTER | |
The continuum estimation is a critical step when modeling spectra,
especially for the cold component, and may contribute to the larger
uncertainties on the inferred cold component crystallinities and sizes
discussed in previous subsection. The continuum may affect the model
outputs in the following way: a high-flux continuum in the
20-30![]() m spectral range leaves very little flux to be fitted
under the spectrum, possibly leading to a composition with few large
and/or featureless grains. A low-flux continuum could, on the other
hand, lean toward large/featureless grains to fill the flux left. We
therefore examine if (whether) such trends are present in the results
of our B2C procedure (or not) for the cold component.
m spectral range leaves very little flux to be fitted
under the spectrum, possibly leading to a composition with few large
and/or featureless grains. A low-flux continuum could, on the other
hand, lean toward large/featureless grains to fill the flux left. We
therefore examine if (whether) such trends are present in the results
of our B2C procedure (or not) for the cold component.
We quantify the level of continuum by integrating the
continuum-substracted spectra between 22 ![]() m and 35
m and 35 ![]() m
(x-axis in Fig. A.3). Low-flux continua have high
integrated fluxes and are located on the right side of the plot in
Fig. A.3, the high-flux continua being on the left
side. The left panel of Fig. A.3 shows the
crystalline fraction for the cold component, as a function of the
integrated flux left once the continuum is substracted. The trend low
continuum - low crystalline fraction is visible for the highest
integrated flux values. But the large dispersion for low integrated
flux values indicates that no strong bias is introduced as we obtain
cases with very high-flux continua but still with very low crystalline
fractions. It remains that for the low-flux continua cases, we cannot
possibly obtain very high crystalline fractions as a lot of flux needs
to be filled to match the spectra. Indeed, amorphous grains are the
best choice to fulfill this requirement, therefore diminishing the
cold component crystalline fraction.
m
(x-axis in Fig. A.3). Low-flux continua have high
integrated fluxes and are located on the right side of the plot in
Fig. A.3, the high-flux continua being on the left
side. The left panel of Fig. A.3 shows the
crystalline fraction for the cold component, as a function of the
integrated flux left once the continuum is substracted. The trend low
continuum - low crystalline fraction is visible for the highest
integrated flux values. But the large dispersion for low integrated
flux values indicates that no strong bias is introduced as we obtain
cases with very high-flux continua but still with very low crystalline
fractions. It remains that for the low-flux continua cases, we cannot
possibly obtain very high crystalline fractions as a lot of flux needs
to be filled to match the spectra. Indeed, amorphous grains are the
best choice to fulfill this requirement, therefore diminishing the
cold component crystalline fraction.
The influence of the continuum on the estimated mass-averaged grain
size is shown on the right panel of Fig. A.3. A very
weak and dispersed anti-correlation is found between the two
parameters. We obtain a ![]() value of -0.12 with a significance
probability P = 0.17, meaning that the adopted shape for the
continuum is not strongly influencing the inferred mean grain
size. The trend is mostly caused by a few low-flux continua objects
modeled with large grains.
value of -0.12 with a significance
probability P = 0.17, meaning that the adopted shape for the
continuum is not strongly influencing the inferred mean grain
size. The trend is mostly caused by a few low-flux continua objects
modeled with large grains.
To conclude, the continuum estimation is a challenging problem for the cold component and its adopted shape will always have an impact on the results for the crystallinity and grain size at the same time. Still, we have checked that, statistically speaking, we are not introducing a strong and systematic bias with our simple, two free parameter continuum.
A.3 Importance of silica and necessity for large grains
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13909_f28.ps}
\vspace*{-3mm} \end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg180.png)
|
Figure A.4:
Change in reduced
|
| Open with DEXTER | |
Usually, Mg-rich silicates are considered for the dust mineralogy in
proto-planetary disks (e.g. Henning & Meeus 2009). But both
Olofsson et al. (2009) and Sargent et al. (2009) attribute some features
in IRS spectra of young stars to silica (composition SiO2). To
gauge the importance of silica in our B2C compositional approach, we
run the B2C model with and without silica. Many fits were improved
adding silica in the dust population (as shown for one example in
Fig. A.5, the 20-22 ![]() m range being the spectral range
where the improvement is the more noticeable). As can be seen on the
right panel of Fig. A.4, showing the reduced
m range being the spectral range
where the improvement is the more noticeable). As can be seen on the
right panel of Fig. A.4, showing the reduced
![]() for simulations with and without silica, many fits
are improved when silica is included, demonstrating the non-negligible
importance of silica for our B2C model.
for simulations with and without silica, many fits
are improved when silica is included, demonstrating the non-negligible
importance of silica for our B2C model.
We have also critically examined the need for large, amorphous,
6.0 ![]() m-sized grains in the B2C model as they are almost
featureless contrary to the 0.1 and 1.5
m-sized grains in the B2C model as they are almost
featureless contrary to the 0.1 and 1.5 ![]() m-sized grains. We
therefore run the B2C procedure on the 58 same objects with only 0.1
and 1.5
m-sized grains. We
therefore run the B2C procedure on the 58 same objects with only 0.1
and 1.5 ![]() m-sized grains. Left panel of Fig. A.4 shows
that the mean value of the reduced
m-sized grains. Left panel of Fig. A.4 shows
that the mean value of the reduced
![]() for all the
simulations is augmented by 2.50 when using only two grain sizes,
showing that the majority of the fits are improved using three grain
sizes instead of two.
for all the
simulations is augmented by 2.50 when using only two grain sizes,
showing that the majority of the fits are improved using three grain
sizes instead of two.
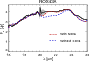
|
Figure A.5: Blowup on the fit to the ROX43A spectrum, performed with silica (red dot-dashed line) and without (blue dashed line). |
| Open with DEXTER | |
One can also worry about the influence of the offset ![]() values on the inferred grain sizes. As a large offset value leads to
larger flux below the continuum-substracted spectrum, it may indeed
favor larger grains. We therefore examined if there was any
correlation between the fraction of large 6.0
values on the inferred grain sizes. As a large offset value leads to
larger flux below the continuum-substracted spectrum, it may indeed
favor larger grains. We therefore examined if there was any
correlation between the fraction of large 6.0 ![]() m-sized grains and
the
m-sized grains and
the ![]() values, and we quantified these relations with
correlation coefficients. Considering the warm large grains and the
values, and we quantified these relations with
correlation coefficients. Considering the warm large grains and the
![]() offsets, we find a
offsets, we find a ![]() value of 0.04 with a
significance probability of P = 0.69. For the cold large grain
fraction and the
value of 0.04 with a
significance probability of P = 0.69. For the cold large grain
fraction and the ![]() values, we obtain
values, we obtain
![]() and P =
0.70. This means that there is no significant influence of the
offsets
and P =
0.70. This means that there is no significant influence of the
offsets ![]() on the inferred grain sizes.
on the inferred grain sizes.
Table A.1: Dust composition derived using the ``B2C'' procedure for 58 objects from our sample.
Table A.2:
Dust temperatures, continuum parameters (blackbody temperature and offset
![]() )
derived using the ``B2C'' procedure for 58 objects from our sample.
)
derived using the ``B2C'' procedure for 58 objects from our sample.
![\begin{figure}
\par\mbox{\includegraphics[width=4cm,origin=bl]{spectra/spe_0.ps}...
...e_26.ps}\includegraphics[width=4cm,origin=bl]{spectra/spe_27.ps} }\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg1339.png)
|
Figure A.6: Fits to the 58 objects using the B2C procedure. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=4cm,origin=bl]{spectra/spe_28.ps...
...e_54.ps}\includegraphics[width=4cm,origin=bl]{spectra/spe_55.ps} }\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg1340.png)
|
Figure A.6: continued. |
| Open with DEXTER | |
| Figure A.6: continued |
|
| Open with DEXTER | |
Footnotes
- ... decomposition
![[*]](/icons/foot_motif.png)
- Appendix A is only available in electronic form at http://www.aanda.org
- ... accepted
![[*]](/icons/foot_motif.png)
- The implementation of a Metropolis-Hastings rule to decide on whether a jump should be accepted or rejected with a certain probability did not improve the fitting process, while increasing the calculation time
All Tables
Table 1: Cloud-to-cloud variations for several parameters from the spectral decomposition.
Table 2: X-ray luminosities for a subset of our stellar sample.
Table A.1: Dust composition derived using the ``B2C'' procedure for 58 objects from our sample.
Table A.2:
Dust temperatures, continuum parameters (blackbody temperature and offset
![]() )
derived using the ``B2C'' procedure for 58 objects from our sample.
)
derived using the ``B2C'' procedure for 58 objects from our sample.
All Figures
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13909_f01.ps}\par {\hspace*...
...ics[width=13cm,clip]{13909_f02.ps}\hspace*{1.5cm}}\vspace*{-4mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg20.png)
|
Figure 1:
Blowup of the opacities (in units of cm2 g-1) used to model the IRS spectra. The solid line is for
0.1 |
| Open with DEXTER | |
| In the text | |

|
Figure 2: Detailed example of B2C modeling steps for the object Sz 96. From top to bottom: the original spectrum and the estimated continuum (top panel), the continuum substracted spectrum and the fit to the warm component (in orange, 2nd panel), the residuals from the fit to the warm component and the fit to this cold component (in blue, 3rd panel), the final fit to the entire spectrum (in green) and the various contributions (4th panel), the relative residuals between the original spectrum and the final fit (last panel). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=16cm,origin=bl]{13909_f04.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg65.png)
|
Figure 3:
Examples of probabilities distributions for
the fit to the Sz 96 spectrum. From the top left panel, clockwise,
are displayed the probability distributions for the warm olivine,
pyroxene, enstatite and forsterite grains. On each panel are
represented 0.1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{ \includegraphics[width=7cm]{13909_f05.ps} \includegrap...
...th=7cm]{13909_f07.ps} \includegraphics[width=7cm]{13909_f08.ps} }
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg67.png)
|
Figure 4:
Examples of B2C fits over the entire IRS
spectral range for four objects: IRS 60,
Hn 9, SSTc2d J161159.8-382338 and
Sz 96. The warm component is displayed in dotted
orange line, the cold component in dashed blue line, and final
fit to the entire spectrum in green. The dot-dashed grey line
represents the continuum. The light grey enveloppe represents
the 3- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,origin=bl]{13909_f09.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg71.png)
|
Figure 5: Mean grain sizes for the cold component as a function of the mean grain size for the warm component |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,origin=bl]{13909_f10.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg88.png)
|
Figure 6: Flaring indices F30/F13 as a function of the warm mass-averaged mean grain size. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,origin=bl]{13909_f11.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg96.png)
|
Figure 7: Grain sizes distribution, for warm (red circles and dotted line) and cold (blue squares and dashed line) component. The MRN reference distribution (-3.5 index) is the black plain line. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,origin=bl]{13909_f12.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg108.png)
|
Figure 8:
Crystalline fraction of the cold component (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=8.8cm,origin=bl]{13909_f...
...ps}\includegraphics[angle=0,width=8.8cm,origin=bl]{13909_f14.ps} }\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg109.png)
|
Figure 9:
Left panel: crystalline distributions for warm component (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[angle=0,width=9cm,origin=bl]{13909_f15.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg116.png)
|
Figure 10:
Crystalline fraction for the warm (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,origin=bl]{13909_f16.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg119.png)
|
Figure 11:
Warm crystalline fraction
|
| Open with DEXTER | |
| In the text | |

|
Figure 12: Mean composition for warm and cold components according to the results of the 58 objects processed. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=8cm,origin=bl]{13909_f18...
...phics[angle=0,width=8cm,origin=bl]{13909_f19.ps} }\vspace*{-2mm} \end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg128.png)
|
Figure 13: Distribution for the warm (red circles and dotted histogram), cold (blue squares and dashed histogram) for enstatite ( left panel) and forsterite (right panel) crystalline abundances. |
| Open with DEXTER | |
| In the text | |

|
Figure 14:
Crystalline fraction for the warm component
(
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=8cm,origin=bl]{13909_f21...
...raphics[angle=0,width=8cm,origin=bl]{13909_f22.ps} }\vspace*{-2mm}\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg162.png)
|
Figure 15:
Left panel: mass-averaged grain sizes for the warm component, as a function of the strength of the 10 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,origin=bl]{13909_f23.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg171.png)
|
Figure 16:
Crystalline fraction for the warm component (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13909_f24.ps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg176.png)
|
Figure A.1: Results for the fits to the 58 synthetic spectra to test our ``B2C'' procedure. The x-axis shows the dispersion in grain size (ratio of inferred over input mean mass-averaged grain sizes) and the y-axis the ratio between inferred and input crystallinity. Red open circles correspond to the warm component, and blue open squares to the cold component. The filled circles are mean values, with error bars corresponding to standard deviations. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13909_f25.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg177.png)
|
Figure A.2: Ratios between output over input crystallinity fractions as a function of the input crystallinity fractions, for the fits to the 58 synthetic spectra. Red open circles are results for the warm component and blue open squares are for the cold component. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=9cm,origin=bl]{13909_f26.ps}\includegraphics[angle=0,width=9cm,origin=bl]{13909_f27.ps} }
\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg178.png)
|
Figure A.3:
Left panel: crystalline fraction for the cold
component as a function of the integrated continuum substracted
flux in the range 22-35 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13909_f28.ps}
\vspace*{-3mm} \end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg180.png)
|
Figure A.4:
Change in reduced
|
| Open with DEXTER | |
| In the text | |

|
Figure A.5: Blowup on the fit to the ROX43A spectrum, performed with silica (red dot-dashed line) and without (blue dashed line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=4cm,origin=bl]{spectra/spe_0.ps}...
...e_26.ps}\includegraphics[width=4cm,origin=bl]{spectra/spe_27.ps} }\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg1339.png)
|
Figure A.6: Fits to the 58 objects using the B2C procedure. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=4cm,origin=bl]{spectra/spe_28.ps...
...e_54.ps}\includegraphics[width=4cm,origin=bl]{spectra/spe_55.ps} }\end{figure}](/articles/aa/full_html/2010/12/aa13909-09/Timg1340.png)
|
Figure A.6: continued. |
| Open with DEXTER | |
| In the text | |
| |
Figure A.6: continued |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



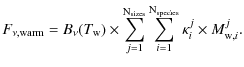
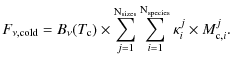
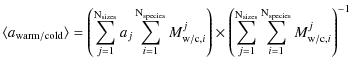
![$\displaystyle \int_{a-\delta a/2}^{a+\delta a/2} {\rm d}n(a)
= \frac{K_a}{1+p} ...
...frac{\delta a}{2}\right)^{1+p}
- \left(a-\frac{\delta a}{2}\right)^{1+p}\right]$](/articles/aa/full_html/2010/12/aa13909-09/img99.png)