| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 23 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913909 | |
| Published online | 27 September 2010 | |
Online Material
Appendix A: Validation
A.1 Procedure validation
We evaluate the robustness of our procedure by fitting synthetic spectra with known abundances, temperatures and continua. This allows to check whether these quantities could be recovered when the spectra are processed with the B2C procedure. To this end, we used the best fit, synthetic spectra for the 58 objects analyzed in this paper (and presented in Sect. 3), as fake, but representative observations for serving as inputs to our B2C procedure. We reconstructed these synthetic spectra using the outputs of the fitting process on the original data. Namely, the same continuum emission, the same relative abundances for the dust species and their corresponding temperatures. The uncertainties chosen for the synthetic spectra are those of the original observed spectra.
Figure A.1 shows the ratio between the output and input crystallinity, as a function of the ratio between the output and input grain sizes, for both the warm and cold components. The plot shows ratios of about 1 on both axis, especially for the cold component (blue squares on the figure), suggesting some best fits obtained with the procedure may not be unique. But from a statistical point view, the B2C procedure produces reproducible results as the mean ratios between output and input quantities remain close to 1 (vertical and horizontal bars on the figure).
More precisely, the warm component crystallinity is slightly
overestimated by 22% with a dispersion (i.e. the standard deviation)
about this value of 30%. The inferred cold component crystallinity
is satisfactorily reproduced at the 2% level with respect to the
input value, and the dispersion, 35%, is rather similar to that for
the crystallinity of the warm grains. The mean mass-averaged size of
the warm grains is slightly underestimated by ![]() % with respect
to the input value, while the mean mass-averaged size of the cold
grains is well reproduced but with a larger dispersion (
% with respect
to the input value, while the mean mass-averaged size of the cold
grains is well reproduced but with a larger dispersion (![]() %).
%).
A closer look at the dispersion of the calculated crystalline fraction
as a function of the input crystallinity is shown in
Fig. A.2 for the 58 fits to synthetic spectra, for
both the warm (red open circles) and cold (blue open squares)
components. The over-estimation of the warm component crystalline
fractions seen in Fig. A.1 is mostly visible for objects with
low-crystalline fractions (below 20%). For the cold component, it
actually tends to be rather underestimated for large crystalline
fractions (above ![]() 40%). The overall trend for both the warm and
cold components is that the dispersion raises with the decreasing
crystallinity. This finds an explanation in the fact that objects
showing high crystalline fractions display strong, high-contrast
crystalline features that are less ambiguously matched by theoretical
opacities than objects with lower crystalline fractions.
40%). The overall trend for both the warm and
cold components is that the dispersion raises with the decreasing
crystallinity. This finds an explanation in the fact that objects
showing high crystalline fractions display strong, high-contrast
crystalline features that are less ambiguously matched by theoretical
opacities than objects with lower crystalline fractions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13909_f24.ps}
\vspace*{-3mm}
\end{figure}](/articles/aa/olm/2010/12/aa13909-09/Timg176.png)
|
Figure A.1: Results for the fits to the 58 synthetic spectra to test our ``B2C'' procedure. The x-axis shows the dispersion in grain size (ratio of inferred over input mean mass-averaged grain sizes) and the y-axis the ratio between inferred and input crystallinity. Red open circles correspond to the warm component, and blue open squares to the cold component. The filled circles are mean values, with error bars corresponding to standard deviations. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13909_f25.ps}
\end{figure}](/articles/aa/olm/2010/12/aa13909-09/Timg177.png)
|
Figure A.2: Ratios between output over input crystallinity fractions as a function of the input crystallinity fractions, for the fits to the 58 synthetic spectra. Red open circles are results for the warm component and blue open squares are for the cold component. |
| Open with DEXTER | |
A.2 Influence of the continuum on the cold component
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=9cm,origin=bl]{13909_f26.ps}\includegraphics[angle=0,width=9cm,origin=bl]{13909_f27.ps} }
\end{figure}](/articles/aa/olm/2010/12/aa13909-09/Timg178.png)
|
Figure A.3:
Left panel: crystalline fraction for the cold
component as a function of the integrated continuum substracted
flux in the range 22-35 |
| Open with DEXTER | |
The continuum estimation is a critical step when modeling spectra,
especially for the cold component, and may contribute to the larger
uncertainties on the inferred cold component crystallinities and sizes
discussed in previous subsection. The continuum may affect the model
outputs in the following way: a high-flux continuum in the
20-30![]() m spectral range leaves very little flux to be fitted
under the spectrum, possibly leading to a composition with few large
and/or featureless grains. A low-flux continuum could, on the other
hand, lean toward large/featureless grains to fill the flux left. We
therefore examine if (whether) such trends are present in the results
of our B2C procedure (or not) for the cold component.
m spectral range leaves very little flux to be fitted
under the spectrum, possibly leading to a composition with few large
and/or featureless grains. A low-flux continuum could, on the other
hand, lean toward large/featureless grains to fill the flux left. We
therefore examine if (whether) such trends are present in the results
of our B2C procedure (or not) for the cold component.
We quantify the level of continuum by integrating the
continuum-substracted spectra between 22 ![]() m and 35
m and 35 ![]() m
(x-axis in Fig. A.3). Low-flux continua have high
integrated fluxes and are located on the right side of the plot in
Fig. A.3, the high-flux continua being on the left
side. The left panel of Fig. A.3 shows the
crystalline fraction for the cold component, as a function of the
integrated flux left once the continuum is substracted. The trend low
continuum - low crystalline fraction is visible for the highest
integrated flux values. But the large dispersion for low integrated
flux values indicates that no strong bias is introduced as we obtain
cases with very high-flux continua but still with very low crystalline
fractions. It remains that for the low-flux continua cases, we cannot
possibly obtain very high crystalline fractions as a lot of flux needs
to be filled to match the spectra. Indeed, amorphous grains are the
best choice to fulfill this requirement, therefore diminishing the
cold component crystalline fraction.
m
(x-axis in Fig. A.3). Low-flux continua have high
integrated fluxes and are located on the right side of the plot in
Fig. A.3, the high-flux continua being on the left
side. The left panel of Fig. A.3 shows the
crystalline fraction for the cold component, as a function of the
integrated flux left once the continuum is substracted. The trend low
continuum - low crystalline fraction is visible for the highest
integrated flux values. But the large dispersion for low integrated
flux values indicates that no strong bias is introduced as we obtain
cases with very high-flux continua but still with very low crystalline
fractions. It remains that for the low-flux continua cases, we cannot
possibly obtain very high crystalline fractions as a lot of flux needs
to be filled to match the spectra. Indeed, amorphous grains are the
best choice to fulfill this requirement, therefore diminishing the
cold component crystalline fraction.
The influence of the continuum on the estimated mass-averaged grain
size is shown on the right panel of Fig. A.3. A very
weak and dispersed anti-correlation is found between the two
parameters. We obtain a ![]() value of -0.12 with a significance
probability P = 0.17, meaning that the adopted shape for the
continuum is not strongly influencing the inferred mean grain
size. The trend is mostly caused by a few low-flux continua objects
modeled with large grains.
value of -0.12 with a significance
probability P = 0.17, meaning that the adopted shape for the
continuum is not strongly influencing the inferred mean grain
size. The trend is mostly caused by a few low-flux continua objects
modeled with large grains.
To conclude, the continuum estimation is a challenging problem for the cold component and its adopted shape will always have an impact on the results for the crystallinity and grain size at the same time. Still, we have checked that, statistically speaking, we are not introducing a strong and systematic bias with our simple, two free parameter continuum.
A.3 Importance of silica and necessity for large grains
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13909_f28.ps}
\vspace*{-3mm} \end{figure}](/articles/aa/olm/2010/12/aa13909-09/Timg180.png)
|
Figure A.4:
Change in reduced
|
| Open with DEXTER | |
Usually, Mg-rich silicates are considered for the dust mineralogy in
proto-planetary disks (e.g. Henning & Meeus 2009). But both
Olofsson et al. (2009) and Sargent et al. (2009) attribute some features
in IRS spectra of young stars to silica (composition SiO2). To
gauge the importance of silica in our B2C compositional approach, we
run the B2C model with and without silica. Many fits were improved
adding silica in the dust population (as shown for one example in
Fig. A.5, the 20-22 ![]() m range being the spectral range
where the improvement is the more noticeable). As can be seen on the
right panel of Fig. A.4, showing the reduced
m range being the spectral range
where the improvement is the more noticeable). As can be seen on the
right panel of Fig. A.4, showing the reduced
![]() for simulations with and without silica, many fits
are improved when silica is included, demonstrating the non-negligible
importance of silica for our B2C model.
for simulations with and without silica, many fits
are improved when silica is included, demonstrating the non-negligible
importance of silica for our B2C model.
We have also critically examined the need for large, amorphous,
6.0 ![]() m-sized grains in the B2C model as they are almost
featureless contrary to the 0.1 and 1.5
m-sized grains in the B2C model as they are almost
featureless contrary to the 0.1 and 1.5 ![]() m-sized grains. We
therefore run the B2C procedure on the 58 same objects with only 0.1
and 1.5
m-sized grains. We
therefore run the B2C procedure on the 58 same objects with only 0.1
and 1.5 ![]() m-sized grains. Left panel of Fig. A.4 shows
that the mean value of the reduced
m-sized grains. Left panel of Fig. A.4 shows
that the mean value of the reduced
![]() for all the
simulations is augmented by 2.50 when using only two grain sizes,
showing that the majority of the fits are improved using three grain
sizes instead of two.
for all the
simulations is augmented by 2.50 when using only two grain sizes,
showing that the majority of the fits are improved using three grain
sizes instead of two.
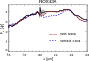
|
Figure A.5: Blowup on the fit to the ROX43A spectrum, performed with silica (red dot-dashed line) and without (blue dashed line). |
| Open with DEXTER | |
One can also worry about the influence of the offset ![]() values on the inferred grain sizes. As a large offset value leads to
larger flux below the continuum-substracted spectrum, it may indeed
favor larger grains. We therefore examined if there was any
correlation between the fraction of large 6.0
values on the inferred grain sizes. As a large offset value leads to
larger flux below the continuum-substracted spectrum, it may indeed
favor larger grains. We therefore examined if there was any
correlation between the fraction of large 6.0 ![]() m-sized grains and
the
m-sized grains and
the ![]() values, and we quantified these relations with
correlation coefficients. Considering the warm large grains and the
values, and we quantified these relations with
correlation coefficients. Considering the warm large grains and the
![]() offsets, we find a
offsets, we find a ![]() value of 0.04 with a
significance probability of P = 0.69. For the cold large grain
fraction and the
value of 0.04 with a
significance probability of P = 0.69. For the cold large grain
fraction and the ![]() values, we obtain
values, we obtain
![]() and P =
0.70. This means that there is no significant influence of the
offsets
and P =
0.70. This means that there is no significant influence of the
offsets ![]() on the inferred grain sizes.
on the inferred grain sizes.
Table A.1: Dust composition derived using the ``B2C'' procedure for 58 objects from our sample.
Table A.2:
Dust temperatures, continuum parameters (blackbody temperature and offset
![]() )
derived using the ``B2C'' procedure for 58 objects from our sample.
)
derived using the ``B2C'' procedure for 58 objects from our sample.
![\begin{figure}
\par\mbox{\includegraphics[width=4cm,origin=bl]{spectra/spe_0.ps}...
...e_26.ps}\includegraphics[width=4cm,origin=bl]{spectra/spe_27.ps} }\end{figure}](/articles/aa/olm/2010/12/aa13909-09/Timg1339.png)
|
Figure A.6: Fits to the 58 objects using the B2C procedure. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=4cm,origin=bl]{spectra/spe_28.ps...
...e_54.ps}\includegraphics[width=4cm,origin=bl]{spectra/spe_55.ps} }\end{figure}](/articles/aa/olm/2010/12/aa13909-09/Timg1340.png)
|
Figure A.6: continued. |
| Open with DEXTER | |
| Figure A.6: continued |
|
| Open with DEXTER | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


