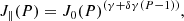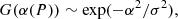| Issue |
A&A
Volume 660, April 2022
|
|
|---|---|---|
| Article Number | L5 | |
| Number of page(s) | 9 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202142855 | |
| Published online | 05 April 2022 | |
Letter to the Editor
The first ground-level enhancement of solar cycle 25 on 28 October 2021⋆
1
Institute for Astronomy, Astrophysics, Space Applications and Remote Sensing (IAASARS), National Observatory of Athens, I. Metaxa & Vas. Pavlou St., 15236 Penteli, Greece
e-mail: atpapaio@astro.noa.gr
2
IRAP, Université Toulouse III-Paul Sabatier, CNRS, CNES, Toulouse, France
3
Space Physics and Astronomy Research Unit and Sodankylä Geophysical Observatory, University of Oulu, Oulu, Finland
4
Department of Physics and Astronomy, University of Turku, 20500 Turku, Finland
5
Institut für Experimentelle und Angewandte Physik, Christian-Albrechts-Universität zu Kiel, 24118 Kiel, Germany
Received:
7
December
2021
Accepted:
14
February
2022
Aims. The first relativistic solar proton event of solar cycle 25 was detected on 28 October 2021 by neutron monitors (NMs) on the ground and particle detectors on board spacecraft in near-Earth space. This is the first ground-level enhancement (GLE) of the current cycle. A detailed reconstruction of the NM response together with the identification of the solar eruption that generated these particles is investigated based on in situ and remote-sensing measurements.
Methods. In situ proton observations from a few MeV to ∼500 MeV were combined with the detection of a solar flare in soft X-rays, a coronal mass ejection, radio bursts, and extreme ultraviolet (EUV) observations to identify the solar origin of the GLE. Timing analysis was performed, and a relation to the solar sources was outlined.
Results. GLE73 reached a maximum particle rigidity of ∼2.4 GV and is associated with type III, type II, and type IV radio bursts and an EUV wave. A diversity of time profiles recorded by NMs was observed. This points to the event having an anisotropic nature. The peak flux at E > 10 MeV was only ∼30 pfu and remained at this level for several days. The release time of ≥1 GV particles was found to be ∼15:40 UT. GLE73 had a moderately hard rigidity spectrum at very high energies (γ ∼ 5.5). Comparison of GLE73 to previous GLEs with similar solar drivers is performed.
Key words: Sun: coronal mass ejections (CMEs) / Sun: heliosphere / Sun: flares / solar-terrestrial relations / Sun: particle emission
Movies are available at https://www.aanda.org
© ESO 2022
1. Introduction
Ground-level enhancements (GLEs) represent the high-energy tail of solar energetic particle (SEP) events. They require acceleration processes capable of producing ≥1 GV (in rigidity) particles with sufficient intensity to allow their secondary products to reach the terrestrial ground and be detected by neutron monitors (NMs; e.g. Poluianov et al. 2017, and references therein). Due to their fast propagation, relativistic protons in GLEs are particularly useful for the identification of SEP sources at the Sun (Aschwanden 2012). The relationship between manifestations of solar activity and energetic protons has been investigated in a series of works (e.g. Belov et al. 2005; Gopalswamy et al. 2012; Mäkelä et al. 2015; Firoz et al. 2019; Kouloumvakos et al. 2019). However, given the relation of GLEs to both strong solar flares and fast and wide coronal mass ejections (CMEs), their acceleration site cannot be unambiguously identified. Detailed studies of specific GLE events have been conducted (e.g. Bombardieri et al. 2008; Mishev et al. 2018), but the conditions and processes that lead to such strong SEP events are still not completely understood. GLEs usually have a gradual proton component with E > 10 MeV that lasts for several days and leads to a significant SEP peak flux. Hence, GLEs are thought to be dominated by CME-driven shocks (see e.g. Kahler et al. 2012; Nitta et al. 2012). On the other hand, studies of the timing of GLE events have shown evidence for two distinct components, one driven by reconnection processes that lead to the so-called prompt component and the other associated with the expanding CME-driven shock that gives rise to the delayed component (e.g. Vashenyuk et al. 2006; McCracken et al. 2008; Moraal & McCracken 2012). Therefore, the debate about the exact nature of GLE mechanisms is still ongoing (see e.g. Kouloumvakos et al. 2020; Kocharov et al. 2021).
Ground-level enhancements are rare, with a rate of ∼0.9 events per year (i.e. only 73 events in ∼80 years of observations; Vainio et al. 2017). These events have primarily been recorded by NMs on the ground, and their lower-energy components have been seen by spacecraft in near-Earth space. Thus, their analysis has been hampered by the lack of identification from other vantage points within the heliosphere. However, in recent years, with the launch of the Solar Terrestrial Relations Observatory (STEREO) twin mission (Kaiser et al. 2008) and the landing of the Mars Science Laboratory on Mars (Grotzinger et al. 2012), GLE71 (17 May 2012) and GLE72 (10 September 2017) have been identified and investigated as multi-spacecraft events (see e.g. Rouillard et al. 2016; Battarbee et al. 2018; Guo et al. 2018; Cohen & Mewaldt 2018). Adding to this, GLEs have only been investigated based on recordings made in the inner heliosphere for a handful of cases (e.g. Cliver 2006; Reames et al. 2013). Nonetheless, present-day missions such as Solar Orbiter (SolO; Müller et al. 2020), Parker Solar Probe (PSP; Fox et al. 2016), and BepiColombo (Benkhoff et al. 2010) may provide a new view on open scientific questions on the origin of relativistic particles since they offer concurrent measurements of protons and complementary electromagnetic observations from a set of vantage points in the inner heliosphere. The present Letter combines measurements of GLE73 – the first such event recorded in solar cycle 25 (SC25) – from near-Earth space and from the ground together with observations of the CME evolution, context solar information, and modelling of SEPs based on NM recordings.
2. Observations
2.1. Overview
The first GLE event (GLE73) of SC25 was observed by several NMs around the Earth (see Table C.1) on 28 October 2021. Figure 1 shows an overview of observations during the GLE73 event. The peak intensity was maximum for the two conventional NM stations located on the Antarctic plateau, ∼7.3% for Dome C at Concordia (DOMC) and 5.4% for the South Pole (SOPO). Bare (lead-free) NMs at the same sites detected a higher response: 14.0% for Dome B (DOMB) and 6.6% for South Pole Bare (SOPB). Energetic protons were also observed by the Solar and Heliospheric Observatory (SOHO)/Energetic and Relativistic Nuclei and Electron (ERNE) instrument (Torsti et al. 1995) at a range of energies (see Appendix A). Figure 1b depicts three proton channels of ERNE. GLE73 was associated with an X1.0 class flare starting at 15:17 UT and peaking at 15:35 UT (see Fig. 1c). The source active region (AR) NOAA AR12887 was located at W02S26 – in the Heliographic Stonyhurst (HGS) coordinate system at 15:20 UT – as observed from Earth’s viewpoint. In addition, from metric to kilometric wavelengths (radio domain), type III, type II, and IV radio bursts were also observed in association with the solar event. In particular, the start time of the first type III radio burst is marked at 15:28 UT (see Fig. 1d), which further coincides with the start of a type II radio burst1. The group of type III bursts is evident from ∼15:30–15:50 UT, and a metric type IV radio burst is also marked at ∼15:37 UT (see the inset in Fig. 1d).
 |
Fig. 1. GLE73 on 28 October 2021. Panel a: increase (in percent) of several NMs based on 5-minute de-trended NM data. Panel b: SOHO/ERNE proton flux. Panel c: SXR flux observed by GOES, denoting an X1.0 solar flare (red curve; left axis). The vertical dashed black line corresponds to the start time of the flare. The height of the WL shock is shown with the magenta squares from measurements at the plane-of-sky near the CME leading edge. The dashed blue line is a linear fit to the height and extrapolated back to the surface of the Sun. Panel d: dynamic radio spectrum observed by Wind/WAVES. The dashed black line corresponds to the start time of the identified type III burst at ∼15:28 UT. The inset figure denotes the type II burst (in blue), the storm of type III bursts (in magenta), and the type IV burst (in green). |
2.2. The CME and the EUV wave
GLE73 was also associated with an extreme ultraviolet (EUV) wave that was observed in the low corona by EUV imagers – the Atmospheric Imaging Assembly (AIA) of the Solar Dynamics Observatory (SDO; Lemen et al. 2011) and STEREO-A/EUVI Howard et al. (2008) – and with a CME and white light (WL) shock wave that was observed higher in the corona by the SOHO/LASCO (Brueckner et al. 1995) and STEREO-A coronagraphs (Howard et al. 2008). In Fig. 2, we show remote-sensing observations during the solar event. Extreme ultraviolet observations show a classic picture of an EUV wave, namely a circular propagating bright front forming at ∼15:28 UT. The EUV wave expanded coherently towards every direction and evolved clearly as a global wave from the Earth’s viewpoint, engulfing the visible disk by 16:20 UT (see the online movie).
 |
Fig. 2. Selected snapshots of EUV and WL coronagraphic observations before and during the GLE73 event on 28 October 2021. Left panel: a running-difference image in EUV from SDO/AIA at 193 Å. The EUV wave is circled to indicate its location. The footpoints of the Parker spirals connected to STEREO-A (red), SolO (blue), and Earth (green) are shown with the coloured crosses. Most of the footpoints of the magnetic field lines connected to Earth (from PFSS) gather close to the region highlighted with a green circle. We indicate the location of ARs that the pressure (shock) wave interacted with during its expansion. The middle and right panels show running-difference images from the LASCO-C2 and STEREO-A/COR2 coronagraphs, respectively. We outline the location of the shock wave and indicate the CME. We indicate the locations where the pressure (shock) wave interacted with coronal streamers (SI) and the previous CME (P-CME). |
The CME was well observed by two different spacecraft, namely STEREO-A and SOHO, that were separated by 38° (see also Fig. A.1). At LASCO/C2 and STEREO-A/COR1, the CME was observed for the first time, at 15:48 UT at ∼2.83 R⊙ and a position angle (PA) of ∼185° and at 15:36 UT at ∼1.91 R⊙ and a PA of ∼230°, respectively. Both viewpoints reveal the emergence of a broad CME forming a halo and a clear pressure wave in front moving faster than the erupting plasma. The wave appears to interact with coronal streamers located on the CME flanks (see Fig. 2). There is also a narrow and slow CME that erupted a few hours before GLE73, from an AR located just behind the western solar limb. The western flank of the WL pressure (shock) seems to interact with the southern section of legs of this previous CME. From a linear fit to the height-time measurements, we obtained a plane-of-sky CME speed at its leading edge (PA: ∼185°) of the combined LASCO/C2 and C3 field of view of ∼1240 ± 40 km s−1 (see Fig. 1c). In the same direction we obtained for the WL shock a plane-of-sky speed of ∼1640 ± 40 km s−1.
2.3. Neutron monitor data
During GLE73, differences in the time profiles of the cosmic-ray intensity are evident, as revealed by the Fort Smith (FSMT), DOMC, SOPO, Oulu (OULU), and Peawanuck (PWNK) NMs presented in Fig. 1a. Herein, we use five-minute integrated de-trended NM data retrieved from the International GLE Database (IGLED)2. Neutron monitor data are also presented in the Neutron Monitor Database. One can see that the event revealed a typical gradual increase and moderate anisotropy (see details in Sects. 3.1 and 3.4) during the onset since a moderate count-rate increase is recorded by the stations looking in the sunward direction (i.e. FSMT, PWNK, and SOPO). As can be seen in Fig. 1a, during GLE73 the flux remained above the background level for almost 4.5 hours. The NMs situated at high-altitude polar stations (i.e. DOMC and SOPO) recorded the greatest count-rate increases. The rapid rise as shown by the FSMT, SOPO, and PWNK NM intensity time profile (Fig. 1) indicates that energetic protons had reasonable access to the Sun-Earth-connecting field lines. For twelve NMs and the two bare NMs, the onset and peak time, as well as the maximum increase (in percent), were calculated using the de-trended NM data (Usoskin et al. 2020), as discussed in Appendix C. All results are presented in Table C.1.
3. Results
3.1. Modelling the neutron monitor response
The analysis of GLEs based on NM data consists of several consecutive steps (see Smart et al. 2000). A detailed description of the model used in this work is given in Mishev et al. (2014) and Mishev & Poluianov (2021). This method has recently been applied to a series of GLEs (i.e. Mishev et al. 2017, 2018). Figure 3 shows the calculated viewing directions of the NMs used in this analysis at around the onset of GLE73 (15:50 UT) for particles of 1 to 5 GV, accordingly 0.7–5 GV for the high-altitude polar NMs, whilst in the analysis a rigidity range of up to 20 GV was implied. The FSMT, SOPO, PWNK, and Nain NMs possess viewing directions that are close to the nominal sunward direction, whilst the Inuvik (INVK) NM had a viewing direction close to the nominal anti-sunward direction. The SOPO and FSMT NMs observed an earlier onset, with a more rapid rise being exhibited by FSMT and PWNK and a gradual rise exhibited by INVK. Naturally, this is related to the location of those stations.
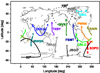 |
Fig. 3. Viewing directions of NMs in the GSE coordinates at around the onset of GLE73 at 15:50 UT on 28 October 2021. Geomagnetic conditions were slightly disturbed (Kp = 1.0). The colour lines, acronyms, and numbers depict the asymptotic directions, NM stations, and rigidities in the range 1–5 GV, respectively. The line of equal pitch angles relative to the anisotropy axis is plotted for 30° for the sunward direction (solid black line) and for 150° for the anti-sunward direction (dashed black line). |
Employing the model presented in Appendix C, we derived the spectra (see Eq. (C.1)), pitch-angle distribution (PAD), and apparent source position (see Eq. (C.2)) of the solar protons during the main phase of GLE73. The spectra gradually softened in the course of the event, specifically during the initial and main phases of the event, the latter corresponding to about 17:30–18:20 UT, that is, during the peak intensity of the event (see the discussion in e.g. Mishev et al. 2021). The results are presented in Fig. 4, and the details are given in Table C.2. The derived spectra are moderately hard with moderate steepening (δγ). Moreover, we derived a moderately anisotropic angular distribution fitted with a function similar to a Gaussian, without any signature of protons arriving from the anti-sunward direction nor a complicated PAD as depicted in Mishev et al. (2014). The derived angular distribution gradually broadens during the main phase of the event.
 |
Fig. 4. Derived SEP rigidity spectra (left panel) and PADs (right panel) during GLE73 on 28 October 2021. The solid black line denotes the GCR flux, which corresponds to the time period of the GLE 73 occurrence (see text for details). All times in the legend are in UT and refer to the start of the corresponding five-minute interval over which the data are integrated. |
3.2. In situ particles
GLE73 was clearly recorded by particle instruments on near-Earth orbiting spacecraft, including ERNE on board SOHO, the Space Environment in Situ Suite (SEISS) on the Geostationary Operational Environmental Satellite (GOES; Kress et al. 2020), and the High Energy Telescope (HET) of the Energetic Particle Detector on SolO (Rodríguez-Pacheco et al. 2020). Figure 1b shows the recordings from SOHO/ERNE for a set of three energy channels with effective energies of 15.4, 29.1, and 57.4 MeV. Figure A.2 shows the 5-minute-averaged recordings of solar particles on GOES/SEISS (6.5–500 MeV), SOHO/ERNE (15.4–57.4 MeV), and SolO/HET (13.68–89.46 MeV), together with the recordings of the BCB counter of SolO/HET (E > 157 MeV) (see details in Freiherr von Forstner et al. 2021). In addition, Fig. A.1 shows the relative position of spacecraft at 15:15 UT and indicates that, in addition to GOES and SOHO, SolO was close to Earth, at a distance of 0.80 AU.
3.3. Relation to solar sources
For the first arriving particles, it is possible to perform time-shifting analysis (Vainio et al. 2013) to infer their release time at the Sun, the solar release time (SRT). A low-end energy limit of particles recorded by a sea-level NM station is ∼1 GV (i.e. 433 MeV), and thus the corresponding mean velocity for such energetic protons would be u = 0.73c. For GLE73, particles with rigidities of up to ∼2.4 GV (1.6 GeV) have been identified, with a mean velocity of u = 0.93c. The length of the Parker spiral, L, can be computed based on the solar wind speed during the event. During GLE73, the solar wind speed was slow, VSW = 300 km s−1, leading to L = 1.28 AU. For the first arriving particles, we assumed scatter-free propagation and calculated the expected SRT of the relativistic protons, trel, adding 500 s for comparison with remote-sensing measurements at 1 AU (e.g. radio observations; Papaioannou et al. 2014). For the SOPO NM station, which registered the earlier onset, we obtained tonset = 15 : 45 UT (see Table C.1). The travel time of the relativistic protons of ∼2.4 GV was calculated to be ∼11 min and the corresponding anticipated trel ∼ 15 : 42 UT. For a set of rigidities ≥1 GV, trel ranges from 15:39–15:42 UT. Since 5-minute resolution NM data are used, there is a 5-minute uncertainty in these calculations.
From SDO/AIA images, we tracked the expansion of the EUV wave towards the footpoints of the magnetic field lines connected to Earth, which we determined using the potential field source surface (PFSS) model and global photospheric magnetic maps (see Appendix B). We find that the footpoints were located ∼72° west of AR12887. The release time of the relativistic particles for GLE73 seems to connect well to the time that the EUV wave passed by the location of the footpoints magnetically connected to Earth (see Fig. B.1 at ∼15:39 UT). Comparing with the soft X-ray (SXR) and radio observations, we find that the release of ∼2.4 GV particles (∼15:42 UT) occurred ∼5 minutes after the flare peak time and 12 minutes after the start of the first type III ratio burst and the type II ratio burst (Fig. 1). Around the release time of the energetic protons (R ≥ 1 GV, which ranges between ∼15:39 and 15:42 UT) there is radio emission from a group of the type III radio bursts and a moving type VI radio burst (see Fig. 1d). At the release time of the ∼2.4 GV particles, the WL shock is located at a height of ∼2.32 R⊙. Table B.1 provides a timeline of events during GLE73 based on the measurements and calculations.
3.4. Comparison with other GLEs
Since 1976 there have only been five GLEs associated with a ≤X1.0 SXR flare (i.e. GLE30, GLE32, GLE58, GLE62, and GLE71). However, only GLE58 is associated with a central (E09) X1.0 flare. Figure 5 shows the time distribution of all GLEs since 1976 with respect to the E > 10 MeV proton peak flux, IP, detected by the series of GOES satellites. Despite the similar flare flux and position, GLE58 (orange square) has an IP that is 6.7 times larger than that of GLE73 (red square). GLE40 and GLE50 (purple squares) have similar IP (∼30 pfu) to GLE73, but both were limb events (> W85). Around the time of release of the 2.4 GV particles, the height of the CME and the WL shock was ∼1.84 R⊙ and ∼2.32 R⊙, respectively. Both values are lower than the mean values reported for other poorly connected GLEs (see Gopalswamy et al. 2012). Also, the median plane-of-sky (projected) speed for GLEs is ∼1810 km s−1 (see Gopalswamy et al. 2012), whereas the GLE73 CME (WL shock) plane-of-sky speed from LASCO C2 and C3 was estimated to be ∼1240 km s−1 (∼1640 km s−1).
 |
Fig. 5. Peak proton flux (IP) at E > 10 MeV for GLEs that occurred from 1976 to 2021 (blue squares). GLE58 (orange square), GLE40 and GLE50 (purple squares), and GLE73 (red square) are indicated. Mean (1850 pfu) and median (321 pfu) values of the peak proton flux are presented as horizontal dashed pink lines. Monthly and smoothed monthly sunspot numbers are shown as grey and black lines. |
4. Conclusions
In this work a summary of observations for GLE73 – which took place on 28 October 2021 and was the first such event of SC25 – is presented. Detailed modelling and reconstruction of the spectral and angular characteristics of high-energy SEPs in the vicinity of the Earth were performed. Data from ground-based NMs, together with space-borne data, were employed in the corresponding data analysis. One of the characteristic aspects of this GLE is its association with a central-disk (W02) X1.0 flare (fairly atypical for GLEs) and a CME (of ∼1240 km s−1) driving a WL shock (of ∼1640 km s−1). The main results of the study are:
-
During the main phase of GLE73, the rigidity spectrum was moderately hard (γ ∼ 5.5) and with significant steepness, δγ ∼ 0.4. During this stage of the event, the derived PAD was relatively wide (σ2 ≈ 4.5 rad2).
-
The event was characterised by a directional particle flux arriving from the sunward direction, and hence GLE73 was characterised by a relatively strong anisotropy.
-
The SRT of the very high-energy particles was found to be ∼15:40 UT, and around this SRT the CME-driven shock was located at a height of ∼2.32 (±0.2) R⊙.
-
The timing of the EUV wave evolution towards the field lines magnetically connected to Earth and the inferred release time of high-energy protons seem to be in good agreement.
Movies
Movie 1 associated with Fig. 2 (SDO_AIA_20211028_Extended_full) Access here
Movie 2 associated with Fig. B.1 (AIA_and_ConnectFLs_v2) Access here
Acknowledgments
The authors acknowledge the International Space Science Institute and the supported International Team 441: HEROIC. AP acknowledges support from NASA/LWS project NNH19ZDA001N-LWS. AK, RV and JG acknowledge financial support from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 101004159 (SERPENTINE). AK and AR acknowledge the ANR COROSHOCK project (ANR-17-CE31-0006-01). AM and AP acknowledge the support by the Academy of Finland (project 330064 QUASARE). KH acknowledges the support of the DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets (HE 8392/1-1)”. AP and KH also acknowledge the supported International Team 464: ETERNAL. IU acknowledges a partial support from the Academy of Finland (project ESPERA No. 321882). RV and JG acknowledge the support of Academy of Finland (FORESAIL, grants 312357 and 336809). We acknowledge the NMDB database (www.nmdb.eu) founded under the European Union’s FP7 programme (contract no. 213007), and the PIs of individual neutron monitors. Italian polar program PNRA (via the LTCPAA PNRA 2015/AC3 and the BSRN PNRA OSS-06 projects), the French Polar Institute IPEV and FINNARP are acknowledged for the hosting of DOMB/DOMC NMs.
References
- Alken, P., Thacbault, E., Beggan, C., et al. 2021, Earth. Planets Space, 73, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Arge, C. N., Henney, C. J., Hernandez, I. G., et al. 2013, AIP Conf. Ser., 1539, 11 [NASA ADS] [Google Scholar]
- Aschwanden, M. J. 2012, Space Sci. Rev., 171, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Battarbee, M., Guo, J., Dalla, S., et al. 2018, A&A, 612, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belov, A., Garcia, H., Kurt, V., Mavromichalaki, H., & Gerontidou, M. 2005, Sol. Phys., 229, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Benkhoff, J., Van Casteren, J., Hayakawa, H., et al. 2010, Planet. Space Sci., 58, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Bombardieri, D., Duldig, M., Humble, J., & Michael, K. 2008, ApJ, 682, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- Brueckner, G., Howard, R., Koomen, M., et al. 1995, in The SOHO mission (Springer), 357 [CrossRef] [Google Scholar]
- Caballero-Lopez, R. 2016, J. Geophys. Res. A: Space Phys., 121, 7461 [NASA ADS] [CrossRef] [Google Scholar]
- Cliver, E. 2006, ApJ, 639, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, C., & Mewaldt, R. 2018, Space Weather, 16, 1616 [NASA ADS] [CrossRef] [Google Scholar]
- Cooke, D., Humble, J., Shea, M., et al. 1991, Il Nuovo Cimento C, 14, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Cramp, J., Duldig, M., Flückiger, E., et al. 1997, J. Geophys. Res., 102, 237 [NASA ADS] [Google Scholar]
- Desorgher, L. 2005, in MAGNETOCOSMICS http://cosray.unibe.ch/~laurent/magnetocosmics/ [Google Scholar]
- Firoz, K., Gan, W., Moon, Y.-J., Rodríguez-Pacheco, J., & Li, Y. 2019, ApJ, 883, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, N., Velli, M., Bale, S., et al. 2016, Space Sci. Rev., 204, 7 [Google Scholar]
- Freiherr von Forstner, J. L., Dumbović, M., Möstl, C., et al. 2021, A&A, 656, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gleeson, L. J., & Axford, W. 1968, ApJ, 154, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Gopalswamy, N., Xie, H., Yashiro, S., et al. 2012, Space Sci. Rev., 171, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Grotzinger, J. P., Crisp, J., Vasavada, A. R., et al. 2012, Space Sci. Rev., 170, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, J., Dumbović, M., Wimmer-Schweingruber, R. F., et al. 2018, Space Weather, 16, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R. A., Moses, J., Vourlidas, A., et al. 2008, Space Sci. Rev., 136, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Kahler, S., Cliver, E., Tylka, A., & Dietrich, W. 2012, Space Sci. Rev., 171, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, M. L., Kucera, T., Davila, J., et al. 2008, Space Sci. Rev., 136, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Kocharov, L., Omodei, N., Mishev, A., et al. 2021, ApJ, 915, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Kouloumvakos, A., Rouillard, A. P., Wu, Y., et al. 2019, ApJ, 876, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Kouloumvakos, A., Rouillard, A. P., Share, G. H., et al. 2020, ApJ, 893, 76 [CrossRef] [Google Scholar]
- Kress, B. T., Rodriguez, J. V., & Onsager, T. G. 2020, in The GOES-R Series (Elsevier), 243 [CrossRef] [Google Scholar]
- Kurt, V., Belov, A., Kudela, K., et al. 2019, Sol. Phys., 294, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kuwabara, T., Bieber, J., Clem, J., et al. 2006, Space Weather, 4, 1 [NASA ADS] [Google Scholar]
- Lara, A., Borgazzi, A., & Caballero-Lopez, R. 2016, Adv. Space Res., 58, 1441 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Akin, D. J., Boerner, P. F., et al. 2011, The Solar Dynamics Observatory (Springer), 17 [Google Scholar]
- Mäkelä, P., Gopalswamy, N., Akiyama, S., Xie, H., & Yashiro, S. 2015, ApJ, 806, 13 [Google Scholar]
- McCracken, K., Moraal, H., & Stoker, P. 2008, J. Geophys. Res. Space Phys., 113, A12101 [Google Scholar]
- Mishev, A., & Poluianov, S. 2021, Sol. Phys., 296, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Mishev, A., & Usoskin, I. 2020, J. Space Weather Space Clim., 10, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mishev, A., Kocharov, L., & Usoskin, I. 2014, J. Geophys. Res. Space Phys., 119, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Mishev, A., Poluianov, S., & Usoskin, I. 2017, J. Space Weather Space Clim., 7, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mishev, A., Usoskin, I., Raukunen, O., et al. 2018, Sol. Phys., 293, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Mishev, A. L., Koldobskiy, S. A., Kovaltsov, G. A., Gil, A., & Usoskin, I. G. 2020, J. Geophys. Res. Space Phys., 125, e2019JA027433 [CrossRef] [Google Scholar]
- Mishev, A., Koldobskiy, S., Kocharov, L., & Usoskin, I. 2021, Sol. Phys., 296, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Moraal, H., & McCracken, K. 2012, Space Sci. Rev., 171, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, D., Cyr, O. S., Zouganelis, I., et al. 2020, A&A, 642, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nitta, N., Liu, Y., DeRosa, M., & Nightingale, R. 2012, Space Sci. Rev., 171, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Papaioannou, A., Souvatzoglou, G., Paschalis, P., Gerontidou, M., & Mavromichalaki, H. 2014, Sol. Phys., 289, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Poluianov, S., Usoskin, I., Mishev, A., Shea, M., & Smart, D. 2017, Sol. Phys., 292, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Reames, D. V., Ng, C. K., & Tylka, A. J. 2013, Sol. Phys., 285, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Pacheco, J., Wimmer-Schweingruber, R., Mason, G., et al. 2020, A&A, 642, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rouillard, A. P., Plotnikov, I., Pinto, R. F., et al. 2016, ApJ, 833, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Rouillard, A. P., Pinto, R. F., Vourlidas, A., et al. 2020, A&A, 642, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smart, D., Shea, M., & Flückiger, E. 2000, Cosmic Rays and Earth, 93, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Torsti, J., Valtonen, E., Lumme, M., et al. 1995, Sol. Phys., 162, 505 [CrossRef] [Google Scholar]
- Tsyganenko, N. A. 1989, Planet. Space Sci., 37, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Usoskin, I. G., Alanko-Huotari, K., Kovaltsov, G. A., & Mursula, K. 2005, J. Geophys. Res. Space Phys., 110, A12108 [NASA ADS] [CrossRef] [Google Scholar]
- Usoskin, I., Gil, A., Kovaltsov, G., Mishev, A., & Mikhailov, V. 2017, J. Geophys. Res., 122, 3875 [NASA ADS] [CrossRef] [Google Scholar]
- Usoskin, I., Koldobskiy, S., Kovaltsov, G., et al. 2020, A&A, 640, A17 [CrossRef] [EDP Sciences] [Google Scholar]
- Vainio, R., Valtonen, E., Heber, B., et al. 2013, J. space weather Space clim., 3, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vainio, R., Raukunen, O., Tylka, A. J., Dietrich, W. F., & Afanasiev, A. 2017, A&A, 604, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vashenyuk, E., Balabin, Y. V., Perez-Peraza, J., Gallegos-Cruz, A., & Miroshnichenko, L. 2006, Adv. Space Res., 38, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Vos, E., & Potgieter, M. 2015, ApJ, 815, 119 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Near-Earth measurements of the SEP event of 28 October 2021
At the time of GLE73, SolO, STEREO-A, and PSP were trailing Earth by -3°, -38°, and -54°, respectively, while BepiColombo was leading Earth by 90°. Figure A.1 shows the positions of various spacecraft at the heliosphere and the Parker spirals connecting each location. A measured solar wind speed was used for each spacecraft when available3; otherwise, a speed of 350 km s−1 was assumed. Using the measured solar wind speeds shown in the legend of Fig. A.1, we calculated the location of the footpoints of the nominal Parker spirals for Earth, STEREO-A, and SolO. The footpoints connected to Earth, STEREO-A, and SolO were located at W81N05, W31N07, and W63N02, respectively (in the HGS system at 15:20 UT).
 |
Fig. A.1. View of the ecliptic plane from solar north, showing the positions of various spacecraft on 28 October 2021 at 15:15 UT. The Parker spirals are shown for each spacecraft. The data are from the Solar MAgnetic Connection Haus tool (https://solar-mach.github.io/). |
GLE73 was clearly recorded by near-Earth spacecraft GOES and SOHO as well as by SolO, which was in a favourable position to record it. The analysis of GLE73 using all heliospheric vantage points is beyond the scope of this Letter, and we concentrated instead on the near-Earth spacecraft and SolO, which is the least separated from Earth (see Fig. A.1). The time history of SEP measurements during GLE73 as recorded from GOES/SEISS (6.5-500 MeV), SOHO/ERNE (15.4-57.4 MeV), SolO/HET (13.68-89.46 MeV), and the BCB counter (E>157 MeV; counts/min; Freiherr von Forstner et al. 2021) are presented in Fig. A.2. High-energy protons at each spacecraft (all indicated with a red line in each panel) seem to have a prompt increase: GOES/P10 (275-500 MeV) has an onset time at 15:55 UT, SOHO/ERNE (at 57.4 MeV) records the event at 16:18 UT, and the BCB counter of SolO (Fig. A.2, third panel from the top; brown line) has an onset time at 15:40 UT. We note, however, that at the lowest energies there seems to be some high-energy contamination in the GOES channels (see Fig. A.2, top panel).
 |
Fig. A.2. Energetic particle recordings of GLE73 in the near-Earth space. From top to bottom: 5-minute-averaged GOES/SEISS differential fluxes; SOHO/ERNE fluxes; and SolO/HET measurements, including the recordings of the SolO/HET/BCB counter. |
Appendix B: Magnetic connectivity using the PFSS model
Since the magnetic configurations in the low corona are more complex than the simple Parker spiral model employed in Fig. 2, we also used the PFSS model and global photospheric magnetic maps to calculate the magnetic field configuration in the low corona4(Rouillard et al. 2020). This gives some further context to the magnetic connectivity of Earth. For the input magnetic maps, we used the maps provided by the Air Force data assimilative photospheric flux transport (ADAPT) model (Arge et al. 2013). The ADAPT maps are global magnetograms of the photospheric magnetic flux. Then we used the PFSS model and the global maps of the radial magnetic field at the photosphere and calculated the magnetic field from the solar surface to 3.0 R⊙, which is the assumed height of the source surface. From the location of the footpoint of the Parker spiral at the source surface, we determined the field lines connected to Earth. We found that most of the footpoints of the magnetic field lines connected to Earth gather to the west of AR12886, which was located at W59S19 (e.g. ∼57° west of AR12887). Specifically, we found that the average location of the footpoints was at W74S25 and that they thinned out for about 10° from this location. In addition, Fig. B.1 provides the combined outputs of the PFSS model and the evolution of the EUV wave at the inferred release time (i.e. 15:39 UT) of the high-energy particles (≥1 GV).
 |
Fig. B.1. Evolution of the EUV wave and PFSS magnetic field lines for Earth (green) presented at ∼15:39 UT. The location of the heliospheric current sheet is shown with the red line. See online movie. |
Timeline of events for GLE73.
Appendix C: Analysis of neutron monitor measurements
C.1. Measurements
Inspection of the NM data from various stations around the world indicated the presence of particles with a rigidity of up to ∼2 GV. The Newark NM, with a vertical cutoff rigidity of 2.4 GV, recorded an increase of marginal significance that may or may not be related to GLE73. The de-trended NM data (Usoskin et al. 2020) were used in the study. Essentially, the de-trended data account for smooth temporal variability in the baseline, allowing for a clear estimation of the contribution of solar particles in GLEs, free from the effect of short-time variability of galactic cosmic rays (GCRs) due to interplanetary transients and local anisotropy. Figure C.1 illustrates the recordings of the Calgary (CALG) NM and shows that in the recordings of this station GLE73 occurred on the background of a strong diurnal wave caused by the local GCR anisotropy.
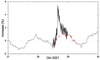 |
Fig. C.1. Pressure-corrected count rate (5-minute data between 12–24 UT on 28 October 2021, and hourly otherwise) of CALG NM, in percent with respect to the pre-increase level of 353 cnts/sec (13-15 UT on 28 October 2021), as indicated by the dotted black line. The dashed red line depicts a parabolic-shaped GCR background due to the diurnal wave, with respect to which the GLE strength is calculated. The data are available at IGLED2. |
Moreover, the anisotropy is usually assessed by a direct comparison of count rates of northern and southern near-polar NMs. For GLE73, we compared the count rate of two sub-polar NMs, namely Thule (THUL) and Jang Bogo (JBGO), both of which have similar characteristics (i.e. R = 0.30 GV and an altitude of 260 m and 30 m, respectively). This comparison directly indicates the presence (or not) of north-south anisotropy. As can be seen in Fig. C.2, the difference (red line) remained close to 0% (mean = 0.02%, median = 0.06%) during GLE73, and thus the comparison does not reveal any significant north-south anisotropy component.
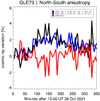 |
Fig. C.2. Evaluation of the north-south anisotropy of GLE73. Variations using two sub-polar stations, THUL (north, blue line) and JBGO (south, black line), and their corresponding difference (red line) are shown. |
Additionally, in the case of an isotropic GLE, high-latitude NMs situated at altitudes near sea level should display almost the same increases caused by SEPs. There are 11 such NM stations with a nominal cutoff rigidity RC< 1.4 GV (Kurt et al. 2019). Figure C.3 shows a comparison of the averaged data of eight of these stations (blue line) against the recordings of the FSMT NM (black line). The fact that FSMT is the only NM to show a large increase compared to all other high-latitude stations indicates a moderate longitudinal anisotropy of GLE73 in the first ∼2 hrs of the event. As can be seen in Fig. C.3, the difference (red line) had a maximum of ∼3(±0.72)% during GLE73 at around ∼16:40-16:50 UT (mean = 0.92%, median = 0.87%).
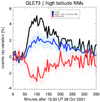 |
Fig. C.3. Evaluation of high-latitude NMs during GLE73. Variations using the FSMT NM (solid black line) and the mean of eight high-latitude NMs (solid blue line) and their corresponding difference (red line) are shown. The blue and the pink ribbons depict the 1σ error. |
Table C.1 provides the characteristics (onset, peak time, and maximum increase in percent) of GLE73. Column 1 provides the name (conventional acronym) of the NM used in the analysis, Col. 2 the GLE onset time (in UT), Col. 3 the peak time (also in UT), and Col. 4 the maximum increase (in percent) of the NM station. All products were calculated based on 5-minute de-trended NM data (Usoskin et al. 2020). Although finer time resolution data (i.e. 1-minute) would in principal facilitate a better relation to the solar source, the statistical fluctuations for such a moderate GLE, however, would be too large. The high-altitude and high-latitude stations DOMC and SOPO, with a vertical cutoff rigidity of 0.10 GV, allow the registration of lower-energy particles compared to the bulk of NMs, that is, they are the more sensitive (Kuwabara et al. 2006; Mishev & Poluianov 2021). As a result, these NMs recorded the most intense flux during GLE73 of all the NMs. At the same time, the bare NMs at these locations (i.e. DOMB and SOPB) recorded the most pronounced signals of solar particles for GLE73 (see Table C.1).
Characteristics of GLE73 as recorded by NMs.
C.2. Calculation of the asymptotic directions
A straightforward computation of the rigidity cutoffs and asymptotic directions of the allowed trajectories (Cooke et al. 1991) requires a combination of the international geomagnetic reference field geomagnetic model (Alken et al. 2021), for the internal field model, with the Tsyganenko 89 model, for the external field (Tsyganenko 1989). All computations of the particle transport in the geomagnetic field were performed with the MAGNETOCOSMICS code (Desorgher 2005). It is plausible to assume that the first nearly relativistic protons arriving in the vicinity of the Earth propagate along the interplanetary magnetic field. Therefore, an NM whose asymptotic cone is nearly aligned with the interplanetary magnetic field is expected to register the earliest signal over the background (i.e. the event onset) and possibly the greatest count-rate increase (Bombardieri et al. 2008; Papaioannou et al. 2014).
C.3. Modelling the response of neutron monitors
In the model employed in this work, a modified power-law rigidity spectrum of SEPs is assumed:
where J∥(P) is the particle flux arriving from the Sun along the symmetry axis, whose direction is defined by the geographic coordinate angles Λ and ψ; γ is the power-law spectral exponent at a rigidity P = 1 GV; and δγ is the rate of the spectrum steepening. The PAD is assumed to be similar to a Gaussian:
where α is the pitch angle and σ is the parameter that corresponds to the width of the PAD. The pitch angle is defined as the angle between the asymptotic direction and the axis of anisotropy. We note that a steady convergence and reliable solution are usually obtained when the merit function, 𝒟 (i.e. the residual according to Mishev et al. 2021), is ∼ 5, yet for weak events it can be about 12–15 (for details, see e.g. Vashenyuk et al. 2006; Mishev et al. 2021, and the discussion therein) (see Table C.2). For the GCR spectrum, we employed a parametrisation based on the force-field model (Gleeson & Axford 1968), the full details are given in Usoskin et al. (2005), where the local interstellar spectrum is considered according to Vos & Potgieter (2015). The modulation is considered following the procedure from Usoskin et al. (2017). Here, the modelling of the NM response is performed with a new altitude-dependent NM yield function (Mishev et al. 2020), that is, each NM is modelled with a yield function corresponding to the exact station altitude, leading to significant improvement of the unfolding procedure compared to previous studies (e.g. Cramp et al. 1997; Mishev et al. 2021). Here we rescaled the DOMC/DOMB mini NMs to a standard 6NM64, similarly to Caballero-Lopez (2016) and Lara et al. (2016).
Derived spectral and angular characteristics during several stages of GLE 73 on 28 October 2021.
All Tables
Derived spectral and angular characteristics during several stages of GLE 73 on 28 October 2021.
All Figures
 |
Fig. 1. GLE73 on 28 October 2021. Panel a: increase (in percent) of several NMs based on 5-minute de-trended NM data. Panel b: SOHO/ERNE proton flux. Panel c: SXR flux observed by GOES, denoting an X1.0 solar flare (red curve; left axis). The vertical dashed black line corresponds to the start time of the flare. The height of the WL shock is shown with the magenta squares from measurements at the plane-of-sky near the CME leading edge. The dashed blue line is a linear fit to the height and extrapolated back to the surface of the Sun. Panel d: dynamic radio spectrum observed by Wind/WAVES. The dashed black line corresponds to the start time of the identified type III burst at ∼15:28 UT. The inset figure denotes the type II burst (in blue), the storm of type III bursts (in magenta), and the type IV burst (in green). |
| In the text | |
 |
Fig. 2. Selected snapshots of EUV and WL coronagraphic observations before and during the GLE73 event on 28 October 2021. Left panel: a running-difference image in EUV from SDO/AIA at 193 Å. The EUV wave is circled to indicate its location. The footpoints of the Parker spirals connected to STEREO-A (red), SolO (blue), and Earth (green) are shown with the coloured crosses. Most of the footpoints of the magnetic field lines connected to Earth (from PFSS) gather close to the region highlighted with a green circle. We indicate the location of ARs that the pressure (shock) wave interacted with during its expansion. The middle and right panels show running-difference images from the LASCO-C2 and STEREO-A/COR2 coronagraphs, respectively. We outline the location of the shock wave and indicate the CME. We indicate the locations where the pressure (shock) wave interacted with coronal streamers (SI) and the previous CME (P-CME). |
| In the text | |
 |
Fig. 3. Viewing directions of NMs in the GSE coordinates at around the onset of GLE73 at 15:50 UT on 28 October 2021. Geomagnetic conditions were slightly disturbed (Kp = 1.0). The colour lines, acronyms, and numbers depict the asymptotic directions, NM stations, and rigidities in the range 1–5 GV, respectively. The line of equal pitch angles relative to the anisotropy axis is plotted for 30° for the sunward direction (solid black line) and for 150° for the anti-sunward direction (dashed black line). |
| In the text | |
 |
Fig. 4. Derived SEP rigidity spectra (left panel) and PADs (right panel) during GLE73 on 28 October 2021. The solid black line denotes the GCR flux, which corresponds to the time period of the GLE 73 occurrence (see text for details). All times in the legend are in UT and refer to the start of the corresponding five-minute interval over which the data are integrated. |
| In the text | |
 |
Fig. 5. Peak proton flux (IP) at E > 10 MeV for GLEs that occurred from 1976 to 2021 (blue squares). GLE58 (orange square), GLE40 and GLE50 (purple squares), and GLE73 (red square) are indicated. Mean (1850 pfu) and median (321 pfu) values of the peak proton flux are presented as horizontal dashed pink lines. Monthly and smoothed monthly sunspot numbers are shown as grey and black lines. |
| In the text | |
 |
Fig. A.1. View of the ecliptic plane from solar north, showing the positions of various spacecraft on 28 October 2021 at 15:15 UT. The Parker spirals are shown for each spacecraft. The data are from the Solar MAgnetic Connection Haus tool (https://solar-mach.github.io/). |
| In the text | |
 |
Fig. A.2. Energetic particle recordings of GLE73 in the near-Earth space. From top to bottom: 5-minute-averaged GOES/SEISS differential fluxes; SOHO/ERNE fluxes; and SolO/HET measurements, including the recordings of the SolO/HET/BCB counter. |
| In the text | |
 |
Fig. B.1. Evolution of the EUV wave and PFSS magnetic field lines for Earth (green) presented at ∼15:39 UT. The location of the heliospheric current sheet is shown with the red line. See online movie. |
| In the text | |
 |
Fig. C.1. Pressure-corrected count rate (5-minute data between 12–24 UT on 28 October 2021, and hourly otherwise) of CALG NM, in percent with respect to the pre-increase level of 353 cnts/sec (13-15 UT on 28 October 2021), as indicated by the dotted black line. The dashed red line depicts a parabolic-shaped GCR background due to the diurnal wave, with respect to which the GLE strength is calculated. The data are available at IGLED2. |
| In the text | |
 |
Fig. C.2. Evaluation of the north-south anisotropy of GLE73. Variations using two sub-polar stations, THUL (north, blue line) and JBGO (south, black line), and their corresponding difference (red line) are shown. |
| In the text | |
 |
Fig. C.3. Evaluation of high-latitude NMs during GLE73. Variations using the FSMT NM (solid black line) and the mean of eight high-latitude NMs (solid blue line) and their corresponding difference (red line) are shown. The blue and the pink ribbons depict the 1σ error. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.