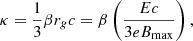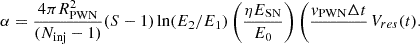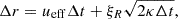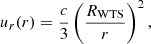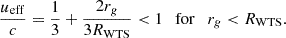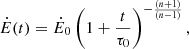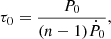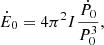| Issue |
A&A
Volume 698, May 2025
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202452726 | |
| Published online | 06 June 2025 | |
Hadronic emission from the environment of the Crab Pulsar Wind Nebula by re-accelerated particles
1
Erlangen Centre for Astroparticle Physics (ECAP), Friedrich-Alexander-Universität Erlangen-Nürnberg, Nikolaus-Fiebiger-Str. 2, D 91058 Erlangen, Germany
2
Department of Physics, Clarendon Laboratory, Parks Road, Oxford OX1 3PU, United Kingdom
3
Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany
⋆ Corresponding author: samuel.spencer@fau.de
Received:
23
October
2024
Accepted:
9
April
2025
Context. The observation of peta-electronvolt (PeV) γ-ray photons from the Crab Nebula by the Large High Altitude Air Shower Observatory (LHAASO) has revitalised the possibility of a secondary population of hadrons producing the highest energy emission through neutral pion decay. Despite previous studies modelling this population, the origin of such high-energy hadronic particles remains unclear.
Aims. We consider possible acceleration scenarios for multi-PeV particles in the Crab Nebula environment, including one in which high-energy protons produced at the supernova remnant’s outer shock diffuse into the pulsar wind nebula (PWN). Particles that reach the Crab Pulsar’s wind termination shock can be accelerated to the required energies, and subsequently interact with the dense filaments surrounding the nebula.
Methods. We performed particle transport simulations of this scenario, including the effects of the expansion of the PWN into the surrounding supernova ejecta.
Results. We find that this results in PeV photons being produced over the lifetime of the Crab system, without over-estimating the flux at lower energies or exceeding the energy budget of the Crab Pulsar. This results in a reasonable match with the LHAASO data at the highest energies. We also present predictions for the resulting all-flavour neutrino flux, finding it to be approximately an order of magnitude below the sensitivity of current generation instruments.
Key words: ISM: supernova remnants / gamma rays: general
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Crab Nebula is the remnant of a star purported to have exploded in 1054 AD (Lundmark 1921). It is the most widely studied object in very high-energy (VHE) γ-ray astrophysics and was the first (and brightest persistent) teraelectronvolt (TeV) γ-ray source detected from the ground using the Imaging Atmospheric Cherenkov Telescope (IACT) technique (e.g. Weekes et al. 1989; Aharonian et al. 2004, 2006; Albert et al. 2008). More recently, a High-Energy Stereoscopic System (H.E.S.S.)-only analysis found that the γ-ray emission from the Crab Nebula has an extension of (52.2 ± 2.9stat ± 6.6sys)″ at TeV energies (H.E.S.S. Collaboration 2020). A joint analysis with the Fermi Large Area Telescope (Fermi-LAT) and H.E.S.S. yielded r68 = (0.82 ± 0.29stat)′ (Aharonian et al. 2024). The latter analysis found strong evidence for a decreasing size as a function of energy in the γ-ray regime up to ∼100 TeV; the energy-dependent morphology in this range is likely lepton-dominated. Furthermore, pulsed emission from the central pulsar, PSR J0534+2200, has also been detected at TeV photon energies by the Major Atmospheric Gamma Imaging Cherenkov (MAGIC) telescope (Ansoldi et al. 2016) and the Very Energetic Radiation Imaging Telescope Array System (VERITAS) (Nguyen & VERITAS Collaboration 2015). This pulsar is located at a distance of 2 kpc from Earth Kaplan et al. (2008) and has a spin-down luminosity of 5 × 1038 erg s−1 (Smith et al. 2023).
As pointed out by Atoyan & Aharonian (1996), the production of the TeV γ-ray emission purely via π0 decay can be ruled out on energetic grounds. Thus, the primary emission mechanism for γ rays above 100 GeV from the nebula is generally accepted to be the inverse-Compton (IC) scattering of photons in the nebula by energetic electrons and/or positrons. The target photons come from a variety of background radiation fields, even though at photon energies greater than 100 TeV, the cosmic microwave background (CMB) dominates (Cao 2021). The wind termination shock (WTS) of the ultra-relativistic wind of the pulsar, located at ≈0.13 pc from the pulsar (Weisskopf et al. 2012), is believed to be the site of acceleration of the TeV-emitting particles (e.g. Rees & Gunn 1974; Bell 1992; Amato & Arons 2006; Giacinti & Kirk 2018). However, the details of the acceleration remain unclear. The magnetic field structure of the Crab Nebula has also recently been examined by the Imaging X-ray Polarimetry Explorer (IXPE) mission, revealing a predominantly toroidal magnetic field (Bucciantini et al. 2023), as expected for an oblique rotating pulsar (e.g. Coroniti 1990; Michel 1994; Bogovalov 1999).
Although a purely hadronic origin for the giga-electron volt-TeV (GeV-TeV) emission was ruled out, Atoyan & Aharonian (1996) proposed that a hard component could in principle dominate at higher energies. Such a scenario becomes increasingly favourable at ultra-high energies, where the Klein-Nishina suppression affects even CMB photons (e.g. Dirson & Horns 2023). The recent detection of the PeV γ-ray emission by the Large High-Altitude Air Shower Observatory (LHAASO) (Cao 2021) has re-opened this debate.
Previous studies exploring the role of hadronic emission in the context of the LHAASO results (e.g. Liu & Wang 2021; Peng et al. 2022; Nie et al. 2022) do not address the origin of the multi-PeV particles required to explain the observations. However, even the processes underlying the energisation of IC-emitting particles are uncertain. It is broadly accepted that the pulsar wind termination shock plays the dominant role, though exactly how it does so remains a topic of active investigation. Different proposed models include, for example, a resonant cyclotron absorption of the pairs (e.g. Amato et al. 2003; Amato & Arons 2006) or directly via relativistic shock acceleration (Giacinti & Kirk 2018; Giacinti et al. 2022).
The resonant cyclotron absorption mechanism does not accelerate ions efficiently. However, to produce the observed energetic pairs, the mechanism would require the pulsar wind to be energetically dominated by a cold ion component with a large bulk Lorentz factor of Γwind > 106. Protons and/or ions embedded in such a wind, should they exist, would be thermalised at the shock and injected into the nebula at multi-PeV energies. Despite observational arguments supporting large bulk Lorentz factors (e.g. Kennel & Coroniti 1984b), it remains uncertain whether they can be realised in practice (see Kirk et al. 2009, for a review)1. If the ions are not energetically dominant, or the wind has a substantially lower bulk Lorentz factor, one could consider if relativistic shock acceleration can occur at the termination shock. Giacinti & Kirk (2018) have shown that particles of one charge can undergo multiple Fermi cycles at the shock in the equatorial region due to the field reversal across the equator. Both scenarios would require a non-negligible proton and/or nucleon component in the wind, whose presence is currently unconstrained (though see for example Bednarek & Protheroe 1997; Nie et al. 2022).
Alternative routes for PeV proton acceleration include diffusive shock acceleration at the outer blast wave of the supernova remnant (SNR) associated with the progenitor of the Crab Pulsar. However, favourable wind conditions of the progenitor star are needed for particles to exceed PeV energies (Bell et al. 2013). As pointed out by Bell (1992), lower-energy protons accelerated at the outer shock can cross the nebula via a grad B drift and interact with the relativistic termination shock of the pulsar wind (see also Lucek & Bell 1994; Bell & Lucek 1996; Ohira et al. 2018).
Global magneto-hydrodynamic (MHD) simulations of the Crab system predict a complex magnetic field topology in the enclosed pulsar wind nebula (PWN) (Porth et al. 2014), through which particles can diffuse against the outward-directed flow. We considered the possibility that protons accelerated early in the evolution of the supernova forward shock populate a reservoir of energetic particles in the region between the PWN boundary and this forward shock at later times. Following Bell (1992), we explored the possibility that particles of a sufficiently high energy can in principle penetrate the nebula and reach the WTS. We applied a simple radial diffusion model and did not consider the role of drift motions. There, protons can be re-accelerated, before escaping the nebula and subsequently re-interacting with gas in the reservoir. A schematic of our proposed scenario is shown in Fig. 1. The existence of finger-like structures in the PWN, seen in the infrared and believed to be caused by Rayleigh-Taylor instabilities at the PWN boundary, supports this hypothesis. Their presence suggests that material is encroaching into the PWN from the surrounding SNR (Hester 2008). The goal of this work is to determine whether this proposed scenario can account for the highest-energy LHAASO γ-ray flux points reaching ≳1 PeV.
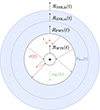 |
Fig. 1. Schematic of our proposed scenario. Hadronic particles with position r(t) (shown in red) are initially shocked by the SNR forward shock RSNR, fs. They then travel from the reservoir region (volume VRes, shown in blue) between the RSNR, fs and the PWN radius to the pulsar wind termination shock RWTS. Following re-acceleration, they advect outwards with the pulsar wind (velocity vW, shown by the green arrow) to hit the reservoir region from which they originated. The black star denotes the pulsar’s position. In a system as old as Crab, the supernova reverse shock RSNR, rs still travels outwards. |
The outline of the remainder of this paper is as follows: In Sect. 2, we first explain how we made analytic estimates of the diffusion coefficient in the nebula and the resulting γ-ray flux. We then introduce the theory of an expanding PWN. Next, we present the Monte-Carlo simulation procedure we adopted and our modelling of the resulting γ-ray emission. In Sect. 3 we compare the results of this modelling to the LHAASO data and to the available energy budget from the pulsar, before making an estimate of the resulting neutrino flux. In Sect. 4, we present our conclusions.
2. Methods
2.1. Motivation and estimates
Working with the hypothesis that the γ-ray flux at and above PeV energies is dominated by hadronic emission, the LHAASO flux of ϕ(Eγ > 1015 eV)≳10−14 erg/cm2/s can be used to constrain the total energy of protons and other nuclei. This yields wtot(E > PeV)≈1046/⟨nH⟩ erg, irrespective of the acceleration process. Here ⟨nH⟩ is the average gas target density surrounding the nebula. This can be compared against the kinetic energy provided by the supernova of ESNR ≈ 1051 erg, or the integrated energy released by the central pulsar Epulsar ≫ 1049 erg. The latter inequality assumes that the spin-down power was larger in the past. It is evident that a modest efficiency of less than a fraction of a percent would be sufficient in either scenario to account for the required PeV protons energetically.
Modelling the multi-wavelength observations of the Crab PWN generally indicates that the root mean square field inside the nebula is BPWN ≈ 100 μG. The transport of energetic particles in this field is sensitive to both its global topology and the details of the MHD turbulence embedded in the flow. Based on recent X-ray polarisation measurements (Bucciantini et al. 2023), it appears that the radial component of the field is sub-dominant in the nebula, and, thus, the radial diffusion coefficient should not exceed the Bohm limit. Adopting present-day parameters for the nebula, one can estimate an upper limit on the radial diffusion length of 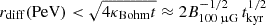 pc (i.e. comparable to the expected present-day radius of the nebula). This is consistent with the results of 3D MHD simulations of radial diffusion in the Crab Nebula by Porth et al. (2016), who found an almost energy-independent radial diffusion coefficient of ≲1027 cm2 s−1 for test particles with Lorentz factors of γ ≪ 1010. With such a short radial diffusion length, ions that recently interacted with the wind termination shock remain inside the nebula, whereas those entering from outside at the current epoch have a negligible probability of reaching the wind termination shock through diffusion alone (in this work, we do not consider drift motions as done in Bell 1992). Knowledge of the time history and internal structure of the SNR is therefore important for hadronic models of the PeV γ-ray emission.
pc (i.e. comparable to the expected present-day radius of the nebula). This is consistent with the results of 3D MHD simulations of radial diffusion in the Crab Nebula by Porth et al. (2016), who found an almost energy-independent radial diffusion coefficient of ≲1027 cm2 s−1 for test particles with Lorentz factors of γ ≪ 1010. With such a short radial diffusion length, ions that recently interacted with the wind termination shock remain inside the nebula, whereas those entering from outside at the current epoch have a negligible probability of reaching the wind termination shock through diffusion alone (in this work, we do not consider drift motions as done in Bell 1992). Knowledge of the time history and internal structure of the SNR is therefore important for hadronic models of the PeV γ-ray emission.
As mentioned in the introduction, we consider the possibility that, during the early stages of SNR expansion, a fraction of the energy processed by the forward shock was converted to cosmic rays (CRs). The particles that accumulate downstream of the external shock enclose the PWN, forming a reservoir of relativistic ions that, for simplicity, we assume to be comprised exclusively of protons. According to the standard CR-SNR origins model (e.g. Ginzburg & Syrovatskii 1964), approximately 10% of the SNR’s kinetic energy should be converted to CRs over its lifetime. Given the relatively young age of the Crab Pulsar, we do not expect the total energy in the reservoir to exceed this.
It is possible to constrain the total energy by requiring that the emission from the reservoir does not dominate the IC emission from the nebula at sub-PeV energies. This also serves as a consistency check of our proposed model. Assuming the non-thermal proton distribution in the reservoir is a power law, dN/dE ∝ E−s above 1 GeV, the γ-ray flux at Earth is approximately
where we introduced the efficiency parameter η as the fraction of the total kinetic energy of the SNR in CRs above a GeV, wtot(E > GeV) = ηESN. Assuming s ≳ 2 and that the cutoff in the proton distribution extends well beyond several PeVs, the above numerical values alone could accommodate the LHAASO measurements. While this cannot be ruled out based on current observational constraints, it requires that the SNR shock both accelerates and confines particles to energies well beyond a PeV inside the remnant. This presents a challenge for current theoretical models (Bell et al. 2013).
If, on the other hand, protons accelerated at the SNR’s external shock reach some maximum energy ≪PeV, these CRs could fill the volume between the PWN and the outer SNR shock with the desired reservoir. The resulting hadronic emission from these particles would cut off below the LHAASO energy range, with the flux level being negligible compared to that of the IC emission. Similar arguments can be used to rule out a dominant leptonic contribution from the SNR.
2.2. PWN evolution
For the spherically symmetric evolution of the system, we followed the approach of van der Swaluw et al. (2001). In their model, the PWN radius satisfies
where RS is the Sedov radius given by
ESN = 1051 erg is the supernova energy, and Mej = 3M⊙ is the supernova ejecta mass. Assuming an interstellar medium (ISM) density of n = 0.1 cm−3, tS is the Sedov time given by tS ≈ 103 years in this case. The velocity of the outer radius of the PWN, vPWN, as a function of time is given by dRPWN/dt,
at the current stage of the Crab’s evolution. The WTS radius is fixed at 5% of the PWN radius at each time step, such that the size of the WTS at the current time is approximately correct (0.1 pc).
2.3. Simulation procedure
We sought to determine what fraction of the particles in the CR reservoir can interact with the WTS and be accelerated to higher energies. This required a number of assumptions on the nature of the particle transport in the nebula and the acceleration process itself. Analytic treatments of particle acceleration at relativistic shocks were complicated by the fact that the ratio of the shock velocity to the speed of light is not a small parameter that can be exploited (see for example Kirk et al. 2023). To proceed, we made a number of simplifying assumptions. We assumed that the system is spherically symmetric and that it can be approximately treated with the following non-relativistic transport equation:
where f(r, p, t) is the isotropic part of the distribution function, ur(r) is the radial fluid velocity, and κ is the radial diffusion coefficient. In general, Eq. (4) requires that the distribution remains close to isotropic and the flow satisfies ur ≪ c, both of which break down in the vicinity of the relativistic shock. We discuss how we avoided this complication below.
Defining F = 4πp34πr2f, Eq. (4) can be recast in the form
where 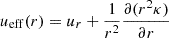 is the effective radial velocity and y = ln(E/E0). We chose E0 = 1 GeV. For simplicity, we further assumed that κ is constant and uniform in the nebula and has a Bohm scaling of
is the effective radial velocity and y = ln(E/E0). We chose E0 = 1 GeV. For simplicity, we further assumed that κ is constant and uniform in the nebula and has a Bohm scaling of
where rg is the particle gyroradius, E is its energy, Bmax is the magnetic field strength, and β a free parameter that we set to unity. We set the magnetic field strength to 112 μG in order to reproduce the synchrotron and IC emission from X-ray wavelengths to PeV at the current epoch with single-zone models (Cao 2021).
Equation (5) is in the standard Fokker-Planck form, which lends itself readily to a stochastic differential equation (SDE) approach (e.g. Achterberg & Krulls 1992; Gardiner 1994; Marcowith & Kirk 1999). In this approach, a large number of pseudo-particles are integrated in time, generating a particle distribution that is equivalent to that produced by the Fokker-Planck equation.
Particles are continuously injected at the outer surface of the PWN at r = RPWN(t). The region between the PWN and the rest of the SNR interior is assumed to be a uniform reservoir of CRs with an energy density of ⟨ucr⟩=ηESN/VRes, where 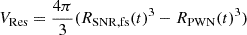 is the reservoir’s volume. For simplicity, we considered RSNR, fs(t) the solution of McKee & Truelove (1995). Both Vres and η are, in reality, time-dependent. However, since we know neither the history of the external medium in the early stages of the SNR nor the CR escape history, we considered η as a fixed value.
is the reservoir’s volume. For simplicity, we considered RSNR, fs(t) the solution of McKee & Truelove (1995). Both Vres and η are, in reality, time-dependent. However, since we know neither the history of the external medium in the early stages of the SNR nor the CR escape history, we considered η as a fixed value.
The energy distribution of CRs in the reservoir was considered to be a power law F ∝ (E/E0)−S with S > 1, where the particles likely to be re-accelerated have energies between the limits E1 = 1 TeV and E2 = 50 TeV. Particles were injected at each time step and chosen in such a way that the integrated energy density matches that in the reservoir. This implies a numerical weighting factor of 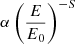 for each macro-particle. At each time step, we injected Ninj macro-particles, logarithmically spaced between ln(E1/E0) and ln(E2/E0), such that α is given by
for each macro-particle. At each time step, we injected Ninj macro-particles, logarithmically spaced between ln(E1/E0) and ln(E2/E0), such that α is given by
For the results presented, the number of macro-particles injected per time step is Ninj = 2000. The evolution of α over time is shown in Fig. 2.
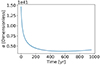 |
Fig. 2. Values of α at injection over the duration of the simulation. The α (determined by Eq. (7)) is assigned to each particle at injection and acts as a weighting factor in the particle spectrum upon escape. |
The injected particles were evolved using a standard SDE formalism. At each time step, each pseudo-particle’s radius r was updated such that
where ξR is a random number following a standard normal distribution centred at zero with a standard deviation of unity.
The flow profile in the nebula was chosen to satisfy
following the low-magnetisation wind-bubble solution (Weaver et al. 1977) (see also Kennel & Coroniti 1984a). Since ur is divergence-free, no change in the particle’s energy occurs during any time step unless the diffusive step results in a pseudo-particle crossing the internal WTS boundary. As stated earlier, the transport equation cannot capture the physics near the shock. We circumvented this issue by simply doubling the particle’s energy (as is expected at an ultra-relativistic shock, see Achterberg et al. 2001) and reflecting its position downstream so that rnew = RWTS + |RWTS − rold|. We note that for Bohm diffusion, the effective radial velocity for any particle on the shock surface is
Since rg = RWTS corresponds to the Hillas limit for relativistic shocks (Hillas 1984), this condition is satisfied. Provided the time step is chosen such that 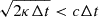 , the maximum energy cannot exceed the Hillas limit, since outward radial advection must exceed the diffusive step. For our chosen values, the Hillas limit is EHillas ≈ 1016 eV for protons.
, the maximum energy cannot exceed the Hillas limit, since outward radial advection must exceed the diffusive step. For our chosen values, the Hillas limit is EHillas ≈ 1016 eV for protons.
The free parameters used in the simulation are shown in Table 1. The computational domain covers only the region, rWTS < r < rPWN. We recorded any particle that has been transported outside the domain (r > rPWN), but only if it has interacted with the WTS at least once. These particles were injected back into the reservoir and assumed to remain there.
Fixed parameters set in the simulation with associated values based on previous literature.
2.4. γ-ray spectrum
We used the GAMERA package (Hahn 2015; Hahn et al. 2022) to infer the γ-ray spectrum from the protons interacting with the reservoir based on the cross-section parameterisations of Kafexhiu et al. (2014). We considered the reservoir to be a static target with a density of 5 cm−3, using the proton spectra from the simulation at 969 years as the input proton distribution. It should be noted that the normalisation of the hadronic spectrum here is effectively a free parameter given the assumptions about the density in the target material and the fraction of the supernova energy in the population of re-accelerated hadrons. To model the hadronic emission, we employed the SYBIL 2.1 (Ahn et al. 2009) code as supported by GAMERA.
3. Results and discussion
3.1. Comparison to γ-ray data
Figure 3 shows instantaneous steps of our simulations at selected times, displaying particle energy relative to the maximum injection energy as a function of radius from the pulsar. This shows that the majority of re-accelerated particles interact with the WTS comparatively early (with the first interactions occurring around 30 years), before advecting outwards with the wind. The majority of interactions occur at ∼100 years. After ∼650 years, the simulations effectively freeze out, with no high-energy particles shocked or remaining within the PWN, as expected. These results further indicate that protons re-accelerated at the WTS are, as anticipated, outliers. If the contrary were true, their emission would potentially exceed the observed flux at lower energies. Secondary electrons and positrons produced through the secondary hadronic population’s proton-proton interactions would not be detectable above the existing IC emission from the primary electrons.
 |
Fig. 3. Instantaneous steps of the simulation over time. At each time step, the distribution of particle energies compared to the maximum injection particle energy is shown as a function of distance from the pulsar. A small number of particles with energy ratios greater than one can be seen, corresponding to interactions with the WTS. The PWN radius was constrained to reach the current size at the end of the simulation (969 years). At late times (≳650 years), there are no interactions with the WTS, and very few shocked particles remain within the nebula. |
Figure 4 shows the spectrum of re-accelerated protons that exit the PWN and merge with the CR reservoir with a clear break at ∼1 PeV. We found the resulting γ-ray spectrum using GAMERA and compared it to the LHAASO flux points in Fig. 5. Here, we adopted the multi-band leptonic model fit from Dirson & Horns (2023) for the IC component. Our re-acceleration model matched the data reasonably well, indicating that a hadronic re-acceleration scenario cannot be excluded as the origin of the highest-energy emission. A longer integration time with LHAASO or with such next-generation detectors as the Cherenkov Telescope Array Observatory (CTAO) will help constrain this hadronic scenario further. In particular, the improved angular resolution of CTAO (∼0.02° at 100 TeV) could help determine if the highest-energy γ rays correlate with the position of the target gas that sits outside the nebula (CTAO Consortium 2021). A very small number of particles (∼10s out of ∼108 injected) interacting with the shock more than ten times appears to account for the highest-energy emission. This can be seen in Fig. 6. These tend to be the particles injected with lower energies as a result of the injection statistics. To confirm that the pulsar can provide sufficient power to re-accelerate the protons, we compared the energy gained by the pseudo-particles at the WTS to the pulsar spin-down luminosity over time, Ė(t), defined as
 |
Fig. 4. Spectrum of re-accelerated protons that have escaped the PWN at the final time step. The Poisson errors on these measurements are shown. The x-axis errors denote the size of the bins. A power-law fit of E2dN/dE up to 1 PeV, normalised to 1 TeV, is shown for comparison to highlight the spectral break. |
 |
Fig. 5. Hadronic Crab spectra as modelled using GAMERA with SIBYLL 2.1. The IC spectra from Dirson & Horns (2023) is also shown. |
 |
Fig. 6. Re-weighted particle energies on escape from the PWN as a function of the number of interactions with the WTS. Only a small number of the ∼108 total particles injected over the PWN’s history ever reach the WTS, and a few tens of these can interact with the shock ≳10 times. |
where Ė0 is the spin-down luminosity at birth and n is the braking index (fixed at 2). The characteristic age of the pulsar τ0 is given by
where P0 is the Crab Pulsar birth period and Ṗ0 is the birth period derivative. We took the values P0 = 18.3 ms and Ṗ0 = 6.4 × 10−13 s s−1 from Zhang et al. (2020). To calculate Ė0 we used the following equation from Gaensler & Slane (2006),
where I = 1045 g cm2 is the neutron star’s moment of inertia. The results of this comparison are shown in Fig. 7. To match the highest-energy LHAASO flux point, we chose η to be 7 × 10−5. This suggests that in our scenario only a small portion of the pulsar’s spin-down luminosity would ultimately go into the re-acceleration of CRs. We also performed simulations with S in the range 1.1–1.3 and with E2 set to 25 TeV and 75 TeV; the effect on the spectrum was minor and would not change our conclusions, especially given the freedom in the choice of η.
 |
Fig. 7. Spin-down energy output of the pulsar compared to the total energy injected by the pulsar into re-accelerated hadrons at the WTS. |
3.2. Predicted neutrino flux
The neutrino flux we predict from our secondary hadronic population, according to the prescription of Kelner et al. (2006), is shown in Fig. 8. Consistent with Peng et al. (2022), we find that the predicted neutrino flux is substantially below the sensitivity threshold of such current generation instruments as the IceCube neutrino observatory (IceCube Collaboration 2023) and the upcoming Cubic Kilometre Neutrino Telescope (KM3Net) detector (Adrián-Martínez et al. 2016). This could be in tension with the hotspot associated with the Crab Nebula identified in the recent cascade event analysis by the IceCube collaboration (IceCube Collaboration 2023).
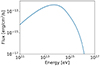 |
Fig. 8. Neutrino flux prediction for our re-acceleration model. For reference, the current generation of neutrino detectors have an optimal sensitivity at 100 TeV of approximately 10−12 erg cm−2 s−1 (Aartsen et al. 2019). |
4. Conclusions
In this study, we performed particle transport simulations to discern whether the highest-energy emission from the Crab Nebula, as observed by LHAASO, could have a hadronic contribution. We based our simulations on a physically motivated re-acceleration scenario. Our results show that, in principle, protons have sufficient time to travel from the region between the PWN radius and the SNR forward shock to the WTS, interact multiple times with the WTS, and travel back again. Our model provides a reasonable quality match to the LHAASO data without over-estimating the flux at lower energies. This indicates that a hadronic scenario cannot be excluded. Our results motivate additional realistic 3D simulations to further explore this scenario. Possible extensions of this model could consider the reverberation phase in older systems, where the combination of the SNR reverse shock crushing the PWN (Ohira et al. 2018) and re-acceleration at the central WTS may produce a greater number of PeV particles.
See also Kirk & Giacinti (2019) for a study of the impact of protons on the Crab Pulsar wind.
Acknowledgments
S. Spencer and A. Mitchell are supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project Number 452934793.
References
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2019, Eur. Phys. J. C, 79, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Achterberg, A., & Krulls, W. M. 1992, A&A, 265, L13 [NASA ADS] [Google Scholar]
- Achterberg, A., Gallant, Y. A., Kirk, J. G., & Guthmann, A. W. 2001, MNRAS, 328, 393 [Google Scholar]
- Adrián-Martínez, S., Ageron, M., Aharonian, F., et al. 2016, J. Phys. G: Nucl. Part. Phys., 43, 084001 [Google Scholar]
- Aharonian, F., Akhperjanian, A., Beilicke, M., et al. 2004, ApJ, 614, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Benkhali, F. A., Aschersleben, J., et al. 2024, Spectrum and extension of the inverse-Compton emission of the Crab Nebula from a combined Fermi-LAT and H.E.S.S. analysis [Google Scholar]
- Ahn, E.-J., Engel, R., Gaisser, T. K., Lipari, P., & Stanev, T. 2009, Phys. Rev., D, 80 [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2008, ApJ, 674, 1037 [CrossRef] [Google Scholar]
- Amato, E., & Arons, J. 2006, ApJ, 653, 325 [Google Scholar]
- Amato, E., Guetta, D., & Blasi, P. 2003, A&A, 402, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ansoldi, S., Antonelli, L. A., Antoranz, P., et al. 2016, A&A, 585, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Atoyan, A. M., & Aharonian, F. A. 1996, MNRAS, 278, 525 [NASA ADS] [Google Scholar]
- Bednarek, W., & Protheroe, R. J. 1997, Phys. Rev. Lett., 79, 2616 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1992, MNRAS, 257, 493 [Google Scholar]
- Bell, A. R., & Lucek, S. G. 1996, MNRAS, 283, 1083 [Google Scholar]
- Bell, A. R., Schure, K. M., Reville, B., & Giacinti, G. 2013, MNRAS, 431, 415 [Google Scholar]
- Bogovalov, S. V. 1999, A&A, 349, 1017 [Google Scholar]
- Bucciantini, N., Ferrazzoli, R., Bachetti, M., et al. 2023, Nat. Astron., 7, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, Z., et al. 2021, Science, 373, 425 [Google Scholar]
- Coroniti, F. V. 1990, ApJ, 349, 538 [Google Scholar]
- CTAO Consortium 2021, CTAO Instrument Response Functions - prod5 version v0.1 [Google Scholar]
- Dirson, L., & Horns, D. 2023, A&A, 671, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fesen, R. A., Shull, J. M., & Hurford, A. P. 1997, AJ, 113, 354 [Google Scholar]
- Gaensler, B. M., & Slane, P. O. 2006, ARA&A, 44, 17 [Google Scholar]
- Gardiner, C. W. 1994, Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences (Springer) [Google Scholar]
- Giacinti, G., & Kirk, J. G. 2018, ApJ, 863, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Giacinti, G., Reville, B., & Kirk, J. 2022, in 37th International Cosmic Ray Conference, 913 [Google Scholar]
- Ginzburg, V. L., & Syrovatskii, S. I. 1964, The Origin of Cosmic Rays (New York: Macmillan) [Google Scholar]
- H.E.S.S. Collaboration 2020, Nat. Astron., 4, 167 [Google Scholar]
- Hahn, J. 2015, in GAMERA - A Modular Framework For Spectral Modeling In VHE Astronomy [Google Scholar]
- Hahn, J., Romoli, C., & Breuhaus, M. 2022, GAMERA: Source modeling in gamma astronomy, Astrophysics Source Code Library [record ascl:2203.007] [Google Scholar]
- Hester, J. J. 2008, ARA&A, 46, 127 [Google Scholar]
- Hillas, A. M. 1984, ARA&A, 22, 425 [Google Scholar]
- IceCube Collaboration, 2023 Science, 380, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Kafexhiu, E., Aharonian, F., Taylor, A. M., & Vila, G. S. 2014, Phys. Rev. D, 90, 123014 [Google Scholar]
- Kaplan, D. L., Chatterjee, S., Gaensler, B. M., & Anderson, J. 2008, ApJ, 677, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S. R., Aharonian, F. A., & Bugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [Google Scholar]
- Kennel, C. F., & Coroniti, F. V. 1984a, ApJ, 283, 694 [CrossRef] [Google Scholar]
- Kennel, C. F., & Coroniti, F. V. 1984b, ApJ, 283, 710 [Google Scholar]
- Kirk, J. G., & Giacinti, G. 2019, ApJ, 884, 62 [Google Scholar]
- Kirk, J. G., Lyubarsky, Y., & Petri, J. 2009, in Astrophysics and Space Science Library, ed. W. Becker, 357, 421 [Google Scholar]
- Kirk, J. G., Reville, B., & Huang, Z.-Q. 2023, MNRAS, 519, 1022 [Google Scholar]
- Liu, R.-Y., & Wang, X.-Y. 2021, ApJ, 922, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Lucek, S. G., & Bell, A. R. 1994, MNRAS, 268, 581 [Google Scholar]
- Lundmark, K. 1921, PASP, 33, 225 [Google Scholar]
- Marcowith, A., & Kirk, J. G. 1999, A&A, 347, 391 [NASA ADS] [Google Scholar]
- McKee, C. F., & Truelove, J. K. 1995, Phys. Rep., 256, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, F. C. 1994, ApJ, 431, 397 [Google Scholar]
- Nguyen, T., & VERITAS Collaboration 2015, in 34th International Cosmic Ray Conference (ICRC2015), 34, 828 [Google Scholar]
- Nie, L., Liu, Y., Jiang, Z., & Geng, X. 2022, ApJ, 924, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Ohira, Y., Kisaka, S., & Yamazaki, R. 2018, MNRAS, 478, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Q.-Y., Bao, B.-W., Lu, F.-W., & Zhang, L. 2022, ApJ, 926, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Porth, O., Komissarov, S. S., & Keppens, R. 2014, MNRAS, 438, 278 [Google Scholar]
- Porth, O., Vorster, M. J., Lyutikov, M., & Engelbrecht, N. E. 2016, MNRAS, 460, 4135 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., & Gunn, J. E. 1974, MNRAS, 167, 1 [CrossRef] [Google Scholar]
- Smith, D. A., Abdollahi, S., Ajello, M., et al. 2023, ApJ, 958, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Stephenson, F. R., & Green, D. A. 2003, J. Astron. Hist. Heritage, 6, 46 [NASA ADS] [CrossRef] [Google Scholar]
- van der Swaluw, E., Achterberg, A., Gallant, Y. A., & Tóth, G. 2001, A&A, 380, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weaver, R., McCray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [Google Scholar]
- Weekes, T. C., Cawley, M. F., Fegan, D. J., et al. 1989, ApJ, 342, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Elsner, R. F., Kolodziejczak, J. J., O’Dell, S. L., & Tennant, A. F. 2012, ApJ, 746, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, X., Chen, Y., Huang, J., & Chen, D. 2020, MNRAS, 497, 3477 [Google Scholar]
All Tables
Fixed parameters set in the simulation with associated values based on previous literature.
All Figures
 |
Fig. 1. Schematic of our proposed scenario. Hadronic particles with position r(t) (shown in red) are initially shocked by the SNR forward shock RSNR, fs. They then travel from the reservoir region (volume VRes, shown in blue) between the RSNR, fs and the PWN radius to the pulsar wind termination shock RWTS. Following re-acceleration, they advect outwards with the pulsar wind (velocity vW, shown by the green arrow) to hit the reservoir region from which they originated. The black star denotes the pulsar’s position. In a system as old as Crab, the supernova reverse shock RSNR, rs still travels outwards. |
| In the text | |
 |
Fig. 2. Values of α at injection over the duration of the simulation. The α (determined by Eq. (7)) is assigned to each particle at injection and acts as a weighting factor in the particle spectrum upon escape. |
| In the text | |
 |
Fig. 3. Instantaneous steps of the simulation over time. At each time step, the distribution of particle energies compared to the maximum injection particle energy is shown as a function of distance from the pulsar. A small number of particles with energy ratios greater than one can be seen, corresponding to interactions with the WTS. The PWN radius was constrained to reach the current size at the end of the simulation (969 years). At late times (≳650 years), there are no interactions with the WTS, and very few shocked particles remain within the nebula. |
| In the text | |
 |
Fig. 4. Spectrum of re-accelerated protons that have escaped the PWN at the final time step. The Poisson errors on these measurements are shown. The x-axis errors denote the size of the bins. A power-law fit of E2dN/dE up to 1 PeV, normalised to 1 TeV, is shown for comparison to highlight the spectral break. |
| In the text | |
 |
Fig. 5. Hadronic Crab spectra as modelled using GAMERA with SIBYLL 2.1. The IC spectra from Dirson & Horns (2023) is also shown. |
| In the text | |
 |
Fig. 6. Re-weighted particle energies on escape from the PWN as a function of the number of interactions with the WTS. Only a small number of the ∼108 total particles injected over the PWN’s history ever reach the WTS, and a few tens of these can interact with the shock ≳10 times. |
| In the text | |
 |
Fig. 7. Spin-down energy output of the pulsar compared to the total energy injected by the pulsar into re-accelerated hadrons at the WTS. |
| In the text | |
 |
Fig. 8. Neutrino flux prediction for our re-acceleration model. For reference, the current generation of neutrino detectors have an optimal sensitivity at 100 TeV of approximately 10−12 erg cm−2 s−1 (Aartsen et al. 2019). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



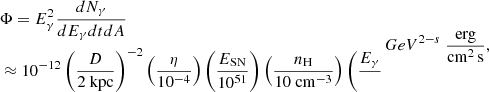
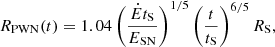
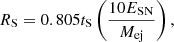
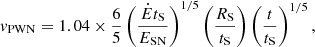
![$$ \begin{aligned} \frac{\partial f}{\partial t}+u_r\frac{\partial f}{\partial r} = \frac{1}{r^2}\frac{\partial }{\partial r}\left[ {r^2 \kappa }\frac{\partial f}{\partial r}\right] + \frac{1}{3r^2} \frac{\partial r^2 u_r}{\partial r} p \frac{\partial f}{\partial p}, \end{aligned} $$](/articles/aa/full_html/2025/06/aa52726-24/aa52726-24-eq6.gif)
![$$ \begin{aligned} \frac{\partial F}{\partial t} + \frac{\partial \,}{\partial r}\left[u_{\rm eff} F - \frac{\partial \,}{\partial r}(\kappa F) \right] - \frac{\partial \,}{\partial y}\left[\frac{1}{r^2} \frac{\partial r^2 u_r}{\partial r} \, F\right]=0 , \end{aligned} $$](/articles/aa/full_html/2025/06/aa52726-24/aa52726-24-eq7.gif)