| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | L2 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201527289 | |
| Published online | 17 November 2015 | |
Online material
Appendix A: Effects of Pturb on a 1.5 M⊙ stellar model and derived stellar parameters
In this section we discuss the comparison between tracks with and without the inclusion of Pturband eturb in the calculation of a 1.5M⊙stellar models. We emphasize that, different from massive stars (Grassitelli et al. 2015), the convective velocities for intermediate-mass stars do not exceed the local sound speed and no limitation of vc is necessary.
During the main-sequence phase (Teff ≳ 5800 K), the two tracks do not present appreciable differences; as the tracks approach the terminal-age main-sequence, the model with Pturb presents a displacement on the order of ≈10 K toward lower effective temperatures. A similar behavior is also found for the post-main-sequence evolution, corresponding to a difference in radius on the order of ≈1% or less. In line with the results of Grassitelli et al. (2015) for the massive stellar models (including a 7M⊙stellar track), we consider the effects of turbulence on the hydrostatic models to be small, and do not directly include them in the calculations of the stellar tracks in Fig. 1.
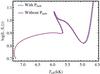 |
Fig. A.1
HR diagram showing evolutionary tracks of a 1.5M⊙model with (blue dashed) and without (purple continuous) turbulent pressure. |
| Open with DEXTER | |
υsini and υmacvalues derived for the analysed stars.
Appendix B: Convective timescales and mixing length
The results of an estimate of the convective timescales are shown in Fig. B.1. The convective timescale τconv has been computed as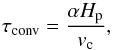 (B.1)where Hp is the local pressure scale height. At the center of the hydrogen convective zone, where we obtain the highest convective velocities, the timescale for convection is on the order of five minutes. At the upper border instead (i.e., at the convective boundary close to the surface) the timescale increases from 1 up to ≈10 days or more. Thus the convective timescales vary by ≈4 orders of magnitude within the last mixing length of the convective zone. This makes a direct comparison with the observed periods difficult. Numerical simulations are necessary in order to show whether observed mode lifetimes are compatible with stochastic excitation.
(B.1)where Hp is the local pressure scale height. At the center of the hydrogen convective zone, where we obtain the highest convective velocities, the timescale for convection is on the order of five minutes. At the upper border instead (i.e., at the convective boundary close to the surface) the timescale increases from 1 up to ≈10 days or more. Thus the convective timescales vary by ≈4 orders of magnitude within the last mixing length of the convective zone. This makes a direct comparison with the observed periods difficult. Numerical simulations are necessary in order to show whether observed mode lifetimes are compatible with stochastic excitation.
The absolute values given here and in Sect. 3 depend upon the adopted value of the mixing-length parameter α. For α = 1, the turbulent pressure fraction decreases to a maximum of 5% as a consequence of smaller convective velocities, while an increase of α (e.g., α = 1.8) leads to transonic convective velocities. Changing α also changes the position of the local peak of ![]() , e.g., the position of the peak decreases by 300 K when adopting α = 1.
, e.g., the position of the peak decreases by 300 K when adopting α = 1.
 |
Fig. B.1
Convective timescale (color coded) as a function of the effective temperature and optical depth throughout part of the evolution of a 1.9 M⊙ model (same as Fig. 2). In the center of the hydrogen convective zone, where we find the higher contribution from Pturb, the convective timescales are ≈ 10-2 days, while at the edges of the hydrogen convective zone τconv increases up to ≈ 101−102 days. |
| Open with DEXTER | |
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


