| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 26 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526113 | |
| Published online | 30 September 2015 | |
Online material
Appendix A: Rotation scheme integration and tests
 |
Fig. A.1
Results at 23.3 Gyr for the two-ring test. Two rings rotate in opposite directions around a 1 × 1011 M⊙ mass located at (0,0). When the frame of reference rotates (all but the standard GEAR code), it rotates around the point (100,0). The points should continue to orbit at 50 kpc and 100 kpc represented by two black rings. The standard GEAR code in a non-rotating frame is shown with blue crosses. In a rotating frame of reference, the results of calculating the forces at every time step is shown with yellow squares, using the half time step velocity (Mid-v) as green points, and the iteration scheme (It-v) with red triangles. Only every 20th point is shown for clarity. |
| Open with DEXTER | |
Because of the non-symplectic nature of the leapfrog integrator, care needs to be taken when dealing with the rotating reference frame to advance the velocity at each step due to the accelerations dependence on the velocity.
We test a few schemes through two tests: first, a simple system of rotating rings, and also a dwarf that only experiences tidal forces as in NRJ14.
First, we consider a system of two simple rings, each comprising a number of particles of negligible mass (we use 1000 particles of mass 0.01 M⊙) in circular orbits at 50 kpc and 100 kpc around a 1 × 1011 M⊙ point mass (modelled as a Plummer sphere with a softening of 0.5 kpc). If the central mass is considered the origin, then the rotating box is positioned at (100,0) and is set to orbit in the same direction as the outer ring (clockwise), giving the outer ring zero velocity in the rotating frame of reference. The inner ring is set to rotate in the opposite direction (anti-clockwise in this case). This system is then simulated for 23.3 Gyr (5000 time units in our set up), just shy of 2.5 rotations of the outer ring. We show the results in Fig. A.1. We note that all errors here are time step dependent, with all methods performing well at small time steps, however, large differences are seen at the time steps selected by the code.
 |
Fig. A.2
Stellar mass for the dwarf only experiencing tidal forces in the standard GEAR implementation (blue) and in the rotating reference with the Mid-v scheme (green dash) and with the It-v scheme (red dash-dot) and the It-v scheme with a low step size (green dotted). The beginning of the orbit is shown with a vertical dotted line. For the first ~1.5 Gyr, the stellar mass is basically the same with similar bursts (see Fig. A.3), beyond this, however, the Mid-v scheme flattens out, still producing stars for another ~1.5 Gyr, but at a lower rate. The drop in stellar mass at the end in the rotation schemes is due to stellar particles being deleted as they cross the boundaries. This drop is lower in the low step size due to better simulation of the dwarf core (see Fig. A.4). |
| Open with DEXTER | |
 |
Fig. A.3
Star formation rate for the dwarf only experiencing tidal forces in the standard GEAR implementation (blue, top) and in the rotating reference with the Mid-v scheme (green, middle) and with the It-v scheme (red, bottom). The beginning of the orbit is shown with a vertical dotted line. For the first ~1.5 Gyr, the bursts are similar between all cases with short bursts of ~ 4 × 10-4 M⊙ (and a slightly extended one in the normal GEAR code), which leads to a similar chemical evolution. Beyond this point however, Mid-v run drops to ~ 1 × 10-4 M⊙ before becoming extremely low levels around 6 Gyr. Suggesting that the change in density profile impacts the star formation rate, and subsequently the feedback and chemical evolution within the dwarf. |
| Open with DEXTER | |
 |
Fig. A.4
Smoothed density in a central 1 kpc slice (logarithmic from maximum density at simulation start to 1% of this) through the centre of the dwarf in the three schemes. Each box is 10 kpc in width and height. The standard GEAR scheme is on the left column, Mid-v scheme in second column, It-v scheme with natural step sizes in the third column, and the It-v scheme with limited step sizes in the right column. From top to bottom, the slices take place at 2 Gyr (simulation start), 4.8 Gyr (perigalacticon), 7.6 Gyr (apogalacticon), and 10.4 Gyr (perigalacticon). In the rotating frame schemes, the dwarf is rotated back to the host galaxy frame of reference to be directly comparable with the standard GEAR scheme. As should be the case, the density profiles are identical at the simulation start, by the first perigalacticon, however (second row), the Mid-v scheme is less dense in the centre and slightly over dense in the tidal tails; this central under density is carried over to the first apogalacticon (third row) before the Mid-v dwarf is effectively destroyed at the next perigalacticon (bottom panel). The It-v dwarf survives these passages in slightly better shape, particularly at the second perigalacticon where it still retains a slightly denser core. When limiting step sizes to those typical of the RPS simulations, the It-v scheme performs quite well, possessing a similar core to the normal GEAR scheme at each point. |
| Open with DEXTER | |
As the periodic box is in a circular orbit, this test only evaluates the Coriolis and centrifugal forces. In the ideal case, the two rings (shown with black circles) maintains their orbits for all time, and this appears in the standard GEAR code (blue crosses; we note that this is identical to the standard Gadget-2 code, with an external potential force added) without the rotating reference frame. Inside the rotating reference frame, calculating the forces at the standard time step (yellow squares) and using the half-time step velocity inside the fictitious forces gradually introduces errors that build in time, with the inner ring expanding to a radius of ~65 kpc and the outer ring staying constant (a sign that the centrifugal force is being evaluated accurately). We find better results (green points) if we calculate the fictitious forces using an approximated future velocity (Mid-v) generated by the following:  Updating ω or q to an approximation does not greatly change the result here. In this case, the rings seem to suffer minimal contraction or expansion.
Updating ω or q to an approximation does not greatly change the result here. In this case, the rings seem to suffer minimal contraction or expansion.
We display one further case (It-v, red triangles).This form performs better in other tests, although it is seemingly more sensitive to step size (at low-step size all methods perform similarly) and in pure dark matter simulations (which tend towards larger step sizes) should be avoided. Here, the mid point is approximated as per above, but then it is approximated again using this calculated value. Here, we also assume that the angular velocity changes slightly across a time step, but that the acceleration in the angular velocity is negligible. We find  A second test is to compare the results with just tidal forces, particularly focusing on the star formation present within the dwarf. We follow the same method as in NRJ14, simulating a dwarf in isolation, before inserting it within the potential of a host galaxy. We choose an orbit with a perigalacticon of 80 kpc and an apogalacticon of 200 kpc, injecting the dwarf after 2 Gyr of evolution in isolation. This is the same simulated dwarf we use below, and its properties may be found in more detail in Sect. 3. The host halo parameters are the same as used in the main simulations and are shown in Table 1. The effects of just tides are discussed in detail in NRJ14, and here we just investigate the density profile, which provides resistance against ram pressure stripping, and star formation, which affects the chemical evolution of the dwarf, to compare the codes. Here we implement the particle deletion scheme discussed below in Sect. 2.3, but this has minimal effects on the dynamics of the dwarf (we do not follow it all the way to destruction). We compare the standard GEAR code (with slight updates from NRJ14), with the mid-point velocity scheme and the iterated velocity scheme for each property with the normal GEAR selected step sizes and the iterated velocity scheme limited to the typical step size GEAR chooses for the main simulations (~0.094 Myr).
A second test is to compare the results with just tidal forces, particularly focusing on the star formation present within the dwarf. We follow the same method as in NRJ14, simulating a dwarf in isolation, before inserting it within the potential of a host galaxy. We choose an orbit with a perigalacticon of 80 kpc and an apogalacticon of 200 kpc, injecting the dwarf after 2 Gyr of evolution in isolation. This is the same simulated dwarf we use below, and its properties may be found in more detail in Sect. 3. The host halo parameters are the same as used in the main simulations and are shown in Table 1. The effects of just tides are discussed in detail in NRJ14, and here we just investigate the density profile, which provides resistance against ram pressure stripping, and star formation, which affects the chemical evolution of the dwarf, to compare the codes. Here we implement the particle deletion scheme discussed below in Sect. 2.3, but this has minimal effects on the dynamics of the dwarf (we do not follow it all the way to destruction). We compare the standard GEAR code (with slight updates from NRJ14), with the mid-point velocity scheme and the iterated velocity scheme for each property with the normal GEAR selected step sizes and the iterated velocity scheme limited to the typical step size GEAR chooses for the main simulations (~0.094 Myr).
We show the stellar mass in Fig. A.2 and the star formation rate in Fig. A.3. It is immediately obvious that the various schemes produce different star formation histories; while the standard GEAR code (top panels in both) experiences a period of extended star formation. In both of the other cases, this continues the bursty nature of the isolated dwarf (before the dashed line). That the GEAR code changes from a star formation history characterised by bursts to one with a gradual period of star formation (at least initially) is likely related to the lack of pause in cooling that occurs when beginning a simulation from a snapshot (see NRJ14, for a discussion of this), why this does not occur with the other two is not known, but the star formation histories are similar apart from this initial region and that suggests it will not greatly affect the final results.
A more noticeable change occurs in the density profile of the dwarf as shown in Fig. A.4. Here the mid-v scheme (middle column) has a lower central density from the first perigalacticon passage (second row), which gets worse as time goes on. That much of the star formation occurs soon after input (and the dwarf is quenched in all cases) suggests that the schemes differ more in their estimation of the dynamical effects than in the chemical evolution of the systems. The changes in the star formation (of order 20%) between the simulations is not a great concern when simulating dwarfs and is roughly the amount produced by changing random seeds.
Appendix B: Particle deletion/creation scheme
The creation and deletion of particles is not without error. The creation of particles ignores things like pressure when deciding where particles are placed and their velocity, and the deletion relies on experimental values which are context dependent.
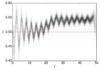 |
Fig. B.1
Two-dimensional histogram of the velocity and position of the particles in a wind tunnel (darker shades represent more particles there). The expected velocity is shown with a red dashed line at 0.5. The creation/deletion of particles introduces waves into the box, which are damped with position, and the deletion of the particles leads to a rising velocity towards the outer edge of the box. |
| Open with DEXTER | |
 |
Fig. B.2
Two-dimensional histogram of the ram pressure force (divided by the expected) and position of the particles in a wind tunnel (darker shades represent more particles there). The expected ram pressure force is shown with a red dashed line at 1.0. Here, we see that the creation/deletion of particles introduces waves into the box, with a rising velocity towards the outer edge of the box. |
| Open with DEXTER | |
 |
Fig. B.3
Ratio of the ram pressure force near the centre of the box to the expected versus radius for a sample orbit. The region of the orbit decreasing in galactocentric distance is shown in blue, while the region of increasing distance is shown in red. |
| Open with DEXTER | |
The simplest test case to examine what errors we can expect is a simple wind tunnel. Even here however there are a number of free parameters to consider: the velocity, pressure, and internal energy of the particles all influence the final error. We consider a wind tunnel of length 50 (50 kpc in physical units) and inject particles with a velocity of 0.5 (103 km s-1). All particles have a density of 9 × 10-8 (3.7 × 10-5 cm-3) and an internal energy generated from a temperature of 2 × 106 K. These conditions and velocity are similar to a dwarf orbiting at the outer edge of the halo. Although this box is not rotating, we delete particles if they come within 0.1 of the outer edge (this is smaller than the value used for the rotating box, but as discussed below, the rotation minimises the backwards wave).
We display the velocity of the particles as a function of position in Fig. B.1, and the ram pressure force divided by the true velocity in Fig. B.2 at a time of 10. The creation and deletion of the particles introduce standing waves into the box, which are damped in amplitude towards the middle. Beyond the middle, the deletion of particles (and the subsequent vacuum it creates) increases the velocity beyond the centre. This creates a slight increase in velocity, which travels backwards before settling at a value of ~0.55 ± 0.02. If a deletion region of size 0.5 is used in the wind tunnel, the velocity instead settles at a value of ~0.8. The change in velocity and changes in density due to the waves introduces a spread in ram pressure at the centre from about 90% of the true value to about 130%.
We also consider the effects of the orbit changing, which introduces a pressure gradient across the box. The periodic box is placed in an orbit with a perigalacticon of 80 kpc and apogalacticon of 200 kpc, identical to that used in Appendix A, in a box of side 50 kpc, a gas particle mass of 6.0 × 103 M⊙, and a halo density profile as per Sect. 3.2. We show the results in Fig. B.3 as a function of the radius of the orbit. Here, the pressure gradient results in a slight underestimation of the ram pressure at perigalacticon (by about ~10%), while being slightly above at apogalacticon. It is clear that over the densest fastest region of the orbit, any dwarf likely experiences a slight underestimation of the ram pressure, with the overestimation that occurs towards apogalacticon.
Notably, the larger error appears to be as the dwarf increases in galactocentric distance (i.e. approaching apogalacticon), and suggests that the scheme has more trouble accounting for a decrease in pressure than the increase in pressure associated with infall.
The choice to base it on the current positions of the dwarf results in creating an effective delay in the density of the halo reaching the dwarf (since the particles have to travel half the box). As the orbit can change on these scales, the solution to this problem would require integrating the pivot point forward and inserting the particles at its future density. Given the correction factor, this is not a trivial solution, particularly at perigalacticon where the impact is biggest, however, future versions of the code will attempt to incorporate this solution.
Appendix C: Particle creation
At simulation start, the positions of particles of an SPH glass (of Nglass particles) in a unit cube are passed through to memory. At each time step, of size Δt, particles of mass mgas are injected with a density corresponding to the halo halo at density ρhalo. Particles are inserted by mapping the volume required to be filled by the particles to the glass cube. We show a schematic of the particle creation in Fig. C.1 to assist in the understanding.
|
Fig. C.1
Particle creation schematic. The periodic box is shown in the left panel. The SPH glass is shown on the right. When particles need to be created (below the dashed line), a region of the SPH glass is selected (right panel, grey shading) according to Eq. (C.1). The positions of the particles within this region is then scaled to match the boundaries of the particle creation region, resulting in the grey points. The velocity of the particles is then set according to Eq. (12), and the other properties based on the assumed halo profile. At the next time step, the region of glass selected would start at the top of the shaded region (0.1 in the right-hand box) repeating the glass in any dimension when necessary. |
|
| Open with DEXTER | |
If the number of particles required to fill the entire box (of side L) is Nhalo = ρhaloL3mgas, then the volume at each time step that needs to be filled corresponds to a rectangular prism (x × y × z) on the glass of size, 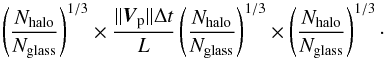 (C.1)All particles within this prism, and moving the prism along the velocity axis at each time step, are “accreted", that is, a new gas particle is created at the position (Nhalo/Nglass)− 1 / 3(xg,yg,zg), where (xg,yg,zg) is the position of the particle on the glass relative to the origin of the prism. As (Nhalo/Nglass)− 1 / 3 is not, in general, equal to one the periodicity is lost, but we find using a glass is still considerably better than randomly distributing halo particles in the new volume.
(C.1)All particles within this prism, and moving the prism along the velocity axis at each time step, are “accreted", that is, a new gas particle is created at the position (Nhalo/Nglass)− 1 / 3(xg,yg,zg), where (xg,yg,zg) is the position of the particle on the glass relative to the origin of the prism. As (Nhalo/Nglass)− 1 / 3 is not, in general, equal to one the periodicity is lost, but we find using a glass is still considerably better than randomly distributing halo particles in the new volume.
Appendix D: Comparison of baryon free satellites and halos
We compare here the mass and orbital evolution of a satellite with dark matter only and one with baryons and dark matter that orbits in the rotating reference frame without the external host coronae being present. The baryon free model, NBF-50, is created by evolving the same original dark matter potential without dwarfs and inserting it on the same orbit as NRPS-50, which has a perigalacticon of 50 kpc and an apogalacticon of 200 kpc. The tidal model, NTO-50, is simply the NISO model inserted at 2 Gyr on the same orbit of 50 kpc perigalacticon and 200 kpc apogalacticon, but with no Milky Way-like hot halo. In both cases, the models were limited to a maximum step size of ~0.094 Myr, and the step size GEAR quickly selects for the ram pressure simulations; all other parameters are the same as for the RPS cases.
These two models provide complementary tests. NBF-50 ensures any orbital evolution is not due to dynamical friction or errors in the particle creation/deletion, creating spurious gravitational attractions behind the dwarf. NTO-50 checks that the mass evolution is not a by-product of the rotation scheme or only due to tidal influences. Both models, without any form of hydrodynamic drag, also provide a test that the orbital evolution is not a by-product of the rotation scheme.
Appendix D.1: Mass evolution
We show the dark matter mass of the NTO-50 and NBF-50 models and NRPS-50 as a function of time in Fig. D.1. Similar to Arraki et al. (2014), the removal of baryons in NBF-50 produces a dramatic loss in dark matter density (and therefore mass within the 1 kpc and 3 kpc boundaries), although the mass loss is slightly under that found by Arraki et al. possibly attributable to the instantaneous removal of the baryons here. The tidal model NTO-50 retains the central mass density of NRPS-50, and tracks it closely until the first perigalacticon.
At the first perigalacticon, mass is lost from all models, however, it is dramatically more from NRPS-50 than NBF-50 or NTO-50, which lose ~30–50% within 3 kpc. This is compared to NRPS-50 which because of the ram pressure loses more than 70%. By the next perigalacticon, the NRPS-50 model is destroyed into a stream, while both the NBF-50 and NTO-50 models survive until the present day.
That both models undergo tidal stripping but retain their general structure confirms that the ram pressure stripping of gas acts synergistically with tidal stripping to remove mass from the dwarf, including its dark matter mass.
 |
Fig. D.1
Mass of dark matter within 1 kpc (thin lines) and 3 kpc (thick lines) for the NRPS-50 (cyan), NBF-50 (brown), and NTO-50 (pink) models. |
| Open with DEXTER | |
 |
Fig. D.2
Orbital evolution of NRPS-50 (cyan), NBF-50 (brown), and NTO-50 (pink). Line styles are as per Fig. 15. |
| Open with DEXTER | |
Appendix D.2: Orbital evolution
We compare the orbital evolution (see Sect. 4.6) between the three models in Fig. D.2. Notably, neither NBF-50 or NTO-50 show a change in orbital energy, as these orbital energies are always approximately the equal to the infall energy. Similarly, their peri- and apogalacticons remain approximately constant. NBF-50 does show a minor drop in apogalacticon of order 5 kpc, which can be regarded as the error arising because of the halo generation method. Notably, this is still much smaller than the 50 kpc drop in apogalacticon NRPS-50 suffers at the first perigalacticon. The constant nature of these peri- and apogalacticons increases the confidence that the drag experienced on the dwarf is due to a hydrodynamic interaction between the gas of a dwarf and the hot halo, which is then gravitationally coupled to the dark matter of the dwarf.
Appendix E: Drag of a dwarf galaxy
The drop in energy throughout a dwarf’s orbit (Fig. 15) and subsequent orbital change suggests that hydrodynamic drag is non-negligible when considering the evolution of a dwarf. By comparing the energy change to the mass nearby the coefficient of drag of the galaxy can be calculated. If the kinetic energy at time step i is Ek,i and potential energy Ep,i then the coefficient of drag at the time step i is given by  (E.1)We consider the mass of the dwarf within 10 kpc of the centre, and assume the energy change is simply the energy per unit mass of the centre multiplied by the mass. The choice of area is much more ambiguous, consisting of a clumpy medium, and it is not clear what reference should be chosen as hot gas may stream through parts of the structure. At each snapshot we select the total area of the dwarf, which exceeds a column density in the direction of motion of nH = 1 × 1021 cm-2 averaged over 0.25 kpc2 cells. This boundary is not the only potential choice, but seems to correspond to the area of the dwarf through which hot gas cannot easily flow.
(E.1)We consider the mass of the dwarf within 10 kpc of the centre, and assume the energy change is simply the energy per unit mass of the centre multiplied by the mass. The choice of area is much more ambiguous, consisting of a clumpy medium, and it is not clear what reference should be chosen as hot gas may stream through parts of the structure. At each snapshot we select the total area of the dwarf, which exceeds a column density in the direction of motion of nH = 1 × 1021 cm-2 averaged over 0.25 kpc2 cells. This boundary is not the only potential choice, but seems to correspond to the area of the dwarf through which hot gas cannot easily flow.
As the coefficient of drag generally depends on the Reynolds number of the flow, we calculate the Reynolds number3 at each time step as well, assuming the reference length is the same as the radius of a circle with equivalent area to the reference area. We plot the mean coefficient of drag versus Reynolds number in Fig. E.1 for the NRPS-50 model for the first 1.5 Gyr (450 snapshots) and the NRPS-100 model for ~8 Gyr (2000 snapshots). This time selection avoids the recreation event in NRPS-50, which leads to significant errors and stream formation in
NRPS-100. We also show a fit to the coefficient of drag to a smooth sphere versus Reynolds number (Eq. (7) of Mikhailov & Freire 2013) and see that although the coefficient of drag on the dwarf is much higher (as could be expected from the shape of the dwarf), it follows a similar trait of rapidly dropping until Re ~200 where Cd ~ 3–10 before dropping down to Cd ~ 1.
 |
Fig. E.1
Coefficient of drag of a dwarf galaxy throughout its orbit against the Reynolds number of the flow (calculated using the hot gas viscosity, not the numerical). The solid lines show the mean of the coefficient of drag for NRPS-50 (cyan) and NRPS-100 (magenta) within each (logarithmic) Reynolds number bin. Dashed lines show the standard deviation on each bin. A fit to the changing coefficient of drag of a sphere versus Reynolds number from Mikhailov & Freire (2013) is shown with a black line. |
| Open with DEXTER | |
The large amount of scatter at low Reynolds number is not in itself surprising, with the dwarf changing shape numerous times due to internal feedback, which is minimised at high Reynolds number because of the higher containing pressure. This large degree of scatter (and the dependence of Cd on area) makes it difficult to approximate the orbital change in semi-analytic models.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


