| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 22 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425587 | |
| Published online | 19 June 2015 | |
Online material
Appendix A: Testing gas hydrodynamics equations
Our numerical scheme for solving the equations of gas hydrodynamics (1)–(4) can be tested using a conventional set of test problems suitable for cylindrical coordinates. Below, we provide the results of six essential test problems, each designed to test the code performance at various physical circumstances. The code has also performed well on two additional tests: the two interacting blast waves and the Noh (or implosion) problems, but we do not provide the results for the sake of conciseness.
Appendix A.1: Sod shock-tube test
This test is often used to assess the ability of a numerical algorithm to accurately track the position of relatively weak shock waves and contact discontinuities. Initial conditions involve two discontinuous states along the z-axis, with a hot dense gas on the left and cold rarified gas on the right. More specifically, we set the pressure and density at z ∈ [ 0−0.5 ] to 1.0, while at z ∈ [ 0.5−1.0 ] the pressure is 0.1 and density is 0.125. The velocity of a γ = 1.4 gas is initially zero everywhere.
Filled circles in Fig. A.1 show the results of the Sod shock-tube test computed with a resolution of 200 grid zones and C2 = 4 (the number of zones over which the shock is spread), while the solid lines plot the analytic solution at t = 0.235. It is evident that the code tracks well the positions of shock waves and contact discontinuities, which are resolved by 3–4 zones, in accordance with the chosen value of C2. Decreasing C2 results in sharper shocks and contact discontinuities but may increase the magnitude of anomalous spikes in the specific energy (bottom-right panel), and hence is not recommended. Increasing C2 to 6 produces results similar to those for C2 = 4, except that the shocks and contact discontinuities are now resolved by 5−6 zones.
Appendix A.2: Sedov point explosion
The Sedov explosion problem tests the code’s ability to deal with strong shocks. In contrast to the Sod shock-tube test, in which shock waves were of a pure planar geometry, this test involves a spherically symmetric strong shock wave. Hence, the point explosion is a powerful test on the code’s ability to render spherically symmetric structures on an essentially nonspherical grid stencil.
 |
Fig. A.1
Sod shock tube problem for the gas density (upper-left), velocity (upper-right), pressure (lower-left), and specific internal energy (lower-right). The numerical solution is shown by open circles, while the analytical one is plotted by solid lines. |
| Open with DEXTER | |
 |
Fig. A.2
Sedov point explosion test for the explosion energy 1051 erg and background density n = 0.01 cm-3. The analytic solution is shown by the red lines, while the numerical solutions along the z-axis, r-axis, and diagonal z = r are shown by the black, pink, and blue lines, respectively. The top left panel presents the solution for the tensor artificial viscosity with C2 = 6 ; the top right panel, for the scalar artificial viscosity and C2 = 3; the bottom left panel, for the tensor artificial viscosity and C2 = 3; and the bottom right panel, for the tensor artificial viscosity with off-diagonal terms set to zero and C2 = 6. |
| Open with DEXTER | |
To initialize the explosion, we consider a cold (T = 10 K) homogeneous medium with number density n = 10-2 cm-3 and inject 1051 ergs of thermal energy (equivalent to one supernova) into the innermost grid cell. The adopted resolution is 300 × 300 grid cells and the size of each cell is 1.0 pc in each coordinate direction (z and r). We do not inject energy into a central sphere comprising a few cells near the coordinate origin, which is the usual practice to alleviate the problem of a nonspherical geometry. Instead, we consider the most difficult situation when energy is injected in just one, essentially cylindrical innermost cell.
Figure A.2 compares our derived density distributions along the z-axis (black line), the r-axis (pink line), and the diagonal z = r (blue line with circles) with the analytic solution given by the red line (Sedov 1959) at t = 1 Myr after the explosion. In particular, numerical simulations in the top left panel are obtained using the tensor artificial viscosity (AV) as defined in Sect. 4, while the density distribution in the top right panel is obtained using the “classic” scalar AV, as described by Richtmyer & Morton (1995). It is evident that the tensor AV yields a much better agreement with the analytic solution. The expanding shell has almost a perfect spherical shape (all three lines showing the numerical solution virtually coincide), notwithstanding the fact that the energy was injected into a cylindrically shaped innermost cell. On the other hand, the Richtmyer & Morton scalar AV yields a notable deviation from sphericity along the r and z axes, as seen in the top right panel of Fig. A.2. The Richtmyer & Morton solution also slightly overshoots the analytical solution. Regardless of the AV prescription used, the shock front is resolved by 2−3 grid zones.
We want to emphasize that all components of the artificial viscosity tensor Q should be used, including the off-diagonal terms. Neglecting the latter, as is done in, e.g., Stone & Norman (1992), leads to a significant deterioration of the numerical solution. The bottom right panel in Fig. A.2 demonstrates the effect of zeroing the off-diagonal terms in Q. As one can see, the numerical solution is skewed, notably undershooting the position of the shock front in the r-direction and along the diagonal direction but reproducing the shock front rather well in the z-direction.
A caution should be paid when choosing the AV softener C2. As one can notice in Fig. A.2, the test was done with different values of C2 for the tensor and scalar AV, 6 and 3, respectively. If we choose C2 = 3 for the tensor AV, the position of the shock front notably undershoots the analytic solution, as is illustrated in the bottom left panel of Fig. A.2. Fortunately, once the proper value of C2 is found, the tensor AV algorithm performs well regardless of the energy input, background density, or numerical resolution. We demonstrate this in Fig. A.3 showing the tensor AV performance for various choices of the input parameters as indicated in each panel and C2 = 6. It is evident that the test results are virtually insensitive to a particular choice of initial conditions.
The sensitivity of the Sedov test to a particular choice of the AV softener C2 is a well-known problem of numerical codes that evolve the internal energy (e.g., Tasker et al. 2008). Switching to the total energy helps to eliminate this problem (e.g., Clarke 2010). However, in numerical codes that make use of a staggered grid as our own, with vector and scalar variables defined at different positions on the grid, solving for the total energy equation is not a good option as it inevitably requires interpolating between the internal and kinetic energies to obtain the total energy (Clarke 2010) or applying corrections after each time step to conserve the total energy (Vshivkov et al. 2011). In either case, this practice, according to our experience, often comes at a cost of degraded performance on other test problems and is not recommended. Instead, we show that a proper choice of the artificial viscosity softener can help to resolve this problem without resorting to the total energy equation.
 |
Fig. A.3
Sedov point explosion test for various explosion energies, background densities, and numerical resolutions as indicated in each panel. The tensor artificial viscosity with C2 = 6 is used for every plot. The line meaning is the same as in Fig. A.2. |
| Open with DEXTER | |
Appendix A.3: Collapse of a pressure-free sphere
The gravitational collapse of a pressure-free sphere is used to assess the code’s ability to accurately treat converging spherical flows in cylindrical coordinates. This test is also useful for estimating the performance of the gravitational potential solver on dynamical problems (our solver does well on the static configurations such as spheres and ellipsoids). To run this test, we set a cold homogeneous sphere of unit radius and density (for convenience, the gravitational constant is also set to unity) and let it collapse under its own gravity. The analytic solution to this problem only exists in the limit of an infinite cloud radius, describing the collapse of every mass shell (Hunter 1962). In the cylindrical geometry, however, we consider a cloud of finite radius with a sharp outer boundary to preserve the cloud sphericity. As a result, a rarefaction wave develops after the onset of the collapse, propagating toward the coordinate origin and necessitating complicated corrections to the analytic solution (Truelove et al. 1998).
The left panel in Fig. A.4 compares the results of our numerical simulations with the “uncorrected” analytic solution of (Hunter 1962, red line) at t = 0.535 (or 0.985 that of the free-fall time) when the initial density has increased by nearly three orders of magnitude. As in the previous test, we plot the numerically derived density along the z-axis (black line), r-axis (green line), and the z = r diagonal (blue line with circles). The numerical resolution is 200 × 200 grid zones. The cloud’s outer boundary is somewhat smeared out because of the action of the rarefaction wave. The peak density is also about 1% smaller than that predicted from the analytic solution. On the other hand, the code performs well on preserving sphericity of the collapsing cloud. In the right panel, we turn off the volume averaging corrections applied to the advection of the r-momentum in the r-direction as described in Blondin & Lufkin (1993), which results in the development of an artificial density spike near the z-axis and also in the distortion of a spherically symmetric collapse. This test demonstrates the utility of the volume averaging corrections introduced originally by Blondin & Lufkin (1993) in the PPA advection scheme in non-Cartesian coordinates.
|
Fig. A.4
Collapse of a pressure-free sphere showing the gas density at 0.985 that of the free-fall time. The left and right panels show the test results with and without the volume averaging corrections as described in Blondin & Lufkin (1993). The line meaning is the same as in Fig. A.2. |
|
| Open with DEXTER | |
Appendix A.4: Collapse of a rotating sphere
This test is invoked to assess the code’s ability to conserve angular momentum. The setup consists of a isothermal (T = 10 K) homogeneous sphere of unit radius and density, which rotates at a constant angular velocity Ω0. The latter is found from the requirement that the ratio β of the rotational energy ![]() to gravitational energy
to gravitational energy ![]() is equal to 5%. Here, I = 2M0R2/ 5 is the moment of inertia of a homogeneous sphere of radius R and mass M0. The adopted value of β = 0.05 is close to an upper limit found in rotating prestellar molecular cloud cores and DM halos.
is equal to 5%. Here, I = 2M0R2/ 5 is the moment of inertia of a homogeneous sphere of radius R and mass M0. The adopted value of β = 0.05 is close to an upper limit found in rotating prestellar molecular cloud cores and DM halos.
In the absence of any mechanisms for angular momentum redistribution, the mass with specific angular momentum less than or equal to K = ωr2, where ω is the angular velocity at a distance r from the z-axis, should be conserved and equal to (Norman et al. 1980), 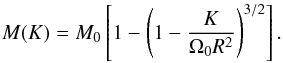 (A.1)A deviation from Eq. (A.1) would manifest the nonconservation of angular momentum in the numerical algorithm.
(A.1)A deviation from Eq. (A.1) would manifest the nonconservation of angular momentum in the numerical algorithm.
 |
Fig. A.5
Specific angular momentum spectrum M(K), calculated using Eq. (A.1), for a collapsing sphere at 1.03tff. The analytic spectrum is shown with the solid line, while the test results are plotted with open circles. |
| Open with DEXTER | |
The solid line in Fig. A.5 shows the initial mass spectrum M(K), whereas the open circles present the mass spectrum obtained at time 1.03 × tff = 0.551, where tff is the free-fall time for a nonrotating sphere of the same density and radius. The numerical resolution is 200 × 200 grid zones. By t = 0.551, the density near the center of the sphere has increased by more than three orders of magnitude, but the deviation of the mass spectrum from the initial configuration is negligible everywhere except at lowest values of K. This deviation is a manifestation of angular momentum nonconservation near the rotational axis caused by imperfections in the interpolation procedure across the inner r-boundary. Nevertheless, the total mass of gas that suffers form the angular momentum nonconservation is just below 1%, and therefore should not affect notably the global evolution.
Appendix A.5: Kelvin-Helmholtz instability
The Kelvin-Helmholtz instability (KHI) occurs at the interface between two fluid moving with different velocities. In the context of this paper, this instability operates at the interface between the hot supernova ejecta and the cold swept-up shell and may cause an accelerated disintegration of the latter (e.g., Vorobyov & Basu 2005). Therefore, it is essential that the code be able to demonstrate the development of the KHI as expected from the linear perturbation theory.
The initial setup involves two fluids moving in opposite directions along the z-axis with the relative velocity vz,rel = 0.2cs, where cs = 0.06 is the sound speed. The interface between the fluids is located at r = 0.5 and the densities of the inner and outer fluids are ρin = 1.0 and ρout = 0.1, respectively. We use periodic boundary conditions and the resolution is 200 × 200 grid zones on the 1.0 × 1.0 computational domain.
To trigger the instability, we impose a sinusoidal perturbation on the radial velocity vr of the form ![]() (A.2)where the amplitude and wavelength of the perturbation are δvr = vz,rel/ 100 and λ = 1/6, respectively. The perturbation is applied to five neighboring grid zones on both sides of the fluid interface.
(A.2)where the amplitude and wavelength of the perturbation are δvr = vz,rel/ 100 and λ = 1/6, respectively. The perturbation is applied to five neighboring grid zones on both sides of the fluid interface.
 |
Fig. A.6
Development of the KHI at different moments in time (see text for more detail). |
| Open with DEXTER | |
Figure A.6 demonstrates the growth of the KHI with time. There are six growing vortices, in agreement with the wavelength of the perturbation λ = 1/6, and the growth time is approximately 50−60, again in agreement with the characteristic growth time of the KHI for our choice of the fluid density and velocity, 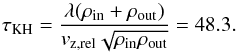 (A.3)We should note here that, for this particular test, gravity can be neglected. Therefore, all modes of perturbation, irrespective of their wavelengths (or wavenumbers) are unstable (see Vieser & Hensler 2007, for stability criteria when gravity is taken into account).
(A.3)We should note here that, for this particular test, gravity can be neglected. Therefore, all modes of perturbation, irrespective of their wavelengths (or wavenumbers) are unstable (see Vieser & Hensler 2007, for stability criteria when gravity is taken into account).
Appendix A.6: Overstability of a radiative shock
A useful test problem for hydrodynamic codes with optically thin radiative cooling is described in Stone & Norman (1993). The test involves setting a unform flow of gas with velocity v0 against a reflecting wall. An adiabatic reflection shocks forms immediately at the wall and propagates upstream with velocity vsh = v0/ 3. After approximately one cooling time, the shock loses its pressure support and is then advected back to the wall at vsh ≲ −v0. After reflecting off the wall, the shock again becomes adiabatic and propagates outward to repeat the cycle.
 |
Fig. A.7
Shock position versus time of a one-dimensional radiative shock during overstable oscillations. The shock positions for the flow velocities of 120 km s-1, 130 km s-1, and 150 km s-1 are plotted with solid, dash-dotted, and dotted lines, respectively. |
| Open with DEXTER | |
Figure A.7 presents the test results for the cooling function with solar metallicity and ionization fraction fion = 10-3. Gas heating is turned off for this test. The initial setup is identical to that described in Stone & Norman (1993), i.e., the initial gas number density and temperature are set to 10 cm-3 and 104 K, respectively. The position of the shock front for three flow velocities of 120 km s-1, 130 km s-1 and 150 km s-1 are plotted with the solid, dash-dotted, and dashed lines, respectively. The shock position demonstrates regular pulses, as expected. The amplitude and period of the observed oscillations are somewhat different from those presented in Stone & Norman (1993), which simply reflect the difference in the adopted cooling functions. The upstream velocity of the adiabatic shock is close to the expected value, v0/ 3. For instance, in the case of v0 = 150 km s-1, the maximum upstream velocity of the shock is 47 km s-1. This test demonstrates the reliability of our solution scheme for the gas cooling and heating described in Sect. 3.
Appendix B: Testing stellar hydrodynamics equations
Testing the stellar hydrodynamics Eqs. (6)−(8) presents a certain challenge since stellar systems are described by a stellar dispersion tensor, which may be anisotropic, rather than by an isotropic pressure. Fortunately, some of the test problems considered above can be adapted to stellar hydrodynamics as well. The matter is that the equations of stellar hydrodynamics can be formally made identical to those of gas hydrodynamics for a specific set of initial conditions (note that the continuity equations are always identical). Indeed, for a one-dimensional flow along the z-direction (with zero gravity and no star formation), Eqs. (7) and (8) become 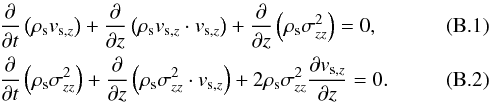 These equations become identical to the corresponding gas dynamics equations for ρgvz and ϵ, if we set
These equations become identical to the corresponding gas dynamics equations for ρgvz and ϵ, if we set ![]() ,
, ![]() , and γ = 3 (see Mitchell et al. 2013, for details). This fact allows us to directly compare the performance of both stellar and gas hydrodynamics code on some test problems considered in Sect. A or use analytic solutions available from the gas dynamics.
, and γ = 3 (see Mitchell et al. 2013, for details). This fact allows us to directly compare the performance of both stellar and gas hydrodynamics code on some test problems considered in Sect. A or use analytic solutions available from the gas dynamics.
Appendix B.1: Sod shock-tube test
The initial setup for this test is identical to that considered in Sect. A.1. We run the test along the z-axis and set ![]() and ρs at z ∈ [ 0−0.5 ] to 1.0, while at z ∈ [ 0.5−1.0 ] the z-component of the stress tensor is 0.1 and stellar density is 0.125.
and ρs at z ∈ [ 0−0.5 ] to 1.0, while at z ∈ [ 0.5−1.0 ] the z-component of the stress tensor is 0.1 and stellar density is 0.125.
 |
Fig. B.1
Sod shock-tube problem for the stellar density (upper-left), velocity (upper-right), z-component of the stress tensor (lower-left), and square of the z-velocity dispersion (lower-right). The numerical solution is shown by open circles, while the analytical solution is plotted by solid lines. |
| Open with DEXTER | |
Our numerical results for C2s = 4 and t = 0.14 (open circles) are compared against the analytical solution (solid lines) in Fig. B.1. It is seen that our numerical scheme correctly reproduces the position of shock waves and contact discontinuities in the stellar fluid. On the other hand, small-scale oscillations are evident at shock positions, perhaps reflecting the lack of energy dissipation due to the collisionless nature of stellar hydrodynamics. An increase in the coefficient of artificial viscosity helps to reduce the amplitude of spurious oscillations but simultaneously increases the shock smearing and hence is only recommended if these oscillations lead to numerical instabilities.
Appendix B.2: Collapse of a cold sphere and angular momentum conservation
The collapse of a cold stellar sphere, both with and without rotation, produces very similar results to those presented in Sects. A.3 and A.4 and will not be repeated here. This ensures that our stellar hydrodynamics part is expected to perform well on problems involving gravitational contraction/expansion with and without rotation.
Appendix C: Testing the chemical evolution routines
It is currently common to find hydrodynamical codes coupled with passive scalars (or other numerical techniques), which are able to follow the evolution of the metals in a simulation. However, usually no test is performed to check the numerical accuracy of these routines. Actually, since a very vast literature on analytical solutions of the chemical evolution of galaxies and other astronomical objects exists (see, e.g., Tinsley 1980; Matteucci 2001; Hensler & Recchi 2010, and references therein) it is indeed not difficult to benchmark the chemical evolution routines of a chemodynamical code.
The “closed box” model of chemical evolution is based on the following assumptions: (i) the system is uniform and closed (there are no inflows or outflows); (ii) the IMF does not change with time; (iii) the gas is well mixed at any time; and (iv) stars more massive than a certain threshold mass Mthr die instantaneously whereas stars less massive than Mthr live forever. This last assumption, although very restrictive, is fulfilled if we look at specific chemical elements, in particular O and the other α-elements, since they are mostly synthesized by Type II SNe and the (long-living) low- and intermediate-mass stars contribute negligibly to their production.
In a system made up of only gas and stars (DM does not play any role here) we define the quantities, 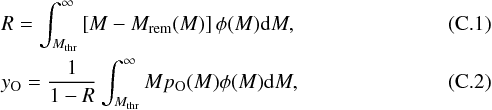 where Mtot = Mgas + Mstars, Mrem(M) is the remnant mass after a star of mass M has died and MpO(M) is the oxygen mass newly synthesized by the star of mass M (pO(M) is the true yield of O). Under the initial condition Mgasf(0) = Const. = Mtot, Mstars(0) = 0, XO(0) = X0 we find that
where Mtot = Mgas + Mstars, Mrem(M) is the remnant mass after a star of mass M has died and MpO(M) is the oxygen mass newly synthesized by the star of mass M (pO(M) is the true yield of O). Under the initial condition Mgasf(0) = Const. = Mtot, Mstars(0) = 0, XO(0) = X0 we find that 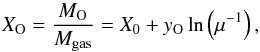 (C.3)
(C.3)
where μ = Mgas/Mtot. This is the famous analytical solution of the closed box model, which only depends on the gas fraction μ.
We have integrated numerically Eqs. (C.1) and (C.2) by using the values of Mrem(M) and MpO(M) tabulated by Woosley & Weaver (1995), using Z = 0.01Z⊙ as initial metallicity. We do not use Z = 0 as initial metallicity for two reasons: firstly, for Z(0) = 0 the cooling is very low and the resulting star formation is too weak; secondly, the yields pO(M) tabulated by Woosley & Weaver (1995) at this metallicity oscillate considerably and that makes the calculation of yO by means of Eq. (C.2) less accurate. By properly choosing a reference volume in the computational box (namely a volume encompassing all the metals produced and advected within a time span of 100 Myr), we can thus calculate the variation of μ with time and, from it, the analytical evolution of the oxygen mass fraction XO with time. This is plotted in Fig. C.1 (solid line), together with the direct numerical calculation of MO/Mgas, averaged over the same volume (dashed line). The two curves only converge after ~30 Myr. This is expected because we have to ensure that Type II SNe of all initial masses contribute to the production of O and ~30 Myr is approximately the lifetime of the less massive SNeII. After a time of ~40 Myr the two curves almost overlap, demonstrating that our chemical routines are able to accurately follow the overall chemical evolution of a galaxy.
 |
Fig. C.1
Evolution with time of the mass fraction of oxygen as derived from the analytical expression Eq. (C.3) (solid line) and from our numerical simulation (dashed line). See text for more detail. |
| Open with DEXTER | |
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


