| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 6 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201526041 | |
| Published online | 11 June 2015 | |
Online material
Appendix A: Supplementary figure
 |
Fig. A.1
Spitzer IRS spectrum of GoHam (continuous black line) and fit (diamonds) using the PAHTAT model. The mid-IR optical depth derived with the model is shown in red. The positions and bandwidths of the VISIR PAH1 and PAH2 filters are indicated. This spectrum includes GoHam a and b, the absorption is dominated by the disk mid-plane. |
| Open with DEXTER | |
Appendix B: Model
Appendix B.1: Model description
We modeled GoHam b as a spherical clump of constant density nb and radius rb. The presence of this clump results in a localized excess of column density with a profile along the cut as a function of position p (Fig. 3) of parabolic form: ![]() (B.1)where pb is the position of GoHam b in the cross cut, that is, 4.25′′. The resulting mid-IR optical depth τb due to GoHam b is then
(B.1)where pb is the position of GoHam b in the cross cut, that is, 4.25′′. The resulting mid-IR optical depth τb due to GoHam b is then ![]() (B.2)where Cext is the dust cross-section per unit of H atom. The mid-IR emission along the cut, corrected for the extinction by GoHam b, can then be recovered by
(B.2)where Cext is the dust cross-section per unit of H atom. The mid-IR emission along the cut, corrected for the extinction by GoHam b, can then be recovered by ![]() (B.3)where IIR(p) is the observed mid-IR emission profile shown in Fig. 3. In addition, we computed the emission in the 13CO(2−1) line as a function of p:
(B.3)where IIR(p) is the observed mid-IR emission profile shown in Fig. 3. In addition, we computed the emission in the 13CO(2−1) line as a function of p: ![]() (B.4)where Δv is the width of the line measured to be 1.7 km s-1, Ωff is the beam-filling factor equal to
(B.4)where Δv is the width of the line measured to be 1.7 km s-1, Ωff is the beam-filling factor equal to ![]() , where a and b are the minor and major axis of the beam, that is, a = 1.14′′ and b = 1.52′′. K is a Gaussian kernel of width equal to b, which is the angular resolution along the cut shown in Fig. 3 (since the major axis of the beam is almost aligned north-south, see Bujarrabal et al. 2009, as is our cross cut).
, where a and b are the minor and major axis of the beam, that is, a = 1.14′′ and b = 1.52′′. K is a Gaussian kernel of width equal to b, which is the angular resolution along the cut shown in Fig. 3 (since the major axis of the beam is almost aligned north-south, see Bujarrabal et al. 2009, as is our cross cut). ![]() is the brightness temperature of the 13CO(2−1) line that is equal to zero for p<pb − rb and p>pb + rb. For the other values of p, the brightness is equal to (optically thick line)
is the brightness temperature of the 13CO(2−1) line that is equal to zero for p<pb − rb and p>pb + rb. For the other values of p, the brightness is equal to (optically thick line) 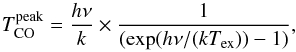 (B.5)where Tex is the excitation temperature, which we fixed at 16 K, that is, the temperature of the disk midplane derived by Bujarrabal et al. (2009). Tex could be higher than this value in the internal parts of the clump, but this is not critical in the estimation of rb , which is a function of the square root of Tex. Overall, the parameters of the model are the density of GoHam b nb, the radius of GoHam b rb, and the dust cross-section Cext. For interstellar dust, the cross section is typically Cext = 2.5 × 10-23 cm2 per H atom at 8.6 and 11.2 μm (Weingartner & Draine 2001). In disks, however, this value is expected to decrease significantly due to grain growth, typically by a factor of 10 in the mid-IR (Andrews et al. 2009; D’Alessio et al. 2001). We therefore considered these two extreme cases and their effects on the parameters derived by the model.
(B.5)where Tex is the excitation temperature, which we fixed at 16 K, that is, the temperature of the disk midplane derived by Bujarrabal et al. (2009). Tex could be higher than this value in the internal parts of the clump, but this is not critical in the estimation of rb , which is a function of the square root of Tex. Overall, the parameters of the model are the density of GoHam b nb, the radius of GoHam b rb, and the dust cross-section Cext. For interstellar dust, the cross section is typically Cext = 2.5 × 10-23 cm2 per H atom at 8.6 and 11.2 μm (Weingartner & Draine 2001). In disks, however, this value is expected to decrease significantly due to grain growth, typically by a factor of 10 in the mid-IR (Andrews et al. 2009; D’Alessio et al. 2001). We therefore considered these two extreme cases and their effects on the parameters derived by the model.
Appendix B.2: Adjustment of the parameters nb and rb
First, rb was adjusted so as to reproduce the observed emission profile of ICO as shown in Fig. 3. Once the value of rb is adjusted, the following step consists of adjusting the parameter nb so as to obtain a symmetric ![]() profile, which is what is expected in a disk without any clump. The result of this procedure is shown in Fig. 3. From the adjusted values of nb and rb, we can derive the clump mass,
profile, which is what is expected in a disk without any clump. The result of this procedure is shown in Fig. 3. From the adjusted values of nb and rb, we can derive the clump mass, ![]() (B.6)where μ is the mean molecular weight and mH the proton mass. The parameters used in the model and those derived from the fit for the two values of Cext are summarized in Table B.2.
(B.6)where μ is the mean molecular weight and mH the proton mass. The parameters used in the model and those derived from the fit for the two values of Cext are summarized in Table B.2.
Main physical parameters of the GoHam disk.
Main physical parameters of the GoHam b candidate protoplanet in the model.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


