| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425057 | |
| Published online | 10 June 2015 | |
Online material
Appendix A: Fit of component C8
Appendix A.1: Introduction
The trajectory of C8 is observed for the first 5 mas, but the map of 1928+738 (Fig. 1) shows that the VLBI jet turns after about 10 mas (Lister & Homan 2005).
In a first step, we tried to find a solution that can explain the long-term turn using a BBH system, in a second step we study the influence of a third black hole or a second BBH system on the solution and correct the coordinates of Kun et al. (2014) for this perturbation. We finally determine the characteristics of the BBH system ejecting C8 using the corrected coordinates.
We used the method developed by Roland et al. (2008) and Roland et al. (2013).
Appendix A.2: Solution using the coordinates of Kun et al. (2014)
The solution obtained corresponds to a VLBI ejection with an asymptotic direction of ΔΞ ≈ 182°.
The main characteristics of the BBH system ejecting C8 are that the two black holes are associated with the components CS and Cg, and the VLBI component C8 is ejected by the VLBI core, that is component Cg (there is no indication that the origin of the ejection is offset). The radius of the BBH system is Rbin ≈ 220 μas ≈ 0.98 pc. The ratio MCg/MCS is ≈4, which is the inverse of the mass ratio found from fitting the coordinates of C1 (Appendix D) and the ratio Tp/Tb is ≈129.
The ratio MCg/MCS is a free parameter of the model and the value MCg/MCS ≈ 4 comes from the fit of the coordinates of C8 (see Fig. A.1).
We find also that the inclination angle is io ≈ 26° and the angle between the accretion disk and the rotation plane of the BBH system is Ω ≈ 9.2°. The bulk Lorentz factor of the VLBI component is γc ≈ 5.5 and the origin of the ejection of the VLBI component is to ≈ 1993.9.
 |
Fig. A.1
Determining of the parameter MCg/MCS. We calculated χ2(MCg/MCS) fitting of the coordinates of C8, which provides the value of the ratio MCg/MCS, i.e. MCg/MCS ≈ 4. |
| Open with DEXTER | |
 |
Fig. A.2
Variations of the distance and the apparent speed of component C8 assuming a constant bulk Lorentz factor γc ≈ 5.5. Top pannel: from the plot of the variations of the distance we deduce the mean speed: 4.86 mas/19.7 yr ≈247 μas/yr. Bottom pannel: despite the high value of the inclination angle, we observe a superluminal motion with a mean speed ≈4.1 c. |
| Open with DEXTER | |
 |
Fig. A.3
Fits of the two coordinates W(t) and N(t) of component C8 of 1928+738. They correspond to the solution with Tp/Tb ≈ 130, MCg/MCS ≈ 4, and io ≈ 26°. The points are the observed coordinates of component C8. The VLBI coordinates and their error bars are taken from Kun et al. (2014). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
| Open with DEXTER | |
The variations of the distance and the apparent speed of component C8 are shown in Fig. A.2. Component C8 moves with a mean apparent speed vap ≈ 4.1 c, a value similar to that obtained by Lister et al. (2013).
The fits of the two coordinates W(t) and N(t) of the component C8 of 1928+738 are shown in Fig. A.3.
Appendix A.3: Determining the solution family
For the inclination angle previously found, i.e., io ≈ 26°, Tp/Tb ≈ 129, MCg/MCS ≈ 4, and Rbin ≈ 220 μas, we gradually varied Va between 0.001 c and 0.45 c. The function χ2(Va) remained constant, indicating a degeneracy of the solution. We deduced the range of variation of the BBH system parameters. They are given in Table A.1.
Table A.1 provides the range of the BBH system parameters ejecting C8. To obtain the final range of the two BBH systems Cg-CS and BHC6-BH4 one has to make the intersection of the ranges of BBH systems parameters found after the fits of C8, C1 and C6 (see Sect. 8).
For Va,Cg = 0.1 c, the total mass of the BBH system ejecting C8 is MCg + MCS ≈ 1.26 × 1010 M⊙.
Appendix A.4: Determining the size of the accretion disk
From the knowledge of the mass ratio MCg/MCS ≈ 4 and the ratio Tp/Tb ≈ 130, we calculated in the previous section the mass of the ejecting black hole MCg, the orbital period Tb, and the precession period Tp for each value of Va.
The rotation period of the accretion disk, Tdisk, is given by Eq. (2). Thus we calculated the rotation period of the accretion disk, and assuming that the mass of the accretion disk is Mdisk ≪ MCg, the size of the accretion disk is given by Eq. (3). We found that the size of the accretion disk does not depend on Va and is Rdisk ≈ 0.028 mas ≈ 0.124 pc.
Ranges for the BBH system parameters ejecting C8.
Appendix B: Circular orbit correction of C8 coordinates
The long-term turn of the VLBI trajectory at about 10 mas can be explained by the BBH system associated with CS and Cg. However, components C5 and C6 are ejected by either a third black hole or a second BBH system, therefore we estimated the influence of the slow rotation of the BBH system Cg-CS around the mass ejecting C5 and C6 and correct the coordinates of C8 for this perturbation to determine of the characteristics of the BBH system ejecting C8 anew.
We call MBH3 the mass ejecting C6, and because the long term turn can partly be explained by the BBH system Cg-CS, we should have MBH3/ (MCg + MCS) < 1. We calculated the circular orbit correction for MBH3/ (MCg + MCS) = 1/10, 1 and 10 and found a non-mirage solution only if MBH3/ (MCg + MCS) < 1. To continue, we therefore arbitrarily chose the ratio MBH3/ (MCg + MCS) = 1/10. To estimate the influence of the choice of this value on the final numerical result one could calculate the circular orbit correction, assuming, for instance, MBH3/ (MCg + MCS) = 1/5. This choice MBH3/ (MCg + MCS) = 1/5 does not change the conclusion but simply the numerical result.
Using the parameters of the solution found in Appendix A, Va = 0.1 c, we have MCg + MCS ≈ 1.26 × 1010 M⊙ and then MBH3 ≈ 1.26 × 109 M⊙. As the distance between the BBH system Cg-CS and BH3 is ≈1.35 mas (see Appendix G), the corresponding orbital period of rotation of Cg-CS around BH3 is Tbin ≈ 11 671 yr. Keeping the geometrical parameters of the solution found in Appendix A, we calculated the trajectory and the tangent to the trajectory. At a given time, knowing the coordinates, WCO(t), NCO(t), of the trajectory of the VLBI component due to the slow circular orbit motion, and the coordinates, Wtan(t), Ntan(t), of the VLBI component along the tangent trajectory, the VLBI coordinates corrected for the slow orbital motion are 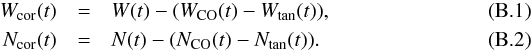 We plot in Fig. B.1 the trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected for the slow orbital motion.
We plot in Fig. B.1 the trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected for the slow orbital motion.
 |
Fig. B.1
Trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected from the slow orbital motion. |
| Open with DEXTER | |
Using the corrected VLBI coordinates, we determined the characteristics of the BBH system ejecting component C8 anew. The result is given in Sect. 5.
Appendix C: Fit of component C7a
We assumed that component C7a belongs to the component family ejected by the black hole Cg. To verify this hypothesis and the consistency of the model found, we used the characteristics of the BBH system Cg-CS and the characteristics of the geometrical parameters of the trajectory of C8 to fit the coordinates of component C7a.
If C7a has been ejected by Cg, we have to fit the coordinates of C7a using the characteristics of the BBH system Cg-CS found in Appendix A, that is, Cg is the origin of the ejection, Tp ≈ 103 998 yr, Tp/Tb ≈ 129, Rbin ≈ 0.220 μas and MCg/MCS ≈ 4, and using the same geometrical parameters than those found to fit the trajectory of C8, that is, ΔΞ ≈ 182°, Ω ≈ 9.2°, Ro ≈ 28 pc and Td ≈ 710 yr.
Then we calculate χ2(io) starting from io ≈ 26° and assuming that the parameters, φo the phase of the precession at to, γc the bulk Lorentz, Ψo the phase of the BBH system at to and to the time origin of the ejection of the component, are free parameters.
The best fit is obtained for io ≈ 20°. The bulk Lorentz factor is γ ≈ 4.1 and the time origin of the ejection is to ≈ 1992. The trajectory of C7a is shown in Fig. C.1. We obtain a very good fit of each coordinate showing that component C7a has been ejected by Cg, the characteristics of the BBH system Cg-CS are correct and the solution found for the ejection of component C8 is the correct one.
 |
Fig. C.1
Trajectory of C7a assuming that it has been ejected by the black hole Cg of the BBH system Cg-CS and using the characteristics of the BBH system Cg-CS obtained during the fit of component C8 and the geometrical parameters of the trajectory of C8. |
| Open with DEXTER | |
Appendix D: Fit of component C1
The solution obtained corresponds to a VLBI ejection with an asymptotic direction of ΔΞ ≈ 182°.
The main characteristics of the solution of the BBH system associated with 1928+738 are that: the VLBI component C1 is not ejected by the VLBI core Cg, but by component CS (there is a weak indication that the origin of the ejection is offset in the direction of CS, this weak indication is due to the lack of observations of C1 for the beginning of the trajectory), the coordinates of CS are XCS ≈ − 0.07 mas and YCS ≈ + 0.21 mas. The radius of the BBH system is Rbin ≈ 220 μas ≈0.98 pc, the ratio MCS/MCg is ≈1/4, which is the inverse of the mass ratio found from fitting the coordinates of C8 (Appendix A) and the ratio Tp/Tb is ≈53.
The ratio MCS/MCg is a free parameter of the model, and the value MCS/MCg ≈ 0.25 comes from the fit of the coordinates of C1 (see Fig. D.1). The fit of C1 provides a mass ratio MCS/MCg ≈ 0.25, which is the inverse of the mass ratio MCg/MCS ≈ 4 obtained from the fit of component C8. This shows that components C1 and C8 are not ejected by the same black hole.
We find that the inclination angle is io ≈ 23°, the angle between the accretion disk and the rotation plane of the BBH system is Ω ≈ 10.3°. The bulk Lorentz factor of the VLBI component is γc ≈ 5.9, and the origin of the ejection of the VLBI component is to ≈ 1967.
 |
Fig. D.1
Determining the parameter MCS/MCg. We calculated χ2(MCS/MCg) fitting of the coordinates of C1, which provides the value of the ratio MCS/MCg, i.e. MCS/MCg ≈ 0.25. |
| Open with DEXTER | |
 |
Fig. D.2
Variations of the distance and the apparent speed of component C1 assuming a constant bulk Lorentz factor γc ≈ 5.9. Top pannel: from the plot of the variations of the distance we deduce the mean speed: 16 mas /46 yr ≈ 350 μas/yr. Bottom pannel: despite the high value of the inclination angle, we observe a superluminal motion with a mean speed ≈4.7 c. |
| Open with DEXTER | |
 |
Fig. D.3
Fit of the two coordinates W(t) and N(t) of component C1 of 1928+738. They correspond to the solution with Tp/Tb ≈ 53, MCS/MCg ≈ 1/4, and io ≈ 23°. The points are the observed coordinates of component C1 that were corrected for the offsets ΔW ≈ − 70 μas and ΔN ≈ + 210 μas. The VLBI coordinates and their error bars are taken from Kun et al. (2014). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
| Open with DEXTER | |
The variations of the distance and the apparent speed of component C1 are shown in Fig. D.2. We find that component C1 moves with a mean apparent speed vap ≈ 4.7c, which is slower than obtained by Lister et al. (2013).
The fit of the two coordinates W(t) and N(t) of the component C1 of 1928+738 is shown in Fig. D.3. The points are the observed coordinates of component C1 that were corrected for the offsets ΔW ≈ − 70 μas and ΔN ≈ + 210 μas, and the red lines are the coordinates of the component trajectory calculated using the BBH model.
Appendix D.1: Determining the solution family
For the inclination angle previously found, that is, io ≈ 23°, Tp/Tb ≈ 53, MCS/MCg ≈ 1/4, and Rbin ≈ 220 μas, we gradually varied Va between 0.001 c and 0.45 c. The function χ2(Va) remained constant, indicating a degeneracy of the solution. We deduced the range of variation of the BBH system parameters. They are given in Table D.1.
Ranges for the BBH system parameters ejecting C1.
Table D.1 provides the range of the BBH system parameters ejecting C1. To obtain the final range of the two BBH systems Cg-CS and BHC6-BH4 one has to make the intersection of the ranges of BBH systems parameters found after the fits of C8, C1 and C6 (see Sect. 8).
For Va,CS = 0.1 c, the total mass of the BBH system ejecting C1 is MCg + MCS ≈ 1.87 × 109 M⊙. The total mass of the BBH system ejecting C1 is the same as the total mass of the BBH system ejecting C8 if Va,CS ≈ 0.232 c, that is, the propagation speeds of the perturbations are different for different trajectory families (see Sect. 8 for the determination of the propagation speeds of the perturbations of three trajectory families if MCg + MCS ≈ 8 × 108 M⊙).
Appendix D.2: Determining the size of the accretion disk
From the knowledge of the mass ratio MCs/MCg ≈ 1/4 and the ratio Tp/Tb ≈ 53, we calculated in the previous section the mass of the ejecting black hole MCS, the orbital period Tb, and the precession period Tp for each value of Va.
The rotation period of the accretion disk, Tdisk, is given by Eq. (2). Thus we calculated the rotation period of the accretion disk, and assuming that the mass of the accretion disk is Mdisk ≪ MCS, the size of the accretion disk is given by Eq. (3). We found that the size of the accretion disk does not depend on Va and is Rdisk ≈ 0.013 mas ≈ 0.058 pc.
Appendix E: Circular orbit correction of C1 coordinates
We calculated the circular orbit correction for MCg + MCS = 10 ∗ (MBHC6 + MBH4).
Using the parameters of the solution found in Appendix D, that is, for Va = 0.1 c, we have MCg + MCS ≈ 1.9 × 109 M⊙ and then MBHC6 + MBH4 ≈ 1.9 × 108 M⊙. As the distance between the two BBH systems is ≈1.35 mas (see Appendix G), the corresponding orbital period of rotation of Cg-CS around BHC6-BH4 is Tbin ≈ 30 320 yr. Keeping the geometrical parameters of the solution found in Appendix D, we calculated the trajectory and the tangent to the trajectory. At a given time, knowing the coordinates, WCO(t), NCO(t), of the trajectory of the VLBI component due to the slow circular orbit motion, and the coordinates, Wtan(t), Ntan(t), of the VLBI component along the tangent trajectory, the VLBI coordinates corrected from the slow orbital motion are given by Eqs. (B.1) and (B.2).
We plot in Fig. E.1 the trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected for the slow orbital motion.
 |
Fig. E.1
Trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected from the slow orbital motion. |
| Open with DEXTER | |
Using the corrected VLBI coordinates, we determined the characteristics of the BBH system ejecting component C1 anew. The result is given in Sect. 6.
Appendix F: Fit of component C9
We assumed that component C9 belongs to the component family ejected by the black hole CS. To verify this hypothesis and the consistency of the model found, we used the characteristics of the BBH system Cg-CS and the characteristics of the geometrical parameters of the trajectory of C1, to fit the coordinates of components C9.
If C9 has been ejected by CS, we have to fit the coordinates of C9 using the characteristics of the BBH system Cg-CS found in Appendix D, that is, CS is the origin of the ejection, Tp ≈ 101 866 yr, Tp/Tb ≈ 53, Rbin ≈ 0.220 μas and MCS/MCg ≈ 0.25. Using the same geometrical parameters than those found to fit the trajectory of C1, that is, ΔΞ ≈ 182°, Ω ≈ 10.3°, Ro ≈ 56 pc and Td ≈ 1278 yr.
To begin, the coordinates of C9 given by Kun et al. (2014) were corrected for the offsets ΔXC9 ≈ − 0.07 mas and ΔYC9 ≈ + 0.21 mas.
Then we calculated χ2(io) starting from io ≈ 23° and assuming that the parameters φo the phase of the precession at to, γc the bulk Lorentz, Ψo the phase of the BBH system at to and to the time origin of the ejection of the component, are free parameters.
The best fit is obtained for io ≈ 20°. The bulk Lorentz factor is γ ≈ 4.3 and the time origin of the ejection is to ≈ 1993.3. The trajectory of C9 is shown in Fig. F.1. We obtain a very good fit of each coordinate showing that component C9 has been ejected by CS, the characteristics of the BBH system Cg-CS are correct and the solution found for the ejection of component C1 is the correct one.
 |
Fig. F.1
Trajectory of C9 assuming that it has been ejected by the black hole CS of the BBH system Cg-CS and using the characteristics of the BBH system Cg-CS obtained during the fit of component C1 and the geometrical parameters of the trajectory of C1. |
| Open with DEXTER | |
Appendix G: Fit of component C6
The component C6 is not ejected by CS or Cg but is ejected by a third black hole. We can show that this third black hole belongs to a second BBH system. We assumed that C6 is ejected by a single black hole and applied the precession model. We studied the solution χ2(io) in the interval 2° ≤ io ≤ 50° and we found that
-
1.
solutions with γ< 30 exist only in the interval 2° ≤ io ≤ 17° (see Fig. G.1);
-
2.
the solution with γ< 30 is a mirage solution, that is, the curve χ2(io) is convex and does not show a minimum; moreover, the bulk Lorentz factor γ diverges when io → 17° (see Fig. G.2); and
-
3.
the precession period corresponding to the solution is 1200 yr ≤ Tprec ≤ 2000 yr. This precession period is too short to be explained by either the Lense-Thirring effect, that is a spinning black hole, or the precession due to the rotation of the black hole ejecting C6 around the BBH system Cg-CS.
However, if the black hole ejecting C6 belongs to a second BBH system, the corresponding solution is no longer a mirage solution, that is, the curve χ2(io) is concave and shows a minimum. We call the black hole ejecting component C6, BHC6, and the second black hole of the second BBH system, BH4.
 |
Fig. G.1
Assuming that component C6 is ejected by a single black hole, we applied the precession model and calculated χ2(io) in the interval 2° ≤ io ≤ 50° starting from 6 different values of the inclination angle, namely io = 5°, 50°, 40°, 35°, 30°, and 20°. Solutions with γ< 30 only exist in the interval 2° ≤ io ≤ 17°. Top panel: curves χ2(io) calculated starting from 6 different values of the inclination angle. Bottom panel: bulk Lorentz factor γ of to the solution χ2(io). |
| Open with DEXTER | |
 |
Fig. G.2
Assuming that component C6 is ejected by a single black hole, we applied the precession model and the solution with γ< 30 is a mirage solution, that is, the curve χ2(io) is convex and it does not show a minimum; moreover, the bulk Lorentz factor γ diverges when io → 17°. Top panel: curve χ2(io) is convex and it does not show a minimum. Bottom panel: bulk Lorentz factor γ diverges when io → 17°. |
| Open with DEXTER | |
In this section we present the characteristics of the BBH system BHC6-BH4 using the coordinates of C6 given by Kun et al. (2014).
The main characteristics of the solution of the BBH system ejecting C6 are that the coordinates of BHC6 are XBHC6 ≈ − 0.11 mas and YBHC6 ≈ − 1.30 mas (assuming that the origin is associated with Cg). None of the two black holes are associated with a stationary VLBI component, meaning that, they are not strong sources. The radius of the BBH system is Rbin ≈ 140 μas ≈ 0.62 pc. Calling the mass of the black hole ejecting C6, MBHC6, and the mass of the other black hole, MBH4, the ratio MBHC6/MBH4 is ≈0.3, and the ratio Tp/Tb is ≈1456.
We find that the inclination angle is io ≈ 21°, the angle between the accretion disk and the rotation plane of the BBH system is Ω ≈ 3.6°. The bulk Lorentz factor of the VLBI component is γc ≈ 4.6, and the time origin of the ejection of the VLBI component is to ≈ 1994.7.
The variations of the distance and the apparent speed of component C6 are shown in Fig. G.3. Component C6 moves with a mean apparent speed vap ≈ 4.4 c, which is similar to the value obtained by Lister et al. (2013).
 |
Fig. G.3
Variations of the distance and the apparent speed of component C6 assuming a constant bulk Lorentz factor γc ≈ 4.6. Top panel: from the plot of the variations of the distance we deduce the mean speed: 3 mas/7.8 yr ≈385 μas/yr. Bottom panel: despite the high value of the inclination angle, we observe a superluminal motion with a mean speed ≈4.4 c. |
| Open with DEXTER | |
The fit of the two coordinates W(t) and N(t) of the component C6 of 1928+738 is shown in Fig. G.4. The points are the observed coordinates of component C6 that were corrected for the offsets ΔW ≈ + 110 μas and ΔN ≈ + 1300 μas, and the red lines are the coordinates of the component trajectory calculated using the BBH model.
 |
Fig. G.4
Fit of the two coordinates W(t) and N(t) of component C6 of 1928+738. They correspond to the solution with Tp/Tb ≈ 1500, MBHC6/MBH4 ≈ 0.3, and io ≈ 21°. The points are the observed coordinates of component C6 that were corrected for the offsets ΔW ≈ + 110 μas and ΔN ≈ + 1300 μas. The VLBI coordinates and their error bars are taken from Kun et al. (2014). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
| Open with DEXTER | |
Appendix G.1: Determining the solution family
For the inclination angle previously found, that is, io ≈ 21°, Tp/Tb ≈ 1500, MBHC6/MBH4 ≈ 0.3, and Rbin ≈ 140 μas, we gradually varied Va between 0.001 c and 0.45 c. The function χ2(Va) remained constant, indicating a degeneracy of the solution. We deduced the range of variation of the BBH system parameters. They are given in Table G.1.
Ranges for the BBH system parameters ejecting C6.
Table G.1 provides the range of the BBH system parameters ejecting C6. To obtain the final range of the two BBH systems Cg-CS and BHC6-BH4 one has to make the intersection of the ranges of BBH systems parameters found after the fits of C8, C1 and C6 (see Sect. 8).
For Va,CS = 0.1 c, the total mass of the BBH system ejecting C1 is MCg + MCS ≈ 1.87 × 109 M⊙. The total mass of the BBH system ejecting C6 is MBHC6 + MBH4 = (MCg + MCS)/10 if Va,BHC6 ≈ 0.030 c, meaning that the propagation speeds of the perturbations are different for different trajectory families (see Sect. 8 for the determination of the propagation speeds of the perturbations of three trajectory families if MCg + MCS ≈ 8 × 108 M⊙).
Appendix G.2: Determining the size of the accretion disk
From the knowledge of the mass ratio MBHC6/MBH4 ≈ 0.3 and the ratio Tp/Tb ≈ 1500, we calculated in the previous section the mass of the ejecting black hole MBHC6, the orbital period Tb, and the precession period Tp for each value of Va.
The rotation period of the accretion disk, Tdisk, is given by Eq. (2). Thus we calculated the rotation period of the accretion disk, and assuming that the mass of the accretion disk is Mdisk ≪ MBHC6, the size of the accretion disk is given by Eq. (3). We found that the size of the accretion disk does not depend on Va and is Rdisk ≈ 0.00096 mas ≈ 0.0043 pc.
Appendix H: Circular orbit correction of C6 coordinates
We calculated the circular orbit correction for MBHC6 + MBH4 = (MCg + MCS)/10.
Using the parameters of the solution found in Appendix G, that is, for Va,C6 = 0.1 c, the mass of the BBH system ejecting C6 is MBHC6 + MBH4 ≈ 2.5 × 109 M⊙ and then MCg + MCS ≈ 2.5 × 1010 M⊙. We could calculate the circular orbit correction for a different value of Va to have a mass MCg + MCS equal to the mass used in Appendix B, but because of the degeneracy of the solution, the result will be the same.
The distance between the two BBH systems is ≈1.35 mas (see Appendix G), the corresponding orbital period of rotation of Cg-CS around BHC6-BH4 is Tbin ≈ 8837 yr. Keeping the geometrical parameters of the solution found in Appendix G, we calculated the trajectory and the tangent to the trajectory. At a given time, knowing the coordinates, WCO(t), NCO(t), of the trajectory of the VLBI component due to the slow circular orbit motion, and the coordinates, Wtan(t), Ntan(t), of the VLBI component along the tangent trajectory, the VLBI coordinates corrected from the slow orbital motion are given by Eqs. (B.1) and (B.2).
We plot in Fig. H.1, the trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected for the slow orbital motion.
 |
Fig. H.1
Trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected from the slow orbital motion. |
| Open with DEXTER | |
Using the corrected VLBI coordinates, we determined of the characteristics of the BBH system ejecting component C6 anew. The result is given in Sect. 7.
Appendix I: Fit of component C5
We assumed that component C5 belongs to the component family ejected by the black hole BHC6. To verify this hypothesis and the consistency of the model found, we used the characteristics of the BBH system BHC6-BH4 and the characteristics of the geometrical parameters of the trajectory of C6 to fit the coordinates of components C5.
If C5 has been ejected by BHC6, we have to fit the coordinates of C5 using the characteristics of the BBH system BHC6-BH4 found in Appendix G, that is BHC6 is the origin of the ejection, Tp ≈ 1 344 545 yr, Tp/Tb ≈ 1456, Rbin ≈ 0.140 μas and MBHC6/MBH4 ≈ 0.3. Using the same geometrical parameters as those found to fit the trajectory of C6, that is ΔΞ ≈ 165°, Ω ≈ 3.6°, Ro ≈ 103 pc and Td ≈ 1500 yr.
To begin, the coordinates of C5 given by Kun et al. (2014) were corrected for the offsets ΔXC5 ≈ + 0.10 mas and ΔYC5 ≈ + 1.30 mas.
Then we calculated χ2(io) starting from io ≈ 21° and assuming that the parameters, φo the phase of the precession at to, γc the bulk Lorentz, Ψo the phase of the BBH system at to and to the time origin of the ejection of the component, are free parameters.
The best fit is obtained for io ≈ 20°. The bulk Lorentz factor is γ ≈ 4.3 and the time origin of the ejection is to ≈ 1991. The trajectory of C5 is shown in Fig. I.1. We obtain a very good fit of each coordinate showing that component C5 has been ejected by BHC6, the characteristics of the BBH system BHC6-BH4 are correct and the solution found for the ejection of component C6 is the correct one.
 |
Fig. I.1
Trajectory of C5 assuming that it has been ejected by the black hole BHC6 of the BBH system BHC6-BH4 and using the characteristics of the BBH system BHC6-BH4 obtained during the fit of component C6 and the geometrical parameters of the trajectory of C6. |
| Open with DEXTER | |
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


