| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425057 | |
| Published online | 10 June 2015 | |
Structure of the nucleus of 1928+738⋆
1 Institut d’Astrophysique, UPMC Univ. Paris 06, CNRS, UMR 7095, 98bis Bd Arago, 75014 Paris, France
e-mail: roland@iap.fr
2 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
3 Department of Experimental Physics, University of Szeged, Dóm tér 9, 6720 Szeged, Hungary
4 Department of Theoretical Physics, University of Szeged, Tisza Lajos krt 84-86, 6720 Szeged, Hungary
5 Laboratoire d’Astrophysique, Observatoire de Grenoble, 414 rue de la Piscine, Domaine Universitaire, 38400 Saint-Martin d’ Hères, France
6 Observatoire de Paris, SYRTE, CNRS, UPMC, CRGS, 75014 Paris, France
Received: 26 September 2014
Accepted: 16 December 2014
Modeling trajectories of VLBI components ejected by the nucleus of 1928+738 shows that the VLBI jet contains three trajectory families, meaning that the VLBI components are ejected from three different origins. The fit of components C1, C6, and C8 indicates that the nucleus of 1928+738 contains two binary black hole systems. The first is associated with the stationary components Cg and CS and is characterized by a radius Rbin,1 ≈ 0.220 mas; both black holes ejected VLBI components almost regularly between 1990 and 2010. The second binary black hole system is not associated with stationary components and is characterized by a radius Rbin,2 ≈ 0.140 mas; it ejected only three VLBI components between 1994 and 1999. The two black hole systems are separated by ≈1.35 mas. We briefly discuss the consequences of the existence of binary black holes systems in radio quasars to make the link between radio quasars and Gaia.
Key words: astrometry / galaxies: jets / galaxies: individual: 1928+738
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
VLBI observations of compact radio sources show that the ejection of VLBI components does not follow a straight line, but wiggles. These observations suggest a precession of the accretion disk. By studying the observed wiggles, several authors reported evidence that nuclei of extragalactic radiosources contain binary black hole (BBH) systems (see Britzen et al. 2001 for 0420-014; Lobanov & Roland 2005 for 3C 345; Roland et al. 2008 for 1803+784; Roland et al. 2013 for 1823+568 and 3C 279; and Roos et al. 1993; Kun et al. 2014; and this work for 1928+738). BBH systems can form when galaxies merge (Begelman et al. 1980), and the detection of BBH systems associated with nuclei of extragalactic radio sources can explain why extragalactic radio sources are associated with elliptical galaxies and why quasars (quasi-stellar radio sources) represent about 5% of the quasi-stellar objects (QSO; Britzen et al. 2001). For a review of massive BBH systems, see Colpi & Dotti (2011).
A BBH system produces three perturbations of the VLBI ejection by
-
1.
the precession of the accretion disk;
-
2.
the motion of the two black holes around the center of gravity of the BBH system; and
-
3.
the possible motion of the BBH system around either a third black hole or another BBH system. This third perturbation produces a change of the VLBI jet direction. It is observed for 1928+738 (Fig. 1), 3C 345 (Lister & Homan 2005), and 3C 454.3 (Lister et al. 2009a), for instance1.
A BBH system induces several consequences, which are that
-
1.
even if the angle between the accretion disk and the rotation plane of the BBH system is zero, the ejection does not follow a straight line (because of the rotation of the black holes around the center of gravity of the BBH system);
-
2.
the two black holes can have accretion disks with different angles with the rotation plane of the BBH system and can eject VLBI components; in this case, we observe two different trajectory families, meaning that the trajectories are ejected from two different origins; a good example of a source showing two tajectory families is 3C 279 (Roland et al. 2013);
-
3.
if the VLBI core is associated with one black hole, and if the VLBI component is ejected by the second black hole, there will be an offset between the VLBI core and the origin of the ejection of the VLBI component; this offset will correspond to the radius of the BBH system; a good example of a component ejected with a large offset from the VLBI core is component C5 of 3C 279 (Roland et al. 2013).
BBH systems affect several domains of astronomy and astrophysics. As indicated in Britzen et al. (2001), nuclei of extragalactic radio sources that contain BBH systems will be good candidates to be observed with low-frequency gravitational wave detectors like eLISA. Britzen et al. (2001) showed that the typical life time of BBH systems associated with nuclei of extragalactic radio sources is between 5 to 10 billion yr, and during the final phase of the collapse they are observable for about 2.5 yr. Britzen et al. (2001) also estimated that there will be about one collapse of BBH systems associated with extragalactic radio sources every 2.5 yr.
BBH systems in nuclei of extragalactic radio sources also have consequences for the realization of celestial frames. The absolute position of radio sources as measured by geodetic VLBI shows a standard deviation (rms) larger than 0.1 mas (see Sect. 8). This floor is partly due to the source structure and constitutes a limit to the stability of a quasar-based celestial frame axes (e.g., Fey et al. 2009; Lambert 2013).
The structure of the paper will be as follows:
-
in Sect. 2 we recall the parameters of the model;
-
In Sect. 3 we report the properties of the radio source 1928+738.
We found from modeling and fitting the ejections of components C1, C5, C6, C7a, C8, and C9 that the nucleus of 1928+738 contains at least three black holes ejecting the VLBI components. We show that the three black holes belong to two BBH systems, namely Cg-CS and BHC6-BH4. The black hole associated with the stationary component CS ejected components C1 and C9, the black hole associated with the stationary component Cg ejected components C8 and C7a, the third black hole BHC6, which ejected C6 and C5, is not detected in radio. In Sect. 4 we explain to which trajectory family the different components belong.
To precisely determine the two BBH systems,
-
1.
we found the characteristics of the BBH system using the coordinates given by Kun et al. (2014);
-
2.
we estimated the perturbation due to the slow rotation of the BBH system Cg-CS around the second BBH system BHC6-BH4 assuming MBHC6 + MBH4 = (MCS + MCg)/10 and corrected the coordinates given by Kun et al. (2014) for this perturbation, finally;
-
3.
we used the corrected coordinates to find the final characteristics of the BBH system.
In Sects. 5 and 6 we give the solution of fitting components C8 and C1 after correction for the slow rotation of the BBH system Cg-CS around the second BBH system BHC6-BH4. In Sect. 7 we provide the solution of fitting component C6 after correction of the slow rotation of the BBH system BHC6-BH4 around the BBH system Cg-CS.
Finally, in Sect. 8 we study the consequences of BBH systems in nuclei of extragalactic radio sources to link radio positions obtained from VLBI observations and Gaia.
The fits of C1, C5, C6, C7a, C8, and C9 using the coordinates given by Kun et al. (2014) and the circular orbit corrections are given in Appendices.
2. Model parameters
A VLBI component is a relativistically ejected cloud of e− − e+. It corresponds to the relativistic beam in the two-fluid model. It follows the perturbed magnetic field lines, which means that its motion is not ballistic. We call x,y, and z the coordinates of a point source component. For details of the model geometry, the two-fluid model, the perturbation of the VLBI ejection, and the coordinates of the VLBI component see Roland et al. (2008) and Roland et al. (2013).
The possible free parameters of the model (for more details see Roland et al. 2013) are
-
io the inclination angle;
-
φo the phase of the precession at t = 0;
-
ΔΞ the rotation angle in the plane perpendicular to the line of sight, also the asymptotic direction of the jet;
-
Ω the opening angle of the precession cone;
-
Ro the maximum amplitude of the perturbation;
-
Tp the precession period of the accretion disk;
-
Td the characteristic time for the damping of the beam perturbation,
-
M1 the mass of the black hole ejecting the radio jet;
-
M2 the mass of the secondary black hole;
-
γc the bulk Lorentz factor of the VLBI component;
-
ψo the phase of the BBH system at t = 0;
-
Tb the period of the BBH system;
-
to the time of the origin of the ejection of the VLBI component;
-
Va the propagation speed of the perturbations;
-
nrad is the number of steps to describe the extension of the VLBI component along the beam;
-
ΔW and ΔN the possible offsets of the origin of the VLBI component.
Because M1 and M2 are free parameters, the ratio M1/M2 is a free parameter as well.
The parameter Va can be used to study the degeneracy of the solutions, therefore we can keep it constant to find the solution. The range of values that we study for parameter Va is 0.001 × c ≤ Va ≤ 0.45 × c2.
The parameter nrad is known when the size of the VLBI component is known.
This means that, practically, the problem we have to solve is a problem with 15 free parameters.
We investigated the different possible scenarios with regard to the sense of the accretion disk rotation and the sense of the orbital rotation of the BBH system. These possibilities correspond to ± ωp(t − z/Va) and ± ωb(t − z/Va). Because the sense of the precession is always opposite to the sense of the orbital motion (Katz 1997), we studied the two cases denoted by +− and −+, where we have ωp(t − z/Va), −ωb(t − z/Va) and −ωp(t − z/Va), ωb(t − z/Va), respectively (ωp and ωb are defined by ωp = 2π/Tp and ωb = 2π/Tb).
3. Radio source 1928+738
The radio source S5 1928+738 is a core-dominated quasar at a redshift of 0.302 (Lawrence et al. 1986). It is associated with a bright optical blazar whose magnitude is mR ≈ 15 to 16 (Healey et al. 2008). The jet morphology is two-sided on kpc scales, the southern part being more pronounced (Murphy et al. 1993). On pc scales the source is one-sided. The map of 1928+738 (Fig. 1) shows that the VLBI jet turns after about 10 mas Lister & Homan (2005). Close to the nucleus, the ejection direction is characterized by ΔΞ ≈ 163°, and after about 10 mas, the VLBI jet turns and has an asymptotic direction characterized by ΔΞ ≈ 182°, which corresponds to the large-scale jet direction observed with the VLA (Murphy et al. 1993). As mentioned in Sect. 1, the VLBI jet turn might be an indication that the nucleus of 1928+738 contains either three black holes or two BBH systems. We show below that components C5 and C6 are ejected by either a third black hole or a second BBH system, which means that we need to estimate the influence of the slow rotation of the BBH system Cg-CS around the mass ejecting C5 and C6, and we need to correct the coordinates given by Kun et al. (2014) for this perturbation to obtain the precise characteristics of the BBH system Cg-CS.
 |
Fig. 1 VLBI image of S5 1928+738 observed on 28 Aug. 2003 and obtained by Lister & Homan (2005). The VLBI jet turns after about 10 mas, and the asymptotic direction is characterized by ΔΞ ≈ 182°, which corresponds to the direction of the large-scale jet observed with the VLA (Murphy et al. 1993). This long-term turn is characteristic of the slow rotation of the BBH system around a third black hole or a second BBH system. We indicate the positions of the two stationary components Cg and CS, which are associated with the two black holes of the BBH system Cg-CS, the position of the black hole BHC6, which ejected components C5, C6, and C7b, and finally, the positions of components C1, C6, and C8 whose ejections have been fitted. |
The VLBI observations of S5 1928+738 used in the present work were taken between 1994.67 and 2013.06 at 15 GHZ in the framework of the MOJAVE Survey, Lister et al. (2009a) and Lister et al. (2009b). Kun et al. (2014) decomposed the brightness distribution of the jet for its components by using the Caltech software package Difmap (Shepherd 1997). The core and the jet components were fitted by circular Gaussian. For details about the error calculation and component identification see Kun et al. (2014). We considered the VLBI core to be associated with component Cg; Kun et al. (2014) considered that the VLBI core is associated with component CS. We therefore corrected the original coordinates of Kun et al. (2014) to take into account this new origin. When we refer to the coordinates of Kun et al. (2014), they correspond to the coordinates corrected to take into account the origin of Cg.
The kinematics of the jet reveals superluminal motion of its components. The jet components show outward motion, except for the northernmost component, component CS, which is observed at a quasi-stationary position compared to the core. Sixteen components appear at 15 GHZ, that is, 10–14 on average in one epoch. The separation of the different components from the core is shown in Fig. 2. The radio map of 1928+738, observed on 28 Aug. 2003, is shown in Fig. 1.
The redshift of the source is zs ≈ 0.302, and using Ho ≈ 71 km s-1 Mpc-1 for the Hubble constant, the luminosity distance of the source is Dl ≈ 1552 Mpc and the angular distance Da = Dl/ (1 + z)2. Thus 1 mas ≈ 4.44 pc.
Observations were performed at 15 GHZ, and the beam size was mostly circular and equal to beam ≈0.5 mas. We adopted as lowest values of the error bars the values (ΔW)min ≈ beam/15 ≈ 34 μas and (ΔN)min ≈ beam/15 ≈ 34 μas for the west and north coordinates, meaning that, when the error bars obtained from the VLBI data reduction were smaller than (ΔW)min or (ΔN)min, they were enlarged to the lowest values (see Roland et al. 2013 for details concerning this choice).
It has been suggested by Lister & Homan (2005) that the lowest values for the error bars should be ≈beam/5, but Roland et al. (2013) showed that the correct lowest values for the error bars adopted at 15 GHz are given by 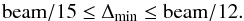 (1)The fit of VLBI coordinates of components of 3C 345 (work in progress) indicates that the adopted values for the lowest values of the error bars, using Eq. (1), are correct for frequencies between 8 GHz and 22 GHz. At lower frequencies, the minimum values may be higher than beam/12 as a result of strong opacity effects, and at 43 GHz, the minimum values are also probably higher (≈20 μas).
(1)The fit of VLBI coordinates of components of 3C 345 (work in progress) indicates that the adopted values for the lowest values of the error bars, using Eq. (1), are correct for frequencies between 8 GHz and 22 GHz. At lower frequencies, the minimum values may be higher than beam/12 as a result of strong opacity effects, and at 43 GHz, the minimum values are also probably higher (≈20 μas).
There are two important points concerning the lowest values used for the error bars. The lowest values were chosen empirically, but the adopted values were justified a posteriori by comparing of the value of χ2 of the final solution and the number of constraints used to make the fit. Indeed, the reduced χ2 has to be close to 1. The adopted lowest value of the error bars also includes typical errors caused by opacity effects, which shift the measured position at different frequencies (Lobanov 1998).
 |
Fig. 2 Separation from the core for the different VLBI components obtained by Kun et al. (2014) for source 1928+738 using from MOJAVE data (Lister et al. 2009b). We fitted components C1, C6, and C8, which have been ejected by black holes Cg, CS, and BHC6. To check the consistency of the model, we fitted components C7a, C9, and C5, which have been ejected by black holes Cg, CS, and BHC6. |
We modeled and fit the coordinates W(t) and N(t) of components C8, C1, and C6 which, as our modeling shows, have been ejected by the three different black holes Cg, CS, and BHC6 (Fig. 2, Sects. 5–7), and to check the consistency of the model, we fit the coordinates of components C7a, C9, and C5, which have been ejected by Cg, CS, and BHC6 (see Appendices C, F and I).
The model and fit of components C8, C1, C6, C7a, C9, and C5 were obtained with the sense of the rotation of the accretion disks −ωp(t − z/Va) and the sense of the orbital rotation of the BBH systems + ωb(t − z/Va).
4. Trajectory families in the VLBI jet
From modeling the ejections of components C8, C1, C6, C7a, C9, and C5, we found that the VLBI jet is a blend of three trajectory families, meaning that the nucleus of 1928+738 contains at least three black holes ejecting VLBI components. The first one corresponds to the VLBI components ejected by CS, the second one corresponds to the VLBI components ejected by Cg, and the third one to the VLBI components ejected by the third black hole, which we call BHC6.
In this section we indicate to which trajectory family the components belong. When no fit of the component has been made we indicate the possible membership of the component using the trajectories, the distance from the core variations, and the flux densities variations, and we give the time origin of the ejection. We used the data and component identifications from Kun et al. (2014).
Component C1: Modeling the ejection of C1, we found after correcting for the circular orbit that the mass ratio MCS/MCg is MCS/MCg ≈ 1/3, indicating that component C1 cannot be ejected by the same black hole as component C8, which means that C1 is not ejected by Cg, but by CS (see Sect. 6, Figs. D.2, D.3 and 3). C1 defines the first trajectory family and has been ejected by the black hole associated with CS, whose coordinates are XCS ≈ − 0.07 mas and YCS ≈ + 0.21 mas, and its to ≈ 1967.
Component C2 follows the same trajectory as C1, meaning that it has probably been ejected by CS, and its to ≈ 1975 (Fig. 3).
Component C3 follows the same trajectory as C8, that is, it has probably been ejected by the black hole associated with Cg, whose coordinates are XCS = 0.0 mas, YCS + 0.0 mas, and its to ≈ 1986 (Fig. 3).
Component C4 probably is a blend of the two components C4a and C4b. The beginning of the trajectory, C4a that is, from 1996 to 2008.6, is the same as C8, which means that it has probably been ejected by Cg and its to ≈ 1987. The end of the trajectory, C4b that is, the last eight points from 2008.9 to 2013.1, is the same as C1, and its to ≈ 1990 (Fig. 3).
Component C5 follows the same trajectory as C6 which is different from C1 and C8. To determine whether that component C5 belongs to the component family ejected by the black hole BHC6 and to check the consistency of the model, we used the characteristics of the BBH system BHC6-BH4 and the characteristics of the geometrical parameters of the trajectory of C6 to fit the coordinates of component C5 (see Figs. I.1 and 4). C5 is ejected by the black hole BHC6, which means that it belongs to the third trajectory family, and its to ≈ 1991.
Component C6 defines the third trajectory family. It is ejected by the third black hole, BHC6, whose coordinates are XBHC6 ≈ − 0.10 mas, YBHC6 ≈ − 1.30 mas (see Sect. 7, Figs. G.3, G.4, 4 and 6), and its to ≈ 1994.5.
Component C7 is a blend of the two components C7a and C7b. The beginning of the trajectory (from 1994.5 to 2002.5), C7a, is the same as C8. To determine whether component C7a belongs to the component family ejected by the black hole Cg and to verify the consistency of the model, we used the characteristics of the BBH system Cg-CS and those of the geometrical parameters of the trajectory of C8 to fit the coordinates of components C7a (see Figs. C.1 and 3). C7a belongs to the second trajectory family. It has been ejected by Cg and its to ≈ 1992. The end of the trajectory, C7b, is the same as that of C5 and C6, which means that C7b has been ejected by BHC6, and its to ≈ 1998.5 (Fig. 4).
 |
Fig. 3 Two trajectory families associated with the VLBI components ejected by CS and the VLBI components ejected by Cg. The two families separate clearly after 1 mas. Components C1 and C9 have been ejected by CS and components C2, C4b, and C11b probably by CS. They form the first VLBI trajectory family. Components C8 and C7a have been ejected by Cg, and components C3, C4a, C10 and C11a probably by Cg. They form the second VLBI trajectory family. The VLBI coordinates are taken from Kun et al. (2014). |
Component C8: Modeling the ejection of C8, we found after correcting for the circular orbit that the mass ratio MCg/MCS is MCg/MCS ≈ 3, and there no offset of the origin of the ejection, indicating that component C8 cannot be ejected by the same black hole as component C1, which means that C8 is not ejected by CS, but by Cg (see Sect. 5, Figs. A.2, A.3 and 3). C8 defines the second trajectory family and has been ejected by Cg and its to ≈ 1993.8.
Component C9 follows the same trajectory as C1. To determine whether component C9 belongs to the component family ejected by the black hole CS and to verify the consistency of the model, we used the characteristics of the BBH system Cg-CS and those of the geometrical parameters of the trajectory of C1 to fit the coordinates of components C9 (see Figs. F.1 and 3). C9 belongs to the first trajectory family. It has been ejected by CS, and its to ≈ 1995.
Component C10 follows the same trajectory as C8, meaning that it has been probably ejected by Cg, and its to ≈ 1997.8 (Fig. 3).
Component C11 is a blend of the two components, C11a and C11b. The beginning of the trajectory, C11a, follows the same trajectory as C8, meaning that it has been probably ejected by Cg, and its to ≈ 1998 (Fig. 3). The end of the trajectory, C11b, follows the same trajectory as C9, it has been probably ejected by CS, and its to ≈ 2003 (Fig. 3).
The trajectories of the next components are not long enough to determine whether their trajectories are similar to those of C1 or C8. However, none of then are ejected by BHC6. So, Cg or CS have ejected components C12 to C16. The to of C12 is to ≈ 2002.5, that of C14 is to ≈ 2006.5, that of C15 is to ≈ 2009, and that of C16 is to ≈ 2010. Component C13 may be a blend of two components that have been ejected by Cg or CS, and 2005 ≤ to ≤ 2007.
We found that the VLBI components follow three different trajectory families, meaning that the nucleus of 1928+738 contains at least three black holes. However, we show below that the fit of the ejection of C6 cannot be explained simply by a third black hole, but indicates that C6 is ejected by a second BBH system. This mean that the nucleus of 1928+738 contains two BBH systems. We call Cg and CS the two black holes of the first BBH system and BHC6 and BH4 the two black holes of the second BBH system.
As indicated in Sect. 1, the BBH system Cg-CS orbits the second BBH system BHC6-BH4, therefore we corrected for this slow rotation to precisely determine of the two BBH system parameters.
We modeled and fit the coordinates of components C8, C1, and C6 and deduced the characteristics of the two BBH systems (see Sects. 5–8). To check the consistency of the model, we used the characteristics of the two BBH systems and the geometrical parameters of the trajectories of C8, C1, and C6 to fit the coordinates of components C7a, C9, and C5 which have been ejected by Cg, CS, and BHC6 (see Appendices C, F and I).
 |
Fig. 4 Trajectory family associated with the VLBI components ejected by the third black hole BHC6. Components C5 and C6 have been ejected by BHC6, and C7b has probably been ejected by BHC6. They form the third VLBI trajectory family. The VLBI coordinates are taken from Kun et al. (2014). |
We plot in Fig. 5 the time origin of the component ejected by the three black holes of the nucleus of 1928+738 during the period from 1985 to 2015. We find that there is no obvious periodicity in the ejection time of the VLBI components, black hole BHC6, ejected components only during the period from 1991 to 1999, and black hole Cg ejects about two time more components than black hole CS.
 |
Fig. 5 Time origin of the component ejected by the three black holes of the nucleus of 1928+738 during the period from 1985 to 2015. |
5. Fit of component C8
To precisely determine of the characteristics of the BBH system ejecting component C8, we first found the characteristics of the BBH system Cg-CS using the coordinates of C8 given by Kun et al. (2014), see Appendix A. Then we estimated the perturbation by the slow rotation of the BBH system Cg-CS around the second BBH system BHC6-BH4 assuming MBHC6 + MBH4 = (MCS + MCg)/10 and corrected the coordinates given by (Kun et al. 2014) for this perturbation, see details in Appendix B. Finally, we used the corrected coordinates to find the final characteristics of the BBH system Cg-CS.
Here we present the solution to the fit of the coordinates of C8, which have been corrected for the slow motion of the BBH system Cg-CS around the BBH system BHC6-BH4.
The main characteristics of the BBH system ejecting C8 are that, the VLBI component C8 is ejected by the VLBI core, that is, component Cg (there is no indication of an offset of the origin of the ejection). The two black holes are associated with components CS and Cg, the radius of the BBH system is Rbin ≈ 220 μas ≈0.98 pc. The ratio MCg/MCS is ≈3, which is the inverse of the mass ratio found from fitting the coordinates of C1 (Sect. 6) and the ratio Tp/Tb is ≈107.
The ratio MCg/MCS is a free parameter of the model and is determinated by the fit of the coordinates of C8.
We find also that the inclination angle is io ≈ 18.5° and the asymptotic ejection direction is Ξ ≈ 165°. The angle between the accretion disk and the rotation plane of the BBH system is Ω ≈ 2.7°, and the bulk Lorentz factor of the VLBI component is γc ≈ 5.9. The origin of the ejection of the VLBI component is to ≈ 1993.8.
Compared with the first solution found in Appendix A, this new solution is characterized by a smaller inclination angle, a lower mass ratio MCg/MCS, a smaller angle between the accretion disk and the rotation plane of the BBH system, and an asymptotic direction of the VLBI jet, ΔΞ ≈ 165° indicating that the long-term turn of the VLBI jet observed at about 10 mas is due to the rotation of the BBH system Cg-CS around the BBH system BHC6-BH4.
5.1. Determining the solution family
For the inclination angle previously found, that is, io ≈ 18.5°, Tp/Tb ≈ 107, MCg/MCS ≈ 3, and Rbin ≈ 220 μas, we gradually varied Va between 0.001 c and 0.45 c. The function χ2(Va) remained constant, indicating a degeneracy of the solution. We deduced the range of variation of the BBH system parameters. They are given in Table 1.
Ranges for the BBH system parameters ejecting C8.
Table 1 provides the range of the BBH system parameters ejecting C8. To obtain the final range of the two BBH systems Cg-CS and BHC6-BH4, one has to make the intersection of the ranges of BBH system parameters found after the fits of C8, C1, and C6 (this is described in Sect. 8).
5.2. Determining the size of the accretion disk
From the knowledge of the mass ratio MCg/MCS ≈ 3 and the ratio Tp/Tb ≈ 107, we calculated in the previous section the mass of the ejecting black hole MCg, the orbital period Tb, and the precession period Tp for each value of Va.
The rotation period of the accretion disk, Tdisk, is given by (Britzen et al. 2001) 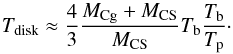 (2)Thus we calculated the rotation period of the accretion disk, and assuming that the mass of the accretion disk is Mdisk ≪ MCg, the size of the accretion disk Rdisk is
(2)Thus we calculated the rotation period of the accretion disk, and assuming that the mass of the accretion disk is Mdisk ≪ MCg, the size of the accretion disk Rdisk is 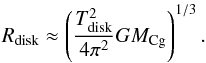 (3)We found that the size of the accretion disk does not depend on Va and is Rdisk ≈ 0.027 mas ≈ 0.120 pc.
(3)We found that the size of the accretion disk does not depend on Va and is Rdisk ≈ 0.027 mas ≈ 0.120 pc.
6. Fit of component C1
To precisely determine of the characteristics of the BBH system ejecting component C1, we found the characteristics of the BBH system Cg-CS using the coordinates of C1 given by Kun et al. (2014), see Appendix D. We also estimated the perturbation due to the slow rotation of the BBH system Cg-CS around the second BBH system BHC6-BH4 assuming MBHC6 + MBH4 = (MCS + MCg)/10 and corrected the coordinates given by Kun et al. (2014) for this perturbation, see see details in Appendix E. Finally, we used the corrected coordinates to find the final characteristics of the BBH system Cg-CS.
Here we present the solution to the fit of the coordinates of C1 which have been corrected from the slow motion of the BBH system Cg-CS around the BBH system BHC6-BH4.
The main characteristics of the BBH system ejecting C1 are that, the VLBI component C1 is not ejected by the VLBI core Cg, but by component CS (there is a weak indication that the origin of the VLBI ejection is offset in the direction of CS, which is due to the lack of observations of C1 for the beginning of the trajectory). The coordinates of CS are XCS ≈ − 0.07 mas and YCS ≈ + 0.21 mas. The radius of the BBH system is Rbin ≈ 220 μas ≈0.98 pc. The ratio MCS/MCg is ≈1/3, which is the inverse of the mass ratio found by fitting the coordinates of C8 (Sect. 5) and the ratio Tp/Tb is ≈31.
The ratio MCS/MCg is a free parameter of the model, and the value MCS/MCg ≈ 1/3 comes from the fit of the coordinates of C1. The fit of C1 provides a mass ratio MCS/MCg ≈ 1/3, which is the inverse of the mass ratio MCg/MCS ≈ 3 obtained from the fit of component C8. This shows that components C1 and C8 are not ejected by the same black hole and demonstrates the consistency of the method. It is remarkable to find this result with only parts of the complete trajectories of C1 and C8.
We find that the inclination angle is io ≈ 19°, and the asymptotic ejection direction is Ξ ≈ 162°. The angle between the accretion disk and the rotation plane of the BBH system is Ω ≈ 2.4°. The bulk Lorentz factor of the VLBI component is γc ≈ 10.2, and the origin of the ejection of the VLBI component is to ≈ 1966.2.
Compared with the first solution found in Appendix D, this new solution is characterized by a smaller inclination angle, a smaller angle between the accretion disk and the rotation plane of the BBH system, and an asymptotic direction of the VLBI jet, ΔΞ ≈ 162°, which indicates that the long-term turn of the VLBI jet observed at about 10 mas is due to the rotation of the BBH system Cg-CS around the BBH system BHC6-BH4.
6.1. Determining the solution family
For the inclination angle previously found, that is, io ≈ 19°, Tp/Tb ≈ 31, MCS/MCg ≈ 1/3, and Rbin ≈ 220 μas, we gradually varied Va between 0.001 c and 0.45 c. The function χ2(Va) remained constant, indicating that the solution is degenerate. We deduced the range of variation of the BBH system parameters. They are given in Table 2.
Ranges for the BBH system parameters ejecting C1.
Table 2 provides the range of the BBH system parameters ejecting C1. To obtain the final range of the two BBH systems Cg-CS and BHC6-BH4, one has to make the intersection of the ranges of BBH systems parameters found after the fits of C8, C1, and C6 (this is described in Sect. 8).
6.2. Determining the size of the accretion disk
From the knowledge of the mass ratio MCs/MCg ≈ 1/3 and the ratio Tp/Tb ≈ 31, we calculated in the previous section the mass of the ejecting black hole MCS, the orbital period Tb, and the precession period Tp for each value of Va.
The rotation period of the accretion disk, Tdisk, is given by Eq. (2). Thus we calculated the rotation period of the accretion disk, and assuming that the mass of the accretion disk is Mdisk ≪ MCS, the size of the accretion disk is given by Eq. (3). We found that the size of the accretion disk does not depend on Va and is Rdisk ≈ 0.021 mas ≈ 0.093 pc.
7. Fit of component C6
The component C6 is not ejected by CS or Cg, but is ejected by a third black hole, which belongs to a second BBH system. We call the black hole ejecting component C6 BHC6 and the fourth black hole BH4. To begin, we assumed that C6 is ejected by a single black hole and applied the precession model. We studied the solution χ2(io) in the interval 2° ≤ io ≤ 50° and found that solutions with γ< 30 only exist, in the interval 2° ≤ io ≤ 17° (see Fig. G.1), and the solution with γ< 30 is a mirage solution, meaning that the curve χ2(io) is convex and does not show a minimum; moreover, the bulk Lorentz factor γ diverges when io → 17° (see Fig. G.2); see more details in Appendix G.
To precisely determine of the characteristics of the BBH system ejecting component C6, we found the characteristics of the BBH system BHC6-BH4 using the coordinates of C6 given by Kun et al. (2014), see Appendix G, then we estimated the perturbation due to the slow rotation of the BBH system BHC6-BH4 around the second BBH system Cg-CS assuming MBHC6 + MBH4 = (MCS + MCg)/10 and corrected the coordinates given by Kun et al. (2014) from this perturbation, see details in Appendix H, finally we used the corrected coordinates to find the final characteristics of the BBH system BHC6-BH4.
The main characteristics of the solution of the BBH system ejecting C6 are that the coordinates of BHC6 are XBHC6 ≈ −0.11 mas and YBHC6 ≈ −1.30 mas (assuming that the origin is associated with Cg). None of the two black holes are associated with a stationary VLBI component, meaning that they are not strong sources. The radius of the BBH system is Rbin ≈ 140 μas ≈0.62 pc. Calling MBHC6 the mass of the black hole ejecting C6 and MBH4 the mass of the other black hole, the ratio MBHC6/MBH4 is ≈0.12, and the ratio Tp/Tb is ≈50.
We find that the inclination angle is io ≈ 23°, and the asymptotic ejection direction is Ξ ≈ 165°. The angle between the accretion disk and the rotation plane of the BBH system is Ω ≈ 1.9°. The bulk Lorentz factor of the VLBI component is γc ≈ 5.7, and the origin of the ejection of the VLBI component is to ≈ 1994.5.
Compared with the first solution found in Appendix G, this new solution is characterized by a similar inclination angle, a smaller angle between the accretion disk and the rotation plane of the BBH system, and a smaller mass ratio MBHC6/MBH4.
7.1. Determining the solution family
For the inclination angle previously found, that is, io ≈ 23°, Tp/Tb ≈ 50, MBHC6/MBH4 ≈ 0.12, and Rbin ≈ 140 μas, we gradually varied Va between 0.001 c and 0.45 c. The function χ2(Va) remained constant, indicating that the solution is degenerate. We deduced the range of variation of the BBH system parameters. They are given in Table 3.
Ranges for the BBH system parameters ejecting C6.
Table 3 provides the range of the BBH system parameters ejecting C6. To obtain the final range of the two BBH systems Cg-CS and BHC6-BH4, one has to make the intersection of the ranges of BBH systems parameters found after the fits of C8, C1, and C6 (this is described in Sect. 8).
7.2. Determining the size of the accretion disk
From the knowledge of the mass ratio MBHC6/MBH4 ≈ 0.12 and the ratio Tp/Tb ≈ 50, we calculated in the previous section the mass of the ejecting black hole MBHC6, the orbital period Tb, and the precession period Tp for each value of Va.
The rotation period of the accretion disk, Tdisk, is given by Eq. (2). Thus we calculated the rotation period of the accretion disk, and assuming that the mass of the accretion disk is Mdisk ≪ MBHC6, the size of the accretion disk is given by Eq. (3). We found that the size of the accretion disk does not depend on Va and is Rdisk ≈ 0.006 mas ≈ 0.027 pc.
8. Discussion and conclusion
Modeling the ejections of components C8, C1, C6, C7a, C9, and C5, we found that the VLBI components follow three different trajectory families, that is, the nucleus of 1928+738 contains at least three black holes. The fit of the ejection of C6 cannot be explained simply by a third black hole but indicates that C6 is ejected by a second BBH system, which means that the nucleus of 1928+738 contains two BBH systems.
To precisely determine the characteristics of the BBH systems, we found the characteristics of the BBH system ejecting a component using the coordinates of the component given by Kun et al. (2014). We estimated the perturbation due to the slow rotation of the BBH system ejecting the component around the second BBH system assuming MBHC6 + MBH4 = (MCS + MCg)/10 and corrected the coordinates given by Kun et al. (2014) for this perturbation. Finally, we used the corrected coordinates to find the final characteristics of the BBH system.
The characteristics of the two BBH systems are the following: the distance between the two BBH systems is ≈1.35 mas ≈6.0 pc. The first BBH system is composed by the components Cg and CS, the radius of the BBH system is Rbin,1 ≈ 220 μas ≈ 0.98 pc, the mass ratio of the two black holes is MCg = 3 × MCS, and the coordinates of the two black holes are XCg = 0, YCg = 0 (by definition) and XCS ≈ − 70 μas, YCS ≈ + 210 μas. The two black holes of the second BBH system, BHC6 and BH4, are not associated with stationary VLBI components, which means that they are weak radio sources, the radius of the BBH system is Rbin,2 ≈ 140 μas ≈ 0.62 pc, the mass ratio of the two black holes is MBHC6 = 0.12 × MBH4 and the coordinates of the black hole BHC6 is XBHC6 ≈ − 100 μas, YCS ≈ − 1300 μas and the coordinates of BH4 are unknown.
 |
Fig. 6 Structure of the nucleus of 1928+738. The nucleus of 1928+738 contains two BBH systems separated by ≈1.35 mas ≈ 6 pc. The first BBH system is composed of components Cg and CS and has a size Rbin,1 ≈ 220 μas ≈ 0.98 pc. The second BBH system is composed of BHC6 and BH4, which are not detected in radio, and it has a size Rbin,2 ≈ 140 μas ≈ 0.62 pc. The position of BH4 is unknown. |
We found that the inclination angle is between io ≈ 18.5° and io ≈ 23.5°.
Combining the constraints obtained using the fits of components C1, C6, and C8, that is, making the intersection of the ranges of the BBH systems parameters given in Tables 1–3, we can deduce the characteristics of the BBH systems associated with the nucleus of 1928+738. They are: the total mass of the BBH system Cg-CS is 3 × 106 M⊙≤ MCg + MCS ≤ 1.2 × 1011 M⊙, and the period of the BBH system Cg-CS is 265 yr ≤ Tbin ≤ 52 200 yr. The size of the accretion disk around Cg is Rdisk,Cg ≈ 0.027 mas ≈0.12 pc and the rotation period of the disk is 13.2 yr ≤ Tdisk,Cg ≤ 2590 yr. The size of the accretion disk around CS is Rdisk,CS ≈ 0.021 mas ≈0.093 pc and the rotation period of the disk is 15.5 yr ≤ Tdisk,Cg ≤ 3040 yr. The total mass of the BBH system BHC6-BH4 is 3 × 105 M⊙≤ MBHC6 + MBH4 ≤ 1.2 × 1010 M⊙, and the period of the BBH system BHC6-BH4 is 420 yr ≤ Tbin ≤ 84 600 yr. The size of the accretion disk around BHC6 is Rdisk,Cg ≈ 0.006 mas ≈0.027 pc and the rotation period of the disk is 12.4 yr ≤ Tdisk,Cg ≤ 2500 yr.
Combining the constraints obtained using the fits of components C1, C6, and C8 reduce the range of the parameters obtained for each fit separately.
Roos et al. (1993) assumed that the mass of the nucleus was ≈108 M⊙, and Kelly & Bechtold (2007) estimated the mass of the nucleus to be ≈8 × 108 M⊙. If we assume MCg + MCS ≈ 8 × 108 M⊙, we therefore have MCg ≈ 6 × 108 M⊙ and MCS ≈ 2 × 108 M⊙. The orbital period of the BBH system (Cg-CS) is Tbin ≈ 3195 yr, and the rotation periods of the accretion disks around Cg and CS are Tdisk,Cg ≈ 159 yr and Tdisk,CS ≈ 186 yr. Assuming MBHC6 + MBH4 ≈ (MCg + MCS)/10 ≈ 8 × 107 M⊙, we have MBHC6 ≈ 8.7 × 106 M⊙ and MBH4 ≈ 7.1 × 107 M⊙. The orbital period of the BBH system (BHC6-BH4) is Tbin ≈ 5130 yr, and the rotation period of the accretion disk around BHC6 is Tdisk,Cg ≈ 152 yr. We found the orbital period of the two black hole systems, with a mean distance ≈1.35 mas, it is Tbin ≈ 46 300 yr. We deduced the propagation speeds of the different trajectory families. The propagation speed of the family corresponding to the ejection of C8 is Va,Cg ≈ 0.045 c, the propagation speed of the family corresponding to the ejection of C1 is Va,CS ≈ 0.064 c, and the propagation speed of the family corresponding to the ejection of C6 is Va,BHC6 ≈ 0.016 c.
During the period of observations, of about 20 years, the black holes associated with CS and Cg almost regularly ejected VLBI components, but the second BBH system ejected only three components within eight years (Fig. 5). Note that there is no periodicity for the ejection of VLBI components.
Kun et al. (2014) found that the flux density of first two mas of the VLBI jet was quasi-periodic with a period of ≈4.5 yr. The first two mas can contain VLBI components ejected by Cg and CS. The blueshift factor corresponding to component C1, ejected by CS, is ≈0.08, and the blueshift factor corresponding to component C8, ejected by Cg, is ≈0.18. The quasi-period observed by Kun et al. (2014) was related to the ejection of new VLBI components, and it corresponds to a value of between ≈25 yr and ≈56 yr in the quasar frame. This period corresponds to a fraction of between 1/8 and 1/3 of the rotation periods of the accretion disks but does not correspond to the orbital period of the BBH system.
For 1928+738, our modeling shows that the nucleus contains two BBH systems on the pc scale. The sizes of the binary systems are Rbin,1 ≈ 0.22 mas ≈0.98 pc, Rbin,2 ≈ 0.14 mas ≈0.62 pc, and the distance between the two BBH systems is ≈1.35 mas ≈6 pc. Deane et al. (2014) reported the detection of a triple system with a size of ≈7.4 kpc with a binary system with a size of ≈140 pc. The interpretation of Deane et al. (2014) has been challenged by Wrobel et al. (2014). For the formation of triple supermassive black hole systems, see Hoffman & Loeb (2007) and Kulkarni & Loeb (2012). As indicated in the Introduction, the ejection of VLBI components can be perturbed by the motion of the BBH system around a third black hole or another BBH system. The VLBI observations show a signature of this kind of perturbation: a triple black hole system or a double BBH system in the nucleus. Close to the nucleus, short-period wiggles are observed, followed by a single turn that changes the ejection direction by a large angle, which can be 45 deg. The best-known sources showing this behavior and containing a triple system or two BBH systems are 3C 345 (work in progress) and 3C 454.3.
If a BBH system forms, it evolves rapidly, after the merging of two galaxies, to reach a critical radius Rbin ~ 1 pc (Yu & Tremaine 2002; Merritt 2004). Then it loses energy by emitting gravitational waves and takes several billions years to collapse (Britzen et al. 2001). This explains that the typical size of the BBH system found in nuclei of extragalactic radio sources is 0.25 pc ≤ Rbin ≤ 1.5 pc (Roland 2014). A typical BBH system with a size of ≈1 pc and containing two similar black holes of 108 M⊙ is characterized by an orbital period of 6600 yr. The mean speed of the two black holes is ≈950 km s-1. If the inclination angle of the source is io ≤ 10°, the difference between the radial speeds of the emission lines of the two cloud systems associated with the two black holes will be ΔVr ≤ 165 km s-1. This result shows why it is difficult to detect BBH systems from studying the broadline spectra of quasars, and that the most efficient method to find BBH systems and to determine their characteristics is to study the kinematics of ejected VLBI components.
 |
Fig. 7 Rms of the coordinate time series of the most frequently observed quasars in the geodetic VLBI monitoring program of the International VLBI Service (IVS) for Geodesy and Astrometry (Lambert 2014) as a function of the number of sessions. |
As shown in Fig. 7, the position of radio sources as measured by geodetic VLBI shows displacements larger than 0.1 mas in rms. This floor is obviously not only due to changes in the radio source structure: several other limiting factors such as the mismodeling of the troposphere wet delay and the noise introduced by site-dependent correlated errors play a non-negligible role. For 1928+738, the size of the BBH system associated with Cg and Cs is 0.22 mas and the distance between the two BBH systems is 1.35 mas. The corresponding coordinate time series (Fig. 8), computed after observations of the geodetic VLBI monitoring program of the International VLBI Service for Geodesy and Astrometry (IVS; Schuh & Behrend 2012; Lambert priv. comm.) is close to 0.3 mas, which agrees with the size of the former BBH system and the fact that this BBH system is much more active than the latter. For geodetic VLBI observations, 1928+738 therefore appears to be a single BBH system of size 0.22 mas. However, the radio center detected by geodetic VLBI will follow the emitting black hole, and significant displacements of about the size of the BBH system are expected. Evidence of such a correspondence between the size of the BBH system, generally larger than 0.1 mas, and the rms of the coordinate time series has been reported in Roland (2014), although this study considered only very few sources and must be extended to other sources. If this holds true, the astrometric precision of VLBI will be limited in the future by the size of the BBH systems, even at frequencies higher than the current 8.6 GHZ band used for the ICRF2. Determing of the numbers and sizes of BBH systems in quasar nuclei will therefore be crucial in the future realization of reference frames, especially for the choice of the so-called defining sources that define the system axes and that should be, in principle, as point-like as possible.
 |
Fig. 8 Coordinate time series (mean removed and shifted by 2 mas for α and −2 mas for δ) of 1928+738 obtained from analyzing data of the geodetic VLBI monitoring program of the IVS (Lambert, priv. comm.). |
The same remarks apply to the Gaia optical reference frame (Perryman et al. 2001). If the nucleus of the radio quasar contains a BBH system and if the two black holes are active, three different cases scenarios are possible:
-
1.
if the radio core and the optical core are associated with the same BH, then the distance between the radio core and the optical core depends on the opacity effect, which will be weak if the inclination angle is small,
-
2.
if the radio core and the optical core are associated with different black holes, then the distance between the radio core and the optical core is about the size of the BBH system (corrected for the possible opacity effect), and
-
3.
if the two black holes are emitting in the optical, then Gaia will provide a mean position between the two optical cores. This position will be different from the positions of the two radio cores.
Because quasars vary strongly and rapidly, during the 5 years of observations of Gaia, the 3 different cases can happen for a given source.
Although 1928+738 is associated with a bright optical quasar and the radio positions of the two radio emitting black holes are known, the high value of the inclination angle implies that the opacity effect can be significant. The two black holes are active and ejecting VLBI components, which hinders using 1928+738 to obtain the precise link between the radio positions and the optical position obtained by Gaia.
Online material
Appendix A: Fit of component C8
Appendix A.1: Introduction
The trajectory of C8 is observed for the first 5 mas, but the map of 1928+738 (Fig. 1) shows that the VLBI jet turns after about 10 mas (Lister & Homan 2005).
In a first step, we tried to find a solution that can explain the long-term turn using a BBH system, in a second step we study the influence of a third black hole or a second BBH system on the solution and correct the coordinates of Kun et al. (2014) for this perturbation. We finally determine the characteristics of the BBH system ejecting C8 using the corrected coordinates.
We used the method developed by Roland et al. (2008) and Roland et al. (2013).
Appendix A.2: Solution using the coordinates of Kun et al. (2014)
The solution obtained corresponds to a VLBI ejection with an asymptotic direction of ΔΞ ≈ 182°.
The main characteristics of the BBH system ejecting C8 are that the two black holes are associated with the components CS and Cg, and the VLBI component C8 is ejected by the VLBI core, that is component Cg (there is no indication that the origin of the ejection is offset). The radius of the BBH system is Rbin ≈ 220 μas ≈ 0.98 pc. The ratio MCg/MCS is ≈4, which is the inverse of the mass ratio found from fitting the coordinates of C1 (Appendix D) and the ratio Tp/Tb is ≈129.
The ratio MCg/MCS is a free parameter of the model and the value MCg/MCS ≈ 4 comes from the fit of the coordinates of C8 (see Fig. A.1).
We find also that the inclination angle is io ≈ 26° and the angle between the accretion disk and the rotation plane of the BBH system is Ω ≈ 9.2°. The bulk Lorentz factor of the VLBI component is γc ≈ 5.5 and the origin of the ejection of the VLBI component is to ≈ 1993.9.
 |
Fig. A.1 Determining of the parameter MCg/MCS. We calculated χ2(MCg/MCS) fitting of the coordinates of C8, which provides the value of the ratio MCg/MCS, i.e. MCg/MCS ≈ 4. |
 |
Fig. A.2 Variations of the distance and the apparent speed of component C8 assuming a constant bulk Lorentz factor γc ≈ 5.5. Top pannel: from the plot of the variations of the distance we deduce the mean speed: 4.86 mas/19.7 yr ≈247 μas/yr. Bottom pannel: despite the high value of the inclination angle, we observe a superluminal motion with a mean speed ≈4.1 c. |
 |
Fig. A.3 Fits of the two coordinates W(t) and N(t) of component C8 of 1928+738. They correspond to the solution with Tp/Tb ≈ 130, MCg/MCS ≈ 4, and io ≈ 26°. The points are the observed coordinates of component C8. The VLBI coordinates and their error bars are taken from Kun et al. (2014). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
The variations of the distance and the apparent speed of component C8 are shown in Fig. A.2. Component C8 moves with a mean apparent speed vap ≈ 4.1 c, a value similar to that obtained by Lister et al. (2013).
The fits of the two coordinates W(t) and N(t) of the component C8 of 1928+738 are shown in Fig. A.3.
Appendix A.3: Determining the solution family
For the inclination angle previously found, i.e., io ≈ 26°, Tp/Tb ≈ 129, MCg/MCS ≈ 4, and Rbin ≈ 220 μas, we gradually varied Va between 0.001 c and 0.45 c. The function χ2(Va) remained constant, indicating a degeneracy of the solution. We deduced the range of variation of the BBH system parameters. They are given in Table A.1.
Table A.1 provides the range of the BBH system parameters ejecting C8. To obtain the final range of the two BBH systems Cg-CS and BHC6-BH4 one has to make the intersection of the ranges of BBH systems parameters found after the fits of C8, C1 and C6 (see Sect. 8).
For Va,Cg = 0.1 c, the total mass of the BBH system ejecting C8 is MCg + MCS ≈ 1.26 × 1010 M⊙.
Appendix A.4: Determining the size of the accretion disk
From the knowledge of the mass ratio MCg/MCS ≈ 4 and the ratio Tp/Tb ≈ 130, we calculated in the previous section the mass of the ejecting black hole MCg, the orbital period Tb, and the precession period Tp for each value of Va.
The rotation period of the accretion disk, Tdisk, is given by Eq. (2). Thus we calculated the rotation period of the accretion disk, and assuming that the mass of the accretion disk is Mdisk ≪ MCg, the size of the accretion disk is given by Eq. (3). We found that the size of the accretion disk does not depend on Va and is Rdisk ≈ 0.028 mas ≈ 0.124 pc.
Ranges for the BBH system parameters ejecting C8.
Appendix B: Circular orbit correction of C8 coordinates
The long-term turn of the VLBI trajectory at about 10 mas can be explained by the BBH system associated with CS and Cg. However, components C5 and C6 are ejected by either a third black hole or a second BBH system, therefore we estimated the influence of the slow rotation of the BBH system Cg-CS around the mass ejecting C5 and C6 and correct the coordinates of C8 for this perturbation to determine of the characteristics of the BBH system ejecting C8 anew.
We call MBH3 the mass ejecting C6, and because the long term turn can partly be explained by the BBH system Cg-CS, we should have MBH3/ (MCg + MCS) < 1. We calculated the circular orbit correction for MBH3/ (MCg + MCS) = 1/10, 1 and 10 and found a non-mirage solution only if MBH3/ (MCg + MCS) < 1. To continue, we therefore arbitrarily chose the ratio MBH3/ (MCg + MCS) = 1/10. To estimate the influence of the choice of this value on the final numerical result one could calculate the circular orbit correction, assuming, for instance, MBH3/ (MCg + MCS) = 1/5. This choice MBH3/ (MCg + MCS) = 1/5 does not change the conclusion but simply the numerical result.
Using the parameters of the solution found in Appendix A, Va = 0.1 c, we have MCg + MCS ≈ 1.26 × 1010 M⊙ and then MBH3 ≈ 1.26 × 109 M⊙. As the distance between the BBH system Cg-CS and BH3 is ≈1.35 mas (see Appendix G), the corresponding orbital period of rotation of Cg-CS around BH3 is Tbin ≈ 11 671 yr. Keeping the geometrical parameters of the solution found in Appendix A, we calculated the trajectory and the tangent to the trajectory. At a given time, knowing the coordinates, WCO(t), NCO(t), of the trajectory of the VLBI component due to the slow circular orbit motion, and the coordinates, Wtan(t), Ntan(t), of the VLBI component along the tangent trajectory, the VLBI coordinates corrected for the slow orbital motion are 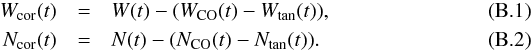 We plot in Fig. B.1 the trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected for the slow orbital motion.
We plot in Fig. B.1 the trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected for the slow orbital motion.
 |
Fig. B.1 Trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected from the slow orbital motion. |
Using the corrected VLBI coordinates, we determined the characteristics of the BBH system ejecting component C8 anew. The result is given in Sect. 5.
Appendix C: Fit of component C7a
We assumed that component C7a belongs to the component family ejected by the black hole Cg. To verify this hypothesis and the consistency of the model found, we used the characteristics of the BBH system Cg-CS and the characteristics of the geometrical parameters of the trajectory of C8 to fit the coordinates of component C7a.
If C7a has been ejected by Cg, we have to fit the coordinates of C7a using the characteristics of the BBH system Cg-CS found in Appendix A, that is, Cg is the origin of the ejection, Tp ≈ 103 998 yr, Tp/Tb ≈ 129, Rbin ≈ 0.220 μas and MCg/MCS ≈ 4, and using the same geometrical parameters than those found to fit the trajectory of C8, that is, ΔΞ ≈ 182°, Ω ≈ 9.2°, Ro ≈ 28 pc and Td ≈ 710 yr.
Then we calculate χ2(io) starting from io ≈ 26° and assuming that the parameters, φo the phase of the precession at to, γc the bulk Lorentz, Ψo the phase of the BBH system at to and to the time origin of the ejection of the component, are free parameters.
The best fit is obtained for io ≈ 20°. The bulk Lorentz factor is γ ≈ 4.1 and the time origin of the ejection is to ≈ 1992. The trajectory of C7a is shown in Fig. C.1. We obtain a very good fit of each coordinate showing that component C7a has been ejected by Cg, the characteristics of the BBH system Cg-CS are correct and the solution found for the ejection of component C8 is the correct one.
 |
Fig. C.1 Trajectory of C7a assuming that it has been ejected by the black hole Cg of the BBH system Cg-CS and using the characteristics of the BBH system Cg-CS obtained during the fit of component C8 and the geometrical parameters of the trajectory of C8. |
Appendix D: Fit of component C1
The solution obtained corresponds to a VLBI ejection with an asymptotic direction of ΔΞ ≈ 182°.
The main characteristics of the solution of the BBH system associated with 1928+738 are that: the VLBI component C1 is not ejected by the VLBI core Cg, but by component CS (there is a weak indication that the origin of the ejection is offset in the direction of CS, this weak indication is due to the lack of observations of C1 for the beginning of the trajectory), the coordinates of CS are XCS ≈ − 0.07 mas and YCS ≈ + 0.21 mas. The radius of the BBH system is Rbin ≈ 220 μas ≈0.98 pc, the ratio MCS/MCg is ≈1/4, which is the inverse of the mass ratio found from fitting the coordinates of C8 (Appendix A) and the ratio Tp/Tb is ≈53.
The ratio MCS/MCg is a free parameter of the model, and the value MCS/MCg ≈ 0.25 comes from the fit of the coordinates of C1 (see Fig. D.1). The fit of C1 provides a mass ratio MCS/MCg ≈ 0.25, which is the inverse of the mass ratio MCg/MCS ≈ 4 obtained from the fit of component C8. This shows that components C1 and C8 are not ejected by the same black hole.
We find that the inclination angle is io ≈ 23°, the angle between the accretion disk and the rotation plane of the BBH system is Ω ≈ 10.3°. The bulk Lorentz factor of the VLBI component is γc ≈ 5.9, and the origin of the ejection of the VLBI component is to ≈ 1967.
 |
Fig. D.1 Determining the parameter MCS/MCg. We calculated χ2(MCS/MCg) fitting of the coordinates of C1, which provides the value of the ratio MCS/MCg, i.e. MCS/MCg ≈ 0.25. |
 |
Fig. D.2 Variations of the distance and the apparent speed of component C1 assuming a constant bulk Lorentz factor γc ≈ 5.9. Top pannel: from the plot of the variations of the distance we deduce the mean speed: 16 mas /46 yr ≈ 350 μas/yr. Bottom pannel: despite the high value of the inclination angle, we observe a superluminal motion with a mean speed ≈4.7 c. |
 |
Fig. D.3 Fit of the two coordinates W(t) and N(t) of component C1 of 1928+738. They correspond to the solution with Tp/Tb ≈ 53, MCS/MCg ≈ 1/4, and io ≈ 23°. The points are the observed coordinates of component C1 that were corrected for the offsets ΔW ≈ − 70 μas and ΔN ≈ + 210 μas. The VLBI coordinates and their error bars are taken from Kun et al. (2014). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
The variations of the distance and the apparent speed of component C1 are shown in Fig. D.2. We find that component C1 moves with a mean apparent speed vap ≈ 4.7c, which is slower than obtained by Lister et al. (2013).
The fit of the two coordinates W(t) and N(t) of the component C1 of 1928+738 is shown in Fig. D.3. The points are the observed coordinates of component C1 that were corrected for the offsets ΔW ≈ − 70 μas and ΔN ≈ + 210 μas, and the red lines are the coordinates of the component trajectory calculated using the BBH model.
Appendix D.1: Determining the solution family
For the inclination angle previously found, that is, io ≈ 23°, Tp/Tb ≈ 53, MCS/MCg ≈ 1/4, and Rbin ≈ 220 μas, we gradually varied Va between 0.001 c and 0.45 c. The function χ2(Va) remained constant, indicating a degeneracy of the solution. We deduced the range of variation of the BBH system parameters. They are given in Table D.1.
Ranges for the BBH system parameters ejecting C1.
Table D.1 provides the range of the BBH system parameters ejecting C1. To obtain the final range of the two BBH systems Cg-CS and BHC6-BH4 one has to make the intersection of the ranges of BBH systems parameters found after the fits of C8, C1 and C6 (see Sect. 8).
For Va,CS = 0.1 c, the total mass of the BBH system ejecting C1 is MCg + MCS ≈ 1.87 × 109 M⊙. The total mass of the BBH system ejecting C1 is the same as the total mass of the BBH system ejecting C8 if Va,CS ≈ 0.232 c, that is, the propagation speeds of the perturbations are different for different trajectory families (see Sect. 8 for the determination of the propagation speeds of the perturbations of three trajectory families if MCg + MCS ≈ 8 × 108 M⊙).
Appendix D.2: Determining the size of the accretion disk
From the knowledge of the mass ratio MCs/MCg ≈ 1/4 and the ratio Tp/Tb ≈ 53, we calculated in the previous section the mass of the ejecting black hole MCS, the orbital period Tb, and the precession period Tp for each value of Va.
The rotation period of the accretion disk, Tdisk, is given by Eq. (2). Thus we calculated the rotation period of the accretion disk, and assuming that the mass of the accretion disk is Mdisk ≪ MCS, the size of the accretion disk is given by Eq. (3). We found that the size of the accretion disk does not depend on Va and is Rdisk ≈ 0.013 mas ≈ 0.058 pc.
Appendix E: Circular orbit correction of C1 coordinates
We calculated the circular orbit correction for MCg + MCS = 10 ∗ (MBHC6 + MBH4).
Using the parameters of the solution found in Appendix D, that is, for Va = 0.1 c, we have MCg + MCS ≈ 1.9 × 109 M⊙ and then MBHC6 + MBH4 ≈ 1.9 × 108 M⊙. As the distance between the two BBH systems is ≈1.35 mas (see Appendix G), the corresponding orbital period of rotation of Cg-CS around BHC6-BH4 is Tbin ≈ 30 320 yr. Keeping the geometrical parameters of the solution found in Appendix D, we calculated the trajectory and the tangent to the trajectory. At a given time, knowing the coordinates, WCO(t), NCO(t), of the trajectory of the VLBI component due to the slow circular orbit motion, and the coordinates, Wtan(t), Ntan(t), of the VLBI component along the tangent trajectory, the VLBI coordinates corrected from the slow orbital motion are given by Eqs. (B.1) and (B.2).
We plot in Fig. E.1 the trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected for the slow orbital motion.
 |
Fig. E.1 Trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected from the slow orbital motion. |
Using the corrected VLBI coordinates, we determined the characteristics of the BBH system ejecting component C1 anew. The result is given in Sect. 6.
Appendix F: Fit of component C9
We assumed that component C9 belongs to the component family ejected by the black hole CS. To verify this hypothesis and the consistency of the model found, we used the characteristics of the BBH system Cg-CS and the characteristics of the geometrical parameters of the trajectory of C1, to fit the coordinates of components C9.
If C9 has been ejected by CS, we have to fit the coordinates of C9 using the characteristics of the BBH system Cg-CS found in Appendix D, that is, CS is the origin of the ejection, Tp ≈ 101 866 yr, Tp/Tb ≈ 53, Rbin ≈ 0.220 μas and MCS/MCg ≈ 0.25. Using the same geometrical parameters than those found to fit the trajectory of C1, that is, ΔΞ ≈ 182°, Ω ≈ 10.3°, Ro ≈ 56 pc and Td ≈ 1278 yr.
To begin, the coordinates of C9 given by Kun et al. (2014) were corrected for the offsets ΔXC9 ≈ − 0.07 mas and ΔYC9 ≈ + 0.21 mas.
Then we calculated χ2(io) starting from io ≈ 23° and assuming that the parameters φo the phase of the precession at to, γc the bulk Lorentz, Ψo the phase of the BBH system at to and to the time origin of the ejection of the component, are free parameters.
The best fit is obtained for io ≈ 20°. The bulk Lorentz factor is γ ≈ 4.3 and the time origin of the ejection is to ≈ 1993.3. The trajectory of C9 is shown in Fig. F.1. We obtain a very good fit of each coordinate showing that component C9 has been ejected by CS, the characteristics of the BBH system Cg-CS are correct and the solution found for the ejection of component C1 is the correct one.
 |
Fig. F.1 Trajectory of C9 assuming that it has been ejected by the black hole CS of the BBH system Cg-CS and using the characteristics of the BBH system Cg-CS obtained during the fit of component C1 and the geometrical parameters of the trajectory of C1. |
Appendix G: Fit of component C6
The component C6 is not ejected by CS or Cg but is ejected by a third black hole. We can show that this third black hole belongs to a second BBH system. We assumed that C6 is ejected by a single black hole and applied the precession model. We studied the solution χ2(io) in the interval 2° ≤ io ≤ 50° and we found that
-
1.
solutions with γ< 30 exist only in the interval 2° ≤ io ≤ 17° (see Fig. G.1);
-
2.
the solution with γ< 30 is a mirage solution, that is, the curve χ2(io) is convex and does not show a minimum; moreover, the bulk Lorentz factor γ diverges when io → 17° (see Fig. G.2); and
-
3.
the precession period corresponding to the solution is 1200 yr ≤ Tprec ≤ 2000 yr. This precession period is too short to be explained by either the Lense-Thirring effect, that is a spinning black hole, or the precession due to the rotation of the black hole ejecting C6 around the BBH system Cg-CS.
However, if the black hole ejecting C6 belongs to a second BBH system, the corresponding solution is no longer a mirage solution, that is, the curve χ2(io) is concave and shows a minimum. We call the black hole ejecting component C6, BHC6, and the second black hole of the second BBH system, BH4.
 |
Fig. G.1 Assuming that component C6 is ejected by a single black hole, we applied the precession model and calculated χ2(io) in the interval 2° ≤ io ≤ 50° starting from 6 different values of the inclination angle, namely io = 5°, 50°, 40°, 35°, 30°, and 20°. Solutions with γ< 30 only exist in the interval 2° ≤ io ≤ 17°. Top panel: curves χ2(io) calculated starting from 6 different values of the inclination angle. Bottom panel: bulk Lorentz factor γ of to the solution χ2(io). |
 |
Fig. G.2 Assuming that component C6 is ejected by a single black hole, we applied the precession model and the solution with γ< 30 is a mirage solution, that is, the curve χ2(io) is convex and it does not show a minimum; moreover, the bulk Lorentz factor γ diverges when io → 17°. Top panel: curve χ2(io) is convex and it does not show a minimum. Bottom panel: bulk Lorentz factor γ diverges when io → 17°. |
In this section we present the characteristics of the BBH system BHC6-BH4 using the coordinates of C6 given by Kun et al. (2014).
The main characteristics of the solution of the BBH system ejecting C6 are that the coordinates of BHC6 are XBHC6 ≈ − 0.11 mas and YBHC6 ≈ − 1.30 mas (assuming that the origin is associated with Cg). None of the two black holes are associated with a stationary VLBI component, meaning that, they are not strong sources. The radius of the BBH system is Rbin ≈ 140 μas ≈ 0.62 pc. Calling the mass of the black hole ejecting C6, MBHC6, and the mass of the other black hole, MBH4, the ratio MBHC6/MBH4 is ≈0.3, and the ratio Tp/Tb is ≈1456.
We find that the inclination angle is io ≈ 21°, the angle between the accretion disk and the rotation plane of the BBH system is Ω ≈ 3.6°. The bulk Lorentz factor of the VLBI component is γc ≈ 4.6, and the time origin of the ejection of the VLBI component is to ≈ 1994.7.
The variations of the distance and the apparent speed of component C6 are shown in Fig. G.3. Component C6 moves with a mean apparent speed vap ≈ 4.4 c, which is similar to the value obtained by Lister et al. (2013).
 |
Fig. G.3 Variations of the distance and the apparent speed of component C6 assuming a constant bulk Lorentz factor γc ≈ 4.6. Top panel: from the plot of the variations of the distance we deduce the mean speed: 3 mas/7.8 yr ≈385 μas/yr. Bottom panel: despite the high value of the inclination angle, we observe a superluminal motion with a mean speed ≈4.4 c. |
The fit of the two coordinates W(t) and N(t) of the component C6 of 1928+738 is shown in Fig. G.4. The points are the observed coordinates of component C6 that were corrected for the offsets ΔW ≈ + 110 μas and ΔN ≈ + 1300 μas, and the red lines are the coordinates of the component trajectory calculated using the BBH model.
 |
Fig. G.4 Fit of the two coordinates W(t) and N(t) of component C6 of 1928+738. They correspond to the solution with Tp/Tb ≈ 1500, MBHC6/MBH4 ≈ 0.3, and io ≈ 21°. The points are the observed coordinates of component C6 that were corrected for the offsets ΔW ≈ + 110 μas and ΔN ≈ + 1300 μas. The VLBI coordinates and their error bars are taken from Kun et al. (2014). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
Appendix G.1: Determining the solution family
For the inclination angle previously found, that is, io ≈ 21°, Tp/Tb ≈ 1500, MBHC6/MBH4 ≈ 0.3, and Rbin ≈ 140 μas, we gradually varied Va between 0.001 c and 0.45 c. The function χ2(Va) remained constant, indicating a degeneracy of the solution. We deduced the range of variation of the BBH system parameters. They are given in Table G.1.
Ranges for the BBH system parameters ejecting C6.
Table G.1 provides the range of the BBH system parameters ejecting C6. To obtain the final range of the two BBH systems Cg-CS and BHC6-BH4 one has to make the intersection of the ranges of BBH systems parameters found after the fits of C8, C1 and C6 (see Sect. 8).
For Va,CS = 0.1 c, the total mass of the BBH system ejecting C1 is MCg + MCS ≈ 1.87 × 109 M⊙. The total mass of the BBH system ejecting C6 is MBHC6 + MBH4 = (MCg + MCS)/10 if Va,BHC6 ≈ 0.030 c, meaning that the propagation speeds of the perturbations are different for different trajectory families (see Sect. 8 for the determination of the propagation speeds of the perturbations of three trajectory families if MCg + MCS ≈ 8 × 108 M⊙).
Appendix G.2: Determining the size of the accretion disk
From the knowledge of the mass ratio MBHC6/MBH4 ≈ 0.3 and the ratio Tp/Tb ≈ 1500, we calculated in the previous section the mass of the ejecting black hole MBHC6, the orbital period Tb, and the precession period Tp for each value of Va.
The rotation period of the accretion disk, Tdisk, is given by Eq. (2). Thus we calculated the rotation period of the accretion disk, and assuming that the mass of the accretion disk is Mdisk ≪ MBHC6, the size of the accretion disk is given by Eq. (3). We found that the size of the accretion disk does not depend on Va and is Rdisk ≈ 0.00096 mas ≈ 0.0043 pc.
Appendix H: Circular orbit correction of C6 coordinates
We calculated the circular orbit correction for MBHC6 + MBH4 = (MCg + MCS)/10.
Using the parameters of the solution found in Appendix G, that is, for Va,C6 = 0.1 c, the mass of the BBH system ejecting C6 is MBHC6 + MBH4 ≈ 2.5 × 109 M⊙ and then MCg + MCS ≈ 2.5 × 1010 M⊙. We could calculate the circular orbit correction for a different value of Va to have a mass MCg + MCS equal to the mass used in Appendix B, but because of the degeneracy of the solution, the result will be the same.
The distance between the two BBH systems is ≈1.35 mas (see Appendix G), the corresponding orbital period of rotation of Cg-CS around BHC6-BH4 is Tbin ≈ 8837 yr. Keeping the geometrical parameters of the solution found in Appendix G, we calculated the trajectory and the tangent to the trajectory. At a given time, knowing the coordinates, WCO(t), NCO(t), of the trajectory of the VLBI component due to the slow circular orbit motion, and the coordinates, Wtan(t), Ntan(t), of the VLBI component along the tangent trajectory, the VLBI coordinates corrected from the slow orbital motion are given by Eqs. (B.1) and (B.2).
We plot in Fig. H.1, the trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected for the slow orbital motion.
 |
Fig. H.1 Trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected from the slow orbital motion. |
Using the corrected VLBI coordinates, we determined of the characteristics of the BBH system ejecting component C6 anew. The result is given in Sect. 7.
Appendix I: Fit of component C5
We assumed that component C5 belongs to the component family ejected by the black hole BHC6. To verify this hypothesis and the consistency of the model found, we used the characteristics of the BBH system BHC6-BH4 and the characteristics of the geometrical parameters of the trajectory of C6 to fit the coordinates of components C5.
If C5 has been ejected by BHC6, we have to fit the coordinates of C5 using the characteristics of the BBH system BHC6-BH4 found in Appendix G, that is BHC6 is the origin of the ejection, Tp ≈ 1 344 545 yr, Tp/Tb ≈ 1456, Rbin ≈ 0.140 μas and MBHC6/MBH4 ≈ 0.3. Using the same geometrical parameters as those found to fit the trajectory of C6, that is ΔΞ ≈ 165°, Ω ≈ 3.6°, Ro ≈ 103 pc and Td ≈ 1500 yr.
To begin, the coordinates of C5 given by Kun et al. (2014) were corrected for the offsets ΔXC5 ≈ + 0.10 mas and ΔYC5 ≈ + 1.30 mas.
Then we calculated χ2(io) starting from io ≈ 21° and assuming that the parameters, φo the phase of the precession at to, γc the bulk Lorentz, Ψo the phase of the BBH system at to and to the time origin of the ejection of the component, are free parameters.
The best fit is obtained for io ≈ 20°. The bulk Lorentz factor is γ ≈ 4.3 and the time origin of the ejection is to ≈ 1991. The trajectory of C5 is shown in Fig. I.1. We obtain a very good fit of each coordinate showing that component C5 has been ejected by BHC6, the characteristics of the BBH system BHC6-BH4 are correct and the solution found for the ejection of component C6 is the correct one.
 |
Fig. I.1 Trajectory of C5 assuming that it has been ejected by the black hole BHC6 of the BBH system BHC6-BH4 and using the characteristics of the BBH system BHC6-BH4 obtained during the fit of component C6 and the geometrical parameters of the trajectory of C6. |
Acknowledgments
We thank the referee for very useful comments, and one of us (J.R.) thanks Bertha Sese for enlightening discussions. This research has made use of data from the MOJAVE database that is maintained by the MOJAVE team (Lister et al. 2009a) and part of this work was supported by the COST Action MP0905 Black Holes in a Violent Universe.
References
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Britzen, S., Roland, J., Laskar, J., et al. 2001, A&A, 374, 784 [Google Scholar]
- Colpi, M., & Dotti, M. 2011, Adv. Sci. Lett., 4, 181 [CrossRef] [Google Scholar]
- Deane, R. P., Paragi, Z., Jarvis, M. J., et al. 2014, Nature, 511, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Fey, A. L., Gordon, D. G., Jacobs, C. S., et al. 2009, in Bundesamts für Kartographie und Geodäsie, ed. Frankfurt am Main [Google Scholar]
- Healey, S. E., Romani, R. W., Cotter, G., et al. 2008, ApJS, 175, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, L., & Loeb, A. 2007, MNRAS, 377, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, J. I. 1997, ApJ, 478, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C., & Bechtold, J. 2007, ApJS, 168, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, G., & Loeb, A. 2012, MNRAS, 422, 1306 [NASA ADS] [CrossRef] [Google Scholar]
- Kun, E., Gabányi, K. É., Karouzos, M., Britzen, S., & Gergely, L. Á. 2014, MNRAS, 445, 1370 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, S. 2013, A&A, 553, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lawrence, C. R., Pearson, T. J., Readhead, A. C. S., & Unwin, S. C. 1986, AJ, 91, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., & Homan, D. C. 2005, AJ, 130, 1389 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Aller, H. D., Aller, M. F., et al. 2009a, AJ, 137, 3718 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009b, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Aller, M. F., Aller, H. D., et al. 2013, AJ, 146, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P. 1998, A&A, 330, 79 [NASA ADS] [Google Scholar]
- Lobanov, A. P., & Roland, J. 2005, A&A, 431, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merritt, D. 2004, Coevolution of Black Holes and Galaxies (Cambridge University Press), 263 [Google Scholar]
- Murphy, D. W., Browne, I. W. A., & Perley, R. A. 1993, MNRAS, 264, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roland, J. 2014, in Proc. Journées 2013: Systèmes de référence spatio-temporels: Scientific developments from highly accurate space-time reference systems, Observatoire de Paris, 16–18 September 2013, ed. N. Capitaine, 28 [Google Scholar]
- Roland, J., Britzen, S., Kudryavtseva, N. A., Witzel, A., & Karouzos, M. 2008, A&A, 483, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roland, J., Britzen, S., Caproni, A., et al. 2013, A&A, 557, A85 [Google Scholar]
- Roos, N., Kaastra, J. S., & Hummel, C. A. 1993, ApJ, 409, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Schuh, H., & Behrend, D. 2012, J. Geodyn., 61, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Shepherd, M. C. 1997, in Astronomical Data Analysis Software and Systems VI, eds. G. Hunt, & H. Payne, ASP Conf. Ser., 125, 77 [Google Scholar]
- Wrobel, J. M., Walker, R. C., & Fu, H. 2014, ApJ, 792, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Q., & Tremaine, S. 2002, MNRAS, 335, 965 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 VLBI image of S5 1928+738 observed on 28 Aug. 2003 and obtained by Lister & Homan (2005). The VLBI jet turns after about 10 mas, and the asymptotic direction is characterized by ΔΞ ≈ 182°, which corresponds to the direction of the large-scale jet observed with the VLA (Murphy et al. 1993). This long-term turn is characteristic of the slow rotation of the BBH system around a third black hole or a second BBH system. We indicate the positions of the two stationary components Cg and CS, which are associated with the two black holes of the BBH system Cg-CS, the position of the black hole BHC6, which ejected components C5, C6, and C7b, and finally, the positions of components C1, C6, and C8 whose ejections have been fitted. |
| In the text | |
 |
Fig. 2 Separation from the core for the different VLBI components obtained by Kun et al. (2014) for source 1928+738 using from MOJAVE data (Lister et al. 2009b). We fitted components C1, C6, and C8, which have been ejected by black holes Cg, CS, and BHC6. To check the consistency of the model, we fitted components C7a, C9, and C5, which have been ejected by black holes Cg, CS, and BHC6. |
| In the text | |
 |
Fig. 3 Two trajectory families associated with the VLBI components ejected by CS and the VLBI components ejected by Cg. The two families separate clearly after 1 mas. Components C1 and C9 have been ejected by CS and components C2, C4b, and C11b probably by CS. They form the first VLBI trajectory family. Components C8 and C7a have been ejected by Cg, and components C3, C4a, C10 and C11a probably by Cg. They form the second VLBI trajectory family. The VLBI coordinates are taken from Kun et al. (2014). |
| In the text | |
 |
Fig. 4 Trajectory family associated with the VLBI components ejected by the third black hole BHC6. Components C5 and C6 have been ejected by BHC6, and C7b has probably been ejected by BHC6. They form the third VLBI trajectory family. The VLBI coordinates are taken from Kun et al. (2014). |
| In the text | |
 |
Fig. 5 Time origin of the component ejected by the three black holes of the nucleus of 1928+738 during the period from 1985 to 2015. |
| In the text | |
 |
Fig. 6 Structure of the nucleus of 1928+738. The nucleus of 1928+738 contains two BBH systems separated by ≈1.35 mas ≈ 6 pc. The first BBH system is composed of components Cg and CS and has a size Rbin,1 ≈ 220 μas ≈ 0.98 pc. The second BBH system is composed of BHC6 and BH4, which are not detected in radio, and it has a size Rbin,2 ≈ 140 μas ≈ 0.62 pc. The position of BH4 is unknown. |
| In the text | |
 |
Fig. 7 Rms of the coordinate time series of the most frequently observed quasars in the geodetic VLBI monitoring program of the International VLBI Service (IVS) for Geodesy and Astrometry (Lambert 2014) as a function of the number of sessions. |
| In the text | |
 |
Fig. 8 Coordinate time series (mean removed and shifted by 2 mas for α and −2 mas for δ) of 1928+738 obtained from analyzing data of the geodetic VLBI monitoring program of the IVS (Lambert, priv. comm.). |
| In the text | |
 |
Fig. A.1 Determining of the parameter MCg/MCS. We calculated χ2(MCg/MCS) fitting of the coordinates of C8, which provides the value of the ratio MCg/MCS, i.e. MCg/MCS ≈ 4. |
| In the text | |
 |
Fig. A.2 Variations of the distance and the apparent speed of component C8 assuming a constant bulk Lorentz factor γc ≈ 5.5. Top pannel: from the plot of the variations of the distance we deduce the mean speed: 4.86 mas/19.7 yr ≈247 μas/yr. Bottom pannel: despite the high value of the inclination angle, we observe a superluminal motion with a mean speed ≈4.1 c. |
| In the text | |
 |
Fig. A.3 Fits of the two coordinates W(t) and N(t) of component C8 of 1928+738. They correspond to the solution with Tp/Tb ≈ 130, MCg/MCS ≈ 4, and io ≈ 26°. The points are the observed coordinates of component C8. The VLBI coordinates and their error bars are taken from Kun et al. (2014). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
| In the text | |
 |
Fig. B.1 Trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected from the slow orbital motion. |
| In the text | |
 |
Fig. C.1 Trajectory of C7a assuming that it has been ejected by the black hole Cg of the BBH system Cg-CS and using the characteristics of the BBH system Cg-CS obtained during the fit of component C8 and the geometrical parameters of the trajectory of C8. |
| In the text | |
 |
Fig. D.1 Determining the parameter MCS/MCg. We calculated χ2(MCS/MCg) fitting of the coordinates of C1, which provides the value of the ratio MCS/MCg, i.e. MCS/MCg ≈ 0.25. |
| In the text | |
 |
Fig. D.2 Variations of the distance and the apparent speed of component C1 assuming a constant bulk Lorentz factor γc ≈ 5.9. Top pannel: from the plot of the variations of the distance we deduce the mean speed: 16 mas /46 yr ≈ 350 μas/yr. Bottom pannel: despite the high value of the inclination angle, we observe a superluminal motion with a mean speed ≈4.7 c. |
| In the text | |
 |
Fig. D.3 Fit of the two coordinates W(t) and N(t) of component C1 of 1928+738. They correspond to the solution with Tp/Tb ≈ 53, MCS/MCg ≈ 1/4, and io ≈ 23°. The points are the observed coordinates of component C1 that were corrected for the offsets ΔW ≈ − 70 μas and ΔN ≈ + 210 μas. The VLBI coordinates and their error bars are taken from Kun et al. (2014). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
| In the text | |
 |
Fig. E.1 Trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected from the slow orbital motion. |
| In the text | |
 |
Fig. F.1 Trajectory of C9 assuming that it has been ejected by the black hole CS of the BBH system Cg-CS and using the characteristics of the BBH system Cg-CS obtained during the fit of component C1 and the geometrical parameters of the trajectory of C1. |
| In the text | |
 |
Fig. G.1 Assuming that component C6 is ejected by a single black hole, we applied the precession model and calculated χ2(io) in the interval 2° ≤ io ≤ 50° starting from 6 different values of the inclination angle, namely io = 5°, 50°, 40°, 35°, 30°, and 20°. Solutions with γ< 30 only exist in the interval 2° ≤ io ≤ 17°. Top panel: curves χ2(io) calculated starting from 6 different values of the inclination angle. Bottom panel: bulk Lorentz factor γ of to the solution χ2(io). |
| In the text | |
 |
Fig. G.2 Assuming that component C6 is ejected by a single black hole, we applied the precession model and the solution with γ< 30 is a mirage solution, that is, the curve χ2(io) is convex and it does not show a minimum; moreover, the bulk Lorentz factor γ diverges when io → 17°. Top panel: curve χ2(io) is convex and it does not show a minimum. Bottom panel: bulk Lorentz factor γ diverges when io → 17°. |
| In the text | |
 |
Fig. G.3 Variations of the distance and the apparent speed of component C6 assuming a constant bulk Lorentz factor γc ≈ 4.6. Top panel: from the plot of the variations of the distance we deduce the mean speed: 3 mas/7.8 yr ≈385 μas/yr. Bottom panel: despite the high value of the inclination angle, we observe a superluminal motion with a mean speed ≈4.4 c. |
| In the text | |
 |
Fig. G.4 Fit of the two coordinates W(t) and N(t) of component C6 of 1928+738. They correspond to the solution with Tp/Tb ≈ 1500, MBHC6/MBH4 ≈ 0.3, and io ≈ 21°. The points are the observed coordinates of component C6 that were corrected for the offsets ΔW ≈ + 110 μas and ΔN ≈ + 1300 μas. The VLBI coordinates and their error bars are taken from Kun et al. (2014). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
| In the text | |
 |
Fig. H.1 Trajectory of the VLBI component due to the slow circular orbit motion, the tangent trajectory, the VLBI coordinates given by Kun et al. (2014), and the coordinates corrected from the slow orbital motion. |
| In the text | |
 |
Fig. I.1 Trajectory of C5 assuming that it has been ejected by the black hole BHC6 of the BBH system BHC6-BH4 and using the characteristics of the BBH system BHC6-BH4 obtained during the fit of component C6 and the geometrical parameters of the trajectory of C6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


