| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 11 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201425016 | |
| Published online | 06 March 2015 | |
Online material
Appendix A: Rigid-body approximation
In this appendix we compare the time scale of motions of galaxies modeled as rigid bodies with the time scale of their internal dynamics. In particular, we consider the (rigid) oscillations of elliptical galaxies (a similar analysis has been carried out in Ciotti & Giampieri 1997) and the precession of spiral galaxies. We show below that internal dynamics is much faster than rigid-body dynamics, thus confirming the results of Ciotti & Dutta (1994) for elliptical galaxies.
Appendix A.1: General case
We assume that the distribution of mass of the galaxy only depends on the elliptical radius ![]() and that its principal axes are aligned with the coordinate axes:
and that its principal axes are aligned with the coordinate axes: 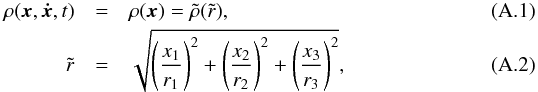 where r1, r2 and r3 are the semi-axes of the ellipsoid (ρ = 0 for
where r1, r2 and r3 are the semi-axes of the ellipsoid (ρ = 0 for ![]() ). Then the inertia tensor is
). Then the inertia tensor is 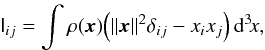 (A.3)where δ is the Kronecker delta, and we placed the center of mass of the galaxy in the origin. With this definition, the moment of inertia
(A.3)where δ is the Kronecker delta, and we placed the center of mass of the galaxy in the origin. With this definition, the moment of inertia ![]() along the unit vector
along the unit vector ![]() is
is ![]() (A.4)For an elliptical mass distribution whose principal axes are parallel to the coordinate axes we obtain
(A.4)For an elliptical mass distribution whose principal axes are parallel to the coordinate axes we obtain 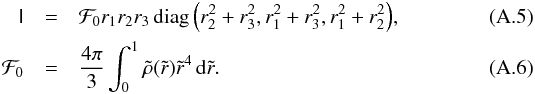 The potential energy W of a body subject to the action of the external field Uext(x) (whose Laplacian is null in the region occupied by the galaxy) is (Jackson 1998)
The potential energy W of a body subject to the action of the external field Uext(x) (whose Laplacian is null in the region occupied by the galaxy) is (Jackson 1998) 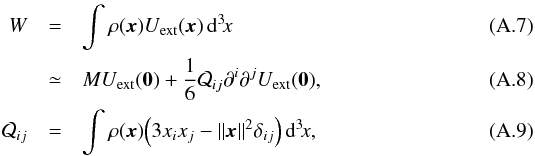 where M and
where M and ![]() are the mass and the quadrupole tensor of the body. For an elliptical mass distribution with principal axes parallel to the coordinate axes we obtain
are the mass and the quadrupole tensor of the body. For an elliptical mass distribution with principal axes parallel to the coordinate axes we obtain 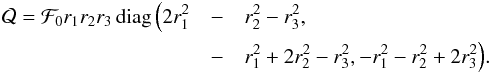 (A.10)
(A.10)
Appendix A.2: Elliptical galaxies: oscillation period
For a Keplerian potential, the galaxy energy is 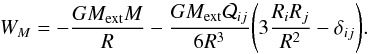 (A.11)Without loss of generality, let
(A.11)Without loss of generality, let ![]() be diagonal and let θ and ϕ be the angles between the
be diagonal and let θ and ϕ be the angles between the ![]() axis and R and between the
axis and R and between the ![]() axis and
axis and ![]() , in a spherical coordinate system (see Fig. A.1). In other words, we consider a coordinate system whose axes are parallel to the principal axes of the galaxy.
, in a spherical coordinate system (see Fig. A.1). In other words, we consider a coordinate system whose axes are parallel to the principal axes of the galaxy.
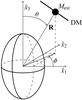 |
Fig. A.1
Spherical coordinate system adopted in the text, Keplerian (Mext) and DM filament cases. |
| Open with DEXTER | |
Having kept ![]() diagonal, we have to rotate the tidal tensor. Considering that
diagonal, we have to rotate the tidal tensor. Considering that ![]() , we find
, we find 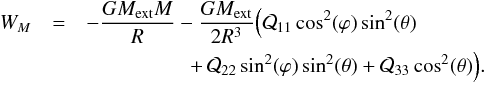 (A.12)We can in principle determine the oscillation equations of the galaxy via the Euler-Lagrange equations, using the correct kinetic energy expression. This approach leads to complex equations and therefore we assume that (i) the elliptical distribution of mass is prolate (i.e., r1 = r2 = req<r3), from which I11 = I22 = Ieq and
(A.12)We can in principle determine the oscillation equations of the galaxy via the Euler-Lagrange equations, using the correct kinetic energy expression. This approach leads to complex equations and therefore we assume that (i) the elliptical distribution of mass is prolate (i.e., r1 = r2 = req<r3), from which I11 = I22 = Ieq and ![]() ; and (ii) there are no initial intrinsic rotation (
; and (ii) there are no initial intrinsic rotation (![]() ) or precession motions; there could be only nutation (
) or precession motions; there could be only nutation (![]() ). Using the Euler-Lagrange equations, we then obtain
). Using the Euler-Lagrange equations, we then obtain ![]() (A.13)We explicitly note that this equation is not self-consistent: in fact, in principle it should be completed with the equations of the relative motion between the galaxy center of mass and the monopole. However, we are not interested in a complete treatment of the problem, but only in an analytic estimate of the time scale of an oscillation. Therefore we assume, without clarifying the physical mechanism that would permit this, that the relative position between the external monopole and the galaxy is fixed, and that only the orientation of the galaxy can vary. With these assumptions, Eq. (A.13)is sufficient to describe the dynamics of the system. To obtain the time scale of an oscillation, we make the small-angle approximation (θ ≪ 1) and recall that
(A.13)We explicitly note that this equation is not self-consistent: in fact, in principle it should be completed with the equations of the relative motion between the galaxy center of mass and the monopole. However, we are not interested in a complete treatment of the problem, but only in an analytic estimate of the time scale of an oscillation. Therefore we assume, without clarifying the physical mechanism that would permit this, that the relative position between the external monopole and the galaxy is fixed, and that only the orientation of the galaxy can vary. With these assumptions, Eq. (A.13)is sufficient to describe the dynamics of the system. To obtain the time scale of an oscillation, we make the small-angle approximation (θ ≪ 1) and recall that ![]() (prolate galaxy), obtaining the pendulum equation. Considering that the components of I and
(prolate galaxy), obtaining the pendulum equation. Considering that the components of I and ![]() are of the same order of magnitude, we find that the period tosc,M of an oscillation is
are of the same order of magnitude, we find that the period tosc,M of an oscillation is 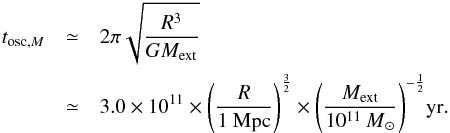 (A.14)We remark that Eq. (A.14)is reminiscent of the expression of the free-fall time tff ∝ (Gρ)− 1/2 ∝ tosc,M × (D/ 2R)3/2, being D the diameter of the galaxy. Using the values adopted here for the external mass Mext = 1011M⊙ and for the distance R = 500 kpc, the period is tosc,M ≃ 1.0 × 1011 yr, which is greater than the age of the Universe5 (the numerical integration of Eq. (A.13)is in accordance with the approximate result).
(A.14)We remark that Eq. (A.14)is reminiscent of the expression of the free-fall time tff ∝ (Gρ)− 1/2 ∝ tosc,M × (D/ 2R)3/2, being D the diameter of the galaxy. Using the values adopted here for the external mass Mext = 1011M⊙ and for the distance R = 500 kpc, the period is tosc,M ≃ 1.0 × 1011 yr, which is greater than the age of the Universe5 (the numerical integration of Eq. (A.13)is in accordance with the approximate result).
This period has to be compared with the time scale on which the shape of a galaxy changes, because of the external gravitational field. A rough estimate of this is the time necessary for a star to travel across the galaxy (e.g., Fleck & Kuhn 2003) ![]() (A.15)where σv is the stellar velocity dispersion and D is the diameter of the galaxy. For D ≃ 40 kpc and σv ≃ 200 km s-1, we obtain tcross,ell ≃ 2 × 108 yr ≪ tosc,M. In other words, an elliptical galaxy, not aligned with the gravitational tidal field, deforms itself before completing a rigid oscillation.
(A.15)where σv is the stellar velocity dispersion and D is the diameter of the galaxy. For D ≃ 40 kpc and σv ≃ 200 km s-1, we obtain tcross,ell ≃ 2 × 108 yr ≪ tosc,M. In other words, an elliptical galaxy, not aligned with the gravitational tidal field, deforms itself before completing a rigid oscillation.
If we consider a DM filament along the ![]() axis, using Eq. (41), we can write the galaxy energy as
axis, using Eq. (41), we can write the galaxy energy as 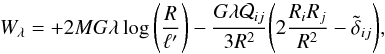 (A.16)where ℓ′ is an arbitrary constant introduced to have an adimensional logarithmic argument, and
(A.16)where ℓ′ is an arbitrary constant introduced to have an adimensional logarithmic argument, and ![]() . As before, we rotate the coordinate frame in such a way that
. As before, we rotate the coordinate frame in such a way that ![]() be diagonal6 (see Fig. A.1), we use spherical coordinates and assume that the galaxy is prolate, that there are no proper rotation nor precession motions, and that the position of the galaxy is fixed. We then obtain
be diagonal6 (see Fig. A.1), we use spherical coordinates and assume that the galaxy is prolate, that there are no proper rotation nor precession motions, and that the position of the galaxy is fixed. We then obtain ![]() (A.17)Using the same approximations as before and Eq. (45), we may estimate the period of a small rigid oscillation of the galaxy
(A.17)Using the same approximations as before and Eq. (45), we may estimate the period of a small rigid oscillation of the galaxy 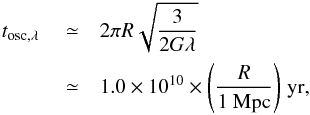 (A.18)which in the case considered throughout the paper (R = 500 kpc) corresponds to 5.0 × 109 yr. This is shorter than the period of oscillation found in the Keplerian case, but nevertheless greater than tcross,ell. We therefore have to drop the rigid-body approximation and deepen the description of elliptical galaxies to account for the internal degrees of freedom, as done in Sect. 3 and Appendix B.
(A.18)which in the case considered throughout the paper (R = 500 kpc) corresponds to 5.0 × 109 yr. This is shorter than the period of oscillation found in the Keplerian case, but nevertheless greater than tcross,ell. We therefore have to drop the rigid-body approximation and deepen the description of elliptical galaxies to account for the internal degrees of freedom, as done in Sect. 3 and Appendix B.
Appendix A.3: Spiral galaxies: precession period
The key feature that distinguishes spiral galaxies from elliptical ones is the dominance of ordered motions over chaotic ones, that is, the characterizing presence of the angular momentum. If we place a rigid body with an angular momentum in an external field, it starts precessing. In this subsection we estimate the precession period for a spiral galaxy, taken as a rigid body.
The precession period tprec of a rotating rigid body is 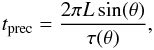 (A.19)where L is the angular momentum of the spiral galaxy, θ is the angle between L and the external force, and τ(θ) is the amount of the momentum of the external force. In spiral galaxies the luminous mass distribution is very different from that of the dark matter; in our calculation we can detach the two contributions because the DM distribution is (approximately) spherical and does not generate a torque on the visible mass, in which we are interested. To determine the total stellar angular momentum L⋆, we can use the rigid-body formula L⋆ = I⋆ 33ω⋆. In spiral galaxies stars at different distances from the center of the galaxy have different angular velocities (ω⋆ = ω⋆(ℓ), where ℓ is the distance from the symmetry axis of the spiral). Therefore it is sensible to use a weighted angular velocity
(A.19)where L is the angular momentum of the spiral galaxy, θ is the angle between L and the external force, and τ(θ) is the amount of the momentum of the external force. In spiral galaxies the luminous mass distribution is very different from that of the dark matter; in our calculation we can detach the two contributions because the DM distribution is (approximately) spherical and does not generate a torque on the visible mass, in which we are interested. To determine the total stellar angular momentum L⋆, we can use the rigid-body formula L⋆ = I⋆ 33ω⋆. In spiral galaxies stars at different distances from the center of the galaxy have different angular velocities (ω⋆ = ω⋆(ℓ), where ℓ is the distance from the symmetry axis of the spiral). Therefore it is sensible to use a weighted angular velocity ![]() , defined as
, defined as 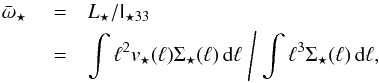 (A.20)where Σ⋆(ℓ) is the projected stellar surface density at distance ℓ from the spiral symmetry axis and v⋆(ℓ) is the stellar tangential velocity. In spiral galaxies, the stellar tangential velocity is approximately constant, v⋆(ℓ) ≃ v⋆, and the stellar column density follows an exponential law with length scale ℓ0, Σ⋆(ℓ) = Σ0exp( − ℓ/ℓ0). We then obtain
(A.20)where Σ⋆(ℓ) is the projected stellar surface density at distance ℓ from the spiral symmetry axis and v⋆(ℓ) is the stellar tangential velocity. In spiral galaxies, the stellar tangential velocity is approximately constant, v⋆(ℓ) ≃ v⋆, and the stellar column density follows an exponential law with length scale ℓ0, Σ⋆(ℓ) = Σ0exp( − ℓ/ℓ0). We then obtain  (A.21)Using this expression in Eqs. (A.13)and (A.17), we find for an oblate galaxy (r3<r1 = r2 = req)
(A.21)Using this expression in Eqs. (A.13)and (A.17), we find for an oblate galaxy (r3<r1 = r2 = req) 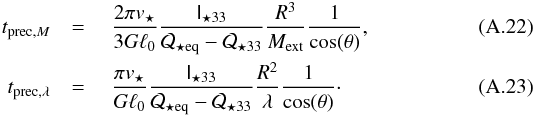 Assuming v⋆ = 200 km s-1 and ℓ0 = 10 kpc, we obtain
Assuming v⋆ = 200 km s-1 and ℓ0 = 10 kpc, we obtain 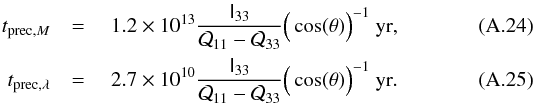 Therefore the time scale is longer than or similar to the age of the Universe, and it is also longer than the deformation time of spiral galaxies (similarly to that of the elliptical galaxy).
Therefore the time scale is longer than or similar to the age of the Universe, and it is also longer than the deformation time of spiral galaxies (similarly to that of the elliptical galaxy).
Appendix B: Equipotential approximation
In Sect. 3 we have obtained the expression of the intrinsic ellipticity of an early-type galaxy subjected to an external tidal field. To do so, we have calculated the luminous quadrupole, making use of the stellar distribution function. In this appendix we present another approach, which is less complete but has the advantage of having a clear and simple physical understanding. In particular, we model the deformation of the galaxy by means of the equipotential surfaces of the total gravitational potential. In this approach, we “assume[s] that the local galaxy density is produced approximately by stars near their zero-velocity surfaces” (Ciotti & Dutta 1994). As in Sect. 3, (i) we start with an unperturbed spherical galaxy; (ii) we take an external tidal potential and add it to the (unperturbed) galaxy potential, thus ignoring the changes in the galaxy potential induced by the deformation of the galaxy (see also Ciotti & Dutta 1994; Bertin & Varri 2008); and (iii) we assume that the galaxy immediately reacts to a change of the external gravity field by modifying its shape accordingly (see Sect. 3 for details).
Appendix B.1: General case
In the absence of external fields, the galaxy potential U0 obeys the Poisson equation ![]() (B.1)where ρ0 is the unperturbed galaxy mass distribution. We now introduce a (weak) external potential Uext, so that U0 → U = U0 + Uext. The introduction of the external field changes the equipotential surfaces of the galaxy. Given a volume
(B.1)where ρ0 is the unperturbed galaxy mass distribution. We now introduce a (weak) external potential Uext, so that U0 → U = U0 + Uext. The introduction of the external field changes the equipotential surfaces of the galaxy. Given a volume ![]() enclosed by a particular equipotential surface
enclosed by a particular equipotential surface ![]() at energy E0 of the unperturbed potential, we consider the corresponding equipotential surface
at energy E0 of the unperturbed potential, we consider the corresponding equipotential surface ![]() for U
for U![]() (B.2)The energy shift δE is chosen in such a way that the mass inside the surface does not change:
(B.2)The energy shift δE is chosen in such a way that the mass inside the surface does not change: 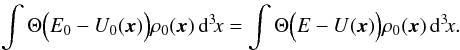 (B.3)A Taylor expansion of the right-hand side of Eq. (B.3)for low δE − Uext gives
(B.3)A Taylor expansion of the right-hand side of Eq. (B.3)for low δE − Uext gives 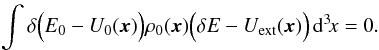 (B.4)Since ρ0 has spherical symmetry, ρ0 and ∇U0 are uniform on
(B.4)Since ρ0 has spherical symmetry, ρ0 and ∇U0 are uniform on ![]() , and we finally obtain
, and we finally obtain 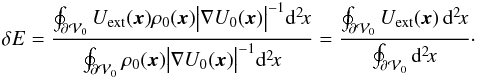 (B.5)If Uext ≡ Utidal = Φijxixj, that is, the external potential is a tidal one, δE is equal to zero, because Φij is traceless and
(B.5)If Uext ≡ Utidal = Φijxixj, that is, the external potential is a tidal one, δE is equal to zero, because Φij is traceless and ![]() has spherical symmetry.
has spherical symmetry.
We use the galaxy logarithmic potential of Eq. (28). If we introduce an external tidal potential, the equipotential surface becomes an ellipsoid (see Fig. B.1). We place the galaxy center at the origin and align the coordinate axes along the eigenvectors of the tidal tensor Φij. Then, we can evaluate the deviation from the circular shape of a particular equipotential surface with radius rmax<rtr by expanding to first order its semi-axis variations δi in Eq. (B.2), 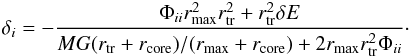 (B.6)We kept for generality δE, even if it vanishes for an external tidal field. Equation (B.6)allows us to compute the intrinsic ellipticity of a particular isophotal of a galaxy subject to a tidal field as observed along any direction. For this, we just have to project an ellipsoid with semi-axes rmax + δ1, rmax + δ2 and rmax + δ3 along the line of sight. For example, if the ellipsoid is observed along
(B.6)We kept for generality δE, even if it vanishes for an external tidal field. Equation (B.6)allows us to compute the intrinsic ellipticity of a particular isophotal of a galaxy subject to a tidal field as observed along any direction. For this, we just have to project an ellipsoid with semi-axes rmax + δ1, rmax + δ2 and rmax + δ3 along the line of sight. For example, if the ellipsoid is observed along ![]() , we would have from Eq. (3)
, we would have from Eq. (3)![]() (B.7)
(B.7)
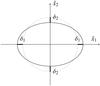 |
Fig. B.1
Schematic representation of the deformation of a two-dimensional contour of an equipotential surface. The dotted line is the unperturbed contour, the solid line the perturbed contour. In the tidal approximation, the variations along the positive and negative directions are the same. |
| Open with DEXTER | |
Appendix B.2: Particular cases
For the Keplerian tidal field (38), placing the external spherical galaxy at R = (R,0,0), using (B.7), and assuming rmax,rtr ≪ R, we obtain (Fig. 2) 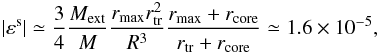 (B.8)where in the last step we used Mext = 1011M⊙, rmax = 10 kpc and R = 500 kpc. We note that εs = O(R-3), and that the ellipticity becomes lower for inner equipotential surfaces.
(B.8)where in the last step we used Mext = 1011M⊙, rmax = 10 kpc and R = 500 kpc. We note that εs = O(R-3), and that the ellipticity becomes lower for inner equipotential surfaces.
For an external DM filament directed along the line of sight and distant R = 500 kpc from the galaxy, if we assume7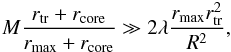 (B.9)we obtain from Eqs. (41), (45)and (B.7)(Fig. 2)
(B.9)we obtain from Eqs. (41), (45)and (B.7)(Fig. 2) 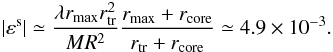 (B.10)We observe that in this case the dependence on the distance is εs = O(R-2); again, inner equipotential surfaces have lower ellipticity.
(B.10)We observe that in this case the dependence on the distance is εs = O(R-2); again, inner equipotential surfaces have lower ellipticity.
The values obtained through the equipotential approximation (B.8)and (B.10)are higher than those obtained through the distribution function method (39)and (46); the reason is that with the equipotential approximation we only consider an outer isopotential surface, which is more deformed than the inner ones. Instead with the distribution function method, more realistically, we are “weighting the ellipticities of the isophotes” of the galaxy from its center to rmax. Equations (B.8)and (B.10)have the same dependence on R as was found with the distribution function method (see Fig. 2).
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


