| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 36 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201323310 | |
| Published online | 11 June 2014 | |
Online material
Herschel observations. All are part of the OT1 seymour 1 program except when specified.
Herschel photometry.
Submm flux at 870 μm with LABOCA in this paper and at 850 μm for all the rest.
Main results from the SED fitting.
Appendix A: Notes on sources
B2 0902+34 (WCD with three detections): this object is the only radio galaxy from our sample to be most likely dominated by synchrotron emission (Archibald et al. 2001). We therefore treat this galaxy as if it were actually a member of the UL class for the purposes of fitting its SED.
4C 23.56 (WD with five detections): this object is the prototypical case where the IR emission is dominated by the emission from the AGN. There are other pieces of evidence from other wavelengths to support this dominance. For instance, rest frame UV shows strong polarisation (Cimatti et al. 1998); the IRAC colours are characteristic of sources dominated by AGN emission in rest frame near-IR (Fig. 13 De Breuck et al. 2010); X-ray emission is also prominent and suggestive of emission from an AGN. This radio source can be seen as having the most extreme AGN contribution to its SED in our sample. We stress that the Mullaney AGN template satisfactorily reproduces the SED of 4C 23.56 without any modification. This indicates that the AGN DecompIR template can be a good representation of AGN emission in our sample.
4C 41.17 (WCD with seven detections): of course, with a radio galaxy dominated by its AGN in the infrared, it would be interesting to have the opposite, a radio galaxy dominated with its IR SED dominated by star formation; 4C 41.17 very likely represents such a case. This radio source has a SB dominated SED, and can be reproduced well by the SB6 template. A more complete SED decomposition confirms this results (Rocca-Volmerange et al. 2013).
Appendix B: AGN or SB dominated?
 |
Fig. B.1
From top to bottom, AGN fraction at 10, 50 and 100 μm against the total infrared luminosity. The colour and symbols correspond to the classes defined in Sect. 3.2. |
| Open with DEXTER | |
We note that fAGN is defined as the ratio SAGN/SSB where S is the flux of the AGN and the SB respectively, at 10, 50, and 100 μm. Figure B.1 plots the 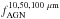 fraction as a function of the total infrared luminosity,
fraction as a function of the total infrared luminosity, 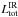 (see Sect. 3.1). This fraction of AGN emission at 10, 50, and 100 μm allow us to check whether the emission at the probed wavelength is dominated by AGN emission or not.
(see Sect. 3.1). This fraction of AGN emission at 10, 50, and 100 μm allow us to check whether the emission at the probed wavelength is dominated by AGN emission or not.
The top plot shows that, independently from the classification introduced in Sect. 3.2, the AGN contributes at least 50% of the flux at 10 μm. In contrast, at 100 μm (bottom plot), the AGN is generally at the ≲10% level. However, we can see that even at such long wavelengths, the contribution of the AGN can, from time to time, be exceptionally high (almost 50%). This last value could refer to extreme objects such as 4C 23.56 or to extended dust emission (Dicken et al. 2010). At 50 μm (middle plot), we can clearly see that AGN can be from dominant to completely negligible. We conclude that even trying to define classes to potentially differentiate between AGN and SB dominated objects from data is almost impossible for high-redshift radio galaxies. Only a SED decomposition as presented in Sect. 4 can finally settle this question.
Appendix C: Bolometric correction
In order to derive AGN intrinsic properties, the AGN bolometric luminosity is needed. Hard X-rays provide the best approximation to the bolometric luminosity as most of the material along the line of sight is optically transparent. We do not possess X-ray measurements for our entire sample and so we make use of the calculated infrared luminosities. Numerous attempts to derive bolometric correction factors have been done (e.g. Elvis et al. 1994; Haas et al. 2003; Marconi et al. 2004; Krawczyk et al. 2013; Hao et al. 2014; Scott & Stewart 2014). Although essential, they are subject to significative variation from object to object. For our SED range, Elvis et al. (1994) and Richards et al. (2006) provide some correction factors depending on the observed wavelength. This correction factor can be as small as 2 and as high as 20 for X-rays, depending mainly on the morphology. Here, we want an approximation of this factor for our sources.
First, we can use a purely geometrical approach. Assuming the torus around AGN to be optically thick at all wavelengths, it absorbs light from across the electromagnetic spectrum and re-radiates in IR. We can use the statistical distribution of Type 1 and Type 2 AGN in the sky (Barthel 1989). The solid angle for an opening angle of 45°corresponds to a factor ~2. This is expected to be the minimum correction.
Second, we can assume that the nuclei in Type 2 and Type 1 AGN are similar. Using a Type 1 radio loud AGN template from Elvis et al. (1994) and assuming that the total IR luminosity does not depend strongly on orientation, the bolometric correction factor is ~6. Doing the same exercise with the Richards et al. (2006) template gives a correction factor of ~5.
Third, some sources in our sample possess X-ray observations (Carilli et al. 2002). Integrating the energy over X-rays, it appears that X-rays do not present the most significative contribution to the bolometric luminosity.
As the radio emission is highly directional (i.e. subject to strong beaming effects), its inclusion in the bolometric factor is highly uncertain. Type 2 AGN SEDs show that the integrated radio energy is roughly at the X-ray level. Its contribution to the total energy should not be the most significant.
Estimation of the bolometric correction is rather difficult and uncertain. Nevertheless, the geometric approach and the moderate contribution from X-rays and radio indicates that most of the light comes from the UV-optical from the central AGN part and the reprocessed light from the dust. Therefore, a factor of 6 seems appropriate in the case of radio galaxies to convert 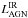 to
to 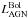 .
.
Appendix D: Summary of the global uncertainties
Since we are using various approximations throughout this paper that can have an impact on this analysis, we summarise here each of these and discuss their possible impact on our interpretation.
-
(i)
The validity of the MBH–MBulge relation at high-redshift de-serves some attention. The first part of this relation is to considerthe estimated stellar mass as the mass of the bulge or spheroid ofindividual galaxies. HST observations have shown that radiogalaxies have elliptical light profiles (van Breugelet al. 1998; Pentericciet al. 1999, 2001; Zirmet al. 2003). Nevertheless, thesedeterminations represent the radially averaged or globalbest-fit light profile with moderate-to-low signal-to-noiseand the possible presence and contribution from substruc-ture and heavily obscured younger disc components cannotbe excluded in the profile fitting (see Hatchet al. 2013). After all, our estimatesof the star formation rates suggest that obscuration could be im-portant and since the gas supporting such intense star formationwould be highly dissipative and could easily be in a disc. However,the stellar masses estimated by De Breuck et al. (2010) are measured in the rest-frame H band, minimizing the impact of extinction and also sampling more appropriately the older population (modulo the contribution from young super-giants). The measured mass can therefore be considered as the total mass of the system and at least, in principle, sensitive to the older generations of stars in the host galaxy (Rocca-Volmerange et al. 2013). Considering the MBH–MBulge relation itself, Jahnke et al. (2009) estimate that the MBH-Mstel relation shows little variation from z = 1.4 to z = 0.
-
(ii)
The radiative efficiency of the accretion, ϵ, is not well-constrained and is certainly not a constant. This factor can vary from 0.06 to 0.42, related to the spin of the black hole (Krolik 1999). There are attempts to constrain the spin of radio loud AGN in the literature. Martínez-Sansigre & Rawlings (2011) show that black hole spins tend to be lower at higher redshift even with the presence of a bimodal distribution. As these constraints are quite poor at high-redshift, it is impossible to draw a conclusion on the possible value of ϵ, but perhaps a range of a few is reasonable (a factor of 3 at most).
-
(iii)
The correction factor to estimate the bolometric luminosity,
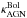 , shows a wide variety of possible values. Pure geometric considerations imply that
, shows a wide variety of possible values. Pure geometric considerations imply that 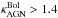 and is unlikely to be >10 for the conversion of IR luminosity to bolometric luminosity (see Appendix C for details). We assumed
and is unlikely to be >10 for the conversion of IR luminosity to bolometric luminosity (see Appendix C for details). We assumed 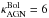 for the ensemble of radio galaxies. This correction is not expected to differ strongly from this value as the energy is mostly radiated in IR in our object and we have now good coverage of this part of the SED. However, a factor as low as 2 is not unreasonable (see Appendix C).
for the ensemble of radio galaxies. This correction is not expected to differ strongly from this value as the energy is mostly radiated in IR in our object and we have now good coverage of this part of the SED. However, a factor as low as 2 is not unreasonable (see Appendix C). -
(iv)
The calculated sSFR are dependant on the canonical law used to transform
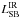 into SFR and the stellar mass. While the Kennicutt (1998) relation seems to represent most star forming galaxies, some discrepancies are expected as it is dependent of the star formation law. Calzetti (2012) lists the impact of the approximation on the different SFR indicators at various wavelengths. This also depends on τ and the adopted IMF; the variation can be a factor of a few (up to ~6). In addition, the IMF can induce a factor of ~2 in the stellar masses estimates (e.g. Marchesini et al. 2009). This effect will move the points horizontally in Fig. 9.
into SFR and the stellar mass. While the Kennicutt (1998) relation seems to represent most star forming galaxies, some discrepancies are expected as it is dependent of the star formation law. Calzetti (2012) lists the impact of the approximation on the different SFR indicators at various wavelengths. This also depends on τ and the adopted IMF; the variation can be a factor of a few (up to ~6). In addition, the IMF can induce a factor of ~2 in the stellar masses estimates (e.g. Marchesini et al. 2009). This effect will move the points horizontally in Fig. 9. -
(v)
The AGN SED can present a wide variation (e.g. Nenkova et al. 2008; Fritz et al. 2006). As mentioned, our generic AGN SED can miss a part of the extended flux from the AGN heating of the NLR (e.g. Dicken et al. 2009; Pier & Krolik 1993). However, as we are dealing with integrated luminosities over the 8–1000 μm range, the calculated
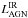 is expected to differ strongly only with a drastic change of the AGN SED which is unlikely (Sect. 4.2). The most probable case would be that we underestimated the AGN contribution; therefore, all corresponding values will be increased by the same factor, increasing the offset from the local MBH–MBulge relation.
is expected to differ strongly only with a drastic change of the AGN SED which is unlikely (Sect. 4.2). The most probable case would be that we underestimated the AGN contribution; therefore, all corresponding values will be increased by the same factor, increasing the offset from the local MBH–MBulge relation.
 |
Fig. D.1
SEDs of the 70 radiogalaxies sorted by RA. IRS and MIPS data taken from De Breuck et al. (2010), PACS and SPIRE data in Table 3, and submm data in Table 4. Filled diamonds are the firm detections (>3σ), open diamonds the weak detections (2σ<Fgal< 3σ), and downward triangles the 3σ upper limits. The red downward triangles mark to the most constraining upper limit. Continuous line represents for fitted components, depending on the class: AGN for WD, SB for CD, and sum of AGN and SB for WCD (as marked in the figure legend). The six stamps correspond to the MIPS (24 μm) and the five Herschel observations when available, with north at the top, east at the left, centred on the radio coordinates of the radio galaxy. Each stamp covers 2 × 2 arcmin. We also overplot the IRS spectra when available for the source (Seymour et al. 2008; Rawlings et al. 2013). |
| Open with DEXTER | |
 |
Fig. D.1
continued. |
| Open with DEXTER | |
 |
Fig. D.1
continued. |
| Open with DEXTER | |
 |
Fig. D.1
continued. |
| Open with DEXTER | |
 |
Fig. D.1
continued. |
| Open with DEXTER | |
 |
Fig. D.1
continued. |
| Open with DEXTER | |
 |
Fig. D.1
continued. |
| Open with DEXTER | |
 |
Fig. D.1
continued. |
| Open with DEXTER | |
 |
Fig. D.1
continued. |
| Open with DEXTER | |
 |
Fig. D.1
continued. |
| Open with DEXTER | |
 |
Fig. D.1
continued. |
| Open with DEXTER | |
 |
Fig. D.1
continued. |
| Open with DEXTER | |
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


