| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 33 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201323248 | |
| Published online | 27 May 2014 | |
Online material
Estimated parameters.
Appendix A: MIR photometry of the HRS
Statistics of the MIR photometry from IRAC and WISE.
For the purpose of this study, we perform MIR photometry at 8, 12, and 22 μm from Spitzer/IRAC and WISE data. We thus present here the flux densities at these wavelengths for all of the HRS galaxies.
Appendix A.1: Spitzer/IRAC 8 μm
One of the output results from Draine & Li (2007) models is the PAH fraction of the total dust mass of a galaxy. Because one of the largest PAH emission features is expected at 7.7 μm, we need the IRAC (Fazio et al. 2004) 8 μm images to constrain this part of the SED.
We retrieved 8 μm images available for 129 HRS galaxies from the Spitzer Data Archive9. The FWHM of the PSF of the IRAC fourth channel is 1.9′′ and the maps have a pixel size of 0.6′′. As a first step, we convert the images from MJy/sr to μJy/pixel, and then remove all of the problematic pixels (NaN) by replacing them by the median value of the surrounding pixels. We remove the stars and background sources visible at 8 μm using the IRAF/imedit task from all of the images. We then extract the flux densities using apertures adapted to each galaxies to take all of the IR emission into account, and minimize the contamination from background features. As the images have small fields of view, we do not estimate residual background emission from circular annuli (as we do for WISE and Herschel/SPIRE photometry) but from the mean value of multiple 10 × 10 pixels boxes around the galaxies. IRAC flux densities need to be corrected for aperture effects to take the diffuse scattering of incoming photons through the IRAC array10 into account. We thus apply aperture corrections on our measurements using the parameters provided in Table 4 of Dale et al. (2007).
For the error calculation, we proceed as in Boselli et al. (2003b) using the same boxes as for the background residual estimation. We thus take two terms into account, one being the pixel-to-pixel error (the mean value of the standard deviation in all of the boxes) and the other one being the sky error due to large scale structures (the standard deviation of the mean values in all of the boxes). To this stochastic error, we add quadratically a calibration error of 10% as indicated in Dale et al. (2007). Galaxies with a signal-to-noise lower than 3 are considered as undetected, and an upper limit of 3σ is given.
In Table A.2, we give the IRAC 8 μm flux densities of the HRS galaxies. A flag is associated with the measurements with the following code: 0 for undetected galaxies, 1 for detected galaxies, and 2 for galaxies for which the measurement suffers from source blending.
 |
Fig. A.1
Comparison between our Spitzer/IRAC 8 μm flux density measurements and Spitzer/IRAC data from the literature. The one-to-one relationship is the solid black line. The ratios between the HRS IRAC 8 μm and the literature 8 μm flux densities are shown in the lower panel. |
| Open with DEXTER | |
MIR photometry of the HRS galaxies.
To check the validity of our IRAC photometry, we search for IRAC 8 μm flux densities already available for HRS galaxies on NED and make the comparison (Fig. A.1). We find eight galaxies in common with the SINGS sample (the Spitzer Infrared Nearby Galaxies Survey, Kennicutt et al. 2003; Dale et al. 2007), one galaxy in common with Panuzzo et al. (2007), and two galaxies to be compared with Willmer et al. (2009). The only point that deviates from the one-to-one relationship is the data point of Panuzzo et al. (2007). It corresponds to the flux density of NGC 4435, which is very close to NGC 4438. This proximity can be problematic as outlined by Panuzzo et al. (2007) and the difference in the measurement may come from how the emission from NGC 4438 is treated. This comparison shows that our measurements are consistent with the 8 μm data taken from the literature with a mean ratio of 0.93 ± 0.04.
Appendix A.2: WISE 12 and 22 μm
NASA’s telescope WISE (Wright et al. 2010) performed an all sky survey in four NIR and MIR bands. For the purpose of this work, we use WISE data at 12 and 22 μm, observed with a resolution of 6.5′′, and 12.0′′, respectively. WISE scanned the sky with 8.8 s exposures at 12 and 22 μm (the W3 and W4 bands), each with a 47′ field of view, providing at least eight exposures per position on the ecliptic and increasing depth toward the ecliptic poles. The individual frames were combined into coadded images with a pixel size of 1.375′′. WISE achieved 5σ point source sensitivities better than 1 and 6 mJy in unconfused regions on the ecliptic in the W3 and W4 bands. Sensitivity improves toward the ecliptic poles due to denser coverage and lower zodiacal background. We retrieve the images of all of the HRS galaxies at 12 and 22 μm from the WISE Science Archive11. We perform aperture photometry using the DS9/Funtools program “Funcnts”. For each galaxy, the aperture, where the flux of the galaxy is estimated, and the background annulus, where the emission from the background is estimated, are defined “manually”. They are chosen to encompass all of the emission from the galaxy and avoid any contamination from foreground/background sources.
 |
Fig. A.2
Comparison between WISE flux density measurements and NIR/MIR ancillary data available from the literature at 12 and 22 μm (left and right panels, respectively). The one-to-one relationship is the solid black line. The WISE to literature flux density ratios are shown in the lower panels. |
| Open with DEXTER | |
To convert the counts extracted into Jy, we use the factors provided by the Explanatory Supplement to the WISE Preliminary Data Release Products12, Sect. II.3.f, 2.9045 × 10-6 Jy/DN and 5.2269 × 10-5 Jy/DN at 12 and 22 μm, respectively. For WISE photometry of extended sources, Jarrett et al. (2013) recommended three corrections to be applied to all measurements. The first one is an aperture correction that accounts for the WISE absolute photometric calibration method using PSF profile fitting. This correction is 0.03 mag and −0.03 mag at 12 and 22 μm, respectively. The second correction is a color correction that accounts for the spectral signature of the source convolved with WISE relative system response (RSR). Because our SED fitting method integrates the models into the filters of the bands before comparing them with the data, we do not need to apply this correction. The third correction comes from a discrepancy between the WISE photometric standard “blue” stars and “red” galaxies related to an error in the W4 RSR, as described in Wright et al. (2010) and Jarrett et al. (2011). Following Jarrett et al. (2013), we apply a correction factor of 0.92 to the 22 μm flux densities of all of the spirals and disk galaxies. This correction is thus applied to HRS galaxies with morphological type of Sa and later.
We determine the errors in the measurements following the method described for the IRAC data. However, because of a correlated noise with a typical length scale larger than 10 pixels, we use 50 × 50 boxes rather than 10 × 10 pixels. Galaxies with a signal-to-noise lower than 3 are considered as undetected, and an upper limit of 3σ is given.
In Table A.2, we give the WISE 12 and 22 μm flux densities of the HRS galaxies. As for IRAC measurements, a flag is provided with the following code: 0 for undetected galaxies, 1 for detected galaxies and 2 for galaxies for which the measurement suffer from sources blending.
To check the validity of our measurements, we compared our results to the NIR and MIR ancillary data available for the HRS galaxies in Fig. A.2. We use the Spitzer/IRAC 8 μm from this work and the Spitzer/MIPS 24 of Bendo et al. (2012b). Even if the 8 μm filter from IRAC and the 12 μm filter from WISE are not overlapping enough to make a reliable comparison, and knowing that the emission process at the two wavelengths differ, we plot the comparison to identify possible outliers and thus possible issues with the photometry. IRAS data at 12 and 25 μm are also available for some of the HRS galaxies (Sanders et al. 2003; Moshir & et al. 1990; Thuan & Sauvage 1992; Soifer et al. 1989; Young et al. 1996). Some shifts in the relation can be due to the different wavelength of the data and the different response curve of the filters. There is a good correlation between IRAS and WISE data at 12 μm, but WISE flux densities tend to be higher than IRAS ones. The mean 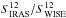 is 1.11 with a standard deviation of 0.79. We note that the relation becomes very dispersed for flux densities below ≈80 mJy. The relation between the IRAC 8 μm and the WISE 12 μm measured in this work is good, with a standard deviation of 0.43 for the IRAC to WISE flux density ratio, and a mean value of the ratio of 1.08. There might be an effect due to the difference of wavelength, however it is difficult to quantify it as the 8 μm lies completely in the PAH emission domain.
is 1.11 with a standard deviation of 0.79. We note that the relation becomes very dispersed for flux densities below ≈80 mJy. The relation between the IRAC 8 μm and the WISE 12 μm measured in this work is good, with a standard deviation of 0.43 for the IRAC to WISE flux density ratio, and a mean value of the ratio of 1.08. There might be an effect due to the difference of wavelength, however it is difficult to quantify it as the 8 μm lies completely in the PAH emission domain.
There is good agreement between MIPS 24 μm and WISE 22 μm measurements with a mean MIPS to WISE flux density ratio of 1.22 ± 0.44. Even if very dispersed, the relation between IRAS 25 μm and WISE 22 μm flux densities is good. However, as noticed at 12 μm, the relation becomes very dispersed for 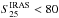 mJy.
mJy.
Appendix B: Removing the stellar contribution
In global galaxies, the emission in the 2−10 μm range is due to both the old stellar population and the dust (very small grains + PAHs). The contribution of these two components varies differently with the type of the galaxies, the former being dominant in ETG, the latter in star forming systems. Given that the Draine & Li (2007) models deal only with the dust component, we have to remove the stellar contribution first. This has been historically done by considering the Rayleigh-Jeans tail of the stellar emission peaked at ≈1−2 μm determined using a blackbody with T ≈ 3000 K, using the typical SED of ETG not showing any evidence of the presence of dust, or using stellar SEDs derived, for instance, from the Starburst99 models (e.g., Boselli et al. 1998; Helou et al. 2004; Draine et al. 2007). In this work, we use the CIGALE code (Noll et al. 2009), which allows us to compute the stellar SED of a galaxy using stellar population models from (Maraston 2005) convolved with a given star formation history (SFH). We refer the reader to Noll et al. (2009) for a complete description of the code.
 |
Fig. B.1
Evolution of S8 μm/S2 μm, S12 μm/S2 μm, and S22 μm/S2μm flux density ratios with τ, the e-folding rate of the exponentially decreasing SFR. |
| Open with DEXTER | |
 |
Fig. B.2
SED decomposition. Red diamonds are flux densities of the late type galaxy M 99 normalized to 2 μm. Grey triangles are flux densities of all HRS early-type galaxies normalized to 2 μm. Dashed red, green, and blue lines represents black body laws with different temperatures. Purple, magenta, cyan and orange lines represents models from Maraston (2005) convolved by CIGALE with an exponentially decreasing SFH for different e-foldings τ. |
| Open with DEXTER | |
Depending on their morphological types, the stellar populations of galaxies have very different characteristics. The elliptical and lenticular galaxies (ETG) are dominated by an old stellar population emitting in NIR whereas stellar populations of late-type galaxies are younger, emitting in UV. To properly remove the stellar contribution from the MIR emission, we need to take these differences into account.
Here, we consider an SFH with a decreasing exponential shape and an e-folding time τ. If the e-folding time of the SFH is very small (1−2 Gyr) then all of the stars are created in a very short time and evolve to become, at the age of the Universe, a very old population. On the contrary, a large e-folding (≈10−20 Gyr) corresponds to a quasi-constant SFR and stars are still being created at the age of the Universe.
To understand the impact of the choice of τ on MIR colors, we show on Fig. B.1 the variation of MIR flux densities from the models normalized to 2 μm with τ. Strong variations are seen for the 8 to 2 μm flux density ratios and the 12 to 2 μm flux density ratios (36% and 40%, respectively), whereas a very weak variation is seen at 22 μm. These variations stress the fact that estimates of the stellar emission in MIR strongly depends on the SFH of the galaxy and thus on its morphological type. Small values of τ correspond to a high S8 μm/S2 μm ratio, which is consistent with an important old stellar population. Thus, choosing a τ of 2 Gyr would lead to a SFH compatible with ETGs. With τ = 10 Gyr, there is less variation in the 8 to 2 μm flux density ratio. This smaller ratio implies a smaller flux density at 8 μm, which is what we expect for late-type galaxies.
To estimate the counterpart of the MIR emission due to stars in a late-type galaxy, Helou et al. (2004) used the stellar population models of Starburst 99 (Leitherer et al. 1999). Assuming that the 3.6 μm emission was purely stellar, they obtained stellar contribution factors of 0.596, 0.399, 0.232, and 0.032 at 4.5, 5.8, 8.0 and 24.0 μm, respectively. Draine et al. (2007) proposed similar values obtained from a blackbody emission with a temperature of 5000 K (0.260, 0.0326 at 8.0, and 24.0 μm, respectively). We use blackbodies of different temperatures and stellar population models computed from CIGALE and present the resulting stellar emission normalized at 2 μm in Fig. B.2. For comparison, we show the normalized observed flux densities of all the early-type galaxies of the HRS as well as those of M 99, a typical late-type galaxy of our sample. Differences in the stellar contributions are seen depending on the model (blackbody or models from CIGALE) and on the assumption on the temperature or the e-folding time. Both methods, blackbody or more complex models, pull uncertainties due to the assumption on the parameters (temperature or e-folding time). However, using the models from CIGALE allows us to take the observed differences between the stellar populations of the ETGs and LTGs into account. We thus decide to use the stellar population models computed by CIGALE, with a population aged of 13 Gyr, and consider these differences by using different e-folding times: τ = 2 Gyr for the ETGs and τ = 10 Gyr for the LTGs. In Table B.1, we calculate the coefficients and the associated errors corresponding to the stellar contribution for several NIR and MIR bands (from J to IRAS 60 μm), normalized to different bands (from J to IRAC 1). Our coefficients are in good agreement with those of Helou et al. (2004) and Draine et al. (2007), i.e., 0.589, 0.396, 0.244, and 0.044 at 4.5, 5.8, 8.0, and 24.0 μm, respectively, for the late-type galaxies.
Stellar contribution in NIR and MIR bands for early-type galaxies (ETG) and late-type galaxies (LTG).
Appendix C: Draine & Li (2007) parameters of the HRS galaxies
Even if this work is focused on the study of the dust properties of a subsample of gas-rich galaxies from the HRS, we apply the SED fitting procedure presented in Sect. 4.4 to all of the HRS galaxies. First, we removed the MIR stellar emission using the coefficients presented in Appendix B. In order to have fiducial corrected MIR flux densities, we impose the following criterion. If a galaxy has a corrected flux density lower than 2σ at 8 or 12 μm, then this galaxy is removed from the sample. At longer wavelengths, the contribution from the stellar populations to the IR emission is considered negligible.
Of the 322 HRS galaxies, 270 fulfill this criterion. However, from these 270 galaxies, we remove five that were not detected in PACS and SPIRE bands, thus having no constraints on the FIR and submm part of the SED: HRS 90, HRS 155, HRS 240, HRS 291, and HRS 316. We run our fitting procedure on 265 galaxies: 20 early-type galaxies and 245 late-type galaxies.
We present the results from the fits of the galaxies not analyzed in this work (20 early-type galaxies and 99 Hi-deficient galaxies) in Table C.1.
Estimated parameters.
Appendix D: Comparison between the properties of the gas-rich galaxies and the output of DL07 models
While we describe the main results of the comparison between the output parameters of DL07 and the properties of the gas-rich galaxy sample in Sect. 5, we describe here, for each output parameters, the relations with these properties. These relations are presented in Fig. D.1. The Spearman coefficient is provided for every relation. With a number of objects larger than 100, a correlation is expected to be real with a Spearman correlation coefficient larger than 0.40.
 |
Fig. D.1
Comparison between the output parameters of the Draine & Li (2007) models and different physical variables. Galaxies are color-coded according their morphological type. In red: the Sa, Sab, Sb; in green: the Sbc, Sc, Scd, and in blue: the Sd, Im and BCD. The Spearman correlation coefficient of each relation is provided. Galaxies with a 24 μm measurement are represented by filled symbols, galaxies with 22 μm with empty symbols. |
| Open with DEXTER | |
Appendix D.1: PAH emission
The fraction of PAH correlates with all of the parameters, except the birthrate parameter, with ρ ranging from 0.45 to 0.73. The relation between the fraction of PAH, the metallicity, and the stellar mass is described in Sect. 5.
There is a weak relation between the fraction of PAH contributing to the total IR luminosity and the SFR (ρ = 0.45). We would expect a tighter correlation as PAHs are often used as SFR indicators although many caveats on this assumption have been discussed in the literature (Boselli et al. 2004; Wu et al. 2005; Calzetti et al. 2007; Zhu et al. 2008; Kennicutt et al. 2009). Indeed, the destruction of PAH in regions where the ISRF is too intense, such as PDRs, can affect the relation between the SFR and 8 μm luminosity. This leads to a weak anticorrelation with the birthrate parameter as well, and a moderate relation with the Hα surface brightness that directly probes star formation. It seems that galaxies experiencing a star formation episode, i.e., with higher b, have lower qPAH. Indeed, previous works found that the PAH emission is inhibited within star-forming regions relative to other star formation tracers (e.g., Helou et al. 2004; Calzetti et al. 2005; Bendo et al. 2006, 2008; Pérez-González et al. 2006; Gordon et al. 2008). Another relation is found between qPAH and the H-band surface brightness, linked to what was previously noticed by Calzetti et al. (2007) and Bendo et al. (2008) who showed that 8 μm emission is also contributed by dust heated by the diffuse nonionizing stellar component. A correlation is also found between the fraction of PAH and the FUV attenuation (ρ = 0.58). However, the trend seen on the related panel is difficult to interpret, as the relation, if real, appears to be nonlinear.
Appendix D.2: Relative contribution of PDR and diffuse regions
Here we only consider galaxies for which MIPS 24 μm measurements are available (filled symbols on Fig. D.1) to have the strongest constraint on γ (see Sect. 4.3). There is a moderate relation between γ and the birthrate parameter (ρ = 0.44). When γ increases, the contribution of the PDR to the emission of the IR SED increases. As b is linked to the hardness of the UV radiation field, both quantities are correlated. Although weak, these relations between γ and b, and γ and the metallicity are consistent as the most metal poor objects are also the most star forming. We also notice a trend between γ and the metallicity, with a Spearman correlation coefficient of ρ = −0.39. The PDR contribution to the IR SED increases when the metallicity decreases. This confirms the tendency between γ and the stellar mass already noticed from the shape of the IR SED in Fig. 4. Furthermore, when γ increases, the IR peaks widen (Fig. 4). These two points confirm the results of Smith et al. (2012a) who performed a panchromatic analysis of the SED of a 250 μm selected sample of galaxies and found that low-mass galaxies have broader IR peaks. This relation also implies that the IR SED of the most massive galaxies is dominated by the emission of the diffuse component.
Appendix D.3: Interstellar radiation field
The ISRF is characterized by the parameters Umin, which quantifies the ISRF of the diffuse stellar component, and ⟨ U ⟩, the dust heating rate parameter, which is calculated from Umin, γ, and Umax (fixed to 106). Relations between ⟨ U ⟩ and the integrated properties of the galaxies are thus linked to the relations between Umin, γ, and these properties.
The relation between the intensity of the diffuse ISRF and the Hα and H-band surface brightnesses are discussed in Sect. 5. A weak correlation is observed between the birthrate parameter b and ⟨ U ⟩, with ρ = 0.48. The dust heating parameter ⟨ U ⟩ provides a direct measurement of the mean interstellar radiation field of the galaxy. This confirms the results of Boselli et al. (2010b) and Boselli et al. (2012) who found a correlation between b and the S60/S100 flux density ratio, sensitive to the dust temperature.
Appendix D.4: Infrared luminosity
An expected trend is seen between the LIR and M∗ as the most massive galaxies are also the most luminous as a scale effect (Kennicutt 1990). We recover the strong relation between the LIR and the SFR as well (Devereux & Young 1990; Devereux et al. 1995; Buat & Xu 1996; Kennicutt et al. 2009). Indeed, the LIR is widely used as a proxy for the SFR (e.g., Scoville & Young 1983; Buat & Xu 1996; Kennicutt 1998; Kennicutt et al. 2009; Kennicutt & Evans 2012).
We observe a moderate relation between the LIR and the metallicity (ρ = 0.58). Finally, there is also a moderate trend between the LIR and the FUV attenuation (ρ = 0.50). The energy absorbed in UV is reemitted by the dust in IR, one would expect to find a tighter relation between these two properties. Indeed, Smith et al. (2012a) found that the FIR/optical ratio increases with the LIR indicating that the galaxies with the higher IR luminosities are also the most obscured. However, by definition, A(FUV) is the infrared to UV luminosity ratio. These two quantities are thus not independent.
Appendix D.5: Dust mass
As expected, the dust mass and the stellar mass are tightly linked with a Spearman correlation coefficient of 0.83, as a scaling effect. There is also a strong correlation between the dust mass and the SFR. A weak global trend appears with the metallicity (ρ = 0.44). Indeed, the dust mass is larger in the most massive galaxies that are also the most metal-rich (Tremonti et al. 2004).
From Fig. D.1, we conclude that all of the integrated properties, except the FUV attenuation, correlate moderately to strongly with at least one of the output of Draine & Li (2007) models: the stellar mass to the fraction of PAH, the SFR to the fraction of PAH, the birthrate parameter moderately with γ and ⟨ U ⟩, ΣHα and μe(H) with Umin and qPAH, and the metallicity with qPAH and moderately with γ. All of these properties drive the shape of the IR SED. We confirm the results of Boselli et al. (2012) who found that the metallicity, the intensity of the ionizing and nonionizing radiation field, and the birthrate parameter are key parameters in the dust emission observed in the FIR.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


