| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201322658 | |
| Published online | 27 February 2014 | |
Online material
Appendix A: asymmetric-drift correction
To calculate the asymmetric-drift correction, we start from Eq. (4-33) of Binney & Tremaine (1987), which describes a stationary, axisymmetric stellar system embedded in a gravitational potential Φ(R,z): 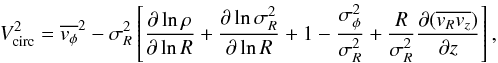 (A.1)where vR, vz, and vφ are the components (in cylindrical coordinates) of the velocity of a star, ρ is the stellar density,
(A.1)where vR, vz, and vφ are the components (in cylindrical coordinates) of the velocity of a star, ρ is the stellar density, 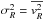 ,
, 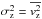 ,
, 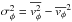 , and
, and 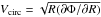 . The observed stellar rotation curve vrot provides
. The observed stellar rotation curve vrot provides 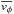 . Note that Eq. (A.1) does not require that the velocity dispersion is smaller than the rotation velocity. Following Weijmans et al. (2008), we write
. Note that Eq. (A.1) does not require that the velocity dispersion is smaller than the rotation velocity. Following Weijmans et al. (2008), we write 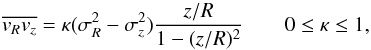 (A.2)where κ = 0 and κ = 1 correspond, respectively, to the extreme cases of a velocity ellipsoid aligned with the cylindrical (R, z, φ) and spherical (r, θ, φ) coordinate systems. Using higher-order velocity-moments of the collisionless Boltzmann equation, Weijmans et al. (2008) obtained the following expressions (see their Appendix A):
(A.2)where κ = 0 and κ = 1 correspond, respectively, to the extreme cases of a velocity ellipsoid aligned with the cylindrical (R, z, φ) and spherical (r, θ, φ) coordinate systems. Using higher-order velocity-moments of the collisionless Boltzmann equation, Weijmans et al. (2008) obtained the following expressions (see their Appendix A): 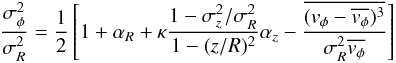 (A.3)and
(A.3)and 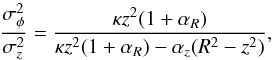 (A.4)where
(A.4)where 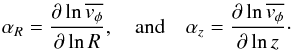 (A.5)The last term of Eq. (A.3) vanishes if the velocity ellipsoid is symmetric around
(A.5)The last term of Eq. (A.3) vanishes if the velocity ellipsoid is symmetric around 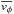 . Since we want to estimate Vcirc at R ≃ Rd, this higher-order term can be safely ignored, as
. Since we want to estimate Vcirc at R ≃ Rd, this higher-order term can be safely ignored, as 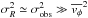 in the inner galaxy regions.
in the inner galaxy regions.
We now assume that the galaxy is in cylindrical rotation, i.e. 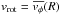 . Observationally, it is difficult to obtain information on the rotation velocities above the galaxy plane. A negative velocity gradient in the vertical direction, however, would produce an observable feature: asymmetric line profiles with a tail toward the systemic velocity. This means that a Gauss-Hermite polynomial-fit to the line profiles should give high values of the h3 term. This effect is observed, for example, in the lagging H I haloes of spiral galaxies (e.g., Fraternali et al. 2002). The stellar, absorption-line profiles of gas-poor dwarfs, instead, are quite symmetric and have | h3 | ≲ 0.1 (Halliday et al. 2001; Spolaor et al. 2010; Howley et al. 2013), implying that any vertical velocity gradient is relatively small. It is reasonable, therefore, to assume cylindrical rotation such that αz = 0. Thus, Eq. (A.4) gives σφ = σz.
. Observationally, it is difficult to obtain information on the rotation velocities above the galaxy plane. A negative velocity gradient in the vertical direction, however, would produce an observable feature: asymmetric line profiles with a tail toward the systemic velocity. This means that a Gauss-Hermite polynomial-fit to the line profiles should give high values of the h3 term. This effect is observed, for example, in the lagging H I haloes of spiral galaxies (e.g., Fraternali et al. 2002). The stellar, absorption-line profiles of gas-poor dwarfs, instead, are quite symmetric and have | h3 | ≲ 0.1 (Halliday et al. 2001; Spolaor et al. 2010; Howley et al. 2013), implying that any vertical velocity gradient is relatively small. It is reasonable, therefore, to assume cylindrical rotation such that αz = 0. Thus, Eq. (A.4) gives σφ = σz.
Since we are interested in the inner circular-velocity gradient, we also assume that the galaxy is in solid-body rotation, i.e. 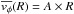 . All the Sphs in our sample, indeed, show nearly solid-body rotation curves out to the last measured point (cf. van Zee et al. 2004b) and thus αR = 1. Consequently, Eq. (A.3) gives σφ = σR (neglecting the higher-order term). Therefore, using observationally-motivated assumptions, we find that the Sphs in our sample can be approximated as isotropic rotators with σR = σz = σφ = σobs.
. All the Sphs in our sample, indeed, show nearly solid-body rotation curves out to the last measured point (cf. van Zee et al. 2004b) and thus αR = 1. Consequently, Eq. (A.3) gives σφ = σR (neglecting the higher-order term). Therefore, using observationally-motivated assumptions, we find that the Sphs in our sample can be approximated as isotropic rotators with σR = σz = σφ = σobs.
Finally, we assume that the scale height of the galaxy is constant with radius. Thus, we have ∂lnρ/∂lnR = ∂lnΣ/∂lnR, where Σ is the surface density profile (traced by the surface brightness profile). Assuming a Sérsic profile (Sérsic 1963), the asymmetric-drift-corrected circular velocity is given by 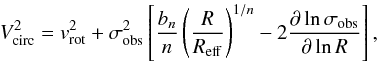 (A.6)where Reff is the effective radius, n is the Sérsic index, and bn is a constant that depends on n (see Ciotti 1991; Ciotti & Bertin 1999).
(A.6)where Reff is the effective radius, n is the Sérsic index, and bn is a constant that depends on n (see Ciotti 1991; Ciotti & Bertin 1999).
For rotating Sphs, the surface brightness profile can be fitted by an exponential law, thus n = 1 and b1 = 1.678. We also assume that σobs is constant with radius, as the observations generally provide only the mean value  . Therefore, Eq. (A.6) simplifies to
. Therefore, Eq. (A.6) simplifies to 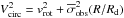 , where Rd = 1.678Reff is the exponential scale length. In this case, the error δV/R on Vcirc/R is given by
, where Rd = 1.678Reff is the exponential scale length. In this case, the error δV/R on Vcirc/R is given by 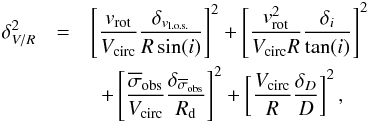 (A.7)where D and i are, respectively, the galaxy distance and inclination (cf. with Eq. (3)).
(A.7)where D and i are, respectively, the galaxy distance and inclination (cf. with Eq. (3)).
Appendix B: tables
Appendix B.1: Tables B1 and B3: structural and dynamical properties of gas-rich dwarfs (BCDs and Irrs)
Column (1) gives the galaxy name. Columns (2)−(4) give the assumed distance, the distance indicator, and the corresponding reference. Columns (5)−(8) give the R-band absolute magnitude MR, the central R-band surface brightness 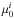 (corrected for inclination), the scale length Rd, and the reference for the surface photometry. The structural parameters were derived from an exponential fit to the outer parts of the surface brightness profiles. All the quantities have been corrected for Galactic extinction, but not for internal extinction. Column (9) gives the galaxy inclination, derived by fitting a tilted-ring model to the H I velocity field and/or by building 3D model-cubes. Columns (10)−(13) give the circular velocity VRd at Rd, the circular velocity Vlast at the last measured point, the radius at Vlast, and the reference for the H I rotation curves. Values of Vlast in italics indicate rotation curves that do not reach the flat part. Column (14) gives the circular-velocity gradient VRd/Rd.
(corrected for inclination), the scale length Rd, and the reference for the surface photometry. The structural parameters were derived from an exponential fit to the outer parts of the surface brightness profiles. All the quantities have been corrected for Galactic extinction, but not for internal extinction. Column (9) gives the galaxy inclination, derived by fitting a tilted-ring model to the H I velocity field and/or by building 3D model-cubes. Columns (10)−(13) give the circular velocity VRd at Rd, the circular velocity Vlast at the last measured point, the radius at Vlast, and the reference for the H I rotation curves. Values of Vlast in italics indicate rotation curves that do not reach the flat part. Column (14) gives the circular-velocity gradient VRd/Rd.
Sample of starbursting dwarfs: structural and dynamical properties.
Sample of starbursting dwarfs: gas and star-formation properties.
Appendix B.2: Tables B2 and B4: gas and star formation properties of gas-rich dwarfs (BCDs and Irrs)
Column (1) gives the galaxy name. Columns (2) and (3) give the gas metallicity and the respective reference. Values in italics indicate abundances derived using “strong-line” calibrations; we assigned to them a conservative error of 0.2 (cf. Berg et al. 2012). All the other abundances have been derived using the Te-method. Columns (4)−(6) give the H I mass, the mean H I surface density within Ropt = 3.2Rd (corrected for inclination), and the reference for the H I observations. Columns (7)−(9) give the Hα+[N II]equivalent width, the Hα star formation rate (SFR), and the reference for the Hα observations. SFRs have been calculated using the Kennicutt (1998a) calibration and have not been corrected for internal extinction. Columns (10) and (11) give the ratio SFR/Mbar and the SFR surface density (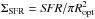 ). Mbar has been estimated using the baryonic Tully-Fisher relation as calibrated by McGaugh (2012) with an accuracy of ~10%. Values of SFR/Mbar in italics indicate galaxies with rotation curves that do not reach the flat part, thus they may be slightly underestimated. Columns (12) and (13) give the global and local gas depletion times τglobal and τlocal. τglobal considers the total atomic gas mass of the galaxy, whereas τlocal considers the atomic gas mass within Ropt.
). Mbar has been estimated using the baryonic Tully-Fisher relation as calibrated by McGaugh (2012) with an accuracy of ~10%. Values of SFR/Mbar in italics indicate galaxies with rotation curves that do not reach the flat part, thus they may be slightly underestimated. Columns (12) and (13) give the global and local gas depletion times τglobal and τlocal. τglobal considers the total atomic gas mass of the galaxy, whereas τlocal considers the atomic gas mass within Ropt.
Appendix B.3: Table B5: structural and dynamical properties of gas-poor dwarfs (Sphs)
Column (1) gives the galaxy name. Columns (2)−(6) give the R-band absolute magnitude, the inclination i, the central surface brightness (corrected for i), the scale length, and the reference for the surface photometry. The inclination was estimated from the observed ellipticities using Eq. (6) with q0 = 0.35. The structural parameters were derived from an exponential fit to the outer parts of the surface brightness profiles. All the quantities have been corrected for Galactic extinction, but not for internal extinction. Columns (7)−(11) give the rotation velocity at Rd, the rotation velocity vlast at the last measured point, the radius at vlast, the mean velocity dispersion, and the reference for the stellar spectroscopy. All rotation velocities have been corrected for inclination. Columns (12)−(14) give the circular velocity at Rd, the circular velocity at Rlast, and the circular-velocity gradient. All the circular velocities have been corrected for asymmetric-drift (see Appendix A).
Sample of irregulars: structural and dynamical properties.
Sample of irregulars: gas and star-formation properties.
Sample of rotating spheroidals in the Virgo cluster.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


