| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 17 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201322252 | |
| Published online | 28 November 2013 | |
Online material
Appendix A: Addendum to averaged models
Appendix A.1: Reversed granulation
To illustrate the effects of the remapping of the 3D atmospheric structures on new reference depth scales, we show slices of temperature contours from our TO-simulation in Fig. A.1.
 |
Fig. A.1
Temperature contours from our model with Teff = 6500 K and log g = 4.5 with [Fe / H] = 0.0 (left) and − 3.0 (right). The top panels display horizontal slices with the reversed granulation pattern imprinted in the temperature map (from 3 to 7 × 103 K) taken at ~ 230 km above the surface, which is also indicated in the second panel (dashed lines). The panels below show vertical slices (T-contours from 2 to 17 × 103 K) ranging from − 5.0 ≤ log τRoss ≤ 5.0 on layers of constant geometrical height (second), column mass density (third) and Rosseland optical depth (last panel). These panels include isocontours of the temperature (5, 10 and 12 × 103 K; yellow lines) and density (0.1, 1.0 and 2.5 × 10-7g / cm3; blue lines) and both increase with decreasing vertical depth. We show also lines of constant optical depth (second) and geometrical depth (third and last) indicated with white lines. |
| Open with DEXTER | |
We show horizontal temperature maps taken in the upper atmosphere (top panel) and three vertical slices with different reference depth scales, which include geometrical z (second panel), column mass density m (third panel), and Rosseland optical depth (bottom panel). Furthermore, we indicate three different isocontours of the temperature (yellow) and density (blue lines) in Fig. A.1, and we also show lines of constant optical depth τRoss (white lines in top panel) or geometrical depth z (middle and bottom panels).
The downdrafts just below the optical surface, which are denser and cooler than the lighter and hotter surrounding granules, are easily identified (by the prominent changes in T,ρ and τRoss above the downflows, e.g. x ≈ 1.8 Mm). Owing to the lower temperatures in the downdrafts compared with the granules, the same optical depth value is reached at lower geometrical depths, meaning that the emergent radiation in the intergranular lanes originate in much deeper geometrical heights. The corrugation of the optical depth on geometrical depth scale is therefore most pronounced in the downdrafts (see isocontour of log τRoss = 2.0 in second panel of Fig. A.1).
The opposite is true for the upper atmospheric layers because of the phenomenon of reversed granulation (Rutten et al. 2004; Cheung et al. 2007), namely, above the granules, cooling by adiabatic expansion is dominant, while above the inter granular lanes the radiative reheating and mechanical compression are more important for the energy balance. At lower metallicity and higher Teff, the radiative heating above granules is reduced by the weakening of spectral line features. The resulting reduction in radiative reheating leads to significantly cooler temperatures (see top panel in A.1) and a lower pressure support, and as a consequence the atmospheric layers at a given constant optical depth subside toward lower geometrical heights, closer to the optical surface. Therefore, the temperature contrast is enhanced in the upper atmosphere. The subsiding of the atmosphere is similar to what we found earlier, namely that the density range spanned in the atmosphere is significantly reduced at lower metallicity (see Fig. 16 in Paper I). Finally, the enhancement of the reversed granulation and the temperature contrast results in strongly corrugated surfaces of constant optical depth at the top of metal-poor simulations. We note that we also found an enhanced intensity-contrast for metal-poor stars (see Paper I).
The remapping of the individual columns of the 3D structure from geometrical depth to optical depth entails a change of perspective between the old and the new scales in terms of the distribution of values of a particular physical variable at a given constant reference depth. This is again most obvious in the downdrafts in the convection zone (see line of constant geometrical depth at z = 0.2 Mm in bottom panel of Fig. A.1). Properties from deeper geometrical heights are mapped onto layers at lower optical depth, and the temperature differences between upflowing and downflowing regions are reduced, which results in a less of a temperature contrast and in minimum-maximum ranges (see Sect. 4.1). On the other hand, the deviations in the density are significantly enhanced, which will clearly alter the statistical properties, in particular the mean values.
In the upper atmospheric layers of the solar metallicity case, the optical depth is corrugated only a small amount, therefore the transformation does not affect the temperature and density much (compare the upper flat blue line with the two lower corrugated ones in the bottom panel of Fig. A.1). However, the corrugation of the optical depth in the upper atmosphere is rather large for hotter metal-poor stars owing to the enhanced reversed granulation. As a result, the effects of remapping on the optical depth scale for the temperature and density is fairly substantial in these simulations. And the distribution of the thermodynamic properties is broadened, such that the meaning of the horizontal average is weakened (see Fig. 6).
In a similar way, the translation to column mass density naturally reduces the variations in density thanks to its definition of the reference depth scale, which is the depth-integrated density. Therefore, the resulting density fluctuations are rather small in layers at constant column mass density. The variation in temperature is slightly lower than in the averages on geometrical depth, but larger than in the averages on optical depth, as one would expect.
We stress once again that the different reference depth scales are equivalent to each other in terms of the spatial remapping of the 3D atmospheric structures. What differs of course is the statistical properties of physical variables on layers of constant depth, which vary depending on the choice of reference depth scale. One has to consider two important aspects concerning the horizontal averaging, the first being what kind of quantity is considered, and the second which reference depth scale is accounted for. Therefore, the statistical properties of the density and temperature are relatively distinctive depending on which reference depth scale is considered (see Sect. 4).
Appendix A.2: Hydrostatic equilibrium
The Stagger-code directly solves the discretized time-dependent, RHD equations (see Paper I) for the conservation of mass, momentum, and energy. The conservation properties are reflected in the mean ⟨3D⟩z stratifications of relaxed, quasi-stationary 3D hydrodynamical models averaged on layers of constant geometrical depth. In particular, the geometrical averages appear over time to be close to hydrostatic equilibrium5. To elucidate this further, we analyze the horizontal and time-average of the momentum equation 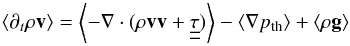 (A.1)with pth being the thermodynamic pressure, v the velocity field, and
(A.1)with pth being the thermodynamic pressure, v the velocity field, and 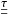 the viscosity stress tensor. Due to the averaging, the only remaining spatial dependence is the vertical one. Divergence terms thus reduce to vertical derivatives, i.e., ∇·⟨X⟩ = ∂z⟨X⟩. The time derivative ⟨∂tρv⟩ vanishes on time average as our model atmospheres are relaxed, hence quasi-stationary. The inertial term reduces to turbulent pressure
the viscosity stress tensor. Due to the averaging, the only remaining spatial dependence is the vertical one. Divergence terms thus reduce to vertical derivatives, i.e., ∇·⟨X⟩ = ∂z⟨X⟩. The time derivative ⟨∂tρv⟩ vanishes on time average as our model atmospheres are relaxed, hence quasi-stationary. The inertial term reduces to turbulent pressure 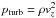 , so we obtain ⟨∇·(ρvv)⟩ = ∂z⟨pturb⟩. The divergence of the viscous stress tensor,
, so we obtain ⟨∇·(ρvv)⟩ = ∂z⟨pturb⟩. The divergence of the viscous stress tensor, 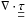 , vanishes on average. The last two terms yield ∂z⟨pth⟩ and ⟨ρg⟩, and we retrieve the equation for hydrostatic equilibrium with
, vanishes on average. The last two terms yield ∂z⟨pth⟩ and ⟨ρg⟩, and we retrieve the equation for hydrostatic equilibrium with 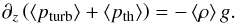 (A.2)In Fig. A.2 we show the hydrostatic equilibrium in the form of ρgdz / dptot = 1 for the temporal and geometrical averaged ⟨3D⟩z stratifications, which are very close to hydrostatic equilibrium. We emphasize that the hydrostatic equilibrium is only fulfilled by considering the total pressure ptot, as given in Eq. (A.2), which includes the non-thermal turbulent pressure that occupies a significant fraction of ptot at the top and in the SAR (see Fig. 21 in Paper I).
(A.2)In Fig. A.2 we show the hydrostatic equilibrium in the form of ρgdz / dptot = 1 for the temporal and geometrical averaged ⟨3D⟩z stratifications, which are very close to hydrostatic equilibrium. We emphasize that the hydrostatic equilibrium is only fulfilled by considering the total pressure ptot, as given in Eq. (A.2), which includes the non-thermal turbulent pressure that occupies a significant fraction of ptot at the top and in the SAR (see Fig. 21 in Paper I).
 |
Fig. A.2
Deviations from the hydrostatic equilibrium vs. optical depth. Dashed lines: ⟨3D⟩z averages; dotted lines: ⟨3D⟩m; solid lines: ⟨3D⟩Ross. |
| Open with DEXTER | |
Furthermore, one can find in Fig. A.2 that the averages on a new reference depth scales feature distinctive deviations from hydrostatic equilibrium (see ⟨3D⟩Ross and ⟨3D⟩m). The transformation of to a new reference depth scale maps all three components of Eq. (A.2) – geometrical depth z, density ρ, and total pressure ptot – away from its hydrostatic equilibrium state. Also, the geometrical depth z loses its strict physical meaning through such a transformation as a mean value. The mean stratifications on constant Rosseland optical depth ⟨3D⟩Ross deviate slightly at the top and significantly in the SAR from the hydrostatic equilibrium (⟨3D⟩500 is very similar). The largest departures can be found in the SAR. Furthermore, the amplitude of the discrepancy from hydrostatic equilibrium increases for higher Teff and lower log g.
 |
Fig. A.3
Deviations between the spatially and temporally averaged pressure (top) and opacity (bottom) and the values derived from the EOS, i.e. X(⟨ρ⟩,⟨ε⟩), vs. optical depth. Dashed lines: ⟨3D⟩z averages; dotted lines: ⟨3D⟩m; solid lines: ⟨3D⟩Ross. |
| Open with DEXTER | |
Appendix A.3: Deviations from the EOS
In 3D RHD simulations, the thermodynamic state of a simulation is self-consistently determined by the EOS. This means in particular that any thermodynamic variable depends on only two independent variables (namely the gas density ρ and the internal energy ε) in a well-defined way. However, the internal self-consistency is broken by reductions like temporal or spatial averaging.
This can be easily understood by investigating the behavior of a function f(X) on a 3D cube of quantity X. For small fluctuations X′ = X − ⟨X⟩ around the horizontal average at a given depth in the model atmosphere, a Taylor-expansion of f up to second order yields 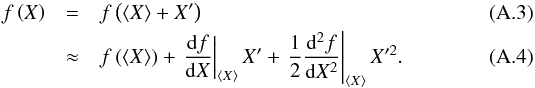 The horizontal average of this expression evaluates to
The horizontal average of this expression evaluates to 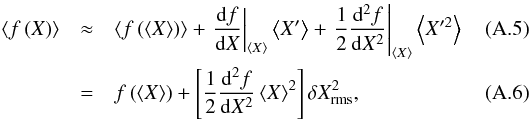 where the definition of the contrast δXrms was used in the last equation (see Eq. (3) in Sect. 4.1). The linear term in Eq. (A.5) vanishes as ⟨X′⟩ = 0 by definition. It is immediately clear that
where the definition of the contrast δXrms was used in the last equation (see Eq. (3) in Sect. 4.1). The linear term in Eq. (A.5) vanishes as ⟨X′⟩ = 0 by definition. It is immediately clear that 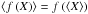 holds for linear functions. It is thus the non-linearity of f that causes a departure of
holds for linear functions. It is thus the non-linearity of f that causes a departure of 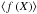 from f(⟨X⟩), because the departure scales with the square of the contrast δXrms.
from f(⟨X⟩), because the departure scales with the square of the contrast δXrms.
The discussion can be easily expanded to functions of two variables f(X,Y), since they are found in the EOS.
As a consequence, deriving thermodynamic quantities from averaged independent variables, ⟨ρ⟩ and ⟨ε⟩, will lead to inconsistent outcomes. The mean pressure in a given layer of the 3D cube will deviate from the pressure calculated with the EOS from mean density and mean internal energy, ⟨pth⟩ ≠ pth(⟨ρ⟩,⟨ε⟩). Therefore, with ⟨3D⟩ we face another level of complexity.
To quantify the deviations, we compute the temperature T, pressure pth, opacity κRoss, and electron number density nel from the EOS by employing the mean independent variables ⟨ρ⟩ and ⟨ε⟩. Then, we determine the relative disagreement as 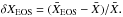 In Fig. A.3, we display the deviations of thermal pressure
In Fig. A.3, we display the deviations of thermal pressure 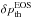 and opacity
and opacity  . As suggested by Eq. (A.6), we find the maximal deviations typically below the optical surface in the SAR, where the large fluctuations take place due to the overturning and to the presence of convective motions with their highly asymmetric up and downflows. The mean value thus toddles between the bimodal distribution. Furthermore, we find a strong variation in the δXEOS with stellar parameter, which increases for higher Teff and lower log g. Depending on which reference depth scale is applied, the disagreement δXEOS are distinct.
. As suggested by Eq. (A.6), we find the maximal deviations typically below the optical surface in the SAR, where the large fluctuations take place due to the overturning and to the presence of convective motions with their highly asymmetric up and downflows. The mean value thus toddles between the bimodal distribution. Furthermore, we find a strong variation in the δXEOS with stellar parameter, which increases for higher Teff and lower log g. Depending on which reference depth scale is applied, the disagreement δXEOS are distinct.
This loss of consistency caused by dimensional reduction means that mean ⟨3D⟩ models can never entirely substitute full 3D models, especially for spectral line formation applications (Uitenbroek & Criscuoli 2011). The mean stratifications are nothing more than statistically meaningful representations of stellar atmospheres, while only the complete 3D data set describes their physical state completely. In 1D model atmospheres, such internal consistency is maintained at all times, since no spatial averaging of non-linear variables is involved in the construction of 1D models.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


