| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321600 | |
| Published online | 20 September 2013 | |
Online material
Appendix A: Modeling details
 |
Fig. A.1
Spectral energy distribution (black line) of our best fit model, compared to dereddened photometry (AV = 0.3, Q11) from the literature (Q11, Tilling et al. 2012; Cutri et al. 2011; Ishihara et al. 2010; Egan et al. 2003; Helou & Walker 1988). The stellar photosphere is shown as the thin dashed line. |
| Open with DEXTER | |
Comparison of observed and model fluxes.
Adopted model.
Appendix A.1: Parametric dust and gas structure
We adopt the overall disk properties derived by Q11 from fitting the broadband spectral energy distribution and spatial extent of their mm data: a disk mass Mdisk = 0.089 M⊙, with an inner edge Rin = 0.6 AU and a critical radius RC = 150 AU. We define the surface density as (e.g. Andrews et al. 2009): 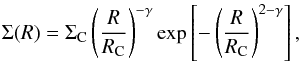 (A.1)where we set the surface density power law index, γ, equal to 1, the value for a self-similar accretion disk in steady-state (Hartmann et al. 1998). We adopt the gas-to-dust ratio of 154 from Q11 as well as their two component dust grain population (small and large) used to simulate dust settling. Both populations are made of a 60%/40% mix of astronomical silicates and graphite, and follow a power law grain size distribution n(a) ∝ a-3.5 (Draine 2006) with a minimum grain size amin = 0.005 μm for both populations. The small grain population has a maximum grain size amax,small = 0.25 μm, and the large population has amax,large = 1 mm. The small grain component is set to include 1.6% of the dust mass (fsmall = 0.016).
(A.1)where we set the surface density power law index, γ, equal to 1, the value for a self-similar accretion disk in steady-state (Hartmann et al. 1998). We adopt the gas-to-dust ratio of 154 from Q11 as well as their two component dust grain population (small and large) used to simulate dust settling. Both populations are made of a 60%/40% mix of astronomical silicates and graphite, and follow a power law grain size distribution n(a) ∝ a-3.5 (Draine 2006) with a minimum grain size amin = 0.005 μm for both populations. The small grain population has a maximum grain size amax,small = 0.25 μm, and the large population has amax,large = 1 mm. The small grain component is set to include 1.6% of the dust mass (fsmall = 0.016).
The vertical distribution is modeled as a Gaussian with angular scale height 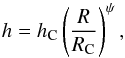 (A.2)where hC is the angular scale height at the characteristic radius RC and ψ describes the power-law disk flaring. We set ψ = 0.066, for consistency with the modeling of Tilling et al. (2012). The two dust component populations have independent scale heights (hC) of hsmall and hlarge, respectively, which we adjust to match the spectral energy distribution (discussed below).
(A.2)where hC is the angular scale height at the characteristic radius RC and ψ describes the power-law disk flaring. We set ψ = 0.066, for consistency with the modeling of Tilling et al. (2012). The two dust component populations have independent scale heights (hC) of hsmall and hlarge, respectively, which we adjust to match the spectral energy distribution (discussed below).
The gas density distribution produced by the physical model of Q11 is approximately Gaussian at low heights and has a long “tail” to large heights (cf. their Fig. 7). In order to approximate this, we have constructed the gas density distribution using a two-component model with independently varying scale heights for the main component (hmain) and the lower mass, larger scale height tail (htail). In addition, we vary the distribution of gas mass between these two components, with a term ftail describing the fraction of the total gas mass in the tail.
Appendix A.2: Determining the disk parameters
With this framework in place, we adjust parameters to match the SED and CO line fluxes in the literature for HD 163296. We carried out continuum radiative transfer modeling using the 2D code RADMC (Dullemond & Dominik 2004), which receives as input stellar properties and a dust density structure and outputs the resulting temperature structure. It includes a ray-tracing code, Raytran, for producing the model spectral energy distribution. We adjusted hsmall and hlarge in order to approximate the temperature structure found in Q11 (cf. their Fig. 9), which came from a self-consistent vertical structure calculation. We made further small adjustments to these parameters in order to match the SED. Our adopted disk model has small- and large-grain scale heights of 0.08 and 0.06, respectively, and we show the resulting SED in Fig. A.1. In our further modeling, we assume the gas temperature matches the mean dust temperature calculated in this modeling, which is a reasonable approximation in the dense regions upon which we focus.
After setting the dust parameters, we adjust hmain, htail, and ftail to approximate the gas density structure found in Q11 (their Fig. 9). We fine-tune these parameters by comparing our modeled fluxes of CO and its isotopologues with the observed fluxes of Q11, focusing on the low-J rotational lines that are expected to come largely from the cool outer disk regions studied here. We assume a relative CO abundance [CO]/[H] ≈ 10-4 (Frerking et al. 1982), which drops to zero at hydrogen column
densities less than 2 × 1021 cm-2 due to photodissociation (Visser et al. 2009) and at temperatures less than 19 K due to freezeout (Qi et al. 2011). We also assume a ratio of 12C to 13C of 75, and ratios of 16O to 18O and 17O of 500 and 1750, respectively (Frerking et al. 1982). To generate our model line emission, we input our adopted dust density and temperature structure, along with the model gas density structure, to the line radiative transfer code LIME (Brinch & Hogerheijde 2010), and we achieve a match to the observed line fluxes within ~50%.
The gas “tail” has a scale height htail = 0.2 and includes 5% of the gas mass (ftail), while the “main” gas component has a scale height hmain = 0.1. In Table A.1, we list the integrated fluxes of the CO lines which we use to determine the disk gas structure. Table A.2 lists and categorizes all disk modeling parameters, as well as the range of explored values or the reference from which the fixed value was adopted. In both tables, we repeat the HCO+, H13CO+, and DCO+ properties discussed in the main body of the text.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


