| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321600 | |
| Published online | 20 September 2013 | |
ALMA imaging of the CO snowline of the HD 163296 disk with DCO+⋆
1 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: gmathews@strw.leidenuniv.nl
2 SRON Netherlands Institute for Space Research, PO Box 800, 9700 AV Groningen, The Netherlands
3 Academia Sinica Institute of Astronomy and Astrophysics (ASIAA), PO Box 23-141, 10617 Taipei, Taiwan
4 Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
5 National Astronomical Observatory of Japan (NAOJ), 2-21-1 Osawa, Mitaka, 181-8588 Tokyo, Japan
6 NAOJ Chile Observatory
7 European Southern Observatory, Karl Schwarzschild Str 2, 85748 Garching bei München, Germany
8 Joint ALMA Observatory (JAO), Alonso de Cordova 3107, Vitacura, Santiago, Chile
9 National Radio Astronomical Observatory (NRAO), 520 Edgemont Road, Charlottesville, VA 22903, USA
10 INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
Received: 29 March 2013
Accepted: 11 July 2013
Context. The high spatial resolution and line sensitivity of the Atacama Large Millimeter/submillimeter Array (ALMA) opens the possibility of resolving emission from molecules in large samples of circumstellar disks. With an understanding of the conditions under which these molecules can have high abundance, they can be used as direct tracers of distinct physical regions. In particular, DCO+ is expected to have an enhanced abundance within a few Kelvin of the CO freezeout temperature of 19 K, making it a useful probe of the cold disk midplane.
Aims. We aim to use line emission from DCO+ to directly resolve the CO “snowline” – the region at which the gas-phase CO abundance drops due to freezeout – and determine the temperature boundaries of the region of DCO+ emission in the HD 163296 disk. This will serve as a test of deuteration models based on enhanced formation of the parent molecule H2D+ and a direct probe of midplane disk structure and ionization.
Methods. We compare ALMA line observations of HD 163296 to a grid of models based on the best fit physical model of Qi et al. (2011, ApJ, 740, 84). We vary the upper- and lower-limit temperatures of the region in which DCO+ is present as well as the abundance of DCO+ in order to fit channel maps of the DCO+J = 5–4 line. To determine the abundance enhancement compared to the general interstellar medium, we carry out similar fitting to HCO+J = 4–3 and H13CO+J = 4–3 observations.
Results. ALMA images show centrally peaked extended emission from HCO+ and H13CO+. DCO+ emission lies in a resolved ring from ~110 to 160 AU. The outer radius approximately corresponds to the size of the CO snowline as measured by previous lower resolution observations of CO lines in this disk. The ALMA DCO+ data now resolve and image the CO snowline directly.
Conclusions. In the best fitting models, HCO+ exists in a region extending from the 19 K isotherm to the photodissociation layer with an abundance of 3 × 10-10 relative to H2. DCO+ exists within the 19–21 K region of the disk with an abundance ratio [DCO+]/[HCO+] = 0.3. This represents a factor of 104 enhancement of the DCO+ abundance within this narrow region of the HD 163296 disk. Such a high enhancement has only previously been seen in prestellar cores. The inferred abundances provide a lower limit to the ionization fraction in the midplane of the cold outer disk (≳4 × 10-10), and suggest the utility of DCO+ as a tracer of its parent molecule H2D+.
Key words: stars: pre-main sequence / protoplanetary disks / submillimeter: stars / stars: individual: HD 163296
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Circumstellar disks of gas and dust are the environments in which planets form, as well as many molecules which may be transported to planets. Understanding the density and temperature structure of these disks, in particular the dense midplane, is necessary to understand the dynamic and chemical processes involved (Williams & Cieza 2011). However, directly probing the midplane is difficult. Many of the most abundant molecules, such as CO and HCO+, are present throughout much of the disk but have high opacity. Optically thin isotopologues such as C18O or H13CO+ may have detectable emission from the midplane, but it is confused by emission from higher layers. In addition, much of the midplane becomes unobservable as CO and other tracers freeze onto grains due to low temperatures at large radii.
DCO+ has been suggested as an excellent tracer of the disk midplane near the freezeout region of CO because the decline in temperature provides an ideal environment for gas-phase DCO+ formation. It is formed in the gas phase primarily by the transfer of a deuterium atom from the H2D+ ion to a CO molecule (Wootten 1987).
Chemical models predict the enhanced formation of the parent molecule H2D+ at low temperatures from the reaction 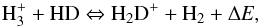 (1)where ΔE ~ 220 K (Roberts & Millar 2000). This effect is further enhanced by the reduction in the H2 ortho/para ratio at low temperatures, where the energy difference between the ortho ground state (J = 1) and para ground state (J = 0) otherwise provides internal energy for the back reaction (ΔE ~ 170 K, Maret & Bergin 2007; Pagani et al. 2009).
(1)where ΔE ~ 220 K (Roberts & Millar 2000). This effect is further enhanced by the reduction in the H2 ortho/para ratio at low temperatures, where the energy difference between the ortho ground state (J = 1) and para ground state (J = 0) otherwise provides internal energy for the back reaction (ΔE ~ 170 K, Maret & Bergin 2007; Pagani et al. 2009).
The parent molecule of H2D+, H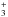 , is effectively destroyed by CO (Jørgensen et al. 2004), which can remain in the gas phase down to a temperature of ~ 20 K. Thus a reduction in the CO abundance will make HD the preferred destroyer of H
, is effectively destroyed by CO (Jørgensen et al. 2004), which can remain in the gas phase down to a temperature of ~ 20 K. Thus a reduction in the CO abundance will make HD the preferred destroyer of H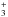 and lead to an enhancement of H2D+. The increase in H2D+ formation, in turn, is expected to enhance the formation of DCO+.
and lead to an enhancement of H2D+. The increase in H2D+ formation, in turn, is expected to enhance the formation of DCO+.
However, CO is also one of the parent molecules of DCO+, so while DCO+ formation is aided by a decrease in CO abundance, it will also be constrained at temperatures where too little CO remains in the gas phase. A balance between low temperatures and CO abundance is required to enhance DCO+ abundance.
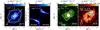 |
Fig. 1 Left: integrated emission map of HCO+ (blue) from 0–12 km s-1 with contours showing 3, 10, and 17σ emission (σ = 25 mJy beam-1 km s-1). The white-bordered black line shows the positions from which we constructed the position–velocity diagram (middle-left), and the gray box shows the smaller region for which we show H13CO+ and DCO+ line emission (middle-right and right). Middle-left: the HCO+ position–velocity diagram. The magenta curves show the Keplerian velocity profile for an assumed stellar mass of 2.3 M⊙, disk inclination of 44°, and systemic velocity of 5.8 km s-1. Middle-right: integrated emission map of H13CO+ (green) from 0.8–10.4 km s-1 with contours showing 3, 5, and 7σ emission (σ = 14 mJy beam-1 km s-1). Right: integrated emission map of DCO+ (red) from 0.8–10.4 km s-1 with contours showing 3 and 5σ emission (σ = 18 mJy beam-1 km s-1). The 19 K contour of the midplane temperature at a radius of 155 AU in the model disk is overlaid on the DCO+ emission using a white-bordered black ellipse. In the maps of integrated emission, the ~0 |
These factors have led to models predicting that the DCO+ abundance will be enhanced in a narrow range of temperatures of a few Kelvin near the CO freezeout temperature of ~ 20 K, which successfully explain emission from pre-stellar cores (e.g., Caselli et al. 1999; Pagani et al. 2012). In disks, line emission from DCO+ is then expected to trace the rise in formation of its parent molecule, H2D+ at increasing radii. H2D+ serves as the basis of many deuteration processes, and is one of the principal ions in cold dense gas. DCO+ emission will not rise indefinitely, instead it will form a ring which is truncated at the midplane ~20 K isotherm, the CO “snowline” where the gas phase CO abundance drops due to freezeout onto grains (e.g., Aikawa et al. 2002; Willacy 2007). Tracing the CO snowline is of importance to theories of planet formation because of the increase in the surface density of solids which can accelerate the growth of larger bodies.
While ions such as HCO+ and DCO+ are expected to trace low temperature conditions within the disk, they can also provide limits on the ionization fraction (e.g., Öberg et al. 2011b), a key parameter governing accretion in the disk. At ionization fractions (xion) less than 10-13, the magneto-rotational instability that drives viscous accretion breaks down due to a lack of conductivity. This creates “dead zones” (Gammie 1996), which in turn provide one mechanism of enhancing planet formation by the generation of high pressure vortices that trap large dust grains, thus increasing grain growth efficiency (e.g., Barge & Sommeria 1995; Varnière & Tagger 2006). Direct assessment of the ionization fraction will serve to test recently proposed mechanisms by which cosmic rays, one of the primary ionization mechanisms, might be excluded from a circumstellar disk by the young star’s stellar winds and magnetic field (Cleeves et al. 2013).
Single dish observations have previously revealed emission from DCO+ towards two T Tauri stars, TW Hya (van Dishoeck et al. 2003; Guilloteau et al. 2006), with interferometric observations suggesting a ringlike morphology for DCO+ in TW Hya (Qi et al. 2008; Öberg et al. 2012). Comparison with HCO+ has indicated a disk averaged DCO+/HCO+ abundance ratio of ~0.04 (TW Hya, van Dishoeck et al. 2003), which is a factor of 1000 higher than the interstellar medium [D]/[H] abundance of ≈10-5 (Watson 1976). Even higher abundances have been seen in dark clouds such as L1544 (DCO+/HCO+ = 0.12, Caselli et al. 1999). Later observations with the Sub-Millimeter Array (SMA) have detected DCO+ in several additional disks, though not with sufficient resolution to see the details of the morphology (Öberg et al. 2010, 2011a,b).
Nearby gas-rich disks provide ideal sites for examination of the cold disk midplane using DCO+. One such system is the Herbig Ae star HD 163296 (α = 17h56m21.29s, δ = −21°57′21 87, J2000, spectral type A1, Houk & Smith-Moore 1988), which is relatively nearby (122 pc, Perryman et al. 1997) and young (4 Myr, van den Ancker et al. 1998). It has long served as a prototype for studies of gas and dust rich protoplanetary disks (e.g., Mannings & Sargent 1997). Previous studies have determined that it has a relatively massive disk (0.07–0.08 M⊙) and a gas-to-dust ratio from 100 to 150 (e.g., Qi et al. 2011; Tilling et al. 2012). The disk is observed at an inclination of 44°, and position angle of ~133° east-of-north. Due to its high luminosity (~ 40 L⊙), the 20 K region is at a large radius which can be resolved with science verification data from the Atacama Large Millimeter/submillimeter Array (ALMA). The massive disk has a high total line-of-sight column density of DCO+ and the intermediate inclination means that vertical and radial spatial information can be obtained, as well as kinematic information.
87, J2000, spectral type A1, Houk & Smith-Moore 1988), which is relatively nearby (122 pc, Perryman et al. 1997) and young (4 Myr, van den Ancker et al. 1998). It has long served as a prototype for studies of gas and dust rich protoplanetary disks (e.g., Mannings & Sargent 1997). Previous studies have determined that it has a relatively massive disk (0.07–0.08 M⊙) and a gas-to-dust ratio from 100 to 150 (e.g., Qi et al. 2011; Tilling et al. 2012). The disk is observed at an inclination of 44°, and position angle of ~133° east-of-north. Due to its high luminosity (~ 40 L⊙), the 20 K region is at a large radius which can be resolved with science verification data from the Atacama Large Millimeter/submillimeter Array (ALMA). The massive disk has a high total line-of-sight column density of DCO+ and the intermediate inclination means that vertical and radial spatial information can be obtained, as well as kinematic information.
Qi et al. (2011, henceforth Q11) measured the radius of the CO snowline in the disk around HD 163296 by fitting high spectral resolution visibility data from the SMA with models of 13CO emission incorporating a sharp drop in abundance as a function of distance from the star. They estimated that the CO snowline of HD 163296 lies at a distance of 155 AU, corresponding to a midplane temperature of 19 K in their physical model.
In this paper, we present resolved imaging of DCO+ line emission from HD 163296 and examine the utility of DCO+ as a tracer of disk structure. The paper is structured as follows. In Sect. 2, we describe the observations and data reduction, and present our results in Sect. 3. We compare the disk properties to models in Sect. 4 and explore the implications for further disk studies in Sect. 5. We summarize our findings in Sect. 6.
2. Observations
Band 7 observations of HD 163296 were carried out on June 9, 11, 22, and July 6, 2012 for a total on-source time of 59.4 minutes as part of the ALMA science verification program 2011.0.000010.SV. Median precipitable water vapor levels (pwv) were 1.8, 0.7, 0.3, and 0.7 mm, respectively. The ALMA array included between 17 and 20 12m diameter antennas and baselines from 13m to 402m. The four correlator bands were centered on the CO J = 3–2, HCO+J = 4–3, H13CO+J = 4–3, and DCO+J = 5–4 transitions at 345.796, 356.734, 346.998, and 360.170 GHz, with channel widths of 122.1, 122.1, 244.1, and 30.5 kHz, and total bandwidths of 468.8, 468.8, 937.5, and 117.2 MHz, respectively. For gain, bandpass, and flux calibration, we used J1733-130, J1924-292, and Neptune, respectively.
We used the Common Astronomy Software Applications package (CASA, McMullin et al. 2007) to carry out calibration and imaging of the visibility datasets. Self-calibration was carried out for both phases and amplitudes using line free channels. We used the CLEAN algorithm with natural weighting and circular clean masks with diameters of ~9′′, 5′′, and 5′′ to produce channel maps of the HCO+, H13CO+, and DCO+ lines, respectively. The image cubes have a velocity resolution of 0.4 km s-1 and pixel size of 0 15 in each data cube. The synthesized beam size is ~0
15 in each data cube. The synthesized beam size is ~0 65 × 0
65 × 0 44, at a position angle of ~90°.
44, at a position angle of ~90°.
In this paper we examine the emission from HCO+ and its isotopologues, with a focus on DCO+. Discussion of the CO line emission from the disk may be found in de Gregorio-Monsalvo et al. (2013) and in Chapillon et al. (in prep.), while Klaassen et al. (2013), discuss CO line emission associated with the disk wind.
3. Results
In Table 1, we list the rms noise limits found in map regions and channels showing no emission, as well as the spatially and spectrally integrated emission in each line. We also present the line fluxes of our adopted model (discussed below). Line emission is detected at velocities between 0 and 12 km s-1 in HCO+, and at velocities of 0.8 to 10.4 km s-1 in H13CO+ and DCO+. All three lines have a central LSR (local standard of rest) velocity of 5.8 km s-1, consistent with previous observations (e.g., Mannings & Sargent 1997, Q11). In Fig. 1, we show the integrated maps of the emission from all three isotopologues in the velocity ranges given above.
3.1. Morphology
The HCO+ emission exhibits a smooth spatial profile that peaks at the stellar position. We fit an ellipse to the 3σ contour of the integrated emission map, and find that it has major and minor axes of 7 8 and 5
8 and 5 3 and a position angle of 133° east of north. Under the assumption of a flat disk these correspond to a disk with an outer radius of 475 AU observed at an inclination of 47°, comparable to previous inclination determinations. The position–velocity diagram in Fig. 1 shows that the line-of-sight velocities along the disk major axis exhibit a Keplerian velocity profile.
3 and a position angle of 133° east of north. Under the assumption of a flat disk these correspond to a disk with an outer radius of 475 AU observed at an inclination of 47°, comparable to previous inclination determinations. The position–velocity diagram in Fig. 1 shows that the line-of-sight velocities along the disk major axis exhibit a Keplerian velocity profile.
H13CO+ emission is only detected near the center of the disk, with the 2σ contour extending 1 4 from the disk center (170 AU).
4 from the disk center (170 AU).
DCO+ emission is not detected at the stellar position but is confined to an annulus in the integrated emission map with outer major and minor axes of 3 3 and 2
3 and 2 2, and inner major and minor axes of 1
2, and inner major and minor axes of 1 4 and 1
4 and 1 0. This suggests DCO+ emission originates in a ring with a central radius of ~ 140 AU and a width less than 110 AU (i.e. extending from a radius of at least 95 AU to less than 195 AU). This approximately corresponds to the CO snowline found by Q11 from lower resolution SMA observations of CO and its isotopologues, a relation we explore in more detail below. We show the midplane 19 K contour at a radius of 155 AU from our adopted model (see Sect. 4) in Fig. 1. There is an apparent peak in emission to the northwest. However, in this work we address the large scale structure, and do not attempt to model variations within that structure.
0. This suggests DCO+ emission originates in a ring with a central radius of ~ 140 AU and a width less than 110 AU (i.e. extending from a radius of at least 95 AU to less than 195 AU). This approximately corresponds to the CO snowline found by Q11 from lower resolution SMA observations of CO and its isotopologues, a relation we explore in more detail below. We show the midplane 19 K contour at a radius of 155 AU from our adopted model (see Sect. 4) in Fig. 1. There is an apparent peak in emission to the northwest. However, in this work we address the large scale structure, and do not attempt to model variations within that structure.
Observational and modeling results.
3.2. Estimated column densities
H13CO+ is expected to have an abundance a factor of 75 less than HCO+, corresponding to the 12C/13C abundance ratio in the interstellar medium (Frerking et al. 1982). We assume that the H13CO+J = 4–3 line is optically thin and can be used to estimate the median molecular column density in the disk. The H13CO+J = 4–3/HCO+J = 4–3 intensity ratio for positions and velocities where H13CO+ is detected has a median value of 0.18, confirming the high optical depth of HCO+ with τ ≈ 16 under the assumption of local thermodynamic equilibrium (LTE).
We use the online RADEX 1D non-LTE radiative transfer tool1 (van der Tak et al. 2007) to make an initial estimate of the column density. Assuming a kinetic temperature TK = 40 K and gas density nH2 = 107 cm-3 (intermediate values from the disk model of Q11), and assuming ΔV = 1 km s-1, we adjust the HCO+ and H13CO+ column densities until the model intensity ratios match the median observed intensity ratio. We find line of sight column densities of 2.1 × 1014 cm-2 and 2.8 × 1012 cm-2 for HCO+ and H13CO+, respectively. Correcting for the disk inclination, these are vertical column densities of 1.5 × 1014 cm-2 and 2.0 × 1012 cm-2.
The column density sensitivity of our observations is estimated using RADEX, as well. For each transition, we convert the 3σ limits in our maps of integrated line emission to antenna temperature. We then assume gas densities and temperatures typical of the expected emission regions. For HCO+ and H13CO+, we assume the same TK and nH2 values as above, and for DCO+ we assume nH2 = 109 cm-3 and TK = 19 K (values from the midplane CO snowline of Q11). Our integrated maps have approximate column density sensitivities of 1.7 × 1012, 0.7 × 1012, and 2.5 × 1012 cm-2 for HCO+, H13CO+, and DCO+, respectively. These estimates do not reflect the variation in density and temperature across the regions in which these molecules exist, factors that require more detailed radiative transfer modeling as described in the following section.
4. Modeling
4.1. Physical structure
Analysis of the DCO+ spatial distribution requires a physical model which specifies the temperature and gas density as a function of both radius and height in the disk. We use a parametric disk model to approximate the best-fit model of Q11, with parameters adjusted to fit the spectral energy distribution and line fluxes for CO and its isotopologues in the literature. The details of the density and temperature structure of our disk model, as well as our radiative transfer models and ray-tracing, can be found in Appendix A. Simulated observations of our models, mimicking the (u,v) coverage of the data, were carried out using the built-in simulation tasks of CASA.
We used this spectral energy distribution (SED) -constrained model as the basis for constructing a grid of HCO+, H13CO+, and DCO+ models, with energy levels, transition frequencies, and Einstein A coefficients taken from the Leiden Atomic and Molecular Database2 (Schöier et al. 2005). We manually varied the isotopologue abundances, and in the case of DCO+ the region in which it is abundant (discussed below), and compared the resulting channel maps to the observations.
4.2. Molecular abundances
The HCO+ and H13CO+ abundances χHCO+ and χH13CO+, respectively) are taken to be constant within the region populated by the parent CO molecule. This region is bounded on the upper side by photodissociation (i.e., below the height where a hydrogen column density of NH2 = 2 × 1021 cm-2 is reached, adopted from the translucent-cloud modeling of Visser et al. 2009) and on the lower side by the 19 K CO freezeout zone (Q11). Outside this region we treat the abundance as zero. We explored HCO+ abundances relative to H2 ranging from 10-11 to 10-5 in logarithmic steps of 0.5 (corresponding to factors ~3) and setting the H13CO+ abundance to 1/75 that of HCO+. We find a best simultaneous match to the HCO+ and H13CO+ integrated intensities and channel maps with a HCO+ abundance of 3 × 10-10, and a corresponding H13CO+ abundance of 4 × 10-12. These constant abundances are adopted throughout this work.
We carried out a similar manual fit to the DCO+J = 5–4 emission. Our DCO+ models include the same assumption of a uniform abundance (χDCO+) within the region of DCO+ enhancement, and an abundance of zero outside of this region. However, the region in which DCO+ is enhanced is defined by both high temperature and low temperature cutoffs, Thigh,DCO+ and Tlow,DCO+. Above Thigh,DCO+, DCO+ cannot form in large quantities due to the destruction of H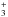 and H2D+ by gas phase CO and ortho-H2, respectively. Below Tlow,DCO+ it cannot form due to a lack of gas phase CO. We find that a χDCO+ of 1 × 10-10 at temperatures between Thigh,DCO+ = 21 K and Tlow,DCO+ = 19 K provides the best fit to both the total flux and to channel maps. We compare fluxes from our adopted model to the observed fluxes in Table 1.
and H2D+ by gas phase CO and ortho-H2, respectively. Below Tlow,DCO+ it cannot form due to a lack of gas phase CO. We find that a χDCO+ of 1 × 10-10 at temperatures between Thigh,DCO+ = 21 K and Tlow,DCO+ = 19 K provides the best fit to both the total flux and to channel maps. We compare fluxes from our adopted model to the observed fluxes in Table 1.
Figure 2 presents the comparison between our best fit DCO+ model and the observations in the large lower left panel, for 2 km s-1 wide channel maps centered at 4, 6, and 8 km s-1, respectively. We simultaneously display these maps in blue, green, and red scaled uniformly above 3σ, and overlay the 3 and 5σ model contours in the same velocity ranges (in these broad channel maps, σ = 15 mJy beam-1 km s-1).
 |
Fig. 2 Comparison of integrated intensities of our DCO+ models (contours, 3 and 5σ, σ = 15 mJy beam-1 km s-1) to the observations (image, colors show intensities from 3σ). Colors indicate the velocities included in constructing the zeroth moment maps. Clockwise from the upper left, small figures show: 1) decreasing Tlow,DCO+ and Thigh,DCO+ by 3 K, 2) raising Tlow,DCO+ and Thigh,DCO+ by 4 K, 3) broadening the temperature range from 2 K to 4 K, with χDCO+ halved to maintain the same total DCO+J = 5–4 line flux, 4) reduction of χDCO+ by a factor of 3, and 5) raising χDCO+ by a factor of 3. |
The five small panels of Fig. 2 show how the emission varies if we change the temperature range and abundance of DCO+. The panels show: 1) if we decrease the temperature bounds by 3 K or 2) increase them by 4 K, 3) if we broaden the temperature range by a factor of two (while halving the abundance to maintain approximately the same integrated emission), or if we 4) decrease the abundance by a factor of 3, or 5) increase it by a factor of 3. These effects highlight the relation between disk properties and observables: the temperature range in which DCO+ has high abundance primarily sets the observed spatial region of emission, while the abundance adjusts the strength of that emission.
In Fig. 3, we illustrate the HCO+ and DCO+ regions of our adopted model and the molecular column density as a function of radius in the disk. Due to the increasing physical thickness of the DCO+ region, decreasing gas density, and our assumption of a constant abundance, the DCO+ column density is relatively constant from 110 to 150 AU, corresponding to the brightest region of observed emission.
 |
Fig. 3 Top: regions of non-zero HCO+ (blue) and DCO+ (red) abundance, overlaid with contours indicating the hydrogen density (solid gray lines) and temperature (dashed gray lines). The 19 and 21 K contours are shown with a thick dark gray line. The region containing HCO+ is bounded on the upper and lower sides by CO photodissociation and by freezeout at 19 K, respectively. The DCO+ region is bounded by the temperature range 19–21 K. Bottom: the column density of HCO+ and its isotopologues (colored lines), with the 19 K CO snowline indicated by the thick dark gray dashed line. The broad plateau of the DCO+ column density from ~110–150 AU explains the ring morphology seen in line emission. The 3σ line sensitivities (from Sect. 3.2) are shown with the horizontal gray lines. |
5. Discussion
5.1. Why a ring?
The data constrain DCO+ emission to a narrow ring near the previously inferred CO snowline, and our models constrain the physical parameters of this region. Three factors combine to restrict the detection of DCO+ to a narrow ring:
- 1.
As the temperature decreases to 21 K, theCO abundance begins to drop due to freezeout andallows the effective formation of one of the parent molecules ofDCO+, H2D+. In addition, the ortho/para ratio of H2 drops to ~ 10-3,inhibiting the back reaction of H2D+ with H2. These lowtemperatures are first reached at a radius of ~ 110 AU,and the DCO+ column density will rise as its abundance becomesenhanced (Fig. 3, 21 K contour).
- 2.
Where the temperature drops below 19 K (i.e. at radii greater than 155 AU in the midplane), the other parent molecule of DCO+, CO, will be largely removed from the gas phase due to freezeout. This will in turn reduce the DCO+ column density (Fig. 3, 19 K contour). The temperature bounded region is present at larger radii above the midplane, but at these heights, DCO+ emission faces a third constraint.
- 3.
The gas density, nH2, decreases with height above the midplane, in turn reducing the column density of DCO+. This is illustrated by comparing the top and bottom panels of Fig. 3. The column density decreases at the CO snowline at 155 AU (bottom, vertical dashed gray line). This is the radius where the 19 K temperature contour rises above the midplane (top, thick dashed gray line). As the 19 K isotherm rises in the disk, the gas density, and the corresponding column densities, decrease (top, solid contours).
At low optical depths and nearly constant temperature, the integrated intensity will be an approximately linear function of column density. We can infer from Fig. 3 that the outer edge of the broad peak of DCO+ emission traces the CO snowline in the midplane, while emission at larger radii traces a layer of constant temperature that rises from the midplane of the disk. Under our enrichment scenario, the inner edge indicates where the formation rate of H2D+ rises.
In our model, the column density of DCO+ drops by a factor of ~4 from 150 to 200 AU. In the current observations, the peak intensity is 6σ, suggesting that only a factor of 3 improvement in sensitivity is needed to probe this disk structure to a radius of ~200 AU. With twice as many antennas, the full ALMA array will be able to accomplish such an observation with only ~2 h integration time.
5.2. Probing the vertical structure
Models with a factor of 3 increase in column density – which could be achieved either by increasing the relative abundance or the overall gas density – lead to much larger structures being detectable in the model images (see panels 4 and 5 of Fig. 2). This is due to an increase in the column density at larger radii in the disk. As this is also the region where the 19 K isotherm rises from the midplane, this suggests the utility of DCO+ not just as a probe of the regions of enhanced H2D+ formation and the midplane CO snowline, but also with higher sensitivity observations a probe of the vertical disk structure.
In combination with detailed chemical models, this provides constraints on the degree of vertical mixing, as DCO+ that moves upward from this region will be destroyed, and that which moves down in the disk will freeze out on grains.
5.3. Sensitivity to Thigh and Tlow
At a radius of 155 AU, the disk midplane temperature changes at a rate of ≈1 K per 20 AU. Small changes in the modeled DCO+ temperature range then correspond to large changes in the physical emission region. The resolution of the beam, 0 44, corresponds to about 50 AU at the distance of HD 163296, therefore differences of 2.5 K in Thigh,DCO+ and Tlow,DCO+ will lead to resolvable differences in the radial distribution of line emission. The center of the temperature range can decrease by less than 3 K and increase by less than 4 K (see panels 1 and 2 of Fig. 2). The width of the temperature range in which DCO+ exists cannot be much larger than 2 K, as the ring of emission becomes too wide (see panel 3 of Fig. 2). Changes in the position of emission in the disk will also lead to changes in the line of sight velocity, with the velocity changing on a scale of ≈0.2 km s-1 per 20 AU. Thigh,DCO+ and Tlow,DCO+ cannot shift far from ~20 K as the ring both changes in size and the emission shifts to different velocities.
44, corresponds to about 50 AU at the distance of HD 163296, therefore differences of 2.5 K in Thigh,DCO+ and Tlow,DCO+ will lead to resolvable differences in the radial distribution of line emission. The center of the temperature range can decrease by less than 3 K and increase by less than 4 K (see panels 1 and 2 of Fig. 2). The width of the temperature range in which DCO+ exists cannot be much larger than 2 K, as the ring of emission becomes too wide (see panel 3 of Fig. 2). Changes in the position of emission in the disk will also lead to changes in the line of sight velocity, with the velocity changing on a scale of ≈0.2 km s-1 per 20 AU. Thigh,DCO+ and Tlow,DCO+ cannot shift far from ~20 K as the ring both changes in size and the emission shifts to different velocities.
5.4. Enhancement of DCO+
While DCO+ is restricted to a much smaller vertical area of the disk than HCO+, the regions in which these ions are abundant overlap near the CO snowline. Under our assumption of a uniform HCO+ abundance within the region from the CO snowline to the CO photodissociation limit at NH2 = 2 × 1021 cm-2, the relative abundance of DCO+ to HCO+ is as high as 0.3 within the sub-region which lies near 20 K. This represents a local enhancement by a factor of at least 104 over the ISM [D]/[H] ratio of ≈10-5 (Watson 1976), and is a higher deuteration than that observed in pre-stellar cores where CO is also frozen out (e.g., Caselli et al. 1999). Some models of vertical chemical structure predict that the HCO+ abundance begins declining above the region of enhanced DCO+ abundance (Aikawa & Nomura 2006). In such a scenario, the local DCO+ to HCO+ abundance ratio would be even higher. While H13CO observations could provide constraints on this scenario, distentangling the midplane emission from that in higher layers in the disk requires more detailed modeling of the HCO+ abundance structure and higher signal-to-noise H13CO+ data.
In the images presented here, DCO+ emission covers approximately 1/4 of the observed HCO+ emission area (Fig. 1). In our model, the vertical thickness of the DCO+ region is also approximately 1/4 that of the HCO+ region (Fig. 3). Taking both geometric effects into account, the disk averaged abundance ratio is approximately 0.02, comparable to the disk-averaged abundance ratio found in TW Hya (0.04, van Dishoeck et al. 2003).
5.5. Ionization fraction
The model HCO+ and DCO+ abundances provide a lower limit to the ionization fraction of the disk. In the warm molecular disk where HCO+ is present, the ionization fraction must be at least 3 × 10-10. Assuming that it continues to be present into the cold midplane region where the DCO+ abundance is enhanced (as it is in our simple model), the minimum ionization fraction would be 4 × 10-10 (HCO+ + DCO+). This is at least an order of magnitude higher than that found in the cool molecular layer of DM Tau described by Öberg et al. (2011b). This is also three orders of magnitude higher than the critical ionization fraction at which dead zones form. Observations of other region specific ions (e.g., H2D+ outside the CO snowline, Öberg et al. 2011b) will allow for estimation of the importance of this mechanism for planet formation throughout the disk.
5.6. Comparison to other disks
The scenario we have modeled here for HD 163296 is consistent with that described for DM Tau by Öberg et al. (2011b), wherein they find that unresolved DCO+ emission can be fit using an enhanced DCO+ abundance in the temperature range of 16–20 K. This temperature range is slightly lower and broader than that found here.
DCO+J = 3–2 emission has been mapped towards TW Hya by Qi et al. (2008) and can also be fit by a ring-like morphology. They simulate a three-layer disk structure by assuming a model in which the molecular column density is a function of distance from the star, and the abundance at any given radius is constant within the middle layer. They fit a power law radial column density profile for each molecule in their study, as well as a vertical structure defined relative to the hydrogen column density. Under this model, they find that DCO+ emission is best fit by either a model in which its column density increases away from the star with a sharp truncation at 90 AU, or by a two-part power law function which increases to 70 AU, and then decreases. In both models, the DCO+ exists in a layer extending from hydrogen column densities of 0.1 to 10 times 1.59 × 1021 cm-2, the “disk surface”. This region has temperatures ranging from ~16–50 K, and densities from ~107–108 cm-3. Midplane temperatures at this radius are ~ 10 K.
The 19 K midplane isotherm in TW Hya lies at 30 AU in the Qi et al. (2008) model. DCO+ in this disk therefore does not appear to trace the same isotherm as in HD 163296 and in pre-stellar cores. Either some mechanism acts to inhibit the low temperature enhancement of DCO+ at 30 AU, or alternatively, some process generates a second peak in DCO+ around 70 AU as seen by the SMA.
One possibility is related to the formation of H2D+, the DCO+ parent molecule. Whereas we have focused on the reduction of CO abundance allowing for greater formation of H2D+ from H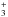 , other molecules can serve to inhibit its formation (therefore inhibiting its reaction products, such as DCO+). H
, other molecules can serve to inhibit its formation (therefore inhibiting its reaction products, such as DCO+). H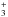 can also react with N2. Perhaps the 70 AU radius in TW Hya traces N2 freezeout which occurs at slightly lower temperatures (Bisschop et al. 2006) resulting in a second peak in H2D+. If some residual CO was present, due to mixing from warmer layers or release from grains, then DCO+ could form.
can also react with N2. Perhaps the 70 AU radius in TW Hya traces N2 freezeout which occurs at slightly lower temperatures (Bisschop et al. 2006) resulting in a second peak in H2D+. If some residual CO was present, due to mixing from warmer layers or release from grains, then DCO+ could form.
Alternatively, the underlying model of gas and dust density and temperature could be in need of revision. Recent SMA continuum observations (Andrews et al. 2012) indicate the mm-emitting dust disk is truncated at 60 AU. This would have far reaching effects on the thermal structure and disk chemistry, including the potential release of CO into the gas phase due to increased penetration of ultraviolet radiation (an effect noted by Andrews et al.). This could allow the gas-phase formation of DCO+ even outside the CO snowline.
At 30 AU, it is also possible that the ortho-to-para ratio of H2 has not dropped to the low levels of ~10-3 expected for these low midplane temperatures and required to enhance H2D+ abundance. The ortho-to-para conversion is governed by the H+ + ortho-H2 → H+ + para-H2 reaction, which has a timescale that is proportional to the H+ abundance. For an H+ abundance of at most 10-12 with respect to H2 (Walsh et al. 2012) the timescale is at least 3 × 105 yr for a density of 109 cm-3 and rate coefficient of 1.1 × 10-10 cm3 s-1 at 10 K (Pagani et al. 2013). If some high temperature event (e.g., a recent flare) has reset the H2 ortho/para ratio to a high temperature value in the inner disk temporarily, it may not have equilibrated back to the low value needed to boost the H2D+ abundance at the 30 AU radius. Note that the ortho-H2 S(1) line at 17 μm has been detected toward TW Hya (Najita et al. 2010) and interpreted to arise from radii out to 30 AU (Gorti et al. 2011). Even though the mid-infrared emission arises from the warm surface layers, some of this ortho-H2 may have been mixed down to the midplane.
A superthermal abundance of ortho-H2 also has other chemical consequences, most notably in driving the reaction N+ + ortho-H2 → NH+ + H, which triggers the nitrogen chemistry leading to NH3. The strong Herschel-HIFI detection of NH3 in the TW Hya disk (Hogerheijde et al., in prep.) would be consistent with this scenario.
Ultimately, this discussion points to the need for high spatial resolution ALMA mapping of DCO+ and other molecules sensitive to CO freezeout (e.g., Qi et al. 2013a) in the TW Hya and other disks to determine the relative importance of the H2D+ enhancement versus CO freeze-out.
5.7. Dependence on physical models
Here we relate the observed emission to physical/chemical properties via an adopted structure model for the disk. This model has been constrained via observations that trace various regions of the disk (e.g., the SED and CO observations). CO observations in particular are primarily sensitive to a thin surface layer between the height where photodissociation of CO no longer effectively operates and the height where the lines become optically thick. Even the emission of optically thin isotopologues of CO are strongly affected by the emission from these surface layers, and only partially probe the disk midplane. Because our DCO+ observations are thought to probe the disk midplane, it is appropriate to investigate the dependence of our results on the details of the adopted physical model.
Compared to our model, which is based on the work of Q11, the best-fit disk structure of de Gregorio-Monsalvo et al. (2013) has 1–3 K lower temperatures and factor ~1.5 higher densities in the 100–150 AU midplane region. Using this model, we find that our observations are best described if DCO+ is enhanced between temperatures of 16 and 20 K (compared to 19–21 K found using the Q11 model). The best fit DCO+ abundance is ~7 × 10-11, compared to 1 × 10-10 for the Q11 model. These higher densities affect the H13CO+ abundance in a similar fashion, leading to an HCO+ abundance of ~2 × 10-10. The differences in gas density affect the molecular abundance in the same manner, leading to a similar localized DCO+/HCO+ ratio of ~0.3.
Although the details of the best-fit model clearly depend on the adopted disk structure, the general characteristics remain unchanged: DCO+ is a sensitive tracer of the narrow temperature range where CO freezes out and H2D+ starts to increase in abundance. Other high-resolution observations of species that also trace this transition (e.g., N2H+; see Qi et al. 2013b) will further constrain the parameter range of allowed models.
6. Conclusions
We have presented ALMA Science Verification images of the HCO+J = 4–3, H13CO+J = 4–3, and DCO+J = 5–4 emission from the HD 163296 circumstellar disk. While HCO+ traces the entire disk and is detected at the stellar position, the DCO+ emission is seen in a ring tracing the region between the rise of H2D+ formation and the CO snowline. Using radiative transfer modeling, we have shown that the emission can be matched by a model in which DCO+ has high abundance within a limited temperature range near the CO freezeout temperature (from 19 to 21 K). This emission traces the previously determined CO snowline. Comparison of the modeled abundances indicates a [DCO+]/[HCO+] ratio of 0.3, the highest yet observed. This in turn suggests that gas phase deuteration processes can lead to local enhancements of the abundance of DCO+ on the order of a factor of 104, comparable to that observed in some dark clouds. The high abundance of these ions also indicates that the ionization fraction must be ≳10-10 in the cold midplane, three orders of magnitude higher than necessary to maintain the MHD turbulence that powers viscous accretion.
Future high sensitivity, high resolution observations with ALMA will allow for the direct imaging of many chemical processes in disks. These studies will provide important constraints on models of disk physical structure even in the vertical direction. In conjunction with tracers of the disk surface (e.g. CO) and the bulk gas (e.g. C18O), we are entering the era of “disk tomography” where disks can be mapped in a region-by-region fashion. This will, in turn, allow us to study chemistry and dynamics as they vary throughout the disk.
Online material
Appendix A: Modeling details
 |
Fig. A.1 Spectral energy distribution (black line) of our best fit model, compared to dereddened photometry (AV = 0.3, Q11) from the literature (Q11, Tilling et al. 2012; Cutri et al. 2011; Ishihara et al. 2010; Egan et al. 2003; Helou & Walker 1988). The stellar photosphere is shown as the thin dashed line. |
Comparison of observed and model fluxes.
Adopted model.
Appendix A.1: Parametric dust and gas structure
We adopt the overall disk properties derived by Q11 from fitting the broadband spectral energy distribution and spatial extent of their mm data: a disk mass Mdisk = 0.089 M⊙, with an inner edge Rin = 0.6 AU and a critical radius RC = 150 AU. We define the surface density as (e.g. Andrews et al. 2009): ![\appendix \setcounter{section}{1} \begin{equation} \Sigma (R) = \Sigma_{\rm C} \left ( \frac{R}{R_{\rm{C}}} \right ) ^{-\gamma} \exp \left [-\left (\frac{R}{R_{\rm{C}}} \right )^{2-\gamma} \right ], \end{equation}](/articles/aa/full_html/2013/09/aa21600-13/aa21600-13-eq132.png) (A.1)where we set the surface density power law index, γ, equal to 1, the value for a self-similar accretion disk in steady-state (Hartmann et al. 1998). We adopt the gas-to-dust ratio of 154 from Q11 as well as their two component dust grain population (small and large) used to simulate dust settling. Both populations are made of a 60%/40% mix of astronomical silicates and graphite, and follow a power law grain size distribution n(a) ∝ a-3.5 (Draine 2006) with a minimum grain size amin = 0.005 μm for both populations. The small grain population has a maximum grain size amax,small = 0.25 μm, and the large population has amax,large = 1 mm. The small grain component is set to include 1.6% of the dust mass (fsmall = 0.016).
(A.1)where we set the surface density power law index, γ, equal to 1, the value for a self-similar accretion disk in steady-state (Hartmann et al. 1998). We adopt the gas-to-dust ratio of 154 from Q11 as well as their two component dust grain population (small and large) used to simulate dust settling. Both populations are made of a 60%/40% mix of astronomical silicates and graphite, and follow a power law grain size distribution n(a) ∝ a-3.5 (Draine 2006) with a minimum grain size amin = 0.005 μm for both populations. The small grain population has a maximum grain size amax,small = 0.25 μm, and the large population has amax,large = 1 mm. The small grain component is set to include 1.6% of the dust mass (fsmall = 0.016).
The vertical distribution is modeled as a Gaussian with angular scale height 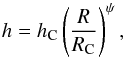 (A.2)where hC is the angular scale height at the characteristic radius RC and ψ describes the power-law disk flaring. We set ψ = 0.066, for consistency with the modeling of Tilling et al. (2012). The two dust component populations have independent scale heights (hC) of hsmall and hlarge, respectively, which we adjust to match the spectral energy distribution (discussed below).
(A.2)where hC is the angular scale height at the characteristic radius RC and ψ describes the power-law disk flaring. We set ψ = 0.066, for consistency with the modeling of Tilling et al. (2012). The two dust component populations have independent scale heights (hC) of hsmall and hlarge, respectively, which we adjust to match the spectral energy distribution (discussed below).
The gas density distribution produced by the physical model of Q11 is approximately Gaussian at low heights and has a long “tail” to large heights (cf. their Fig. 7). In order to approximate this, we have constructed the gas density distribution using a two-component model with independently varying scale heights for the main component (hmain) and the lower mass, larger scale height tail (htail). In addition, we vary the distribution of gas mass between these two components, with a term ftail describing the fraction of the total gas mass in the tail.
Appendix A.2: Determining the disk parameters
With this framework in place, we adjust parameters to match the SED and CO line fluxes in the literature for HD 163296. We carried out continuum radiative transfer modeling using the 2D code RADMC (Dullemond & Dominik 2004), which receives as input stellar properties and a dust density structure and outputs the resulting temperature structure. It includes a ray-tracing code, Raytran, for producing the model spectral energy distribution. We adjusted hsmall and hlarge in order to approximate the temperature structure found in Q11 (cf. their Fig. 9), which came from a self-consistent vertical structure calculation. We made further small adjustments to these parameters in order to match the SED. Our adopted disk model has small- and large-grain scale heights of 0.08 and 0.06, respectively, and we show the resulting SED in Fig. A.1. In our further modeling, we assume the gas temperature matches the mean dust temperature calculated in this modeling, which is a reasonable approximation in the dense regions upon which we focus.
After setting the dust parameters, we adjust hmain, htail, and ftail to approximate the gas density structure found in Q11 (their Fig. 9). We fine-tune these parameters by comparing our modeled fluxes of CO and its isotopologues with the observed fluxes of Q11, focusing on the low-J rotational lines that are expected to come largely from the cool outer disk regions studied here. We assume a relative CO abundance [CO]/[H] ≈ 10-4 (Frerking et al. 1982), which drops to zero at hydrogen column
densities less than 2 × 1021 cm-2 due to photodissociation (Visser et al. 2009) and at temperatures less than 19 K due to freezeout (Qi et al. 2011). We also assume a ratio of 12C to 13C of 75, and ratios of 16O to 18O and 17O of 500 and 1750, respectively (Frerking et al. 1982). To generate our model line emission, we input our adopted dust density and temperature structure, along with the model gas density structure, to the line radiative transfer code LIME (Brinch & Hogerheijde 2010), and we achieve a match to the observed line fluxes within ~50%.
The gas “tail” has a scale height htail = 0.2 and includes 5% of the gas mass (ftail), while the “main” gas component has a scale height hmain = 0.1. In Table A.1, we list the integrated fluxes of the CO lines which we use to determine the disk gas structure. Table A.2 lists and categorizes all disk modeling parameters, as well as the range of explored values or the reference from which the fixed value was adopted. In both tables, we repeat the HCO+, H13CO+, and DCO+ properties discussed in the main body of the text.
Acknowledgments
This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.00010.SV. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. Astrochemistry in Leiden is supported by NOVA, KNAW and EU A-ERC grant 291141 CHEMPLAN. D.H. is additionally supported by SRON. IdGM acknowledges the Spanish MICINN grant AYA2011-30228-C03 (co-funded with FEDER funds). A.H. acknowledges support from the Millennium Science Initiative, Chilean Ministry of Economy: Nucleus P10-022-F. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
References
- Aikawa, Y., & Nomura, H. 2006, ApJ, 642, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Aikawa, Y., van Zadelhoff, G. J., van Dishoeck, E. F., & Herbst, E. 2002, A&A, 386, 622 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., et al. 2012, ApJ, 744, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Barge, P., & Sommeria, J. 1995, A&A, 295, L1 [NASA ADS] [Google Scholar]
- Bisschop, S. E., Fraser, H. J., Öberg, K. I., van Dishoeck, E. F., & Schlemmer, S. 2006, A&A, 449, 1297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinch, C., & Hogerheijde, M. R. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Cleeves, L., Adams, F. C., & Bergin, E. A. 2013, ApJ, 772, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Wright, E. L., Conrow, T., et al. 2011, Explanatory Supplement to the WISE Preliminary Data Release Products, Tech. Rep. [Google Scholar]
- de Gregorio-Monsalvo, I., Ménard, F., Dent, W., et al. 2013, A&A, DOI: 10.1051/.../201321603 [Google Scholar]
- Draine, B. T. 2006, ApJ, 636, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, A&A, 417, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Egan, M. P., Price, S. D., Kraemer, K. E., et al. 2003, VizieR Online Data Catalog: V/114 [Google Scholar]
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Gorti, U., Hollenbach, D., Najita, J., & Pascucci, I. 2011, ApJ, 735, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Guilloteau, S., Piétu, V., Dutrey, A., & Guélin, M. 2006, A&A, 448, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., & Walker, D. W. 1988, in Infrared astronomical satellite (IRAS) catalogs and atlases, The small scale structure catalog, 7 [Google Scholar]
- Houk, N., & Smith-Moore, M. 1988, Michigan Catalogue of Two-dimensional Spectral Types for the HD Stars, Declinations –26 °.0 to –12 °.0, 4 (Ann Arbor: Univ. Michigan) [Google Scholar]
- Ishihara, D., Onaka, T., Kataza, H., et al. 2010, A&A, 514, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2004, A&A, 416, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klaassen, P. D., Juhasz, A., Mathews, G. S., et al. 2013, A&A, 555, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannings, V., & Sargent, A. I. 1997, ApJ, 490, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S., & Bergin, E. A. 2007, ApJ, 664, 956 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Najita, J. R., Carr, J. S., Strom, S. E., et al. 2010, ApJ, 712, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2010, ApJ, 720, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2011a, ApJ, 734, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Qi, C., Wilner, D. J., & Andrews, S. M. 2011b, ApJ, 743, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Qi, C., Wilner, D. J., & Hogerheijde, M. R. 2012, ApJ, 749, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Pagani, L., Vastel, C., Hugo, E., et al. 2009, A&A, 494, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Bourgoin, A., & Lique, F. 2012, A&A, 548, L4 [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Lesaffre, P., Jorfi, M., et al. 2013, A&A, 551, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Qi, C., Wilner, D. J., Aikawa, Y., Blake, G. A., & Hogerheijde, M. R. 2008, ApJ, 681, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., D’Alessio, P., Öberg, K. I., et al. 2011, ApJ, 740, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Öberg, K. I., & Wilner, D. J. 2013a, ApJ, 765, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Öberg, K. I., Wilner, D. J., et al. 2013b, Science, 341, 630 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Roberts, H., & Millar, T. J. 2000, A&A, 361, 388 [NASA ADS] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tilling, I., Woitke, P., Meeus, G., et al. 2012, A&A, 538, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Ancker, M. E., de Winter, D., & Tjin A Djie, H. R. E. 1998, A&A, 330, 145 [NASA ADS] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Thi, W.-F., & van Zadelhoff, G.-J. 2003, A&A, 400, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Varnière, P., & Tagger, M. 2006, A&A, 446, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walsh, C., Nomura, H., Millar, T. J., & Aikawa, Y. 2012, ApJ, 747, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, W. D. 1976, Rev. Mod. Phys., 48, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Willacy, K. 2007, ApJ, 660, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Wootten, A. 1987, in Astrochemistry, eds. M. S. Vardya, & S. P. Tarafdar, IAU Symp., 120, 311 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: integrated emission map of HCO+ (blue) from 0–12 km s-1 with contours showing 3, 10, and 17σ emission (σ = 25 mJy beam-1 km s-1). The white-bordered black line shows the positions from which we constructed the position–velocity diagram (middle-left), and the gray box shows the smaller region for which we show H13CO+ and DCO+ line emission (middle-right and right). Middle-left: the HCO+ position–velocity diagram. The magenta curves show the Keplerian velocity profile for an assumed stellar mass of 2.3 M⊙, disk inclination of 44°, and systemic velocity of 5.8 km s-1. Middle-right: integrated emission map of H13CO+ (green) from 0.8–10.4 km s-1 with contours showing 3, 5, and 7σ emission (σ = 14 mJy beam-1 km s-1). Right: integrated emission map of DCO+ (red) from 0.8–10.4 km s-1 with contours showing 3 and 5σ emission (σ = 18 mJy beam-1 km s-1). The 19 K contour of the midplane temperature at a radius of 155 AU in the model disk is overlaid on the DCO+ emission using a white-bordered black ellipse. In the maps of integrated emission, the ~0 |
| In the text | |
 |
Fig. 2 Comparison of integrated intensities of our DCO+ models (contours, 3 and 5σ, σ = 15 mJy beam-1 km s-1) to the observations (image, colors show intensities from 3σ). Colors indicate the velocities included in constructing the zeroth moment maps. Clockwise from the upper left, small figures show: 1) decreasing Tlow,DCO+ and Thigh,DCO+ by 3 K, 2) raising Tlow,DCO+ and Thigh,DCO+ by 4 K, 3) broadening the temperature range from 2 K to 4 K, with χDCO+ halved to maintain the same total DCO+J = 5–4 line flux, 4) reduction of χDCO+ by a factor of 3, and 5) raising χDCO+ by a factor of 3. |
| In the text | |
 |
Fig. 3 Top: regions of non-zero HCO+ (blue) and DCO+ (red) abundance, overlaid with contours indicating the hydrogen density (solid gray lines) and temperature (dashed gray lines). The 19 and 21 K contours are shown with a thick dark gray line. The region containing HCO+ is bounded on the upper and lower sides by CO photodissociation and by freezeout at 19 K, respectively. The DCO+ region is bounded by the temperature range 19–21 K. Bottom: the column density of HCO+ and its isotopologues (colored lines), with the 19 K CO snowline indicated by the thick dark gray dashed line. The broad plateau of the DCO+ column density from ~110–150 AU explains the ring morphology seen in line emission. The 3σ line sensitivities (from Sect. 3.2) are shown with the horizontal gray lines. |
| In the text | |
 |
Fig. A.1 Spectral energy distribution (black line) of our best fit model, compared to dereddened photometry (AV = 0.3, Q11) from the literature (Q11, Tilling et al. 2012; Cutri et al. 2011; Ishihara et al. 2010; Egan et al. 2003; Helou & Walker 1988). The stellar photosphere is shown as the thin dashed line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


