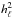| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | L4 | |
| Number of page(s) | 10 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201321382 | |
| Published online | 01 May 2013 | |
Online material
Appendix A: The LGMCA method
The GMCA framework
The generalized morphological component analysis (GMCA) method is based on blind source separation (BSS, Bobin et al. 2013). In the framework of BSS, each of the five WMAP frequency channels are modeled as a linear combination of n components: 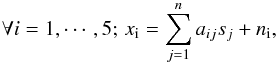 (A.1)where sj stands for the jth component, aij is a scalar that models the contribution of the jth component to channel i, and ni models the instrumental noise. This problem is more conveniently recast into the matrix formulation
(A.1)where sj stands for the jth component, aij is a scalar that models the contribution of the jth component to channel i, and ni models the instrumental noise. This problem is more conveniently recast into the matrix formulation 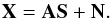 (A.2)In practice, the number of components is set to n = 5, which allows for more degrees of freedom to obtain a clean CMB map while keeping A invertible. In constrast to standard approaches in astrophysics (see Bobin et al. 2013, and references therein), the GMCA relies on the sparsity of the components S in the wavelet domain. Taking the data to the wavelet representation only alters the statistical distribution of the data coefficients without affecting its information content. A wavelet transform tends to grab the informative coherence between pixels while averaging the noise contributions, thus enhancing the structure in the data. This allows one to better distinguish components that do not share the same sparse distribution in the wavelet domain. In addition, sparsity has the ability to be more sensitive to non-Gaussian processes, which has been shown to improve the foreground separation method.
(A.2)In practice, the number of components is set to n = 5, which allows for more degrees of freedom to obtain a clean CMB map while keeping A invertible. In constrast to standard approaches in astrophysics (see Bobin et al. 2013, and references therein), the GMCA relies on the sparsity of the components S in the wavelet domain. Taking the data to the wavelet representation only alters the statistical distribution of the data coefficients without affecting its information content. A wavelet transform tends to grab the informative coherence between pixels while averaging the noise contributions, thus enhancing the structure in the data. This allows one to better distinguish components that do not share the same sparse distribution in the wavelet domain. In addition, sparsity has the ability to be more sensitive to non-Gaussian processes, which has been shown to improve the foreground separation method.
With A as the mixing matrix and Φ as a wavelet transform, we assume that each source sj can be sparsely represented in Φ; sj = αjΦ. The multichannel noiseless data Y can be written as 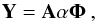 (A.3)where α is a Ns × T matrix whose rows are αj.
(A.3)where α is a Ns × T matrix whose rows are αj.
This means that the sparsity of the sources in Φ translates into sparsity of the multichannel data Y. The GMCA algorithm seeks an unmixing scheme through estimating A, which leads to the sparsest sources S. This is expressed by the following optimization problem (written in the augmented Lagrangian form) 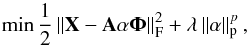 (A.4)where typically p = 0 (or its relaxed convex version with p = 1) and ∥X∥F = sqrt(trace(XTX)) is the Frobenius norm.
(A.4)where typically p = 0 (or its relaxed convex version with p = 1) and ∥X∥F = sqrt(trace(XTX)) is the Frobenius norm.
Local GMCA
The local-GMCA (LGMCA) algorithm (Bobin et al. 2013) has been introduced as an extension of GMCA:
-
multi-frequency instruments generally provide observationsthat do not share the same resolution. For example, the WMAPfrequency channels have a resolution that ranges from 13.2 arcmin for the W band to 52.8 arcmin for the K band. This makes the linear mixture model underlying the GMCA algorithm invalid. It is customary to alleviate this problem by degrading the frequency channels down to a common resolution prior to applying any component separation technique (the official CMB map provided by the WMAP consortium has a resolution of 1 degree). For this purpose, the data are decomposed in the wavelet domain, and at each wavelet scale we only use the observations with invertible beams and then degrade the maps to a common resolution. This allows us to estimate a CMB map with a resolution of 15 arcmin.
-
most foreground emissions (e.g. thermal dust, synchrotron, free-free) have electromagnetic spectra that are not spatially constant. In the framework of GMCA, this translates into a mixing matrix A that also varies across the pixels. Dealing with the variation across pixels of the electromagnetic spectrum of some of the components, the LGMCA estimates the mixing matrices on patches at various wavelet scales with band-dependent size.
The LGMCA algorithm has been implemented and evaluated on simulated Planck data in (Bobin et al. 2013).
Appendix B: LGMCA parameters for WMAP data
As described in Appendix A, LGMCA mixing matrices are estimated from a set of input channels at a given resolution on a patch of data at a given wavelet scale. For WMAP data, the parameters used by the LGMCA to compute these matrices are described in Table B.1. Figure B.1 displays the filters in spherical harmonics defining the wavelet bands at which the derived weights (by inverting these mixing matrices) were applied.
Parameters used in LGMCA to process the WMAP data with ancillary data.
 |
Fig. B.1
Filters defining the wavelet bands used in LGMCA. |
| Open with DEXTER | |
Appendix C: Simulations
In this section, the LGMCA algorithm is applied to data simulated by the Planck Sky Model (PSM) developed by Delabrouille and collaborators2 (Delabrouille et al. 2013). The PSM models the astrophysical foregrounds in the range of frequencies probed by WMAP, the simulated instrumental noise, and the beams. In detail, the simulations were obtained as follows.
-
Frequency channels: the simulated data comprised the 5 WMAP channels at frequency 23, 33, 41, 61, and 94 GHz. The frequency-dependent beams are perfectly isotropic PSFs; their profiles were obtained as the mean value of the beam transfer functions of at each frequency as provided by the WMAP consortium (nine years version).
-
Instrumental noise: instrumental noise was generated according to a Gaussian distribution with the covariance matrix provided by the WMAP consortium (nine years version).
-
Cosmic microwave background: the CMB map is a Gaussian random realization whose theoretical power spectrum is defined as the WMAP (nine years) best-fit power spectrum (from the six cosmological parameters model). The simulated CMB is perfectly Gaussian, and no non-Gaussianity (e.g. lensing, ISW, fNL) was added. This will allow for non-Gaussianity tests under the null assumption in the sequel.
-
Dust emissions: the Galactic dust emissions is composed of two distinct dust emissions: thermal dust and spinning dust (a.k.a. anomalous microwave emission). Thermal dust is modeled with the Finkbeiner model (Finkbeiner et al. 1999), which assumes that two hot/cold dust populations contribute to the signal in each pixel. The emission law of thermal dust varies across the sky.
-
Synchrotron emission: the synchrotron emission, as simulated by the PSM, is an extrapolation of the Haslam 408 MHz map (Haslam et al. 1982). The emission law of the synchrotron emission is an exact power law with a spatially varying spectral index.
-
Free-free emission: the spatial distribution of free-free emission is inspired by the Hα map built from the SHASSA and WHAM surveys. The emission law is a perfect power law with a fixed spectral index.
-
Point sources: infrared and radio sources were added based on existing catalogs at that time (including WMAP7 sources). In the following, the brightest point sources are masked prior to the evaluation results.
A simulated WMAP dataset was produced for each of the nine years. This allows to process the simulated data in the same manner as the WMAP data are processed.
Component separation
 |
Fig. C.1
Estimated CMB map power spectrum from simulated WMAP (nine years). |
| Open with DEXTER | |
 |
Fig. C.2
Estimated CMB map, noise, and remaining foreground power spectra from simulated WMAP (nine years) at 15 arcmin resolution. |
| Open with DEXTER | |
 |
Fig. C.3
Comparisons between LGMCA and ILC at 1 degree resolution. Estimated CMB map, noise, and remaining foreground power spectra from simulated WMAP (nine years). Additionally, the amplitudes have been amplified by |
| Open with DEXTER | |
 |
Fig. C.4
Legendre coefficients of the wavelet filters employed for non-Gaussianity analyses at 1 degree (left) and 15 arcmin (right). These wavelets are well localized in pixel space, allowing a fine analysis per latitude band. |
| Open with DEXTER | |
 |
Fig. C.5
Comparison of skewness levels in the LGMCA (red) and ILC (blue) maps at 1 degree computed for various wavelet scales. These statistics were centered on the expected value and normalized from a set of 100 simulations of CMB and noise (see text). |
| Open with DEXTER | |
 |
Fig. C.6
Comparison of centered and normalized kurtosis in the LGMCA (red) and ILC (blue) maps at 1 degree computed for various wavelet scales. The same mask and set of simulations where employed as in Fig. C.5. |
| Open with DEXTER | |
 |
Fig. C.7
Centered and normalized skewness and kurtosis in the LGMCA map at 15 arcmin computed for various wavelet scales. A 75% mask and a set of 100 simulations of CMB and noise were used to compute these statistics (see text). |
| Open with DEXTER | |
 |
Fig. C.8
Centered and normalized skewness in the LGMCA map at 15 arcmin computed for various wavelet scales and locations. The same mask and set of simulations were employed to derive the statistic as in Fig. C.7. |
| Open with DEXTER | |
 |
Fig. C.9
Centered and normalized kurtosis in the LGMCA map at 15 arcmin computed for various wavelet scales and locations. The same mask and set of simulations were employed the statistic as in Fig. C.7. |
| Open with DEXTER | |
The same templates and parameters as listed in Table B.1 were used for the LGMCA. We also implemented an ILC as for the WMAP9 release: first computing the weights in the same regions as for the WMAP9 release, then smoothing them to 1.5 degree, and finally applying them to the data at 1 degree in the same regions as defined in the official WMAP9 product. Note that no post-processing was performed to subtract the ILC bias due to foreground propagation as in the official product. This allows us to compare with the simulations the relative performance of the LGMCA and a localized ILC in pixel space at a resolution of 1 degree.
Recovered maps and power spectra
The power spectrum was computed following the procedure described in Sect. 3. Figure C.1 displays the theoretical power-spectrum in black and the LGMCA estimated power-spectrum in red. The pseudo-spectrum of the input map is shown in blue; these points would correspond to a perfect estimation of the CMB map where only cosmic variance is a source of uncertainty. The larger 1σ red errors originate from the error from the remaining instrumental noise. In this experiment, 75% of the sky coverage was used; the mask we used is a combination of point sources and Galactic masks. These two plots show that the power-spectrum of the CMB map estimated after component separation does not show any statistically significant bias.
Using simulations allows a precise decomposition of the CMB estimation error into its different components: CMB, remaining instrumental noise, and foregrounds. For that purpose we applied the inversion parameters estimated with LGMCA independently to the simulated foregrounds and the instrumental noise. The resulting maps give the exact level of contamination of the CMB estimated by LGMCA. Figure C.2 shows the power spectra of the CMB as well as the residual noise and foregrounds that contaminate the estimated map. The resolution of the map estimated with LGMCA is 15 arcmin; therefore the different spectra in Fig. C.2 remain at the same resolution and are not deconvolved to infinite resolution. Again, exactly the same sky coverage of 75% was used in this experiment which quantifies the exact level of foreground contamination of the estimated CMB power spectrum displayed in Fig. C.1. The two panels of Fig. C.2 first show that the main source of contamination is the remaining instrumental noise, which predominates for ℓ > 600. This translates to the large error bars of the estimated power spectrum at small scales in Fig. C.1. For very low-ℓ (ℓ < 20), the contribution of both the remaining noise and foregrounds is less than 1%, which is far below the error related to the cosmic variance. In this experiment, the level of foreground contamination seems to be below 1% at all scales. This very low level has to be tempered: the ancillary data, namely the composite all-sky H-alpha map of (Finkbeiner 2003) and the Finkbeiner thermal dust template (Finkbeiner et al. 1999) were also used within the PSM to produce the simulations of the free-free emission and thermal dust emission. We therefore expect the level of residual foregrounds to be higher when the LGMCA is applied to the real WMAP data. Interestingly, we also applied the LGMCA with exactly the same parameters except that only the WMAP maps without ancillary data were used. The contamination levels are featured in Fig. C.2 as the dashed line. If using templates indeed lowers the level of the remaining foregrounds, their contribution is still much lower than the level of CMB. Noise is therefore the main source of contamination in the final CMB estimate, whether external templates are used or not.
Finally, in Fig. C.3 all components were propagated using weights computed by ILC and LGMCA. This figure illustrates that LGMCA is more efficient at lowering noise levels (due to the high amplification of noise in the ILC map when the 1 degree deconvolution is performed) and foreground contamination (due to localization and the use of templates) than the computed ILC map.
Higher order statistics – non-Gaussianities
The level of non-Gaussianity in the recovered CMB map provides a sanity check to measure and localize any remaining foreground contamination in the recovered CMB map, since in this case the CMB is generated as a Gaussian random field. In this work, we computed the non-Gaussianity levels from the recovered CMB maps for LGMCA and ILC at 1 degree, and for the LGMCA map at 15 arcmin. The 75% mask was employed and sparse inpainting was performed to interpolate the signal inside the mask (Starck et al. 2013). The skewness and kurtosis were then computed on the simulation inside these masks on different wavelet scales using an isotropic undecimated wavelet on the sphere (Starck et al. 2006), with the wavelet filters in spherical harmonic space described in Fig. C.4. These statistics were then centered on the expected value (computed by propagating only the simulated noise and CMB) and normalized by the standard deviation computed from a set of 100 CMB and noise realizations. These statistics were also computed at different latitude bands for each wavelet scale to assess the level of foreground contamination in the maps at various scales and positions.
The comparison between LGMCA and ILC at 1 degree is displayed in Figs. C.5 and C.6. For both methods, the skewness and kurtosis are compatible with the error bars due to propagated noise and cosmic variance, with a maximal detection at 2.5σ close to the Galactic center. The same tests were also performed for the LGMCA map at the full resolution of 15 arcmin
and are displayed in Figs. C.7–C.9. The difference observed between the LGMCA non-Gaussianity levels and those computed from the simulation without foregrounds is compatible with the errors expected at that resolution.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.